The Spectrum of Density Fluctuations of Noble Gases Probed by THz Neutron and X-ray Spectroscopy
Abstract
:1. Introduction
1.1. The Dynamics of Molecules at Mesoscopic Scales
1.2. The Departure from Hydrodynamic Regime and the Onset of Relaxation Processes
1.3. The Central Role of Noble Gases
2. Measurements of the THz Spectrum of Noble Gases up to the 1990s
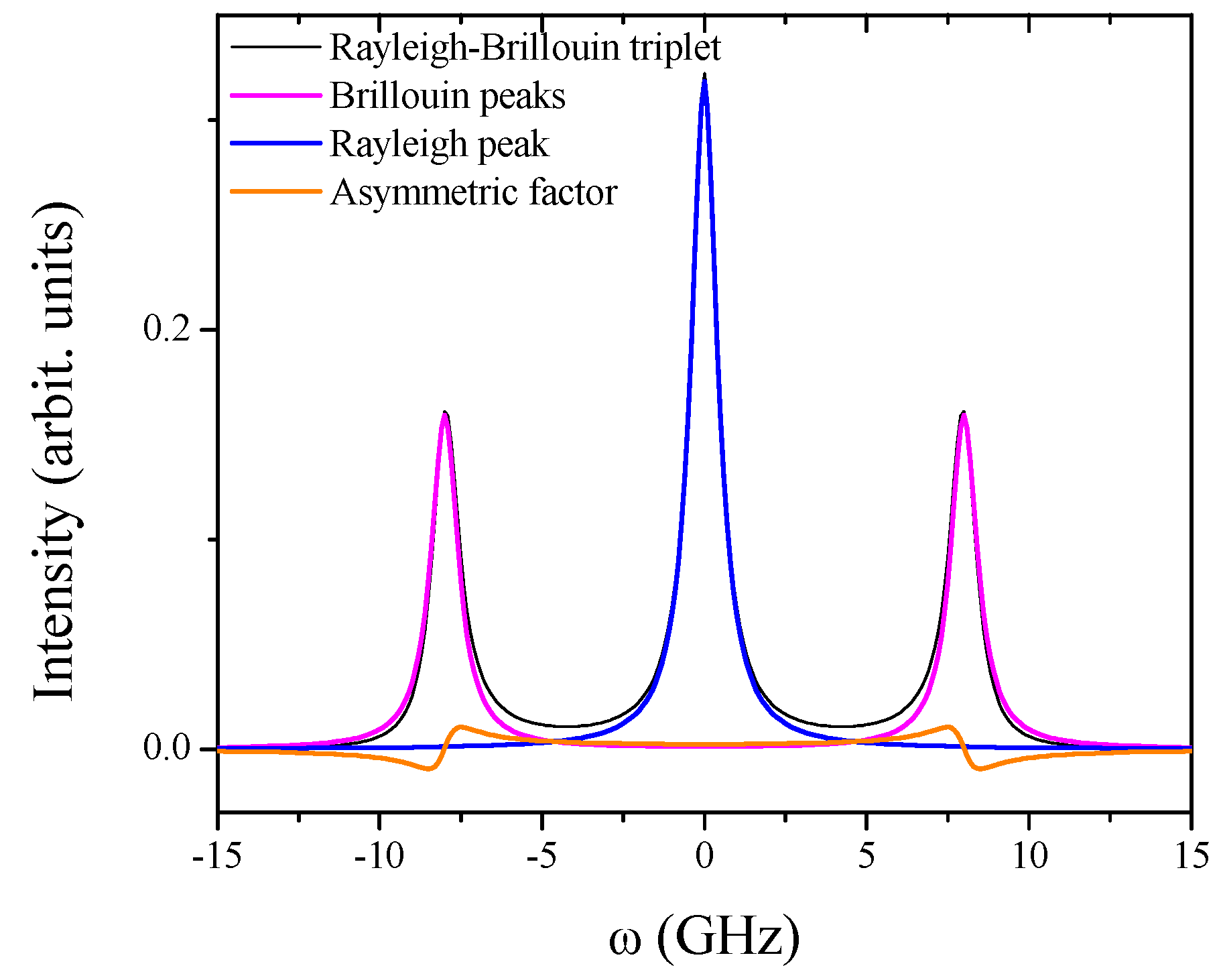
2.1. The Spectral Line-Shape in the Continuous Limit
- (1)
- The heat diffusion (Rayleigh) central peak, which relates to entropy fluctuations diffusing at constant pressure (P).
- (2)
- The two Brillouin acoustic side peaks, connected to P-fluctuations propagating at constant entropy.
- (3)
- An additional contribution (term ∝ b) asymmetric around the Brillouin peaks position having negative tails. This term distorts the Lorentzian terms 1) and 2) ultimately enabling the convergence of the spectral moments , with n ≤ 2.
2.2. 1922–1969: From Theoretical Prediction to Actual Measurements
2.3. 1964–1967: Seeking for a Triplet Shape at Mesoscopic Scales
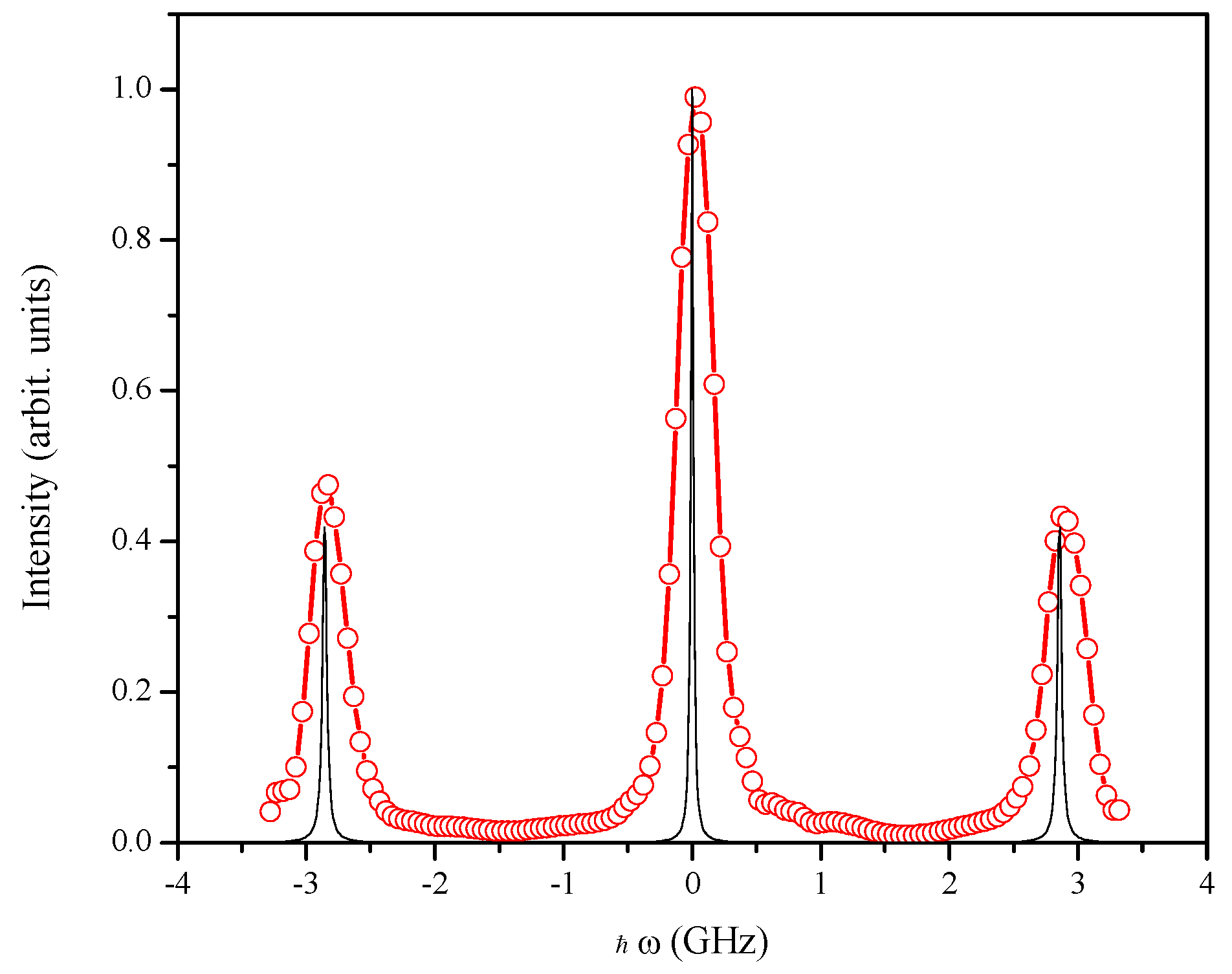
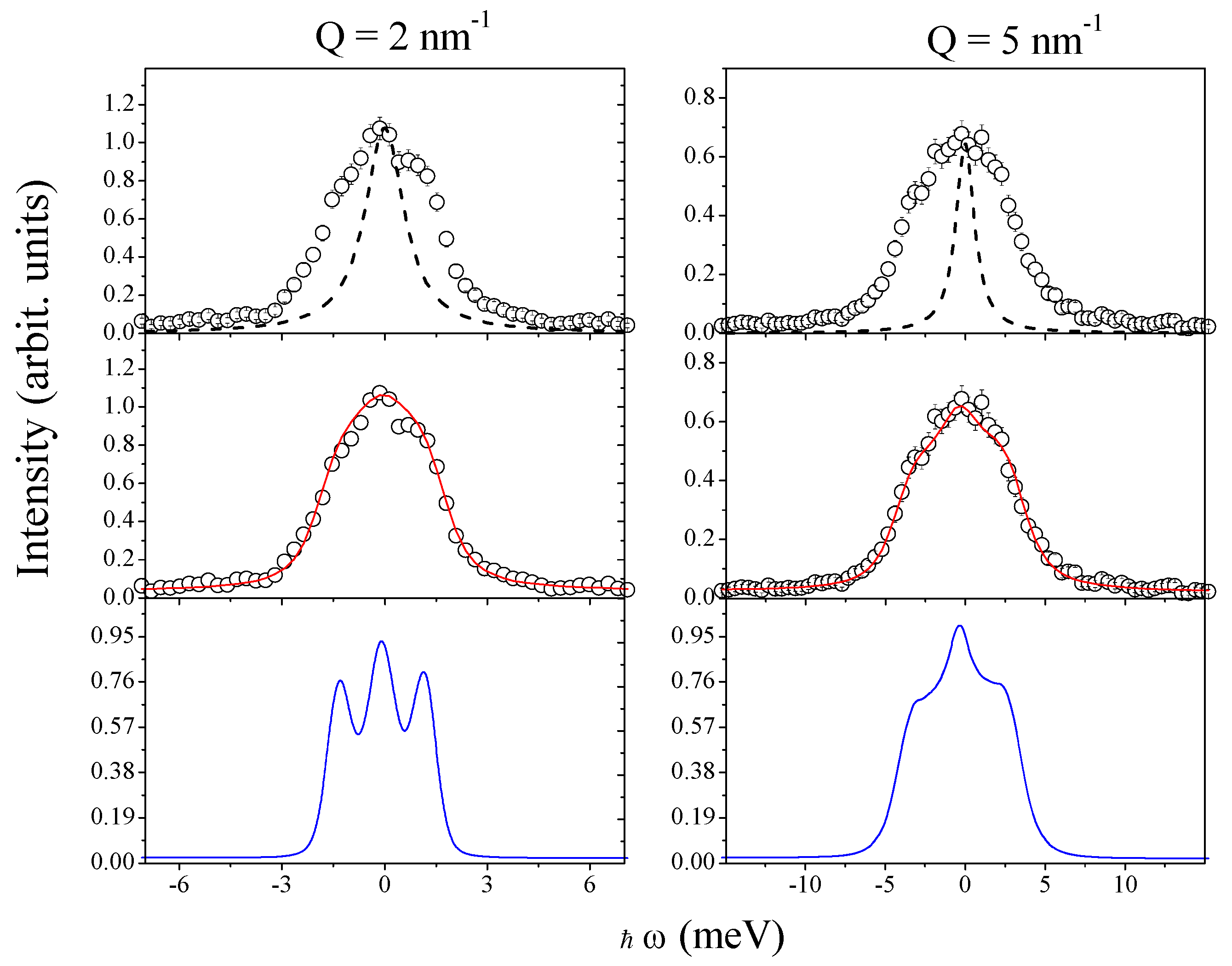
2.4. 1971: First Evidences of a Rayleigh-Brillouin triplet beyond the Continuous Limit
2.5. 1973–1975: First Signatures of A Viscoelastic Behavior in Real and Simulated Noble Gases
2.6. 1978–1987: The Failure of the Three Modes Description High Q in Liquid Noble Gases and the Test of Kinetic and Mode Coupling Theories
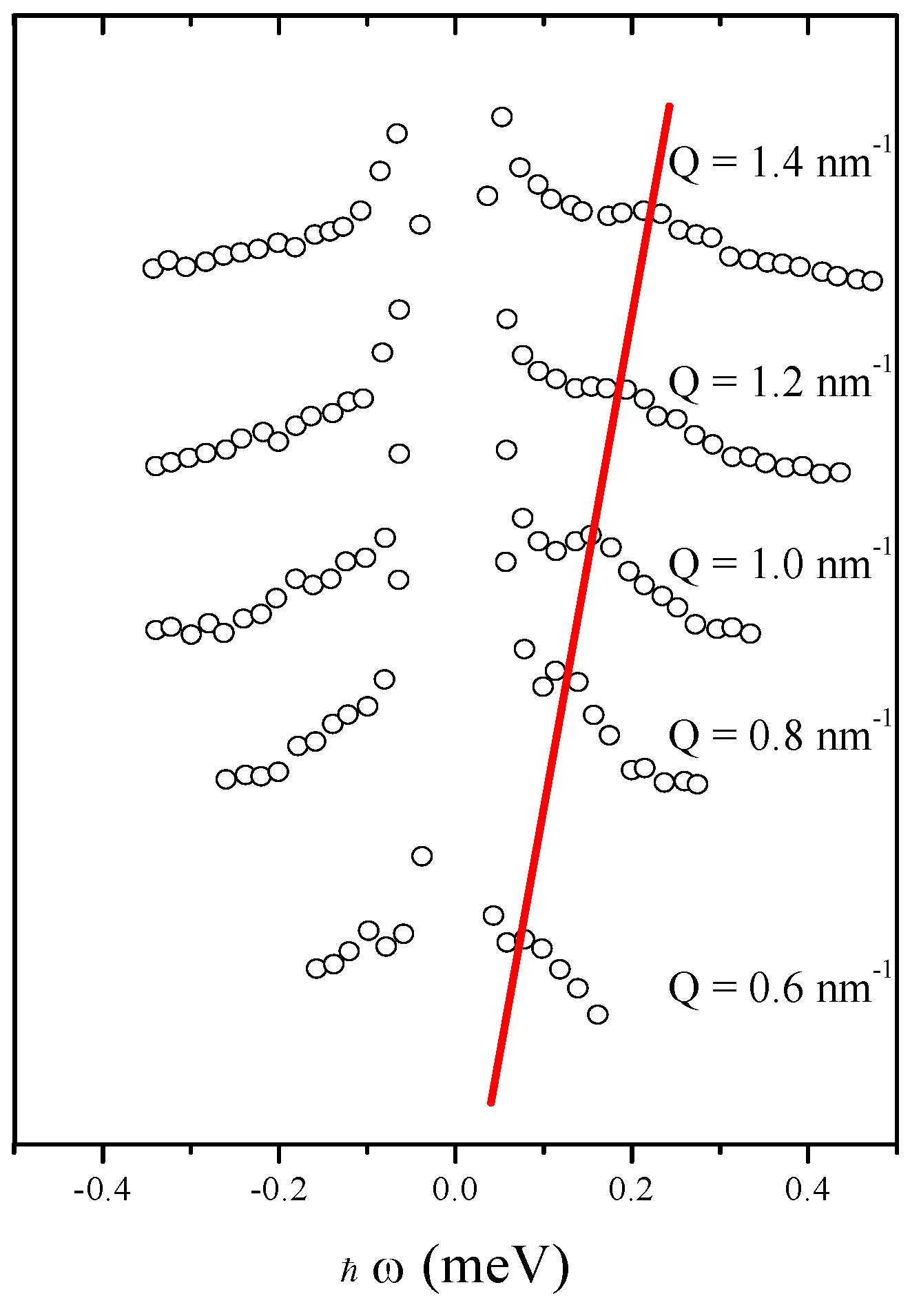
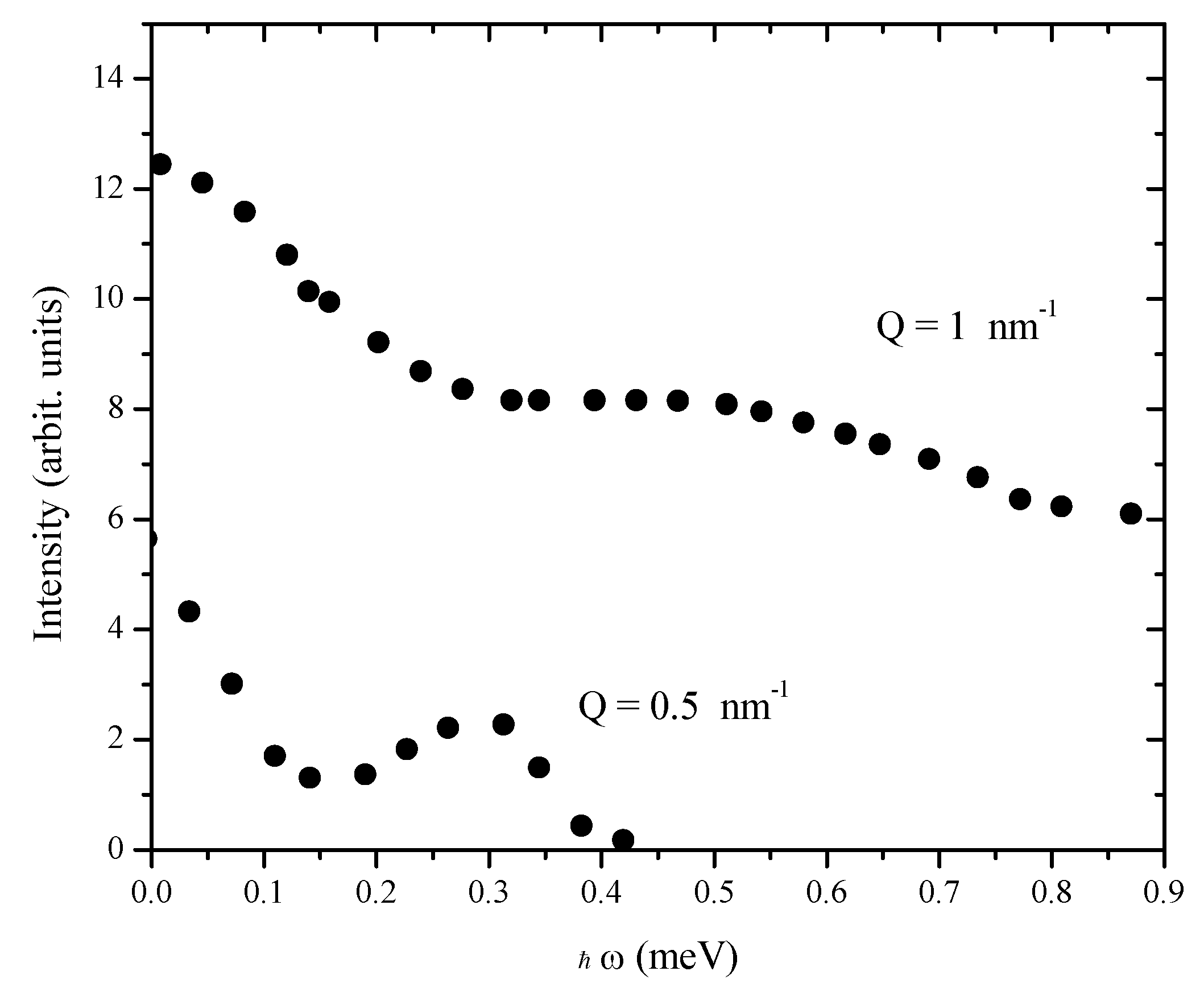
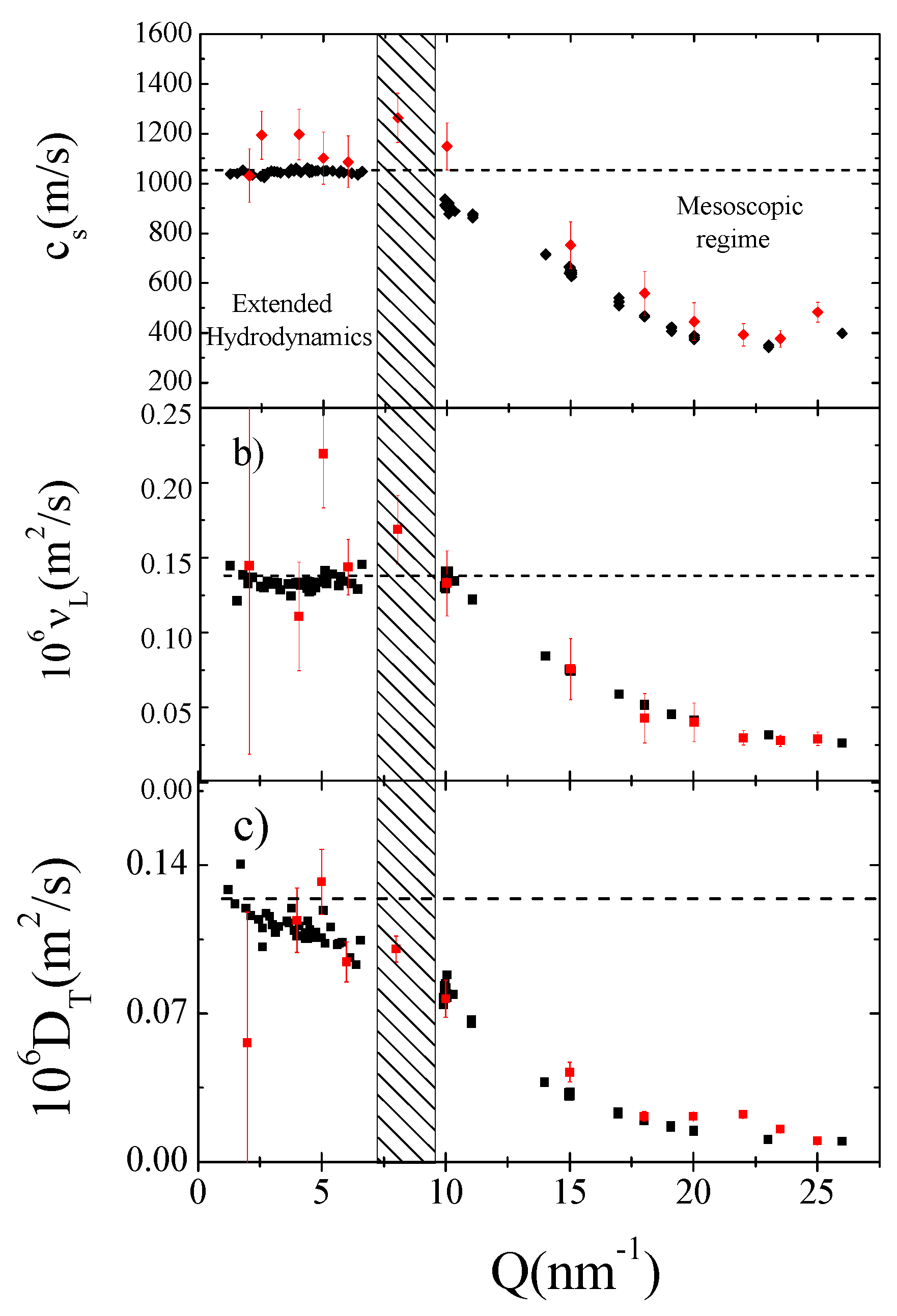
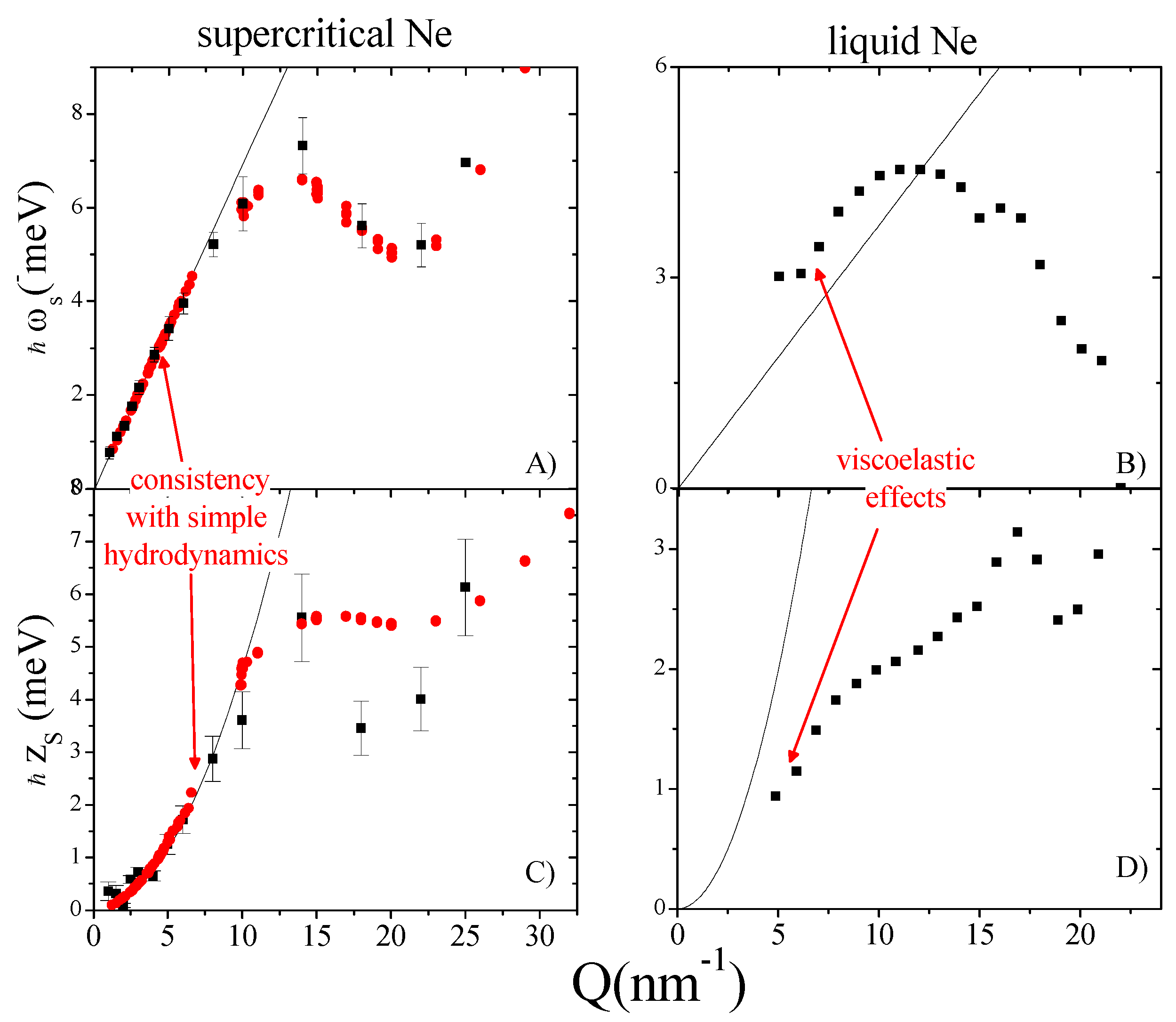
2.7. 1990: “Extended Hydrodynamics Modes” up to Q ≈ 1 nm−1
2.8. 1998: First IXS Measurements of the THz Spectrum of Noble Gases
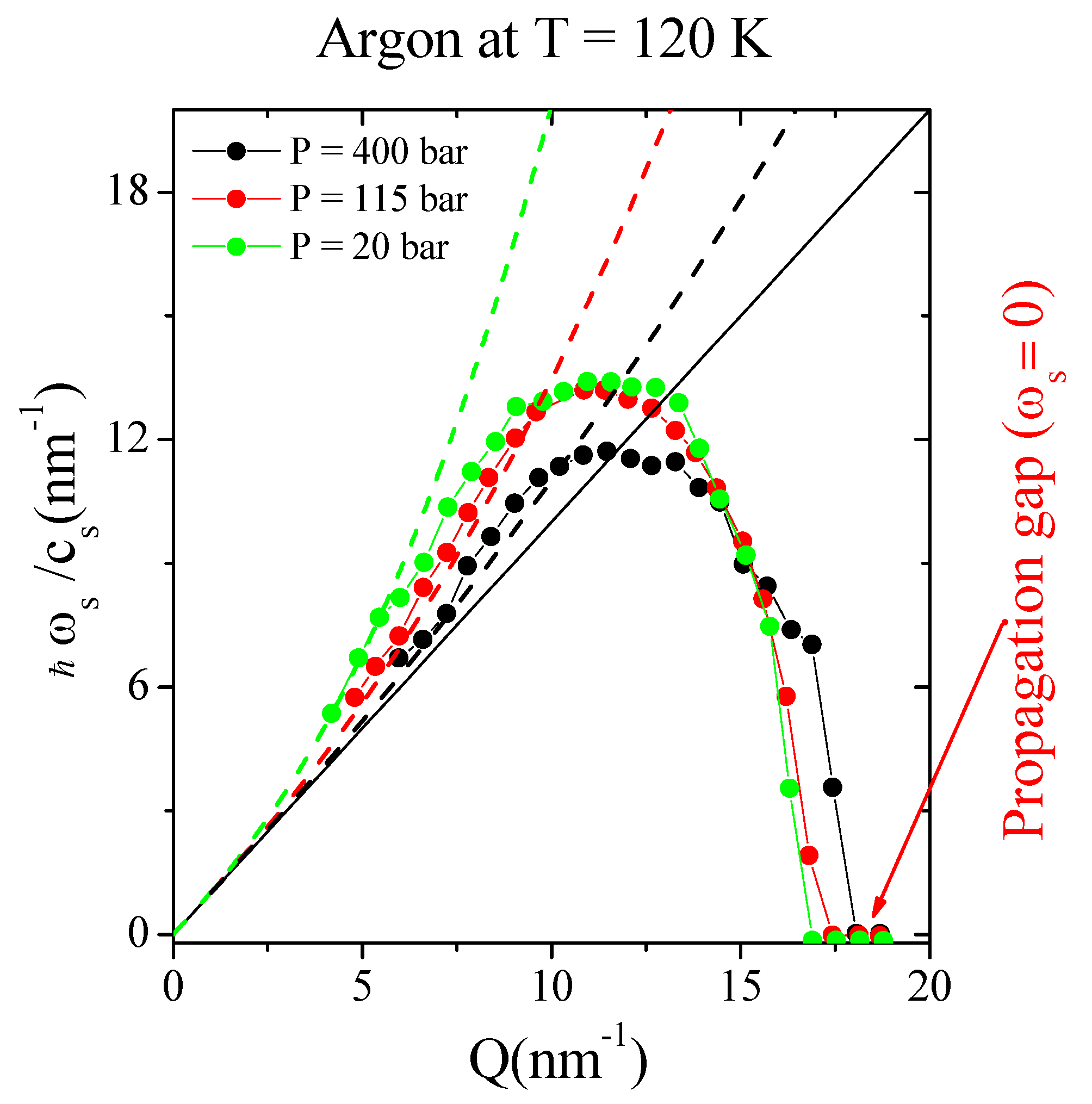
2.9. The Onset of a Positive Sound Dispersion in Liquid Noble Gases
3. A Model for the Measured Spectral Shape
3.1. The Memory Function Formalism
- The antisymmetric matrix is the proper frequency of the system, which describes the oscillatory behavior of . This matrix depends on equilibrium (static) properties of the system. Here the symbol indicates a statistical (thermal) average.
- The variable is the random fluctuating force. Noticeably, the presence of the term implies that , namely that the fluctuating force is orthogonal (statistically uncorrelated) to .
- The matrix is memory matrix, or memory function if υ = 1, as in the cases of interest here. It is worth noticing that the integrand in Equation (4) includes all values between 0 and t, “weighted” by the memory, which thus defines the ability of the system to keep memory of the past.
- (1)
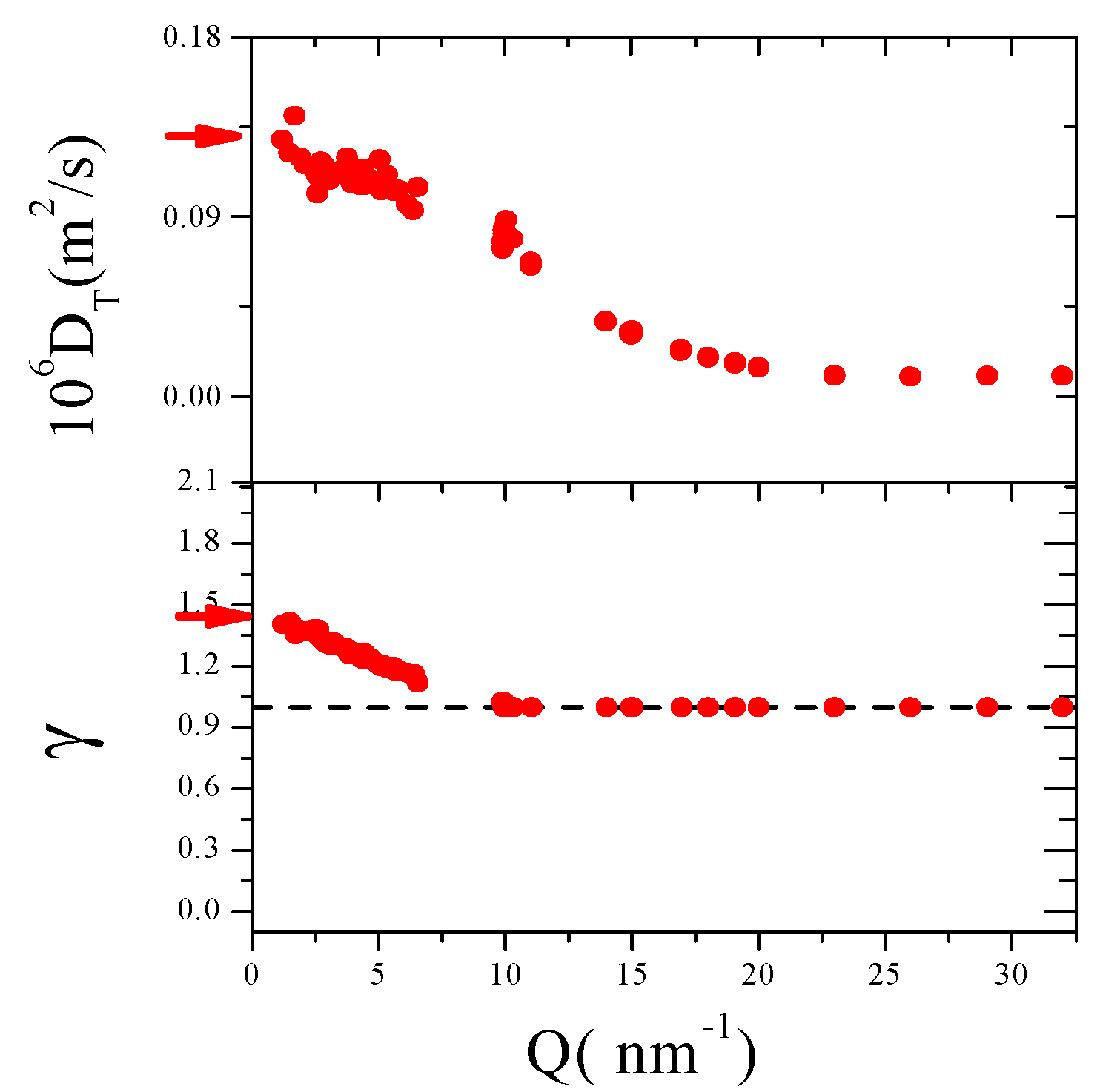
- The thermal contribution. The first term describes diffusive thermal motions triggered by spontaneous temperature gradients. Its timescale and amplitude are and respectively, with DT, cT, γ and being the generalized diffusivity, the isothermal velocity and the constant pressure to constant volume specific heats ratio.
- (2)
- The viscous relaxation contribution. The second term accounts for relaxation processes affecting the viscosity and having a timescale and amplitude , where is the generalized infinite frequency or “elastic” sound velocity of the sample.
- (3)
- The instantaneous contribution. The last term accounts for the coupling of density fluctuations with the ultra-fast vibrational dynamics here accounted by a δ(t) profile. It was often found that the amplitude has a quadratic Q-dependence and is essentially insensitive to thermodynamic changes [20].
- (1)
- In principle, structural relaxation phenomena in highly viscous systems can be better described by assuming a stretched exponential rather than a simple exponential time-decay of the memory function [17,74,75]. However, the use of this model would introduce an unwanted additional parameter (the stretching coefficient) and, perhaps more importantly, its Fourier transform cannot be cast on an analytical form. Fortunately, for simplest systems as noble gases, of interest in this paper, it is reasonable to assume that the simple exponential decay is a rather accurate approximation.
- (2)
- A second remark concerns the possible presence in the spectrum of a second inelastic excitation as observed in systems as diverse as liquid water [73,76,77,78], tetrahedrally arranged glasses [79], glass formers [80] liquid metals [81,82,83,84,85], complex biophysical samples [86,87,88] and mixtures [89]. The presence of this low frequency mode in the S(Q,ω) is customarily ascribed to the onset of shear mode propagation, although this assignment could seem suspicious as S(Q,ω) couples primarily with longitudinal movements only. In a liquid, the onset of shear waves in the spectrum of density fluctuations can only occur via the so-called longitudinal-transverse coupling [73,76,90], that is a mixing between acoustic modes having orthogonal polarization. The presence of this mode-mixing is not properly accounted for by any known analytic model for the memory function. However, such a coupling has never been observed in noble gases, likely due to the highly isotropic character of their interatomic interaction, and will not be discussed in the remainder of this paper.
3.2. The Departure from the Hydrodynamic Shape of the Spectrum
3.3. The Simple Viscoelastic Model
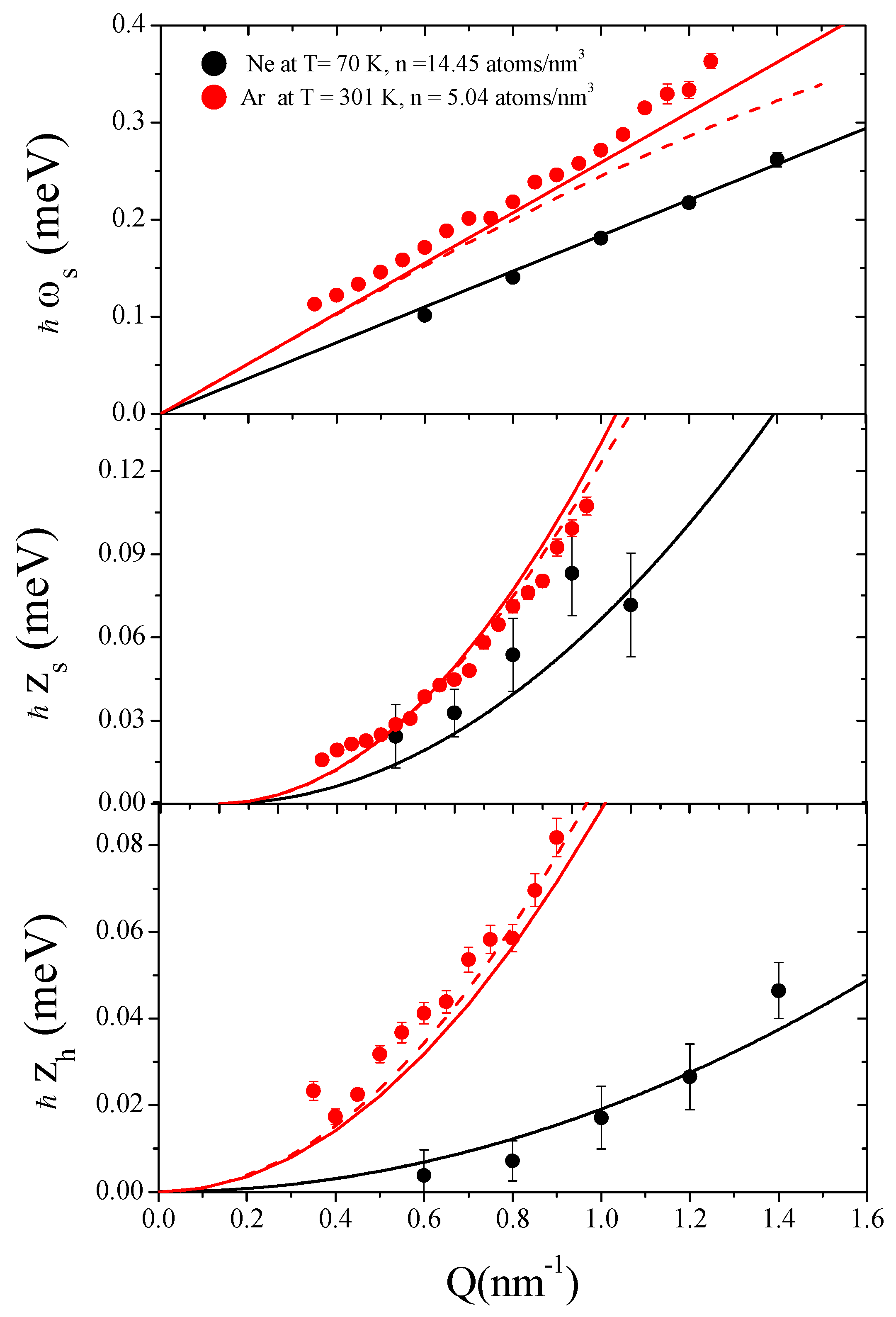
4. 2001–2007: The Memory Function-Based Modeling of IXS Spectra of Noble Gases
- (1)
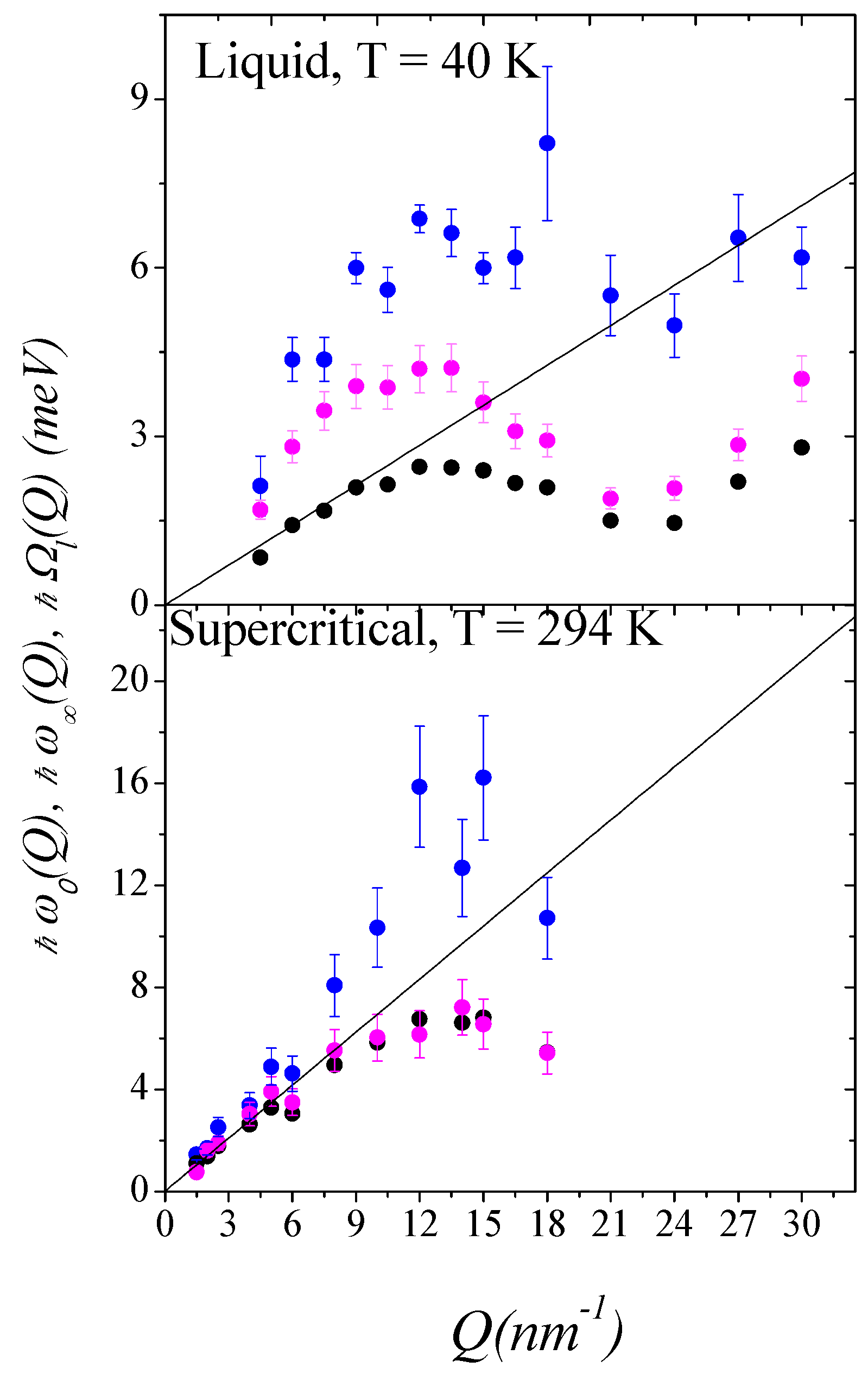
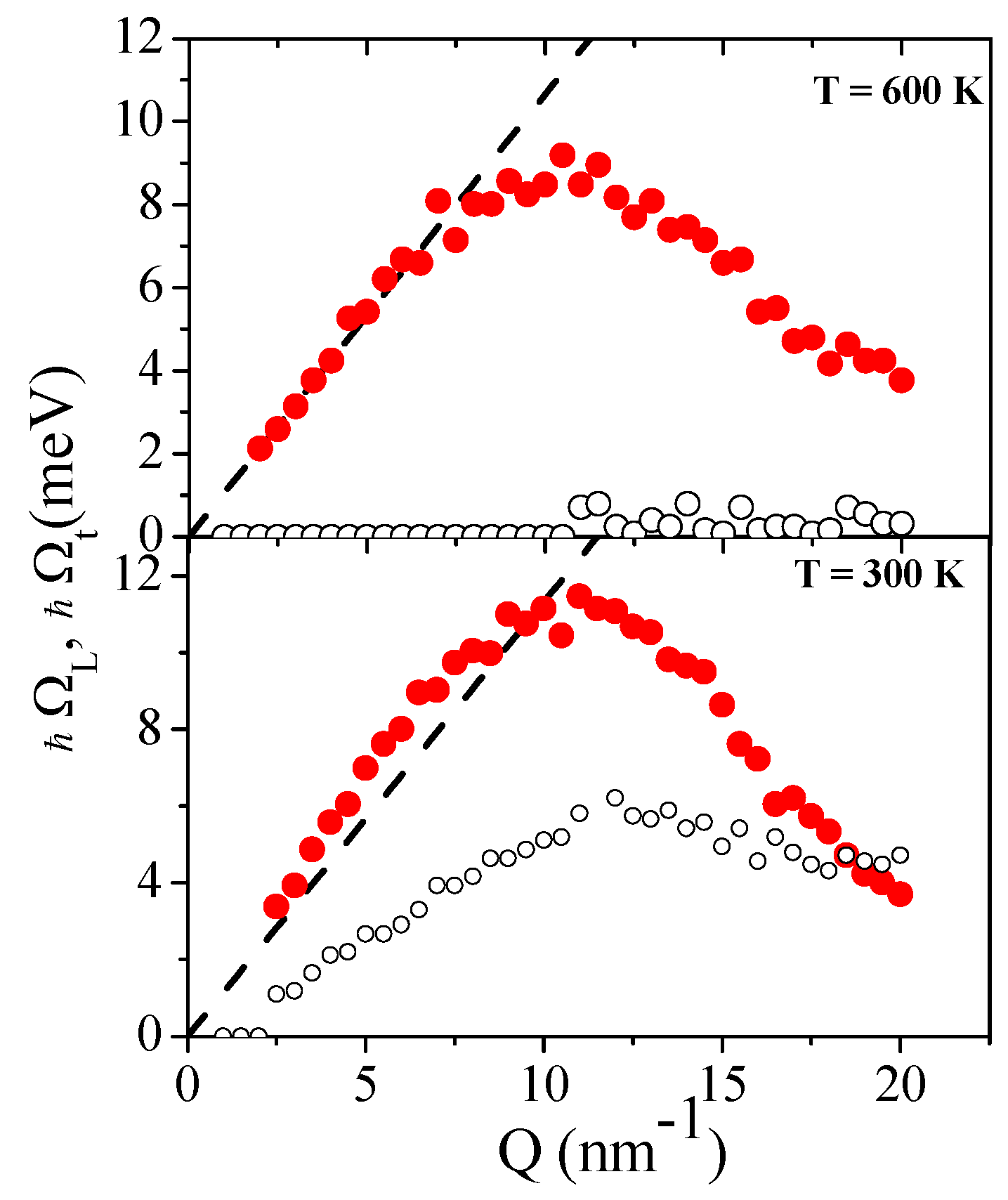
- the liquid phase datum bears evidence for the more-than-linear behavior of Ωl (purple dots) for Q ≤ 10 nm−1, i.e., the systematic bending of Ωl upwards the hydrodynamic linear law and toward ω∞ (the mentioned PSD effect) . Conversely, the liquid phase point is characterized by a sizable PSD.
- (2)
- At higher Qs one can observe the “backward transition” of Ωl from ω∞ to ω0, which is actually joined for Q larger than the position of the first di QM (≈22 nm−1).
- (3)
- Again, viscoelastic effects disappear in deeply supercritical conditions (lower panel) since ω0, Ωl and ω∞ merge into each other (at least at the lowest Qs), thus suggesting that the viscous relaxation term in Equation (9) has a vanishing strength.
4.1. Microscopic vs. Structural Relaxations
- (1)
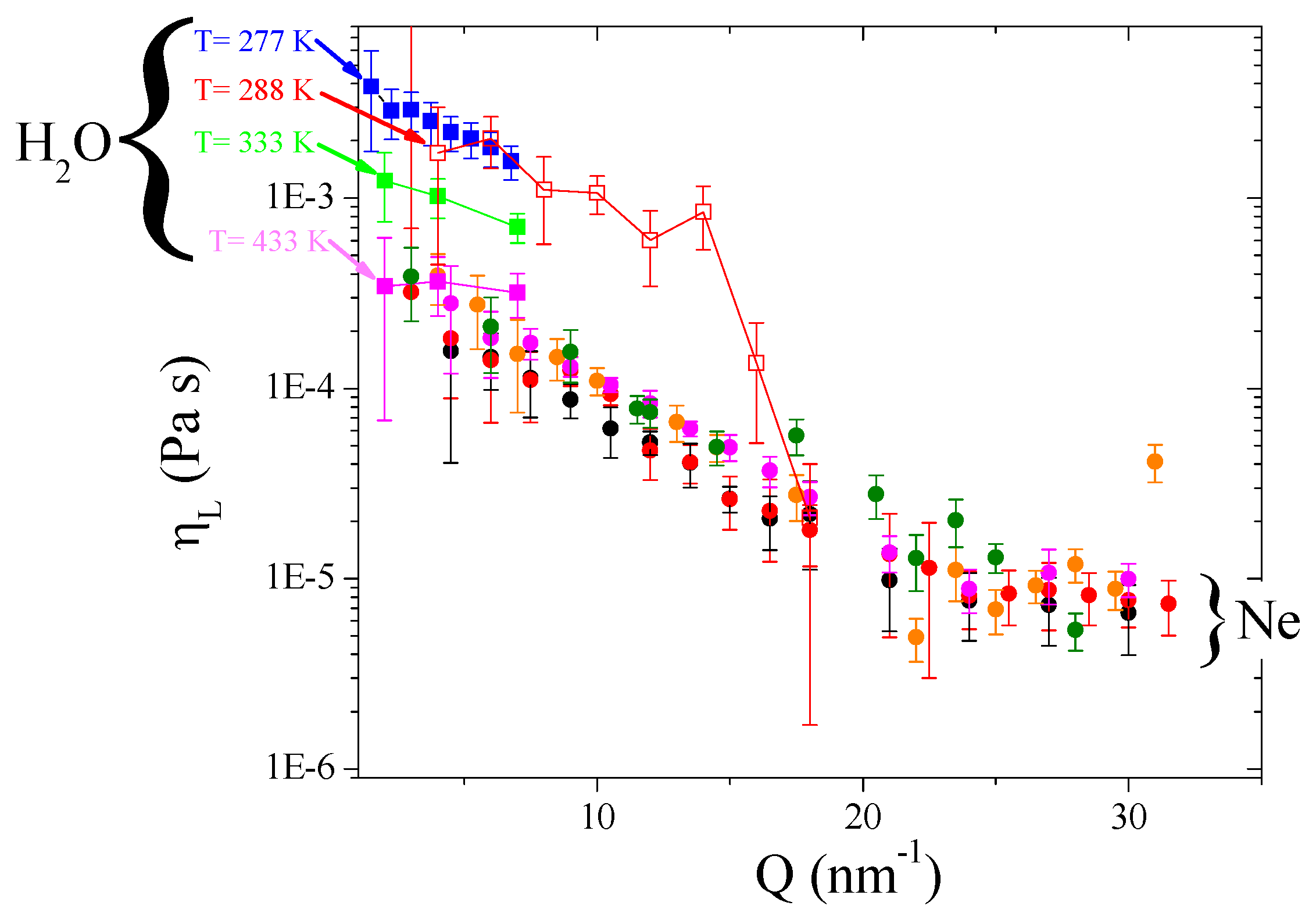
- Viscosity curves of Ne are only weakly dependent on thermodynamic conditions, although the macroscopic viscosity in the spanned thermodynamic interval undergoes important variations. Combined thermodynamic [72] and bulk viscosity data [28] of neon lead to estimate a more than 300% variation of ηl within the probed thermodynamic range, clearly non reproduced by mesoscopic measurements. Conversely, viscosity data of water in the same plot have a T dependence as sharp as the one of macroscopic viscosity [96]. This discrepancy is likely due to the large weight of structural processes in water, especially at the low Qs covered by data of [13]. Structural relaxations, owing to their collective nature can only be observed over long distances, or, equivalently, at high Qs and are expectedly dominating in associate liquids.
- (2)
- High T values of ηl approach from above low-Q neon data. This seems consistent with the inferred link between structural relaxation and local readjustment of the hydrogen bond (HB) network in water [12,13]. At the highest Ts the average number of HBs per molecule is sensibly lower which weakens the strength of structural relaxations [13,19].
- (3)
- The strong Q-dependence of ηl in water suggests that at Q higher than the values covered by Ref. [13], viscosity curves of water and neon tend to get closer to each other also considering that the latter have an essentially flat Q-dependence at high Qs. This impression is confirmed by ηl data derived from extremely high resolution INS measurements of on deuterated water (line + open squares symbols) at T = 288 K, which covered a Q-range larger than those of other water data reported in the same plot.
4.2. 2001–2003: Quantum Effects on the Line-Shape
- Diffraction effects are relevant only when Λ matches the length-scales over wich the interparticle potential U(rij) varies apppreciably.
- Exchange effects are instead relevant when Λ becomes comparable with interatominc centers of mass distance and are thus observable only for small mass atoms, for which such a distance can be relatively small. These effects only emerge at very low temperature and responsible for few “spectacular” quanto-mechanical manifestations, such as, e.g., Bose condensation and superfluidity.
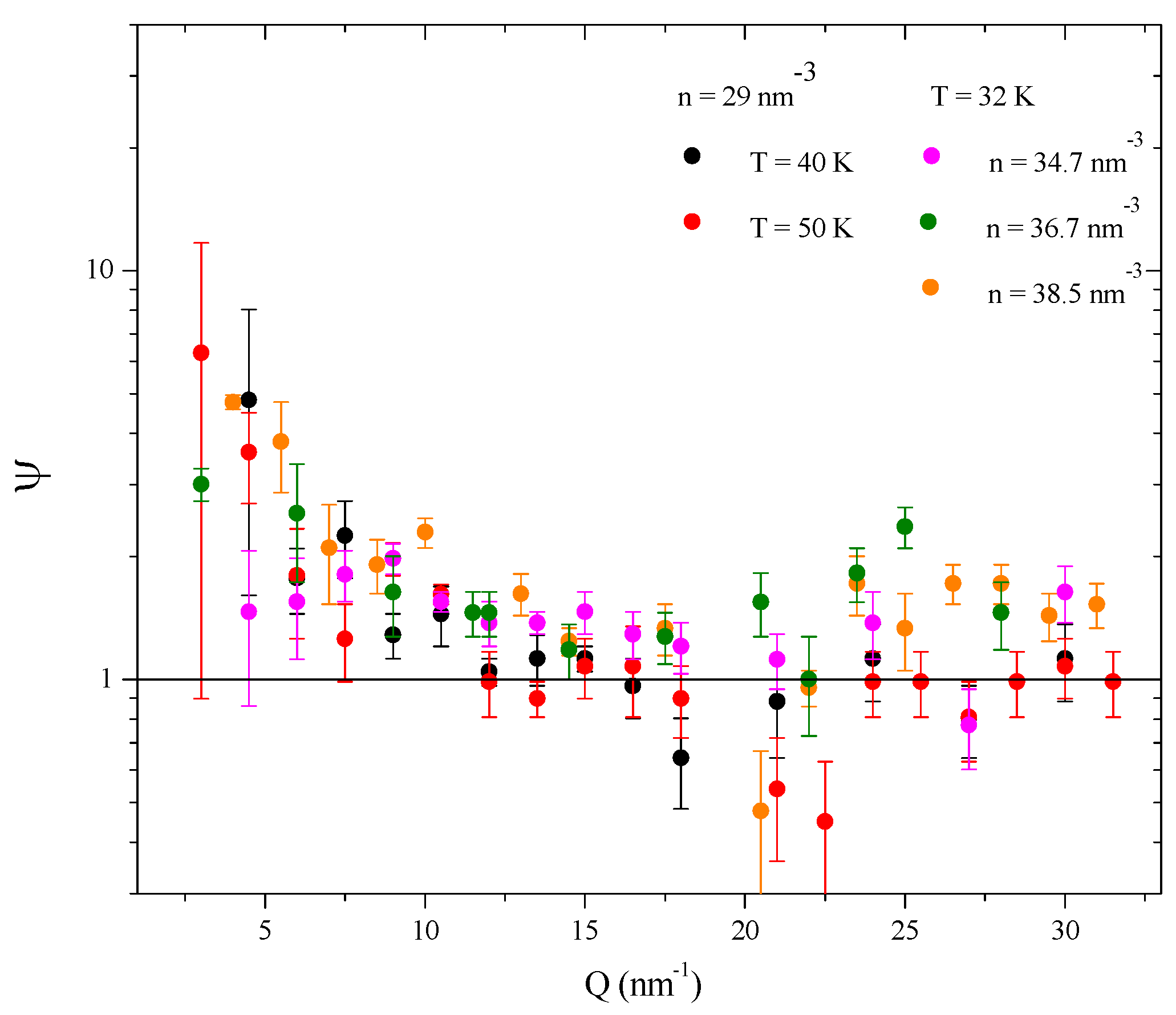
5. 2006-Present: Toward a New Vision of the Supercritical Phase
- (1)
- A gas-like domain, featured by the absence of PSD effects and the related inability of the fluid to support transverse wave propagation and
- (2)
- A liquid-like domain in which the system exhibits merely viscoelastic features such as a sizable PSD and the onset of shear mode propagation.
6. Conclusions and Future Perspectives
Acknowledgments
Conflicts of Interest
References
- Lovesey, S.W. Theory of Neutron Scattering from Condensed Matter; Clarendon Press: Oxford, UK, 1984; Volume 1. [Google Scholar]
- Sinha, S.K. Theory of inelastic X-ray scattering from condensed matter. J. Phys. Condens. Matter. 2001, 13, 7511–7523. [Google Scholar] [CrossRef]
- Berne, B.J.; Pecora, R. Dynamic Light Scattering; John Wiley: New York, NY, USA, 1976. [Google Scholar]
- Zwanzig, R. Lectures in Theoretical Physiscs; Brittin, W., Ed.; Wiley-Inerscience: New York, NY, USA, 1961; Volume 3, pp. 106–141. [Google Scholar]
- Mori, H. A continued-fraction representation of the time-correlation functions. Prog. Theor. Phys. 1965, 34, 399–416. [Google Scholar] [CrossRef]
- Cunsolo, A.; Pratesi, G.; Verbeni, R.; Colognesi, D.; Masciovecchio, C.; Monaco, G.; Ruocco, G.; Sette, F. Microscopic relaxation in supercritical and liquid neon. J. Chem. Phys. 2001, 114, 2259–2267. [Google Scholar] [CrossRef]
- Bencivenga, F.; Cunsolo, A.; Krisch, M.; Monaco, G.; Orsingher, L.; Ruocco, G.; Sette, F.; Vispa, A. Structural and collisional relaxations in liquids and supercritical fluids. Phys. Rev. Lett. 2007, 98, 085501. [Google Scholar] [CrossRef] [PubMed]
- Bencivenga, F.; Cunsolo, A.; Krisch, M.; Monaco, G.; Ruocco, G.; Sette, F. Adiabatic and isothermal sound waves: The case of supercritical nitrogen. Europhys. Lett. 2006, 75, 70–76. [Google Scholar] [CrossRef]
- Scopigno, T.; Balucani, U.; Ruocco, G.; Sette, F. Evidence of two viscous relaxation processes in the collective dynamics of liquid lithium. Phys. Rev. Lett. 2000, 85, 4076–4079. [Google Scholar] [CrossRef] [PubMed]
- Scopigno, T.; Balucani, U.; Ruocco, G.; Sette, F. Inelastic X-ray scattering study of the collective dynamics in simple liquid metals. J. Non-Cryst. Solids 2002, 312–314, 121–127. [Google Scholar] [CrossRef]
- Scopigno, T.; Ruocco, G.; Sette, F. Microscopic dynamics in liquid metals: The experimental point of view. Rev. Mod. Phys. 2005, 77, 881–933. [Google Scholar] [CrossRef]
- Cunsolo, A.; Ruocco, G.; Sette, F.; Masciovecchio, C.; Mermet, A.; Monaco, G.; Sampoli, M.; Verbeni, R. Experimental determination of the structural relaxation in liquid water. Phys. Rev. Lett. 1999, 82, 775–778. [Google Scholar] [CrossRef]
- Monaco, G.; Cunsolo, A.; Ruocco, G.; Sette, F. Viscoelastic behavior of water in the terahertz-frequency range: An inelastic X-ray scattering study. Phys. Rev. E 1999, 60, 5505–5521. [Google Scholar] [CrossRef]
- Angelini, R.; Giura, P.; Monaco, G.; Ruocco, G.; Sette, F.; Verbeni, R. Structural and microscopic relaxation processes in liquid hydrogen fluoride. Phys. Rev. Lett. 2002, 88, 255503. [Google Scholar] [CrossRef] [PubMed]
- Fioretto, D.; Buchenau, U.; Comez, L.; Sokolov, A.; Masciovecchio, C.; Mermet, A.; Ruocco, G.; Sette, F.; Willner, L.; Frick, B.; et al. High-frequency dynamics of glass-forming polybutadiene. Phys. Rev. E 1999, 59, 4470–4475. [Google Scholar] [CrossRef]
- Scarponi, F.; Comez, L.; Fioretto, D.; Palmieri, L. Brillouin light scattering from transverse and longitudinal acoustic waves in glycerol. Phys. Rev. B 2004, 70, 054203. [Google Scholar] [CrossRef]
- Giugni, A.; Cunsolo, A. Structural relaxation in the dynamics of glycerol: A joint visible, UV and X-ray inelastic scattering study. J. Phys. Condens. Matter. 2006, 18, 889–902. [Google Scholar] [CrossRef]
- Comez, L.; Fioretto, D.; Monaco, G.; Ruocco, G. Brillouin scattering investigations of fast dynamics in glass forming systems. J. Non-Cryst. Solids 2002, 307, 148–153. [Google Scholar] [CrossRef]
- Bencivenga, F.; Cimatoribus, A.; Gessini, A.; Izzo, M.G.; Masciovecchio, C. Temperature and density dependence of the structural relaxation time in water by inelastic ultraviolet scattering. J. Chem. Phys. 2009, 131, 144502. [Google Scholar] [CrossRef] [PubMed]
- Bencivenga, F.; Cunsolo, A.; Krisch, M.; Monaco, G.; Ruocco, G.; Sette, F. High frequency dynamics in liquids and supercritical fluids: A comparative inelastic X-ray scattering study. J. Chem. Phys. 2009, 130, 064501. [Google Scholar] [CrossRef] [PubMed]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Boon, J.P.; Yip, S. Molecular Hydrodynamics; Courier Dover Publications: Dover, UK, 1980. [Google Scholar]
- Bafile, U.; Guarini, E.; Barocchi, F. Collective acoustic modes as renormalized damped oscillators: Unified description of neutron and X-ray scattering data from classical fluids. Phys. Rev. E 2006, 73, 061203. [Google Scholar] [CrossRef] [PubMed]
- Brillouin, L. Diffusion of light and X-rays by a transparent homogeneous body. Ann. Phys. 1922, 17, 88. [Google Scholar]
- Landau, L.; Placzek, G. The structure of undisplaced scattered lines. Physik. Z. Sowjet. 1934, 5, 172. [Google Scholar]
- Fabelinskii, I. Some aspects of the molecular scattering of light in liquids. Phys. Usp. 1957, 63, 355–410. [Google Scholar] [CrossRef]
- Fleury, P.A.; Boon, J.P. Brillouin scattering in simple liquids—Argon and neon. Phys. Rev. 1969, 186, 244–254. [Google Scholar] [CrossRef]
- Castillo, R.; Castaneda, S. The bulk viscosity in dense fluids. Int. J. Thermophys. 1988, 9, 383–390. [Google Scholar] [CrossRef]
- Rouch, J.; Lai, C.C.; Chen, S.H. Brillouin-scattering studies of normal and supercooled water. J. Chem. Phys. 1976, 65, 4016–4021. [Google Scholar] [CrossRef]
- Fleury, P.; Boon, J.-P. Laser light scattering in fluid systems. Advances in Chemical Physics 1973, 24, 1–93. [Google Scholar]
- Chen, S.H.; Eder, O.J.; Egelstaf, P.; Haywood, B.C.G.; Webb, F.J. Co-operative modes of motion in simple liquids. Phys. Lett. 1965, 19, 269–271. [Google Scholar] [CrossRef]
- Kroô, N.; Borgonovi, G.; Skôld, K.; Larsson, K.-E. Inelastic scattering of cold neutrons by condensed argon. In Proceedings of the Symposium on Inelastic Scattering of Neutrons, Bombay, India, 15–19 December 1964; IAEA: Bombay, India, 1964. [Google Scholar]
- Sköld, K.; Larsson, K.E. Atomic motion in liquid argon. Phys. Rev. 1967, 161, 102–116. [Google Scholar] [CrossRef]
- Randolph, P.D.; Singwi, K.S. Slow-neutron scattering and collective motions in liquid lead. Phys. Rev. 1966, 152, 99. [Google Scholar] [CrossRef]
- Rahman, A. Propagation of density fluctuations in liquid rubidium: A molecular-dynamics study. Phys. Rev. Lett. 1974, 32, 52–54. [Google Scholar] [CrossRef]
- Price, D.L. Effects of a volume-dependent potential on equilibrium properties of liquid sodium. Phys. Rev. A 1971, 4, 358–363. [Google Scholar] [CrossRef]
- Bell, H.G.; Kollmar, A.; Alefeld, B.; Springer, T. Investigation of collective excitations in liquid neon by means of neutron-scattering at small scattering vectors. Phys. Lett. A 1973, 45, 479–480. [Google Scholar] [CrossRef]
- Henshaw, D.G.; Woods, A.D.B. Modes of atomic motions in liquid helium by inelastic scattering of neutrons. Phys. Rev. 1961, 121, 1266–1274. [Google Scholar] [CrossRef]
- Dorner, B.; Plesser, T.; Stiller, H. Brillouin scattering of neutrons from liquids. Discuss. Faraday Soc. 1967, 43, 160–168. [Google Scholar] [CrossRef]
- Bell, H.; Moellerwenghoffer, H.; Kollmar, A.; Stockmeyer, R.; Springer, T.; Stiller, H. Neutron Brillouin-scattering in fluid neon. Phys. Rev. A 1975, 11, 316–327. [Google Scholar] [CrossRef]
- Ailawadi, N.K.; Rahman, A.; Zwanzig, R. Generalized hydrodynamics and analysis of current correlation functions. Phys. Rev. A 1971, 4, 1616–1625. [Google Scholar] [CrossRef]
- Levesque, D.; Verlet, L.; Kürkijarvi, J. Computer "experiments" on classical fluids. Iv. Transport properties and time-correlation functions of the lennard-jones liquid near its triple point. Phys. Rev. A 1973, 7, 1690–1700. [Google Scholar] [CrossRef]
- Van Well, A.A.; Verkerk, P.; de Graaf, L.A.; Suck, J.B.; Copley, J.R.D. Density-fluctuations in liquid argon—Coherent dynamic structure factor along the 120-K isotherm obtained by neutron-scattering. Phys. Rev. A 1985, 31, 3391–3414. [Google Scholar] [CrossRef] [PubMed]
- De Schepper, I.M.; Verkerk, P.; van Well, A.A.; de Graaf, L.A. Short-wavelength sound modes in liquid argon. Phys. Rev. Lett. 1983, 50, 974–977. [Google Scholar] [CrossRef]
- Verkerk, P.; van Well, A.A.; de Schepper, I.M. Disappearance of the sound-propagation gap in liquid argon at very high-densities. J. Phys. C: Solid State Phys. 1987, 20, L979–L982. [Google Scholar] [CrossRef]
- Van Well, A.A.; de Graaf, L.A. Density fluctuations in liquid argon. Ii. Coherent dynamic structure factor at large wave numbers. Phys. Rev. A 1985, 32, 2384–2395. [Google Scholar] [CrossRef] [PubMed]
- De Schepper, I.M.; Verkerk, P.; van Well, A.A.; de Graaf, L.A. Non-analytic dispersion relations in liquid argon. Phys. Lett. A 1984, 104, 29–32. [Google Scholar] [CrossRef]
- McGreevy, R.L.; Mitchell, E.W.J. Collective modes in molten alkaline earth chlorides: III. Inelastic neutron scattering from molten MGCL2 and CACL2. J. Phys. C Solid State Phys. 1985, 18, 1163–1178. [Google Scholar] [CrossRef]
- Crevecoeur, R.M.; Verberg, R.; de Schepper, I.M.; de Graaf, L.A.; Montfrooij, W. Overdamped phonons in fluid helium at 4 K. Phys. Rev. Lett. 1995, 74, 5052–5055. [Google Scholar] [CrossRef] [PubMed]
- Montfrooij, W.; de Graaf, L.A.; de Schepper, I.M. Viscoelastic behavior of helium at 39-K and 114-bar. Phys. Rev. A 1991, 44, 6559–6563. [Google Scholar] [CrossRef] [PubMed]
- Zuilhof, M.J.; Cohen, E.G.D.; de Schepper, I.M. Sound-propagation in fluids and neutron-spectra. Phys. Lett. A 1984, 103, 120–125. [Google Scholar] [CrossRef]
- De Gennes, P.G. Liquid dynamics and inelastic scattering of neutrons. Physica 1959, 25, 825–839. [Google Scholar] [CrossRef]
- Lovesey, S.W. Comment on “short-wavelength sound modes in liquid argon”. Phys. Rev. Lett. 1984, 53, 401. [Google Scholar] [CrossRef]
- De Schepper, I.M.; Verkerk, P.; van Well, A.A.; de Graaf, L.A.; Cohen, E.G.D. de Schepper et al. Respond. Phys. Rev. Lett. 1985, 54, 158. [Google Scholar] [CrossRef]
- Hansen, J.-P.; McDonald, I.R. Chapter 3—Static properties of liquids: Thermodynamics and structure. In Theory of Simple Liquids, 3rd ed.; Hansen, J.-P., McDonald, I.R., Eds.; Academic Press: Burlington, VT, USA, 2006; pp. 46–77. [Google Scholar]
- Cohen, E.G.D. Fifty years of kinetic theory. Physica A 1993, 194, 229–257. [Google Scholar] [CrossRef]
- Yip, S. Renormalized kinetic-theory of dense fluids. Annu. Rev. Phys. Chem. 1979, 30, 547–577. [Google Scholar] [CrossRef]
- Kamgar-Parsi, B.; Cohen, E.G.; de Schepper, I.M. Dynamical processes in hard-sphere fluids. Phys. Rev. A 1987, 35, 4781–4795. [Google Scholar] [CrossRef] [PubMed]
- Rabinovich, V.A.; Vasserman, A.A.; Nedostup, V.I.; Veksler, L.S. Thermophysical Properties of Neon, Argon, Krypton, and Xenon; Hemisphere Pub. Corp.: Washington, DC, USA, 1987. [Google Scholar]
- Postol, T.A.; Pelizzari, C.A. Neutron-scattering study of thermally excited density fluctuations in a dense classical fluid. Phys. Rev. A 1978, 18, 2321–2336. [Google Scholar] [CrossRef]
- Ernst, M.H.; Haines, L.K.; Dorfman, J.R. Theory of transport coefficients for moderately dense gases. Rev. Mod. Phys. 1969, 41, 296–316. [Google Scholar] [CrossRef]
- Bafile, U.; Verkerk, P.; Barocchi, F.; de Graaf, L.A.; Suck, J.; Mutka, H. Onset of depature from linearized hydrodynamic behavior in argon gas studied with neutron brillouin scattering. Phys. Rev. Lett. 1990, 65, 2394–2397. [Google Scholar] [CrossRef] [PubMed]
- Balucani, U.; Zoppi, M. Dynamics of the Liquid State; Clarendon Press Oxford: Oxford, UK, 1994. [Google Scholar]
- Krisch, M.; Sette, F. Neutron and X-ray Spectroscopy; Springer Verlag: Berlin, Germany, 2007; pp. 317–370. [Google Scholar]
- Cunsolo, A.; Pratesi, G.; Ruocco, G.; Sampoli, M.; Sette, F.; Verbeni, R.; Barocchi, F.; Krisch, M.; Masciovecchio, C.; Nardone, M. Dynamics of dense supercritical neon at the transition from hydrodynamical to single-particle regimes. Phys. Rev. Lett. 1998, 80, 3515–3518. [Google Scholar] [CrossRef]
- Cunsolo, A.; Pratesi, G.; Rosica, F.; Ruocco, G.; Sampoli, M.; Sette, F.; Verbeni, R.; Barocchi, F.; Krisch, M.; Masciovecchio, C.; et al. Is there any evidence of a positive sound dispersion in the high frequency dynamics of noble gases? J. Phys. Chem. Sol. 2000, 61, 477–483. [Google Scholar] [CrossRef]
- Cunsolo, A. Relaxation phenomena in the THZ dynamics of simple fluids probed by inelastic X-ray scattering. PhD Thesis, Université J. Fourier, Grenoble, France, 1999. [Google Scholar]
- Verkerk, P.; van Well, A.A. Short wavelength sound dispersion in liquid argon close to solidification. Physica B + C 1986, 136, 168–171. [Google Scholar] [CrossRef]
- Cowley, R.A.; Woods, A.D.B. Neutron scattering from liquid helium at high energies. Phys. Rev. Lett. 1968, 21, 787–789. [Google Scholar] [CrossRef]
- Montfrooij, W.; de Graaf, L.A.; de Schepper, I.M. Propagating microscopic temperature-fluctuations in a dense helium fluid at 13.3-K. Phys. Rev. B 1992, 45, 3111–3114. [Google Scholar] [CrossRef]
- Van Well, A.A.; de Graaf, L.A. Density fluctuations in liquid neon studied by neutron scattering. Phys. Rev. A 1985, 32, 2396–2412. [Google Scholar] [CrossRef] [PubMed]
- Thermodynamic Data are from the Database. Available online: http://webbook.nist.gov/chemistry/form-ser.html (accessed on 1 September 2015).
- Pontecorvo, E.; Krisch, M.; Cunsolo, A.; Monaco, G.; Mermet, A.; Verbeni, R.; Sette, F.; Ruocco, G. High-frequency longitudinal and transverse dynamics in water. Phys. Rev. E 2005, 71, 011501. [Google Scholar] [CrossRef] [PubMed]
- Torre, R.; Bartolini, P.; Righini, R. Structural relaxation in supercooled water by time-resolved spectroscopy. Nature 2004, 428, 296–299. [Google Scholar] [CrossRef] [PubMed]
- Masciovecchio, C.; Santucci, S.C.; Gessini, A.; Di Fonzo, S.; Ruocco, G.; Sette, F. Structural relaxation in liquid water by inelastic UV scattering. Phys. Rev. Lett. 2004, 92, 255507. [Google Scholar] [CrossRef] [PubMed]
- Sampoli, M.; Ruocco, G.; Sette, F. Mixing of longitudinal and transverse dynamics in liquid water. Phys. Rev. Lett. 1997, 79, 1678–1681. [Google Scholar] [CrossRef]
- Cimatoribus, A.; Saccani, S.; Bencivenga, F.; Gessini, A.; Izzo, M.G.; Masciovecchio, C. The mixed longitudinal-transverse nature of collective modes in water. New J. Phys. 2010, 12, 053008. [Google Scholar] [CrossRef]
- Cunsolo, A.; Kodituwakku, C.N.; Bencivenga, F.; Frontzek, M.; Leu, B.M.; Said, A.H. Transverse dynamics of water across the melting point: A parallel neutron and X-ray inelastic scattering study. Phys. Rev. B 2012, 85. [Google Scholar] [CrossRef]
- Cunsolo, A.; Li, Y.; Kodituwakku, C.N.; Wang, S.; Antonangeli, D.; Bencivenga, F.; Battistoni, A.; Verbeni, R.; Tsutsui, S.; Baron, A.Q.; et al. Signature of a polyamorphic transition in the Thz spectrum of vitreous GEO2. Sci. Rep. 2015, 5, 14996. [Google Scholar] [CrossRef] [PubMed]
- Scopigno, T.; Pontecorvo, E.; Di Leonardo, R.; Krisch, M.; Monaco, G.; Ruocco, G.; Ruzicka, B.; Sette, F. High-frequency transverse dynamics in glasses. J. Phys. Condens. Matter. 2003, 15, S1269–S1278. [Google Scholar] [CrossRef]
- Hosokawa, S.; Inui, M.; Kajihara, Y.; Matsuda, K.; Ichitsubo, T.; Pilgrim, W.C.; Sinn, H.; Gonzalez, L.E.; Gonzalez, D.J.; Tsutsui, S.; et al. Transverse acoustic excitations in liquid Ga. Phys. Rev. Lett. 2009, 102, 105502. [Google Scholar] [CrossRef] [PubMed]
- Giordano, V.M.; Monaco, G. Inelastic X-ray scattering study of liquid Ga: Implications for the short-range order. Phys. Rev. B 2011, 84, 052201. [Google Scholar] [CrossRef]
- Hosokawa, S.; Inui, M.; Kajihara, Y.; Matsuda, K.; Ichitsubo, T.; Pilgrim, W.C.; Sinn, H.; Gonzalez, L.E.; Gonzalez, D.J.; Tsutsui, S.; et al. Transverse excitations in liquid Ga. Eur. Phys. J. 2011, 196, 85–93. [Google Scholar]
- Hosokawa, S.; Munejiri, S.; Inui, M.; Kajihara, Y.; Pilgrim, W.C.; Ohmasa, Y.; Tsutsui, S.; Baron, A.Q.; Shimojo, F.; Hoshino, K. Transverse excitations in liquid sn. J. Phys. Condens. Matter. 2013, 25, 112101. [Google Scholar] [CrossRef] [PubMed]
- Hosokawa, S.; Pilgrim, W.C.; Sinn, H.; Alp, E.E. The possibility of transverse excitation modes in liquid Ga. J. Phys. Condens. Matter. 2008, 20, 114107. [Google Scholar] [CrossRef] [PubMed]
- Paciaroni, A.; Orecchini, A.; Haertlein, M.; Moulin, M.; Conti Nibali, V.; De Francesco, A.; Petrillo, C.; Sacchetti, F. Vibrational collective dynamics of dry proteins in the terahertz region. J. Phys. Chem. B 2012, 116, 3861–3865. [Google Scholar] [CrossRef] [PubMed]
- Violini, N.; Orecchini, A.; Paciaroni, A.; Petrillo, C.; Sacchetti, F. Neutron scattering investigation of high-frequency dynamics in glassy glucose. Phys. Rev. B 2012, 85, 134204. [Google Scholar] [CrossRef]
- Li, M.D.; Chu, X.Q.; Fratini, E.; Baglioni, P.; Alatas, A.; Alp, E.E.; Chen, S.H. Phonon-like excitation in secondary and tertiary structure of hydrated protein powders. Soft Matter. 2011, 7, 9848–9853. [Google Scholar] [CrossRef]
- Cunsolo, A.; Kodituwakku, C.N.; Bencivenga, F.; Said, A.H. Shear propagation in the terahertz dynamics of water-glycerol mixtures. J. Chem. Phys. 2013, 139, 184507. [Google Scholar] [CrossRef] [PubMed]
- Balucani, U.; Brodholt, J.P.; Vallauri, R. Dynamical properties of liquid water. J. Phys. Condens. Matter. 1996, 8, 9269–9274. [Google Scholar] [CrossRef]
- Debye, P. Zur theorie der spezifischen wärmen. Ann. Phys. 1912, 344, 789–839. [Google Scholar] [CrossRef]
- Lovesey, S.W. Density fluctuations in classical monatomic liquids. J. Phys. C Solid State Phys. 1971, 4, 3057–3064. [Google Scholar] [CrossRef]
- Magazu, S.; Maisano, G.; Majolino, D.; Mallamace, F.; Migliardo, P.; Aliotta, F.; Vasi, C. Relaxation process in deeply supercooled water by mandelstam-brillouin scattering. J. Phys. Chem. 1989, 93, 942–947. [Google Scholar] [CrossRef]
- Maisano, G.; Migliardo, P.; Aliotta, F.; Vasi, C.; Wanderlingh, F.; Darrigo, G. Evidence of anomalous acoustic behavior from brillouin-scattering in supercooled water. Phys. Rev. Lett. 1984, 52, 1025–1028. [Google Scholar] [CrossRef]
- Cunsolo, A.; Nardone, M. Velocity dispersion and viscous relaxation in supercooled water. J. Chem. Phys. 1996, 105, 3911–3917. [Google Scholar] [CrossRef]
- Franks, F. Water: A Comprehensive Treatise; Plenum: New York, NY, USA, 1972; Volume 1. [Google Scholar]
- Coester, F. Principle of detailed balance. Phys. Rev. 1951, 84, 1259. [Google Scholar] [CrossRef]
- Verbeni, R.; Cunsolo, A.; Pratesi, G.; Monaco, G.; Rosica, F.; Masciovecchio, C.; Nardone, M.; Ruocco, G.; Sette, F.; Albergamo, F. Quantum effects in the dynamics of he probed by inelastic X-ray scattering. Phys. Rev. E 2001, 64, 021203. [Google Scholar] [CrossRef] [PubMed]
- Monaco, G.; Cunsolo, A.; Pratesi, G.; Sette, F.; Verbeni, R. Deep inelastic atomic scattering of X-rays in liquid neon. Phys. Rev. Lett. 2002, 88, 227401. [Google Scholar] [CrossRef] [PubMed]
- Cunsolo, A.; Monaco, G.; Nardone, M.; Pratesi, G.; Verbeni, R. Transition from the collective to the single-particle regimes in a quantum fluid. Phys. Rev. B 2003, 67, 024507. [Google Scholar] [CrossRef]
- Rabani, E.; Reichman, D.R. A self-consistent mode-coupling theory for dynamical correlations in quantum liquids: Rigorous formulation. J. Chem. Phys. 2002, 116, 6271–6278. [Google Scholar] [CrossRef]
- Gotze, W.; Mayr, M.R. Evolution of vibrational excitations in glassy systems. Phys. Rev. E 2000, 61, 587–606. [Google Scholar] [CrossRef]
- De Schepper, I.M.; Cohen, E.G.; Bruin, C.; van Rijs, J.C.; Montfrooij, W.; de Graaf, L.A. Hydrodynamic time correlation functions for a lennard-jones fluid. Phys. Rev. A 1988, 38, 271–287. [Google Scholar] [CrossRef] [PubMed]
- Gorelli, F.; Santoro, M.; Scopigno, T.; Krisch, M.; Ruocco, G. Liquidlike behavior of supercritical fluids. Phys. Rev. Lett. 2006, 97, 245702. [Google Scholar] [CrossRef] [PubMed]
- Simeoni, G.G.; Bryk, T.; Gorelli, F.A.; Krisch, M.; Ruocco, G.; Santoro, M.; Scopigno, T. The widom line as the crossover between liquid-like and gas-like behaviour in supercritical fluids. Nat. Phys. 2010, 6, 503–507. [Google Scholar] [CrossRef]
- Widom, B. Phase Transitions and Critical Phenomena; Domb, C.G., Ed.; Academic Press: Waltham, MA, USA, 1972; Volume 2. [Google Scholar]
- Zemansky, Y. Heat and Thermodynamics : An Intermediate Textbook, 7th ed.; McGraw-Hill: New York, NY, USA, 1937. [Google Scholar]
- Bolmatov, D.; Zhernenkov, M.; Zavyalov, D.; Stoupin, S.; Cai, Y.Q.; Cunsolo, A. Revealing the mechanism of the viscous-to-elastic crossover in liquids. J. Phys. Chem. Lett. 2015, 6, 3048–3053. [Google Scholar] [CrossRef] [PubMed]
- Brazhkin, V.V.; Fomin, Y.D.; Lyapin, A.G.; Ryzhov, V.N.; Tsiok, E.N.; Trachenko, K. “Liquid-gas” transition in the supercritical region: Fundamental changes in the particle dynamics. Phys. Rev. Lett. 2013, 111, 145901. [Google Scholar] [CrossRef] [PubMed]
- Frenkel, J. Kinetic Theory of Liquids; Oxford University Press: Oxford, UK, 1947. [Google Scholar]
- Brazhkin, V.V.; Fomin, Y.D.; Lyapin, A.G.; Ryzhov, V.N.; Trachenko, K. Two liquid states of matter: A dynamic line on a phase diagram. Phys. Rev. E 2012, 85, 031203. [Google Scholar] [CrossRef] [PubMed]
- Bolmatov, D.; Musaev, E.T.; Trachenko, K. Symmetry breaking gives rise to energy spectra of three states of matter. Sci. Rep. 2013, 3, 2794. [Google Scholar] [CrossRef] [PubMed]
- Bolmatov, D.; Brazhkin, V.V.; Trachenko, K. The phonon theory of liquid thermodynamics. Sci. Rep. 2012, 2, 421. [Google Scholar] [CrossRef] [PubMed]
- Bolmatov, D.; Zavyalov, D.; Zhernenkov, M.; Musaev, E.T.; Cai, Y.Q. Unified phonon-based approach to the thermodynamics of solid, liquid and gas states. Ann. Phys. 2015, 363, 221–242. [Google Scholar] [CrossRef]
- Bolmatov, D.; Brazhkin, V.V.; Trachenko, K. Thermodynamic behaviour of supercritical matter. Nat. Commun. 2013, 4, 2331. [Google Scholar] [CrossRef] [PubMed]
- Bolmatov, D.; Zhernenkov, M.; Zav’yalov, D.; Stoupin, S.; Cunsolo, A.; Cai, Y.Q. Thermally triggered phononic gaps in liquids at thz scale. Sci. Rep. 2016, 6, 19469. [Google Scholar] [CrossRef] [PubMed]
- Shvyd’ko, Y. X-ray Optics—High-Energy-Resolution Applications, Optical Science; Springer: Berlin, Germany; New York, NY, USA, 2004; Volume 98. [Google Scholar]
- Shvyd’ko, Y.; Stoupin, S.; Shu, D.; Collins, S.P.; Mundboth, K.; Sutter, J.; Tolkiehn, M. High-contrast sub-millivolt inelastic X-ray scattering for nano- and mesoscale science. Nat. Commun. 2014, 5, 4219. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.Q.; Coburn, D.S.; Cunsolo, A.; Keister, J.W.; Honnicke, M.G.; Huang, X.R.; Kodituwakku, C.N.; Stetsko, Y.; Suvorov, A.; Hiraoka, N.; et al. The ultrahigh resolution ixs beamline of nsls-II: Recent advances and scientific opportunities. J. Phys. Conf. Ser. 2013, 425, 202001. [Google Scholar] [CrossRef]
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cunsolo, A. The Spectrum of Density Fluctuations of Noble Gases Probed by THz Neutron and X-ray Spectroscopy. Appl. Sci. 2016, 6, 64. https://doi.org/10.3390/app6030064
Cunsolo A. The Spectrum of Density Fluctuations of Noble Gases Probed by THz Neutron and X-ray Spectroscopy. Applied Sciences. 2016; 6(3):64. https://doi.org/10.3390/app6030064
Chicago/Turabian StyleCunsolo, Alessandro. 2016. "The Spectrum of Density Fluctuations of Noble Gases Probed by THz Neutron and X-ray Spectroscopy" Applied Sciences 6, no. 3: 64. https://doi.org/10.3390/app6030064
APA StyleCunsolo, A. (2016). The Spectrum of Density Fluctuations of Noble Gases Probed by THz Neutron and X-ray Spectroscopy. Applied Sciences, 6(3), 64. https://doi.org/10.3390/app6030064




