Motion Pattern Recognition Based on Surface Electromyography Data and Machine Learning Classifiers: Preliminary Study

Featured Application

The findings described in this paper could be used in physiotherapy to define the level of activity of chosen superficial muscles of the upper limbs, as well as to develop algorithms to control assistant and guidance mode in mechatronic devices, such as exoskeletons and prostheses, used in rehabilitation.

Abstract

Objective: The aim of this preliminary study was to recognize motion patterns by classifying time series features extracted from electromyography (EMG) data of the upper limb muscles. Methods: In this study, we tested six machine learning (ML) classification models (decision trees, support vector machines, linear discriminant, quadratic discriminant, k-nearest neighbors, and efficient logistic regression) to classify time series features segmented from processed EMG data that were acquired from eight superficial muscles of two upper limbs over performing given physical activities in two main stages (supination and neutral forearm configuration) in initial and target (isometric) positions. Results: Findings indicate that in aiming to classify stages of the upper limb with the highest performance, the following ML models should be used: (1) K-NN cityblock (F1 equals 0.973/0.992) and K-NN minkowski (0.966/0.992) for the left limb in initial or target position; (2) K-NN seuclidean (0.959/0.985) and K-NN minkowski (0.957/0.986) for the right limb in initial position; (3) K-NN cityblock (0.966/0.986), K-NN seuclidean (0.959/0.985), and K-NN minkowski (0.957/0.986) for the right limb in target position. Conclusions: Upper limb positions tested in this study can be recognized based on classification of surface EMG data by using the k-nearest neighbors models (K-NN cityblock, K-NN seuclidean or K-NN minkowski) that have to be trained separately for the right and left upper limbs.

1. Introduction

The analysis of motion patterns of the human body is crucial in sport biomechanics and clinical applications along with medical diagnosis, treatment, and rehabilitation [1]. Electromyography (EMG) is a fundamental technique used to measure the electrical activity of muscles by applying either needle EMG or surface EMG (sEMG). Both methods have been extensively studied and sEMG has gained significant attention because of its non-invasive nature and a broad range of applications, e.g., (1) classification of human movements, gait or posture analysis; (2) control of an exoskeleton, robotic arm or prosthetic devices by using wearable sensors; (3) human–machine interaction (interface); (4) diagnosis of neuromuscular disorders [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26].

Recent advances in machine learning (ML) and artificial intelligence (AI) have significantly improved the analysis of EMG data, especially in classifying EMG patterns to recognize limb or hand movements in different physical activities. The literature shows evidence referring to application of various supervised ML techniques to recognize patterns of EMG data, e.g., support vector machine (SVM), random forest (RF), decision tree (DT), k-nearest neighbors (KNNs), logistic regression (LR), naive Bayes, extra tree, ensemble bagged trees, and ensemble subspace discriminant [15,16,17,18,19,20,23,24]. For example, the study [27] evaluates the efficiency of ML algorithms, including SVM, LR, and an artificial neural network (ANN) by using acquired sEMG data to recognize seven shoulder motions of healthy subjects. This study reports mean accuracy of 97.29% for SVM, 96.79% for ANN, and 95.31% for LR. Furthermore, a study [28] uses the K-NN classifier and reports that the peak accuracy of sEMG features a classification of 99.23% for testing protocol composed of relaxation, holding a pen, grabbing a bottle, and lifting a 2 kg weight. Moreover, a paper [29] compares results of K-NN and RF classifiers to separate sEMG data collected from upper limb muscles at different angles of forearm flexion. This study concludes that RF outperformed K-NN classification accuracy.

Advanced AI techniques, such as deep learning models, have also been applied in biomechanics. For example, the paper [30] presents a model with a hybrid architecture combining the convolutional neural network (CNN) and the recurrent neural network (RNN) to classify the human hand motions by using sEMG data downloaded from publicly available databases (external ones) [24,31]. The authors report an average classification accuracy that is within the range of [82.2%; 97.7%]. Furthermore, the study [10] presents high accuracy results for the CNN-based view pooling technique to recognize the gestures by considering sEMG data. To classify hand gestures in dexterous robotic telemanipulation, the paper [25] compares several approaches of ML (including RF) and CNN along with transformer-based models. This paper indicates that while deep learning models achieve high accuracy, RF provided an optimal trade-off between time of classification and its accuracy, and it might be treated as well-suited for real-time applications.

Evidence referring to the fusion of electroencephalography (EEG) and sEMG signals for classification has shown promising results, especially in controlling a wearable exoskeleton. For example, the paper [32] describes the feasibility of a CNN-based EEG-EMG fusion approach for multi-class movement detection and reports an average classification accuracy of 80.51%. Moreover, the study [11] presents a hybrid human–machine interface created to classify gait phases by applying the Bayesian fusion of EEG and EMG classifiers. Additionally, an optimization approach based on general non-linear fusion function “α-integration” is applied for EEG pattern recognition in epileptic patients [33].

To improve the efficiency of feature extraction from sEMG data, the paper [34] describes an implementation of the smooth wavelet packet transform (SWPT) and a hybrid model composing of CNN, the long short-term memory (LSTM) enhanced with a convolutional block attention module (CBAM) and fused with accelerometer data. This study reports an average accuracy of 92.159% for gesture recognition tasks. Furthermore, a study [35] reports an accuracy of 92% for sEMG data multiclassification by applying the Back-Propagation–LSTM model to recognize six motions, but the authors did not specify these motions in detail.

Among traditional pattern recognition methods, one can find evidence related to the application of ML algorithms that include K-NN, SVM, RF, and linear discriminant analysis (LDA) [36]. These classifiers are favored for their simplicity, very fast computation times, and high accuracy. Additionally, one can find studies that describe an application of ANN to analyze EMG data [37]. Furthermore, the paper [38] proposes using a “symbolic transition network” to estimate a fatigue index based on sEMG data features. On the other hand, the study [39] describes the ensemble classifiers, including RF, along with SVM and ANN to recognize neuromuscular disorders by using clinical and simulated EMG data.

It is important to note that recognition of human motions, which is based on the sEMG data classification, requires solving a problem related to the compositions of the EMG features. Moreover, one needs to use a proper domain of sEMG data (time, frequency, or time–frequency) along with a proper type of data (subject-wise or group of subjects) [40,41]. Also, this issue should be related to the device used to collect sEMG data and its sampling rate, i.e., low-sampling sEMG device (e.g., Myo Armband [42]), clinical sEMG device, or high-density sEMG device [43,44,45,46]. Additionally, a proper metric (metrics) should be used to analyze the classification results based on the sEMG features [47].

The purpose of this study was to test the hypothesis, which states that it is possible to recognize motion patterns tested by classifying electrophysiological data (sEMG time-series) with chosen ML classifiers. In this study, we tested six ML algorithms implemented in the MATLAB (R2023b) environment: decision trees, support vector machines, linear discriminant and quadratic discriminant, k-nearest neighbors, and efficient logistic regression. The main contributions of this work are as follows: (1) new testing protocol that is feasible for practical applications and can be applied to determine whether upper limb dominance requires the use and training of different ML models to classify the motions of each upper limb; (2) elaboration of new dataset of healthy population that is composed of EMG time series features, which can be easily adapted for real-time controlling in mechatronic devices, such as exoskeletons and prostheses, used in rehabilitation.

2. Materials and Methods

To recognize motion patterns and to assess the accuracy of chosen ML models, sEMG data (EMG data) and acceleration were collected on a group of 27 healthy subjects: 16 males (age 22.81 ± 3.43 years, height 184.19 ± 5.81 cm, weight 81.59 ± 13.44 kg), and 11 females (age 22.33 ± 3.67 years, height 166.33 ± 5.81 cm, weight 61.67± 7.43 kg). Subjects tested in this study had no musculoskeletal, postural, neurological, or psychological disorders. Non-invasive testing was approved by the Ethics Committee (Ethics Committee Approval of Gdansk University of Technology from 29 January 2020). Each examined subject signed informed consent before testing. The study was conducted at the Laboratory of Biomechanics (Gdansk University of Technology, Gdansk, Poland).

In this study, we used an experimental protocol that involved two main stages performed in the given sequence: the first was a supination stage (related to forearm supination position) and the second was a neutral stage (related to forearm neutral position). Each main stage included six alternatively performed initial positions along with five or six target positions (the number was dependent on the subject’s physical condition) (Figure 1). The initial position involved maintaining fully extended upper limbs along the body without keeping up any external weight and trying to maintain both over 10–20 sec in a specific configuration: supination in supination stage, and neutral in neutral stage. The target position required maintaining both forearms in a given isometric configuration (supination in the supination stage, and neutral in the neutral stage) while both forearms and arms were flexed at the elbow joints at the right angle in the sagittal plane and were simultaneously loaded with two 3 kg dumbbells that were maintained through a hand grip over 10 sec. It is worth noting that in each target position, these two dumbbells were simultaneously given to the subject by the investigator, and after a defined time range, these dumbbells were simultaneously taken away by the investigator, and after that, the subject was able to return to the initial position. Throughout the whole test, which included two main stages, each subject stood on both feet (in shoes, feet apart) by maintaining upright trunk posture without performing motions in both humeral joints (glenohumeral joints) and shoulder girdle joints.

Before conducting an examination, each subject was given a demonstration of the initial and target positions in each main stage, and after that, they familiarized himself/herself with the demonstrated activities. Following this, an experimental protocol was carried out. The number of trials (six initial positions and five (or six) target positions in each main stage) was established to avoid fatigue along with the learning effect. Each trial was performed by providing a verbal instruction. After completing each stage, the subject was given at least a 5 min break. An assessment of maximum voluntary contraction (MVC) was conducted after 20 min of completion of the last trial of the entire examination. This MVC testing involved separate testing for each upper limb over three times with at least 5 min of rest during each MVC testing.

To collect sEMG and acceleration data, we used eight wireless Trigno Avanti™ sensors of the Delsys Trigno^® Wireless Biofeedback System (Natick, MA, USA) [https://delsys.com/trigno-avanti/ (accessed on 17 November 2025)] distributed by Technomex (Gliwice, Poland). Each Trigno Avanti™ sensor (14 g weight and 27 × 37 × 13 mm dimensions) features both an EMG unit and an inertial measurement unit (IMU). Each sensor was attached to the skin by using a disposable Delsys adhesive sensor interface. The EMG units measure surface EMG data without requiring any additional reference electrode. Eight sensors were attached on the properly prepared skin surface over the tested muscle bellies identified through palpation. Each sensor was oriented in a specific way according to Delsys’ recommendation, i.e., sensor silver contacts were positioned in a perpendicular direction with respect to the muscle fibers of each tested belly [48]. Each EMG sensor has an anti-aliasing filter operating within a frequency range of [20 Hz; 450 Hz] with a sampling rate of 1926 Hz in 11 mV range, while each IMU collects acceleration data with a sampling rate of 148 Hz within a range of [−16 g; 16 g]. The analog-to-digital converter for the EMG unit has a resolution of 16 bits.

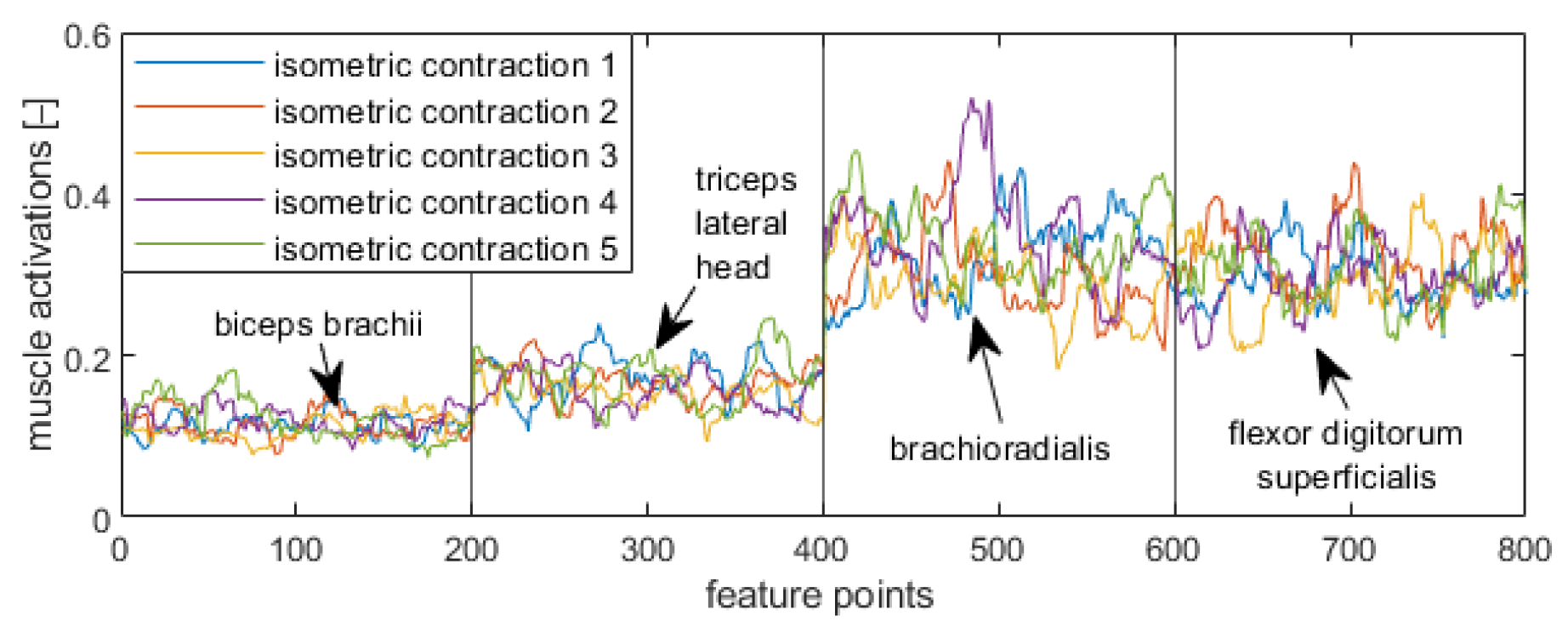
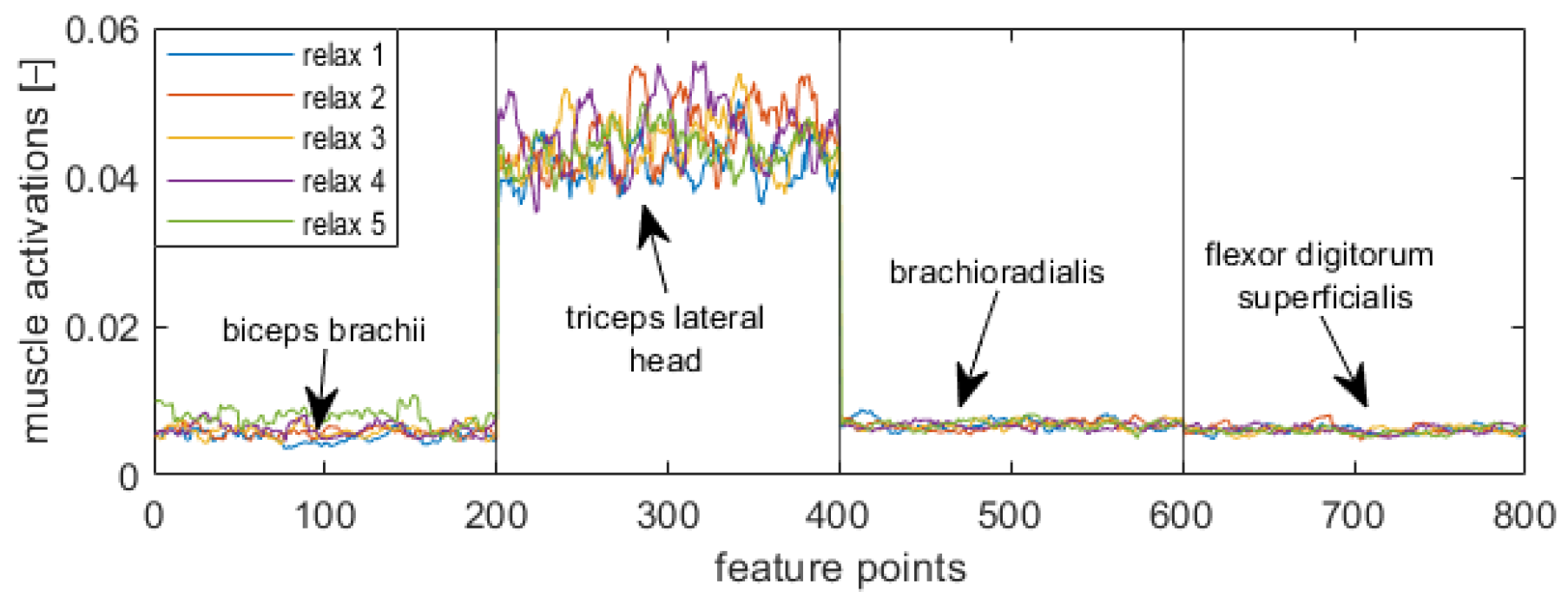
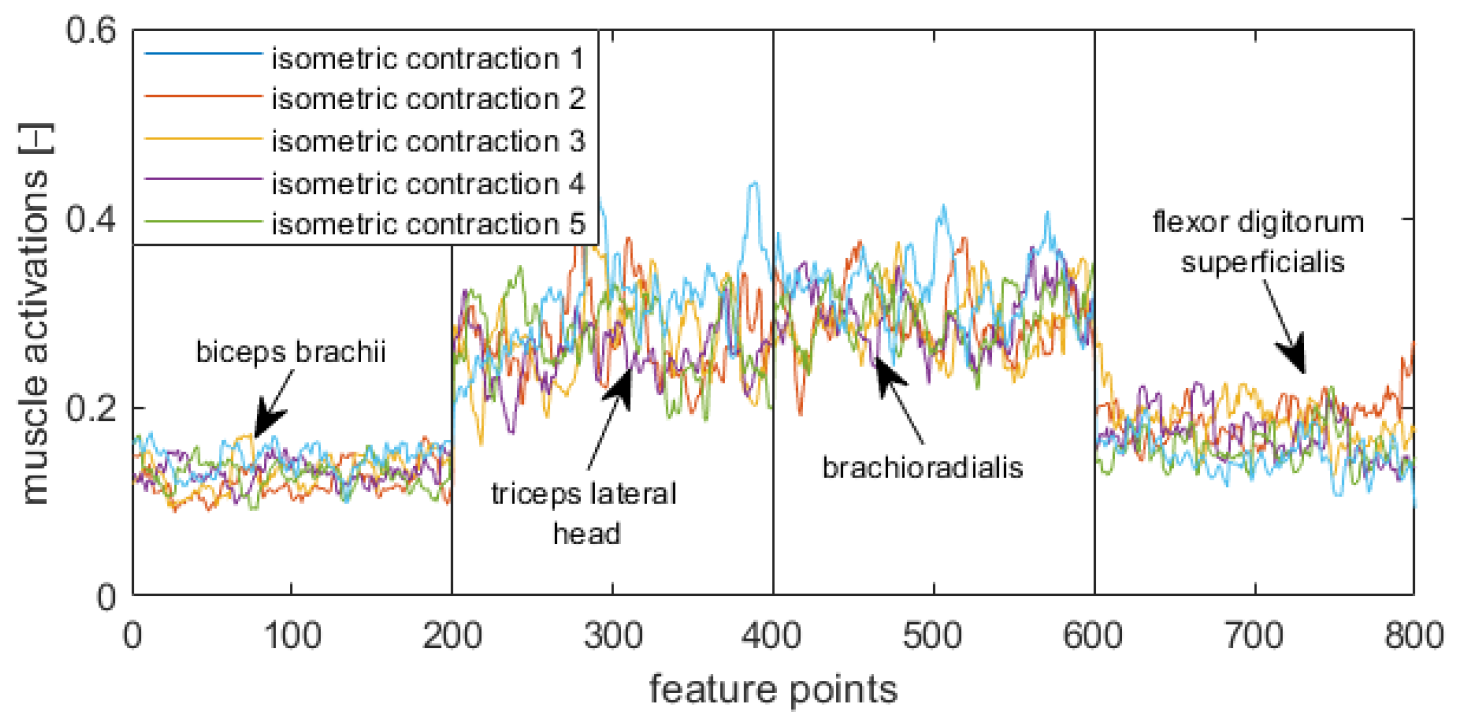
Eight Trigno Avanti™ sensors were attached to the bellies of following muscles: left biceps brachii (EMG1), left triceps lateral head (EMG 2), left brachioradialis (EMG 3), left flexor digitorium superficialis (EMG 4), right biceps brachii (EMG 5), right triceps lateral head (EMG 6), right brachioradialis (EMG 7), and right flexor digitorium superficialis (EMG 8) (Figure 2). The tested muscles are superficial ones that were chosen based on reports described in [38,49]. In each main stage, the initial position was labeled as “Relax”, whereas a target position was labeled as “Isometric” (Figure 3).

The commercial Delsys software (EMGworks Acquisition 4.7.3.0) was used to synchronously collect and record raw sEMG data along with acceleration data. To process the raw sEMG data, we used the EMGworks Analysis software 4.8.0 to filter, rectify, and smooth by using the root mean square (RMS) algorithm with a 125 msec window with 10 msec overlapping. The processed sEMG (time series) was transmitted to the MATLAB software (R2023b), normalized with respect to MVC, and segmented by using the code developed by the authors. Segmentation of EMG data was performed based on the onset/offset of EMG data along with accelerometer data (x,y,z) of both arms by especially focusing on the sensor 4 (EMG4 and Accelerometer 4) and sensor 8 (EMG8 and Accelerometer 8) (Figure 4). The onset/offset threshold of the accelerometer data was defined as a range with no more than 0.05 g. Each segmentation window related to the initial/target position was supplemented by a visual inspection along with defined time range, in which measured data of both arms met given requirements. Next, processed and normalized EMG data were extracted from all-segmentation windows, normalized to the motion timing (to 100%), resampled to 1000 points, and divided into five equal parts, which were treated as five EMG patterns.

In this study, each feature was created by concatenating four EMG patterns into a single vector: for the left upper limb (time series of EMG1, EMG2, EMG3, EMG4) and for the right upper limb (time series of EMG5, EMG6, EMG7, EMG8).

To identify the best ML classifiers for recognition of features composed of sEMG patterns, in this research, we created four datasets composed of features: (1) for the right upper limb in a supination stage (730 initial/730 target positions); (2) for the left upper limb in a supination stage (730 initial/730 target positions); (3) for the right upper limb in a neutral stage (685 initial/725 target positions); (4) for the left upper limb in a neutral stage (685 initial/725 target positions). Figure 5, Figure 6, Figure 7 and Figure 8 display visualizations of features related to a target position in a supination stage (Figure 5), initial position in a supination stage (Figure 6), target position in a neutral stage (Figure 7), and initial position in a neutral stage (Figure 8).

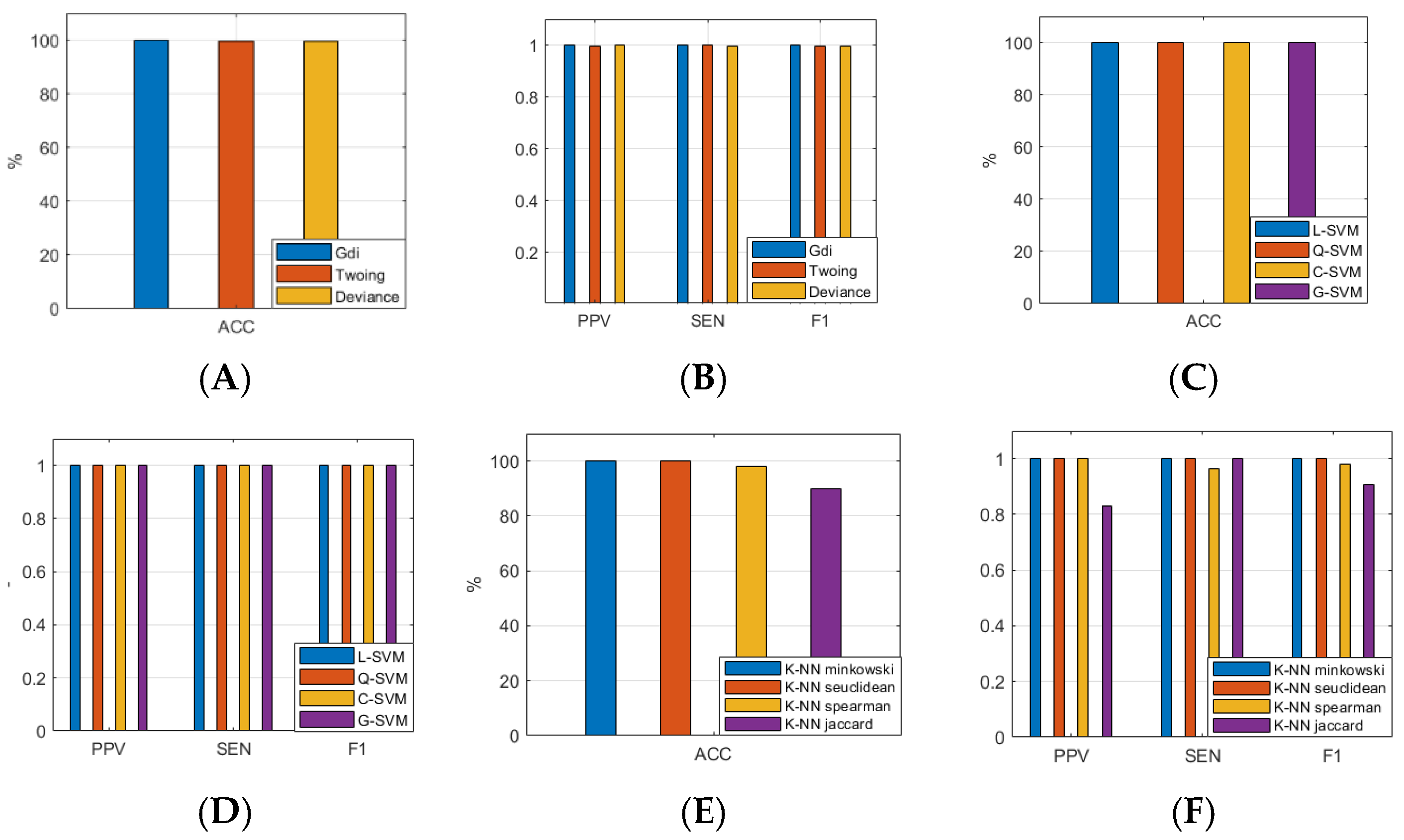
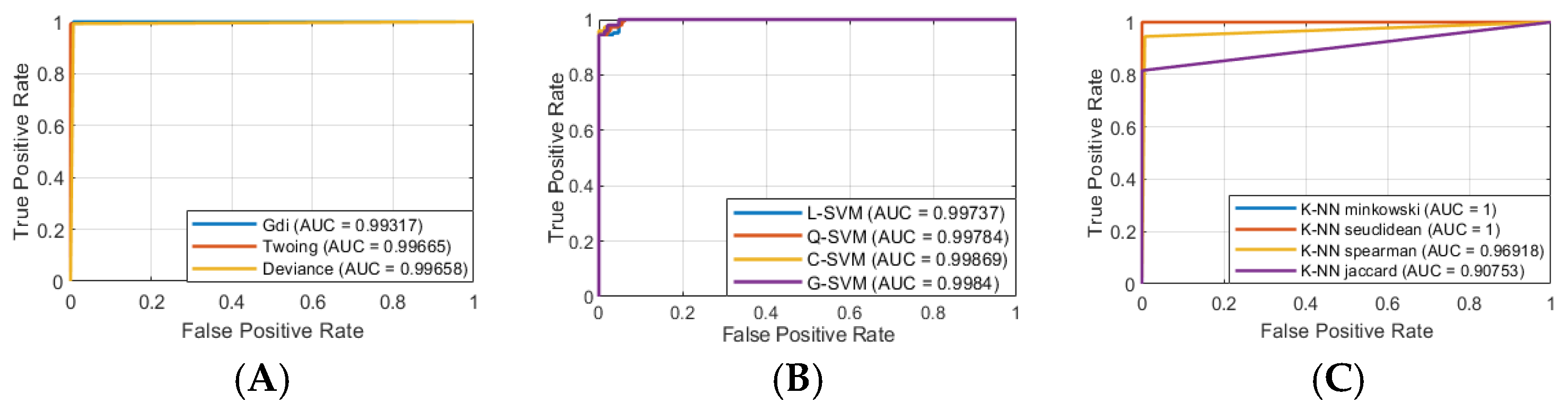
In this study, we tested twenty-three ML algorithms from the Classification Learner App (MATLAB R2023b):

(1)

Decision tree (Gini’s diversity index (Gdi), Twoing rule (Twoing), maximum deviance reduction (deviance));

(2)

Support vector machines (linear (L-SVM), quadratic (Q-SVM), cubic (C-SVM), and Gaussian (G-SVM));

(3)

Linear discriminant (LD);

(4)

Quadratic discriminant (QD);

(5)

K-nearest neighbors (Euclidean (K-NN Euclidean), cityblock (K-NN cityblock), chebychev (K-NN chebychev), cosine (K-NN cosine), correlation (K-NN correlation), minkowski (K-NN minkowski), seuclidean (K-NN seuclidean), spearman (K-NN spearman), jaccard (K-NN jaccard));

(6)

Efficient logistic regressions (average stochastic gradient descent (ELR asgd), stochastic gradient descent (ELR sgd), Broyden–Fletcher–Goldfarb–Shanno quasi-Newton algorithm (ELR bfgs), limited-memory BFGS (ELR lbfgs), sparse reconstruction by separable approximation (ELR sparsa)).

Each selected ML algorithm was trained and tested by using a proper database that was trial-wise and was randomly divided into balanced training and testing groups (80% and 20%) with the k-fold cross-validation (k = 5).

Hyperparameters used in the presented ML models were selected through a trial-and-error method (Table S1). All three models of decision trees (Gdi, Twoing, and Deviance) were implemented with a maximum of 100 splits without surrogate decision splits. All four models of support vector machines (L-SVM, Q-SVM, C-SVM, and G-SVM) were used with one box constraint level, auto kernel scale mode, and standardized data. All nine models of k-nearest neighbors (K-NN Euclidean, K-NN cityblock, K-NN chebychev, K-NN cosine, K-NN correlation, K-NN minkowski, K-NN seuclidean, K-NN spearman, K-NN jaccard) were implemented using one neighbor, equal distance weight, and standardized data. All five models of efficient logistic regressions (ELR asg, ELR sgd, ELR bfgs, ELR lbfgs, ELR sparsa) were implemented by using auto regularization strength (Lambda) and relative coefficient tolerance (Beta tolerance) of 0.0001.

To recognize motion patterns, we evaluated ML classification models by solving two main tasks:

(1)

Task A involved classifying between initial and target positions of the left arm in a supination stage (ASL), initial and target positions of the right arm in a supination stage (ASR), initial and target positions of the left arm in a neutral stage (ANL), and initial and target positions of the right arm in a neutral stage (ANR);

(2)

Task B involved classifying between supination and neutral stages of the left arm in an initial position (BSNLI), supination and neutral stages of the left arm in a target position (BSNLT), supination and neutral stages of the right arm in an initial position (BSNRI), and supination and neutral stages of the right arm in a target position (BSNRT).

These main tasks were solved in two steps. First, 23 classifiers were used to address the ASL and ASR tasks. Second, we analyzed the performance results of these tasks and selected the best 15 classifiers (Twoing, Deviance, Q-SVM, C-SVM, G-SVM, QD, K-NN Euclidean, K-NN cityblock, K-NN chebychev, K-NN cosine, K-NN minkowski, K-NN seuclidean, ELR bfgs, ELR lbfgs, ELR sparsa) to tackle the ANL and ANR tasks. Next, we used these 15 classifiers to solve the BSNLI, SNLT, BSNRI, and BSNRT tasks. To solve task A, we used prepared databases: (1) for supination stage, we used 1460 features (730/730) to address the ASR and ASL tasks; (2) for neutral stage, we applied random downsampling and used 1370 features (685/685) to solve the ANR and ANL tasks. To handle task B, we used prepared datasets: (1) 1415 features to solve BSNLI and BSNRI tasks; (2) 1455 features to solve BSNLT and BSNRT tasks.

3. Results

Results of binary classification models were evaluated using the following metrics: accuracy, recall (sensitivity), precision, and F1-score [50]. Accuracy (ACC) was defined by the following equation:

$$ACC={\displaystyle \frac{TPR+TNR}{TPR+FPR+TNR+FNR}}\times 100\%$$

(1)

where TPR is true positive rate; TNR is true negative rate; FPR is false positive rate; FNR is false negative rate.

The recall (SEN), the precision (PPV), and F1-score (F1) were calculated using the following relations (2), (3), and (4):

$$SEN={\displaystyle \frac{TPR}{TPR+FNR}}$$

(2)

$$PPV={\displaystyle \frac{TPR}{TPR+FPR}}$$

(3)

$$F_1={\displaystyle \frac{2·SEN·PPV}{SEN+PPV}}$$

(4)

In this paper, we presented the results of classification related to the following tasks:

(1)

For the ASL in

Table 1. Results of classification of the left arm in a supination stage (ASL task).

No.	Classifier	ACC [%]	PPV [−]	SEN [−]	F1 [−]
1.	Gdi	99.658	1.000	0.993	0.997
2.	Twoing	99.772	0.995	1.000	0.998
3.	Deviance	99.772	1.000	0.995	0.998
4.	L-SVM	100.000	1.000	1.000	1.000
5.	Q-SVM	100.000	1.000	1.000	1.000
6.	C-SVM	100.000	1.000	1.000	1.000
7.	G-SVM	100.000	1.000	1.000	1.000
8.	LD	95.662	0.997	0.916	0.955
9.	QD	98.744	0.976	1.000	0.988
10.	K-NN Euclidean	100.000	1.000	1.000	1.000
11.	K-NN cityblock	100.000	1.000	1.000	1.000
12.	K-NN chebychev	100.000	1.000	1.000	1.000
13.	K-NN cosine	100.000	1.000	1.000	1.000
14.	K-NN correlation	98.174	0.995	0.968	0.981
15.	K-NN minkowski	100.000	1.000	1.000	1.000
16.	K-NN seuclidean	100.000	1.000	1.000	1.000
17.	K-NN spearman	98.174	1.000	0.963	0.981
18.	K-NN jaccard	89.840	0.832	1.000	0.908
19.	ELR asgd	97.717	0.995	0.959	0.977
20.	ELR sgd	97.717	1.000	0.954	0.977
21.	ELR bfgs	100.000	1.000	1.000	1.000
22.	ELR lbfgs	100.000	1.000	1.000	1.000
23.	ELR sparsa	99.543	1.000	0.991	0.995

, Figure 9 and Figure S1 along with chosen confusion matrices in Figure 10, and chosen ROC curves in Figure 11 and Figure S13;

(2)

For the ASR in

Table 2. Results of classification of the right arm in a supination stage (ASR task).

No.	Classifier	ACC [%]	PPV [−]	SEN [−]	F1 [−]
1.	Gdi	99.315	0.993	0.993	0.993
2.	Twoing	99.886	1.000	0.998	0.999
3.	Deviance	99.886	0.998	1.000	0.999
4.	L-SVM	97.717	0.997	0.957	0.977
5.	Q-SVM	98.288	1.000	0.966	0.983
6.	C-SVM	98.288	1.000	0.966	0.983
7.	G-SVM	98.288	1.000	0.966	0.983
8.	LD	95.206	0.993	0.911	0.950
9.	QD	96.233	0.972	0.952	0.962
10.	K-NN Euclidean	99.658	1.000	0.993	0.997
11.	K-NN cityblock	100.000	1.000	1.000	1.000
12.	K-NN chebychev	99.658	1.000	0.993	0.997
13.	K-NN cosine	100.000	1.000	1.000	1.000
14.	K-NN correlation	96.918	1.000	0.938	0.968
15.	K-NN minkowski	100.000	1.000	1.000	1.000
16.	K-NN seuclidean	100.000	1.000	1.000	1.000
17.	K-NN spearman	97.603	1.000	0.952	0.975
18.	K-NN jaccard	90.753	1.000	0.815	0.898
19.	ELR asgd	96.233	1.000	0.925	0.961
20.	ELR sgd	96.233	1.000	0.925	0.961
21.	ELR bfgs	98.288	0.993	0.973	0.983
22.	ELR lbfgs	97.945	0.986	0.973	0.979
23.	ELR sparsa	98.630	1.000	0.973	0.986

, Figure 12 and Figure S2, along with chosen confusion matrices in Figure 13, and chosen ROC curves in Figure 14 and Figure S14;

(3)

For the ANL in

Table 3. Results of classification of the left arm in a neutral stage (ANL task).

No.	Classifier	ACC [%]	PPV [−]	SEN [−]	F1 [−]
1.	Twoing	99.635	0.998	0.995	0.996
2.	Deviance	99.392	0.993	0.995	0.994
3.	Q-SVM	99.513	0.995	0.995	0.995
4.	C-SVM	99.757	0.995	1.000	0.998
5.	G-SVM	99.757	0.995	1.000	0.998
6.	QD	97.445	0.992	0.956	0.974
7.	K-NN Euclidean	99.765	0.999	0.996	0.998
8.	K-NN cityblock	99.713	0.996	0.998	0.997
9.	K-NN chebychev	99.505	0.995	0.995	0.995
10.	K-NN cosine	99.140	0.997	0.985	0.991
11.	K-NN minkowski	99.530	0.992	0.998	0.995
12.	K-NN seuclidean	99.661	0.995	0.998	0.996
13.	ELR bfgs	98.297	0.990	0.976	0.983
14.	ELR lbfgs	98.054	0.990	0.971	0.980
15.	ELR sparsa	97.445	0.990	0.959	0.974

, Figure 15 and Figure S3 along with chosen confusion matrices in Figure 16, and chosen ROC curves in Figure 17 and Figure S15;

(4)

For the ANR in

Table 4. Results of classification of the right arm in a neutral stage (ANR task).

No.	Classifier	ACC [%]	PPV [−]	SEN [−]	F1 [−]
1.	Twoing	99.270	0.998	0.988	0.993
2.	Deviance	99.513	1.000	0.990	0.995
3.	Q-SVM	99.726	1.000	0.995	0.997
4.	C-SVM	99.635	0.998	0.995	0.996
5.	G-SVM	99.726	1.000	0.995	0.997
6.	QD	97.810	0.990	0.966	0.978
7.	K-NN Euclidean	99.392	0.990	0.998	0.994
8.	K-NN cityblock	99.392	0.990	0.998	0.994
9.	K-NN chebychev	99.148	1.000	0.983	0.991
10.	K-NN cosine	99.392	0.993	0.995	0.994
11.	K-NN minkowski	99.392	0.993	0.995	0.994
12.	K-NN seuclidean	99.757	0.998	0.998	0.998
13.	ELR bfgs	97.689	0.976	0.978	0.977
14.	ELR lbfgs	97.323	0.978	0.968	0.973
15.	ELR sparsa	96.959	0.978	0.961	0.969

, Figure 18 and Figure S4 along with chosen confusion matrices in Figure 19, and chosen ROC curves in Figure 20 and Figure S16;

(5)

For the BSNLI in

Table 5. Results of classification of supination and neutral stages of the left arm in an initial position (BSNLI task).

No.	Method	PPV [−]		SEN [−]		F1 [−]
		Mean	SD	Mean	SD	Mean	SD
1.	Twoing	0.922	0.018	0.935	0.018	0.928	0.011
2.	Deviance	0.927	0.021	0.924	0.020	0.925	0.015
3.	Q-SVM	0.807	0.019	0.818	0.031	0.812	0.021
4.	C-SVM	0.916	0.020	0.927	0.019	0.921	0.014
5.	G-SVM	0.896	0.018	0.813	0.027	0.852	0.017
6.	QD	0.549	0.057	0.210	0.033	0.304	0.041
7.	K-NN Euclidean	0.963	0.013	0.957	0.015	0.960	0.008
8.	K-NN cityblock	0.961	0.011	0.985	0.009	0.973	0.007
9.	K-NN chebychev	0.956	0.017	0.953	0.018	0.954	0.014
10.	K-NN cosine	0.961	0.014	0.963	0.015	0.962	0.009
11.	K-NN minkowski	0.958	0.015	0.974	0.014	0.966	0.009
12.	K-NN seuclidean	0.965	0.013	0.977	0.014	0.971	0.009
13.	ELR bfgs	0.622	0.038	0.493	0.037	0.549	0.034
14.	ELR lbfgs	0.615	0.035	0.470	0.044	0.532	0.038
15.	ELR sparsa	0.607	0.051	0.334	0.036	0.430	0.039

and Figure S5 along with chosen confusion matrices in Figure S9, chosen ROC curves in Figure 21A and Figure S17, and PR curves in Figure S21;

(6)

For the BSNLT in

Table 6. Results of classification of supination and neutral stages of the left arm in a target position (BSNLT task).

No.	Method	PPV [−]		SEN [−]		F1 [−]
		Mean	SD	Mean	SD	Mean	SD
1.	Twoing	0.951	0.015	0.935	0.02	0.943	0.013
2.	Deviance	0.959	0.013	0.958	0.016	0.958	0.01
3.	Q-SVM	0.905	0.021	0.823	0.024	0.862	0.016
4.	C-SVM	0.970	0.014	0.919	0.024	0.944	0.015
5.	G-SVM	0.966	0.014	0.897	0.023	0.930	0.013
6.	QD	0.821	0.039	0.508	0.036	0.627	0.03
7.	K-NN Euclidean	0.996	0.004	0.990	0.006	0.993	0.004
8.	K-NN cityblock	0.998	0.003	0.986	0.008	0.992	0.004
9.	K-NN chebychev	0.973	0.013	0.960	0.016	0.966	0.011
10.	K-NN cosine	0.970	0.014	0.969	0.012	0.969	0.011
11.	K-NN minkowski	0.992	0.005	0.992	0.006	0.992	0.004
12.	K-NN seuclidean	0.994	0.006	0.997	0.005	0.996	0.005
13.	ELR bfgs	0.803	0.024	0.761	0.031	0.781	0.022
14.	ELR lbfgs	0.816	0.026	0.756	0.029	0.785	0.022
15.	ELR sparsa	0.793	0.028	0.744	0.035	0.767	0.027

and Figure S6 along with chosen confusion matrices in Figure S10, chosen ROC curves in Figure 21B and Figure S18, and PR curves in Figure S22;

(7)

For the BSNRI in

Table 7. Results of classification of supination and neutral stages of the right arm in an initial position (BSNRI task).

No.	Method	PPV [−]		SEN [−]		F1 [−]
		Mean	SD	Mean	SD	Mean	SD
1.	Twoing	0.924	0.015	0.919	0.022	0.921	0.013
2.	Deviance	0.934	0.015	0.931	0.016	0.932	0.013
3.	Q-SVM	0.801	0.028	0.811	0.027	0.806	0.023
4.	C-SVM	0.917	0.020	0.941	0.016	0.928	0.014
5.	G-SVM	0.887	0.017	0.906	0.024	0.897	0.018
6.	QD	0.548	0.060	0.199	0.031	0.291	0.040
7.	K-NN Euclidean	0.967	0.015	0.973	0.012	0.970	0.009
8.	K-NN cityblock	0.964	0.015	0.968	0.012	0.966	0.008
9.	K-NN chebychev	0.940	0.015	0.933	0.019	0.936	0.011
10.	K-NN cosine	0.936	0.017	0.950	0.015	0.943	0.012
11.	K-NN minkowski	0.957	0.011	0.956	0.013	0.957	0.010
12.	K-NN seuclidean	0.946	0.013	0.972	0.011	0.959	0.007
13.	ELR bfgs	0.563	0.038	0.313	0.034	0.402	0.035
14.	ELR lbfgs	0.608	0.047	0.350	0.029	0.444	0.033
15.	ELR sparsa	0.574	0.057	0.219	0.031	0.316	0.037

and Figure S7 along with chosen confusion matrices in Figure S11, chosen ROC curves in Figure 21C and Figure S19, and PR curves in Figure S23;

(8)

For the BSNRT in

Table 8. Results of classification of supination and neutral stages of the right arm in a target position (BSNRT task).

No.	Method	PPV [−]		SEN [−]		F1 [−]
		Mean	SD	Mean	SD	Mean	SD
1.	Twoing	0.944	0.017	0.923	0.021	0.933	0.015
2.	Deviance	0.932	0.020	0.936	0.018	0.934	0.015
3.	Q-SVM	0.861	0.019	0.906	0.027	0.882	0.017
4.	C-SVM	0.939	0.019	0.947	0.017	0.943	0.014
5.	G-SVM	0.972	0.014	0.939	0.016	0.955	0.011
6.	QD	0.667	0.023	0.730	0.030	0.697	0.023
7.	K-NN Euclidean	0.991	0.006	0.986	0.010	0.989	0.006
8.	K-NN cityblock	0.995	0.005	0.977	0.011	0.986	0.006
9.	K-NN chebychev	0.966	0.013	0.964	0.014	0.965	0.008
10.	K-NN cosine	0.969	0.015	0.977	0.016	0.973	0.012
11.	K-NN minkowski	0.990	0.008	0.982	0.010	0.986	0.007
12.	K-NN seuclidean	0.988	0.007	0.982	0.009	0.985	0.006
13.	ELR bfgs	0.723	0.029	0.758	0.029	0.740	0.024
14.	ELR lbfgs	0.718	0.020	0.759	0.027	0.737	0.016
15.	ELR sparsa	0.715	0.028	0.731	0.040	0.723	0.031

and Figure S8 along with chosen confusion matrices in Figure S12, chosen ROC curves in Figure 21D and Figure S20, and PR curves in Figure S24.

Results of classification (ACC, SEN, PPV, F1) of task A (ASL, ASR, ANL, ANR) are presented as an average by assuming that a target position was treated as a true rate, whereas an initial position was treated as a negative rate. Furthermore, results of classification (SEN, PPV, F1) of task B are presented as an average by assuming the following: (1) a target position of neutral stage was treated as true rate, whereas a target position of supination stage was treated as negative rate for tasks BSNLT and BSNRT; (2) an initial position of neutral stage was treated as true rate, whereas an initial position of supination stage was treated as negative rate for tasks BSNLI and BSNRI.

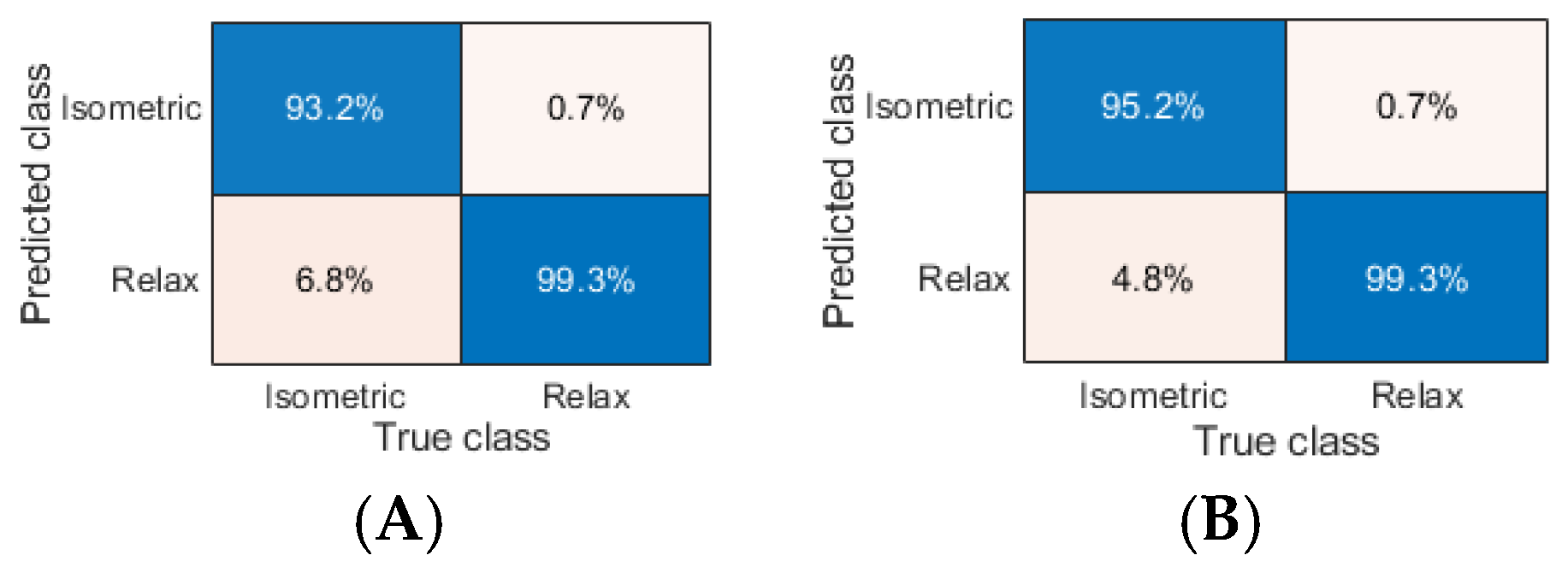
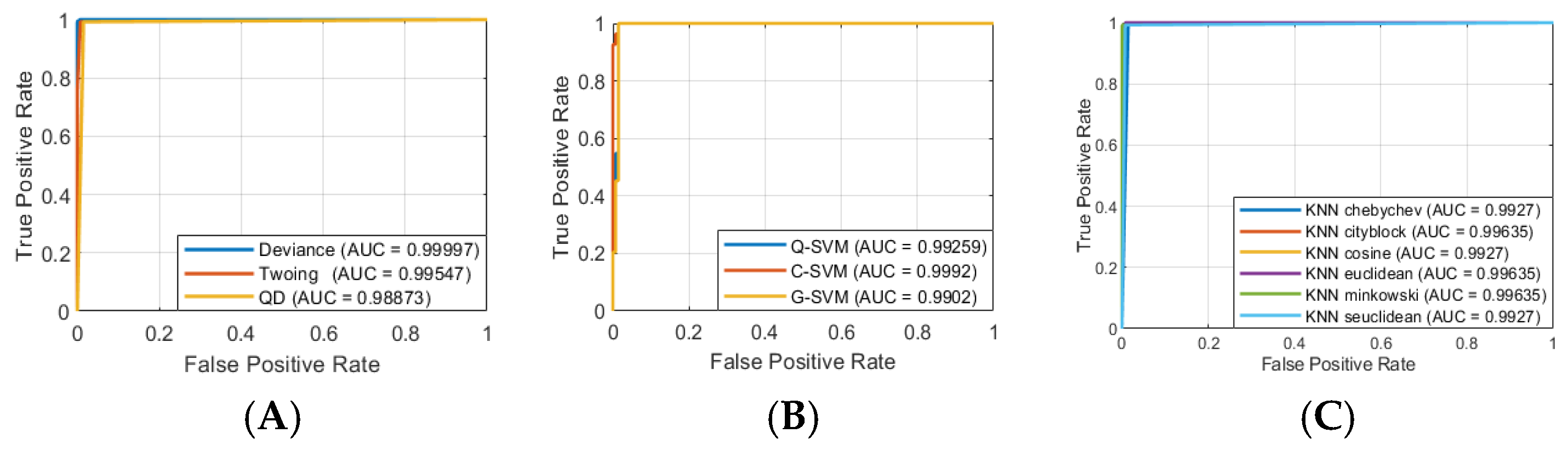
Considering the results of the ASL task, we identified the ML models that split sEMG data with the highest performance related to the following:

(1)

ACC of 100% along with F1 of 1.000 (L-SVM, Q-SVM, C-SVM, G-SVM, K-NN Euclidean, K-NN cityblock, K-NN chebychev, K-NN cosine, K-NN minkowski, K-NN seuclidean, ELR bfgs, and ELR lbfgs, respectively);

(2)

ACC of 99.772% (Twoing and Deviance), 99.658% (Gdi), and 99.543% (ELR sparsa);

(3)

F1 of 0.998 (Twoing and Deviance), 0.997 (Gdi), and 0.995 (ELR sparsa).

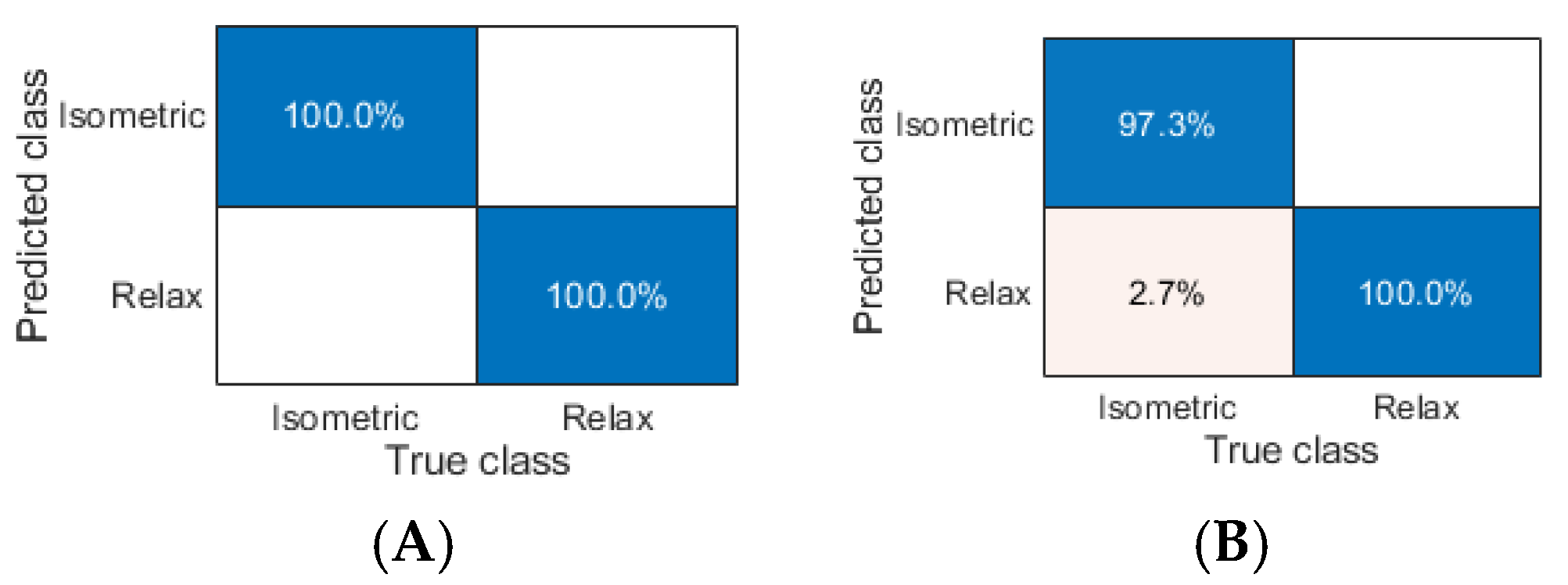
Analyzing the results of the ASR task, we found the following ML models that classified sEMG data with the highest metrics:

(1)

ACC of 100% along with F1 equaled 1.000 (K-NN cityblock, K-NN cosine, K-NN minkowski, and K-NN seuclidean, respectively);

(2)

ACC of 99.886% (Twoing and Deviance), 99.658% (K-NN Euclidean and K-NN chebychev), and 99.315% (Gdi);

(3)

F1 of 0.999 (Twoing and Deviance), 0.997 (K-NN Euclidean and K-NN chebychev), and 0.993 (Gdi).

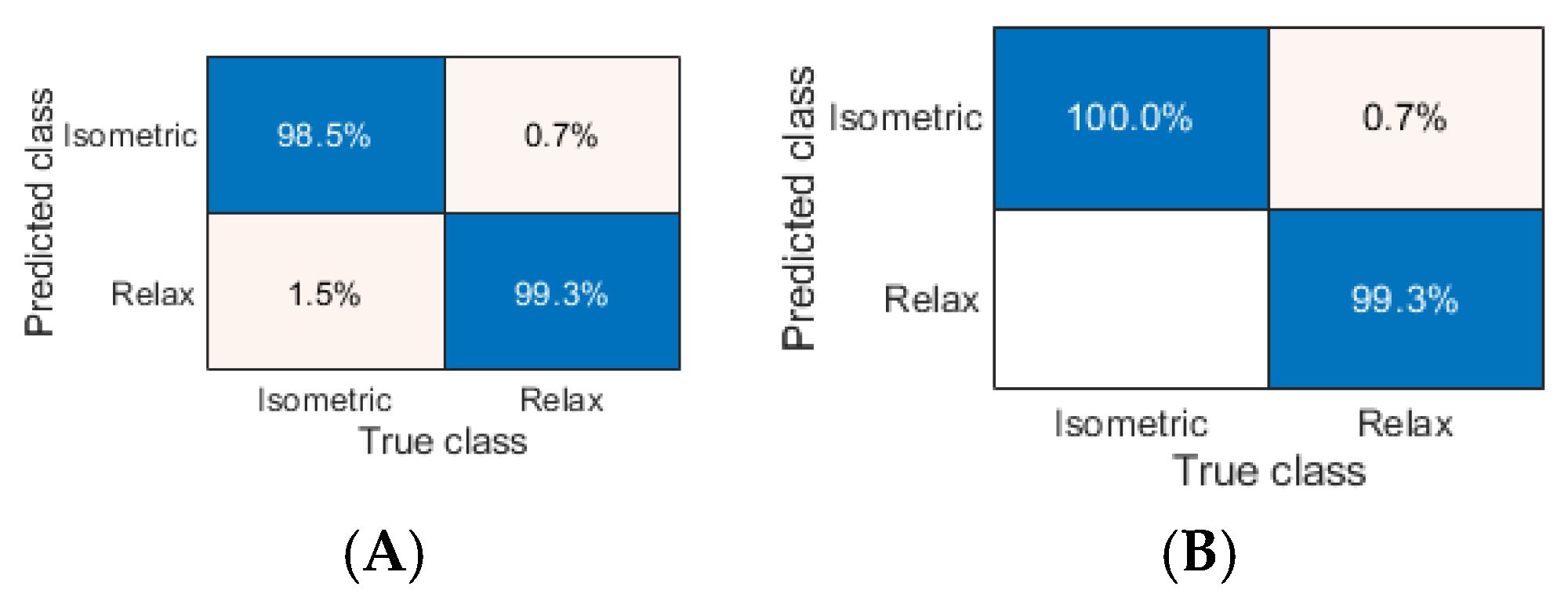
Next, we considered results of the classification of the ANL task and identified the following ML models that split sEMG data with the highest performance:

(1)

ACC of 99.765% (K-NN Euclidean);

(2)

ACC of 99.757% (C-SVM and G-SVM), 99.713% (K-NN cityblock), and 99.661% (K-NN seuclidean);

(3)

F1 of 0.998 (C-SVM, G-SVM and K-NN Euclidean);

(4)

F1 of 0.997 (K-NN cityblock), 0.996 (Twoing and K-NN seuclidean), and 0.995 (Q-SVM, K-NN chebychev, K-NN minkowski).

After this, we analyzed the results of the classification of the ANR task and identified the following ML models that separated sEMG data with the highest metric:

(1)

ACC of 99.757% along F1 equaled 0.998 (K-NN seuclidean);

(2)

ACC of 99.726% (Q-SVM and G-SVM), 99.635% (C-SVM), and 99.513% (Deviance);

(3)

F1 of 0.997 (Q-SVM and G-SVM), 0.996 (C-SVM), and 0.995 (Deviance).

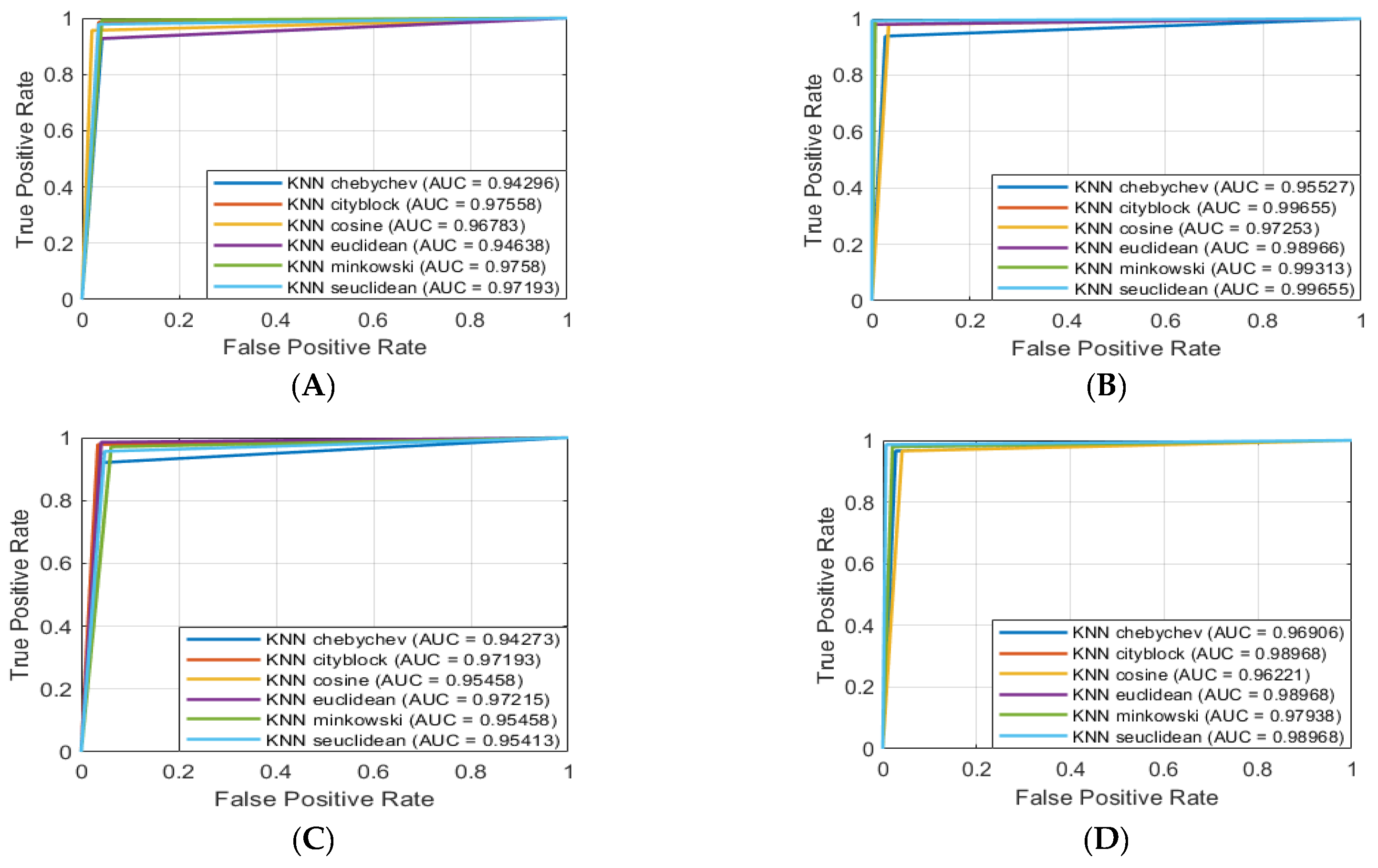
Considering results of the BSNLI task, we identified the following ML models that divide the sEMG data with the highest performance:

(1)

F1 of 0.973 (K-NN cityblock);

(2)

F1 of 0.971 (K-NN seuclidean), 0.966 (K-NN minkowski), and 0.962 (K-NN cosine).

Analyzing results of the BSNLT tasks, we identified the following ML models that separated sEMG data with the highest metrics:

(1)

F1 of 0.996 (K-NN seuclidean);

(2)

F1 of 0.993 (K-NN Euclidean), 0.992 (K-NN minkowski and K-NN cityblock), and 0.969 (K-NN cosine).

Next, we considered results of the classification of the BSNRI tasks and identified the following ML models that split the sEMG data with the highest performance:

(1)

F1 of 0.970 (K-NN Euclidean);

(2)

F1 of 0.966 (K-NN cityblock), 0.959 (K-NN seuclidean), and 0.957 (K-NN minkowski).

After this, we analyzed the results of classification of the BSNRT tasks and identified the following ML models that split the sEMG data with the highest metrics:

(1)

F1 of 0.989 (K-NN Euclidean);

(2)

F1 of 0.986 (K-NN cityblock and K-NN minkowski), 0.985 (K-NN seuclidean), and 0.973 (K-NN cosine).

Considering the best results of B tasks (BSNLI, BSNLT, BSNRI, BSNRT), we identified three models that have the best classification performances in each B task: K-NN cityblock, K-NN minkowski, K-NN seuclidean. Aiming to define whether these models could be alternatively used in practice, we identified statistically significant differences in results of these models by applying the following methods: (1) for results with a normal distribution we used the analysis of variance (one-way ANOVA) (ANOVA) with Tukey HSD post hoc test; (2) for results with a non-normal distribution, we used the Kruskal–Wallis ANOVA test (non-parametric one-way ANOVA) (Kruskal) with Dunnett’s post hoc test. To define a normal distribution requirement, we used the Shapiro–Wilk test. We assumed statistically significant threshold p (p ≤ 0.05) and used Bonferroni correction in tests. Considering F1 score results, we put the results of analysis in

Table 9. Results of analysis of variances (+++ statistically significant differences).

Task B	F1	K-NN Cityblock and K-NN Minkowski	K-NN Minkowski and K-NN Seuclidean	K-NN Seuclidean and K-NN CITYBLOCK
BSNLI	ANOVA (p ≤ 0.007) +post hoc	-	+++	+++
BSNLT	Kruskal (p ≤ 0.0001) +post hoc	-	+++	+++
BSNRI	Kruskal (p ≤ 0.0055) +post hoc	+++	-	+++
BSNRT	ANOVA	-	-	-

. It is important to note that the results of models BSNLI, BSNLT, BSNRI have statistically significant differences, whereas the results of model BSNRT do not show any statistically significant differences.

4. Discussion

In the scope of this study, we applied supervised classification algorithms [51] and tested chosen ML classifiers (decision trees, support vector machines, linear discriminant, quadratic discriminant, k-nearest neighbors, efficient logistic regressions) to recognize motion patterns by classifying time series features extracted from processed EMG data that were acquired from eight superficial muscles of both upper limbs while performing given physical activities. We only focused on the time domain of features composed of EMG patterns. We explored 23 ML classifier models to split the features obtained from a supination stage. Next, among these models, we identified the best 15 models (with the highest performance) to classify the features obtained from a neutral stage. After this, we applied these 15 models to classify data merged from both the supination and neutral stages. All ML models were trained and tested by using a database obtained from healthy subjects without division by sex (59% male and 41% female).

Analyzing all results of classifications of task A (ASL, ASR, ANL, ANR), we identified the following ML models that classified sEMG data with the highest performance (Table 1, Table 2, Table 3 and Table 4):

(1)

ACC for the left arm in a supination stage (ACC range of [99.543%; 100.000%]): L-SVM, Q-SVM, C-SVM, G-SVM, K-NN Euclidean, K-NN cityblock, K-NN chebychev, K-NN cosine, K-NN minkowski, K-NN seuclidean, ELR bfgs, ELR lbfgs, Twoing, Deviance, Gdi and ELR sparsa (Table 1);

(2)

ACC for the right arm in a supination stage (ACC range of [99.315%; 100.000%]): K-NN cityblock, K-NN cosine, K-NN minkowski, K-NN seuclidean, Twoing, Deviance, K-NN Euclidean, K-NN chebychev and Gdi (Table 2);

(3)

ACC for the left arm in a neutral stage (ACC range of [99.713%; 99.661%]): K-NN Euclidean, C-SVM, G-SVM, K-NN cityblock and K-NN seuclidean (Table 3);

(4)

ACC for the right arm in a neutral stage (ACC range of [99.635; 99.513]%): K-NN seuclidean, Q-SVM, G-SVM, C-SVM and Deviance (Table 4);

(5)

F1 for the left arm in a supination stage (F1 range of [0.995; 1.000]): L-SVM, Q-SVM, C-SVM, G-SVM, K-NN Euclidean, K-NN cityblock, K-NN chebychev, K-NN cosine, K-NN; minkowski, K-NN seuclidean, ELR bfgs, ELR lbfgs, Twoing Deviance, Gdi and ELR sparsa (Table 1);

(6)

F1 for the right arm in a supination stage (F1 range of [0.993; 1.000]): K-NN cityblock, K-NN cosine, K-NN minkowski, K-NN seuclidean, Twoing, Deviance, K-NN Euclidean, K-NN chebychev and Gdi (Table 2);

(7)

F1 for the left arm in a neutral stage (F1 range of [0.995; 0.998]): C-SVM, G-SVM, K-NN Euclidean, K-NN cityblock, Twoing, K-NN seuclidean, Q-SVM, K-NN chebychev and K-NN minkowski (Table 3);

(8)

F1 for the right arm in a neutral stage (F1 range of [0.995; 0.998]): K-NN seuclidean, Q-SVM, G-SVM, C-SVM and Deviance (Table 4).

Considering the results of classification of Task A in a supination stage, we identified the following ML models that separated sEMG data with the highest performance for both limbs: (a) four models (K-NN cityblock, K-NN cosine, K-NN minkowski, and K-NN seuclidean) that classified data with the highest performance (ACC = 100%, F1 = 1.000, PPV = 1.000, and SEN = 1.000); (b) five models (Twoing, Deviance, Gdi, K-NN Euclidean, and K-NN chebychev) that classified data with ACC ≥ 99.658% along with F1 ≥ 0.997 for the left arm, and ACC ≥ 99.315% along with F1 ≥ 0.993 for the right arm. Furthermore, analyzing the results of classification of Task A in a neutral stage, we found the following ML models that separated sEMG data with the highest performance for both limbs: (1) K-NN seuclidean (for the left arm with ACC = 99.661% along with F1= 0.996; for the right arm with ACC = 99.757% along with F1 = 0.998); (2) G-SVM and C-SVM (for the left arm with ACC = 99.757% along with F1 = 0.998; for the right arm with ACC ≥ 99.635% along with F1 ≥ 0.996).

Analyzing all results of classification of Task B (BSNLT, BSNRT, BSNLI, BSNRI), which used data merged from supination and neutral stages, we identified the following ML models with the best performance that can be used (Table 5, Table 6, Table 7 and Table 8):

(1)

To identify a target position in neutral and supination stage for both limbs (BSNLT and BSNRT): K-NN seuclidean (for the right/left arm F1 equals 0.985/0.996), K-NN Euclidean (for the right/left arm F1 equals 0.989/0.993), K-NN minkowski (for the right/left arm F1 equals 0.986/0.992), and K-NN cityblock (for the right/left arm F1 equals 0.986/0.992) (Table 6 and Table 8);

(2)

To identify an initial position in neutral and supination stage for both limbs (BSNLI and BSNRI): K-NN cityblock (for the right/left arm F1 equals 0.966/0.973), K-NN seuclidean (for the right/left arm F1 equals 0.959/0.971), and K-NN minkowski (for the right/left arm F1 equals 0.957/0.966) (Table 5 and Table 7);

(3)

To identify an initial or target position in neutral along with supination stage for the left limb: K-NN cityblock (for initial/target position F1 equals 0.973/0.992), K-NN seuclidean (for initial/target position F1 equals 0.971/0.996), K-NN minkowski (for initial/target position F1 equals 0.966/0.992), K-NN cosine (for initial/target position F1 equals 0.962/0.969) (Table 5 and Table 6);

(4)

To identify an initial or target position in neutral along with supination stage for the right limb: K-NN Euclidean (for initial/target position F1 equals 0.970/0.989), K-NN cityblock (for initial/target position F1 equals 0.966/0.986), K-NN seuclidean (for initial/target position F1 equals 0.959/0.985), K-NN minkowski (for initial/target position F1 equals 0.957/0.986) (Table 7 and Table 8).

Moreover, analyzing all presented findings related to the tasks B along with results of analysis of variance (Table 9), we identified that one can use K-NN cityblock or K-NN minkowski to classify data related to the BSNLI and BSNLT task. With respect to the right upper limb we found the following: (1) to handle the BSNRI task one can apply K-NN minkowski or K-NN seuclidean; (2) to tackle the BSNRT task, one can apply K-NN cityblock or K-NN seuclidean, or K-NN minkowski.

Additionally, we performed MonteCarlo experiments for the best models of task A and task B and put the results in Tables S2–S6. Results related to the tasks A (Table S2) are very close to the ones presented in Table 1, Table 2, Table 3 and Table 4. This similarity can be related to the different muscle activities occurring in the initial and target position of each upper limb. However, results related to the best models of tasks B show following differences: (1) smaller ones for BSNLT models (Table 6 vs. Table S4) and BSNRT models (Table 8 vs. Table S6); (2) higher ones for BSNLI models (Table 5 vs. Table S3) and BSNRI models (Table 7 vs. Table S5). These findings can be related to the physiology of tested muscles, especially to the compositions of time series EMG data that are dependent on the configuration of the forearm with respect to the arm along with influence of gravity force and maintaining external load.

In

Table 10. Results of classification reported in the literature.

Article	Algorithm/Type of Classification	ACC [%]	PPV [%]	SEN [%]	F1 [%]
[6]	SVM RBF/multi	90.69	-	62.10	-
[27]	K-NN/multi	99.23	98.47	98.45	98.46
[30]	CNN and Bi-LSTM/multi	98.33	-	-
[33]	BP-LSTM/multi	92.00	91.00	-	96.00
[37]	RF + SVM/binary	99.70	-	-	99.70
[43]	K-NN/multi	94.00	-	-	-
[47]	SVM/multi	83.21	-	-	-
[48]	K-NN/multi	99.50	-	99.60 and 98.80	-
[49]	SVM Cubic/multi	95.83	96.09	-	95.86
[51]	HGS-SCNN/multi	99.44	-	-	99.44
[52]	ResNet-50/multi	94.41	-	-	95.96

, we present the best results reported in the literature. We found that our results are consistent with those presented in the literature. However, to the authors knowledge, our results are related to the novel protocol of testing and they pertain to binary classification. Moreover, there are some specific factors that have a huge impact on classification results: (1) examined limb movement with used external loading; (2) examined muscles along with the type of EMG sensors used for data acquisition, especially the sampling frequency; (3) composition of sEMG patterns’ features; (4) data processing algorithm; (5) ML algorithm used for classification. That is why it is not possible to directly compare our results with published ones. Regarding the K-NN models used for classification, three papers [28,46,52] report high accuracy results: (a) forearm-hand activities based on sEMG data [28]; (b) hand motions based on sEMG features [46]; (c) types of neuromuscular disorder based on needle EMG data [52]. Furthermore, high-performance results of classification obtained with SVM models based on sEMG data are described in [6] (eight hand movements), [51] (six categories of motion), [53] (seven hand gestures). Also, the paper [39] presents high-performance results of classification of neuromuscular disorders by using the SVM-RF model and needle EMG data. Moreover, high-performance results of classification obtained with ANN models are described in [23,54] or with more complex neural network architectures: (1) the EMGHandNet model composed of CNN and Bi-LSTM architecture [31]; (2) the HGS-SCNN model by using sEMG transformed to images ((1-D) CNN) [55]; (3); the ResNet-50 model pre-trained (ImageNet) [56]; (4) the BP (back-propagation)—LSTM model [35]. Additionally, there are studies reporting classification accuracy obtained with application of different ML algorithms, e.g., [23] presents accuracy results of 95.02% (LDA), 94.63% (SVM), 90.05% (kNN), and 86.66% (DT). However, these results are related to the multiclassification of the upper limb motion that is different with respect to the motions tested in our study.

Considering the findings presented in this study, we conclude that different ML models should be used to classify muscle activity of the right and left upper limbs in supination stage and in neutral stage. This conclusion is agreed with the physiology of the muscular system. First, upper limb dominance influences muscular activity patterns. Second, tested muscles are differently activated in tested forearm positions (stages), because musculoskeletal configurations of the upper limb segments (arm, forearm, and hand) are different in supination and neutral forearm configuration with respect to the gravity force. Moreover, the muscular system is a redundant one, and muscles work in groups according to habituated neurological and motor patterns. That is why different configurations of the skeletal system require different neurological and motor patterns. Furthermore, these patterns depend on the subject’s anthropometric proportions, biomechanical characteristics, limb dominance, and the degree of familiarity with motions tested in this study (i.e., agility acquired through previous physical activities like sport, playing musical instruments, or dance). Moreover, a study [31] declares that results of classification of subject-wise data are higher compared to the aggregate data. All these factors should be considered as a reason that originated from the inter- and intra-differences in muscle activity.

From a practical perspective, the best ML models identified in this study can be used to help clinicians identify activity states of tested muscles, for example, in rehabilitation of neuromuscular disorders, and application in ergonomics or military areas, especially when using an external passive or active device [57].

The limitations of this study are as follows. First, in this study, we did not use multiclassification models or more complex models composed of ensembles of ML classifiers or deep learning models. Second, this paper does not cover the results of pronation forearm configuration.

5. Conclusions

The aim of this preliminary study was to recognize motion patterns by classifying time series features extracted from electromyography (EMG) data of the upper limb muscles. To reach this goal, we identified ML methods of supervised classification that could be used to recognize the states of tested muscles based on surface EMG data. In this study, we only focused on two stages of the forearm (supination and neutral) related to initial and target positions. We evaluated six main ML classifiers: decision trees (Gdi, Twoing, Deviance), support vector machines (L-SVM, Q-SVM, C-SVM and G -SVM), linear discriminant (LD), quadratic discriminant (QD), k-nearest neighbors (K-NN Euclidean, K-NN city block, K-NN, K-NN cosine, K-NN correlation, K-NN minkowski, K-NN seuclidean, K-NN spearman, K-NN jaccard), and efficient logistic regressions (ELR asgd, ELR sgd, ELR bfgs, ELR lbfgs, ELR sparsa). To the authors’ knowledge, the results presented in this study are new ones with respect to the tested motions and tested muscles along with the feature compositions used for classification.

In this study, we present solutions for binary classification tasks that were trained and tested by using our own four datasets. Analyzing all classification results of task A, we identified the following high-performance ML models that can be used to split the sEMG data to recognize a target or initial position for both limbs:

(1)

In supination stage—six k-nearest neighbors’ models (K-NN cityblock, K-NN cosine, K-NN minkowski, and K-NN seuclidean, K-NN Euclidean and K-NN chebychev) and three decision tree models (Twoing, Deviance, Gdi);

(2)

In neutral stage—one k-nearest neighbors’ model (K-NN seuclidean) and two SVM models (G-SVM and C-SVM).

(3)

Analyzing classifications results of task B, we found the following:

(4)

For both limbs, four K-nearest neighbors’ models (K-NN seuclidean, K-NN Euclidean, K-NN minkowski, K-NN cityblock) can be applied to split the sEMG data into neutral or supination stage in target position;

(5)

For both limbs three k-nearest neighbors’ models (K-NN cityblock, K-NN seuclidean, K-NN minkowski) can be applied to split the sEMG data into neutral or supination stage in initial position;

(6)

For the left limb four k-nearest neighbors’ models (K-NN cityblock, K-NN seuclidean, K-NN minkowski, K-NN cosine) can be used to divide sEMG data related to initial or target position in neutral or supination stage;

(7)

For the right limb four k-nearest neighbors’ models (K-NN Euclidean, K-NN cityblock, K-NN seuclidean, K-NN minkowski) can be used to divide sEMG data related to initial or target position in neutral or supination stage.

Moreover, analyzing all results of tasks solved in this study, we found that to classify data with the highest performance one can apply the following:

(1)

K-NN seuclidean model in all A tasks;

(2)

K-NN cityblock and K-NN minkowski models for the left limb in initial or target position (BSNLI and BSNLT tasks);

(3)

K-NN minkowski and K-NN seuclidean models for the right limb in initial position (BSNRI task);

(4)

K-NN cityblock or K-NN minkowski or K-NN seuclidean models for the right limb in target position (BSNRT task).

In this study, a pattern classification was performed by considering features composed of four EMG patterns recorded on each upper limb. Each EMG pattern is a time series of post-processed sEMG data. An application of such features has clinical and biomechanical reasons, because muscles are functioning in groups. Moreover, sEMG data are irregular, complex physiological signals that reflect muscle activation being a time–spatial summation of motor units. That is why postprocessing of these data should be properly conducted along with data denoising.

It is worth noting that we cannot point out only one model of classification, which is able to split sEMG data with the highest results of ACC and/or F1 metrics for both arms in supination and neutral stages to recognize the tested positions (target or initial). We recommend using different ML models to accurately identify muscle activity of the left and right upper limbs. Applying ML classification models, one can discriminate and/or classify EMG data (or recognize EMG patterns) to diagnose different musculoskeletal disorders (e.g., Duchenne muscular dystrophy, stroke, or aging), to monitor the progress of the disorder or rehabilitation strategy, especially in evaluating a progress of functional recovery in applied rehabilitation or a somatosensory rehabilitation program, to control the functioning of wearable robotics devices or external prosthetic devices or other external devices (e.g., an exoskeleton) through setting the proper mode of function (assistance or guidance mode). Additionally, the tested ML algorithms could be applied to control human–robot interactions in industrial digital production or digital twin applications. Moreover, it is worth noting that the classification toolboxes that were used in this study are working in a very fast way, which is crucial for real-time controlling.

Future research encompasses the following: (1) elaborating and publishing the external sEMG dataset of a healthy population; (2) classifying results in pronation forearm configuration and more complex motions used in activities of daily living; (3) testing more complex models composed of ensembles of ML classifiers and/or deep learning models to determine whether these complex models are more effective than those used in this study.