Fatigue Life Prediction and Reliability Analysis of Reinforced Concrete Bridge Decks Based on an XFEM–ANN–Monte Carlo Hybrid Framework

Abstract

This study proposes a hybrid computational framework that integrates the Extended Finite Element Method (XFEM), Artificial Neural Network (ANN), and Monte Carlo simulation to evaluate the fatigue crack propagation and reliability of reinforced concrete (RC) bridge decks. First, XFEM was employed to simulate crack initiation and propagation under cyclic loading based on the statistical distributions of the Paris law parameters C and m. The fatigue life data generated from these simulations were used to train a multilayer feedforward ANN optimized with the Adam algorithm and the ReLU activation function. The trained network achieved a high prediction accuracy (R² = 0.99, MAPE = 0.977%) and demonstrated strong generalization capability for predicting the XFEM-derived fatigue life. Subsequently, 10,000 Monte Carlo samples of C and m were analyzed using the trained ANN to perform probabilistic fatigue life assessment. The results revealed a nonlinear degradation pattern in reliability: the structural reliability remained high at low fatigue cycles but decreased sharply once a critical threshold of approximately 1.45 × 10⁹ cycles was reached. When actual bridge traffic was considered, the deck maintained a reliability of 0.99 after 23 years and 0.95 after 67 years of service. Compared with the XFEM, the ANN-based prediction improved computational efficiency by more than 10⁴ times while maintaining satisfactory accuracy. The proposed hybrid framework effectively combines deterministic simulation, probabilistic analysis, and data-driven modeling, providing a rapid and reliable approach for predicting fatigue life and evaluating the reliability of concrete bridge structures.

1. Introduction

Bridges are essential components of transportation infrastructure, and their long-term service performance is strongly influenced by the fatigue behavior of reinforced concrete (RC) bridge decks subjected to millions of vehicle load cycles. Under repeated loading, microcracks in the tensile zone gradually coalesce into visible fatigue cracks, resulting in stiffness degradation, corrosion initiation, and a decline in load-bearing capacity [1,2,3,4]. Accurately predicting fatigue life and reliability is thus essential for the safety and durability of existing bridge structures.

Traditional fatigue assessment methods, including the S–N curve approach and Miner’s linear cumulative damage rule, have been widely used in engineering design due to their simplicity. However, these empirical methods fail to account for the nonlinear, stochastic, and scale-dependent nature of concrete fatigue behavior [5,6,7]. Moreover, they cannot capture the influence of random material heterogeneity, stress redistribution, and multi-axial stress states, which are common in real bridge decks [8,9].

To address these limitations, advanced numerical simulation methods have been developed to analyze the propagation of fatigue cracks in RC components. Among them, the Extended Finite Element Method (XFEM) allows crack growth modeling without remeshing and provides an effective means to capture crack initiation and propagation in quasi-brittle materials [10]. Moës et al. [11] developed a finite element method that models crack growth without remeshing. This work laid the foundation for the later XFEM. Jin et al. [12] developed a coupled XFEM–Continuum Damage Mechanics (CDM) model for asphalt concrete, which accurately reproduced the fatigue crack growth and stiffness reduction observed in semicircular bending and three-point bending tests. Gontarz et al. [13] developed an XFEM-based algorithm in Abaqus for predicting crack paths in concrete-like composites. Numerical simulations of three-point bending tests showed cracks bypassing aggregate grains under various configurations. These studies have verified XFEM’s ability to reproduce crack growth paths and stress intensity evolution in concrete. Nevertheless, direct XFEM-based fatigue analysis remains computationally intensive and highly sensitive to uncertain parameters such as the tensile strength, fracture energy, and the Paris law constants C and m [14,15,16]. Chen et al. [17] analyzed fatigue crack growth in self-compacting concrete based on Paris’ law, showing that the fitted parameters C and m change with loading frequency and stress level. Miarka et al. [18] proposed a method linking S–N curves to Paris’ law and found that the empirical constants C and m change with the applied stress level across different concrete mixtures.

In the field of stochastic fatigue modeling, probabilistic approaches, notably the Monte Carlo simulation, have been employed to quantify the randomness of material and loading parameters [19]. Llanos et al. [20] applied the Monte Carlo method using OpenSeesPy to evaluate flexural demand in RC beams under vertical loads. Félix et al. [21] integrated carbonation and chloride diffusion models with the Monte Carlo method to estimate the probability of reinforcement depassivation in RC structures. These studies improved the interpretability of fatigue life predictions but often required thousands of repeated deterministic analyses, making them computationally prohibitive. To mitigate this challenge, data-driven surrogate models, such as artificial neural networks (ANNs), have been increasingly utilized to approximate complex fatigue behavior with reduced computational requirements. Shi et al. [22] developed an ANN-based model for predicting concrete fatigue life, in which a group random-weighted dynamic time warping barycentric averaging (GRW-DBA) method was applied to augment limited fatigue datasets and improve model accuracy. Lunardi et al. [23] developed a hybrid machine learning model combining ANN, random forests (RFs), and support vector regression (SVR) to predict concrete fatigue life, highlighting the effects of stress ratio and loading frequency. However, most existing ANN models rely on purely empirical datasets and lack integration with physics-based methods, which limits their reliability under parameter uncertainty [24].

In summary, the fatigue degradation of concrete bridge decks involves multiple sources of uncertainty, including material randomness, variations in cyclic loading, and complex crack propagation behavior. To address these challenges, this study develops a hybrid probabilistic learning framework that integrates the physical modeling capability of the XFEM, the uncertainty quantification of the Monte Carlo simulation, and the computational efficiency of ANNs. The proposed framework enables accurate fatigue life prediction and reliability evaluation under stochastic material parameters while markedly improving computational efficiency compared with conventional numerical simulations. As illustrated in Figure 1, the overall workflow consists of three interrelated components: (1) XFEM-based fatigue simulation for generating fatigue life data; (2) ANN surrogate modeling for learning the nonlinear mapping between material parameters and fatigue life; and (3) Monte Carlo-based reliability evaluation for quantifying probabilistic fatigue performance. This study bridges deterministic modeling and data-driven prediction, offering a unified and scalable methodology for predicting fatigue life and assessing the reliability of concrete bridge structures.

2. Methodology

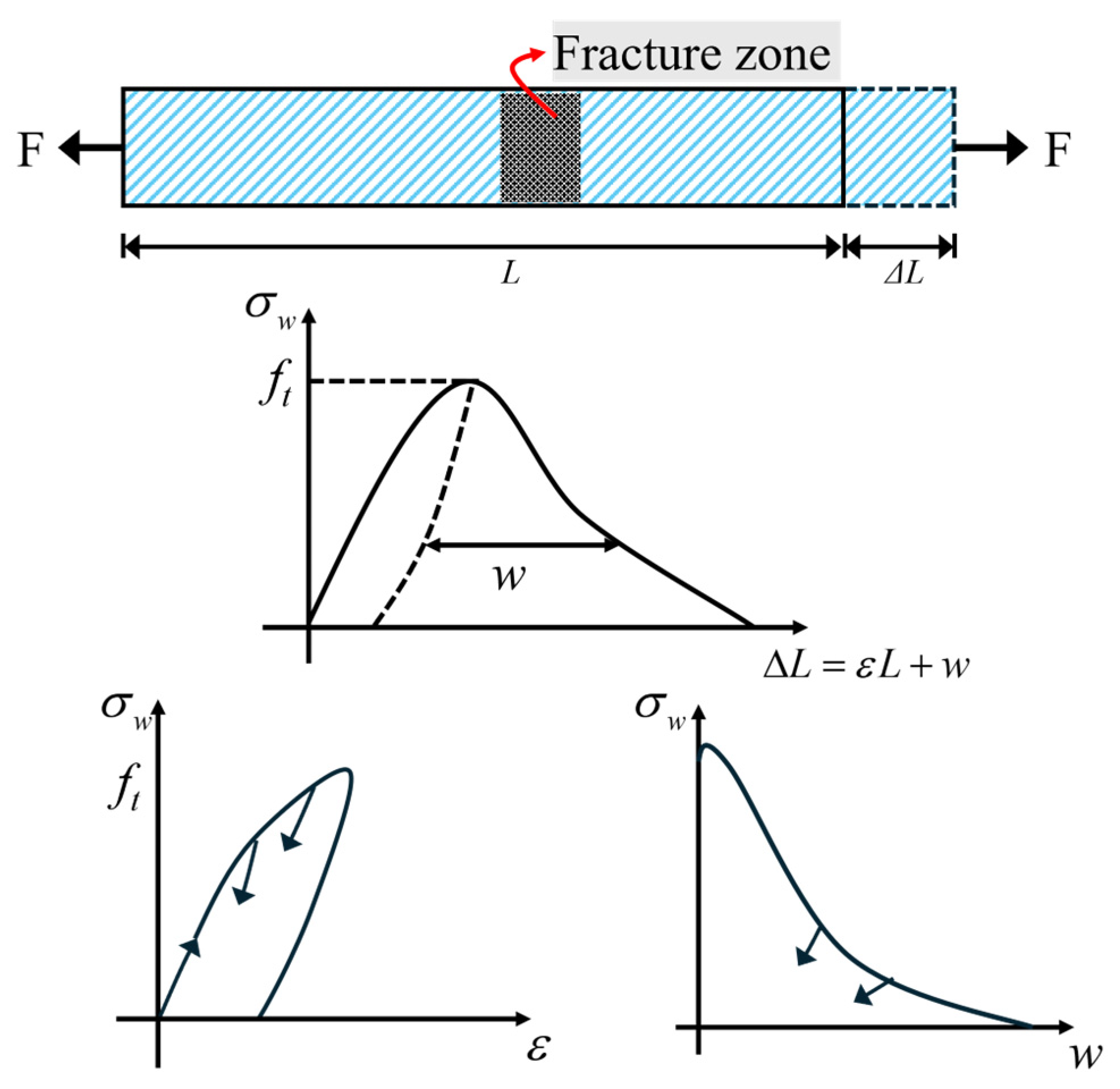
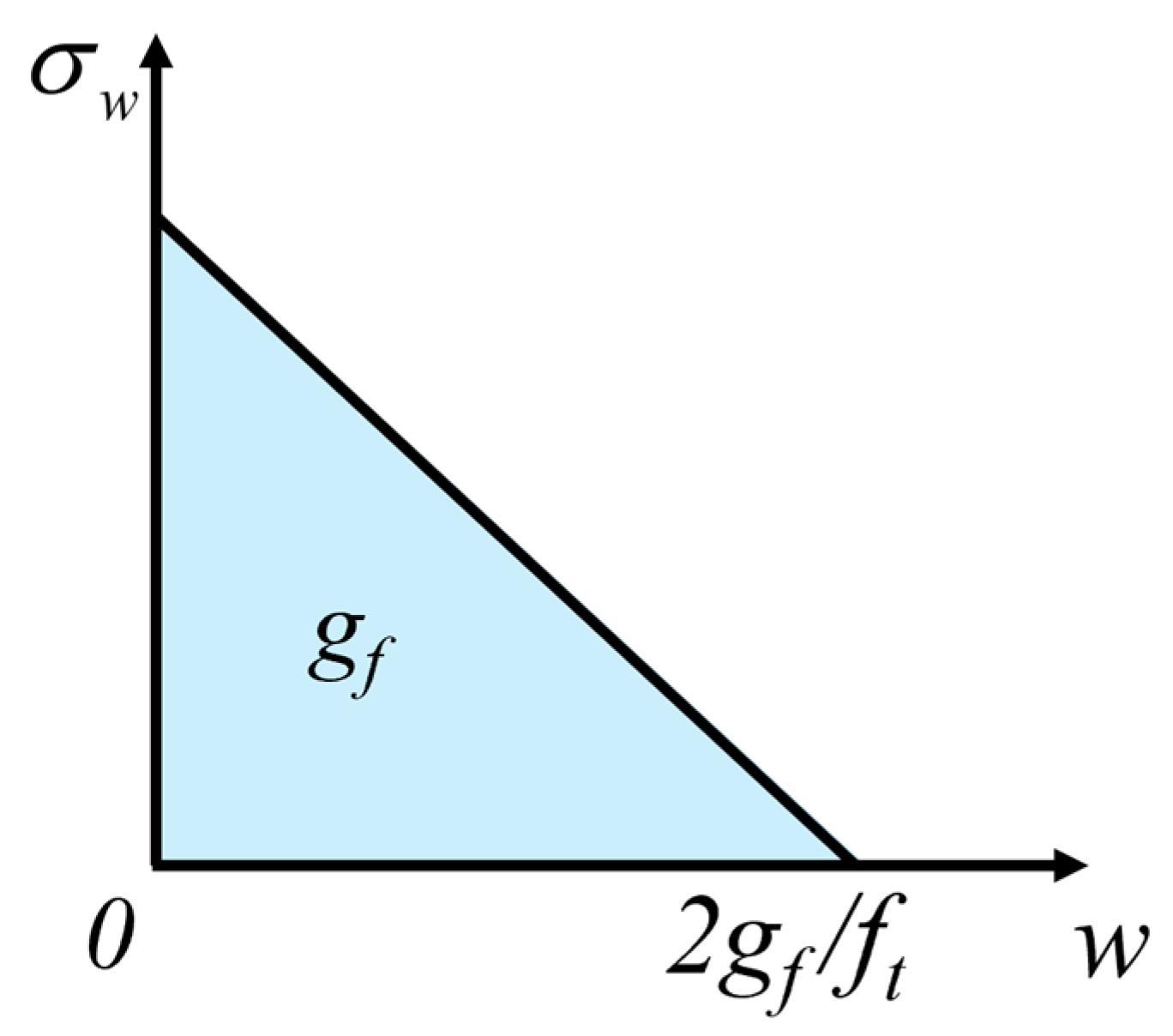
2.1. Virtual Crack Model

The development and coalescence of micro-cracks govern the fracture of quasi-brittle materials, such as concrete, within a finite region ahead of the macroscopic crack tip. This region, referred to as the fracture process zone (FPZ), controls energy dissipation and the apparent size effect of nominal strength [25,26]. Conventional linear-elastic fracture mechanics (LEFM) assumes an ideally brittle crack and ignores the nonlinear stress redistribution within the FPZ, which limits its applicability to concrete. To address this limitation, cohesive-zone-type models were developed to represent progressive stress transfer inside the FPZ. Among them, the virtual crack model (VCM) proposed by Hillerborg and co-workers has become the most representative formulation [27].

The fundamental mechanism of the VCM is illustrated in Figure 2, which depicts the formation of a cohesive fracture zone and the corresponding stress–displacement relationship obtained from a uniaxial tensile test. In the VCM, a fictitious crack carrying cohesive stresses is introduced ahead of the real crack. The tensile stress transmitted across the crack surfaces gradually decreases with increasing crack-opening displacement w, representing a progressive degradation of cohesion. In this study, a linear softening relationship is employed to characterize the fracture process zone, as given in Equation (1). This formulation captures the total energy dissipation capacity, the governing physics of macroscopic fatigue crack propagation, while minimizing the number of independent statistical variables that are difficult to calibrate experimentally.

$${\sigma }_w=f_t\left(1-{\displaystyle \frac{w}{w_c}}\right),$$

(1)

where f_t is the tensile strength and w_c denotes the critical crack-opening displacement corresponding to the complete loss of cohesion. The total fracture energy G_f, defined as the energy required to create a unit area of new fracture surface, can be obtained by integrating the stress–displacement curve, as given in Equation (2):

$$G_f={\displaystyle {\int }_0^{w_c}{\sigma }_w}dw,$$

(2)

The special case of a linear-softening relationship represented by Equation (1) is illustrated in Figure 3, which shows the progressive reduction in cohesive stress with increasing crack opening displacement and the corresponding local energy dissipation g_f (equivalent to the fracture energy G_f in the case where both crack and ligament sizes are large enough relative to the coarse aggregate size) in the FPZ equals 0.5f_tw_c.

To describe the influence of structural size—here referring to the beam depth W, which governs the size effect through its ratio to the fracture-process characteristic length—Bažant et al. [29] introduced the characteristic length l_ch, as defined in Equation (3):

$$l_{ch}={\displaystyle \frac{E{G}_f}{f_t^2}},$$

(3)

where E is the elastic modulus of concrete, and G_f is, as defined earlier, the material fracture energy, representing the energy dissipated per unit crack area during quasi-brittle fracture. When the specimen size W is comparable to l_ch, both the strength and fracture energy govern the behavior because the fracture process zone remains sufficiently large for strength to be significant, while its decreasing relative size simultaneously introduces fracture energy dissipation-dominated effects; as W/l_ch increases, the fracture mode gradually shifts from fracture-energy-controlled failure to strength-controlled failure [26].

The mechanism of the fracture process zone (FPZ) and its interaction with specimen geometry are illustrated in Figure 4. As shown in Figure 4a, when geometrically similar beams with different depths (W) are compared, the relative size of the FPZ decreases with increasing specimen size, and its position moves farther from the beam boundaries. This subfigure illustrates the well-known size effect, where larger beams exhibit a smaller FPZ-to-depth ratio due to a more localized stress concentration at the crack tip [30,31]. In contrast, Figure 4b compares large specimens with increasing crack lengths a. It reveals that as the crack length increases, the FPZ becomes increasingly localized relative to the structural dimensions, indicating a shift toward fracture-toughness-dominated behavior, in which the absolute FPZ size becomes negligible. Figure 4c shows the case where the uncracked ligament (W-a) is kept identical to that of the geometrically similar specimens in Figure 4a. In this configuration, the FPZ interacts with the back boundary, highlighting the boundary effect on quasi-brittle fracture. From a mechanics viewpoint, the cohesive-stress distribution assumed in the VCM can be regarded as a one-dimensional abstraction of the internal stress field within the FPZ. The gradual decay of cohesive stress represents the progressive transition from micro-crack bridging to complete separation.

This equivalence allows the VCM to capture the size-dependent fracture response of concrete without relying on empirical calibration. By consistently linking the tensile strength (f_t), fracture energy (G_f), and characteristic length (l_ch), the model provides a unified mechanical framework for describing crack initiation and propagation in quasi-brittle materials.

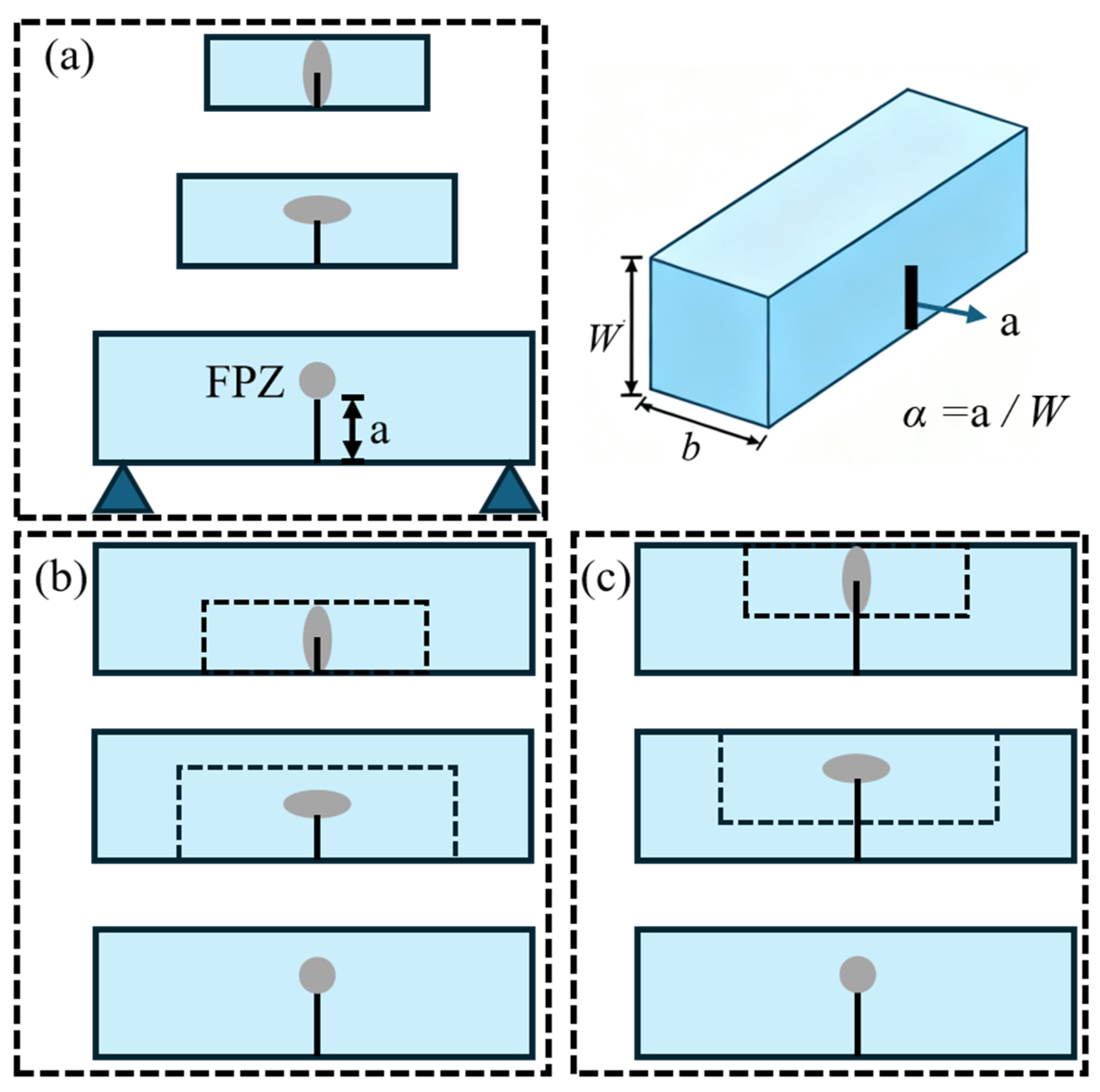
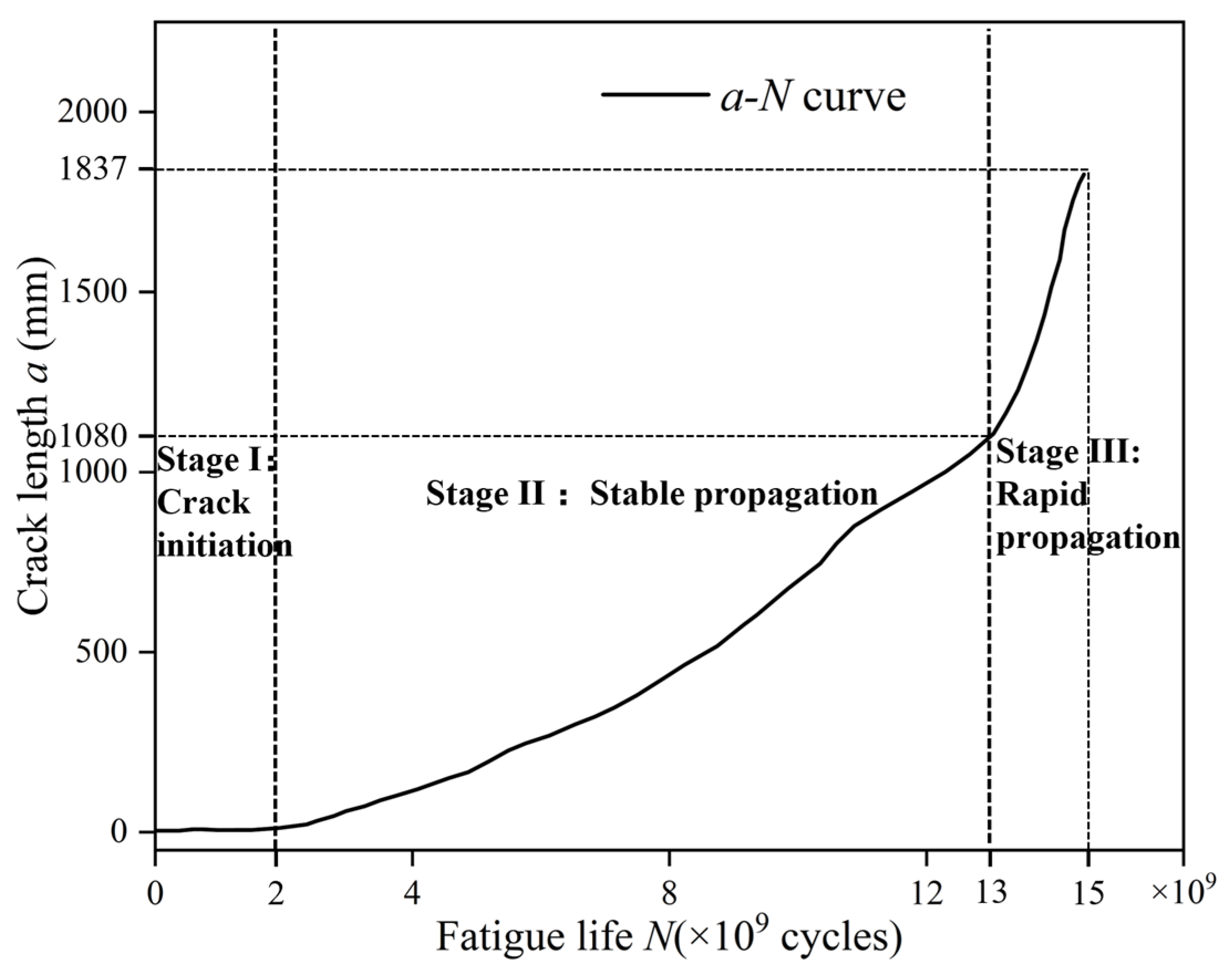
2.2. Fatigue Crack Growth and Size Effect Correction

The fatigue-crack-growth behavior of concrete is generally described by the Paris law, as shown in Equation (4):

$${\displaystyle \frac{da}{dN}}=C{\left(\Delta K\right)}^m,$$

(4)

where da/dN is the crack-growth rate, ΔK is the stress intensity factor range, and C and m are empirical material constants. For a crack initiating at a₀ and propagating to a critical length a_c, the total fatigue life N_f can be evaluated by integrating Equation (4), as expressed in Equation (5):

$$N_f={\displaystyle {\int }_{a_0}^{a_c}\frac{1}{C{\left(\Delta K\right)}^m}}da,$$

(5)

Although Paris’ law is widely used for concrete fatigue, its empirical parameters C and m may vary with specimen geometry, moisture condition, loading frequency, and stress ratio. These parameters are typically obtained from controlled laboratory tests and are applicable only within the calibrated range. Beyond the empirical sensitivities, an additional limitation arises from the quasi-brittle nature of concrete: the FPZ ahead of the crack tip introduces a distinct size dependence that the classical Paris equation cannot capture. To account for this, Bažant et al. [29] proposed a size-effect-based modification of Paris’ law, as expressed in Equation (6):

$${\displaystyle \frac{da}{dN}}=C{\left(1+{\displaystyle \frac{W_{0c}}{W}}\right)}^{m/2}{(\Delta K)}^m,$$

(6)

where W_0c is the characteristic length related to the fatigue process zone and W is the specimen depth. When W → ∞, Equation (5) reduces to the classical Paris form.

This expression reveals that smaller specimens exhibit higher apparent crack-growth rates owing to the greater relative influence of the FPZ. The modified relationship successfully unifies fatigue data from different structural sizes. It provides a consistent link between fracture parameters (f_t, G_f, l_ch) and fatigue life prediction, as developed in subsequent sections.

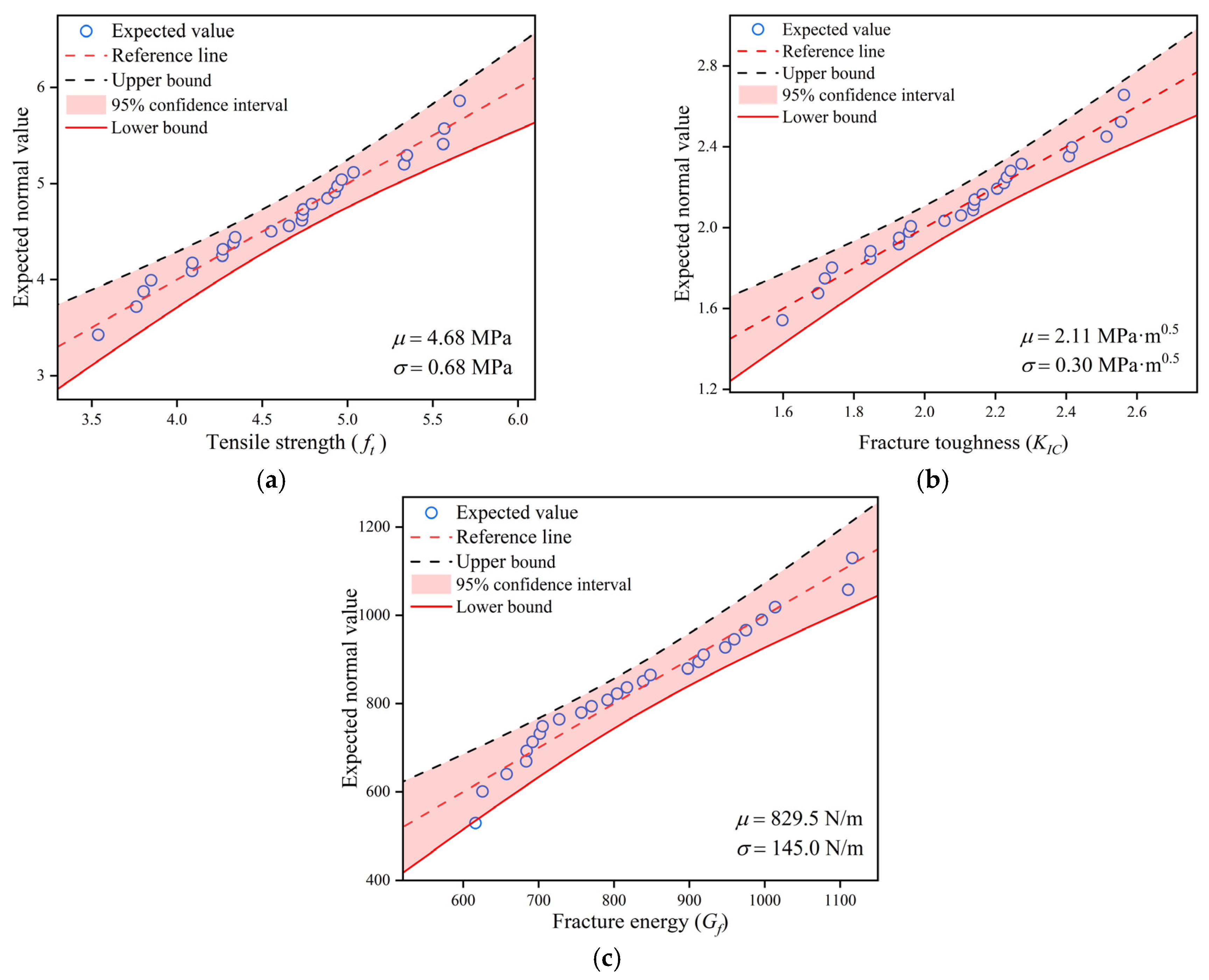
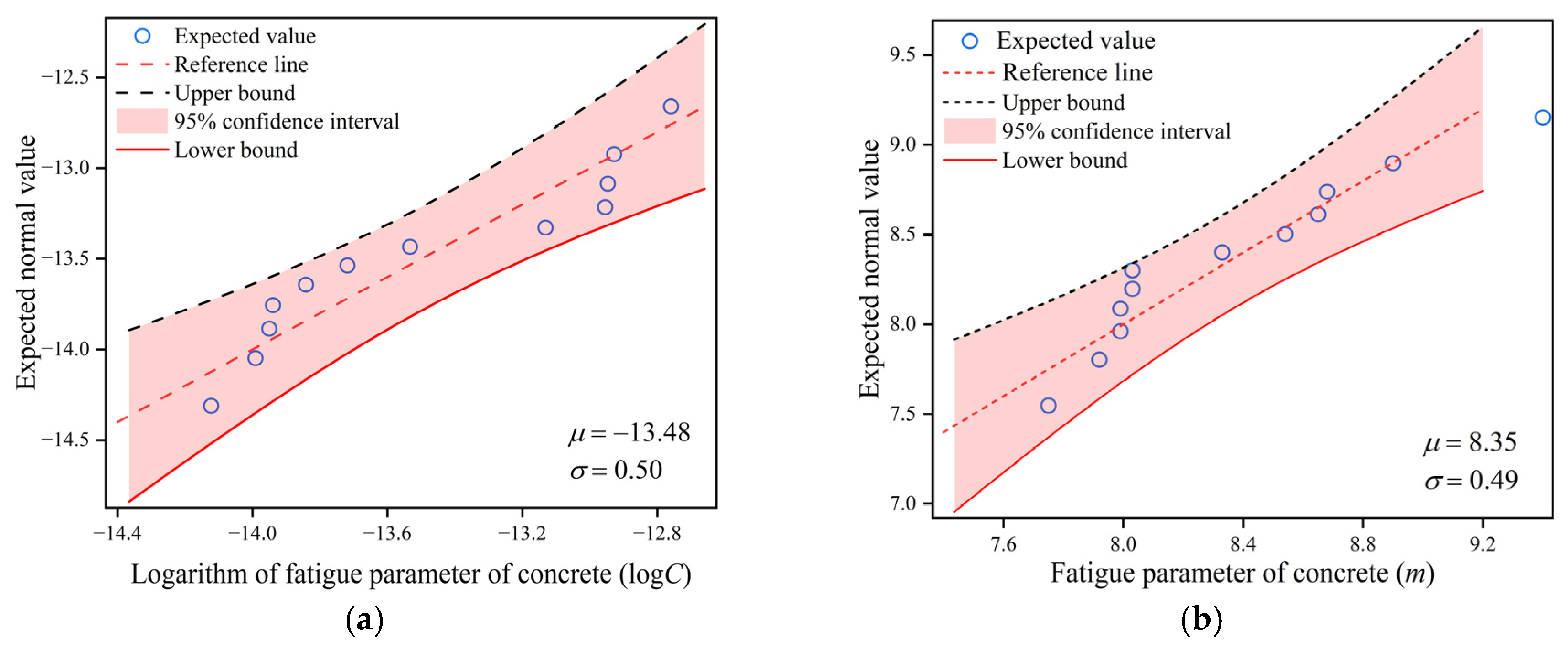
2.3. Statistical Characterization of Material Parameters

For the static fracture characterization, the experimental data were obtained from the study conducted by Zhuo [32]. Based on the complete load–crack opening response, the tensile strength f_t, fracture toughness K_IC, and fracture energy G_f were determined. Statistical analysis demonstrated that these parameters approximately follow a normal distribution, with mean values of f_t = 4.68 MPa, K_IC = 2.11 MPa·m^0.5, and G_f = 829.5 N/m. The fitted probability distribution curves, shown in Figure 5, exhibit clear linear correlations between the theoretical and experimental quantiles, confirming the validity of the standard distribution assumption. Most data points fall within the 95% confidence bounds, suggesting limited dispersion and good material homogeneity. Such consistency ensures that the static fracture behavior can be reliably represented by a single set of characteristic parameters, providing a stable foundation for the cohesive-crack simulations in the following sections.

Following the fatigue tests and size-effect adjustments proposed by Kirane et al. [33], regression analysis of the experimental results yielded log C = −13.48 ± 0.50 and m = 8.35 ± 0.49. Please note that the unit of da/dN is mm/cycle and ΔK is in MPa·m^0.5 when deriving the material parameters. The statistical evaluation of these parameters, as illustrated in Figure 6, shows a well-defined linear trend within the 95% confidence interval, verifying the applicability of the normal distribution hypothesis. The relatively low dispersion of m indicates a stable sensitivity of crack propagation to stress amplitude. At the same time, the scatter in C primarily reflects the micro-scale variability of crack-tip damage accumulation.

Overall, the experimentally derived parameters f_t, K_IC, G_f, C, and m exhibit consistent mechanical and statistical characteristics. These verified parameters ensure the reliability and reproducibility of the material input for the subsequent XFEM-based fatigue–fracture coupled simulations.

3. XFEM Simulation

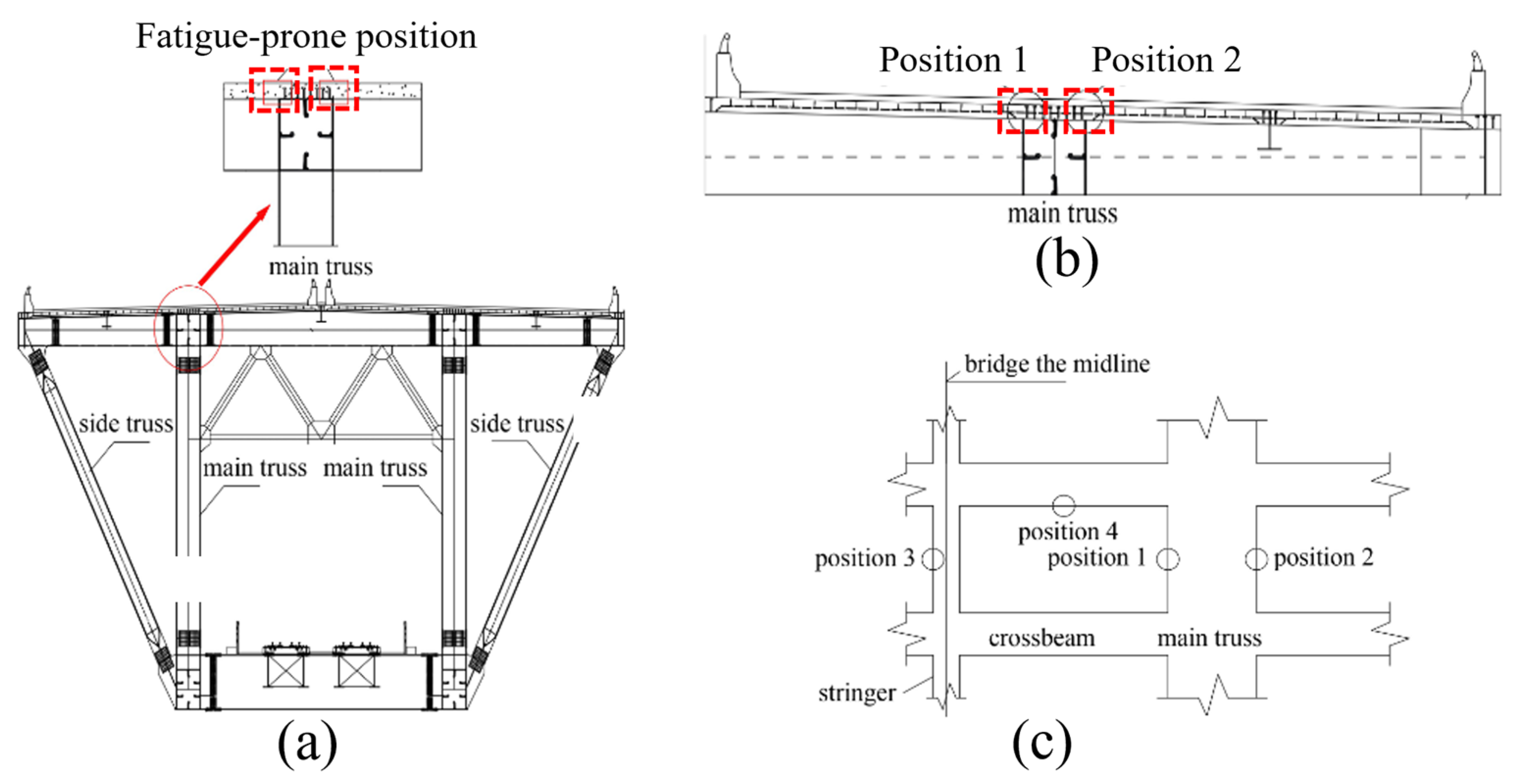
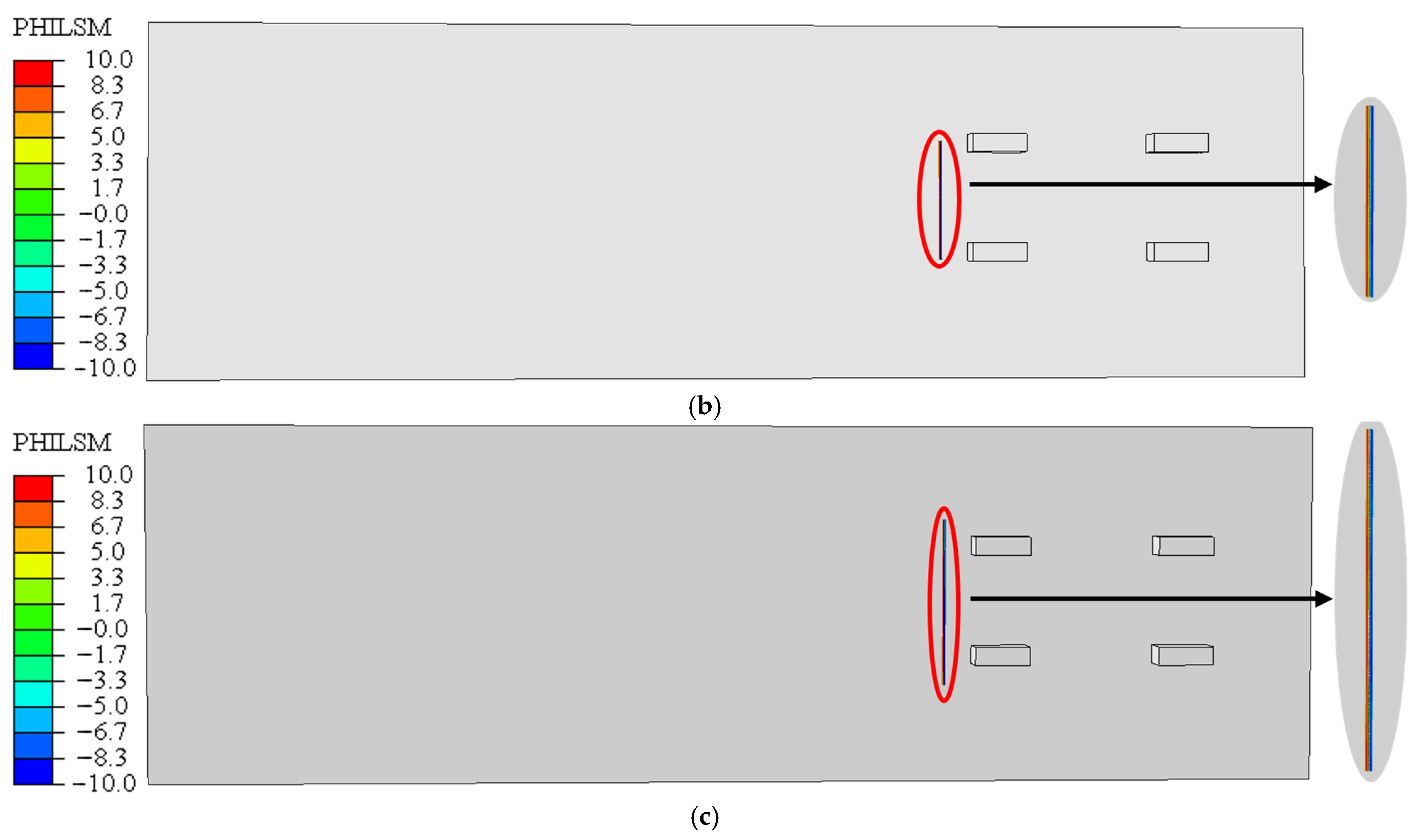
3.1. Prototype Bridge and Identification of Fatigue-Prone Regions

This study is based on the Nansha Port long-span dual-purpose highway–railway steel truss bridge located in Guangdong Province, China. A finite element model of the steel–concrete composite bridge deck was established to investigate the initiation and propagation of fatigue cracks under cyclic loading. As one of the largest-span continuous steel truss bridges of its kind in China, the Nansha Port Bridge possesses high engineering significance and represents a notable achievement in research. The bridge adopts a three-span continuous system (102 m + 175 m + 102 m), in which the concrete deck slab acts compositely with the main truss’s upper chord. Field inspections and long-term monitoring revealed fatigue cracks in the tensile surface region of the deck near the main truss, identifying it as a fatigue-prone area. Figure 7 illustrates the typical cross-section of the bridge, highlighting the fatigue-sensitive position located above the main truss.

To further analyze the fatigue damage mechanism in this critical region with high computational efficiency, a localized finite element model was developed. This model represents a refined substructure of the bridge deck, explicitly focusing on the fatigue-prone zone above the main truss node, extracted from the global system to enable fine-mesh XFEM simulations. Figure 7 presents the numerical model configurations: (a) shows the overall finite element model of the bridge, including the highway deck, truss members, and boundary conditions; (b) provides an enlarged view of the mid-span region to capture the stress transfer and deformation behavior near the main truss; and (c) focuses on the interface between the upper chord and the concrete deck, where the fatigue-prone areas (hotspots) are identified. This modeling approach effectively captures the stress concentration and crack evolution behavior of the steel–concrete composite structure under cyclic loading, forming a reliable basis for subsequent fatigue life assessment.

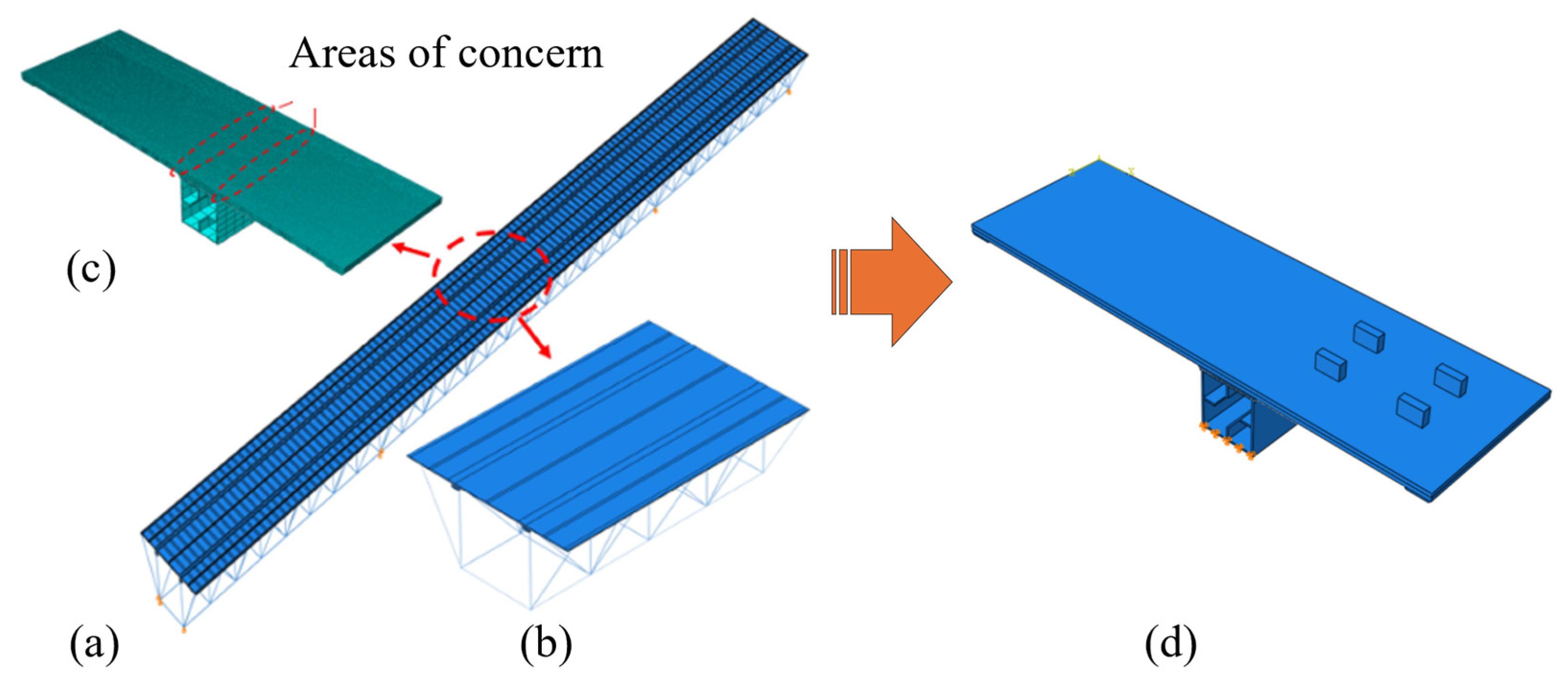
3.2. Finite Element Modeling of the Composite Bridge Deck

In the local finite-element model, the main upper chord of the truss, highway crossbeams, longitudinal girders, bottom steel plates, structural reinforcement, and concrete deck were modeled separately to capture their mechanical interactions. PBL (Perfobond Leiste) shear connectors were embedded between the concrete deck and the underlying steel beams to ensure effective composite action. Because this study focuses on the negative-moment region of the upper concrete deck, the interface between the deck and the steel beams was simulated using the Tie constraint to achieve a complete interaction. Similarly, the connections between the longitudinal girders, crossbeams, and the bottom plate, as well as between the bottom plate and the concrete deck, were all defined using Tie constraints to guarantee coordinated deformation of the entire composite system. This constraint enforces a perfect bond by coupling all active degrees of freedom (translational and rotational) of the contacting surfaces, thereby preventing any relative motion (sliding or separation) between the components and ensuring full composite action.

To better reflect the actual composite behavior, the reinforcing bars were modeled with the Embed constraint, allowing them to be fully embedded within the concrete slab while neglecting bond-slip effects. The concrete deck was modeled using solid elements (C3D8R), and the reinforcement was modeled using truss elements (T3D2). The material constitutive models exhibited nonlinear elastic–plastic behavior for steel and a damaged plasticity model for concrete, capturing stiffness degradation under cyclic loading.

The loading condition is simplified as a surface load corresponding to the mid-rear axle of the standard fatigue truck model, as determined in previous studies [34]. The amplitude and loading path were determined according to the Specifications for Design of Highway Steel Bridges (JTG D64-2015) [35], where a single-vehicle fatigue load of 4 × 120 kN was applied. Boundary constraints were imposed to simulate the realistic support conditions of the bridge deck, with one end fixed and the other allowing longitudinal displacement to avoid over-constraint.

Figure 8 illustrates the finite-element configuration of the Nansha Port Bridge model. Subfigure (a) shows the overall continuous-span system; (b) highlights the mid-span region near the main truss where stress concentration occurs; (c) presents a local enlarged view of the fatigue-prone interface zone; and (d) displays the refined local model used for the subsequent XFEM-based fatigue-crack propagation analysis. This hierarchical modeling approach enables the accurate capture of stress distribution in the bridge deck and the identification of critical regions susceptible to fatigue cracking.

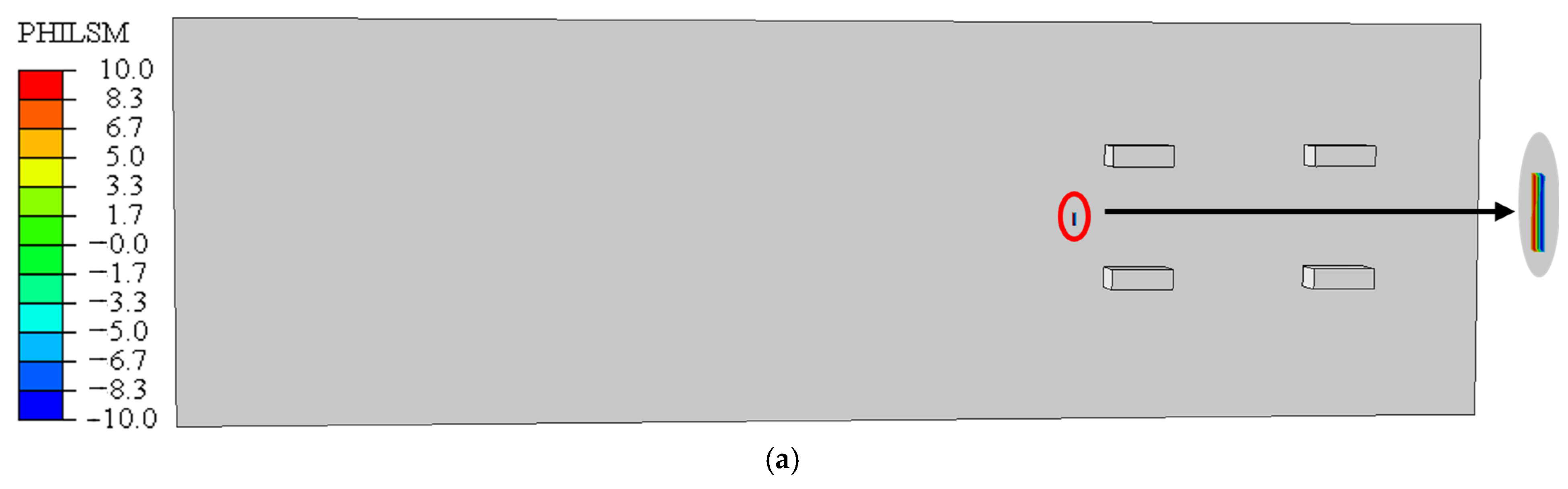
3.3. XFEM-Based Fatigue Crack Propagation and Material Parameters

In the interaction definition, the concrete deck above the main truss was set as the cracking region. A predefined crack measuring 1 mm × 1 mm was introduced at the mid-span location where the transverse tensile stress of the deck was maximal. The crack was positioned at the center of the mesh partition to ensure computational convergence. Fatigue crack propagation was simulated using the direct cyclic step in Abaqus, where each loading cycle corresponded to one analysis increment, allowing for the explicit simulation of crack evolution under repeated traffic loading.

For illustration,

Table 1. Concrete fatigue parameters for fatigue life calculation with XFEM.

Parameters	C	m	C1	C2	C3	C4
Value	1.11 × 10−13	7.92	155	–0.046	1.73549 × 10−7	3.96

lists the material parameters adopted in the XFEM simulation for one set of arbitrarily selected fatigue crack growth constants reported in Reference [33]. Parameters C of 1.11 × 10⁻¹³ and m of 7.92 represent the fundamental Paris law constants obtained from fatigue tests, describing the material-level relationship between the crack-growth rate and the stress-intensity-factor range. In the XFEM implementation, the Paris law expressed in terms of ΔK is converted into the energy-release-rate form da/dN = C₃·(ΔG)^C4, where ΔG = (ΔK)²/E, and the equivalent coefficients C₃ = C·(0.001 × E × (1 − R)/(1 + R))^m/2 and C₄ = m/2 correspond to the transformed parameters in the energy-based formulation. The elastic modulus of concrete E was 41,240 MPa, and the load ratio R, defined as the ratio of minimum and maximum fatigue load, was 0.0588 [33]. A unit conversion of 0.001 is necessary because N for load and mm for length were used in Abaqus analysis, and K has the unit of MPa·mm^0.5, differing from that used to derive the C and m values in [33]. Parameter C₁ serves as the scaling coefficient linking ΔK and ΔG, while C₂ defines the threshold behavior during crack initiation. All these parameters were determined through regression fitting of experimental fatigue data to ensure that the numerical model accurately reproduces the three-stage fatigue degradation process of concrete.

Figure 9 shows the XFEM-simulated crack evolution in the fatigue-prone region of the bridge deck. The crack initiates from the prefabricated notch (Figure 9a) and rapidly propagates in the longitudinal direction under cyclic loading (Figure 9b). As observed in the XFEM simulation results, with continued fatigue loading, the crack length and opening displacement increase progressively, accompanied by the enlargement of the local damage zone around the crack tips. At the critical stage (Figure 9c), crack growth accelerates rapidly, corresponding to the steep rise observed in the a–N curve in Figure 10. This process clearly demonstrates the typical three-stage behavior of fatigue cracking—initiation, stable propagation, and rapid acceleration—and agrees well with the stress distribution obtained from numerical analysis, confirming the reliability of the local modeling approach.

During the simulation, the crack length (a) was recorded as a function of the number of load cycles (N). As shown in Figure 10, the a–N curve exhibits a characteristic three-stage trend: an initial rapid-growth stage, a stable propagation stage, and a final accelerated-growth stage. The crack length increases progressively with the number of cycles until it reaches the critical value (a_c = 1837 mm), corresponding to through-thickness cracking. The fatigue life (N_f) is defined as the number of cycles corresponding to a = a_c, at which point the structure is considered to have reached fatigue failure. The XFEM-predicted a–N relationship effectively captures the fatigue damage evolution of the composite bridge deck, providing reliable data for subsequent ANN-based fatigue life prediction and reliability evaluation.

4. Artificial Neural Network

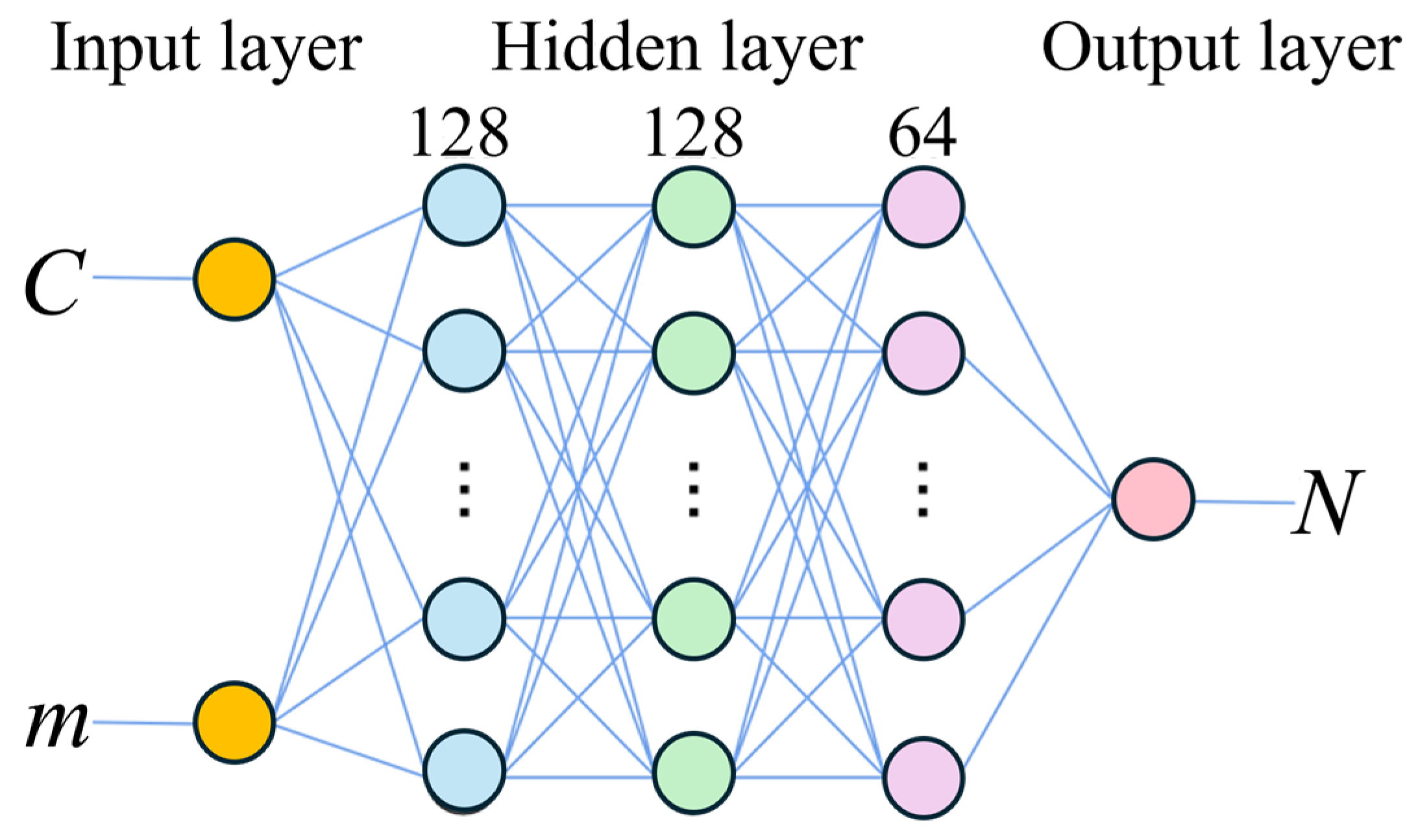
4.1. Structure of BP Neural Network

To overcome the high computational cost of repeated XFEM simulations under stochastic material parameters, a back-propagation (BP) neural network was constructed as a surrogate model to approximate the mapping between fatigue parameters and the fatigue life of the bridge deck. Compared with the deterministic numerical analyses described in Section 3, this data-driven model provides an efficient and robust approach for rapidly predicting fatigue life while preserving the essential nonlinear characteristics of fatigue damage evolution. The surrogate model enables thousands of fatigue life estimations to be performed within seconds, making it particularly suitable for large-scale probabilistic reliability analysis [36].

The proposed neural network is a multilayer feedforward structure consisting of an input layer, several hidden layers, and an output layer. The forward propagation process can be expressed as Equation (7):

$$\widehat{y}=f^{\left(L\right)}(W^{\left(L\right)}\dots f^{\left(2\right)}(W^{\left(2\right)}{f}^{\left(1\right)}(W^{\left(1\right)}X+b^{\left(1\right)})+b^{\left(2\right)})\dots +b^{\left(L\right)}),$$

(7)

where X is the input vector, $\widehat{y}$ is the network output, W^(l) and b^(l) represent the weight matrix and bias vector of the l-th layer, and f^(l)(·) is the activation function. Through the iterative adjustment of weight and bias parameters via the back-propagation algorithm, the BP network is capable of approximating complex, nonlinear relationships between inputs and outputs.

In this study, the ANN surrogate was designed according to the characteristics of the XFEM-based fatigue results. The input layer contains two neurons corresponding to the logarithmic fatigue parameters log C and m, which govern the propagation rate according to Paris’ law. Three hidden layers with 128, 128, and 64 neurons were employed to provide sufficient expressive capacity while avoiding over-parameterization and instability. The output layer consists of a single neuron representing the predicted logarithmic fatigue life, log N_f. The overall network configuration is illustrated in Figure 11. The hidden layers employ the Rectified Linear Unit (ReLU) activation function, as defined as Equation (8). This offers low computational cost, avoids gradient vanishing, and ensures faster convergence compared with sigmoid or tanh functions. Each neuron receives a weighted sum of all outputs from the preceding layer, and bias terms are introduced to enhance the flexibility and nonlinearity of the mapping.

$$f(x)=\max (0,x),$$

(8)

The network was trained using supervised learning, where the input–output pairs (log C, m)→(log N_f) were obtained from XFEM simulations with different parameter combinations. The loss function was defined as the mean squared error (MSE) between the predicted and reference fatigue life, as expressed in Equation (9):

$$\mathrm{MSE}={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{\left(\log N_{f,i}^{\mathrm{ANN}}-\log N_{f,i}^{\mathrm{XFEM}}\right)}^2},$$

(9)

where n denotes the number of training samples. The optimization of network parameters was conducted using the Adam algorithm, which combines the advantages of adaptive learning rate and momentum updating to accelerate convergence. The training process was terminated when the loss function no longer decreased significantly with additional epochs, indicating convergence.

During training, both the training and validation loss curves were monitored to evaluate the model’s convergence and generalization performance. As presented in Section 4.3, the MSE values gradually stabilized after approximately 150 iterations, and the final error remained below 10⁻³, suggesting that the trained network can accurately reproduce the XFEM-derived fatigue life. The relationship between predicted and reference values followed a near 1:1 trend, confirming that the surrogate model successfully captured the nonlinear dependence of fatigue life on the governing parameters.

Once trained, the BP neural network functions as a physics-informed surrogate model that embeds the fatigue mechanisms revealed by XFEM within an efficient computational framework. It preserves the physical dependence of fatigue life on the material parameters log C and m, while enabling the rapid estimation of fatigue life for numerous stochastic realizations. This approach bridges deterministic numerical simulation and probabilistic reliability analysis, allowing the neural network to replace the XFEM model in the subsequent Monte Carlo procedure described in Section 5. As a result, the fatigue life distribution and failure probability under random material conditions can be efficiently estimated with high accuracy.

4.2. Data Collection and Preprocessing

In this study, the fatigue life dataset was constructed based on the finite element results of the composite bridge deck described in the previous section. The XFEM-based simulations provided reliable fatigue life values under various combinations of material parameters, which were subsequently used to train and validate the BP neural network model. To ensure the statistical representativeness of the dataset, the two fatigue crack growth parameters in Paris’ law, C and m, were first analyzed statistically using available experimental and numerical results from previous studies. It was found that both parameters follow approximately normal distributions, as expressed in Equations (10) and (11):

$$\log C~N\left(-13.48,0.5\right),$$

(10)

$$m~N(8.35,0.49),$$

(11)

Based on these distributions, 100 random combinations of parameters were generated using Python’s (version 3.13.5) random sampling functions, ensuring that the sampled data conformed to their respective probability distributions. For each sampled pair of (C, m), the corresponding fatigue life N_f was calculated using the XFEM fatigue analysis framework described in Section 3.3. Consequently, each data entry in the dataset consisted of two input variables (C, m) and one output variable (N_f), forming the basis for supervised neural network training.

To enable effective learning and performance evaluation, the entire dataset was divided into a training set and a testing set using a stratified random split. The training subset accounted for 80% of the total samples, while the remaining 20% were reserved for independent testing. This ratio ensured that sufficient data were available for parameter optimisation while maintaining an adequate number of samples for assessing model generalisation and avoiding overfitting.

Prior to neural network training, data normalization and feature scaling were applied to enhance the numerical stability of the model. Because the magnitudes of C and m differ by several orders of magnitude, direct input without scaling would lead to uneven gradient updates and reduced convergence speed. To address this issue, all input and output variables were standardized to a uniform scale. Each feature was normalized to have a mean of zero and a standard deviation of one, as expressed in Equation (12):

$$X_{scaled}={\displaystyle \frac{x-\mu }{\sigma }},$$

(12)

where μ and σ denote the mean and standard deviation of the original feature values, respectively. This preprocessing step not only accelerates convergence but also improves model accuracy by reducing sensitivity to the original data scale. Moreover, normalization prevents the dominance of large-valued features during back-propagation, allowing the optimization process to treat all variables with equal importance.

To further enhance model robustness, data augmentation was implemented by applying small random perturbations to the input features within ±2% of their mean values. This strategy mimics the inherent uncertainty in material properties and boundary conditions observed in actual structures, thereby improving the model’s generalization ability when predicting fatigue life under unseen parameter combinations.

Through this process, a standardized and statistically consistent dataset was established and used to train the BP neural network for predicting the fatigue life of the composite bridge deck. The comprehensive preprocessing workflow, including distribution fitting, random sampling, data partitioning, and normalization, ensures that the trained network captures the essential probabilistic characteristics of fatigue degradation while maintaining computational efficiency and numerical stability.

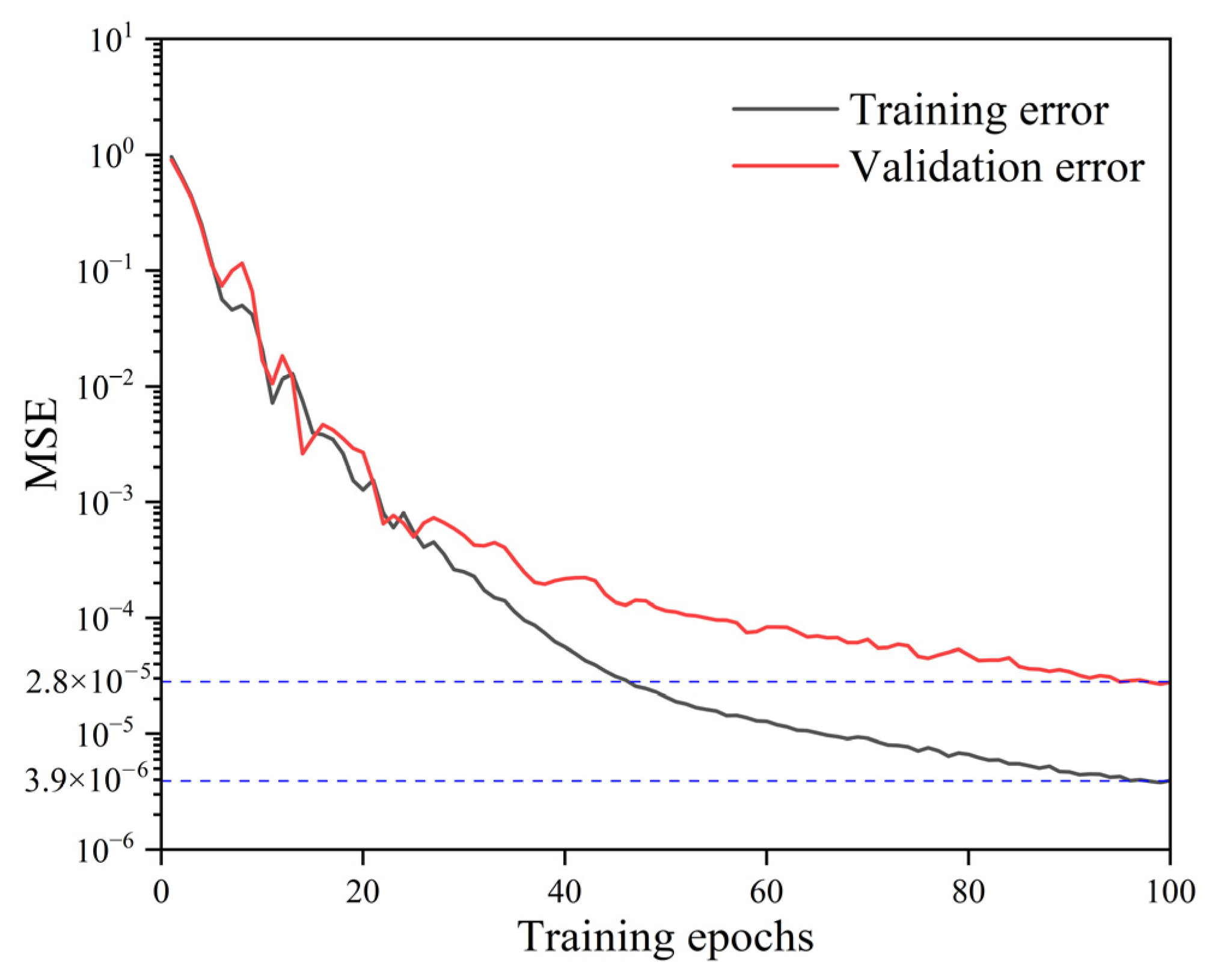
4.3. Model Evaluation and Verification

The neural network model was implemented using the Keras framework in Python, and its parameters were optimized with the adaptive moment estimation algorithm. The Adam combines the advantages of momentum-based stochastic gradient descent and the RMSProp algorithm, thereby maintaining robust convergence across nonlinear and high-dimensional problems [37]. Its iterative update process considers both the first and second moment estimates of the gradients, as expressed in Equations (13)–(17):

$$m_t={\beta }_1{m}_{t-1}+\left(1-{\beta }_1\right)g_t,$$

(13)

$$v_t={\beta }_2{v}_{t-1}+\left(1-{\beta }_2\right)g_t^2,$$

(14)

$${\widehat{m}}_t=m_t/\left(1-{\beta }_1^t\right),$$

(15)

$${\widehat{v}}_t=v_t/\left(1-{\beta }_2^t\right),$$

(16)

$${\theta }_{t+1}={\theta }_t-{\displaystyle \frac{\eta }{\sqrt{{\widehat{v}}_t}+\epsilon }}\cdot {\widehat{m}}_t,$$

(17)

where θ_t denotes the model parameters at iteration t; m_t and v_t are the first- and second-moment estimates (mean and variance) of the gradient g_t; η is the learning rate (set to 0.001); and β₁ and β₂ are exponential decay rates for the two moments, typically 0.9 and 0.999, respectively. The small constant ϵ (10⁻⁷) prevents division by zero. By adaptively scaling the learning rate of each parameter, Adam accelerates convergence and prevents oscillations during training.

The mean squared error (MSE) was used as the primary loss function to quantify the discrepancy between the predicted and reference fatigue life, as expressed in Equation (18):

$$\mathrm{MSE}={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2},$$

(18)

where n denotes the number of samples, y_i and ${\widehat{y}}_i$ represent the reference and predicted values, respectively. To provide complementary perspectives on prediction accuracy, two additional evaluation metrics were employed: the mean absolute error (MAE) and mean absolute percentage error (MAPE), defined in Equations (19) and (20):

$$\mathrm{MAE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|y_i-{\widehat{y}}_i\right|,$$

(19)

$$\mathrm{MAPE}={\displaystyle \frac{100\%}{n}}\sum _{i=1}^n\left|{\displaystyle \frac{y_i-{\widehat{y}}_i}{y_i}}\right|,$$

(20)

The MSE penalizes larger errors more heavily, providing sensitivity to outliers; the MAE reflects the average magnitude of errors in the same units as the data; and the MAPE expresses the relative prediction deviation, which facilitates interpretation in percentage terms. The joint use of these metrics ensures a comprehensive assessment of model precision and robustness.

During training, the standardized input data were fed into the network, which iteratively updated weights and biases through back-propagation according to the Adam optimization scheme. Each epoch involved forward propagation to compute predicted fatigue life values, followed by comparison with the reference XFEM results to minimize the loss. Figure 12 illustrates the evolution of training and validation errors. The MSE curves show a rapid decrease within the first 30 epochs, followed by gradual stabilization. After approximately 100 epochs, both curves converged smoothly, indicating that the model had reached a stable learning state without overfitting. The final MSE of the training and validation sets was 3.9 × 10⁻⁶ and 2.8 × 10⁻⁵, respectively, confirming both numerical stability and consistent generalization capability.

To further validate the predictive accuracy, the relationship between the predicted and actual fatigue life values was analyzed, as shown in Figure 13. The predicted points closely align with the ideal line y = x, and the coefficient of determination reached R² = 0.99. The mean absolute percentage error (MAPE) of 0.977% demonstrates the model’s ability to reproduce XFEM-derived fatigue life results accurately. The close clustering of points along the 1:1 line also indicates that prediction errors are uniformly distributed across the fatigue life range, with no systematic bias toward overestimation or underestimation.

Overall, these results confirm that the trained BP neural network effectively captures the nonlinear mapping between fatigue parameters and fatigue life within the stochastic domain considered in this study. The convergence trend of MSE and the high correlation coefficient collectively verify the accuracy and reliability of the surrogate model. Consequently, the ANN model can replace time-consuming XFEM simulations for probabilistic fatigue life prediction, significantly improving the computational efficiency while maintaining a high fidelity to the physical degradation behavior observed in the finite element analysis.

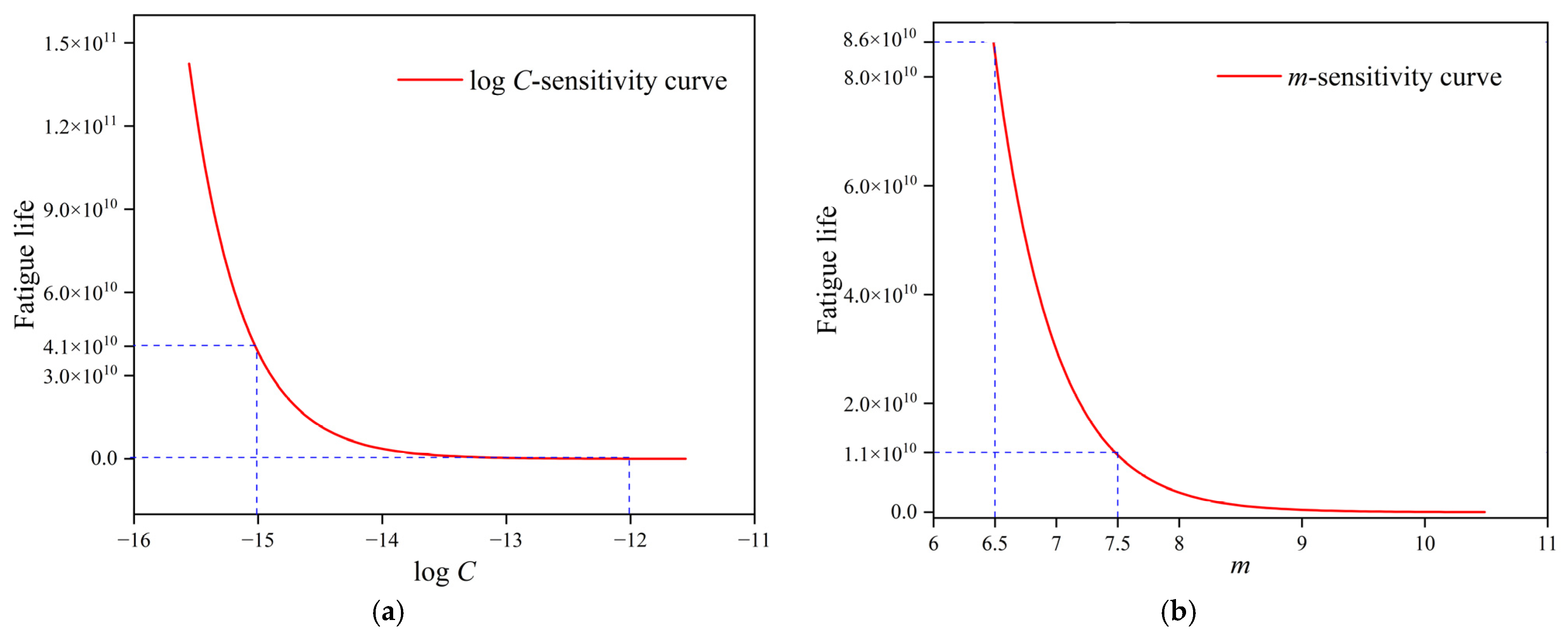
4.4. Sensitivity Analysis of Parameters

To examine the influence of the Paris law parameters C and m on the fatigue life prediction and to verify whether the ANN has correctly captured the underlying physical dependencies, a sensitivity analysis was conducted using the trained ANN model. In this analysis, one parameter was varied within its probabilistic range. At the same time, the other was fixed at its mean value, allowing the independent effect of each parameter on fatigue life to be quantified. The results are presented in Figure 14, where Figure 14a illustrates the sensitivity of fatigue life to variations in log C, and Figure 14b shows the relationship between m and the fatigue life.

As shown in Figure 14a, the predicted fatigue life decreases sharply with increasing log C, following a typical logarithmic-type decay. This negative correlation reflects the physical role of parameter C in Paris’ law, where a larger C corresponds to a higher crack-growth rate under the same stress-intensity range, thereby reducing the number of cycles required for failure. Within the analyzed range, when log C increases from –15 to –12, the fatigue life decreases by nearly one order of magnitude, indicating that small fluctuations in C can lead to significant changes in fatigue performance.

A similar trend is observed in Figure 14b for parameter m, which governs the sensitivity of the crack-growth rate to variations in stress intensity. As m increases from 6.5 to 7.5, the predicted fatigue life decreases sharply, indicating a strong amplification effect of the Paris exponent on crack propagation. When m exceeds approximately 8.5, the fatigue life approaches a very low level, and the decreasing trend gradually levels off. This behavior is consistent with the Paris law mechanism, in which a larger exponent amplifies the effect of load fluctuations on the crack propagation speed.

Comparing Figure 14a and Figure 14b, it can be seen that variations in m cause a more drastic reduction in fatigue life than those in log C. Quantitatively, within their respective statistical ranges, an increase of 10% in m leads to an approximately 30–40% reduction in predicted fatigue life, whereas an equivalent variation in C results in about a 20% decrease. Hence, parameter m exhibits stronger sensitivity and dominates the overall uncertainty of fatigue life prediction. This finding suggests that accurate calibration of m is more crucial for ensuring the reliability of fatigue assessment in steel–concrete composite structures.

Overall, the sensitivity analysis confirms that both parameters C and m exert strong adverse effects on fatigue life, and their influence becomes increasingly significant in the upper parameter ranges. These results highlight the importance of incorporating parameter uncertainty into fatigue life assessment frameworks. In practical engineering applications, adopting conservative estimates of C and m is recommended to ensure the durability and reliability of bridge deck structures under long-term cyclic loading.

5. Fatigue Life Reliability Analysis

5.1. Monte Carlo-Based Reliability Evaluation

To obtain the reliability of fatigue life prediction, the Monte Carlo method was used to generate large-scale random samples of the Paris law parameters C and m. In this framework, uncertainty is introduced by treating log C and m as random variables whose scatter reflects the variability observed in fatigue experiments. Because the statistical evaluation of these parameters shows a clear linear trend within the confidence bounds and does not deviate noticeably from normality (as demonstrated in Figure 6), normal distributions were adopted to describe their probabilistic characteristics in the sampling process. Based on these distributions, 10,000 random pairs of log C and m were generated to represent a wide range of possible material conditions. The sampled parameters were subsequently fed into the trained ANN model to estimate the corresponding fatigue life for each realization.

The fatigue life results were subsequently ranked in ascending order. Each sample was assigned a corresponding reliability level according to its cumulative probability of occurrence as R = 1 − i/(k + 1), where i denotes the sample order and k is the total number of samples (10,000 in this study). Therefore, the highest fatigue life value was assigned a reliability level of 0.0001, while the lowest fatigue life value corresponded to 0.9999. This treatment ensures that even the most favorable case retains a finite probability of failure. The calculated fatigue life and reliability results are summarized in

Table 2. Illustration of predicted fatigue life based on a Monte Carlo simulation and ANN. Note that fatigue life is arranged in ascending order, and the corresponding reliability is calculated.

No.	C	m	Fatigue Life N	Reliability R
1	3.04172 × 10−12	8.837	5.93 × 106	0.9999
2	1.14668 × 10−12	9.281	6.09 × 106	0.9998
3	9.72082 × 10−13	9.122	9.89 × 106	0.9997
…	…	…	…	…
9998	3.56685 × 10−15	6.882	2.81 × 1011	0.0003
9999	3.62076 × 10−16	7.775	4.32 × 1011	0.0002
10,000	2.17557 × 10−15	6.892	4.35 × 1011	0.0001

, which presents the predicted fatigue lives and their associated reliability levels based on the Monte Carlo simulation.

As illustrated in Figure 15, the fatigue life reliability curve R (red) and the cumulative failure probability curve F (black) exhibit complementary trends with increasing fatigue life N. At low cycle counts (N < 1.97 × 10⁸), the bridge deck slab maintains a very high reliability, with R remaining above 0.90 and F close to 0, indicating that fatigue failure is unlikely in the early stage. As N increases from 1.97 × 10⁸ to 5.36 × 10⁹, the reliability decreases rapidly while the failure probability rises steeply. This stage corresponds to the primary degradation region, where fatigue damage accumulates quickly, and the structure becomes increasingly vulnerable to failure. Beyond about N ≈ 1.45 × 10⁹, the rate of reliability reduction becomes more pronounced, indicating a characteristic transition from stable damage accumulation to accelerated deterioration. As the fatigue life approaches N ≈ 5.36 × 10⁹, the reliability drops to about 0.20, indicating a high risk of fatigue failure. The zoomed-in subplot in Figure 15 highlights the early fatigue life ranges, making the rapid drop in reliability and the corresponding increase in failure probability more clearly visible.

By converting the fatigue life to its logarithmic form, the reliability curve of the logarithmic fatigue life is obtained, as shown in Figure 16. The curve exhibits an S-shaped distribution, closely resembling a cumulative distribution function. This suggests that the logarithmic fatigue life approximately follows a normal distribution, consistent with typical probabilistic characteristics of fatigue damage in concrete.

5.2. Conversion to Service Time and Computational Efficiency Comparison

According to the study by Sun [38], the investigated bridge carries an average daily traffic volume of approximately 4593 vehicles, represented by the most frequently encountered three-axle trucks. The corresponding annual traffic volume can be calculated using Equation (21):

$$4593\times 365=1,676,445\mathrm{vehicles}/\mathrm{year},$$

(21)

The number of effective loading cycles induced by each vehicle passage depends on the structural detail configuration and truck axle arrangement. For the specific composite deck under consideration, finite element analysis and live load testing have shown that the bridge deck is a locally stressed structural component whose length of influence line is relatively short. Each passage of the three-axle truck during service causes one large alternating stress cycle [39]. Therefore, the fatigue life expressed in load cycles can be converted into service time (years), providing a more intuitive assessment of the bridge’s operational safety over its service period. The corresponding reliability levels for R = 0.99, R = 0.95, and R = 0.90 are summarized in

Table 3. Fatigue reliability of the bridge deck and associated service time in years.

Reliability (R)	Fatigue Life (Cycles)	Service Time (Years)
0.99	3.82 × 107	23
0.95	1.13 × 108	67
0.90	1.97 × 108	118

. As shown, with increasing service years, the risk of fatigue failure gradually increases and the reliability decreases. After approximately 23 years of service, the bridge reliability drops to 0.99; after 67 years, it decreases to 0.95, indicating a significant probability of fatigue cracking in the deck slab. At around 118 years, the reliability falls to 0.90, suggesting that critical regions require focused inspection and preventive maintenance.

To further highlight the engineering applicability of the proposed framework, the computational efficiency of the XFEM-based simulation and the ANN prediction model was compared. The XFEM approach involves stepwise crack-growth analysis under cyclic loading, requiring nonlinear convergence, which is computationally intensive. In this study, one complete XFEM fatigue simulation for a single parameter set required approximately 6–8 h on a workstation equipped with an Intel Xeon processor and 64 GB RAM. In contrast, once the ANN model was trained, it could predict fatigue life for 10,000 Monte Carlo samples within several seconds, representing an efficiency gain of more than four orders of magnitude.

It should be noted that the number of XFEM-derived samples is limited (100 sets) due to the high computational cost of each simulation. However, since the input parameter space is low-dimensional and exhibits smooth monotonic behavior, the ANN is employed as a local surrogate to approximate the XFEM-derived fatigue life mapping within this confined domain. Hyperparameter tuning showed that the selected architecture (128–128–64) provides a good balance between accuracy and stability, and the closely related training and validation loss curves indicate that the network does not experience overfitting under these conditions. Moreover, despite the substantial speed advantage, the ANN maintained excellent accuracy, with a determination coefficient of R² = 0.99 and a mean absolute percentage error (MAPE) of 0.977%. Therefore, the ANN can serve as an effective surrogate model for large-scale reliability analysis, allowing for rapid probabilistic evaluation of fatigue life under parameter uncertainties. The combined use of XFEM and ANN provides a hybrid computational framework that ensures both the high fidelity of numerical simulation and the efficiency required for practical engineering applications. This approach greatly enhances the feasibility of fatigue assessment in real bridge structures, where a large number of variable combinations must be evaluated under limited computational resources.

6. Conclusions

In this study, a comprehensive framework integrating the Extended Finite Element Method (XFEM), Artificial Neural Network (ANN), and Monte Carlo simulation was developed to investigate the fatigue crack propagation and reliability of a reinforced concrete bridge deck. The main findings are summarized as follows:

(1)

Based on the statistical characteristics of the Paris law parameters C and m, 100 sets of random parameter combinations were generated from normal distributions using Python’s random sampling functions. The XFEM was employed to simulate crack initiation and propagation under cyclic loading, and the resulting fatigue life data served as the foundation for the subsequent ANN training and verification.

(2)

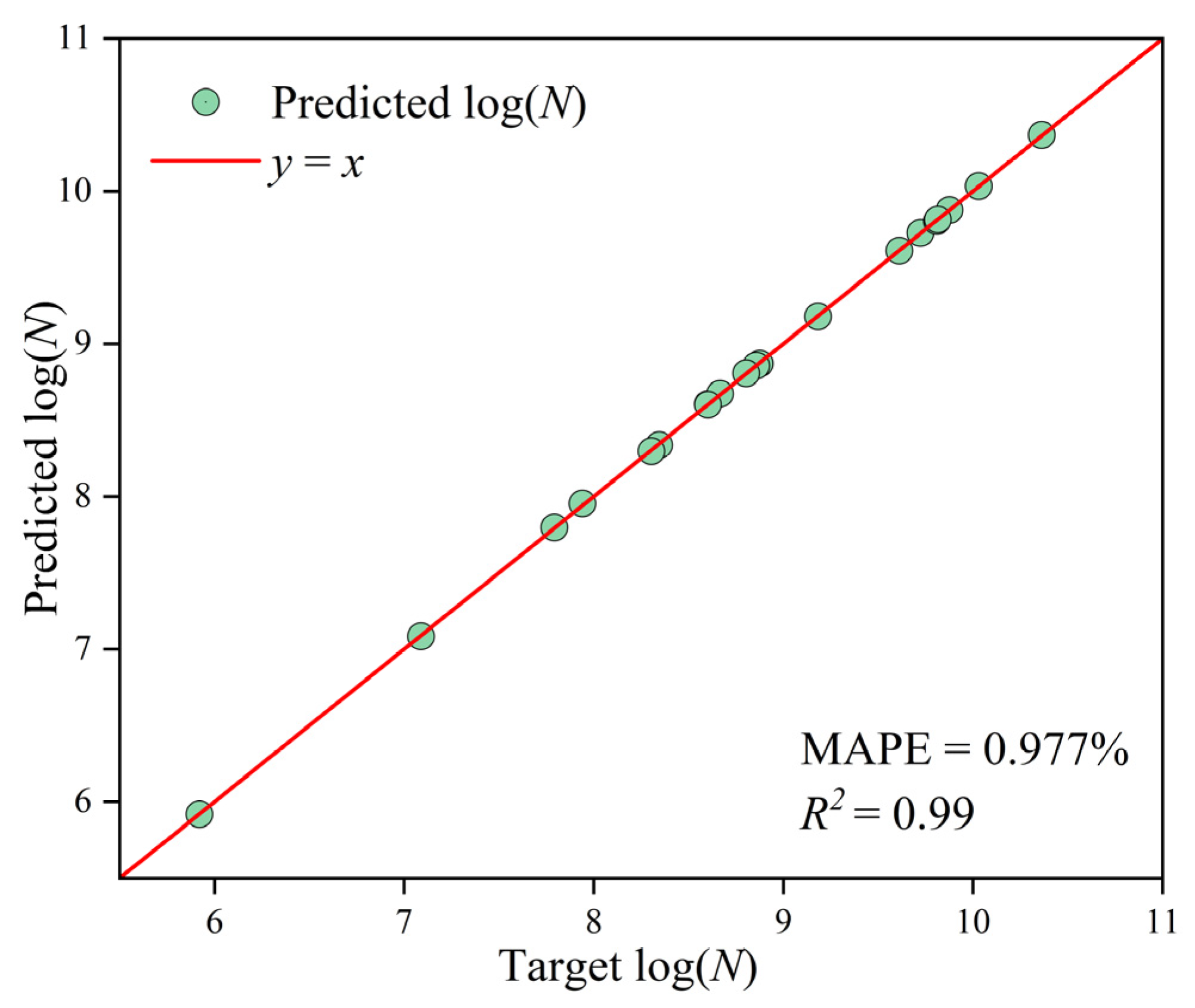
A feedforward back-propagation neural network with three hidden layers (128–128–64) was constructed in Python using the ReLU activation function and Adam optimization algorithm. The model was trained by minimizing the Mean Squared Error (MSE) and evaluated through Mean Absolute Error (MAE) and Mean Absolute Percentage Error (MAPE). The optimized ANN achieved R² = 0.99 and MAPE = 0.977%, demonstrating high prediction accuracy and good generalization for fatigue life estimation of the bridge deck.

(3)

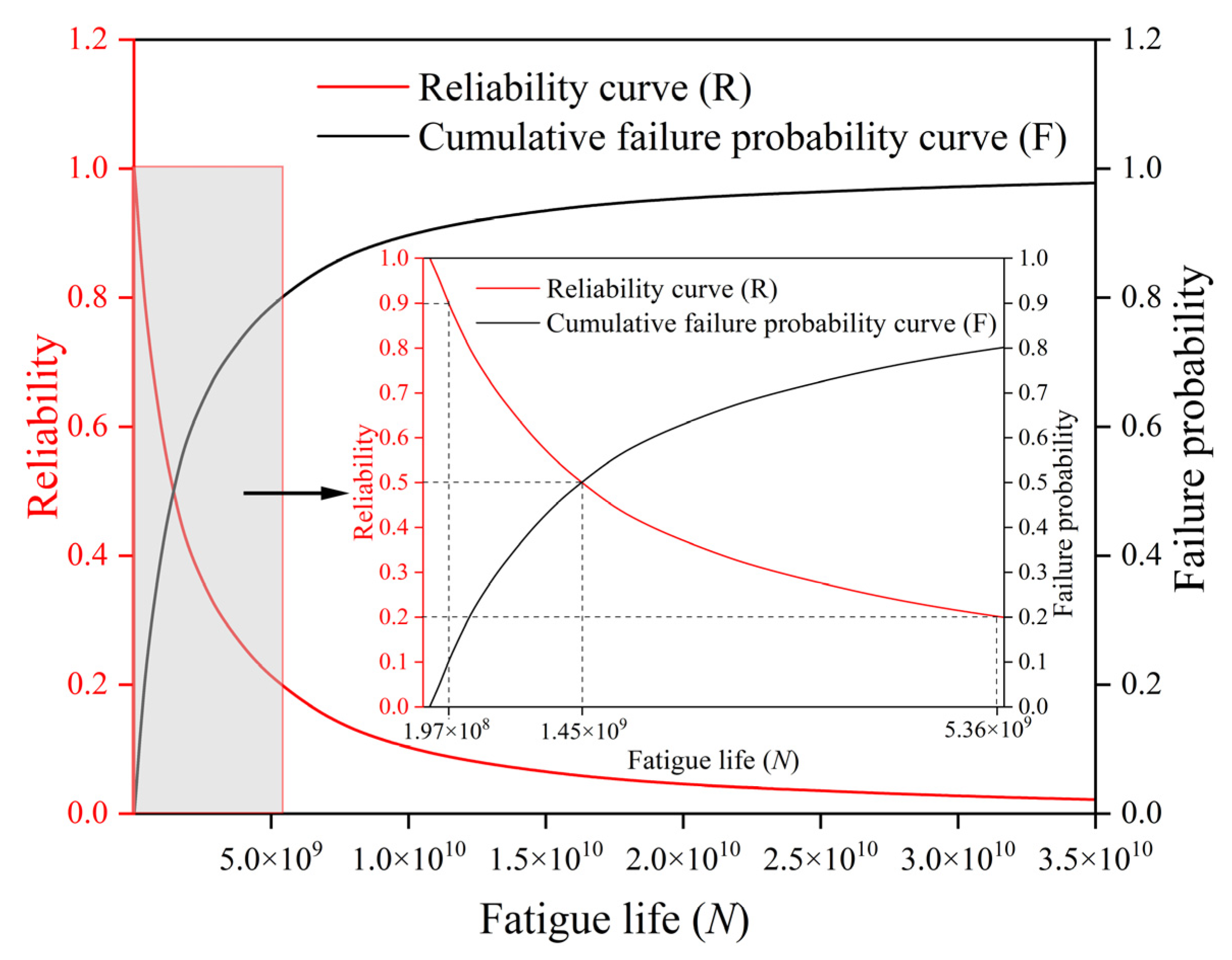
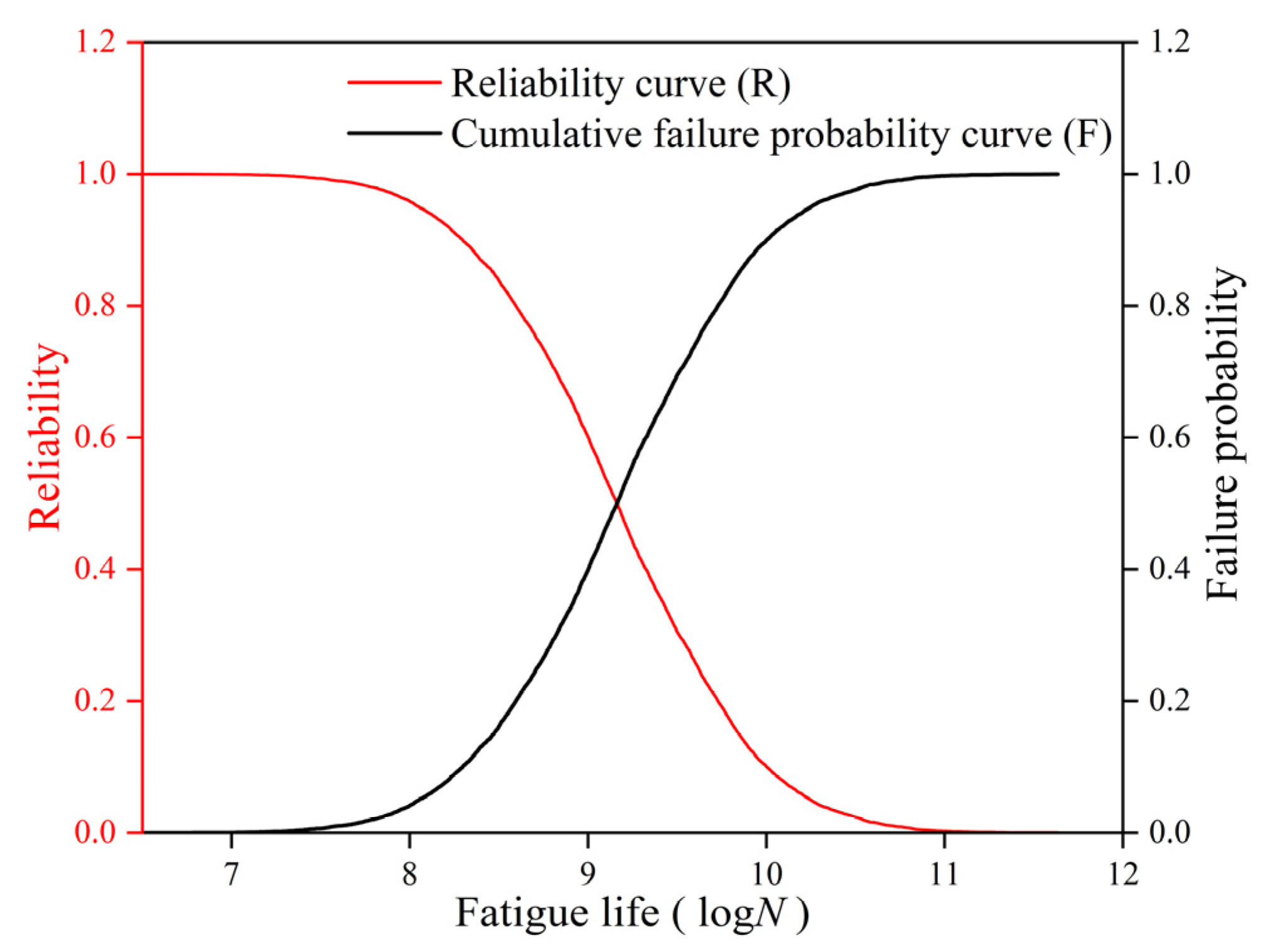
The trained ANN model was coupled with the Monte Carlo simulation to perform 10,000 random samplings of parameters C and m, enabling rapid fatigue life prediction under multiple parameter combinations. The resulting reliability curves exhibited a nonlinear degradation pattern, in which the reliability remained high under low fatigue cycles but dropped sharply once a critical threshold of approximately 1.45 × 10⁹ cycles was reached. Considering the actual bridge traffic volume of approximately 4593 vehicles per lane per day, the analysis indicated that the bridge deck maintained a reliability level of 0.99 after 23 years of service and decreased to 0.95 after 67 years, implying an increasing risk of fatigue cracking during long-term operation.

(4)

Compared with XFEM, which requires 6–8 h to complete a single fatigue simulation, the trained ANN model can predict 10,000 parameter combinations within seconds, improving computational efficiency by more than four orders of magnitude. This hybrid XFEM–ANN–Monte Carlo framework effectively bridges deterministic simulation and probabilistic modeling, offering a practical and efficient tool for large-scale reliability evaluation of concrete bridge decks.

Although the proposed method exhibits strong predictive capability and computational efficiency, several limitations remain. First, the current framework focuses exclusively on material-parameter uncertainties, thereby representing an idealized scenario that isolates material variability. Critical real-world factors, such as stochastic traffic loading (e.g., axle weights, lateral wander) and environmental effects (e.g., temperature, freeze–thaw cycles), were not included in this phase. Second, the ANN was trained on 100 XFEM samples, which constrains the precision of the response surface mapping and introduces epistemic uncertainty into the probabilistic results. Future work should incorporate stochastic loading effects, expand the training dataset by using additional XFEM simulations, and explore advanced models, such as Bayesian neural networks or deep residual networks, to enhance robustness and interpretability. Furthermore, the assumption of an initial crack with a fixed geometry can be relaxed by introducing variable crack sizes and orientations to simulate realistic fatigue initiation scenarios. Crucially, experimental validation through laboratory tests and field monitoring will be conducted to substantiate the proposed hybrid framework.