Design and Performance Evaluation of Double-Curvature Impellers for Centrifugal Pumps

Abstract

The efficiency of centrifugal pumps is strongly influenced by impeller blade design; however, studies on double-curvature impellers remain limited. This research evaluates the impact of double-curvature impellers on pump performance through experimental measurements. Five impeller configurations were tested experimentally, and their hydraulic behavior was analyzed at three rotational speeds: 1400, 1700, and 1900 rpm. For each impeller–speed combination, 12 measurement points were recorded, capturing suction and discharge pressures, flow rate, rotational velocity, electrical parameters, and power consumption. Additionally, four impellers with double-curvature designs of 15%, 25%, and 35% were developed to improve flow guidance between blades and enhance the hydraulic performance of the pump. Quantitatively, the double-curvature impellers demonstrated performance improvements over the baseline configuration, achieving increases in hydraulic head of approximately 5–10% and peak efficiency gains of 4–8 percentage points (equivalent to 10–18% relative improvement), particularly in mid-range flow conditions. These enhancements confirm the beneficial role of blade double curvature in reducing internal losses and improving flow guidance. The results were used to derive head–flow and efficiency–flow relationships, demonstrating that specific double-curvature configurations can enhance pump performance compared to the original design.

1. Introduction

Centrifugal pumps are fundamental components across domestic, industrial, agricultural, and civil sectors, accounting for approximately 10% of global electricity usage [1]. This significant energy footprint has driven research towards enhancing hydraulic efficiency, reducing energy losses, and adapting to modern operational demands. Among the strategies explored, the optimization of impeller geometry has emerged as a critical factor in improving overall performance, particularly through curvature-based design innovations that modify internal flow characteristics.

The integration of centrifugal pumps continues to expand across sectors. Chai et al. [2] investigated their application in small-scale pumped hydro storage, while Gu et al. [3] examined their role in thermal management for electric vehicles. Pump-as-turbine (PAT) configurations have also gained traction for energy recovery purposes [4], and Li et al. [5] proposed multistage pump designs to enhance performance under high-pressure regimes. These studies collectively underscore the need for geometrical adaptability in modern pumping systems.

Recent advancements in computational tools and data-driven approaches have significantly influenced impeller design methodologies. Xin et al. [6] utilized machine learning to accelerate the design process, and genetic algorithms were employed by Yang et al. [7], Zhang et al. [8] to optimize blade profiles with measurable gains in efficiency and head. Ntiri Asomani et al. [9] extended this direction using surrogate modeling based on CFD data, while Wang et al. [10] validated a one-dimensional theoretical model against experiments. In parallel, Mentzos et al. [11] highlighted the impact of blade shape on two-phase flow control through experimental and numerical methods.

Hydrodynamic instability, including flow separation and cavitation, remains a persistent challenge. Wang et al. [12,13] demonstrated the critical influence of inlet blade angles and turbulence intensity on stall mechanisms, while Ye et al. [14] showed that trailing-edge modifications can reduce unsteady flow structures and improve hydraulic stability. These studies point to the importance of blade shape refinement in achieving robust performance under off-design conditions.

Hybrid experimental-numerical approaches have proven especially effective in validating and improving pump models. Fontana and Masi [15] combined CFD with leakage flow experiments to accurately predict axial thrust and energy consumption in multistage pumps. Similarly, innovative blade geometries have been proposed to better control internal flow dynamics. For instance, Chai et al. [2] introduced a double-bend impeller based on the Stodola equation, revealing the relationship between entropy generation and hydraulic losses, while Oro et al. [16] analyzed how radial gap sizes affect velocity fluctuations and pressure pulsations within the impeller.

The need for experimental validation remains essential, particularly for complex or cost-intensive designs. Hu et al. [17], Liu et al. [18], Ma et al. [19] applied advanced optimization methods—such as PSO, LSSVR, and machine learning—to improve blade profiles and diffuser geometries. Their results confirmed that detailed geometric adjustments can significantly enhance hydraulic performance, particularly in cryogenic and high-demand systems.

Experimental optimization strategies have yielded substantial performance benefits. Sun et al. [20] employed the Taguchi method to identify influential design parameters, while Wang et al. [21] and Wu et al. [22] demonstrated that experimental refinement can improve efficiency and head by up to 8.8%. Duan et al. [23] further showed that outlet blade profile modifications reduce energy losses and stabilize flow under varying loads.

Curvature of the impeller blades has been identified as a key design parameter influencing head, efficiency, and flow rate. Yang et al. [7], Abuchar-Curi et al. [24] found that increasing blade curvature leads to improved hydraulic efficiency through better flow guidance. Capurso et al. [1] demonstrated how a double-suction impeller could reduce slip losses, while Zhang et al. [25] implemented parametric adjustments in blade thickness and angle to enhance performance.

Recent studies also highlight structural robustness and multi-criteria optimization. Yuan et al. [26], Shi et al. [27] optimized impellers to balance mechanical strength with energy efficiency, and Chang et al. [28] incorporated wavelet-based vortex analysis to evaluate loss mechanisms. While high-curvature designs may increase power demand at elevated flow rates, the corresponding improvements in head and efficiency often justify the trade-off.

Despite these advances, a critical gap persists in the systematic experimental evaluation of impellers with double-curvature profiles. Most studies have concentrated on individual geometric features or numerical simulations, leaving a need for comprehensive physical validation under variable operating conditions. This study addresses this gap by proposing an experimental framework to evaluate centrifugal pump impellers with various double-curvature configurations. This study aims to determine the double-curvature parameters that improve hydraulic head and efficiency while minimizing specific energy consumption, thereby contributing to the development of high-performance centrifugal pump designs for application in energy-intensive sectors.

While previous studies have explored the effect of blade curvature on internal flow guidance and pump performance, including our earlier work on double-curvature impellers supported by 3D CFD analysis [24], the present study expands this line of research in two fundamental ways. First, it provides a fully experimental validation under controlled laboratory conditions, allowing direct measurement of hydraulic head, efficiency, and power consumption across multiple operating regimes. Second, and more importantly, this work introduces the integration of flow-directing elements within the impeller passage—an innovation not examined in prior studies. These elements are designed to improve flow alignment between the primary and secondary curvature regions, thereby enhancing guidance and reducing internal losses. This dual contribution underscores the novel scope of the present work and differentiates it from existing literature on curvature-based impeller optimization.

This work presents an experimental evaluation of five impeller configurations, including four with double-curvature designs (15%, 25%, and 35%). Tests were performed at multiple rotational speeds, and key performance indicators such as head, efficiency, and power consumption were measured under controlled conditions. The findings demonstrate that certain double-curvature geometries can provide measurable improvements in hydraulic performance over conventional designs, reinforcing the role of impeller optimization in the development of energy-efficient pumping systems.

2. Materials and Methods

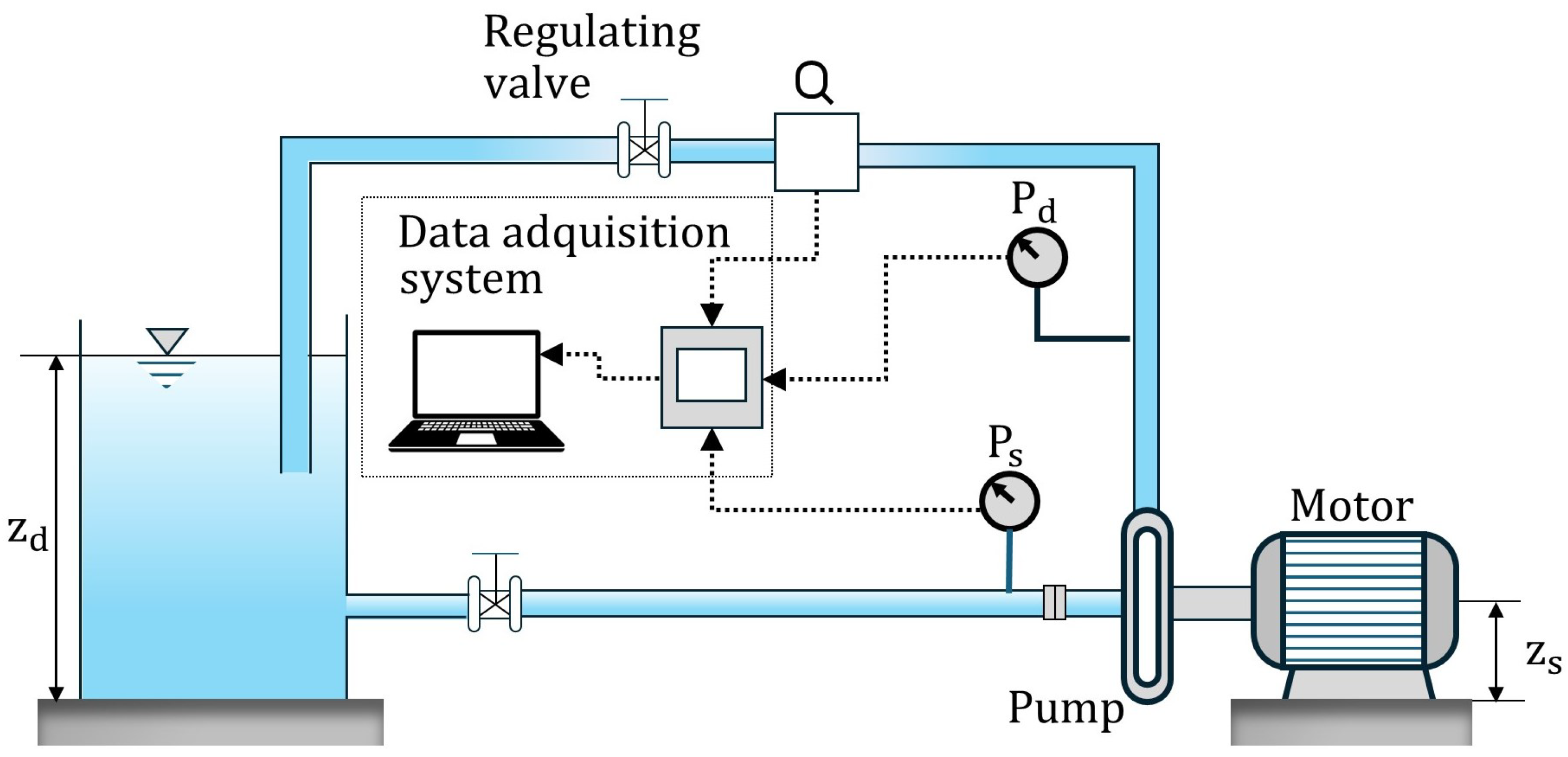
2.1. Experimental Setup

An experimental setup was configured at Universidad Tecnológica de Bolívar to evaluate the hydraulic performance of different impeller designs. The experimental facility was designed to measure key parameters such as flow rate, pressure head, and power consumption under controlled conditions.

A centrifugal pump (IG-IHM Eurolinea 3 × 18 model) with a 2 HP electric motor operating at 1750 rpm was used for the tests. The pump operates at 220 V and 60 Hz. The experimental setup consisted of a closed-loop system incorporating a suction tank, a discharge pipeline, and instrumentation for real-time data acquisition. The total length of the pipe used for the experimental loop is approximately 4 m, and the suction and discharge diameters are 40 mm. All experiments were conducted using water as the working fluid. To ensure the reliability and reproducibility of the experimental measurements, all instrumentation was selected in accordance with the accuracy requirements of ASME PTC 8.2–1990 [29]. Suction and discharge pressures were recorded with Autonics analog pressure gauges with a full-scale accuracy of ±0.5%. Flow rate was measured using a Signet 8550 electromagnetic flowmeter with an accuracy of ±0.8% of the reading. Electrical power inputs were obtained with a FLUKE 1735 power analyzer, which provides an accuracy of approximately ±1%. All sensors underwent a warm-up period of at least ten minutes prior to data collection to guarantee stability. Data acquisition was carried out using a LabView-based system operating at a sampling frequency of 100 Hz. At each flow condition, the pump was allowed to reach steady-state operation, which was defined as a period during which the measured pressure and flow signals varied by less than 1% over ten consecutive seconds.

Measurement uncertainty was quantified following the propagation rules defined by ASME PTC 8.2–1990. The uncertainties associated with flow rate, differential pressure, rotational speed, electrical power, and temperature were used to estimate combined uncertainties for the calculated hydraulic head and pump-motor efficiency. The uncertainty of the head was determined by propagating the uncertainties of pressure difference and velocity terms through the Bernoulli-based formulation. As for the tested operating conditions, the resulting uncertainty in hydraulic head ranged between ±1.5% and ±2.0%. Similarly, the uncertainty of the overall pump-motor efficiency ranged between ±2.5% and ±3.0%. The system included:

• High-precision sensors: Autonics pressure gauges for suction and discharge pressures.
• Flow measurement: Signet 8550 flow transmitters to ensure accurate volumetric flow readings.
• Power and efficiency monitoring: FLUKE 1735 Power Logger energy analyzer to measure motor power consumption.
• Speed control: A variable frequency drive (VFD) to regulate motor speed at 1400, 1700, and 1900 rpm.
• Data acquisition system: Developed in LabView, it is capable of recording 100 data points per second and providing averaged values.

The experimental system included two 5000 L tanks with positive suction, ensuring stable operating conditions. A schematic representation of the experimental setup is shown in Figure 1. In this study, the hydraulic head generated by the pump was determined using the pressure difference between the discharge and suction measurement sections. Because the experimental facility operates as a closed-loop recirculating system (See Figure 1), the classical Bernoulli formulation can be simplified. The suction and discharge pipes have similar diameters, resulting in practically equal flow velocities at both locations, and thus the velocity head difference is negligible. Likewise, the suction and discharge tanks are at the same elevation, eliminating any static height contribution. Under these conditions, the pump head equals the total head loss of the loop and is determined directly from the measured differential pressure.

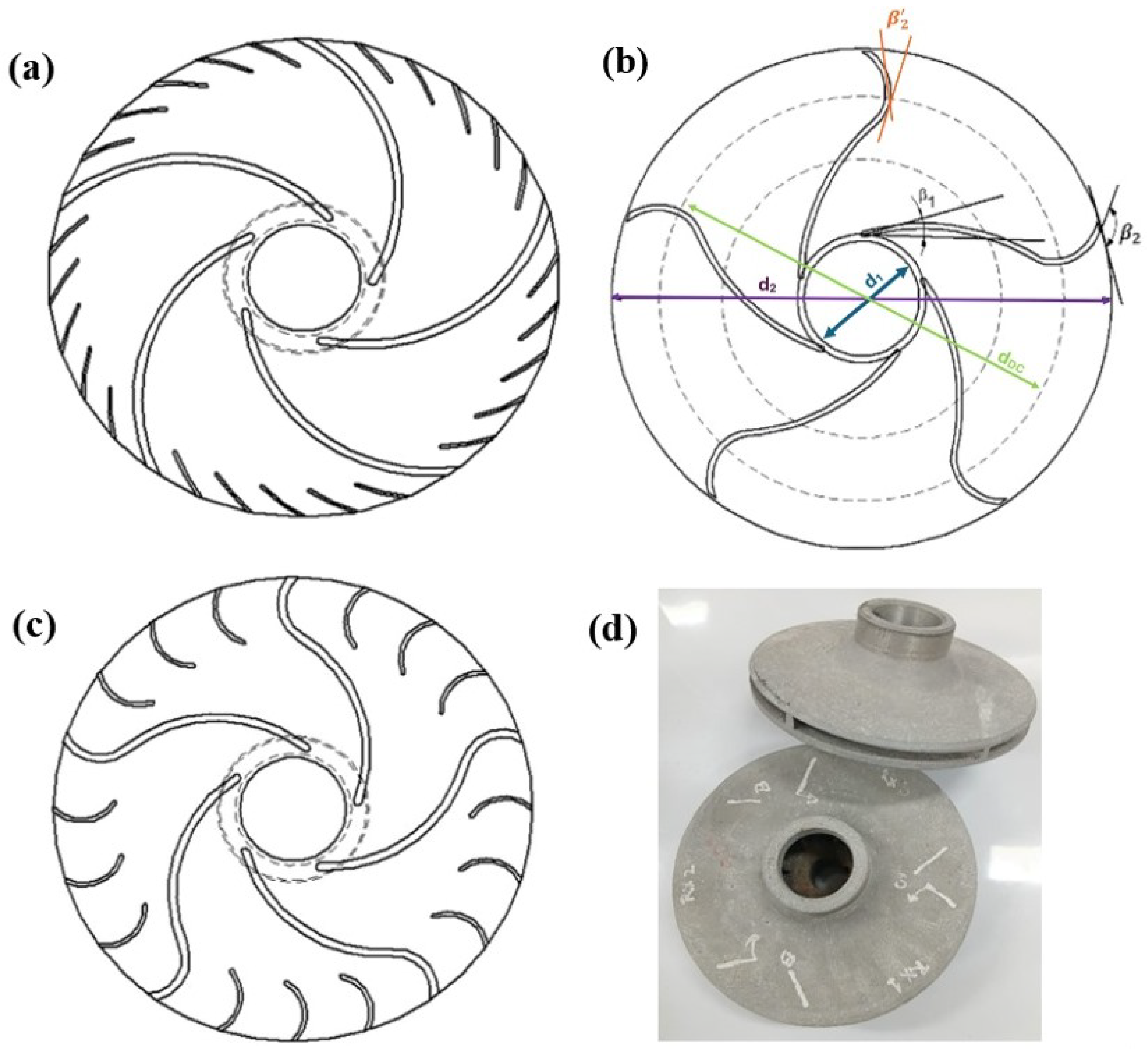
2.2. Impeller Characteristics

The impellers analyzed in this study were designed with different geometric configurations to evaluate their impact on pump performance. Their design was based on fundamental fluid dynamics principles, considering key parameters:

• ${\beta }_1$: Impeller inlet blade angle.
• ${\beta }_2$: Primary impeller outlet blade angle.
• ${\beta }_2^{\prime }$: Secondary outlet blade angle in double-curvature impellers.
• $DC$ (%): Percentage of double curvature (15%, 25%, or 35%).
• $d_{DC}$: Double-curvature transition diameter.

The impellers evaluated in this study included a baseline configuration (original impeller, IO) and four modified variants incorporating different levels of double curvature, each defined by a specific Number of Splitter Blades (NSB). The curvature percentages were chosen based on both prior experience and the geometric characteristics identified as relevant to the study. The corresponding $d_{DC}$ diameter was then computed following the formulation given in Equation (1). The geometric parameters associated with these designs are summarized in

Table 1. Characteristics of the tested impellers.

Impeller	${\mathit{\beta }}_1$ (°)	${\mathit{\beta }}_2$ (°)	${\mathit{\beta }}_2^{\prime }$ (°)	$\mathit{DC}$ (%)	${\mathit{d}}_{\mathit{DC}}$ (mm)	NSB
IO	27	30	-	-	-	5
I2	27	135	30	35	133.2	3
I3	27	80	30	35	133.2	3
I4	27	135	30	15	159.9	5
I5	27	80	30	25	146.6	3

.

$$d_{DC}=d_2-(d_2-d_1)·DC$$

(1)

where $d_2$ and $d_1$ are the impeller outlet and inlet diameters, respectively, and $DC$ is the percentage of double curvature expressed as a decimal.

A visual representation of the impeller configurations is provided in Figure 2.

2.3. Testing Procedure

The experimental plan involved testing impellers with different configurations and adjusting rotational speeds using a VFD. The selected speeds were 1400, 1700, and 1900 rpm.

Before each test, the maximum flow rate ($Q_{max}$) was measured by fully opening the regulating valve. The flow rate increment was computed as:

$$\mathrm{\Delta }Q={\displaystyle \frac{Q_{max}}{n-1}}$$

(2)

A total of $n=$ 12 flow rate points were measured for each impeller.

2.4. Head Calculation

The pump head H for the system was determined using the equation:

$$H={\displaystyle \frac{P_d-P_s}{\rho g}}$$

(3)

where $P_d$ and $P_s$ denote the discharge and suction pressures (Pa), respectively; $\rho$ is the density of water (kg/m³); g is the gravitational acceleration (m/s²). Several curve-fitting models were evaluated to identify the most accurate representation of the experimental head–flow rate relationship.

2.5. Pump-Motor Unit Efficiency Calculation

The pump-motor system efficiency ($\eta$) was calculated as:

$$\eta ={\displaystyle \frac{QH{\gamma }_w}{N_e}}$$

(4)

where $N_e$ corresponds to the electrical power input to the motor (W), as measured directly by the energy analyzer. Since $N_e$ represents the electrical consumption of the motor, the efficiency $\eta$ computed from Equation (4) denotes the overall pump–motor unit efficiency. To identify the most suitable model for representing efficiency as a function of flow rate, various curve-fitting methods were evaluated.

3. Results and Discussion

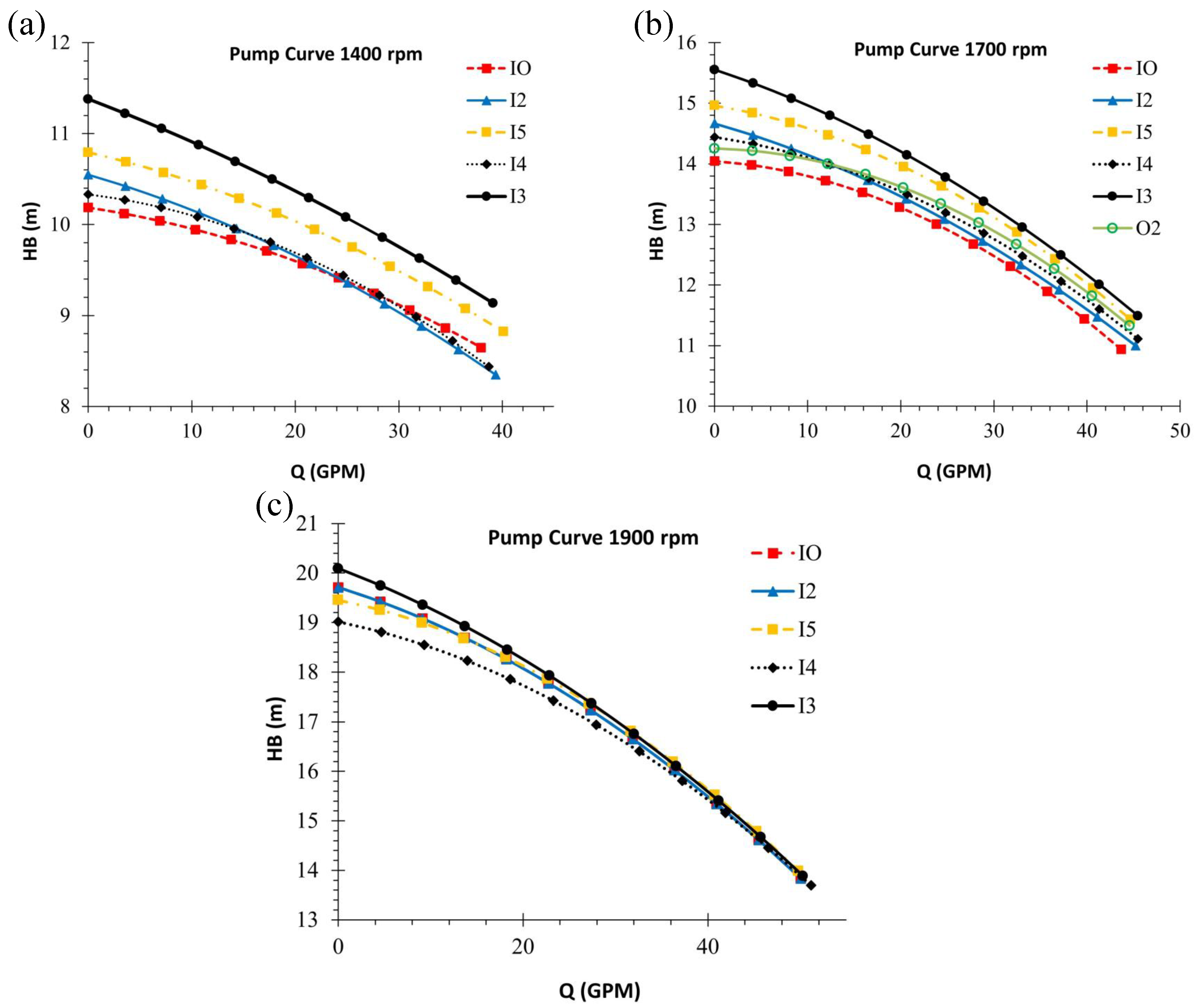
3.1. Head–Flow Rate Relationship

The experimental results for the head–flow rate relationship of the tested impellers are presented in Figure 3. These curves illustrate the effect of different impeller designs on the pump head. The IO served as the baseline for comparison, while the modified impellers with varying degrees of double curvature exhibited distinct performance trends.

It was observed that impellers with higher double-curvature percentages (25% and 35%) generated a greater head across the tested flow rates. This improvement can be attributed to the enhanced flow guidance provided by the curved blades, which reduced energy losses due to flow separation and secondary flows. However, at higher flow rates, the increase in head became less pronounced, suggesting a possible saturation effect of the curvature modification. The mathematical correlation between head and flow rate was obtained using a second-order polynomial fit:

$$H=A{Q}^2+BQ+C$$

(5)

where A, B, and C are empirical coefficients derived from experimental data. The goodness-of-fit for these equations was validated, with all cases showing a correlation coefficient ($R^2$) above 99%, as shown in

Table 2. Head–flow rate equation coefficients for the tested impellers at different rotational speeds.

Impeller	$\mathit{\omega }$ (rpm)	A	B	C	${\mathit{R}}^2$
IO	1400	$-6.22\times {10}^{-4}$	$-1.70\times {10}^{-2}$	10.19	99.32
	1700	$-1.38\times {10}^{-3}$	$-1.07\times {10}^{-2}$	14.05	98.66
	1900	$-1.18\times {10}^{-3}$	$-5.84\times {10}^{-2}$	19.71	99.18
I2	1400	$-5.83\times {10}^{-4}$	$-3.29\times {10}^{-2}$	10.55	99.35
	1700	$-8.33\times {10}^{-4}$	$-4.34\times {10}^{-2}$	14.67	99.21
	1900	$-1.10\times {10}^{-3}$	$-6.09\times {10}^{-2}$	19.72	99.26
I3	1400	$-3.58\times {10}^{-4}$	$-3.29\times {10}^{-2}$	11.38	97.90
	1700	$-8.56\times {10}^{-4}$	$-5.04\times {10}^{-2}$	15.55	99.27
	1900	$-1.04\times {10}^{-3}$	$-7.09\times {10}^{-2}$	20.09	99.49
I4	1400	$-8.99\times {10}^{-4}$	$-1.41\times {10}^{-2}$	10.33	99.82
	1700	$-1.10\times {10}^{-3}$	$-2.27\times {10}^{-2}$	14.44	99.42
	1900	$-1.27\times {10}^{-3}$	$-3.89\times {10}^{-2}$	19.02	99.64
I5	1400	$-5.63\times {10}^{-4}$	$-2.66\times {10}^{-2}$	10.79	98.92
	1700	$-1.20\times {10}^{-3}$	$-2.53\times {10}^{-2}$	14.96	99.26
	1900	$-1.46\times {10}^{-3}$	$-3.73\times {10}^{-2}$	19.45	99.34

, indicating strong agreement between the model and the experimental data.

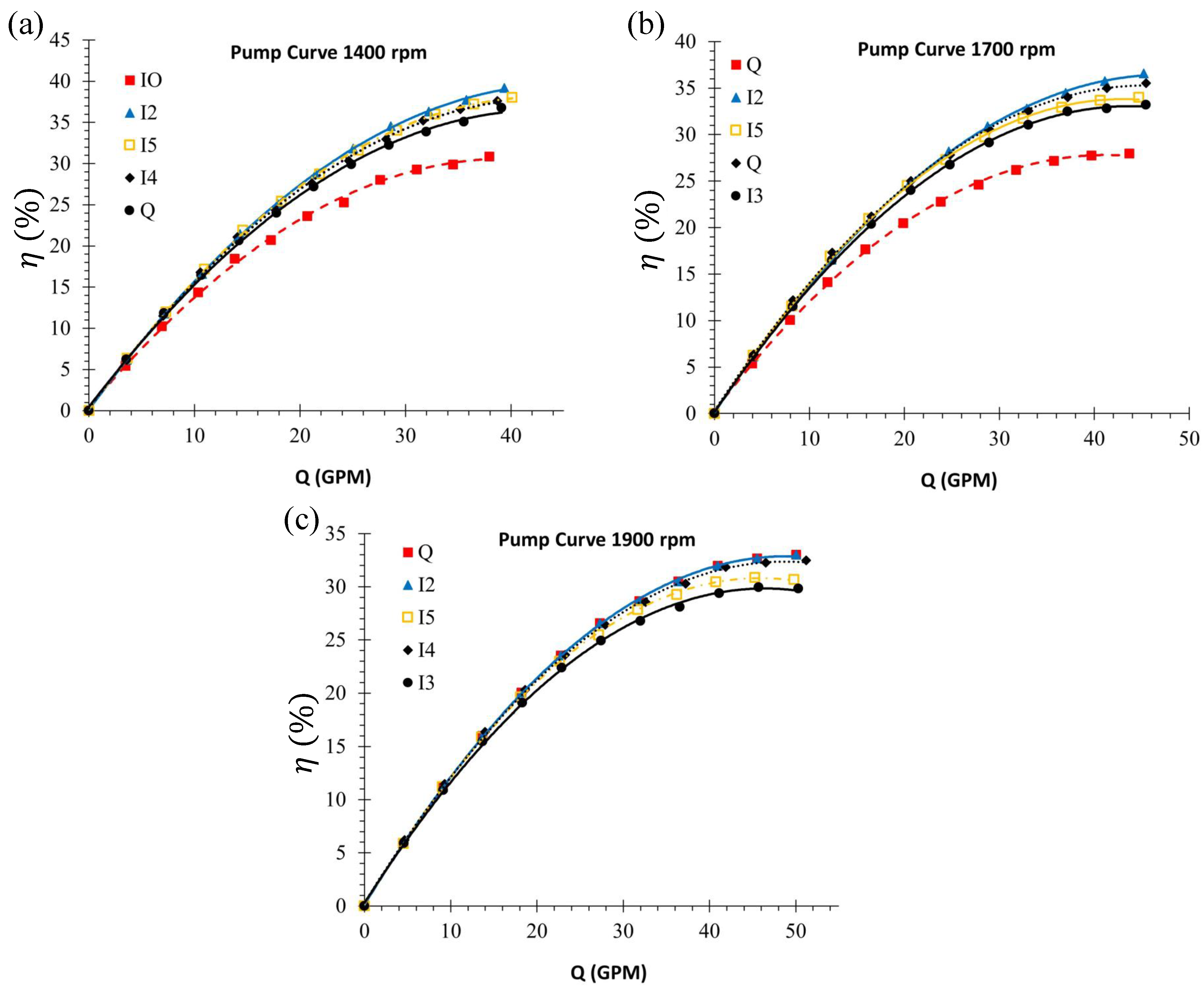
3.2. Pump-Motor Efficiency

The efficiency of the pump-motor unit was evaluated for each impeller configuration. The results, summarized in

Table 3. Efficiency equation coefficients for the tested impellers at different rotational speeds.

Impeller	$\mathit{\omega }$ (rpm)	D	E	F	${\mathit{R}}^2$
IO	1400	$3.79\times {10}^{-1}$	$1.53$	$-1.93\times {10}^{-2}$	99.87
	1700	$3.10\times {10}^{-1}$	$1.33$	$-1.62\times {10}^{-2}$	99.95
	1900	$1.18\times {10}^{-1}$	$1.34$	$-1.37\times {10}^{-2}$	99.99
I2	1400	$1.11\times {10}^{-1}$	$1.75$	$-1.95\times {10}^{-2}$	99.99
	1700	$1.05\times {10}^{-1}$	$1.53$	$-1.61\times {10}^{-2}$	99.99
	1900	$1.44\times {10}^{-1}$	$1.38$	$-1.21\times {10}^{-2}$	99.97
I3	1400	$4.76\times {10}^{-1}$	$1.67$	$-1.95\times {10}^{-2}$	99.92
	1700	$1.84\times {10}^{-1}$	$1.50$	$-1.72\times {10}^{-2}$	99.98
	1900	$2.91\times {10}^{-1}$	$1.27$	$-1.37\times {10}^{-2}$	99.96
I4	1400	$3.00\times {10}^{-1}$	$1.72$	$-1.97\times {10}^{-2}$	99.95
	1700	$3.36\times {10}^{-1}$	$1.54$	$-1.70\times {10}^{-2}$	99.96
	1900	$3.06\times {10}^{-1}$	$1.32$	$-1.35\times {10}^{-2}$	99.95
I5	1400	$1.83\times {10}^{-1}$	$1.76$	$-2.05\times {10}^{-2}$	99.98
	1700	$1.80\times {10}^{-1}$	$1.56$	$-1.81\times {10}^{-2}$	99.98
	1900	$1.73\times {10}^{-1}$	$1.34$	$-1.46\times {10}^{-2}$	99.98

, show the variation in efficiency as a function of flow rate.

The efficiency was computed using the equation:

$$\eta =D+EQ+F{Q}^2$$

(6)

where D, E, and F are empirical coefficients determined experimentally.

As expected, the efficiency followed a parabolic trend with respect to flow rate (See Figure 4), reaching a peak value before gradually decreasing at higher flow conditions. The double-curvature impellers exhibited slightly higher efficiency compared to the original impeller, particularly in the mid-range flow rates. This improvement is attributed to the smoother fluid passage and reduced turbulence losses introduced by the modified blade profiles.

3.3. Power Consumption Analysis

To evaluate the energy demand of each impeller design, the electrical power consumption of the motor was analyzed at maximum flow rate conditions for different rotational speeds. The results, shown in

Table 4. Maximum flow rate of the impeller (GPM) for each rotational speed.

Impeller	1400 rpm	1700 rpm	1900 rpm
IO	37.95	43.68	50.04
I2	39.35	45.20	50.04
I3	39.09	45.46	50.29
I4	38.71	45.46	51.18
I5	40.11	44.69	49.78

, indicate the maximum flow rates achieved by each impeller at 1400, 1700, and 1900 rpm. At 1400 rpm, the double-curvature designs provide clear benefits. For instance, at the maximum flow rate, impeller I3 (25% double curvature) increases the head from 8.65 m to 9.55 m (+10.4%). The overall pump–motor efficiency improves from 30.6% to 36.0% (relative increase ≈+17%). At 1700 rpm, the trend persists. Impeller I3 provides an increase in head from 10.95 m to 11.49 m (+4.9%). The unit efficiency increases from 27.5% to 32.8% (relative gain ≈+19%). Impeller I4 (35% double curvature) yields an even larger efficiency improvement (from 27.5% to 35.2%, ≈+28%) with a reduction in electrical power of about 17%. At 1900 rpm, the efficiency power balance is more neutral but still favorable in terms of performance. For example, comparing the baseline impeller IO with the 35% double-curvature impeller I4, the flow rate increases from 50.0 to 51.2 GPM, These quantitative comparisons show that, particularly at 1400 and 1700 rpm, the double-curvature impellers simultaneously increase head and flow capacity while reducing electrical power consumption and improving efficiency, and at 1900 rpm they provide higher capacity with only a modest increase in power at essentially unchanged efficiency.

The data suggest that impellers with higher double-curvature percentages achieved slightly higher maximum flow rates, which is consistent with the observed increase in head. However, this also implies a greater energy demand, as more power is required to maintain these higher flow rates. Despite the increased power demand, the efficiency gains obtained through the modified impeller geometries suggest that the trade-off between energy consumption and hydraulic performance remains favorable.

3.4. Discussion of Experimental Findings

The results indicate that the introduction of double curvature in the impeller blades leads to an overall improvement in pump performance, particularly in terms of head generation and efficiency. The 25% double-curvature impeller exhibited the best balance between head increase and efficiency gain, while the 35% impeller provided the highest head but with a marginal efficiency drop at high flow rates.

From a practical perspective, the findings suggest that impeller modifications should be optimized to balance energy consumption and hydraulic performance, depending on the specific operational requirements of the pump system.

4. Conclusions

This study presented an experimental investigation into the hydraulic performance of centrifugal pump impellers with varying levels of double curvature. The results offer clear evidence that blade curvature significantly influences head, efficiency, flow rate capacity, and energy consumption. Based on the findings, the following conclusions can be drawn:

• Head–flow rate performance: Impellers incorporating double-curvature profiles exhibited a consistent improvement in head generation compared to the baseline (uncurved) impeller. The 25% and 35% curvature configurations demonstrated the highest head values, indicating that blade curvature enhances pressure rise capabilities across a wide range of flow conditions.
• Hydraulic efficiency improvement: The adoption of double-curvature geometries led to increased pump-motor efficiency, particularly in mid-range flow rates. This improvement is attributed to enhanced flow guidance and reduced internal losses due to minimized turbulence and flow separation.
• Energy consumption considerations: While impellers with higher curvature (notably 35%) resulted in a moderate increase in power consumption at maximum flow rates, the observed gains in hydraulic performance suggest a favorable trade-off. The results indicate that performance enhancements can be achieved without disproportionate energy penalties.
• Flow rate capacity enhancement: Double-curvature impellers achieved superior maximum flow rates across all tested rotational speeds. Notably, the I4 impeller (35% curvature) delivered the highest flow rate at 1900 rpm, followed closely by I3 (25%) and I2 (15%), confirming the influence of blade geometry on volumetric capacity.
• Most favorable design configuration: Among all evaluated configurations, the 25% double-curvature impeller offered the best compromise between improved head, enhanced efficiency, and manageable energy consumption. Although the 35% design delivered higher head, it exhibited diminishing returns in efficiency and energy performance.
• Practical and industrial relevance: The results support the application of double-curvature impellers in energy-intensive industrial environments where performance optimization is critical. These findings reinforce the role of geometric refinement in centrifugal pump design and highlight the need for continued research into curvature parameterization and scaling for larger pump systems.

Future work will focus on expanding the present experimental analysis through high-fidelity CFD simulations to better characterize the internal flow structures induced by double-curvature geometries and to identify the mechanisms responsible for the observed performance variations. Additional impeller designs with different NSB and a wider range of curvature parameters will also be evaluated to refine the understanding of geometrical influences on hydraulic performance. These efforts will contribute to developing more generalized design guidelines for double-curvature impellers and to enhancing the predictive capability of performance models for centrifugal pumps.