Detection of Weak Radar Return Signals Based on Pseudo-Time Domain Algorithm

Abstract

When the signal-to-noise ratio (SNR) falls below −10 dB, signals are considered weak. Radar systems, particularly those on small platforms like drones and satellites, often face this challenge due to limited power, resulting in low transmit power and weak signals. Additionally, ambient noises in the detection environment can further obscure the echo signal, leading to low SNR. Satellite-based radar systems are further constrained by processing capabilities and limitations in data transmission bandwidth and communication time windows. As a result, received radar signals are often transformed into a frequency spectrum and relayed to ground stations for offline processing. To address these challenges, this study proposes a novel method that treats the frequency spectrum of the echo signal as an impulse signal and interprets the frequency domain as a “pseudo-time domain”. By applying conventional time-domain waveform detection methods, such as wavelet analysis, in this “pseudo-time domain”, we can significantly enhance the success rate and accuracy of offline detection for weak echo signals. Numerical simulations show that this approach can handle SNR as low as −34 dB or even lower, which achieves notable denoising effects and improves signal quality. In cases where the SNR reaches −40 dB, the detection success rate exceeds 95% in most instances. Outdoor experiments also maintain a 90% accuracy rate even at −34 dB SNR.

1. Introduction

The deployment of radar systems on miniaturized platforms such as drones and satellites confronts a critical technical challenge: the coupling effect between power-constrained transmission systems and strong background noise in complex electromagnetic environments yields received signals with characteristically low signal-to-noise ratios (SNR $<-10$ dB) [1,2]. This weak signal characteristic not only substantially elevates false alarm probabilities but also fundamentally undermines the reliability of conventional detection frameworks [3,4]. In such strong noise environments, the effective identification of weak signals primarily relies on two methodological frameworks: linear and nonlinear analytical approaches. As a core linear analysis technique, time-domain, frequency-domain, and time-frequency joint analysis methods achieve feature extraction by investigating signal characteristics in the time-frequency distribution. Particularly, the time-frequency joint analysis methodology overcomes the limitations of conventional single-domain representations through the construction of time-frequency distribution maps, enabling precise characterization of signal transient features. Its principal advantage lies in a multidimensional representation capability that effectively resolves the non-stationary characteristics of complex signals.

Among time-frequency joint analysis methods, wavelet transform has emerged as a research focus due to its unique dual-domain filtering capability [5,6]. Compared with the single-domain frequency representation of the Fourier transform, wavelet decomposition achieves effective noise suppression through multiscale feature extraction while preserving temporal signal details [7,8,9]. Current research demonstrates varying performance limits: a modulus maxima detection-based wavelet reconstruction strategy enables lidar echo denoising within the 8 dB to 1 dB [10], while frequency-domain accumulation combined with temporal wavelet transform accomplishes signal recovery at SNR = $-20$ dB [11]. Recent advancements include multilayer autocorrelation-based detection for weak sinusoidal signals (−18 dB to −20 dB) [12] and range-guided wavelet transform achieving echo denoising at 1.37 dB [13]. A two-step noise reduction strategy has been reported to process −19 dB weak signals [14]. Although these studies have reached a minimum SNR of $-20$ dB, more effective denoising methods for lower SNR conditions remain imperative.

Recent efforts have integrated wavelet denoising with deep learning to reduce computational load and adapt to complex data environments. Representative work includes a completely unsupervised deep learning framework for high-frequency time series monitoring, demonstrating enhanced unsupervised monitoring capabilities [15,16]. And the method of combining wavelet denoising with long-term and short-term memory (LSTM) network is used to study the denoising effect in the SNR range of $-6$ dB to $+24$ dB [17]. Furthermore, wavelet denoising techniques have been specifically applied in hydroacoustic signal processing [18], seismic analysis [19], and target detection [20,21,22,23]. Cross-domain research documented in [24] confirms wavelet transform’s capability for defect identification under extreme noise conditions (SNR $<-40$ dB), suggesting potential applicability to radar signal detection. However, existing wavelet-based denoising studies predominantly focus on temporal waveform analysis. Although some exploratory attempts employ frequency-domain methods such as spectral accumulation [25] and frequency filtering [26], conventional frequency filtering only eliminates out-of-band noise, while in-band noise components persistently degrade useful signal integrity.

To address the aforementioned challenges, this paper proposes a radar weak echo signal detection method based on a pseudo-time-domain algorithm. This method constructs a two-stage processing flow comprising pure noise/signal analysis and received signal parsing through spectral data mapping into pseudo-time-domain sequences. On the satellite end, the spectral data of received signals undergoes preprocessing via frequency-domain filters to compress transmission data volume. During the ground-based offline processing stage, noise suppression and signal-to-noise ratio (SNR) enhancement are achieved through a time-domain wavelet transform algorithm in the pseudo-time-domain. Experimental results demonstrate that the pseudo-time-domain-based denoising process significantly improves the SNR of weak echo signals, enhances detection success rates and accuracy, achieves breakthroughs in detection precision under SNR conditions as low as −40 dB, and simultaneously opens new dimensions for applying deep learning to spaceborne radar signal processing.

2. Introduction to Denoising Methods

This study is entirely based on signal spectra. It defines the frequency domain as a “pseudo-time domain”, where the frequency domain features of the detected signals, including but not limited to signal spectra and power spectra, are regarded as waveforms in this pseudo-time domain. Specific structures within the pseudo-time domain waveforms, corresponding to specific frequency domain features, are identified using waveform detection methods. Therefore, the subject of this research is the frequency domain waveform of signals. After converting time-domain signals into frequency domain signals, denoising and detection of received signals can also be carried out in the “pseudo-time domain” using time-domain denoising methods.

The chosen denoising method in this paper is the Discrete Wavelet Transform (DWT) [27]. The DWT allows for multiscale analysis of signals, enabling the localization, detection, and extraction of useful signals within a specific range.

In this paper, the entire process of denoising and detecting weak return signals is illustrated in Figure 1, which involves five steps.

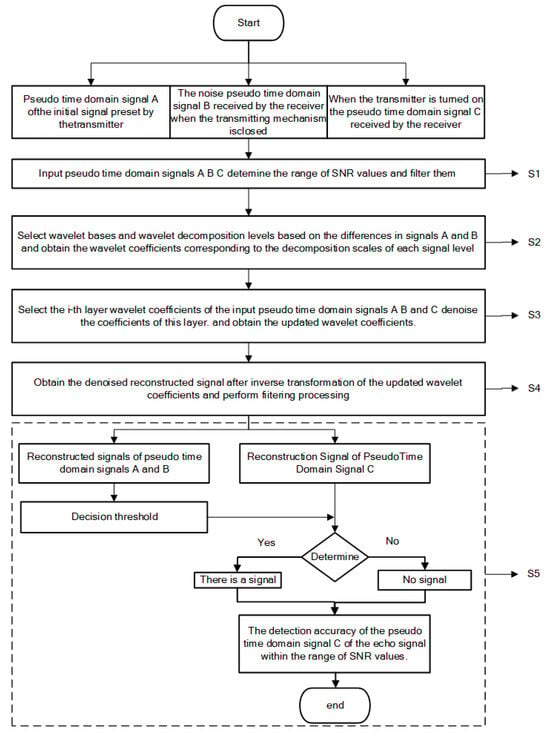
Figure 1. Flow chart of signal denoising.

Step 1: The input pseudo-time domain signals come in three forms. Background noise, which occurs when the transmitter is off and the receiver detects noise, is the sum of spatial environmental noise, system thermal noise from the receiver, and other external interferences. This signal is in the time domain, with its corresponding frequency domain signal denoted as pseudo-time domain signal A. The reference signal is the initially preset signal from the transmitter, also in the time domain, with its frequency domain signal represented as pseudo-time domain signal B. The received signal, which may or may not contain the transmission signal, is the signal received by the receiver when the transmitter is turned on. This signal is in the time domain, with its frequency domain signal referred to as pseudo-time domain signal C. Upon inputting pseudo-time domain signals A, B, and C, the range of SNR for the signal to be detected is determined, and filtering is applied.

Step 2: Based on the differences in pseudo-time domain signals A and B, wavelet bases and wavelet decomposition levels are selected to decompose the pseudo-time domain signals. This decomposition yields wavelet coefficients corresponding to different decomposition scales in the pseudo-time domain. Traditional wavelet decomposition is performed in the time domain, but in Step 2, the decomposition is conducted in the pseudo-time domain. Methods to determine the decomposition level n include, but are not limited to, the following approaches:

$$\begin{array}{c}\hfill {log}_2\left({\displaystyle \frac{\frac{F_s}{2}}{f}}\right)<n{<log}_2\left({\displaystyle \frac{\frac{F_s}{2}}{f}}\right)+1\end{array}$$

(1)

n, representing the wavelet decomposition level, is an integer value determined by the receiver’s sampling rate and the signal frequency.

Step 3: Select the i-th level wavelet coefficients corresponding to the input pseudo-time domain signals A, B, and C. Denoise this level of coefficients, resulting in updated wavelet coefficients. Traditional thresholding methods include three types: hard thresholding [28], soft thresholding [29], and forced denoising [30,31,32]. In this paper, select the i-th level wavelet coefficients $A_1$, $B_1$, and $C_1$ corresponding to pseudo-time domain signals A, B, and C. Based on Equations (2)–(4), the coefficients $d_{i1,k}$ at this level are denoised to obtain the updated wavelet coefficients $d_{i2,k}$, Therefore, the updated $A_{i2}$, $B_{i2}$, and $C_{i2}$ are obtained. The denominator a is determined by analyzing multiple sets of background noise at this layer, which influences the detection signal accuracy. Here, ${\sigma }_n$ denotes the global noise standard deviation, and ${\sigma }_i$ represents the noise standard deviation of the background noise at the i-th layer. For the i-th wavelet coefficients, the layer-specific threshold is defined as ${\lambda }_i$.

$$\begin{array}{c}\hfill {\sigma }_i={\displaystyle \frac{\mathrm{median}\left(\right|d_i\left|\right)}{a}}\end{array}$$

(2)

$$\begin{array}{c}\hfill \begin{array}{c}{\lambda }_i={\displaystyle \frac{{\sigma }_i^2}{\sqrt{max\left({\sigma }_i^2-{\sigma }_n^2,0\right)}}}\hfill \end{array}\end{array}$$

(3)

$$\begin{array}{c}\hfill d_{i2,k}=sign\left(d_{i1,k}\right)·max\left(\left|d_{i1,k}\right|-{\lambda }_i,0\right)\end{array}$$

(4)

Step 4: Perform an inverse transform on the updated wavelet coefficients to obtain the denoised reconstructed signal, followed by filtering.

Step 5: Determine the decision threshold for the reconstructed signals of pseudo-time domain signals A and B. Detect the reconstructed signal of input pseudo-time domain signal C, and determine the presence of a signal. This process yields the detection accuracy of the pseudo-time domain signal C for the SNR range in question.

3. Experimental Results and Analysis

3.1. Simulation Experiment Results and Discussion

The received signals used in this paper include Gaussian white noise with a single-frequency sine signal and Gaussian white noise without it. The expression for the received signal is as follows:

$$\begin{array}{cc}\hfill x_1\left(t\right)& =n\left(t\right)+s\left(t\right)\hfill \\ \hfill x_2\left(t\right)& =n\left(t\right)\hfill \end{array}$$

(5)

where $s\left(t\right)$ is the single-frequency sine signal, and $n\left(t\right)$ is the Gaussian white noise.

Parameters are set as follows: the frequency of the sine signal is $F=50$ Hz, the SNR is set to SNR = −24 dB. Based on the SNR, zero-mean Gaussian white noise is added to the sine signal. The sampling frequency is $F_s=1000$ Hz, and the number of sampling points is $N=4096$.

From Figure 2, it can be observed that at a SNR of −24 dB, the sine signal is completely masked by noise in both the time domain and the pseudo-time domain. In the pseudo-time domain, the noise intensity exceeds that of the signal. The distinction between the received signal with the added sine signal and the background noise signal is almost imperceptible. Therefore, under low SNR conditions, direct signal identification is not possible, and the task of signal detection and extraction becomes highly challenging.

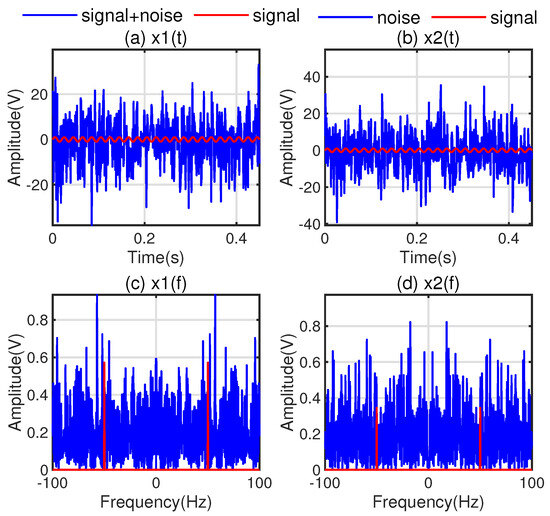
Figure 2. Waveforms of received signals at SNR = −24 dB. (a) Time-domain waveform of signal $x_1\left(t\right)$; (b) Time-domain waveform of signal $x_2\left(t\right)$; (c) Pseudo-time-domain waveform of signal $x_1\left(t\right)$; (d) Pseudo-time-domain waveform of signal $x_2\left(t\right)$.

For signals with a specific frequency, the bandwidth of the band-pass filter is set to $2d$ Hz, so the frequency range of the received signal after filtering is $(F-d,F+d)$ Hz. In this study, the received signals after preprocessing are in the frequency bands of (−60, −40) Hz and $(40,60)$ Hz. The signals used in Figure 2a,c are the received signals containing the sinusoidal signal spectrum, while those in Figure 2b,d are the received signals without the sinusoidal signal spectrum. The SNR of the received signal changes from approximately −24 dB to approximately −9 dB after filtering in Figure 3a,b. The received signal after filtering is subjected to wavelet decomposition and denoising, and the reconstructed waveform after denoising is compared with the original received signal waveform. After denoising, the SNR of the received signal is significantly increased, as shown in Figure 3c,d.

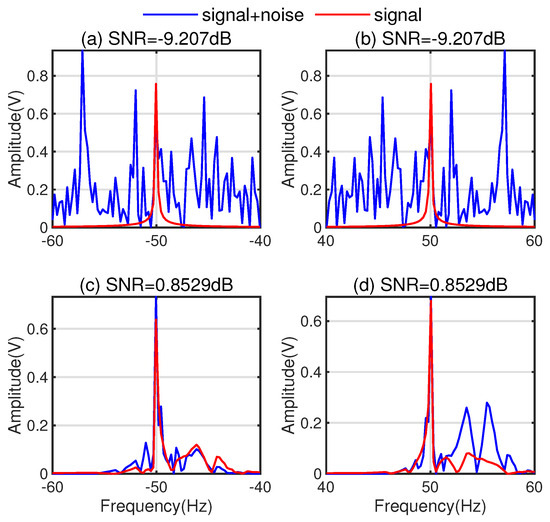
Figure 3. Signal waveforms of received signals before and after denoising. (a,b) show the signal waveforms before wavelet denoising, while (c,d) show the signal waveforms after wavelet transformation.

A single set of data cannot adequately validate the accuracy of the method. Therefore, this paper performs denoising on 1000 sets of received signals multiple times, compares the results with the transmission conditions, and calculates the detection probability to verify the effectiveness and feasibility of the method.

The relationship between SNR and detection rate is shown in Figure 4. It can be seen that within the range of $\mathrm{SNR}\ge -34$ dB, the detection accuracy is $100\%$. Within the range of $\mathrm{SNR}<-34$ dB, the detection rate decreases as the SNR decreases. When the SNR is $-40$ dB, the detection success rate can exceed $95\%$. Therefore, the simulation results can verify that the method adopted in this paper is an effective denoising method.

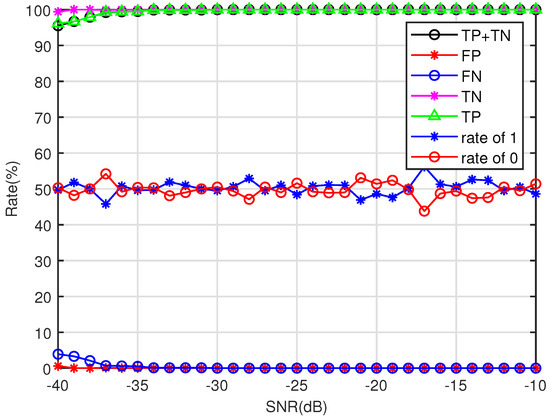
Figure 4. Relationship between SNR and detection rate. In the figure, TP represents the probability of correctly identifying the presence of a signal. TN represents the probability of correctly identifying the absence of a signal. FP represents the false alarm probability, which is the probability of identifying the presence of a signal when there is none. FN represents the miss probability, which is the probability of identifying the absence of a signal when there is one. TP + TN represents the total probability of correctly identifying received signals.

3.2. Results and Analysis of Outdoor Experiments

At the position marked in red in the Figure 5, multiple sets of background noise signals were received by a signal reception system. The signal reception system consisted of a loop antenna, Universal Software Radio Peripheral (USRP) X410 (National Instruments, Austin, TX, USA), a computer, and other equipment. The outdoor experiment flowchart is shown in Figure 6.

Figure 5. Location of outdoor experiment.

Figure 6. Flowchart of the outdoor experiment.

The open-loop experiment conducted in the outdoor environment captured all signals received by the transceiver from system startup to shutdown, as illustrated in Figure 7. The acquired time-domain waveform is partitioned into three characteristic segments: initial transient noise, stable external environmental noise, and post-shutdown system noise. Specifically, multiple stable segments from the second phase are selected as experimental background noise. The normalized time-domain waveform of the selected background noise is shown in Figure 8a, with corresponding pseudo-temporal domain representations provided in Figure 8b,c. These pseudo-temporal profiles reveal four distinct peaks from other interference sources, corresponding to spectral components at $\pm 1$ kHz and $\pm 15.875$ kHz.

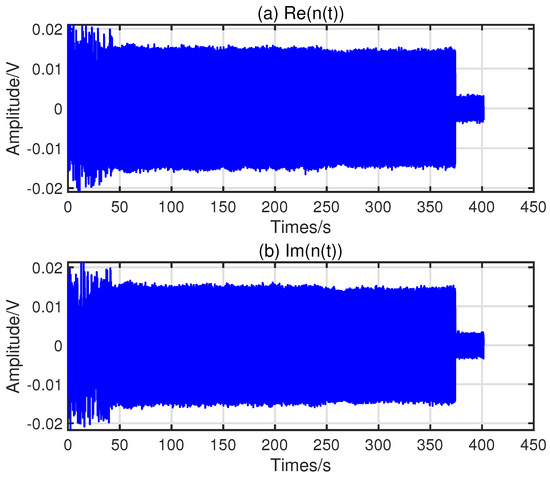
Figure 7. Time domain diagram of received signal, (a) real part, (b) imaginary part.

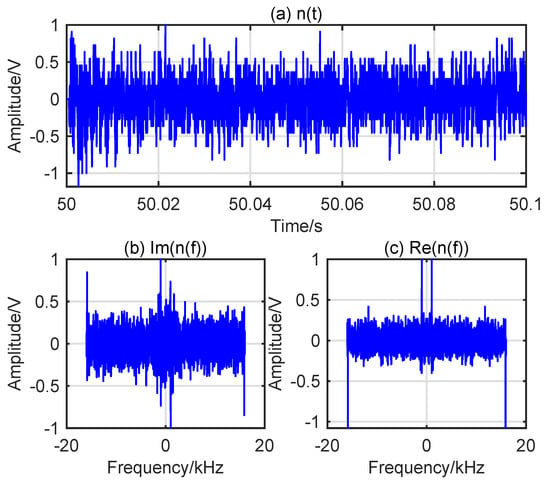
Figure 8. The waveform diagrams of the background noise signal, where Figure (a) is the time-domain waveform, and Figure (b,c) are the pseudo-time-domain waveforms, respectively.

After adding the reference signal to the background noise to form a −30 dB received signal and normalizing it, the time-domain waveform is shown in Figure 9a, and the pseudo-time-domain waveforms are presented in Figure 9b,c. In Figure 9b, the two peaks of the red reference signal correspond to the spectral positions of the 10 kHz signal, which are completely masked by the noise. The denoising comparison of the received signal with an SNR of $-30$ dB is shown in Figure 10. Figure 10a shows the pseudo-time-domain waveform of the received signal with the reference signal, and Figure 10b shows the pseudo-time-domain waveform of the received signal without the reference signal. From Figure 10a, it can be seen that the peaks at the frequency positions of the pseudo-time-domain waveform of the received signal with the reference signal are significantly larger after denoising. From Figure 10b, it can be seen that the peaks at the frequency positions of the pseudo-time-domain waveform of the received signal without the reference signal are much smaller after denoising.

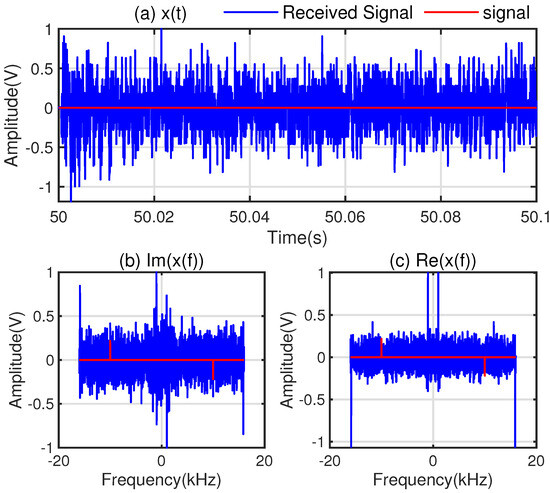
Figure 9. The time-domain waveform and the pseudo-time-domain waveform of the received signal.

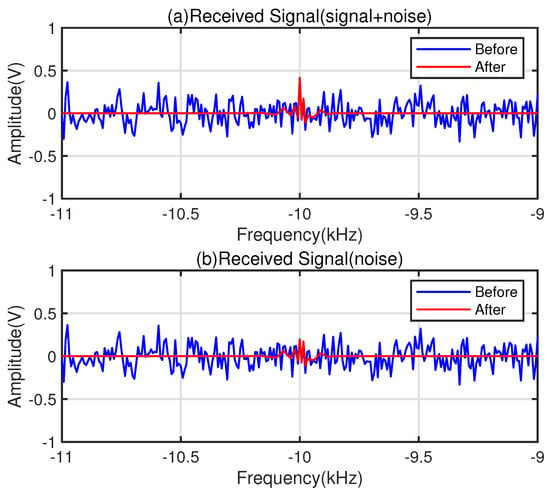
Figure 10. Waveform diagrams before and after denoising: (a) Waveform of the noise signal before and after denoising, (b) Waveform of the received signal before and after denoising.

Through multiple experiments with 1000 sets of signals randomly added in the SNR range from $-40$ dB to $-10$ dB, the results obtained using the denoising method presented in this paper are shown in Figure 11. As the SNR increases, the detection accuracy gradually improves. When the SNR is greater than or equal to $-25$ dB, the detection rate reaches $100\%$, and it exceeds $99\%$ at an SNR of $-28$ dB.

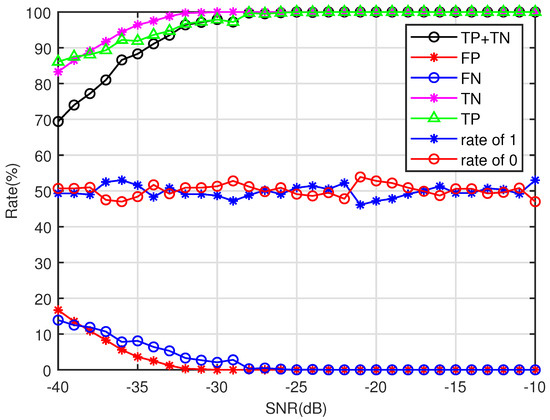
Figure 11. Detection probability plots for 1000 groups, each with a distinct SNR.

The comparison between the SNR values that can be processed in this article and other literature is shown in Table 1. In the selection of SNR for detecting radar signals, the minimum SNR value in other literature is $-20$ dB. The method proposed in this article achieves detection accuracy close to the theoretical limit in simulation experiments at $SNR=-40$ dB.

Table 1. Performance Comparison of Different Methods.

Paper Number	SNR	Method
Reference [10]	8 dB, 1 dB	Wavelet Decomposition + Max Modulus Detection
Reference [11]	−20 dB	Frequency-domain Accumulation + Wavelet Transform
Reference [12]	−18 dB, −20 dB	Multi-layer Autocorrelation + Wavelet Transform
Reference [13]	1.37 dB	Wavelet Transform + Range Guidance
Reference [14]	−19 dB	Two-step De-noising Strategy (TSDS)
proposed method	−40 dB to −10 dB	Pseudo-time De-noising Domain +
		Wavelet Decomposition +
		AdaptiveThreshold Detection

4. Conclusions

This study, based on signal spectra, defines the frequency domain as a “pseudo-time domain” and employs wavelet transform to identify specific structures within the pseudo-time domain waveforms. By applying wavelet transform in the “pseudo-time domain”, thresholds are established according to the characteristics of the transmitted signal and background noise after wavelet decomposition. This process effectively removes noise, significantly enhances the signal-to-noise ratio (SNR), and achieves a high detection success rate. Numerical simulations demonstrate that this method can handle received signals with SNR as low as $-34$ dB or even lower, substantially increasing the SNR and achieving a notable denoising effect. When the SNR is $-40$ dB, the maximum detection success rate can exceed $95\%$. Outdoor experimental results show that the accuracy remains at $90\%$ even when the SNR is $-34$ dB.

Therefore, this method can accurately detect weak signals with very low SNRs and is compatible with existing time-domain denoising methods. It effectively improves the weak signal detection accuracy of low-power radars installed on small platforms such as unmanned aerial vehicles and satellites, enabling the detection of signals at longer distances without altering hardware conditions.

However, it should be noted that the denoising and threshold determination in this method are based on the analysis of reference signals and background noise, which can be computationally intensive. Future work will therefore focus on incorporating deep learning techniques to reduce this computational load, while further optimizing the method to enhance its robustness in more complex environments and exploring its potential applications in other low-SNR scenarios.

5. Patents

The content of this paper has been filed for a patent, titled “A Method for Detecting Weak Return Signals Based on a Wavelet Transform Algorithm in the Pseudo-Time Domain”, with the patent number ZL202110940896.1.