Abstract
The increasing penetration of renewable energy generation in recent years has introduced significant changes and challenges to modern power systems. One of the most critical challenges is the reduction in system inertia, which decreases grid stability and subsequently weakens the electrical network. To address this issue, grid-forming (GFM) converters have emerged as a promising solution to maintain stability in weak grids. This paper proposes three novel control schemes for GFM converters and compares them with the performance of another topology recently published by the same authors. The four evaluated control schemes are based on the virtual flux variable which allows current limiting without using internal current loops, improving the stability of the control system. The assessment includes methods based on PI regulators, using the mathematical flatness property of differential algebra, direct control (DC), and model predictive control (MPC). The results demonstrate the robustness and correct operation of all four control strategies as GFM converters. Furthermore, through tests involving disturbances such as frequency variations, voltage sags, phase jumps, and transitions to islanded mode, their differences in terms of dynamic response, switching frequency, and current quality are clearly evidenced.
1. Introduction
The global energy landscape has undergone a profound transformation due to the increasing integration of renewable energy sources (RES) into power systems to mitigate carbon emissions. Over the past decade, the annual deployment of RES capacity has surpassed that of conventional generation technologies, such as fossil fuels and nuclear power. Recent reports from the International Renewable Energy Agency (IRENA) [1] and the European Network of Transmission System Operators for Electricity (ENTSO-E) [2] highlight that certain electrical networks are approaching scenarios of 100% RES penetration during specific timeframes. This shift has been facilitated by inverter-based resources (IBRs), which play a crucial role in integrating RES into electrical grids [3,4].
The increasing integration of IBRs has transformed power systems, bringing both benefits and new challenges. Unlike synchronous generators (SGs), IBRs lack inherent inertia, reducing grid strength and making the system more susceptible to disturbances [5]. To enable the integration of these technologies, grid-following (GFL) converters have traditionally been used as the primary control method. These converters operate as a current source with current control loops to regulate power injection and rely on phase-locked loops (PLLs) for synchronization [6]. However, their dependence on the grid voltage for operation makes them less effective in weak grids, where PLL performance deteriorates, potentially leading to instability [7]. Furthermore, GFL converters can neither operate autonomously in islanded mode nor contribute to system restoration during blackouts [8,9].
To overcome these limitations, GFM converters have emerged as an alternative solution capable of providing voltage and frequency regulation without requiring an external reference. Unlike GFL converters, which behave as controlled current sources, GFM converters emulate voltage sources, adjusting their output dynamically to support grid stability. This capability allows them to provide essential functions such as inertial response, frequency regulation, blackstart restoration, and improved performance in weak grids [10,11]. As a result, GFM converters are becoming a key technology in power systems with a high share of renewable energy, ensuring a more stable and resilient electrical network. Table 1 shows a summary of the different control techniques adopted for these types of converters.
According to the literature, various control methodologies have been proposed for GFM converters [12,13]. The first category is known as droop control, a technique designed to mimic the behavior of a SG governor [14,15,16,17,18]. This approach is widely used due to its simplicity and ease of implementation; however, it does not inherently provide inertial response. To address this limitation, a second category, referred to as synchronous machine-based controllers, has been developed. These controllers allow GFM converters to emulate inertial response and provide damping capabilities, enhancing their dynamic performance [19,20,21,22,23,24]. Lastly, a third category consists of nonlinear control algorithms, among which virtual oscillation-based control (VOC) stands out as one of the most widely adopted approaches [25,26,27,28,29].
On the other hand, there are several techniques for controlling the voltage vector of a power converter regardless of the methodology implemented, with Field-Oriented Control (FOC) being the most widely used. This approach, commonly applied to electrical machines, involves transforming the three-phase system variables into a synchronous reference frame, defined by axes rotating at a predetermined speed. This transformation enables the decoupled control of both the converter’s voltage and frequency using two PI controllers, which generate the desired reference voltages, obtaining good dynamics and waveforms [30,31,32,33]. Finally, a pulse width modulation (PWM) algorithm, which sets a switching frequency, is used to generate the switching pattern of the converter. Another approach for controlling a converter is to apply the flatness property of differential algebra. This property enables the complete characterization of a system’s dynamics through a specific set of flat outputs once the system is identified as flat. Consequently, by imposing a desired trajectory on these outputs, it is possible to ensure full control over all system variables, both in steady-state and during transient conditions [34,35,36]. Theoretically, this technique shows better performance than PI regulators for transitions between equilibrium points, especially in a nonlinear system [37]. In addition, the simple implementation and parameterization of this type of technique are two of its benefits. Like vector control, this type of technique also needs to use PWM to generate the switching pattern.
Alternatively, DC is an approach that regulates a key variable of the converter without relying on conventional internal control loops. Instead of using PWM, it operates based on switching tables and hysteresis regulators [38,39,40]. This method provides a fast dynamic response and high robustness; however, due to its variable switching frequency, it can introduce resonances in the system. Another control method widely explored in the literature is MPC. This technique relies on a mathematical model of the system to predict the future behavior of the converter’s variables and determine the optimal control action through a defined cost function [41,42,43,44,45]. Additionally, it does not require a PWM, as it directly selects the optimal switching states of the converter. Therefore, as well as the DC, MPC operates with a variable switching frequency, although this can be addresed through the cost function [46,47].
Finally, an essential aspect in the design of GFM is the implementation of current limitation mechanisms, as these converters can withstand significantly lower overcurrents compared to SGs [48]. The literature presents various strategies to mitigate overcurrents during critical disturbances, such as voltage sags. One proposed approach involves switching the converter to GFL mode during disturbances. However, as previously discussed, this method can lead to stability issues [49,50]. Another widely implemented technique is saturating the current regulators, but this can adversely affect the control angle, potentially compromising the converter’s stability [51,52,53]. The use of virtual impedances is also a common solution [54,55]; however, its design and parameterization remain a complex challenge [56]. More recently, a novel control architecture has been proposed to limit current in a straightforward manner. This approach is a synchronous machine-based controller and is based on virtual flux-oriented control (VFOC), eliminating conventional current control loops, which enhances system robustness and stability [57]. Additionally, by incorporating two control blocks that influence both the control angle and the magnitude of the reference flux, this method effectively limits both active and reactive currents, demonstrating strong performance even in commercial converters [58].

Table 1.
Summary of GFM control methods and current limitation strategies.
Table 1.
Summary of GFM control methods and current limitation strategies.
| GFM Approach | Class | Definition | Advantages/Disadvantages |
|---|---|---|---|
| Methodology | Droop control [14,15,16,17,18] | Mimics the behavior of a SG governor | ✓ Simple implementation
✗ Does not provide inertial response |
| Synchronous machine-based controllers [19,20,21,22,23,24] | Mimics the behavior of a SG | ✓ Emulates inertial response and provides damping capabilities
✗ Output power can be more oscillating | |
| Nonlinear control algorithms [25,26,27,28,29] | Emulates the dynamics of a weakly nonlinear oscillator using a single dead-zone oscillator | ✓ No need to determine any control angle
✓ Allows the synchronization of several converters running in parallel ✗ Does not provide inertial emulation or fault-ride through capability | |
| Voltage Vector Control | Field-Oriented Control [30,31,32,33] | Decouples control of both the converter’s voltage and frequency using two PI controllers | ✓ Good dynamics and waveforms
✓ Fixed switching frequency (PWM) |
| Flatness theory [34,35,36] | Ensures full control over all system variables by imposing a desired trajectory on flat outputs | ✓ Easy implementation
✓ Fixed switching frequency (PWM) | |
| Direct control [38,39,40] | Regulates a key variable of the converter without relying on conventional internal control loops | ✓ Fast dynamic response and high robustness
✗ Variable switching frequency | |
| Model predictive control [41,42,43,44,45] | Uses a mathematical model to predict the converter’s future behavior and determine the optimal control action | ✓ Fast transient performance, inclusion of nonlinearities and constraints
✗ Variable switching frequency (can be addresed through the cost function) | |
| Current Limitation | Switch to GFL control [49,50] | Uses a backup PLL | ✗ May cause instabilities |
| Saturate regulators [51,52,53] | Saturates the reference currents of the internal current control | ✗ Can adversely affect the control angle, potentially compromising the converter’s stability | |
| Virtual impedances [54,55,56] | Increase the converter’s output impedance | ✓ Balances current limitation and stability
✗ Requires complex design | |
| Virtual-flux-based control [57,58] | Does not use current control loops | ✓ Easy design and implementation, limiting current in a robust way |
Nomenclature:✓ for advantages and ✗ for disadvantages.
This paper proposes, as its main contributions, three new control schemes based on the virtual flux variable. However, unlike the vector control approach presented in [57], the new schemes are based on flatness theory, DC, and MPC. Their performance as GFM is evaluated and compared following the requirements set by the National Energy System Operator (NESO) [59,60], using the results obtained on a Hardware-in-the-Loop (HIL) platform.
This study is structured as follows. Section II describes the implemented system and how the virtual flux variable is measured. Section III presents the four control algorithms to be compared. Then, Section IV presents the results obtained for the different tests on the HIL platform, and finally, Section V summarizes the conclusions and future work.
2. System Description and Virtual Flux Measurement
Figure 1 illustrates the schematic of a two-level Voltage Source Converter (VSC) connected to the grid through a filter, where and represent the inductance and resistance of the coil, respectively. The converter current i is measured at this point, while the capacitance is where the output voltage v is measured. The parameter e represents the internally generated voltage of the converter.
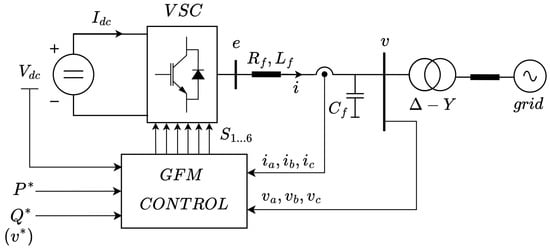
Figure 1.
Generic diagram of a GFM.
On the side of the inverter, both the current () and voltage () are measured. Using these measurements, along with the reference values for active power () and reactive power (), the four control schemes analyzed in this article can be implemented. These schemes generate the corresponding switching pattern defined by the six switching signals ().
On the other hand, from the schematic shown in Figure 1, the following electrical equation can be obtained, if is neglected
In practical applications, the inductors used in power converter filters are designed with a high quality factor, with a typical ratio of around 10 or higher. Therefore, the impedance of the inductor is dominated by the inductive term, making the resistive component negligible in comparison.
As described in [57], the grid voltage v can be expressed as
where represents the grid flux. Substituting (2) into (1) yields
The derivative term in (3) represents the variable known as virtual flux, which can be expressed as
Once the converter is connected to the grid, the grid voltage and the converter output voltage become equal (v). Therefore, isolating the grid flux in (2) and substituting it into (4), the virtual flux of the converter can be expressed as
As discussed in [57], the expressions for active power (P) and reactive power (Q) are given by
where represents the reactance of the system based on the grid frequency (), and is the phase angle between the converter’s internal voltage and its terminal voltage . Since the internal voltage is directly related to the virtual flux , its adjustment enables the regulation of both active and reactive power in the converter.
3. Control Schemes
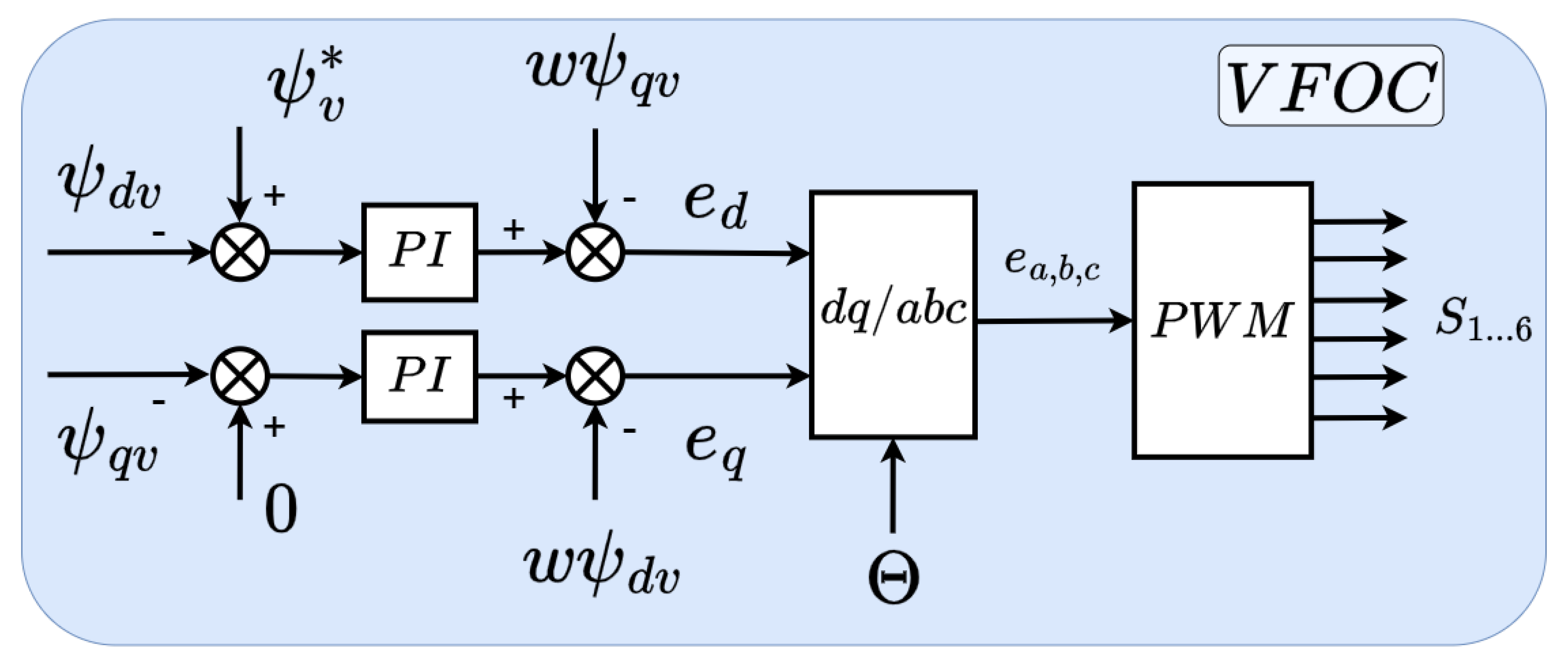
In this section, the four control schemes compared in this article are developed, starting with a summary of the model based on virtual flux-oriented control (VFOC), which is shown in Figure 2 and has already been validated by the same authors even in a commercial converter [58]. Next, the implementation of flatness-based control (FBC), direct control (DC), and model predictive control (MPC) are detailed as a function of the virtual flux variable. The three proposed models attempt to replace the block located on the right side in Figure 2 (VFOC) by other methods of voltage vector control.
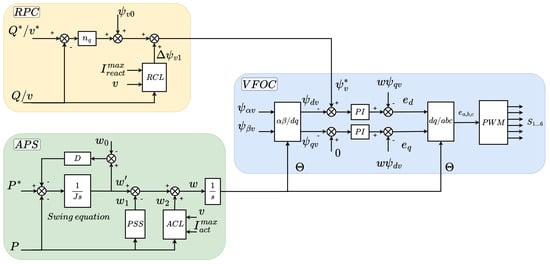
Figure 2.
Virtual flux-oriented control scheme.
3.1. Virtual Flux-Oriented Control
As shown in Figure 2, the original control scheme consists of three control loops. The first one, located in the upper left part of Figure 2, is referred to as the Reactive Power Control (RPC). This block enables the decision of whether to regulate the reactive power (PQ mode) or the converter voltage (PV mode), with the second case being used for the tests performed in this article. A proportional controller, with gain, determines the reference magnitude of the virtual flux to be imposed on the converter, .
The terms and correspond to the nominal flux, set at 1 p.u., and the output of the reactive current limiter (RCL) block, respectively. The latter is responsible for limiting the reactive current supplied by the converter by adjusting the reference flux magnitude whenever the predefined limits are exceeded. Therefore, the calculation of the reference flux can be expressed as
The second control loop, referred to as Active Power Synchronization (APS), is located in the lower left part of Figure 2. This loop determines the control angle , allowing the converter to emulate the inertial response of a SG and damp power oscillations. The first stage of the loop calculates the term which emulates the swing equation of a SG, where J represents the virtual moment of inertia, defined as twice the inertia constant H, and the damping coefficient D.
Next, the terms and are introduced. The first, , corresponds to the output of the Power System Stabilizer (PSS), responsible for damping the active power response. The second, , is the output of the active current limiter (ACL), which operates similarly to the reactive current limiter but regulates the active current of the converter by adjusting the control angle. Thus, the control angle used for Park transformations is obtained through the following equation
Finally, the virtual flux-oriented control (VFOC) loop is implemented. In this loop, the components of the virtual flux are regulated using two PI controllers along with the feedforward signals (, ) to compensate the cross-coupling terms. Once the reference voltages and are obtained, an inverse Park transformation is applied, followed by a PWM modulation scheme to generate the converter’s switching signals .
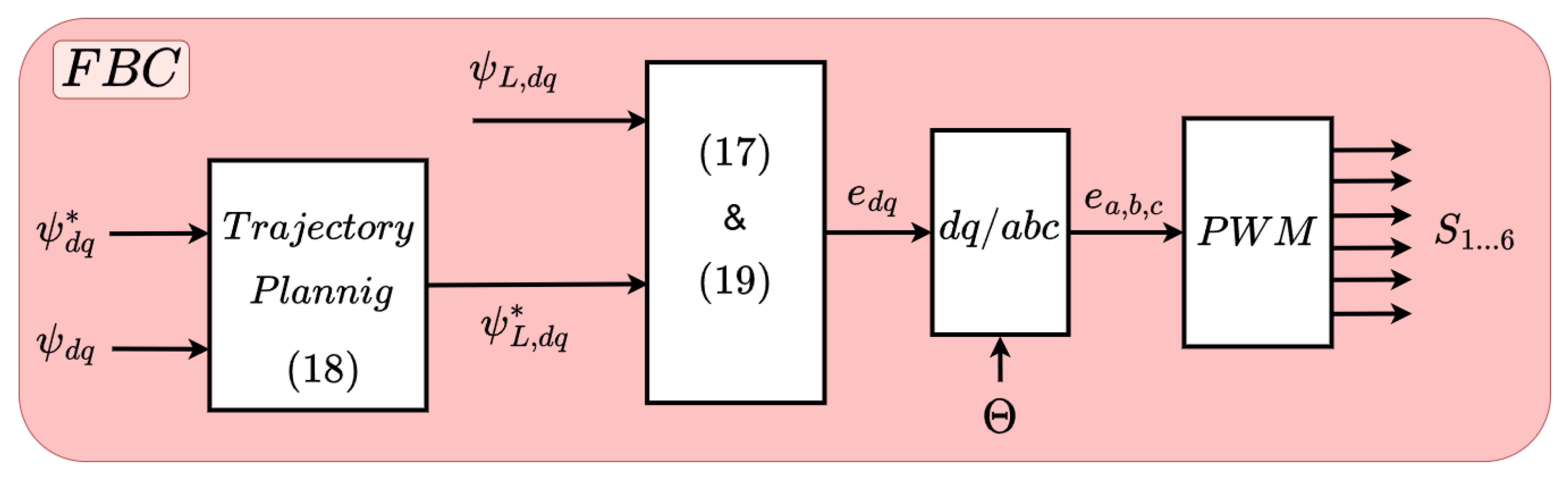
3.2. Flatness-Based Control
The concept of flatness originates from differential algebra [61] and describes a particular class of systems whose dynamics and trajectories can be fully determined by a specific set of variables. A system is considered differentially flat if there exists an appropriately chosen output variable, referred to as the ‘flat output’, from which all state variables and control inputs can be explicitly expressed as algebraic functions, using only a finite number of derivatives of this output without the need to integrate any differential equations [34,36]. More formally, consider a system represented by
where represents the state vector and denotes the input vector. The system is said to be differentially flat if, and only if, all states and inputs can be rewritten as algebraic functions of a chosen system output y and a finite number of its derivatives
From (4), the flux generated in the filter inductor can be expressed as
The variable is proposed as the flat output of the system, which can be expressed in terms of the current i, serving as the system’s state variable
As observed, this satisfies the first condition in (11) required for the system to be classified as differentially flat. From (4), the current can be solved, expressing the state vector as a function of the system output, thereby fulfilling the second condition given in (12)
Finally, the internal voltage e, obtained from (3), is considered as the system input. This voltage can be rewritten in terms of the derivative of the selected output
Thus, the third and final condition from (13) is also satisfied, ensuring that the system can be classified as differentially flat.
As previously discussed, one of the key properties of differentially flat systems is that all system dynamics can be fully characterized through the selected flat output. Consequently, by imposing a trajectory on this output, it is possible to ensure that all system variables are properly controlled both in steady-state and during transient conditions. In the proposed control system, the reference output is chosen as the inductor flux , which its components can be obtained as
where represents the reference flux magnitude obtained from the RPC loop shown in Figure 2, while is set to 0. In addition, represents the measured grid flux. To ensure that the system follows the reference accurately, a second-order control law is proposed to eliminate steady-state errors in both components, given by
Solving for (which corresponds to the derivative of the system’s output variable, ), and substituting the result into (17), the internal converter voltages can be determined. Furthermore, for the Park transformations (-abc), the control angle obtained in the APS loop , depicted in Figure 2, is used. These values are then used to compute the duty cycles required for the PWM modulator, which ultimately determines the switching states of the power semiconductors. Thus, the VFOC control block depicted in Figure 2 can be replaced by the proposed control scheme illustrated in Figure 3.
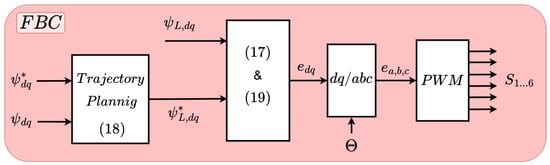
Figure 3.
Flatness-based control scheme.
For parameter tuning, is set to 0.7, while is chosen such that it satisfies
Therefore, in the experiments conducted, was selected to be ten times lower than , where is derived from the fixed switching frequency . In addition, from a practical standpoint, in order to simplify the algorithm implementation, the term in (19) was neglected, as its removal does not significantly impact the system’s dynamic performance.
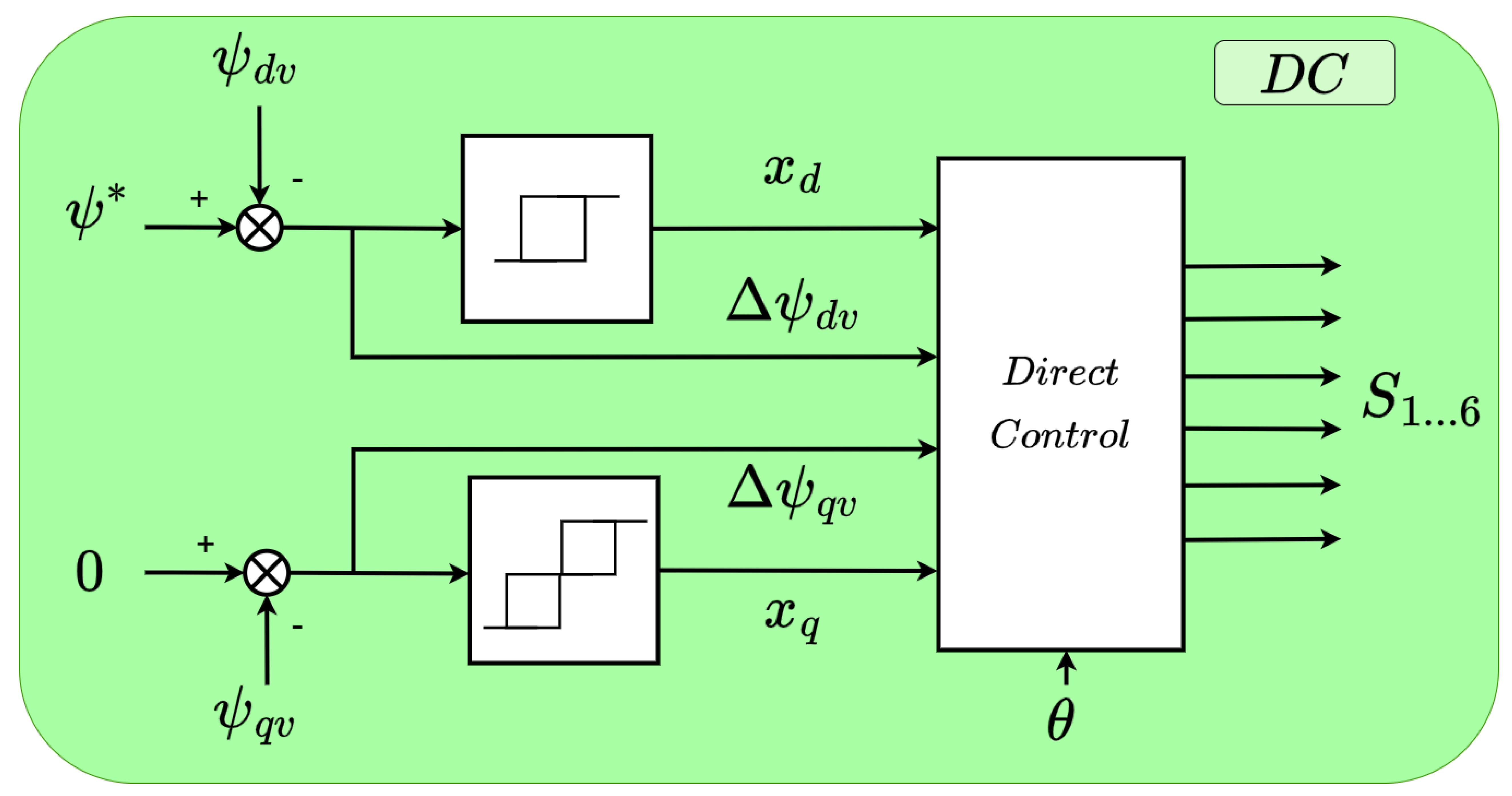
3.3. Direct Control
During the design of the original control scheme [57], the direct relationship between the converter’s internal voltage and its virtual flux was established as
This relationship allows active and reactive power regulation through virtual flux control. Leveraging this direct relationship, a direct control approach can be implemented for the main control loops, theoretically improving system dynamics under fast transients. The proposed direct control scheme is illustrated in Figure 4, where two hysteresis controllers and a control logic unit replace the PI regulators from the VFOC scheme. This control method determines the optimal switching pattern for the IGBTs and the duration for which each switching state should be applied, ensuring that the virtual flux follows its reference values as closely as possible.
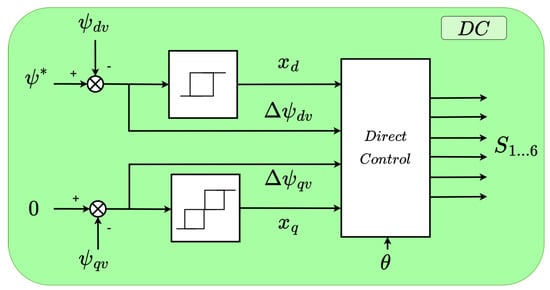
Figure 4.
Direct control scheme.
The outputs of the two hysteresis regulators are denoted as and , where their values depend on the number of levels in the respective hysteresis controllers. For the d-component of the flux, a two-level regulator is selected, meaning that can take values of either 1 or . In contrast, the q-component is regulated using a three-level hysteresis controller, allowing to take values of 1, 0, or . A three-level regulator is chosen for the q-component because precise control of this variable is essential for ensuring proper synchronization between the converter and the grid. The values of and depend on the measured error in each flux component, and , the hysteresis bandwidth, and the position within the hysteresis cycle. In the experimental tests conducted in this study, the bandwidth for both hysteresis controllers was set to p.u.
To determine the switching pattern applied to the converter, a control logic based on twelve sectors and eight possible switching vectors has been implemented, as shown in Figure 5. These eight switching vectors are numbered 0 to 7 and are depicted in blue in Figure 5. Each vector has associated with it a possible conbination for the IGBTSs defined as with , , being the state of the converter’s upper IGBTs corresponding to phase , respectively. For the lower switches of each phase, the negated state of the upper switch is used , , . Finally, the vectors and are known as null vectors, and the choice of using one or the other is made on the basis of the one that requires the minimum switching state variations to reduce the number of commutations and average switching frequency.
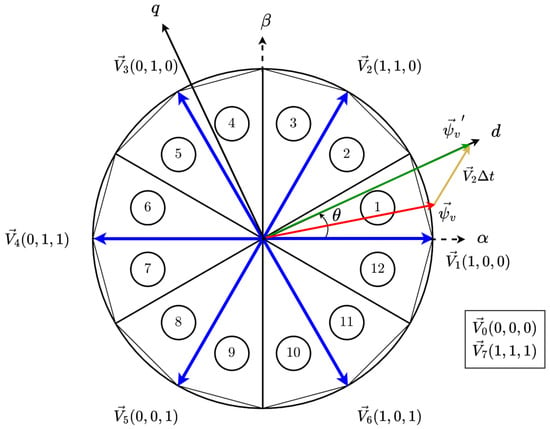
Figure 5.
Vector diagram of direct control and example of its application in sector 1.
An example of direct control operation is illustrated in Figure 5, where the virtual flux vector reaches a new value after applying a voltage vector for a duration .
Furthermore, to select the appropriate voltage vector to be applied, a decision must be made regarding whether to prioritize the error in or . In the developed control algorithm, the component with the larger error is given higher priority. Based on these conditions, the switching logic for direct control is summarized in Table 2.

Table 2.
Direct control logic.
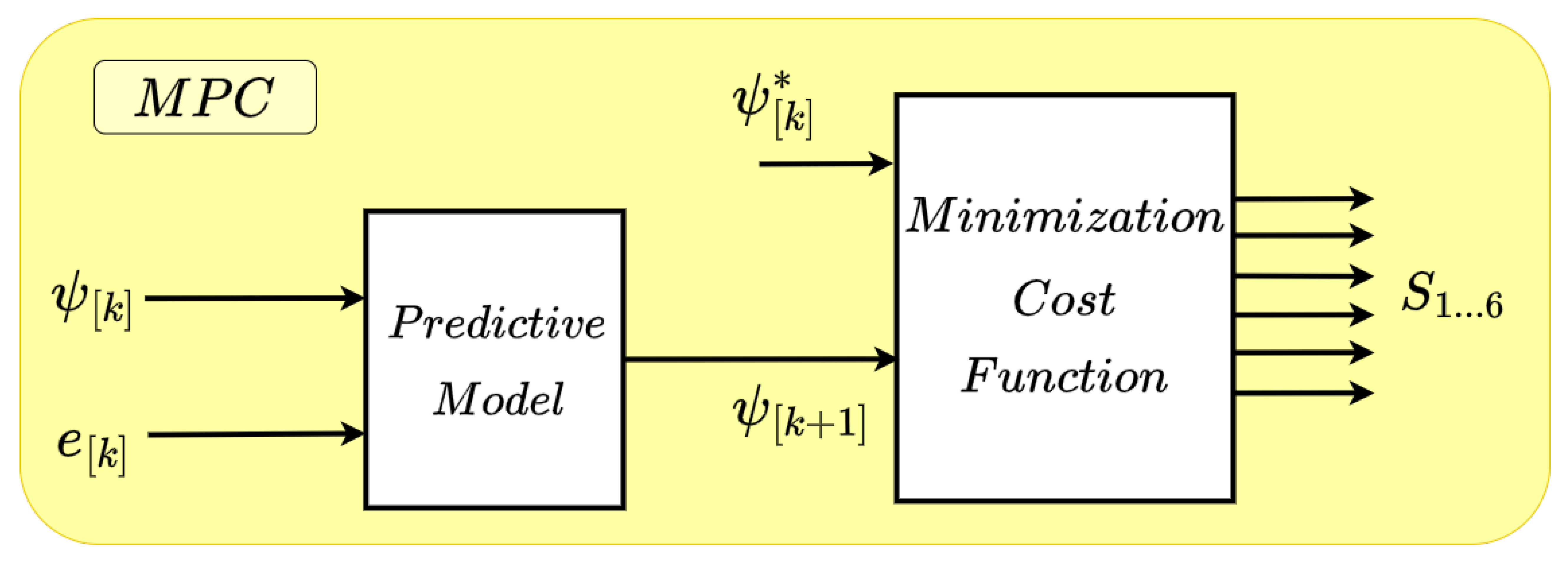
3.4. Model Predictive Control
The control of a power electronic converter can be defined as the application of the appropriate control action to ensure that the control variable follows its reference value as closely as possible. To determine the optimal control action, a MPC strategy can be employed. In this case, a predictive control algorithm has been designed, similar to the one detailed in [41].
At a given time instant , the control variable is evaluated, and based on its value, one of the possible control actions is applied. These actions correspond to a finite set of switching states that can be programmed, matching the seven vectors previously defined for the DC algorithm. To determine the optimal control action, the control variable is first predicted for each possible action using a discrete prediction function
where n represents the number of possible control actions. In this case, the control variable is the virtual flux , obtained from the equation previously demonstrated in [57].
Discretizing (23) for a sampling time , the following expression is obtained
which leads to the prediction function for the virtual flux
where is the virtual flux measured at the current time step, and is the converter’s internal voltage applied during the sampling period. This value is determined by the switching state, as shown in Table 3.

Table 3.
Possible switching states and voltage vectors for a three-phase inverter.
Once all possible virtual flux values are computed, the optimal voltage vector is selected using a cost function, which minimizes the error between the predicted control variable and its reference value. The cost function used in this case is
where is the reference flux calculated in the RPC loop, and is the predicted flux for each possible control action. To obtain the components of both fluxes, the control angle obtained in the APS has been used, allowing the converter to provide inertial response. The voltage vector leading to the lowest cost is applied to the converter, resulting in the control scheme illustrated in Figure 6. This approach aims to minimize the error between the measured virtual flux and the computed reference value. The quadratic cost function is selected since it penalizes or increases the cost for large errors (>1), while it is less reactive to smaller errors (0–1).
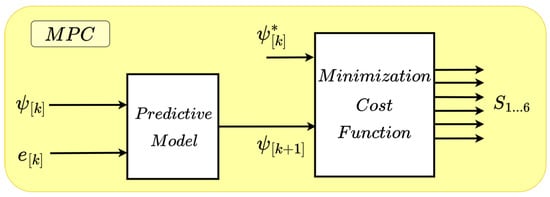
Figure 6.
Model predictive control scheme.
It is important to note that this predictive control method ideally assumes that there is enough time within each control period to measure the variables, compute predictions, and execute the control action. However, in practical implementations, it is often challenging to complete all these tasks within a single sampling period, leading to an overlapping of computation and control execution.
To address this issue, a two-step prediction approach is proposed instead of predicting only the next switching state. This concept is explained in [41] and depicted in Figure 7. Essentially, the described prediction process is first executed to determine the optimal voltage vector. Then, once this vector is selected, the control variable’s future state is predicted. The entire prediction algorithm is then repeated, but this time using the estimated flux from the first step as the measured value. This results in predicting the appropriate voltage vector two sampling periods ahead, ensuring that measurement acquisition, control computation, and control execution do not overlap within a single sampling period . Naturally, the sampling period must be longer than the total time required for measuring, computing, and executing the control algorithm.
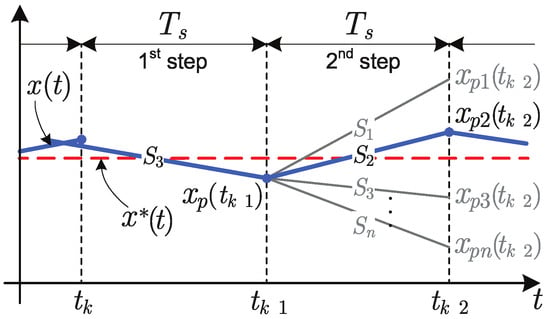
Figure 7.
MPC operation with a two-step prediction horizon [41].
4. HIL Results and Comparison
This section presents a comparative analysis of the four control schemes based on the requirements established for GFM by NESO, which outlines the essential functionalities and performance criteria expected from GFM converters operating in Great Britain. A concise summary of the core requirements is presented below:
- Reactive Power Capability: GFM units must be capable of both generating and absorbing reactive power.
- Voltage Regulation: GFM converters are expected to maintain control over their internal voltage vector, both in magnitude and angle, regardless of grid or load conditions.
- Active Power Control: These converters must emulate the behavior of synchronous machines, supplying active power in response to control setpoints.
- Frequency Support: GFM units should respond to frequency deviations by adjusting their active power output, thereby contributing to system frequency stability.
- Damping of Oscillations: PSS or equivalent mechanisms are encouraged to mitigate low-frequency oscillations. In this case, prior validation has been conducted by the authors using Hardware-in-the-Loop simulations [62].
- Fault Ride Through and Dynamic Current Injection: GFM converters must remain connected during grid faults and must be able to inject reactive current rapidly to support voltage recovery.
- ROCOF Response: These units must be able to provide inertial response by injecting active power during periods of high rate of change of frequency (ROCOF), in addition to regular frequency support.
- Phase Jump Response: In events involving sudden phase angle changes between the converter and the grid, the system must manage transient power exchanges to maintain stability.
To evaluate their performance as established by NESO, several tests have been conducted, including frequency variations in the grid, phase jumps, voltage sags, and grid disconnection to assess islanded operation. These tests have been performed in the Hardware-in-the-Loop (HIL) setup shown in Figure 8. The experimental setup consists of a real-time RTDS simulator, where the plant depicted in Figure 1 has been modeled, and a dSpace controller board executing the control algorithms. The parameters used for both platforms can be found in Appendix A.

Figure 8.
HIL setup.
Throughout all the tests, the same nomenclature has been used for all signals. Results corresponding to the virtual flux-oriented control scheme are represented in blue with the subscript “VFOC”. The results for the control scheme based on flatness theory are shown in red with the subscript “FBC”. The direct control results are displayed in green with the subscript “DC”, and finally, the model predictive control results are represented in yellow with the subscript “MPC”.
4.1. Frequency Variation
During this test, the grid frequency was reduced by 2.5 Hz with a Rate of Change of Frequency (ROCOF) of 2 Hz/s at t = 0.5 s, as depicted in the upper first of Figure 9. As observed in the second plot, the converter starts injecting active power proportionally to the frequency deviation. The injection of active power leads to a change in the voltage magnitude. To compensate for this effect, given that the converter operates as a PV node, it begins to absorb reactive current as shown in the third plot of Figure 9, ensuring that the voltage magnitude remains at 1 p.u. Since the constant D has been set to 50, for a 2.5% variation in frequency the converter would have to supply 250% of its rated steady state power, which would cause severe damage to the equipment. Therefore, the active current limiter starts to act, not allowing the maximum current of the converter, set at 1.25 p.u., to be exceeded, as shown in the last plot of Figure 9. This confirms that the converter is capable of injecting active power to the system during frequency variations while ensuring the proper operation of the active current limiter across all four control schemes evaluated. Furthermore, in terms of dynamic response, the converter exhibits nearly identical performance for all four control strategies analyzed.
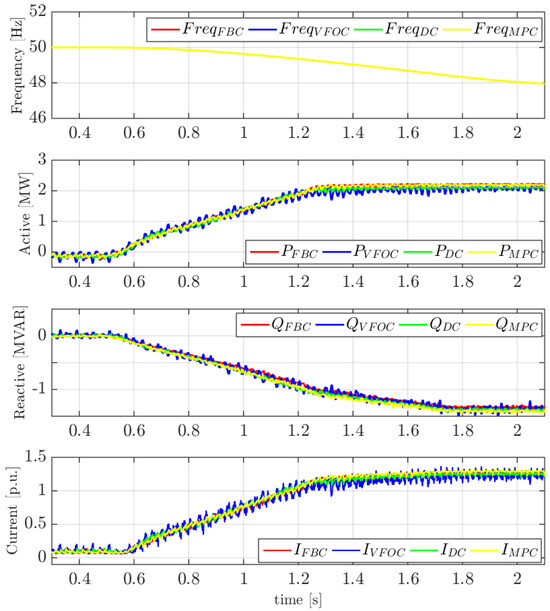
Figure 9.
Frequency, active and reactive power and current during a frequency variation.
On the other hand, Figure 10 shows the output current waveforms of the converter once the active current limiter is activated. As observed, the proposed models achieve a similar waveform quality, except for the VFOC, which exhibits slight distortions compared to the other control algorithms.
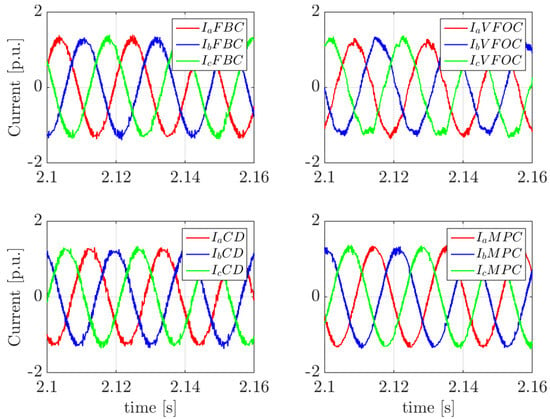
Figure 10.
Instantaneous currents during a frequency variation.
4.2. Phase Jump
In this test, a 20° phase jump is induced in the grid at t = 0.5 s, and the results are presented in Figure 11. The first plot illustrates the grid frequency measured through a PLL, which experiences a temporary disturbance at the moment of the phase jump before stabilizing back to its nominal value. The second and third plots display the active and reactive power measured during the test, respectively. Similar to the previous case, the reactive power dynamics remain almost identical across all four control algorithms, with the FBC method exhibiting slightly higher oscillations compared to the others.
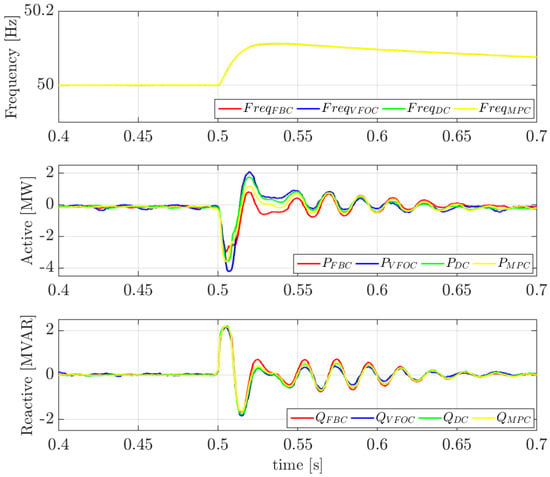
Figure 11.
Frequency, active and reactive power during a phase jump.
On the other hand, significant differences emerge in the active power response of the converter under this rapid disturbance, which directly impacts the APS. While all control schemes reach steady state in approximately the same timeframe, the VFOC and DC algorithms exhibit higher oscillations at the time when phase jump occurs, with VFOC being the most affected (reaching a peak of −4 MW). In contrast, FBC proves to be the most resilient, only reaching a peak of less than 3 MW and displaying the least deviation during this type of disturbance.
4.3. Low Voltage Ride-Through
This test shows the response to a balanced three-phase voltage sag with a depth of 50% and a duration of 250 ms in the grid. Figure 12 presents the instantaneous voltage waveforms during sag for the four control algorithms. As observed, in all cases, the converter withstands voltage sags successfully and maintains stability after recovery, although differences in waveform characteristics can be noted. Both FBC and MPC exhibit resonance effects, distorting the voltage waveform, whereas the DC control introduces noticeable noise in the voltages. In contrast, the VFOC approach maintains voltages more effectively.
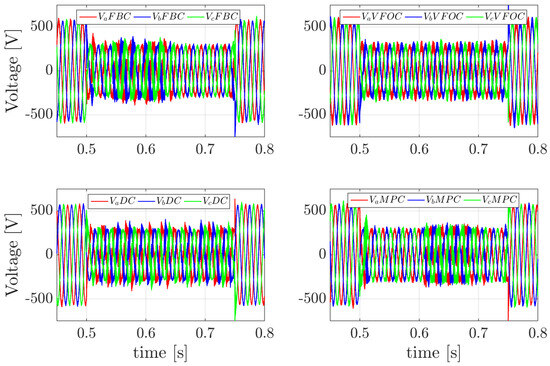
Figure 12.
Instantaneous voltages during a three-phase fault.
Figure 13 illustrates the components of the virtual flux generated by the converter. The d-component behaves similarly across all four control strategies, although MPC shows a slightly lower magnitude compared to the others. However, significant differences are observed in the q-component behavior. Both MPC and FBC introduce noise in this component, which affects the waveform of the voltages and currents injected by the converter. This noise originates from the reactive current limiter. The reason why it impacts MPC and FBC but not DC and VFOC is that these two methods do not directly control the reference flux modulus calculated in the RPC. Instead, FBC regulates the flux produced in the filter inductor, , while MPC operates based on a future estimation of the virtual flux, .
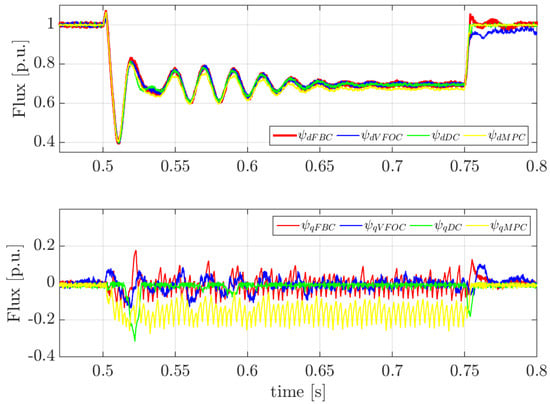
Figure 13.
Flux components during a three-phase fault.
Another key observation is that the q-component of MPC remains shifted (around −0.15 p.u.) compared to the other methods, leading to differences in the power response of the converter during the voltage sag, as will be analyzed later. Lastly, regarding dynamic response, DC proves to be the fastest control algorithm, responding quickly to both the entry and the exit of the voltage sag, whereas VFOC exhibits the slowest recovery once the disturbance clears.
Figure 14 and Figure 15 illustrate the active and reactive power of the converter, along with the output current magnitude, during which both the entry and exit of the voltage sag. All four control strategies behave similarly and according to (8), delivering a reactive current during the sag limited by the reactive current limiter. However, when analyzing the dynamic response at the entry of the fault, VFOC exhibits the most pronounced impact, generating a higher current peak (around 2.5 p.u.) compared to the other control schemes. Once the three-phase fault occurs, DC stabilizes the fastest, whereas MPC takes the longest to settle.
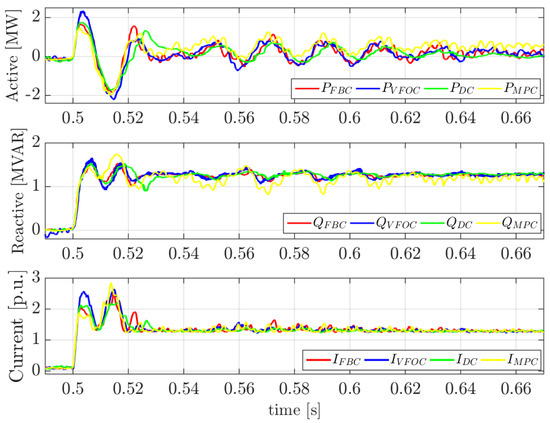
Figure 14.
Active and reactive power and current modulus during the voltage fault entry.
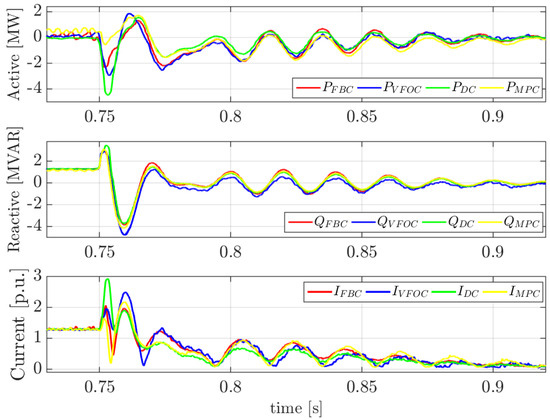
Figure 15.
Active and reactive power and current modulus during the voltage fault exit.
Additionally, an important distinction is observed in the power delivered by the converter in this scenario. Unlike VFOC, FBC, and DC, the MPC strategy provides slightly less reactive power and instead injects a small amount of active power. This causes a shift in the control angle, leading to a nonzero q-component of the flux, as evidenced in Figure 13.
Regarding the exit from the voltage sag, DC is the most affected, producing the highest current peak (around 3 p.u.) at the moment of the fault clearing. On the other hand, as also reflected in the flux components in Figure 13, VFOC exhibits the slowest recovery, taking the longest to return to its pre-fault operating condition. Meanwhile, MPC and FBC demonstrate a nearly identical dynamic response throughout the process.
Finally, Figure 16 presents the instantaneous converter output currents during the voltage sag, where the reactive current limiter is actively operating. Both MPC and FBC exhibit highly distorted currents, introducing the noise observed in the q-component of the flux shown in Figure 13.
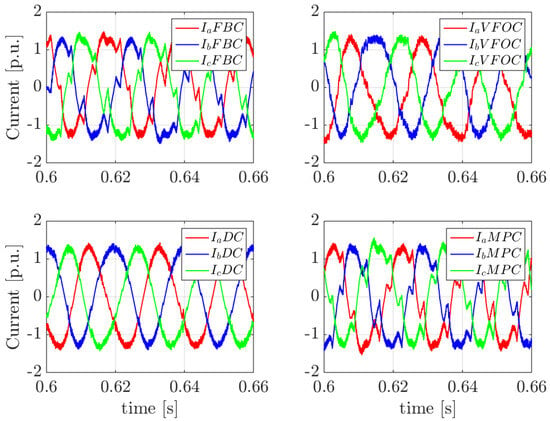
Figure 16.
Instantaneous currents during a three-phase fault.
4.4. Islanded Mode Operation
For this test, a three-phase resistive load is first connected at point v in Figure 1. Then, at t = 0.5 s, the grid is disconnected, leaving the converter supplying the load in islanded mode. Figure 17 illustrates the output voltage magnitude of the converter, the frequency measured through a PLL, and the active and reactive power.
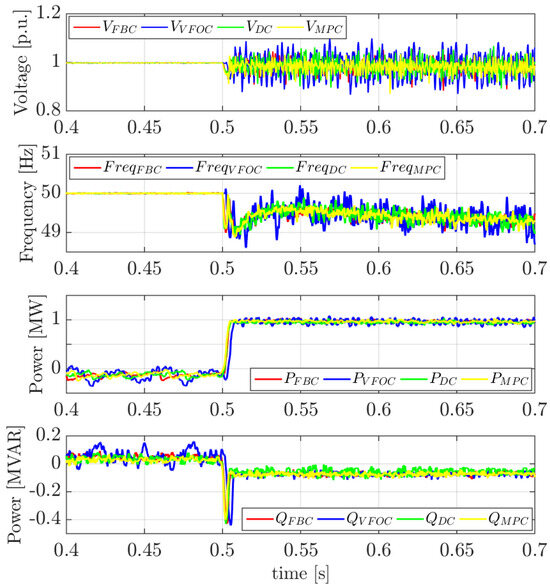
Figure 17.
Voltage, frequency, and active and reactive power during the transition to islanded mode.
At the moment of grid disconnection, the converter successfully supplies the load while maintaining the nominal voltage (1 p.u.) in all four cases. However, as observed in the first graph of Figure 17, the VFOC algorithm exhibits more noise in the voltage waveform compared to the other control schemes. In the second graph of the same figure, a slight decrease in frequency is observed in the four systems due to the droop control and the value of the connected load. The last two graphs show that once the grid is disconnected, which was initially supplying the load, the converter increases its active and reactive power to the necessary levels to maintain the required voltage and frequency. Regarding dynamic performance, all four control strategies exhibit almost identical behavior in this scenario.
Furthermore, Figure 18 displays the instantaneous output current waveforms of the converter for the four control schemes at the moment of grid disconnection. As can be seen, their behavior in islanded mode is quite similar across all cases. However, the VFOC system introduces some noise into the waveforms, which aligns with the observations made in Figure 17.
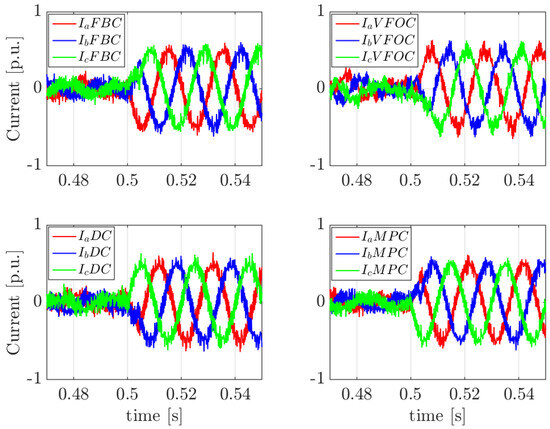
Figure 18.
Instantaneous currents during the transition to islanded mode.
4.5. Switching Frequency Comparison
Finally, the switching frequency () of each control algorithm has been analyzed in Figure 19, given that one of the key characteristics of DC and MPC is their variable switching frequency operation. To assess this, a Fast Fourier Transform (FFT) was used to estimate the spectrum of the voltage between phase a of the converter and the negative terminal of the DC bus, , which value conmutates between 0 and .
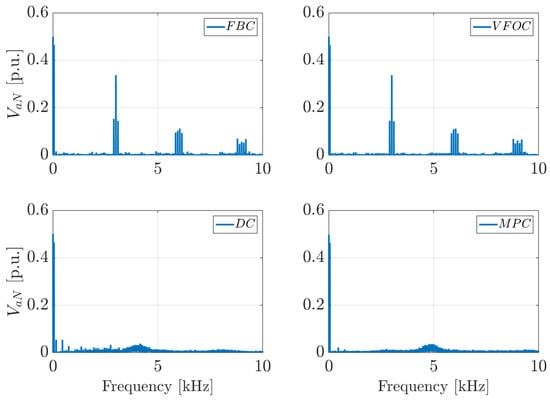
Figure 19.
Switching frequencies.
The first two graphs, corresponding to the FBC and VFOC, exhibit similar harmonic profiles since both use PWM for voltage modulation, which enforces a fixed switching frequency. As seen in both cases, the dominant harmonic components, aside from the component and the fundamental frequency, appear at the predefined switching frequency of 3000 Hz, as well as in its neighboring frequencies and higher multiples, albeit with lower intensity. This behavior is industrially accepted [41].
On the other hand, for the DC and MPC models, the harmonic concentration is more dispersed, indicating that the switching frequency varies dynamically. In the case of DC, the switching frequency predominantly concentrates around 4000 Hz, with the presence of low-frequency harmonics, which could potentially introduce operational issues. Meanwhile, for MPC, the harmonic content in the voltage fluctuates around 5000 Hz. The fact that these control strategies operate at a higher switching frequency is a notable drawback, although both control schemes can be adjusted to operate at other switching frequencies, particularly MPC, where modifications to the cost function could control the switching frequency and voltage spectrum [46,47]. Higher switching frequencies lead to increased switching losses in the power semiconductors and impose greater computational demands on the control hardware.
5. Discusion and Conclusions
The primary goal of this paper is to propose three novel control methods based on the virtual flux control variable, applied to grid-forming converters. These methods rely on three different strategies: the flatness property, direct control, and a predictive model. The results demonstrate that the newly designed systems can successfully operate as grid-forming converters, albeit with some minor differences. To validate the performance of these methods, their behavior has been compared to the original VFOC control scheme previously developed by the same authors, with the key conclusions summarized in Table 4. The nomenclature used was two green ticks for the algorithms that obtained the best response, one green tick for a suitable response, one red cross for a less favorable response, and two red crosses for the worst cases.

Table 4.
Virtual flux methods comparison.
Regarding their ability to provide inertial response and the performance of the active current limiter, all four control schemes achieve this functionality and a nearly identical response. However, during a phase jump, the original VFOC system is the most affected, followed by DC. In contrast, FBC exhibits the most robust behavior, while MPC achieves an optimal performance in this scenario.
When analyzing the performance during voltage sags, the DC method demonstrates the best response both during the sag’s entry and throughout its duration. On the other hand, the reactive current limiter introduces significant noise in the FBC and MPC methods, leading to distorted output currents. Upon sag clearance, the DC control shows a worse performance, presenting a higher current peak and slower recovery.
In terms of their grid-forming performance in islanded mode, all four control strategies show similar behavior, maintaining system stability and the desired operating conditions. Finally, in terms of switching frequency, both the DC and MPC techniques operate with variable switching frequencies, which results in higher average switching frequencies. Nevertheless, as discussed earlier, MPC switching frequency could be regulated through an appropriate cost function adjustment.
In future work, it is recommended to explore potential strategies to mitigate the weaknesses identified in each control method. For instance, developing an improved approach to better limit the reactive current in the FBC and MPC schemes could significantly enhance their performance. Additionally, further investigation into optimizing the switching patterns of the DC and MPC techniques might yield better efficiency and power quality.
Author Contributions
Conceptualization, J.D.F., J.E.-G., S.A.G., S.K., H.R. and J.L.R.A.; methodology, J.D.F., J.E.-G., S.A.G., S.K., H.R. and J.L.R.A.; software, J.D.F.; validation, J.D.F., J.E.-G., S.A.G., S.K., H.R. and J.L.R.A.; formal analysis, J.D.F., J.E.-G., S.A.G., S.K., H.R. and J.L.R.A.; investigation, J.D.F., J.E.-G.; resources, S.A.G. and J.L.R.A.; data curation, J.D.F.; writing—original draft preparation, J.D.F.; writing—review and editing, J.E.-G., S.A.G., S.K., H.R. and J.L.R.A.; visualization, J.D.F.; supervision, J.E.-G., S.A.G., S.K., H.R. and J.L.R.A.; project administration, S.A.G. and J.L.R.A.; funding acquisition, S.A.G. and J.L.R.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Spanish Research Agency under Grant TED2021-130468B-I00 MCIN/AEI/MCIN/AEI/10.13039/501100011033. NextGenerationEU/PRTR: CONTRIBUTION OF GRID FORMING CONVERTERS TO POWER SYSTEMS STABILITY AND OPERABILITY WITH HIGH PENETRATION OF RENEWABLE ENERGY SOURCES (GFM-RES). This work was also supported, in part, by the following projects from the Agencia Nacional de Investigacion y Desarrollo (ANID): AC3E (ANID/Basal/AFB240002), SERC Chile (ANID/FONDAP/1523A0006).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Joaquín Eloy-García was employed by the company Ingenia Power Solutions SL. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ACL | Active Current Limiter; |
| APS | Active Power Synchronization; |
| DC | Direct Control; |
| ENTSO-E | European Network of Transmission System Operators for Electricity; |
| FBC | Flatness-Based Control; |
| FOC | Field-Oriented Controller; |
| GFL | Grid-following; |
| GFM | Grid-forming; |
| HIL | Hardware-in-the-Loop; |
| IBR | Inverter-Based Resources; |
| IRENA | International Renewable Energy Agency; |
| MPC | Model Predictive Control; |
| NESO | National Energy System Operator; |
| PSS | Power System Stabilizer; |
| PLL | Phase-Locked Loop; |
| PWM | Pulse Width Modulation; |
| RES | Renewable Energy Source; |
| RCL | Reactive Current Limiter; |
| ROCOF | Rate of Change of Frequency; |
| RPC | Reactive Power Controller; |
| SG | Synchronous Generator; |
| VFOC | Virtual-Flux Orientation Control; |
| VSC | Voltage Source Controller; |
| VOC | Virtual Oscillation-based Controller. |
Appendix A
Appendix A.1. System Parameters
| Parameter | Value | Units |
| DC voltage, | 1200 | V |
| Converter rated power, | 2 | MVA |
| Converter rated voltage (line to line), | 690 | V |
| Filter resistance, | 0.7104 | mΩ |
| Filter inductance, | 200 | μH |
| Filter capacitance, | 200 | μF |
| Nominal frequency, | 50 | Hz |
| Switching frequency, | 3000 | Hz |
Appendix A.2. Control System Parameters
| Parameter | Value | Units |
| Damping constant, D | 50 | p.u. |
| Inertia constant, H | 3.5 | s |
| PSS time constant, | 1.2 | s |
| PSS constant, | 0.01 | p.u. |
| RCL gain, | 0.15 | p.u. |
| RCL gain, | 0.15 | p.u. |
| Damping factor, | 0.7 | p.u. |
| Natural frequency, | 2000 | rad/s |
References
- International Renewable Energy Agency (IRENA). Renewable Energy Statistics. 2021. ISBN: 978-92-9260-356-4. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2021/Aug/IRENA_Renewable_Energy_Statistics_2021.pdf (accessed on 1 May 2025).
- Christensen, P.; Andersen, G.K.; Seidel, M.; Bolik, S.; Engelken, S.; Knueppel, T.; Krontiris, A.; Wuerflinger, K.; Bülo, T.; Jahn, J.; et al. High Penetration of Power Electronic Interfaced Power Sources and the Potential Contribution of Grid Forming Converters; ENTSO-E 2020; ENTSO: Brussels, Belgium, 2020. [Google Scholar]
- Zarei, S.F.; Mokhtari, H.; Ghasemi, M.A.; Blaabjerg, F. Reinforcing Fault Ride Through Capability of Grid Forming Voltage Source Converters Using an Enhanced Voltage Control Scheme. IEEE Trans. Power Deliv. 2019, 34, 1827–1842. [Google Scholar] [CrossRef]
- Zhang, Q.; Mao, M.; Ke, G.; Zhou, L.; Xie, B. Stability problems of PV inverter in weak grid: A review. IET Power Electron. 2020, 13, 2165–2174. [Google Scholar] [CrossRef]
- Li, Y.; Gu, Y.; Green, T.C. Revisiting Grid-Forming and Grid-Following Inverters: A Duality Theory. IEEE Trans. Power Syst. 2022, 37, 4541–4554. [Google Scholar] [CrossRef]
- Rosso, R.; Wang, X.; Liserre, M.; Lu, X.; Engelken, S. Grid-Forming Converters: Control Approaches, Grid-Synchronization, and Future Trends—A Review. IEEE Open J. Ind. Appl. 2021, 2, 93–109. [Google Scholar] [CrossRef]
- Wu, H.; Wang, X. Design-oriented transient stability analysis of PLL-synchronized voltage-source converters. IEEE Trans. Power Electron. 2020, 35, 3573–3589. [Google Scholar] [CrossRef]
- Tielens, P.; Van Hertem, D. The relevance of inertia in power systems. Renew. Sustain. Energy Rev. 2016, 55, 999–1009. [Google Scholar] [CrossRef]
- Matevosyan, J.; MacDowell, J.; Miller, N.; Badrzadeh, B.; Ramasubramanian, D.; Isaacs, A.; Quint, R.; Quitmann, E.; Pfeiffer, R.; Urdal, H.; et al. A future with inverter-based resources: Finding strength from traditional weakness. IEEE Power Energy Mag. 2021, 19, 18–29. [Google Scholar] [CrossRef]
- Zhang, L.; Harnefors, L.; Nee, H.-P. Power-synchronization control of grid-connected voltage-source converters. IEEE Trans. Power Syst. 2010, 25, 809–8200. [Google Scholar] [CrossRef]
- Anttila, S.; Döhler, J.S.; Oliveira, J.G.; Boström, C. Grid forming inverters: A review of the state of the art of key elements for microgrid operation. Energies 2022, 15, 5517. [Google Scholar] [CrossRef]
- Mohammed, N.; Udawatte, H.; Zhou, W.; Hill, D.J.; Bahrani, B. Grid-Forming Inverters: A Comparative Study of Different Control Strategies in Frequency and Time Domains. IEEE Open J. Ind. Electron. Soc. 2024, 5, 185–214. [Google Scholar] [CrossRef]
- Zhang, H.; Xiang, W.; Lin, W.; Wen, J. Grid forming converters in renewable energy sources dominated power grid: Control strategy, stability, application, and challenges. J. Mod. Power Syst. Clean Energy 2021, 9, 1239–1256. [Google Scholar] [CrossRef]
- Fazal, S.; Haque, M.E.; Arif, M.T.; Gargoom, A. Droop Control Techniques for Grid Forming Inverter. In Proceedings of the 2022 IEEE PES 14th Asia-Pacific Power and Energy Engineering Conference (APPEEC), Melbourne, Australia, 20–23 November 2022; pp. 1–6. [Google Scholar]
- Mohiuddin, S.M.; Qi, J. A Unified Droop-Free Distributed Secondary Control for Grid-Following and Grid-Forming Inverters in AC Microgrids. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; pp. 1–5. [Google Scholar]
- Awal, M.A.; Yu, H.; Lukic, S.; Husain, I. Droop and Oscillator Based Grid-Forming Converter Controls: A Comparative Performance Analysis. Front. Energy Res. 2020, 8, 168. [Google Scholar] [CrossRef]
- Du, W.; Chen, Z.; Schneider, K.P.; Lasseter, R.H.; Nandanoori, S.P.; Tuffner, F.K.; Kundu, S. A Comparative Study of Two Widely Used Grid-Forming Droop Controls on Microgrid Small-Signal Stability. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 963–975. [Google Scholar] [CrossRef]
- Unruh, P.; Nuschke, M.; Strauß, P.; Welck, F. Overview on Grid-Forming Inverter Control Methods. Energies 2020, 13, 2589. [Google Scholar] [CrossRef]
- Li, D.; Zhu, Q.; Lin, S.; Bian, X.Y. A self-adaptive inertia and damping combination control of VSG to support frequency stability. IEEE Trans. Energy Convers. 2017, 32, 397–398. [Google Scholar] [CrossRef]
- Ashabani, M.; Jung, J. Synchronous voltage controllers: Voltage-based emulation of synchronous machines for the integration of renewable energy sources. IEEE Access 2020, 8, 49497–49508. [Google Scholar] [CrossRef]
- Bevrani, H.; Ise, T.; Miura, Y. Virtual synchronous generators: A survey and new perspectives. Electr. Power Syst. Res. 2014, 54, 244–254. [Google Scholar] [CrossRef]
- Li, M.; Huang, W.; Tai, N.; Yang, L.; Duan, D.; Ma, Z. A dual-adaptivity inertia control strategy for virtual synchronous generator. IEEE Trans. Power Syst. 2020, 35, 594–604. [Google Scholar] [CrossRef]
- Colombino, M.; Groß, D.; Brouillon, J.; Dörfler, F. Global phase and magnitude synchronization of coupled oscillators with application to the control of grid-forming power inverters. IEEE Trans. Autom. Control 2019, 64, 4496–45119. [Google Scholar] [CrossRef]
- Yu, M.; Roscoe, A.J.; Booth, C.D.; Dysko, A.; Ierna, R.; Zhu, J.; Grid, N.; Urdal, H. Use of an inertia-less virtual synchronous machine within future power networks with high penetrations of converters. In Proceedings of the 2016 Power Systems Computation Conference, Genoa, Italy, 20–24 June 2016. [Google Scholar]
- Sinha, M.; Dörfler, F.; Johnson, B.B.; Dhople, S.V. Uncovering droop control laws embedded within the nonlinear dynamics of van der pol oscillators. IEEE Trans. Control Netw. Syst. 2017, 4, 347–3587. [Google Scholar] [CrossRef]
- Awal, M.A.; Yu, H.; Tu, H.; Lukic, S.M.; Husain, I. Hierarchical control for virtual oscillator based grid-connected and islanded microgrids. IEEE Trans. Power Electron. 2020, 35, 988–1001. [Google Scholar] [CrossRef]
- Johnson, B.B.; Sinha, M.; Ainsworth, N.G.; Dörfler, F.; Dhople, S.V. Synthesizing virtual oscillators to control islanded inverters. IEEE Trans. Power Electron. 2016, 31, 6002–6015. [Google Scholar] [CrossRef]
- Awal, M.A.; Husain, I. Unified virtual oscillator control for gridforming and grid-following converters. IEEE J. Emerg. Sel. Topics Power Electron. 2021, 9, 4573–4586. [Google Scholar] [CrossRef]
- Azizi Aghdam, S.; Agamy, M. Virtual oscillator-based methods for grid-forming inverter control: A review. IET Renew. Power Gener. 2022, 16, 835–855. [Google Scholar] [CrossRef]
- Sadeque, F.; Fateh, F. On Control Schemes for Grid-Forming Inverters. In Proceedings of the IEEE Kansas Power and Energy Conference (KPEC), Manhattan, KS, USA, 25–26 April 2022; pp. 1–6. [Google Scholar]
- Nurunnabi, M.; Li, S.; Das, H.S. Control and Operation Evaluation of Grid-Forming Inverters with L, LC, and LCL Filters. In Proceedings of the 2023 IEEE Power & Energy Society General Meeting (PESGM), Orlando, FL, USA, 16–20 July 2023; pp. 1–5. [Google Scholar]
- Reißner, F.; Weiss, G. Robust and Adaptive Tuning of PI Current Controllers for Grid-Forming Inverters. IEEE Open J. Ind. Electron. Soc. 2025, 6, 115–129. [Google Scholar] [CrossRef]
- Qoria, T.; Gruson, F.; Colas, F.; Guillaud, X.; Debry, M.-S.; Prevost, T. Tuning of Cascaded Controllers for Robust Grid-Forming Voltage Source Converter. In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018; pp. 1–7. [Google Scholar]
- Houari, A.; Renaudineau, H.; Martin, J.-P.; Pierfederici, S.; Meibody-Tabar, F. Flatness-Based Control of Three-Phase Inverter With Output LC Filter. IEEE Trans. Ind. Electron. 2012, 59, 2890–2897. [Google Scholar] [CrossRef]
- Gensior, A.; Woywode, O.; Rudolph, J.; Guldner, H. On differential flatness trajectory planning observers and stabilization for dc-dc converters. IEEE Trans. Circuits Syst. I Reg. Pap. 2006, 53, 2000–2010. [Google Scholar] [CrossRef]
- Renaudineau, H.; Lopez, D.; Flores-Bahamonde, F.; Kouro, S. Flatness-based control of a boost inverter for PV microinverter application. In Proceedings of the 2017 IEEE 8th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Florianopolis, Brazil, 17–20 April 2017; pp. 1–6. [Google Scholar]
- Mungporn, P.; Thounthong, P.; Sikkabut, S.; Yodwong, B.; Chunkag, V.; Kumam, P.; Bizon, N.; Nahid-Mobarakeh, B.; Pierfederici, S. Dynamics improvement of 3-phase inverter with output LC-filter by using differential flatness based control for grid connected applications. In Proceedings of the 2016 19th International Conference on Electrical Machines and Systems (ICEMS), Chiba, Japan, 13–16 November 2016; pp. 1–6. [Google Scholar]
- Alonso-Martínez, J.; Eloy-García, J.; Arnaltes, S. Direct power control of grid connected PV systems with three level NPC inverter. Sol. Energy 2010, 84, 1175–1186. [Google Scholar]
- Maissa, M.; Kouider, L. Direct power control technique for Grid-tied two levels VSI inverter fed by photovoltaic system. In Proceedings of the 2023 1st International Conference on Renewable Solutions for Ecosystems: Towards a Sustainable Energy Transition (ICRSEtoSET), Djelfa, Algeria, 6–8 May 2023; pp. 1–5. [Google Scholar]
- Kulikowski, K.; Sikorski, A. New DPC Look-Up Table Methods for Three-Level AC/DC Converter. IEEE Trans. Ind. Electron. 2016, 63, 7930–7938. [Google Scholar] [CrossRef]
- Kouro, S.; Cortes, P.; Vargas, R.; Ammann, U.; Rodriguez, J. Model Predictive Control—A Simple and Powerful Method to Control Power Converters. IEEE Trans. Ind. Electron. 2009, 56, 1826–1838. [Google Scholar] [CrossRef]
- Heydari, R.; Young, H.; Flores-Bahamonde, F.; Vaez-Zadeh, S.; Gonzalez-Castano, C.; Sabzevari, S.; Rodriguez, J. Model-Free Predictive Control of Grid-Forming Inverters With LCL Filters. IEEE Trans. Power Electron. 2022, 37, 9200–9211. [Google Scholar] [CrossRef]
- Kumar, D.; Kumar, C. Model Predictive Control of Isolated Three-Phase Four-Wire Grid Forming Converter. In Proceedings of the 2023 11th National Power Electronics Conference (NPEC), Guwahati, India, 14–16 December 2023; pp. 1–5. [Google Scholar]
- Cortés, P.; Kouro, S.; La Rocca, B.; Vargas, R.; Rodríguez, J.; Leon, J.I.; Vazquez, S.; Franquelo, L.G. Guidelines for weighting factors design in Model Predictive Control of power converters and drives. In Proceedings of the 2009 IEEE International Conference on Industrial Technology, Churchill, VIC, Australia, 10–13 February 2009; pp. 1–7. [Google Scholar]
- Pérez-Guzmán, R.E.; Rivera, M.; Vicencio, N.; Wheeler, P.W. Model-based Predictive Control in Three-Phase Inverters. In Proceedings of the 2020 IEEE International Conference on Industrial Technology (ICIT), Buenos Aires, Argentina, 26–28 February 2020; pp. 499–504. [Google Scholar]
- Aguirre, M.; Kouro, S.; Rojas, C.A.; Rodriguez, J.; Leon, J.I. Switching Frequency Regulation for FCS-MPC Based on a Period Control Approach. IEEE Trans. Ind. Electron. 2018, 65, 5764–5773. [Google Scholar] [CrossRef]
- Aguirre, M.; Kouro, S.; Rojas, C.A.; Vazquez, S. Enhanced Switching Frequency Control in FCS-MPC for Power Converters. IEEE Trans. Ind. Electron. 2021, 68, 2470–2479. [Google Scholar] [CrossRef]
- Zubiaga, M.; Cardozo, C.; Prevost, T.; Sanchez-Ruiz, A.; Olea, E.; Izurza, P.; Khan, S.H.; Arza, J. Enhanced TVI for Grid Forming VSC under Unbalanced Faults. Energies 2021, 14, 6168. [Google Scholar] [CrossRef]
- Oureilidis, K.O.; Demoulias, C.S. A fault clearing method in converter-dominated microgrids with conventional protection means. IEEE Trans. Power Electron. 2016, 31, 4628–4640. [Google Scholar] [CrossRef]
- Shi, K.; Song, W.; Xu, P.; Fang, Z.; Ji, Y. Low-voltage ride-through control strategy for a virtual synchronous generator based on smooth switching. IEEE Access 2017, 6, 2703–2711. [Google Scholar] [CrossRef]
- Huang, L.; Xin, H.; Wang, Z.; Zhang, L.; Wu, K.; Hu, J. Transient stability analysis and control design of droop-controlled voltage source converters considering current limitation. IEEE Trans. Smart Grid 2017, 10, 578–591. [Google Scholar] [CrossRef]
- Jiang, S.; Zhu, Y.; Xu, T.; Konstantinou, G. Current-Synchronization Control of Grid-Forming Converters for Fault Current Limiting and Enhanced Synchronization Stability. IEEE Trans. Power Electron. 2024, 39, 5271–5285. [Google Scholar] [CrossRef]
- Jiang, S.; Xu, T.; Konstantinou, G. Current Synchronization Loop for Enhanced Fault Tolerance and Fast Recovery in Grid-Forming Converters. In Proceedings of the IECON 2023—49th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 16–19 October 2023; pp. 1–6. [Google Scholar]
- Lu, X.; Wang, J.; Guerrero, J.M.; Zhao, D. Virtual-impedance-based fault current limiters for inverter dominated ac microgrids. IEEE Trans. Smart Grid 2018, 9, 1599–1612. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.W.; Blaabjerg, F.; Loh, P.C. Virtualimpedance-based control for voltage-source and current-source converters. IEEE Trans. Power Electron. 2015, 30, 7019–70375. [Google Scholar] [CrossRef]
- Groß, D.; Dörfler, F. Projected grid-forming control for current-limiting of power converters. In Proceedings of the 2019 57th Annual Allerton Conference on Communication, Control and Computing (Allerton), Monticello, IL, USA, 24–27 September 2019; pp. 326–333. [Google Scholar]
- Rodríguez-Amenedo, J.L.; Gómez, S.A.; Zubiaga, M.; Izurza-Moreno, P.; Arza, J.; Fernández, J.D. Grid-Forming Control of Voltage Source Converters Based on the Virtual-Flux Orientation. IEEE Access 2023, 11, 10254–10274. [Google Scholar] [CrossRef]
- Fernández, J.D.; Navarro, E.R.; Amenedo, J.L.R.; Eloy-García, J.; Gómez, S.A. Operation of a Grid-Forming Converter Controlled by the Flux Vector. IEEE Access 2025, 13, 7040–7052. [Google Scholar] [CrossRef]
- NGESO: Grid Forming Best Practice Grid. April 2023. Available online: https://www.neso.energy/document/278491/download (accessed on 31 January 2025).
- NGESO, GC0137: Minimum Specification Required for Provision of GB Grid Forming (GBGF) Capability. 2021. Available online: https://www.neso.energy/document/220511/download (accessed on 5 April 2025).
- Fliess, M.; Lévine, J.; Martin, P.; Rouchon, P. Flatness and defect of non-linear systems: Introductory theory and examples. Int. J. Control 1995, 61, 1327–1361. [Google Scholar] [CrossRef]
- Dolado, J.; Rodríguez Amenedo, J.L.; Arnaltes, S.; Eloy-Garcia, J. Improving the Inertial Response of a Grid-Forming Voltage Source Converter. Electronics 2022, 11, 2303. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).