1. Introduce
Pathologists can analyze morphological features such as cell size, texture, and shape to assist in diagnosing malignant tumors, determining treatment methods, or conducting in-depth research [
1]. Specifically, through instance segmentation of cells, researchers can accurately quantify cellular characteristics, including the cell count and size within tumor tissues, thereby supporting the quantitative analysis, grading, and staging of malignancies [
2]. The prerequisite for these procedures involves large-scale cellular-level analysis of digital tissue samples, which renders manual cell analysis practically infeasible due to its high labor intensity and significant inter-observer variability. This necessitates the urgent development of automated cell analysis methods [
3].
Most existing fully supervised automated cell analysis algorithms are based on convolutional neural networks (CNNs), which have achieved remarkable progress in the medical field and digital pathology [
4,
5,
6]. Among them, UNet [
7], a widely used CNN architecture for image segmentation, has been applied to cell instance segmentation [
8]. Researchers have also proposed numerous UNet-based variants, such as UNet++ [
9] and UNet3+ [
10]. In these methods, the semantic gap between feature maps of encoder and decoder subnetworks is reduced by redesigning skip connections, thereby enhancing segmentation performance. However, despite merging coarse-grained deep features and fine-grained shallow features at the same scale via skip connections, UNet-based encoder–decoder networks exhibit inefficient non-local contextual modeling across arbitrary positions, limiting their performance in segmenting complex histopathological images [
11]. To address these challenges, researchers have developed novel approaches. For example, Hover-Net [
12] uses a fully convolutional neural network to extract image features and identifies candidate cell regions through post-processing. These candidate regions are further processed and filtered to generate final segmentation masks, achieving instance segmentation of individual cells. CIA-Net [
13] incorporates two decoders, with each responsible for segmenting nuclei or contours. By bidirectionally aggregating specific features, it leverages spatial and textural dependencies between nuclei and contours to enhance performance on both tasks. Nevertheless, such methods rely on complex pixel grouping post-processing to extract object instances, and their performance is highly dependent on segmentation results and grouping strategies [
14].
Fully supervised deep learning methods have significantly enhanced the automation level of cell segmentation through end-to-end feature learning. However, these methods rely heavily on large quantities of high-quality annotated data for training, which enables models to achieve high segmentation accuracy even in complex backgrounds. This reliance on extensive annotations poses challenges, including high costs, time-consuming processes, and inconsistent annotation quality due to the need for pathologist involvement in medical image labeling. To address these limitations, semi-supervised learning methods have gradually gained attention. These methods integrate a small amount of labeled data with a large volume of unlabeled data, reducing data acquisition costs while enhancing model generalization and robustness. For example, Mean Teacher [
15] leverages consistency regularization to utilize unlabeled data for performance improvement, FixMatch [
16] combines pseudo-labeling with strong–weak data augmentation strategies to significantly boost segmentation accuracy, and Cross Pseudo Supervision [
17] mitigates pseudo-label noise via mutual supervision between dual networks. Additionally, generative adversarial network (GAN)-based methods such as SegAN [
18] exploit distributional information in unlabeled data through adversarial training mechanisms, thereby further improving segmentation model robustness. Despite these advances, efficiently leveraging unlabeled data remains a challenge. The insufficient exploration of unlabeled data or failure to find optimal correlations between unlabeled and labeled data can lead to suboptimal model performance. Designing self-supervised constraints, consistency regularization, or GAN-based mechanisms can uncover implicit distributional patterns and contextual information in unlabeled data. Nevertheless, current semi-supervised methods for medical images still face challenges such as pseudo-label noise propagation and feature disentanglement, necessitating the urgent development of novel learning paradigms adapted to cellular characteristics [
19]. Furthermore, designing a robust cell segmentation model framework remains crucial.
In this paper, we propose a semi-supervised method for nuclear instance segmentation. A class-adaptive sampling strategy is employed to guide the model to focus on rare classes and dynamically adapt to data distributions, thereby effectively addressing class imbalance issues. Additionally, a region-adaptive attention mechanism is introduced to improve the morphological accuracy of segmentation masks by dynamically assigning higher weights to critical regions. We present comparative results on two independent multi-tissue histology image datasets and demonstrate state-of-the-art performance compared to other recently proposed methods. The contributions of this work can be summarized as follows:
A category-adaptive sampling method is designed to guide the model to prioritize rare classes and dynamically adapt to data distributions. This prevents fixed sampling strategies from causing model reliance on artificially set balancing ratios and effectively addresses long-tailed data distribution issues.
A strong–weak contrast consistency method is developed, generating two strong perturbations and one weak perturbation to substantially expand the perturbation space, learn perturbation-invariant feature representations, and enhance the model’s discriminative ability for critical cellular features.
A region-adaptive attention mechanism is designed to strengthen key regions through dynamic weighting, guiding the model to focus on learning discriminative features of challenging regions such as blurred boundaries or overlapping cells, thereby improving the morphological accuracy of segmentation masks.
3. Methods
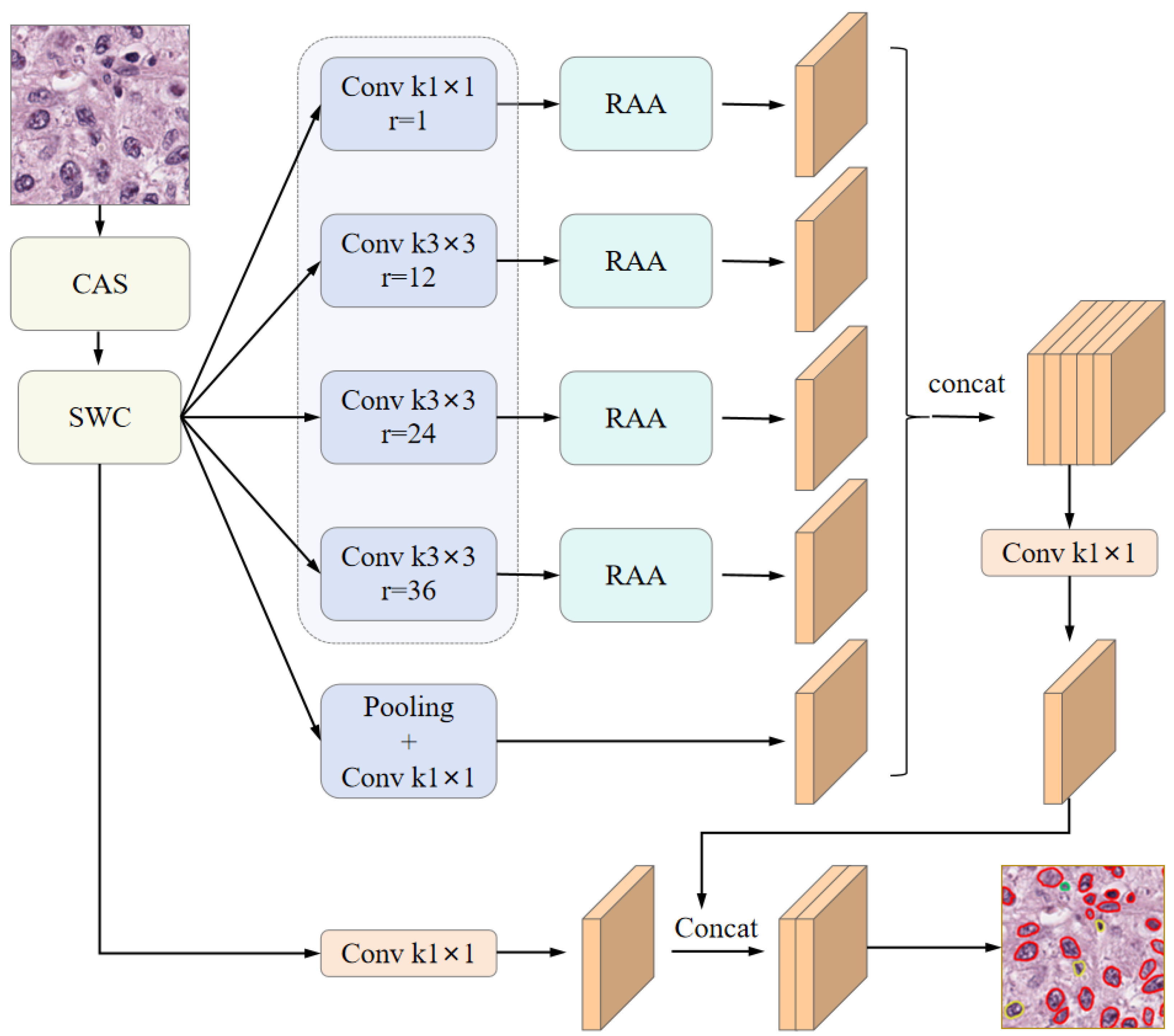
In this study, we adopted DeepLabv3 [
36] as the backbone architecture for the segmentation network. Based on this foundation, we proposed a novel category-adaptive sampling (CAS) strategy to enhance dataset sampling efficiency. To facilitate semi-supervised learning, we incorporated a strong–weak consistency (SWC) mechanism that enforces contrastive consistency between strongly and weakly augmented views. Furthermore, we introduced a region-adaptive attention (RAA) module to emphasize discriminative regional features from the dilated convolutional outputs. By integrating these components, we developed a semi-supervised segmentation framework—termed CSRA-Net. The overall network architecture is illustrated in
Figure 1. In this study, we adopted DeepLabv3 [
36] as the backbone architecture for the segmentation network. Based on this foundation, we propose a novel Category-Adaptive Sampling (CAS) strategy to enhance dataset sampling efficiency. To facilitate semi-supervised learning, we incorporate a Strong-Weak Consistency (SWC) mechanism that enforces contrastive consistency between strongly and weakly augmented views. Furthermore, we introduce a Region-Adaptive Attention (RAA) module to emphasize discriminative regional features from the dilated convolutional outputs. By integrating these components, we develop a semi-supervised segmentation framework—termed CSRA-Net. The overall network architecture is illustrated in
Figure 1.
3.1. Category-Adaptive Sampling Method
In medical image analysis, datasets often suffer from significant class imbalance, where certain tissues or cell types are underrepresented. This imbalance can lead to suboptimal model performance, particularly in recognizing minority classes during training. Conventional techniques such as random oversampling and SMOTE [
37] adopt fixed sampling strategies, which may not fully exploit class-specific information embedded in the training data.
To address this challenge, we proposed a category-adaptive sampling (CAS) strategy that dynamically adjusts the sampling weights based on the imbalance severity of each class. The CAS framework emphasizes the representation of underrepresented classes by incorporating class-specific oversampling factors and adaptive adjustment mechanisms. This dynamic strategy enhances the ability of the model to learn from rare classes and mitigates the negative impact of class imbalance.
Moreover, to improve the stability and robustness of the model while minimizing the risk of overfitting associated with oversampling, we introduced several refinements to the CAS method. These include precise formula derivations, systematic methodological enhancements, and comprehensive implementation details, all of which contribute to improved classification performance on imbalanced datasets.
3.1.1. Calculate the Category Imbalance Ratio
First, the imbalance ratio for each category in the training set was computed to quantify its relative scarcity compared to the majority class. Let
represent the tissue category,
represent the cellular category,
represent the total number of training samples, and
represent the number of samples in the majority class. The category imbalance ratio is defined as Equation (
1):
These imbalance ratios are subsequently used to compute the oversampling factor
for each category. To ensure that rarer classes receive proportionally more sampling attention, an inverse proportionality strategy is adopted. The calculation of
r is defined in Formula (2). Here,
is a constant hyperparameter that controls the overall oversampling intensity, thereby modulating the amplification level across different categories.
3.1.2. Calculate the Sampling Weights of the Sample
For each training sample
i, the overall sampling weight is composed of two components: one corresponding to the tissue category and the other to the cell category. The sampling weight
for the tissue category is determined based on the specific tissue label
associated with the sample. The calculation is defined in Equation (
3):
Here, is an indicator function, denoting whether sample j belongs to the category of the tissue.
The sampling weight
for the cell categories is computed based on the cell class composition of each training sample
i. Since a single sample may contain multiple cell categories, we define a binary vector
, where
denotes the total number of cells of all categories. Each element
in this vector indicates whether sample
i contains cell category
j (1 if present, 0 if otherwise).
3.1.3. Calculate the Total Sampling Weight
Ultimately, the total sampling weight
for each sample
i is computed as a sum of the tissue-level and cell-level sampling weights. This formulation allows for joint consideration of both tissue and cellular category imbalances. The calculation is expressed in Equation (
5):
By incorporating this composite weight into the sampling procedure, the sampling probability of each training sample is dynamically adjusted, enabling the model to more effectively address class imbalance across both tissue and cell categories.
3.1.4. Dynamically Adjust the Oversampling Factor
To effectively address category imbalance while mitigating the risk of overfitting, a periodic oversampling strategy is proposed. Rather than maintaining a fixed oversampling rate throughout training, this strategy periodically updates the oversampling factor to reduce computational overhead per epoch and enhance model generalization. Specifically, the oversampling factor
is updated every predefined interval (e.g., every 10 epochs), and its magnitude is gradually decreased as training progresses. This dynamic adjustment allows the model to focus more on underrepresented categories in early training stages while reducing the influence of oversampling in later stages. The update rule is defined in Equation (
6):
Among them, is the initial oversampling factor, and represents the remainder of the current and the periodic update interval , which determines the adjustment ratio within the current period; is the total number of training rounds, and is the interval of periodic updates (for example, updated once every 10 epochs).
This gradually decreasing oversampling intensity helps prevent overfitting to minority classes in later stages of training and improves the generalization capability of the model.
3.2. Strong–Weak Contrastive Consistency
To enhance the robustness and feature discrimination capability of models in cell segmentation tasks, we proposed a strong–weak contrast consistency (SWC) strategy, which integrates dual-stream perturbation contrast learning, strong–weak perturbation consistency supervision, labeled perturbation supervision mechanisms, and staining normalization enhancement techniques. Below, we provide a detailed explanation of each module along with its mathematical formulation. Additionally,
Figure 2 presents a schematic illustration comparing the SWC strategy with FixMatch [
16] and UniMatch [
25].
As illustrated in
Figure 2, the proposed SWC strategy demonstrates substantial differences compared to existing semi-supervised learning methods, such as FixMatch and UniMatch.
X,
,
,
, and
respectively represent the labeled data, the weakly perturbed features of labeled data, the strongly perturbed features of labeled data, the weakly perturbed features of unlabeled data, and the strongly perturbed features of unlabeled data.
,
,
,
, and
respectively represent the labeled data, the prediction results for labeled data, the prediction results based on strongly perturbed features of labeled data, the prediction results for weakly perturbed unlabeled data, and the prediction results based on strongly perturbed features of unlabeled data. Unlike FixMatch, which depends exclusively on pseudo-label confidence and hard thresholding, SWC incorporates a two-stream perturbation comparison mechanism that aligns representations under both strong and weak perturbations. This mitigates confirmation bias and enhances feature-level consistency. In contrast to UniMatch, our method fully learns perturbation-invariant features by contrasting two strongly perturbed features. Moreover, our approach diverges from both FixMatch and UniMatch in that it applies strong perturbation feature generation not only to unlabeled data but also to labeled data. By constructing perturbation space consistency, our method effectively guides the learning of unlabeled data, thereby further improving the robustness and learning efficiency of the model.
3.2.1. Dual-Stream Perturbation and Contrastive Learning
UniMatch [
25] employs the DusPerb method to expand the perturbation space from two distinct perspectives, thereby fully capturing the diversity of original perturbations. Inspired by this approach, we adopted a similar perturbation strategy in this work. Specifically, for each unlabeled sample
, two strongly augmented feature representations, denoted as
and
, are generated. These perturbations aim to enhance the discriminative representation of cell regions, thereby improving the ability of the model to distinguish cellular structures from complex backgrounds. In addition, we introduced the CutMix [
38] data augmentation technique, which utilizes randomly sampled templates to synthesize images with diverse staining styles. This strategy not only increases data diversity but also overcomes the limitations of using fixed staining templates.
To maximize consistency between the strongly perturbed features, a contrastive learning loss is defined, as shown in Equation (
7):
Among them, N represents the sample quantity, and represent strong disturbance features, is the classifier weight, and C represents the number of classifier weights. By maximizing the similarity between features, the model can learn robust feature representations in complex backgrounds.
3.2.2. Consistent Supervision of Strong and Weak Perturbation
To further enhance the quality of pseudo-labels, a weak perturbation feature
is introduced for the unlabeled data. Pseudo-label
is then generated to ensure that semantic consistency of the original data is preserved under weak perturbations, thereby making the reliability of the results of the model.
The method proposed in UDA [
39] employs RandAugment and back-translation to generate two distinct strongly augmented variants of unlabeled data and computes the consistency loss through pseudo-labeling. This approach ensures that the model remains robust to augmented data. Inspired by this, we incorporated pseudo-labels combined with dual-stream strong perturbation for consistency supervision, and we define the loss function as presented in Equation (
9):
where
denotes a weakly perturbed feature, and
represents a pseudo-label generated from the prediction corresponding to the weakly perturbed input. The weak perturbations cause minimal damage distortion to the original image structure, thereby ensuring that the generated pseudo-labels are closer to the true labels.
and
correspond to strong perturbation features. Consistency loss is computed between the two strong perturbation features and the pseudo-label to ensure model consistency across various perturbation conditions, This approach mitigates bias potentially introduced by a single perturbation and reduces the impact of potential errors in the pseudo-labels. This process further enhances the robustness of feature representations for unlabeled data and improves the stability of pseudo-label generation. Moreover, each unlabeled sample is reused in two strongly perturbed versions, effectively simulating the effects of data augmentation, which is particularly advantageous in scenarios where medical image annotations are limited.
3.2.3. Supervised Mechanism with Label Perturbation
Although consistent supervision using both strong and weak perturbations can effectively enhance the learning performance of unlabeled data, the absence of direct guidance from ground-truth labels may result in the accumulation of pseudo-label errors. Miyato [
40] computed the prediction results for both original samples and perturbed samples, applied consistency loss to ensure stable predictions under perturbations, and suggested that this approach could be extended to labeled data. Therefore, this section introduces consistency supervision for labeled data to provide indirect guidance for the learning process of unlabeled data, thereby assisting the model in correcting cognitive biases and improving its segmentation capability on real-world data. For labeled data
, strong perturbation features
are generated, and the supervised loss is calculated in conjunction with the ground-truth labels
.
This mechanism offers indirect supervision for pseudo-label generation, thereby addressing the model’s cognitive bias toward real data and further improving segmentation performance. Finally, by integrating the contrastive learning loss of unlabeled data, the consistency regularization loss from strong and weak perturbations, and the supervised loss of labeled data, the overall loss function is formulated as shown in Equation (
11):
Among them, and serve as hyperparameters for adjusting the weights of the loss terms. This comprehensive loss function enables collaborative optimization in the learning process of both labeled and unlabeled data, thereby enhancing the model’s robustness and accuracy in scenarios with imbalanced data distribution and complex backgrounds.
3.3. Region-Adaptive Attention Mechanism
In cellular segmentation tasks, the inherent challenges posed by highly heterogeneous morphological and textural characteristics of cells, particularly in regions exhibiting fine structures, low contrast, or ambiguous boundaries, significantly compromise the effectiveness of conventional convolutional neural networks (CNNs) and standard attention mechanisms. These limitations primarily manifest in two aspects: (1) Traditional attention frameworks employ static weighting strategies that fail to adaptively recalibrate feature importance according to regional complexity levels, resulting in insufficient attention allocation to diagnostically critical areas. (2) The inherent confirmation bias in pseudo-labeling processes tends to reinforce erroneous high-confidence predictions during iterative training, thereby exacerbating error propagation and ultimately degrading segmentation accuracy.
To address these critical issues, we proposed a region-adaptive attention (RAA) mechanism based on gradient changes, as illustrated in
Figure 3. By dynamically adjusting focus on different regions, this mechanism mitigates the model’s reinforcement of incorrectly predicted areas, thereby improving segmentation performance in complex regions.
Specifically, each scale
(the four different scale outputs from the encoder) is processed to compute the difficulty score
for each region. This score is derived based on the gradient variation within the region, reflecting the complexity of feature changes in that region. For each region
, its gradient magnitude
is computed, which represents the degree of pixel intensity variation in the region. The variance
in the gradient magnitude for the region is then calculated using Equation (
12) to assess the difficulty level of the region.
Regions with large gradient variance typically exhibit high feature variation, such as blurred boundaries or complex textures, indicating that these regions are more challenging. Consequently, they will receive greater attention in subsequent steps. Based on the gradient variance
, dynamic weights
are assigned to each region to reflect the level of attention required. During computation, the Sigmoid function is applied to map the difficulty score, thereby obtaining the dynamic weights as shown in Equation (
13):
This weight ensures that regions with larger gradient variations (i.e., higher difficulty regions) receive increased attention, enabling the model to concentrate its resources on processing these complex areas more effectively. Through this dynamic adjustment mechanism, the model adaptively prioritizes challenging regions during training while mitigating overfitting to easily distinguishable regions.
Then, a multi-head self-attention mechanism [
41] was adopted to combine features of different scales, and a dynamic weight
was introduced in the attention calculation to further enhance the focus on regions with higher difficulty. Specifically, for each scale
, the corresponding Query, Key, and Value were calculated through Equations (4)–(14):
Among them,
,
, and
are the corresponding weight matrices,
represents the input region tokens, and
is the result of concatenating all scale outputs. The similarity matrix
is calculated through these inputs, and the weighted output
is obtained through Equation (
15) to acquire the feature representation of each region.
Among them,
denotes the instance normalization operation, which serves to normalize the feature matrix of each region. To further enhance the feature representation capability, the DMLP module within the DAT-Net [
42] network structure is applied to the output of each scale. Through deep semantic enhancement, the feature representation is enriched, thereby improving both the expressiveness of features and the model’s ability to understand complex regions. The final feature representation
is obtained via Formula (16).
Finally, through the convolutional layer, the enhanced feature representation is mapped back to the original input space, yielding the final output . These outputs not only capture high-level semantic information but also effectively emphasize complex regions requiring correction.
4. Experiment
4.1. Datasets and Evaluation Metrics
This paper primarily employed two widely-used datasets in medical image nuclei segmentation tasks: the PanNuke [
43] dataset and the Conic [
44] dataset. The PanNuke dataset served as the primary training and evaluation dataset, comprising 7901 images of size 256 × 256 pixels. This dataset encompasses 19 distinct tissue types and five cell categories, namely, tumor cells, non-tumor epithelial cells, inflammatory cells, connective tissue cells, and dead cells. Notably, the dataset exhibits significant class imbalance, particularly a severe underrepresentation of the dead cell category, which is prominently reflected in the statistics of both cell and tissue categories. The Conic dataset consists of H&E-stained colon tissue section images, containing 4981 images of size 256 × 256 pixels. In this dataset, cells are finely categorized into six classes, including epithelial cells, lymphocytes, plasma cells, eosinophils, neutrophils, and connective tissue cells. To evaluate the network’s segmentation accuracy under semi-supervised conditions, the data from the PanNuke and Conic datasets were partitioned, with the distribution presented in
Table 1. A labeled training dataset was created through random sampling from the original training dataset, while the remaining portion formed the unlabeled dataset.
We adopted Precision, Recall, F1-score, and Mean Intersection over Union (MIOU) as the evaluation metrics for the segmentation performance of the semi-supervised model.
where True Positive (TP) represents the count of correctly segmented target pixels, False Positive (FP) denotes the count of pixels from other classes incorrectly segmented as target pixels, and False Negative (FN) indicates the count of target pixels mistakenly segmented as non-target pixels. MIOU is a key metric for assessing the accuracy of semantic segmentation models. It is the ratio of the intersection to the union of the predicted and ground-truth values. It is expressed in Equation (
20):
where
k represents the number of pixel categories, excluding the background class.
4.2. Implementation and Training Details
We conducted all experiments on PyTorch 1.13.1 with Nvidia GeForce GTX 4090. We used mini-batch stochastic gradient descent (SGD) with a momentum 0.9 and weight decay of . The batch size was set to 16, and the training epoch was set to 400. The initial learning rate was 0.005, and it was decayed by cosine annealing with a period of 400.
Upon data loading, the original images and their corresponding labels underwent standardization and augmentation to enhance the model’s robustness and generalization capabilities. First, input images and labels were randomly scaled with a scaling ratio ranging from 0.5 to 2.0 to improve the model’s scale invariance. Additionally, fixed-size cropping was applied to enhance the model’s adaptability to spatial transformations while ensuring that the input data met computational requirements. Meanwhile, distinct invalid region markers were assigned for labeled and unlabeled data to prevent interference from unlabeled data during training. Furthermore, images were randomly horizontally flipped with a 50% probability to improve the model’s adaptability to data from various orientations. For unlabeled data, this study introduced a multi-view augmentation strategy to strengthen the model’s generalization ability and self-supervised learning performance. Specifically, color jittering was applied with an 80% probability to adjust brightness, contrast, saturation, and hue, enabling the model to handle diverse lighting conditions. Random grayscale conversion was applied with a 20% probability to enhance recognition of black-and-white or low-saturation images. Gaussian blur was applied with a 50% probability to simulate real-world blurring effects, thereby improving the model’s ability to learn boundary information.
4.3. Performance Comparisonn
We compared our method with the state-of-the-art methods on the PanNuke and Conic datasets. Both datasets encompass a variety of cell types and exhibit a significant imbalance across these types. As such, they are considered among the most challenging instance segmentation datasets in terms of segmentation complexity. In this experiment, we evaluated the performance of CSRA-Net and compared it with that of the fully supervised network UNet as well as the state-of-the-art semi-supervised methods Fixmatch and Unimatch. All methods were tested under identical conditions, including the same dataset and training settings, to ensure a fair comparison. Furthermore, detailed comparisons were conducted for scenarios where the proportion of labeled data was set to 1/4, 1/8, 1/16, and 1/32, respectively.
Table 2 summarizes the experimental results of the network on the PanNuke dataset. As shown in the table, CSRA-Net achieved superior performance across all annotation ratios (1/4, 1/8, 1/16, and 1/32). The performance outcomes of both FixMatch and UniMatch networks were outperformed by CSRA-Net. Despite being among the state-of-the-art semi-supervised segmentation networks, there existed a noticeable time gap between the introduction of these two models. Nonetheless, their segmentation accuracies were comparable, with the improvement margin between them being less than 0.5%. This suggests that multi-type instance segmentation under complex backgrounds poses an exceptionally high level of difficulty, where even highly sophisticated network designs can only yield marginal accuracy gains. Compared to UNet, CSRA-Net demonstrated significant improvements at all annotation data ratios, particularly in scenarios with extremely limited annotations (1/32), where the F1-score and MIOU increased by 12.75% and 10.70%, respectively. This highlights its effectiveness in learning from small sample annotation data. When compared to FixMatch, CSRA-Net exhibited a relatively modest improvement (approximately 1%) at higher annotation ratios (1/4 and 1/8). However, at lower annotation ratios (1/16 and 1/32), the F1-score increased by 3.29% and 1.77%, while the MIOU improved by 2.67% and 1.60%, respectively. This indicates that CSRA-Net outperforms FixMatch in scenarios with scarce data. In comparison to UniMatch, CSRA-Net maintained a consistent lead across all data ratios, albeit with slightly smaller gains than those observed against FixMatch. Specifically, at the 1/16 and 1/32 data divisions, the improvements in F1-score and MIOU ranged between 1.0% and 1.3%, suggesting that the two methods performed similarly, yet CSRA-Net retained a stable advantage. In contrast to the marginal improvement observed between FixMatch and UniMatch, CSRA-Net achieved an enhancement of approximately 2% across all scenarios, thereby providing further evidence of its effectiveness.
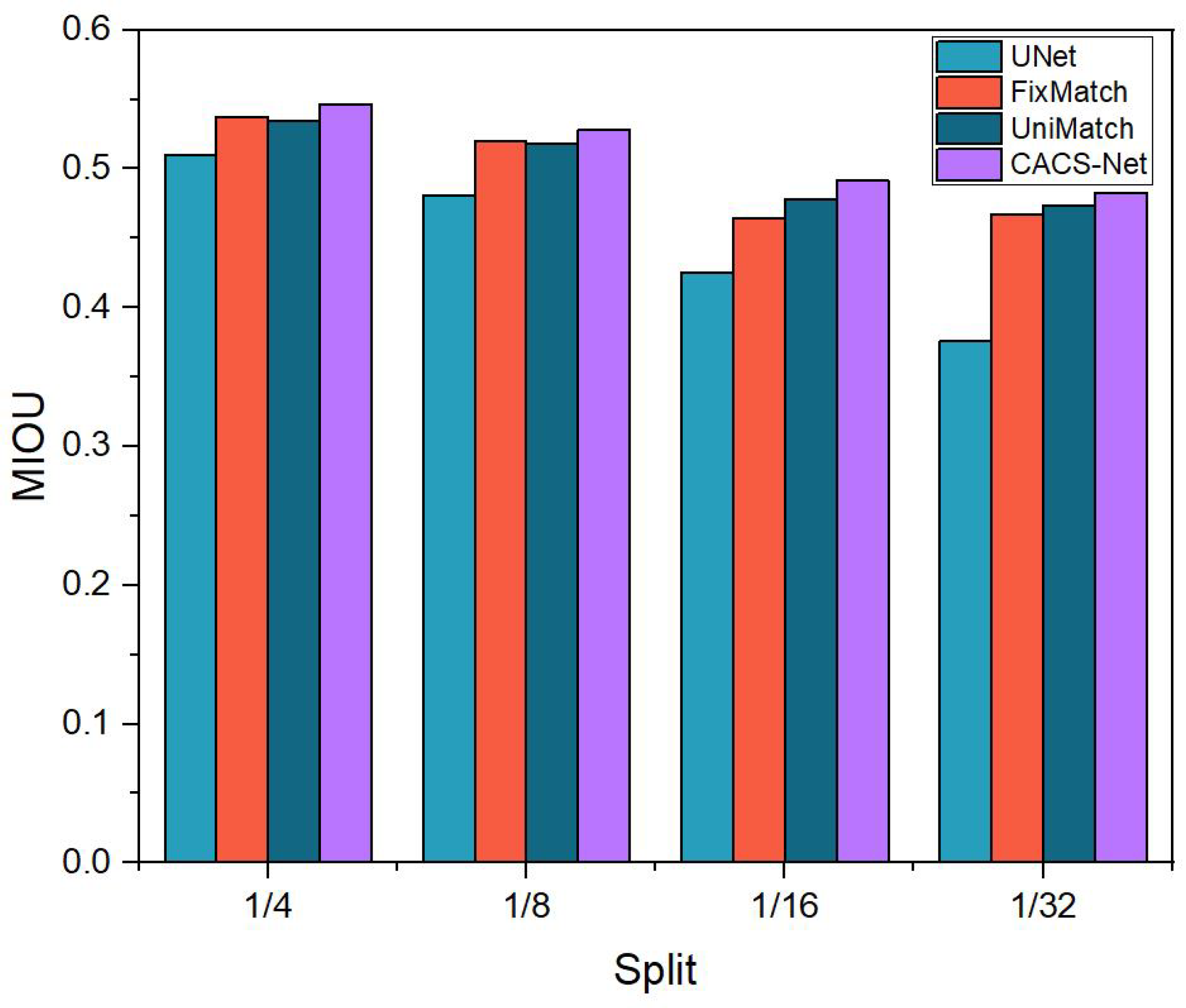
To provide a more intuitive illustration of the MIOU scores for various methods under different proportions of labeled data in the PanNuke dataset,
Figure 4 offers a visual representation. The results shown in the figure demonstrate that CSRA-Net achieved superior segmentation performance across all four scenarios.
Table 3 illustrates the experimental results of CSRA-Net compared to fully supervised methods and the other state-of-the-art semi-supervised approaches on the Conic dataset. Comparable to the findings on the PanNuke dataset, both FixMatch and UniMatch demonstrated weaker performance relative to CSRA-Net. The segmentation accuracy results of these two networks under various conditions were similar, with an average improvement margin between them being less than 1.5%. Specifically, CSRA-Net exhibited an approximate 5% higher average accuracy across different conditions compared to FixMatch and approximately a 2% improvement compared to UniMatch. Compared to UNet, CSRA-Net demonstrated substantial improvements across all data partitions, particularly in the 1/8 and 1/16 scenarios, where the F1-score increased by 8.26% and 9.21%, and the MIOU improved by 5.82% and 6.05%, respectively. When compared to FixMatch, CSRA-Net exhibited consistent enhancements across all data proportions, with notable performance gains in the 1/8 and 1/32 scenarios, where the F1-score rose by 2% and %, and the MIOU increased by 0.7% and 2.7%, respectively. This highlights the superior effectiveness of the semi-supervised strategy SWC proposed in this work over FixMatch. In comparison to UniMatch, CSRA-Net achieved a moderate yet stable improvement across all data partitions, with the F1-score increasing by 1.6–1.9% and the MIOU improving by 0.7–1.3%. These results indicate that CSRA-Net offers distinct advantages in semi-supervised learning scenarios.
To provide a more intuitive illustration of the MIOU scores for various methods under different proportions of labeled data in the Conic dataset,
Figure 5 offers a visual representation. The results shown in the figure demonstrate that CSRA-Net achieved superior segmentation performance across all four scenarios.
In summary, the experiments conducted on the PanNuke and Conic datasets show that CSRA-Net is capable of effectively leveraging limited labeled data to improve segmentation performance. Notably, in scenarios with extremely low labeling ratios (1/8, 1/16, and 1/32), it consistently outperformed other semi-supervised methods (FixMatch and UniMatch) by maintaining stable performance gains. These results validate the effectiveness and strong generalization capability of CSRA-Net in the task of semi-supervised cell instance segmentation.
4.4. Ablation Experiments
To rigorously assess the effectiveness of each component within this framework, a series of ablation experiments were performed on the PanNuke dataset to systematically evaluate the contribution of each module to the overall performance. The PanNuke dataset comprises 19 distinct tissue types and five diverse cell categories, with a significant imbalance across these classes, thereby posing substantial challenges to the segmentation task.
4.4.1. The Function of Individual Modules
Category-adaptive sampling (CAS) enhances the balance of samples across different cell types by dynamically adjusting the sampling strategy for labeled data. This indirectly optimizes the training process of unlabeled data and mitigates the prediction errors caused by class imbalance. The balanced labeled data provide a more uniform supervision signal, enabling the model to comprehensively learn the features of various cell types and generate higher-quality pseudo-labels. This reduces error propagation due to insufficient minority-class samples. During this process, the features learned from balanced batches avoid over-reliance on discriminative patterns of dominant cell types, thereby reducing the likelihood of misclassifying ambiguous cells in unlabeled data as majority classes and improving segmentation and classification accuracy. The benchmark network selected for this study was Deeplabv3. As a prominent model in the segmentation domain, Deeplabv3 demonstrated exceptionally high segmentation accuracy. Even when applied to the highly challenging PanNuke dataset, Deeplabv3 achieved segmentation accuracy comparable to that of state-of-the-art semi-supervised segmentation networks. In recent years, the average improvement achieved by mainstream semi-supervised segmentation networks on the PanNuke dataset has been approximately 0.5%, with no substantial performance gains observed. As shown in
Table 4, when the proportion of labeled data was 1/4, 1/8, 1/16, and 1/32, the F1-score increased by 1.07%, 0.9%, 1.22%, and 1.25%, respectively, and the MIOU score increased by 0.33%, 0.67%, 0.16%, and 0.49%, respectively, after applying the category adaptive sampling strategy in the benchmark network. Compared to the accuracy gains achieved by existing semi-supervised instance segmentation networks, the improvement brought by the category-adaptive sampling strategy is notably more significant, thereby demonstrating its effectiveness.
To verify the strong–weak contrast consistency (SWC) strategy, two strongly perturbed features were generated for an unlabeled cell image sample. Their feature consistency was constrained via contrastive learning to ensure robustness in data augmentation and feature extraction. This strategy compels the model to disregard noise and irrelevant background information in the image, focusing instead on learning the structural and morphological features of the cells, thereby extracting more robust and essential feature representations. In this study, strong perturbations were applied to labeled data to encourage the model to learn perturbation-invariant feature representations, enhancing its adaptability to variations in cell morphology. By applying strong perturbations to both labeled and unlabeled data, the proposed method promotes consistency in the model’s feature space, alleviating optimization bias caused by differences in perturbations between supervised and unsupervised data and achieving a robust integration of supervised and unsupervised signals. As shown in
Table 4, after introducing the perturbation strategy, the model’s performance improved by 1.31%, 1.24%, 1.77%, and 1.65% in the F1-score and by 0.54%, 0.83%, 0.23%, and 1.05% in the MIOU score compared to the baseline network when the proportion of labeled data was 1/4, 1/8, 1/16, and 1/32, respectively. These results demonstrate the effectiveness of this strategy in enhancing the model’s robustness. Compared to the category-adaptive sampling strategy, the strong–weak contrast consistency strategy demonstrated a more pronounced improvement in accuracy, thereby validating its effectiveness in enhancing model robustness.
The region-adaptive attention (RAA) mechanism dynamically adjusts attention according to the complexity of regions, enabling the model to prioritize complex areas. This enhances the accuracy and robustness of cell segmentation while mitigating the adverse effects of erroneous learning during model training. By incorporating gradient changes, adaptive weight computation, and multi-head self-attention, RAA offers an effective enhancement strategy for medical image segmentation tasks, addressing challenges such as variable cell morphology and ambiguous boundaries. Experimental results show that after integrating the RAA method into the network, when the proportion of labeled data was 1/4, 1/8, 1/16, and 1/32, the F1-score improved by 1.65%, 1.59%, 2.42%, and 2.06%, respectively, and the MIOU scores increased by 0.69%, 0.94%, 3.08%, and 1.24%, respectively. As shown in
Table 4, the regional-adaptive attention mechanism demonstrated the highest effectiveness among the three strategies, with its improvement nearly equivalent to the combined effects of the other two. This suggests that in instance segmentation tasks involving complex backgrounds, the adoption of the regional adaptive attention mechanism enables the model to dynamically adjust attention based on regional complexity, directing greater focus toward intricate areas and consequently improving the accuracy of cell segmentation.
4.4.2. The Function of the Combination Module
In the preceding ablation experiments, the designed methods were individually integrated into the baseline network to validate their standalone contributions. The results demonstrate the effectiveness of the proposed methods in addressing the complex task of cell instance segmentation. In the subsequent ablation experiments, a detailed analysis was conducted on the performance improvements achieved by different module combinations under varying proportions of labeled data. As shown in
Table 5, the Base+SWC+RAA scheme consistently outperformed the Base+CAS+SWC scheme across all data partitions, achieving higher F1-score and MIOU improvements. This indicates that the RAA component plays a more critical role in enhancing cell feature extraction and fine-grained information learning. Specifically, under the 1/4, 1/8, 1/16, and 1/32 data partitions, the F1-score of Base+SWC+RAA improved by 1.30%, 0.90%, 1.99%, and 1.92%, respectively, compared to the baseline network. Similarly, the MIOU index improved by 1.18%, 1.20%, 4.25%, and 2.55%, respectively.
Furthermore, CSRA-Net (Base + CAS + SWC + RAA) demonstrated the best performance across all experiments. Compared to the baseline model, this network achieved an average accuracy improvement of 1.5%, outperforming the enhancement observed among mainstream networks and thereby validating the effectiveness of the combined module. Specifically, in the 1/16 data split, its F1-score and MIOU improved by 5.64% and 5.75%, respectively, compared to the baseline. This highlights the significant enhancement in the network’s learning capability achieved through the synergistic interaction of multiple modules in scenarios with limited labeled data. However, in the 1/32 data split, despite achieving the highest improvement among all methods (the F1-score increased by 2.95%, and the MIOU increased by 3.43%), the performance gain was relatively smaller compared to the 1/16 split. This indicates that under conditions of extremely scarce labeled data, the model’s overall performance is constrained, leading to a saturation effect in the contributions of additional modules.
5. Discussion and Conclusions
This paper presents CSRA-Net, a segmentation network based on category-adaptive and attention mechanisms designed for semi-supervised instance segmentation of cell nuclei. To address the prediction bias arising from class imbalance in semi-supervised instance segmentation, we proposed a category-adaptive sampling method. By dynamically adjusting the sampling strategy for labeled data, this method enhances the balance of samples across different cell types, allowing the model to effectively learn the characteristics of various cell types and consequently produce more accurate segmentation results. Secondly, to tackle the segmentation robustness challenge encountered by semi-supervised models, we proposed a strong–weak contrast consistency strategy. This strategy compels the model to disregard noise and irrelevant background information in images while emphasizing the learning of structural and morphological features of cells. Consequently, it enables the extraction of more robust and intrinsic feature representations, thereby improving the model’s robustness. Finally, we proposed a region-adaptive attention mechanism that adaptively adjusts the attention weights based on regional complexity. This enables the model to focus more effectively on complex regions, thereby enhancing the accuracy of segmentation. The proposed network, acting as a universal semi-supervised instance segmentation method, not only provides valuable insights for both semi-supervised and fully supervised segmentation approaches but also effectively tackles the challenges of sample category imbalance and limited segmentation robustness in segmentation tasks.
Despite the satisfactory performance of CSRA-Net, several limitations should be noted. First, the method heavily relies on the quality of pseudo-labels generated during the semi-supervised learning process. Although our strong–weak contrast consistency strategy helps mitigate the impact of noise in pseudo-labels, the potential accumulation of errors in the pseudo-labels remains a challenge. These errors could lead to suboptimal model performance, particularly in complex or ambiguous regions of the images. Additionally, while the dynamic category-adaptive sampling method effectively addresses the issue of class imbalance, it requires careful hyperparameter tuning to ensure optimal performance across different datasets. For instance, the inverse proportional strategy used in our method to calculate the oversampling factor for each class may not achieve ideal balance in cases of extreme class imbalance between cell types.
In future work, we will explore strategies to further improve pseudo-label quality, such as incorporating self-training techniques or refining the adaptive sampling method to better handle extreme class imbalances. Furthermore, reducing the computational overhead of the region-adaptive attention mechanism could enhance the applicability of CSRA-Net in more resource-constrained environments.