Next Article in Journal
Innovative Stackable Multijet-Printed Templates for Precise Veneer Preparation: A Dental Technique
Previous Article in Journal
The Impact of Laser Amplitude on the Radiation Characteristics of the Cross-Collision Between the Relativistic Electron and the Tightly Focused Linearly Polarized Laser
Previous Article in Special Issue
Real-Time Pipeline Leak Detection: A Hybrid Deep Learning Approach Using Acoustic Emission Signals
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 15
Issue 9
10.3390/app15094976
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Optimal Arrangement Strategy of IoT Sensors in Urban Drainage Networks: A Review

by
Yiyi Ma
,
Tianyu Guo
and
Yiran Wang
*
College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China
*
Author to whom correspondence should be addressed.
Appl. Sci. 2025, 15(9), 4976; https://doi.org/10.3390/app15094976
Submission received: 15 March 2025 / Revised: 18 April 2025 / Accepted: 22 April 2025 / Published: 30 April 2025
(This article belongs to the Special Issue Application and Simulation of Fluid Dynamics in Pipeline Systems)
Browse Figures
Versions Notes

Abstract

:
The Urban Drainage Network (UDN) is a type of underground municipal infrastructure responsible for transporting sewage and rainwater. To keep abreast of the hydraulic and water quality conditions of the pipes and to detect problems such as pipe clogging, pollution and leakage, real-time monitoring sensors have been widely adopted, accomplished with the development of IoT technologies. However, the intricate topology and numerous nodes of drainage pipes complicate IoT sensor placement strategies, especially in the selection of sensors and the location of monitoring points. This review examines application cases of IoT sensors in UDNs and some other hydraulic networks, evaluating the characteristics and applicability of various optimal placement methods and theories. A general framework was proposed applicable to the optimal placement of IoT sensors in the UDN, including object classification–method selection–quantitative evaluation. Currently, the quantitative evaluation of monitoring schemes lacks a systematic process, and existing layout methods may not be optimal. Future research can explore dynamic optimization strategies through phased deployment and feedback iteration, which can enhance the accuracy and objectivity of sensor layout design and evaluation.

1. Introduction

The Urban Drainage Network (UDN) is a type of underground municipal infrastructure for transferring and transporting rainwater and sewage. Owing to complex operating conditions, their inspection and maintenance are difficult [1]. Monitoring the operational status of pipeline networks using Internet of Things (IoT) sensors can facilitate the identification of problems such as blockage, pollution, and leakage, owing to factors such as pipeline failure. This is critical to the safe and stable operation of drainage networks. In a UDN, the parameters that are monitored by sensors include water quality and hydraulic parameters. By monitoring the composition of sewage [2,3,4], low water quality and illegal discharge points can be identified in pipelines, and corresponding measures can be implemented to reduce the operational burden of sewage treatment plants during pollution events. Moreover, by monitoring hydraulic parameters such as the flow rate and water level, the flow state inside a pipeline can be evaluated [5,6], and abnormal events, such as blockage, external water infiltration, backflow, and overflow [7,8,9], can be analyzed to guide the operation and maintenance of the network.
Traditional drainage network operation and maintenance rely heavily on regular field surveys [10,11] or sewage and sediment sampling [3,12,13] to obtain network operational data. Currently, high-precision sensors such as flow, level, and current meters are widely utilized in important nodes of UDNs. However, owing to several limitations, including their data temporal resolution, the amount of data collected, and the spatial distribution of sampling points, it is difficult to adequately assess the real-time operational status of the drainage network using regular manual sampling or empirical judgment. Consequently, there is a lag in accident monitoring such as illegal discharge and flood overflow. Thus, it is impossible to reflect real-time hydraulic and water quality status in the pipeline network.
The advancement of IoT technology and the iterative improvement in sensors have led to the development of IoT sensors that facilitate real-time data transmission for safety and health monitoring of structures such as bridges [14] and dams [15], as well as environmental monitoring such as air quality [16]. They are also widely used in the monitoring of hydraulic parameters in water supply projects [17,18,19], surface rivers [20], groundwater [21], and rainfall [22]. Recently, IoT sensors have also been widely used in the monitoring of water quality hydraulic parameters in UDNs. The application of IoT in UDN monitoring is shown in Figure 1.
However, the complexity of sewage composition and variable flow patterns in drainage pipes pose great challenges to the application of IoT monitoring devices and communication technologies. In addition, drainage networks have a complex pipeline network topology, consisting of pipelines at different levels, such as main drains, main sewers, branch pipelines, and connecting pipelines. Therefore, the application of IoT sensors, especially the selection of monitoring locations, is difficult. Numerous studies have been conducted on the optimized layout of sensors. A universal layout strategy has not been established yet. This investigation focused on the monitoring needs and structural characteristics of drainage pipelines, proposed a general framework applicable to the optimal layout of IoT sensors for UDNs and classified the monitored parameters at different nodes, and compared the advantages, disadvantages, and application scopes of different types of sensor layout optimization methods.

2. Literature Sources

In order to systematize the existing research results and support the framework construction, this study first clarifies the strategy and screening criteria of the literature search. The following methodology was used to search and identify relevant literature: First, we categorized the keywords into four different dimensions according to time, type of network, technology, and topic, as shown in Table 1. Time represents the research discussed in this study, mainly up to 31 December 2024; the network types are mainly combined and separated drainage networks. In the other three dimensions, we considered terms and expressions similar to the keyword “optimal placement of IoT sensors in urban drainage networks”, and searched the Web of Science database by combining the terms of “technology” and “network”; connecting them with “and” yielded a total of 189 papers. Next, a further review in conjunction with the abstracts of the literature excluded those that were not relevant to the topic of this study. In order to ensure the comprehensiveness of the research methodology, we referenced and drew on the application of sensors in other similar hydraulic projects to provide a more robust scientific overview and suggestions for the monitoring of drainage networks. Finally, a total of 96 studies were included for discussion in this review.
As can be seen from the buzzwords and high-frequency words related to UDN monitoring in Figure 2, the current monitoring work of UDNs mainly focuses on some water quality indicators (concentration of a certain marker in the drainage network) due to the wide range of water quality characterization parameters, which can be used to identify pollution sources, analyze the trend of pollutant propagation and dispersion, and assess the water environment to facilitate managers to take timely and effective measures. The other part of the monitoring effort focuses on hydraulic characterization parameters such as flow and water level, which are mainly used to study overflow, flooding, leakage, and inflow/infiltration problems in the UDN.
In the process of the literature research, we found that the research and application of IoT sensors on UDN show a rising trend year by year, and these articles mainly focus on the stage of analyzing and applying the collected data on drainage networks. Nevertheless, the importance of the site selection of the monitoring point in the early stage for the whole research should not be ignored, but relatively few studies have been conducted on this key link. The selection of monitoring points is decisive for the effective collection, processing and analysis of subsequent data, but the current attention and research investment in this area are insufficient in the academic community, and this area is in urgent need of further in-depth research and study. This study presents a summary and classification according to the optimization theories and methods used in the study and discusses the optimal arrangement of IoT sensors in drainage networks, with a view to providing scientific guidance for the siting of monitoring points in UDNs.

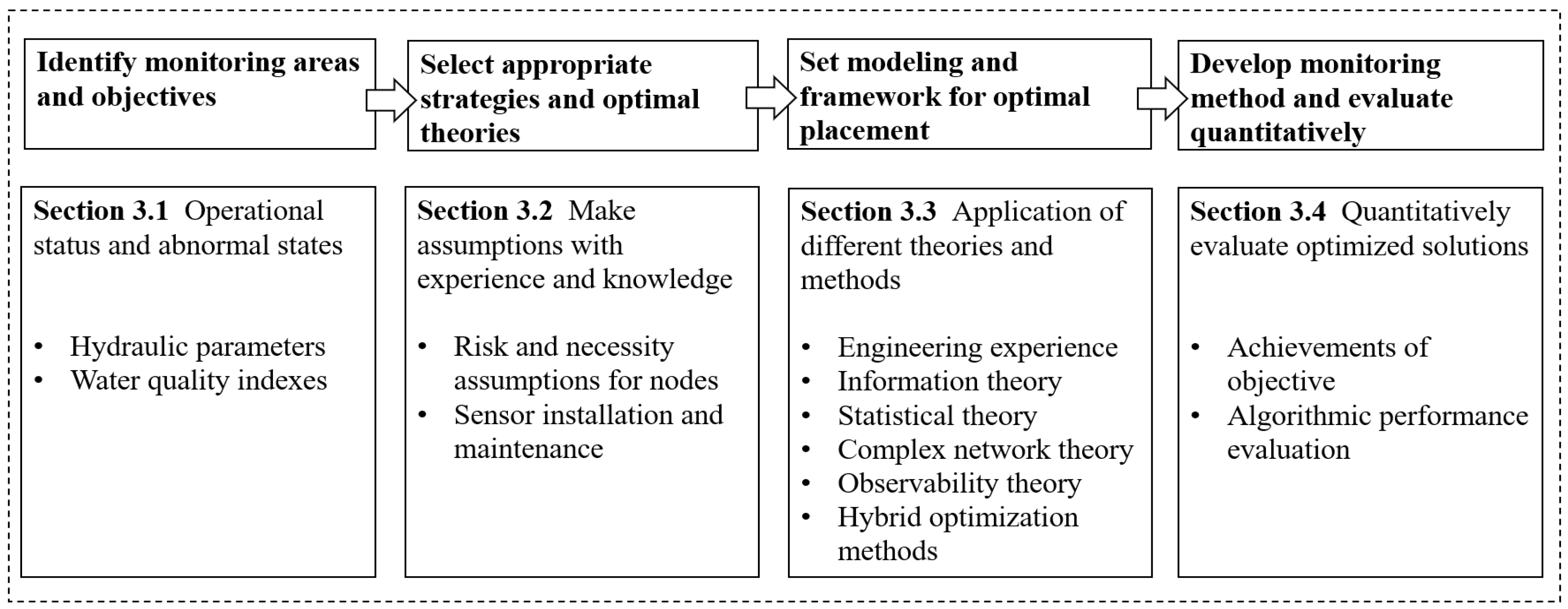
3. Arrangement of IoT Sensors in the Drainage Network

In contrast with the relatively mature methods for optimizing the layout of monitoring points in surface water and water supply networks, there is still a lack of comprehensive guidance for optimizing the placement of IoT sensors in drainage networks. The optimized layout of sensors in drainage networks is similar to the selection of monitoring points in other applications, but there are significant differences in topology, flow characteristics, and water quality monitoring: ① drainage networks are usually simplified as tree-like structures [13,23], with inspection wells and connections represented by nodes [12]; ② the internal environment of pipelines is complex, usually exhibiting alternating open and full flow states; ③ the rainwater and sewage transported inside the pipeline are complex in composition and corrosive. These characteristics account for the difference in the design and layout of IoT sensors in drainage networks compared to other applications.
Sensors should be arranged to provide as much valid data as possible on the targets to be monitored, which is the first step in information analysis [24], planning and management [25,26,27], or the adoption of appropriate measures [28]. The accuracy of decision making depends more on the precision and reliability of data, rather than the volume of the data. Poor-quality datasets may lead to decision-making biases [29,30]. It has been shown that an increase in the number of sensors leads to a sharp decline in the return on scale [2,23]. In Figure 3, we explicitly present a general process applicable to the optimal placement of IoT sensors in UDNs, as well as a description of the content and framework of this review.
Firstly, the study area and monitoring objectives should be identified for the selection of indicator parameters and sensor types. Topological information and data on the drainage network should be collected and organized. Based on various optimization theories and methods, the optimization model and framework were established by incorporating prior knowledge and engineering experience. The monitoring plan was then generated and quantitatively evaluated. The operational status of the drainage network can then be obtained using the IoT monitoring data. Thus, the drainage network can be maintained and promptly managed.

3.1. Classification of Monitoring Objectives

The information provided by nodes and sections of drainage networks in different studies has different meanings and values [6]. For example, to address the information collection needs of a drainage network, the small-scale network in Example 8 of the SWMM (the Storm Water Management Model, which is a comprehensive tool used to simulate urban stormwater runoff and drainage system behavior, widely employed in planning, analysis, and design of stormwater management systems) application manual has been used in several studies as the object. Based on this, several monitoring schemes using different sensor layouts have been developed depending on the objectives [31,32,33]. This included the monitoring of the operational status and the identification of abnormal conditions in the network.

3.1.1. Monitoring of the Operational Status of the Pipeline Network

The assessment and diagnosis of the pipeline network operation states are mainly realized via the real-time monitoring of hydraulic parameters such as flow rate, liquid level, and flow velocity [34]. By analyzing abnormal signals and sharing data across nodes, IoT sensors enable spatial continuity in monitoring, improving the detection and resolution of pipeline network anomalies. The IoT sensors are optimally arranged. Optimal IoT layouts are used to improve the coverage area [35,36], the amount of monitored information, the time of detection [33,37], and the reliability of the monitoring scheme [30,38].
In addition, the monitored data of the drainage network can be used in the calibration of numerical models. The hydraulic and water quality coupling model can be used to solve hydrodynamic problems involving flow velocity, flow rate, and water level. They can also simulate source diffusion and its inverse [39,40]. However, they require more input parameters [41] for calibration. Both the number and spatial location of calibration points can affect the calibration accuracy of the model [42,43]. By optimizing the arrangement of sensors to collect data at the optimal calibration points [44] of the model, the cost of data collection can be reduced while improving the accuracy.

3.1.2. Identification of Abnormal States in Pipeline Networks

(1)
Tracking and Source Tracing of Target Pollutants
By monitoring the composition of sewage such as pH, conductivity [2,4], and other water quality parameters in the drainage network, the tracking and source tracing of illegal discharge in the network can be realized. Based on reverse modeling [45] and the inversion [46] of monitoring data on the transfer and diffusion process of target pollutants, or the establishment of transfer and transport models for these pollutants [20], tracking and source tracing can be achieved. Wastewater treatment plants can be instructed to implement emergency measures in advance to minimize the impact on the treatment process owing to fluctuations in sewage quality in the network.
The drainage network is an important type of infrastructure in cities. Downstream inspection wells collect and reflect the upstream sewage composition information. By monitoring the specific chemical components of wastewater, it is possible to locate and trace target pollutants. In recent years, wastewater-based epidemiology (WBE) has facilitated the tracking and localization of mass epidemic outbreak hotspots [47,48] and illicit drug abuse [49,50]. It has achieved reliable monitoring results in populated areas such as communities [51] and universities [52]. In particular, this method is low cost and allows for wide coverage during the initial screening of large populations compared to the sampling and testing of individuals. An example of this is during the large-scale COVID-19 outbreak [53]. When information about the target is detected in the drainage network, progressive screening of the upstream area can facilitate the localization of infected individuals. Appropriate isolation measures can then be implemented.
(2)
Hotspot Monitoring of Floods and Overflows
The monitoring of water levels in municipal drainage networks via the placement of IoT sensors in flood-prone areas can guide flood emergency response and management, such as in unattended overflow sections of the pipeline network [45], flooding hotspots in the combined drainage network [22], and areas where backflow occurs in rainwater networks during high tides [54]. Through the appropriate positioning of sensors, the scope of investigation can be narrowed for the required measurement. The development of AI technology enables the efficient application of the massive amount of data generation from IoT sensors to flood modeling and prediction. Zhang et al. [55] constructed different neural network models to simulate and predict CSO water levels based on IoT-monitored CSO water-level datasets and rainfall intensity data. C. Cosco et al. [9] considered the three factors of CSO frequency, volume of water, and the amount of pollution, to monitor CSO events in a combined drainage network to minimize their impacts.

3.2. Assumptions for Scheme Design

Before optimizing the layout of IoT sensors, preliminary scheme design is conducted based on premises and assumptions, considering the monitoring objective, drainage network characteristics, and design experience. This can address the information deficit of the design process, anticipate potential problems and risks in advance, and, thus, develop coping strategies in advance.

3.2.1. Risk and Necessity Assumptions for Nodes

In theory, each node and pipeline can be selected as a monitoring point. However, such a large-scale arrangement of monitoring points is not economical. Based on the monitoring objectives, it may be necessary to evaluate the risks and necessity of nodes in different locations to eliminate extraneous nodes and their connecting pipeline segments. There are two main assumptions regarding the necessity of nodes. One is that any node in the pipeline network has an equal probability of being the source in pollutant monitoring. Thus, the nodes have the same weight in the scheme formulation. The other is that the nodes in certain locations in the drainage network have a higher necessity for monitoring. Table 2 lists the assumptions about the risk and necessity of nodal monitoring of UDNs.
Exploiting the idea of Bayesian inference, when arranging sensors, empirical knowledge is used as prior information based on established objectives to classify nodes and assign weights in advance, thereby reducing the number of decision variables and the computational burden during the early stages of establishing the IoT sensor layout optimization model. This is applicable to solving black-box optimization problems, including sensor position selection. Moreover, the results indicate that when only specific monitoring objectives are considered, the probability distribution of prior information does not affect the optimized placement of the sensors, and the optimized result is insensitive to this parameter [13,32]. Therefore, detailed experience and data analysis are not required to create prior information.

3.2.2. Assumptions for Sensor Installation and Maintenance

In theory, the installation and operational costs, failure conditions, and service life of the sensors do not change significantly with the location of installation, and the sensors are assumed to be immune to failure and damage. However, in practical situations, sensor failure and delayed response can have an impact on monitoring, especially in water supply networks [60,61]. The installation and maintenance costs of sensors are linked to their specific location [62], and the actual situation must be considered to guide the installation process. Moreover, the sensors are more susceptible to damage owing to complex sewage composition and the operating environment [8]. Therefore, the operational costs, robustness, and adaptability of the design scheme should be comprehensively considered during the scheme design phase.

3.3. Optimization of Monitoring Point Locations

3.3.1. Design Evaluation Methods Based on Engineering Experience

Decision makers need to comprehensively consider the overall study area and objectives when selecting the location of monitoring points based on engineering experience. The general principles considered include the principle of controllability, as well as the requirements for uniformity, feasibility, representativeness, safety, and installation and maintenance costs [5,6,10,25]. Important nodes in the drainage network [12,63], other than inspection wells, or the selection of important drainage facilities, such as sewage treatment plants [64], discharge outlets [24,65], pump stations [6], and weirs [26], all require special attention. In addition, in some cases, where monitoring points are arranged in a UDN [34,66], the classification of branch pipelines, main sewers, and main drains is conducted based on several factors. These include the connection structure of the network, the location of monitoring points, and monitored parameters. They are determined step by step, and the monitoring points are classified. Ogie et al. [67] considered the high-impact scenarios of sensor monitoring deployment, the high-risk locations of the monitored objects, and the high coverage of the sensor network as the objectives. They set different weights for the objectives based on expert opinions and optimized the objective function to calculate the sensor layout scheme.
In certain UDNs with a long service life, detailed basic data and relevant information are often missing, making it difficult to establish high-precision models. Therefore, expert experience and engineering practice are relied on to select monitoring point locations, and extensive data and information on the operation of drainage networks are acquired. However, for UDNs with complex topology and a large number of pipelines and nodes, it is difficult to directly determine the monitoring point locations based on human experience. For example, the collected data at the discharge outlet and the downstream area can reflect the summary information of the system and facilitate useful observational utility [56,67]. However, the merging of different branch pipelines blurs the details of the spatial information [57]. Thus, the layout of monitoring points should be more scientific and reasonable.

3.3.2. Design Evaluation Methods Based on Information Theory

Information theory can also be used for the design evaluation of optimized sensor layouts. Entropy is defined as a reduction in the uncertainty of a random variable X [68] in information theory. When a signal is observed, the amount of information obtained indirectly measures the reduction in uncertainty. To some extent, the concepts of information and uncertainty can be equated [69]. Information entropy and some of its related concepts, as shown in Table 3, have been applied to the design and evaluation of a variety of hydrological measurement networks, including precipitation [70,71], runoff [72,73,74], water quality [69], groundwater [21,75], polder [26], and water supply networks [6].
Li et al. [76] proposed a generalized maximum information minimum redundancy (MIMR) criterion for the design and evaluation of hydrological networks, which satisfies the three objectives of maximum overall information (joint entropy), maximum information transformation capability (ubiquitous information), and minimum redundancy information (total correlation). The design and evaluation of monitoring schemes based on the MIMR criterion can accurately and efficiently represent information. This criterion has been further supplemented and improved by researchers in the field. Combining heuristics, such as greedy algorithms, genetic algorithms, and evolutionary algorithms, it has also been widely applied to the optimized layout of IoT sensors in UDNs and hydrological network monitoring [1,27].
Based on the principle of information theory, high entropy corresponds to high uncertainty (and high information content) in measurements owing to a large number of possible events [1]. Therefore, locations with high entropy values [37,77] are usually selected as monitoring points. However, points with high information content may not necessarily have high monitoring value. Alfonso and Price [28] introduced the concept of information value when designing hydrological monitoring networks. Different decisions were made based on the information acquired from monitoring points. The resulting consequences corresponded to different information values, and locations with high information values [6,78] served as monitoring points. This method can guide the decision-making process regarding the operational status of water conservancy facilities. A major drawback of entropy-based criteria is that nodes with low redundant information are usually located as far away from each other as possible [77]. As a result, these schemes tend to place sensors on the boundaries of the study area, thus ignoring practical engineering needs. Moreover, population density and socio-geographical issues are not considered [79].

3.3.3. Design Evaluation Methods Based on Statistical Theory

The main idea behind the design and optimization of the monitoring network is to reduce the uncertainty associated with unmonitored locations [26], as well as the redundancy of monitored locations. Statistical theory can handle and analyze massive amounts of data as well as measure and quantify uncertainty. Therefore, statistical theory represented by cluster analysis is widely used in the design of sensor locations for water supply [80,81,82,83]. Cluster analysis groups unlabeled data points into clusters based on similarity. This method also categorizes nodes using the similarity of data patterns or topological relationships. Thus, it is possible to reduce the number of monitoring points while ensuring overall effectiveness, thereby guiding the selection of sensor locations.
However, the number of required clusters for analysis must be determined by decision makers after several tests [22,31] or by using heuristic algorithms [84]. It may not be possible to obtain the optimal cluster partitioning, and the results cannot identify specific sensor location choices within the cluster. Given that the focus is on the similarity of nodes, the benefits and value of single monitoring points are ignored.

3.3.4. Design Evaluation Methods Based on Complex Network Theory

Most optimized IoT sensor arrangements are designed based on the time-series datasets of monitoring points [22] or pollutant transport and dispersion distributions in the pipeline network [35,39,58] based on SWMM pipeline network hydrodynamic simulations. Other methods have also been adopted instead of hydrodynamic models, focusing on the topological structure of drainage networks. The placement of sensors was optimized by evaluating the degree to which each node was affected by abnormal events in the pipeline network. Simone et al. [85] analyzed the potential and feasibility of complex network theory (CNT) in the assessment of the vulnerability and resilience of UDNs, the design of optimal monitoring points, and the study of the propagation of pollutants. They also proposed a series of topology-based indexes and coefficients that were utilized to guide the optimal placement of sensors. This approach considers the relative position and connections between the nodes and facilitates the optimal arrangement and evaluation of the sensors without performing hydraulic simulations, which serves as an alternative approach to solving these types of problems.

3.3.5. Design Evaluation Methods Based on Observability Theory

The observability of a complex system can be defined as the utilization of the minimum number of sensors to collect enough information for the prediction or estimation of the state of areas of the system that are not directly monitored [86]. This facilitates a better understanding of the system’s operational status and improves situational awareness for risk management and decision making. Observability analysis can be used to establish a state space model to ensure that the system’s state can be estimated using sensor measurements. The approach guides the location selection process of sensors in applications such as the evaluation of the pollutant concentration in river networks [11] and the identification of key nodes in flood monitoring networks [87]. In the water supply network, the system’s state can be estimated based on indicators such as node water demand [88], disinfectant (chlorine) concentration [89], and pollutant identification [90], and sensors can then be arranged accordingly. There are few studies on the design and evaluation of the optimized placement of IoT sensors in UDNs based on observability. Zheng et al. [78] used the matrix completion model to improve observability by recovering missing data from unmonitored locations. They quantified the deviation between the predicted value of the water level and the observed value to evaluate the optimized placement scheme of the sensors. The utilization of the minimum number of optimally arranged sensors in a complex network structure to improve the observability of the pipeline network has great application potential for the identification and early warning of abnormal states in the operation of a UDN. In Table 4, we summarize and compare the properties of the above methods in terms of accuracy, robustness, computational costs, and adaptability.

3.3.6. Hybrid Optimization Methods and Application

In this section, we introduce the application of the above optimization theories and methods in the practical engineering of the optimal arrangement of IoT sensors in UDNs, including the type of monitoring indicators, monitoring objectives, the size of the pipe network in the monitoring area, the number of monitoring points, and so on. By using the above optimization theories directly or combining them, or combining multiple models and substituting the model outputs into another model for optimization analysis, the advantages of each method can be better exploited to obtain a more effective monitoring scheme. Table 5 summarizes the specific cases of the current IoT optimization arrangement for a UDN.
In addition, the optimal layout of sensors was transformed into a pollution traceability problem to improve the accuracy and reliability of source identification (SI) [95,96], and the results obtained were used as a reference for the siting of sensors. Compared with the sensor layout, only by virtue of engineering experience, considering the optimized layout through the above method, the number and distribution of sensors in the UDN are more reasonable, and the performance in the specific evaluation indexes has a better effect; alternatively, the original monitoring layout can be used to ensure the monitoring effect remains unchanged, which reduces the number of sensors and reduces the cost of the layout and maintenance [84,92,93]. However, it is necessary to point out that the theoretical optimization obtained by the layout should also be considered in combination with cost, field layout, and other factors.

3.4. Quantitative Evaluation of the Monitoring Scheme

Optimal IoT layouts are determined by comparing multiple approaches, which fall into two main categories: ① assessing monitoring efficiency through defined metrics, and ② evaluating algorithmic complexity in the optimization process and to quantitatively evaluate the different schemes by the algorithms’ performances and related indicators. Evaluation methodology/indicators in Table 5 show some of the quantitative evaluation methods and indicators used by the authors, and in Table 6, we further explain the types and the meaning of evaluation indicators.
Due to the diversity of monitoring objectives, optimization theories, and methods, the quantitative evaluation of the optimal deployment of IoT sensors in UDNs has not yet formed a unified evaluation method and process and even lacks the step of quantitatively evaluating the scheme in some studies. On the basis of the existing research results and with reference to the evaluation of other sensor optimization schemes, the performance, cost, and feasibility of the implementation of the optimization scheme of the sensor design scheme are comprehensively evaluated through the quantification of indicators of different dimensions, including the following: for the formulated monitoring objectives, the collected data can effectively respond to the operational status of the UDN; the arrangement of the sensors is cost-effective, and the scope covers the study area while avoiding data redundancy.

4. Summary and Recommendations

This review focuses on a strategy for the optimal layout of IoT sensors for UDNs, covering the general process, principal methods, and application cases. The main conclusions are listed as follows:
(1)
The monitoring of drainage networks primarily reflects their operational status and detects and identifies abnormal states through hydraulic and water quality parameters. Different monitoring areas correspond to distinct monitoring indexes, which, in turn, gives rise to varying layout schemes. Nevertheless, the arrangement of IoT sensors for different networks should strive to provide the maximum amount of valid information.
(2)
In practical scenarios, multiple types of sensors are required for collaborative monitoring and sensing of UDNs. The sensor arrangement methods, based on information theory, statistical theory, and complex network theory, have their own characteristics and adaptation of application. Modularly combining these methods or employing hybrid optimal strategies can be useful for the design and evaluation of optimal layout solutions.
(3)
The quantitative evaluation of monitoring schemes is mainly conducted based on the degree of objective achievement, performance evaluation indexes of optimization algorithms, comparisons with the original sensor layout scheme, or contrasts in the effects achieved by different optimization methods. Nevertheless, a systematic and standardized quantitative evaluation process and methodology for monitoring schemes remain to be established. The current optimized layout methods may not be optimal and deserve further study.
(4)
The existing research on the optimal layout of sensors predominantly focuses on spatial distribution and quantity. In the future, dynamic optimization strategies can be explored by implementing a phased deployment–feedback iteration approach. In the initial stage, sensors should be preferentially arranged at critical nodes. Subsequently, the arrangement scheme for the next stage can be adjusted and determined according to the collected feedback data and information gain. The dynamic optimization strategy has the potential to enhance the accuracy and objectivity of scheme design and evaluation.

Author Contributions

Conceptualization, T.G. and Y.W.; methodology, T.G. and Y.W.; software, Y.W.; validation, T.G. and Y.W.; formal analysis, Y.W.; investigation, Y.W.; resources, Y.M.; data curation, Y.W.; writing—original draft preparation, T.G. and Y.M.; writing—review and editing, Y.M. and Y.W.; visualization, T.G.; supervision, Y.M.; project administration, Y.M.; funding acquisition, Y.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research study is supported by the National Key R&D Program of China (Grant No. 2023YFC3208905), the Natural Science Foundation of Zhejiang Province (Grant No. LZJWZ23E090009), the National Natural Science Foundation of China (Grant No. 52300122), and the Fundamental Research Funds for the Central Universities (226-2024-00033).

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Fahle, M.; Hohenbrink, T.L.; Dietrich, O.; Lischeid, G. Temporal Variability of the Optimal Monitoring Setup Assessed Using Information Theory. Water Resour. Res. 2015, 51, 7723–7743. [Google Scholar] [CrossRef]
  2. Sikorski, A.; Solano Donado, F.; Kozdrowski, S. Cost-Efficient Coverage of Wastewater Networks by IoT Monitoring Devices. Sensors 2022, 22, 6854. [Google Scholar] [CrossRef] [PubMed]
  3. Banik, B.K.; Alfonso, L.; Torres, A.S.; Mynett, A.; Di Cristo, C.; Leopardi, A. Optimal Placement of Water Quality Monitoring Stations in Sewer Systems: An Information Theory Approach. Procedia Eng. 2015, 119, 1308–1317. [Google Scholar] [CrossRef]
  4. Buras, M.P.; Solano Donado, F. Identifying and Estimating the Location of Sources of Industrial Pollution in the Sewage Network. Sensors 2021, 21, 3426. [Google Scholar] [CrossRef]
  5. Rathi, S.; Gupta, R. Sensor Placement Methods for Contamination Detection in Water Distribution Networks: A Review. Procedia Eng. 2014, 89, 181–188. [Google Scholar] [CrossRef]
  6. Khorshidi, M.S.; Nikoo, M.R.; Sadegh, M. Optimal and Objective Placement of Sensors in Water Distribution Systems Using Information Theory. Water Res. 2018, 143, 218–228. [Google Scholar] [CrossRef]
  7. Salem, M. Urban Areas Management in Developing Countries: Analysis of the Urban Areas Crossed with Risk of Storm Water Drains, Aswan-Egypt. World Acad. Sci. Eng. Technol. Int. J. Transp. Veh. Eng. 2017, 14, 96–102. [Google Scholar]
  8. Alshami, A.; Elsayed, M.; Ali, E.; Eltoukhy, A.E.E.; Zayed, T. Monitoring Blockage and Overflow Events in Small-Sized Sewer Network Using Contactless Flow Sensors in Hong Kong: Problems, Causes, and Proposed Solution. IEEE Access 2023, 11, 87131–87149. [Google Scholar] [CrossRef]
  9. Cosco, C.; Cugueró, M.À.; Tàsies, F.; Aguiló, P.; Gómez, M. Sensor Placement for Combined Sewer System Monitoring in the Besòs River Basin. IFAC-Pap. 2018, 51, 949–956. [Google Scholar] [CrossRef]
  10. He, J. The Design of Urban Waterlogging Online Monitoring and Information Services Digital System and Optimization of Monitoring Points of Urban Waterlogging. Master’s Thesis, South China University of Technology, Guangzhou, China, 2014. [Google Scholar]
  11. Bartos, M.; Kerkez, B. Observability-Based Sensor Placement Improves Contaminant Tracing in River Networks. Water Resour. Res. 2021, 57, e2020WR029551. [Google Scholar] [CrossRef]
  12. Kim, K.; Ban, M.J.; Kim, S.; Park, M.-H.; Stenstrom, M.K.; Kang, J.-H. Optimal Allocation and Operation of Sewer Monitoring Sites for Wastewater-Based Disease Surveillance: A Methodological Proposal. J. Environ. Manag. 2022, 320, 115806. [Google Scholar] [CrossRef] [PubMed]
  13. Larson, R.C.; Berman, O.; Nourinejad, M. Sampling Manholes to Home in on SARS-CoV-2 Infections. PLoS ONE 2020, 15, e0240007. [Google Scholar] [CrossRef] [PubMed]
  14. Hou, S.; Wu, G. A Low-Cost IoT-Based Wireless Sensor System for Bridge Displacement Monitoring. Smart Mater. Struct. 2019, 28, 085047. [Google Scholar] [CrossRef]
  15. Smith, C.; McCain, J.; Downey, A.R.J.; Imran, J. An Open-Source IoT Remote Monitoring System for High-Hazard Dams. In Proceedings of the 2022 IEEE Sensors, Dallas, TX, USA, 30 October–2 November 2022; pp. 1–4. [Google Scholar]
  16. Shaik, R.; Kampara, R.K.; Kumar, A.; Sharma, C.S.; Kumar, M. Metal Oxide Nanofibers Based Chemiresistive H2S Gas Sensors. Coord. Chem. Rev. 2022, 471, 214752. [Google Scholar] [CrossRef]
  17. Rathi, S.; Gupta, R.; Kamble, S.; Sargaonkar, A. Risk Based Analysis for Contamination Event Selection and Optimal Sensor Placement for Intermittent Water Distribution Network Security. Water Resour. Manag. 2016, 30, 2671–2685. [Google Scholar] [CrossRef]
  18. Wu, Y.; Liu, S.; Wu, X.; Liu, Y.; Guan, Y. Burst Detection in District Metering Areas Using a Data Driven Clustering Algorithm. Water Res. 2016, 100, 28–37. [Google Scholar] [CrossRef]
  19. Kim, Y.; Lee, S.J.; Park, T.; Lee, G.; Suh, J.C.; Lee, J.M. Robust Leak Detection and Its Localization Using Interval Estimation for Water Distribution Network. Comput. Chem. Eng. 2016, 92, 1–17. [Google Scholar] [CrossRef]
  20. Ji, C. Optimizing Drainage Network Monitoring and Pollution Tracing Using Machine Learning and Markov Chain Monte Carlo. Master’s Thesis, Shandong University, Jinan, China, 2023. [Google Scholar]
  21. Jia, R.; Wu, J.; Zhang, Y.; Luo, Z. Site Prioritization and Performance Assessment of Groundwater Monitoring Network by Using Information-Based Methodology. Environ. Res. 2022, 212, 113181. [Google Scholar] [CrossRef]
  22. Li, J. Exploring the Potential of Utilizing Unsupervised Machine Learning for Urban Drainage Sensor Placement under Future Rainfall Uncertainty. J. Environ. Manag. 2021, 296, 113191. [Google Scholar] [CrossRef]
  23. Nourinejad, M.; Berman, O.; Larson, R.C. Placing Sensors in Sewer Networks: A System to Pinpoint New Cases of Coronavirus. PLoS ONE 2021, 16, e0248893. [Google Scholar] [CrossRef]
  24. Métadier, M.; Bertrand-Krajewski, J.-L. The Use of Long-Term on-Line Turbidity Measurements for the Calculation of Urban Stormwater Pollutant Concentrations, Loads, Pollutographs and Intra-Event Fluxes. Water Res. 2012, 46, 6836–6856. [Google Scholar] [CrossRef] [PubMed]
  25. Mishra, A.K.; Coulibaly, P. Developments in Hydrometric Network Design: A Review. Rev. Geophys. 2009, 47. [Google Scholar] [CrossRef]
  26. Alfonso, L.; Lobbrecht, A.; Price, R. Information Theory–Based Approach for Location of Monitoring Water Level Gauges in Polders. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
  27. Keum, J.; Coulibaly, P. Information Theory-Based Decision Support System for Integrated Design of Multivariable Hydrometric Networks. Water Resour. Res. 2017, 53, 6239–6259. [Google Scholar] [CrossRef]
  28. Alfonso, L.; Price, R. Coupling Hydrodynamic Models and Value of Information for Designing Stage Monitoring Networks. Water Resour. Res. 2012, 48, W0853. [Google Scholar] [CrossRef]
  29. Keum, J.; Kornelsen, K.C.; Leach, J.M.; Coulibaly, P. Entropy Applications to Water Monitoring Network Design: A Review. Entropy 2017, 19, 613. [Google Scholar] [CrossRef]
  30. Guo, X.; Zhao, D.; Du, P.; Li, M. Automatic Setting of Urban Drainage Pipe Monitoring Points Based on Scenario Simulation and Fuzzy Clustering. Urban Water J. 2018, 15, 700–712. [Google Scholar] [CrossRef]
  31. Wang, S.; Zhang, X.; Wang, J.; Tao, T.; Xin, K.; Yan, H.; Li, S. Optimal Sensor Placement for the Routine Monitoring of Urban Drainage Systems: A Re-Clustering Method. J. Environ. Manag. 2023, 335, 117579. [Google Scholar] [CrossRef]
  32. Sambito, M.; Di Cristo, C.; Freni, G.; Leopardi, A. Optimal Water Quality Sensor Positioning in Urban Drainage Systems for Illicit Intrusion Identification. J. Hydroinformatics 2019, 22, 46–60. [Google Scholar] [CrossRef]
  33. Banik, B.K.; Alfonso, L.; Di Cristo, C.; Leopardi, A.; Mynett, A. Evaluation of Different Formulations to Optimally Locate Sensors in Sewer Systems. J. Water Resour. Plan. Manag. 2017, 143, 04017026. [Google Scholar] [CrossRef]
  34. Fu, X.; Zhang, T.; Li, M.; Li, Y.; Li, X.; Zhou, R.; Wan, R.; Chen, S. Research on the method of monitoring points distribution of urban drainage network. J. Water Resour. Plan. Manag. 2023, 59, 452–456. [Google Scholar] [CrossRef]
  35. Guadagno, V.; Del Giudice, G.; Di Cristo, C.; Leopardi, A.; Simone, A. Impact Coefficient Evaluation for Sensor Location in Sewer Systems. J. Water Resour. Plan. Manag. 2023, 149, 04023063. [Google Scholar] [CrossRef]
  36. Simone, A.; Di Cristo, C.; Guadagno, V.; Del Giudice, G. Sewer Networks Monitoring through a Topological Backtracking. J. Environ. Manag. 2023, 346, 119015. [Google Scholar] [CrossRef] [PubMed]
  37. Banik, B.; Alfonso, L.; Di Cristo, C.; Leopardi, A. Greedy Algorithms for Sensor Location in Sewer Systems. Water 2017, 9, 856. [Google Scholar] [CrossRef]
  38. Simone, A.; Cesaro, A.; Cristo, C.D.; Fecarotta, O.; Morani, M.C. Monitoring Planning for Urban Drainage Networks. IOP Conf. Ser. Earth Environ. Sci. 2023, 1136, 012008. [Google Scholar] [CrossRef]
  39. Chachuła, K.; Nowak, R.; Solano, F. Pollution Source Localization in Wastewater Networks. Sensors 2021, 21, 826. [Google Scholar] [CrossRef]
  40. Shao, Z.; Xu, L.; Chai, H.; Yost, S.A.; Zheng, Z.; Wu, Z.; He, Q. A Bayesian-SWMM Coupled Stochastic Model Developed to Reconstruct the Complete Profile of an Unknown Discharging Incidence in Sewer Networks. J. Environ. Manag. 2021, 297, 113211. [Google Scholar] [CrossRef]
  41. Zhao, D.; Wang, H.; Chen, J.; Sheng, Z. Application and Analysis of Monitoring Technology in Operation and Management of Urban Drainage Network. China Water Wastewater 2012, 28, 11–14. [Google Scholar]
  42. Fattoruso, G.; Agresta, A.; Guarnieri, G.; Lanza, B.; Buonanno, A.; Molinara, M.; Marrocco, C.; De Vito, S.; Tortorella, F.; Francia, G.D. Optimal Sensors Placement for Flood Forecasting Modelling. Procedia Eng. 2015, 119, 927–936. [Google Scholar] [CrossRef]
  43. Walski, T.M. Technique for Calibrating Network Models. J. Water Resour. Plan. Manag. 1983, 109, 360–372. [Google Scholar] [CrossRef]
  44. Clemens, F. Evaluation of a Method for the Design of Monitoring Networks in Urban Drainage. In Proceedings of the Ninth International Conference on Urban Drainage (9ICUD), Portland, OR, USA, 8–13 September 2012; pp. 1–17. [Google Scholar] [CrossRef]
  45. De Vito, S.; Fattoruso, G.; Esposito, E.; Salvato, M.; Agresta, A.; Panico, M.; Leopardi, A.; Formisano, F.; Buonanno, A.; Delli Veneri, P.; et al. A Distributed Sensor Network for Waste Water Management Plant Protection; Andò, B., Baldini, F., Di Natale, C., Marrazza, G., Siciliano, P., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 431, pp. 303–314. [Google Scholar]
  46. He, M.; Zhang, Y.; Ma, Z.; Zhao, Q. Intelligent Optimal Layout of Drainage Pipe Network Monitoring Points Based on Information Entropy Theory. Front. Environ. Sci. 2024, 12, 1401942. [Google Scholar] [CrossRef]
  47. Brosky, H.; Prasek, S.M.; Innes, G.K.; Pepper, I.L.; Miranda, J.; Brierley, P.E.; Slinski, S.L.; Polashenski, L.; Betancourt, W.Q.; Gronbach, K.; et al. A Framework for Integrating Wastewater-Based Epidemiology and Public Health. Front. Public Health 2024, 12, 1418681. [Google Scholar] [CrossRef] [PubMed]
  48. Bibby, K.; Bivins, A.; Wu, Z.; North, D. Making Waves: Plausible Lead Time for Wastewater Based Epidemiology as an Early Warning System for COVID-19. Water Res. 2021, 202, 117438. [Google Scholar] [CrossRef] [PubMed]
  49. Yargeau, V.; Werschler, T. Wastewater-Based Epidemiology as an Input to National Statistics on Recreational Drug Use: A Canadian Pilot Study. Wastewater-Based Epidemiol. 2019, 1319, 137–153. [Google Scholar] [CrossRef]
  50. Huizer, M.; ter Laak, T.L.; de Voogt, P.; van Wezel, A.P. Wastewater-Based Epidemiology for Illicit Drugs: A Critical Review on Global Data. Water Res. 2021, 207, 117789. [Google Scholar] [CrossRef]
  51. Peccia, J.; Zulli, A.; Brackney, D.E.; Grubaugh, N.D.; Kaplan, E.H.; Casanovas-Massana, A.; Ko, A.I.; Malik, A.A.; Wang, D.; Wang, M.; et al. Measurement of SARS-CoV-2 RNA in Wastewater Tracks Community Infection Dynamics. Nat. Biotechnol. 2020, 38, 1164–1167. [Google Scholar] [CrossRef]
  52. Johnson, W.; Reeves, K.; Liebig, J.; Feula, A.; Butler, C.; Alkire, M.; Singh, S.; Litton, S.; O’Conor, K.; Jones, K.; et al. Effectiveness of Building-Level Sewage Surveillance during Both Community-Spread and Sporadic-Infection Phases of SARS-CoV-2 in a University Campus Population. FEMS Microbes 2022, 3, xtac024. [Google Scholar] [CrossRef]
  53. Tshehla, K.S.; Hamam, Y.; Abu-Mahfouz, A.M. State Estimation in Water Distribution Network: A Review. In Proceedings of the 2017 IEEE 15th International Conference on Industrial Informatics (INDIN), Emden, Germany, 24–26 July 2017; pp. 1247–1252. [Google Scholar]
  54. Gold, A.; Anarde, K.; Grimley, L.; Neve, R.; Srebnik, E.R.; Thelen, T.; Whipple, A.; Hino, M. Data from the Drain: A Sensor Framework That Captures Multiple Drivers of Chronic Coastal Floods. Water Resour. Res. 2023, 59, e2022WR032392. [Google Scholar] [CrossRef]
  55. Zhang, D.; Lindholm, G.; Ratnaweera, H. Use Long Short-Term Memory to Enhance Internet of Things for Combined Sewer Overflow Monitoring. J. Hydrol. 2018, 556, 409–418. [Google Scholar] [CrossRef]
  56. Wang, S.; Xu, K.; Zhou, Y. Cost-Effective Sensor Placement Optimization for Large-Scale Urban Sewage Surveillance. Sustain. Cities Soc. 2024, 103, 105250. [Google Scholar] [CrossRef]
  57. Vonach, T.; Tscheikner-Gratl, F.; Rauch, W.; Kleidorfer, M. A Heuristic Method for Measurement Site Selection in Sewer Systems. Water 2018, 10, 122. [Google Scholar] [CrossRef]
  58. Sambito, M.; Freni, G. Strategies for Improving Optimal Positioning of Quality Sensors in Urban Drainage Systems for Non-Conservative Contaminants. Water 2021, 13, 934. [Google Scholar] [CrossRef]
  59. Banik, B.K.; Di Cristo, C.; Leopardi, A. A Pre-Screening Procedure for Pollution Source Identification in Sewer Systems. Procedia Eng. 2015, 119, 360–369. [Google Scholar] [CrossRef]
  60. Berry, J.; Carr, R.D.; Hart, W.E.; Leung, V.J.; Phillips, C.A.; Watson, J.-P. Designing Contamination Warning Systems for Municipal Water Networks Using Imperfect Sensors. J. Water Resour. Plan. Manag. 2009, 135, 253–263. [Google Scholar] [CrossRef]
  61. Zheng, Z.; Zheng, F.; Bi, W.; Du, J.; Duan, H.-F.; Savic, D.; Kapelan, Z. Evaluating the Robustness of Water Quality Sensor Placement Strategies of Water Distribution Systems Considering Possible Sensor Failures and System Changes. J. Water Resour. Plan. Manag. 2022, 148, 04022050. [Google Scholar] [CrossRef]
  62. Berry, J.W.; Hart, W.E.; Phillips, C.A.; Uber, J.G.; Walski, T.M. Water Quality Sensor Placement in Water Networks with Budget Constraints. In Impacts of Global Climate Change; American Society of Civil Engineers: Reston, VA, USA, 2012; pp. 1–11. [Google Scholar] [CrossRef]
  63. Bai, H. Research on the Optimization Design Method of Separated Urban Drainage System under Uncertainty. Ph.D. Thesis, Tsinghua University, Beijing, China, 2016. [Google Scholar]
  64. Boënne, W.; Desmet, N.; Van Looy, S.; Seuntjens, P. Use of Online Water Quality Monitoring for Assessing the Effects of WWTP Overflows in Rivers. Environ. Sci. Process. Impacts 2014, 16, 1510–1518. [Google Scholar] [CrossRef]
  65. Kim, M.; Choi, C.Y.; Gerba, C.P. Development and Evaluation of a Decision-Supporting Model for Identifying the Source Location of Microbial Intrusions in Real Gravity Sewer Systems. Water Res. 2013, 47, 4630–4638. [Google Scholar] [CrossRef]
  66. Guo, X.; Li, M.; Du, P.; Zhao, D.; Zhang, X. Quantification of On-line Monitoring Layout in Urban Drainage Network. China Water Wastewater 2022, 38, 122–131. [Google Scholar] [CrossRef]
  67. Ogie, R.I.; Shukla, N.; Sedlar, F.; Holderness, T. Optimal Placement of Water-Level Sensors to Facilitate Data-Driven Management of Hydrological Infrastructure Assets in Coastal Mega-Cities of Developing Nations. Sustain. Cities Soc. 2017, 35, 385–395. [Google Scholar] [CrossRef]
  68. Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
  69. Ozkul, S.; Harmancioglu, N.B.; Singh, V.P. Entropy-Based Assessment of Water Quality Monitoring Networks. J. Hydrol. Eng. 2000, 5, 90–100. [Google Scholar] [CrossRef]
  70. Kwon, T.; Lim, J.; Yoon, S.; Yoon, S. Comparison of Entropy Methods for an Optimal Rain Gauge Network: A Case Study of Daegu and Gyeongbuk Area in South Korea. Appl. Sci. 2020, 10, 5620. [Google Scholar] [CrossRef]
  71. Yeh, H.-C.; Chen, Y.-C.; Chang, C.-H.; Ho, C.-H.; Wei, C. Rainfall Network Optimization Using Radar and Entropy. Entropy 2017, 19, 553. [Google Scholar] [CrossRef]
  72. Sreeparvathy, V.; Srinivas, V.V. A Fuzzy Entropy Approach for Design of Hydrometric Monitoring Networks. J. Hydrol. 2020, 586, 124797. [Google Scholar] [CrossRef]
  73. Joo, H.; Jun, H.; Lee, J.; Kim, H.S. Assessment of a Stream Gauge Network Using Upstream and Downstream Runoff Characteristics and Entropy. Entropy 2019, 21, 673. [Google Scholar] [CrossRef]
  74. Salman, R.; Nikoo, M.R.; Shojaeezadeh, S.A.; Beiglou, P.H.B.; Sadegh, M.; Adamowski, J.F.; Alamdari, N. A Novel Bayesian Maximum Entropy-Based Approach for Optimal Design of Water Quality Monitoring Networks in Rivers. J. Hydrol. 2021, 603, 126822. [Google Scholar] [CrossRef]
  75. Masoumi, F.; Kerachian, R. Optimal Redesign of Groundwater Quality Monitoring Networks: A Case Study. Environ. Monit. Assess. 2010, 161, 247–257. [Google Scholar] [CrossRef]
  76. Li, C.; Singh, V.P.; Mishra, A.K. Entropy Theory-Based Criterion for Hydrometric Network Evaluation and Design: Maximum Information Minimum Redundancy. Water Resour. Res. 2012, 48, W05521. [Google Scholar] [CrossRef]
  77. Krause, A.; Singh, A.; Guestrin, C. Near-Optimal Sensor Placements in Gaussian Processes: Theory, Efficient Algorithms and Empirical Studies. J. Mach. Learn. Res. 2008, 9, 235–284. [Google Scholar]
  78. Zheng, Y.; Jin, X.; Wei, J.; Zhou, Y.; Zhang, Y. A Novel Framework for Optimization and Evaluation of Sensors Network in Urban Drainage System. Water Res. 2025, 270, 122833. [Google Scholar] [CrossRef] [PubMed]
  79. Yazdi, J. Water Quality Monitoring Network Design for Urban Drainage Systems, an Entropy Method. Urban Water J. 2018, 15, 227–233. [Google Scholar] [CrossRef]
  80. Gautam, D.K.; Kotecha, P.; Subbiah, S. Efficient K-Means Clustering and Greedy Selection-Based Reduction of Nodal Search Space for Optimization of Sensor Placement in the Water Distribution Networks. Water Res. 2022, 220, 118666. [Google Scholar] [CrossRef] [PubMed]
  81. Khaksar Fasaee, M.A.; Monghasemi, S.; Nikoo, M.R.; Shafiee, M.E.; Berglund, E.Z.; Bakhtiari, P.H. A K-Sensor Correlation-Based Evolutionary Optimization Algorithm to Cluster Contamination Events and Place Sensors in Water Distribution Systems. J. Clean. Prod. 2021, 319, 128763. [Google Scholar] [CrossRef]
  82. Peng, S.; Cheng, J.; Wu, X.; Fang, X.; Wu, Q. Pressure Sensor Placement in Water Supply Network Based on Graph Neural Network Clustering Method. Water 2022, 14, 150. [Google Scholar] [CrossRef]
  83. Cheng, L.; Kun, D.; Jia-peng, T.; Wei-xin, D. Optimal Placement of Pressure Sensors in Water Distribution System Based on Clustering Analysis of Pressure Sensitive Matrix. Procedia Eng. 2017, 186, 405–411. [Google Scholar] [CrossRef]
  84. Zhao, W.; Cheng, Y.; Li, M. Optimization of Monitoring Points in Drainage Pipe Network Based on Improved K-means Algorithm. Adm. Tech. Environ. Monit. 2024, 36, 79–83. [Google Scholar] [CrossRef]
  85. Simone, A.; Cesaro, A.; Del Giudice, G.; Di Cristo, C.; Esposito, G.; Fecarotta, O. The Spread of Contaminants in Urban Drainage Networks Based on a Topological Analysis. Environ. Sci. Proc. 2022, 21, 20. [Google Scholar] [CrossRef]
  86. Liu, Y.-Y.; Slotine, J.-J.; Barabási, A.-L. Observability of Complex Systems. Proc. Natl. Acad. Sci. USA 2013, 110, 2460–2465. [Google Scholar] [CrossRef]
  87. Farahmand, H.; Liu, X.; Dong, S.; Mostafavi, A.; Gao, J. A Network Observability Framework for Sensor Placement in Flood Control Networks to Improve Flood Situational Awareness and Risk Management. Reliab. Eng. Syst. Saf. 2022, 221, 108366. [Google Scholar] [CrossRef]
  88. Shao, Y.; Li, K.; Zhang, T.; Ao, W.; Chu, S. Pressure Sampling Design for Estimating Nodal Water Demand in Water Distribution Systems. Water Resour. Manag. 2024, 38, 1511–1527. [Google Scholar] [CrossRef]
  89. Taha, A.F.; Wang, S.; Guo, Y.; Summers, T.H.; Gatsis, N.; Giacomoni, M.H.; Abokifa, A.A. Revisiting the Water Quality Sensor Placement Problem: Optimizing Network Observability and State Estimation Metrics. J. Water Resour. Plan. Manag. 2021, 147, 04021040. [Google Scholar] [CrossRef]
  90. Palleti, V.R.; Narasimhan, S.; Rengaswamy, R.; Teja, R.; Murty Bhallamudi, S. Sensor Network Design for Contaminant Detection and Identification in Water Distribution Networks. Comput. Chem. Eng. 2016, 87, 246–256. [Google Scholar] [CrossRef]
  91. Lee, J.H. Determination of Optimal Water Quality Monitoring Points in Sewer Systems Using Entropy Theory. Entropy 2013, 15, 3419–3434. [Google Scholar] [CrossRef]
  92. Qin, L. The application of cluster analysis in monitoring point optimal of sewer system. J. Guizhou Univ. (Nat. Sci.) 2013, 30, 123–125, 134. [Google Scholar] [CrossRef]
  93. Yuan, J. Research on Hydraulic Modeling and Optimization of Monitoring Points of Urban Drainage System. Master’s Thesis, Hunan University, Changsha, China, 2010. [Google Scholar]
  94. Wu, Y.; Zheng, F.; Yang, Y.; Zhang, K.; Du, K.; Duan, H.; Savic, D.; Kapelan, Z. Enhancing Inflow and Infiltration Detection in Urban Sewer Networks with a New Deterministic Sensor Placement Method. Water Res. 2025, 268, 122591. [Google Scholar] [CrossRef]
  95. Mariacrocetta, S.; Piazza, S.; Freni, G. Bayesian Identification of Brackish Water Infiltration by Lagrangian Sensors. In Proceedings of the 39th IAHR World Congress, Granada, Spain, 19–24 June 2022; International Association for Hydro-Environment Engineering and Research (IAHR): Madrid, Spain; pp. 3718–3720. [Google Scholar]
  96. Salem, A.K.; Abokifa, A.A. Sensor Placement Optimization in Sewer Networks: Machine Learning–Based Source Identification Approach. J. Water Resour. Plan. Manag. 2024, 150, 04024048. [Google Scholar] [CrossRef]
Applsci 15 04976 g001
Figure 1. Demonstrates the application of IoT in drainage network monitoring.
Figure 1. Demonstrates the application of IoT in drainage network monitoring.
Applsci 15 04976 g001
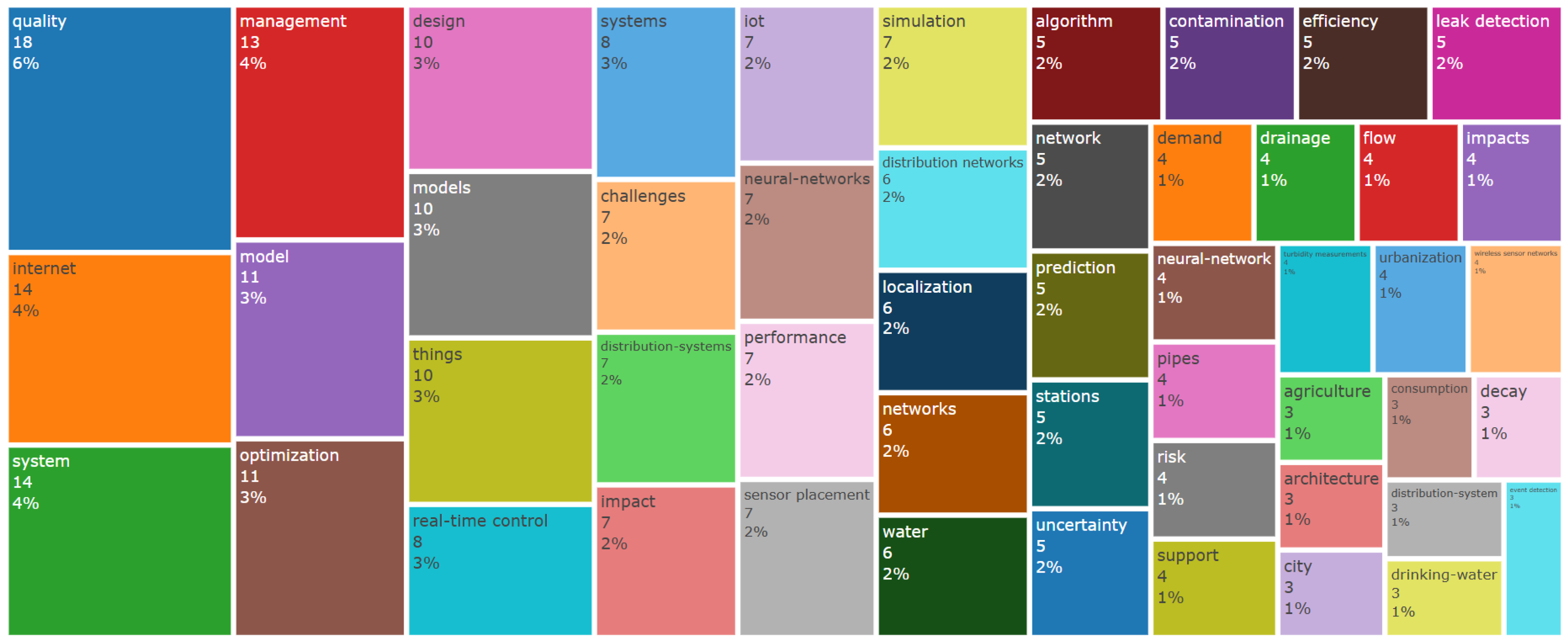
Applsci 15 04976 g002
Figure 2. Hot and high-frequency words related to the monitoring of UDN.
Figure 2. Hot and high-frequency words related to the monitoring of UDN.
Applsci 15 04976 g002
Applsci 15 04976 g003
Figure 3. Process of optimizing the placement of IoT sensors in UDN.
Figure 3. Process of optimizing the placement of IoT sensors in UDN.
Applsci 15 04976 g003
Table 1. Different dimensional keywords used for literature search.
Table 1. Different dimensional keywords used for literature search.
TimeTechnologyNetworkTheme
As of 31 December 2024IoT/sensor
online/real time
monitoring/continuous measurement		Sewer/sewerage/wastewater/drainage
urban networks/system		Optimal/optimization
placement/site/position
Table 2. List of monitoring necessities associated with different types of nodes.
Table 2. List of monitoring necessities associated with different types of nodes.
CategoryType of StudyType of Node
Nodes in certain locations have a higher necessity for monitoringWEB-based drainage network monitoringPriority is given to areas with a high population density such as hospitals, nursing homes, community centers, and inspection wells connected to buildings [12,56].
The location of potentially infected nodes is reflected through Bayesian prior probabilities [13]
Calibration of hydrodynamic modelsThe pipeline where the flow rate changes is the “potential measurement location” [57]
Tracking and source tracing of pollutantsMost pollution events occur in nodes located downstream [32,58]
Different levels of priority are assigned to each potential monitoring site considering CSO frequency, flow rate, and mass of pollutant [9]
A pre-screening procedure based on the concept of pollution matrix is introduced to screen some nodes [59]
Daily monitoringNodes in key topological locations, nodes located in areas with high residential density [31]
Nodes have the same necessity for monitoring [17,33,35]Monitoring and source tracing of pollutants in drainage networksAny node has an equal probability of being the source
Table 3. Formulas and meanings of entropy and its related concepts [76].
Table 3. Formulas and meanings of entropy and its related concepts [76].
Entropy-Based Information MeasureCalculation FormulaMeaning
Entropy (high uncertainty entropy, information entropy or marginal entropy) H X = − ∑ k = 1 K p ( x k ) l o g ⁡ [ p ( x k ) ] Amount of information provided by each monitoring point
Joint entropy (joint information entropy, total entropy, multivariate joint entropy) H X 1 , X 2 … , X N = − ∑ x 1 ∈ X 1 ∑ x 2 ∈ X 2 … ∑ x n ∈ X n p x 1 , x 2 , … x n l o g 2 p ( x 1 , x 2 , … x n ) Total amount of information provided by multiple monitoring points together
Total correlation C X 1 , X 2 , … , X N = ∑ i = 1 N H X i − H ( X 1 , X 2 , … , X N ) Redundancy of information between variables
Transinformation (mutual information) The special cases of total correlation, where n = 2 [26] I X 1 , X 2 = H X 1 + H X 2 − H ( X 1 , X 2 ) Components of redundant information in the monitoring network
Conditional entropy H X 1 | X 2 = H X 1 , X 2 − H X 2 the information loss that occurs during the trans-information process between random variates X1 and X2
Table 4. Performance comparison of main optimized methods.
Table 4. Performance comparison of main optimized methods.
MethodAccuracyRobustnessComputational CostAdaptability
Cluster analysisMedium, dependent on data distribution and algorithm selectionlow, parameters need to be preset, sensitive to noiseModerate algorithmic complexityIdeal for rapid deployment and cost control
Information theoryHigh, quantifying information content through information entropyMedium, relies on data distribution stability, performance degrades with data noise or dynamic changesHigh, requires complex optimization algorithmsNot applicable to old pipe networks or where data is missing
Complex network theoryMedium, based on topology, easy to overlook hydraulic detailsHigh, topologically stableLow, only network analysis required, no complex simulationsNot dependent on hydraulic parameters, but accuracy is limited
Observability theoryHigh, inferring state through mathematical modelingHigh, model parameters optimized for noise immunityHigh, involving matrix operationsEffectiveness is limited when data is extremely sparse
Table 5. Application of optimal theory and methods in UDN.
Table 5. Application of optimal theory and methods in UDN.
TheoryResearchTypeObjectives/IndicatorsSize of Study NetworkMonitoring PointsEvaluation Methodology/Indicators
HydraulicsQualityAreaConduits/
Pipelines		Nodes/
Junctions		Other Water Facilities
Multi-objective optimization + information theory[91] √Maximizing marginal entropy and maximizing trans-information (all entropy variates have positive values)161 ha\80\The outlet + other 7 monitoring points Scheme with maximized joint entropy and minimized total correlation
[3] √Monitoring of pollution of water quality in the sewer network12 sub-catchments, covering an area of 19.71 km2 1909190214 pumps, 14 storage units and 1 treatment plant12
[37] √12 sub-catchments, covering an area of 19.71 km2 1909190214 pumps, 14 storage units and 1 treatment plant14
[79] √4 separate catchment areas\748 candidate sites\20
[78]√ understanding the operating status of UDS and facilitating urban flood early warning. 2.679 km2, is divided into 2693 sub-catchments898878\4 monitoring points (lower budget) or 8 monitoring points (higher budget)Maximize value of information (VOI), minimize trans-information (TE) and minimize economic costs
Complex network theory (CNT)[36] √Evaluating the ability of node to receive pollutants, detecting the maximum amount of information propagated on the network\79771 outfall4In-Relevance-Harmonic Centrality as the indicator
[85] √Analyzing the impact of a pollutant spill at a given node on the entire system, focusing on the role of network topology in pollutant dispersionSWMM example 3 32321 outfall, 1 storage and 1 pump.\node contamination index IC as the indicator
[35] √Analyzing the dispersion of pollutants by calculating the influence coefficients of each node with respect to the installed sensor in the system (usually located at the outfall).\79771 outfall7 monitoring points, with a network coverage equal to 60%impact coefficient (IC) as the indicator
[38] √Analyzing pollutant dispersion at various nodes\79771 outfall7 monitoring points and the prioritization order of the sensors was further consideredtopological impact coefficient (ICT) as the indicator
Multi-objective optimization + Expert advice[67]√ Obtaining water level data to make decisions about the operation of flood control infrastructure\647 waterways57971 pumping stations, 30 floodgates and 11 flood gauges4 sensors in the first phase, which will be expanded to 10 sensors in the following phasesLocations at high risk of monitored phenomena; locations to maximize network coverage; water level information to maximize water temperature infrastructure
Cluster analysis[92]√√Improving monitoring of operational status in sever network\4 main pipelines\\After optimization 10 monitoring points can replace all the initial monitoring pointsStatistical significance analyses based on F-tests and t-tests were performed to compare the data for differences between groups
[93]√√a catchment\\\The original 23 monitoring sites were reduced to 10 sites through optimization
[30]√ 21.5 km219218717 outfalls12The composite indicator compounded from Pearson’s coefficient and Euclidean distance
[84]√√62.88 km2\23 original monitoring points\Reduction of 7 monitoring points Calinski-Harabasz Index, Within-Group Sum of Squares (WGSS), Between-Group Sum of Squares (BGSS)
[31]√√2.63 km27857851 outlet20Scheme with maximized joint entropy and minimized total correlation
[22]√ Flood hotspot monitoring in combined drainage systems7 sub-catchments58602 outfalls3 or 4 Silhouette Coefficient Index (SCI)
[20] √Monitoring of pollution of water quality in the sewer network 139135\8Silhouette Coefficient (SC)
[94]√ detecting inflow and infiltration (I&I) in urban sewer networks15 km28198201 outlet20detection reliability (DR); distribution uniformity (DU)
Table 6. Quantitative evaluation indexes of optimized IoT sensor layout scheme for drainage network.
Table 6. Quantitative evaluation indexes of optimized IoT sensor layout scheme for drainage network.
ClassificationEvaluation IndicatorMeaning
Algorithm performance indicatorAlgorithm running time [2,37,42], hypervolume metric (HV) [56], Silhouette coefficient index (SC) [22], Calinski-Harabaz index (CH) [84].Quantitative evaluation of optimized sensor placement schemes via evaluation of algorithm performance
Mean Absolute Error (MAE), Root Mean Square Error (RMSE), relative RMSE (RRE), coefficient of determination (R2), Nash-Sutcliffe Efficiency (NSE) [20,56,57], Confidence Coefficient, Segregation Likelihood [58], Residual Squared, Correlation Coefficient, Consistency Index [57], Mean of Relative Error MRE [46]. Differences between predicted and actual values obtained by inversion when studying the transport and traceability of pollutants
Assessment of the achievement of objectivesNumber of detected events and event detection rate [39,58], access to monitoring information wherever possible [31,33,84], response time to anomalous events [20,37], reliability of the monitoring network [30,33,37,58,94] uniformity of sensor distribution [94].Assessed by the degree of achievement of monitoring objectives
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Ma, Y.; Guo, T.; Wang, Y. Optimal Arrangement Strategy of IoT Sensors in Urban Drainage Networks: A Review. Appl. Sci. 2025, 15, 4976. https://doi.org/10.3390/app15094976

AMA Style

Ma Y, Guo T, Wang Y. Optimal Arrangement Strategy of IoT Sensors in Urban Drainage Networks: A Review. Applied Sciences. 2025; 15(9):4976. https://doi.org/10.3390/app15094976

Chicago/Turabian Style

Ma, Yiyi, Tianyu Guo, and Yiran Wang. 2025. "Optimal Arrangement Strategy of IoT Sensors in Urban Drainage Networks: A Review" Applied Sciences 15, no. 9: 4976. https://doi.org/10.3390/app15094976

APA Style

Ma, Y., Guo, T., & Wang, Y. (2025). Optimal Arrangement Strategy of IoT Sensors in Urban Drainage Networks: A Review. Applied Sciences, 15(9), 4976. https://doi.org/10.3390/app15094976

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop