Study on Collision Avoidance Behavior in the Social Force-Based Pedestrian–Vehicle Interaction Simulation Model at Unsignalized Intersections
Abstract
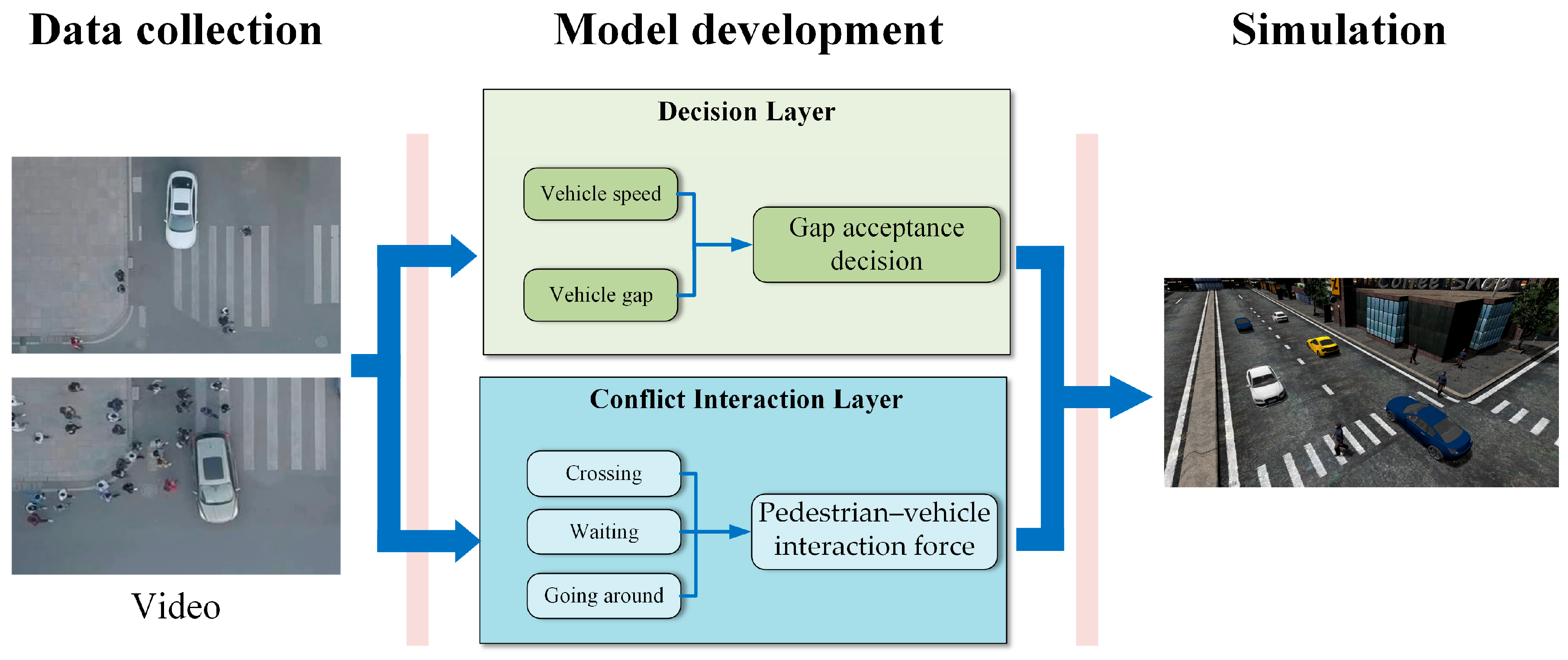
:1. Introduction
- We enhance the ability of pedestrian agents to plan their routes when facing conflicting vehicles by refining the direction and magnitude of the forces they experience at different positions relative to vehicles. This makes pedestrian behavior more realistic and diverse.
- We conduct qualitative and quantitative analyses of both the trajectories and speed of pedestrian–vehicle interaction behaviors in different interaction scenarios and compare them with currently advanced social force-based pedestrian–vehicle interaction models. The results indicate that our model better replicates the observed pedestrian behavior.
2. Related Works
2.1. Data-Driven Models
2.2. Expert Models
3. Pedestrian Agents
3.1. Gap Acceptance Decision
3.2. Force-Based Pedestrian Model Framework
4. Vehicle Agents
4.1. Normal Following
4.2. Yielding Behavior
5. Simulation Results
5.1. Simulation Environment
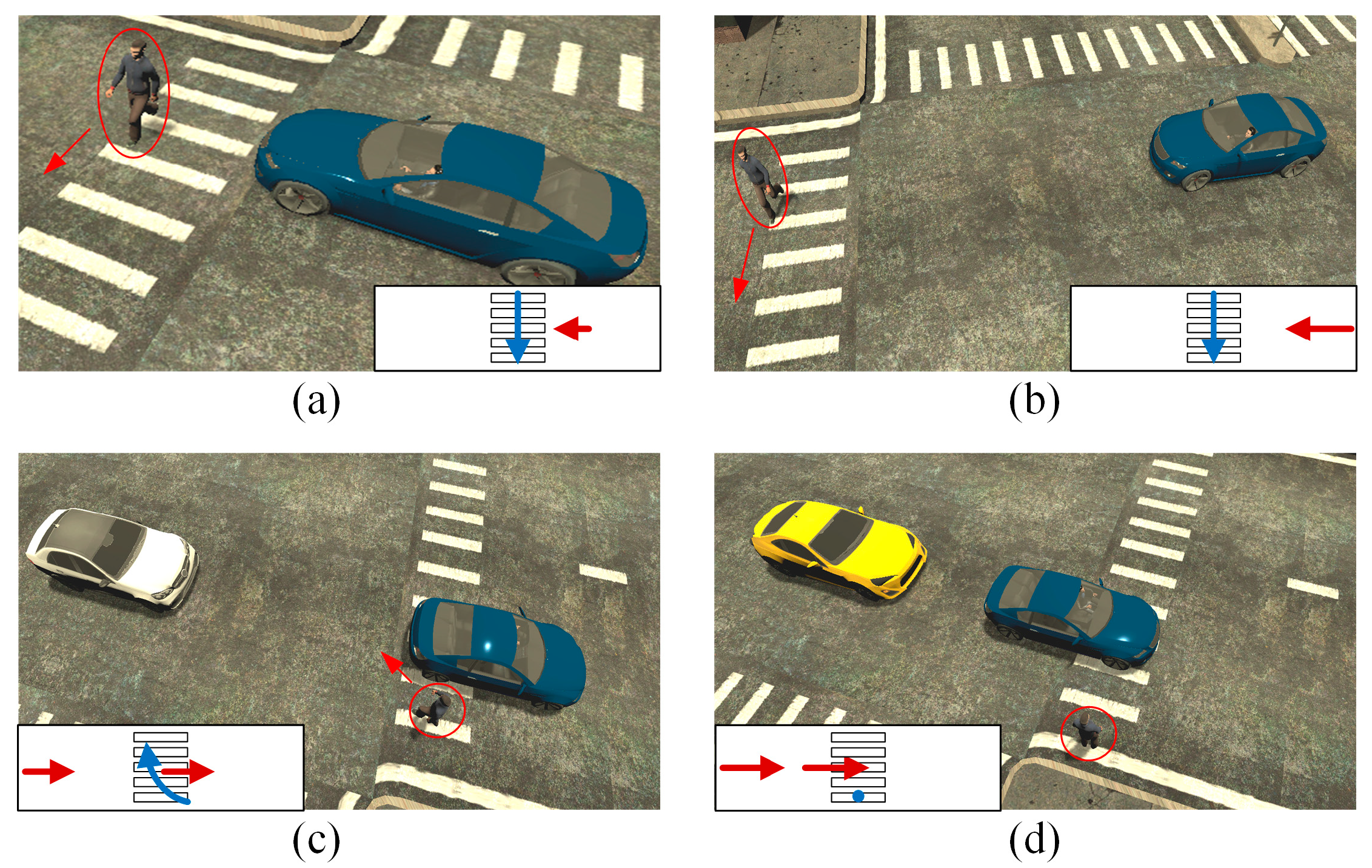
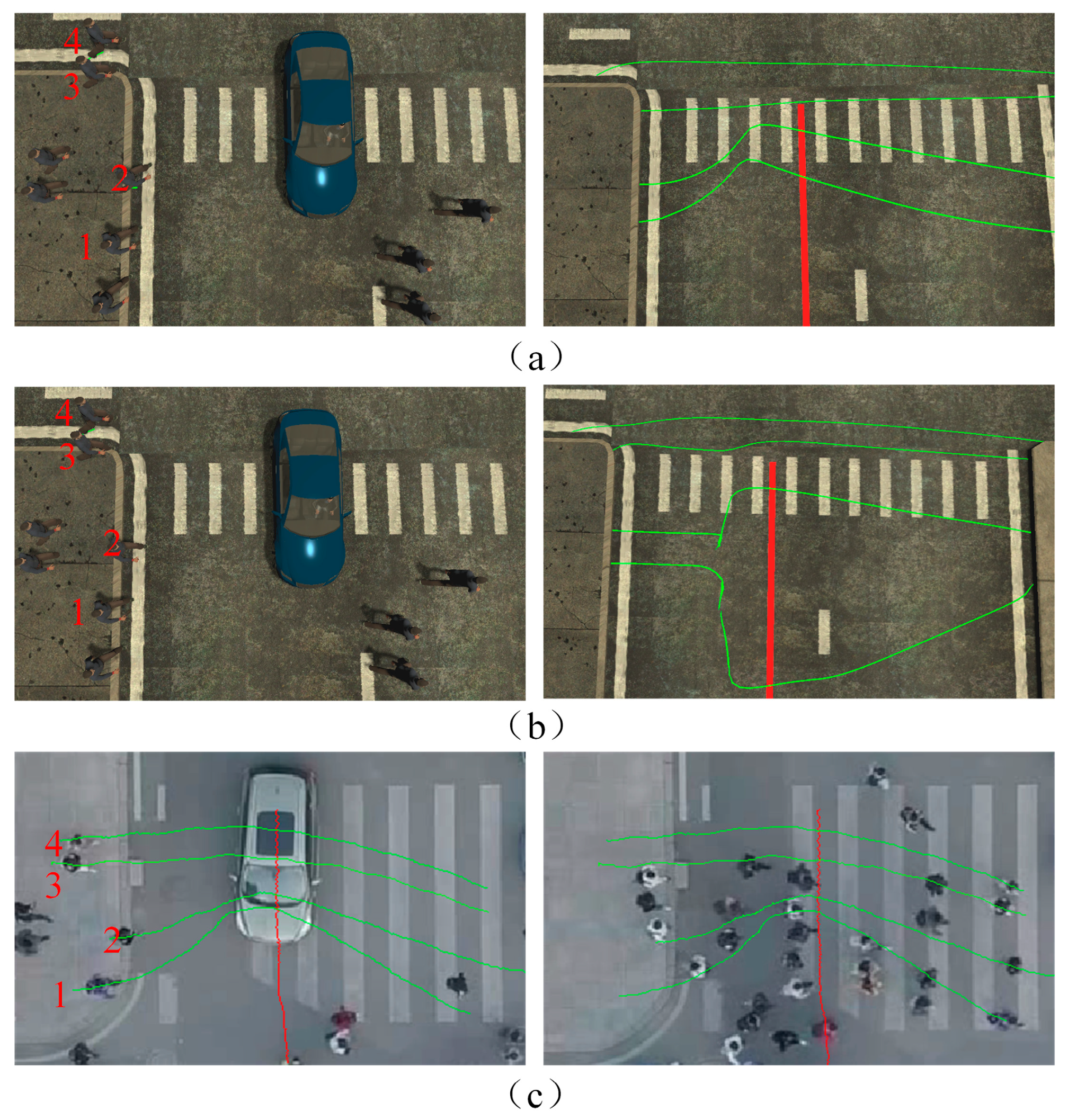
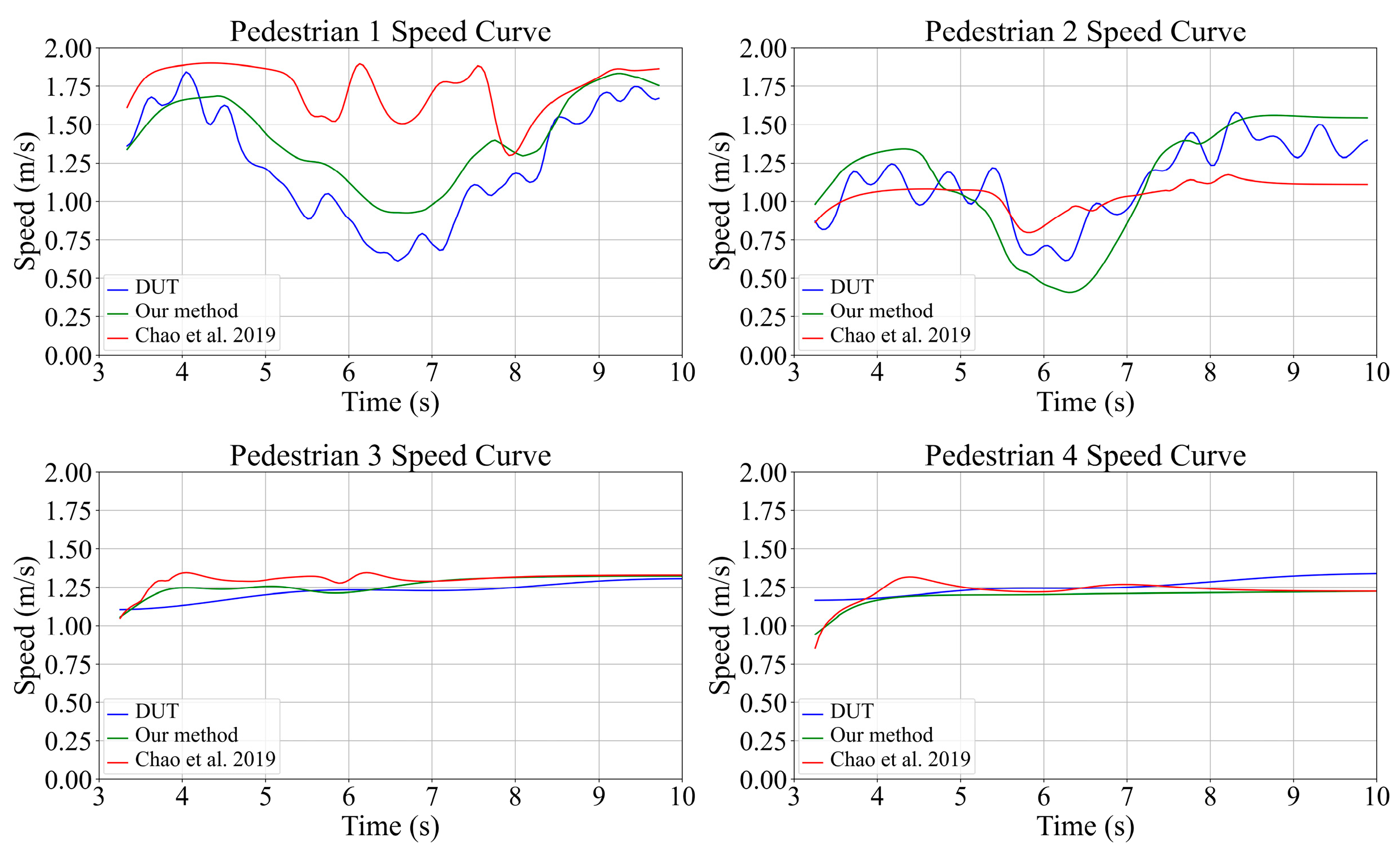
5.2. Pedestrian–Vehicle Interaction
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alver, Y.; Onelcin, P.; Cicekli, A.; Abdel-Aty, M. Evaluation of pedestrian critical gap and crossing speed at midblock crossing using image processing. Accid. Anal. Prev. 2021, 156, 106127. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Chen, F.; Wei, Y. Evaluation of pedestrian crossing behavior and safety at uncontrolled mid-block crosswalks with different numbers of lanes in China. Accid. Anal. Prev. 2019, 123, 263–273. [Google Scholar] [CrossRef] [PubMed]
- Nassereddine, H. Modeling vehicle-pedestrian interactions at unsignalized intersections. J. Transp. Saf. Secur. 2024, 1–19. [Google Scholar] [CrossRef]
- World Health Organization. Global Status Report on Road Safety 2018; World Health Organization: Geneva, Switzerland, 2018. [Google Scholar]
- Han, Y.; Chao, Q.; Jin, X. A simplified force model for mixed traffic simulation. Comput. Animat. Virtual Worlds 2021, 32, e1974. [Google Scholar] [CrossRef]
- Rinke, N.; Schiermeyer, C.; Pascucci, F.; Berkhahn, V.; Friedrich, B. A multi-layer social force approach to model interactions in shared spaces using collision prediction. Transp. Res. Procedia 2017, 25, 1249–1267. [Google Scholar] [CrossRef]
- Chao, Q.; Deng, Z.; Jin, X.J. Vehicle–pedestrian interaction for mixed traffic simulation. Virtual Worlds 2015, 26, 405–412. [Google Scholar] [CrossRef]
- Yang, D.; Li, L.; Redmill, K.; Özgüner, Ü. Top-view trajectories: A pedestrian dataset of vehicle-crowd interaction from controlled experiments and crowded campus. In Proceedings of the 2019 IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; IEEE: New York, NY, USA, 2019. [Google Scholar]
- Chao, Q.; Deng, Z.; Ren, J.; Ye, Q.; Jin, X. Realistic data-driven traffic flow animation using texture synthesis. IEEE Trans. Vis. Comput. Graph. 2017, 24, 1167–1178. [Google Scholar] [CrossRef]
- Ren, J.; Xiang, W.; Xiao, Y.; Yang, R.; Manocha, D.; Jin, X. Heter-sim: Heterogeneous multi-agent systems simulation by interactive data-driven optimization. IEEE Trans. Vis. Comput. Graph. 2019, 27, 1953–1966. [Google Scholar] [CrossRef]
- Alahi, A.; Goel, K.; Ramanathan, V.; Robicquet, A.; Fei-Fei, L.; Savarese, S. Social lstm: Human trajectory prediction in crowded spaces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Cheng, H.; Sester, M. Modeling mixed traffic in shared space using lstm with probability density mapping. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; IEEE: New York, NY, USA, 2018. [Google Scholar]
- Chao, Q.; Bi, H.; Li, W.; Mao, T.; Wang, Z.; Lin, M.C.; Deng, Z. A survey on visual traffic simulation: Models, evaluations, and applications in autonomous driving. Comput. Graph. Forum. 2020, 39, 287–308. [Google Scholar] [CrossRef]
- Peng, G.; Cai, X.; Liu, C.; Cao, B.; Tuo, M. Optimal velocity difference model for a car-following theory. Phys. Lett. A 2011, 375, 3973–3977. [Google Scholar] [CrossRef]
- Kesting, A.; Treiber, M.; Helbing, D. Enhanced intelligent driver model to access the impact of driving strategies on traffic capacity. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 368, 4585–4605. [Google Scholar] [CrossRef] [PubMed]
- Zhu, M.; Wang, X.; Tarko, A. Modeling car-following behavior on urban expressways in Shanghai: A naturalistic driving study. Transp. Res. Part C Emerg. Technol. 2018, 93, 425–445. [Google Scholar] [CrossRef]
- Crociani, L.; Vizzari, G. An integrated model for the simulation of pedestrian crossings. In Proceedings of the Cellular Automata: 11th International Conference on Cellular Automata for Research and Industry, ACRI 2014, Krakow, Poland, 22–25 September 2014; Springer: Berlin/Heidelberg, Germany, 2014. Proceedings 11. [Google Scholar]
- Chen, P.; Wu, C.; Zhu, S. Interaction between vehicles and pedestrians at uncontrolled mid-block crosswalks. Saf. Sci. 2016, 82, 68–76. [Google Scholar] [CrossRef]
- Wu, W.; Chen, R.; Jia, H.; Li, Y.; Liang, Z. Game theory modeling for vehicle–pedestrian interactions and simulation based on cellular automata. Int. J. Mod. Phys. C 2019, 30, 1950025. [Google Scholar] [CrossRef]
- Helbing, D.; Molnar, P. Social force model for pedestrian dynamics. Phys. Rev. E 1995, 51, 4282. [Google Scholar] [CrossRef]
- Anvari, B.; Bell, M.G.; Sivakumar, A.; Ochieng, W.Y. Modelling shared space users via rule-based social force model. Transp. Res. Part C Emerg. Technol. 2015, 51, 83–103. [Google Scholar] [CrossRef]
- Chao, Q.; Jin, X.; Huang, H.-W.; Foong, S.; Yu, L.-F.; Yeung, S.-K. Force-based heterogeneous traffic simulation for autonomous vehicle testing. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; IEEE: New York, NY, USA, 2019. [Google Scholar]
- Xu, M.; Wang, H.; Chu, S.; Gan, Y.; Jiang, X.; Li, Y.; Zhou, B. Traffic simulation and visual verification in smog. ACM Trans. Intell. Syst. Technol. TIST 2018, 10, 1–17. [Google Scholar] [CrossRef]
- Zeng, W.; Chen, P.; Yu, G.; Wang, Y. Specification and calibration of a microscopic model for pedestrian dynamic simulation at signalized intersections: A hybrid approach. Transp. Res. Part C Emerg. Technol. 2017, 80, 37–70. [Google Scholar] [CrossRef]
- Yang, D.; Özgüner, Ü.; Redmill, K. A social force based pedestrian motion model considering multi-pedestrian interaction with a vehicle. ACM Trans. Spat. Algorithms Syst. TSAS 2020, 6, 1–27. [Google Scholar] [CrossRef]
- Zhao, J.; Malenje, J.O.; Wu, J.; Ma, R. Modeling the interaction between vehicle yielding and pedestrian crossing behavior at unsignalized midblock crosswalks. Transp. Res. Part F Traffic Psychol. Behav. 2020, 73, 222–235. [Google Scholar] [CrossRef]
- Schönauer, R.; Stubenschrott, M.; Huang, W.; Rudloff, C.; Fellendorf, M. Modeling concepts for mixed traffic: Steps toward a microscopic simulation tool for shared space zones. Transp. Res. Rec. 2012, 2316, 114–121. [Google Scholar] [CrossRef]
- Tian, K.; Markkula, G.; Wei, C.; Lee, Y.M.; Madigan, R.; Merat, N.; Romano, R. Explaining unsafe pedestrian road crossing behaviours using a psychophysics-based gap acceptance model. Saf. Sci. 2022, 154, 105837. [Google Scholar] [CrossRef]
- Helbing, D.; Farkas, I.; Vicsek, T. Simulating dynamical features of escape panic. Nature 2000, 407, 487–490. [Google Scholar] [CrossRef] [PubMed]







| Parameters | Value | Unit | Description |
|---|---|---|---|
| {200, 500, 15,000} | scale factor of force | ||
| {5, 2.5} | sensitivity to distance | ||
| 7 | minimum conflict distance | ||
| 1.5 | scale factor of | ||
| 0.1 | minimum lateral distance | ||
| [0.7, 1.0] | pedestrian reaction time | ||
| [7, 12] | desired speed of the vehicle | ||
| [2, 3] | maximum acceleration of the vehicle | ||
| [3, 4] | comfortable deceleration of the vehicle | ||
| [1, 2] | jam space headway | ||
| [1, 2] | desired safety time headway |
| Pedestrian 1 | Pedestrian 2 | Pedestrian 3 | Pedestrian 4 | |
|---|---|---|---|---|
| Our method | 0.215/13.39% | 0.195/1.01% | 0.057/3.59% | 0.075/5.00% |
| Chao et al.’s method [22] | 0.591/39.87% | 0.233/7.59% | 0.093/6.45% | 0.076/2.36% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Liu, T.; Liu, Z. Study on Collision Avoidance Behavior in the Social Force-Based Pedestrian–Vehicle Interaction Simulation Model at Unsignalized Intersections. Appl. Sci. 2025, 15, 4885. https://doi.org/10.3390/app15094885
Wang X, Liu T, Liu Z. Study on Collision Avoidance Behavior in the Social Force-Based Pedestrian–Vehicle Interaction Simulation Model at Unsignalized Intersections. Applied Sciences. 2025; 15(9):4885. https://doi.org/10.3390/app15094885
Chicago/Turabian StyleWang, Xuwei, Tingting Liu, and Zhen Liu. 2025. "Study on Collision Avoidance Behavior in the Social Force-Based Pedestrian–Vehicle Interaction Simulation Model at Unsignalized Intersections" Applied Sciences 15, no. 9: 4885. https://doi.org/10.3390/app15094885
APA StyleWang, X., Liu, T., & Liu, Z. (2025). Study on Collision Avoidance Behavior in the Social Force-Based Pedestrian–Vehicle Interaction Simulation Model at Unsignalized Intersections. Applied Sciences, 15(9), 4885. https://doi.org/10.3390/app15094885






