Abstract
The high-filling engineering of airports is common in mountainous cities, and as critical infrastructure for urban development, airports are prone to slope instability under extreme climate and mechanical coupling effects. Therefore, it is essential to investigate the geometric form of failure surfaces under limit stability conditions for airport slopes. The rational determination of the form of the rupture surface of a soil nailing support structure is a key factor in the structural safety of a project. In this study, we analyzed the rupture surface form and reinforcement mechanism of four common soil nailing support structures in engineering. First, we established theoretical model I and verified the consistency of the upper-limit theorem of plastic mechanics and energy conservation in this model. Next, a theoretical analytical model of the rupture surface form was established taking into consideration the existence of tension depth in a certain depth range at the top. The mathematical expressions of the rupture surface form with respect to h/H and L/H were derived by combining plasticity mechanics and energy conservation. Finally, the rupture surface forms of the structure were analyzed for different slope angles of soil nail-supported structures and different friction angles within the soil. The findings were compared with the rupture surface forms in the existing codes and literature. The results showed that L/H decreased continuously with the slope angle of the soil nailing support structure and decreased gradually with an increasing friction angle within the soil. Furthermore, h/H decreased with the slope angle of the soil nailing support structure, but it showed a trend with the increase in soil internal friction angle and the slope angle of the soil nailing support structure. The analysis revealed that only in some specific cases were and closely aligned with the values acquired using standard methods in specifications and the literature. The theoretical analysis provided important reference values for the design and improvement of soil nailing length in soil nailing support structures under certain conditions, thereby ensuring their enhanced stability and strength.
1. Introduction
With the rapid advancement of civil aviation airport construction in China, the number of high-slope projects in mountainous areas has significantly increased. Simultaneously, the frequent occurrence of global extreme weather events [1], such as typhoons, tornadoes, and heavy rainfall, has posed severe challenges to urban infrastructure and transportation systems [2,3]. Figure 1 shows the No. 12 landslide at Panzhihua Airport, which was located in the upper part of a wide and gentle valley area on the east side of the northern section of the airport. It was caused by the instability of the filled body and the reactivation of the old Yujiaoping landslide below. The maximum filling height of the filled body was approximately 128 m, and the maximum width was approximately 433 m (perpendicular to the airport runway direction). At 15:00 on 3 October 2009, the filled body slid, triggering the reactivation of the old landslide. The elevation of the landslide front was 1550 m, and the elevation of the rear edge was 1980 m (the elevation of the airport soil surface area). The height difference between the front and rear edges was approximately 430 m. The landslide was 1600 m long in the longitudinal direction, with a total volume of approximately 5.1 million m3. After the landslide occurred, a huge gap formed in the soil surface area. The horizontal distance from the landslide scarp to the centerline of the runway was only 75 m, and it continued to deform and collapse. Some residential houses and farmland water conservancy facilities below were damaged, and operations at Panzhihua Airport were suspended for a period [3]. Against this backdrop, stability management and disaster prevention in slope engineering have become critical issues for ensuring the safe operation of airports and the sustainable development of regions. Geotechnical reinforcement techniques are now widely used in geotechnical engineering, especially in foundation works. This technology can fully exploit geotechnical energy in order to improve the self-stabilizing ability and reduce the self-weight of a structure and preserve the material, which has significant economic and social benefits [4].
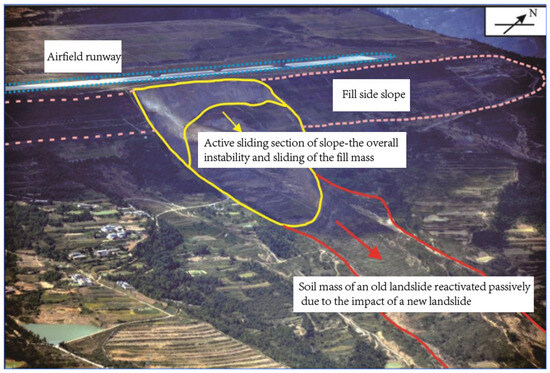
Figure 1.
A large-scale landslide that occurred on the slope of Panzhihua Airport [3].
Owing to the wide range of fields involved in geotechnical engineering, it is a highly comprehensive discipline. It includes geotechnical engineering investigation, soil mechanics, foundation and foundation engineering, the mechanics of materials, structural mechanics, and other multidisciplinary topics. The soil nailing support structure was developed in the 1970s, and its application has grown extensively over the years. However, the theory behind soil nail supports still lags far behind the engineering reality. Although our country has issued several design regulations and norms on soil nail supports [5,6,7], in general, soil nailing support design and calculation methods are not perfect, and many scholars have conducted research on this problem. Yuan [8] conducted theoretical analysis and suggested that after soil nails are installed in the soil, the stress state in the soil body will change and the direction of the principal stress will be deflected. The sliding crack surface of the soil will also change accordingly. Hui et al. [9] assumed that the sliding surface had a parabolic shape and established a search model for the most critical sliding surface using geometric relations and an integral method. Li et al. [10] proposed a new method to determine the potential fracture surface of soil nailing walls based on the relationship between the residual sliding force of soil at the potential fracture surface and the nailing force in the sliding zone. Zhao et al. [11], based on the cantilever beam model, compared the critical instability height of the rock layer with the height of the preset failure surface, dividing the rock layer on the failure surface into stable, active toppling, and passive toppling zones. They proposed a stability calculation method based on the limit equilibrium principle and preliminarily assessed the toppling risk of the slope using the geometric area of the S-zone. Li et al. [12] treated the failure surface of reinforced soil-retaining walls as composed of multiple line segments. Based on the mechanical equilibrium conditions of horizontal soil strips under seismic action, they derived a calculation formula for reinforcement tension related to failure surface parameters and determined the critical failure surface corresponding to the maximum tension value. Zhou et al. [13] conducted theoretical research on the stability of soil slopes by combining the variational method and the limit equilibrium method. They employed the shooting method for numerical solutions, obtaining precise results for the slip surface location, normal stress distribution, and stability coefficient. The effectiveness of the proposed method was validated through comparisons with the slice method and the finite element strength reduction method.
The potential fracture surface of a soil nailing wall can be determined by calculating the maximum axial force of layered soil nailing in the sliding zone. There have also been analyses derived from full-scale tests and model tests. For example, Wang et al. [14] analyzed the deformation of a soil nailing wall and the internal force characteristics of soil nailing through a full-scale test. Shan et al. [15] and Zhang [16] tested the horizontal displacement of the top of the soil nailing wall, the internal force of soil nailing, and the soil pressure during the whole test process through similar model tests. Numerical analysis has also been conducted. Luo et al. [17] used the finite element method to study the evolution of the failure surface and earth pressure distribution during the active limit state of backfill soil under the translation of counterweight-retaining walls. By comparisons with centrifuge tests, they proposed a modified earth pressure calculation model based on the shear state of the failure surface. Zhao et al. [18] applied strength reduction and limit equilibrium theories to analyze the failure mechanisms and stability of homogeneous soil slopes under different geometries using finite difference software. Wang Huanhuan and Guo Mingzhu [19] simulated the toppling failure of anti-dip layered rock slopes under seismic action, finding that increasing the internal friction angle reduces the time taken to reach a new equilibrium state and decreases the maximum horizontal displacement of sliding blocks. Bian et al. [20] and Guo et al. [21] investigated the seismic failure modes of rock slopes with intermittent bedding joints and the deformation mechanisms of fault-controlled creeping bedding landslides, respectively. They revealed the mechanism of soil nailing support. Studies integrating engineering practice have also been conducted. Zhou et al. [22] discussed and optimized the calculation formula of the overall stability safety factor of a soil nailing wall in the technical regulations for building foundation pit support according to different types of sliding surfaces of the soil nailing wall. Liao et al. [23] established the corresponding function of reliability analysis by studying the stability of a soil nailing wall against overall slip and overturning. The corresponding reliability index was calculated using the JC method combined with engineering examples. Lou and Pu [24] monitored the force of a soil nailing support structure in combination with a soft-rock high-slope project. It was found that the working principle of the unearthed nailing support was different from that of the anchor structure and soil nailing wall. Based on the change in soil nailing axial force, the failure mode of the soft-rock high slope was proposed.
Scholars from other countries have also conducted extensive research on this issue. Ahmed et al. [25] simplified the Janbu method to make it more suitable for calculating the safety factor of three-dimensional slopes. Park and Michalowski [26] established a three-dimensional limit equilibrium model based on the Hoek–Brown criterion to evaluate the stability of three-dimensional rock slopes, thus expanding the research field to rock slopes. Brideau et al. [27] systematically and comprehensively expounded and demonstrated the application of the three-dimensional limit equilibrium method in slope engineering through specific research cases. Giger and Krizek [28,29] were the first to analyze the stability of vertical angular notches subjected to local additional loads using the upper-bound method, but they did not deeply analyze the failure surface forms under different slope angles. Some scholars from other countries have also carried out analyses using the finite element method. For example, Tan and Sarma [30] used the finite element method to verify an improved limit equilibrium method incorporating stress acceptability criteria, making the simulation of the failure mechanism of the slip surface more accurate. Noroozi et al. [31] proposed the 3D Key-Group Method for three-dimensional slope stability analysis and established a rigid-body plastic limit equilibrium equation considering three-dimensional effects, but its adaptability to complex boundary conditions is limited.
Although many scholars have analyzed the mechanical characteristics and fracture modes of soil nailing walls and supports from different angles, the rationality and reliability of the existing fracture surface forms have rarely been studied from the perspectives of energy methods and plastic mechanics. These aspects have an important influence on the design length of soil nailing support structures with different slope angles and different soil internal friction angles.
In this study, first, a theoretical analysis model of an inclined plane is established based on the reinforcement mechanism of soil nailing support to verify the rationality of the conservation of energy. Second, a theoretical analysis model of the fracture surface form considering the tension depth at the top is established, and the mathematical expressions of the fracture surface form in terms of h/H and L/H are derived based on the plasticity theory. Finally, based on different slope foot and internal friction angles, the fracture surface forms are discussed. The results are compared with the methods available in the literature. The results provide important insights for understanding the mechanism and mechanical characteristics of soil nailing support at a deeper level and improving its design method. The results also provide significant guidance for the application of soil nailing supports in engineering practices.
2. Four Common Forms of Rupture Surfaces in Engineering
From the literature, it is known that rupture surface shapes can be a circular arc or hyperbolic, parabolic, logarithmic helix, bifurcated, and so on. When designing and making calculations for soil nail support in China, it is usually simplified to four rupture surface forms (shown in Figure 2). Considering Figure 2 as an example, for the same engineering problem, when four different assumed rupture surface forms are used for soil nail support design, the length of the soil nails will differ by several meters. So far, the form of the rupture surface of soil nail supports has remained a controversial issue.
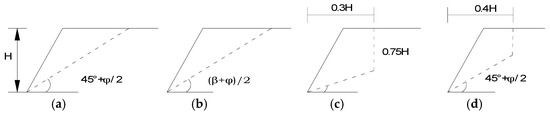
Figure 2.
Four forms of rupture surfaces assumed in engineering.
Figure 2a is from the mandatory standard “Technical Specification for Retaining and Protection of Building Foundation Excavations” (JGJ120-2012) [5] issued by the People’s Republic of China; Figure 2b is from the “Code for Technique of Building Foundation Pit Engineering” [6] edited by the General Institute of Architecture and Research of the Ministry of Metallurgy (YB9258-97); and Figure 2c,d are from the “Methodology of Cheng Liangkui” [32] and “Methodology of Beijing University of Technology” [33], respectively, where β is the slope angle of the soil body, is the friction angle within the soil body, and H is the height of the slope or pit.
3. Reinforcement Mechanism of Soil Nail Support
The soil nail support mechanism is dependent on soil nail inclination, stiffness, soil nail length, spacing, nail–soil interface interaction, soil parameters, and other factors. Accordingly, the aim of this research is to study their roles in said mechanism. Therefore, this study focuses on analyzing the reinforcement mechanism of soil nail support.
The shear strength of a soil body is low, and its tensile strength is almost negligible. In order to provide the soil with a certain tensile capacity, a specific number and density of reinforcing elements must be placed within the soil. The synergistic effect between the soil and reinforced body not only accounts for the soil body’s tensile and shear strength to improve the overall stiffness of the soil body, but also allows the soil to utilize its structural strength potential to the maximum, altering the deformation and failure characteristics of slopes.
The reinforcement theory of soil nail support is based on the interaction at the nail–soil interface, where the tensile capacity of the soil nail is transferred to the soil body, so that the soil body’s strength is reinforced.
Engineering practices and research show that soil nail support can significantly improve the strength and stability of a soil body. In Figure 3 (Zhang et al. [34]), it is evident that the damage strength of the soil nail support is significantly improved, with the two lines being essentially parallel. This indicates that the soil nail support does not significantly change the angle of internal friction. However, the damage envelope of the soil body does not pass through the origin, indicating quasi-viscous cohesion. It can be seen that the lateral deformation of the soil body is restrained owing to the tensile bonding between the nail and soil, thus improving the strength and stability of the soil body.
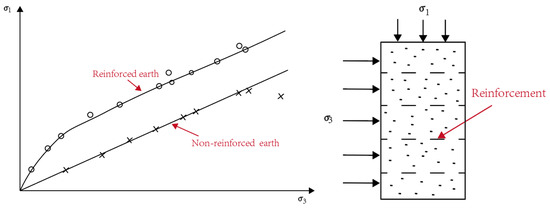
Figure 3.
Experimental effect of soil reinforcement.
Combined with Figure 3, it follows from the M-C theory that for unreinforced soil,
and for reinforced soil,
where and are the maximum and minimum principal stresses, respectively, is the cohesive force, and is the angle of internal friction.
When Equation (2) is deformed, we obtain
such that .
Accordingly, ; c = 0 in the unreinforced soil itself.
Using = 0 in Equation (3), can be considered . At this point, can be transformed into
Equations (2)–(4) indicate that the strength of the soil body increases significantly when the reinforced material is added to the soil body. The increment is shared by or , as shown in the reinforced soil unit in Figure 4, where is the rupture strength of the reinforced soil, is the vertical spacing of the reinforced soil, is the friction angle within the soil, and L is the width of the wedge.
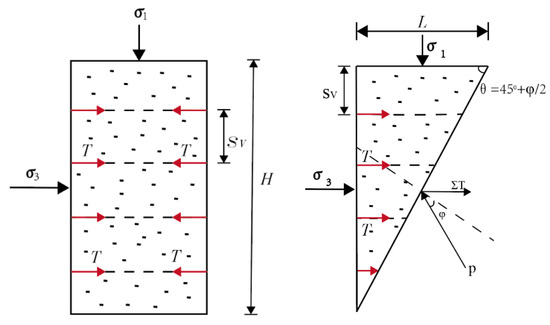
Figure 4.
Soil reinforcement unit.
This is known from the triangular equilibrium condition for forces:
When Equation (2) is substituted into Equation (5) we obtain
At this point, the portion of the cohesion that increases the strength of the soil owing to its reinforcement is
Here, and are the increase in the cohesion and minimum principal stress of the soil after reinforcement, respectively, and is the passive earth pressure coefficient.
Figure 5a [35] shows the stress–strain curves of reinforced soil with the same reinforcement strength but different reinforcement spacings, indicating that the soil strength gradually increases as the number of reinforcement layers increases and the spacing decreases. Figure 5b presents the test results for reinforced soil with the same spacing but different reinforcement strengths. Figure 6 displays the test results for unreinforced soil under different confining pressures. Through a comparison of Figure 5 and Figure 6 [36], it can be concluded that is reasonable and shows excellent agreement with the experimental results.
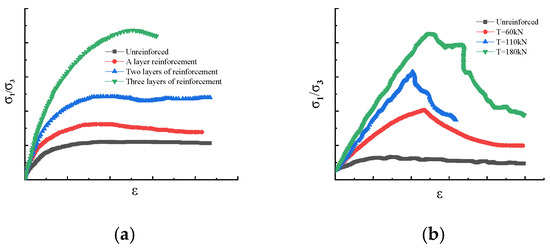
Figure 5.
Effect of reinforcement on strength. (a) Effect of reinforcement spacing. (b) Effect of reinforcement strength.
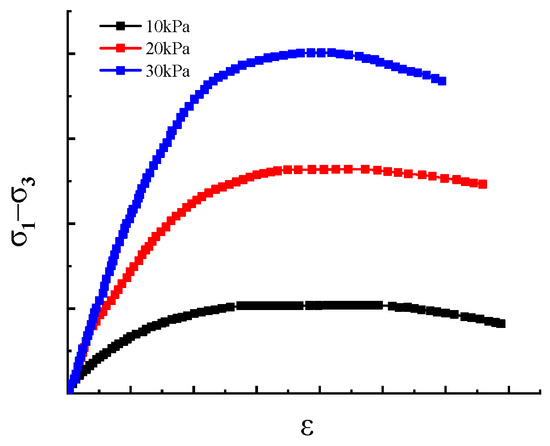
Figure 6.
Effect of confining pressure on strength.
4. Modeling Assumptions and Analysis of Soil Nail Support Reinforcement Theory
4.1. Establishment of Theoretical Model I and Method Verification
In soil mechanics and geotechnical foundations, plasticity theory has always played an important role. Prime examples include the ultimate bearing capacity of foundations, soil slope stability, and soil pressure theories that are established based on the limit analysis method of plasticity theory.
First, five assumptions are made about theoretical model I: (1) the slope of the soil nailing support structure represents a plane strain problem; (2) the slope is assumed to be that of homogeneous cohesive soil, and the soil beneath the slope base is stable; (3) the potential slip plane is an inclined plane (Figure 2a,b), (4) the groundwater level is below the bottom of the slope or there is no groundwater; and (5) there is no overloading on the ground. Based on these assumptions, the soil body under the action of self-weight is divided into two zones—the damage zone and the stress zone—as shown in Figure 7. The stress zone is like a rigid body sliding along the rupture surface with a certain velocity . At this point, both the direction of the sliding speed and the angle of the rupture surface remain constant (φ).
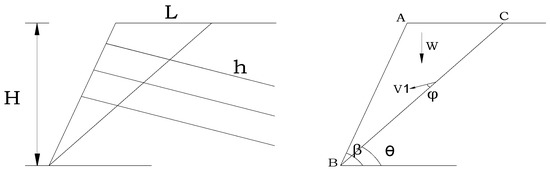
Figure 7.
The rupture surface of the soil nailing support structure is assumed to be an inclined plane.
It should be noted that the following theoretical analysis is derived using continuum mechanics equations (including equilibrium equations, constitutive equations, and kinematic equations). Among them, the equilibrium equations are applicable to static or quasi-static problems. In the kinematic equations, the deformation is assumed to be continuous and small, and the constitutive relationship of the material is assumed to be elastoplastic.
According to the upper-limit theorem of plasticity and the conservation of energy, the power of the work done by the soil under its own weight is equal to the power consumed on the slip surface owing to the action of the cohesive force (including the increase after the reinforcement).
When , we obtain
To reach its full potential and to reach the limit state, the critical height of the soil nailing support structure H is considered a function of the inclination angle () of the slip-cracking surface, in order to determine the extreme value of H when :
From Equation (10), , and the inclination of its slip fracture surface is .
When the slip fracture surface form is assumed to be an inclined plane, it is not only consistent with the slip fracture surface angle (as shown in Figure 2b, when ), but also consistent with the slip fracture surface angle (as shown in Figure 2a). Furthermore, it is consistent with the rupture surface form deduced from Kalman’s formula (Jiang [37]; Casin and Kirkby [38]; Ma et al. [39]; Jiang [40]). This shows that the calculation of the plane fracture surface by this method is fairly reasonable.
4.2. Establishment of Theoretical Model II and Deduction of Simplified Formula
Based on the validation of the rationality of the theoretical method and Zhang Weimin’s research on the limit analysis of a reinforced soil-retaining wall (Li [41]), five assumptions are made: (1) the slope of the soil nailing support structure represents a plane strain problem; (2) the slope is assumed to be that of homogeneous cohesive soil, and the soil beneath the slope base is stable; (3) the potential slip surface is the folded line plane; (4) the groundwater level is below the bottom of the slope or there is no groundwater; and (5) there is no overloading on the ground. It should be noted that except for the fourth point, the rest of the points are described in the same manner as in the previous assumptions.
It should be noted that the following theoretical analysis is still carried out using the equations of continuum mechanics (including equilibrium equations, constitutive equations, and geometric equations). Among them, the equilibrium equations are applicable to static or quasi-static problems. In the geometric equations, it is assumed that the deformation is continuous and small, and the material’s constitutive relationship is assumed to be that of an elastoplastic material.
On the basis of the above assumptions, the soil body under the action of self-weight is divided into a range of damage zones and different stress zones as shown in Figure 8. Where in Figure 8, was the toe of the slope, L was the horizontal length of the failure surface at the slope crest, and H was the depth of the vertical failure surface (Figure 8a). Each stress zone slides along the respective rupture surfaces with different velocities like a rigid body, and the direction of the sliding velocity is at an angle φ to the rupture surface (φ is the angle of internal friction). At the same time, each velocity component consists of a closed vector triangle. According to the related literature (Liang and Sun [42]; Gong [43]), owing to the existence of cohesion (c), the cohesive soil body in the active limit state exhibits tension cracks in a certain depth range at its top and at the depth of the cracks, as indicated by Equation (5).
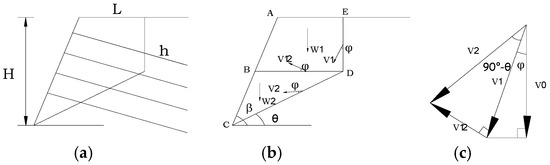
Figure 8.
Assumed rupture surface form for soil nail support.
According to the plastic limit theory mentioned by Gong Xiaonan (Gong [43]), the ultimate load is the smallest among all the loads corresponding to the allowable plastic deformation displacement rate field (Figure 8b). At this point, the soil nailing support structure will break down, and the work done by the soil’s self-weight will be theoretically equal to the total energy expended in plastic deformation.
Here, , and are the rates of plastic deformation displacement in the vector triangle, and , and are the soil slope angle, internal friction angle, and rupture angle, respectively.
According to “Elasticity and Plasticity” by Chen Huifa (Chen et al. [44]), the M-C criterion is used as the yield condition in general geotechnical engineering. At this point, the yield surface equation is given as . According to the classical flow law of plastic mechanics, it is known that when the plastic potential energy surface has the same shape as the yield surface, i.e., if , the flow law is associated with the yield condition using the following equation:
Based on the yield surface equation, which can be solved by combining it with Equation (15) above, we obtain
At this point, it follows that . The energy consumption rate per unit volume on the rupture surface of a soil nail-supported structure is given by . Substituting Equation (16) and the relation into the equation , we obtain
From the above calculations, it is clear that the relationship between the energy dissipation rate and frictional consumption of the soil is not reflected when both positive and shear stresses are present at the rupture surface of the soil nail-supported structure. The primary reason for this is that the frictional depletion between the soils counteracts the shear dilatation depletion that exists between and within the soils.
- (1)
- Power Wi, consumed by the internal forces along the rupture surface in a soil nailing support structure, while taking into account the additional cohesive forces due to the action of soil nails, is given byAt this point,
- (2)
- When work is done by the soil under self-weight at an assumed velocity field rate, power We is given as
Through assuming and combining the above with , according to plasticity theory, the following can be derived when :
From Equation (21), the critical height of the soil nailing support structure when damage occurs can be given by Equation (22):
It can be derived from Equation (22) that the critical height H at which damage occurs to the soil nailing support structure is a function of the angle of slope β and the angle of internal friction φ.
Therefore, we have the following:
;
;
;
;
;
.
Thus, the critical height H, i.e., Equation (22), at which damage occurs in soil nailing support structures, can be converted to
Through combining and , the following equations are obtained:
It should be emphasized here that the study carried out above is based on the analysis of the theoretical model established in Figure 2c,d, which assumes that the rupture surface is the folded line plane.
5. Exploring the Rupture Surface Forms of Soil Nail-Supported Structures
The calculations in the previous subsection resulted in two more succinct scaling relationships, which are detailed in Equation (24), so that the form of the rupture surface when damage occurs to the soil nailing support structure at different slope angles can be analyzed.
- (1)
- Through substituting into Equation (22), the critical height at which damage to the soil nailing support structure occurs can be obtained as
From Equation (26), it can be seen that the rupture surface form of the slope is a function of the angle of internal friction () when has a constant value. Four different internal friction angles (10°, 20°, 30°, and 40°) were used to analyze the rupture surface form of the soil nail-supported structure, as detailed in Table 1 and Figure 9.

Table 1.
Forms of rupture surfaces corresponding to different internal friction angles c (β = 90°).
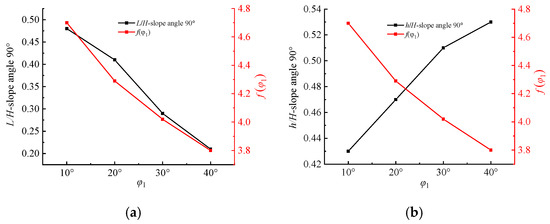
Figure 9.
Geometric dimensions of failure surfaces corresponding to different internal friction angles . (a) Graph of and versus ; (b) graph of and versus .
- (1)
- As the angle of internal friction continues to increase, the rupture surface extends to the top of the pit or slope, thereby reducing the horizontal distance from the edge of the soil nailing support structure. Moreover, the tension cracks in the upper part of the soil nailing support structure gradually increase.
- (2)
- When = 30°, L/H = 0.29 and h/H = 0.51. Under these conditions, the value of L is very close to that of L in the rupture surface form of the “Methodology of Cheng Liangkui” (mentioned in Figure 2c). However, h/H = 0.75 (given in Figure 2c), which is much different from that calculated using the method of the present work.
- (3)
- When = 20°, Table 1 shows that L/H = 0.41. Under these conditions, the value of L is very close to the value of L in the form of rupture surface of the “Methodology of Beijing University of Technology” (mentioned in Figure 2d). This indicates that with the present method, when , the distance from the top edge of the pit or slope to the rupture surface extending to the horizontal ground is close to 0.4H, and regardless of the internal friction angle, the value of L is 0.4H.
- (2)
- Through substituting into Equation (22), the critical height at which damage to the soil nailing support structure occurs can be obtained as
In combining this with the previously derived Equation (24), the values of h/H and L/H in this case can be obtained:
From Equation (28), it can be seen that the rupture surface form of the slope is a function of the angle of internal friction when is a constant value. Four different internal friction angles (10°, 20°, 30°, and 40°) are analyzed for the rupture surface form of the soil nail-supported structure, as detailed in Table 2 and Figure 10.

Table 2.
Forms of rupture surfaces corresponding to different internal friction angles c (β = 80°).
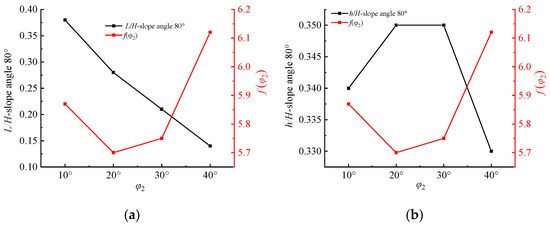
Figure 10.
Geometric dimensions of failure surfaces corresponding to different internal friction angles . (a) Graph of and versus ; (b) graph of and versus .
- (1)
- When = 80°, as the angle of internal friction () continues to increase, the ratio of L/H gradually reduces, and the decrease is greater. The changes in the h/H ratio are reduced compared to in the previous case.
- (2)
- According to Table 2, under the premise of a certain slope angle of the pit or slope, different internal friction angles correspond to different rupture surface forms. In comparing Figure 2c,d, it can be seen that the form of slip fracture damage obtained through engineering experience is only the general shape of the rupture surface rather than all the forms of the slip fracture surface when L/H = 0.3 or 0.4.
Therefore, when the soil nailing support structure is designed according to engineering experience, the length of soil nails may not meet the requirements [45]. This will lead to a significant reduction in the strength and safety of the soil nailing support structure, which can easily lead to engineering accidents. Therefore, in an actual project, when the slope angle has a certain value, it should be designed according to the corresponding rupture surface form of the internal friction angle of different soils, so as to ensure the safety and durability of the soil nailing support structure.
- (3)
- Through substituting into Equation (22), the critical height at which damage to the soil nailing support structure occurs can be obtained as
In combining this with the previously derived Equation (24), the values of h/H and L/H in this case can be obtained:
From Equation (30), it can be seen that the rupture surface form of the slope is a function of the angle of internal friction when is a constant. Four different internal friction angles (10°, 20°, 30°, and 40°) are analyzed for the rupture surface form of the soil nail-supported structure, as detailed in Table 3 and Figure 11.

Table 3.
Forms of rupture surfaces corresponding to different internal friction angles c (β = 70°).
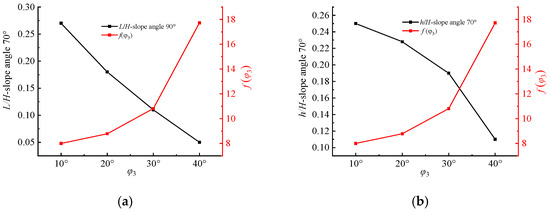
Figure 11.
Geometric dimensions of failure surfaces corresponding to different internal friction angles . (a) Graph of and versus ; (b) graph of and versus .
- (1)
- When the slope angle = 70°, both L/H and h/H start to decrease, while the angle of internal friction continues to increase;
- (2)
To better compare and analyze the variation rules of L/H and h/H in fracture surface forms under slope angles of different soil nailing structures and internal friction angles of different soils, the data in Table 1, Table 2 and Table 3 are sorted, and Figure 12 is obtained. Figure 12 shows the L/H and h/H curves of fracture surface forms under different working conditions. As can be seen from Figure 12, L/H and h/H show different trends: L/H decreases with the slope angle of the soil nailing support structure and gradually decreases with the increase in soil internal friction angle. h/H also decreases with the slope angle of the soil nailing support structure, but h/H shows different trends with an increasing soil internal friction angle. When = 90°, the greater the value, the greater the h/H value. When = 80°, h/H increases first and then decreases with increasing . When =70°, the larger the value, the smaller the h/H value.
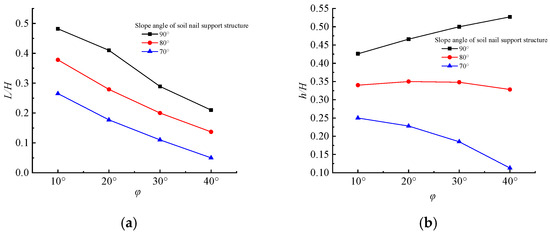
Figure 12.
L/H and h/H curves in the form of the rupture surface under different working conditions: (a) curves of L/H for varying internal friction angles and slope angles and (b) curves of h/H for varying internal friction angles and slope angles.
6. Example Verification
To validate the rationality of the theoretical formulas derived in this study, the soil was assumed to be a homogeneous clay layer, modeled using the Mohr–Coulomb elastoplastic constitutive model. Soil nails were simulated as steel bars with a diameter of 25 mm, represented by solid elements. The soil nails were arranged in a plum blossom pattern with a spacing of 2 m × 2 m, and a total of four layers of soil nails were arranged. Surface-to-surface contact was adopted between the soil nails and the soil; among them, hard contact was used for the normal direction, and Mohr–Coulomb friction contact was used for the tangential direction, with a friction coefficient of 0.4. The numerical model had dimensions of 80 m (length) × 4 m (width) × 12 m (height). Figure 13 and Figure 14 show the geometric model and the mesh model of the numerical computation, respectively. For different working conditions, the slope angles and internal friction angles were set to 70°, 80°, and 90° and 10°, 20°, 30°, and 40°, respectively. Other model parameters are detailed in Table 4. The model boundaries were defined as follows: the bottom was fully fixed, the top surface was a free boundary, and the displacement boundary on one side in the z-direction was set to zero.
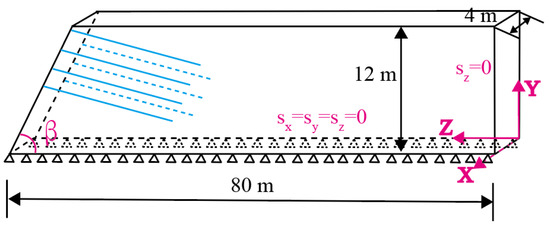
Figure 13.
Numerical geometric model.

Figure 14.
Numerical computation grid.

Table 4.
Numerical calculation of parameters in the model.
Through the use of ABAQUS (version 2020) finite element software, a comparison between numerical calculations and theoretical analysis was made, as shown in Figure 15. In Figure 15, it can be observed that the results from both methods are largely consistent, indicating that the failure surface calculation formula derived from the soil nail reinforcement theory is reliable and reasonable.
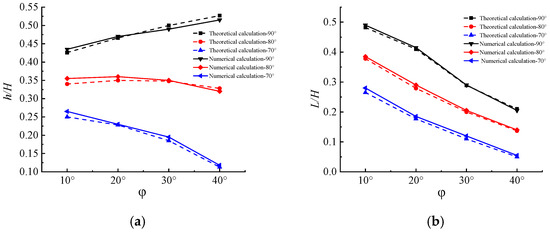
Figure 15.
Curve comparison between theoretical calculation and numerical calculation: (a) curves of L/H for varying internal friction angles and slope angles and (b) curves of h/H for varying internal friction angles and slope angles.
7. Conclusions
Based on the four common forms of fracture surfaces in engineering and the reinforcing mechanism of soil nailing support structures, a theoretical analysis model was established in this paper. Based on the upper-limit theorem of plastic mechanics and the conservation of energy, the mathematical expressions of h/H and L/H in the form of the folded line plane and the angle of failure of the inclined plane were derived. A comparative analysis was made between existing methods in the literature and the proposed methods. The conclusions are presented below.
- (1)
- Four common fracture surface forms in engineering are described, and the strengthening mechanism of internal friction angle and cohesion force after soil nail reinforcement is analyzed. Furthermore, the corresponding mathematical expressions are given.
- (2)
- Through the established theoretical model I and by combining the upper-limit theorem of plastic mechanics and the conservation of energy, the rationality of the assumed model and the used method is verified.
- (3)
- A theoretical analysis model is established considering the fracture surface form with deep drawing in a certain depth range at the top. The mathematical expressions of the fracture surface form in terms of h/H and L/H are derived based on plastic mechanics and energy conservation.
- (4)
- Based on the reinforcement theory of soil nailing support structure, the fracture surface forms of the structure under different slope angles and different soil internal friction angles are analyzed. The fracture surface forms are compared with those in the literature. The results show the following:
- (a)
- L/H gradually decreases with the slope angle of the soil nailing support structure and with an increasing soil internal friction angle . This shows that the horizontal distance between the L value when the fracture surface extends to the top of the slope and the edge of the surface of the soil nailing structure is smaller under this condition.
- (b)
- h/H also decreases with the slope angle of soil nailing support structures, but h/H shows different patterns with an increasing soil internal friction angle. For = 90°, the greater the value, the greater the h/H value. When = 80°, h/H increases first and then decreases with increasing . When = 70°, the larger the value, the smaller the h/H value.
- (c)
- (d)
- When = 90° and = 20°, the value of L/H is close to the value of L/H in the form of the fracture plane in Figure 2d, indicating that when = 90° and , the horizontal distance of the fracture plane extending to the ground is close to 0.4H. Regardless of the angle of internal friction, L is always equal to 0.4H.
By comparing Figure 6 with Figure 2c,d, we can see that the form of rupture surface obtained from engineering experience is remarkably different from that calculated in this study. Numerical analysis has demonstrated the rationality of the theoretical derivation of the failure surface form. The form of slippery cracked surface damage given by engineering experience is only the approximate shape of the rupture surface. If the design of the soil nailing support structure is based on engineering experience, the length of soil nails may not reach the required length of the soil itself, thus decreasing the strength and safety of the soil nailing support structure significantly and causing engineering accidents. Therefore, in an actual project, when the slope angle is fixed, the rupture surface form of the soil nailing support structure should be determined according to the soil parameters in case of any failure. This approach will lead to a more reasonable soil nail length, which would be conducive to reducing the occurrence of engineering accidents.
Author Contributions
Conceptualization, methodology, investigation, model building, F.L. and Z.H.; Data analysis, writing, validation, F.L. and C.J.; verification, visualization, data management, J.H.; writing—review and editing, supervision, Z.H.; writing—commenting and editing, X.M.; verification, review and editing, M.Y. All authors have read and agreed to the published version of the manuscript.
Funding
The work described in this paper was supported by Major Science and Technology Projects in Yunnan Province (CN) (Approval No. 202303AA080011) and Beijing Postdoctoral Science Foundation (zz2024-136). The authors are grateful to all the study participants.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors thank the Science and Technology Department of Yunnan Province and the Beijing Municipal Human Resources and Social Security Bureau for their funding support. The funders had no role in the experimental design, model establishment, data analysis, manuscript writing, or decision to submit this article for publication. The authors thank the anonymous reviewers who provided valuable suggestions that improved the manuscript.
Conflicts of Interest
Authors Feilong Li, Changshan Jiang, Jinbao Han, Xianfeng Meng, and Miaoxian Yao were employed by China Airport Planning and Design Institute Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as potential conflicts of interest.
References
- Deng, E.; Xiang, Q.; Chan, J.C.L.; Dong, Y.; Tu, S.F.; Chan, P.W.; Ni, Y.Q. Increasing temporal stability of global tropical cyclone precipitation. npj Clim. Atmos. Sci. 2025, 8, 11. [Google Scholar] [CrossRef]
- Li, Y.R.; Wu, H.G.; Feng, J.; Lai, T.W. Numerical simulation analysis on the dynamic response of 12# landslide at the Panzhihua Airport of Sichuan Province. Chin. J. Geol. Hazard. Control 2018, 29, 26–31. [Google Scholar]
- Li, D.Y. Numerical Simulation Study on the Movement Process and Mechanism of Landslide No. 12 at Panzhihua Airport. Master’s Thesis, Chengdu University of Technology, Chengdu, China, 2017. [Google Scholar]
- Cheng, L.K.; Zhang, Z.M.; Yang, Z.Y. Practical Technology of Rock and Soil Reinforcement; Seismological Press: Beijing, China, 1994. [Google Scholar]
- JGJ 120-2012; China Academy of Building Research. Technical Specification for Retaining and Protection of Building Foundation Excavations. China Architecture & Building Press: Beijing, China, 2024.
- YB 9258-97; Central Research Institute of Building and Construction Co., Ltd.; MCC Group. Code for Technique of Building Foundation Pit Engineering. Metallurgical Industry Press: Beijing, China, 1997.
- Department of Civil Engineering, Tsinghua University. Specification for Soil Nailing in Foundation Excavations; Standards Press of China: Beijing, China, 1997. [Google Scholar]
- Yuan, H.S. Research on Rupture Angle of Soil-nailing Wall Structure. Constr. Technol. 2011, 40, 41–43. [Google Scholar]
- Hui, C.Y.; Zhu, Y.P.; Ye, S.H. Stability analysis of composite soil-nailing wall with prestressed anchors. Chin. J. Geotech. Eng. 2013, 35, 325–329. [Google Scholar]
- Li, J.J.; Feng, Z.Q.; Dong, J.; Guo, Y.T.; Li, X.B. Determination Method of Soil Nailing Wall’s Potential Slipping Surface. J. North Univ. China (Nat. Sci. Ed.) 2017, 38, 133–139. [Google Scholar]
- Zhao, W.; Wang, R.Q.; Nian, T.K. Analytical method for stability of anti dip rock slope based on flexural toppling failure mode. Chin. J. Rock. Mech. Eng. 2019, 38, 3287–3295. [Google Scholar]
- Li, Q.; Ling, T.Q.; Han, L.F.; Zhang, R.G. Random Search Method of Fracture Surface for Seismic Stability of Reinforced Retaining Wall. J. Southwest Jiaotong Univ. 2021, 56, 801–808. [Google Scholar]
- Zhou, F.X.; Zhu, S.W.; Liang, Y.W.; Zhao, W.C. Exact analysis of soil slope stability by using variational limit equilibrium method. Chin. J. Geotech. Eng. 2023, 45, 1341–1346. [Google Scholar]
- Wang, S.G.; Teng, Y.J.; Duan, Q.W.; Li, Q.R.; Zhang, X.C. Deformation of soil nailing wall and inner forces of soil nails. China Civ. Eng. J. 2015, 50, 97–109. [Google Scholar]
- Shan, R.L.; Zheng, Y.; Wei, L.F. Model tests on supporting mechanism of soil nailing wall in silty clay deep foundation. Chin. J. Geotech. Eng. 2016, 38, 1175–1180. [Google Scholar]
- Zhang, F.L. Model Test Study on Soil Nailing Wall Retaining Structure in Loess Foundation Pit. Master’s Thesis, Lanzhou Jiao tong University, Lanzhou, China, 2013. [Google Scholar]
- Luo, Q.; Xiong, S.J.; Wang, T.F.; Huang, Y.; Zhang, L. Analysis on slip surface characteristics of backfill and earth pressure of balance weight retaining wall under translation movement. J. Southeast Univ. (Nat. Sci. Ed.) 2022, 52, 547–556. [Google Scholar]
- Zhao, L.C.; Liu, Y.J.; Zong, H.; Xu, Y.C.; Wang, B.; Qi, L.M. Study on different slope shapes and stability under same slope angle. China Saf. Sci. J. 2022, 32, 140–144. [Google Scholar]
- Wang, H.H.; Guo, M.Z. Analysis of Toppling Failure of Anti Toppling Rock Slope Based on Numerical Manifold Method. Technol. Earthq. Disaster Prev. 2021, 16, 346–351. [Google Scholar]
- Bian, K.; Liu, J.; Hu, X.J.; Li, P.C.; Chen, L.Z.; Liu, Z.P. Study on failure mode and dynamic response of rock slope with non-persistent joint under earthquake. Rock. Soil. Mech. 2018, 39, 3029–3037. [Google Scholar]
- Guo, S.F.; Fu, J.Y.; Zhang, P.; Li, N. Deformation-damage mechanism and failure mode of creeping bedding rock landslides controlled by faults. China Earthq. Eng. J. 2025, 3, 1–12. [Google Scholar]
- Zhou, Y.; Wang, Z.Z. Improvement of internal stability analysis method of soil nailing wall. Rock. Soil. Mech. 2016, 7, 356–362. [Google Scholar]
- Liao, Y.; Sun, L.J.; Liu, X. Analysis on the Random Variables’ Influence on Outside Stability of Soil Nailed Wall. Sci. Technol. Eng. 2013, 13, 6934–6938. [Google Scholar]
- Lou, G.C.; Bu, J.Q. Field Monitoring of a High Slope of Weak Rocks with Soil-nailing Support and Determination of the Slip Surface. China Civ. Eng. J. 2005, 38, 106–109+114. [Google Scholar]
- Ahmed, A.; Ugai, K.; Yang, Q.Q. Assessment of 3D Slope Stability Analysis Methods Based on 3D Simplified Janbu and Hovland Methods. Int. J. Geomech. 2012, 12, 81–89. [Google Scholar] [CrossRef]
- Park, D.; Michalowski, R.L. Three-dimensional stability assessment of slopes in intact rock governed by the Hoek-Brown failure criterion. Int. J. Rock. Mech. Min. 2020, 137, 104522. [Google Scholar] [CrossRef]
- Brideau, M.A.; Pedrazzini, A.; Stead, D.; Froese, C.; Jaboyedoff, M.; Zeyl, D.V. Three-dimensional slope stability analysis of South Peak, Crowsnest Pass, Alberta, Canada. Landslides 2011, 8, 139–158. [Google Scholar] [CrossRef]
- Giger, M.W.; Krizek, R.J. Stability analysis of vertical cut with variable corner angle. Soils Found. 1975, 15, 63–71. [Google Scholar] [CrossRef] [PubMed]
- Giger, M.W.; Krizek, R.J. Stability of vertical corner cut with concentrated surcharge load. J. Geotech. Eng. Div. 1976, 102, 31–40. [Google Scholar] [CrossRef]
- Tan, D.; Sarma, S.K. Finite element verification of an enhanced limit equilibrium method for slope analysis. Géotechnique 2008, 58, 481–487. [Google Scholar] [CrossRef]
- Noroozi, M.; Jalali, S.E.; Yarahmadi-Bafghi, A.R. 3D key-group method for slope stability analysis. Int. J. Numer. Anal. Met. 2012, 36, 1780–1792. [Google Scholar] [CrossRef]
- Cui, J.Y. Mode Analysis of Sliding Plane for Foundation Pit Anchor. Chin. J. Rock. Mech. Eng. 2003, 22, 337–340. [Google Scholar]
- Zhang, Q.X.; Huo, D.; Wang, B.H. A Method of Designing Soil-nailing Wall Based on Sliding Sphenoid-mass Limit Analysis. Ind. Constr. 2002, 32, 337–340. [Google Scholar]
- Zhang, W.M.; Cai, Z.Y.; Lai, Z.Z. Limit analysis and centrifuge model tests of reinforced retaining wall. Res. Waterborne Transp. 1995, 1, 55–63. [Google Scholar]
- Broms, B.B. Fabric reinforced retaining walls. In Proceedings of the International Geotechnical Symposium on Theory and Practice of Earth Reinforcement, Fukuoka, Japan, 5–7 October 1988; pp. 3–31. [Google Scholar]
- Futaki, M.; Suzuki, H.; Yamato, S. Super large triaxial compression tests on reinforced sand with high strength geogrid. In Proceedings of the 4th International Conference on Geotextiles, Geomembranes and Related Products, The Hague, The Netherlands, 28 May–1 June 1990; Volume 2, pp. 759–764. [Google Scholar]
- Jiang, Z.X. Engineering Application of Culmann’s Formula on Critical Height of Slope. Geotech. Eng. Technol. 2007, 21, 217–220. [Google Scholar]
- Casin, M.A.; Kirkby, M.J. Slope Morphology and Formation Process; Science Press: Beijing, China, 1984. [Google Scholar]
- Ma, P.; Qin, S.Q.; Sun, Q. Computation of lateral soil pressure on soil nailing wall considering cohesion force and cut slope angle. Chin. J. Geotech. Eng. 2007, 29, 1888–1891. [Google Scholar]
- Jiang, Z.X. Discussion on sliding angle formula in “Computation of lateral soil pressure on soil nailing wall considering cohesion force and cut slope angle”. Chin. J. Geotech. Eng. 2008, 06, 952. [Google Scholar]
- Li, G.X. Experimental research and analysis on breaking surface of reinforced earth retaining wall. J. Railway Eng. Soc. 2001, 03, 125–128. [Google Scholar]
- Liang, B.; Sun, Y.Q. A study on the tensile failure of reinforced earth retaining wall with model test. Chin. J. Geotech. Eng. 1995, 17, 83–87. [Google Scholar]
- Gong, X.N. Soil Plastic Mechanics; Zhejiang University Press: Hangzhou, China, 1999. [Google Scholar]
- Chen, H.F.; Sapri, A.F. Elastic and Plastic Mechanics; China Architecture & Building Press: Beijing, China, 2004. [Google Scholar]
- Zhu, Y.P.; Ye, S.H.; Mo, Y. Analysis and treatment of a deep foundation pit accident in Xining, Qinghai Province. Chin. J. Geotech. Eng. 2010, 32, 404–409. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).