Multivariate Regression Analysis for Identifying Key Drivers of Harmful Algal Bloom in Lake Erie
Abstract
1. Introduction
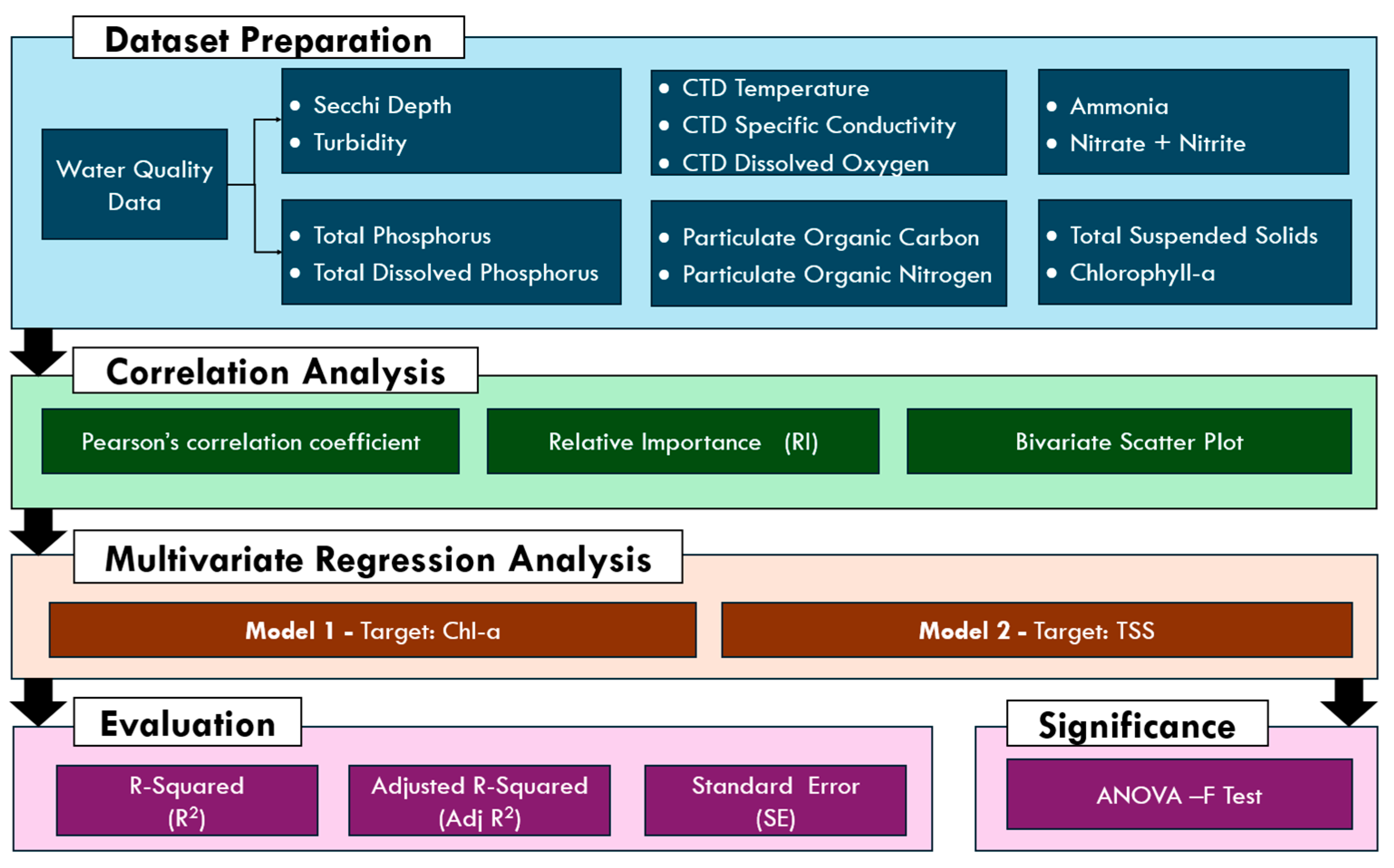
2. Materials and Methods
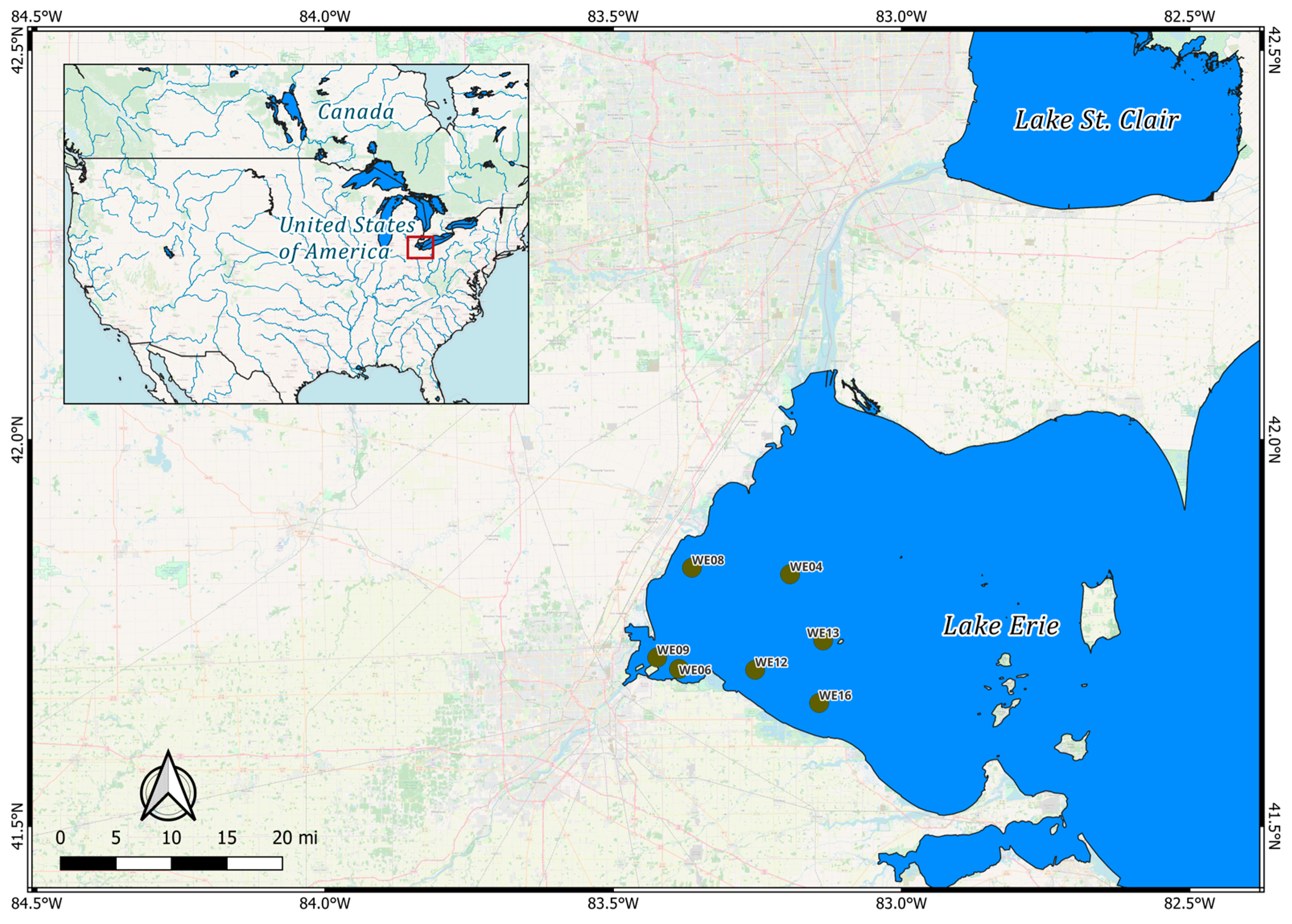
2.1. Study Area and Dataset Preprocessing
2.2. Correlation Analysis
2.3. Multivariate Regression Analysis
2.4. Coefficients of Determination
3. Results and Discussions
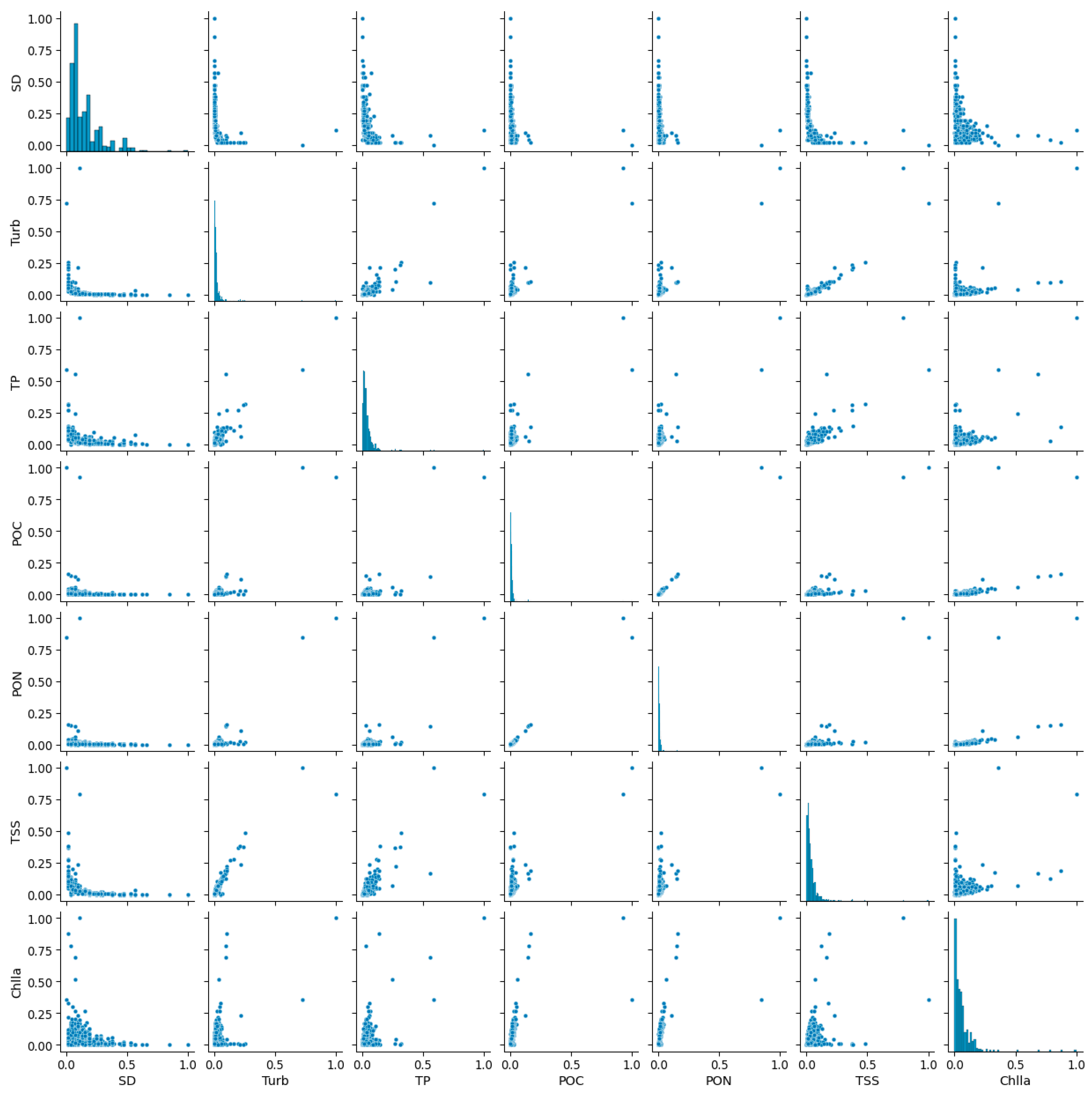
3.1. Data Statistics
3.2. Correlation and Relative Importance
3.3. Multivariate Regression Model Performance
3.4. Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yan, Z.; Kamanmalek, S.; Alamdari, N.; Nikoo, M.R. Comprehensive Insights into Harmful Algal Blooms: A Review of Chemical, Physical, Biological, and Climatological Influencers with Predictive Modeling Approaches. J. Environ. Eng. 2024, 150, 03124002. [Google Scholar] [CrossRef]
- Carmichael, W.W.; Falconer, I.R. Diseases related to freshwater blue-green algal toxins, and control measures. In Algal Toxins in Seafood and Drinking Water; Falconer, I.R., Ed.; Academic Press: London, UK, 1993; pp. 187–209. [Google Scholar]
- Bayar, S.; Demir, I.; Engin, G.O. Modeling leaching behavior of solidified wastes using back-propagation neural networks. Ecotoxicol. Environ. Saf. 2009, 72, 843–850. [Google Scholar] [CrossRef]
- Paerl, H.W.; Paul, V.J. Climate change: Links to global expansion of harmful cyanobacteria. Water Res. 2012, 46, 1349–1363. [Google Scholar] [CrossRef] [PubMed]
- Graham, J.L.; Dubrovsky, N.M.; Eberts, S.M. Cyanobacterial Harmful Algal Blooms and US Geological Survey Science Capabilities. U.S. Geological Survey Report. 2016. Available online: https://pubs.usgs.gov/publication/ofr20161174 (accessed on 23 October 2024).
- Weirich, C.A.; Miller, T.R. Freshwater harmful algal blooms: Toxins and children’s health. Curr. Probl. Pediatr. Adolesc. Health Care 2014, 44, 2–24. [Google Scholar] [CrossRef]
- Yeşilköy, S.; Demir, I. Crop yield prediction based on reanalysis and crop phenology data in the agroclimatic zones. Theor. Appl. Climatol. 2024, 155, 1–14. [Google Scholar] [CrossRef]
- Wells, M.L.; Karlson, B.; Wulff, A.; Kudela, R.; Trick, C.; Asnaghi, V.; Berdalet, E.; Cochlan, W.; Davidson, K.; De Rijcke, M.; et al. Future HAB science: Directions and challenges in a changing climate. Harmful Algae 2020, 91, 101632. [Google Scholar] [CrossRef]
- Tanir, T.; Yildirim, E.; Ferreira, C.M.; Demir, I. Social vulnerability and climate risk assessment for agricultural communities in the United States. Sci. Total Environ. 2024, 908, 168346. [Google Scholar] [CrossRef]
- Greene, S.B.D.; LeFevre, G.H.; Markfort, C.D. Improving the spatial and temporal monitoring of cyanotoxins in Iowa lakes using a multiscale and multi-modal monitoring approach. Sci. Total Environ. 2021, 760, 143327. [Google Scholar] [CrossRef]
- Paerl, H.W.; Gardner, W.S.; Havens, K.E.; Joyner, A.R.; McCarthy, M.J.; Newell, S.E.; Boqiang Qin, B.; Scott, J.T. Mitigating cyanobacterial harmful algal blooms in aquatic ecosystems impacted by climate change and anthropogenic nutrients. Harmful Algae 2016, 54, 213–222. [Google Scholar] [CrossRef]
- Ratté-Fortin, C.; Plante, J.F.; Rousseau, A.N.; Chokmani, K. Parametric versus nonparametric machine learning modelling for conditional density estimation of natural events: Application to harmful algal blooms. Ecol. Modell. 2023, 482, 110415. [Google Scholar] [CrossRef]
- Demiray, B.Z.; Mermer, O.; Baydaroğlu, Ö.; Demir, I. Predicting harmful algal blooms using explainable deep learning models: A comparative study. Water 2025, 17, 676. [Google Scholar] [CrossRef]
- Magnuson, J.J.; Webster, K.E.; Assel, R.A.; Bowser, C.J.; Dillon, P.J.; Eaton, J.G.; Evans, H.E.; Fee, E.J.; Hall, R.I.; Mortsch, L.R.; et al. Potential effects of climate changes on aquatic systems: Laurentian Great Lakes and Precambrian Shield Region. Hydrol. Process. 1997, 11, 825–871. [Google Scholar] [CrossRef]
- Tewari, M.; Kishtawal, C.M.; Moriarty, V.W.; Ray, P.; Singh, T.; Zhang, L.; Treinish, L.; Tewari, K. Improved seasonal prediction of harmful algal blooms in Lake Erie using large-scale climate indices. Commun. Earth Environ. 2022, 3, 195. [Google Scholar] [CrossRef]
- Sterner, R.W.; Keeler, B.; Polasky, S.; Poudel, R.; Rhude, K.; Rogers, M. Ecosystem services of Earth’s largest freshwater lakes. Ecosyst. Serv. 2020, 41, 101046. [Google Scholar] [CrossRef]
- Boegehold, A.G.; Burtner, A.M.; Camilleri, A.C.; Carter, G.; DenUyl, P.; Fanslow, D.; Semenyuk, D.F.; Godwin, C.M.; Gossiaux, D.; Johengen, T.H.; et al. Routine monitoring of western Lake Erie to track water quality changes associated with cyanobacterial harmful algal blooms. Earth Syst. Sci. Data Discuss. 2023, 15, 3853–3868. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Johnson, L.T.; Wynne, T.T.; Baker, D.B. Forecasting annual cyanobacterial bloom biomass to inform management decisions in Lake Erie. J. Great Lakes Res. 2016, 42, 1174–1183. [Google Scholar] [CrossRef]
- Buratti, F.M.; Manganelli, M.; Vichi, S.; Stefanelli, M.; Scardala, S.; Testai, E.; Funari, E. Cyanotoxins: Producing organisms, occurrence, toxicity, mechanism of action and human health toxicological risk evaluation. Arch. Toxicol. 2017, 91, 1049–1130. [Google Scholar] [CrossRef] [PubMed]
- Carmichael, W.W.; Boyer, G.L. Health impacts from cyanobacteria harmful algae blooms: Implications for the North American Great Lakes. Harmful Algae 2016, 54, 194–212. [Google Scholar] [CrossRef]
- Kouakou, C.R.; Poder, T.G. Economic impact of harmful algal blooms on human health: A systematic review. J. Water Health 2019, 17, 499–516. [Google Scholar] [CrossRef]
- Wells, M.L.; Trainer, V.L.; Smayda, T.J.; Karlson, B.S.; Trick, C.G.; Kudela, R.M.; Akira Ishikawa, A.; Bernard, S.; Wulff, A.; Anderson, D.M.; et al. Harmful algal blooms and climate change: Learning from the past and present to forecast the future. Harmful Algae 2015, 49, 68–93. [Google Scholar] [CrossRef]
- Glibert, P.M. Harmful algae at the complex nexus of eutrophication and climate change. Harmful Algae 2020, 91, 101583. [Google Scholar] [CrossRef]
- Zhou, Z.X.; Yu, R.C.; Zhou, M.J. Evolution of harmful algal blooms in the East China Sea under eutrophication and warming scenarios. Water Res. 2022, 221, 118807. [Google Scholar] [CrossRef] [PubMed]
- Su, Y.; Hu, M.; Wang, Y.; Zhang, H.; He, C.; Wang, Y.; Wang, D.; Wu, X.; Zhuang, Y.; Hong, S.; et al. Identifying key drivers of harmful algal blooms in a tributary of the Three Gorges Reservoir between different seasons: Causality based on data-driven methods. Environ. Pollut. 2022, 297, 118759. [Google Scholar] [CrossRef] [PubMed]
- Maze, G.; Olascoaga, M.J.; Brand, L. Historical analysis of environmental conditions during Florida Red Tide. Harmful Algae 2015, 50, 1–7. [Google Scholar] [CrossRef]
- Paerl, H.W.; Hall, N.S.; Calandrino, E.S. Controlling harmful cyanobacterial blooms in a world experiencing anthropogenic and climatic-induced change. Sci. Total Environ. 2011, 409, 1739–1745. [Google Scholar] [CrossRef]
- Hushchyna, K.; Sabir, Q.U.A.; Mclellan, K.; Nguyen-Quang, T. Multicollinearity and multi-regression analysis for main drivers of cyanobacterial harmful algal bloom (CHAB) in the Lake Torment, Nova Scotia, Canada. Environ. Model. Assess. 2023, 28, 1011–1022. [Google Scholar] [CrossRef]
- Katin, A.; Del Giudice, D.; Hall, N.S.; Paerl, H.W.; Obenour, D.R. Simulating algal dynamics within a Bayesian framework to evaluate controls on estuary productivity. Ecol. Modell. 2021, 447, 109497. [Google Scholar] [CrossRef]
- Giere, J.; Riley, D.; Nowling, R.J.; McComack, J.; Sander, H. An investigation on machine-learning models for the prediction of cyanobacteria growth. Fundam. Appl. Limnol. 2020, 194, 85–94. [Google Scholar] [CrossRef]
- Greer, B.; McNamee, S.E.; Boots, B.; Cimarelli, L.; Guillebault, D.; Helmi, K.; Marcheggiani, S.; Panaiotov, S.; Breitenbach, U.; Akçaalan, R.; et al. A validated UPLC–MS/MS method for the surveillance of ten aquatic biotoxins in European brackish and freshwater systems. Harmful Algae 2016, 55, 31–40. [Google Scholar] [CrossRef]
- Li, Z.; Xiang, Z.; Demiray, B.Z.; Sit, M.; Demir, I. MA-SARNet: A one-shot nowcasting framework for SAR image prediction with physical driving forces. ISPRS J. Photogramm. Remote Sens. 2023, 205, 176–190. [Google Scholar] [CrossRef]
- Pamula, A.S.; Gholizadeh, H.; Krzmarzick, M.J.; Mausbach, W.E.; Lampert, D.J. A remote sensing tool for near real-time monitoring of harmful algal blooms and turbidity in reservoirs. J. Am. Water Resour. Assoc. (JAWRA) 2023, 59, 929–949. [Google Scholar] [CrossRef]
- Cheng, K.H.; Chan, S.N.; Lee, J.H. Remote sensing of coastal algal blooms using unmanned aerial vehicles (UAVs). Mar. Pollut. Bull. 2020, 152, 110889. [Google Scholar] [CrossRef] [PubMed]
- Kislik, C.; Dronova, I.; Grantham, T.E.; Kelly, M. Mapping algal bloom dynamics in small reservoirs using Sentinel-2 imagery in Google Earth Engine. Ecol. Indic. 2022, 140, 109041. [Google Scholar] [CrossRef]
- Rolim, S.B.A.; Veettil, B.K.; Vieiro, A.P.; Kessler, A.B.; Gonzatti, C. Remote sensing for mapping algal blooms in freshwater lakes: A review. Environ. Sci. Pollut. Res. 2023, 30, 19602–19616. [Google Scholar] [CrossRef]
- Hartshorn, N.; Marimon, Z.; Xuan, Z.; Cormier, J.; Chang, N.B.; Wanielista, M. Complex interactions among nutrients, chlorophyll-a, and microcystins in three stormwater wet detention basins with floating treatment wetlands. Chemosphere 2016, 144, 408–419. [Google Scholar] [CrossRef] [PubMed]
- Hollister, J.W.; Kreakie, B.J. Associations between chlorophyll-a and various microcystin health advisory concentrations. F1000Research 2016, 5, 151. [Google Scholar]
- Zheng, L.; Wang, H.; Liu, C.; Zhang, S.; Ding, A.; Xie, E.; Li, J.; Wang, S. Prediction of harmful algal blooms in large water bodies using the combined EFDC and LSTM models. J. Environ. Manag. 2021, 295, 113060. [Google Scholar] [CrossRef]
- Bui, H.H.; Ha, N.H.; Nguyen, T.N.D.; Nguyen, A.T.; Pham, T.T.H.; Kandasamy, J.; Nguyen, T.V. Integration of SWAT and QUAL2K for water quality modeling in a data scarce basin of Cau River basin in Vietnam. Ecohydrol. Hydrobiol. 2019, 19, 210–223. [Google Scholar] [CrossRef]
- Wool, T.; Ambrose, R.B., Jr.; Martin, J.L.; Comer, A. WASP 8: The next generation in the 50-year evolution of USEPA’s water quality model. Water 2020, 12, 1398. [Google Scholar] [CrossRef]
- Shin, C.M.; Kim, D.; Song, Y. Analysis of hydraulic characteristics of Yeongsan River and estuary using EFDC model. J. Korean Soc. Water Environ. 2019, 35, 580–588. [Google Scholar]
- Verhamme, E.M.; Redder, T.M.; Schlea, D.A.; Grush, J.; Bratton, J.F.; DePinto, J.V. Development of the Western Lake Erie Ecosystem Model (WLEEM): Application to connect phosphorus loads to cyanobacteria biomass. J. Great Lakes Res. 2016, 42, 1193–1205. [Google Scholar] [CrossRef]
- Wynne, T.T.; Stumpf, R.P.; Tomlinson, M.C.; Fahnenstiel, G.L.; Dyble, J.; Schwab, D.J.; Joshi, S.J. Evolution of a cyanobacterial bloom forecast system in western Lake Erie: Development and initial evaluation. J. Great Lakes Res. 2013, 39, 90–99. [Google Scholar] [CrossRef]
- Baek, S.S.; Kwon, Y.S.; Pyo, J.; Choi, J.; Kim, Y.O.; Cho, K.H. Identification of influencing factors of A. catenella bloom using machine learning and numerical simulation. Harmful Algae 2021, 103, 102007. [Google Scholar] [CrossRef]
- Liu, S.T.; Zhang, L. Surface Chaotic Theory and the Growth of Harmful Algal Bloom. In Surface Chaos and Its Applications; Springer: Singapore, 2022; pp. 299–320. [Google Scholar]
- Baydaroğlu, Ö.; Yeşilköy, S.; Dave, A.; Linderman, M.; Demir, I. Modeling of Harmful Algal Bloom Dynamics and the Model-Based Interactive Framework for Inland Waters. EarthArXiv 2024, 7075. [Google Scholar] [CrossRef]
- Franks, P.J. Recent advances in modelling of harmful algal blooms. In Global Ecology and Oceanography of Harmful Algal Blooms; Springer: Berlin/Heidelberg, Germany, 2018; pp. 359–377. [Google Scholar]
- Janssen, A.B.; Janse, J.H.; Beusen, A.H.; Chang, M.; Harrison, J.A.; Huttunen, I.; Kong, X.; Rost, J.; Teurlincx, S.; Troost, T.A.; et al. How to model algal blooms in any lake on earth. Curr. Opin. Environ. Sustain. 2019, 36, 1–10. [Google Scholar] [CrossRef]
- Tounsi, A.; Abdelkader, M.; Temimi, M. Assessing the simulation of streamflow with the LSTM model across the continental United States using the MOPEX dataset. Neural Comput. Appl. 2023, 35, 22469–22486. [Google Scholar] [CrossRef]
- Wang, P.; Yao, J.; Wang, G.; Hao, F.; Shrestha, S.; Xue, B.; Xie, G.; Peng, Y. Exploring the application of artificial intelligence technology for identification of water pollution characteristics and tracing the source of water quality pollutants. Sci. Total Environ. 2019, 693, 133440. [Google Scholar] [CrossRef]
- Brehob, M.M.; Pennino, M.J.; Handler, A.M.; Compton, J.E.; Lee, S.S.; Sabo, R.D. Estimates of lake nitrogen, phosphorus, and chlorophyll-a concentrations to characterize harmful algal bloom risk across the United States. Earth’s Future 2024, 12, e2024EF004493. [Google Scholar] [CrossRef]
- Yan, Z.; Kamanmalek, S.; Alamdari, N. Predicting coastal harmful algal blooms using integrated data-driven analysis of environmental factors. Sci. Total Environ. 2024, 912, 169253. [Google Scholar] [CrossRef]
- Demir, I.; Beck, M.B. GWIS: A prototype information system for Georgia watersheds. In Proceedings of the Georgia Water Resources Conference: Regional Water Management Opportunities; Warnell School of Forestry and Natural Resources, The University of Georgia: Athens, GA, USA, 2009. [Google Scholar]
- Demir, I.; Jiang, F.; Walker, R.V.; Parker, A.K.; Beck, M.B. Information systems and social legitimacy: Scientific visualization of water quality. In Proceedings of the 2009 IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009; IEEE Press: San Antonio, TX, USA, 2009; pp. 1067–1072. [Google Scholar]
- Gogtay, N.J.; Thatte, U.M. Principles of correlation analysis. J. Assoc. Physicians India 2017, 65, 78–81. [Google Scholar]
- Wang, H.; Zentar, R.; Wang, D. Predicting the compaction parameters of solidified dredged fine sediments with statistical approach. Mar. Georesour. Geotechnol. 2023, 41, 195–210. [Google Scholar] [CrossRef]
- Tian, D.; Xie, G.; Tian, J.; Tseng, K.H.; Shum, C.K.; Lee, J.; Liang, S. Spatiotemporal variability and environmental factors of harmful algal blooms (HABs) over western Lake Erie. PLoS ONE 2017, 12, e0179622. [Google Scholar] [CrossRef]
- Zhou, Z.X.; Yu, R.C.; Zhou, M.J. Resolving the complex relationship between harmful algal blooms and environmental factors in the coastal waters adjacent to the Changjiang River estuary. Harmful Algae 2017, 62, 60–72. [Google Scholar] [CrossRef]
- Kelley, K.; Bolin, J.H. Multiple regression. In Handbook of Quantitative Methods for Educational Research; Brill: Leiden, The Netherlands, 2013; pp. 69–101. [Google Scholar]
- Hair, J.F.; Anderson, R.E.; Babin, B.J.; Black, W.C. Multivariate Data Analysis: A Global Perspective, 7th ed.; Pearson Education: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; García Marquéz, J.R.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Araujo, M.B.; Rahbek, C. How does climate change affect biodiversity? Science 2006, 313, 1396–1397. [Google Scholar] [CrossRef]
- Wheeler, D.C. Geographically weighted regression. In Handbook of Regional Science; Springer: Berlin/Heidelberg, Germany, 2021; pp. 1895–1921. [Google Scholar]
- Helsel, D.R.; Hirsch, R.M. Statistical Methods in Water Resources; U.S. Geological Survey, Techniques of Water-Resources Investigations Book 4; 2002. Available online: https://pubs.usgs.gov/publication/tm4A3 (accessed on 17 April 2025).
- Zuur, A.F.; Ieno, E.N.; Walker, N.J.; Saveliev, A.A.; Smith, G.M. Mixed Effects Models and Extensions in Ecology with R; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Guisan, A.; Zimmermann, N.E. Predictive habitat distribution models in ecology. Ecol. Model. 2000, 135, 147–186. [Google Scholar] [CrossRef]
- Chorus, I.; Welker, M. (Eds.) Toxic Cyanobacteria in Water: A Guide to Their Public Health Consequences, Monitoring and Management, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Igwaran, A.; Kayode, A.J.; Moloantoa, K.M.; Khetsha, Z.P.; Unuofin, J.-L. Cyanobacteria Harmful Algae Blooms: Causes, Impacts, and Risk Management. Water Air Soil Pollut. 2024, 235, 71. [Google Scholar] [CrossRef]
- Havens, K.E. Phosphorus–algal bloom relationships in large lakes of south Florida: Implications for establishing nutrient criteria. Lake Reserv. Manag. 2003, 19, 222–228. [Google Scholar] [CrossRef][Green Version]
- Zhang, X.; Li, Y.; Zhao, J.; Wang, Y.; Liu, H.; Liu, Q. Temporal dynamics of the chlorophyll a–total phosphorus relationship and algal production efficiency: Drivers and management implications. Ecol. Indic. 2024, 158, 111339. [Google Scholar] [CrossRef]
- Wurtsbaugh, W.A.; Paerl, H.W.; Dodds, W.K. Nutrients, eutrophication and harmful algal blooms along the freshwater to marine continuum. Wiley Interdiscip. Rev. Water 2019, 6, e1373. [Google Scholar] [CrossRef]
- Tao, Y.; Ren, J.; Zhu, H.; Li, J.; Cui, H. Exploring Spatiotemporal Patterns of Algal Cell Density in Lake Dianchi with Explainable Machine Learning. Environ. Pollut. 2024, 356, 124395. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.; Pierson, D.C.; Mesman, J.P. Prediction of algal blooms via data-driven machine learning models: An evaluation using data from a well-monitored mesotrophic lake. Geosci. Model Dev. 2023, 16, 35–46. [Google Scholar] [CrossRef]
- Ai, H.; Zhang, K.; Sun, J.; Zhang, H. Short-term Lake Erie algal bloom prediction by classification and regression models. Water Res. 2023, 232, 119710. [Google Scholar] [CrossRef]
- Izadi, M.; Sultan, M.; Kadiri, R.E.; Ghannadi, A.; Abdelmohsen, K. A remote sensing and machine learning-based approach to forecast the onset of harmful algal bloom. Remote Sens. 2021, 13, 3863. [Google Scholar] [CrossRef]
- Qian, J.; Pu, N.; Qian, L.; Xue, X.; Bi, Y.; Norra, S. Identification of driving factors of algal growth in the South-to-North Water Diversion Project by Transformer-based deep learning. Water Biol. Secur. 2023, 2, 100184. [Google Scholar] [CrossRef]
- Gao, L.; Li, X.; Kong, F.; Yu, R.; Guo, Y.; Ren, Y. AlgaeNet: A deep-learning framework to detect floating green algae from optical and SAR imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 2782–2796. [Google Scholar] [CrossRef]
- Parra, L.; Ahmad, A.; Sendra, S.; Lloret, J.; Lorenz, P. Combination of machine learning and RGB sensors to quantify and classify water turbidity. Chemosensors 2024, 12, 34. [Google Scholar] [CrossRef]
| Variable | Unit | Definition |
|---|---|---|
| Secchi Depth | m | Penetration depth of sunlight through the water |
| CTD Temperature | °C | Water temperature at site |
| CTD Specific Conductivity | µS/cm | Conductivity value of water at site |
| CTD Dissolved Oxygen | mg/L | Concentration of dissolved oxygen at site |
| Turbidity | NTU | Cloudiness of a fluid caused by suspended solids |
| Total Phosphorus | µg/L | Concentration of the sum of all phosphorus compounds that occur in various forms at site |
| Total Dissolved Phosphorus | µg/L | Concentration of the portion of phosphorus that is dissolved at site |
| Ammonia | µg/L | Concentration of Ammonia at site |
| Nitrate + Nitrite | mg N/L | Concentration of NOx at site |
| Particulate Organic Carbon | mg/L | Concentration of organic carbon particles suspended in water at site |
| Particulate Organic Nitrogen | mg/L | Concentration of organic nitrogen particles suspended in water at site |
| Total Suspended Solids | mg/L | Concentration of both organic and inorganic particles suspended in water at site |
| Chlorophyll-a | µg/L | Indicator of HABs |
| Variables | Min | Max | Mean | Std. Dev. |
|---|---|---|---|---|
| SD | 0 | 5.3 | 0.796 | 0.694 |
| T | 10.1 | 29.7 | 22.417 | 3.651 |
| Cond | 19.9 | 583.3 | 337.586 | 67.828 |
| DO | 4.2 | 13.0 | 7.478 | 1.217 |
| Turb | 0.95 | 1148.0 | 29.599 | 78.295 |
| TP | 14.87 | 2482.2 | 119.144 | 181.173 |
| TDP | 2.67 | 273.6 | 30.909 | 34.865 |
| A | 0.04 | 561.6 | 39.822 | 56.930 |
| NOx | 0 | 9.5 | 1.308 | 1.676 |
| POC | 0.15 | 219.3 | 3.946 | 15.381 |
| PON | 0.03 | 40.9 | 0.677 | 2.759 |
| TSS | 1.25 | 540.8 | 25.489 | 44.275 |
| Chl-a | 0.71 | 6784.0 | 61.232 | 347.307 |
| RI for Chl-a (100%) | RI for TSS (100%) | |
|---|---|---|
| PON | 24.26 | 28.06 |
| Turb | 22.77 | 35.57 |
| POC | 18.39 | 24.12 |
| TSS | 13.00 | — |
| TP | 10.01 | 6.20 |
| SD | 3.14 | 0.34 |
| DO | 2.44 | 0.00 |
| T | 2.19 | 0.15 |
| TDP | 2.01 | 0.12 |
| A | 1.25 | 0.11 |
| Cond | 0.50 | 0.00 |
| NOx | 0.05 | 0.01 |
| Chl-a | — | 5.34 |
| SD | T | Cond | DO | Turb | TP | TDP | A | NOx | POC | PON | TSS | Chl-a | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SD | 1.00 | 0.12 | −0.13 | −0.05 | −0.23 | −0.27 | −0.15 | −0.06 | −0.01 | −0.12 | −0.11 | −0.35 | −0.06 |
| T | 0.12 | 1.00 | −0.01 | −0.32 | −0.07 | −0.06 | −0.06 | −0.15 | 0.06 | 0.06 | 0.06 | −0.16 | 0.07 |
| Cond | −0.13 | −0.01 | 1.00 | −0.15 | −0.04 | 0.09 | 0.40 | 0.39 | 0.50 | −0.06 | −0.06 | −0.03 | −0.05 |
| DO | −0.05 | −0.32 | −0.15 | 1.00 | 0.10 | 0.03 | −0.31 | −0.32 | −0.23 | 0.16 | 0.16 | 0.06 | 0.19 |
| Turb | −0.23 | −0.07 | −0.04 | 0.10 | 1.00 | 0.88 | 0.11 | 0.06 | 0.05 | 0.89 | 0.91 | 0.93 | 0.75 |
| TP | −0.27 | −0.06 | 0.09 | 0.03 | 0.88 | 1.00 | 0.28 | 0.14 | 0.19 | 0.76 | 0.78 | 0.83 | 0.69 |
| TDP | −0.15 | −0.06 | 0.40 | −0.31 | 0.11 | 0.28 | 1.00 | 0.48 | 0.61 | −0.08 | −0.08 | 0.17 | −0.06 |
| A | −0.06 | −0.15 | 0.39 | −0.32 | 0.06 | 0.14 | 0.48 | 1.00 | 0.46 | −0.09 | −0.09 | 0.12 | −0.08 |
| NOx | −0.01 | 0.06 | 0.50 | −0.23 | 0.05 | 0.19 | 0.61 | 0.46 | 1.00 | −0.09 | −0.08 | 0.09 | −0.07 |
| POC | −0.12 | 0.06 | −0.06 | 0.16 | 0.89 | 0.76 | −0.08 | −0.09 | −0.09 | 1.00 | 0.99 | 0.78 | 0.71 |
| PON | −0.11 | 0.06 | −0.06 | 0.16 | 0.91 | 0.78 | −0.08 | −0.09 | −0.08 | 0.99 | 1.00 | 0.76 | 0.79 |
| TSS | −0.35 | −0.16 | −0.03 | 0.06 | 0.93 | 0.83 | 0.17 | 0.12 | 0.09 | 0.78 | 0.76 | 1.00 | 0.49 |
| Chl-a | −0.06 | 0.07 | −0.05 | 0.19 | 0.75 | 0.69 | −0.06 | −0.08 | −0.07 | 0.71 | 0.79 | 0.49 | 1.00 |
| r | R2 | Adjusted R2 | Std. Error (SE) | |
|---|---|---|---|---|
| Model 1 | 0.986 | 0.973 | 0.972 | 0.008 |
| Model 2 | 0.979 | 0.958 | 0.957 | 0.016 |
| df | SS—Sum of Square | MS—Mean Squares | F-Ratio | p-Value | ||
|---|---|---|---|---|---|---|
| Model 1 | ||||||
| Regression | 5 | 0.989 | 1.98 × 10−1 | 3250.46 | <1 × 10−4 | |
| Residual | 453 | 0.028 | 6.09 × 10−5 | |||
| Total | 458 | 1.017 | ||||
| Model 2 | ||||||
| Regression | 5 | 2.598 | 5.20 × 10−1 | 2067.33 | <1 × 10−4 | |
| Residual | 453 | 0.114 | 2.51 × 10−4 | |||
| Total | 458 | 2.712 | ||||
| Unstandardized Coefficients | Standard Error (SE) | t | p-Value | |
|---|---|---|---|---|
| Model 1 | ||||
| Constant | 0.004 | 0.000 | 7.906 | <0.0001 |
| Turb | 0.113 | 0.038 | 2.963 | 0.0032 |
| TP | −0.035 | 0.012 | −2.837 | 0.0048 |
| POC | −3.453 | 0.076 | −45.688 | <0.0001 |
| PON | 4.115 | 0.091 | 45.380 | <0.0001 |
| TSS | −0.030 | 0.023 | −1.319 | 0.1879 |
| Model 2 | ||||
| Constant | 0.007 | 0.001 | 6.583 | <0.0001 |
| Turb | 1.477 | 0.037 | 40.445 | <0.0001 |
| TP | 0.196 | 0.023 | 8.392 | <0.0001 |
| POC | 2.125 | 0.350 | 6.077 | <0.0001 |
| PON | −2.705 | 0.415 | −6.521 | <0.0001 |
| Chl-a | −0.126 | 0.095 | −1.319 | 0.1879 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mermer, O.; Demir, I. Multivariate Regression Analysis for Identifying Key Drivers of Harmful Algal Bloom in Lake Erie. Appl. Sci. 2025, 15, 4824. https://doi.org/10.3390/app15094824
Mermer O, Demir I. Multivariate Regression Analysis for Identifying Key Drivers of Harmful Algal Bloom in Lake Erie. Applied Sciences. 2025; 15(9):4824. https://doi.org/10.3390/app15094824
Chicago/Turabian StyleMermer, Omer, and Ibrahim Demir. 2025. "Multivariate Regression Analysis for Identifying Key Drivers of Harmful Algal Bloom in Lake Erie" Applied Sciences 15, no. 9: 4824. https://doi.org/10.3390/app15094824
APA StyleMermer, O., & Demir, I. (2025). Multivariate Regression Analysis for Identifying Key Drivers of Harmful Algal Bloom in Lake Erie. Applied Sciences, 15(9), 4824. https://doi.org/10.3390/app15094824








