Reduced-Order Nonlinear Envelope Modeling and Simulation of Resonant Inverter Driving Series Resistor–Inductor–Capacitor Load with Time-Varying Component Values
Abstract
1. Introduction
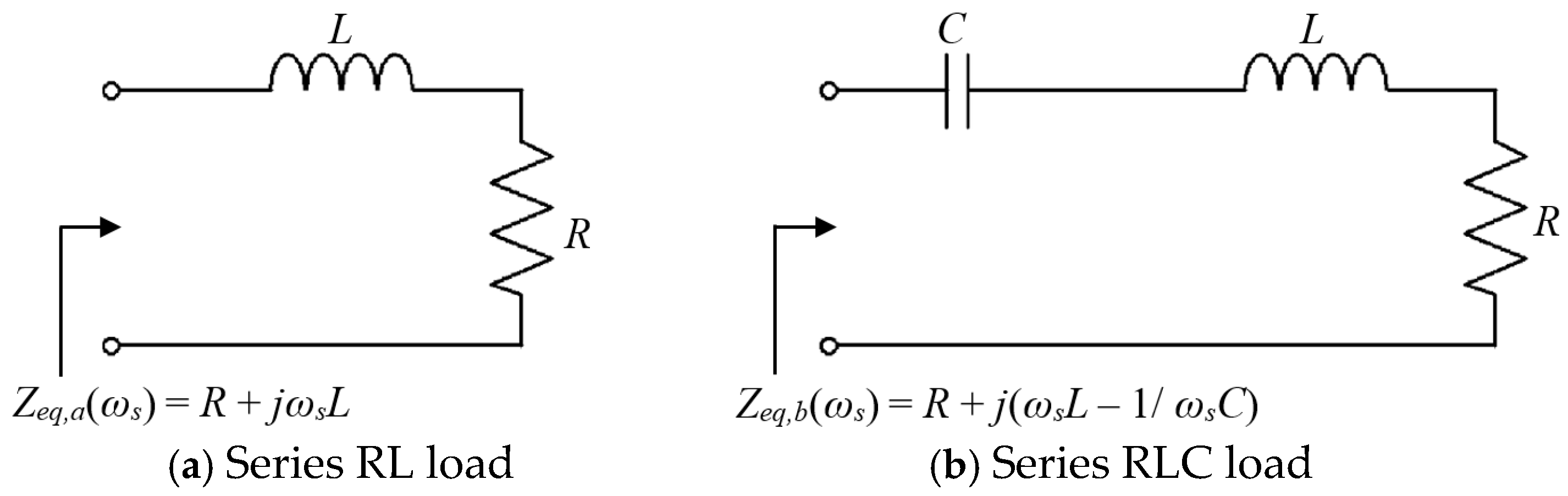
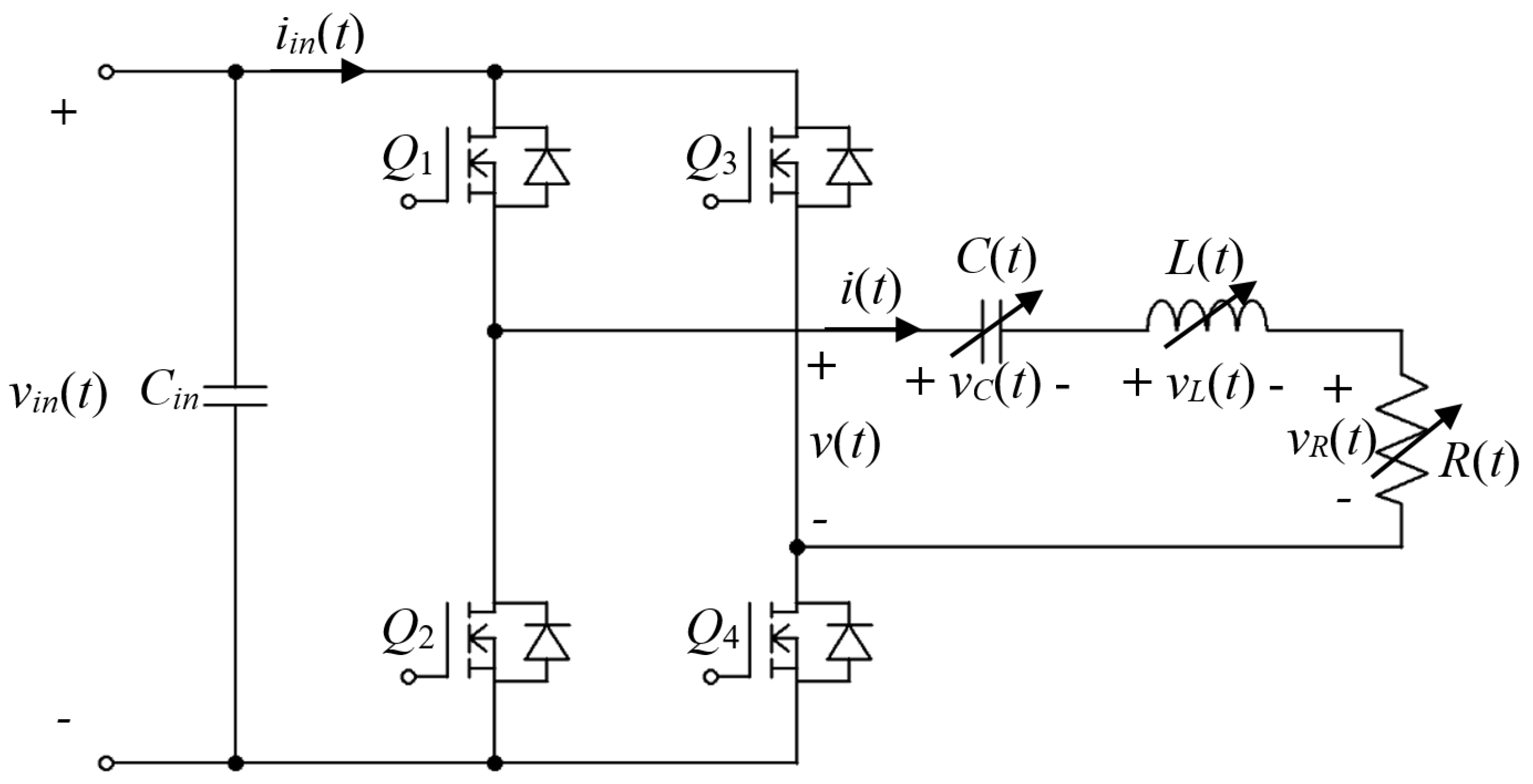
2. System Under Consideration and Basic Assumptions
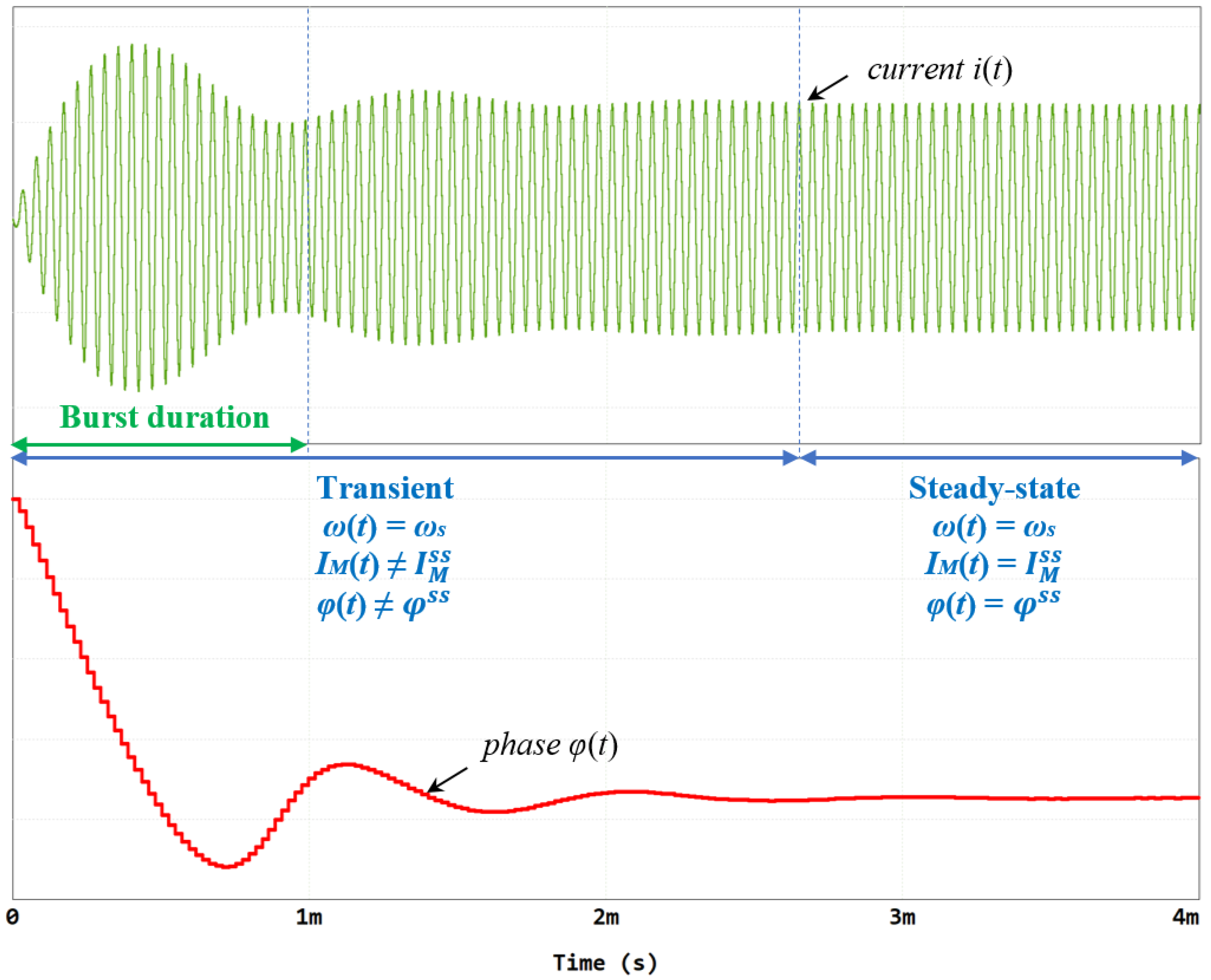
3. Full-Order Envelope Model Derivation
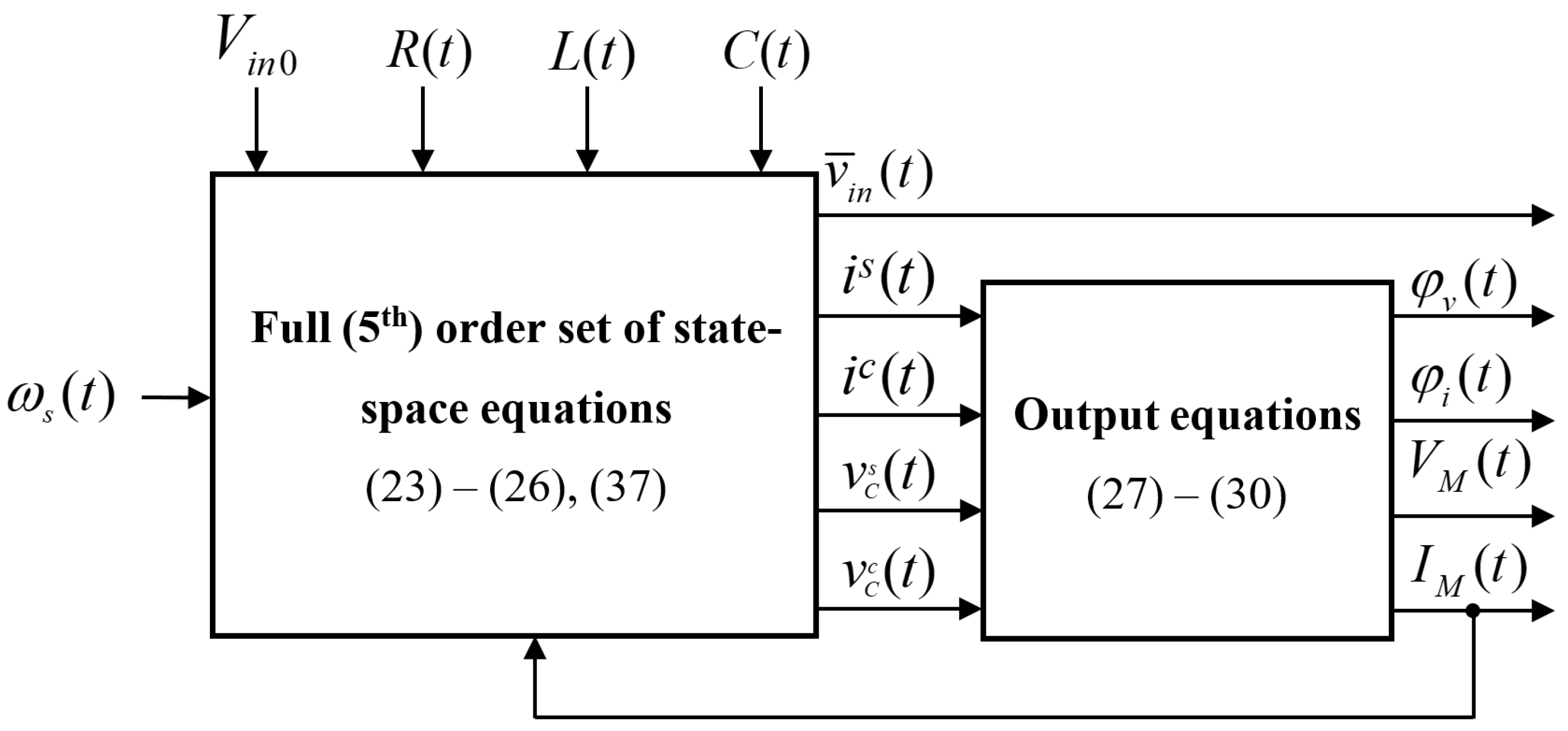
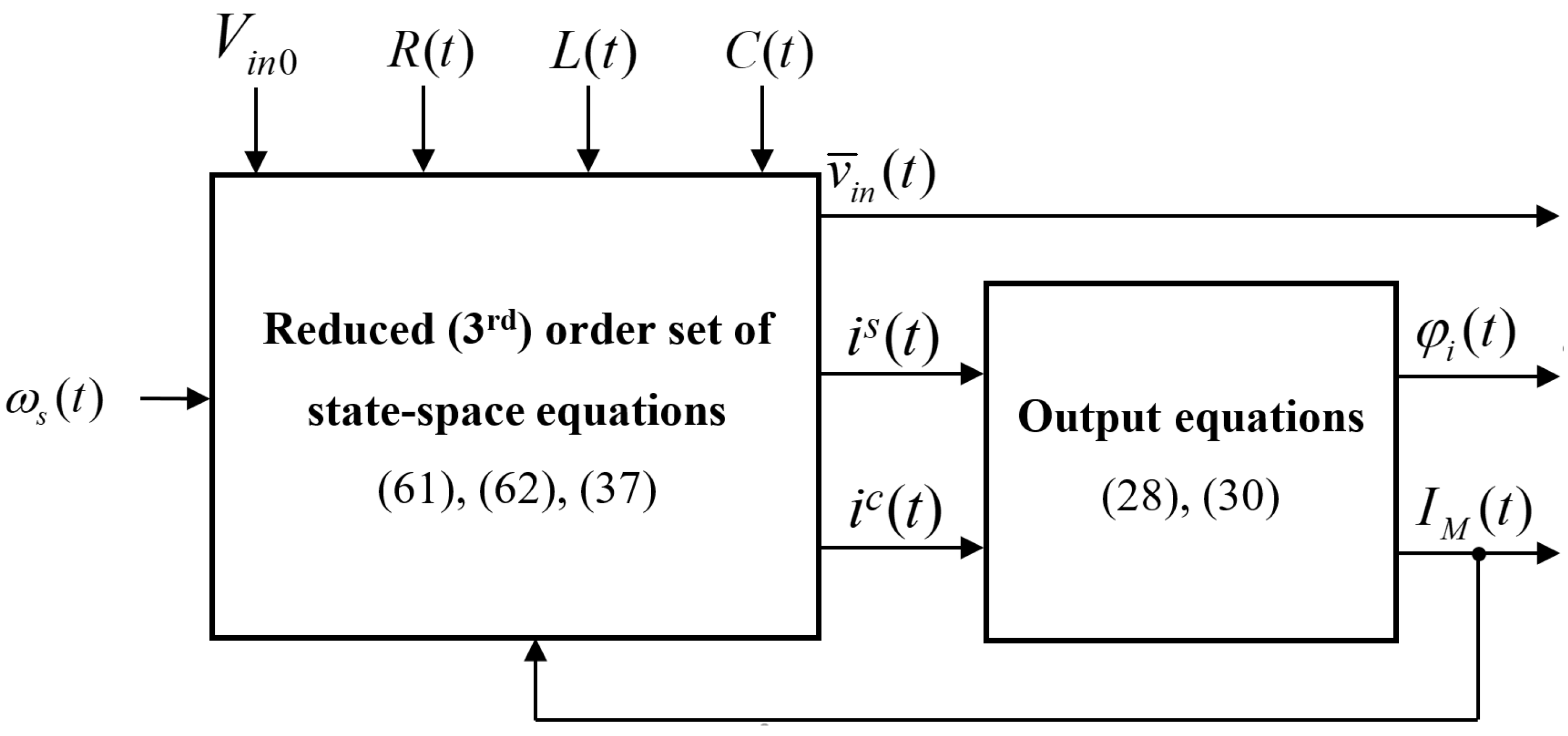
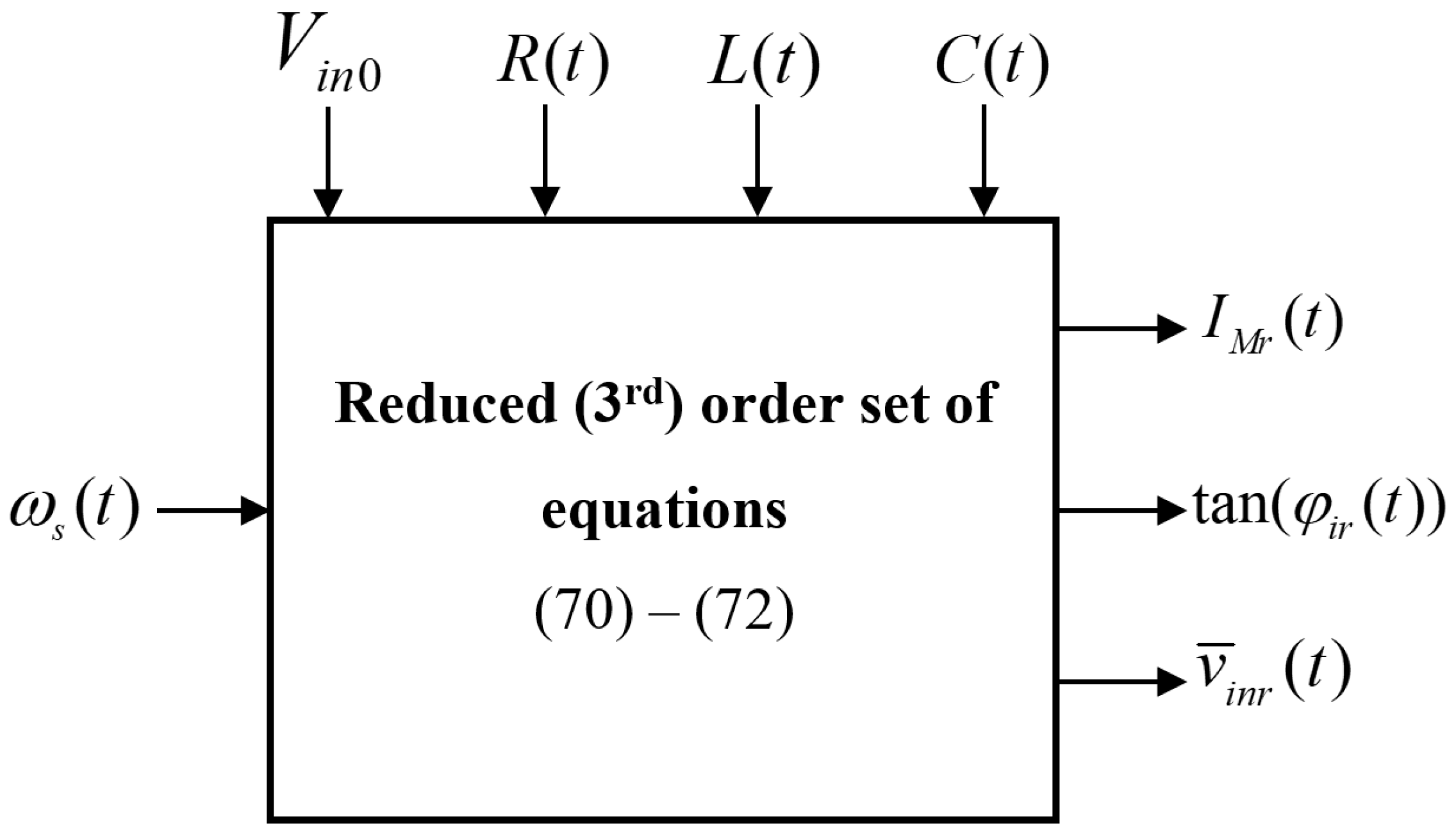
4. Envelope Model Order Reduction
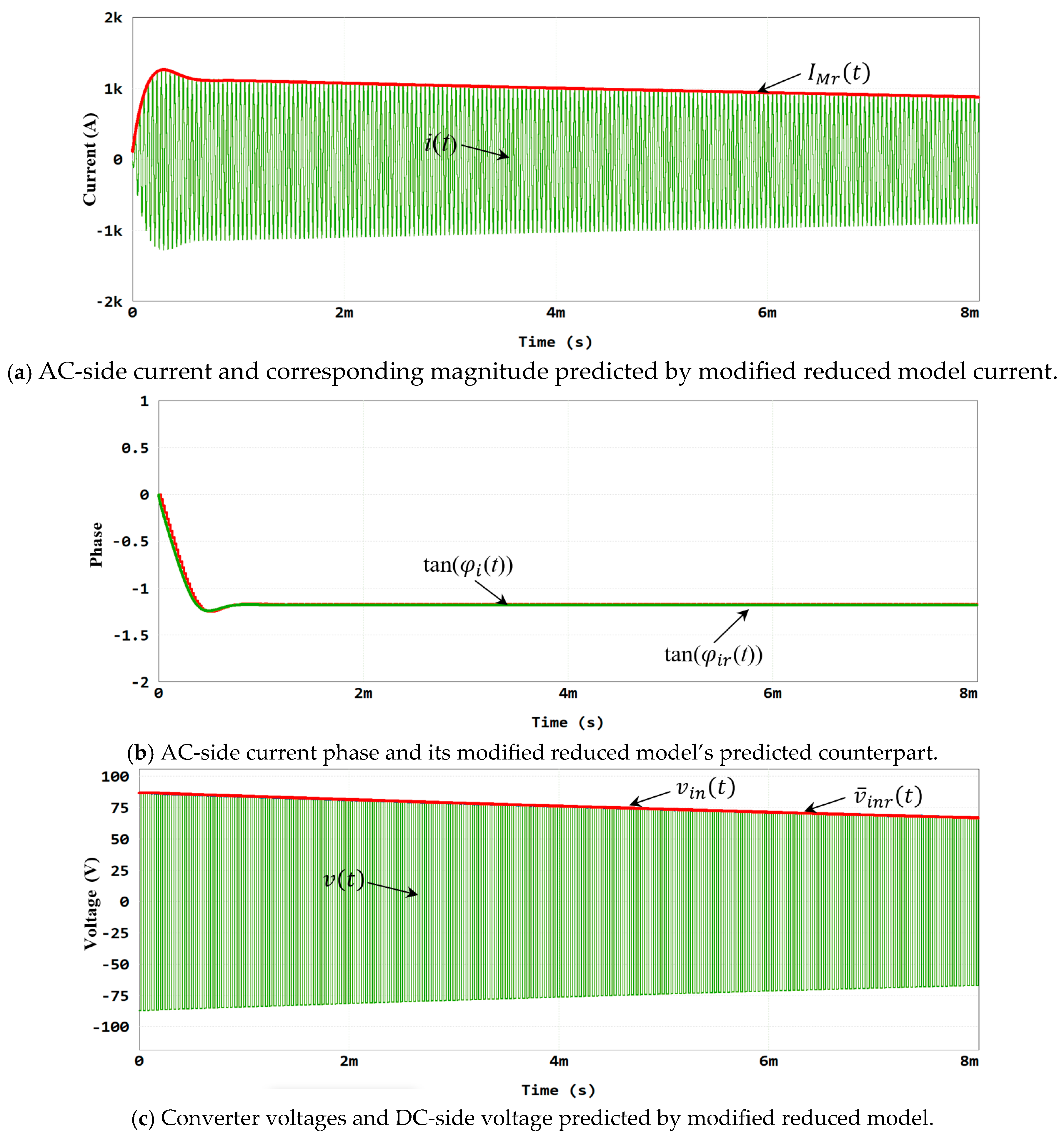
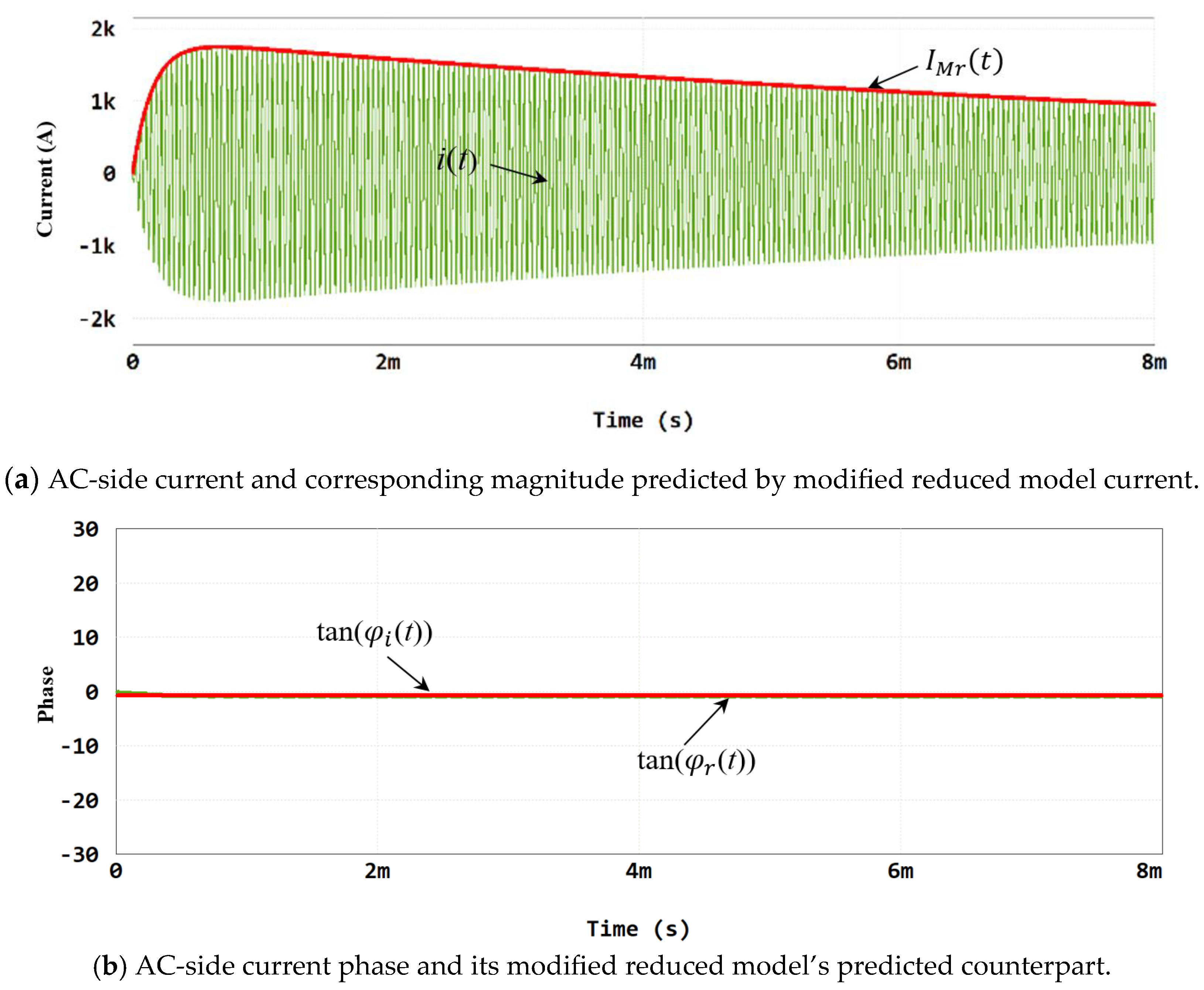
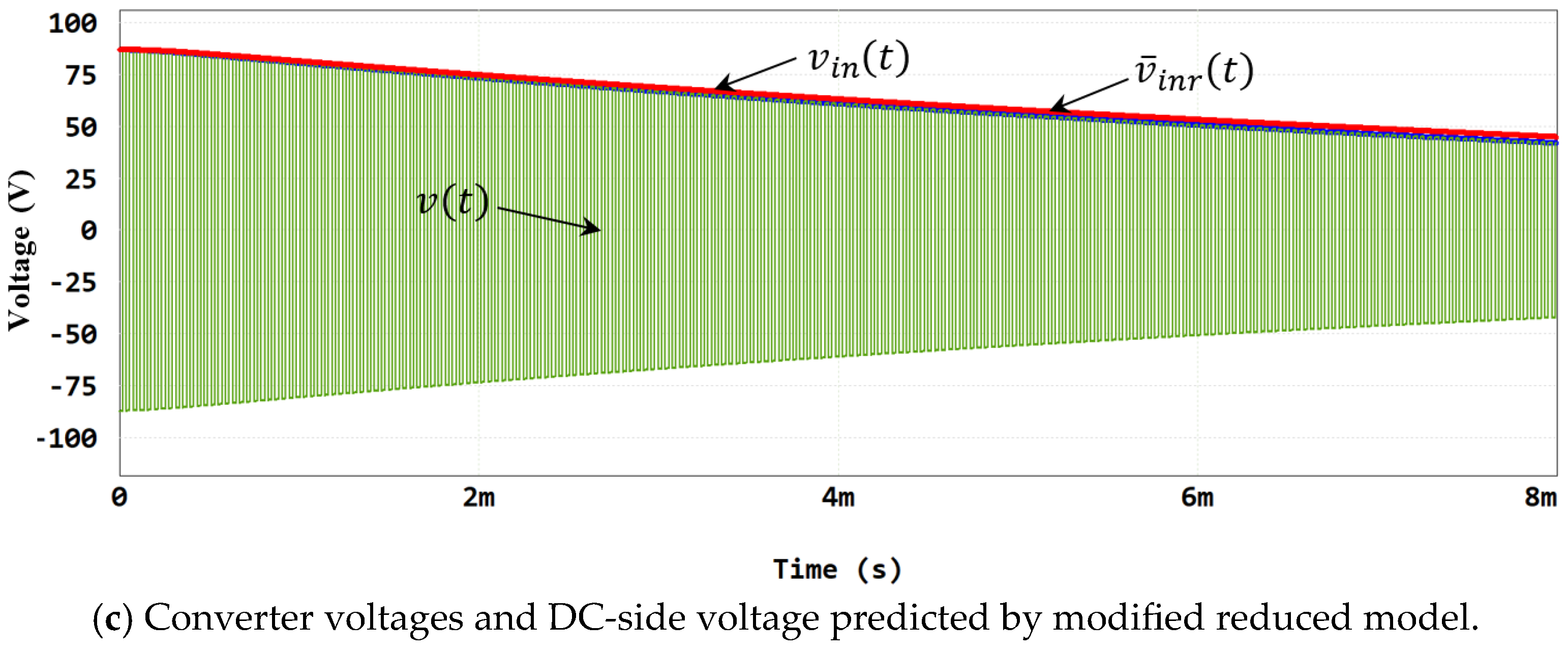
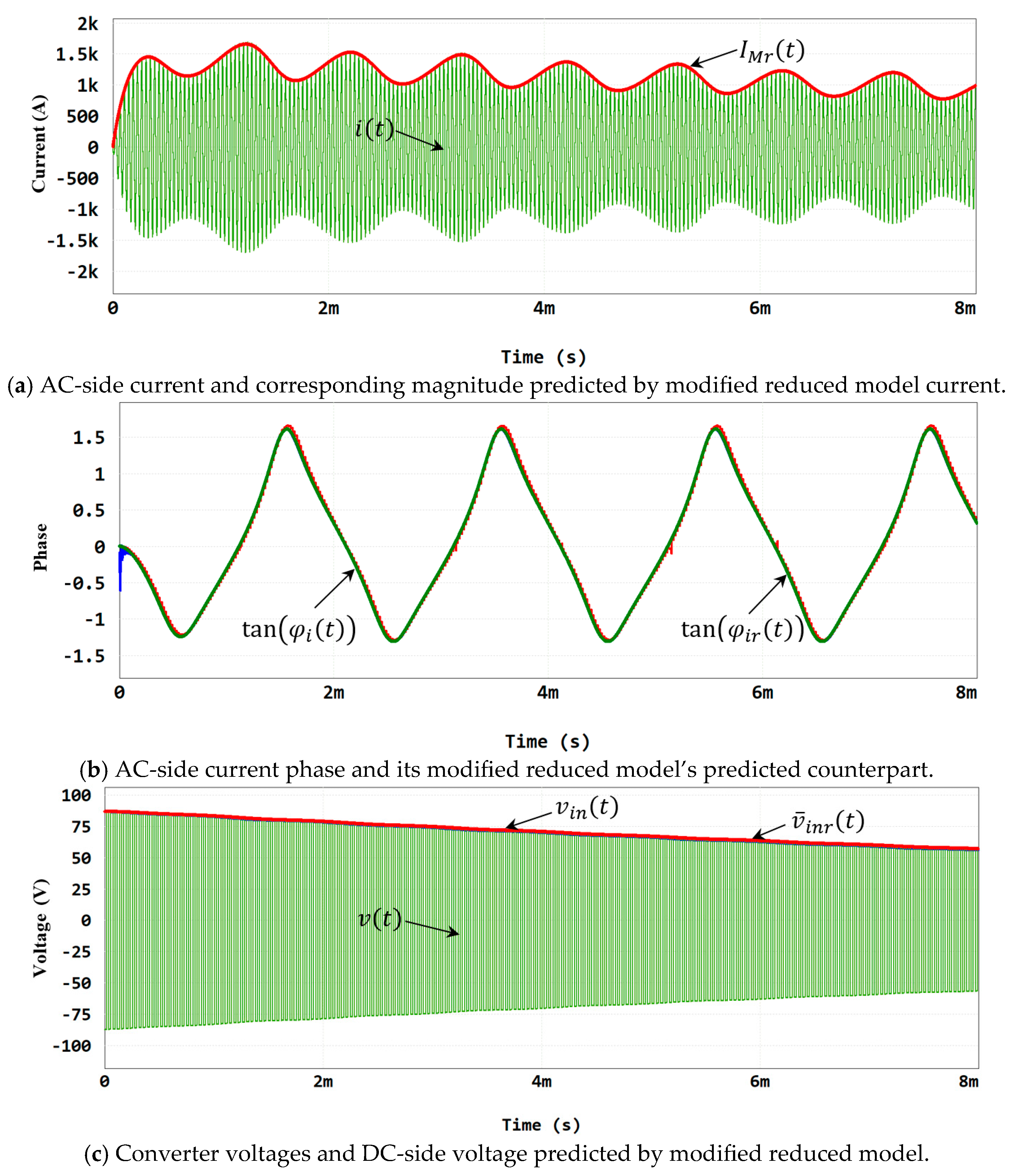
5. Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Garcia-Michelena, P.; Ruiz-Reina, E.; Herrero-Dorca, N.; Chamorro, X. Multiphysics modeling and experimental validation of heat and mass transfer for the vacuum induction melting process. Appl. Therm. Eng. 2024, 243, 122562. [Google Scholar] [CrossRef]
- Vishnuram, P.; Ramachandiran, G.; Sudhakar Babu, T.; Nastasi, B. Induction heating in domestic cooking and industrial melting applications: A systematic review on modelling, converter topologies and control schemes. Energies 2021, 14, 6634. [Google Scholar] [CrossRef]
- Lee, S.-Y.; Gho, J.-S.; Kang, B.-H.; Cho, J.-S. Analysis of Pulse Power Converter for Plasma Application. In Proceedings of the 34th Annual Conference of IEEE Industrial Electronics Society, Orlando, FL, USA, 10–13 November 2008. [Google Scholar]
- Cho, D.; Suh, N.P.; Yoon, U.; Jung, G. Shaped Magnetic Field in Resonance Technology and Its Application to Transportation System. In Proceedings of the International ASME Mechanical Engineering Congress and Exposition, Houston, TX, USA, 13–19 November 2015. [Google Scholar]
- Baimel, D.; Kuperman, A. Multi-regional modeling and operational analysis of LC/S-compensated inductive wireless power transfer link with load-independent current output. Simul. Model. Pract. Theory 2020, 105, 102154. [Google Scholar] [CrossRef]
- Vulfovich, A.; Baimel, D.; Kuperman, A. Modified first harmonic approximation-based modeling of SN-compensated inductive power transfer links operating at load-independent-voltage-output frequency. Simul. Model. Pract. Theory 2021, 111, 102340. [Google Scholar] [CrossRef]
- Hui, S.Y. Planar wireless charging technology for portable electronic products and Qi. Proc. IEEE 2013, 101, 1290–1301. [Google Scholar] [CrossRef]
- Si, P.; Hu, A.P.; Malpas, S.; Budgett, D. A frequency control method for regulating wireless power to implantable devices. IEEE Trans. Biomed. Circuits Syst. 2008, 2, 22–29. [Google Scholar] [CrossRef] [PubMed]
- Baek, S. Trajectory control approach for single-stage soft-switching grid-tied inverters. Appl. Sci. 2024, 14, 10940. [Google Scholar] [CrossRef]
- Aksöz, A. Creating a quasi-resonant induction cooktop integrating zero-voltage switching (ZVS) and load management. Appl. Sci. 2024, 14, 10449. [Google Scholar] [CrossRef]
- Sassonker, I.; Shvartsas, M.; Shoihet, A.; Kuperman, A. Modeling of Electromagnetic Levitation Melting System with Experimental Validation. In Proceedings of the IEEE International Conference on the Science of Electrical Engineering in Israel, Eilat, Israel, 12–14 December 2018. [Google Scholar]
- Sassonker, I.; Kuperman, A. Electro-mechanical modeling of electromagnetic levitation melting system driven by a series resonant inverter with experimental validation. Energy Convers. Manag. 2020, 208, 112578. [Google Scholar] [CrossRef]
- Jang, E.; Kwon, M.J.; Park, S.M.; Ahn, H.M.; Lee, B.K. Analysis and design of flexible-surface induction-heating cooktop with GaN-HEMT-based multiple inverter system. IEEE Trans. Power Electron. 2022, 37, 12865–12876. [Google Scholar] [CrossRef]
- Vulfovich, A.; Kolesnik, S.; Baimel, D.; Cohen, E.; Gutman, M.; Geftler, A.; Kuperman, A. Output characteristics of none-series compensated inductive wireless power transfer link operating at load-independent-voltage-output frequency. Simul. Model. Pract. Theory 2021, 115, 102424. [Google Scholar] [CrossRef]
- Gupta, A.; Yadav, O.P.; DeVoto, D.; Major, J. A Review of Degradation Behavior and Modeling of Capacitors. In Proceedings of the International Technical Conference and Exhibition on Packaging, San Francisco, CA, USA, 27–30 August 2018. [Google Scholar]
- Ji, C.; Zanchetta, P.; Carastro, F.; Clare, J. Repetitive control for high-performance resonant pulsed power supply in radio frequency applications. IEEE Trans. Ind. Appl. 2014, 50, 2660–2670. [Google Scholar] [CrossRef]
- Almer, S.; Jonsson, U. Dynamic phasor analysis of periodic systems. IEEE Trans. Autom. Control 2009, 54, 2007–2012. [Google Scholar] [CrossRef]
- Sassonker, I.; Elkayam, M.; Kuperman, A. Modeling Technique of Large Signal Dynamics for Electromagnetic Levitation Melting System. In Proceedings of the IEEE East-West Design & Test Symposium, Batumi, Georgia, 13–16 September 2019. [Google Scholar]
- Sassonker, I.; Kuperman, A. Envelope dynamics of resonant inverter driven electromagnetic levitation melting system with experimental verification. Mech. Syst. Signal Process. 2020, 140, 106704. [Google Scholar] [CrossRef]
- Sassonker, I.; Sassonker (Elkayam), M.; Shvartsas, M.; Darhovsky, Y.; Shoihet, A.; Kuperman, A. Small-signal modeling and active damping of resonant electromagnetic levitation melting system with experimental verification. Energy Convers. Manag. 2020, 215, 112906. [Google Scholar] [CrossRef]
- Dominguez, A.; Barragan, L.A.; Artigas, J.I.; Otin, A.; Urriza, I.; Navarro, D. Reduced-order models of series resonant inverters in induction heating applications. IEEE Trans. Power Electron. 2017, 32, 2300–2311. [Google Scholar] [CrossRef]
- Li, H.; Wang, K.; Huang, L.; Chen, W.; Yang, X. Dynamic modeling based on coupled modes for wireless power transfer systems. IEEE Trans. Power Electron. 2015, 30, 6245–6253. [Google Scholar] [CrossRef]
- Wang, W.; Song, Q.; Zhang, S.; Li, Y.; Ahmad, M.; Gong, Y. The loss analysis and efficiency optimization of power inverter based on sic mosfets under the high-switching frequency. IEEE Trans. Ind. Appl. 2021, 57, 1521–1534. [Google Scholar] [CrossRef]
- Ge, X.; Wang, Y.; Ren, D.; Tang, M.; Wang, L. A single-input multi-output inverter with voltage boosting for multi-load wireless power transfer systems. Appl. Sci. 2024, 14, 10453. [Google Scholar] [CrossRef]
- Almutairi, S.Z. Dynamic interactions between parallel grid-forming inverters in a microgrid. Appl. Sci. 2023, 13, 6989. [Google Scholar] [CrossRef]
- Elkayam, M.; Frechter, Y.; Sassonker, I.; Kuperman, A. Virtual Impedance Control for Efficient Power Transfer in Electromagnetic Levitation Melting System. In Proceedings of the IEEE Wireless Power Week Conference, London, UK, 18–21 June 2019. [Google Scholar]
- Yin, Y.; Zane, R.; Erickson, R.; Glaser, J. Direct Modeling of Envelope Dynamics in Resonant Inverters. In Proceedings of the 34th IEEE Power Electronics Specialists Conference, Acapulco, Mexico, 15–19 June 2003. [Google Scholar]
- Oliver, J.; Fernandez, C.; Prieto, R.; Cobos, J. Circuit Oriented Model of Rectifiers for Large Signal Envelope Simulation. In Proceedings of the 36th IEEE Power Electronics Specialists Conference, Dresden, Germany, 16 June 2005. [Google Scholar]
- Lineykin, S.; Ben-Yaakov, S. Unified SPICE compatible model for large and small-signal envelope simulation on linear circuits excited by modulated signals. IEEE Trans. Ind. Electron. 2006, 53, 745–751. [Google Scholar] [CrossRef]
- Bertoluzzo, M.; Giacomuzzi, S.; Forato, M. Performance analysis of envelope modelling applied to resonant converters. IEEE Trans. Ind. Electron. 2022, 69, 4046–4055. [Google Scholar] [CrossRef]
- Tian, S.; Lee, F.C.; Li, Q. A simplified equivalent circuit model of series resonant converter. IEEE Trans. Power Electron. 2016, 31, 3922–3931. [Google Scholar] [CrossRef]
- Akler, O.; Siton, Y.; Kuperman, A. Envelope Modeling of Capacitor-Powered Resonant Inverter Feeding a Time-Varying Series RLC Load. In Proceedings of the 18th IEEE International Conference on Compatibility, Power Electronics and Power Engineering, Gdynia, Poland, 24–26 June 2024. [Google Scholar]
- Johansson, L.A.; Ramaswamy, A.; Vikash; Rodwell, M. Coherent Optical Receiver with Linear XOR Phase Detection and Frequency Down-Conversion. In Proceedings of the IEEE MTT-S International Microwave Symposium Digest, Boston, MA, USA, 7–12 June 2009. [Google Scholar]
- Haro-Larrode, M.; Eguia, P.; Santos-Mugica, M. Analysis of voltage dynamics within current control time-scale in a VSC connected to a weak AC grid via series compensated AC line. Electr. Power Syst. Res. 2024, 229, 110189. [Google Scholar] [CrossRef]




| Method | Valid in Steady State | Valid in Transients |
|---|---|---|
| Classical phasor-domain analysis [17] | Yes | No |
| Linearized reduced-order envelope modeling [21] | Yes | Small variations only |
| Energetic coupling envelope modeling [22] | No | Near resonance only |
| Proposed nonlinear reduced-order envelope model | No | Yes |
| Parameter | Value | Unit |
|---|---|---|
| V0 | 87 | V |
| Cin | 80 | mF |
| f1 | 500 | Hz |
| IM0 | 0 | A |
| tan(φ0) | 0 | ---- |
| R0 | 61 | mΩ |
| L0 | 4.6 | μH |
| C0 | 8.58 | μF |
| Parameter | Simulation Parameters | |||||
|---|---|---|---|---|---|---|
| Sim 1 | Sim 2 | Sim 3 | Sim 4 | Sim 5 | Sim 6 | |
| fs [Hz] | 1.05f0 | 0.95f0 | f0 | f0 | f0 | f0 |
| L1 [H] | 0 | 0 | 0 | 0.05L0 | 0.05L0 | 0.05L0 |
| C1 [F] | 0 | 0 | 0 | 0 | 0.05C0 | 0.05C0 |
| R1 [Ω] | 0 | 0 | 0 | 0 | 0 | 0.05R0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akler, O.; Kuperman, A. Reduced-Order Nonlinear Envelope Modeling and Simulation of Resonant Inverter Driving Series Resistor–Inductor–Capacitor Load with Time-Varying Component Values. Appl. Sci. 2025, 15, 4502. https://doi.org/10.3390/app15084502
Akler O, Kuperman A. Reduced-Order Nonlinear Envelope Modeling and Simulation of Resonant Inverter Driving Series Resistor–Inductor–Capacitor Load with Time-Varying Component Values. Applied Sciences. 2025; 15(8):4502. https://doi.org/10.3390/app15084502
Chicago/Turabian StyleAkler, Ohad, and Alon Kuperman. 2025. "Reduced-Order Nonlinear Envelope Modeling and Simulation of Resonant Inverter Driving Series Resistor–Inductor–Capacitor Load with Time-Varying Component Values" Applied Sciences 15, no. 8: 4502. https://doi.org/10.3390/app15084502
APA StyleAkler, O., & Kuperman, A. (2025). Reduced-Order Nonlinear Envelope Modeling and Simulation of Resonant Inverter Driving Series Resistor–Inductor–Capacitor Load with Time-Varying Component Values. Applied Sciences, 15(8), 4502. https://doi.org/10.3390/app15084502







