Study About the Performance of Ascon in Arduino Devices

Abstract

In 2023, the Ascon cipher suite was selected as the winner of the National Institute of Standards and Technology (NIST) standardization process for lightweight cryptography, and has emerged as the leading candidate for cryptographic algorithms in resource-constrained environments. This cipher suite provides authenticated encryption with associated data and hash functionality. NIST’s Ascon proposal consists of two symmetric ciphers, Ascon-128 and Ascon-128a, a hash function, Ascon-HASH, an extendible output function, Ascon-XOF, and a new cipher variant, Ascon-80pq, with increased resistance to quantum attacks. This study presents an overview of the mathematical background, security principles and key properties of the Ascon cipher suite. In addition, a comprehensive performance evaluation of Ascon on various Arduino platforms, such as Arduino DUE, Arduino Mega2560, Arduino Nano Every and Arduino Nano ESP32, is performed. A detailed comparative analysis of these implementations is also provided.

1. Introduction

The Internet of Things (IoT) is experiencing a rapid expansion and increased relevance. By connecting smart devices to the Internet, IoT enables the digitalization of businesses, transportation networks, residential areas, cities, etc. These devices handle large amounts of data, and cryptography has always been responsible for ensuring the authenticity, confidentiality, and integrity of those data. A major challenge arises when these devices lack the computational power and memory to support traditional cryptographic algorithms due to their high processing and storage demands. To solve this problem, Lightweight Cryptography (LwC) is the best option. It should be noted that in order to obtain a lightweight encryption algorithm, two competitions have been announced in recent years: the CAESAR competition [1], organized by an international group of cryptography researchers, and the Lightweight Cryptography competition by NIST [2]. In both competitions, an associated data authenticated encryption scheme has emerged as the winner.

The purpose of this work is to introduce Ascon as the cryptographic algorithm that will be standardized by NIST [3]. Given the rapid development of the IoT, Ascon is expected to be widely deployed in devices with limited computational resources in the near future (for example, see use cases in [4,5]). The main objective of this study is to compare the performance of different implementations of the same software (Ascon family, v1.2) across various devices. This analysis aims to provide insights deciding which device is most suitable, considering diverse applications and requirements of interest for developers and users. For these reasons, this document includes a detailed description of each algorithm and its purpose, as well as an explanation of each of the components involved in the execution of the algorithm. This study includes the analysis of Ascon’s security, presenting fundamental concepts to understand the keys of its security and some known attacks against it. Moreover, a study of Ascon’s performance on four constrained devices of the Arduino family is shown.

Knowing the characteristics of the execution of the reference implementation on different platforms of Ascon family can be of interest. In fact, in [6,7,8], the authors present different studies analyzing three cryptographic algorithms used in lightweight cryptography: AES-128, CHECK, and Ascon, but none of them specifically analyzed all the versions of the Ascon family as we have.

In the present work, we have extended part of the research conducted in [9], where we examined the integration of quantum-safe lightweight cryptography schemes for classical channel authentication in quantum key distribution (QKD) for free-space quantum systems.

One of the main challenges in QKD is authentication, as the security of the quantum channel relies on the ability to establish trust between communicating parties over a classical channel. While QKD enables the exchange of encryption keys with unconditional security, it still requires a classical authentication mechanism to prevent authentication spoofing attacks. Without a robust authentication scheme, an adversary could impersonate legitimate parties, intercept key exchanges, and compromise the integrity of the system.

This challenge is more important in free-space QKD, where the use of mobile nodes, such as drones or satellites, introduces additional constraints on computational power, energy efficiency, and latency. Traditional authentication mechanisms, such as those based on public-key cryptography, are often computationally expensive and vulnerable to quantum attacks, making them unsuitable for future-proof security.

With a focus on applications for mobile nodes and resource-constrained environments, in [9], the feasibility and effectiveness of Ascon-80pq, integrating it into experimental QKD setups, was evaluated. Ascon-80pq, the quantum-resistant lightweight cipher belonging to the Ascon family, offers a compelling solution by providing efficient authenticated encryption with minimal computational overhead. Its high-performance design ensures that authentication can be performed securely, even on hardware with limited resources, without significantly impacting the overall system efficiency. By demonstrating Ascon-80pq’s advantages over other costly alternatives and assessing its protocol performance, this study highlights its potential as a practical authentication mechanism for QKD, ensuring long-term security in the face of emerging quantum threats.

On the other hand, while previous studies have addressed the general efficiency of lightweight cryptographic algorithms in embedded systems, many of them either focus on theoretical performance metrics, simulations, or on high-end platforms with hardware acceleration. Other works explore system-level challenges such as DoS (denial of service)-resilient networked control systems or learning-based security controllers, which, although highly relevant, differ significantly in scope. In contrast, this study provides a practical, empirical performance evaluation of multiple Ascon variants across a diverse set of real-world Arduino devices, ranging from 8 to bit AVR microcontrollers to more powerful 32-bit architectures. The novelty of this work lies in its hands-on benchmarking of Ascon in resource-constrained, low-cost hardware environments, using actual execution metrics (e.g., cycles, memory usage, throughput), which are crucial for developers aiming to adopt Ascon in lightweight IoT deployments without hardware acceleration. This fills a gap in the current literature by providing concrete implementation data directly applicable to practitioners in embedded cryptography.

More specifically, after this introduction, Section 2 provides a detailed description of the Ascon cipher suite, which includes an authenticated encryption algorithm and a hash function. The Ascon’s characteristics as an authenticated encryption and some domains where Arduino-based systems with Ascon are applied, are commented in Section 3. Section 4 contains the essential concepts needed to understand the basis of the security of this type of algorithm and describes the most relevant attacks on Ascon to date. A study of Ascon performance on the four constrained devices of the Arduino family is presented in Section 5, namely Arduino DUE, Arduino Mega2560, Arduino Nano Every, and Arduino Nano ESP32 (Arduino S.r.l., Somerville, MA, USA). The performance of Ascon on these devices highlights its reliability as the emerging standard for lightweight cryptography. Finally, the conclusions of this work are presented in Section 6.

2. The Ascon Cipher Suite

The Ascon cipher suite consists of a family of several algorithms: three versions of an authenticated encryption algorithm with associated data (AEAD) and two hash functions. The key properties, parameter sets, and their respective sizes (in bits) for each Ascon algorithm are summarized below. A more detailed description can be found in the Ascon document submitted to NIST [10].

2.1. Ascon as Authenticated Encryption

For the authenticated encryption process, each Ascon design has an encryption algorithm, denoted by ${\mathcal{E}}_{k,r,a,b}$, and a decryption algorithm, called ${\mathcal{D}}_{k,r,a,b}$. These algorithms have the following parameters:

• The master key, K, which has a length $k=\left|K\right|\le 160$ bits.
• The rate, r, defining the data block size.
• The number of the permutation rounds, a, in the initialization and finalization phases.
• The number of permutation rounds, b, in the intermediate phase.

The input of ${\mathcal{E}}_{k,r,a,b}$ takes k bits of K, 128 bits of a nonce, N, associated data of arbitrary length, A, and a plaintext of arbitrary length, P. Its output consists of an authenticated ciphertext of the same length as P, denoted by C, in addition of a 128-bit authentication tag, which authenticates both the associated data and the encrypted message, i.e.,

$${\mathcal{E}}_{k,r,a,b}(K,N,A,P)=(C,T).$$

(1)

The input of the ${\mathcal{D}}_{k,r,a,b}$ algorithm takes the key, K, the nonce, N, the associated data, A, the ciphertext, C, and the tag, T, giving as output the plaintext, P, if the verification process of the tag, T, is correct, and returns an error, ⊥, if the verification process fails, such that:

$${\mathcal{D}}_{k,r,a,b}(K,N,A,C,T)\in \{P,\perp \}.$$

(2)

There are two initial versions of Ascon: Ascon-128 and Ascon-128a, and due to the quantum threat posed by Shor [11] and Grover [12] algorithms, a variant of Ascon has been added, which is expected to be secure against potential attacks of a quantum computer: Ascon-80pq.

Table 1. Parameters for the three algorithms of the Ascon suite.

Name	Algorithms	Bit Size				Number of Rounds
		K	N	T	r	a	b
Ascon-128	$\mathcal{E},\mathcal{D}$	128	128	128	64	12	6
Ascon-128a	$\mathcal{E},\mathcal{D}$	128	128	128	128	12	8
Ascon-80pq	$\mathcal{E},\mathcal{D}$	160	128	128	64	12	6

shows the three authenticated encryption algorithms of the Ascon suite and their parameters.

2.2. Ascon Hash Functionality

In addition to the encryption/decryption algorithms, the Ascon suite includes two versions of a hash function, Ascon-HASH and Ascon-HASHa, which use a sponge construction [13], i.e., a type of function similar to those used in SHA-3 and SHAKE. The first version of the hash function produces a fixed 256-bit digest, whereas the second one also has two versions, Ascon-XOF and Ascon-XOFa, which provide both digests with a variable length output, l. The number of rounds for the hash versions is represented by four values: the number of rounds during initialization, i, the message absorption, a, the compression of the first block, c, and the compression of the remaining blocks, b.

Moreover, all hash functions in the Ascon suite make use of an extendable output function, denoted as ${\mathcal{X}}_{h,r,a}$, which takes as input the message of arbitrary length, M, and returns a hash, H, of arbitrary but specified length, $l\le h$, where h is the maximal output length bits, 32 bits (with $h=l=256$ for Ascon-HASH and Ascon-HASHa and $h=0$ for unlimited output in Ascon-XOF and Ascon-XOFa), such that:

$${\mathcal{X}}_{h,r,a}(M,l)=H.$$

(3)

Table 2. Parameters for the hash functions defined by Ascon.

Name	Algorithm	Bit Size		Number of Rounds p
		H	r	i	a	c	b
Ascon-HASH	$\mathcal{X}$	256	64	12	12	12	12
Ascon-HASHa	$\mathcal{X}$	256	64	12	8	12	8
Ascon-XOF	$\mathcal{X}$	l	64	12	12	12	12
Ascon-XOFa	$\mathcal{X}$	l	64	12	8	12	8

shows the different sets of parameters for each version of Ascon variants approved by NIST as hash functions, Ascon-HASH and Ascon-XOF.

Ascon-HASH and Ascon-HASHa provide 128-bit security against collision attacks and second pre-image attacks, while, if the output size of l bits is considered, the versions Ascon-XOF and Ascon-XOFa provide at least $min(128,l/2)$ bits of security against collision attacks and at least $min(128,l)$ bits of security against second pre-image attacks.

2.3. State of Ascon

As is well known, a system is said to be stateful if it is designed to remember previous information, which we will call state. Thus, the set of all possible states of a system is called state space. In a discrete system (defined by a finite number of degrees of freedom), the state space is usually finite. The interaction between system states and their environment consist of actions that occur separately, such as the acceptance of an input or the production of an output, which may cause the system to modify or update the state.

In the case of Ascon, all components of the encryption algorithm operate on a finite state of 320 bits, which is modified through a series of permutations (explained in the next section). The 320-bit state is separated into an external part of r bits, denoted as $S_r$, and an internal part of c bits, denoted as $S_c$, where r is the rate and c the capacity such that $c=320-r$ (these parameters depend on the version of Ascon). This state structuring is common in sponge constructions, and in this particular case, the MonkeyDuplex construction [13], where the state is split in the mentioned way.

For a correct application of the round transformations or permutations, the 320-bit state S is divided into five 64-bit register words, $x_i$, $0\le i\le 4$, such that:

$$S=S_r\parallel S_c=x_0\parallel x_1\parallel x_2\parallel x_3\parallel x_4$$

(4)

State S must always be interpreted as a byte-array for the sponge interface, which starts with the most significant bit (MSB) of $x_0$, which is the byte 0, and ends with the lest significant bit (LSB) of $x_4$, which is the byte 39.

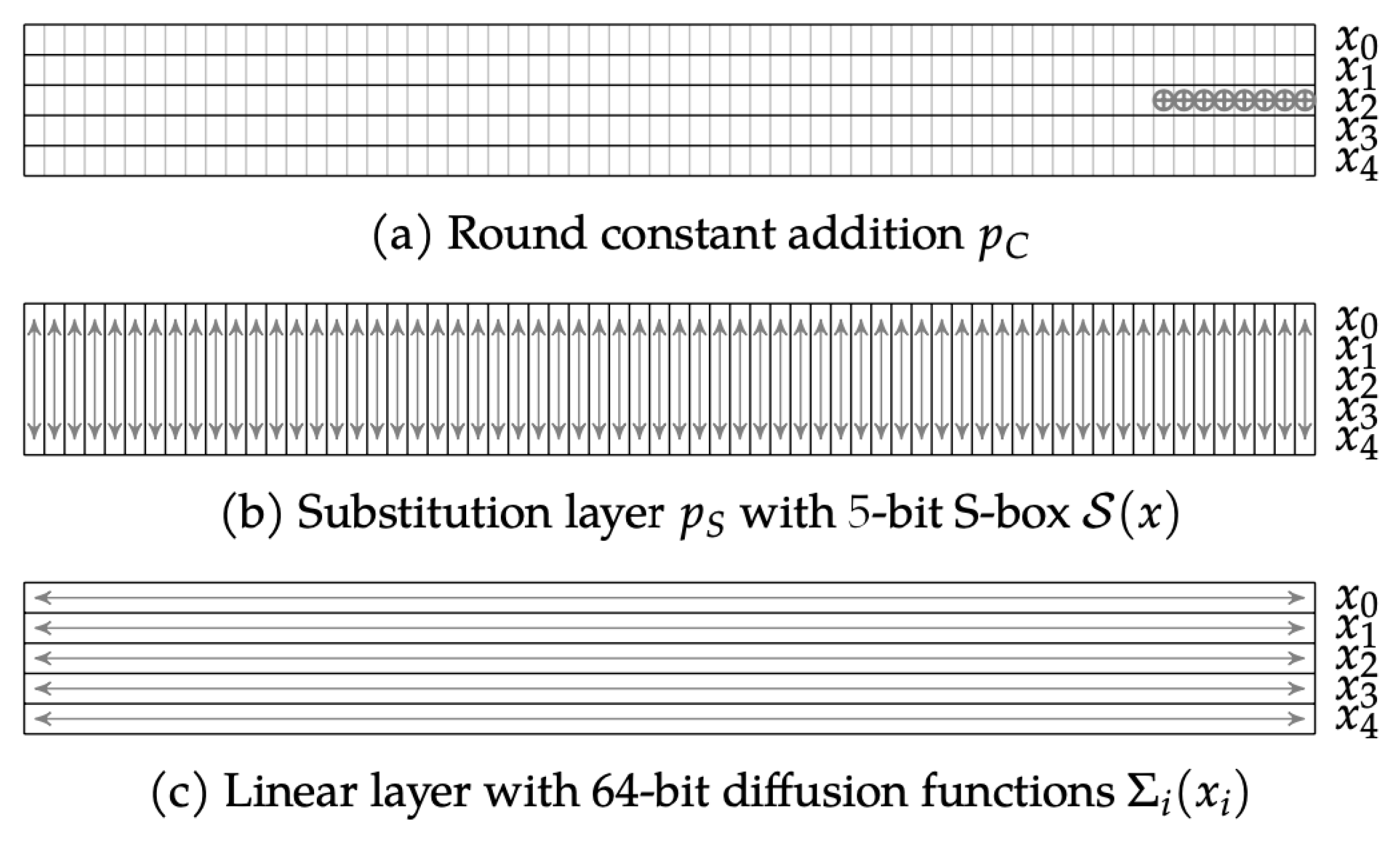
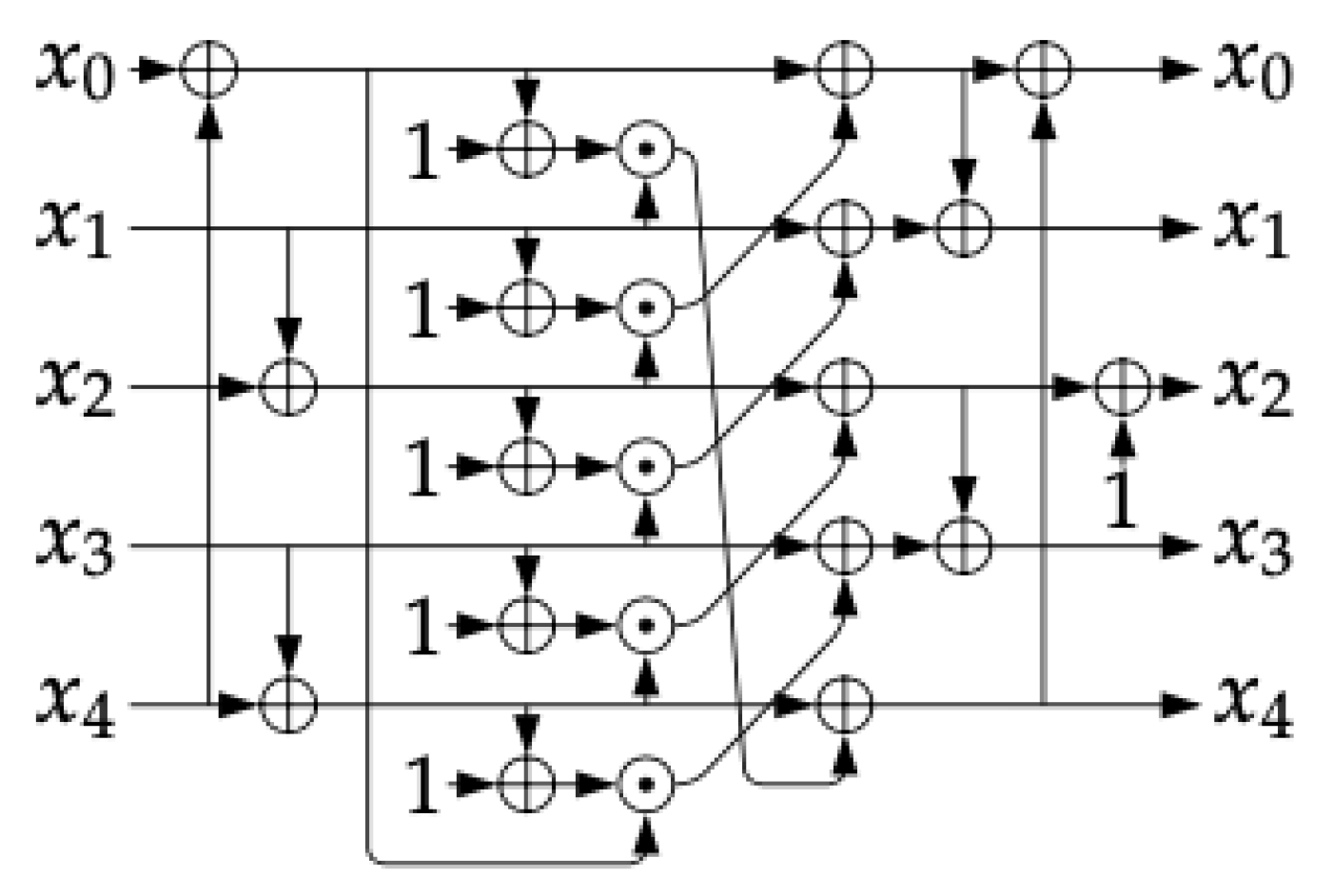
2.4. The Ascon Permutation

The Ascon suite, including the AEAD ciphers and hash algorithms, bases much of its security and efficiency on the two underlying 320-bit permutations, $p^a$ and $p^b$. These permutations are based on the iterative application of the substitution–permutation network (SPN) and each application of the SPN is called round transformation, p. The permutation of both Ascon’s authenticated cipher and its hash functionality has three layers: $p_C$, $p_S$, and $p_L$, such that:

$$p=p_L\circ p_S\circ p_C.$$

(5)

The number of rounds of the two Ascon permutations, $p^a$ and $p^b$, is different and is an adjustable parameter. Figure 1 illustrates the three layers of the permutation p as applied to the five 64-bit register words. The characteristics of such layers will be considered in the next subsections.

2.4.1. Addition of Constants Layer, $p_C$

The first step of the permutation p is the addition of constants layer, $p_C$, which is based on adding a round constant to the register word $x_2$ of the state S in round i. Both index i and r are initialized to 0 and there are differences in the value of r depending on whether $p^a$ or $p^b$ is being applied, i.e., the value of $r=i$ for $p^a$ and $r=i+a-b$ for $p^b$. As a result of this process, the 64-bit $x_2$ register word would be $x_2\leftarrow x_2\oplus c_r$, where $c_r$ is a constant.

Table 3. Specification of round constant $c_r$.

${\mathit{p}}^{\mathit{a}}$	${\mathit{p}}^{\mathit{b}}$	${\mathit{p}}^{\mathit{b}}$		${\mathit{p}}^{\mathit{a}}$	${\mathit{p}}^{\mathit{b}}$	${\mathit{p}}^{\mathit{b}}$
${\mathit{p}}^{\mathbf{12}}$	${\mathit{p}}^{\mathbf{8}}$	${\mathit{p}}^{\mathbf{6}}$	Constant ${\mathit{c}}_{\mathit{r}}$	${\mathit{p}}^{\mathbf{12}}$	${\mathit{p}}^{\mathit{8}}$	${\mathit{p}}^{\mathit{6}}$	Constant ${\mathit{c}}_{\mathit{r}}$
0			000000000000000000f0	6	2	0	00000000000000000096
1			000000000000000000e1	7	3	1	00000000000000000087
2			000000000000000000d2	8	4	2	00000000000000000078
3			000000000000000000c3	9	5	3	00000000000000000069
4	0		000000000000000000b4	10	6	4	0000000000000000005a
5	1		000000000000000000a5	11	7	5	0000000000000000004b

shows the constant $c_r$ (in hexadecimal) used in each round i, distinguishing between the permutations $p^a$ and $p^b$. In particular, $p^{12}$ corresponds to $p^a$ while $p^6$ and $p^8$ correspond to $p^b$, in Ascon-128 and Ascon-128a, respectively.

The round constants have been chosen in such a way that the size is large enough to avoid sliding, rotation, self-similarity, or similar attacks. In addition, the values of the constants have been chosen (one increasing and one decreasing counter for the two halves of the affected byte) so that it is easy to calculate them by a simple counter and inverse operation. Finally, the constants are added to the third word $x_2$ because it allows pipelining with the new or previous operations.

2.4.2. Substitution Layer, $p_S$

The substitution layer, $p_S$, modifies the S-state using 64 parallel applications. For this process, Ascon uses the S-boxes of 5 bits, i.e., it takes 5 bits of input and returns 5 bits of output. The S-box takes one bit from each 64-bit register word vertically and performs a substitution based on

Table 4. Lookup table of the Ascon S-box.

x	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
$S\left(x\right)$	4	11	31	20	26	21	9	2	27	5	8	18	29	3	6	28
x	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31
$S\left(x\right)$	30	19	7	14	0	13	17	24	16	12	1	25	22	10	15	23

. Each 64-bit register word bit contributes one bit to each of the 64 S-boxes, where $x_0$ always contributes with the MSB and $x_4$ with the LSB.

The lookup table goes from 0 to 31, in binary, because it covers all possible combinations of 5 bits in five different positions. Figure 2 represents the S-box and these operations are applied in this bitsliced form, with operations performed on the entire 64-bit words.

The easiest way to implement the S-box is to use a look-up table, but this option has a high area cost. An alternative is to use coordinate functions, which require less area. In algebraic form, the S-Box can be represented by coordinate functions in the following way:

$$\begin{array}{cc}\hfill y_0& =x_4{x}_1\oplus x_3\oplus x_2{x}_1\oplus x_2\oplus x_1{x}_0\oplus x_1\oplus x_0,\hfill \\ \hfill y_1& =x_4\oplus x_2{x}_3\oplus x_3\oplus x_3{x}_1\oplus x_2\oplus x_1{x}_2\oplus x_1\oplus x_0,\hfill \\ \hfill y_2& =x_4{x}_3\oplus x_4\oplus x_2\oplus x_1\oplus 1,\hfill \\ \hfill y_3& =x_4{x}_0\oplus x_3{x}_0\oplus x_4\oplus x_3\oplus x_2\oplus x_1\oplus x_0,\hfill \\ \hfill y_4& =x_4{x}_1\oplus x_4\oplus x_3\oplus x_1{x}_0\oplus x_1,\hfill \end{array}$$

where each $y_i$, $i=0,\dots ,4$, is one of the five 64-bit words, $x_i$, after the S-box has been applied.

2.4.3. Linear Diffusion Layer $p_L$

The linear diffusion layer, $p_L$, applies a linear function $\Sigma$ to each of the 64-bit register words $x_i$, providing diffusion for each one of them:

$$x_i\leftarrow {\Sigma }_i\left(x_i\right),0\le i\le 4.$$

(6)

The functions applied in each layer are defined as follows:

$$\begin{array}{cc}\hfill x_0& \leftarrow {\Sigma }_0\left(x_0\right)=x_0\oplus (x_0⋙19)\oplus (x_0⋙28),\hfill \\ \hfill x_1& \leftarrow {\Sigma }_1\left(x_1\right)=x_1\oplus (x_1⋙61)\oplus (x_1⋙39),\hfill \\ \hfill x_2& \leftarrow {\Sigma }_2\left(x_2\right)=x_2\oplus (x_2⋙1)\oplus (x_2⋙6),\hfill \\ \hfill x_3& \leftarrow {\Sigma }_3\left(x_3\right)=x_3\oplus (x_3⋙10)\oplus (x_3⋙17),\hfill \\ \hfill x_4& \leftarrow {\Sigma }_4\left(x_4\right)=x_4\oplus (x_4⋙7)\oplus (x_4⋙41),\hfill \end{array}$$

where $x_i⋙j$ denotes a right rotation, i.e., a circular shift, of j bits of the 64-bit word $x_i$.

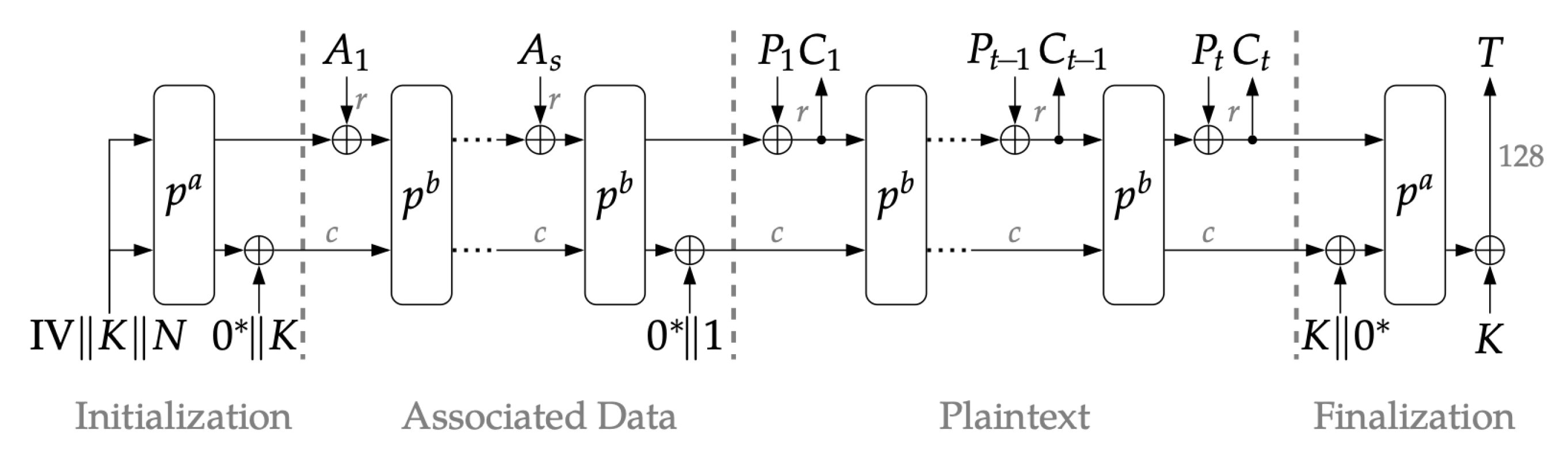
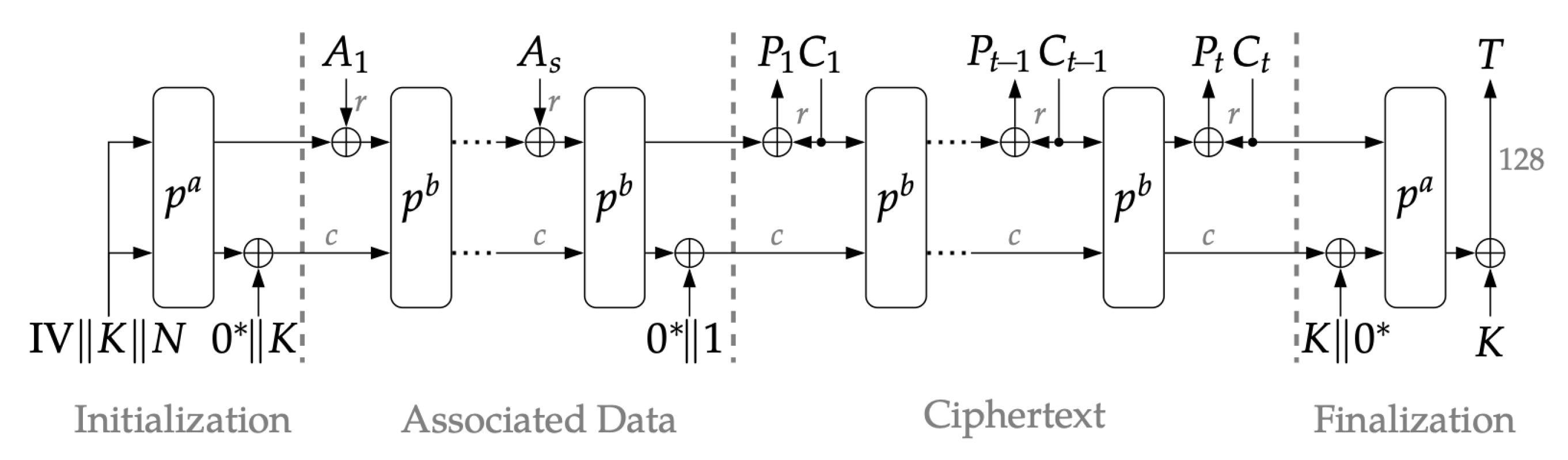
3. Ascon as Authenticated Encryption

As we have mentioned before, specifically in the MonkeyDuplex construction, Ascon’s authenticated encryption process is based on a Duplex construction, in particular the MonkeyDuplex construction, and makes use of a strong initialization and keyed completion function.

3.1. MonkeyDuplex Construction

The security of MonkeyDuplex construction requires the associated data to be unique. In other words, Duplex constructions only ensure the confidentiality of the ciphertext if, for the same key and different messages, the associated data are unique (for more information see [13]). The main features of this scheme are the following:

• It is an object that, upon creation, is loaded with a message authentication code (MAC), a key, and a nonce. Once initialized, duplex calls can be performed by providing an input string and requesting an output string. Its main characteristic is that the output string depends on all the previous input strings, the key, and the nonce.
• The initialization of the b-bit state of the construction is performed by concatenating the key and the nonce, among others, subject to n initial rounds. This is where permutation comes in. If the permutation is good enough in terms of security, the state values of MonkeyDuplex objects with different nonce values can be considered to be independent. In this case, state recovery by an attacker with access to multiple objects gains no advantage over state recovery from a single object.
• The duplexing calls are quantitatively the same as in the Duplex construction. It is possible to reduce the number of rounds of the permutation, without compromising the scheme’s robustness, provided that an initialization protocol is established. As such, differential attacks will be unfeasible, i.e., an attacker would have no knowledge of the difference between the different objects in the MonkeyDuplex construction.
• The difficulty of recovering a state is directly proportional to the number n of rounds of the permutation, and inversely proportional to the size of r. The efficiency is determined by the parameter $r/n$.
  Indeed, a larger value of r allows one to process a larger amount of data per iteration, while a smaller value of n reduces the number of permutation operations required per data block, speeding up the computation. Consequently, the ratio $r/n$ represents the number of useful bits processed per round of permutation applied. The greater $r/n$, the more efficient the scheme, since the amount of data processed per computational unit is maximized.

3.2. Ascon AEAD Operation

As previously mentioned, the different steps and blocks that Ascon must process for encryption and decryption include the key, nonce, associated data, plaintext or ciphertext, and tag (see [10]). Depending on the algorithm version, the nonce is processed or stored to be used in different operations during the cipher operation.

Before block processing, Ascon initializes the cipher status register with an initial value that depends on an initialization vector ($IV$). The value of these $IV$ varies according to the Ascon version and can take the following values:

$$I{V}_{k,r,a,b}\leftarrow k\parallel r\parallel a\parallel b\parallel 0^{160-k}=\left\{\begin{array}{cc}\mathtt{80400}\mathtt{c}\mathtt{0600000000}\hfill & \mathrm{for}\mathrm{Ascon}-128\hfill \\ \mathtt{80800}\mathtt{c}\mathtt{0800000000}\hfill & \mathrm{for}\mathrm{Ascon}-128\mathrm{a}\hfill \\ \mathtt{a}\mathtt{0400}\mathtt{c}\mathtt{06}\hfill & \mathrm{for}\mathrm{Ascon}-80\mathrm{pq}\hfill \end{array}\right.$$

(7)

The initialization algorithm (Algorithm 1) of Ascon consists in storing in the state register, S, the concatenation of the fixed initial vector, $IV$, the key, K, and the nonce, N. Then, the state register, S, is updated with the XOR operation between the result of applying a times the permutation p to the previous state register and the key, K, with a padding of a convenient number of zeros.

Algorithm 1 Initialization process

Input: key $K\in {\{0,1\}}^k,k\le 160$, and nonce $N\in {\{0,1\}}^{128}$ $\hspace{1em}S\leftarrow I{V}_{k,r,a,b}\parallel K\parallel N$ $\hspace{1em}S\leftarrow p^a\left(S\right)\oplus (0^{320-k}\parallel K)$ Output: update S (modifies internal state)

The data association process consists, as shown in Algorithm 2, in dividing the data into blocks of r bits. If the last block is incomplete, a padding is applied. This padding involves adding a 1 immediately after the last bit of the block, followed by 0s until the block reaches a length of r bits. Later, each block is introduced in the state register by means of an XOR operation between the associated data $A_i$ and the internal part of the state, $S_r$. Then, the permutation p is executed b times. The above steps are repeated for each of the blocks $A_i$. Finally, the XOR operation of the state S with a string of 0s and 1s in the LSB is stored in the state register.

Algorithm 2 Processing associated data

Input: associated data $A\in {\{0,1\}}^{*}$ and internal state S  if$\left|A\right|>0$ then     $A_1\cdots A_s\leftarrow$ divide A into r-bits blocks by concatenating $A\parallel 1\parallel 0^{*}$ (padded to make the last block exactly r-bits long)     for$i=1\cdots s$ do        $S\leftarrow p^b\left(\left(S_r\oplus A_i\right)\parallel S_c\right)$     end for  end if   $S\leftarrow S\oplus (0^{319}\parallel 1)$ Output: update S (modifies internal state)

The encryption algorithm, ${\mathcal{E}}_{k,r,a,b}$ is shown in Figure 3. The procedure for encryption plaintext processing follows a similar procedure to that of the associated data, with the difference being that the output of the plaintext processing corresponds to the ciphertext. In fact, in this process (see Algorithm 3), the plaintext is divided into r-bit blocks and if the last block is incomplete, it is padded with zeros. Then, the state register collects the blocks resulting from the XOR operation between the plaintext $P_i$ and the internal part of the state register $S_r$, which corresponds to a block of the ciphertext $C_i$. Once the block is incorporated into the state register, the permutation p is executed, b times. These three steps are repeated for each block of the plaintext, except for the last r-bit block. Finally, the XOR operation between the last plaintext block $P_t$ and the inner part of the state $S_r$, is entered into the state register. The last block of the ciphertext will be the MSB of the $S_r$ state resulting from the last XOR operation. In this case the permutation is not applied again.

Algorithm 3 Encryption (processing plaintext)

Input: plaintext $P\in {\{0,1\}}^{*}$ and internal state S  $P_1\cdots P_t\leftarrow$ divide P into r-bits blocks by concatenating $P\parallel 1\parallel 0^{*}$ (padded to make the last block exactly r-bits long)  for$i=1\cdots t-1$do     $S_r\leftarrow S_r\oplus P_i$     $C_i\leftarrow S_r$     $S\leftarrow p^b\left(S\right)$  end for   $S_r\leftarrow S_r\oplus P_t$   ${\tilde{C}}_t\leftarrow {\lfloor S_r\rfloor }_{\left|P\right|modr}$ Output: ciphertext $C\in {\{0,1\}}^{\left|P\right|}$ and updated state S

On the other hand, the decryption algorithm, ${\mathcal{D}}_{k,r,a,b}$, is illustrated in Figure 4. The decryption (ciphertext processing) is very similar to the encryption. They differ in the order in which the operations are applied, as shown in Algorithm 4. In this case, the ciphertext is also divided into r-bit blocks. As in the previous case, if the last block is incomplete, a pad is added to reach r-bits. Later, the decryption operation involves executing the XOR operation between the encrypted block, $C_i$, and the internal part of the state, $S_r$. The result will be the plaintext P. The value of the state register during the encryption process is recovered by entering the ciphertext C in the internal part of the state register $S_r$. Then, the permutation p is executed b times. The previous three steps are repeated with all the $C_i$ blocks, except for the last one. Using the XOR operation between the last ciphertext block ${\tilde{C}}_t$ and the internal part of the state register $S_r$, the last plaintext block, $P_t$, is calculated. Finally, in the internal part of the state register $S_r$, the result of the XOR operation between this part of the state, and the last block of the plain text $P_t$ (with its corresponding pad if necessary) is entered. This last status update is necessary to complete the finalization process in which the tag to be generated is verified or not.

Algorithm 4 Decryption (processing ciphertext)

Input: ciphertext $C\in {\{0,1\}}^{*}$ and internal state S  $C_1\cdots C_{t-1}{\tilde{C}}_t\leftarrow$r-bit blocks of C, $0\le |{\tilde{C}}_t|<r$  for  $i=1\cdots t-1$do     $P_i\leftarrow S_r\oplus C_i$     $S\leftarrow C_i\parallel S_c$     $S\leftarrow p^b\left(S\right)$  end for   ${\tilde{P}}_t\leftarrow {\lfloor S_r\rfloor }_{|{\tilde{C}}_t|}\oplus {\tilde{C}}_t$   $S_r\leftarrow S_r\oplus ({\tilde{P}}_t\parallel 1\parallel 0^{*})$ Output: plaintext $P\in {\{0,1\}}^{\left|C\right|}$ and updated state S

Two distinct use cases can be identified in the finalization process. If the purpose of the algorithm execution is to encrypt a message, the finalization process generates and transmits a MAC or a tag, T, which depends on the entire previous process (see Algorithm 5). If the purpose of the process is to verify the decryption, the finalization process will compare the tag generated by the decryption process with the tag that was previously generated in the encryption process (see Algorithm 6). For both cases, in the computation of the tag, the state S is updated by executing a times the permutation p to the result of the XOR operation between the state register, a concatenation of r zeros, the key K, and the remaining zeros required to complete the 320 bits of the state. Finally, the tag T is generated through the XOR operation between the r LSB of the S state and the r LSB of the K key.

Algorithm 5 Finalization process (encryption)

Input: key $K\in {\{0,1\}}^k,k\le 160$, and internal state S   $S\leftarrow p^a(S\oplus (0^r\parallel K\parallel 0^{c-k}\left)\right)$   $T\leftarrow {\lceil S\rceil }^{128}\oplus {\lceil K\rceil }^{128}$ Output: tag $T\in {\{0,1\}}^{128}$

Algorithm 6 Finalization process (verification of decryption)

Input: key $K\in {\{0,1\}}^k,k\le 160$, and internal state S   $S\leftarrow p^a(S\oplus (0^r\parallel K\parallel 0^{c-k}\left)\right)$   $T^{*}\leftarrow {\lceil S\rceil }^{128}\oplus {\lceil K\rceil }^{128}$  if$T=T^{*}$then     $F=P_1\parallel \dots \parallel P_{t-1}\parallel {\tilde{P}}_t$  else$F=\perp$  end if Output: F

3.3. Some Application Domains for Ascon in Arduino-Based Systems

Given its efficiency on constrained devices, Ascon has strong potential for adoption in real-world applications such as smart home automation, industrial IoT, automotive keyless entry systems, and wearable health devices. Since Arduino-based microcontrollers are widely used for prototyping and small-scale deployments in these domains, it is important to evaluate how Ascon performs under their typical hardware constraints.

Ascon has been designed for environments where computational resources are severely constrained. Due to its simplicity, efficiency, and minimal memory footprint, Ascon can be deployed on a wide range of microcontrollers, from low-end 8-bit architectures such as those found in Arduino boards, to more specialized 32-bit embedded processors used in automotive, industrial, and medical applications. Arduino microcontrollers, such as those presented in this study, are widely adopted in prototyping, academic research, and small-scale IoT applications. Their open hardware ecosystem, low cost, and broad community support make them ideal platforms for validating lightweight cryptographic algorithms under real-world constraints.

Recent hardware implementations demonstrate that Ascon performs efficiently even on low-power microcontrollers with limited RAM (random access memory) and CPU (central processing unit) cycles, maintaining real-time communication without introducing measurable latency or energy overhead [14,15]. This has enabled its integration into diverse application domains, including the following:

• Home automation and smart devices: In smart home applications, Arduino boards are commonly used to control lighting systems, electronic locks, motion detectors, and environmental sensors. These devices typically communicate over Wi-Fi, Bluetooth, or Zigbee protocols, making them susceptible to replay, spoofing, and man-in-the-middle attacks. Ascon’s lightweight authenticated encryption enables secure communication between nodes, especially in constrained devices with less than 32 KB of RAM [15].
• Smart agriculture and environmental monitoring: Low-power sensor nodes deployed in agricultural environments often rely on boards like Arduino MKR WAN 1310 with LoRa (long-range) connectivity to monitor soil moisture, temperature, or air quality. Because these sensors operate autonomously for long periods, data encryption must be both energy-efficient and robust. Ascon meets these requirements, offering authenticated encryption with a code footprint of less than 10 KB, and minimal CPU usage [16].
• Urban sensing and smart cities: Academic and experimental deployments in smart city infrastructures frequently use Arduino-based networks to monitor variables such as CO₂ levels, traffic density, and ambient noise. These applications require secure transmission of public data across distributed systems. Incorporating Ascon allows end-to-end encryption and data integrity checks, without impacting real-time data acquisition and transmission performance.

While Arduino platforms are sufficient for prototyping and low-volume applications, many industrial, automotive, and medical systems rely on certified microcontrollers with higher performance and robustness requirements. Nevertheless, the demonstrated efficiency of Ascon on constrained devices suggests it can be equally or even more effective in these professional-grade systems, while also contributing to reducing power consumption and production costs, particularly in battery-powered or mass-deployable solutions.

One promising area for such deployment is automotive keyless entry systems. These systems rely on low-frequency RF (radio frequency) transceivers embedded in key fobs and vehicle receivers to authenticate users. However, their vulnerability to relay and replay attacks has been widely documented. Microcontrollers such as the NXP KE15Z or TI CC2640R2F, typically used in these devices, are capable of integrating Ascon as a secure, lightweight alternative to AES, thereby enhancing resistance to cryptographic side-channel and signal-injection attacks [17,18].

In the field of wearable medical devices, data confidentiality and compliance with regulations such as HIPAA (Health Insurance Portability and Accountability Act) or GDPR (General Data Protection Regulation) are paramount. Devices such as ECG (ElectroCardioGram) monitors, smart patches, and glucose sensors transmit biometric data to mobile applications or cloud-based platforms. Ascon’s low memory requirements and efficient computation make it particularly suitable for ARM Cortex-M0/M4 microcontrollers commonly used in these applications, such as the Nordic nRF52832 [19].

Furthermore, industrial control systems (ICS) benefit from integrating Ascon into communication layers between sensors, actuators, and programmable logic controllers (PLCs). In modern factories and critical infrastructures, real-time control commands must be transmitted securely and efficiently. Microcontrollers like the STM32F3 or Microchip PIC32MX have the computational capacity to support Ascon while maintaining deterministic performance, ensuring both safety and security without impacting throughput [20].

4. Security Analysis

In this section, we will summarize the most relevant attacks against Ascon that have been published. These attacks can be divided into two groups: algebraic attacks and side-channel attacks.

4.1. Algebraic Attacks

4.1.1. Differential and Linear Cryptanalysis

As it is well known, differential cryptanalysis is the most commonly type of attack used to break block and stream ciphers, as well as hash functions. This cryptanalysis method consists of studying how certain changes in the input of an algorithm affect the output. That is, the goal is to find a collection of strategies to identify differences in the output through a network of input transformations in order to determine at which points the encryption algorithm exhibits non-random behavior.

Linear cryptanalysis, similarly to differential analysis, is a type of cryptanalysis based on finding close approximations to the action of an encryption algorithm. The most common algorithms to which this type of attack is applied are block ciphers.

The Ascon permutation is built upon two lightweight operations which, individually, do not possess properties that ensure strong resistance against differential or linear attacks. However, when combined, they effectively guarantee the Ascon security. To understand how this type of attack can be executed, it is necessary to review some concepts and definitions that can be extended in [21], such as a differential distribution table or linear approximation table.

For example, differential and linear cryptanalysis are very useful in distinguishing attacks, where an attempt is made to distinguish encrypted data from random data. Furthermore, an algorithm is considered more secure if an attacker cannot distinguish the cryptographic operations of the algorithm from that of a random oracle. Thus, if an attacker could find sufficient relationships between the inputs and outputs, he could use this knowledge to recover parts of the secret key used by the algorithm. A collection of such attacks on the Ascon permutation is compiled in the algorithm’s official submission, see [10].

In [22], the main attacks that have been carried out against Ascon, both in its block cipher and hash function aspects, are discussed. In this case, the most important recommendations point out that the same nonce should not be repeated for two encryptions under the same key.

When the same nonce is reused, the initial internal state of the cipher becomes fixed for every encryption under the same key. This breaks the assumption of input uniqueness required by Ascon’s security model and enables an attacker to treat the cipher as a deterministic Boolean function. In this scenario, algebraic techniques such as cube attacks become applicable, where the cipher is modeled as a multivariate polynomial over the finite field of 2 elements, ${\mathbb{F}}_2$. By evaluating the encryption function over a chosen set of plaintexts (called a cube) and computing the XOR sum of the corresponding outputs (cube-sum vector), the attacker can extract linear or low-degree relations involving internal state bits.

Mathematically, if the cipher behaved like a pseudorandom function, the output vector would appear statistically indistinguishable from random—its Hamming weight would follow a binomial distribution $B(64,0.5)$. However, experiments reported in [23] show that, under nonce reuse and reduced-round conditions, this vector becomes all-zero in approximately $25\%$ of random internal states. This low-probability event does not occur by chance; rather, it reveals specific internal state configurations (e.g., fixed values for the initial bits) that correlate with the algebraic structure of the cipher. In those cases, the attacker can deduce parts of the internal state with high confidence—empirically, with $100\%$ success in the experiments.

These patterns allow for an adaptive chosen-plaintext attack capable of recovering the full 256-bit capacity of Ascon’s internal state, with an online data and time complexity below $2^{40}$. Therefore, while this does not imply a general probabilistic weakness in the full-round Ascon design, it clearly demonstrates that nonce reuse severely compromises confidentiality by enabling probabilistically guided algebraic inference over internal secrets.

Also, the number of blocks of the plaintext and associated data should not be close to the limit protected by the encryption algorithm, which is bounded at $2^{64}$ blocks per key.

Recently, machine learning (ML) techniques have been used to develop differential distinguishers. In this way, in [24] (previously published in [24]), the construction of a differential distinguisher is presented with the objective of being used in the Ascon permutation. Authors show an accuracy of 99.4% for the 4-round distinguisher with $2^{18}$ data complexity.

4.1.2. Cube Attacks

The cube attack is a cryptanalytic technique applied to a variety of symmetric key cryptographic algorithms. The goal of this type of attack is to obtain a set of linear relations between secret bits, so that upon solving these, relations are revealed. These relations between secret bits are obtained by modifying the output bits for all possible inputs. An algorithm is vulnerable to these attacks if, after inputting a key and the associated data, an output bit can be represented as a low-degree polynomial over the finite field of two elements, ${\mathbb{F}}_2$.

Within the range of attacks on the algebraic features of Ascon, conditional cube attacks can be distinguished. In particular, in [25], an attack that recovers the complete state and secret key of Ascon-128a, using seven of the eight rounds of the Ascon permutation in the intermediate phase, is presented. This is the best known attack for this version of the algorithm. Chang et al. also presented a complete state and secret key-recovery attacks for the post-quantum security version Ascon-80pq and Ascon-128 using all six rounds of the permutation in the intermediate phase, i.e., the full number of rounds of the original design [25].

The success of this type of attack relies on the misuse of the nonce N, although Ascon designers claim that the AEAD versions provide a security level of 128 bits and 160 bits in the case of Ascon-80pq when different nonces are used for the same key K. According to the designers, this level of security also holds in a nonce-misuse scenario, as long as the repetition of the nonce is only a few times and the combination of the nonce N and the associated data A remains unique. This type of attack succeeds by exhaustively repeating the same nonce and eliminating or repeating the associated data, as well as violating other features that make the algorithm secure.

For the attack to succeed, it must be assumed that the associated datum A is empty. Moreover, it should be known that $S_0=S_0\left[0\right]\parallel S_0\left[1\right]\parallel S_0\left[2\right]\parallel S_0\left[3\right]\parallel S_0\left[4\right]$ is the input state to the Ascon permutation for the first block of plaintext in the encryption phase. Due to the rate $r=64$, the values of $S_0\left[0\right]$ can be known by choosing the first block of plaintext and thus obtaining the corresponding ciphertext block, while $S_0\left[1\right]\parallel S_0\left[2\right]\parallel S_0\left[3\right]\parallel S_0\left[4\right]$ will remain secret and only depends on the nonce N to change. By means of a family of patterns in which a series of variables and conditions to be fulfilled are defined, along with the requirements of the conditional cube attack and subsequent operations, the entire state $S_0$ is recovered, i.e., $S_0\left[0\right]\parallel S_0\left[1\right]\parallel S_0\left[2\right]\parallel S_0\left[3\right]\parallel S_0\left[4\right]$ for the six intermediate rounds of the Ascon-80pq permutation. With the recovered $S_0$ state and the previously used nonce, the 160-bit key is recovered. This attack and others shown in [25] currently represent the most effective methods in an Ascon nonce-misuse scenario. In any case, these attacks do not compromise the original Ascon security, as the attack would only succeed in a scenario where the algorithm is not implemented with the constraints and instructions that the designers presented in [10].

Moreover, in [26], the authors describe a security model of authenticity under the hypothesis of state recovery. Their analysis considers that the mode aims to guarantee security and authenticity against the key recovery attack even if an adversary can recover the inner state by a leakage, for example. In conclusion, Lefevre and Mennink proved that thanks to its unique key blinding technique, Ascon satisfies this security property.

4.2. Side-Channel Attacks

It is well known that any processor computing a cryptographic primitive is prone to information leaks. Side-channel attacks attempt to obtain information from the implementations performed on cryptographic devices. These attacks are responsible for exploiting such leaks and recovering secret information. They can be divided in time, electromagnetic fields, and power consumption attacks, which are the most common ones regarding Ascon.

Although Ascon is based on the MonkeyDuplex sponge, it has powerful initialization and termination phases. This means that trying to recover the state during an intermediate process between these two phases, or after termination, would not imply being able to recover the keys, in fact it would be a very complicated task. Therefore, power consumption attacks executed during the data processing phases only allow recovering the internal state. On the other hand, attacks performed during the finalization phase are hardly successful, since they have to consider not only many bits of the key, but also several unknown bits of the state that is not related with the final tag. Taking these factors into account, it is easy to deduce that the initialization phase is the easiest phase to find a successful attack to recover the key.

Power analysis attacks consist of the study and exploitation of information leakage by measuring the power consumption of a cryptographic function implemented in a device. There are two types of power attacks: simple power analysis (SPA) and differential power analysis (DPA). In SPA, the attacker needs only a minimum number of power traces to look for patterns that can be related to actions in the cryptographic operation using the key. On the other hand, in DPA, a deeper knowledge of the device and algorithm to be attacked is required, as well as a greater number of traces than in SPA, to model possible situations with certain inputs and power consumption and thus be able to recover the key or parts of it.

In [27], the resistance of Ascon to passive and active side-channel attacks is evaluated. To perform the experiments, the authors use a lightweight implementation on an Artix-7 FPGA (field programmable gate array). In the paper, two attacks are exposed, the first of which is a statistical ineffective fault analysis (SIFA) attack using voltage glitches on the supply pin of the FPGA chip. In this attack, $2^{80}$ correct tags are used as output of the algorithm under fault injection of the S-boxes and thus manage to recover two bits of the secret key. But the main attack of the paper and where the complete key is recovered is the power analysis attack with deep learning (DL) in the initialization phase. This attack is a side-channel attack with reinforcement learning (SCARL). One of the strengths of the attack is that the attacker does not need to have prior knowledge of the leakage model of the cryptographic operation. First, the long short-term memory (LSTM) autoencoder collects a large number of raw power measurements, recognizes the best way to model the data, and generates an intermediate representation of the data. In the next step, using the autoencoder, a representation of an estimated leakage model is created. Finally, using the previously estimated model and a clustering technique, the secret key can be recovered (also see [28]).

In [29] (this work has been also published as [30]), the authors studied the Ascon encryption by considering fault injection attacks, especially under the prism of differential fault analysis (DFA). By using this technique, they recover the complete key. This is performed in two different ways with two fault models. In the first one, by leveraging bit-flip faults, and in the second one by bit-set faults. Moreover, they analyze injecting multiple bit-flip faults at the input of the S-box, which suggests an alternative strategy for compromising the state space.

The main differential power attack against Ascon can be first found in [31] and in more detail in [32]. The experiment was performed by programming in VHDL (VHSIC (very high speed integrated circuit) and HDL (hardware description language)), which is a programming language used to model a digital system using a data flow, behavioral, and structural modeling style: this code has been run on a Sakura-G with a Spartan-6 FPGA.

As already mentioned, for this type of attack, the best option is to target the end of the first permutation round of the initialization phase. As we know, the Ascon state is 320 bits and is divided into five 64-bit words, $x_0,\cdots ,x_4$. When initializing the state, the S-box takes as input 5 bits and returns another 5 bits, and this operation is performed 64 times until the initial state is completely transformed. In this early phase of the algorithm, the 5 bits that the S-box will take first will be composed of $x_0$, corresponding to a constant bit of the initialization vector $IV$, $x_1$ and $x_2$ that will be constant bits belonging to the key, and $x_3$ and $x_4$, which are the bits that will vary according to the nonce set. Samwel and Daemen considered $x_0$ as the sensitive variable, and since its value is known before the first round of permutations, the Hamming distance model was used.

4.3. Side-Channel Attacks Against Arduino Devices

In this subsection, we present the main studies related to side-channel attacks that have been published against Arduino devices. It is noteworthy that most of them only implement the AES cryptosystem.

In [33], the authors implemented correlation power analysis (CPA) attacks using ATmega (ATmega 328 P - PU, Arduino Uno) cryptographic module for configuration and the oscilloscope to obtain the experimental result, and the MATLAB program (R2021b) for the verification process and design technology to analyze countermeasures.

Power analysis attacks against different Arduino boards were presented in [34], but only Speck and AES systems were implemented. Authors concluded that software countermeasures such as random instruction injection and randomly shuffling S-boxes are good enough for their simplicity and cost.

In [35], the authors presented two contributions. First, they show how a complete side-channel test bench can be built with affordable and mainstream components. For this purpose, Durvaux and Durvaux have taken advantage of classic use cases: an AES implementation running on an 8-bit ATmega328P embedded on an Arduino Uno and later on a 32-bit ATSAM3X8E (ARM Cortex-M3) embedded on an Arduino DUE.

Nakanose et al. studied CPA attacks in [36] and they found that light-weight cipher SPECK may not resist side-channel attacks because it requires too few resources for a successful attack. Furthermore, the authors investigated the minimum number of plaintexts needed for attacking it. As a result, it was found that 50 plaintexts are sufficient for a successful attack.

In [37], authors conducted the side-channel attack for the XOR in the final round of the SIMON cryptosystem. As a result, they could attack SIMON with little computational resources and time, which means that this cryptosystem can be weak against side-channel attacks. Furthermore, the authors checked the relationship between the Hamming weight of the round key and the ease of attacking. The authors confirmed that there was no relationship between them.

In [38], Maro et al. presented power analysis traces and practical segmentations of power consumption measurements charts for Russian encryption standard Kuznyechik cipher [39] on original and modified Arduino nano boards.

Finally, in [40], the authors evaluated the effectiveness of the countermeasure based on voltage modulation against CPA and DPA side-channel attacks. The variations in voltage introduce variations in the device current, making it more difficult for the attacker to find the secret key. They implemented the countermeasure on the Arduino platform and tested it for several different voltage sine frequencies. The results shown that the proposed countermeasure is extremely effective against cryptographic attacks.

4.4. Security Bound for Ascon

Until now, most security analysis bounds have treated Ascon as a variant of a duplex construction to establish security. A comprehensive study to establish a tight security bound on Ascon can be found in [41]. The approach of treating Ascon as any variant of a sponge construction is not the most accurate, since it benefits from double-key initialization and double-key finalization that make Ascon a much more robust algorithm than standard sponge constructions. In order to understand the security improvement offered by Ascon, we will now present the known bounds for the standard sponge constructions and the bounds available for Ascon in [41].

It is well known that sponge constructions (including keyed variants such as MonkeyDuplex) have $2^{c/2}$ security bits, where c is the capacity of the sponge. Moreover, a common security bound in the analysis of any duplex AEAD scheme is given by the expression $D·t/2^c$, where D is the data complexity, which is the total number of initializing and duplexing calls to the permutation, and t is the time complexity, which is the total number of calls to the permutation. A condition that is satisfied in most existing security analyses of Ascon and other sponge constructs is that $D·t\ll 2^c$, where in some cases, the D is replaced by $q_D$, which is the number of decryption queries performed by an attacker.

In [41], a strict safety limit is established, which depends on the key k, the capacity c, the state b and the tag $\tau$ sizes. The security bound is

$${\displaystyle \frac{t}{2^{min\{k,c\}}}}+{\displaystyle \frac{D}{2^{min\{\tau ,c\}}}}+{\displaystyle \frac{D·t}{2^b}}.$$

(8)

Comparing this bound with previous work, it is clear that Ascon exceeds the security level of generic duplex constraints. Finally, considering the requirements established by the NIST LwC competition, where $D⩽2^{53}$, $t⩽2^{112}$, $k⩾128$, and $t⩾64$ must be satisfied, the authors conclude that an adequate security level can be achieved in Ascon by defining the capacity as $c=128$ bits (for the b state of 320 bits) and the tag as $t=64$ bits. These changes would result in the rate r to be at least 192 bits, which would be an improvement in efficiency without compromising the security of the algorithm and the permutation.

In addition, it can be stated that the best key-recovery attacks are carried out with the AEAD variants of Ascon with an initialization of 7 rounds, out of the 12 established in [42], while one of the best attacks on the hash variants of Ascon is a pre-image attack that only considers 4 rounds [43]. The most sophisticated attacks of this type combine power analysis attacks with ML techniques (see [28,44]).

Degré et al. consider in [45] the mixed-integer linear programming (MILP) model studied in [43] and they reformulate the same problem in terms of the Boolean satisfiability (SAT), achieving a significant acceleration in time, reducing the memory complexity and removing the heuristic. In addition, in the same paper, the authors study lower bounds for the probability of the permutations of Ascon.

In [46], the authors present a comprehensive analysis of the security of Ascon when considering the reference and a protected implementation and implemented on a 32-bit microcontroller. Weissbart and Picek show their results using CPA and DL tools, giving a practical estimation of the effort required to recover the full key in the authenticated encryption process. According to the authors, an attacker can recover the full key from the reference implementation with 8000 traces and CPA or with 1000 traces and DL.

An ensemble of deep neural networks are used in [47] (and previously in [47]) to attack two different Ascon implementations. The authors employed five multilayer perceptrons or convolutional neural networks to find with, less than 3000 traces, the secret key for a protected implementation of Ascon. Moreover, for an unprotected implementation of Ascon, they identified the key with less than 100 traces.

In [48] (and previously in [48]), the authors extend the pre-image attack framework initially developed in [49] and later improved in [50] against Keccak. The extension proposed by Li et al. [48]. is performed against the hash functionality of Ascon, in fact, against the three-round and four-round Ascon-XOF. The extension is considered in two aspects: The first is a linearize-and-guess approach, which is obtained by studying the algebraic properties of the permutation of Ascon. Then, the authors obtain that the complexity of finding a pre-image for two rounds of Ascon-XOF can be reduced to $2^{27.56}$ guesses from $2^{39}$ guesses, with a 64-bit hash value. In the second aspect, the authors developed an automatic pre-image attack framework based on satisfiability problems using the linearize-and-guess approach. This approach is efficient in finding the optimal structures in an exhaustive way.

Another pre-image attack against two rounds of Ascon-XOF-64 was presented in [51]. This attack has a complexity of $2^{32}$ by means of a guessing strategy. To do this, authors considered a MILP model and then they extend their attack to three rounds with a time complexity of $2^{53}$ when the $IV$ is 0 and of $2^{51}$ for the real $IV$. In addition, Fu et al. [51]. study the behavior of Ascon-HASH against collision attacks. In this case, they consider a linearization of the inverse of S-boxes and propose a collision attack on three rounds against this functionality of Ascon. Moreover, by using this linearization and some two-round connectors, the authors extend this collision attack to 4 and 5 rounds of Ascon-HASH with complexities of $2^{21}$ and $2^{41}$, respectively.

In [52] (and later in [52]), the authors also present more attacks against Ascon-XOF; in particular, they attack the two-round Ascon-XOF in a more efficient way than in [10]. In fact, they consider weakened versions of Ascon-XOF for which all the IV values are set to 0 and the round constants are not considered. These attacks do not suppose a real vulnerability in relation to the security of the full Ascon-XOF.

A systematic study about the security of the different modes of Ascon as authenticated encryption was presented in [53]. In this work, Lefevre and Mennink consider six security models in multi-user setting: (1) nonce-respecting [41], (2) nonce-misuse resistance [54], (3) nonce-misuse resilience [55], (4) leakage resilience [55], (5) state-recovery [26], and (6) release of unverified plaintext analysis [56].

Thus, it can be stated that none of the mentioned attacks violate the security requirements established by NIST; therefore, the Ascon family presents a high degree of security. NIST list the security properties of Ascon in (Section 4.4 in [3]) and they include single-key and multi-key settings, nonce-respecting and nonce-misuse settings, and with or without the truncation option. For example, in the single-key setting, the attacker tries to recover a specific key that is shared by one or several users; whereas in the multi-key setting with n keys, the attacker aims to obtain any of such keys used by the users.

5. Performance Analysis of the Ascon Implementation

Once we presented a detailed description of the Ascon suite in relation to its authenticated encryption and hashing functionalities (Section 2), as well as its main features as a symmetric cryptosystem that make it especially useful in IoT environments (Section 3), and some aspects related to its security, in particular, the assertion that the considered encryption versions can be considered secure (Section 4). In this section, we will present a performance study of the Ascon reference versions in C obtained from the official Github repository [57].

5.1. Selected Arduino Devices

Four different types of Arduino devices were used in this performance comparison: Arduino DUE, Arduino Mega2560, Arduino Nano Every, and Arduino Nano ESP32 (Arduino S.r.l., Somerville, MA, USA, https://www.arduino.cc/en/software/, accessed on 18 February 2025). Each Arduino device has the following characteristics:

• Arduino DUE (Arduino S.r.l., Somerville, MA, USA) is based on a powerful 32-bit SAM3X8E ARM Cortex-M3 ARM microcontroller, with 96 KB of SRAM memory (divided into two banks, one of 64 KB and the other one of 32 KB), and with a 512 KB flash memory for the user application, and a clock speed of 84 MHz.
• Arduino Mega2560 (Arduino S.r.l., Somerville, MA, USA) (less powerful than the previous one) is a board based on the 8-bit AVR CPU core ATmega2560 microcontroller, 256 KB flash memory, of which 8 KB are used by the bootloader, and a clock speed of 16 MHz.
• Arduino Nano Every (Arduino S.r.l., Somerville, MA, USA) is based on an 8-bit AVR CPU core ATMega4809 microcontroller with hardware multiplier, 48 KB flash memory, and a higher clock speed of 20 MHz.
• Arduino Nano ESP32 (Arduino S.r.l., Somerville, MA, USA) has the u-Blox NORA-W106-10B processor, which is based on SP32-S3 RISC-V microcontroller of dual core Xtensa LX7. Note that we have used only one core. It can reach speeds of up to 240 MHz. Its memory has 512 KB SRAM, 384 KB ROM, 8 MB PSRAM, and 16 MB flash.

The mentioned Arduino devices were selected because they are the most used and sold devices. In addition, this selection of devices will allow us to compare two 8-bit and two 32-bit devices with each other and also make a comparison between the 8-bit and 32-bit devices.

All Arduino devices used in this study were programmed in the Arduino IDE (Integrated Development Environment), version 2.3.2 (Arduino S.r.l., Somerville, MA, USA, https://www.arduino.cc/en/software/ (accessed on 18 February 2025), which was installed on a 64-bit PC with 32 GB of RAM and Windows 11 Pro operating system. In order to be tested, the software runs directly on each Arduino device and once the time, cycles, etc. have been calculated within each device, the output data are sent through its serial port and read in the IDE environment on the PC.

In addition, in order to interfere as little as possible with the reference implementations that other users can prefer to use, we have tried to modify the reference versions of the Ascon family as little as possible when implementing them in the different devices. In this way, we modified the generation of random keys and random data for Ascon, for which we have used the rand() function implemented by the Arduinos. In this case, Ascon needs to generate several data: message, key, nonce, etc. The function used is presented as Algorithm 7.

Algorithm 7 Random data generation for Ascon

void RandGen(){    for (i = 0; i < C RYPTO_NPUBBYTES; i++) n[i] = rand()%0xFF;    for (i = 0; i < CRYPTO_KEYBYTES;i++) k[i]=rand()%0xFF;    for (i = 0; i < 16; i++)    {       a[i] = r and()%0xFF;       m[i] = r and()%0xFF;    } }

5.2. Measures in the Encryption/Decryption Operations with Ascon

A series of comparison tables are shown below. They contain different results for the three analyzed versions of Ascon: Ascon-128, Ascon-128a, and Ascon-80pq (see Section 2.1). The implementations we have considered are the reference implementations. The tables collect data related to processor clock cycles. As it is well known, clock cycles are a metric used to evaluate the performance of a cryptographic algorithm in terms of computational efficiency.

For all cases, we considered the following parameters for Ascon-128 and Ascon-128a: 16-bytes for the master key and the nonce, the block size is 16 bytes, and 8 bytes are used for AEAD—whereas for Ascon-80pq, we considered 20-bytes for the master key, 16-bytes for the nonce, 16-bytes for the block size, and 8-bytes for the authenticated data (see Table 1).

Table 5. Number of cycles (Cyc.) and encryptions (Enc.) in the encryption process in Arduino DUE for the three versions of Ascon.

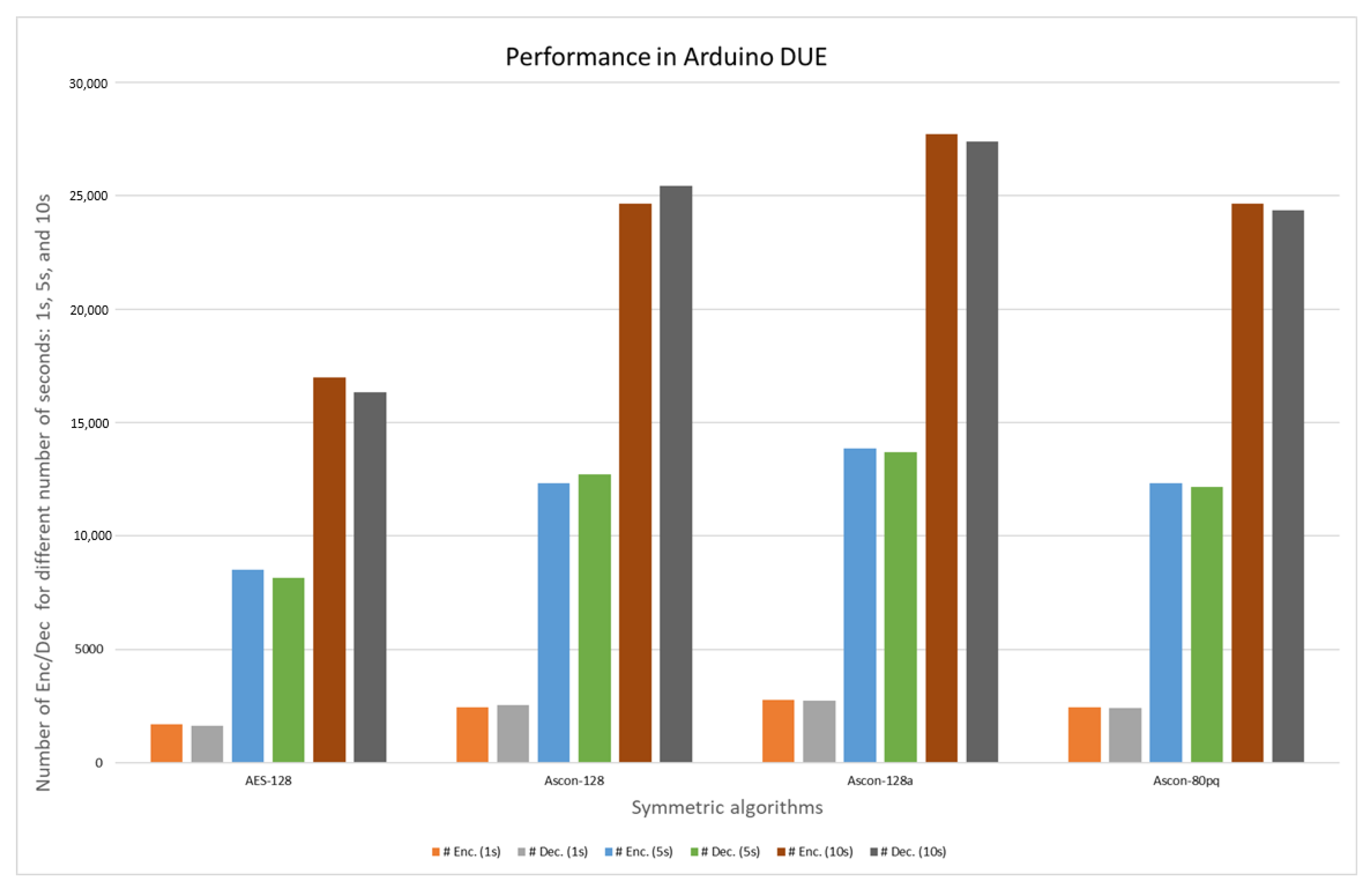
Variant	Number of Cycles and Encryptions in the Encryption Process. Arduino DUE
	# Cyc. (1 s)	# Enc. (1 s)	# Cyc. (5 s)	# Enc. (5 s)	# Cyc. (10 s)	# Enc. (10 s)
Ascon-128	84,025,452	2464	420,008,820	12,320	840,003,108	24,640
Average	33,015	—	33,011	—	33,011	—
Ascon-128a	84,012,768	2772	420,010,248	13,860	840,007,812	27,720
Average	30,661	—	30,664	—	30,663	—
Ascon-80pq	84,015,876	2464	420,022,512	12,320	840,030,492	24,640
Average	34,097	—	34,092	—	34,092	—

and

Table 6. Number of cycles (Cyc.) and decryptions (Dec.) in the decryption operation in Arduino DUE for the three versions of Ascon.

Variant	Number of Cycles and Decryptions in the Decryption Process. Arduino DUE
	# Cyc. (1 s)	# Dec. (1 s)	# Cyc. (5 s)	# Dec. (5 s)	# Cyc. (10 s)	# Dec. (10 s)
Ascon-128	84,013,860	2545	420,003,696	12,723	840,006,636	25,446
Average	33,011	—	33,011	—	33,011	—
Ascon-128a	84,018,480	2740	420,000,840	13,697	840,000,924	27,394
Average	30,663	—	30,663	—	30,663	—
Ascon-80pq	84,028,644	2436	420,031,332	12,178	840,016,884	24,355
Average	34,494	—	34,490	—	34,490	—

show the number of cycles and encryption and decryption operations in some specific periods of time (1 s, 5 s, and 10 s) for both processes of encryption and decryption, for each version of Ascon on an Arduino DUE.

It can be seen that the number of cycles and operations for the encryption and decryption processes in each time period for the three versions of Ascon are very similar. In fact, the average of the number of cycles for Ascon-128 in all cases, whether in encryption or decryption and regardless of the time period, is 33,011, except in the case of encryption with Ascon-128, in which it is 33,015. For Ascon-128a, these values are also very similar, and the averages vary between 30,661 and 30,663. The same occurs for Ascon-80pq, where the averages of cycles are between 34,490 and 34,497 for any period of time.

Comparing the different versions of Ascon among them for this device, it is clear that the number of cycles, on average, for Ascon-128a, are lower than for the other two Ascon versions, whereas the values, on average, for Ascon-80pq are the biggest for the three periods of time considered.

On the other hand,

Table 7. Number of cycles (Cyc.) and encryptions (Enc.) in the encryption operation in Arduino Mega2560 for the three versions of Ascon.

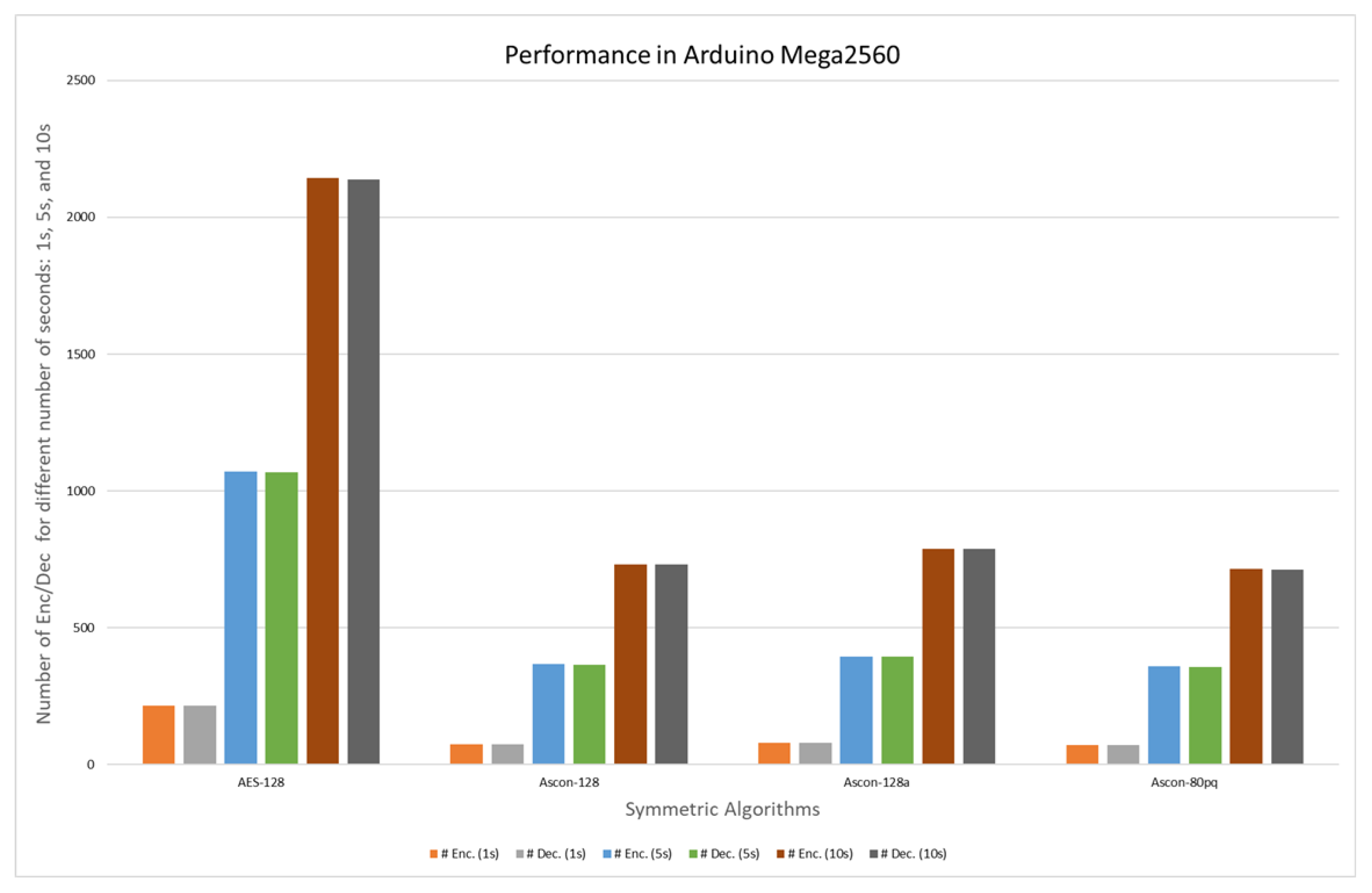
Variant	Number of Cycles and Encryptions in the Encryption Process. Arduino Mega2560
	# Cyc. (1 s)	# Enc. (1 s)	# Cyc. (5 s)	# Enc. (5 s)	# Cyc. (10 s)	# Enc. (10 s)
Ascon-128	16,185,472	74	80,021,696	366	160,035,008	732
Average	221,718	—	219,237	—	219,226	—
Ascon-128a	16,033,152	79	80,134,848	395	160,057,088	789
Average	202,951	—	203,387	—	203,376	—
Ascon-80pq	16,128,000	72	80,161,024	358	160,088,832	715
Average	224,000	—	223,913	—	223,900	—

and

Table 8. Number of cycles (Cyc.) and decryptions (Dec.) in the decryption operation in Arduino Mega2560 for the three versions of Ascon.

Variant	Number of Cycles and Decryptions in the Decryption Process. Arduino Mega2560
	# Cyc. (1 s)	# Dec. (1 s)	# Cyc. (5 s)	# Dec. (5 s)	# Cyc. (10 s)	# Dec. (10 s)
Ascon-128	16,010,816	73	80,053,568	365	160,108,736	730
Average	219,326	—	219,324	—	219,327	—
Ascon-128a	16,075,200	79	80,173,568	394	160,145,664	787
Average	203,483	—	203,486	—	203,488	—
Ascon-80pq	16,195,008	72	80,027,072	356	160,043,072	712
Average	224,930	—	224,795	—	224,779	—

present the number of cycles and encryption and decryption operations in the same considered periods of time for the same processes, for the three versions of Ascon on an Arduino Mega2560. As in the case of Arduino DUE, the number of cycles and the number of encryption and decryption operations in each time period for each process and for the three versions of Ascon are very similar. For this device, the lowest number of cycles, on average, are also obtained for Ascon-128a version for both processes. On its part, the greatest number of cycles, on average, is for Ascon-80pq, again.

Table 9. Number of cycles (Cyc.) and encryptions (Enc.) in the encryption operation in Arduino Nano Every for the three versions of Ascon.

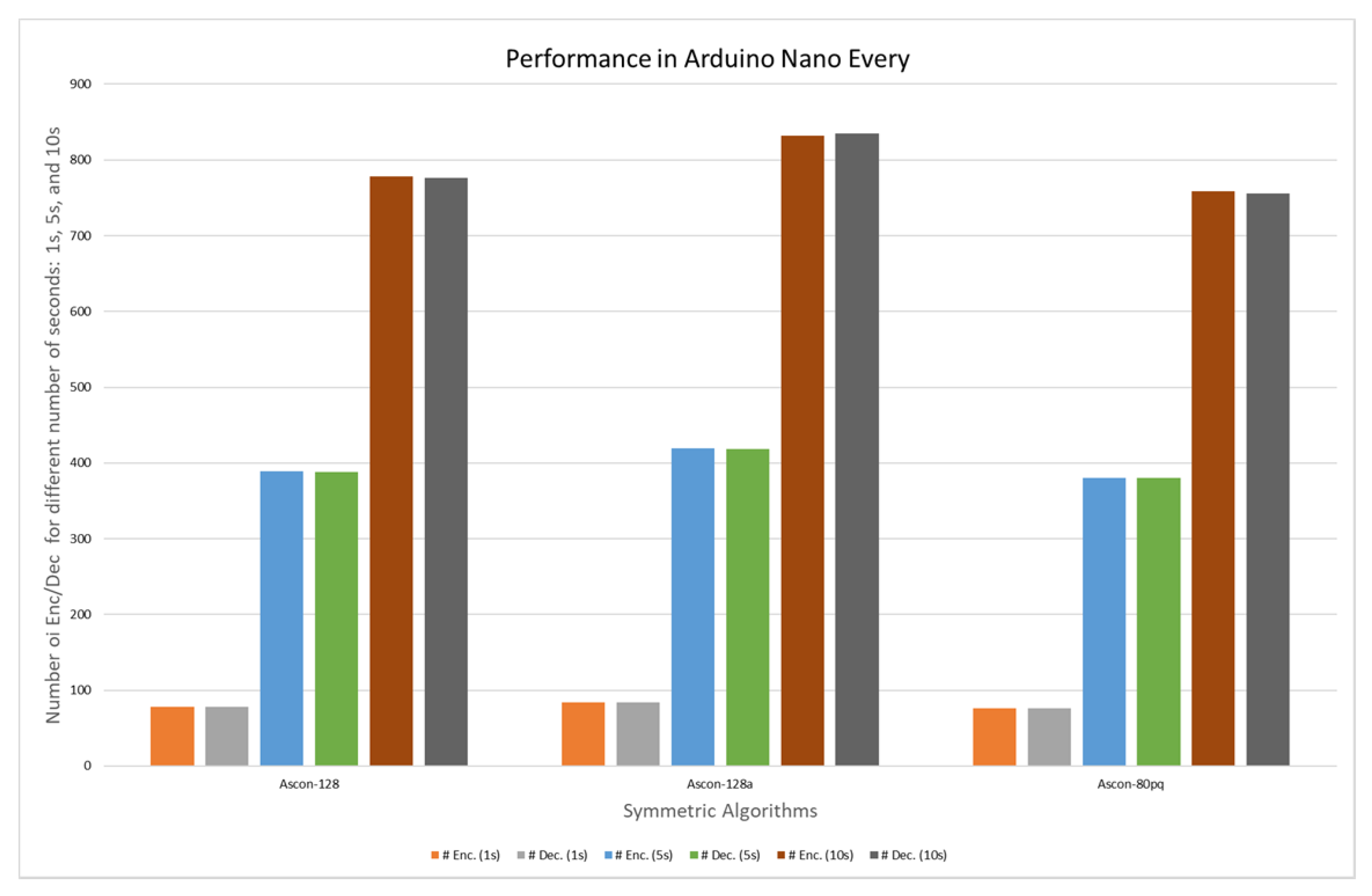
Variant	Number of Cycles and Encryptions in the Encryption Process. Arduino Nano Every
	# Cyc. (1 s)	# Enc. (1 s)	# Cyc. (5 s)	# Enc. (5 s)	# Cyc. (10 s)	# Enc. (10 s)
Ascon-128	16,053,696	78	80,037,120	389	160,065,600	778
Average	205,816	—	206,281	—	206,270	—
Ascon-128a	16,054,656	84	80,055,168	419	160,102,592	832
Average	191,126	—	191,519	—	191,739	—
Ascon-80pq	16,029,760	76	80,122,624	380	160,025,984	759
Average	210,917	—	210,849	—	210,837	—

and

Table 10. Number of cycles (Cyc.) and decryptions (Dec.) in the decryption operation in Arduino Nano Every for the three versions of Ascon.

Variant	Number of Cycles and Decryptions in the Decryption Process. Arduino Nano Every
	# Cyc. (1 s)	# Dec. (1 s)	# Cyc. (5 s)	# Dec. (5 s)	# Cyc. (10 s)	# Dec. (10 s)
Ascon-128	16,097,920	78	80,077,056	388	160,156,672	776
Average	206,383	—	206,384	—	206,387	—
Ascon-128a	16,098,240	84	80,110,912	418	160,030,656	835
Average	191,645	—	191,652	—	191,653	—
Ascon-80pq	16,097,664	76	80,022,400	378	160,034,944	756
Average	211,811	—	211,699	—	211,686	—

show the results obtained in relation to the number of cycles and the encryption and decryption operations for the same previous periods of time with the same processes (encryption and decryption) for the three considered versions of Ascon on an Arduino Nano Every. In this case, again the lowest number of cycles, on average, are also obtained for the Ascon-128a version for both processes, whereas, the biggest number of cycles, on average, corresponds to Ascon-80pq.

Finally,

Table 11. Number of cycles (Cyc.) and encryptions (Enc.) in the encryption operation in Arduino Nano ESP32 for the three versions of Ascon.

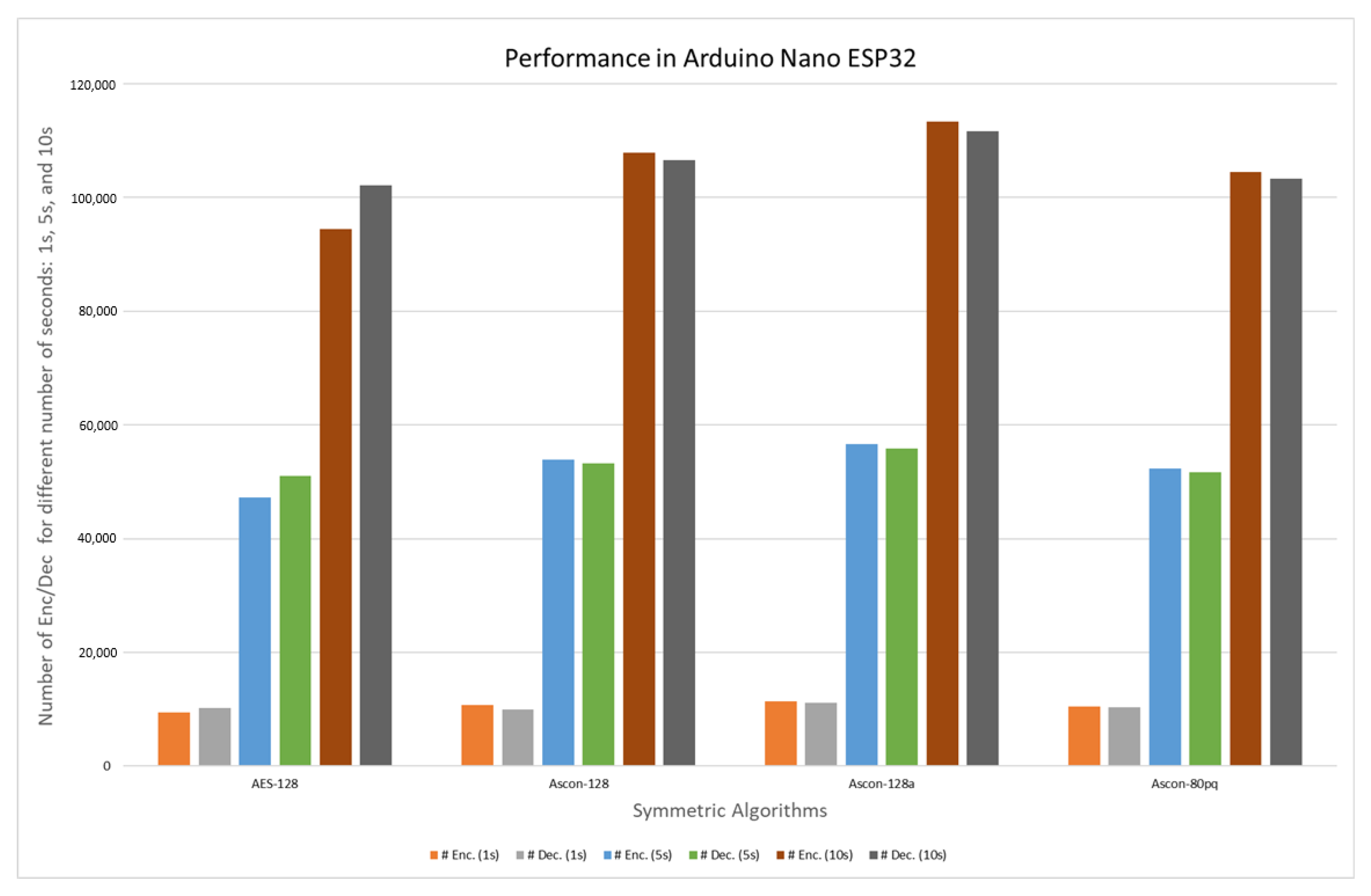
Variant	Number of Cycles and Encryptions in the Encryption Process. Arduino Nano ESP32
	# Cyc. (1 s)	# Enc. (1 s)	# Cyc. (5 s)	# Enc. (5 s)	# Cyc. (10 s)	# Enc. (10 s)
Ascon-128	240,016,080	10,785	1,200,012,240	53,925	2,400,014,160	107,857
Average	22,524	—	22,523	—	22,523	—
Ascon-128a	240,003,120	11,328	1,200,005,760	56,643	2,400,004,800	113,287
Average	21,486	—	21,487	—	21,487	—
Ascon-80pq	240,021,360	10,453	1,200,013,680	52,264	2,400,010,800	104,528
Average	22,961	—	22,960	—	22,960	—

and

Table 12. Number of cycles (Cyc.) and decryptions (Dec.) in the decryption operation in Arduino Nano ESP32 for the three versions of Ascon.

Variant	Number of Cycles and Decryptions in the Decryption Process. Arduino Nano ESP32
	# Cyc. (1 s)	# Dec. (1 s)	# Cyc. (5 s)	# Dec. (5 s)	# Cyc. (10 s)	# Dec. (10 s)
Ascon-128	240,018,720	10,656	1,200,006,960	53,279	2,400,009,600	106,558
Average	2,252,410,656	—	22,523	—	22,523	—
Ascon-128a	240,021,120	11,170	1,200,019,920	55,846	2,400,018,720	111,691
Average	21,488	—	21,488	—	21,488	—
Ascon-80pq	240,003,840	10,328	1,200,008,880	51,644	2,400,016,080	103,289
Average	23,238	—	23,236	—	23,235	—

present the values obtained for the number of cycles and the encryption and decryption operations for the considered periods of time with the same processes (encryption and decryption). We have considered, as in the previous cases, the three versions of Ascon on an Arduino Nano ESP32. Again, the lowest number of cycles, on average, was obtained for Ascon-128a version for both processes—whereas the biggest number of cycles, on average, corresponds to Ascon-80pq. For this Arduino device, one core has been used.

In summary, it can be stated that for the four Arduino devices used and for the three Ascon versions, the number of cycles and the number of encryption and decryption operations for the encryption and decryption processes are similar for each period of time considered. Moreover, for all Arduino devices, the Ascon-128a version presents the lowest values in relation to the number of cycles, on average, and the Ascon-80pq has the biggest values.

Considering Table 7, Table 8, Table 9 and Table 10, it can be seen that the number of cycles and the number of encryption and decryption operations in each variant of Ascon are very similar for both Arduino Mega2560 and Arduino Nano Every. This is because they are composed by the ATmega2560 and ATmega4809 microcontrollers, respectively. Both are 8-bit microcontrollers, and their clock speed is 16 MHz for Arduino Mega2560 and 48 MHz for Arduino Nano Every. In addition, the first one has 256 KB of flash memory, whereas the second one has 48 KB. For all these reasons, Arduino Nano Every needs slightly fewer clock cycles, on average, to perform the same operations than Arduino Mega2560.

In our work, we wish to compare the computing speed of Ascon and AES on different low-cost IoT boards without the help of the possible implementation of cryptographic chips within the processor. For this reason, we do not analyze how much better or worse an 8-bit or 32-bit processor is.

In any case, unlike the 8-bit devices, the two 32-bit Arduinos chosen show, as expected, a much higher average clock cycle rate and a much lower number of encryption and decryption operations (see Table 5, Table 6, Table 11 and Table 12). The main reason for these results is that these two devices have more powerful processors and larger amounts of memory. Furthermore, when comparing the two 32-bit devices, it can be stated that, for both encryption (Table 5 and Table 11) and decryption (Table 6 and Table 12) operations, the number of clock cycles of the Arduino Nano ESP32 is, on average, slightly lower than that of the Arduino DUE; while the number of encryptions and decryptions of the former is about four times higher than for the latter. In summary, we can say that, among the four devices used, the Arduino Nano ESP32 is the one that performs the highest number of encryption and decryption operations per second.

Note that the third columns in Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11 and Table 12 show the number of encryption and decryption operations that each one of the four devices considered is capable of executing in one second. These values provide information on the time complexity of all devices. In fact, the order of the devices in relation to their efficiency, from best to worst, is the following: Arduino Nano ESP32, Aduino DUE, Arduino Nano Every, and Aruino Mega2560, as shown in

Table 13. Averages for the number of encryption and decryption operations in one second for all versions of Ascon family in the Arduino devices.

Name	Nano ESP32		DUE		Nano Every		Mega250
	Enc.	Dec.	Enc.	Dec.	Enc.	Dec.	Enc.	Dec.
Average	10,855.3	10,718	2566.6	2573.6	79.3	79.3	75	74.6

.

In addition, to make a comparison between the number of cycles and the number of encryption and decryption operations for the encryption and decryption processes, respectively, for the Arduino devices and the PC used with Linux,

Table 14. Number of cycles (Cyc.) and encryptions (Enc.) in the encryption operation in a PC with Linux for the three versions of Ascon.

Variant	Number of Cycles and Encryptions in the Encryption Process. Linux PC
	# Cyc. (1 s)	# Enc. (1 s)	# Cyc. (5 s)	# Enc. (5 s)	# Cyc. (10 s)	# Enc. (10 s)
Ascon-128	3,591,863,479	291,229	17,958,761,656	1,472,122	35,918,379,472	2,957,498
Average	12,333	—	12,199	—	12,144	—
Ascon-128a	3,591,926,172	314,703	17,958,959,274	1,566,612	35,917,241,994	3,144,722
Average	11,413	—	11,463	—	11,421	—
Ascon-80pq	3,591,780,396	287,878	17,959,007,943	1,441,062	35,924,275,362	2,637,573
Average	12,476	—	12,462	—	13,620	—

and

Table 15. Number of cycles (Cyc.) and decryptions (Dec.) in the decryption operation in a PC with Linux for the three versions of Ascon.

Variant	Number of Cycles and Decryptions in the Decryption Process. Linux PC
	# Cyc. (1 s)	# Dec. (1 s)	# Cyc. (5 s)	# Dec. (5 s)	# Cyc. (10 s)	# Dec. (10 s)
Ascon-128	3,591,701,259	291,683	17,959,028,616	1,452,898	35,918,447,850	2,921,770
Average	12,332	—	12,199	—	12,144	—
Ascon-128a	3,597,313,614	312,045	17,958,729,660	1,552,602	35,917,223,979	3,103,935
Average	11,430	—	11,463	—	11,421	—
Ascon-80pq	3,591,724,317	285,235	17,958,627,285	1,432,774	35,918,518,506	2,625,828
Average	12,476	—	12,462	—	13,618	—

show the same values as in the previous tables but for the Linux case.

As expected, the number of encryptions and decryptions per second on a PC like the one we used is much higher than on the most efficient Arduino under consideration (Nano ESP32). In fact, it can be said that this number varies between 27 and 28 times more.

5.3. Measures in the Encryption/Decryption Operations with AES

To test the speed of Ascon, the Advanced Encryption Standard cryptographic algorithm [58], with a 128-bit key (AES-128), is introduced in the comparison as this is frequently used in LwC to secure constrained environments. We used the AES implementation that is available in the Github repository [59]. This is a standard implementation of this algorithm, and, moreover, we have chosen this tiny-AES version because it is a version that takes up very little memory, it has no countermeasures, and when encrypting and decrypting a single block, it does not have the ECB operating mode implemented.

We are aware that Ascon and AES are not comparable systems since the properties and characteristics of each are different. However, we include a comparison between them because it can allow the reader to obtain an idea of the efficiency and requirements associated with the implementations of each. This comparison is for information purposes only.

As in the case of the implementation of Ascon in the four Arduino devices, the generation of random keys and random data for AES has been done using the rand() function implemented by the Arduinos. This fact does not interfere with or deteriorate the data obtained since this is done with the same function for all versions of Ascon family and AES. In particular, in the case of AES, the complete function to generate keys and random data is simper than in the case of Ascon and it is shown as Algorithm 8.

Algorithm 8 Random keys and random data for AES.

void RandGen(){    for(i = 0; i < 16; i++){       plain[i] = rand()%0xFF;       key[i] = rand()%0xFF;    } }

Table 16. Number of cycles (Cyc.) and encryptions (Enc.) in the AES-128 encryption operation in Arduino devices.

AES-128	Number of Cycles and Encryptions in the Encryption Process. Arduino Devices
	# Cyc. (1 s)	# Enc. (1 s)	# Cyc. (5 s)	# Enc. (5 s)	# Cyc. (10 s)	# Enc. (10 s)
DUE	84,028,476	1701	420,004,872	8503	840,000,420	17,006
Average	51,393	–	51,401	–	51,404	–
Mega2560	16,064,384	215	80,065,216	1072	160,047,360	2143
Average	75,067	–	74,897	–	74,858	–
Nano ESP 32	240,010,320	9442	1,200,001,440	47,211	2,400,015,360	94,423
Average	23,507	–	23,507	–	23,507	–

and

Table 17. Number of cycles (Cyc.) and decryptions (Dec.) in the AES-128 decryption operation in Arduino devices.

AES-128	Number of Cycles and Decryptions in the Decryption Process. Arduino Devices
	# Cyc. (1 s)	# Dec. (1 s)	# Cyc. (5 s)	# Dec. (5 s)	# Cyc. (10 s)	# Dec. (10 s)
DUE	84,049,140	1635	420,041,244	8171	840,027,552	16,341
Average	51,406	–	51,406	–	51,406	–
Mega2560	16,016,320	214	80,008,000	1069	160,014,912	2138
Average	74,842	–	74,843	–	74,843	–
Nano ESP 32	240,015,840	10,210	1,200,011,280	51,047	2,400,021,360	102,094
Average	23,507	–	23,507	–	23,507	–

show the number of cycles and the number of encryption and decryption operations for AES-128 considering the encryption and decryption processes, respectively, for three Arduino devices: Arduino DUE, Arduino Mega2560, and Arduino Nano ESP32. Here, it is important to emphasize that Arduino Nano Every is not able to support the same AES-128 implementation because it is not able to execute the algorithm due to its memory limitation.

On the other hand, the number of encryptions and decryptions of the Arduino Nano ESP32 for AES-128 is considerably higher than that of the other two devices. In fact, this number is between 43 and 48 times higher than that of the Arduino Mega2560 and between 5 and 7 times higher than that of the Arduino DUE.

To make a comparison related to the space storage and dynamic memory, we present the results obtained for this item in

Table 18. Space storage (Stor.) and dynamic memory (Dyn.) (in bytes) for the Arduino devices.

Algorithm	DUE		Mega2560		Nano Every		Nano ESP32
	Stor.	Dyn.	Stor.	Dyn.	Stor.	Dyn.	Stor.	Dyn.
Ascon-128	14,708	—	11,830	343	13,476	343	290,553	30,736
Ascon-128a	15,300	—	12,990	752	14,641	343	291,289	30,736
Ascon-80pq	14,980	—	12,854	694	14,508	351	297,329	31,112
AES-128	21,200	—	11,478	4922	12,826	265	293,841	30,656

. In this table, we show the measures we obtained for space storage and the dynamic memory used, in bytes, required for each device and for each algorithm, i.e., the number of bytes that each Arduino device uses to store the compiled algorithm (Stor.), and the number of bytes that each algorithm requires to be executed in each device (Dyn.)

As can be seen in Table 18, Arduino Nano ESP32 is the device that uses its greater storage capacity and dynamic memory to achieve the best results in terms of the number of encryptions and decryptions operations in the same time as the other devices. The values for the other three Arduinos are very similar. Note that Arduino DUE does not provide the dynamic memory used.

5.4. Analysis of the Results

Once we have seen the clock cycle data, we will proceed to a comparative analysis of the algorithm’s performance in terms of speed. To do this, we consider the number of encryption and decryption operations shown in Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11 and Table 12, Table 16 and Table 17. Again, we will compare the performance of each Ascon variant in each of the different Arduino devices.

The performance of the three versions of Ascon (see Table 5 and Table 6) together with a standard implementation of AES-128 (see Table 16 and Table 17) on the Arduino DUE is shown in Figure 5. Clearly, all three Ascon versions perform better than AES-128 on the Arduino DUE (the second most powerful board of the four tested), with the Ascon-128a being the fastest version. This is due to the optimization of this feature in its design.

A similar graph is shown comparing the speed performance on the Arduino Mega2560 (see Figure 6). In this case, we have used the values for encryption and decryption operations shown in Table 7, Table 8, Table 16 and Table 17.

It is important to note that AES-128 is more efficient than the three versions of Ascon on the Arduino Mega2560. This may be due to the fact that AES implementations have been developed and optimized over many years. Thus, the AES version is probably designed to perform well on a device with the characteristics of the Arduino Mega2560. Even so, Ascon’s performance on a device such as the Arduino Mega2560 is still excellent, since the post-quantum security version, Ascon-80pq, is capable of performing encryption in as little as 0.013 s.

Figure 7 shows the corresponding comparison about the speed performance on the Arduino Nano Every considering the values for encryption and decryption operations presented in Table 9, Table 10, Table 16, and Table 17.

We have mentioned that Arduino Nano Every is not able to support the considered AES-128 implementation. However, this fact does not affect its behavior in relation to the three Ascon versions, for which excellent results are observed for the performance of a cryptographic algorithm on such a limited device.

As can be seen in Figure 7, the three versions of Ascon have a very similar performance to that offered by the Arduino Mega2560, slightly exceeding it. It is important to see how well Ascon performs on a device as small and limited as the Arduino Nano Every. These data are a clear example that Ascon can be easily implemented in a wide range of IoT devices, thus securing the data they handle.

Finally, Figure 8 shows a comparison of the speed performance on the Arduino Nano ESP32. For this device, we have to consider the values for encryption and decryption operations shown in Table 11, Table 12, Table 16, and Table 17. Here, we can see that the three versions of Ascon and AES-128 present similar performances for Arduino Nano ESP32, although the performance for AES-128 is slightly lower than for the three versions of Ascon.

The collected performance metrics reveal important practical insights into the deployment of Ascon in resource-constrained environments, particularly within the context of embedded and IoT systems. The consistent observation that Ascon-128a outperforms the other variants in terms of cycle efficiency across all tested platforms suggests that it may be the most suitable option when execution speed and low power consumption are critical. This makes Ascon-128a a compelling candidate for devices operating on limited battery life, such as remote sensors or wearable technology, where optimizing computational overhead is essential for extending operational longevity.

In contrast, although Ascon-80pq offers higher theoretical guarantees against quantum adversaries, due to its higher safety margin, it has significantly higher cycle counts and higher computational demands. This overhead may restrict its practicality on ultra constrained 8-bit microcontrollers like the Arduino Mega2560 or Nano Every, where CPU speed and memory availability are inherently limited. Nonetheless, its deployment may still be justified in scenarios where post-quantum resilience is a critical requirement, such as secure firmware updates or long-lifecycle industrial systems.

Furthermore, the throughput gains observed on 32-bit platforms, particularly on the Arduino Nano ESP32, highlight the ability of Ascon to scale effectively with improvements in hardware capabilities. With over 10,000 operations per second and efficient memory utilization, the ESP32 results demonstrate that Ascon can support real-time or high frequency cryptographic tasks when deployed on more capable devices. On 8-bit platforms, while the performance is understandably more limited, encryption still works within acceptable flash and RAM constraints, validating its usability even in the most limited environments.

These findings underscore the versatility and scalability of the Ascon family. They show that, by carefully selecting the variant and hardware platform, developers can strike an effective balance between security requirements, computational efficiency, and system constraints. This flexibility makes Ascon a strong candidate for a wide range of embedded applications, from basic authentication on low-power nodes to high-performance encryption on more powerful IoT gateways.

Moreover, to assess the efficiency of the Ascon cipher on Arduino-based embedded platforms, it is essential to compare its performance with previous implementations targeting more powerful microcontrollers or specialized cryptographic hardware.

Previous studies have demonstrated that Ascon performs efficiently on 32-bit architectures such as ARM Cortex-M processors. For instance, in the reference implementation presented at the NIST Lightweight Cryptography Workshop, Ascon-128 was installed on a 100 MHz Cortex-M4, with an approximate throughput of $17.5$ kbps, which translates to around 137 encryption operations per second with a code size of $9.6$ KB and RAM usage less than 2 KB [15].

In contrast, the experimental results obtained from four different Arduino boards, Mega2560, Nano Every, DUE, and Nano ESP32, demonstrate that Ascon executes efficiently across a range of architectures, despite their constrained resources. On 8-bit AVR microcontrollers, such as the Mega2560 (16 MHz) and Nano Every (48 MHz), encryption throughput reached approximately 75 to 80 operations per second, with flash memory usage ranging from 11 to 15 KB and dynamic memory usage below 750 bytes, depending on the Ascon variant. While modest, these figures confirm that Ascon remains viable even on low-performance platforms without hardware acceleration. Substantial gains were observed on 32-bit boards. The Arduino DUE, equipped with a Cortex-M3 at 84 MHz, achieved an average of ∼2500 encryption operations per second, representing a significant improvement over 8-bit boards. The Arduino Nano ESP32, based on a dual-core Xtensa processor clocked at 240 MHz, achieved over 10,800 operations per second, showcasing the advantage of a more advanced memory system and processing architecture.

Additionally, a high-performance implementation of Ascon was evaluated on an ESP32 Dev Kit under optimized conditions. According to tests by RWeather [60], Ascon-128a achieved an average of $0.86$ cycles per byte for 128-byte message blocks, corresponding to approximately $27.9$ Mbps, or more than 3,400,000 operations per second. This performance significantly exceeds the observed throughput on the Arduino Nano ESP32 and highlights the potential of Ascon when deployed with careful memory management, buffering strategies, and full CPU allocation.

These comparative results illustrate a clear relationship between platform complexity and cryptographic performance. While Ascon scales well with increasing hardware capabilities, its low memory footprint and computational efficiency make it a practical solution even for ultra-constrained platforms such as the Mega2560 and Nano Every. Consequently, Ascon emerges as a robust and scalable cipher for lightweight cryptography across a wide spectrum of IoT and embedded applications.

6. Conclusions

In this work, we have presented the mathematical background, specifications, security foundations, and properties of the Ascon cipher suite, the winner of the Lightweight Cryptography standardization process organized by NIST. After that, we considered an exhaustive study about the Ascon performance on four Arduino devices, namely Arduino DUE, Arduino Mega2560, Arduino Nano Every, and Arduino Nano EPS32. Finally, we have carried out a comparison of the mentioned implementations.

For the four Arduino devices and for the three Ascon versions, the number of cycles and the number of encryption and decryption operations for the processes of encryption and decryption are similar for each period of time considered. In addition, for all Arduino devices, the Ascon-128a version presents the lowest values in relation to the number of cycles, on average, whereas the Ascon-80pq version has the biggest values.

In contrast, the performance of the Arduino DUE and Arduino Nano ESP32 are quite different from the other two devices. As it is shown in Table 5, Table 6, Table 11, and Table 12, both devices consume a significantly higher number of clock cycles, on average, and they are capable of performing a much greater number of encryption and decryption operations within the same time period.

This higher performance of both devices can be attributed to the more powerful hardware of the DUE and the Nano ESP32. They have 32-bit microcontrollers that provide significantly more computational power and efficiency in handling cryptographic tasks compared to the ATmega2560 processor of the Mega2560 and the more limited resources of the Nano Every.

Furthermore, the more powerful processor and larger memory capacity of the Arduino Nano ESP32 play a crucial role in its performance. These features allow for better data handling and the faster execution of all algorithms, especially compared to the other three devices with slower processors or less available memory. This means that the Arduino Nano ESP32 can handle larger datasets or perform cryptographic operations more smoothly without running into memory bottlenecks that affect other devices.

We have also analyzed an implementation of AES-128 on three of the four devices considered in order to compare the results obtained of the Ascon family with another of the standard algorithms which is sometimes used in IoT environments. It has not been possible to use the Arduino Nano Every with AES-128 because this device is not able to support the implementation of AES-128.

From the results obtained, we can state that the three versions of Ascon have a better performance than AES-128 on the Arduino DUE, with the Ascon-128a being the fastest version for this device. However, AES-128 is significantly more efficient than any of the Ascon versions on the Arduino Mega2560. Finally, it should be noticed that the behavior of the three versions of Ascon and AES-128 on the Arduino Nano ESP32 are quite similar, although the algorithm that offers the lowest performance is AES-128, with Ascon 128a being slightly better.

In summary, in the present work we extended a previous work considering different devices and analyzing the efficiency of all versions of the Ascon family in order to have data that allow us to choose, for different use cases, which device an algorithm is more suitable, according to the restrictions imposed by the system to be used. In particular, the obtained results can be of interest for some use cases, for example, a relevant use case could be quantum key distribution in free space with drones, where the ability to operate on resource-constrained hardware is essential. In particular, the Ascon-80pq, which is quantum-resistant, is interesting in the process of an agile transition towards being quantum-resistant.