Abstract
Data acquisition and simultaneous generation of real-time digital terrain models (DTMs) is a demanding task, due to the vast amounts of observations collected by modern technologies and measurement instruments in a short time. Existing methods for generating DTMs with large datasets require significant time and high computing power. Furthermore, these methods often fail to consider fragmentary DTM generation to maintain model continuity by addressing overlaps. Additionally, storing the resulting datasets, generated 3D models, and backup copies consumes excessive memory on computer and server disks. In this study, a novel concept of generating DTMs based on real-time data acquisition using the principles of sequential estimation is proposed. Since DTM generation occurs simultaneously with data acquisition, the proposed algorithm also incorporates data reduction techniques to manage the large dataset. The reduction is achieved using the Optimum Dataset Method (OptD). The effect of the research is the characteristics file that stores information about the DTM. The results demonstrate that the proposed methodology enables the creation of 3D models described by mathematical functions in each sequence and allows for determining the height of any terrain point efficiently. Experimental validation was conducted using airborne LiDAR data. The results demonstrate that data reduction using OptD retains critical terrain features while reducing dataset size by up to 98%, significantly improving computational efficiency. The accuracy of the generated DTM was assessed using root mean square error (RMSE) metrics, with values ranging from 0.041 m to 0.121 m, depending on the reduction level. Additionally, statistical analysis of height differences (ΔZ) between the proposed method and conventional interpolation techniques confirmed the reliability of the new approach. Compared to existing DTM generation methods, the proposed approach offers real-time adaptability, improved accuracy representation per model fragment, and reduced computational overhead.
1. Introduction
Generating digital terrain models (DTMs) based on real-time data acquisition from technologies such as light detection and ranging (LiDAR), multibeam echosounder (MBES), or ground penetrating radar (GPR) for mass data acquisition is very time-consuming and labor-intensive. The first difficulty related to filtering (p1) is the detection of outliers due to multiple reflection [1]. The second challenge (p2) involves performing the filtering process itself, which includes separating points representing the terrain from those representing detail points [2]. The third difficulty (p3) arises from the need to simultaneously generate the DTM while acquiring new data [3]. The fourth challenge (p4) pertains to the method used for generating the DTM [4]. Lastly, the fifth significant issue (p5) is the size of the output file required to store both the acquired data and the generated DTM [5].
Outlier detection, related to the p1 problem, is a technique used to identify unusual or suspicious events or datasets. Anomalies are understood as data points that differ from the norm and are rare compared to other instances in a dataset. Two commonly used methods for anomaly detection are transfer learning and local outlier factors (LOFs). Transfer learning involves using pretrained neural networks to create models more quickly and efficiently [6] while LOFs evaluate an object based on its isolation from other data points in its local environment [7,8].
In the context of solving the second point, i.e., performing filtering, known algorithms can be used. These include progressive morphological filtering (PMF) [9], triangular irregular network (TIN)-based filtering [10], or hierarchical robust interpolation (HRI) [11].
Each of these methods has distinct advantages and limitations depending on the terrain type and data characteristics. PMF is widely applied due to its computational efficiency and ease of implementation. It classifies points based on morphological operations and elevation differences, making it effective for flat or gently sloped terrain. However, PMF struggles with steep areas and complex structures, where selecting an appropriate window size is crucial for reliable results [9]. TIN-based filtering constructs a triangulated model of the ground surface and iteratively refines it by adding points that meet slope or height criteria. This approach is particularly well-suited for steep and irregular terrain, where it preserves terrain features more effectively than PMF. However, it is more computationally demanding and sensitive to noise, often requiring additional post-processing [10]. HRI, in contrast, uses a hierarchical surface fitting approach with robust statistical measures to separate terrain from non-terrain points. This method is highly effective in areas with mixed land cover, such as forests or urban environments, as it better handles outliers and complex surface structures. Nonetheless, HRI requires more parameter tuning and is computationally intensive, making it less suitable for real-time applications [11]. The selection of an appropriate filtering method depends on the specific dataset and application requirements.
Problem p3, concerning simultaneous generation and visualization of DTMs and data acquisition, requires a special approach. This approach should consider the size of the measurement dataset, the DTM generation algorithm, and efficiency. In many cases, the large amount of measurement data interferes with readability, making it difficult to determine and properly interpret the characteristics of the measured objects. For this reason, an important issue related to the management of big data is the reduction in data dimensionality in the context of analysis and visualization. This is one of the more demanding challenges of data analysis because data records are multidimensional. Taking measurements with modern technologies is often supported in real time using computers with dedicated software. Visualization of such large datasets is often impossible, and they are usually unreadable to the user. Additionally, traditional computer systems and technologies limit the ability to act quickly while creating visualizations. Therefore, corporations and scientists around the world are working on improving both data dimension reduction algorithms and innovative approaches to hierarchical data management, as well as the scalability of data structures to visualize data in 2D or 3D, enabling their graphic interpretation.
The aspect that affects the p4 problem is the method of generating the DTM. To generate DTMs, methods based on the TIN or grid structures (also known as raster models) can be used [4]. The TIN model is generally more computationally efficient when dealing with irregularly distributed data, as it only uses points where necessary to define the surface. Grid models can be computationally intensive when the grid resolution is high, leading to large datasets that require significant processing power and memory. Besides using grid or TIN models, mathematical functions can represent terrain, but their applicability and accuracy depend on the context and the complexity of the terrain [12]. Terrain as a regular grid of elevation points is easy to process mathematically but may not capture sharp features like cliffs well. A TIN represents terrain using irregularly spaced points connected by triangles. It adapts to terrain variability better than a grid but is computationally more complex. Mathematical functions provide a concise way to describe terrain features compared to large datasets like grids or TINs. For example, a single equation can represent an entire surface. Calculating elevations using equations is often faster than querying large datasets, especially for analytical tasks like slope, aspect, or contour generation. Moreover, functions can represent terrain at different scales without requiring massive storage. Another important advantage is that mathematical functions can smooth out small-scale noise in terrain data, focusing on general trends and eliminating unnecessary details, and they are ideal for creating synthetic or idealized terrains for testing, modeling, or simulations where real-world data are not available or required [13].
In real-time scenarios, generating or updating large grid models may introduce latency since the model is created by interpolating points on the grid nodes. Consequently, the resulting DTM contains interpolated points rather than actual measurements, which can cause difficulties in the subsequent use of the model and the dataset of points representing this model [5]. The choice of DTM generation method and reduction techniques affects the processing efficiency, which depends on the computing power of the computer and the capabilities of the software used. This can be analyzed by considering the time needed for processing, taking into account the computer’s specifications. The fifth of the mentioned problems (p5) focuses on achieving the smallest possible size of the result file to store the acquired data and the generated DTM. The generated models are stored in raster files or as objects that are part of the software. Both models and files containing measurement data (often from several measurement epochs) can occupy a substantial amount of disk memory.
The aim of this paper is to develop a new concept of DTM generation that takes into account:
- using the OptD reduction algorithm to address the p3 problem;
- adapting sequential estimation to DTM generation to improve existing methods for solving the p4 problem;
- and storing models in the form a characteristics file (a new concept in the literature on the subject), which contains all the necessary information about the model and requires a small amount of disk space (solution to p5). By using this approach, it is possible to determine the real height of any point on the object.
The remainder of this manuscript is organized as follows: Section 2 presents the materials and methods used in our approach, including data reduction techniques and sequential estimation principles. Section 3 details the experimental setup and datasets. Section 4 discusses the results, including computational efficiency and accuracy analyses.
2. Materials and Methods
The new concept of DTM generation from real-time data acquired is based on the OptD method and sequential estimation principles. Among existing techniques for DTM generation, methods such as inverse distance weighting, kriging, nearest neighbor, and spline methods are typically used [14,15]. All these methods give one 3D model after processing. For DTMs generated using the existing methods, the surface is described by one value root mean square error (RMSE). Other errors related to DTM generation are also provided to demonstrate the impact of processing stages on model error or model accuracy depending on the accuracy of the data and measurement technology used [16,17]. For DTMs generated using sequential estimation, the value of for each sequence is calculated. The use of sequential estimation can give a completely different perspective on the accuracy of the generated DTM and is an innovation and novelty in the approach to DTM quality assessment. This means that a significant property of the proposed methodology, namely, the variability of accuracy characteristics of the DTM, can be demonstrated, i.e., determining different accuracies in different fragments of the model.
Moreover, DTM can be stored in the form of a characteristics file, which gives the possibility of calculating the height of a point at any area of object.
2.1. Data Reduction with the OptD Method
Reduction in datasets refers to techniques used to reduce the amount of data in a point cloud while preserving the essential features and structures that are important for visualization, analysis, or further processing. The approaches to data reduction with different sensors are similar because users are always interested in keeping the characteristic observations, for example extremum values, and the ability to save points in areas with a complex structure. It is also important that the reduction algorithm works quickly, which means that it must be computationally simple.
The most commonly used reduction methods include [18,19]:
- uniform grid sampling, which involves dividing the point cloud space into a 3D grid of voxels and selecting one representative point from each voxel;
- voxel grid filtering, where a voxel (3D pixel) is created, and one point (usually the centroid) is chosen to represent all points within that voxel;
- random sampling, which selects a subset of points from the point cloud, though this might not preserve structure well;
- octree-based down-sampling by designing an octree data structure to subdivide the point cloud into hierarchical levels, selecting points based on resolution.
To better illustrate the types of reduction method, Table 1 is presented, which compares reduction methods in terms of data retention, computational efficiency, and impact on accuracy.

Table 1.
Comparison of data reduction methods.
The disadvantage of these of these computationally simple methods is that they lead to the loss of important details, especially in regions of interest such as edges and objects. However, the use of methods such as feature-based reduction [24] or curvature methods [25] is very time-consuming and not suitable for real-time reduction. One of the methods that can be used during reduction is the OptD method [26,27].
The method has been tested in various studies [28,29,30]. The assumption of the OptD method is to reduce the number of observations in datasets using the optimization criterion of the size of the dataset, e.g., percentage p% or the number m of points preserved in the dataset after reduction. During each iteration, the algorithm assesses whether the current tolerance level and the width of the measuring strip allow for meeting the specified percentage of retained points. If the criteria are not met, the tolerance range may be adjusted or width of the measuring strip can be changed. This adjustment helps find the optimal balance between point reduction and the preservation of critical terrain features. By adjusting the strip width, the method can manage the amount of data being processed and ensure that the desired point retention criteria are fulfilled. After each iteration, the algorithm evaluates the remaining points against the set criteria. If the percentage of retained points is above or below the target, the method iteratively refines the tolerance and strip width until the desired conditions are satisfied.
In this way, it is possible to select the optimal dataset, in terms of the introduced optimization criterion, and the user may decide how many observations will remain in the reduced dataset. The OptD method effectively reduces the size of point cloud datasets while retaining essential structural and geometric features. It adapts to the characteristics of the dataset, ensuring optimal reduction even for irregular or complex terrains. The OptD method improves computational performance by significantly reducing the number of points, the method accelerates subsequent processing steps, such as modeling or analysis. Despite reducing the data size, the method maintains high fidelity in representing critical features, ensuring accuracy in the DTM.
The OptD method also has some limitations. The effectiveness of the method depends heavily on the choice of parameters, such as tolerance, which may require fine-tuning for different datasets. In cases where the data contain significant noise or outliers, preprocessing may be necessary to achieve optimal results. These limitations can be eliminated by testing the reduction results using different tolerance ranges and parameter settings. Each dataset is different and requires preliminary testing first.
Tests have shown that the OptD method works effectively in conjunction with filtering methods, such as adaptive TIN models, to enhance data quality further. The OptD method has evolved along with attempts to apply it to various types of data. In [25], observations from a multibeam echosounder were reduced; in paper [31], the optimization concerned data collected from satellite altimetry.
The OptD method has found particular application in the detection of wall defects in buildings [32] and has been used for extraction of off-road objects such as traffic signs, power lines, roadside trees, and light poles [33].
The scheme of the OptD method algorithm for one measuring strip (Li, where i is the number of measuring strip) acquired in real time is presented in Figure 1.
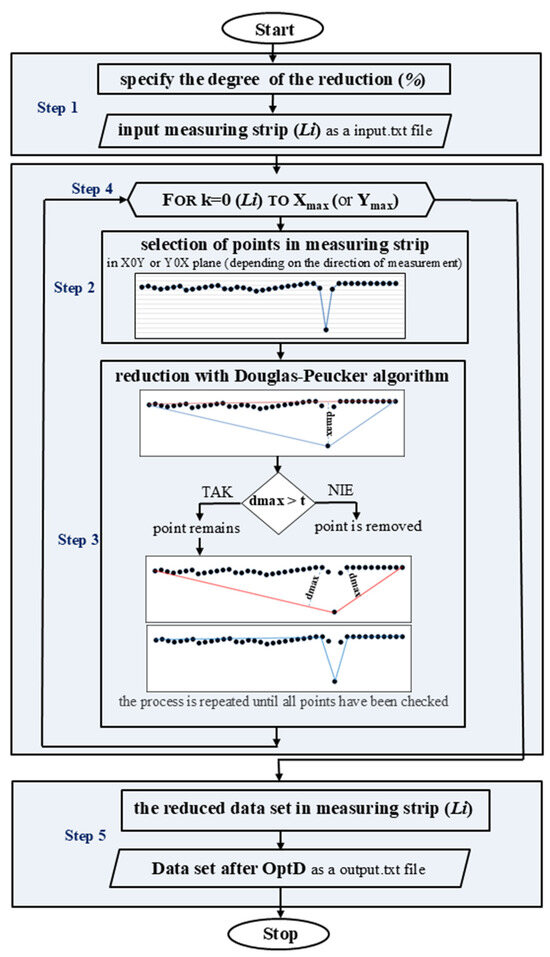
Figure 1.
The OptD method for a single measuring strip, illustrating decisions based on predefined thresholds for data reduction.
The diagram illustrates the OptD method applied to a single measuring strip, outlining the step-by-step decision-making process based on predefined thresholds for data reduction.
- Initial data input. The percentage of points that should remain in the dataset after reduction is determined. Then, the acquired fragment of the dataset is loaded. This fragment contains points that, in the X0Y or Y0X plane (depending on the measurement direction), define the end of the dataset;
FOR loop execution: steps 2, 3, and 4 are performed within a loop that iterates over each measuring strip until all strips are processed:
- 2.
- Projection and preprocessing. To maintain the spatial characteristics of the points, the data are projected onto the X0Z or Y0Z plane instead of the X0Y plane;
- 3.
- Generalization using the Douglas–Peucker algorithm [34]. The algorithm simplifies a line by reducing the number of points while preserving its overall shape. It connects the start and end points of a segment and calculates the perpendicular distance of all intermediate points. Points with a distance (d) below a predefined tolerance (t) are removed, as they do not significantly impact the line’s geometry. This process is recursively repeated until no more points can be removed without exceeding the tolerance;
- 4.
- Iterative processing. A reduced dataset representing the loaded measuring strip is obtained. While the reduction is in progress, the next measuring strip is already being acquired. Once it reaches the required width (determined by the user and measurement type), it enters the OptD algorithm for reduction;
- 5.
- Final data output. The process repeats until the last acquired measuring strip undergoes reduction, ensuring continuous and efficient data reduction while maintaining essential structural details.
This stepwise approach optimizes measurement data storage and processing while preserving key geometric features.
2.2. Sequential Estimation in the Context of DTM Generation
Sequential estimation is a sequential analysis method that is part of inferential statistics and enables staged data processing. The results of calculations from the previous sequence are included in the calculations performed in the next sequence. In processing measurement results, sequential estimation is used to improve the accuracy and reliability of parameter estimates by continuously updating them as new measurement data become available. This is particularly important in contexts where measurements might be noisy. Sequential estimation helps filter out noise from measurements by updating estimates progressively. This is especially beneficial in fields like engineering and signal processing, where measurements are often affected by random noise [35,36].
A very common approach to sequential estimation is Kalman filtering [37]. In the context of DTM generation, both sequential estimation and Kalman filtering can be used for processing and analyzing spatial data, but they differ significantly in their methodologies, applications, and assumptions. Kalman filtering is a recursive algorithm designed for estimating the state of a dynamic system over time. It updates estimates based on new measurements and the previous state, which is particularly useful for time-series data. The Kalman filter consists of two main phases: the prediction step (where it estimates the next state) and the update step (where it incorporates new measurements to refine the estimate). Sequential estimation refers to a broader approach where estimates are updated as new data become available. It is not limited to any specific algorithm and can include various techniques, including Kalman filters. Sequential estimation can handle different types of data and models, making it adaptable to various situations in DTM generation, including both static and dynamic environments. Kalman filtering is particularly effective for integrating time-series measurements, whereas sequential estimation can be employed to improve DTM generation by continuously updating terrain estimates as new data from LiDAR become available [35].
The choice of the sequential estimation method over alternative approaches, such as Kalman filtering, was driven by its adaptability to real-time DTM generation and its ability to manage LiDAR data efficiently. Unlike Kalman filtering, which is optimized for dynamic systems and requires predefined system models, sequential estimation allows flexible integration of new data segments without imposing strong assumptions about temporal dependencies. This approach ensures that each sequence of acquired data contributes to an adaptive and localized model refinement, capturing variations in terrain representation with high accuracy. Moreover, sequential estimation facilitates computational efficiency by enabling incremental updates, reducing memory and processing demands compared to batch-processing techniques. These advantages make it particularly suitable for real-time applications where rapid, high-fidelity DTM updates are required.
The essence of the proposed sequential estimation method in the context of creating the DTM is to generate a 3D model based on a function. The fluctuation of height values in a certain area is approximated by a polynomial equation. The assumption of the proposed solution is to perform calculations to generate the DTM in real time during measurement.
The rules during measurements are presented in Figure 2.
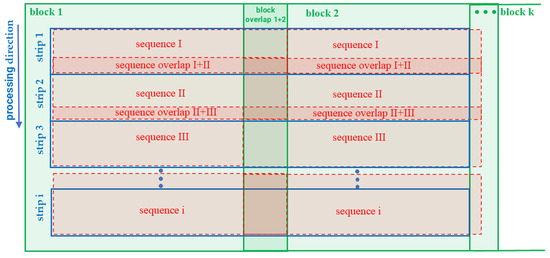
Figure 2.
Rules for acquiring datasets.
Geodetic measurements providing information about the location of points (spatial coordinates) and other data are collected during measurements (e.g., reflection intensity, temperature). The technology most often used to acquire data for DTMs is LiDAR. Measurements are performed continuously with data acquired in blocks (1, 2, …, k). Within each block, following the proposed methodology, observations are acquired in measuring strips (1, 2, …, i). Each measuring strip is acquired at a specific time and has a defined width [38,39]. The principles governing the parameters used during measurements depend on the type of measurement and the technology employed [40,41].
The first acquired measuring strip is subjected to reduction by OptD and undergoes a filtering process using adaptive TIN models [42]. The OptD method can be used before or after filtering [10]. During processing using the OptD method, all points located in the measuring strip are considered. In the X0Z plane (or Y0Z depending on the X and Y axes setting), the reduction process is performed based on the principles of generalization using the Douglas–Peucker method. The following parameters characterizing the dataset after the OptD method are obtained: extremal coordinates (min, max), range (), standard deviation (SD), number of points after reduction, different densities of points in different places of the object, number of iterations, width of the measuring strip, and tolerance (which determines the degree of reduction [42]). Parameters obtained from the reduction process can be directly utilized in sequential processing workflows, improving overall efficiency, and some of them can be used during the sequential estimation process. After the reduction and filtration process, the point cloud representing ground points constitutes the dataset for Sequence I of the calculations. In this step of the proposed concept, appropriate matrices are determined and corrections calculated according to Equation (2) and a polynomial model is adopted . The parameters of the polynomial model are determined, which describes the fragment of the terrain represented by points from the first measuring strip. The second measuring strip is acquired during the processing of the first measuring strip. After the DTM parameters are determined, the data from the second measuring strip are included in sequence I. The dataset from sequence II is also reduced before it enters the computation of sequence II. It is important to consider the sequence overlap (sequence overlap I + II, II + III, i − 1 + i). Overlap is also considered for blocks (block overlap 1 + 2, 2 + 3,…, k − 1 + k).
After the reduction and filtration process in each sequence, the decision should be made regarding the selection of a mathematical model that will be used to build the DTM. This model will be the most favorable approximation of the dataset of observation results. Of the many possibilities, a polynomial model is most often used:
where Zi, Xi, and Yi are the orthogonal coordinates of points obtained from LiDAR measurements; Zi is the height, and Xi and Yi are the rectangular coordinates of the points in the point cloud (i = 1…n; n is the number of points in the dataset), and are parameters.
To fit the area obtained from Equation (1) to the point cloud using the least squares method of the correction equation with respect to the height , the following equation is used:
where: is the correction matrix, represents a coefficient matrix, is a vector of parameters, is the matrix of free terms, and consistently .
The needed parameter estimators can be obtained from the following relationships:
The accuracy of the obtained quantities is assessed by determining, inter alia, the coefficient of variance:
where m is the number of model parameters and is the weight matrix (where: n > m).
Stage 3 of the calculations is loading the , , and coordinates and a new dataset (new fragment of the point cloud) and performing surface prediction using the parameters obtained from sequence I. Predicting the values with dependence (1) results in the following formula:
The heights obtained from the prediction should be verified with the values obtained from direct measurements with LiDAR technology. Verification entails determining the correction to the prediction resulting from the following dependence:
For the values determined in Equation (6), an acceptable tolerance should be created, for example, the following formula (or another criterion adopted by the operator):
where k is a positive coefficient. The given probabilities originate from the Gaussian distribution and correspond to confidence intervals defined by the number of standard deviations from the mean, e.g., k = 1 for probability , k = 1.5 for , and k = 3 for . The final value of depends on the operator performing the calculations.
If all values fall within the acceptable tolerance and condition (7) is fulfilled, the same polynomial model approximating the DTM is adopted as in sequence I. The failure to meet condition (7) (exceeding the tolerance) causes the polynomial model approximating the DTM adopted in sequence I to be changed to a new one. Further calculations are performed according to the following procedure:
where:
- —the vector of corrections to the intercepts of sequence II;
- —the vector of parameters obtained from sequence I included in the calculations of sequence II;
- —a known matrix of coefficients determined for the parameters of sequence I;
- —the vector of the new parameters determined in sequence II;
- —a known matrix of coefficients determined for the new parameters ;
- —the vector of intercepts of sequence II;
- —the vector of parameters (pseudo-observations) obtained from sequence I;
- —the vector of pseudo-observation corrections .
The first equation from dependence (8) concerns the dataset obtained from the second sequence (new observations). The second dependence () concerns corrections to the pseudo-observations obtained from stage I.
Dependence (8) can also be written in the form of a block matrix:
For independent observation results in sequences I and II, the following weight matrix can be written:
where is the sequence I weight matrix and is the weight matrix defined for the new measurement results obtained in sequence II; 0 is zero matrix notation.
The solution of the system of Equation (9) using the least squares method is the estimators:
The coefficient determined after sequence II is calculated from the following formula:
If only new observations are added, dependence (8) can be written as follows:
The solution to problem (13) based on the least squares method takes the form of Equation (9) with a weight matrix such as in Equation (10) and an coefficient determined as in Equation (12).
The implementation of subsequent sequences is performed until the LiDAR measurements are completed. The calculations should also take into account the interrelationships between the measuring strips of the LiDAR, i.e., establish a sequence overlap or additional data. These issues will be considered in future research.
The proposed concept allows for the adjustment of parameters at different stages of the method, to meet a specific user’s needs: width of measuring strips during sequence loading, reduction criteria, such as the number of points after reduction or the tolerance range in the Douglas–Peucker algorithm, the degree of the polynomial model value, and an acceptable tolerance for the values to accept or reject the model from the previous sequence. It is also possible to set all parameters at the input, so as not to interfere with the computational process while the processing is in progress. The approach depends on the user, their experience, and the type of data.
3. Results and Analysis
The research was carried out on LiDAR data obtained from the website https://pzgik.geoportal.gov.pl/imap/ (date of data download 1 October 2023). The data were collected as part of the ISOK Project (IT system for protecting a country against extraordinary threats) from the aircraft platform (airborne laser scanning—ALS). The datasets N-34-114-B-b-4-3-3 with 4 points/m2 were obtained in .las format.
DTMs often rely on multiple data sources, such as a LiDAR point cloud, satellite imagery, or GPS measurements. These datasets must undergo georeferencing to a common coordinate system to ensure seamless integration. Misaligned data can lead to errors in the model, such as incorrect elevation values, distorted slopes, or inaccurate representation of topographic features. In our concept, we used a single type of data: an ALS point cloud. These data were georeferenced, meaning that spatial coordinates were assigned to each point in the dataset, aligning it with a specific geographic coordinate system. This step ensures the data accurately represent the real-world location and can be integrated with other spatial datasets. The research object which was adopted as block 1 is shown in Figure 3.

Figure 3.
Original ALS point cloud in block 1 (RGB color).
The ALS point cloud was processed using the new concept of DTM generation based on real-time data acquisition with sequential estimation and the OptD method. The stages of processing in the measuring strips are presented in Figure 4 to show how the process takes place over time.
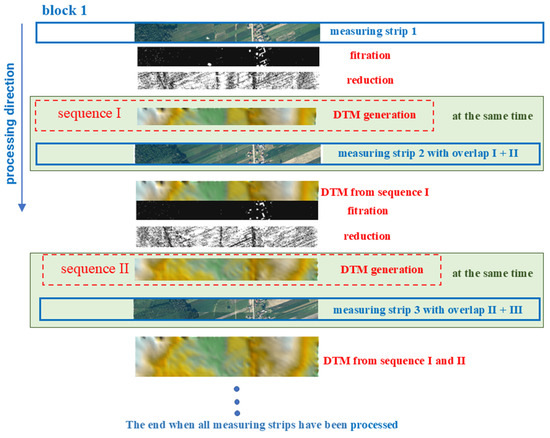
Figure 4.
Stages of processing with the new concept in block 1.
The degree of reduction is important during processing, because a smaller set means a faster DTM generation process.
Different degrees of reduction were used in the study during testing of the new concept. In order to show what the area looks like at different degrees of reduction, preview figures were made. Four variants of reduction, 50%, 30%, 10%, and 2% (percentage of data remaining in the point cloud) were tested. The entire dataset contained 1,998,402 points. After OptD reduction, the following remained in the set: 997,850 points (for 50%), 601,058 points (for 30%), 199,176 points (for 10%), and 40,077 points (for 2%). The final effect after reduction in all strips is presented in Figure 5. The choice of the degree of reduction depends on the user, the density of points, and the purpose of the generated DTM.
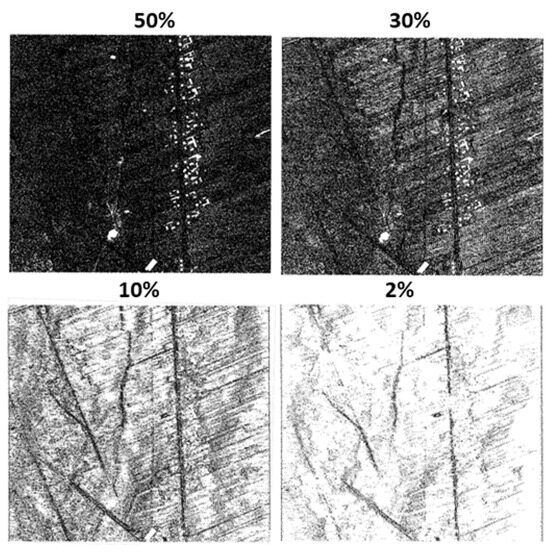
Figure 5.
ALS point clouds representing the ground after applying the OptD method.
Not only different degrees of reduction, but also different widths of measuring strips (15 m—v.1 and 25 m—v.2) were used during processing. The width of the measuring strips depends on the flight altitude and the scanning angle during data acquisition.
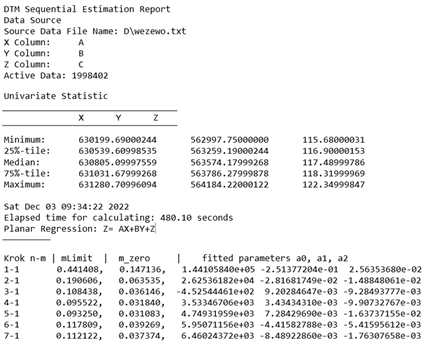
The new concept was used to generate DTMs. The generated models can be stored as a binary file or as a characteristics file: *.txt. For the generated DTMs, the parameter , describing their quality was determined. That parameter was calculated for each sequence, which means that it is different in different places of the generated DTM. Values of , maximum (necessary during processing with sequential estimation), function and model parameters, the average time for creating models in sequences, extreme coordinate values, the name of the input data file, and the number of input data are stored in the form of the characteristics file. Characteristics files were prepared for variants v.1 and v.2 taking into account four options of reduction. A fragment of such a file is presented in Appendix A.
In order to assess the quality of the generated DTMs using the new concept, it was necessary to generate a model using an existing method. The nearest neighbor method was chosen [43]. Given that existing methods generate points on grid nodes, while the method based on sequential estimation defines the model as a mathematical function, the heights of points on the DTM generated using sequential estimation were calculated to correspond to the points at grid nodes of the DTM from the existing method. Following the algorithm presented in Figure 6, the heights of points (node equivalents) were determined for DTM generated using the principles of the new concept. This algorithm can be stored and utilized to determine characteristics at any point within the object. For instance, the algorithm can be read from a file in a Python v. 3.11 program and subsequently invoked to calculate its characteristics or to generate a grid of points using it.
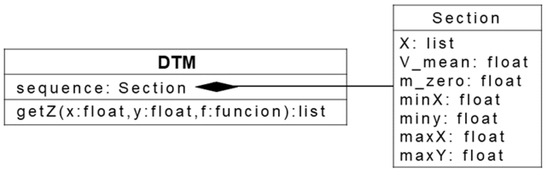
Figure 6.
Scheme for generating Z height values from a characteristics file.
The DTMs were generated with a grid size of 5.0 m so that the grid size was smaller than the measuring strip widths when calculating the function parameters for the sequential estimation method. In Figure 7, the generated DTMs are presented.
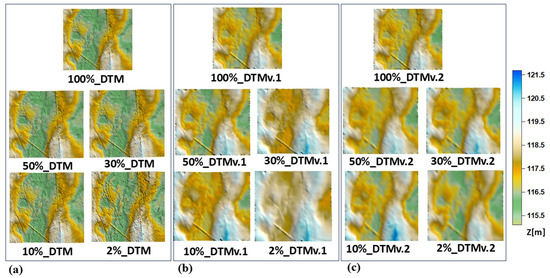
Figure 7.
DTMs: (a) existing method—the nearest neighbor method, (b) DTMs based on points calculated using a Python program after applying the new concept—v.1, (c) DTMs based on points calculated using a Python program after applying the new concept—v.2.
Then, the height differences between the heights (from the new concept) and (from the nearest neighbors method grid interpolation) were calculated. Table 2 summarizes the calculated absolute values of (only minimum, maximum, and mean values are given).

Table 2.
characteristics for differential DTMs.
When analyzing the height differences between the nearest neighbors method model and the model created with new concept, higher values were observed for the model in the variant v.2. However, there were also points where the heights were the same (min values). In models generated from all points (100%), the greatest height differences were observed (1.115 m for the variant v.1, 1.375 m for the variant v.2). Focusing on the values in variant v.1, it is observed that these values are generally smaller compared to those in variant v.2. This indicates that variant v.1 of the generated models exhibits a higher degree of similarity to DTMs produced using the established method.
To assess whether the height differences () between DTMs generated using sequential estimation and the reference nearest neighbor method are statistically significant, a statistical significance test was performed. A non-parametric Wilcoxon signed-rank test was used [44]. The test results indicate a p-value of 0.0625, suggesting that the differences are not statistically significant at the conventional α = 0.05 level, but they are close to the threshold of significance. Additionally, a 95% confidence interval for the mean difference was calculated, indicating a small but consistent deviation between the two methods. These findings suggest that while differences exist, they may not be substantial enough to significantly impact the overall accuracy of the DTM.
In the next stage of results verification, the RMSEs for the DTMs based on the new concept were calculated. DTMs generated from the measurement dataset and from the reduction datasets were assumed as reference models. The speed of DTM generation was also calculated. Additionally, the speed of DTM generation is given. For processing, a computer with processor: Intel Core i7-11800H, RAM size [GB]: 32, disk: 2000 GB SSD, and graphics card: NVIDIA GeForce RTX 3080 was used.
Calculated RMSEs and speeds are presented in Table 3.

Table 3.
RMSE and speed characteristics.
The highest RMSE was recorded for 2%_DTMv.1, and the lowest for 30%_DTMv.1. As is also clear from the considerations presented above, the accuracy of a DTM is always characterized by a single value if it is generated by existing methods or compared with another model. The differences in RMSE between versions v.1 and v.2 can be attributed to several factors. Firstly, the quality and resolution of the data used in each version may impact the accuracy of the results. Version v.1 utilized a higher-resolution DTM, resulting in a lower RMSE. Secondly, the differences in algorithms introduced in v.2 may have improved performance in some cases while degrading it in others.
In the case of a DTM using sequential estimation, is given in each sequence. Therefore, based on the characteristics file, it can be concluded that the variability of accuracy characteristics of the DTM is expressed in each fragment of the area with a different value. We believe this is the right approach because in each fragment of the area, a different number of points is used to build the DTM. The processing times for both variants were comparable and, as expected, decreased with smaller datasets.
Existing methods for DTM creation generate the coordinates of the grid nodes and then give one value of the accuracy calculated from the average height of the entire terrain. It does not take into account the situation in which the number of points is very small in some places.
An example situation is presented in Figure 8. There are only six points in area A and 350 points in area B. The generated DTMs in these areas cannot be described with the same value of the accuracy parameter. A much more accurate model will be generated for area B than for area A.

Figure 8.
Different numbers of points for different fragments of objects, where: A—area with a small number of points, B—area with a large number of points.
In order to verify and compare the results, the following additional study was performed:
- One hundred points were selected from the original ALS dataset and datasets after applying the OptD method;
- The measuring strips in which individual points are located were determined;
- The parameters were found (from the characteristics file) for the sequences in which these points were located;
- The height of each point was calculated and compared with the height in the original ALS point cloud;
- The height difference was calculated.
The calculated differences are summarized in Table 4.

Table 4.
differences between the height of points from the ALS point cloud and the height of points calculated based on the parameters from the characteristics file.
The highest was noticed for the 10% point cloud in variant v.2, and the lowest for the 100% and 50% point clouds in the v.1 and v.2 variants, respectively. Thus, all of them are within the limits 0.010–0.825 m. Such results prove that the characteristics file stores the correct parameters in the individual sequences and the heights obtained from the characteristics file meet the assumptions of the method.
4. Conclusions
This study presents a concept of developing a DTM based on the sequential estimation and the OptD method. The proposed methodology allows the DTM to be saved in a characteristics file (a text file), which occupies less computer memory and is easier to store. In contrast, existing methods save DTMs in model files (binary files). The primary difference between these two approaches is that loading a binary file allows immediate use as part of a program, whereas loading a characteristics file requires “deciphering” the file and constructing the model first. While both approaches ultimately produce the same result, the binary file is more convenient as it is already built and ready to use. On the other hand, the characteristics file contains all the essential information about the model and allows to determine the height of any point on the object when processed.
The application of the OptD method during processing resulted in dataset reduction, which influenced both the efficiency and effectiveness of processing observations using sequential estimation.
The model generated with sequential estimation method has variable DTM accuracy. This means that in each fragment of the model, the value of is different, which proves the variability of the accuracy characteristics of the DTM. Thus, the accuracy of the model is not given by one accuracy value as in the case of the existing methods.
The proposed concept of generating DTMs with prior reduction using the OptD method can be applied during data acquisition when we aim to obtain a model either immediately during measurement or shortly after; for instance, measurements conducted with a multibeam echosounder for comparative navigation purposes. While acquiring data about the bottom of a reservoir, it is possible to generate a bottom model and identify areas requiring more detailed measurements or where obstacles are located. Similarly, during measurements performed with a drone equipped with a LiDAR sensor, we can simultaneously acquire a point cloud and generate a DTM or digital elevation model (DEM).
In this article, only the equation of the plane was used to build the DTM of the studied area. Interesting further research topics include the following:
- the use of a polynomial with higher degrees to create a DTM in more complex terrain configurations;
- the use of a sequential combination of different degrees of polynomials to approximate the measured object.
The conclusion states that the method is novel but lacks specific improvements over existing methods. The authors are invited to clearly state how the proposed method outperforms conventional DTM generation techniques.
Based on the results, the main advantages of the proposed method for developing DTMs using sequential estimation and the OptD method can be formulated as follows:
- Reduced storage space.Saving the DTM in a characteristics file (a text file) requires less computer memory compared to binary files, making data management easier;
- Analytical flexibility.Characteristics files contain essential model information, allowing for height determination at any point after processing;
- Increased processing efficiency.The OptD method reduces datasets, improving the efficiency and effectiveness of observations processed via sequential estimation;
- Variable DTM accuracy.The model shows varying accuracy across different fragments, allowing for tailored precision based on terrain conditions, unlike traditional methods;
- Potential for further development.The methodology supports future research, including the use of higher-degree polynomials for complex terrain modeling;
- Application in data acquisition systems.The method is suitable for implementation in systems that facilitate mass data collection, enhancing its practical utility in various fields.
These and other scientific problems arising from detailed research will be considered in the authors’ subsequent articles. However, it can already be noted that the proposed methodology can be used and implemented in systems supporting mass data acquisition, which are to be used to build DTMs.
Author Contributions
Conceptualization, W.B.-B. and W.K.; methodology, W.B.-B. and W.K.; software, M.B. and W.B.-B.; validation, W.B.-B., W.K. and C.S.; formal analysis, W.B.-B., W.K. and A.M.; investigation, W.B.-B. and W.K.; resources, W.B.-B. and M.B.; data curation, W.B.-B. and C.S.; writing—original draft preparation, W.B.-B. and W.K.; writing—review and editing, W.B.-B. and A.M.; visualization, W.B.-B., M.B. and C.S.; supervision, W.B.-B.; project administration, W.B.-B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
References
- Hodge, V.J.; Austin, J. A survey of outlier detection methodologies. Artif. Intell. Rev. 2004, 22, 85–126. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An easy-to-use airborne LiDAR data filtering method based on cloth simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Glira, P.; PfeifeR, N.; Briese, C.; ReSSl, C. A correspondence framework for ALS strip adjustments based on variants of the ICP algorithm. Photogramm. Fernerkund. Geoinf. 2015, 2015, 275–289. [Google Scholar] [CrossRef]
- Khosravipour, A.; Isenburg, M.; Skidmore, A.K.; Wang, T. Creating better digital surface models from LiDAR points. In Proceedings of the ACRS 2015—36th Asian Conference on Remote Sensing: Fostering Resilient Growth in Asia, Proceedings, Quezon City, Philippines, 24–28 October 2015. [Google Scholar]
- Blaszczak-Bak, W.; Pajak, K.; Sobieraj, A. Influence of datasets decreased by applying reduction and generation methods on digital Terrain models. Acta Geodyn. Geomater. 2016, 13, 361–366. [Google Scholar] [CrossRef]
- Andrew, J.T.A.; Tanay, T.; Morton, E.J.; Griffin, L.D. Transfer Representation-Learning for Anomaly Detection. In Proceedings of the 33rd International Conference on Machine Learning Research, New York, NY, USA, 19–24 June 2016; Volume 48. [Google Scholar]
- Breunig, M.M.; Kriegel, H.P.; Ng, R.T.; Sander, J. LOF: Identifying Density-Based Local Outliers. In Proceedings of the SIGMOD 2000—Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 16–18 May 2000. [Google Scholar] [CrossRef]
- Pirotti, F.; Ravanelli, R.; Fissore, F.; Masiero, A. Implementation and assessment of two density-based outlier detection methods over large spatial point clouds. Open Geospat. Data Softw. Stand. 2018, 3, 14. [Google Scholar] [CrossRef]
- Liu, Y.; Bates, P.D.; Neal, J.C. Bare-earth DEM generation from ArcticDEM and its use in flood simulation. Nat. Hazards Earth Syst. Sci. 2023, 23, 375–391. [Google Scholar] [CrossRef]
- Blaszczak-Bak, W.; Janowski, A.; Kamiñski, W.; Rapiñski, J. Optimization algorithm and filtration using the adaptive TIN model at the stage of initial processing of the ALS point cloud. Can. J. Remote Sens. 2012, 37, 583–589. [Google Scholar] [CrossRef]
- Graham, A.; Coops, N.C.; Wilcox, M.; Plowright, A. Evaluation of ground surface models derived from unmanned aerial systems with digital aerial photogrammetry in a disturbed conifer forest. Remote Sens. 2019, 11, 84. [Google Scholar] [CrossRef]
- Zhou, S.; Zhang, Y.; Yang, J. 3D Mathematical Modeling and Visualization Application Based on Virtual Reality Technology. Comput. Aided Des. Appl. 2023, 20, 1–13. [Google Scholar] [CrossRef]
- Abdeldayem, Z. Automatic Weighted Splines Filter (AWSF): A New Algorithm for Extracting Terrain Measurements from Raw LiDAR Point Clouds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 60–71. [Google Scholar] [CrossRef]
- Stereńczak, K.; Ciesielski, M.; Bałazy, R.; Zawiła-Niedźwiecki, T. Comparison of various algorithms for DTM interpolation from LIDAR data in dense mountain forests. Eur. J. Remote Sens. 2016, 49, 599–621. [Google Scholar] [CrossRef]
- Thomas, K. A New Simplified DSM-to-DTM Algorithm-dsm-to-dtm-step. Preprints 2018, 1, 1–10. [Google Scholar]
- Hodgson, M.E.; Bresnahan, P. Accuracy of Airborne Lidar-Derived Elevation. Photogramm. Eng. Remote Sens. 2013, 70, 331–339. [Google Scholar] [CrossRef]
- Wechsler, S.P. Uncertainties associated with digital elevation models for hydrologic applications: A review. Hydrol. Earth Syst. Sci. 2007, 11, 1481–1500. [Google Scholar] [CrossRef]
- Rehman, M.H.U.; Liew, C.S.; Abbas, A.; Jayaraman, P.P.; Wah, T.Y.; Khan, S.U. Big Data Reduction Methods: A Survey. Data Sci. Eng. 2016, 1, 265–284. [Google Scholar] [CrossRef]
- Mujta, W.; Wlodarczyk-Sielicka, M.; Stateczny, A. Testing the Effect of Bathymetric Data Reduction on the Shape of the Digital Bottom Model. Sensors 2023, 23, 5445. [Google Scholar] [CrossRef]
- Jain, K.; Murty, P.; Flynn, J. Data clustering: A review. ACM Comput. Surv. 1999, 31, 264–323. [Google Scholar] [CrossRef]
- Rusu, R.B.; Cousins, S. 3D is here: Point Cloud Library (PCL). In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011. [Google Scholar] [CrossRef]
- El-Sayed, E.; Abdel-Kader, R.F.; Nashaat, H.; Marei, M. Plane detection in 3D point cloud using octree-balanced density down-sampling and iterative adaptive plane extraction. IET Image Process. 2018, 12, 1595–1605. [Google Scholar] [CrossRef]
- Błaszczak-Bąk, W. New optimum dataset method in LiDAR processing. Acta Geodyn. Geomater. 2016, 13, 381–388. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Y.; Chao, H. Incremental Fuzzy Clustering Based on Feature Reduction. J. Electr. Comput. Eng. 2022, 2022, 8566253. [Google Scholar] [CrossRef]
- Du, X.; Zhuo, Y. A point cloud data reduction method based on curvature. In Proceedings of the 2009 IEEE 10th International Conference on Computer-Aided Industrial Design and Conceptual Design: E-Business, Creative Design, Manufacturing—CAID and CD’2009, Wenzhou, China, 26–29 November 2009; pp. 914–918. [Google Scholar] [CrossRef]
- Błaszczak-Bąk, W.; Sobieraj-Żłobińska, A.; Wieczorek, B. The Optimum Dataset method–examples of the application. E3S Web Conf. 2018, 26, 00005. [Google Scholar]
- Błaszczak-Bąk, W.; Sobieraj-Żłobińska, A.; Kowalik, M. The OptD-multi method in LiDAR processing. Meas. Sci. Technol. 2017, 28, 7500–7509. [Google Scholar]
- Rashdi, R.; Martínez-Sánchez, J.; Arias, P.; Qiu, Z. Scanning Technologies to Building Information Modelling: A Review. Infrastructures 2022, 7, 49. [Google Scholar] [CrossRef]
- Siewczyńska, M.; Zioło, T. Analysis of the Applicability of Photogrammetry in Building Façade. Civ. Environ. Eng. Rep. 2022, 32, 182–206. [Google Scholar] [CrossRef]
- Sánchez-Aparicio, L.J.; Del Pozo, S.; Ramos, L.F.; Arce, A.; Fernandes, F.M. Heritage site preservation with combined radiometric and geometric analysis of TLS data. Autom. Constr. 2018, 85, 24–39. [Google Scholar] [CrossRef]
- Pajak, K.; Blaszczak-Bak, W. Baltic sea level changes from satellite altimetry data based on the OptD method. Acta Geodyn. Geomater. 2019, 16, 235–244. [Google Scholar] [CrossRef]
- Suchocki, C.; Błaszczak-Bąk, W.; Janicka, J.; Dumalski, A. Detection of defects in building walls using modified OptD method for down-sampling of point clouds. Build. Res. Inf. 2020, 49, 197–215. [Google Scholar] [CrossRef]
- Błaszczak-Bąk, W.; Janicka, J.; Suchocki, C.; Masiero, A.; Sobieraj-żłobińska, A. Down-Sampling of large lidar dataset in the context of off-road objects extraction. Geosciences 2020, 10, 219. [Google Scholar] [CrossRef]
- Douglas, D.H.; Peucker, T.K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. Can. Cartogr. 1973, 10, 112–122. [Google Scholar] [CrossRef]
- Gao, B.; Hu, G.; Li, W.; Zhao, Y.; Zhong, Y. Maximum Likelihood-Based Measurement Noise Covariance Estimation Using Sequential Quadratic Programming for Cubature Kalman Filter Applied in INS/BDS Integration. Math. Probl. Eng. 2021, 2021, 9383678. [Google Scholar] [CrossRef]
- Tan, L.; Wang, Y.; Hu, C.; Zhang, X.; Li, L.; Su, H. Sequential Fusion Filter for State Estimation of Nonlinear Multi-Sensor Systems with Cross-Correlated Noise and Packet Dropout Compensation. Sensors 2023, 23, 4687. [Google Scholar] [CrossRef] [PubMed]
- Kim, T.; Park, T.H. Extended kalman filter (Ekf) design for vehicle position tracking using reliability function of radar and lidar. Sensors 2020, 20, 4126. [Google Scholar] [CrossRef]
- Habib, A.; Bang, K.I.; Kersting, A.P.; Chow, J. Alternative methodologies for LiDAR system calibration. Remote Sens. 2010, 2, 874. [Google Scholar] [CrossRef]
- Rentsch, M.; Krzystek, P. Precise quality control of LiDAR strips. In Proceedings of the American Society for Photogrammetry and Remote Sensing Annual Conference 2009, ASPRS 2009, Baltimore, MD, USA, 9–13 March 2009. [Google Scholar]
- Alsadik, B.; Remondino, F. Flight planning for LiDAR-based UAS mapping applications. ISPRS Int. J. Geo inf. 2020, 9, 378. [Google Scholar] [CrossRef]
- Mastor, T.A.; Kamarulzaman, N.; Abidin, M.M.; Samad, A.M.; Hashim, K.A.; Maarof, I.; Zainuddin, K. The Unmanned Aerial Imagery Capturing System (UAiCs) flight planning calculation parameters for small scale format imagery. In Proceedings of the Proceedings—2014 5th IEEE Control and System Graduate Research Colloquium, ICSGRC 2014, Shah Alam, Malaysia, 11–12 August 2014. [Google Scholar] [CrossRef]
- Axelsson, P. DEM Generation from Laser Scanner Data Using adaptive TIN Models. Int. Arch. Photogramm. Remote Sens. 2000, 23, 110–117. [Google Scholar]
- Arun, P.V. A comparative analysis of different DEM interpolation methods. Egypt. J. Remote Sens. Space Sci. 2013, 16, 133–139. [Google Scholar] [CrossRef]
- Candia-Rivera, D.; Valenza, G. Cluster permutation analysis for EEG series based on non-parametric Wilcoxon–Mann–Whitney statistical tests. SoftwareX 2022, 19, 101170. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).