Optimization with Time and Frequency Constraints Using Automatic Differentiation: Application to an Aircraft Electrical Power Channel
Abstract
1. Introduction
- Heuristic methods, which are devoid of derivatives, including techniques such as differential evolution and particle swarm optimization [1,2]. However, the intricate nature of optimization problems associated with power electronic systems, characterized by numerous constraints and complex models, renders the application of derivative-free algorithms quite challenging [3,4];
- For instance, the gradients of such dynamic models in relation to the optimization inputs are particularly elusive due to the occurrence of unpredictable events that can alter the ODE system throughout the dynamic simulation process;
- Furthermore, the sizing criteria must be determined after the steady state of the application has been identified, a condition that remains indeterminate during the design phase. Consequently, it is preferable to simulate the transient state without storing it, thereby conserving memory and eliminating the need for data file writing and reading;
- Regarding Fast Fourier Transform (FFT), many existing methodologies [11,12,13] tend to impose certain prerequisites on the operational model, such as the derivation of frequency-domain characteristics through analytical formulas [14]. Nevertheless, employing FFT can serve as a valuable approach to examining these characteristics through the use of time-domain simulations, provided these operations are computed over a single operating period in a steady state.
2. Methodology
2.1. Hybrid Ordinary Differential Equations (ODEs)
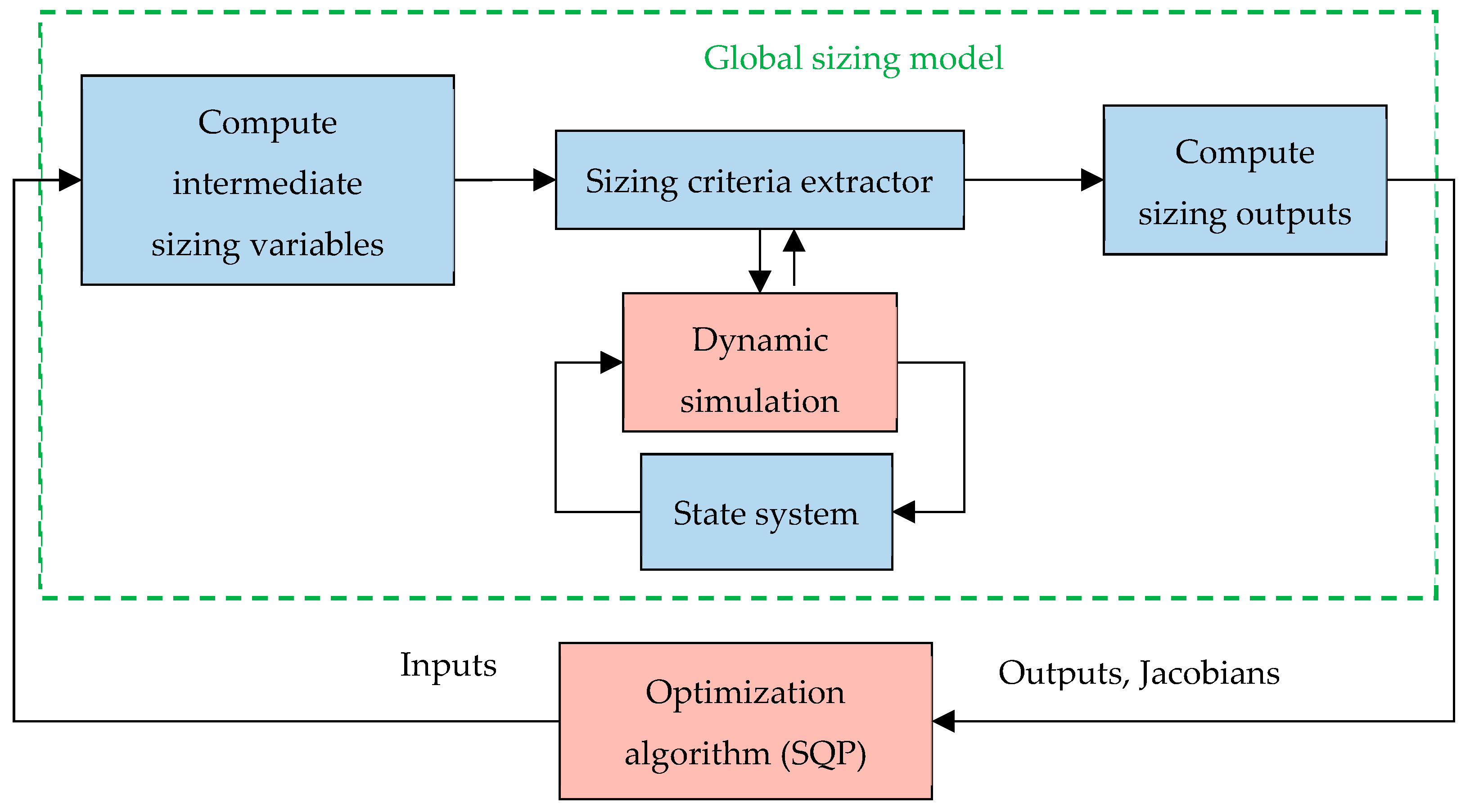
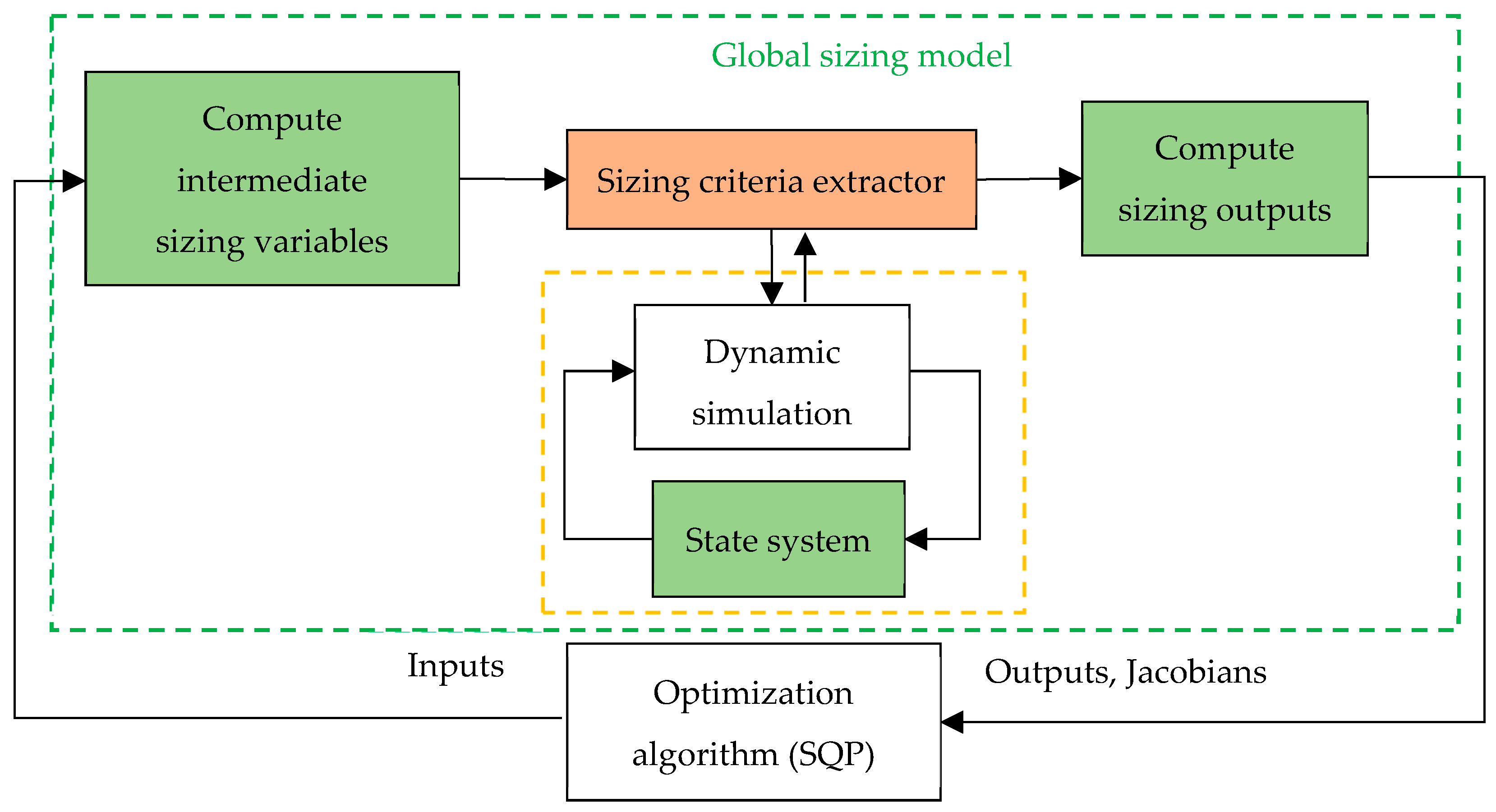
2.2. General Principle of the Methodology
- An ODE system, along with tests designed to detect their variations, enabling the computation of time derivatives of state variables and beyond;
- A time-domain simulator that adeptly resolves problems in regard to ODE systems, yielding the values of state variables throughout the simulation, without necessitating post-processing of the sizing data;
- A criterion for halting the time-domain simulation, which involves the computation of sizing criteria subsequent to the detection of the steady-state conditions;
- An extractor of the sizing criteria that provides both time-domain and frequency-domain features, derived from an FFT computation, and that serve as constraints within the optimization problem;
- The gradient-based optimization algorithm SQP, which adeptly addresses the complexities of nonlinear constrained optimization.
2.3. Derivation Techniques Used
2.3.1. Choice of Derivation Techniques
- For mathematical expressions that vary from one dynamic model to another (e.g., the dynamic model), automatic differentiation (AD) is employed to facilitate user implementation;
- For mathematical expressions that maintain a generic nature across different models (e.g., the computation of sizing criteria), symbolic derivation is utilized to streamline the computational graph of AD [18];
- For the amalgamation of derived numerical methods and mathematical expressions that are generic across different models (e.g., the hybrid ODE solver), a synthesis of AD and symbolic derivation is adopted.
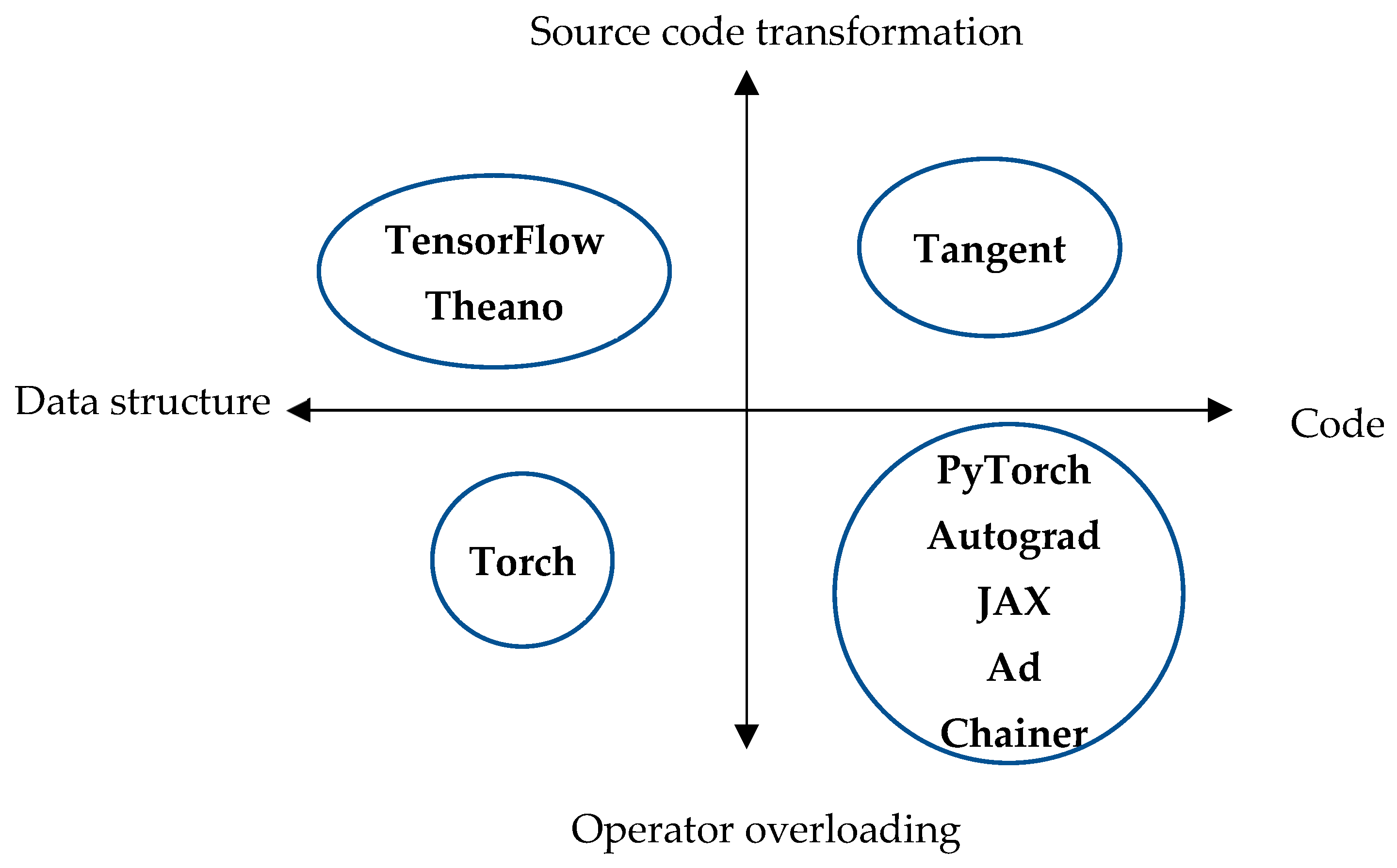
2.3.2. Automatic Differentiation (AD)
- The transformation of source code, which generates a tailored code for the function to be differentiated;
- Operator overloading, which facilitates the real-time computation of derivatives through operations defined within programmed classes.
2.4. Principe of the Hybrid ODE Solver
2.4.1. Resolution Scheme with S-Function Norm
- X is the state vector of length nx, according to the state representation;
- Y is the time output vector of length ny, according to the state representation;
- t is the simulation time;
- I is the sizing input vector of length nI;
- f and g are the vector and C2 class function.
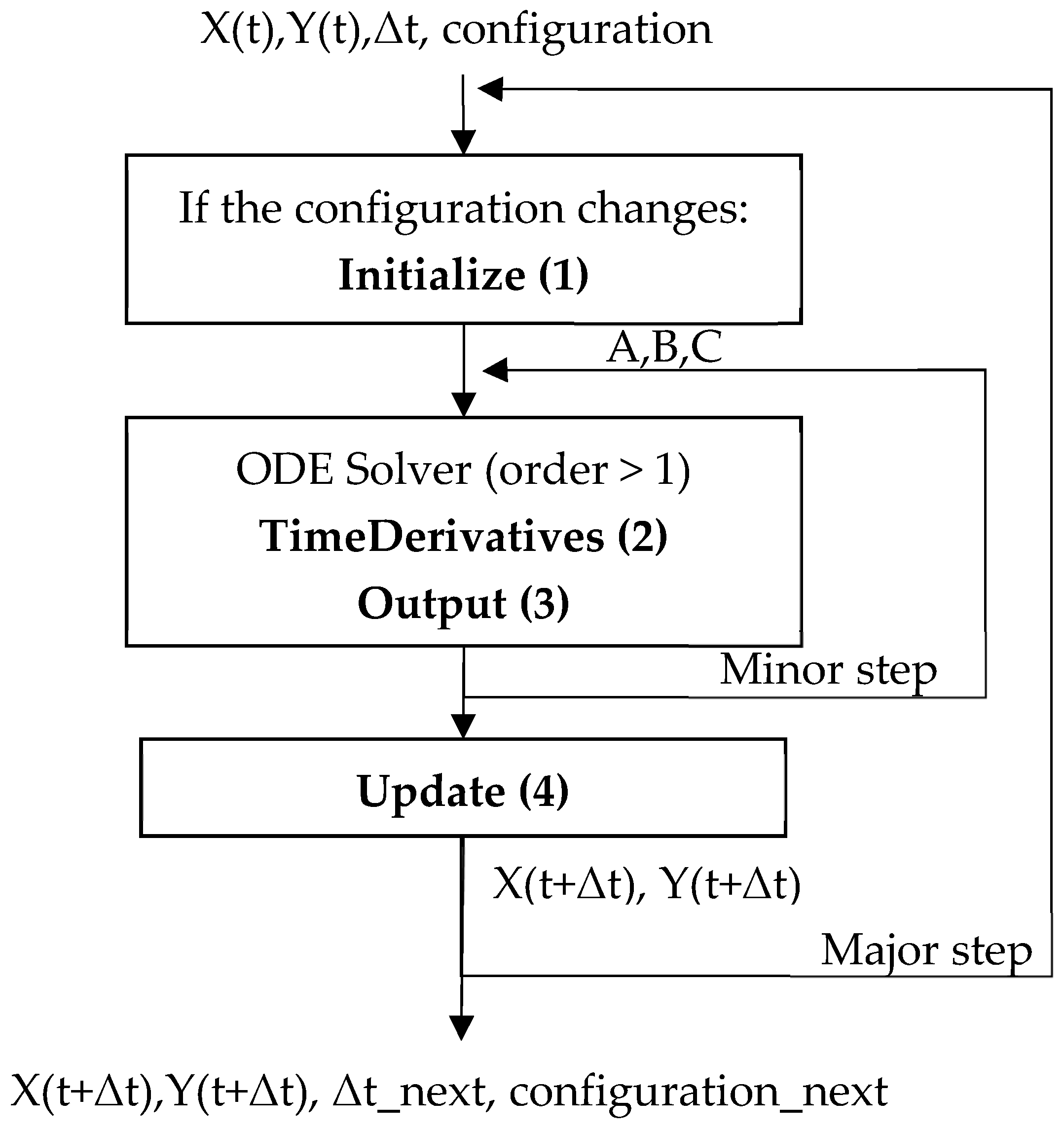
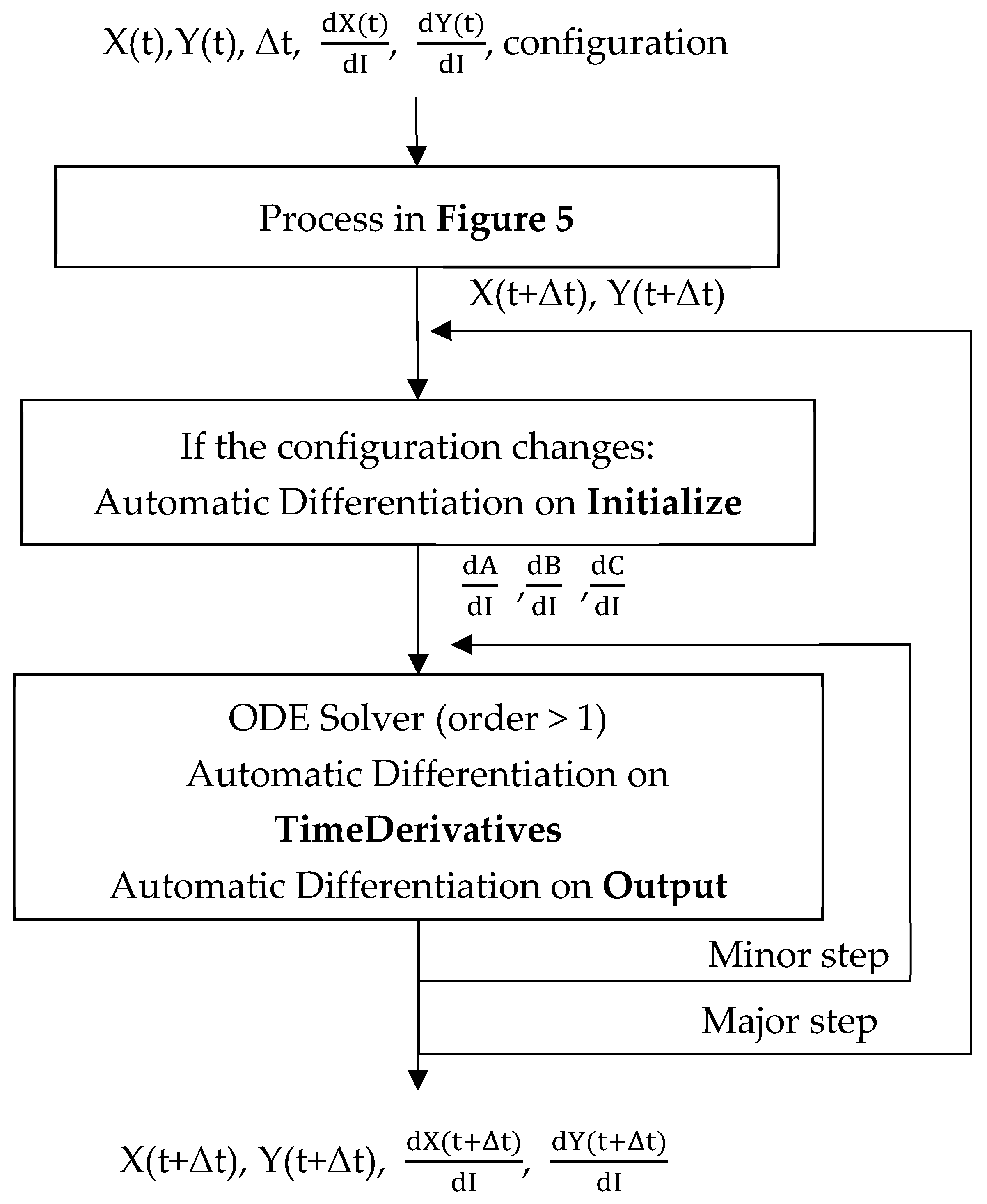
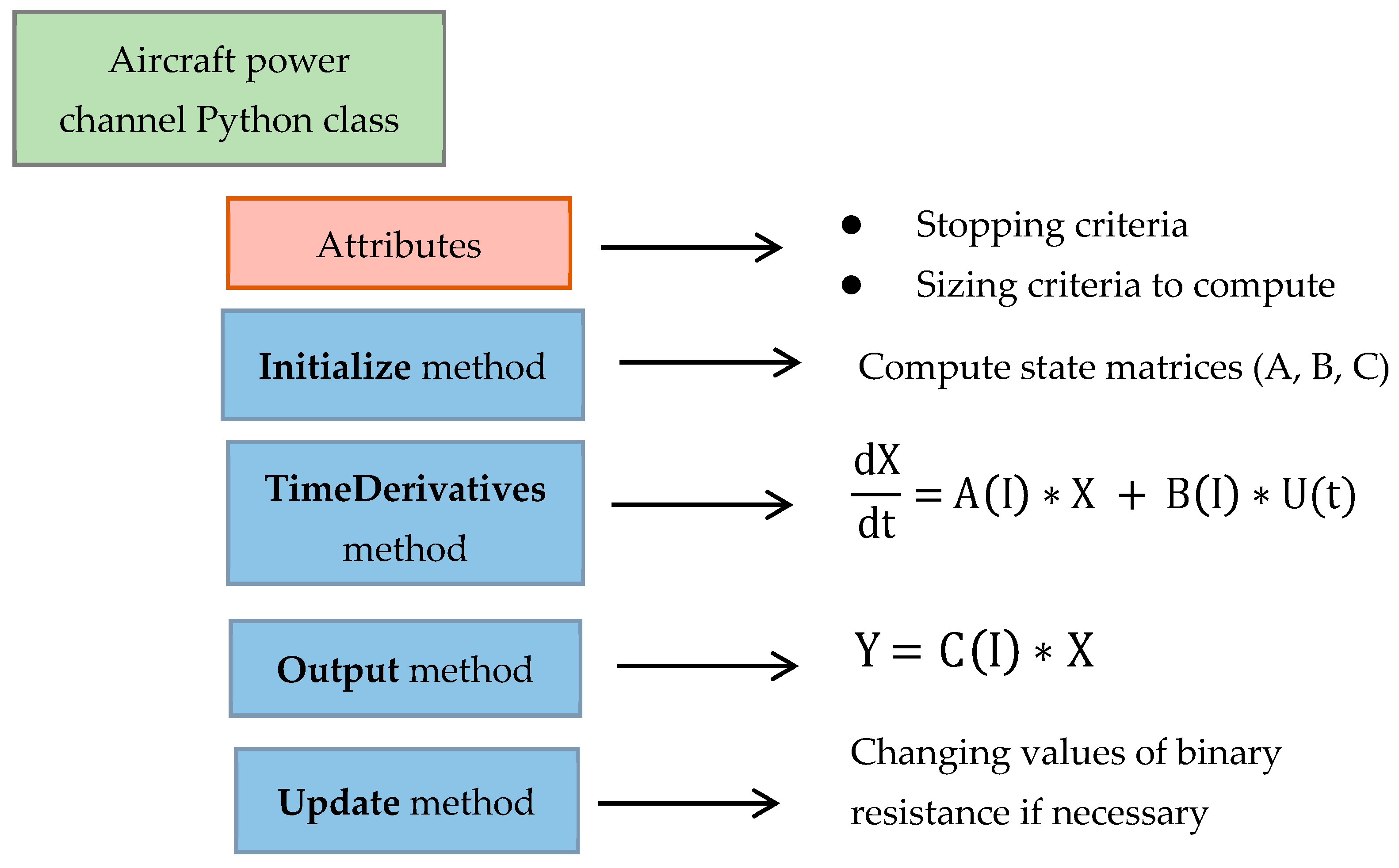
- Initialize (block (1) in Figure 5) provides the state matrices A, B, and C (refer to Appendix A), which are employed to compute the state and output vectors, but only if the circuit configuration has been altered since the previous iteration;
- Output (block (3) in Figure 5) generates the time output vector;
- Update (block (4) in Figure 5) encompasses the necessary tests to modify the variable resistance (representing the switches) values in response to their state.
2.4.2. Gradients of the Hybrid ODE Solver
2.5. Events Management
2.5.1. The Need for an Adaptive Step Size
- As elucidated in the subsequent subsection, certain events transpire during the simulation that necessitate detection in order to modify the model’s configuration. Occasionally, it becomes essential to recompute a simulation point at a prior moment during the simulation. Should a fixed step size be employed for efficiency, it must be exceedingly small, thereby prolonging the computation time of the simulation. Hence, an adaptive time step is favored in this context;
- The simulation must be halted once the sizing criteria have been established. Initially, the steady state of the model must be identified. Subsequently, another operating period must be conducted in a steady state to ascertain the sizing criteria;
- The FFT computation, detailed in the following subsection, necessitates a time-domain simulation recorded at fixed sampling intervals. Consequently, the adaptive time step will be adjusted to capture simulation points that adhere to the sampling period.
2.5.2. Event Detection to Change the Configurations
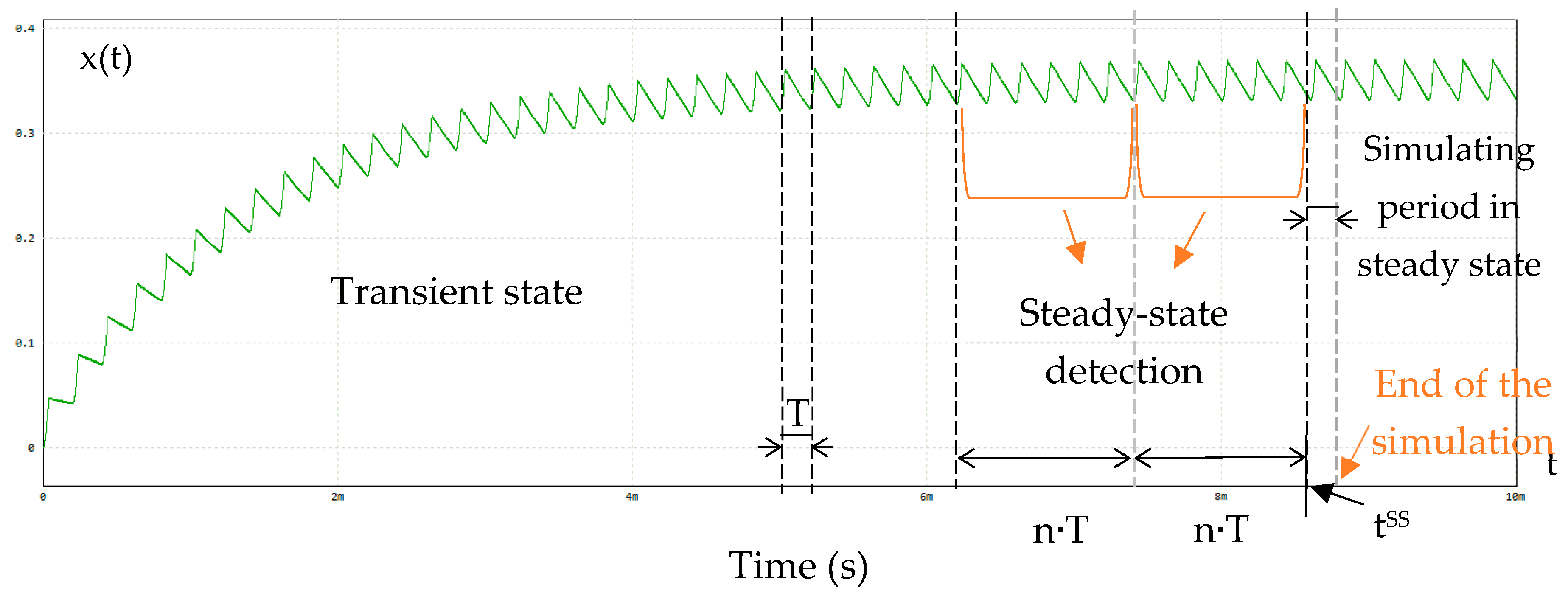
2.5.3. Stopping Criteria: Steady-State Detection
- T is the operating period;
- n is the number of operating periods chosen to detect the steady state;
- tss is the time wherein the steady state is detected.
2.6. Extraction of Sizing Criteria
2.6.1. Time-Domain Features
Extrema Values
2.6.2. Frequency-Domain Features
- x is a component of X, and its FFT;
- M is the number of points in the frequency spectrum.
- Ii is a component of I.
3. Implementation of the Methodology Using the NoLOAD Software
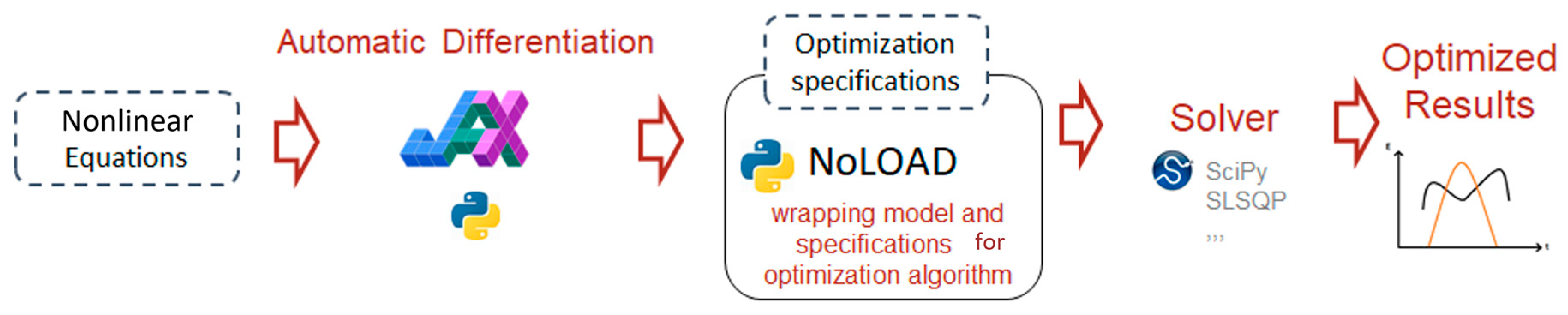
3.1. NoLOAD Software
3.2. Choice of the Solver
- It is widely used in electrical drive problems (containing power electronics models), and is supported by numerous software tools, such as Matlab/Simulink (https://fr.mathworks.com/products/matlab.html);
- Its adaptable variable step size makes it particularly suitable for discrete events and Fast Fourier Transform (FFT) computations.
3.3. Variable Selectivity: Improvement Compared to CADES
3.4. The Automatic Differentiation Library, JAX
3.5. Parts of the Methodology to Be Implemented by the Designer
4. Application to Power Electronics
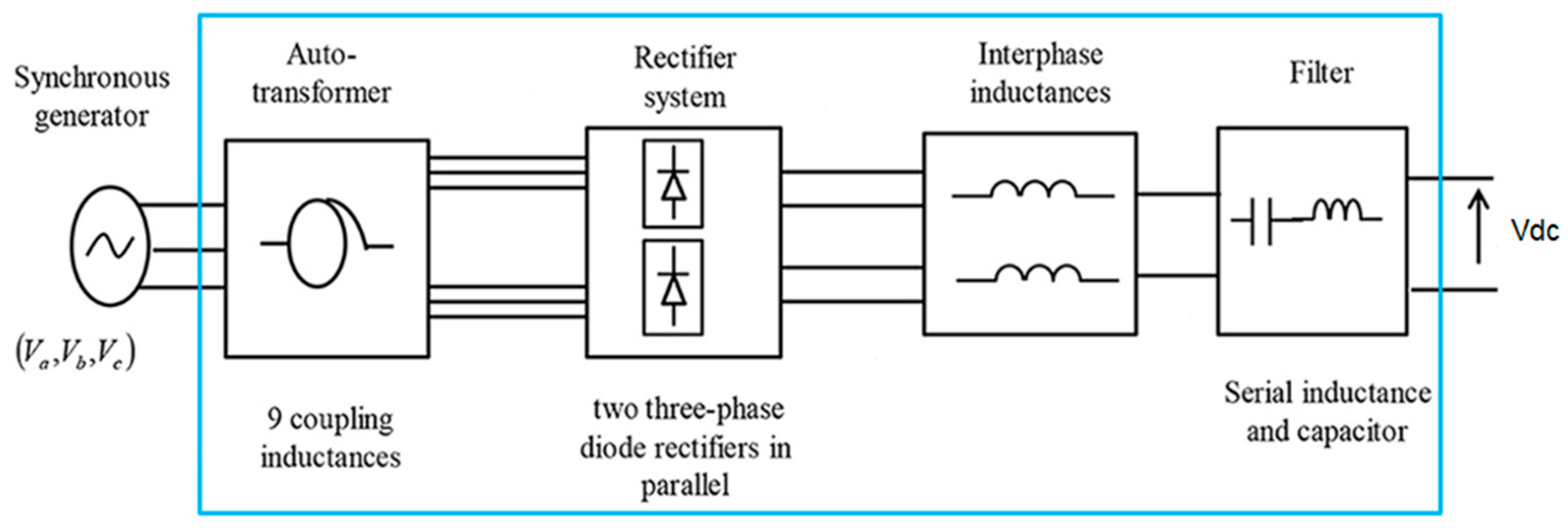
4.1. Presentation of the Application
- (Va, Vb, Vc) = Vs is an AC three-phase voltage source;
- Vdc is the channel output voltage.
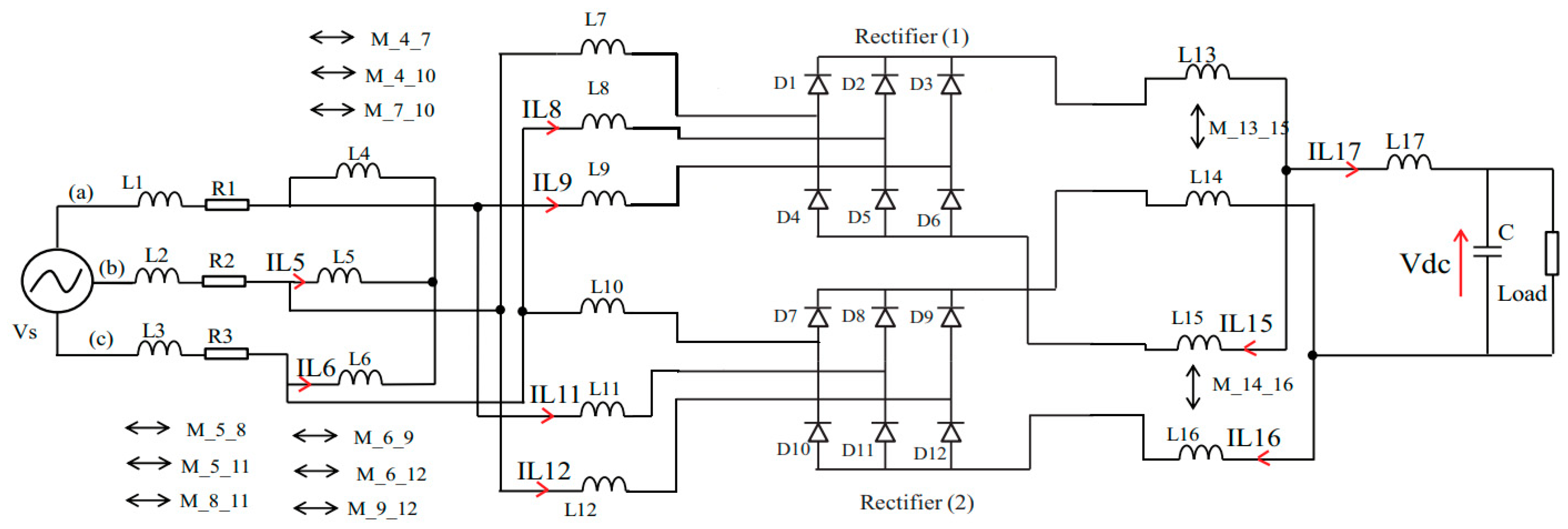
- (a,b,c) corresponds to each of the three-phase of the voltage source.
- f is the frequency of Vs;
- Vdc, iL5, iL6, iL8, iL9, iL11, iL12, iL15, iL16, iL17 are state variables;
- Currents and voltages of diodes D1 to D12 are state outputs, such as the channel input currents iL2, iL3.
- A time-domain simulator (Saber) was employed, in conjunction with a stochastic particle swarm optimization (PSO) algorithm, successfully resolving the optimization challenge within a time span of 2 days for a single run;
- SQP was utilized, alongside a finite difference method, to compute the gradients. An analytical model was crafted to ascertain the frequency-domain characteristics, albeit with a priori knowledge regarding operational modes. This necessitated that the sizing was conducted based on these modes, consequently narrowing the solution space. This optimization problem was also resolved in 2 h for one run.
4.2. Specifications in Terms of the Optimization Problem
4.2.1. Optimization Inputs
4.2.2. Optimization Constraints
- Geometric constraint: the Routh Criterion, which must remain positive. To compute this value, a global equivalent circuit of the aircraft power channel was established, based on an RL series circuit [11]. It was achieved by bringing all the resistance and inductance components to the continuous side. Therefore, the Routh Criterion is applied in this linear continuous system, which represents the global behavior of the system;
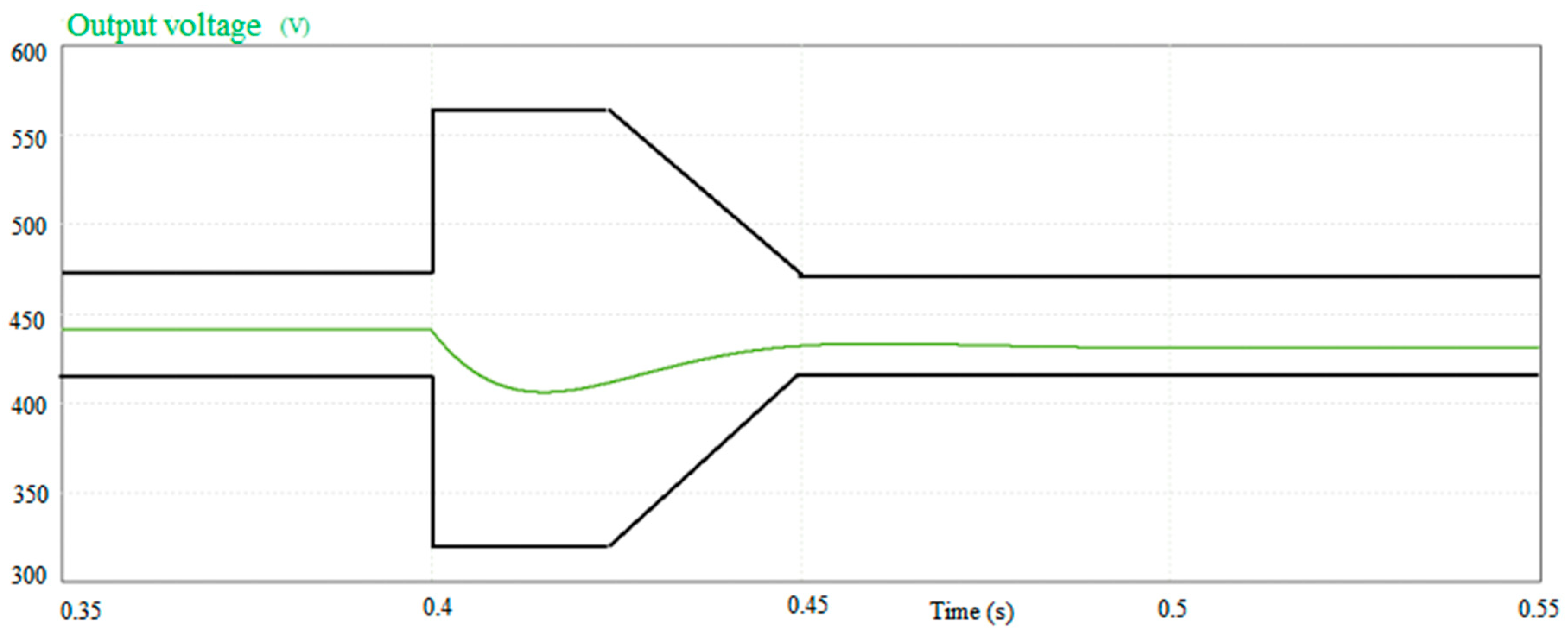
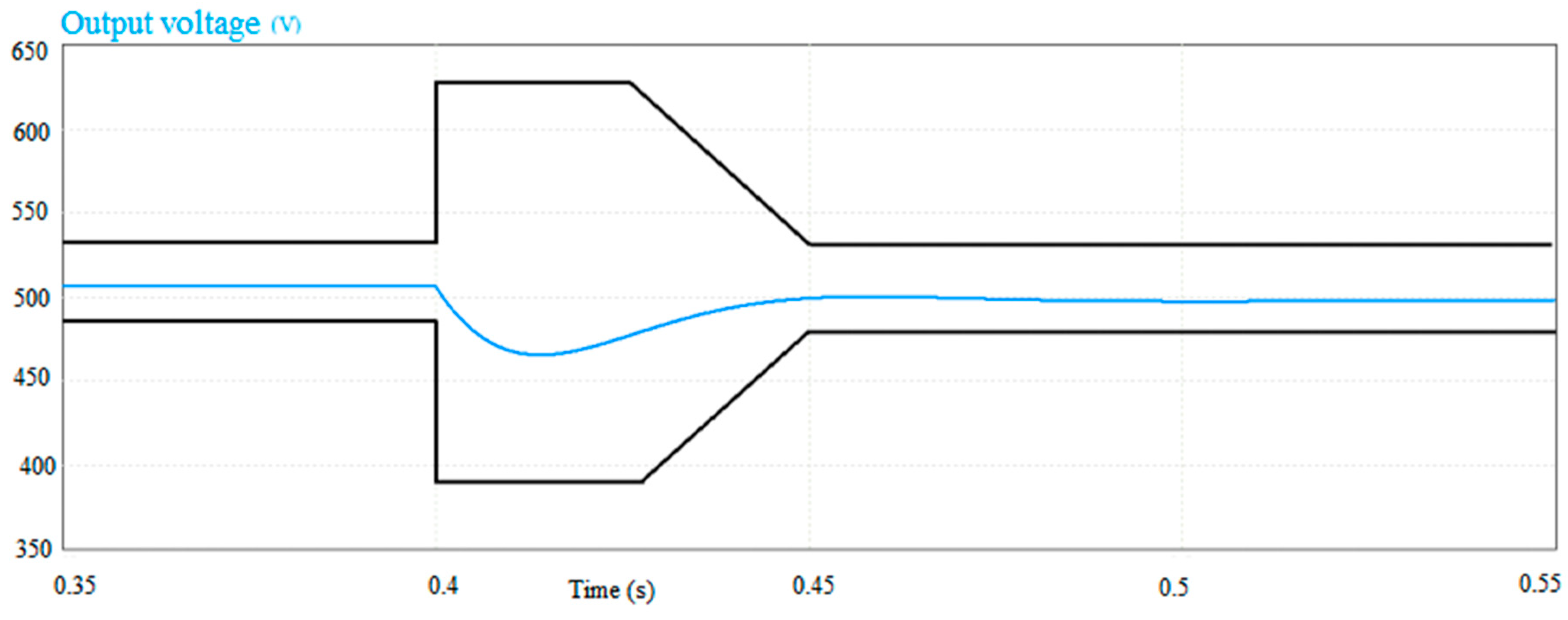
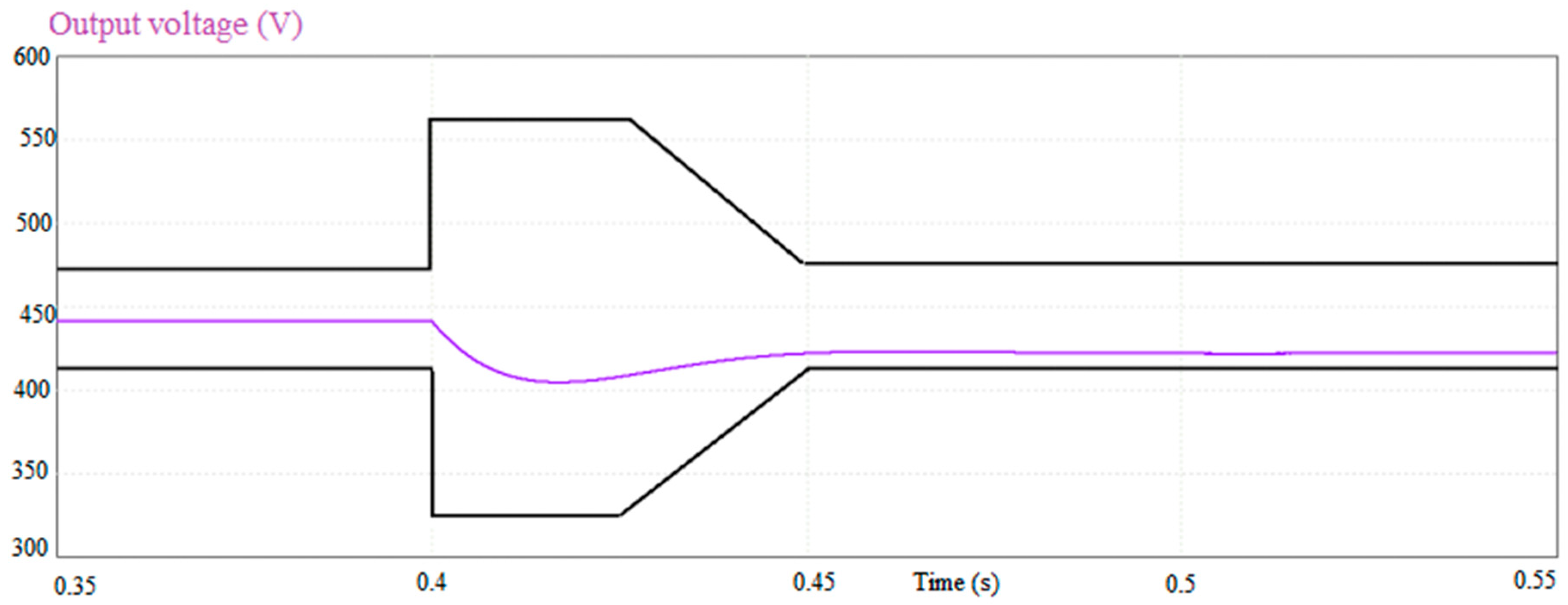
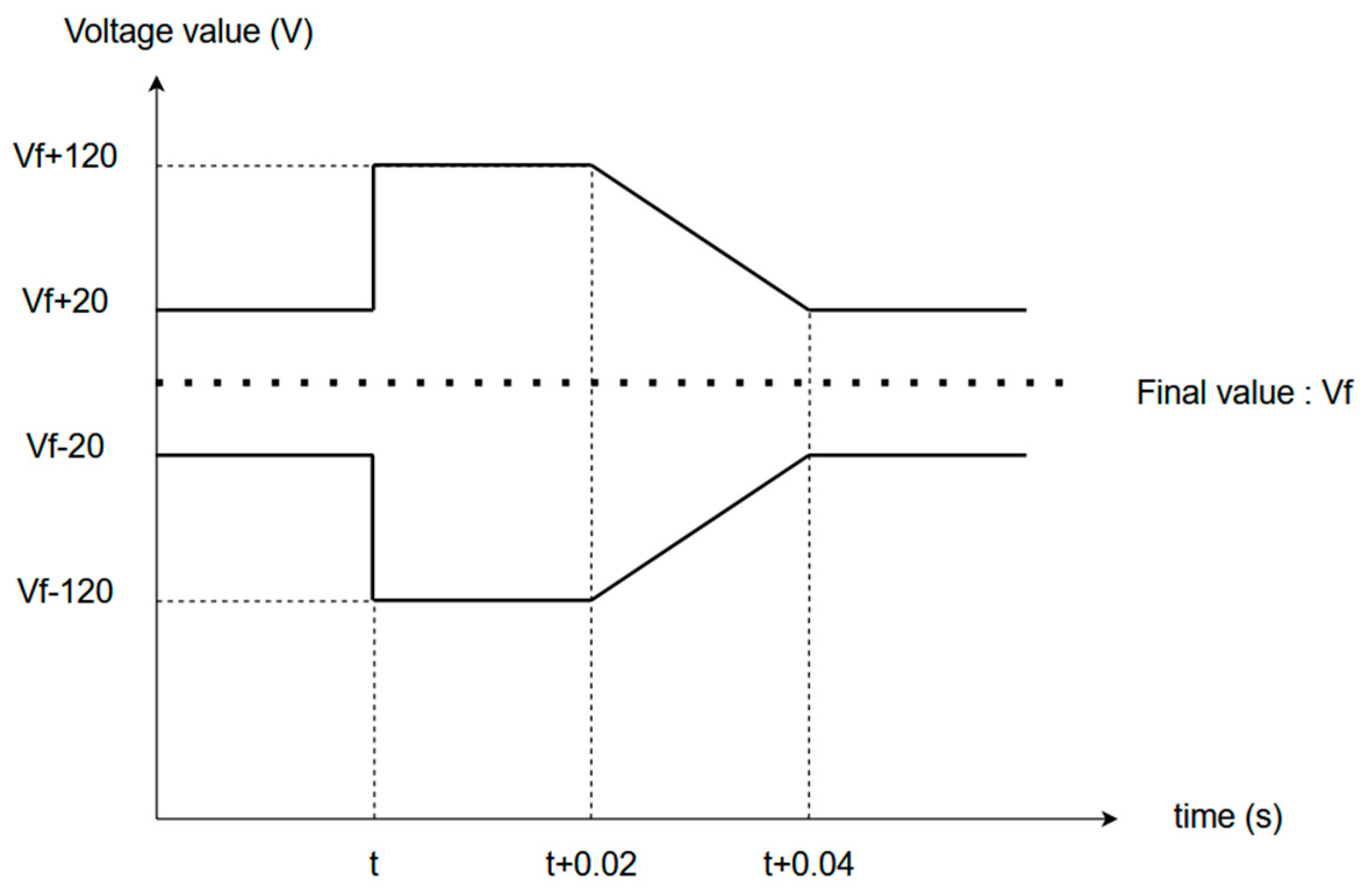
- Time-domain constraint: Upon achieving a steady state, the ‘Load’ resistance depicted in Figure 11 is diminished by one-eighth of its size to induce a disturbance and initiate a new transient state. During this transient phase, the channel’s output voltage (Vdc) must conform to the template illustrated in Figure 12. At each computational interval, should the output voltage (Vdc) deviate from the prescribed template, the constraint value is augmented by the discrepancy between the actual output and the template’s bounds. For the constraint to be satisfied, it must equate to zero. The gradients of this constraint concerning the optimization inputs are derived through automatic differentiation, as no analytical formula exists.
- 1 is the FFT of x when the frequency is equal to the fundamental one (400 Hz);
- k is the harmonic order (from k = 2 for f = 800 Hz, to k = 37 for f = 14800 Hz).
- 1 equality constraint (the time-domain constraint);
- 36 inequality constraints for the frequency-domain constraints (each corresponding performance constrained by an upper bound);
- 1 inequality constraint for the Routh Criteria, which is only constrained by a minimum value (it must be positive).
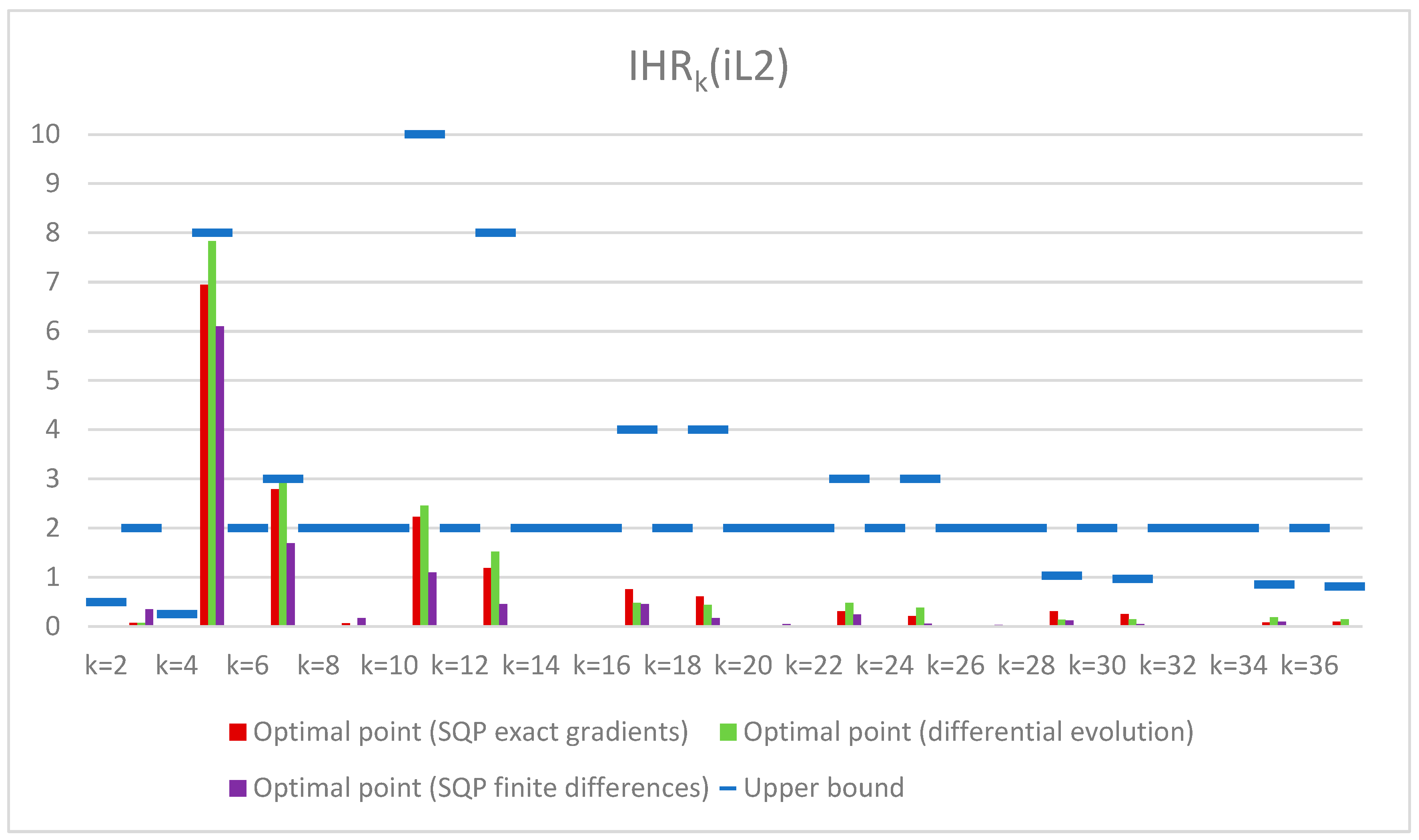
- IHR () means the Individual Harmonic Rate of the channel input current iL2.
4.3. Modelling of the Aircraft Power Channel
- A, B, C are state matrices depending on the optimization inputs, I;
- U is the AC three-phase voltage source vector.
- 600 lines of code, inclusive of the dynamic component’s description;
- 200 intermediate equations that model the electrical parameters derived from the geometric parameters;
- the equations governing the optimization outputs in relation to the optimization inputs (for instance, the total mass of the application and the Routh Criteria).
4.4. The Optimization Procedure
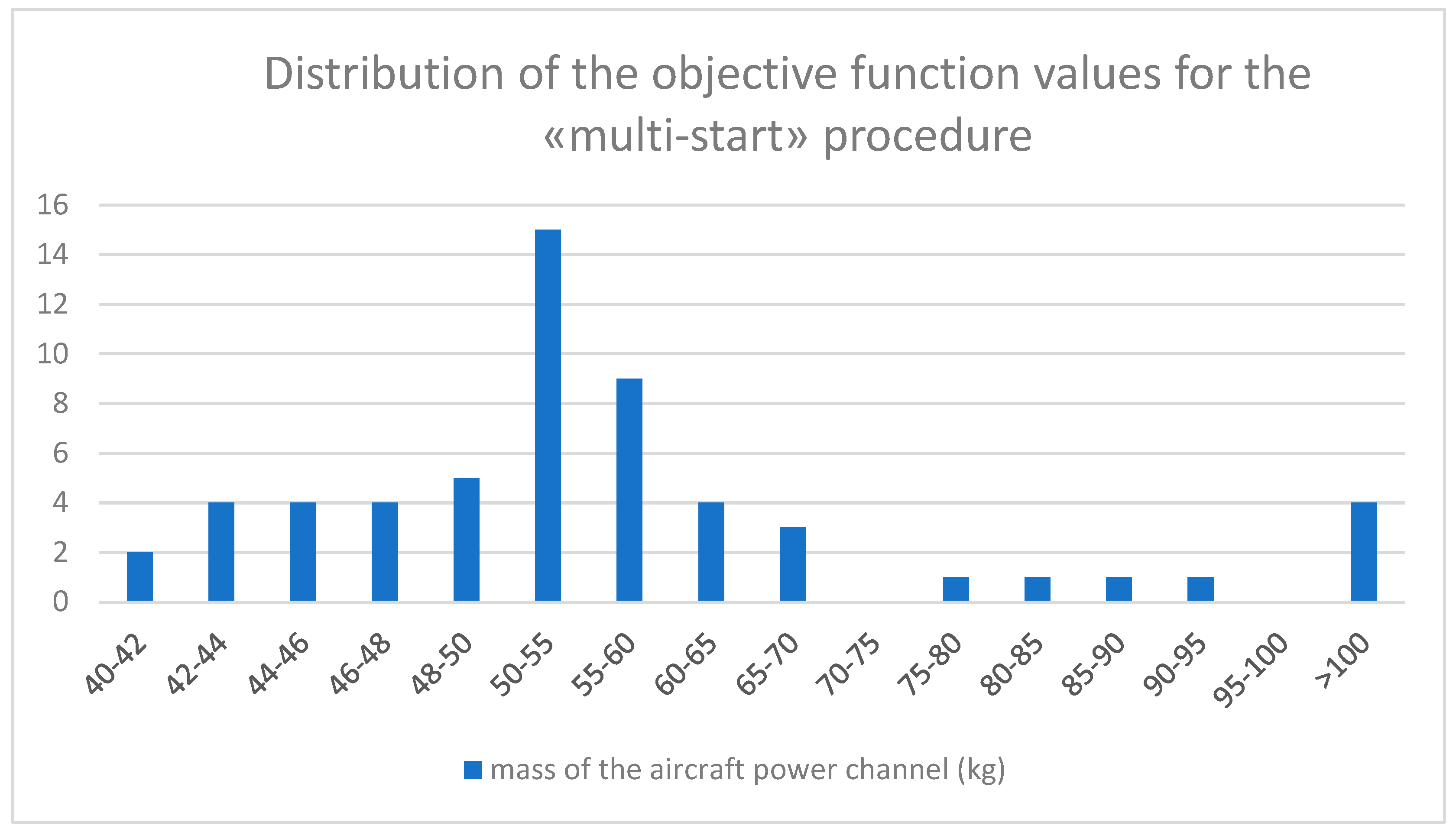
- The SQP algorithm, derived from the SciPy package, employs a «multi-start» strategy. This algorithm is executed ten times, each time initiated from randomly selected starting points, and the optimal solution that most effectively minimizes the objective function is subsequently selected. Thus, the robustness of the SQP will be improved;
- The stochastic differential evolution algorithm, also derived from the SciPy package, operates with a population of 100 individuals and is constrained in regard to a maximum of 500 generations. Given its stochastic nature, this algorithm is executed thrice to ensure that the optimal solution remains consistent across all the iterations.
4.5. The Choice of Parameters for the Simulation
4.6. Results of the Optimization Problem
4.6.1. Application Aspect
4.6.2. Computational Cost Aspect
5. Discussion
- A specialized ‘white-box’ solver has been meticulously crafted to simulate systems governed by ordinary differential equations (ODEs), particularly those that are hybrid in nature. The expressions governing these systems are subject to change in response to unpredictable events;
- This solver possesses the remarkable ability to automatically detect when a power electronics application has attained a steady state;
- It is also equipped to extract salient features from both time-domain and frequency-domain simulations, which can subsequently be utilized as outputs for optimization;
- Furthermore, the solver is amenable to differentiation; the derivatives concerning the optimization inputs are computed through automatic differentiation for time-domain simulations, while formulas are employed for feature extraction.
6. Future Perspectives for the Methodology
- Currently, it addresses optimization problems involving continuous variables; an extension to accommodate discrete variables is necessary;
- The paper presents a sizing approach for power electronics applications. It would be advantageous to extend this methodology to address optimization problems that encompass both sizing and optimal control, such as energy management in regard to microgrids. The integration of optimal control could be incorporated into the dynamic simulations of the proposed methodology;
- Surrogate-based algorithms yield greater precision when gradients are incorporated, thus the methodology should be employed alongside such algorithms to facilitate the sizing of larger systems characterized by state spaces with more dimensions;
- Optimization problems involving a larger number of constraints, and of greater complexity, could, in theory, be addressed using this methodology. However, the limitations regarding the computation of the Jacobian matrix (in relation to the inputs) must be clearly defined;
- The availability of gradients enables the efficient computation of global sensitivity analysis for a model using the DGSM algorithm [51];
- It would be valuable to establish a connection between this methodology and other design environments. Indeed, modeling power electronics applications remains partially manual in nature, as the designer is required to encode the model within Python script. In some instances, this process can be tedious, whereas other environments, such as Matlab/Simulink, provide a more intuitive block-based approach, facilitating ease of use for the designer (especially when incorporating FMU component standards). These aspects could potentially serve as an advanced layer of modeling for NoLOAD. However, it is worth noting that models encapsulated within FMU components become non-differentiable ‘black boxes’, necessitating the evolution of these standards;
- Hybridized optimization approaches, which merge gradient-based and global methods, such as SQP with differential evolution, could have been employed to address our optimization problem, thereby obviating the need for the ‘multi-start’ procedure.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AD | Automatic differentiation |
| FFT | Fast Fourier Transform |
| JIT | Just-In-Time |
| RK | Runge–Kutta |
| SQP | Sequential Quadratic Programming |
Appendix A
- X: Vdc, iL5, iL6, iL8, iL9, iL11, iL12, iL15, iL16, il17;
- Y: iR1, iR2, iR3, iR4, iR5, iR6, iR7, iR7, iR9, iR10, iR11, iR12, iD1, iD2, iD3, iD4, iD5, iD6, iD7, iD8, iD9, iD10, iR0, iR5, iR6, iR11, iR12;
- U: Va, Vb, Vc.
- The si matrices are the sub-matrices of the incidence matrix of the aircraft power channel;
- Rb1 is the diagonal matrix of branch resistances;
- Rm2 is the diagonal matrix of mesh resistances;
- MLb1 is the diagonal matrix of branch inductances;
- MLm2 is the diagonal matrix of mesh inductances;
- MC1 is the diagonal matrix of branch capacitances;
- Id is the identity matrix of the same dimension of Rb1.
Appendix B
| Harmonic Order (k) | Upper Bound (in %) | Initial Point (SQP) | Optimal Point (SQP Exact Gradients/Finite Differences) | Optimal Point (Differential Evolution) |
|---|---|---|---|---|
| k = 2 | IHRk < 0.5 | 0.028 | 0.014/0.023 | 0.005 |
| k = 3 | IHRk < 2 | 0.62 | 0.075/0.35 | 0.077 |
| k = 4 | IHRk < 0.25 | 0.010 | 0.0014/0.011 | 0.0045 |
| k = 5 | IHRk < 8 | 0.79 | 6.94/6.1 | 7.83 |
| k = 6 | IHRk < 2 | 0.0057 | 0.0059/0.007 | 0.0032 |
| k = 7 | IHRk < 3 | 2.80 | 2.80/1.69 | 3.00 |
| k = 8 | IHRk < 2 | 0.0066 | 0.00064/0.0046 | 0.0015 |
| k = 9 | IHRk < 2 | 0.15 | 0.069/0.169 | 0.056 |
| k = 10 | IHRk < 2 | 0.0025 | 0.0029/0.0051 | 0.0020 |
| k = 11 | IHRk < 10 | 0.44 | 2.23/1.10 | 2.45 |
| k = 12 | IHRk < 2 | 0.0033 | 0.0038/0.0034 | 0.0026 |
| k = 13 | IHRk < 8 | 0.78 | 1.19/0.46 | 1.52 |
| k = 14 | IHRk < 2 | 0.0031 | 0.0011/0.0010 | 0.0013 |
| k = 15 | IHRk < 2 | 0.042 | 0.014/0.019 | 0.020 |
| k = 16 | IHRk < 2 | 0.0011 | 0.0014/0.0024 | 0.00039 |
| k = 17 | IHRk < 4 | 0.15 | 0.76/0.46 | 0.48 |
| k = 18 | IHRk < 2 | 0.0016 | 0.0020/0.0020 | 0.0012 |
| k = 19 | IHRk < 4 | 0.26 | 0.61/0.17 | 0.44 |
| k = 20 | IHRk < 2 | 0.0018 | 0.0014/0.0012 | 0.00044 |
| k = 21 | IHRk < 2 | 0.025 | 0.022/0.05 | 0.019 |
| k = 22 | IHRk < 2 | 0.00068 | 0.00015/0.002 | 0.00091 |
| k = 23 | IHRk < 3 | 0.12 | 0.31/0.25 | 0.49 |
| k = 24 | IHRk < 2 | 0.00070 | 0.0015/0.0016 | 0.0011 |
| k = 25 | IHRk < 3 | 0.12 | 0.21/0.061 | 0.38 |
| k = 26 | IHRk < 2 | 0.00088 | 0.00012/0.00039 | 0.00057 |
| k = 27 | IHRk < 2 | 0.038 | 0.013/0.031 | 0.012 |
| k = 28 | IHRk < 2 | 0.00031 | 0.0012/0.0014 | 0.00033 |
| k = 29 | IHRk < 1.035 | 0.064 | 0.31/0.12 | 0.14 |
| k = 30 | IHRk < 2 | 0.00051 | 0.0012/0.0013 | 0.00051 |
| k = 31 | IHRk < 0.968 | 0.047 | 0.25/0.05 | 0.15 |
| k = 32 | IHRk < 2 | 0.00019 | 0.00093/0.00021 | 0.00044 |
| k = 33 | IHRk < 2 | 0.038 | 0.0089/0.013 | 0.011 |
| k = 34 | IHRk < 2 | 0.0000683 | 0.00029/0.0011 | 0.00043 |
| k = 35 | IHRk < 0.857 | 0.043 | 0.083/0.098 | 0.19 |
| k = 36 | IHRk < 2 | 0.00077 | 0.00078/0.00083 | 0.00082 |
| k = 37 | IHRk < 0.811 | 0.052 | 0.100/0.014 | 0.15 |
- Figure A1 illustrates the time-domain constraint associated with the initial point utilized for the SQP method;
- Figure A2 depicts the time-domain constraint for the optimal point derived from SQP employing exact gradients;
- Figure A3 showcases the time-domain constraint for the optimal point obtained through the finite difference method within the SQP framework;
- Figure A4 presents the time-domain constraint for the optimal point identified via differential evolution.

References
- AStork, J.; Eiben, A.E.; Bartz-Beielstein, T. A new taxonomy of global optimization algorithms. Nat. Comput. 2022, 21, 219–242. [Google Scholar] [CrossRef]
- Conn, A.R.; Katya, S.; Luis, N.V. Introduction to Derivative-Free Optimization; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2009. [Google Scholar]
- Larson, J.; Menickelly, M.; Wild, S.M. Derivative-free optimization methods. Acta Numer. 2019, 28, 287–404. [Google Scholar] [CrossRef]
- Kramer, O.; Ciaurri, D.E.; Koziel, S. Derivative-free optimization. In Computational Optimization, Methods and Algorithms; Springer: Berlin/Heidelberg, Germany, 2011; pp. 61–83. [Google Scholar]
- Brilli, A.; Liuzzi, G.; Lucidi, S. An interior point method for nonlinear constrained derivative-free optimization. Optim. Methods Softw. 2021, 1–39. [Google Scholar] [CrossRef]
- Liu, F.; Fredriksson, A.; Markidis, S. A survey of HPC algorithms and frameworks for large-scale gradient-based nonlinear optimization. J. Supercomput. 2022, 78, 17513–17542. [Google Scholar] [CrossRef]
- Haji, S.H.; Abdulazeez, A.M. Comparison of optimization techniques based on gradient descent algorithm: A review. PalArch’s J. Archaeol. Egypt/Egyptol. 2021, 18, 2715–2743. [Google Scholar]
- Khatouri, H.; Benamara, T.; Breitkopf, P. Metamodeling techniques for CPU-intensive simulation-based design optimization: A survey. Adv. Model. Simul. Eng. Sci. 2022, 9, 1. [Google Scholar] [CrossRef]
- Laurent, L.; Le Riche, R.; Soulier, B.; Boucard, P.-A. An overview of gradient-enhanced metamodels with applications. Arch. Comput. Methods Eng. 2017, 26, 61–106. [Google Scholar] [CrossRef]
- Gramacy, R.B.; Gray, G.A.; Le Digabel, S.; Lee, H.K.; Ranjan, P.; Wells, G.; Wild, S.M. Modeling an augmented Lagrangian for blackbox constrained optimization. Technometrics 2016, 58, 1–11. [Google Scholar] [CrossRef]
- Tran, L.N.H.; Gerbaud, L.; Retière, N.; Nguyen Huu, H. Use of SQP optimization algorithm to size a multiphysical system: Application to an aircraft electrical power channel. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2018, 37, 661–680. [Google Scholar] [CrossRef]
- Liu, F.; Fredriksson, A.; Markidis, S. Integrated optimal design for hybrid electric powertrain of future aircrafts. Energies 2022, 15, 6719. [Google Scholar] [CrossRef]
- Ammouri, A.; Salah, T.B.; Morel, H. A spiral planar inductor: An experimentally verified physically based model for frequency and time domains. Int. J. Numer. Model. Electron. Netw. Devices Fields 2017, 31, e2272. [Google Scholar] [CrossRef]
- Voldoire, A.; Schanen, J.-L.; Ferrieux, J.-P.; Sarrazin, B.; Gautier, C.; Ali, M. Using Deterministic Optimization to Compare Interleaved and Coupled Inverters: Results and Experimental Verification. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 5401–5408. [Google Scholar] [CrossRef]
- Shi, H.-J.; Xuan, M.; Oztoprak, F.; Nocedal, J. On the Numerical Performance of Derivative-Free Optimization Methods Based on Finite-Difference Approximations. arXiv 2021, arXiv:2102.09762. [Google Scholar]
- Agobert, L.; Delinchant, B.; Gerbaud, L. Optimization on frequency constraints with FFT using Automatic Differentiation on hybrid ODE applications. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2024, 43, 821–838. [Google Scholar] [CrossRef]
- Boggs, P.T.; Tolle, J.W. Sequential Quadratic Programming. Acta Numer. 1995, 4, 1–51. [Google Scholar] [CrossRef]
- Enciu, P.; Wurtz, F.; Gerbaud, L.; Delinchant, B. AD for optimization in electromagnetism applied to semi analytical models combining composed functions. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2009, 5, 1313–1326. [Google Scholar] [CrossRef]
- Gebremedhin, A.H.; Andrea, W. An introduction to algorithmic differentiation. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2020, 10, e1334. [Google Scholar]
- Forth, S.; Hovland, P.; Phipps, E.; Utke, J.; Walther, A. (Eds.) Recent Advances in Algorithmic Differentiation; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Available online: https://autodiff.org/ (accessed on 20 February 2025).
- Hansen, S.T.; Gomes, C.Â.; Najafi, M.; Sommer, T.; Blesken, M.; Zacharias, I.; Kotte, O.; Mai, P.R.; Schuch, K.; Wernersson, K.; et al. The FMI 3.0 Standard Interface for Clocked and Scheduled Simulations. Electronics 2022, 11, 3635. [Google Scholar] [CrossRef]
- Ozana, S.; Machácek, Z. Implementation of the mathematical model of a generating block in matlab and simulink using s-functions. In Proceedings of the 2009 Second International Conference on Computer and Electrical Engineering, Dubai, United Arab Emirates, 28–30 December 2009; Volume 1, pp. 431–435. [Google Scholar]
- Grace, A.C.W. SIMULAB, An integrated environment for simulation and control. In Proceedings of the 1991 American Control Conference, Edinburgh, UK, 25–28 March 1991. [Google Scholar]
- Shampine, L.F. Some Practical Runge-Kutta Formulas. Math. Comput. 1986, 46, 135–150. [Google Scholar] [CrossRef]
- Kiehl, M. Sensitivity Analysis of ODEs and DAEs—Theory and Implementation Guide. Optim. Methods Softw. 1999, 10, 803–821. [Google Scholar] [CrossRef]
- Serban, R.; Linda, R.P. Efficient computation of sensitivities for ordinary differential equation boundary value problems. SIAM J. Numer. Anal. 2002, 40, 220–232. [Google Scholar] [CrossRef]
- Normand, O.; Catellani, S.; Champenois, G. Use of simulation in failure detection and diagnosis of an electromechanical system. In Proceedings of the European Conference on Power Electronics and Applications, Aalborg, Denmark, 4–8 September 1992; Volume 4. [Google Scholar]
- Maranesi, P.; Naummi, G.; Vanore, A. Computer-aided design of HF converters: New needs, new tools. In Proceedings of the IECON’94-20th Annual Conference of IEEE Industrial Electronics, Bologna, Italy, 5–9 September 1994; Volume 3. [Google Scholar]
- Gerbaud, L.; Diarra, Z.D.; Chazal, H.; Garbuio, L. Obtaining the most exact Jacobian for the time modelling of a power electronics structures to be used by gradient optimisation algorithms. COMPEL—Int. J. Comput. Math. Electr. Electron. Eng. 2022, 41, 2096–2108. [Google Scholar] [CrossRef]
- Oberst, U. The fast Fourier transform. SIAM J. Control Optim. 2007, 46, 496–540. [Google Scholar] [CrossRef]
- Fontes, G.; Ruelland, R.; Morentin, A.; Meynard, T.; Delamare, G.; Videau, N.; Ziani, A. Fast solver to get steady-state waveforms for power converter design. In Proceedings of the PCIM Europe 2018; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 5–7 June 2018; pp. 1–7. [Google Scholar]
- Available online: https://noload-jax.readthedocs.io/en/latest/ (accessed on 20 February 2025).
- Shampine, L.F.; Mark, W.R. The matlab ode suite. SIAM J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef]
- Delinchant, B.; Duret, D.; Estrabaut, L.; Gerbaud, L.; Nguyen Huu, H.; Du Peloux, B.; Wurtz, F. An optimizer using the software component paradigm for the optimization of engineering systems. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2007, 26, 368–379. [Google Scholar] [CrossRef]
- Ma, Y.; Dixit, V.; Innes, M.J.; Guo, X.J.; Rackauckas, C. A comparison of automatic differentiation and continuous sensitivity analysis for derivatives of differential equation solutions. In Proceedings of the 2021 IEEE High Performance Extreme Computing Conference (HPEC), Waltham, MA, USA, 20–24 September 2021. [Google Scholar]
- Margossian, C.C. A review of automatic differentiation and its efficient implementation. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2019, 9, e1305. [Google Scholar] [CrossRef]
- Available online: https://github.com/google/tangent (accessed on 20 February 2025).
- Al-Rfou, R.; Alain, G.; Almahairi, A.; Angermueller, C.; Bahdanau, D.; Ballas, N.; Bastien, F.; Bayer, J.; Belikov, A.; Belopolsky, A.; et al. Theano: A Python framework for fast computation of mathematical expressions. arXiv 2016, arXiv:1605.02688. [Google Scholar]
- Pang, B.; Erik, N.; Ying, N.W. Deep learning with tensorflow: A review. J. Educ. Behav. Stat. 2020, 45, 227–248. [Google Scholar] [CrossRef]
- Nobel, P. Auto_diff: An automatic differentiation package for Python. In Proceedings of the 2020 Spring Simulation Conference (SpringSim), Fairfax, VA, USA, 18–21 May 2020. [Google Scholar]
- Maclaurin, D.; David, D.; Ryan, P.A. Autograd: Effortless Gradients in Numpy. In Proceedings of the ICML 2015 AutoML workshop, Lille, France, 6–11 July 2015; Volume 238. [Google Scholar]
- Kidger, P.; Cristian, G. Equinox: Neural networks in JAX via callable PyTrees and filtered transformations. arXiv 2021, arXiv:2111.00254. [Google Scholar]
- Tokui, S.; Okuta, R.; Akiba, T.; Niitani, Y.; Ogawa, T.; Saito, S.; Yamazaki Vincent, H. Chainer: A deep learning framework for accelerating the research cycle. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2002–2011. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lerer, A. Automatic Differentiation in Pytorch. 2017. Available online: https://openreview.net/pdf?id=BJJsrmfCZ (accessed on 20 February 2025).
- Available online: https://jax.readthedocs.io/en/latest/ (accessed on 20 February 2025).
- Huu, H.N.; Gerbaud, L.; Retiere, N.; Roudet, J.; Wurtz, F. Analytical modeling of static converters for optimal sizing of on-board electrical systems. In Proceedings of the 2010 IEEE Vehicle Power and Propulsion Conference, Lille, France, 1–3 September 2010; pp. 1–6. [Google Scholar]
- Arranz-Gimon, A.; Zorita-Lamadrid, A.; Morinigo-Sotelo, D.; Duque-Perez, O. A review of total harmonic distortion factors for the measurement of harmonic and interharmonic pollution in modern power systems. Energies 2021, 14, 6467. [Google Scholar] [CrossRef]
- Cappuzzo, F.; Broca, O.; Allain, L. Methodologies and processes to achieve earlier virtual integration of aircraft systems. In Proceedings of the 6th European Conference for Aerospace Sciences, Kraków, Poland, 29 June–3 July 2015. [Google Scholar]
- Merdassi, A.; Laurent, G.; Seddik, B. A new automatic average modelling tool for power electronics systems. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008. [Google Scholar]
- Benoît, D.; Hussein, D.; Frédéric, W.; Lauric, G. Derivative Based Global Sensitivity Analysis for Screening and Robustness Studies of Electromagnetic Devices. In Proceedings of the CEFC’14, Annecy, France, 25–28 May 2014; p. ffhal-01000265f. [Google Scholar]
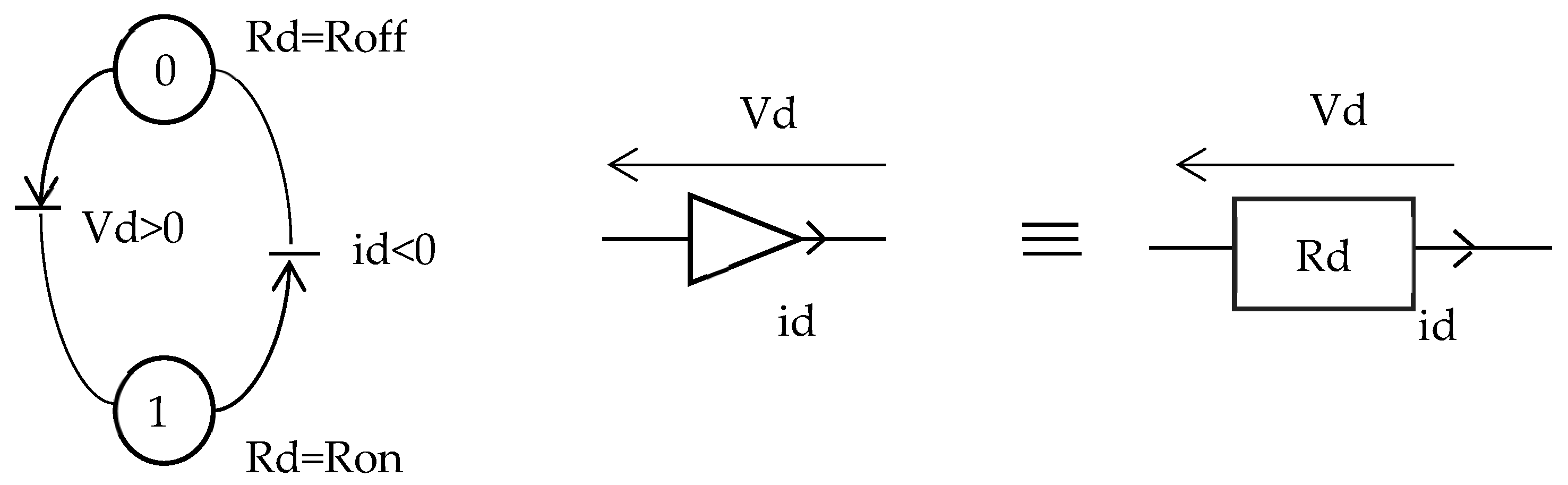
| Name of the Optimization Input and Description | Bounds | |
|---|---|---|
| Min | Max | |
| a1: Coefficient in regard to primary and first secondary coupling matrices | 0.01 | 2.1706 |
| a2: Coefficient in regard to primary and second secondary coupling matrices | 0.01 | 2.1706 |
| kd: Ratio between the winding width and the magnetic core width of the autotransformer | 0.032 | 3.63 |
| np: Number of primary turns for the autotransformer | 10 | 45 |
| kdi: Ratio between the winding width and the magnetic core width of the interphase inductance | 0.02 | 9 |
| ni: Number of primary turns for each interphase inductance | 7 | 203 |
| L17: Filter inductance | 10−6 | 10−4 |
| C: Filter capacitance | 6 × 10−6 | 10−3 |
| kdf: Ratio between the winding width and the magnetic core width of the filter inductance | 0.0013 | 52 |
| nf: Number of filter inductance turns | 1 | 30 |
| Harmonic Order (k) | Upper Bound (in %) |
|---|---|
| k = 3 | IHRk < 2 |
| k = 11 | IHRk < 10 |
| k = 5, 13 | IHRk < 8 |
| k = 17, 19 | IHRk < 4 |
| k = 7, 23, 25 | IHRk < 3 |
| K = 29, 31, 35, 37 | IHRk < 30/k |
| K = 2, 4 | IHRk < 1/k |
| k is a multiple of 3 or is odd | IHRk < 2 |
| Other cases | IHRk < 2 |
| Optimized Inputs | Initial Point (SQP) | Optimal Point (SQP Exact Gradients) | Optimal Point (SQP Finite Differences) | Optimal Point (Differential Evolution) |
|---|---|---|---|---|
| a1 | 0.564 | 0.116 | 0.571 | 0.109 |
| a2 | 0.180 | 0.189 | 0.177 | 0.142 |
| kd | 1.88 | 0.526 | 1.84 | 0.584 |
| np | 14.8 | 37.95 | 15.2 | 41.0 |
| kdi | 2.18 | 0.443 | 2.10 | 0.601 |
| ni | 52.4 | 42.7 | 54.63 | 60.0 |
| L17 | 9.67 × 10−5 | 6.00 × 10−5 | 9.69 × 10−5 | 10−6 |
| C | 9.69 × 10−4 | 8.71 × 10−4 | 9.68 × 10−4 | 5.27 × 10−5 |
| kdf | 43.1 | 0.917 | 0.700 | 0.971 |
| nf | 7.58 | 20.6 | 8.83 | 1.65 |
| Optimized Outputs | Initial Point (SQP) | Optimal Point (SQP Exact Gradients) | Optimal Point (SQP Finite Differences) | Optimal Point (Differential Evolution) |
|---|---|---|---|---|
| Mass of the aircraft power channel (kg) | 138.5 | 41.78 | 95.57 | 39.28 |
| Routh Criteria | 729 (>0) | 1408 (>0) | 975 (>0) | 23 (>0) |
| Transient-state constraint | 0 (=0) | 0 (=0) | 0 (=0) | 0 (=0) |
| Criteria | SQP (Exact Gradients) | SQP (Finite Differences) | Differential Evolution |
|---|---|---|---|
| Number of optimization iterations (one optimization run) | 31 | 13 | 195 |
| Number of model evaluations (one optimization run) | 37 | 149 | 19,985 |
| Number of model gradients evaluations (one optimization run) | 30 | 13 | / |
| Computation time (one optimization run) | 6 min | 1 h 13 min | 2 days 20 h 57 min ≈ 70 h |
| Computation time (with «multi-start» procedure) | 6 min × 58 = 6 h | / | 70 h × 3 = 210 h |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agobert, L.; Gerbaud, L.; Delinchant, B. Optimization with Time and Frequency Constraints Using Automatic Differentiation: Application to an Aircraft Electrical Power Channel. Appl. Sci. 2025, 15, 3624. https://doi.org/10.3390/app15073624
Agobert L, Gerbaud L, Delinchant B. Optimization with Time and Frequency Constraints Using Automatic Differentiation: Application to an Aircraft Electrical Power Channel. Applied Sciences. 2025; 15(7):3624. https://doi.org/10.3390/app15073624
Chicago/Turabian StyleAgobert, Lucas, Laurent Gerbaud, and Benoit Delinchant. 2025. "Optimization with Time and Frequency Constraints Using Automatic Differentiation: Application to an Aircraft Electrical Power Channel" Applied Sciences 15, no. 7: 3624. https://doi.org/10.3390/app15073624
APA StyleAgobert, L., Gerbaud, L., & Delinchant, B. (2025). Optimization with Time and Frequency Constraints Using Automatic Differentiation: Application to an Aircraft Electrical Power Channel. Applied Sciences, 15(7), 3624. https://doi.org/10.3390/app15073624







