Determination of the Fracture Locus of a Cor-Ten Steel at Low and High Triaxiality Ranges
Abstract
1. Introduction
- In the range of negative triaxiality (from −1/3 to 0), the fracture locus can be expressed by an exponential decreasing function.
- In the range of low stress triaxiality (from 0 to 0.4), the fracture locus is best fit by a parabolic function and reaches a local maximum.
- In the range of high stress triaxiality (from 0.4 to 0.95), the fracture locus starts to decrease again according to an exponential function.
- Even if the shape of the fracture locus is specific for each material, as recognized by Bao and Wierzbicki in their study, the general trends of the curve are similar for other metallic materials.
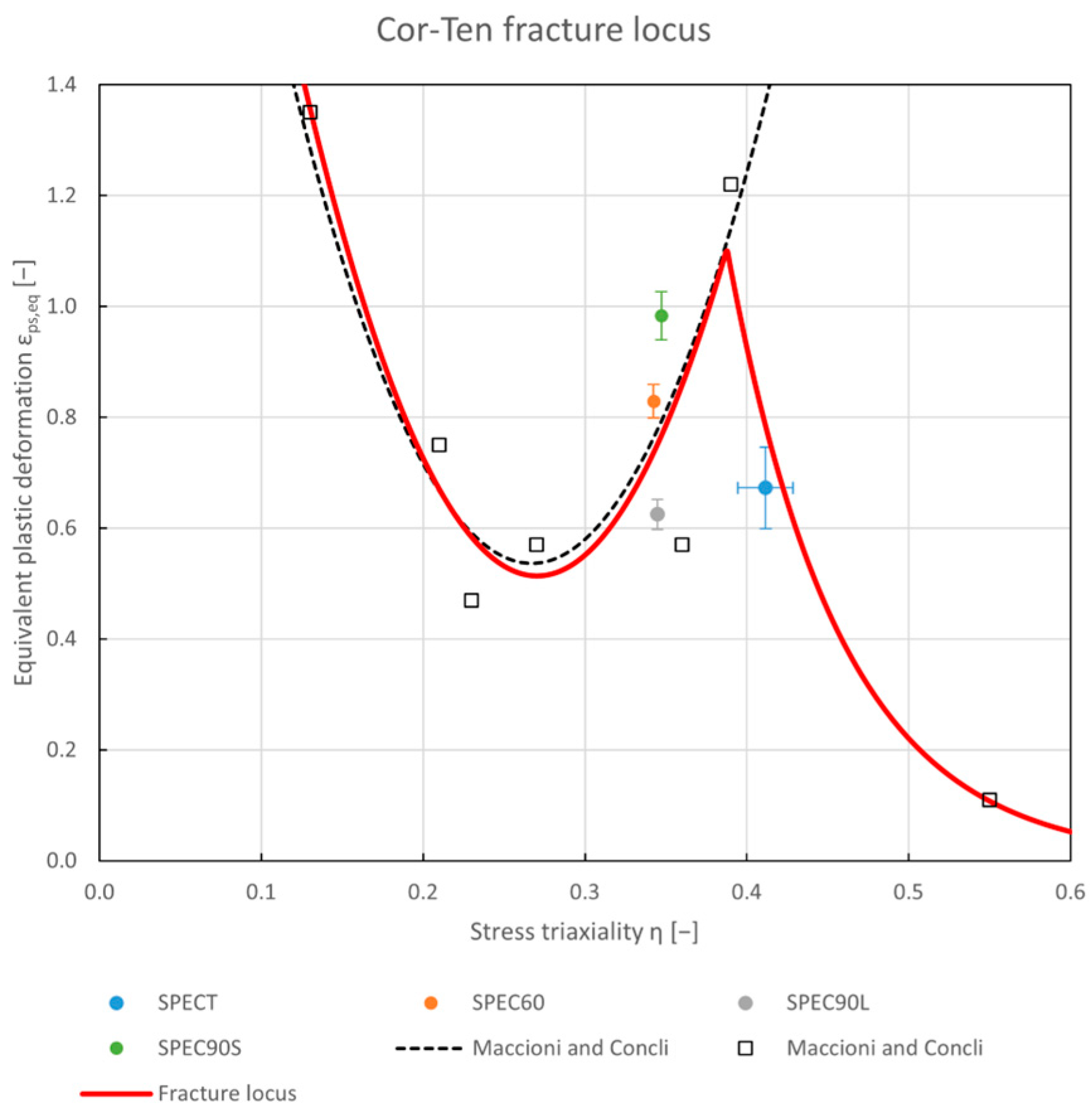
- On the basis of these observations, Maccioni and Concli [6] investigated the fracture locus of a Cor-Ten steel, focusing on the parabolic range. The present study aims to integrate the work carried out by previous authors on this material with the determination of the fracture locus in both the parabolic and exponential ranges, i.e., the low and high triaxiality ranges.
2. Materials and Methods
2.1. Specimens and Tensile Test Machine
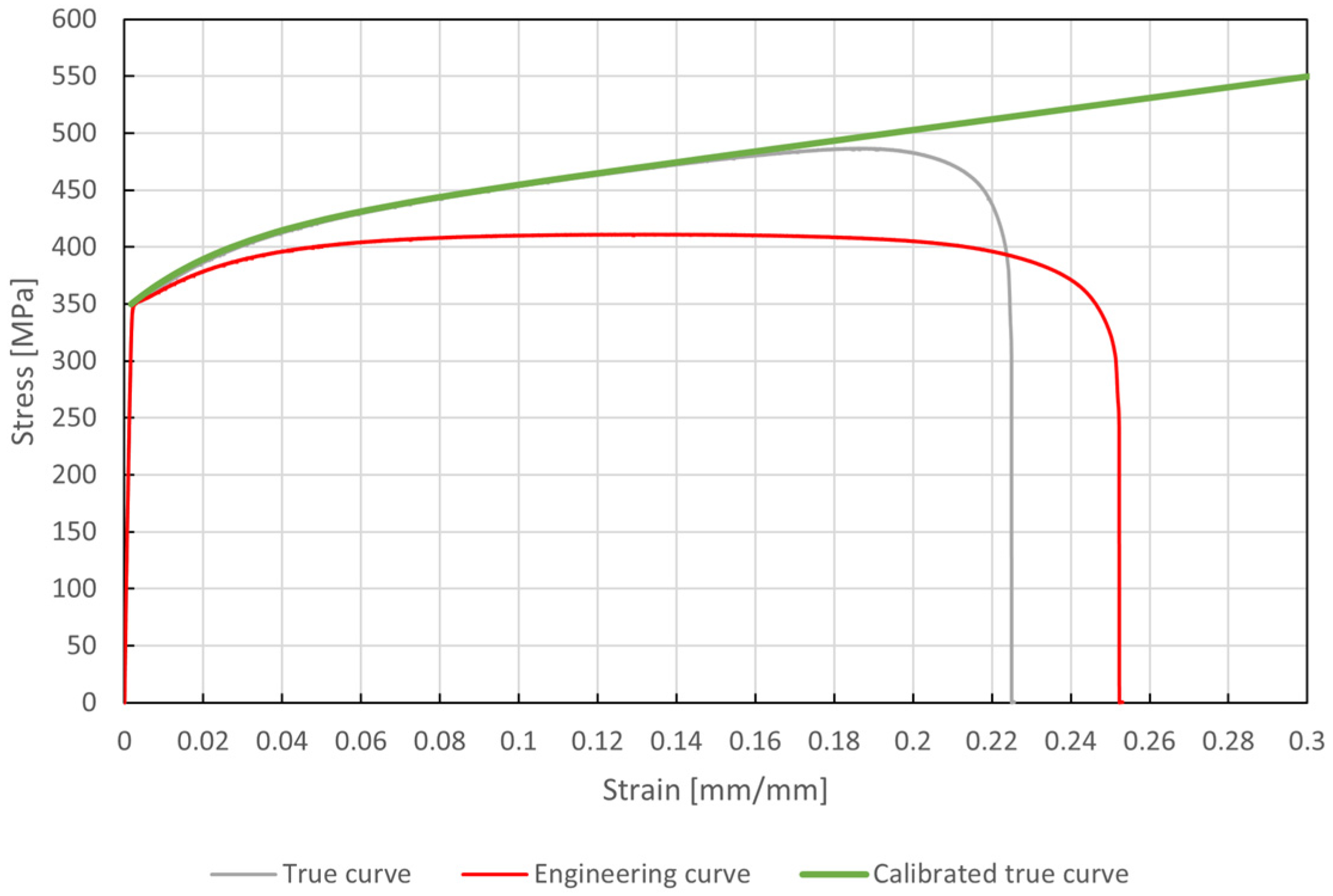
2.2. True Stress–Strain Curve Correction
- Fit the plastic portion of the true stress–strain curve by means of the Voce equation (see Equation (7)), which relates the true stress to the plastic strain through four constants, i.e., .
- Simulate the tensile test by means of a non-linear FEM (Finite Element Method) model taking the Voce equation as an input.
- Compare the force–displacement curve given as an output in the FEM model with the experimental one.
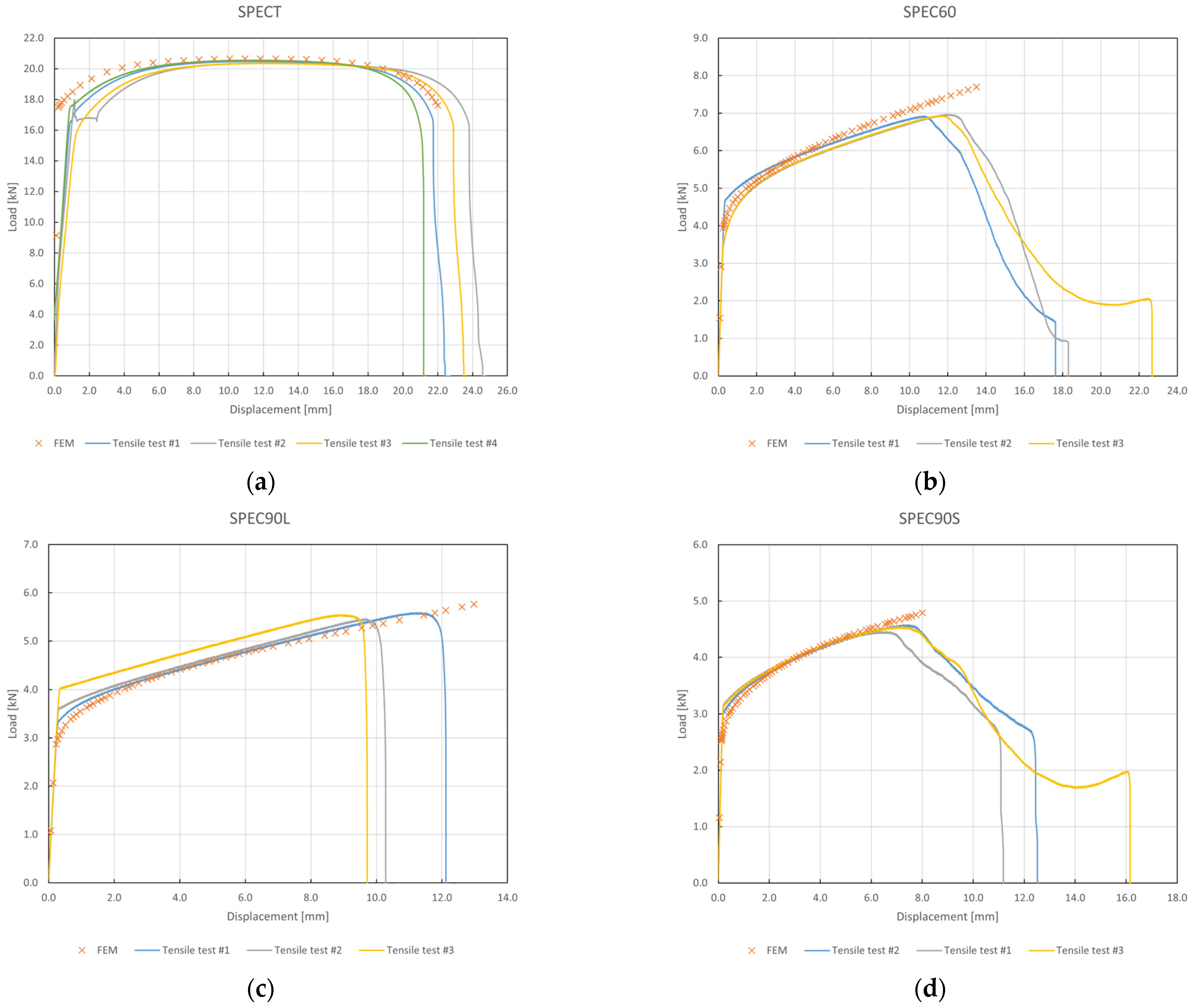
2.3. FEM Validation
3. Results
3.1. Comparison Between FEM and Experimental Results
3.2. Determination of the Fracture Locus
3.3. Stress State Locus
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Budinas, R.G.; Nisbett, J.K. Failure Theories. In Shigley’s Mechanical Engineering Design; McGraw-Hill: New York, NY, USA, 2011; pp. 219–225. [Google Scholar]
- Bao, Y.; Wierzbicki, T. On fracture locus in the equivalent strain and stress triaxiality space. Int. J. Mech. Sci. 2004, 46, 81–98. [Google Scholar] [CrossRef]
- Barsoum, I.; Faleskog, J. Micromechanical analysis on the influence of the Lode parameter on void growth and coalescence. Int. J. Solids Struct. 2011, 48, 925–938. [Google Scholar] [CrossRef]
- Liu, X.; Yan, S.; Rasmussen, K.J.R.; Deierlein, G.G. Experimental investigation of the effect of Lode angle on fracture initiation of steels. Eng. Fract. Mech. 2022, 271, 108637. [Google Scholar] [CrossRef]
- Barsoum, I.; Faleskog, J. Rupture mechanisms in combined tension and shear—Micromechanics. Int. J. Solids Struct. 2007, 44, 5481–5498. [Google Scholar] [CrossRef]
- Maccioni, L.; Concli, F. Fracture locus of a CORTEN steel: Finite Element calibration based on experimental results. Procedia Struct. Integr. 2019, 24, 738–745. [Google Scholar] [CrossRef]
- Murugesan, M.; Jung, D.W. Johnson Cook Material and Failure Model Parameters Estimation of AISI-1045 Medium Carbon Steel for Metal Forming Applications. Materials 2019, 12, 609. [Google Scholar] [CrossRef]
- Suárez, F.; Gálvez, J.C.; Cendón, D.A.; Atienza, J.M. Distinct Fracture Patterns in Construction Steels for Reinforced Concrete under Quasistatic Loading—A Review. Metals 2018, 8, 171. [Google Scholar] [CrossRef]
- Park, N.; Huh, H.; Lim, S.J.; Lou, Y.; Kang, Y.S.; Seo, M.H. Fracture-based forming limit criteria for anisotropic materials in sheet metal forming. Int. J. Plast. 2017, 96, 1–35. [Google Scholar] [CrossRef]
- Liu, Y.; Ikeda, S.; Liu, Y.; Ge, H. Ductile Fracture Investigation of High-Strength Steel SM570 under Low Stress Triaxiality. Metals 2022, 12, 1394. [Google Scholar] [CrossRef]
- Giglio, M.; Manes, A.; Mapelli, C.; Mombelli, D. Relation between Ductile Fracture Locus and Deformation of Phases in Ti–6Al–4V Alloy. ISIJ Int. 2013, 53, 2250–2258. [Google Scholar] [CrossRef][Green Version]
- Peng, J.; Zhou, P.; Wang, Y.; Dai, Q.; Knowles, D.; Mostafavi, M. Stress Triaxiality and Lode Angle Parameter Characterization of Flat Metal Specimen with Inclined Notch. Metals 2021, 11, 1627. [Google Scholar] [CrossRef]
- Annealed 304 Stainless Steel. Available online: https://www.makeitfrom.com/material-properties/Annealed-304-Stainless-Steel (accessed on 2 February 2025).
- EN 1.0038 (S235JR) Non-Alloy Steel. Available online: https://www.makeitfrom.com/material-properties/EN-1.0038-S235JR-Non-Alloy-Steel (accessed on 2 February 2025).
- Cho, Y.; Lee, C.; Yee, J.-J.; Kim, D.-K. Modeling of Ductile Fracture for SS275 Structural Steel Sheets. Appl. Sci. 2021, 11, 5392. [Google Scholar] [CrossRef]
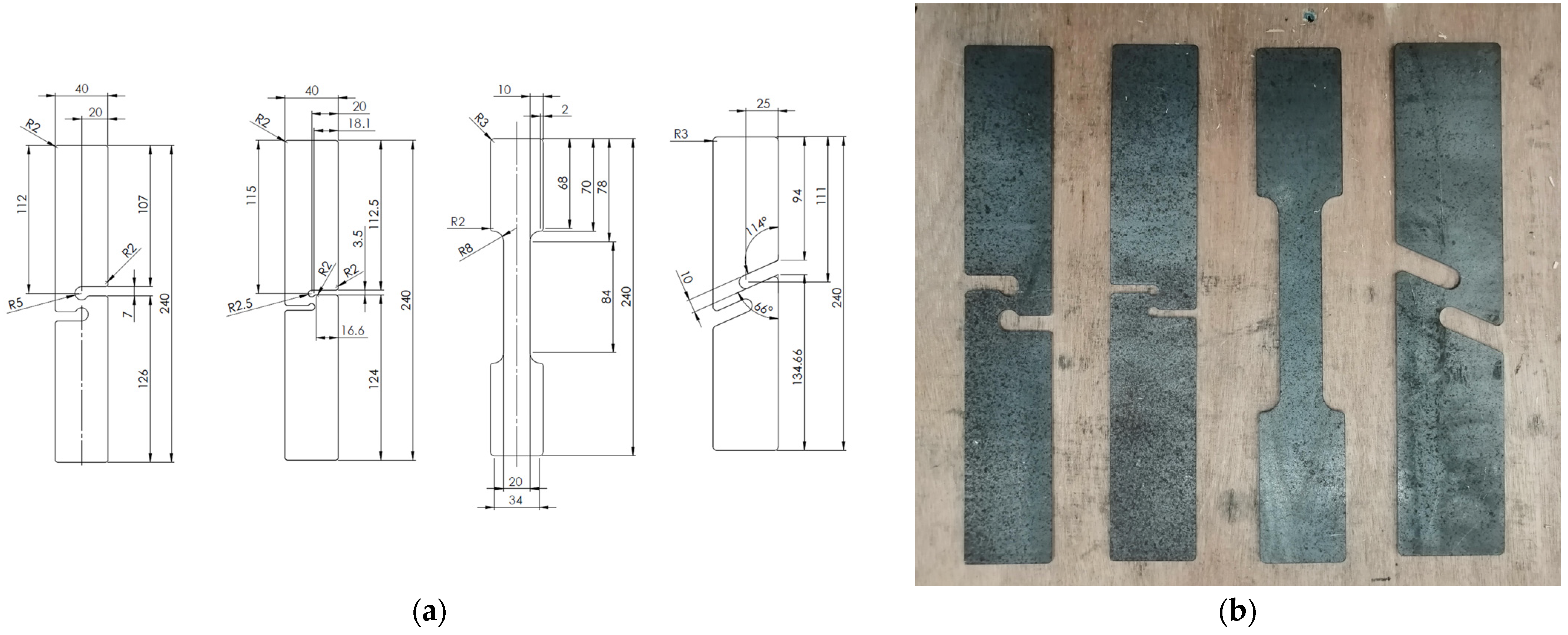




| Elastic Modulus [GPa] | Yield Strength [MPa] | Ultimate Tensile Strength [MPa] | Deformation at Fracture [mm/mm] | Toughness [MJ/m3] |
|---|---|---|---|---|
| 206 | 350 | 411 | 0.25 | 99.4 |
| Specimen | [-] | [mm/mm] | [-] |
|---|---|---|---|
| SPECT | 0.412 ± 0.017 | 0.673 ± 0.074 | 0.75 ± 0.064 |
| SPEC60 | 0.342 ± 0.001 | 0.829 ± 0.030 | 0.97 ± 0.003 |
| SPEC90L | 0.345 ± 0.000 | 0.625 ± 0.027 | 0.96 ± 0.001 |
| SPEC90S | 0.347 ± 0.000 | 0.983 ± 0.044 | 0.96 ± 0.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baruscotti, A.; Miori, N.; Concli, F. Determination of the Fracture Locus of a Cor-Ten Steel at Low and High Triaxiality Ranges. Appl. Sci. 2025, 15, 3569. https://doi.org/10.3390/app15073569
Baruscotti A, Miori N, Concli F. Determination of the Fracture Locus of a Cor-Ten Steel at Low and High Triaxiality Ranges. Applied Sciences. 2025; 15(7):3569. https://doi.org/10.3390/app15073569
Chicago/Turabian StyleBaruscotti, Axel, Nicholas Miori, and Franco Concli. 2025. "Determination of the Fracture Locus of a Cor-Ten Steel at Low and High Triaxiality Ranges" Applied Sciences 15, no. 7: 3569. https://doi.org/10.3390/app15073569
APA StyleBaruscotti, A., Miori, N., & Concli, F. (2025). Determination of the Fracture Locus of a Cor-Ten Steel at Low and High Triaxiality Ranges. Applied Sciences, 15(7), 3569. https://doi.org/10.3390/app15073569








