Abstract
Although the theory of mixed-integer inference is well developed for GNSS parameter estimation, such is not yet the case for the validation and monitoring of mixed-integer GNSS carrier-phase models. It is the goal of this research to contribute to this field by introducing a class of mixed-integer model (MIM) tests for carrier-phase GNSS. Members from this class and their distributional properties are worked out for different model validation applications relevant to GNSS, such as detection, identification, significance testing, and integer testing. The power performance of the various tests is characterized, thereby showing how they are capable of significantly outperforming the customary ambiguity-float tests.
1. Introduction
GNSS model validation and monitoring constitutes an essential part of any GNSS data processing scheme [1,2,3]. Statistical tests are then employed to test for the occurrence of model misspecifications—e.g., pseudorange outliers, carrier-phase slips, or neglected atmospheric delays [4,5,6]—or, in the case of monitoring, to test for the stability of estimated parameters—for instance, in GNSS time-series for displacement, deformation, or landslide studies [7,8,9,10]. To achieve the highest accuracy in GNSS parameter estimation, carrier-phase measurements are generally used, as they have a two orders of magnitude better precision than their pseudorange (code) counterparts [11,12,13]. However, since the interferometric carrier-phase observables are integer-ambiguous, their GNSS models consist of both real-valued and integer-valued parameters; therefore, they are of the mixed-integer type. Although the theory of mixed-integer inference is well developed for GNSS parameter estimation [1,2,3], such is not yet the case for the validation and monitoring of the mixed-integer GNSS carrier-phase models. It is the goal of this study to contribute to this field by introducing a class of ambiguity-resolved model tests for carrier-phase GNSS.
This contribution is organized as follows. In Section 2, we formulate the to-be-tested mixed-integer null and alternative hypotheses of carrier-phase GNSS and introduce our class of mixed-integer model (MIM) tests for their testing. The hypotheses are formulated in a general form such that they apply to any carrier-phase GNSS system of observation equations, whether single-epoch or multi-epoch, single-frequency or multi-frequency, undifferenced, single-differenced or double-differenced, or whether for use with single-GNSS or multi-GNSS. Our MIM test statistic is a function of the least-squares residuals of both null and alternative hypotheses, as well as of their integer admissible ambiguity estimators. As different forms of the test statistic are useful for different applications, we provide various useful relationships between these normed residuals.
To obtain a first insight into the expected performance of the MIM test, we consider two of its limiting cases in Section 3. In the first case, the integerness of the ambiguities is not taken into account, while in the second case, the integer ambiguities are assumed to be known. The first is referred to as ambiguity-float (AF), while the second is referred to as ambiguity-known (AK). In both these limiting cases, the MIM test becomes equal to a -test with well-known power functions (i.e., functions that provide, for a given false-alarm probability, the detection probability as a function of the biases). It is shown that for carrier-phase GNSS, the AK power significantly outperforms the AF power, i.e., when the ambiguities are assumed known, the carrier-phase observables start to act as very precise pseudoranges, thereby contributing significantly to the power improvement of the test. The AK test, however, is not an operational test, since in the case of carrier-phase GNSS, the ambiguities can never be assumed as known, i.e., despite the fact that the ambiguities are known to be integers, they still remain unknown.
Although the AK test cannot be used operationally, its large power difference with the AF test does indicate the great potential of our MIM test, a test that operates in between the AF and AK tests. This is shown in Section 4, where, for different circumstances, different forms of the MIM test statistic are presented together with their associated probability distributions. The MIM test is worked out in Section 4.1 for the case when the null hypothesis is tested against the most relaxed alternative hypothesis. This case of detection requires, in contrast to the general MIM test, only integer ambiguity resolution under the null hypothesis. We also show, when the mixed-integer misclosure vector is used to formulate a derived simple null hypothesis, how its distribution can be used to formulate a highest-density (HD) detection test. This test will have similar performance but is somewhat more difficult to execute. We show an illustrative example in which the power of the MIM test, although not as good as the AK test, is still significantly better than the AF test.
In Section 4.2, we discuss the MIM test for the case of identification, i.e., when the design matrix’ range space of the alternative hypothesis is a strict subspace of the observation space. In this case, integer ambiguity resolution is required under both the null and alternative hypotheses. We prove that the test statistic has a generalized Chi-square distribution if the ambiguity success rate approaches one under the alternative hypothesis. A further insight into the test is provided by neglecting the ambiguity resolution difference of the two hypotheses. This results in a significance test for which the distribution of the test statistic is also given. Again, we also provide the associated HD significance test. For the cases in which full ambiguity resolution is not sufficient for a significant power improvement, we show how partial ambiguity resolution under the alternative hypothesis may drastically improve the power performance.
In Section 4.3, we describe a third important application of the MIM test. This concerns the case under which the ambiguities of the null hypothesis are assumed integer and those under the alternative hypothesis as real-valued. This form of the MIM test is of interest for problems that require integer testing of the ambiguities. Such problems are also of interest for carrier-phase GNSS, since the stability of instrumental hardware delays may not always be such that integerness of the carrier-phase ambiguities is guaranteed. In [14,15], for instance, it is demonstrated that smartphone phase observations may be contaminated by receiver effects that destroy the integer property of the ambiguities. We describe the integer test, its associated distributions, and provide an illustrative example of its power performance. Finally, we provide a summary and conclusions in Section 5.
The following notation is used throughout. We denote a random variable/vector by means of an underscore; thus, is a random variable/vector, while x is not. and stand for the expectation and dispersion of , respectively, and denotes a p-dimensional, normally distributed random vector, with mean (expectation) and variance matrix (dispersion) Q. The Best Linear Unbiased Estimator (BLUE) of a parameter vector x is denoted as and its admissible integer estimator as . denotes the probability of event , the probability density function (PDF) of the continuous random vector , and the probability mass function (PMF) of the integer random vector . The noncentral Chi-square distribution with q degrees of freedom and noncentrality parameter is denoted as . The range space of a matrix M is denoted as , and and denote the p-dimensional spaces of real- and integer numbers, respectively. The -weighted squared norm is denoted as . The BLUE-inverse of a full column rank matrix M is denoted as and the orthogonal projector onto as . Thus, is the orthogonal projector that projects orthogonally on the orthogonal complement of .
2. The Mixed-Integer GNSS Model
In this section, we describe the hypotheses of carrier-phase GNSS and introduce its class of mixed-integer model tests.
2.1. The Null and Alternative Hypotheses
The observation equations of the linear(ized) mixed-integer GNSS model are formulated under the null and alternative hypotheses as
with the observational vector containing the carrier-phase and pseudorange observables; the unknown integer carrier-phase ambiguities; and the unknown real-valued parameters, e.g., position coordinates, atmosphere parameters, receiver and satellite clock parameters, and instrumental biases [1,2,16]. Under , the mean of is assumed shifted by , . Such shifts allow one to model various important GNSS model misspecifications or biases in c. For instance, through the choice of C in , one may model the presence of one or more outliers in the pseudorange data, cycle-slips in the phase data, the presence of neglected atmospheric effects, or in fact any other systematic effect that one failed to take into account under . Various such examples are given in the GNSS Handbooks [2,3].
2.2. The AF and AK Residual Vectors
Residual vectors are generally instrumental in formulating proper test statistics for the testing of a null hypothesis against an alternative hypothesis. In our case of the mixed-integer models of (1), different such residual vectors need to be considered. These are the ambiguity-float (AF) and ambiguity-known (AK) residual vectors of both and . They are defined as
and
The least-squares residual vectors and capture the data-model inconsistency of and in case the ambiguity vector is estimated as an unknown real-valued vector, under and , respectively. Their counterparts, and , do the same; but now, for the case, the ambiguity vectors are assumed known. Note that the AK residuals reduce to their AF counterparts if the ambiguity vector is taken as ambiguity-BLUE. Thus, and , with and being the BLUEs of a under and , respectively, where and .
Various important relations can be established between these residuals. The ones directly relevant for our mixed-integer test statistic are summarized in the following Lemma.
Lemma 1 (Differences normed residuals).
Let and denote the AF-BLUE and AK-BLUE of the bias vector c under , and let and be the BLUEs of a under and , respectively. Then, we can express the differences of the -weighted squared norms of the residual vectors in , , , and as
with ambiguity residuals and .
Proof.
Note that the first two relations of the Lemma, (i) and (ii), establish the link between the - change in normed residuals, on the one hand, and the estimated bias vector, either in AF form or AK form, on the other hand. Therefore, the significance of the estimated bias vectors can be considered a measure of the discrepancy between the two hypotheses. The last two relations of the Lemma establish the link of the AF–AK change in the normed residuals, on the one hand, and the difference between the estimated ambiguities and their assumed values, under and , on the other hand. The AF–AK change in normed residuals is, therefore, a measure for the truthfulness of the assumed ambiguity values.See Appendix A. □
2.3. The Mixed-Integer Model Test
We now introduce our mixed-integer model (MIM) test for testing the hypotheses of (1). Its statistic is designed to measure the - change in model fit, while at the same time doing justice to the integer estimation of the ambiguities under both hypotheses.
Definition 1 (Mixed-Integer Model (MIM) Test).
Note that this MIM test requires the integer estimation of the ambiguities under both hypotheses, and . However, the user still has the freedom in choosing which member from the class of admissible integer estimators to select. An integer estimator , with , is said to be admissible when its pull-in regions , , cover , while being disjoint and integer translational invariant [17]. Popular choices for are integer rounding (IR), integer bootstrapping (IB), integer least-squares (ILS), or vectorial combinations (VIB) of them. The above MIM test becomes equivalent to the LR test if both and are taken as the ILS solutions. ILS is the most complex, but has the advantage of providing the largest possible ambiguity success rate, i.e., the largest probability of correct integer estimation. IR and IB are both simple to execute, whereby IB, especially after ambiguity decorrelation, often obtains a close-to-optimal ambiguity success rate. The freedom in choice of integer estimator implies that the integer estimator choice for need not be the same as the one for . For example, the ILS principle may be chosen to obtain from , while the IB principle is chosen to obtain from . Therefore, such choices should be taken in dependence of the required success rates.Let the change in - model fit be captured by the statistic
and let and be admissible integer estimators of under and (cf. (1)), respectively. Then, the α-level MIM test for rejecting in favor of is defined as
with the critical value satisfying .
3. The AF and AK Tests
To obtain insight on the expected performance of the MIM test, we first consider two of its limiting cases. First, we consider the case when the integerness of the ambiguities is not taken into account, i.e., the ambiguities are treated as real-valued parameters. This is referred to as the ambiguity-float (AF) test. Then, we consider the case when the integer ambiguities are assumed to be completely known. This is referred to as the ambiguity-known (AK) test. Both tests are LR tests and have the property of being uniformly most powerful invariant [2]. We start with the AF test.
3.1. The Ambiguity-Float Test
The AF test statistic is obtained from (4) by replacing and a by their BLUEs under and , respectively. This gives, with the help of Lemma 1,
It is distributed under and as
with noncentrality parameter .
A special case occurs when, under the alternative hypothesis, the mean of is allowed to vary freely over the whole of , i.e., when . Then, and (6) reduces to
This is the test statistic that is used for AF detection, i.e., for testing the ambiguity-float null hypothesis against the most relaxed alternative hypothesis.
3.2. The Ambiguity-Known Test
The AK test statistic is obtained from (4) by setting and assuming a as known. This gives, with the help of Lemma 1,
It is distributed under and as
with noncentrality parameter .
Again, a special case occurs when, under the alternative hypothesis, the mean of is allowed to vary freely over the whole of while a is known, i.e., when . Then, and (6) reduces, with the help of Lemma 1, to
This is the test statistic that is used for AK detection, i.e., for testing the ambiguity-known null hypothesis against the most relaxed ambiguity-known alternative hypothesis.
Note that both detectors, (8) and (11), are expressed in the singular residual vector . A useful alternative expression follows if one makes use of ’s misclosure vector, which has a nonsingular distribution. The misclosure vector is defined as , with being a basis matrix of the null space of , i.e., . Then, , with and . From expressing in as , it follows that
In order to compare the performance of the AF and AK tests, we compare their power. Since the estimator is more precise than , we have and, therefore, . This shows that the power of the AK test will never be smaller than that of the AF test, i.e., . As an example application, we consider the presence testing of a differential tropospheric zenith delay based on a single-epoch, single-frequency, double-differenced (DD) GPS model. Figure 1 shows the power functions of the two tests, thereby illustrating the significant improvement in power that can be achieved with carrier-phase GNSS once all double-differenced ambiguities are known.
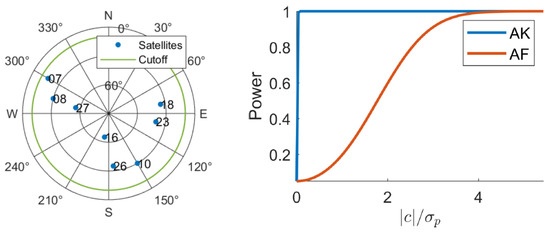
Figure 1.
Tropospheric AK and AF power function curves, computed using their noncentral Chi-square CDF. Left: single-epoch GPS skyplot; Right: single-epoch, L1 GPS, , ambiguity-float (AF) and ambiguity-known (AK) power function curves for tropospheric zenith delay testing.
4. The Ambiguity-Resolved Tests
The previous example has shown that there can be quite a difference in performance between the AK and AF tests in the case of carrier-phase GNSS. This is of course due to the very high precision of the GNSS carrier-phase observables—a precision that really becomes exploited once the ambiguities are known. However, the problem is that, strictly speaking, the AK test cannot be applied in the case of GNSS. Although the ambiguities are known to be integer, they are still unknown. Hence, the best one can do is to estimate the ambiguities as integers and formulate the proper test statistic by taking the uncertainty of the integer estimators into account. For sufficiently high ambiguity success rates, i.e., probabilities of correct integer estimation, one can then generally expect the performance of the MIM test to be better than the AF test and approaching that of the corresponding AK test. We now consider different versions of the MIM test. We start with the case of detection.
4.1. AR Detection
If , then , from which it follows that the statistic (4) becomes dependent only on the -estimators. The AR detector reads, therefore, with ,
Thus, for detection, only integer ambiguity estimation under is required. Also, note that and , being the input to , are independent. The PDF of the mixed-integer misclosure vector follows then as
with, under ,
in which is the PDF of and is the indicator function of the pull-in region of the integer estimator . The PDF of the integer ambiguity residual was already given in [18], Equation (19). Figure 2 (Left) illustrates stepwise (in blue) how it is obtained from in the one-dimensional case. The PDF of (top left) is shown along the x-axis, the PMF of (top right) along the z-axis, and the joint PDF (top middle) is shown in the -plane. This joint PDF consists of slices of translated along the z-axis to the corresponding integers z. The joint PDF of and (bottom left) follows from translating the slices along the x-axis so that they are all centered at the mean value: in this case. The PDF of (bottom right) is then finally obtained by summing over z, i.e., all slices are again translated along the z-axis to the origin. Figure 2 (Right) shows how the shape of the PDF of the ambiguity residual changes with the ambiguity standard deviation and how, under these changes, it compares with the ambiguity-float PDF . It shows that the difference between the two distributions becomes lower the smaller the standard deviation gets.
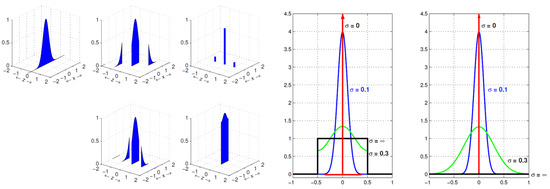
Figure 2.
PDF ambiguity residual: (Left) Stepwise construction (in blue) of from (cf. (15)); (Right) PDF comparison between (left) and (right) for four different values of the standard deviation .
We remark that under (cf. (1)), we have and . When this derived simple null hypothesis is used as the starting point, one can directly make use of (14) to formulate the highest-density (HD) test as an alternative: reject if . It is also an LR-ratio test for testing against . As shown in [18], p. 1124, the HD-formulation does justice to the multimodality of the PDF, while providing an acceptance region with the most concentrated probability. This HD test will, however, due to its infinite sum, be more difficult to execute than the one based on the quadratic form (13); at the same time, due to the commonly high ambiguity success rate carrier-GNSS usages, its performance will be similar to that of (13).
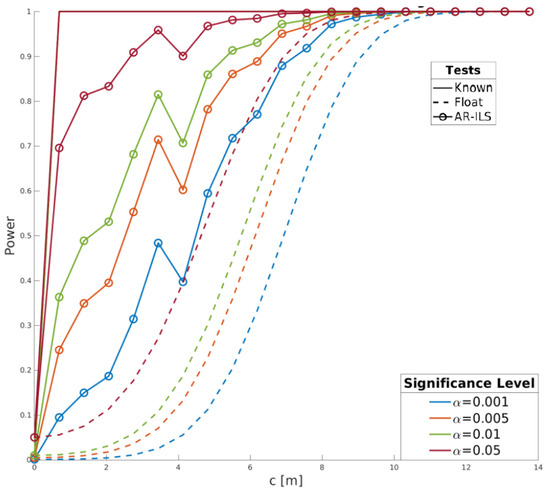
To illustrate the difference in power between the AF and AK detectors, on the one hand, and the operational AR detector (13), on the other hand, we consider as an example application their detection power in the presence of a zenith tropospheric delay bias. As with the other AR test statistics, the power of the AR detector is computed using the Monte Carlo simulation approach of [19]. Figure 3 shows the detection power of the three detectors for a single-frequency, single-epoch, dual constellation (GPS and Galileo), using a mass-market receiver with relatively poor undifferenced pseudorange standard deviation cm. The results show that the AR detector is not as good as the AK detector would be (as the success rate is only ), but that it is significantly better than the AF detector.
4.2. AR Identification
In case is a strict subspace of , then also contributes to the statistic (4), thus implying that integer ambiguity estimation under both and is required. We then have, with the help of Lemma 1 and the short-hand notation and , the following representation for the test statistic:
Comparison with the AF statistic (cf. (6)) shows that now, next to the difference , the ambiguity-resolution based difference is present. It is this added difference, diagnosing the impact of ambiguity resolution under and , that can be expected to improve the power-performance over that of the AF test. To understand what the best possible performance of the test would be, we determine the PDF of (16) for the limiting case that the ambiguity success rate of goes to one, . The following Theorem shows that the limiting distribution is a generalized Chi-squared distribution, i.e., the distribution of the sum of two independent random variables of which the first is Chi-squared distributed and the second is normally distributed.
Note that this statistic also follows directly from the AK test statistic when a in (9) is replaced by the integer estimator . Therefore, it can be seen as a direct ambiguity-resolved generalization of the AK test, having the advantage that now only the integer estimation under needs to be performed. The PDF of was already given in [20], Equation (36), as , with . This result can be used to determine the PDF of (17).
Theorem 1 (Limit distribution of ).
Let and . Then, with the ambiguity success rate under approaching one, the limiting distribution of the test statistic is a generalized Chi-squared distribution, given as
with noncentrality parameter and normal mean .
Proof.
This result shows that the limiting distribution of (16) is equal to that of the AK test statistic (10), under and , in case . The distributions differ, however, under when . Thus, it is the possible bias in under the alternative hypothesis, i.e., , that drives the difference between the two distributions. A further insight into the behavior of the test is obtained when the difference between and is neglected. Using the representation and neglecting the difference between and , we obtainSee Appendix A. □
Lemma 2 (Distribution of ).
Proof.
Note that if the ambiguity success rate goes to one, , the PDF (18) indeed converges to that of the AK test (9). Also note that, as before, we could have used the PDF of directly, by means of the HD test: reject if , to test for the significance of the bias c. Such a test was proposed for outlier testing in [18]. However, as mentioned earlier, such would require dealing with the infinite sum for each individual execution of the test, while at the same time, its GNSS performance will generally be similar to that of (17). Furthermore, for the test statistic , we have its exact distribution available (cf. (18)). The fact that it also consists of an infinite sum is not an issue, since its usage for critical value and power computations can usually be performed off-line at the designing stage, see [19].See Appendix A. □
Although the ambiguity success rates are not required to be as large as needed for ambiguity-fixed GNSS baseline estimation [1], it is clear from the above considerations that they still play a driving role in the performance of the ambiguity-resolved tests. Since it may happen that full ambiguity success rates become drastically reduced when switching from to , particularly when the dimension of c increases, partial ambiguity resolution (PAR) is a strategy to keep the reduction in ambiguity success rate at bay. This is illustrated for ionospheric testing in the example of Figure 4. It shows how PAR can obtain large success rates, thus enabling the conditions of Theorem 1, thereby significantly improving the power compared to that of AF testing.
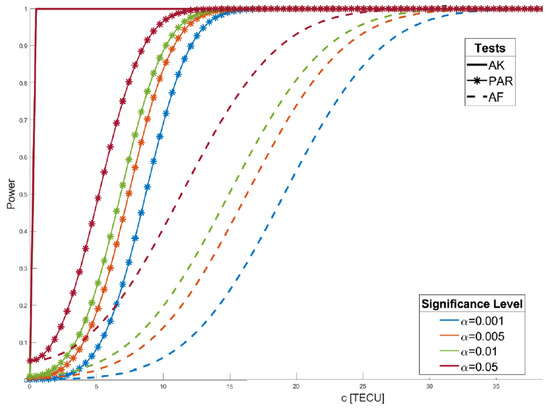
Figure 4.
PAR ionospheric power function compared with AK and AF counterparts for single-epoch, triple-frequency Galileo model with undifferenced pseudorange standard deviation cm. PAR allowed the ambiguity success rate to increase from to .
4.3. AR Integer Testing
The distribution of Theorem 1 considers the case when the integer ambiguity success rate under approaches one, i.e., the case when the integer estimated ambiguity may be considered as known. We now consider the other extreme and assume the ambiguity vector under to be an unknown real-valued parameter instead of integer-valued. The test statistic relevant for this case follows if instead of , the ambiguity-float estimator is used. We obtain, instead of (16), the test statistic
As and are independent, the PDF of the input follows, similarly to (14), as , with . With a assumed as real-valued under , , but integer-valued under , , the statistic (19) is the test statistic to use for integer testing of the ambiguities. When , it simplifies to .
Being able to statistically test for the integerness of estimable ambiguities is important when linking GNSS models. Dependent on how different GNSS systems are combined or on how well receiver hardware delays can be calibrated, real-valued biases may become lumped with the carrier-phase ambiguities, thereby removing the integerness of the estimable ambiguities. For instance, when signals of different systems are integrated, inter-system biases in both the carrier-phase and code data may occur [21,22]. Also, in the case of low-cost, mass-market GNSS receivers, the stability of the hardware delays may not be such that integerness of the carrier-phase ambiguities is guaranteed. For instance, it is demonstrated in [14,15] that smartphone phase observations may indeed be contaminated by receiver effects that destroy the integer property of the ambiguities. Therefore, being able to statistically test for such occurrences becomes important. This is also true in case of opportunistic PNT when one tries to use carrier-phase signals from terrestrial transmitters or LEO communication satellites for precise positioning [23,24].
As an example illustration, we consider the single-epoch, dual-frequency, two-satellite GNSS geometry-free model [1]. The ambiguity bias vector under , propagated into the ambiguity residual , is denoted as . This bias vector is, like the ambiguity residual , confined to the origin-centered pull-in region of the integer ambiguity estimator. Hence, the domain of the power function is confined to this pull-in region as well, which, in case of ILS estimation, is a hexagon. Figure 5 shows, for when is chosen as the ILS estimator, the contour aligns with the color bar of the power function . It clearly shows how the power increases as the ambiguity bias vector moves away from the origin towards the edges of the ILS pull-in region.
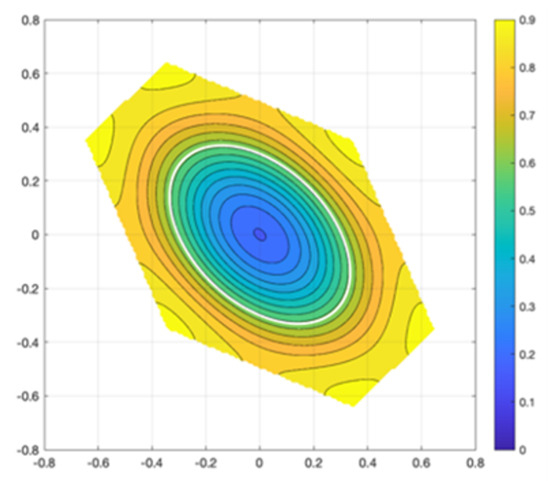
Figure 5.
Contour plot with color bar of the integer testing power function () for a single-epoch, dual-frequency, GNSS geometry-free model. The horizontal and vertical axes are expressed in cycles.
5. Summary and Conclusions
In this contribution, we introduced a class of mixed-integer model (MIM) tests for carrier-phase GNSS and studied its characteristics. As a first indication of its significant power potential, we compared the power performance of two of its limiting forms, the ambiguity-float (AF) test and the ambiguity-known (AK) test. It was shown that for carrier-phase GNSS, the AK test significantly outperforms the AF test. The AK test, however, is not an operational test, since for carrier-phase GNSS, the ambiguities can never be assumed known. Therefore, its best operational alternative is the MIM test for which, for different circumstances, different forms were presented, see Table 1. The relevant probability distributions were also provided, including the highest-density versions of the testing. For the case when the null hypothesis is tested against the most relaxed alternative hypothesis, the MIM test provides ambiguity-resolved detection, while identification is enabled in case the design matrix’ range space of the alternative hypothesis is a strict subspace of the observation space. As a special case of the latter, we also described the significance test, which—in contrast to the general MIM test—only requires integer ambiguity resolution under the alternative hypothesis. As a third field of application, we described how the MIM test specializes to integer testing. Such testing is relevant for carrier-phase GNSS models in which the integerness of ambiguities, or the lack thereof, needs verification—for instance, due to suspected stability issues in its instrumental hardware delays. Several illustrative examples of the MIM test performance were given, demonstrating its improved power over that of the ambiguity-float test. Noteworthy is hereby that such improvements generally do not need the same high ambiguity success rates as required for ambiguity-resolved parameter estimation.

Table 1.
Mixed-integer model (MIM) testing: an overview of the AF, AK, and AR test statistics.
Funding
This research received no external funding.
Data Availability Statement
All data generated or analysed during this study are included in this contribution.
Acknowledgments
Chengyu Yin and Sandra Verhagen provided the graphical and numerical support.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A
Proof of Lemma 1 (Differences normed residuals).
Using the projector product formula, , with , we may express the -residual vector in the -residual vector as . This, together with and the AF-BLUE of c expressed as , having the variance matrix , allows us to write
which proves Lemma 1(i). The resulting Lemma 1(ii), in which is the AK-BLUE of c, is proven in a similar way. To prove Lemma 1(iii), we use the projector product formula , with , to express the AF residual vector in the AK residual vector as . This, together with , , and , allows us to write
which proves Lemma 1(iii). The resulting Lemma 1(iv) is proven in a similar way. □
Proof of Theorem 1 (Limit distribution of ).
As and are both unbiased estimators under , we have, since——that under , and , when . This changes under , since will then have become a biased estimator of a, . Thus, under , we have and , when . Therefore, we have . To determine the distribution of the latter, we make use of its representation
thereby recognizing that is independent of , since is independent of . We now determine the distributions of and separately.
Since , we have and, therefore, . Hence,
with noncentrality parameter .
Proof of Lemma 2 (Distribution of ).
As , and and are independent, we have for any ,
from which the result follows. □
References
- Leick, A.; Rapoport, L.; Tatarnikov, D. GPS Satellite Surveying, 4th ed.; John Wiley and Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Teunissen, P.J.G.; Montenbruck, O. (Eds.) Springer Handbook of Global Navigation Satellite Systems; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Morton, Y.; van Diggelen, F.; Spilker, J., Jr.; Parkinson, B.; Lo, S.; Gao, G. (Eds.) Position, Navigation, and Timing Technologies in the 21st Century: Integrated Satellite Navigation, Sensor Systems, and Civil Applications; Wiley: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Yu, Y.; Yang, L.; Shen, Y.; Sun, N. A DIA Method based on Maximum a Posteriori Estimate for Multiple Outliers. GPS Solut. 2023, 27, 199. [Google Scholar] [CrossRef]
- Zeng, J.; Zhang, Z.; He, X.; Yuan, Y.; Li, Y.; Song, M. Real-time GNSS multiple cycle slip detection and repair based on a controllable geometry-based method in relative positioning. Measurement 2023, 216, 112940. [Google Scholar] [CrossRef]
- Khanafseh, S.; Pullen, S.; Warburton, J. Carrier phase ionospheric gradient ground monitor for GBAS with experimental validation. J. Inst. Navig. 2012, 59, 51–60. [Google Scholar] [CrossRef]
- Perfetti, N. Detection of station coordinate discontinuities within the Italian GPS fiducial network. J. Geod. 2006, 80, 381–396. [Google Scholar] [CrossRef]
- Biagi, L.; Grec, F.C.; Negretti, M. Low-cost GNSS receivers for local monitoring: Experimental simulation, and analysis of displacements. Sensors 2016, 16, 2140. [Google Scholar] [CrossRef] [PubMed]
- Zeng, S.; Kuang, C.; Yu, W. Evaluation of Real-Time Kinematic Positioning and Deformation Monitoring Using Xiaomi Mi 8 Smartphone. Appl. Sci. 2022, 12, 435. [Google Scholar] [CrossRef]
- Huang, G.; Du, S.; Wang, D. GNSS techniques for real-time monitoring of landslides: A review. Satell. Navig. 2023, 4, 10. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Wasle, E. (Eds.) GNSS: Global Navigation Satellite Systems. GPS, GLONASS, Galileo and More; Springer: New York, NY, USA, 2008; ISBN 978-3-211-73012-6. [Google Scholar]
- Khodabandeh, A.; Zaminpardaz, S.; Nadarajah, N. A study on multi-GNSS phase-only positioning. Meas. Sci. Technol. 2021, 32, 095005. [Google Scholar] [CrossRef]
- Song, W.; Zheng, F.; Wang, H.; Shi, C. 100 Picosecond/Sub-10−17 Level GPS Differential Precise Time and Frequency Transfer. Appl. Sci. 2023, 13, 10694. [Google Scholar] [CrossRef]
- Paziewski, J.; Fortunato, M.; Mazzoni, A.; Odolinski, R. An analysis of multi-GNSS observations tracked by recent Android smartphones and smartphone-only relative positioning results. Measurement 2021, 175, 109162. [Google Scholar] [CrossRef]
- Paziewski, J.; Wielgosz, P. Accounting for Galileo–GPS inter-system biases in precise satellite positioning. J. Geod. 2015, 89, 81–93. [Google Scholar] [CrossRef]
- Strang, G.; Borre, K. Linear Algebra, Geodesy, and GPS; Wellesley-Cambridge Press: Wellesley, MA, USA, 1997. [Google Scholar]
- Teunissen, P.J.G. Probabilistic Properties of GNSS Integer Ambiguity Estimation. Earth Planets Space 2000, 52, 801–805. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. Mixed Integer Estimation and Validation for Next Generation GNSS. In Handbook of Geomathematics; Freeden, W., Nashed, M.Z., Sonar, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Chapter 37; pp. 1102–1127. [Google Scholar]
- Yin, C.; Teunissen, P.J.G.; Tiberius, C.C.J.M. Implementation of Ambiguity-Resolved Detector for High-Precision GNSS Fault Detection. In Proceedings of the ION GNSS+ 2024, Baltimore, MD, USA, 16–20 September 2024; pp. 2163–2174. [Google Scholar]
- Teunissen, P.J.G. The probability distribution of the GPS baseline for a class of integer ambiguity estimators. J. Geod. 1999, 73, 275–284. [Google Scholar] [CrossRef]
- Hegarty, C.; Powers, E.; Foville, B. Accounting for timing biases between GPS, modernized GPS, and Galileo signals. In Proceedings of the 36th Annual Precise Time and Time Interval Meeting, Washington, DC, USA, 7–9 December 2004; pp. 307–317. [Google Scholar]
- Montenbruck, O.; Hauschild, A.; Hessels, U. Characterization of GPS/GIOVE sensor stations in the CONGO network. GPS Solut. 2011, 15, 193–205. [Google Scholar] [CrossRef]
- Khalife, J.; Kassas, Z.Z.M. Performance-driven design of carrier phase differential navigation frameworks with megaconstellation LEO satellites. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 2947–2966. [Google Scholar] [CrossRef]
- Stock, W.; Schwarz, R.T.; Hofmann, C.A.; Knopp, A. Survey On Opportunistic PNT With Signals From LEO Communication Satellites. IEEE Commun. Surv. Tutor. 2024, 27, 77–107. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).