Numerical Study of Cavitating Flows in an External Gear Pump with Special Emphasis on Thermodynamic Effects
Abstract
1. Introduction
2. Materials and Methods
2.1. Numerical Calculation Models
2.1.1. Governing Equations
2.1.2. Cavitation Model
2.1.3. Turbulence Model
2.2. Pump Geometry
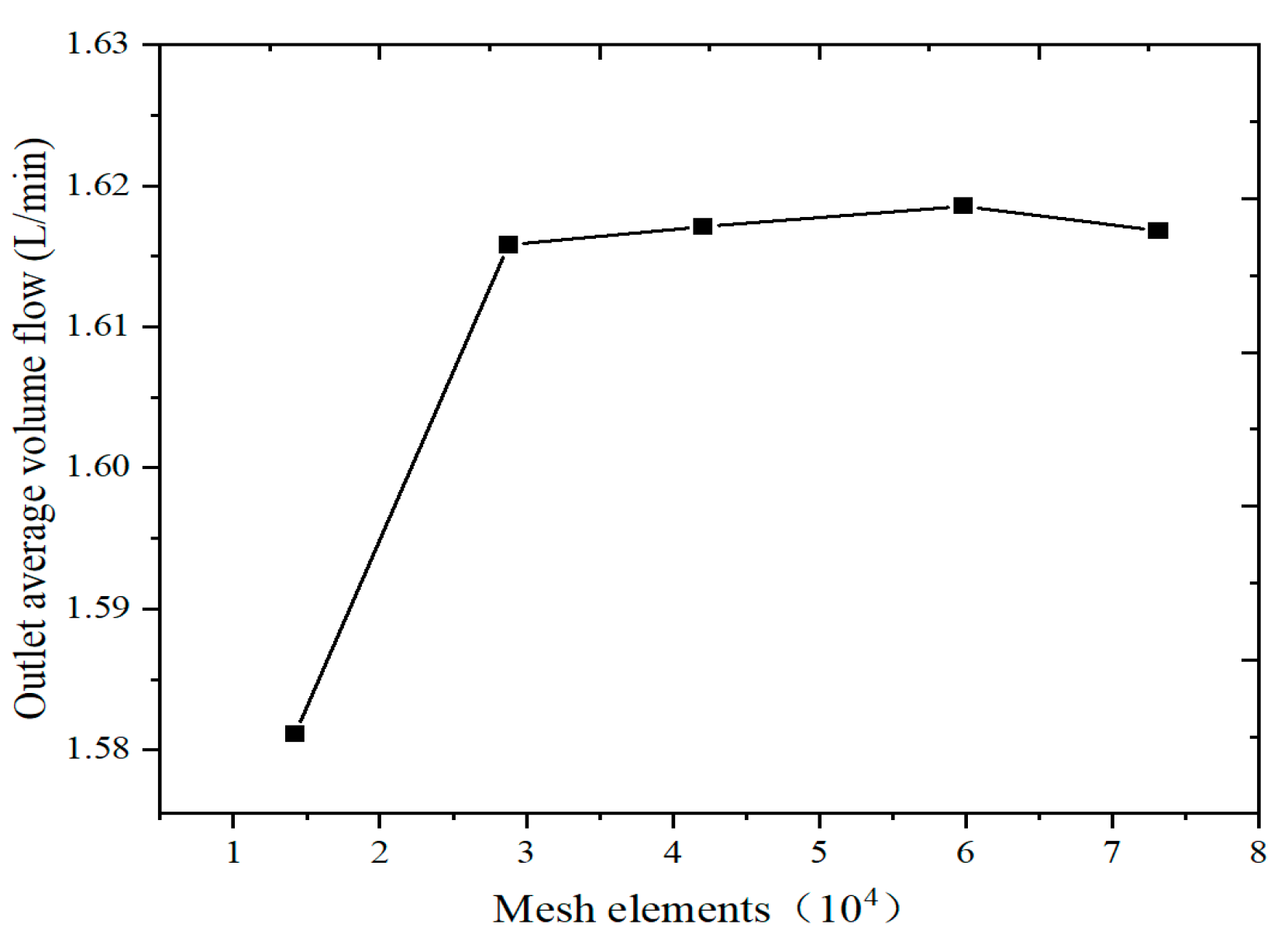
2.3. Numerical Setup and Validation
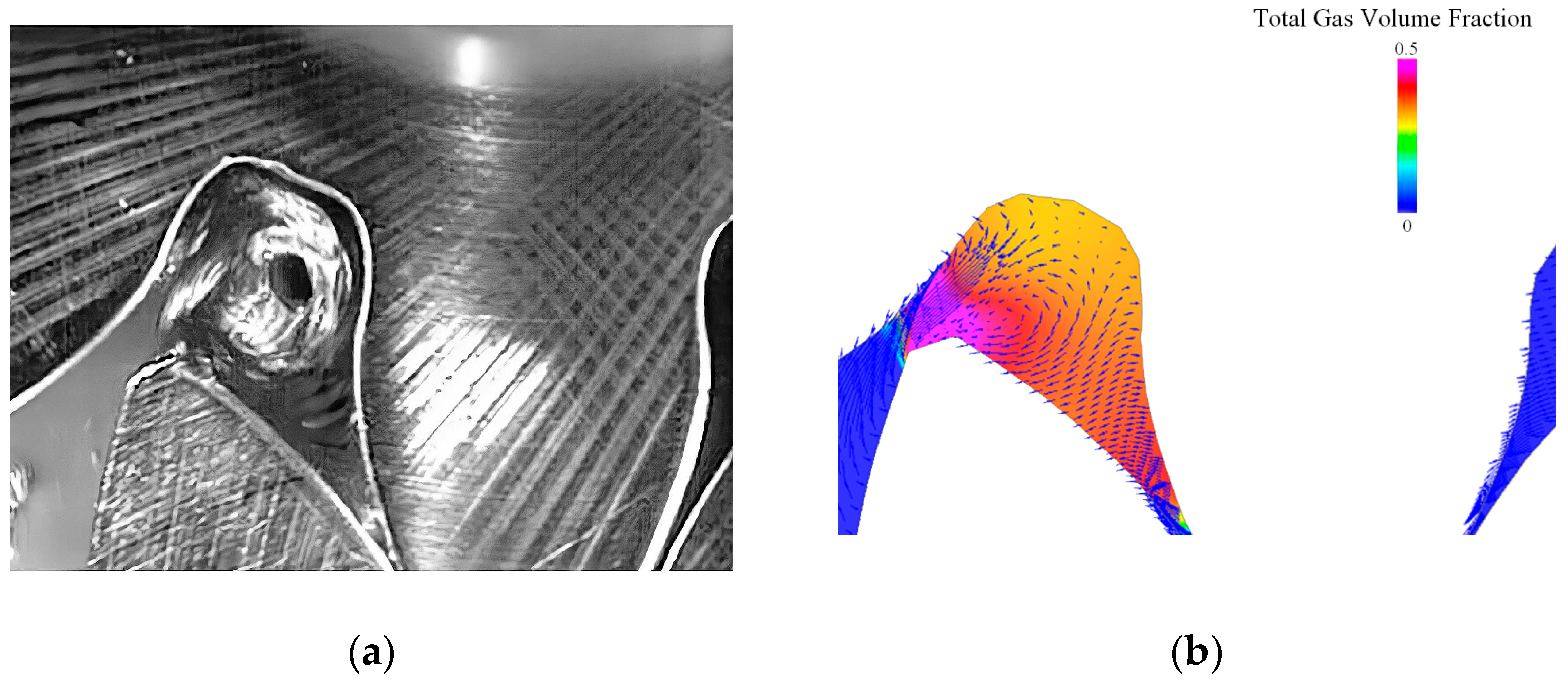
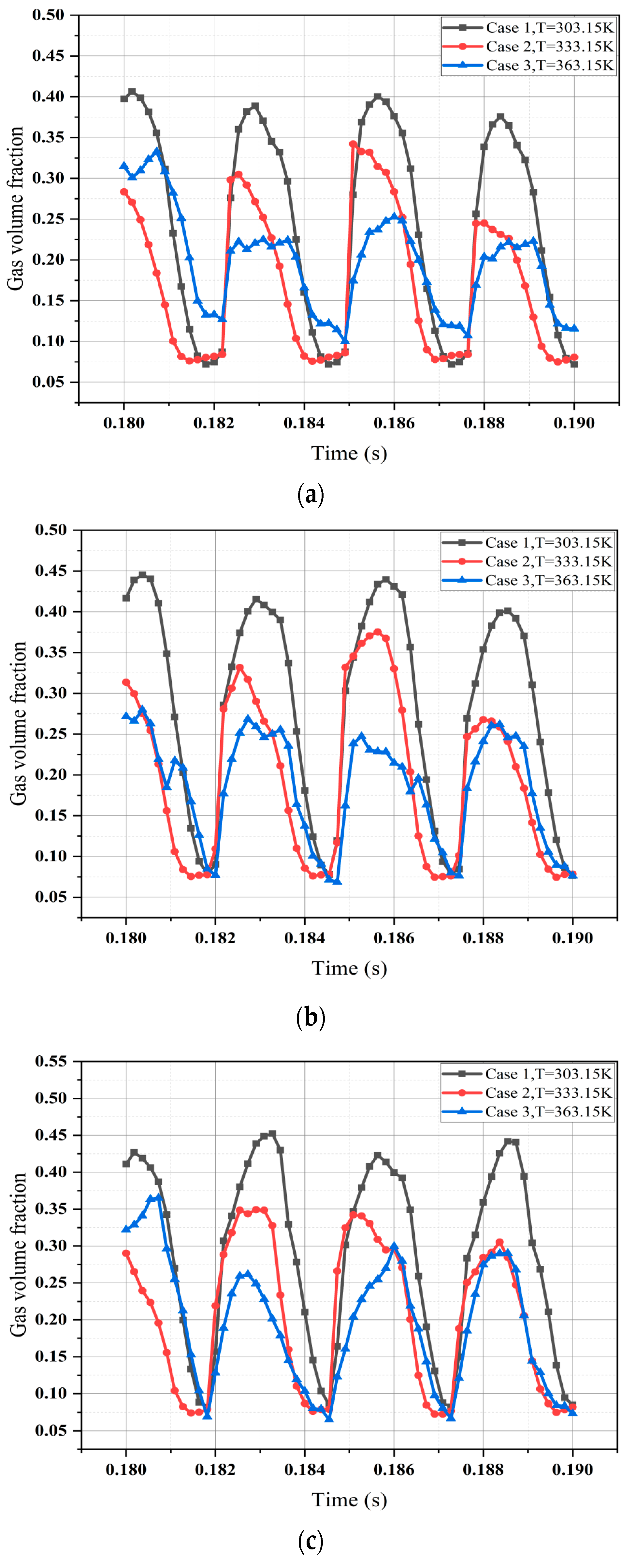
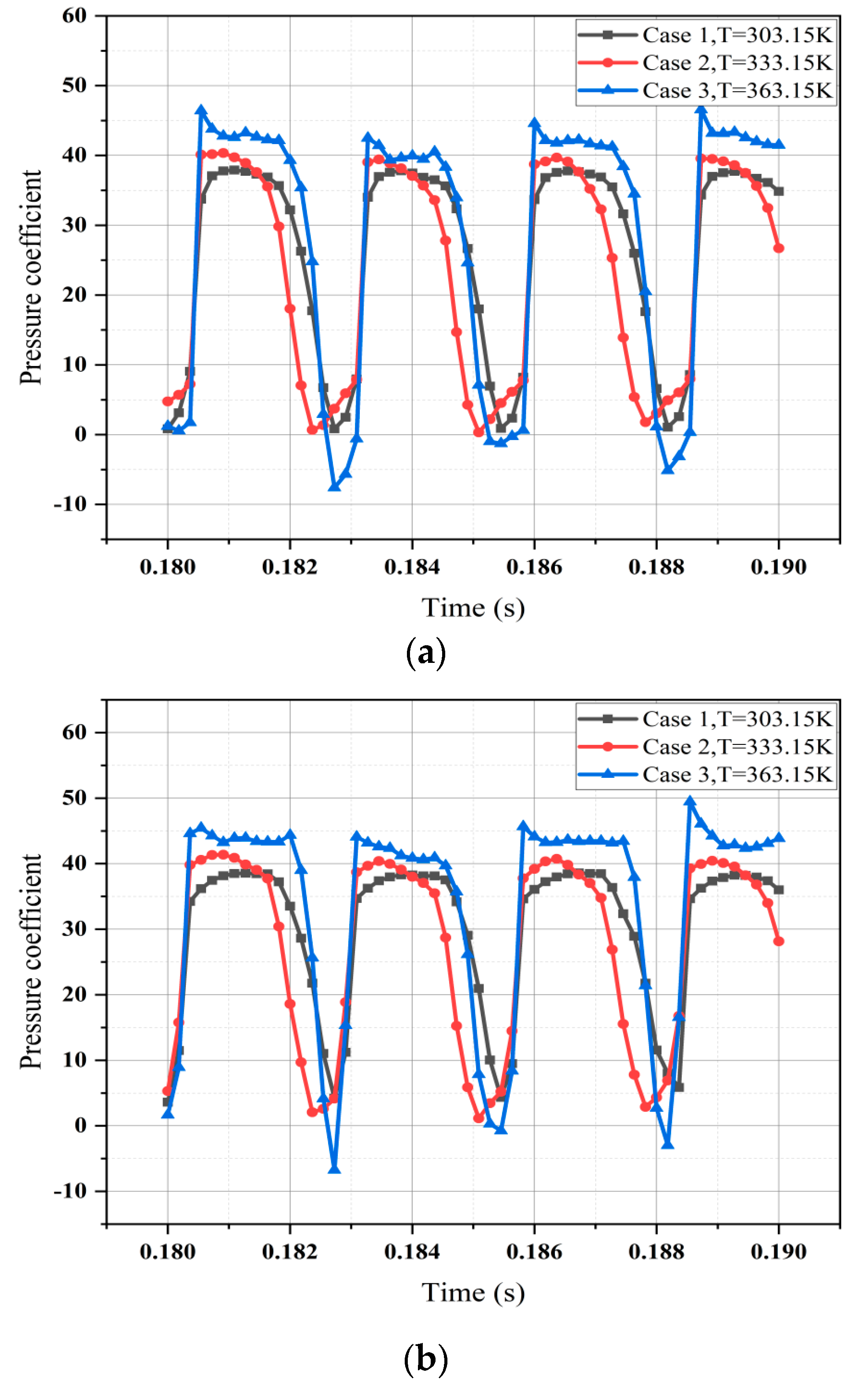
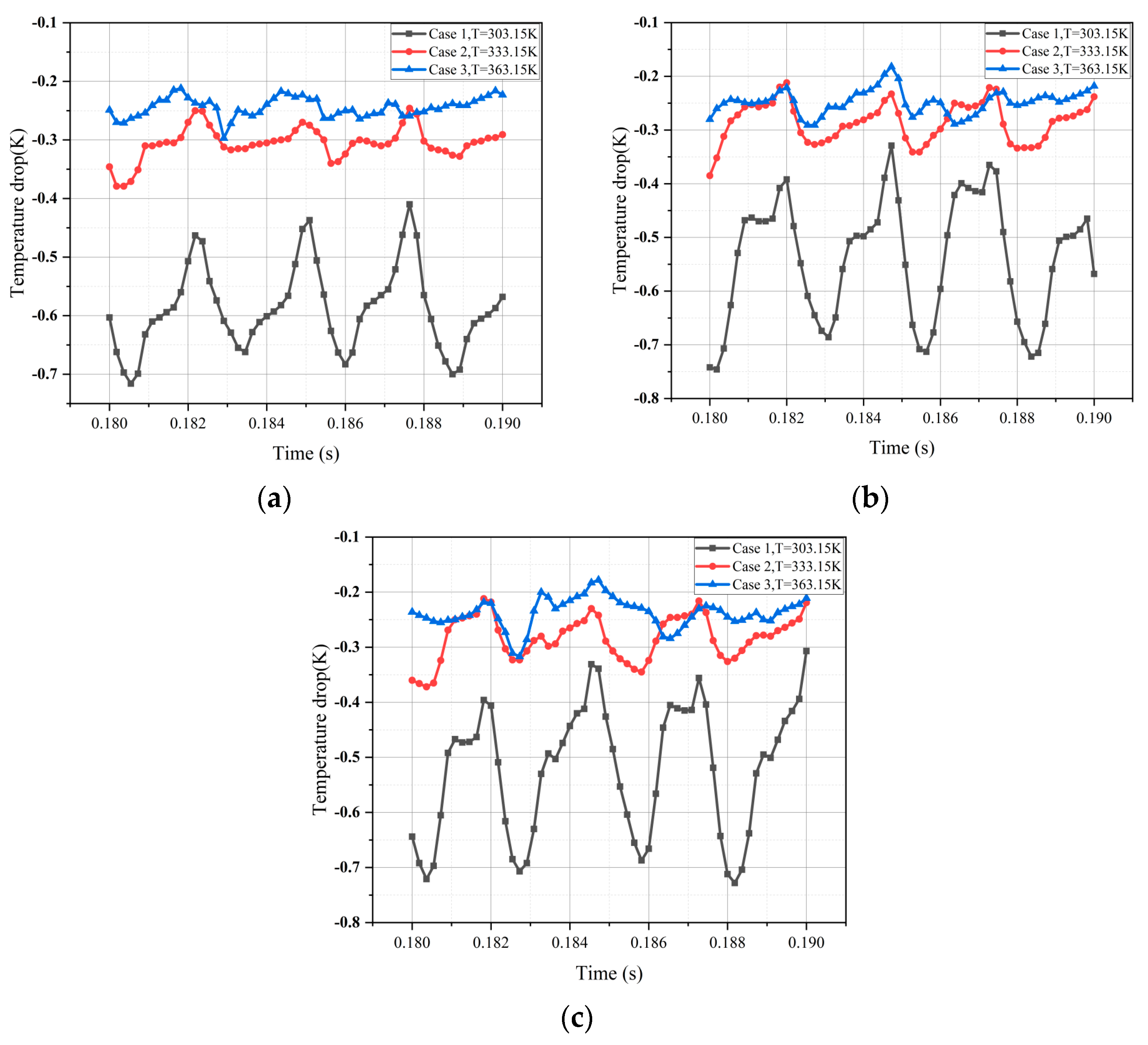
3. Results and Discussion
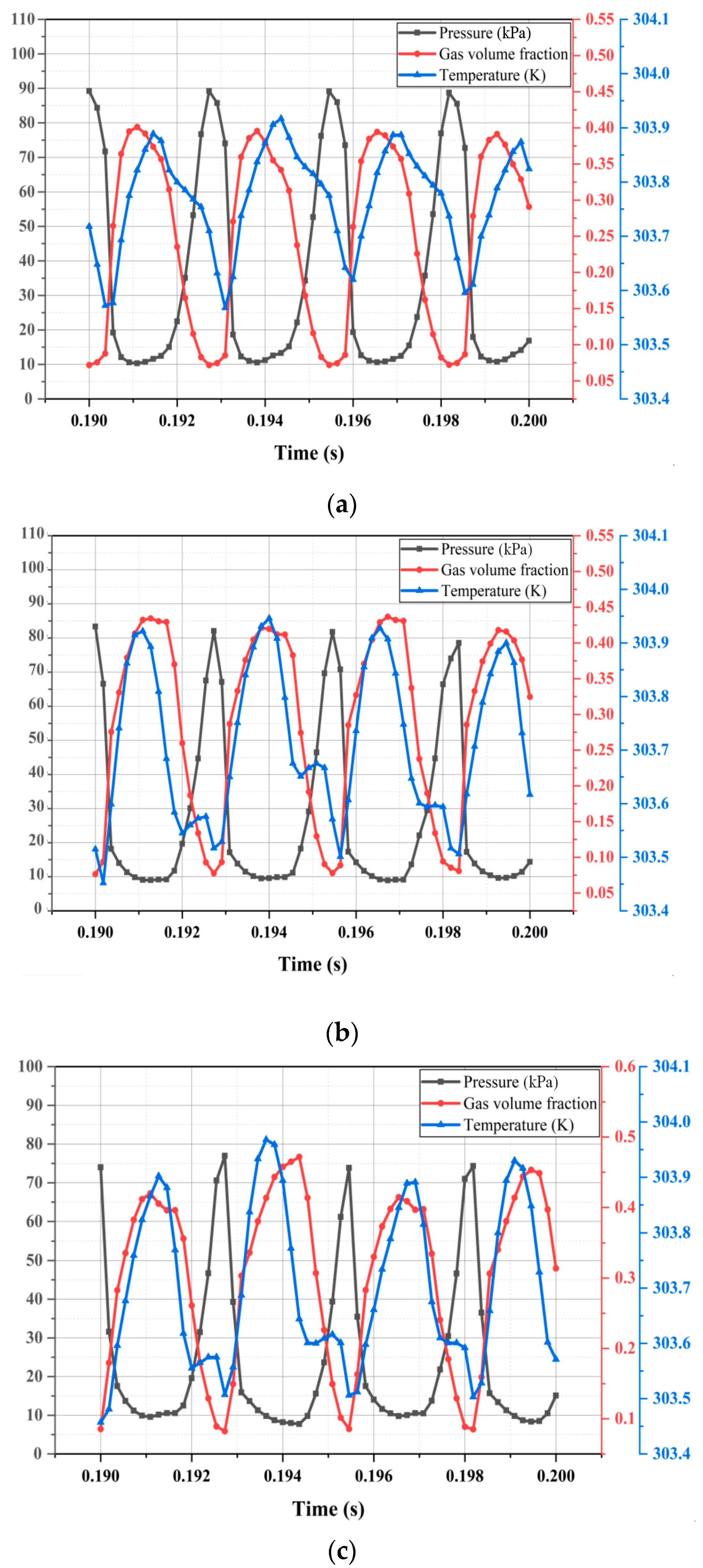
Thermodynamic Effects of Cavitation at Different Temperatures
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brennen, C.E. Cavitation and Bubble Dynamics; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Kim, K.H.; Chahine, G.; Franc, J.P.; Karimi, A. (Eds.) Advanced Experimental and Numerical Techniques for Cavitation Erosion Prediction; Springer: Berlin/Heidelberg, Germany, 2014; Volume 106. [Google Scholar]
- Kubota, A.; Kato, H.; Yamaguchi, H. A New Modelling of Cavitating Flows: A Numerical Study of Unsteady Cavitation on a Hydrofoil Section. J. Fluid Mech. 1992, 240, 59–96. [Google Scholar] [CrossRef]
- Wang, G.; Senocak, I.; Shyy, W.; Ikohagi, T.; Cao, S. Dynamics of Attached Turbulent Cavitating Flows. Prog. Aerosp. Sci. 2001, 37, 551–581. [Google Scholar]
- Ji, B.; Luo, X.; Wu, Y.; Peng, X.; Xu, H. Partially-Averaged Navier–Stokes Method with Modified k–ε Model for Cavitating Flow Around a Marine Propeller in a Non-Uniform Wake. Int. J. Heat Mass Transfer 2012, 55, 6582–6588. [Google Scholar] [CrossRef]
- Chen, T.; Wang, G.; Huang, B.; Wang, K. Numerical Study of Thermodynamic Effects on Liquid Nitrogen Cavitating Flows. Cryogenics 2015, 70, 21–27. [Google Scholar]
- Kato, H. Temperature Depression in Cavity. In Proceedings of the ASME Symposium on Cavitation and Gas-Liquid Flow in Fluid Machinery and Devices, San Diego, CA, USA, 7–11 July 1996; ASME: New York, NY, USA, 1996; pp. 407–413. [Google Scholar]
- Chen, T.; Huang, B.; Wang, G.; Wang, K. Effects of Fluid Thermophysical Properties on Cavitating Flows. J. Mech. Sci. Technol. 2015, 29, 4239–4246. [Google Scholar] [CrossRef]
- Franc, J.P.; Rebattet, C.; Coulon, A. An Experimental Investigation of Thermal Effects in a Cavitating Inducer. J. Fluids Eng. 2004, 126, 716–723. [Google Scholar]
- Cervone, A.; Bramanti, C.; Rapposelli, E.; d’Agostino, L. Thermal Cavitation Experiments on a NACA 0015 Hydrofoil. Fluids Eng. 2006, 128, 326–331. [Google Scholar] [CrossRef]
- Gustavsson, J.P.; Denning, K.C.; Segal, C. Hydrofoil Cavitation Under Strong Thermodynamic Effect. J. Fluid Eng. 2008, 130, 091303. [Google Scholar]
- Petkovšek, M.; Dular, M. IR Measurements of the Thermodynamic Effects in Cavitating Flow. Int. J. Heat Fluid Flow 2013, 44, 756–763. [Google Scholar]
- Hosangadi, A.; Ahuja, V. A Generalized Multi-Phase Framework for Modeling Cavitation in Cryogenic Fluids. In Proceedings of the 33rd AIAA Fluid Dynamics Conference and Exhibit, Orlando, FL, USA, 23–26 June 2003; AIAA: Reston, VA, USA, 2003; p. 4000. [Google Scholar]
- Huang, B.; Wu, Q.; Wang, G. Numerical Investigation of Cavitating Flow in Liquid Hydrogen. Int. J. Hydrogen Energy 2014, 39, 1698–1709. [Google Scholar]
- Rodio, M.G.; De Giorgi, M.G.; Ficarella, A. Influence of Convective Heat Transfer Modeling on the Estimation of Thermal Effects in Cryogenic Cavitating Flows. Int. J. Heat Mass Transfer 2012, 55, 6538–6554. [Google Scholar]
- Liu, S.; Li, S.; Zhang, L.; Wu, Y. A Mixture Model with Modified Mass Transfer Expression for Cavitating Turbulent Flow Simulation. Eng. Comput. 2008, 25, 290–304. [Google Scholar]
- Chen, T.; Wang, G.; Huang, B.; Wang, K.; Xu, H. Numerical Study of Cavitating Flows in a Wide Range of Water Temperatures with Special Emphasis on Two Typical Cavitation Dynamics. Int. J. Heat Mass Transfer 2016, 101, 886–900. [Google Scholar]
- Manco, S.; Nervegna, N. Simulation of an External Gear Pump and Experimental Verification. Proc. JFPS Int. Symp. Fluid Power 1989, 1989, 147–160. [Google Scholar]
- Del Campo, D.; Castilla, R.; Raush, G.A.; Gamez Montero, P.J.; Codina, E. Numerical Analysis of External Gear Pumps Including Cavitation. J. Fluids Eng. 2012, 134, 081105. [Google Scholar]
- Mithun, M.G.; Koukouvinis, P.; Karathanassis, I.K.; Gavaises, M. Numerical Simulation of Three-Phase Flow in an External Gear Pump Using Immersed Boundary Approach. Appl. Math. Model. 2019, 72, 682–699. [Google Scholar]
- Yoon, Y.; Park, B.H.; Shim, J.; Han, Y.O.; Hong, B.J.; Yun, S.H. Numerical Simulation of Three-Dimensional External Gear Pump Using Immersed Solid Method. Appl. Therm. Eng. 2017, 118, 539–550. [Google Scholar]
- Choudhuri, K.; Biswas, N.; Mandal, S.K.; Mitra, C.; Biswas, S. A Numerical Study of an External Gear Pump Operating Under Different Conditions. Mater. Today Proc. 2022; in press. [Google Scholar]
- Bilalov, R.A.; Smetannikov, O.Y. Numerical Study of the Hydrodynamics of an External Gear Pump. J. Appl. Mech. Tech. Phys. 2022, 63, 1284–1293. [Google Scholar]
- Amirante, R.; Distaso, E.; Tamburrano, P. Experimental and Numerical Analysis of Cavitation in Hydraulic Proportional Directional Valves. Energy Convers. Manag. 2014, 87, 208–219. [Google Scholar]
- Casoli, P.; Scolari, F.; Rundo, M.; Lettini, A.; Rigosi, M. CFD Analyses of Textured Surfaces for Tribological Improvements in Hydraulic Pumps. Energies 2020, 13, 5799. [Google Scholar] [CrossRef]
- Casoli, P.; Vescovini, C.M.; Rundo, M. One-Dimensional Fluid Dynamic Modeling of a Gas Bladder Hydraulic Damper for Pump Flow Pulsation. Energies 2023, 16, 3368. [Google Scholar] [CrossRef]
- Tacconi, J.; Shahpar, S.; King, A.; Olufeagba, J.P.; Khan, R.; Sant, I.; Yates, M. Elasto-Hydrodynamic Model of Hybrid Journal Bearings for Aero-Engine Gear Fuel Pump Applications. J. Tribol. 2022, 144, 031604. [Google Scholar]
- Casari, N.; Fadiga, E.; Pinelli, M.; Randi, S.; Suman, A. Pressure Pulsation and Cavitation Phenomena in a Micro-ORC System. Energies 2019, 12, 2186. [Google Scholar] [CrossRef]
- Li, W.; Yu, Z.; Kadam, S. An Improved Cavitation Model with Thermodynamic Effect and Multiple Cavitation Regimes. Int. J. Heat Mass Transfer 2023, 205, 123854. [Google Scholar]
- Kim, S.E. A Numerical Study of Unsteady Cavitation on a Hydrofoil. In Proceedings of the CAV2009—7th International Symposium on Cavitation, Ann Arbor, MI, USA, 16–20 August 2009. [Google Scholar]
- Singhal, A.K.; Athavale, M.M.; Li, H.; Jiang, Y. Mathematical Basis and Validation of the Full Cavitation Model. J. Fluids Eng. 2002, 124, 617–624. [Google Scholar]
- Zhang, Y.; Ren, X.; Wang, Y.; Li, X.; Ito, Y.; Gu, C. Investigation of the Cavitation Model in an Inducer for Water and Liquid Nitrogen. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 6939–6952. [Google Scholar]
- Launder, B.E.; Spalding, D.B. The Numerical Computation of Turbulent Flows. In Numerical Prediction of Flow, Heat Transfer, Turbulence and Combustion; Pergamon: Oxford, UK, 1983; pp. 96–116. [Google Scholar]
- Shen, X.; Zhang, D.; Xu, B.; Jin, Y.; Gao, X. Experimental and Numerical Investigation on Pressure Fluctuation of the Impeller in an Axial Flow Pump. In Fluids Engineering Division Summer Meeting; American Society of Mechanical Engineers: New York, NY, USA, 2019; Volume 59087, p. V005T05A013. [Google Scholar]
- Li, M.X. Study on Dynamic Evolution Process and Influence of Gas Phase in Gear Pump Cavitation. Ph.D. Dissertation, Lanzhou University of Technology, Lanzhou, China, 2019. [Google Scholar]
- Roache, P.J. Quantification of Uncertainty in Computational Fluid Dynamics. Annu. Rev. Fluid Mech. 1997, 29, 123–160. [Google Scholar]
- Antoniak, P.; Stryczek, J. Visualization Study of the Flow Processes and Phenomena in the External Gear Pump. Arch. Civ. Mech. Eng. 2018, 18, 1103–1115. [Google Scholar]

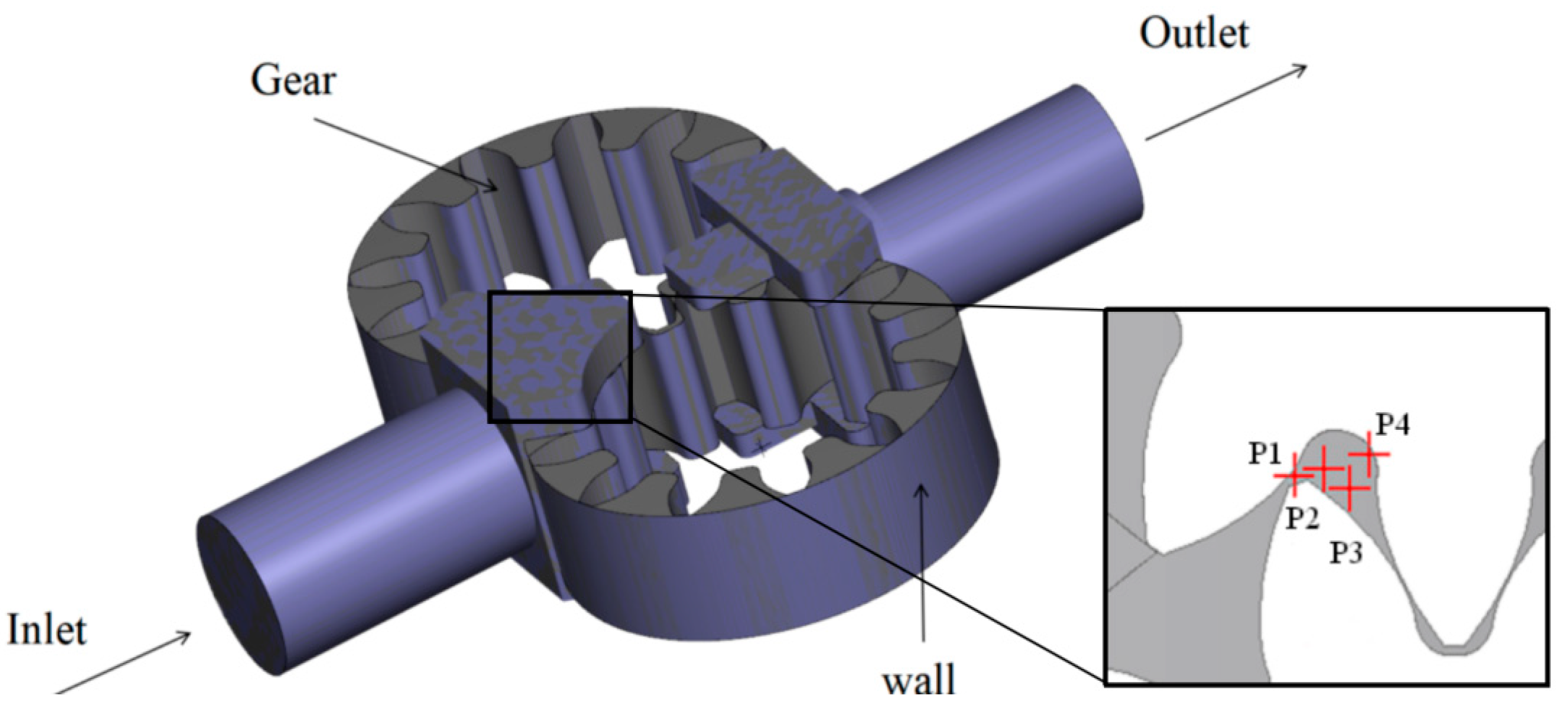



| Parameters | Value | Description |
|---|---|---|
| m | 3 | Module |
| Z | 11 | Tooth number |
| d | 33 | Reference circle diameter (mm) |
| aw | 20 | Pressure angle (°) |
| ha | 9 | Addendum (mm) |
| hf | 4.5 | Dedendum (mm) |
| da | 42 | Addendum circle diameter (mm) |
| df | 28.5 | Dedendum circle diameter (mm) |
| a | 33 | Center distance (mm) |
| ∆d | 2.55 | Center distance change (mm) |
| d′ | 35.55 | Actual center distance (mm) |
| B | 5 | Face width (mm) |
| ∆x | 0.05 | Intertooth clearance (mm) |
| Case | Temperatures (K) | Gear Speed (r/min) | Absolute Inlet Pressure (Pa) | Absolute Outlet Pressure (Pa) |
|---|---|---|---|---|
| 1 | 303.15 | 1000 | 91,019 | 1,091,019 |
| 2 | 333.15 | 1000 | 101,325 | 1,101,325 |
| 3 | 363.15 | 1000 | 177,283 | 1,177,283 |
| Mesh | Elements | Outlet Average Volume Flow (L/min) | GCI/% |
|---|---|---|---|
| I | 47,000 | 1.312 | |
| II | 140,000 | 1.581 | 19.8 |
| III | 420,000 | 1.617 | 2.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Liu, Y.; Li, Z.; Yin, X.; Chen, T. Numerical Study of Cavitating Flows in an External Gear Pump with Special Emphasis on Thermodynamic Effects. Appl. Sci. 2025, 15, 3529. https://doi.org/10.3390/app15073529
Wu X, Liu Y, Li Z, Yin X, Chen T. Numerical Study of Cavitating Flows in an External Gear Pump with Special Emphasis on Thermodynamic Effects. Applied Sciences. 2025; 15(7):3529. https://doi.org/10.3390/app15073529
Chicago/Turabian StyleWu, Xiaomi, Yiyang Liu, Zhixing Li, Xinxin Yin, and Tairan Chen. 2025. "Numerical Study of Cavitating Flows in an External Gear Pump with Special Emphasis on Thermodynamic Effects" Applied Sciences 15, no. 7: 3529. https://doi.org/10.3390/app15073529
APA StyleWu, X., Liu, Y., Li, Z., Yin, X., & Chen, T. (2025). Numerical Study of Cavitating Flows in an External Gear Pump with Special Emphasis on Thermodynamic Effects. Applied Sciences, 15(7), 3529. https://doi.org/10.3390/app15073529







