An MT-InSAR-Based Procedure for Detecting and Interpreting Vertical Ground Deformation Anomalies During Phases of Unrest at Campi Flegrei Caldera, Italy
Abstract
1. Introduction
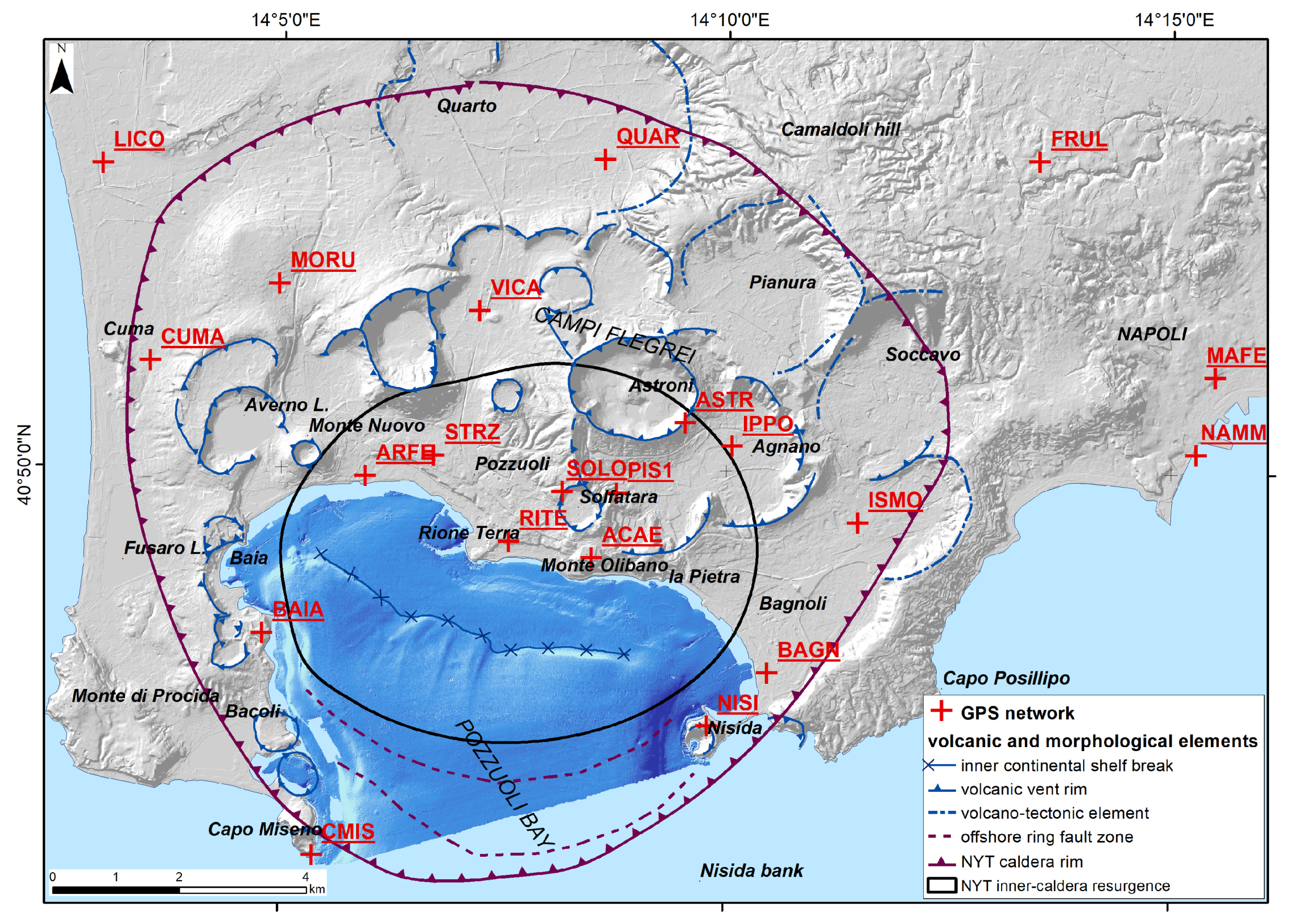
2. Study Area
Ground Deformation in Historical Times
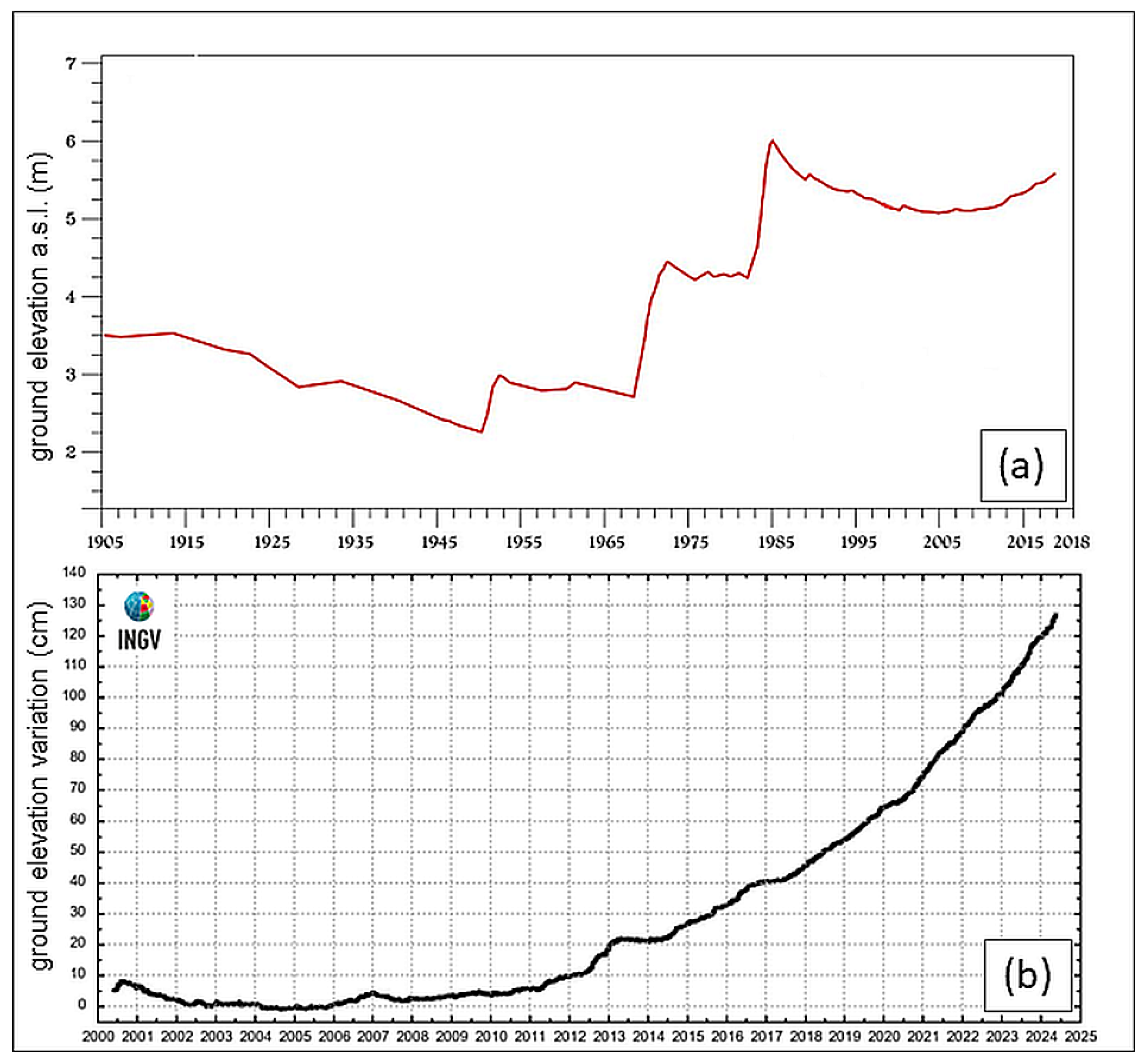
3. Methods
3.1. Satellite Radar Interferometric Dataset
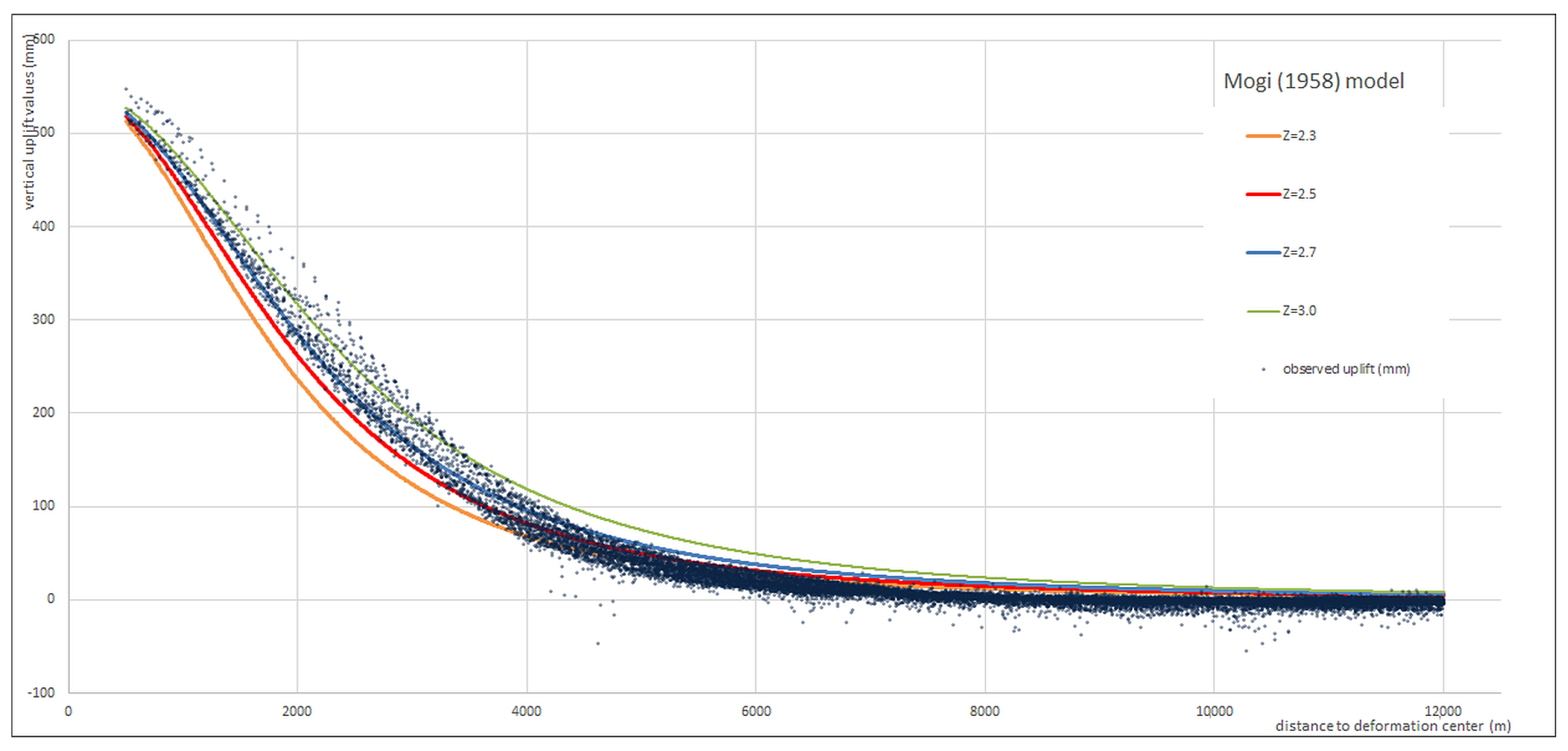
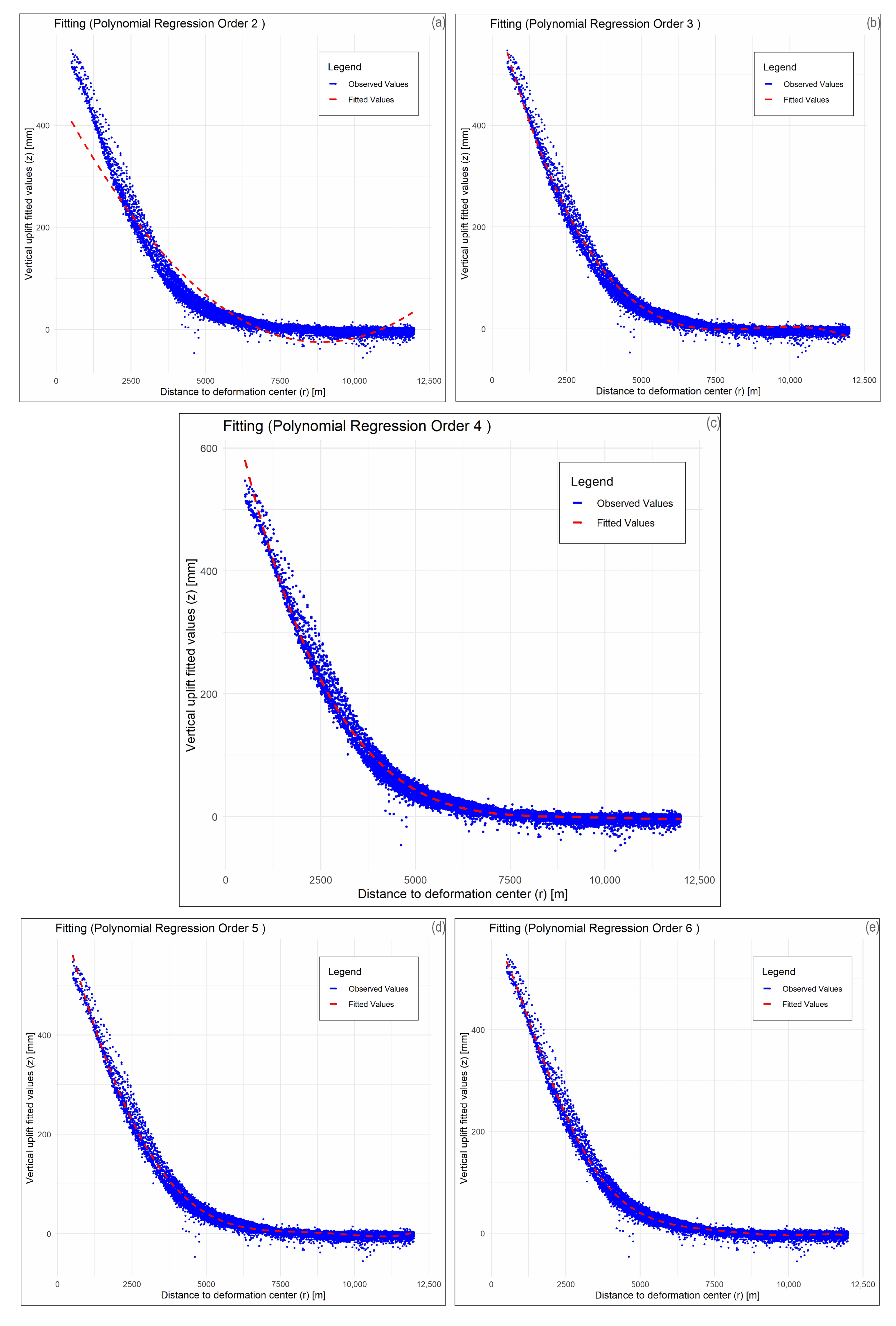
3.2. Ortho Vertical Dataset Processing for Best Fitting Axial–Symmetric Model
- x = r (distance to the deformation center);
- y = z (vertical uplift value in the EGMS ortho-vertical dataset).
3.3. Calculation of Vertical Ground Deformation Residuals
3.4. Residuals’ Analysis and Comparison with Seismic and Volcano-Tectonic Datasets
- (a)
- The INGV national earthquake list, available at https://terremoti.ingv.it/en (accessed on 28 Novembre 2024);
- (b)
- The INGV Osservatorio Vesuviano regional earthquake list, specifically referring to the Campi Flegrei volcanic area for years 1983–1984 and 2005–2024 [79], available at https://terremoti.ov.ingv.it/gossip/flegrei/years.html (accessed on 28 Novembre 2024).
3.5. Cross-Checking with Coeval GPS Datasets
- x = distance to the deformation center;
- y = vertical uplift value in the vertical GPS dataset.
4. Results
4.1. Trends in Vertical and Horizontal Ground Deformation
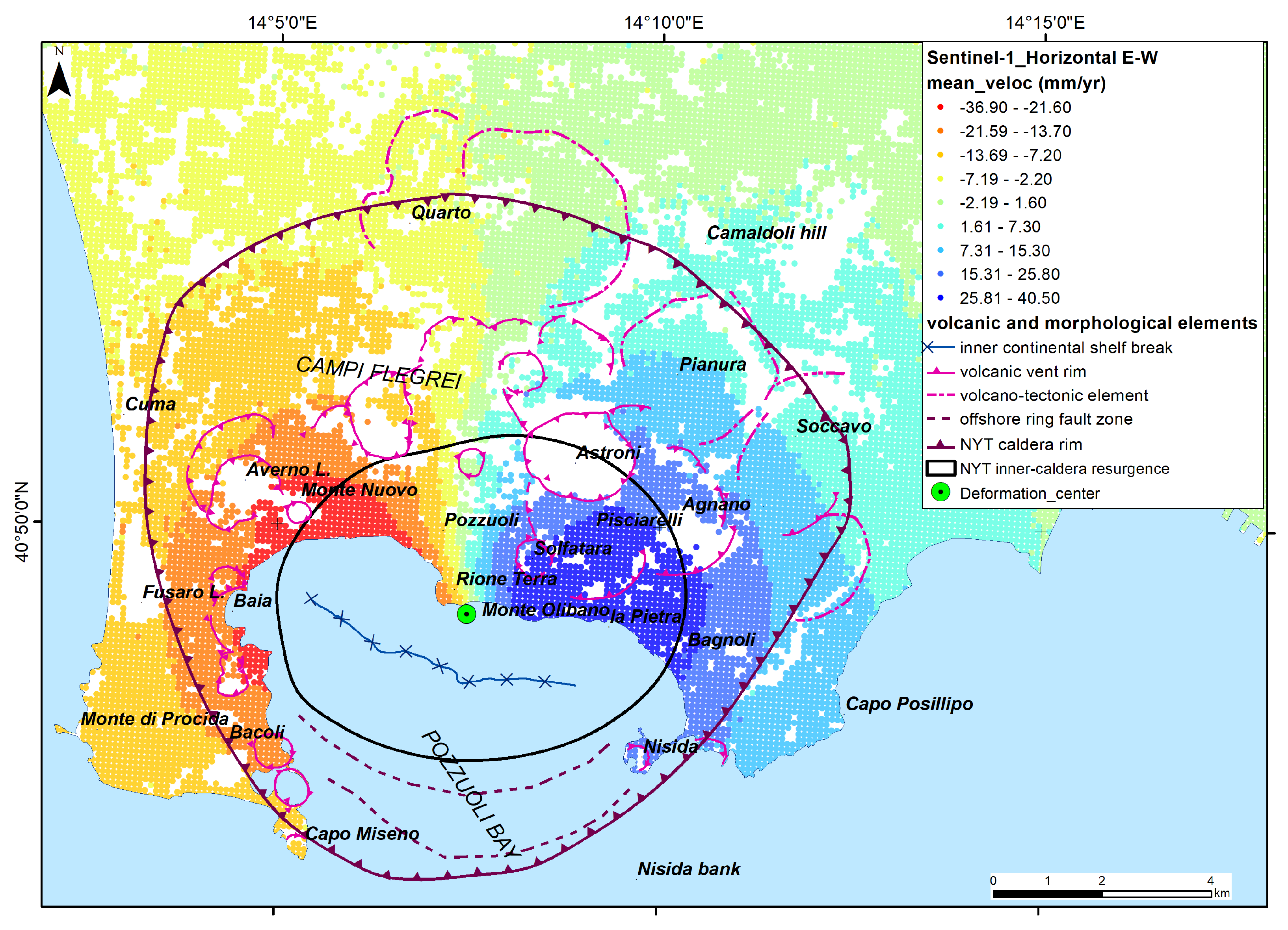

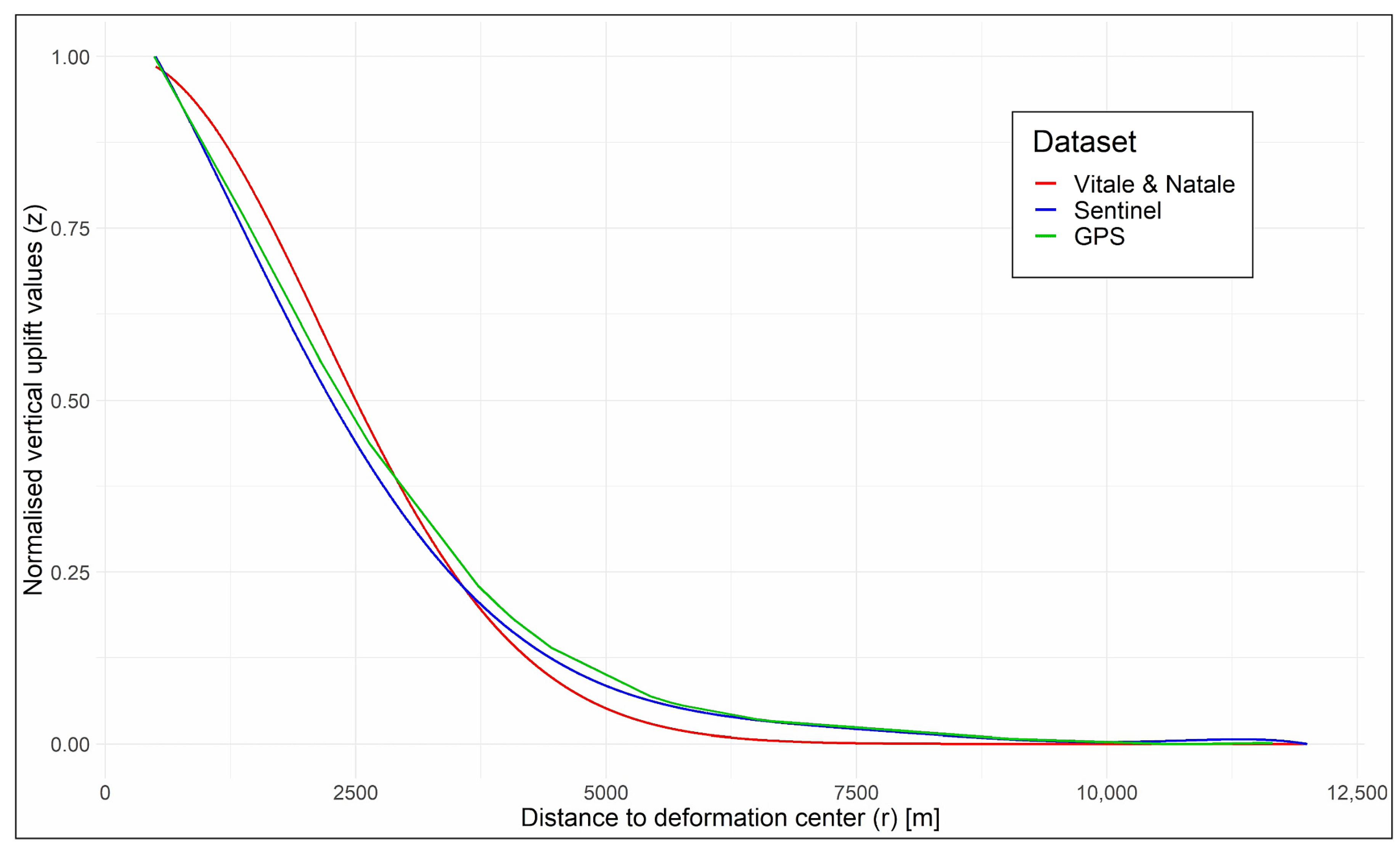
4.2. Vertical Ground Deformation Shape
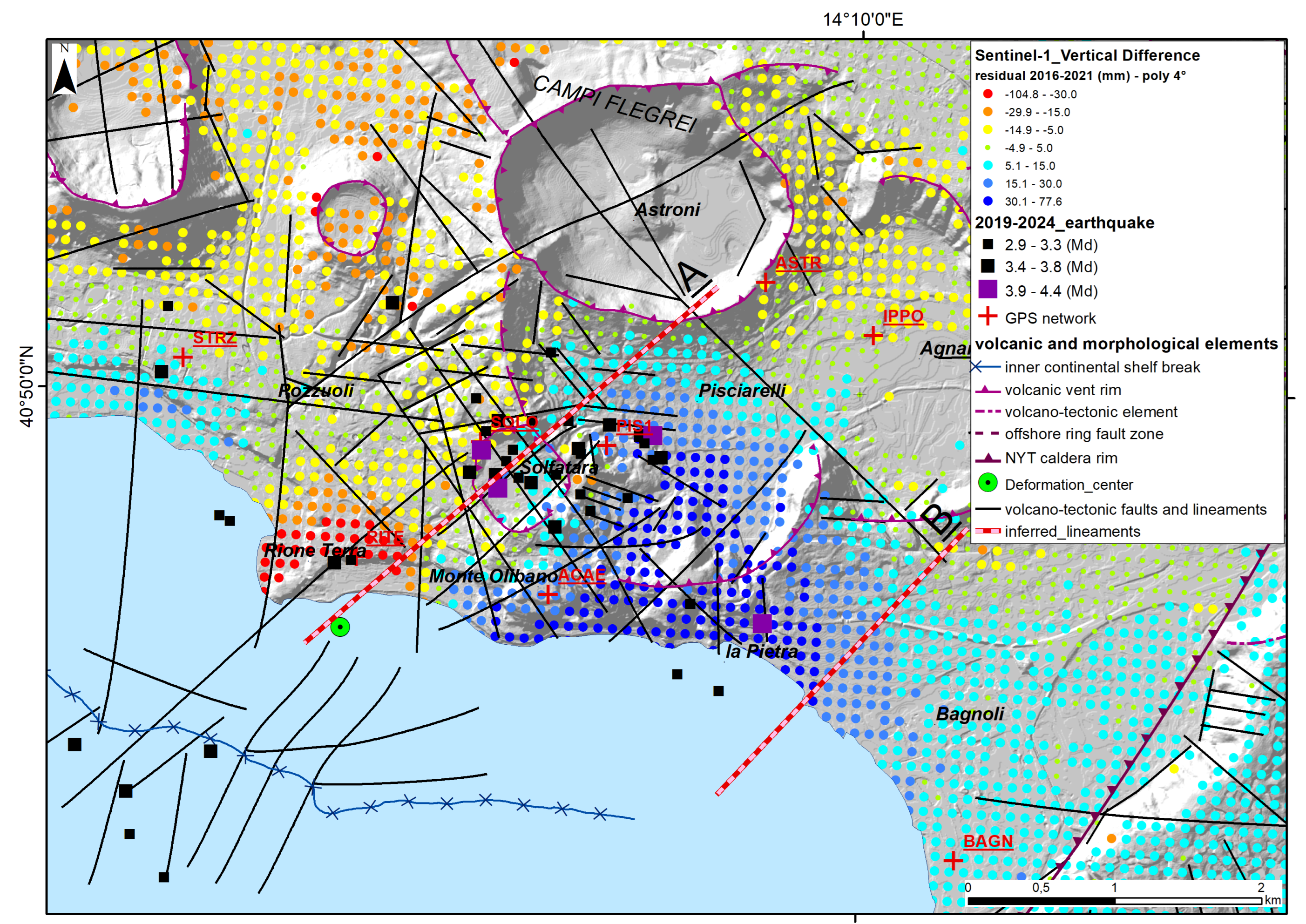
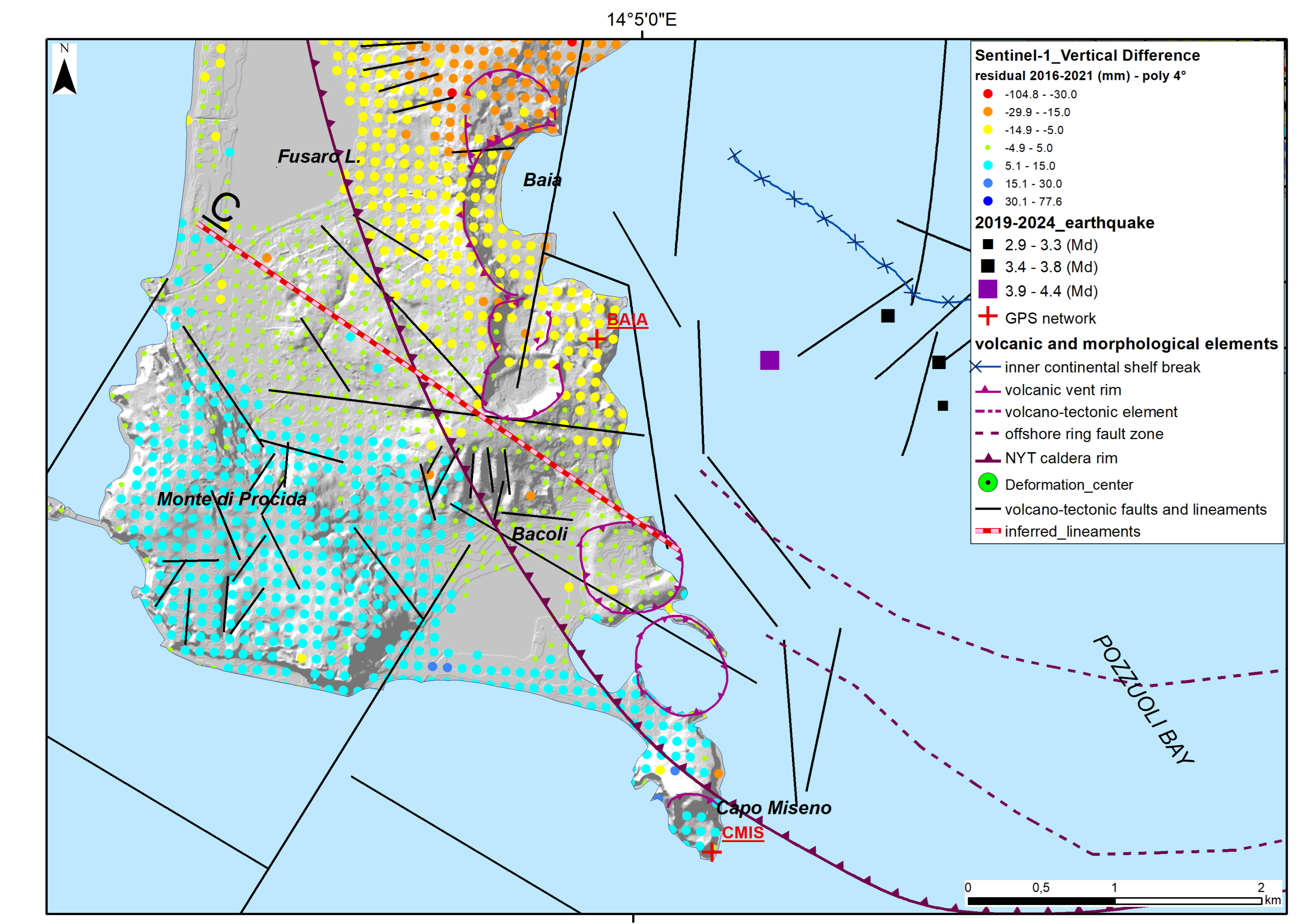
4.3. Differences Between Predicted and Observed Vertical Ground Displacements
- A well-marked SW-NE-oriented line (A) goes from the caldera deformation center to Pisciarelli and Agnano and separates sectors characterized by about 60–75 mm of difference in vertical ground deformation.
- An ill-defined SSW-NNE-oriented line (B) between Bagnoli and La Pietra separates sectors characterized by +15 mm to +45 mm of uplift anomaly (about 30 mm of difference in total).
- A well-marked WNW-ESE-oriented line (C) goes from Baia to Fusaro Lake and separates sectors characterized by −15 mm to +15 mm of uplift anomaly (about 30 mm of difference in total).
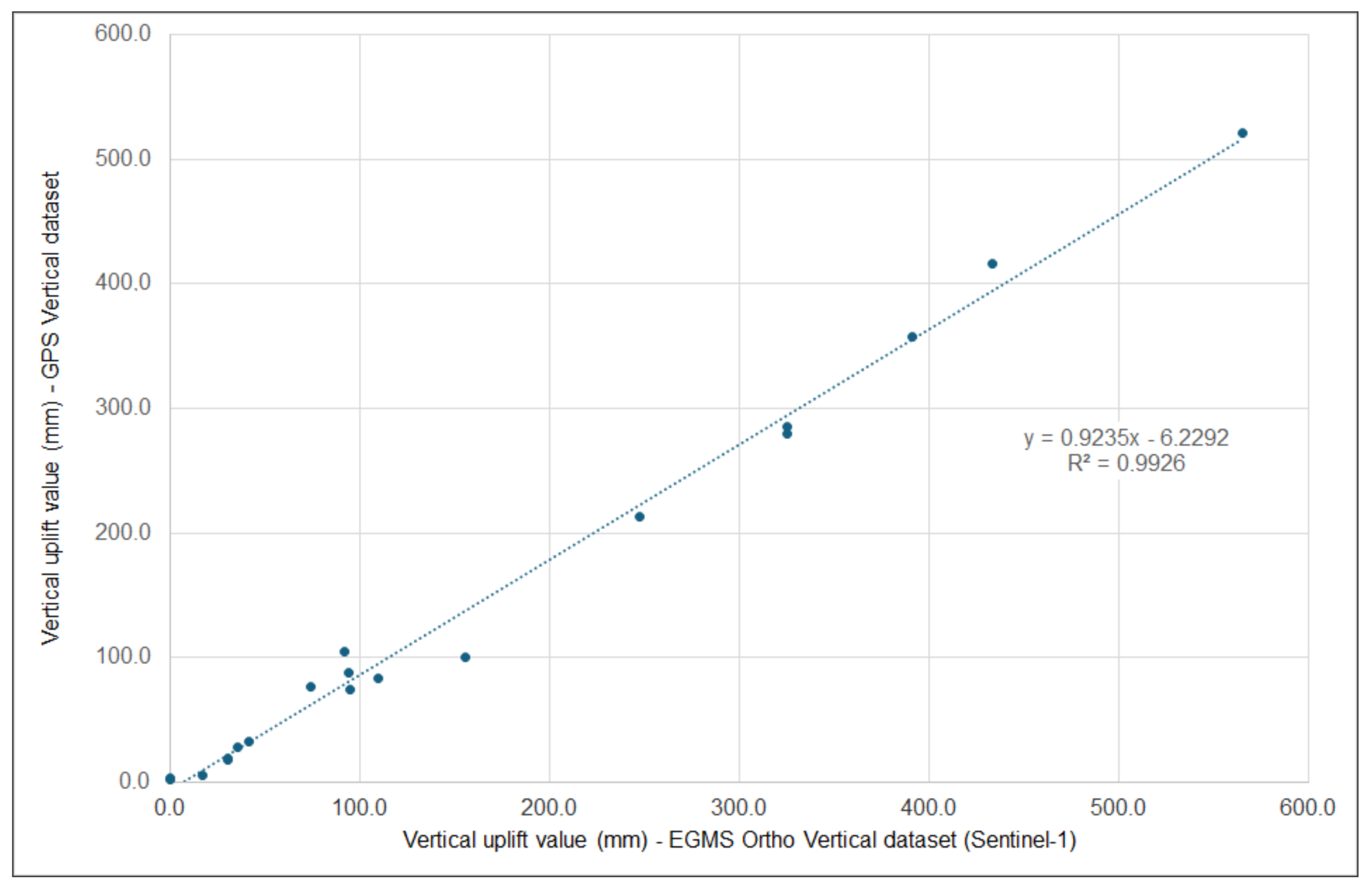
4.4. Comparison Between Sentinel-1 and GPS Datasets
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Galetto, F.; Acocella, V.; Caricchi, L. Caldera resurgence driven by magma viscosity contrasts. Nat. Commun. 2017, 8, 1750. [Google Scholar] [CrossRef] [PubMed]
- Marsh, B.D. On the mechanics of caldera resurgence. J. Geophys. Res. 1984, 89, 8245–8251. [Google Scholar] [CrossRef]
- Kennedy, B.; Wilcock, J.; Stix, J. Caldera resurgence during magma replenishment and rejuvenation at Valles and Lake City calderas. Bull. Volcanol. 2012, 74, 1833–1847. [Google Scholar] [CrossRef]
- De Silva, S.L.; Mucek, A.E.; Gregg, P.M.; Pratomo, I. Resurgent Toba—Field, chronologic, and model constraints on time scales and mechanisms of resurgence at large calderas. Front. Earth Sci. 2015, 3, 25. [Google Scholar] [CrossRef]
- De Natale, G.; Pingue, F.; Allard, P.; Zollo, A. Geophysical and geochemical modelling of the 1982-1984 unrest phenomena at Campi Flegrei caldera (southern Italy). J. Volcanol. Geotherm. Res. 1991, 48, 199–222. [Google Scholar] [CrossRef]
- Hurwitz, S.; Christiansen, L.B.; Hsieh, P.A. Hydrothermal fluid flow and deformation in large calderas: Inferences from numerical simulations. J. Geophys. Res. 2007, 112, B02206. [Google Scholar] [CrossRef]
- Troise, C.; De Natale, G.; Schiavone, R.; Somma, R.; Moretti, R. The Campi Flegrei caldera unrest: Discriminating magma intrusions from hydrothermal effects and implications for possible evolution. Earth-Sci. Rev. 2019, 188, 108–122. [Google Scholar] [CrossRef]
- Acocella, V. Bridging the gap from caldera unrest to resurgence. Front. Earth Sci. 2019, 7, 173. [Google Scholar] [CrossRef]
- Newhall, C.G.; Dzurisin, D. Historical Unrest at large Calderas of the World. US Geological Survey. Bulletin 1988, 1855, 1–1108. [Google Scholar] [CrossRef]
- Phillipson, G.; Sobradelo, R.; Gottsmann, J. Global volcanic unrest in the 21st century: An analysis of the first decade. J. Volcanol. Geotherm. Res. 2013, 264, 183–196. [Google Scholar] [CrossRef]
- Acocella, V.; Di Lorenzo, R.; Newhall, C.; Scandone, R. An overview of recent (1988 to 2014) caldera unrest: Knowledge and perspectives. Rev. Geophys. 2015, 53, 896–955. [Google Scholar] [CrossRef]
- Charlton, D.; Kilburn, C.; Edwards, S. Volcanic unrest scenarios and impact assessment at Campi Flegrei caldera, Southern Italy. J. Appl. Volcanol. 2020, 9, 7. [Google Scholar] [CrossRef]
- Barberi, F.; Corrado, G.; Innocenti, F.; Luongo, G. Phlegraean fields 1982-1984: Brief chronicle of a volcano emergency in a densely populated area. Bull Volcanol. 1984, 47, 175–185. [Google Scholar] [CrossRef]
- Johnston, D.; Scott, B.J.; Houghton, B.; Paton, D.; Dowrick, D.J.; Villamor, P.; Savage, J. Social and economic consequences of historic caldera unrest at the Taupo volcano, New Zealand and the management of future episodes of unrest. Bull. New Zealand Soc. Earthq. Eng. 2002, 35, 215–230. [Google Scholar] [CrossRef]
- Kuester, I.; Forsyth, S. Rabaul eruption risk: Population awareness and preparedness survey. Disasters 1985, 9, 179–182. [Google Scholar] [CrossRef]
- Benson, C. Volcanoes and the economy. In Volcanoes and the Environment; Marti, J., Ernst, G.G.J., Eds.; Cambridge University Press: Cambridge, UK, 2006; pp. 440–467. [Google Scholar]
- De Natale, G.; Troise, C.; Somma, R. Invited perspectives: The volcanoes of Naples: How can the highest volcanic risk in the world be effectively mitigated? Nat. Hazards Earth Syst. Sci. 2020, 20, 2037–2053. [Google Scholar] [CrossRef]
- INGV, 2024. Bollettino di Sorveglianza Campi Flegrei, mese di Giugno 2024. INGV, Sezione di Napoli–Osservatorio Vesuviano. p. 51. Available online: https://www.ov.ingv.it/index.php/monitoraggio-e-infrastrutture/bollettini-tutti/bollett-mensili-cf/anno-2024-3/1652-bollettino-mensile-campi-flegrei-2024-06/file (accessed on 28 November 2024).
- Amoruso, A.; Crescentini, L. Clues of Ongoing Deep Magma Inflation at Campi Flegrei Caldera (Italy) from Empirical Orthogonal Function Analysis of SAR Data. Remote Sens. 2022, 14, 5698. [Google Scholar] [CrossRef]
- Amoruso, A.; Crescentini, L.; Sabbetta, I. Paired deformation sources of the Campi Flegrei caldera (Italy) required by recent (1980–2010) deformation history. J. Geophys. Res. Solid Earth 2014, 119, 858–879. [Google Scholar] [CrossRef]
- Macedonio, G.; Giudicepietro, F.; D’Auria, L.; Martini, M. Sill intrusion as a source mechanism of unrest at volcanic calderas. J. Geophys. Res. Solid Earth 2014, 119, 3986–4000. [Google Scholar] [CrossRef]
- Woo, J.Y.L.; Kilburn, C.R.J. Intrusion and deformation at Campi Flegrei, southern Italy: Sills, dikes, and regional extension. J. Geophys. Res. 2010, 115, B12210. [Google Scholar] [CrossRef]
- Moretti, R.; Troise, C.; Sarno, F.; De Natale, G. Caldera unrest driven by CO2-induced drying of the deep hydrothermal system. Sci. Rep. 2018, 8, 8309. [Google Scholar]
- Zollo, A., N. Maercklin, M. Vassallo, D. Dello Iacono, J. Virieux, and P. Gasparini. Seismic reflections reveal a massive melt layer feeding Campi Flegrei caldera. Geophys. Res. Lett. 2008, 35, L12306. [Google Scholar] [CrossRef]
- Giudicepietro, F.; Casu, F.; Bonano, M.; De Luca, C.; De Martino, P.; Di Traglia, F.; Di Vito, M.A.; Macedonio, G.; Manunta, M.; Monterroso, F.; et al. First evidence of a geodetic anomaly in the Campi Flegrei caldera (Italy) ground deformation pattern revealed by DInSAR and GNSS measurements during the 2021–2023 escalating unrest phase. Int. J. Appl. Earth Obs. Geoinf. 2024, 132, 104060. [Google Scholar] [CrossRef]
- Scotto di Uccio, F.; Lomax, A.; Natale, J.; Muzellec, T.; Festa, G.; Nazeri, S.; Convertito, V.; Bobbio, A.; Strumia, C.; Zollo, A. Delineation and fine-scale structure of fault zones activated during the 2014–2024 unrest at the Campi Flegrei caldera (Southern Italy) from high precision earthquake locations. Geophys. Res. Lett. 2024, 51, e2023GL107680. [Google Scholar] [CrossRef]
- Tramelli, A.; Convertito, V.; Godano, C. b value enlightens different rheological behaviour in Campi Flegrei caldera. Commun. Earth Env. 2024, 5, 275. [Google Scholar] [CrossRef]
- Pappalardo, L.; Civetta, L.; D’Antonio, M.; Deino, A.; Di Vito, M.; Orsi, G.; Carandente, A.; de Vita, S.; Isaia, R.; Piochi, M. Chemical and Sr-isotopical evolution of the Phlegraean magmatic system before the Campanian Ignimbrite and the Neapolitan Yellow Tuff eruptions. J. Volcanol. Geotherm. Res. 1999, 91, 141–166. [Google Scholar] [CrossRef]
- Scarpati, C.; Sparice, D.; Perrotta, A. A crystal concentration method for calculating ignimbrite volume from distal ash fall deposits and a reappraisal of the magnitude of the Campanian Ignimbrite. J. Volcanol. Geotherm. Res. 2014, 280, 67–75. [Google Scholar] [CrossRef]
- Orsi, G.; De Vita, S.; Di Vito, M. The restless, resurgent Campi Flegrei nested caldera (Italy): Constraints on its evolution and configuration. J. Volcanol. Geotherm. Res. 1996, 74, 179–214. [Google Scholar] [CrossRef]
- Rosi, M.; Vezzoli, L.; Aleotti, P.; De Censi, M. Interaction between caldera collapse and eruptive dynamics during the Campanian Ignimbrite eruption, Phlegraean Fields, Italy. Bull Volcanol. 1996, 57, 541–554. [Google Scholar] [CrossRef]
- De Vivo, B.; Rolandi, G.; Gans, P.B.; Calvert, A.; Bohrson, W.A.; Spera, F.J.; Belkin, H.E. New constraints on the pyroclastic eruptive history of the Campanian volcanic plain (Italy). Mineral. Petrol. 2001, 73, 47–65. [Google Scholar] [CrossRef]
- Deino, A.L.; Orsi, G.; de Vita, S.; Piochi, M. The age of the Neapolitan Yellow Tuff caldera-forming eruption (Campi Flegrei caldera—Italy) assessed by 40Ar/39Ar dating method. J. Volcanol. Geotherm. Res. 2004, 133, 157–170. [Google Scholar] [CrossRef]
- Orsi, G.; D’Antonio, M.; de Vita, S.; Gallo, G. The Neapolitan Yellow Tuff, a large-magnitude trachytic phreato-plinian eruption: Eruptive dynamics, magma withdrawal and caldera collapse. J. Volcanol. Geotherm. Res. 1992, 53, 275–287. [Google Scholar] [CrossRef]
- Wohletz, K.; Orsi, G.; De Vita, S. Eruptive mechanisms of the Neapolitan Yellow Tuff interpreted from stratigraphic, chemical, and granulometric data. J. Volcanol. Geotherm. Res. 1995, 67, 263–290. [Google Scholar] [CrossRef]
- De Natale, G.; Troise, C.; Mark, D.; Mormone, A.; Piochi, M.; Di Vito, M.A.; Isaia, R.; Carlino, S.; Barra, D.; Somma, R. The Campi Flegrei Deep Drilling Project (CFDDP): New insight on caldera structure, evolution and hazard implications for the Naples area (Southern Italy). Geochem. Geophys. Geosystems 2016, 17, 4836–4847. [Google Scholar] [CrossRef]
- De Natale, G.; Rolandi, G.; Kilburn, C.R.J.; Troise, C.; Somma, R.; Di Vincenzo, G.; Rolandi, R.; Woo, J.; Cole, P.D. The Campanian Ignimbrite of Southern Italy: A Fissure Eruption or Caldera-Forming Event? Earth Plan. Sci. Lett. 2025; in press. [Google Scholar]
- Rolandi, G.; De Natale, G.; Kilburn, C.R.J.; Troise, C.; Somma, R.; Di Lascio, M.; Fedele, A.; Rolandi, R. The 39 ka Campanian Ignimbrite eruption: New data on source area in the Campanian Plain. In Vesuvius, Campi Flegrei, and Campanian Volcanism; Vivo, B., Belkin, H.E., Rolandi, G., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; Chapter 8; pp. 175–205. [Google Scholar]
- Rolandi, G.; Di Lascio, M.; Rolandi, R. The Neapolitan yellow tuff eruption as the source of 507 the Campi Flegrei caldera. In Vesuvius, Campi Flegrei, and Campanian Volcanism; De Vivo, B., Belkin, H.E., Rolandi, G., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 273–296. [Google Scholar]
- Orsi, G.; Civetta, L.; Del Gaudio, C.; de Vita, S.; Di Vito, M.A.; Isaia, R.; Petrazzuoli, S.M.; Ricciardi, G.P.; Ricco, C. Short-term deformations and seismicity in the resurgent Campi Flegrei caldera (Italy): An example of active block-resurgence in a densely populated area. J. Volcan. Geoth. Res. 1999, 91, 415–451. [Google Scholar] [CrossRef]
- Sacchi, M.; Pepe, F.; Corradino, M.; Insinga, D.D.; Molisso, F.; Lubritto, C. The Neapolitan 1217 Yellow Tuff caldera offshore the Campi Flegrei: Stratal architecture and kinematic reconstruction 1218 during the last 15 ky. Mar. Geol. 2014, 354, 5–33. [Google Scholar] [CrossRef]
- Sacchi, M.; Matano, F.; Molisso, F.; Passaro, S.; Caccavale, M.; Di Martino, G.; Guarino, A.; Innangi, S.; Tamburrino, S.; Tonielli, R.; et al. Geological framework of the Bagnoli–Coroglio coastal zone and continental shelf, Pozzuoli (Napoli) Bay. Chem. Ecol. 2020, 36, 529–549. [Google Scholar] [CrossRef]
- Di Vito, M.A.; Isaia, R.; Orsi, G.; Southon, J.D.; De Vita, S.; D’Antonio, M.; Pappalardo, L.; Piochi, M. Volcanism and deformation since 12,000 years at the Campi Flegrei caldera (Italy). J. Volcanol. Geotherm. Res. 1999, 91, 221–246. [Google Scholar] [CrossRef]
- Isaia, R.; Marianelli, P.; Sbrana, A. Caldera unrest prior to intense volcanism in Campi Flegrei (Italy) at 4.0 ka BP: Implications for caldera dynamics and future eruptive scenarios. Geophys. Res. Lett. 2009, 36, L21303. [Google Scholar] [CrossRef]
- Di Renzo, V.; Arienzo, I.; Civetta, L.; D’Antonio, M.; Tonarini, S.; Di Vito, M.A.; Orsi, G. The magmatic feeding system of the Campi Flegrei caldera: Architecture and temporal evolution. Chem. Geol. 2011, 281, 227–241. [Google Scholar] [CrossRef]
- Smith, V.C.; Isaia, R.; Pearce, N.J.G. Tephrostratigraphy and glass compositions of post-15 kyr Campi Flegrei eruptions: Implications for eruption history and chronostratigraphic markers. Quat. Sci. Rev. 2011, 30, 3638–3660. [Google Scholar] [CrossRef]
- Lirer, L.; Luongo, G.; Scandone, R. On the volcanological evolution of Campi Flegrei. EOS 1987, 68, 226–233. [Google Scholar] [CrossRef]
- De Vita, S.; Orsi, G.; Civetta, L.; Carandente, A.; D’Antonio, M.; Deino, A.; di Cesare, T.; Di Vito, M.A.; Fisher, R.V.; Isaia, R.; et al. The Agnano–Monte Spina eruption (4100 years BP) in the restless Campi Flegrei caldera (Italy). J. Volcanol. Geotherm. Res. 1999, 91, 269–301. [Google Scholar] [CrossRef]
- Dellino, P.; Dioguardi, F.; Isaia, R.; Sulpizio, R.; Mele, D. The impact of pyroclastic density currents duration on humans: The case of the AD 79 eruption of Vesuvius. Sci. Rep. 2021, 11, 49–59. [Google Scholar] [CrossRef] [PubMed]
- Di Vito, M.; Lirer, L.; Mastrolorenzo, G.; Rolandi, G. The 1538 Monte Nuovo eruption (Campi Flegrei, Italy). Bull. Volcanol. 1987, 49, 608–615. [Google Scholar] [CrossRef]
- Di Vito, M.; Acocella, V.; Aiello GBarra, D.; Battaglia, M.; Carandente, A.; Del Gaudio, C.; de Vita, S.; Ricciardi, G.P.; Ricco, C.; Scandone, R.; et al. Magma transfer at Campi Flegrei caldera (Italy) before the 1538 AD eruption. Sci. Rep. 2016, 6, 32245. [Google Scholar] [CrossRef]
- Piochi, M.; Mastrolorenzo, G.; Pappalardo, L. Magma ascent and eruptive processes from textural and compositional features of Monte Nuovo pyroclastic products, Campi Flegrei, Italy. Bull. Volcanol. 2005, 67, 663–678. [Google Scholar] [CrossRef]
- Guidoboni, E.; Ciuccarelli, C. The Campi Flegrei caldera: Historical revision and new data on seismic crises, bradyseisms, the Monte Nuovo eruption and ensuing earthquakes (1582 AD). Bull. Volcanol. 2011, 73, 655–677. [Google Scholar] [CrossRef]
- Rolandi, G.; Troise, C.; Sacchi, M.; di Lascio, M.; De Natale, G. The 1538 eruption at Campi Flegrei resurgent caldera: Implications for future unrest and eruptive scenarios. EGUsphere 2024, 2024, 1–60. [Google Scholar] [CrossRef]
- De Natale, G.; Troise, C.; Pingue, F.; Mastrolorenzo, G.; Pappalardo, L.; Battaglia, M.; Boschi, E. The Campi Flegrei caldera: Unrest mechanisms and hazards. Geol. Soc. Lond. Spec. Publ. 2006, 269, 25–45. [Google Scholar] [CrossRef]
- Vitale, S.; Isaia, R. Fractures and faults in volcanic rocks (Campi Flegrei, Southern Italy): Insight into volcano-tectonic processes. Int. J. Earth Sci. 2014, 103, 801–819. [Google Scholar] [CrossRef]
- Natale, J.; Camanni, G.; Ferranti, L.; Isaia, R.; Sacchi, M.; Spiess, V.; Steinmann, L.; Vitale, S. Fault systems in the ofshore sector of the Campi Flegrei caldera (southern Italy): Implications for nested caldera structure, resurgent dome, and volcano-tectonic evolution. J. Struct. Geol. 2022, 163, 104723. [Google Scholar] [CrossRef]
- Steinmann, L.; Spiess, V.; Sacchi, M. The Campi Flegrei caldera (Italy): Formation and evolution in interplay with sea-level variations since the Campanian Ignimbrite eruption at 39 ka. J. Volcanol. Geotherm. Res. 2016, 327, 361–374. [Google Scholar] [CrossRef]
- Steinmann, L.; Spiess, V.; Sacchi, M. Post-collapse evolution of a coastal caldera system: Insights from a 3D multichannel seismic survey from the Campi Flegrei caldera (Italy). J. Volcanol. Geotherm. Res. 2018, 349, 83–98. [Google Scholar] [CrossRef]
- Isaia, R.; Vitale, S.; Di Giuseppe, M.G.; Iannuzzi, E.; Tramparulo, F.D.A.; Troiano, A. Stratigraphy, structure and volcano-tectonic evolution of Solfatara maar diatreme (Campi Flegrei, Italy). Geol. Soc. Am. Bull 2015, 127, 1485–1504. [Google Scholar] [CrossRef]
- Rosi, M.; Sbrana, A. Phlegrean fields. Quaderni de la ricerca scientifica. Cons. Naz. Delle Ric. 1987, 114, 1–175. [Google Scholar]
- Campi Flegrei. Active Volcanoes of the World; Orsi, G., D’Antonio, M., Civetta, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2022; pp. 201–217. [Google Scholar]
- Parascandola, A. I Fenomeni Bradisismici del Serapeo di Pozzuoli; Stabilmento tipografico G. Genovese: Napoli, Italy, 1947; pp. 1–117. [Google Scholar]
- Morhange, C.; Bourcier, M.; Laborel, J.; Giallanella, C.; Goiran, J.P.; Crimaco, L.; Vecchi, L. New data on historical relative sea level movements in Pozzuoli, Phlaegrean Fields, southern Italy. Phys. Chem. Earth Part A 1999, 24, 349–354. [Google Scholar] [CrossRef]
- Bellucci, F.; Woo, J.; Kilburn, C.R.J.; Rolandi, G. Mechanisms of activity and unrest at large calderas. Geol. Soc. Lond. Spec. Publ. 2006, 269, 141–158. [Google Scholar] [CrossRef]
- Battaglia, M.; Troise, C.; Obrizzo, F.; Pingue, F.; De Natale, G. Evidence for fluid migration as the source of deformation at Campi Flegrei caldera (Italy). Geophys. Res. Lett. 2006, 33, L01307. [Google Scholar] [CrossRef]
- D’Auria, L.; Pepe, S.; Castaldo, R.; Giudicepietro, F.; Macedonio, G.; Ricciolino, P.; Tizzani, P.; Casu, F.; Lanari, R.; Manzo, M.; et al. Magma injection beneath the urban area of Naples: A new mechanism for the 2012–2013 volcanic unrest at Campi Flegrei caldera. Sci. Rep. 2015, 5, 13100. [Google Scholar] [CrossRef]
- Lima, A.; De Vivo, B.; Spera, F.J.; Bodnar, R.J.; Milia, A.; Nunziata, C.; Belkin, H.E.; Cannatelli, C. Thermodynamic model for uplift and deflation episodes (Bradyseism) associated with magmatic hydrothermal activity at the Campi Flegrei active volcanic center (Italy). Earth Sci. Rev. 2009, 97, 44–58. [Google Scholar] [CrossRef]
- Todesco, M.; Neri, A.; Esposti Ongaro, T.; Papale, P.; Rosi, M. Pyroclastic flow dynamics and hazard in a caldera setting: Application to Phlegrean Fields (Italy). Geochem. Geophys. Geosyst. 2006, 7, Q11003. [Google Scholar] [CrossRef]
- Cannatelli, C.; Spera, F.J.; Bodnar, R.J.; Lima, A.; De Vivo, B. Ground movement (bradyseism) in the Campi Flegrei volcanic area: A review. De Vivo, B., Harvey, E., Belkin, Rolandi, G., Vesuvius, Flegrei, C., Volcanism, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 407–433. [Google Scholar] [CrossRef]
- Del Gaudio, C.; Aquino, I.; Ricciardi, G.P.; Ricco, C.; Scandone, R. Unrest episodes at Campi Flegrei: A reconstruction of vertical ground movements during 1905–2009. J. Volcanol. Geotherm. Res. 2010, 195, 48–56. [Google Scholar] [CrossRef]
- Barberi, F.; Cassano, E.; La Torre, P.; Sbrana, A. Structural evolution of Campi Flegrei caldera in light of volcanological and geophysical data. J. Volcanol. Geotherm. Res. 1991, 48, 33–49. [Google Scholar] [CrossRef]
- Ricco, C.; Petrosino, S.; Aquino, I.; Del Gaudio, C.; Falanga, M. Some Investigations on a Possible Relationship between Ground Deformation and Seismic Activity at Campi Flegrei and Ischia Volcanic Areas (Southern Italy). Geosciences 2019, 9, 222. [Google Scholar] [CrossRef]
- Falanga, M.; Aquino, I.; De Lauro, E.; Petrosino, S.; Ricco, C. New insights on ground deformation at Campi Flegrei caldera inferred from kinematics and dynamics investigation of borehole tilt. Earth Space Sci. 2023, 10, e2022EA002702. [Google Scholar] [CrossRef]
- Kilburn, C.R.J.; De Natale, G.; Carlino, S. Progressive approach to eruption at Campi Flegrei caldera in southern Italy. Nat. Commun. 2017, 8, 15312. [Google Scholar] [CrossRef]
- De Natale, G.; Pingue, F. Ground Deformations in Collapsed Caldera Structures. J. Volcanol. Geotherm. Res. 1993, 57, 19–38. [Google Scholar] [CrossRef]
- De Natale, G.; Petrazzuoli, S.M.; Pingue, F. The effect of collapse structures on ground deformations in calderas. Geophys. Res. Lett. 1997, 24, 1555–1558. [Google Scholar] [CrossRef]
- Iuliano, S.; Matano, F.; Caccavale, M.; Sacchi, M. Annual rates of ground deformation (1993-2010) at Campi Flegrei, Italy, revealed by Persistent Scatterer Pair (PSP)—SAR Interferometry. Int. J. Remote Sens. 2015, 36, 6160–6191. [Google Scholar] [CrossRef]
- Ricciolino, P.; Lo Bascio, D.; Esposito, R. GOSSIP—Database sismologico Pubblico INGV-Osservatorio Vesuviano. Istituto Nazionale di Geofisica e Vulcanologia (INGV). 2024. Available online: https://terremoti.ov.ingv.it/gossip/ (accessed on 28 November 2024).
- Ortolani, F.; Pagliuca, S. Principali effetti superficiali del bradisismo di Pozzuoli (Campania) e relazioni con le caratteristiche geologico-tecniche dei terreni. Mem. Soc. Geol. It. 1988, 41, 963–968. [Google Scholar]
- Pingue, F.; Petrazzuoli, S.M.; Obrizzo, F.; Tammaro, U.; De Martino, P.; Zuccaro, G. Monitoring system of buildings with high vulnerability in presence of slow ground deformations (The Campi Flegrei, Italy, case). Measurement 2011, 44, 1628–1644. [Google Scholar] [CrossRef]
- Somma, R.; Iuliano, S.; Matano, F.; Molisso, F.; Passaro, S.; Sacchi, M.; Troise, C.; De Natale, G. High-resolution morpho-bathymetry of Pozzuoli Bay, southern Italy. J. Maps 2016, 12, 222–230. [Google Scholar] [CrossRef]
- Bottiglieri, M.; Falanga, M.; Tammaro, U.; De Martino, P.; Obrizzo, F.; Godano, C.; Pingue, F. Characterization of GPS time series at the Neapolitan volcanic area by statistical analysis. J. Geophys. Res. 2010, 115, B10416. [Google Scholar] [CrossRef]
- De Martino, P.; Dolce, M.; Brandi, G.; Scarpato, G.; Tammaro, U. The Ground Deformation History of the Neapolitan Volcanic Area (Campi Flegrei Caldera, Somma-Vesuvius Volcano, and Ischia Island) from 20 years of continuous GPS observations (2000–2019). Rem. Sens. 2021, 13, 2725. [Google Scholar] [CrossRef]
- Hanseen, R.F. Radar Interferometry: Data Interpretation and Error Analysisf; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001; ISBN 978-0792369455. [Google Scholar]
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett. 2004, 31, L23611. [Google Scholar] [CrossRef]
- Vilardo, G.; Isaia, R.; Ventura, G.; De Martino, P.; Terranova, C. InSAR Permanent Scatterer analysis reveals fault re-activation during inflation and deflation episodes at Campi Flegrei caldera. Remote Sens. Environ. 2010, 114, 2373–2383. [Google Scholar] [CrossRef]
- Gabriel, A.K.; Goldstein, R.M.; Zebker, H.A. Mapping small elevation changes over large areas: Differential radar interferometry. J. Geophys. Res. 1989, 94, 9183–9191. [Google Scholar] [CrossRef]
- Massonnet, D.; Feigl, K.L. Radar interferometry and its application to changes in the Earth’s surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef]
- Kalavrezou, I.-E.; Castro-Melgar, I.; Nika, D.; Gatsios, T.; Lalechos, S.; Parcharidis, I. Application of Time Series IN-SAR (SBAS) Method Using Sentinel-1 for Monitoring Ground Deformation of the Aegina Island (Western Edge of Hel-lenic Volcanic Arc). Land 2024, 13, 485. [Google Scholar] [CrossRef]
- Poland, M.P.; Zebker, H.A. Volcano geodesy using InSAR in 2020; the past and next decades. Bull. Volcanol. 2022, 84, 27. [Google Scholar] [CrossRef]
- Beccaro, L.; Tolomei, C.; Gianardi, R.; Sepe, V.; Bisson, M.; Colini, L.; De Ritis, R.; Spinetti, C. Multitemporal and multisensory InSAR analysis for ground displacement field assessment at Ischia volcanic island (Italy). Remote Sens. 2021, 13, 4253. [Google Scholar] [CrossRef]
- Ezquerro, P.; Bru, G.; Galindo, I.; Montserrat, O.; García-Davalillo, J.C.; Sánchez, N.; Montoya, I.; Palamá, R.; Mateos, R.M.; Pérez-López, R.; et al. Analysis of SAR-derived products to support emergency management during volcanic crisis: La Palma case study. Remote Sens. Environ. 2023, 295, 113668. [Google Scholar] [CrossRef]
- Matano, F. Analysis and Classification of Natural and Human-Induced Ground Deformations at Regional Scale (Campania, Italy) Detected by Satellite Synthetic-Aperture Radar Interferometry Archive Datasets. Remote Sens. 2019, 11, 2822. [Google Scholar] [CrossRef]
- Vilardo, G.; Ventura, G.; Terranova, C.; Matano, F.; Nardò, S. Ground deformation due to tectonic, hydrothermal, gravity, hydrogeological and anthropic processes in the Campania Region (Southern Italy) from Permanent Scatterers Synthetic Aperture Radar Interferometry. Remote Sens. Environ. 2009, 113, 197–212. [Google Scholar] [CrossRef]
- Crosetto, M.; Solari, L.; Balasis-Levinsen, J.; Bateson, L.; Casagli, N.; Frei, M.; Oyen, A.; Moldestad, D.A.; Mróz, M. Deformation monitoring at European Scale: The Copernicus Ground Motion Service. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, 43, 141–146. [Google Scholar] [CrossRef]
- Shahbazi, S.; Crosetto, M.; Barra, A. Ground Deformation Analysis Using Basic Products of the Copernicus Ground Motion Service. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, 43, 6–11. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote. Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A new algorithm for processing interferometric data-stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Iannaccone, G.; Guardato, S.; Donnarumma, G.P.; De Martino, P.; Dolce, M.; Macedonio, G.; Chierici, F.; Beranzoli, L. Measurement of seafloor deformation in the marine sector of the Campi Flegrei caldera (Italy). J. Geophys. Res. Solid Earth 2018, 123, 66–83. [Google Scholar] [CrossRef]
- Vitale, S.; Natale, J. Combined volcano-tectonic processes for the drowning of the Roman western coastal settlements at Campi Flegrei (southern Italy). Earth Planets Space 2023, 75, 38. [Google Scholar] [CrossRef]
- Mogi, K. Relations between the eruptions of various volcanoes and the deformations of the ground surfaces around them. Earthq. Res. Inst. 1958, 36, 99–134. [Google Scholar]
- Natale, J.; Vitale, S.; Repola, L.; Monti, L.; Isaia, R. Geomorphic analysis of digital elevation model generated from vintage aerial photographs: A glance at the pre-urbanization morphology of the active Campi Flegrei caldera. Geomorphology 2024, 460, 109267. [Google Scholar] [CrossRef]
- Natale, J. Geomorphic Analysis of Digital Elevation Model Generated from Vintage Aerial Photographs: A Glance at the Pre-Urbanization Morphology of the Active Campi Flegrei Caldera. OSF Data Repository. 2024. Available online: https://osf.io/tx9hv/ (accessed on 27 November 2024).
- Natale, J.; Ferranti, L.; Isaia, R.; Marino, C.; Sacchi, M.; Spiess, V.; Steinmann, L.; Vitale, S. Integrated on-land-offshore stratigraphy of the Campi Flegrei caldera: New insights into the volcano-tectonic evolution in the last 15 kyr. Basin Res. 2022, 34, 855–882. [Google Scholar] [CrossRef]
- De Martino, P.; Dolce, M.; Brandi, G.; Scarpato GTammaro, U. Campi Flegrei cGPS Daily Timeseries (2000–2019) [Data set]. Zenodo 2022. [Google Scholar] [CrossRef]
- De Martino, P.; Dolce, M.; Brandi, G.; Scarpato, G. Campi Flegrei cGPS Weekly Positions Time Series [Data set]. Zenodo 2023. [Google Scholar] [CrossRef]
- Bevilacqua, A.; Neri, A.; De Martino, P.; Isaia, R.; Novellino, A.; Tramparulo, F.D.A.; Vitale, S. Radial interpolation of GPS and leveling data of ground deforma-tion in a resurgent caldera: Application to Campi Flegrei (Italy). J. Geod. 2020, 94, 24. [Google Scholar] [CrossRef]
- EGMS. Dataset Validated Ortho 2015–2021 (Vector). European Ground Motion Service. 2024. Available online: https://sdi.eea.europa.eu/catalogue/srv/api/records/943e9cbb-f8ef-4378-966c-63eb761016a9?language=all (accessed on 28 November 2024).
- Lundgren, P.; Usai, S.; Sansosti, E.; Lanari, R.; Tesauro, M.; Fornaro, G.; Berardino, P. Modeling surface deformation observed with synthetic aperture radar interferometry at Campi Flegrei caldera. J. Geophys. Res. 2001, 106, 19355–19366. [Google Scholar] [CrossRef]
- Isaia, R.; Di Giuseppe, M.G.; Natale, J.; Troiano, A.; Tramparulo, F.D.A.; Vitale, S. Volcano-tectonic setting of the Pisciarelli Fumarole Field, Campi Flegrei caldera, southern Italy: Insights into fluid circulation patterns and hazard scenarios. Tectonics 2021, 40, e2020TC006227. [Google Scholar] [CrossRef]
- Petrosino, S.; De Siena, L. Fluid migrations and volcanic earthquakes from depolarized ambient noise. Nat. Commun. 2021, 12, 6656. [Google Scholar] [CrossRef]
- Moretti, R.; De Natale, G.; Troise, C. A geochemical and geophysical reappraisal to the significance of the recent unrest at Campi Flegrei caldera (Southern Italy). Geochem. Geophys. Geosystems 2017, 18, 1244–1269. [Google Scholar] [CrossRef]
- De Natale, G.; Iannaccone, G.; Martini, M.; Zollo, A. Seismic sources and attenuation properties at Campi Flegrei volcanic area. Pure Appl. Geoph. 1987, 125, 883–917. [Google Scholar] [CrossRef]
- De Novellis, V.; Carlino, S.; Castaldo, R.; Tramelli, A.; De Luca, C.; Pino, N.A.; Pepe, S.; Convertito, V.; Zinno, I. The 21st August 2017 Ischia (Italy) earthquake source model inferred from seismological, GPS and DInSAR measurements. Geophys. Res. Lett. 2018, 45, 17296. [Google Scholar] [CrossRef]
- De Natale, G.; Zollo, A.; Ferraro, A.; Virieux, J. Accurate fault mechanism determinations for a 1984 earthquake swarm at Campi Flegrei caldera (Italy) during an unrest episode: Implications for volcanological research. J. Geophys. Res. 1995, 100, 24167–24185. [Google Scholar] [CrossRef]
- Troise, C.; De Natale, G.; Pingue, F.; Zollo, A. A model for earthquake generation during unrest episodes at Campi Flegrei and Rabaul calderas. Geophys. Res. Lett. 1997, 24, 1575–1578. [Google Scholar] [CrossRef]
- Mc Tigue, D.F. Elastic stress and deformation near a finite spherical magma body: Resolution of the point source paradox. J. Geophys. Res. 1987, 92, 12931–12940. [Google Scholar] [CrossRef]


| EGMS Dataset | Number of Points | Mean Velocity (mm/yr) | Velocity Range | Mean RMSE |
|---|---|---|---|---|
| Ortho Vertical | 23,970 | + 3.62 | −13.7 to + 91.2 | 1.18 |
| Ortho East/West | 23,970 | −0.16 | −36.9 to + 40.5 | 1.29 |
| Polynomial Degree | Adjusted R2 | RMSE |
|---|---|---|
| 20th degree | 0.9894 | 8.2356 |
| 10th degree | 0.9893 | 8.2927 |
| 9th degree | 0.9892 | 8.3092 |
| 8th degree | 0.9892 | 8.3109 |
| 7th degree | 0.9892 | 8.3315 |
| 6th degree | 0.9891 | 8.3536 |
| 5th degree | 0.9879 | 8.7886 |
| 4th degree | 0.9871 | 9.0848 |
| 3rd degree | 0.9830 | 10.4242 |
| 2nd degree | 0.8999 | 25.3370 |
| Polynomial Degree | Polynomial Equation |
|---|---|
| 6 | 596.3 − 9.748e-02x − 5.892e-05x2 + 2.244e-08x3 − 3.099e-12x4 + 1.951e-16x5 − 4.691e-21x6 |
| 5 | 672.0 − 2.305e-01x + 1.887e-05x2 + 1.642e-09x3 − 3.054e-13x4 + 1.156e-17x5 |
| 4 | 715.4 − 2.892e-01x + 4.391e-05x2 − 2.963e-09x3 + 7.463e-14x4 |
| 3 | 650.6 − 2.264e-01x + 2.588e-05x2 − 9.708e-10x3 |
| 2 | 461.7 − 1.096e-01x + 6.178e-06x2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matano, F.; Casaburi, A.; De Natale, G. An MT-InSAR-Based Procedure for Detecting and Interpreting Vertical Ground Deformation Anomalies During Phases of Unrest at Campi Flegrei Caldera, Italy. Appl. Sci. 2025, 15, 3344. https://doi.org/10.3390/app15063344
Matano F, Casaburi A, De Natale G. An MT-InSAR-Based Procedure for Detecting and Interpreting Vertical Ground Deformation Anomalies During Phases of Unrest at Campi Flegrei Caldera, Italy. Applied Sciences. 2025; 15(6):3344. https://doi.org/10.3390/app15063344
Chicago/Turabian StyleMatano, Fabio, Annarita Casaburi, and Giuseppe De Natale. 2025. "An MT-InSAR-Based Procedure for Detecting and Interpreting Vertical Ground Deformation Anomalies During Phases of Unrest at Campi Flegrei Caldera, Italy" Applied Sciences 15, no. 6: 3344. https://doi.org/10.3390/app15063344
APA StyleMatano, F., Casaburi, A., & De Natale, G. (2025). An MT-InSAR-Based Procedure for Detecting and Interpreting Vertical Ground Deformation Anomalies During Phases of Unrest at Campi Flegrei Caldera, Italy. Applied Sciences, 15(6), 3344. https://doi.org/10.3390/app15063344







