Study on the Lubrication and Anti-Friction Characteristics of the Textured Raceway of the Ball Screws Based on Elastohydrodynamic Lubrication
Abstract
1. Introduction
2. Grinding Surface Topography of the Screw Raceway
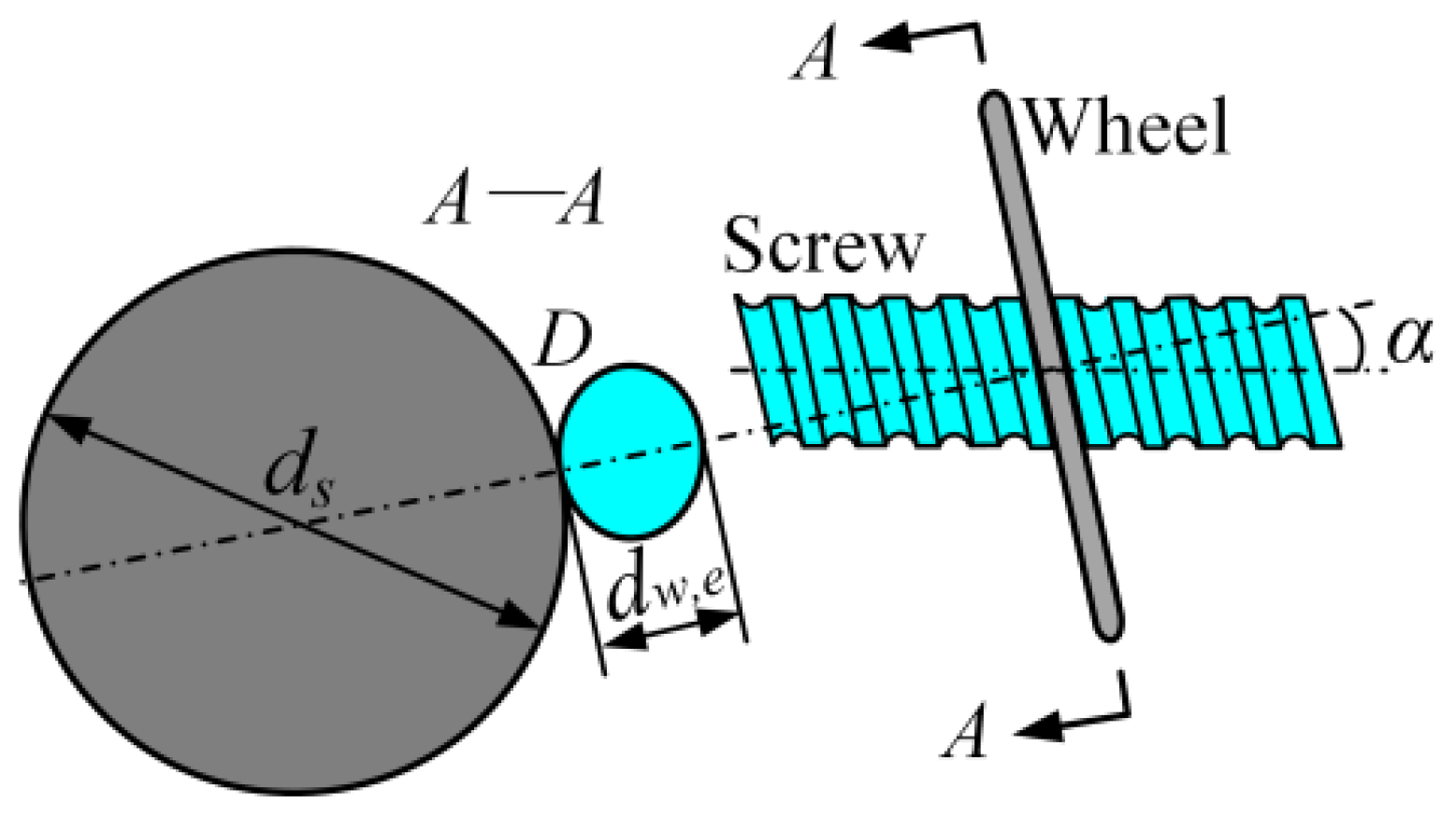
2.1. Surface Topography Characteristics of Grinding Wheel
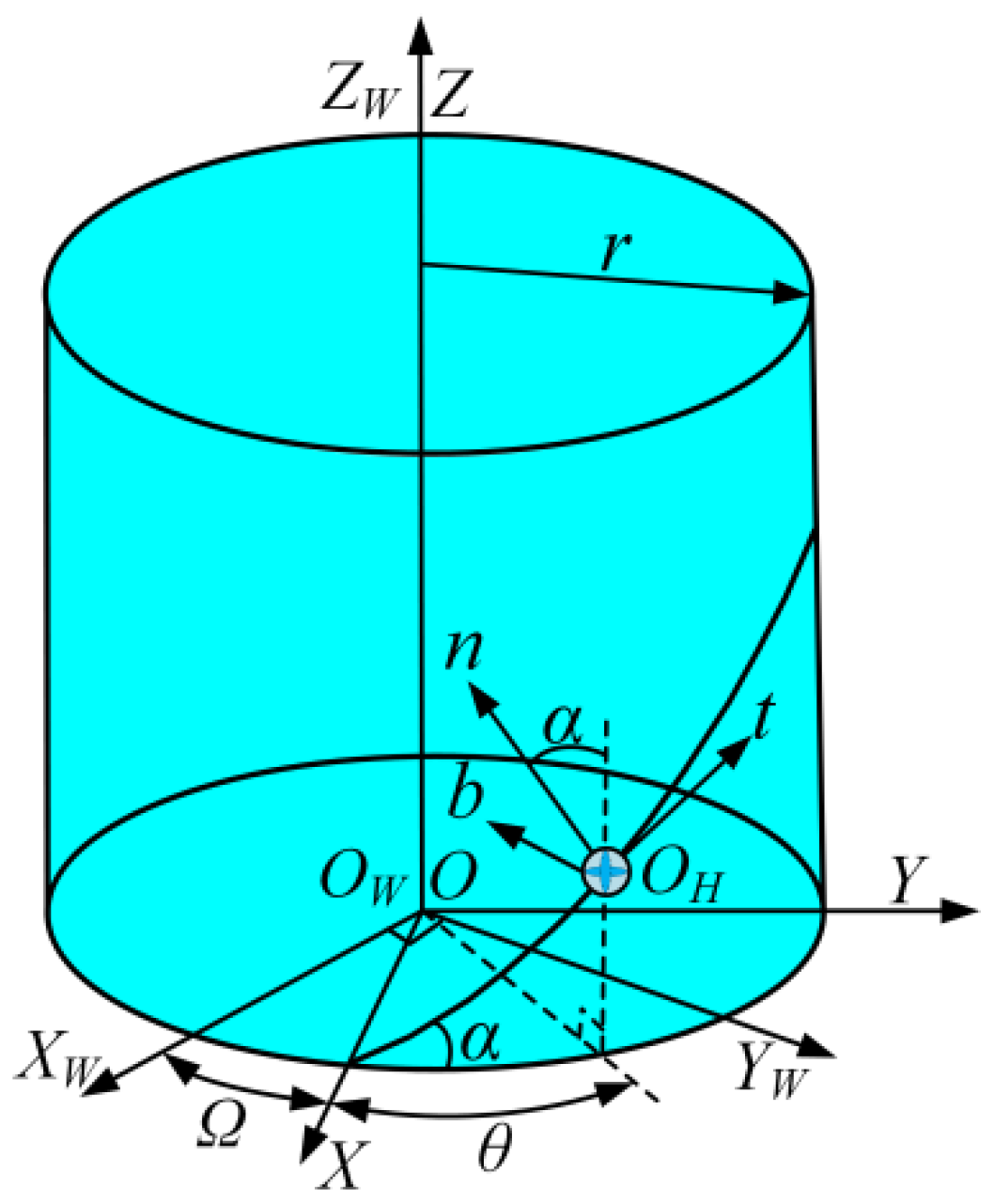
2.2. Grinding Kinematics
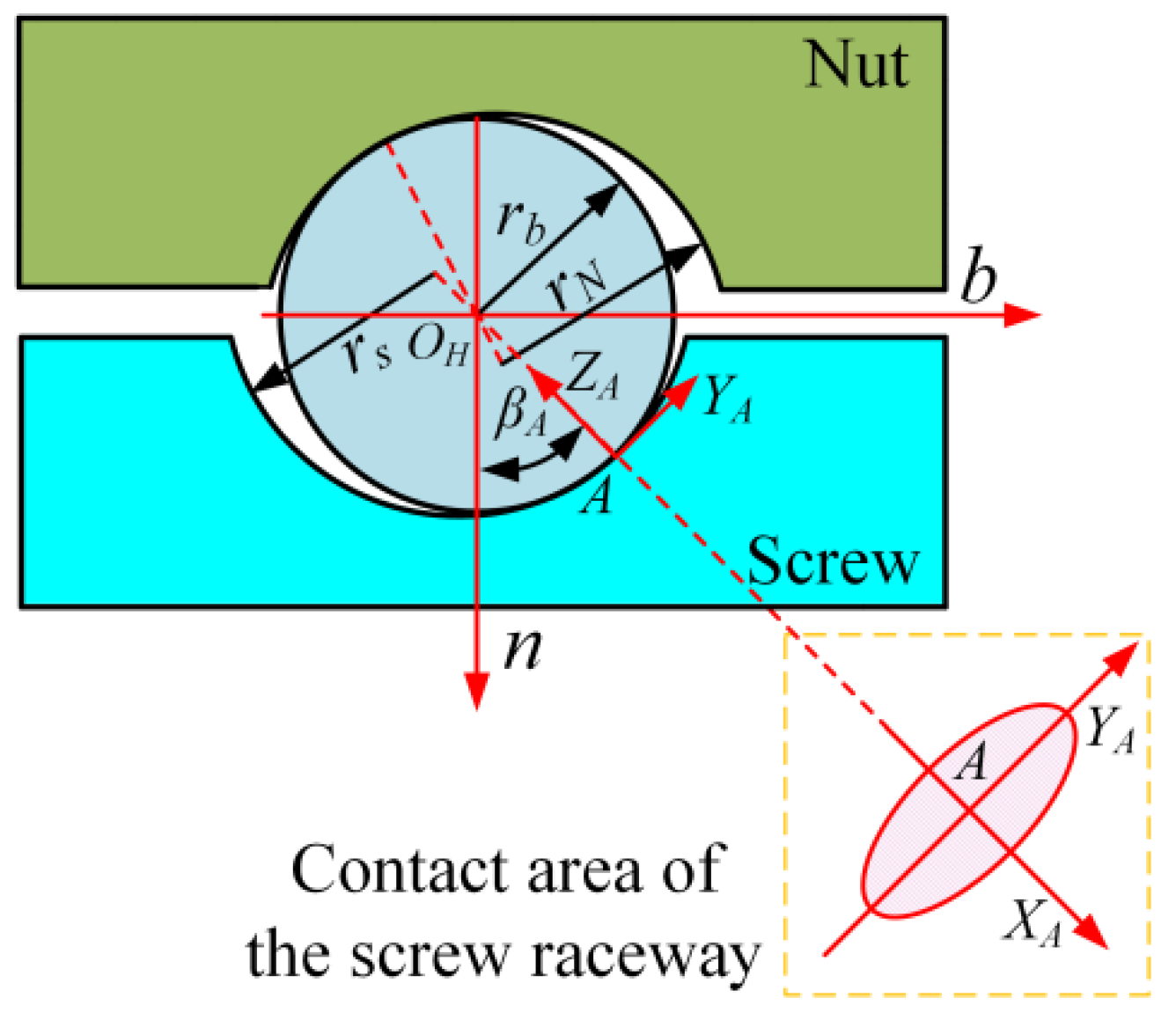
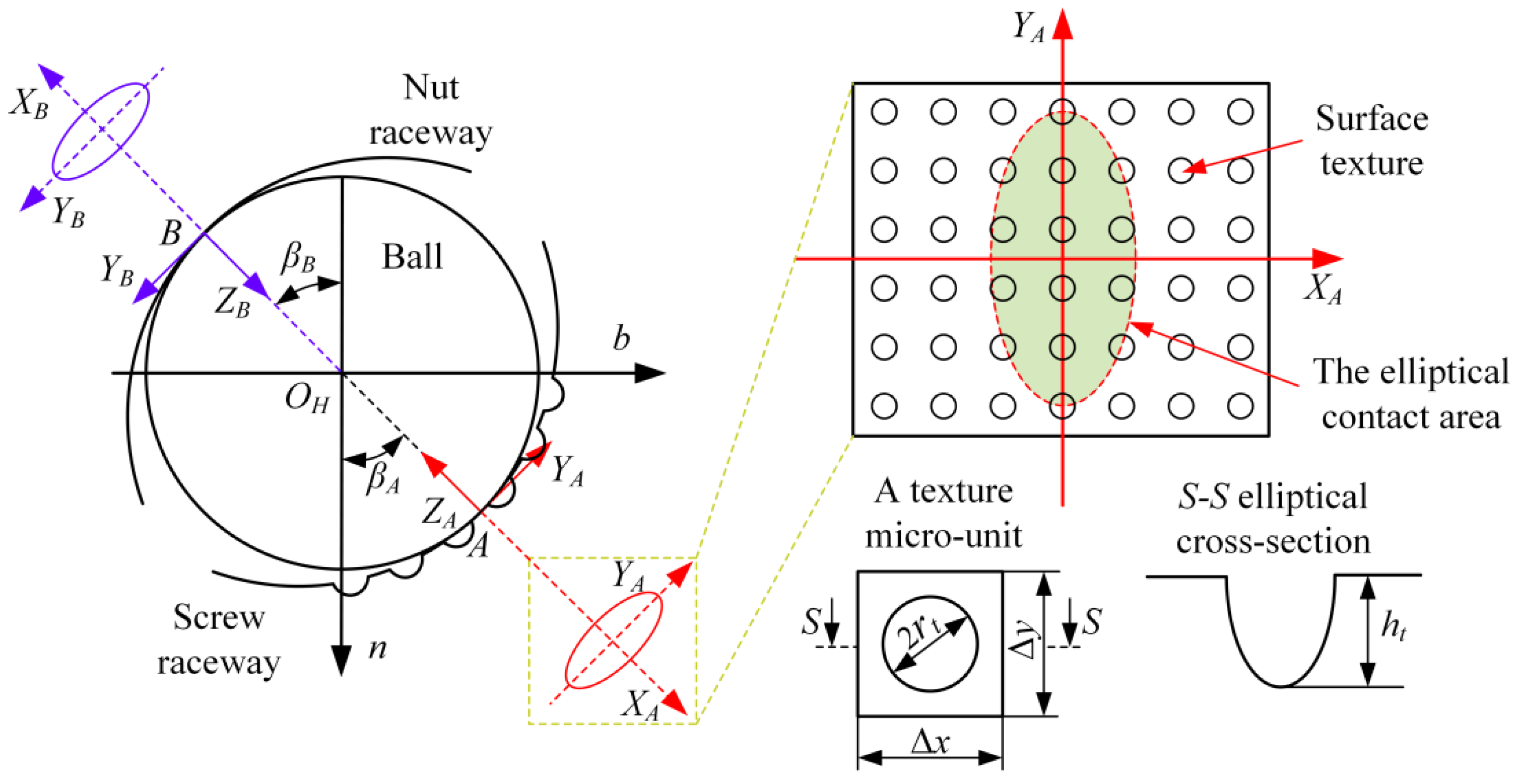
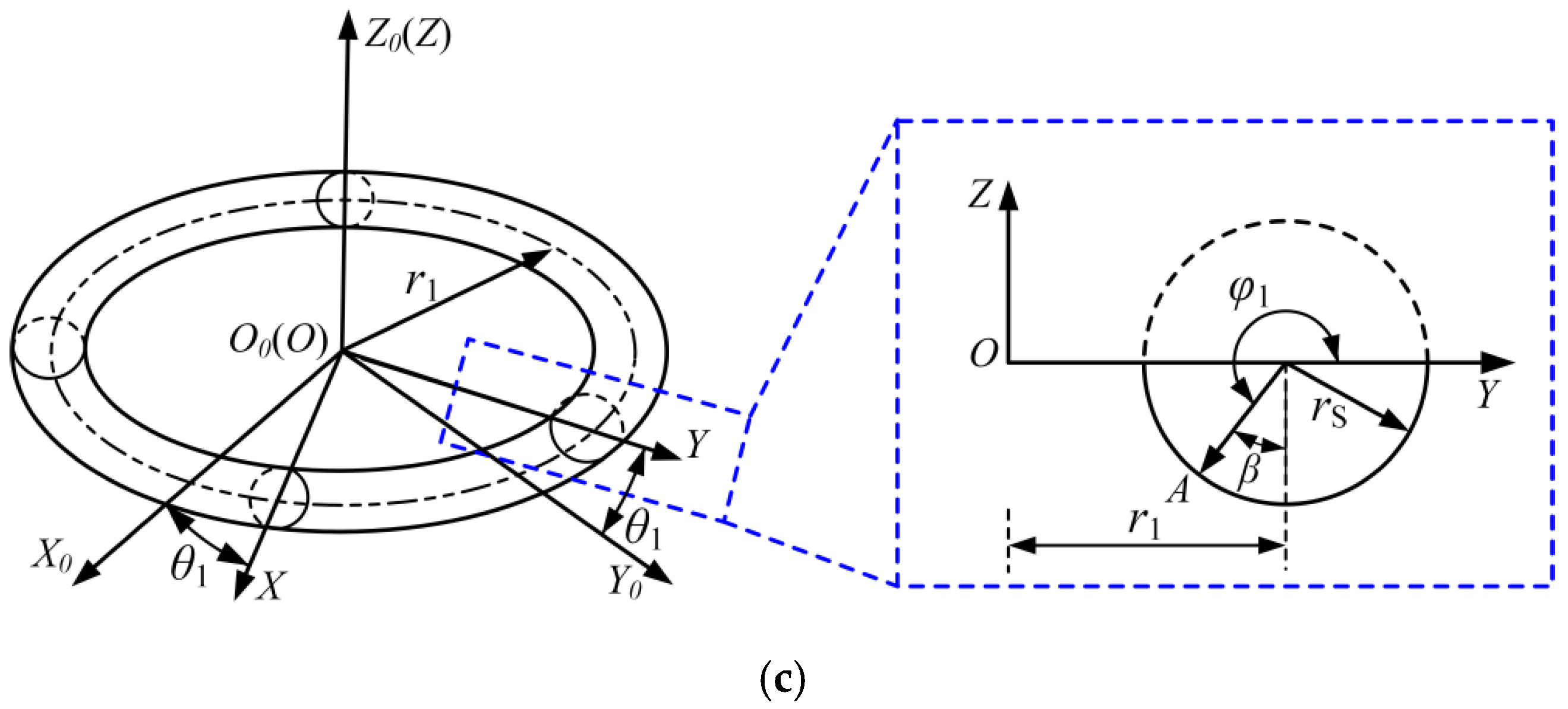
2.3. Modeling of the Geometric Model of the Screw Raceway
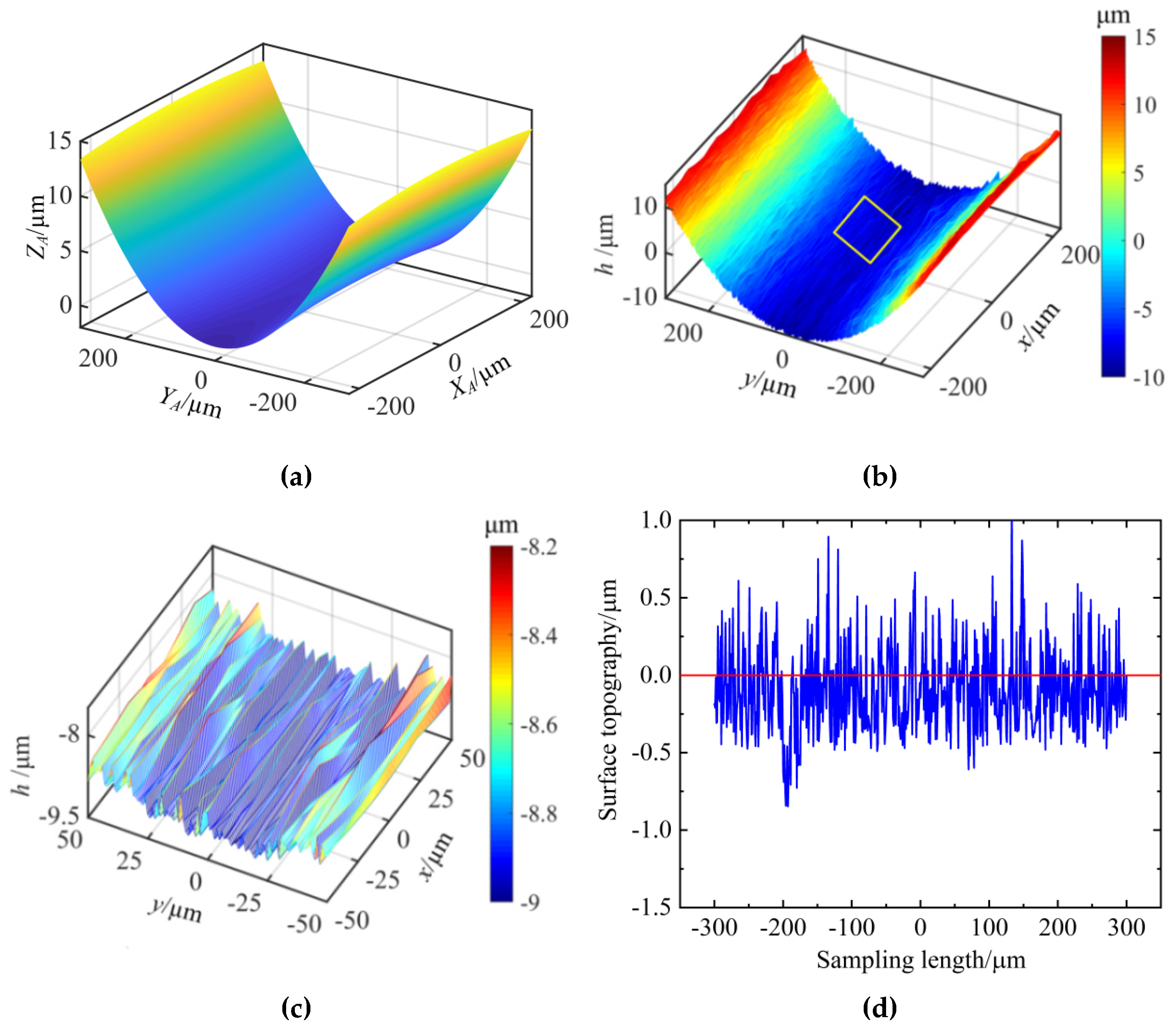
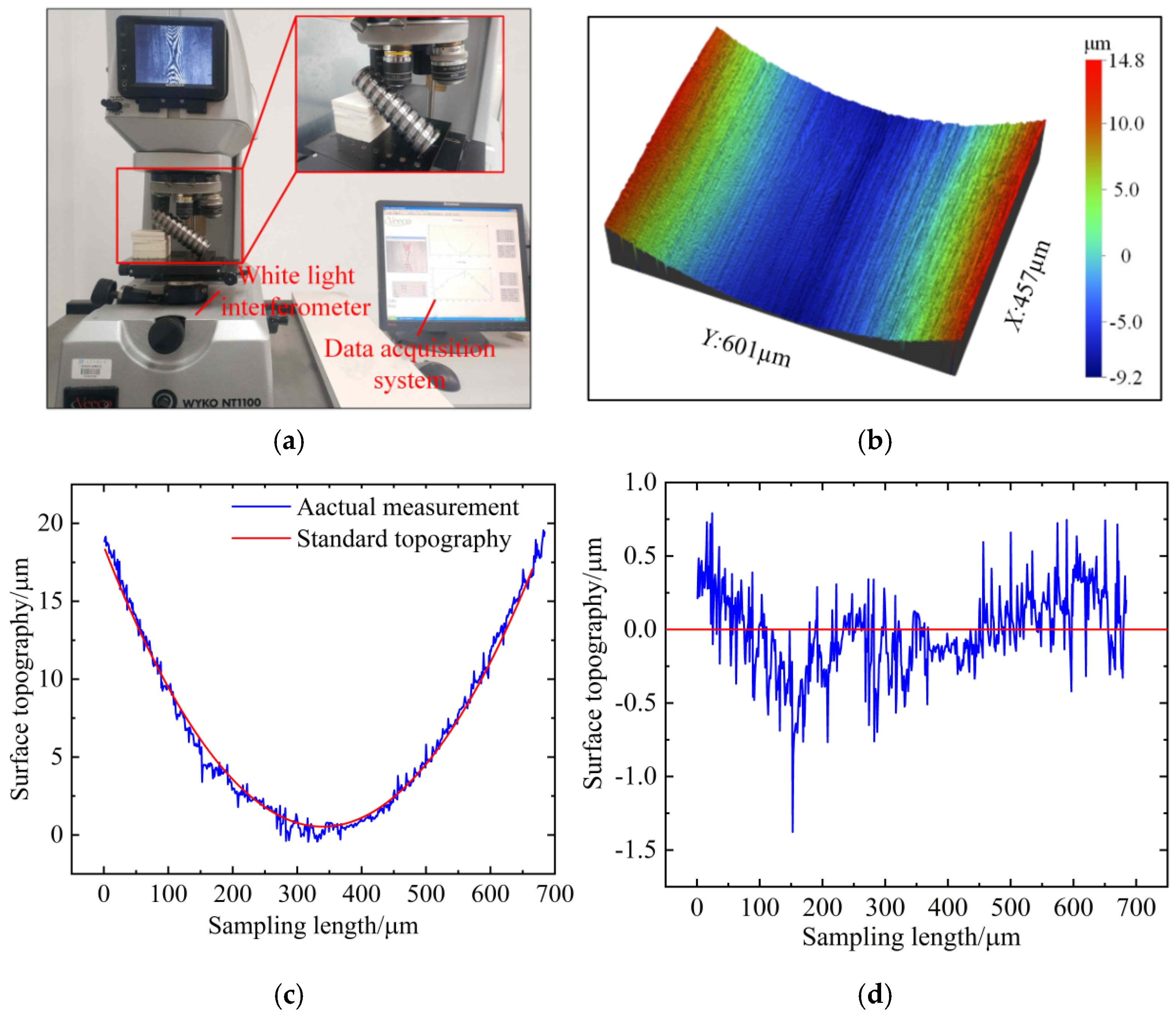
2.4. Measuring the Ground Surface Topography of the Screw Raceway
3. The EHL Model of the Textured Raceway of Ball Screws
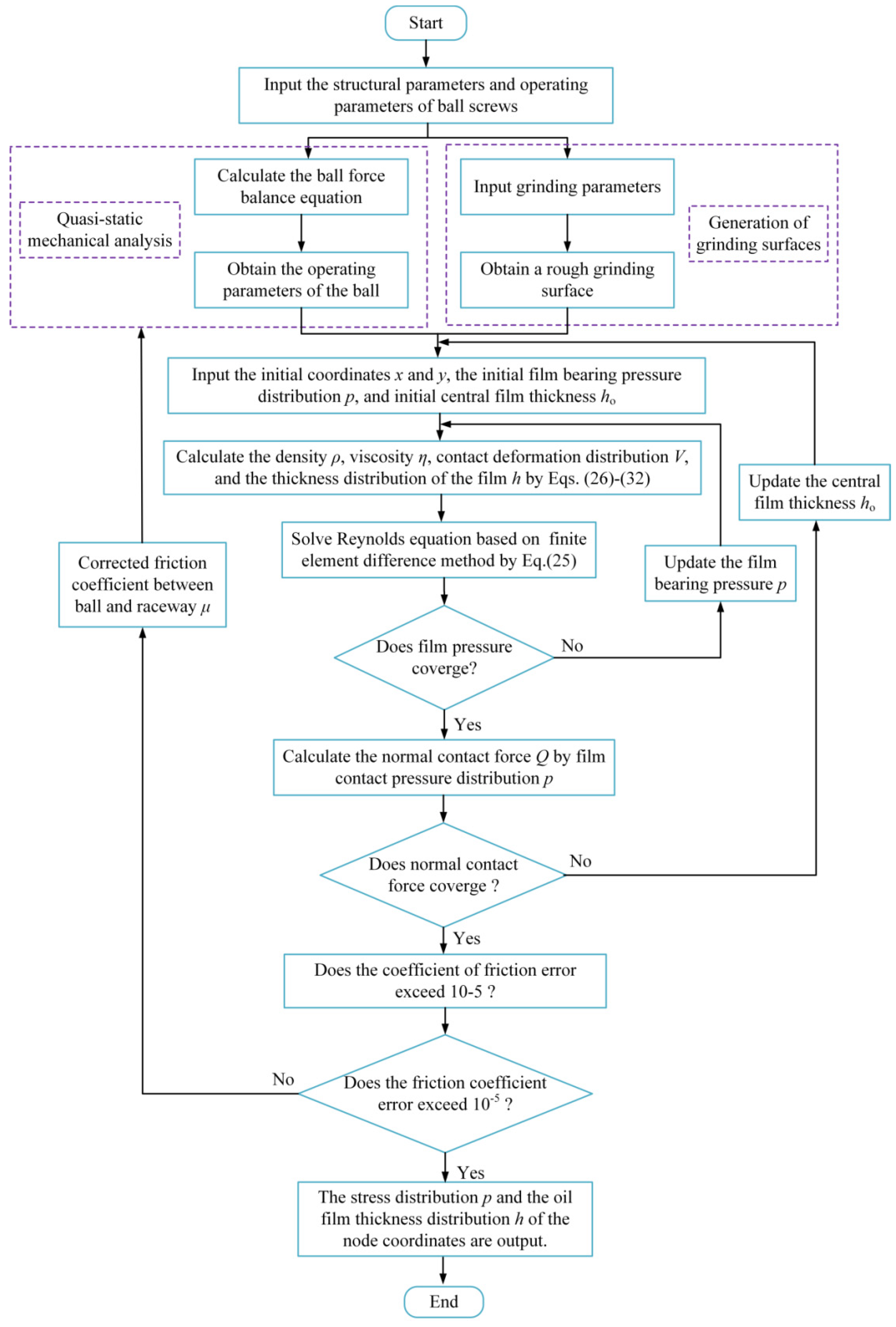
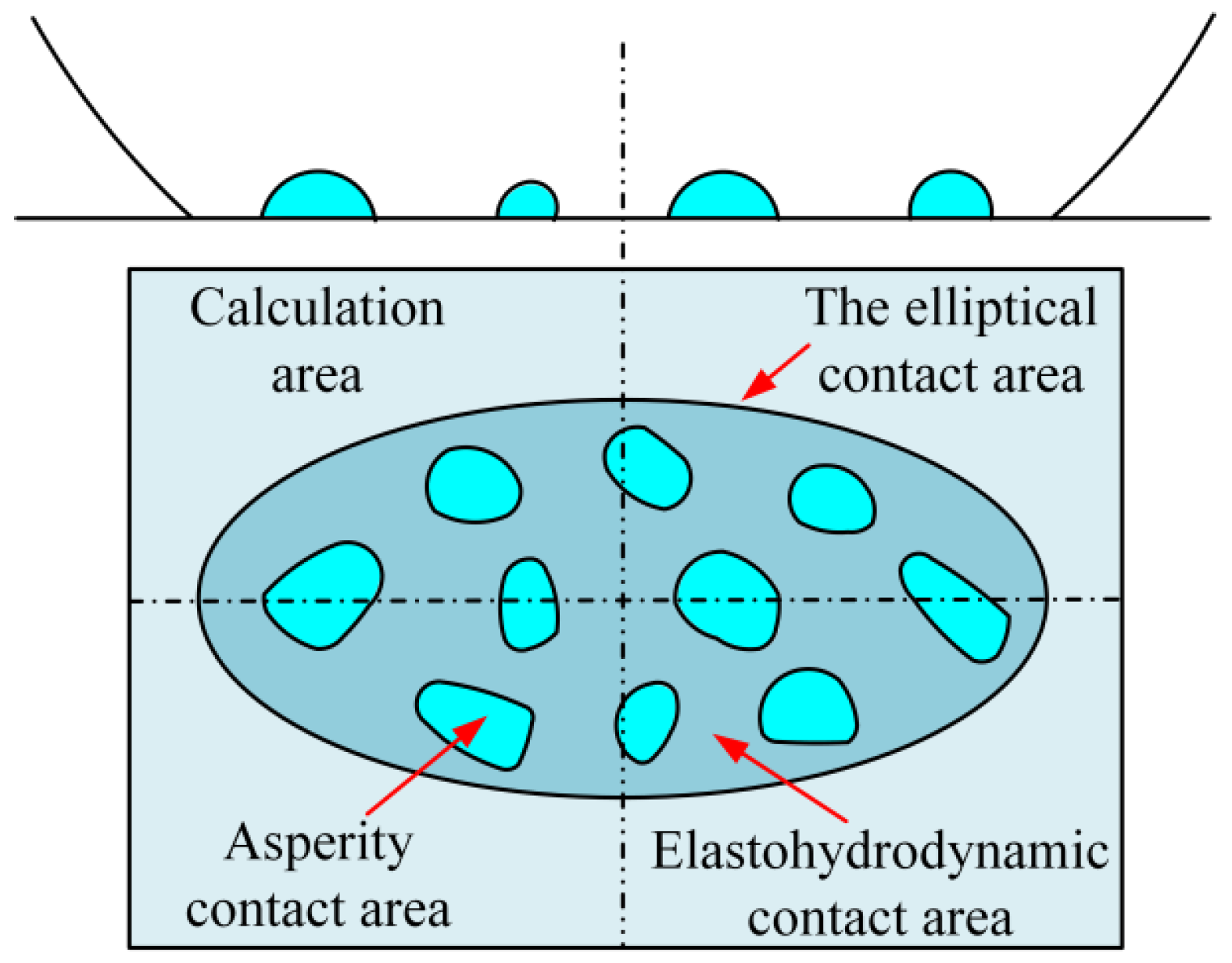
3.1. The EHL Model of the Textured Raceway of Ball Screws
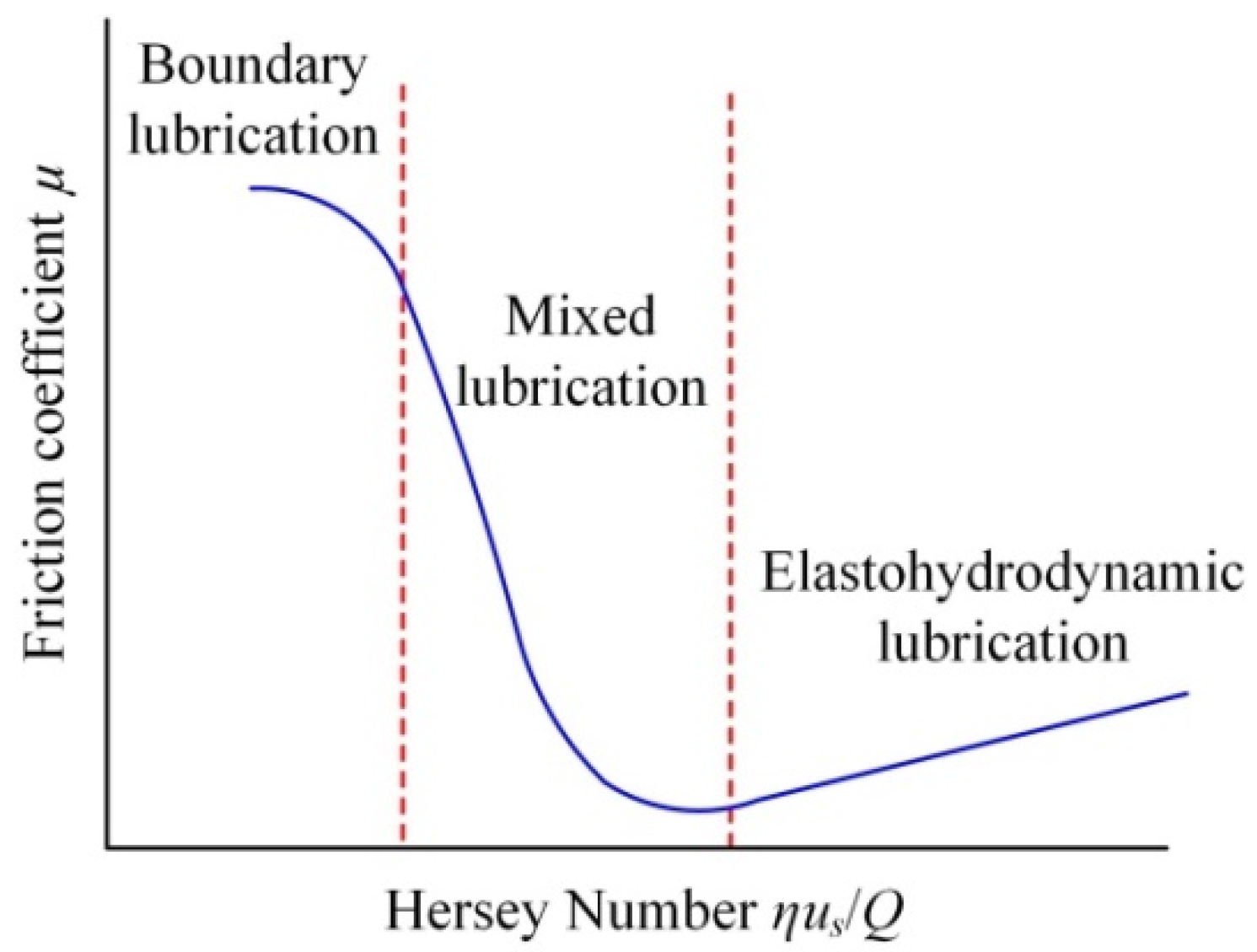
3.2. Calculation of Friction Coefficient and Friction Torque
4. Analysis of Anti-Friction Characteristics of Textured Raceway of the Ball Screws
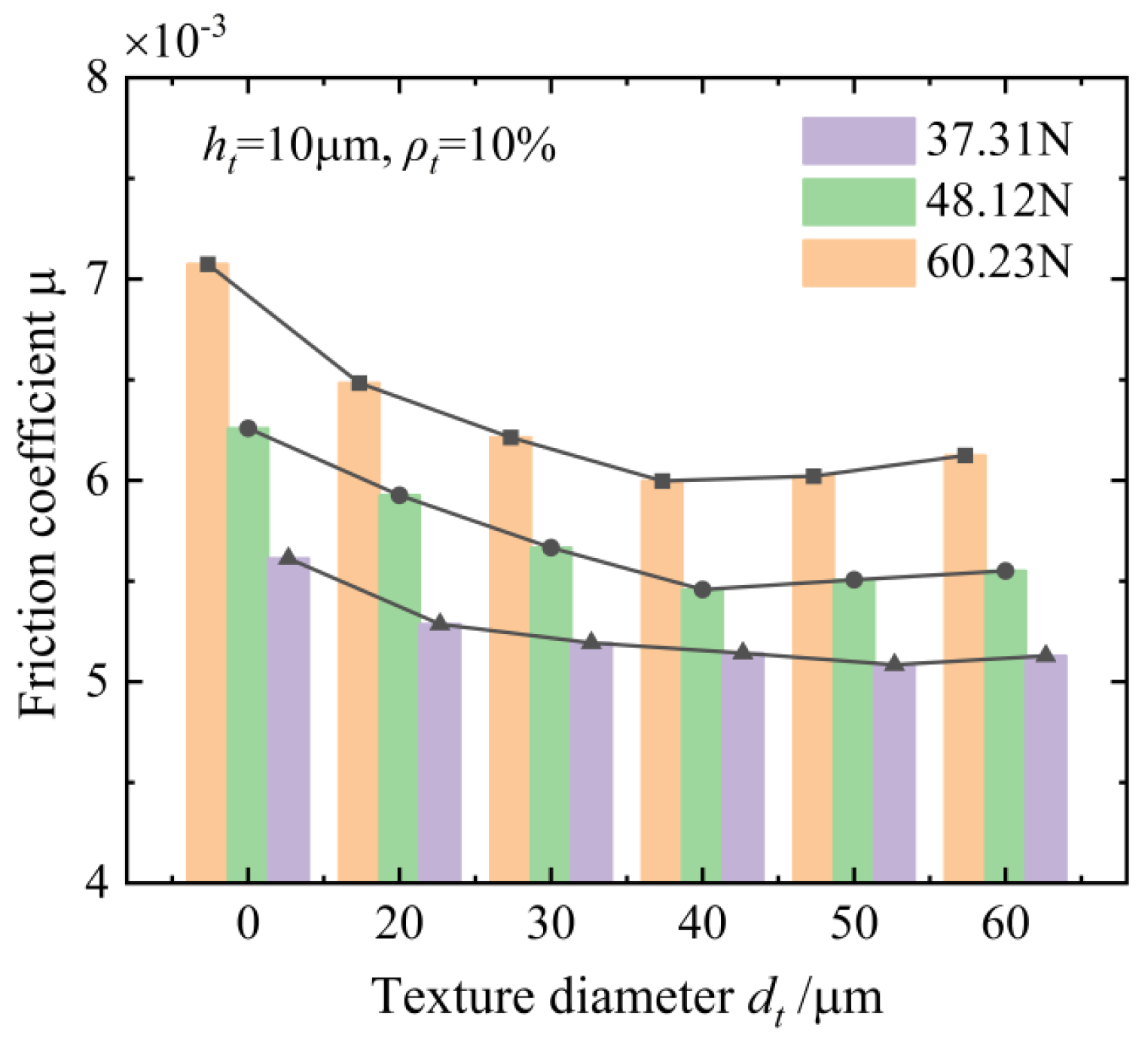
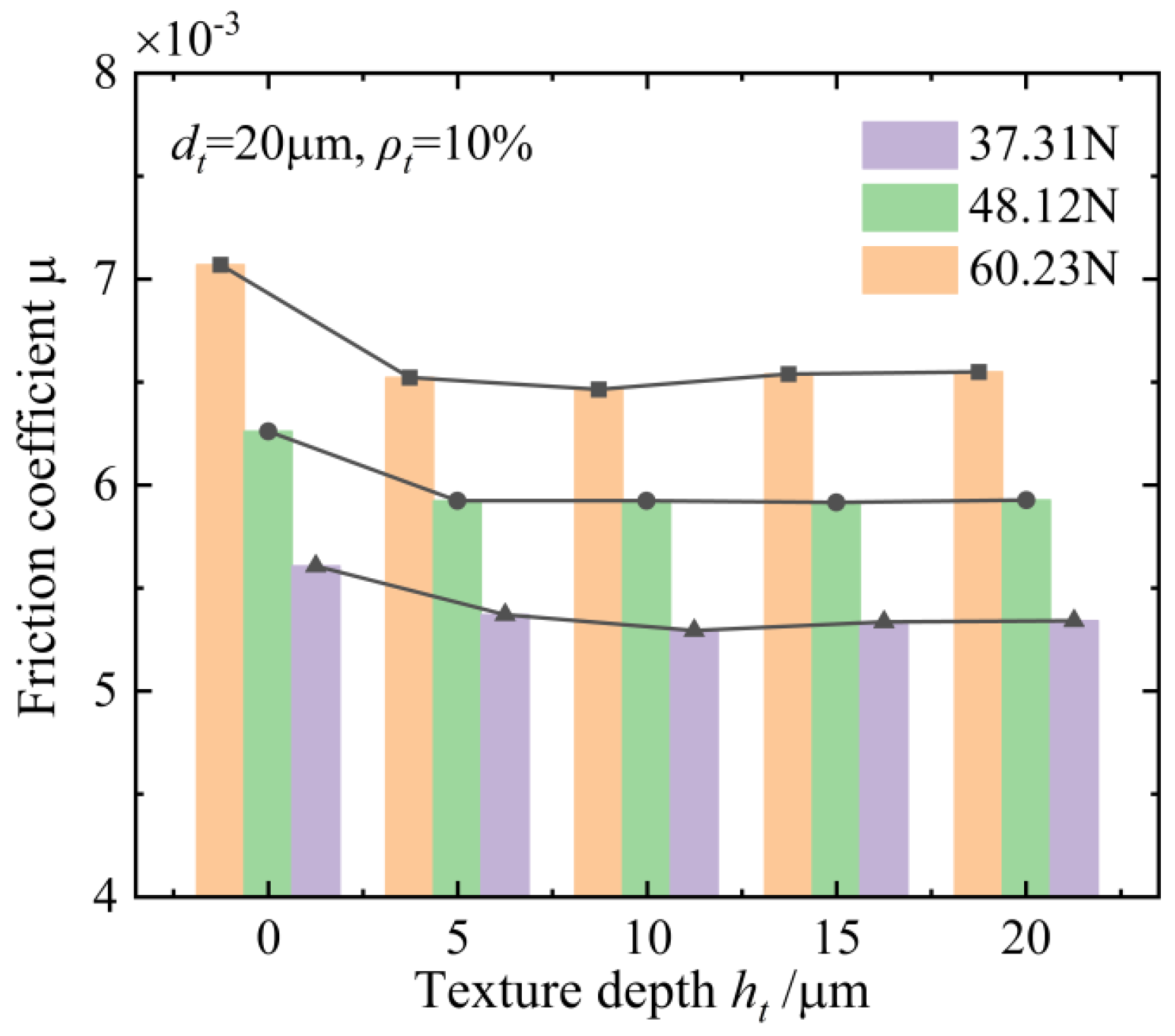
4.1. The Geometric Features of the Textures
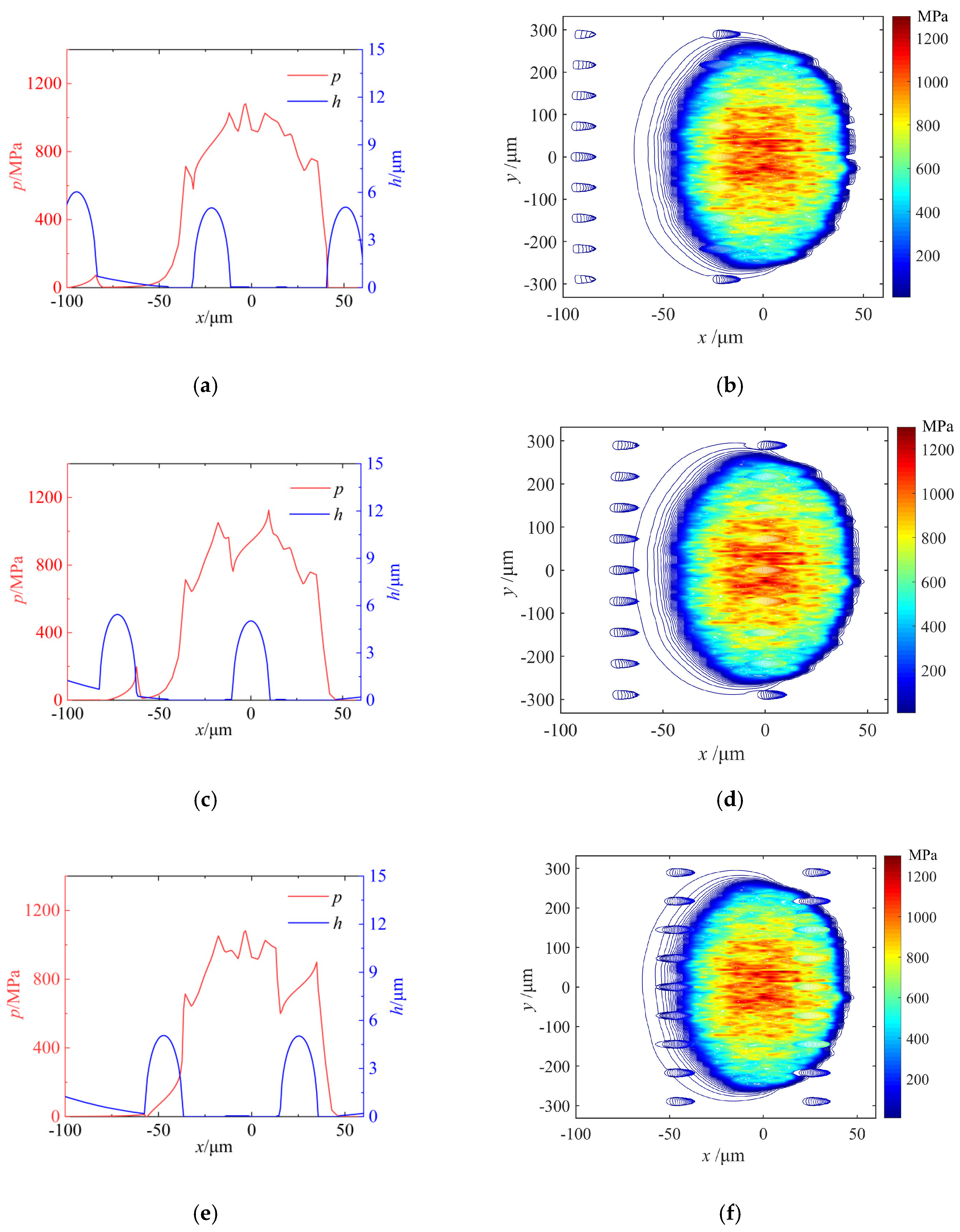
4.2. Analysis of EHL Characteristics of Textured Raceway of the Ball Screws
4.3. Influence of the Axial Loads on the Anti-Friction Characteristics of the Textured Raceway of the Ball Screws
4.4. Influence of the Rotation Speeds on the Anti-Friction Characteristics of the Textured Raceway of the Ball Screws
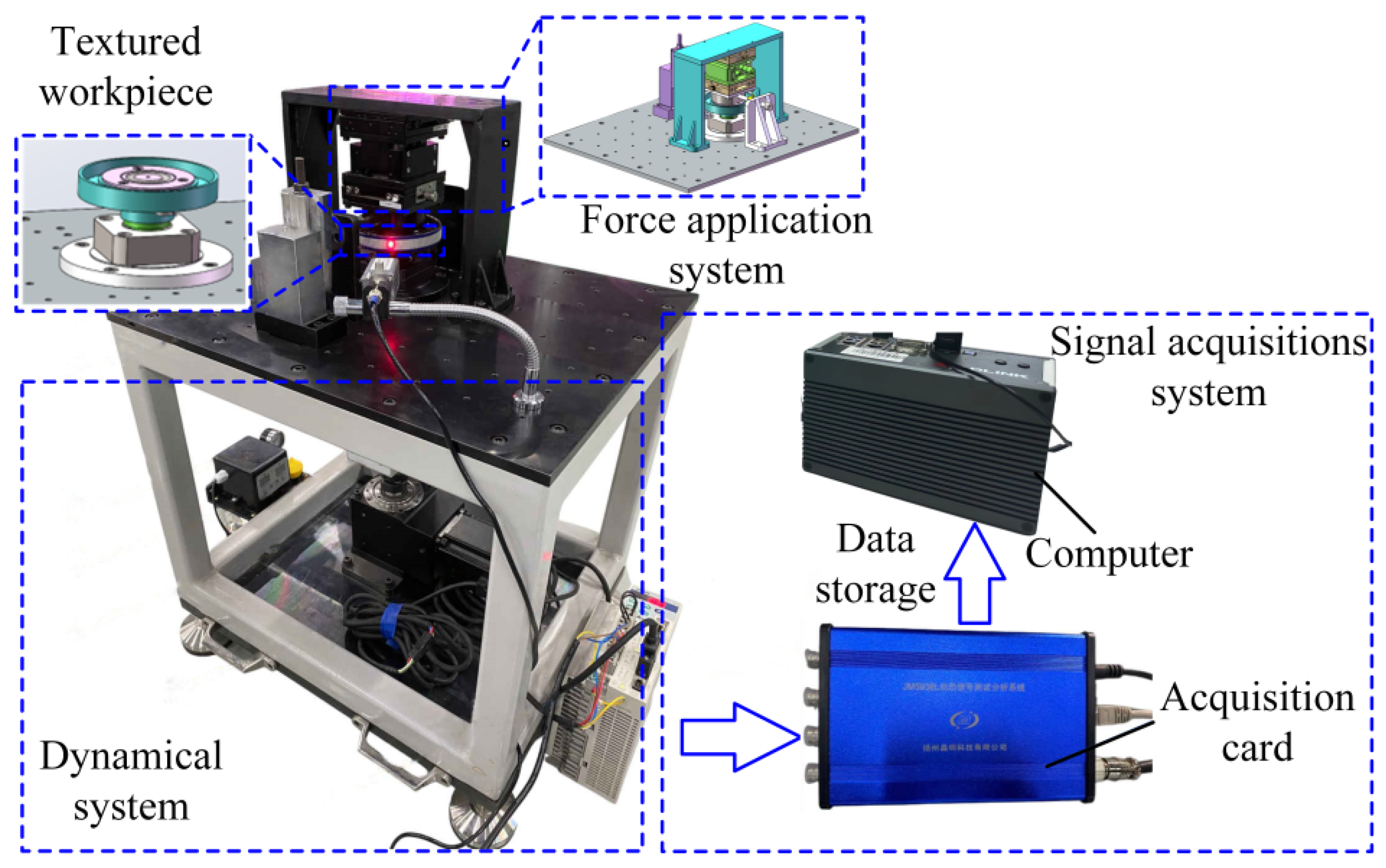
5. The Proof-of-Principle Experiments of the Textured Raceway of the Ball Screws
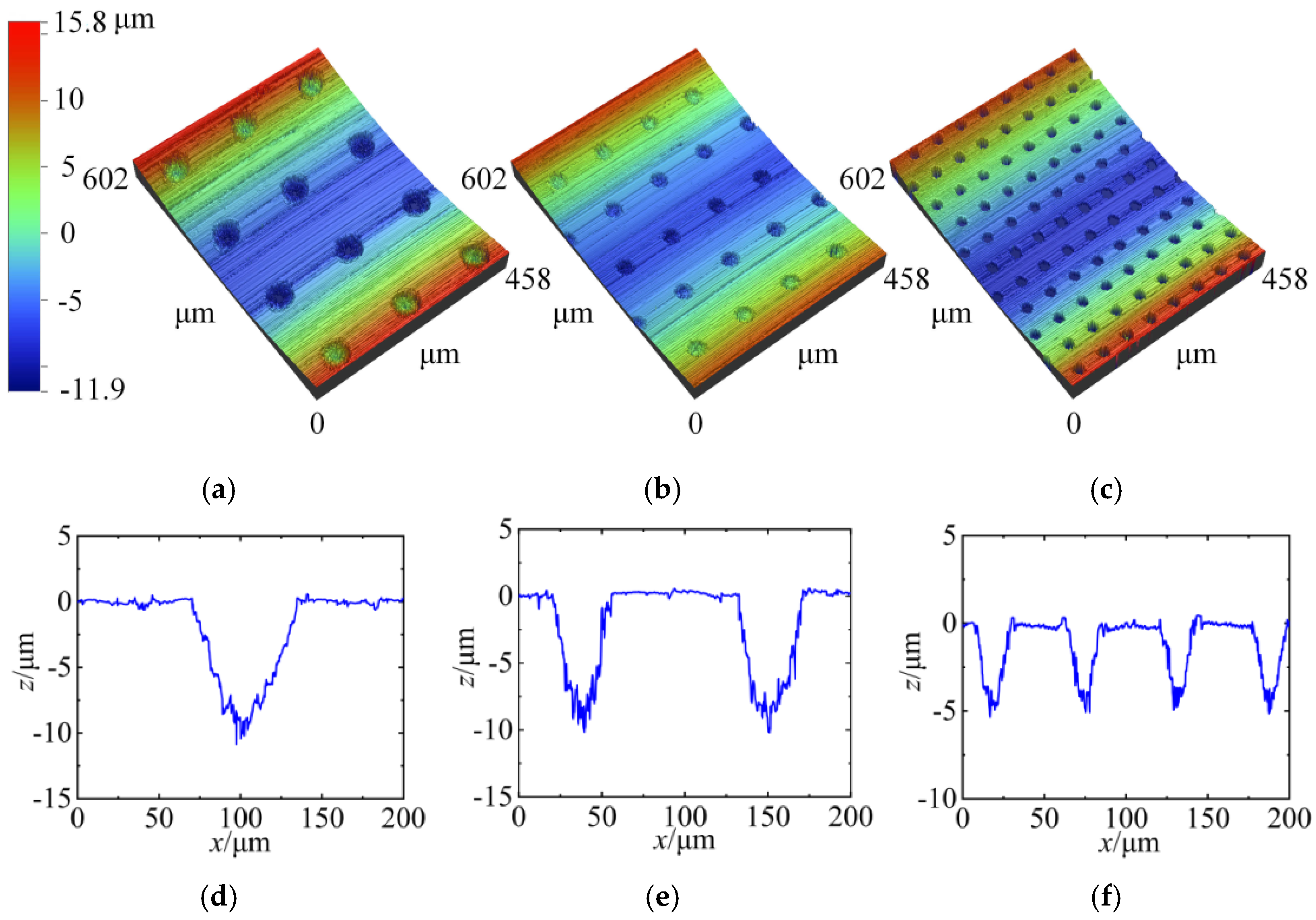
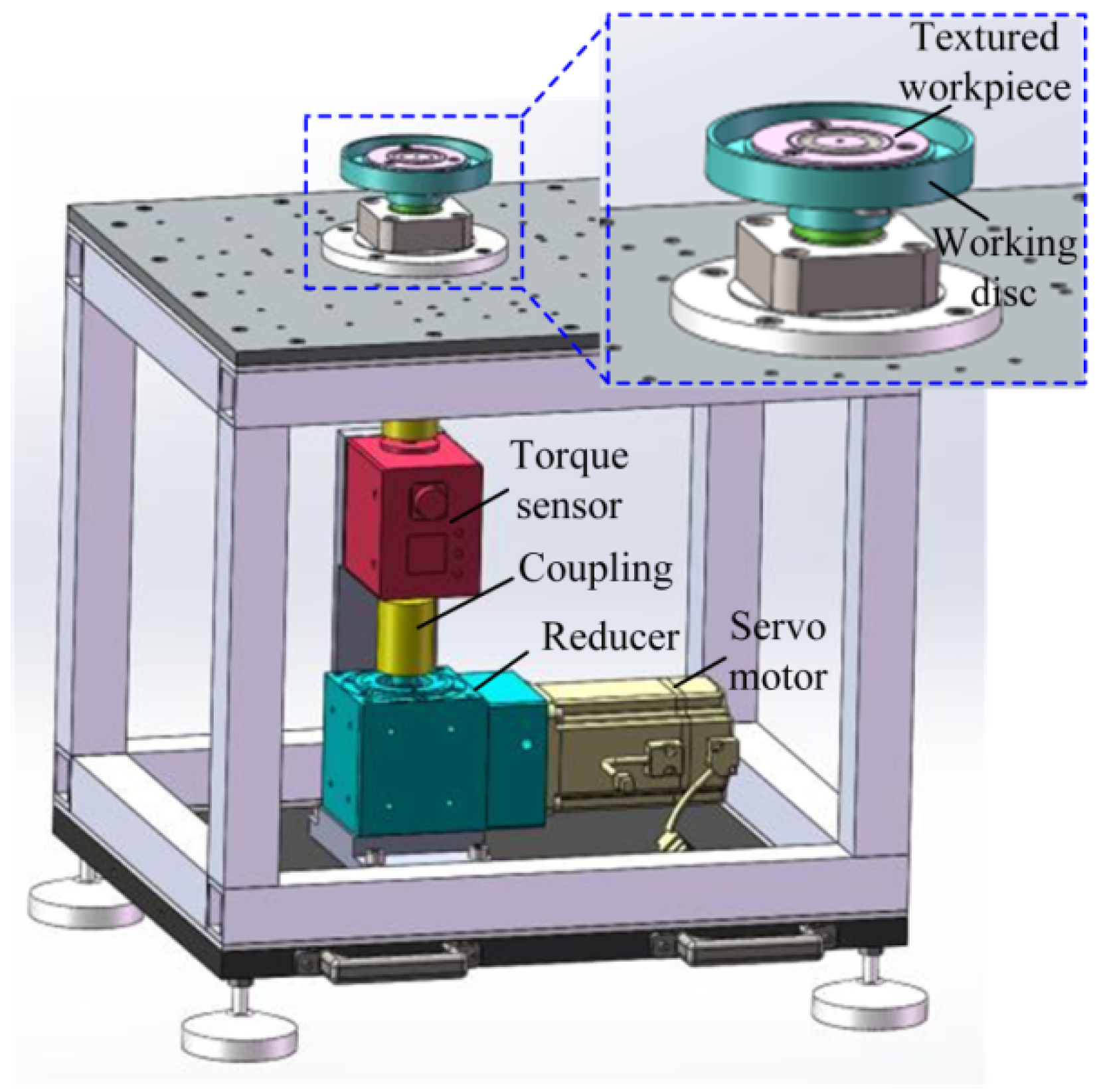
5.1. Design and Manufacture the Textured Workpieces
5.2. Experimental Principle and Scheme
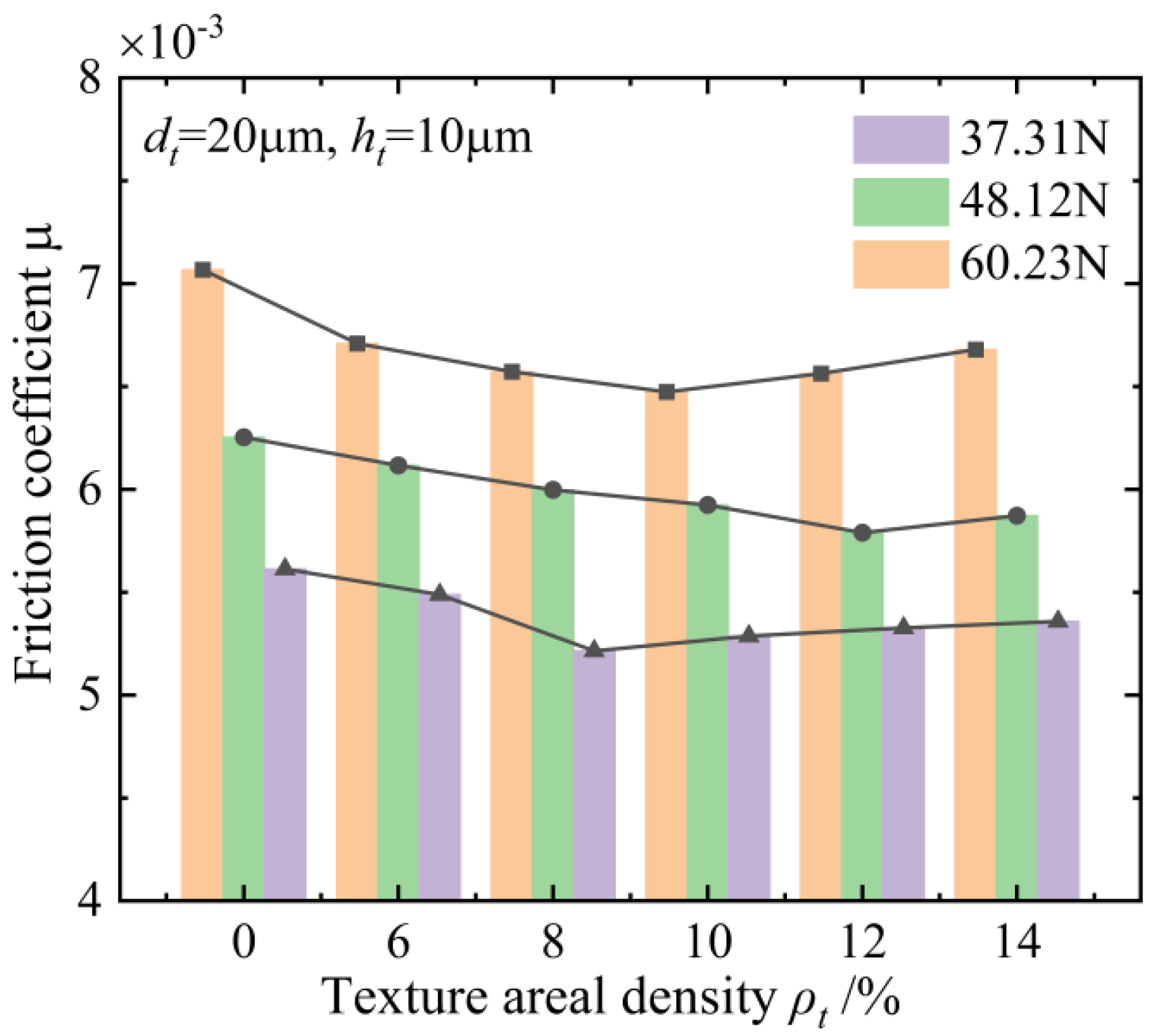
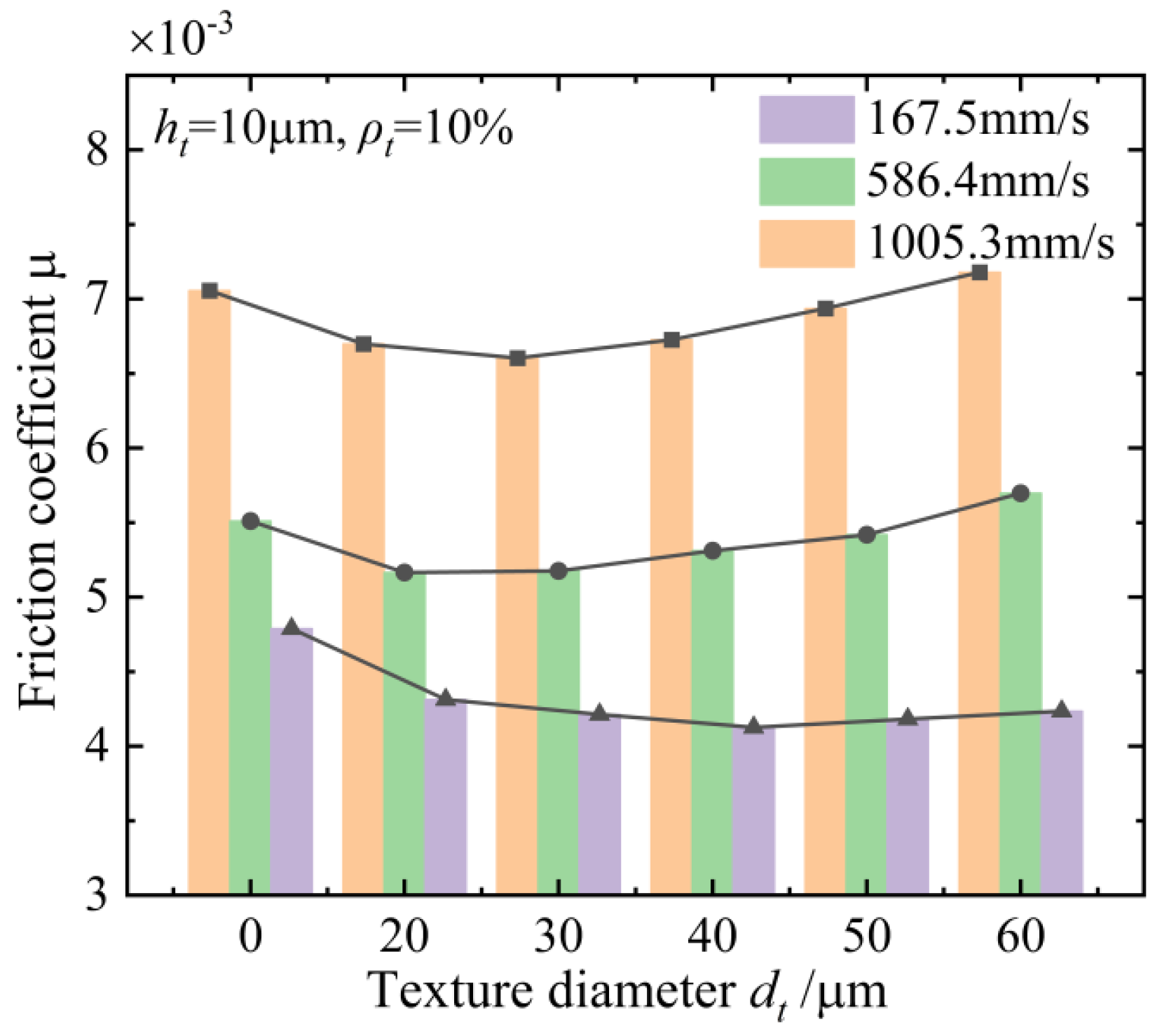
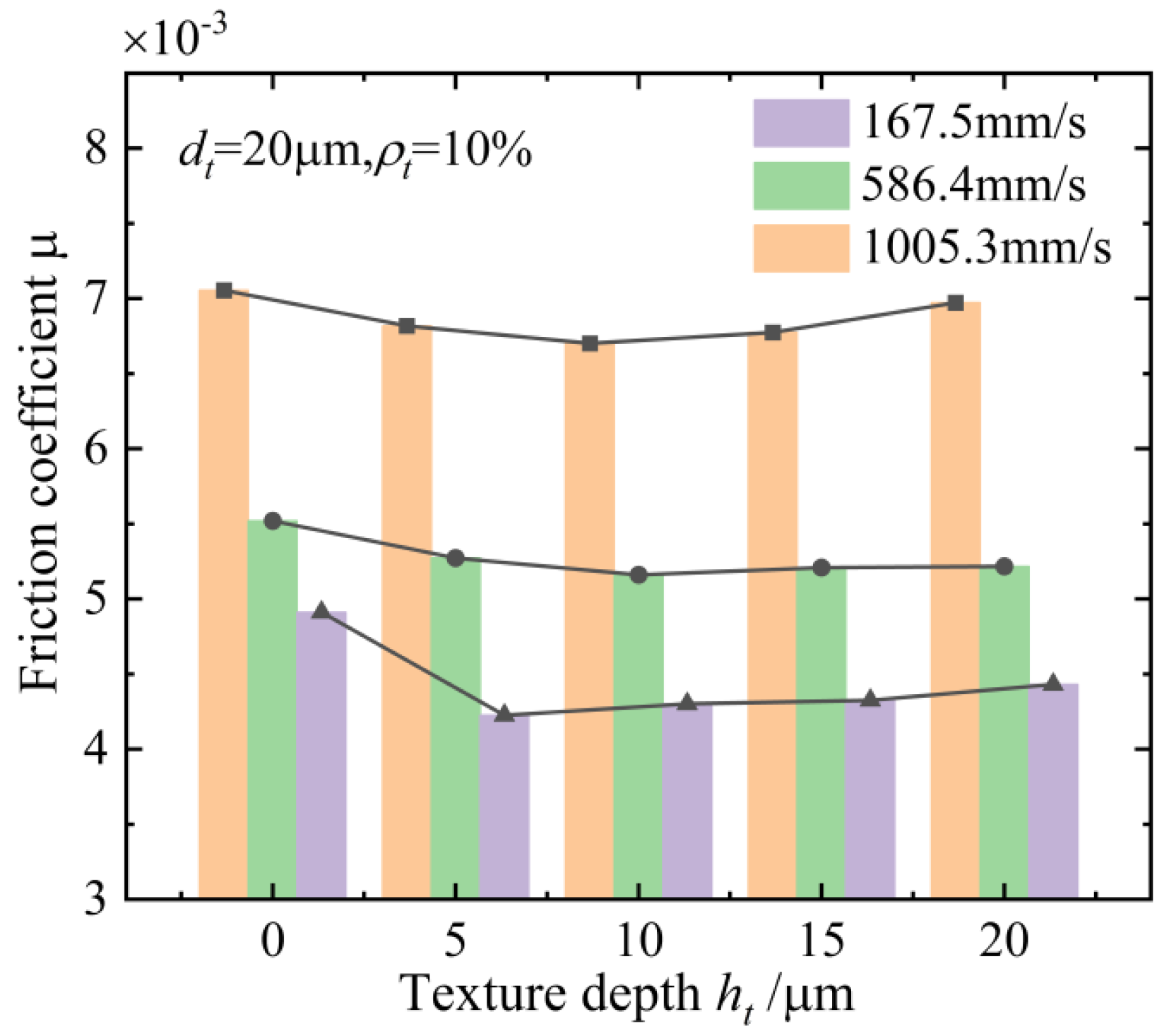
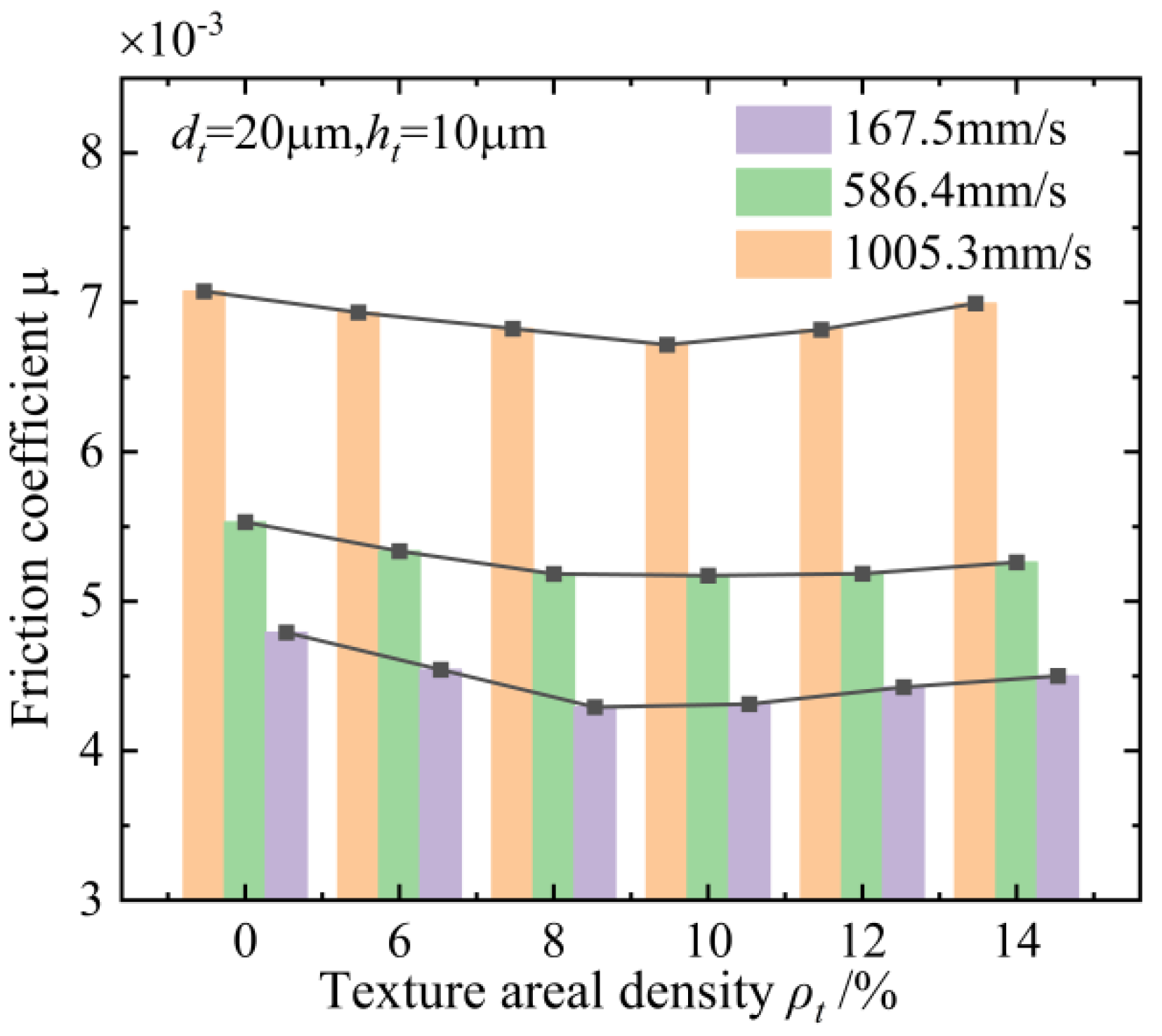
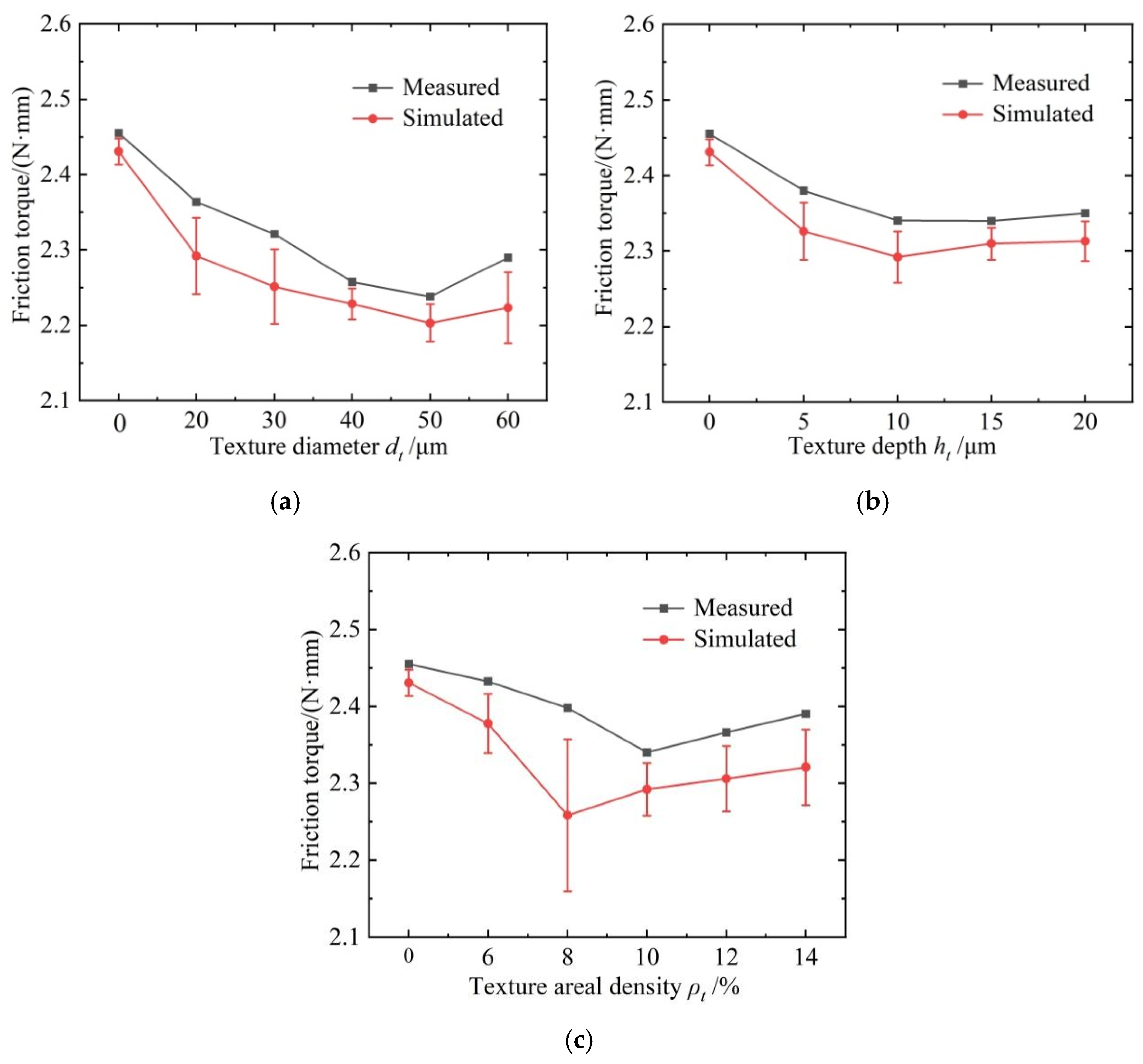
5.3. Analysis of Experimental Results
6. Conclusions
- Theoretical simulation and experimental measurement of the ground surface topography of the screw raceways are conducted based on the formation mechanism of the grinding surface and the geometric model of the screw raceway. The actual measurement and theoretical simulation of the surface roughness of the screw raceway are 0.2128 μm and 0.2072 μm, respectively, and the relative error is only 2.63% to verify the correctness of the forming mechanism of the grinding surface topography of the screw raceway.
- The influence of geometric features of the textures on the anti-friction effect under different rotation speeds and axial loads of the ball screws is investigated and discussed. The textured raceway of the ball screws provides a micro-hydrodynamic pressure perturbation effect that reduces the friction coefficient of the contact system of the ball screws by 15.2% at a normal contact force of 60.23 N, an entrainment speed of 167.5 m/s, a texture diameter of 40 μm, a texture depth of 10 μm, and a texture areal density of 10%.
- The results of the experiments show that the variation trend of the friction-reducing property with the change in the geometric features of the manufactured textures is well in accordance with the theoretical simulation, and the maximum and minimum relative errors are 6.2% and 1.3%, respectively. The correctness of the EHL model of the textured raceway of the ball screws and the effectiveness of the friction reduction effect of the surface texture technology of the ball screws are verified.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notation
| a | the grinding depth of the wheel |
| a1, a2 | the coaxial error parameters of the textured workpiece |
| α | the spiral angle of the ball screws |
| b1, b2 | the coaxial error parameters of the textured workpiece |
| c | coaxial error parameters of the textured workpiece |
| dave | the average diameter of the abrasive particles |
| de | the equivalent diameter of the grinding wheel |
| ds, dw. | the diameters of the grinding wheel and the screw |
| fo | the shear friction coefficient of the oil film |
| Fpre | the preload force |
| Fs | the friction force between the ball and the raceway |
| FSA, FSB | the friction force between the ball and the screw raceway and the nut raceway |
| gm,n | the surface of the workpiece is uniformly discretized into grids, and all grid points form a matrix |
| g(m, n) | the height of the point (m,n) on the surface of the workpiece relative to the global coordinate system |
| h | the oil film thickness distribution in the contact area |
| hi,j | the height of the cutting edge of the abrasive grains on the wheel surface |
| hmax | the maximum height of the cutting edge of the abrasive grain |
| hmin | the minimum oil film thickness |
| ht | the maximum depth of the texture |
| h0 | the oil film thickness in the center of the elliptical contact area. |
| hi,j | all grid points on the surface of the grinding wheel are characterized by a matrix |
| h(i, j) | the height of the cutting edge of the abrasive grain at the point (i, j) |
| ho, hp | the oil film thickness distribution in the non-textured area and textured area on the raceway surface of the ball screws |
| i, j | the position of the abrasive grain in the circumferential and radial directions on the surface of the grinding wheel |
| L | the lead of the ball screw |
| LA, LB | the friction arms of the screw and the nut raceway |
| LD | the distance between the contact point of the ball and the bearing raceway and the rotation axis of the textured workpiece |
| Li,j | the arc length of the rotational movement of the abrasive cutting edge |
| M | the grit number |
| M1, M2 | the friction torques of the ball and bearing |
| M3 | the friction torque due to the coaxial error of the textured workpiece |
| MS | the friction torque of the ball screws |
| ME | the friction torque measured in the experiment |
| nb | the number of working balls in a nut |
| n | the rotation speed of the grinding wheel |
| ND | the number of balls in the bearing raceway |
| p | the bearing capacity of the oil film |
| pa, pf | the bearing stress distribution of the asperity and the oil film in the elliptical contact area |
| pc | the cavitation pressure of the oil film |
| the parameter expression of the cross-sectional arc of the screw raceway at contact point A | |
| the parameter equation of the screw raceway in the coordinate system OXYZ | |
| Q | the total normal contact force of the ball |
| Qa | the normal force of the asperity contact |
| QAQD | the normal contact forces of the balls in the circular raceway and the bearing raceway |
| rb | the radius of the ball |
| rt | the radius of the texture |
| rs | the radius of gyration of the cutting edge of the abrasive grain |
| ri,j | the radial distance from the abrasive grain Gi,j to the center of the grinding wheel |
| Rx, Ry | the equivalent curvature radius in the x and y directions of the contact area |
| R(x, y) | the rough surface of the grinding raceway |
| Rq | the root mean square of the roughness of the screw raceway |
| t | the time taken for the grain G1 to rotate an angle θ |
| the coordinate transformation matrix from the coordinate system OXYZ to the Frenet–Serret coordinate system OHtnb of the helical trajectory of the ball center | |
| the coordinate transformation matrix from the Frenet–Serret coordinate system OHtnb to the contact coordinate system AXAYAZA | |
| u1, u2 | the linear velocities of the ball and raceway along the tangent direction of the spiral trajectory of the ball center |
| us | the entrainment speed of the oil film |
| vs, vw | the speeds of the grinding wheel and the screw |
| vw, vs | the feed speed of the workpiece and the circumferential speed of the grinding wheel |
| vs,e, vw,e | the equivalent speeds of the grinding wheel and the screw |
| Vg | the density of the wheel |
| V(x, y) | the elastic contact deformation in the elliptical contact area between the ball and the screw raceway |
| xin, yin | the coordinates at the entrance of the contact area between the ball and the raceway |
| xout, yout | the coordinates at the exit of the contact area between the ball and the raceway |
| S | the wheel structure number |
| μ | the friction coefficient and friction force between the ball and the raceway |
| μ1 | the mean value of the normal distribution |
| μa | the static friction coefficient of the raceway surface |
| μT, μD | the friction coefficients at the contact points of circular raceway and bearing raceway |
| θ | the rotation angle of the abrasive grain |
| σ | the variance of the normal distribution |
| βA | the contact angle between the ball and the screw raceway |
| βAS | the central angle corresponding to the cross-sectional arc of the screw raceway |
| βA0 | the range of the central angle of the screw raceway |
| Δx, Δy | the grid spacing |
| Δxs, Δys | the distances between the abrasive grains in the circumferential and axial directions of the grinding wheel |
| ΔOi,j | the offset distance of the local coordinate system in the x-direction is equal to the movement distance of the workpiece |
| ΔZi,j | the translation distance of the local coordinate system relative to the global coordinate system in the z-direction |
| ρ, η | the density and viscosity of the lubricating oil |
| ρ0, η0 | the environmental density and environmental viscosity of lubricating oil |
| ρt | the areal density of the texture on the screw raceway surface |
| Ω | the elliptical contact area between the ball and the screw raceway |
| Ωo, Ωh | the oil film-bearing area of the non-textured and textured in the elliptical contact area |
| the shear strain rate of the lubricating oil film | |
| τ, τ0 | the shear stress and the characteristic shear stress of the lubricating oil film |
| Λ | the film thickness ratio |
| τi,j | the shear force distribution of the oil film |
Appendix A. The Expression of the Transformation Matrixes
References
- Zhang, Y.; Zhou, C.; Feng, H. A meticulous friction torque model for a lubricated ball screw considering the surface roughness. Tribol. Int. 2023, 190, 109014. [Google Scholar] [CrossRef]
- Li, C.; Xu, M.; Song, W.; Zhang, H. A review of static and dynamic analysis of ball screw feed drives, recirculating linear guideway, and ball screw. Int. J. Mach. Tools Manuf. 2023, 188, 104021. [Google Scholar] [CrossRef]
- Li, T.-J.; Zhang, Y.-M.; Su, Y.; Zhang, K.; Wang, Y.-B.; Gao, S.-Z. Dynamic reliability of thermally deduced positioning precision of ball screw systems based on random moving difference method. J. Manuf. Syst. 2021, 61, 171–182. [Google Scholar] [CrossRef]
- Xie, Z.; Li, J.; Tian, Y.; Du, P.; Zhao, B.; Xu, F. Theoretical and experimental study on influences of surface texture on lubrication performance of a novel bearing. Tribol. Int. 2024, 193, 109351. [Google Scholar] [CrossRef]
- Zhao, J.; Lin, M.; Song, X.; Wei, N. A modeling method for predicting the precision loss of the preload double-nut ball screw induced by raceway wear based on fractal theory. Wear 2021, 486–487, 204065. [Google Scholar] [CrossRef]
- Sayfidinov, K.; Cezan, S.D.; Baytekin, B.; Baytekin, H.T. Minimizing friction, wear, and energy losses by eliminating contact charging. Sci. Adv. 2018, 4, eaau3808. [Google Scholar] [CrossRef]
- Holmberg, K.; Laukkanen, A.; Hakala, T.; Ronkainen, H.; Suhonen, T.; Wolski, M.; Podsiadlo, P.; Woloszynski, T.; Stachowiak, G.; Gachot, C.; et al. Topography orientation effects on friction and wear in sliding DLC and steel contacts, part 3: Experiments under dry and lubricated conditions. Wear 2021, 486–487, 204093. [Google Scholar] [CrossRef]
- Holmberg, K.; Erdemir, A. The impact of tribology on energy use and CO2 emission globally and in combustion engine and electric cars. Tribol. Int. 2019, 135, 389–396. [Google Scholar] [CrossRef]
- Kharanzhevskiy, E.V.; Ipatov, A.G.; Makarov, A.V.; Gil’mutdinov, F.Z. Towards eliminating friction and wear in plain bearings operating without lubrication. Sci. Rep. 2023, 13, 17362. [Google Scholar] [CrossRef]
- Woydt, M. The importance of tribology for reducing CO2 emissions and for sustainability. Wear 2021, 474–475, 203768. [Google Scholar] [CrossRef]
- Rosenkranz, A.; Costa, H.L.; Baykara, M.Z.; Martini, A. Synergetic effects of surface texturing and solid lubricants to tailor friction and wear—A review. Tribol. Int. 2021, 155, 106792. [Google Scholar] [CrossRef]
- Shah, R.; Gashi, B.; Hoque, S.; Marian, M.; Rosenkranz, A. Enhancing mechanical and biomedical properties of protheses—Surface and material design. Surfaces Interfaces 2021, 27, 101498. [Google Scholar] [CrossRef]
- Boidi, G.; Grützmacher, P.G.; Kadiric, A.; Profito, F.J.; Machado, I.F.; Gachot, C.; Dini, D. Fast laser surface texturing of spherical samples to improve the frictional performance of elasto-hydrodynamic lubricated contacts. Friction 2021, 9, 1227–1241. [Google Scholar] [CrossRef]
- Han, D.; Wang, L.; Zhang, S.; Zhang, Q.; Wang, C.; Li, W. The impact of synergistic action of methacrylic acid/zinc oxide/carbon nanotubes on metal Friction and wear. Wear 2024, 546–547, 205342. [Google Scholar] [CrossRef]
- Wang, B.; Lai, W.; Li, S.; Huang, S.; Zhao, X.; You, D.; Tong, X.; Li, W.; Wang, X. Self-lubricating coating design strategy for titanium alloy by additive manufacturing. Appl. Surf. Sci. 2022, 602, 154333. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, S. Effect of moderately high temperature heat treatment on surface morphology and structure of quartz fibers. Appl. Surf. Sci. 2012, 258, 4698–4701. [Google Scholar] [CrossRef]
- Cai, S.; Chen, G.; Zhou, C. Research and application of surface heat treatment for multipulse laser ablation of materials. Appl. Surf. Sci. 2015, 355, 461–472. [Google Scholar] [CrossRef]
- Oláh, A.; Croitoru, C.; Tierean, M.H. Surface properties tuning of welding electrode-deposited hardfacings by laser heat treatment. Appl. Surf. Sci. 2018, 438, 41–50. [Google Scholar] [CrossRef]
- Amanov, A.; Karimbaev, R. Improvement in frictional and fatigue performances of AISI 4150H steel by dual ultrasonic nanocrystal surface modification for ball screw applications. Tribol. Int. 2021, 161, 107092. [Google Scholar] [CrossRef]
- Tang, W.; Zhou, Y.; Zhu, H.; Yang, H. The effect of surface texturing on reducing the friction and wear of steel under lubricated sliding contact. Appl. Surf. Sci. 2013, 273, 199–204. [Google Scholar] [CrossRef]
- Niu, Y.; Hao, X.; Xia, A.; Wang, L.; Liu, Q.; Li, L.; He, N. Effects of textured surfaces on the properties of hydrodynamic bearing. Int. J. Adv. Manuf. Technol. 2022, 118, 1589–1596. [Google Scholar] [CrossRef]
- Scaraggi, M.; Mezzapesa, F.P.; Carbone, G.; Ancona, A.; Tricarico, L. Friction properties of lubricated laser-microtextured-surfaces: An experimental study from boundary-to hydrodynamic-lubrication. Tribol. Lett. 2013, 49, 117–125. [Google Scholar] [CrossRef]
- Shinde, A.; Pawar, P.; Gaikwad, S.; Kapurkar, R.; Parkhe, A. Numerical Analysis of Deterministic Micro-Textures on the Performance of Hydrodynamic Journal Bearing. Mater. Today Proc. 2018, 5, 5999–6008. [Google Scholar] [CrossRef]
- Ye, Q.; Chang, Q.; Shen, Z. The Influence of Surface Texture Depth on the Load Bearing Capacity of Oil Film. Lubr. Eng. 2012, 5, 39–42. [Google Scholar]
- Convert, L.; Bourillot, E.; François, M.; Pocholle, N.; Baras, F.; Politano, O.; Costil, S. Laser textured titanium surface characterization. Appl. Surf. Sci. 2022, 586, 152807. [Google Scholar] [CrossRef]
- Zhang, D.; Zhao, F.; Li, Y.; Li, P.; Zeng, Q.; Dong, G. Study on tribological properties of multi-layer surface texture on Babbitt alloys surface. Appl. Surf. Sci. 2016, 390, 540–549. [Google Scholar] [CrossRef]
- Brizmer, V.; Kligerman, Y.; Etsion, I. A laser surface textured parallel thrust bearing. Tribol. Trans. 2003, 46, 397–403. [Google Scholar] [CrossRef]
- Wang, X.; Adachi, K.; Otsuka, K.; Kato, K. Optimization of the surface texture for silicon carbide sliding in water. Appl. Surf. Sci. 2006, 253, 1282–1286. [Google Scholar] [CrossRef]
- Fu, Y.; Ji, J.; Bi, Q. The Influence of Partially Textured Slider with Oriented Parabolic Grooves on the Behavior of Hydrodynamic Lubrication. Tribol. Trans. 2012, 55, 210–217. [Google Scholar] [CrossRef]
- Ryk, G.; Kligerman, Y.; Etsion, I. Experimental Investigation of Laser Surface Texturing for Reciprocating Automotive Components. Tribol. Trans. 2002, 45, 444–449. [Google Scholar] [CrossRef]
- Wang, X.; Liu, W.; Zhou, F.; Zhu, D. Preliminary investigation of the effect of dimple size on friction in line contacts. Tribol. Int. 2009, 42, 1118–1123. [Google Scholar] [CrossRef]
- Costa, H.; Hutchings, I. Hydrodynamic lubrication of textured steel surfaces under reciprocating sliding conditions. Tribol. Int. 2007, 40, 1227–1238. [Google Scholar] [CrossRef]
- Morris, N.; Leighton, M.; De la Cruz, M.; Rahmani, R.; Rahnejat, H.; Howell-Smith, S. Combined numerical and experimental investigation of the micro-hydrodynamics of chevron-based textured patterns influencing conjunctional friction of sliding contacts. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2015, 229, 316–335. [Google Scholar] [CrossRef]
- Etsion, I. Surface texturing for in-cylinder friction reduction. In Tribology and Dynamics of Engine and Powertrain; Woodhead Publishing: New Delhi, India, 2010; pp. 458–469+470e. [Google Scholar]
- Overby, A. CNC Machining Handbook: Building, Programming, and Implementation; McGraw-Hill: New York, NY, USA, 2010. [Google Scholar]
- Roeland, C.J. Correlation Aspect of the Viscosity-Temperature-Pressure Relation of Lubrication Oils. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1966. [Google Scholar]
- Dowson, D.; Higginson, G.R. A Numerical Solution to the Elasto-Hydrodynamic Problem. J. Mech. Eng. Sci. 1959, 1, 6–15. [Google Scholar] [CrossRef]





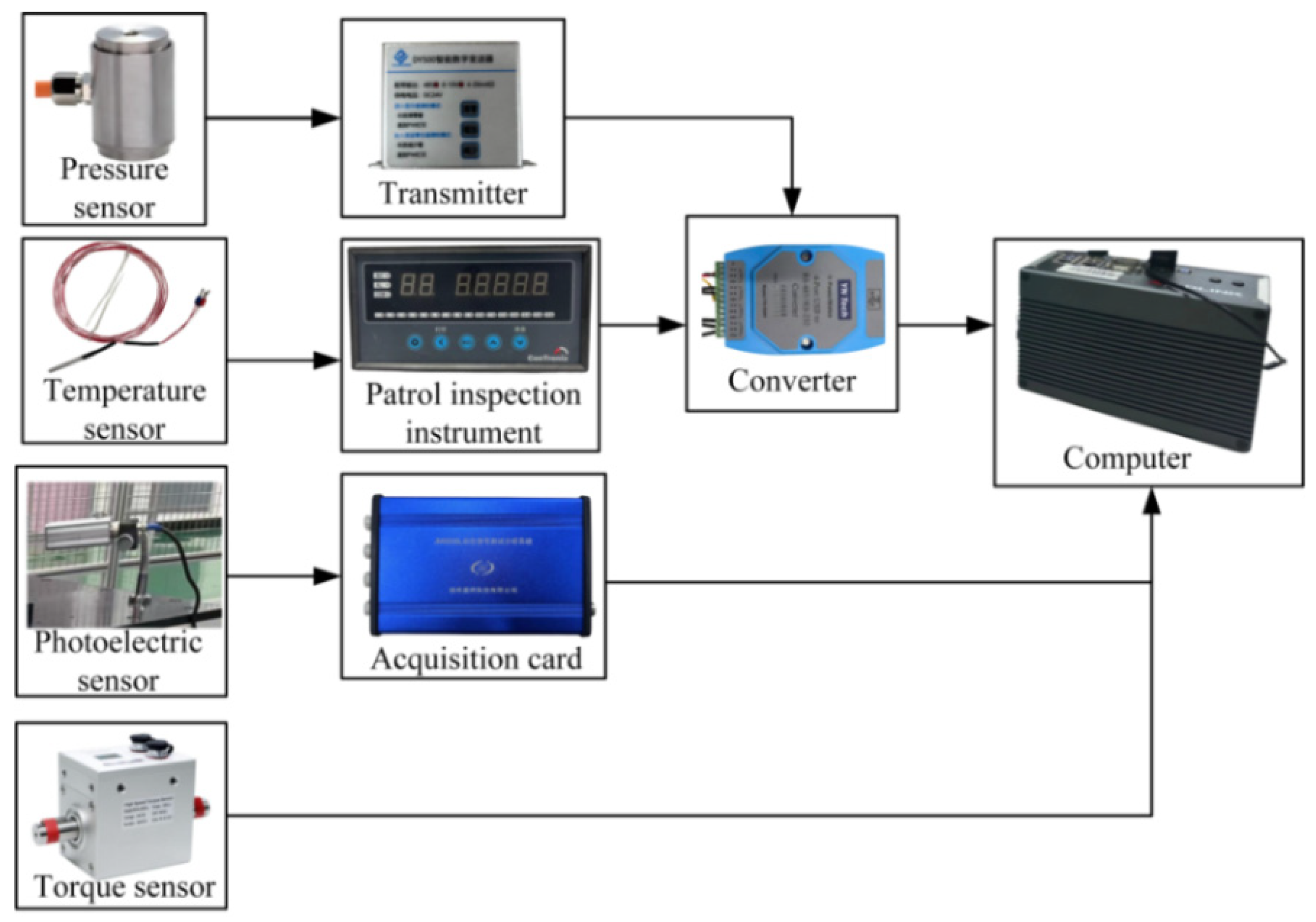

| The Parameter Names | The Parameter Value |
|---|---|
| Workpiece feed speed vw (m/s) | 0.1 |
| Ball diameter 2rb (mm) | 5.953 |
| The nominal radius r (mm) | 16 |
| Wheel diameter ds (mm) | 310 |
| Grinding depth a (µm) | 5 |
| The preload force Fpre (N) | 1500 |
| Lead of ball screw L (mm) | 10 |
| The rotation speed of the grinding wheel n (r/min) | 3000 |
| Workpiece#1 | Areal density ρt | Depth ht/μm | Diameter dt/μm | |||
| 10% | 10 | 30 | 40 | 50 | 60 | |
| Workpiece #2 | Areal density ρt | Diameter dt/μm | Depth ht/μm | |||
| 10% | 20 | 5 | 10 | 15 | 20 | |
| Workpiece #3 | Depth ht/μm | Diameter dt/μm | Areal density ρt | |||
| 10 | 20 | 6% | 8% | 12% | 14% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wang, M.; Gao, X.; Gao, P.; Yang, X.; Cui, X. Study on the Lubrication and Anti-Friction Characteristics of the Textured Raceway of the Ball Screws Based on Elastohydrodynamic Lubrication. Appl. Sci. 2025, 15, 3343. https://doi.org/10.3390/app15063343
Zhang Y, Wang M, Gao X, Gao P, Yang X, Cui X. Study on the Lubrication and Anti-Friction Characteristics of the Textured Raceway of the Ball Screws Based on Elastohydrodynamic Lubrication. Applied Sciences. 2025; 15(6):3343. https://doi.org/10.3390/app15063343
Chicago/Turabian StyleZhang, Yunfei, Min Wang, Xiangsheng Gao, Peng Gao, Xuefei Yang, and Xiwen Cui. 2025. "Study on the Lubrication and Anti-Friction Characteristics of the Textured Raceway of the Ball Screws Based on Elastohydrodynamic Lubrication" Applied Sciences 15, no. 6: 3343. https://doi.org/10.3390/app15063343
APA StyleZhang, Y., Wang, M., Gao, X., Gao, P., Yang, X., & Cui, X. (2025). Study on the Lubrication and Anti-Friction Characteristics of the Textured Raceway of the Ball Screws Based on Elastohydrodynamic Lubrication. Applied Sciences, 15(6), 3343. https://doi.org/10.3390/app15063343






