Abstract
High-powered, heavy-duty diesel engines are widely used in transportation, construction, railways, and marine applications. Optimizing valvetrain dynamics is crucial for improving fuel efficiency and reducing emissions. This study presents an integrated multibody dynamics (MBD) and experimental validation approach for a novel heavy-duty diesel engine valvetrain design. The development of the kinematic and dynamic models was motivated by the necessity to analyze valvetrain behavior, identify operational challenges, and optimize key parameters such as the position of the elephant foot and valve lift. The optimized design was validated through experimental testing using vibration measurements at multiple engine points. The results demonstrate that the proposed modifications effectively mitigate valve bounce, improve stability, and enhance engine performance. The validated model provides a foundation for further advancements in valvetrain optimization, contributing to improved efficiency in heavy-duty diesel engines.
1. Introduction
The use of multibody dynamic analysis has become a crucial aspect in the design and development of heavy-duty diesel engines. This is mainly because it enables accurate simulation and prediction of the dynamic behavior of engine components, such as the valvetrain, which plays a decisive role in engine operation, ensuring precise valve timing and, consequently, optimal combustion and power output [1,2]. The opening and closing of engine valves, synchronized with the crankshaft’s rotation, require precise coordination. However, this synchronized motion can cause problematic phenomena such as valve bounce, discrepancies between actual and theoretical valve lifts, delayed valve openings, and advanced valve closing times [3].
Hu et al. investigated the influence of cam speed and valve clearance on jump and bounce phenomena, concluding that both factors significantly affect the occurrence of these problems [4]. Similarly, Sarıdemir and Saruhan analyzed inertial forces and found that reducing valve lift could mitigate the risk of valve jump [5].
Ali et al. studied the effects of valvetrain misalignment on valve and guide interactions in automotive engines, focusing on intentional misalignments [6]. Their findings emphasized the asymmetric load distribution influenced by damping interactions between the valve tip and the roller finger follower. Contact losses in valvetrain systems, especially at high engine speeds, have significant consequences, including disrupted valve timing and reduced engine performance. Andreatta and Pederiva underscored the importance of dynamic analysis to predict contact losses and optimize valvetrain design [7].
Busch highlighted how the interaction between camshaft speed and system stability affects oscillatory behavior [8]. Oscillations in valvetrain systems arise from the inherent dynamics of the components and their interactions. Even minor disturbances can cause the finger follower to deviate from its intended position. Due to limited lateral clearance, this deviation leads to the follower striking clearance boundaries, causing large misalignment angles. These misalignments result in significant variations in the contact forces between the cam and the roller, which contribute to oscillatory behavior. At low camshaft speeds, the system exhibits instability similar to that of an inverted pendulum, making it highly susceptible to perturbations.
John and Agarwal addressed the issue of valve float by investigating the effect of increasing the rocker arm ratio to achieve larger valve lifts with smaller cam lifts [9]. This adjustment reduced cam velocities and accelerations, effectively mitigating valve float. They also experimented with increasing spring stiffness, which resulted in higher Hertz stress. The stiffer spring required a greater force from the cam to overcome resistance, leading to elevated contact forces at the cam and roller interface. Consequently, this increased Hertz stress posed challenges for the durability of the components.
This study presents a comprehensive methodology for valvetrain system analysis by integrating kinematic and dynamic modeling approaches. While previous studies in the literature often focus on either kinematic or dynamic modeling separately, this study combines both approaches to achieve a more holistic analysis. Kinematic modeling is used to determine fundamental motion characteristics, whereas dynamic modeling provides a detailed examination of system vibrations, contact forces, and interactions between components. Additionally, the validation process in this study is conducted through engine vibration measurements, allowing for a direct comparison between experimental data and model predictions. This approach not only contributes to valvetrain design optimization but also offers a valuable framework for validating dynamic analyses through engine vibration data.
2. Materials and Methods
Kinematic analysis serves as a foundational tool for characterizing the operation of a valvetrain. It enables preliminary calculations of loads and stresses while providing input data for engine thermal analysis. However, MBD analysis is critical to predict the vibrational behavior of the valve train, calculate dynamic loads and stresses, and identify potential component failures or contact losses, particularly at high engine speeds [10].
MBD modeling assumes greater importance at elevated engine speeds, where inertial forces become substantial. Conversely, at lower speeds, such as during idle, the effects of dynamics are less pronounced, and kinematic models often yield reasonable approximations. Dynamic models also account for variables such as spring preload and residual cylinder pressure, which significantly influence valve movement and system loads, factors that are not directly addressed in kinematic analyzes.
In essence, kinematic modeling provides a simplified representation of motion, whereas dynamic modeling offers a more comprehensive understanding of the interactions between forces and system behavior. Both approaches are integral to the thorough analysis of valve train performance, with dynamic modeling becoming increasingly essential under high-speed operating conditions.
Kinematic modeling focuses on the analysis of motion, highlighting parameters such as displacement, velocity, and acceleration of components, including valves. Dynamic modeling, on the other hand, expands this scope by incorporating the forces that influence motion. Factors such as mass, stiffness, and damping are considered in dynamic models to facilitate an understanding of the vibrational behavior of the system. While kinematic models are relatively straightforward and provide an initial understanding of system motion, dynamic models are more intricate, accounting for the interactions of forces and their effects on component behavior.
The FEV Virtual Dynamics 2019.1 software was used for kinematic and dynamic modeling and simulations in this study. This software, built on ADAMS, developed by Mechanical Dynamics, Incorporated (MDI) for the simulation of mechanical system motion in the time and frequency domain, utilizes ISO-certified processes to ensure precise equation formulation and reliable solution algorithms, validated through comparisons with published results and quality assurance standards [11]. It incorporates virtual prototyping into the engine development process, effectively bridging the gap between specialized industry tools and general-purpose simulation software [12]. This software combines engine-specific knowledge with a tailored interface and architecture, incorporating specialized elements such as push rods, gas forces, dynos, and valves, which can be refined to varying levels of detail depending on the development stage and data availability.
The methodology of this study follows a four-stage process integrating kinematic modeling, dynamic simulation, experimental validation, and optimization. First, kinematic modeling is performed to define the cam profile, analyze displacement, velocity, and acceleration, and predict initial valve motion characteristics. Next, an MBD simulation is performed that incorporates mass, stiffness, damping, and external forces to analyze the interactions between valvetrain components, including contact forces and system vibrations. The definition types of the parts in the kinematic and dynamic models and their percentage distribution by mass are shown in Table 1. In the experimental validation phase, vibration accelerations are measured at multiple engine points and compared with simulation results to refine the model and ensure accuracy. Finally, the final optimization and validation stage involves adjusting key parameters such as spring stiffness, cam profile, and damping characteristics to improve valvetrain stability and performance. This integrated approach ensures a comprehensive analysis and validation of the proposed valvetrain design.

Table 1.
Part definitions in kinematic and dynamic model.
2.1. Kinematic Design
The cam profile plays a critical role in determining valve train performance by governing valve motion, acceleration, and contact forces, which in turn influence stress levels within the components. To minimize stress-inducing accelerations, it is essential to reduce abrupt changes in the curvature of the cam profile. The schematic of the kinematic model used in this study is shown in Figure 1. Within the software, cam profile designs were generated to achieve the desired lift values for both intake and exhaust models. Separate cam profiles were created for the intake and exhaust systems of the right and left banks. These profiles were subsequently positioned on the camshaft in accordance with the engine’s firing order.
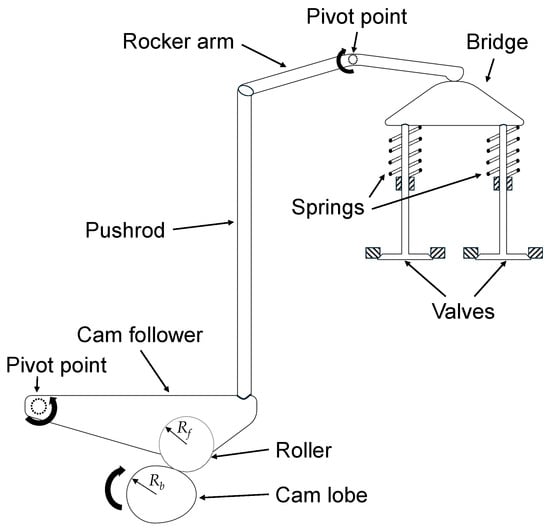
Figure 1.
Kinematic MBD model of valvetrain.
Optimizing valve motion is crucial to achieving the desired engine performance characteristics while mitigating stress concentrations. This requires careful consideration of the dynamic interaction between contact forces and elastic deformation. To address these multifaceted requirements, the design process incorporates acceleration values in the development of the lift profile. In the kinematic model, the cold lash is specified as a constant value when creating the cam profile. In the dynamic model, this clearance is defined between the elephant foot and the bridge. The valve opening ramp zone is for compensating for the specified lash values, as shown by the lift profile acceleration values in Figure 2 (0° crank angle indicates the beginning of the power stroke here and after).
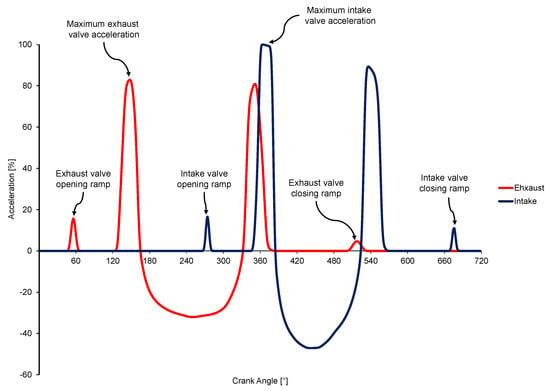
Figure 2.
Lift profile acceleration values.
The valve acceleration profile also significantly impacts the gas exchange process in the engine. Rapid acceleration and deceleration of the valve can improve airflow into and out of the cylinder, potentially improving engine power and efficiency. However, these aggressive acceleration profiles must be carefully balanced against the adverse effects of excessive valvetrain oscillations, which can compromise the stability and durability of the system [13].
Optimizing the valve acceleration profile involves striking a balance between maximizing engine performance and minimizing negative dynamic effects. This often requires tuning the acceleration curve to suppress oscillations, particularly during the valve deceleration phase. In addition, the valve closing velocity is a key factor affecting the noise, vibration and harshness (NVH) characteristics, as well as the durability of the valve, seat, and spring retainer.
The vertical displacement of the cam follower is determined by the cam profile. For a simple harmonic motion cam, the displacement can be expressed as follows:
where is the displacement of the cam follower, is the radius of the cam base circle, is the radius of the roller, is the lift of the cam lobe, and is the angular position of the cam shaft. The pushrod is assumed to be rigid, so its length remains constant. The vertical displacement of the pushrod at the rocker arm end is moving with the ratio is as follows:
where is the horizontal distance from the end of the pushrod to the pivot point and is the horizontal distance from the roller to the pivot point. The angular displacement of the rocker arm is related to the vertical displacement of the pushrod as follows:
This equation accounts for the effect of the pivot on the motion before it reaches the rocker arm. The pushrod transfers its motion to the rocker arm, which has a length ratio is:
where is the length from the pivot of the rocker to the contact of the valve and is the length from the pivot of the rocker to the contact of the pushrod. The relationship between the angular displacement of the rocker arm and the vertical displacement of the valve is the following:
Substituting , the valve displacement is then the following:
The final kinematic equation is as follows:
2.2. Dynamic Design
Dynamic valvetrain models are crucial for understanding and predicting the behavior of diesel engines. The dynamic model of the valvetrain was developed to analyze the system’s behavior under operating conditions across various rotational speeds. The parameters of stiffness damping and penetration depth were defined in the contact points between the parts. The values of the static and dynamic friction coefficients were also defined.
The multi-mass spring approach used to obtain forces under dynamic conditions is based on the discretization of the spring. In this study, the spring model is defined by dividing the spring mass into five segments to represent a section of the spring wire. This method enables the consideration of spring fluctuation due to internal dynamic effects. The model parameters are the wire dimensions and the Young’s modulus and Poisson’s ratio properties of the material. The torsional stiffness of each wire segment was utilized to assess the equivalent translational spring stiffness. To incorporate the nonlinear behavior of the spring, which arises from the changing number of active coils during a compression, the interaction between the coils was integrated into the model.
To verify a dynamic valvetrain model, the diesel engine dynamic model has created in Figure 3. The results of the measurements were then compared to the predictions of the dynamic valvetrain model. The cam follower motion is governed by the following:
where is the cam follower displacement, is the cam reaction force, is the force transmitted to the pushrod. The force transformation at the pivot gives the following:
where is the lever ratio from cam follower to pushrod, is the cam follower force. The pushrod is defined as a multi-mass system:
is the force transmitted to the rocker arm, is the pushrod displacement. The rocker arm rotates about its pivot, introducing rotational dynamics:
where is the moment of inertia of the rocker arm, is the rocker arm displacement. The spring is subject to spring force, damping, and inertia:
where is the rocker force at the valve side, and is the valve spring force with preload.
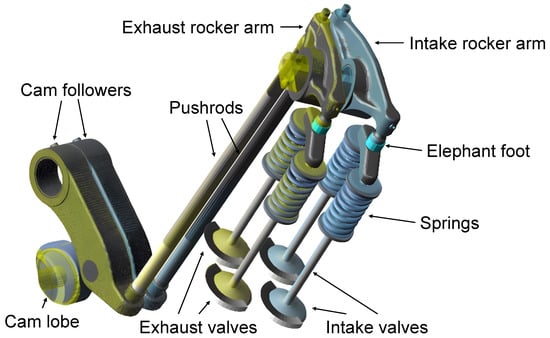
Figure 3.
Dynamic MBD model of valvetrain.
The coupled equations of the system are the following:
where is the overall mass matrix, is the overall damping matrix, is the stiffness matrix, and is the overall force matrix.
The results of the dynamic analysis were used to evaluate key performance and durability parameters of the mechanism. The key measured parameters included the force between the cam and the follower, which was used to assess the risk of separation within the mechanism. The engine speed at which follower separation begins was identified, and the system was deemed safe for brief operation above these speeds. The Hertzian pressure between the cam and the follower was also calculated to evaluate the wear conditions on the cam lobe. Additional forces analyzed included those acting on the bearings of the follower, the push rod, the rocker arm, and the rocker bearing. The relative motion of the elephant foot on the valve bridge and the forces between the valve bridge and the rocker arm were also examined. Furthermore, the drive torque of the valve train for a single cylinder was calculated and the dynamic valve opening profiles were compared to the kinematic profiles. Valve seating velocities and valve backlash were analyzed in relation to seating dynamics. Valve springs were modeled as a mass-elastic system with five degrees of freedom and linear stiffness to accurately capture their dynamic behavior.
Valve springs are critical components that significantly impact engine performance and reliability. The stiffness of valve springs directly influences the engine’s operating dynamics, making it a key parameter in determining both performance and durability. Excessively stiff springs increase engine friction, leading to power losses, while overly soft springs can cause valve float at high engine speeds. Therefore, determining the optimal valve spring stiffness is essential. In this study, a parametric analysis method known as the full factorial optimization methodology was employed to optimize valve spring stiffness. Different spring characteristics were analyzed to identify the most suitable configuration.
The full factorial optimization methodology allows for a systematic variation and evaluation of specific design parameters by considering all possible combinations of factor levels. In this study, the primary parameters affecting spring stiffness—wire diameter, number of coils, free length, and spring diameter—were identified. During the optimization process, these parameters were varied within a defined range, and simulations were conducted for each configuration. The simulation analyses considered performance criteria such as valve float occurrence, spring deformation under different engine speeds, spring force, and dynamic response time.
Based on these analyses, valve opening times were dynamically optimized. The design was validated by correlating the timing results with a thermodynamic model. In addition, alternative designs for the rocker arm were evaluated, and the optimal configuration was achieved by adjusting the spring parameters to achieve the desired performance. This study demonstrates the importance of accurate dynamic valvetrain models for predicting the vibration behavior of diesel engines.
2.3. Model Correlation
The valvetrain system, a complex assembly of interacting components, is a significant source of vibration within an internal combustion engine [14,15,16,17]. Rapid and repetitive movements of the camshaft, followers, pushrods, rocker arms, valves, and springs generate a complex interplay of inertial, impact, frictional, and torsional forces that directly contribute to engine vibration. Impact forces, primarily resulting from valve closing events and potential tappet/follower impacts, transmit impulsive vibrations through the cylinder head and engine block. Simultaneously, inertia forces arising from accelerating and decelerating valvetrain components induce oscillations, while friction within sliding contacts creates irregular vibrations. Torsional vibrations within the camshaft and timing drive system further exacerbate the problem, causing valve timing variations and structural stress. These vibrations are transmitted through the engine structure, which causes increased noise. Precise modeling of the valvetrain is critical to simulating the impact of its behavior on the engine structure and validating experimental data.
The engine test is performed by measuring the vibration acceleration. The validation of the simulation results for the dynamic model in diesel engines was carried out through a structured comparison with the experimental test data on the Horiba test bench shown in Figure 4. The simulation framework was developed using the FEV Virtual Engine software suite, which allowed a detailed finite element model (FEM) of the engine to be constructed in Figure 5. This model incorporated accurate geometric representations of the engine components, such as the cylinder block, crankshaft, camshaft, and mounting points, along with material properties, including stiffness and damping characteristics obtained from the data sheets. In order to calculate the vibration in the system, the modal characteristics of the components at their operating speeds and corresponding frequencies, the directions and magnitudes of the forces depending on time and rpm are defined in the model. In the crank subsystem, connecting rods, pistons, and all bolts and fasteners are modeled with one-dimensional elements. The crankshaft, Torsional Vibration Damper (TVD), and flywheel are modeled with three-dimensional second-order tetrahedral elements. Second-order tetrahedral elements were used to create the finite element model of the engine block. Liners and flywheel housing parts are modeled with second-order tetrahedral elements, and they are connected to each other and to the engine block using one-dimensional and rigid elements. The main bearing caps are connected to the engine block at the respective positions. The simulations generated outputs including vibration acceleration distributions on flywheel housing and crankcase surfaces.

Figure 4.
Engine test bench.

Figure 5.
Vibration measurement points on engine and dynamic model: (a) FEM model vibration request points. (b) Flywheel housing measurement point. (c) Crankcase vibration measurement point.
Experimental validation was carried out on a prototype eight-cylinder diesel engine under test bench conditions that matched the simulation setup. The engine was instrumented with accelerometers to measure surface vibration accelerations. A synchronized data acquisition system recorded the signals at high resolution to ensure an accurate representation of transient behavior. The tests were performed under motored engine operation, with engine speeds ranging from 650 rpm to 1600 rpm. The engine was operated at constant speed by the dynamometer during the measured rpm. Horiba dynamometer is used for test specifications listed in Table 2.

Table 2.
Horiba dynamometer specifications.
To validate the simulation, multiple comparison surfaces were used. Crankcase and flywheel housing are one of the critical components for noise energy [18]. For this reason, measurements were taken from the points of these parts that were closest to the engine mounts. Vibration accelerations were compared in terms of the measurement points specified in the root mean square (RMS). RMS data were applied to quantify the alignment of the simulation results with the test data. Mechanical vibrations were recorded as an RMS on two surfaces with the PCE Instruments PCE-VT 3700 (HAHN+KOLB Werkzeuge GmbH, Ludwigsburg, Germany) vibration data device specifications given in Table 3.

Table 3.
Specifications for accelerometer-PCE-VT 3700.
An iterative refinement process was employed to address any discrepancies between the simulation and the test results. Adjustments were made to the simulation model by refining boundary conditions, updating material properties, and incorporating additional damping effects observed during experimental tests. Input forces were recalibrated as needed to ensure greater accuracy. This iterative approach allowed for progressive improvement of the simulation model, leading to final results that demonstrated close agreement with the experimental data. Specifically, vibration velocities deviated by less than 5%, consistent between simulations and experiments. The validated model provides a solid foundation for valvetrain design optimization.
3. Experimental Verification and Discussion
3.1. Acceleration Measurement
One of the most important parameters for vibration analysis is the amplitude [19]. The amplitude describes the severity of the vibration, so machines with higher amplitudes are more prone to vibrations. The overall vibration measurements are usually expressed in terms of the root mean square amplitude (RMS). RMS amplitude represents the energy of vibration and is directly related to the root mean square abundance. For vibration measurements, it is necessary to select points close to the vibration source [20].
Simulation and test results on flywheel housing correlation are shown in Figure 6. The largest relative difference occurs at 1600 rpm. In general, the simulation values tend to be slightly higher than the test results and the deviations become more pronounced at higher speeds, despite these differences, the variations remain within a reasonable range.
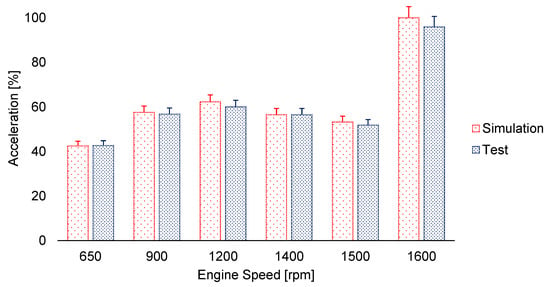
Figure 6.
Test and simulation results on flywheel housing point.
The simulation and test results on the crankcase correlation are shown in Figure 7. The comparison between test and simulation results reveals that the simulation consistently predicts slightly higher values across all rpm levels. The increasing deviation at higher speeds suggests that damping factors and component flexibility models should be fine-tuned to improve simulation accuracy.
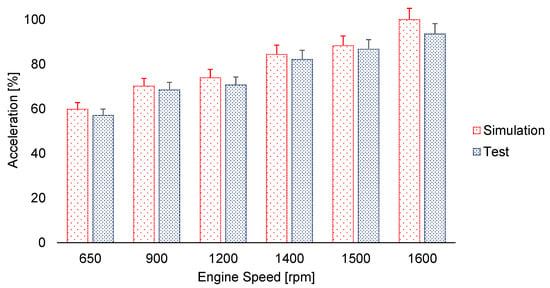
Figure 7.
Test and simulation results on crankcase point.
The differences between experimental and simulation results can be attributed to several factors, including the modeling of components, experimental uncertainties, and model simplifications and assumptions [21]. In the context of this study, the divergence between test and simulation results is attributed to discrepancies in modeling assumptions and the parameters of experimental conditions.
3.2. Lift Profile Optimization
The cam lobe profile determines the valve’s motion and influences acceleration and contact forces, affecting stress levels in components. Slender components like bars and beams in the valve train exhibit flexibility, impacting the system’s dynamics, especially at high speeds [22]. As a result of these dynamic effects, tilt motion on the bridge part, the valve bounce, and no-contact phenomenon conditions occur. In addition, there is a difference between the kinematically targeted lift profile and the dynamically achieved lift. This changes the duration of the targeted valve overlap. Valve overlap is an important engine performance parameter because it provides effective scavenging and is included in the targeted valve lift profile. Valve overlap, defined as the time that both intake and exhaust valves are open simultaneously, is influenced by the dynamic behavior of the valve train. However, in real-world operating conditions, factors such as mechanical limitations and dynamic forces at high engine speeds can prevent the targeted valve overlap from being achieved. During optimization studies, solutions to the valve bounce, which causes deviations from the intended valve lift, help to achieve the desired valve overlap. By optimizing the dynamic opening curves of the valves to be closer to the kinematic profile that represents the theoretically ideal valve lift, valve bounce is reduced, and the desired overlap is maintained. The targeted valve lift profiles shown in Figure 8 were used in the cam lobe design.
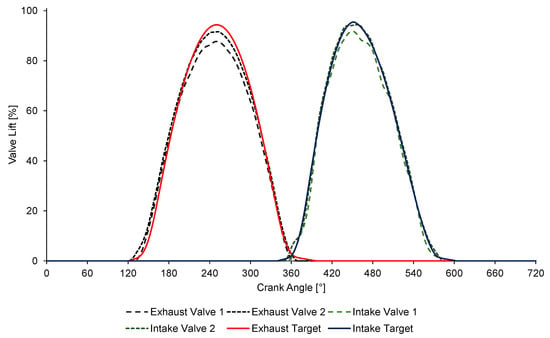
Figure 8.
Targeted valve lift profiles and dynamic valve lift profiles achieved in optimized design.
According to the results of the dynamic analysis of the valve train with the new spring parameters, the thermodynamic targets are met. As a result of the dynamic analysis, the separation between the follower and the lobe, the difference between the valve opening heights and the valve reopening after closing remained within the limits. Simulations were performed to evaluate the elephant foot position at three different points. Design positions are shown in Figure 9. The first position is determined to ensure that the contact zone occurs at the midpoint in the static position when the valve is closed. The second position was determined to ensure that the contact zone occurs at the midpoint of the bridge part, when the valve is at maximum opening. The third position was determined to ensure that the contact zone occurs at the midpoint of the bridge part at the instant of maximum force on the elephant foot.
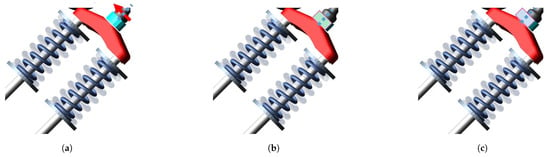
Figure 9.
Vibration measurement points on engine and dynamic model: (a) Contact at midpoint with valve closed. (b) Centered position with the valve at half the maximum opening. (c) Centered position at the moment of maximum force on the valve.
The characteristics of the valve spring, including stiffness and damping, play a vital role in the dynamics of the valvetrain [23]. The spring characteristics are optimized to improve rebound and no-contact points.
3.3. Discussion
The present study explores the optimization of valve effective opening, with the objective of attaining thermodynamic targets. This is achieved by maintaining maximum acceleration in the opening region. However, this approach resulted in separation between the cam lobe and the follower. To address this issue, both the spring tension and lift acceleration was modified. The Version 1 design features no-contact points, where the force between the camshaft and the follower is zero, shown in Figure 10. The Version 2 design indicates that the contact between the cam lobe and the follower is maintained during the lift phase, and concurrently, the amount of force fluctuation is diminished, signifying that the system is more stable.
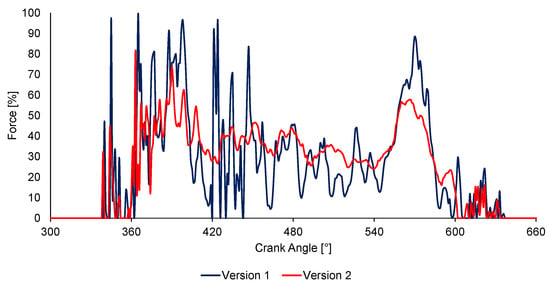
Figure 10.
Force between the cam lobe and the follower.
The reduction in force variations provides a more uniform load on the cam lobe and follower, which reduces Hertzian pressure. Since this force is transferred directly from the crankshaft gear to the camshaft gear, the power demand on the crankshaft is reduced thus increasing the power output of the engine. The elimination of sudden force fluctuations ensures that the valve lift functions with complete accuracy.
Although increased spring forces enabled greater maximum acceleration, this method introduced challenges in manufacturability. The desired curve in the opening and closing regions was achieved by staying within the maximum allowable concavity limits of the machining equipment. However, high acceleration values during the closing phase, particularly at high engine speeds, resulted in valve bounce issue optimized result is shown in Figure 11. In the closing phase 2%, the bouncing is solved. This was mitigated by increasing spring forces, though there was a limit to this solution due to the torque requirements of the camshaft. However, excessive spring forces diverted a substantial portion of the engine’s torque to the camshaft, a result that was sub-optimal.
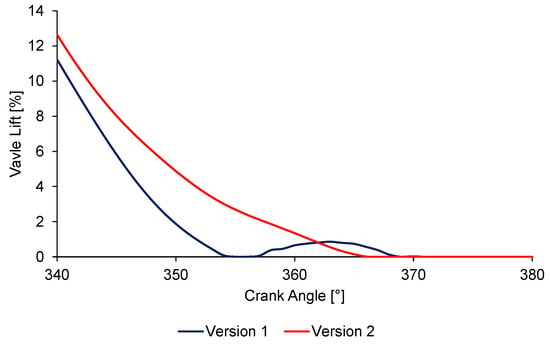
Figure 11.
Enlarged visualization of the valve closing phase.
To address the tilting motion of the valve bridge, which led to uneven opening between the two valves, adjustments were made to the position of the rocker arm. Statically balancing the rocker arm at its midpoint was determined to minimize the tilting motion, ensuring more uniform valve operation.
As shown in Figure 12, the simulation results of the Version 1 design exhibited two distinct peak behaviors, characterized by the initiation of closure and subsequent reopening. The enhanced positioning of the elephant foot in the Version 2 design facilitated the desired behavior of the valve, which began to close after the lift reached its maximum value.
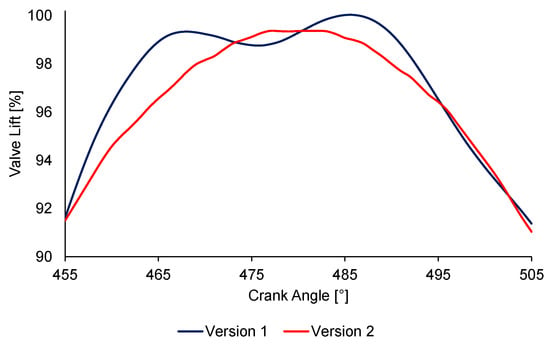
Figure 12.
Enlarged visualization of the maximum valve lift phase.
4. Conclusions
This study proposed an integrated approach that combined MBD modeling and experimental validation to optimize the valvetrain system of a heavy-duty diesel engine. By combining kinematic and dynamic analyses, the research identified and mitigated critical challenges, including valve bounce, no-contact points, and valve-bridge tilting motion. Experimental validation through vibration measurements confirmed the accuracy of the simulation models, demonstrating close correlation with real-world engine performance.
The optimization of cam profiles, spring parameters, and valve bridge geometry resulted in significant improvements in stability, reducing unwanted oscillations and ensuring more efficient valve operation. The refined model successfully predicted and controlled key parameters affecting engine performance, including valve lift and timing accuracy. Furthermore, the study highlighted the importance of integrating numerical modeling with experimental validation to enhance valvetrain reliability, providing a robust framework for future advancements in valvetrain design, contributing to the overall efficiency of heavy-duty diesel engines.
Consequently, future research has the potential to explore further refinements in timing and accessory drive mechanisms and torsional vibration properties, with the objective of enhancing valvetrain performance under varying operational conditions.
Author Contributions
Conceptualization, M.A.Ö. and O.Ö.; methodology, M.A.Ö. and O.Ö.; software, M.A.Ö.; validation, M.A.Ö. and O.Ö.; formal analysis, M.A.Ö. and O.Ö.; investigation, M.A.Ö. and O.Ö.; resources, M.A.Ö. and O.Ö.; data curation, M.A.Ö.; writing—original draft preparation, M.A.Ö. and O.Ö.; writing—review and editing, M.A.Ö. and O.Ö.; visualization, M.A.Ö.; supervision, O.Ö.; project administration, O.Ö.; funding acquisition, M.A.Ö. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors would like to acknowledge that this paper is submitted in partial fulfilment of the requirements for PhD degree at Yildiz Technical University. This study is based on the work carried out as part of the Novel 8V160B engine development project developed within TÜBİTAK RUTE. The authors would like to note that all numerical values in this study have been normalized to maintain the confidentiality of the project. We express our gratitude to TÜBİTAK RUTE for providing the resources and support that made this research possible.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FEM | Finite Element Model |
| MBD | Multibody Dynamics |
| MDI | Mechanical Dynamics, Incorporated |
| NVH | Noise Vibration Harshness |
| RMS | Root Mean Square |
| rpm | revolution per minute |
| TVD | Torsional Vibration Damper |
References
- Roshan, R.; Priest, M.; Neville, A.; Morina, A.; Xia, X.; Green, J.; Warrens, C.; Payne, M. Friction modelling in an engine valve train considering the sensitivity to lubricant formulation. Proc. Inst. Mech. Eng. Part J Eng. Tribol. 2009, 223, 413–424. [Google Scholar] [CrossRef]
- Lee, W.; Jung, T.Y.; Lee, S. Dynamic Characteristics Prediction Model for Diesel Engine Valve Train Design Parameters Based on Deep Learning. Electronics 2023, 12, 1806. [Google Scholar] [CrossRef]
- Zhou, C.; Hu, B.; Chen, S.; He, L. An enhanced flexible dynamic model and experimental verification for a valve train with clearance and multi-directional deformations. J. Sound Vib. 2017, 410, 249–268. [Google Scholar] [CrossRef]
- Hu, B.; Zhou, C.; Wang, H.; Yin, L. Prediction and validation of dynamic characteristics of a valve train system with flexible components and gyroscopic effect. Mech. Mach. Theory 2021, 157, 104222. [Google Scholar] [CrossRef]
- Sarıdemir, S.; Saruhan, H. Experimental analysis of maximum valve lift effects in cam-follower system for internal combustion engines. J. Mech. Sci. Technol. 2014, 28, 3443–3448. [Google Scholar] [CrossRef]
- Ali, M.Y.; Sanders, T.; Ejakov, M.A.; Adimi, R.; Boucke, A.; Lang, J.; Knoll, G. Effect of valvetrain components misalignment on valve and guide interactions in automotive engines. SAE Int. J. Engines 2017, 10, 668–679. [Google Scholar] [CrossRef]
- Andreatta, É.C.; Pederiva, R. Valve Train Kinematic and Dynamic Simulation; Technical Report, SAE Technical Paper; SAE International: Warrendale, PA, USA, 2016. [Google Scholar]
- Busch, M. Stability analysis for nonlinear valve train systems in automotive engines. Arch. Appl. Mech. 2021, 91, 823–840. [Google Scholar] [CrossRef]
- John, A.P.; Agarwal, V.K. Evaluation and Comparative Study of ValveTrain Layouts with Different Rocker Ratio; Technical Report; SAE Technical Paper: Warrendale, PA, USA, 2014. [Google Scholar]
- Eret, A. Valve Dynamic Investigations and Measurements. In Dynamic and Fatigue Assessment of Heavy-Duty Engine Valves; Springer: Berlin/Heidelberg, Germany, 2024; pp. 73–133. [Google Scholar]
- Ryan, R. ADAMS—Multibody system analysis software. In Multibody Systems Handbook; Springer: Berlin/Heidelberg, Germany, 1990; pp. 361–402. [Google Scholar]
- Ortmann, C.; Skovbjerg, H. Powertrain analysis applications using ADAMS/Engine powered by FEV Part I: Valve spring. In Proceedings of the International Adams Users Conference, Rome, Italy, 15–27 November 2000. [Google Scholar]
- Ernst, R.; Schamel, A.R.; Meyer, J. Advanced optimization techniques in valvetrain design. SAE Trans. 1993, 102, 1835–1851. [Google Scholar]
- Yakovenko, A.; Shatrov, M.; Alekseev, I.; Predein, A.; Trofimenko, Y.V. Research of diesel structure-borne noise using modern modeling methods. In Proceedings of the 2022 Systems of Signals Generating and Processing in the Field of on Board Communications, Moscow, Russia, 15–17 March 2022; IEEE: Piscatway, NJ, USA, 2022; pp. 1–5. [Google Scholar]
- Klarin, B.; Vock, C.; Nolfe, C.; De Stefanis, D.; Cardone, C.; Pappalardo, T.; Grasso, C. Enhanced Power Unit NVH Simulation with MBD Solver AVL EXCITE; Technical Report; SAE Technical Paper: Warrendale, PA, USA, 2005. [Google Scholar]
- Liang, J.; Mao, Z.; Liu, F.; Kong, X.; Zhang, J.; Jiang, Z. Multi-sensor signals multi-scale fusion method for fault detection of high-speed and high-power diesel engine under variable operating conditions. Eng. Appl. Artif. Intell. 2023, 126, 106912. [Google Scholar] [CrossRef]
- Lin, T.; Tan, A. Characterizing the signal pattern of a four-cylinder diesel engine using acoustic emission and vibration analysis. In Proceedings of the World Conference on Acoustic Emission-2011 (WCAE-2011), Beijing, China, 24–26 August 2011; WCAE: London, UK, 2011; pp. 506–515. [Google Scholar]
- Lakshminarayanan, P.; Agarwal, A.K. Design and Development of Heavy Duty Diesel Engines: A Handbook; Springer Nature: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Nithin, S.; Hemanth, K.; Shamanth, V. A review on combustion and vibration condition monitoring of IC engine. Mater. Today Proc. 2021, 45, 65–70. [Google Scholar] [CrossRef]
- Ahirrao, N.; Bhosle, S.; Nehete, D. Dynamics and vibration measurements in engines. Procedia Manuf. 2018, 20, 434–439. [Google Scholar] [CrossRef]
- Armentani, E.; Caputo, F.; Esposito, L.; Giannella, V.; Citarella, R. Multibody simulation for the vibration analysis of a turbocharged diesel engine. Appl. Sci. 2018, 8, 1192. [Google Scholar] [CrossRef]
- Hu, B.; Li, Y.; Yin, L. Theoretical and Experimental Analysis of Dynamic Characteristics for a Valve Train System. Sensors 2021, 21, 6328. [Google Scholar] [CrossRef] [PubMed]
- Jelenschi, L.; Scutaru, M.L.; Marin, M.; Cofaru, C. Modelling the Valvetrain of the Car Engine to Study the Effects of Valve Rotation. Appl. Sci. 2022, 12, 3393. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).