Parameter Study and Engineering Verification of the Hardening Soil Model with Small-Strain Stiffness for Loess in the Xi’an Area
Abstract
1. Introduction
2. The Parameters and Introduction of the Hardening Soil Model with Small-Strain Stiffness Model
3. The Indoor Tests on Loess Materials
3.1. Test Purpose
3.2. Test Procedure
- (1)
- Standard consolidation test
- (a)
- In the consolidation container, the following were placed in order from bottom to top: large permeable stones, filter paper, a ring-knife containing the saturated soil sample (with the ring-knife facing downward), filter paper, and small permeable stones. Then, the guide ring was placed and covered with the pressure cap. The permeable stones and filter paper had been pre-soaked to moisten them.
- (b)
- Water was injected into the grooves around the ring-knife to ensure that the saturated sample remained unaffected by water evaporation during consolidation. During the test, the water in the grooves was replenished as needed.
- (c)
- The crossbeam used to apply vertical pressure was lowered, ensuring that the bolts at the bottom of the crossbeam were securely fitted into the concave holes on the upper part of the pressure cover. Then, the dial indicator was installed and adjusted to zero.
- (d)
- The vertical load was applied in five sequential stages: 50 kPa, 100 kPa, 200 kPa, 400 kPa, and 800 kPa. For each load level, the dial indicator reading was allowed to stabilize before the next load level was applied.
- (e)
- The readings of the dial indicator were recorded after each level of load had stabilized.
- (2)
- Triaxial consolidation drained shear test
- (a)
- Water-head saturation: The water head outside the pressure chamber was set to approximately 1 m higher than the top of the sample. Under the influence of gravitational potential energy, water gradually seeped upward from the bottom of the sample, while gas was expelled through the exhaust pipe at the top of the sample.
- (b)
- Back-pressure saturation: Water-head saturation often fails to fully saturate the sample, making back-pressure saturation necessary. The back pressure was set to 100 kPa, the confining pressure to 110 kPa, and the test duration to 3 h.
- (c)
- B-value detection: The back pressure and undrained conditions were kept unchanged, and the confining pressure was increased by 30 kPa. Then, the pore water pressure coefficient B was measured. When , the sample was considered saturated.
- (d)
- Consolidation: The back pressure was maintained at the level of the saturated back pressure, and the effective confining pressure was set to 100 kPa, meaning that the confining pressure was 100 kPa greater than the back pressure. The consolidation time was 1 to 2 days.
- (e)
- Drained shear: The confining pressure was kept constant, and the strain rate was controlled with an equal strain rate of 0.008 mm/min to ensure that the pore water in the sample was fully drained. The test was stopped when the strain of the sample reached 20% or when the sample exhibited significant strain softening.
- (3)
- Triaxial consolidation drained loading−unloading shear test
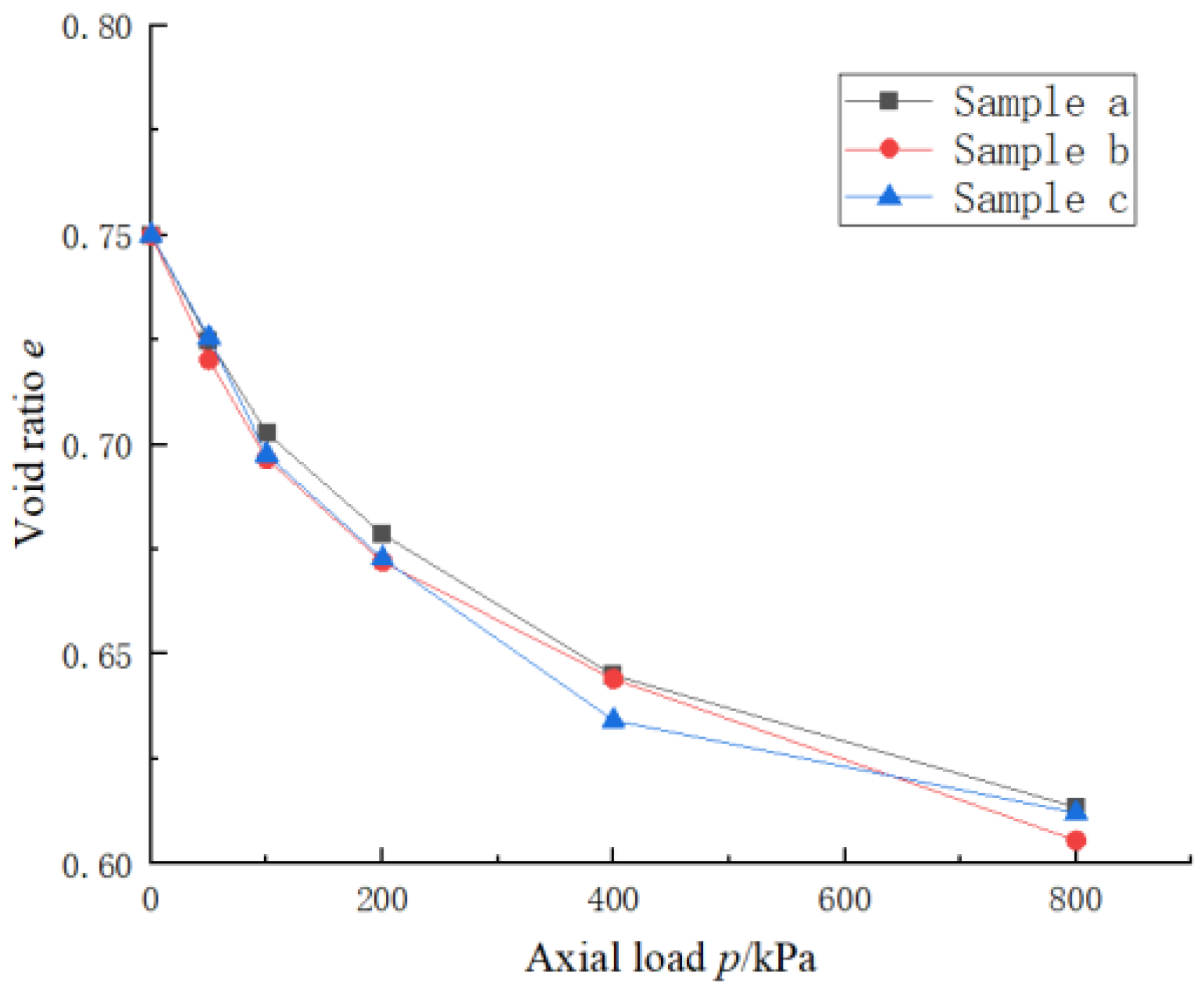
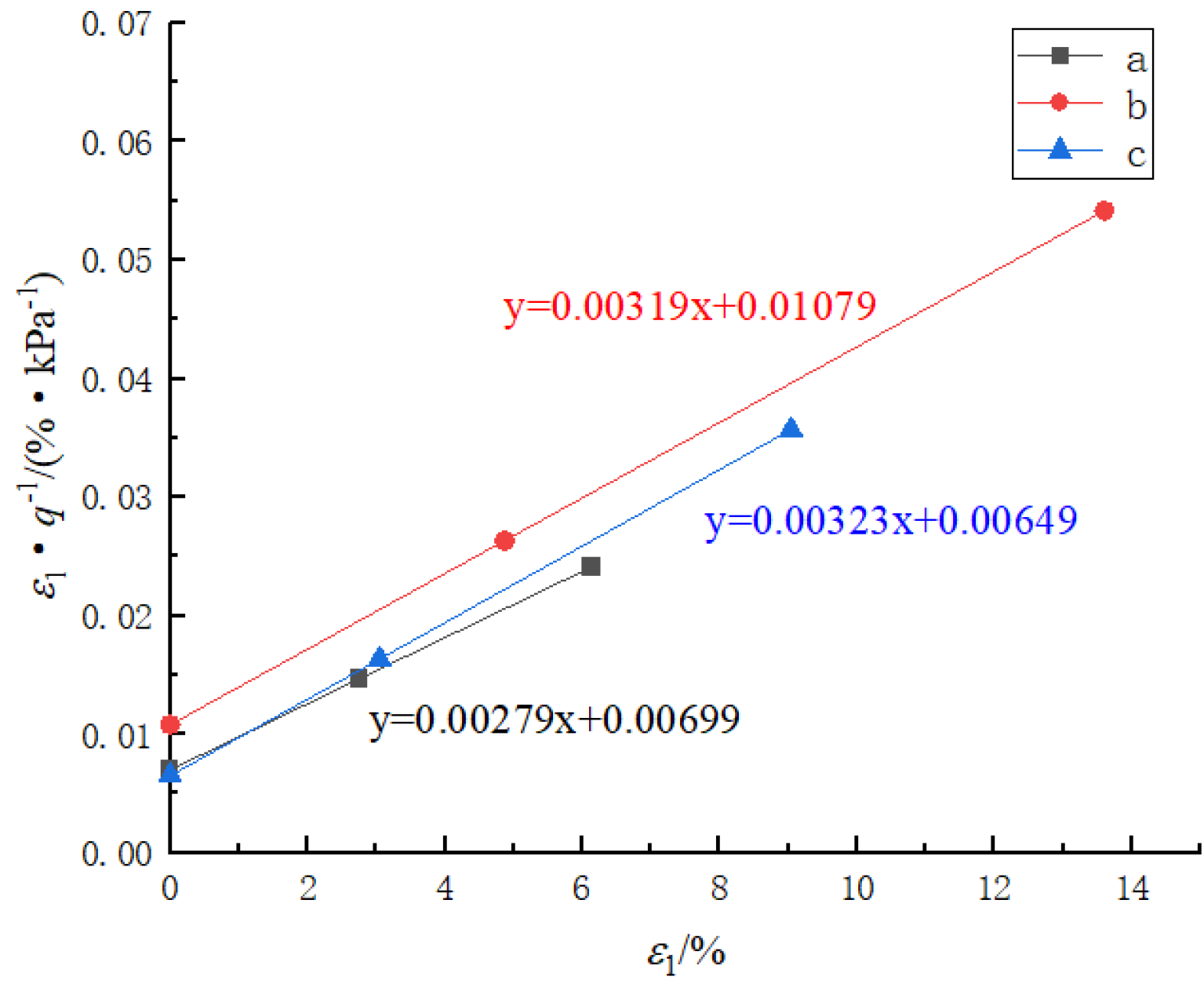
3.3. Tests Result
4. Selection of HSS Model Parameters
5. Engineering Verification
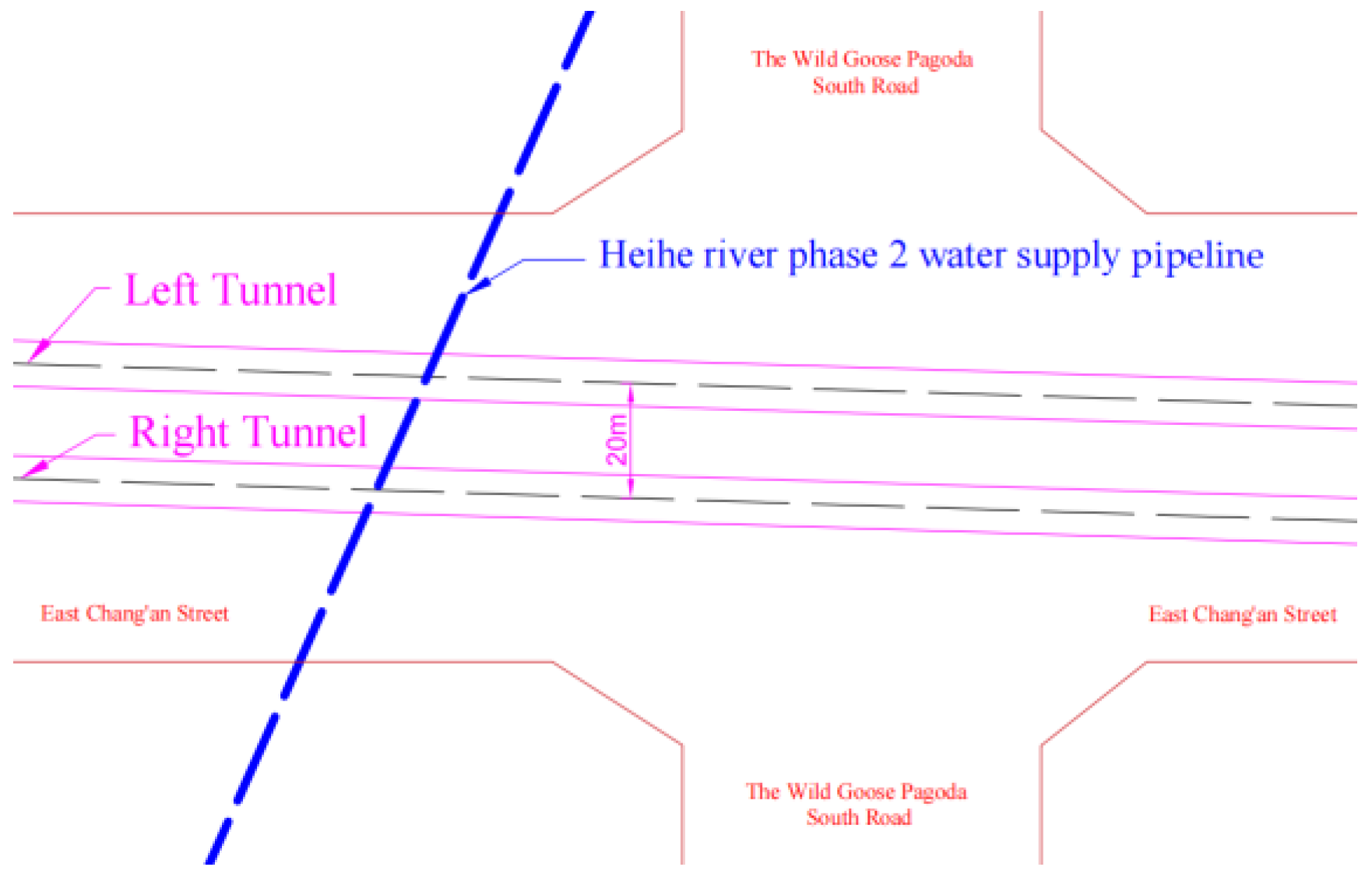
5.1. Project Overview
5.2. Modeling
5.3. Analysis of Simulated Result
6. Conclusions
- (1)
- The proportional relationship between the small-strain moduli in the HSS model for Xi’an loess was obtained through indoor tests. Numerical simulations were performed for various values of the initial dynamic shear modulus . Through a comparison of the simulation results with the field monitoring data, it was found that when the ratio of , , , and in the HSS model is 1:0.96:1.25:6.2:12.4, and , the simulation results are closest to the field monitoring data. This can provide a reference for similar engineering analyses in the Xi’an loess region.
- (2)
- By fitting the data, a functional relationship between the coefficient of earth pressure at rest and the water content w, void ratio e, and over-consolidation ratio OCR for loess was established. The deviation between the values calculated using this fitting formula and the test data is within 15%, providing an empirical method for determining the K value of Xi’an loess.
- (3)
- Through numerical analysis of the section between Shen Zhou 2nd Road Station and Dong Chang’an Street Station on Xi’an Metro Line 15, it was found that compared to the M−C and HS models, the HSS model results are closer to the field monitoring data. The HSS model is more suitable for projects with stricter settlement requirements, and it also validates the feasibility of applying the HSS parameters proposed in this paper.
- (4)
- The above conclusions are derived from the study of loess in the Xi’an area, and further research is needed to determine whether they are applicable to loess in other regions. Future studies will conduct experiments on loess from more regions and at different depths to analyze and summarize the patterns of HSS model parameters for loess in various areas.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jafari, M. System identification of a soil tunnel based on a hybrid artificial neural network–numerical model approach. Iran. J. Sci. Technol.-Trans. Civ. Eng. 2020, 44, 560–572. [Google Scholar] [CrossRef]
- Zhao, X.; Li, Z.; Dai, G.; Wang, H.; Yin, Z.; Cao, S. Numerical Study on the Effect of Large Deep Foundation Excavation on Underlying Complex Intersecting Tunnels. Appl. Sci. 2022, 12, 4530. [Google Scholar] [CrossRef]
- Han, Y.; Ye, W.; Wei, Q. Research on the Influence of New Shield Tunnel to Adjacent Existing Tunnel. Appl. Mech. Mater. 2013, 295–298, 2985–2989. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, M. Geotechnical influence on existing subway tunnels induced by multiline tunneling in Shanghai soft soil. Comput. Geotech. 2014, 56, 121–132. [Google Scholar] [CrossRef]
- Atkinson, J.; Sallförs, G. Experimental determination of stress-strain-time characteristics in laboratory and in-situ tests. General Report. In Proceedings of the 10th European Conference on Soil Mechanics and Foundation Engineering, Florence, Italy, 26–30 May 1991; pp. 915–956. [Google Scholar]
- Wang, Z.; Wang, H.; Qi, K.; Zai, J. Summary and evaluation of experimental investigation on small strain of soil. Rock Soil Mech. 2007, 28, 1518–1524. [Google Scholar]
- Burland, J. Ninth Laurits Bjerrum Memorial Lecture: “Small is beautiful”—The stiffness of soils at small strains. Can. Geotech. J. 1989, 26, 499–516. [Google Scholar] [CrossRef]
- Attewell, P.; Farmer, I. Ground deformations resulting from shield tunnelling in London Clay. Can. Geotech. J. 1974, 11, 380–395. [Google Scholar] [CrossRef]
- Mair, R. Developments in geotechnical engineering research: Application to tunnels and deep excavations. In Proceedings of the Institution of Civil Engineers, London, UK, 20 January 1993; pp. 27–41. [Google Scholar]
- Zheng, G.; Yang, X.; Zhou, H.; Du, Y.; Sun, J.; Yu, X. A simplified prediction method for evaluating tunnel displacement induced by laterally adjacent excavations. Comput. Geotech. 2018, 95, 119–128. [Google Scholar] [CrossRef]
- Ardakani, A.; Bayat, M.; Javanmard, M. Numerical modeling of soil nail walls considering Mohr Coulomb, hardening soil and hardening soil with small-strain stiffness effect models. Geomech. Eng. 2014, 6, 391–401. [Google Scholar] [CrossRef]
- Mu, L.; Huang, M. Small strain based method for predicting three-dimensional soil displacements induced by braced excavation. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2016, 52, 12–22. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, W.; Goh, A. Numerical investigation of pile responses caused by adjacent braced excavation in soft clays. Int. J. Geotech. Eng. 2018, 15, 783–797. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, G.; Zhang, L.; Jiang, H. Application of HSS Model in Shield Simulation and Parameter Sensitivity Research. Chin. J. Undergr. Space Eng. 2020, 16, 618–625. [Google Scholar]
- Xiao, S.; Xu, M.; Lan, R. Choice of Soil Constitutive Models in Numerical Analysis of Foundation Pit Excavation Based on FLAC3D. In Proceedings of the 2023 International Conference on Green Building, Civil Engineering and Smart City (GBCESC 2023); Lecture Notes in Civil Engineering. Springer: Singapore, 2023; Volume 328. [Google Scholar] [CrossRef]
- Wang, T.; Deng, T.; Deng, Y.; Yu, X.; Zou, P.; Deng, Z. Numerical Simulation of Deep Excavation Considering Strain-Dependent Behavior of Soil: A Case Study of Tangluo Street Station of Nanjing Metro. Int. J. Civil. Eng. 2023, 21, 541–550. [Google Scholar] [CrossRef]
- Hsiung, B.; Dao, S. Evaluation of Constitutive Soil Models for Predicting Movements Caused by a Deep Excavation in Sands. Electron. J. Geotech. Eng. 2014, 19, 17325–17345. [Google Scholar]
- Liang, F.; Jia, Y.; Ding, Y.; Huang, M. Experimental study on parameters of HSS model for soft soils in Shanghai. Chin. J. Geotech. Eng. 2017, 39, 269–278. [Google Scholar]
- Gu, X.; Wu, R.; Liang, F.; Gao, G. On HSS model parameters for Shanghai soils with engineering verification. Rock Soil Mech. 2021, 42, 833–845. [Google Scholar]
- Benz, T. Small Strain Stiffness of Soils and Its Numerical Consequences. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2006. [Google Scholar]
- Hardin, B.O.; Black, W.L. Closure to “Vibration Modulus of Normally Consolidated Clay”. J. Soil. Mech. Found. Div. 1969, 95, 1531–1537. [Google Scholar] [CrossRef]
- Hardin, B.O.; Drnevich, V.P. Shear Modulus and Damping in Soils: Design Equations and Curves. J. Soil. Mech. Found. Division. 1972, 98, 667–692. [Google Scholar] [CrossRef]
- Jian, T.; Kong, L.; Bo, W.; Wang, J.; Liu, B. Experimental study on the influence of water content on the small strain shear modulus of undisturbed loess. Chin. J. Geotech. Eng. 2022, 44, 160–165. [Google Scholar]
- Zhong, P. Research on Deformation Characteristics of Loess Foundation Pit Excavation Based on HSS Model. Master’s Thesis, Chang’an University, Xi’an, China, 2023. [Google Scholar]
- Liu, D. Parameter Inversion of Small Strain Hardened Soil Constitutive Model Based on GA-BP and Its Application in Foundation Pit Engineering. Master’s Thesis, Chang’an University, Xi’an, China, 2022. [Google Scholar]
- Liao, J.; Zhu, Q.; Wang, Z.; Dai, Z. Comparison of Simulating Loess Deformation by Two Advanced and Conventional Constitutive Models. Chin. J. Undergr. Space Eng. 2023, 19, 784–792. [Google Scholar]
- Li, L.; Liu, J.; Li, K.; Huang, H.; Ji, X. Study of parameters selection and applicability of HSS model in typical stratum of Jinan. Rock Soil Mech. 2019, 40, 4021–4029. [Google Scholar] [CrossRef]
- Lu, Y. Research on the Impact and Control Measures of Shield Tunnel Construction on Adjacent Bridges Based on HSS Model; University of Jinan: Jinan, China, 2018. [Google Scholar]
- DG/TJ 508–61–2018; Technical Code for Excavation Engineering. Tongji University Press: Shanghai, China, 2018.
- Xu, W.; Liu, C.; Hu, K.; Fan, Y.; Tai, J.; Ren, X.; Feng, X. Experimental study on parameters of hardening soil small-strain model for soft soil in Wuhan. Saf. Environ. Eng. 2024, 31, 88–99. [Google Scholar] [CrossRef]
- Lin, D. Experimental Study and Engineering Application of Small Strain Soil Hardening Model Parameters. Master’s Thesis, Zhejiang University, Zhejiang, China, 2022. [Google Scholar] [CrossRef]
- Meng, R. Parameter tests and engineering applications of small-strain hardening soil model of mucky silty clay in Hangzhou. J. Chengdu Univ. Technol. Sci. Technol. Ed. 2024, 51, 303–315. [Google Scholar]
- Lu, T.; Liu, S.; Cai, G.; Wu, K.; Li, Z. Method and application of parameter determination for small strain hardened soil model based on SCPTU testing. J. Ground Improv. 2023, 5, 451–459. [Google Scholar]
- Wang, X.; Gu, X.; Liu, H.; Lai, H.; Wu, C. Experimental Study on Main Parameters of HSS Model for Marine Soil in Dafeng Sea Area, Jiangsu Province. Mech. Eng. 2024, 46, 316–322. [Google Scholar]
- Dong, X.; Zhou, F.; Zhu, R.; Wang, X.; Zeng, L. Sensitivity analysis and determination method of parameters for small strain soil hardening model. Sci. Technol. Eng. 2024, 24, 6366–6376. [Google Scholar]
- Rafa, S. Cyclic lateral response of piles in dry sand: Effect of pile slenderness. In Proceedings of the Seventh International Jordanian Civil Engineering Conference (JICEC07) Reconstruction of Damaged Zones “The Role of Civil Engineering”, Chengdu, China, 9–11 May 2017. [Google Scholar]
- Brinkgreve, R.B.J.; Kappert, M.H.; Bonnier, P.G. Hysteretic damping in a small-strain stiffness model. Environ. Sci. 2007, 737–742. Available online: https://www.researchgate.net/profile/R-Brinkgreve/publication/267411874_Hysteretic_damping_in_a_small-strain_stiffness_model/links/54b4edbc0cf26833efd0453b/Hysteretic-damping-in-a-small-strain-stiffness-model.pdf (accessed on 2 November 2024).
- Fernando, S. Importance of small-strain stiffness on the prediction of the displacements of a flexible retaining wall on stiff clay. In Proceedings of the 17th European Conference on Soil Mechanics and Geotechnical Engineering, ECSMGE 2019—Proceedings, Reykjavik, Iceland, 1–6 September 2019. [Google Scholar]
- Peteris, S.; Kaspars, B. Applicability of Small Strain Stiffness Parameters for Pile Settlement Calculation. Procedia Eng. 2017, 172, 999–1006. [Google Scholar] [CrossRef]
- Kima, T.; Jung, Y. Optimizing Material Parameters to Best Capture Deformation Responses in Supported Bottom-up Excavation: Field Monitoring and Inverse Analysis. KSCE J. Civ. Eng. 2022, 26, 3384–3401. [Google Scholar] [CrossRef]
- Jesús, F.; Cláudio, P. Non-linear critical speed in high-speed ballasted railways with ground reinforcement. Transp. Geotech. 2024, 48, 101325. [Google Scholar]
- Wang, Y. Study on Triaxial Shear Characteristics of Loess Under K0 Consolidation Conditions. Master’s Thesis, Chang’an University, Xi’an, China, 2023. [Google Scholar] [CrossRef]
- Bolton, M. The strength and dilatancy of sands. Géotechnique 1986, 36, 65–78. [Google Scholar] [CrossRef]
- Zhang, W.; Goh, A.; Feng, X. A simple prediction model for wall deflection caused by braced excavation in clays. Comput. Geotech. 2015, 63, 67–72. [Google Scholar] [CrossRef]
- Brinkgreve, R.; Kumarswamy, S.; Swolfs, W. PLAXIS Version 2015 Manual. The Netherlands. 2015. Available online: https://pdfcoffee.com/plaxis-10-pdf-free.html (accessed on 2 November 2024).
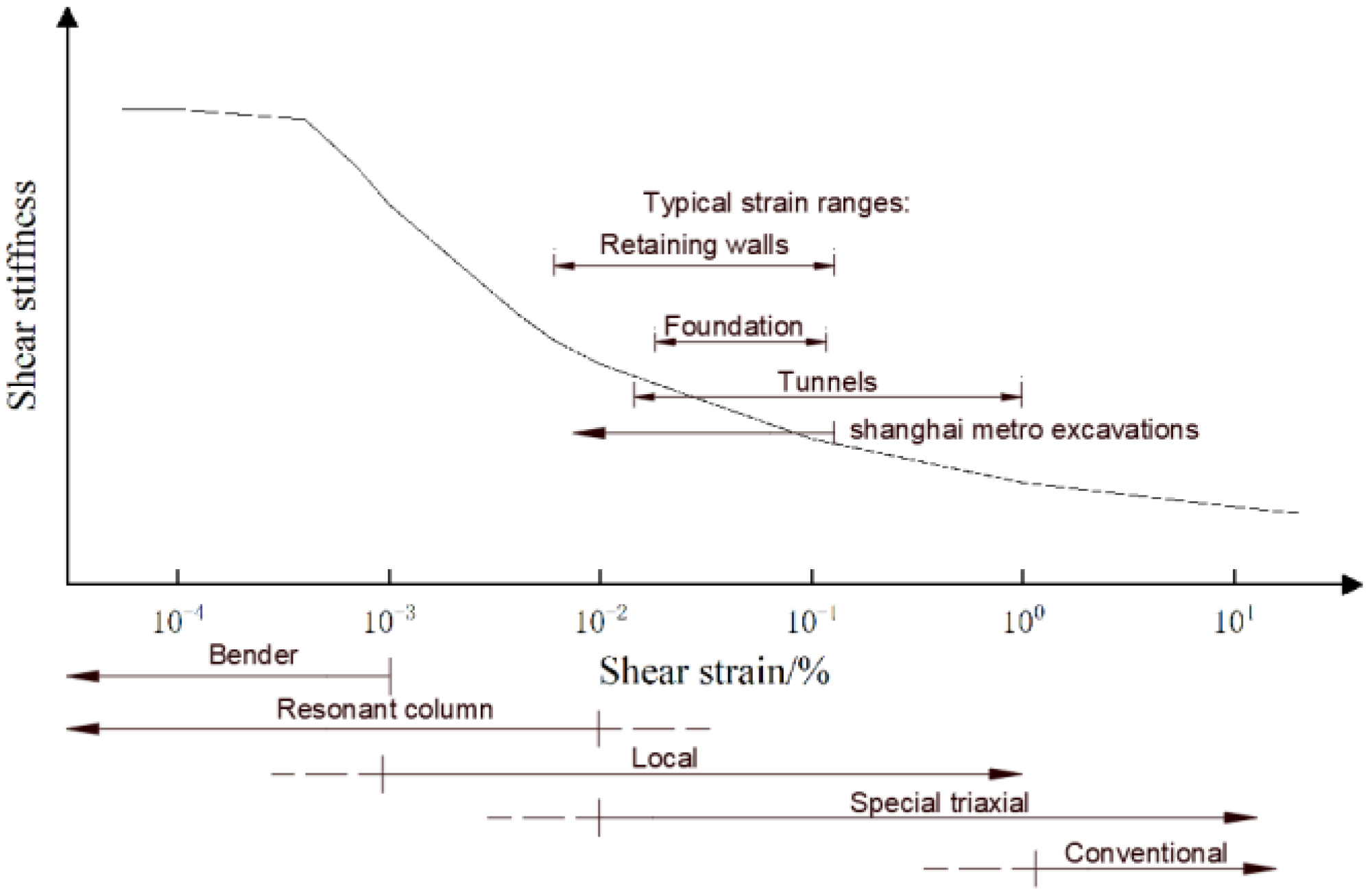







| Model Category | Elasticity or Plasticity | Shear Hardening | Compression Hardening | Dilatancy | Small-Strain Characteristic | Stress Path Dependence |
|---|---|---|---|---|---|---|
| Linear Elastic | Elasticity | × | × | × | × | × |
| D−C | Elasticity | √ | √ | × | × | √ |
| M−−C | Perfect Elastoplasticity | × | × | √ | × | × |
| DP | Elastoplasticity | √ | × | √ | × | × |
| HS | Plasticity | √ | √ | √ | × | √ |
| HSS | Plasticity | √ | √ | √ | √ | √ |
| Parameter | Parameter Name | HS | HSS |
|---|---|---|---|
| Effective cohesion of soil | √ | √ | |
| Effective internal friction angle of soil | √ | √ | |
| Dilation angle of soil | √ | √ | |
| Failure ratio as determined by triaxial drainage shear test | √ | √ | |
| Loading−unloading Poisson’s ratio | √ | √ | |
| Initial coefficient of earth pressure at rest | √ | √ | |
| Reference stress | √ | √ | |
| m | Power exponent related to the modulus stress | √ | √ |
| Reference secant modulus as determined by triaxial consolidation drainage shear test | √ | √ | |
| Tangent modulus under reference stress as determined by standard consolidation test | √ | √ | |
| Loading and unloading modulus as determined by triaxial drainage shear loading−unloading test | √ | √ | |
| Initial dynamic shear modulus | - | √ | |
| Shear strain corresponding to the attenuation of shear modulus to 70% of the initial shear modulus | - | √ |
| Soil Sample | Dry Density | Water Content w/% | Void Ratio /m |
|---|---|---|---|
| Loess | 1.562 | 21 | 0.75 |
| Region | Soil Sample | ||||
|---|---|---|---|---|---|
| Gaoxiong [17] | Sand | - | 1 | 3 | 2.42 |
| Tongchuan [24] | Loess | 0.93 | 12.46 | 7.6 | 2.23 |
| Xi’an [25] | Loess | 1.77 | 1.61 | 5.29 | 1.73 |
| Yan’an [26] | Loess | - | 1.2 | 3 | 3 |
| Jinan [27] | Clay | 1 | 1 | 8 | 1.5 |
| Jinan [28] | Silty clay | - | 0.91 | 6.97 | 1.74 |
| Shanghai [18] | Soft clay | 0.63~1.06 | 1.08~1.2 | 6.7~11.6 | 0.8~1.2 |
| Shanghai [29] | Clay | 0.9 | 1.2 | 6~8 | 2.5~4.9 |
| Wuhan [30] | Silty clay | 0.7~0.8 | 0.7~1.5 | 3.7~5.8 | 2.1~3.0 |
| Hangzhou [31] | Clay | 0.92 | 1.18 | 6.53 | 2 |
| Hangzhou [32] | Silty clay | 0.73~1 | 1~2.22 | 5~8.97 | 1.3~3 |
| Suzhou [33] | Silty clay, Silt | - | 0.8 | 4 | 3.8~4.55 |
| Yancheng [34] | Silty clay | 0.84 | 1.5 | 5.56 | 1.57~1.73 |
| Changzhou [35] | Clay, Silty clay | - | 1.33~1.50 | 3.6~4.3 | 1.6~2.0 |
| Paris, France [36] | Sand | - | 1 | 2.5 | 1.89 |
| London, Britain [37] | Clay | - | 2 | 5.3 | 4.16 |
| Lisbon, Portugal [38] | Stiff clay | - | 1 | 3 | 2.3 |
| Jurmala, Latvia [39] | Subglacial till | - | 1 | 3 | 2.96 |
| Incheon, South Korea [40] | Sediment | - | 1.25 | 3 | 2.65 |
| Ledsgård, Sweden [41] | Clay | - | 1 | 3 | 2.53~3.03 |
| Soil Layer Name | Unit Weight | Natural Water Content | Void Ratio | Over-Consolidation Ratio | Compression Modulus | Consolidated Quick Shear Test | |
|---|---|---|---|---|---|---|---|
| Cohesion | Internal Friction Angle | ||||||
| w | e | OCR | c | ||||
| % | - | - | MPa | kPa | |||
| I Plain Fill | 15.7 | - | - | - | - | 0 | 5.0 |
| II 3-1 New Loess | 16.97 | 19.5 | 0.887 | 2.41 | 10.1 | 34.0 | 23.5 |
| III 3-2 Paleosol | 18.52 | 18.7 | 0.713 | 1.34 | 11.2 | 34.0 | 24.0 |
| IV 4-1-1 Old Loess | 16.87 | 21.2 | 0.925 | 1.30 | 9.7 | 34.0 | 24.0 |
| V 4-1-2 Old Loess | 19.52 | 21.2 | 0.768 | 1.03 | 6.6 | 33.5 | 22.5 |
| VI 4-2-2 Old Loess | 19.72 | 24.1 | 0.688 | 1.01 | 7.5 | 34.0 | 24.0 |
| Soil Layer Name | ||||
|---|---|---|---|---|
| II 3-1 New Loess | 9.7 | 12.6 | 62.6 | 0.40 |
| III 3-2 Paleosol | 10.8 | 14 | 69.4 | 0.39 |
| IV 4-1-1 Old Loess | 9.3 | 12.1 | 60.1 | 0.43 |
| V 4-1-2 Old Loess | 6.3 | 8.3 | 40.9 | 0.43 |
| VI 4-2-2 Old Loess | 7.2 | 9.4 | 46.5 | 0.47 |
| Structure | Thickness | Unit Weight | Elastic Modulus | Poisson’s Ratio |
|---|---|---|---|---|
| m | GPa | - | ||
| Lining of tunnel | 0.35 | 24.1 | 34.5 | 0.2 |
| Lining of Heihe Water Pipeline | 0.3 | 23.5 | 25.5 | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; Du, Q. Parameter Study and Engineering Verification of the Hardening Soil Model with Small-Strain Stiffness for Loess in the Xi’an Area. Appl. Sci. 2025, 15, 1278. https://doi.org/10.3390/app15031278
Hu J, Du Q. Parameter Study and Engineering Verification of the Hardening Soil Model with Small-Strain Stiffness for Loess in the Xi’an Area. Applied Sciences. 2025; 15(3):1278. https://doi.org/10.3390/app15031278
Chicago/Turabian StyleHu, Jiayuan, and Qinwen Du. 2025. "Parameter Study and Engineering Verification of the Hardening Soil Model with Small-Strain Stiffness for Loess in the Xi’an Area" Applied Sciences 15, no. 3: 1278. https://doi.org/10.3390/app15031278
APA StyleHu, J., & Du, Q. (2025). Parameter Study and Engineering Verification of the Hardening Soil Model with Small-Strain Stiffness for Loess in the Xi’an Area. Applied Sciences, 15(3), 1278. https://doi.org/10.3390/app15031278






