A Data-Driven Method for Determining DRASTIC Weights to Assess Groundwater Vulnerability to Nitrate: Application in the Lake Baiyangdian Watershed, North China Plain
Abstract
1. Introduction
2. Methodology
2.1. Modification of the DRASTIC Model
2.2. Revision of Rating Scores and Weights
2.2.1. Common Weighting Methods
2.2.2. Modification of the Weights Based on the Data-Driven Method
2.2.3. Monte Carlo Method
2.2.4. Genetic Algorithm
2.3. Harmonization of Scales
2.4. Verification of the Vulnerability Assessment Performance
3. Case Study
3.1. Study Area
3.2. Dataset and Computation
3.2.1. Nitrate Concentration Data Collection
3.2.2. Hydrogeological Parameter Dataset
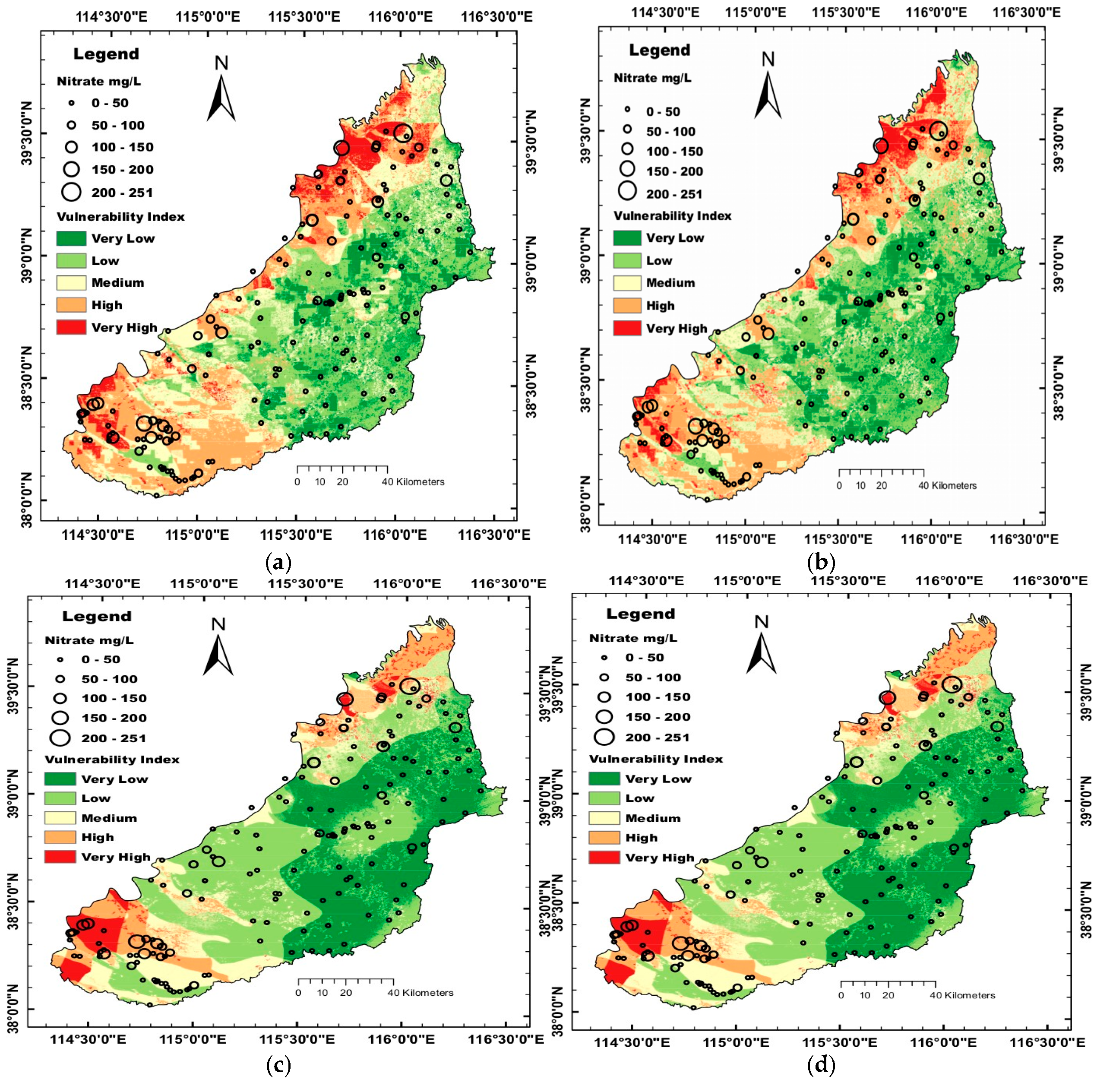
4. Results
4.1. Application of the Common and Pesticide DRASTIC Models
4.2. Optimization of the DRASTIC Model with Respect to the Vulnerability to Nitrate
4.2.1. Revision of the Rating Scores
4.2.2. Revision of the Weights
- (1)
- Using single-parameter sensitivity analysis
- (2)
- Using correlation analysis
- (3)
- Using logistic regression
- (4)
- Using data-driven methods
4.2.3. Verification of the Assessment Performance Based on Nitrate Concentration Changes
5. Discussion
5.1. Impact of Revising Rating Scores
5.2. Impact of Revision Weights
5.3. Verification of the Assessment Performance
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, H.; Li, X.; Li, X.; Cui, J.; Zhang, W.; Xu, W. Optimizing the DRASTIC method for nitrate pollution in groundwater vulnerability assessments: A case study in China. Pol. J. Environ. Stud. 2017, 27, 95–107. [Google Scholar] [CrossRef] [PubMed]
- Javadi, S.; Hashemy, S.; Mohammadi, K.; Howard, K.; Neshat, A. Classification of aquifer vulnerability using K-means cluster analysis. J. Hydrol. 2017, 549, 27–37. [Google Scholar] [CrossRef]
- Douglas, S.; Dixon, B.; Griffin, D.W. Assessing intrinsic and specific vulnerability models ability to indicate groundwater vulnerability to groups of similar pesticides: A comparative study. Phys. Geogr. 2018, 39, 487–505. [Google Scholar] [CrossRef]
- Pacheco, F.; Martins, L.; Quininha, M.; Oliveira, A.S.; Fernandes, L.S. Modification to the DRASTIC framework to assess groundwater contaminant risk in rural mountainous catchments. J. Hydrol. 2018, 566, 175–191. [Google Scholar] [CrossRef]
- Voutchkova, D.D.; Schullehner, J.; Rasmussen, P.; Hansen, B. A high-resolution nitrate vulnerability assessment of sandy aquifers (DRASTIC-N). J. Environ. Manag. 2021, 277, 111330. [Google Scholar] [CrossRef]
- Antonakos, A.; Lambrakis, N. Development and testing of three hybrid methods for the assessment of aquifer vulnerability to nitrates, based on the DRASTIC model, an example from NE Korinthia, Greece. J. Hydrol. 2007, 333, 288–304. [Google Scholar] [CrossRef]
- Huan, H.; Wang, J.; Teng, Y. Assessment and validation of groundwater vulnerability to nitrate based on a modified DRASTIC model: A case study in Jilin City of northeast China. Sci. Total Environ. 2012, 440, 14–23. [Google Scholar] [CrossRef]
- Barbulescu, A. Assessing groundwater vulnerability: DRASTIC and DRASTIC-like methods: A review. Water 2020, 12, 1356. [Google Scholar] [CrossRef]
- Fannakh, A.; Farsang, A. DRASTIC, God, and SI approaches for assessing groundwater vulnerability to pollution: A review. Environ. Sci. Eur. 2022, 34, 77. [Google Scholar] [CrossRef]
- Aller, L.; Bennet, T.; Leher, J.H.; Petty, R.J.; National Water Well Association. DRASTIC: A Standardized System for Evaluating Groundwater Pollution Potential Using Hydrogeologm Settings; EPA/600/2 85/018_296; United States Environmental Protection Agency: Ada, OK, USA, 1985. [Google Scholar]
- Aller, L.; Bennet, T.; Leher, J.H.; Petty, R.J. DRASTIC: A Standardized System for Evaluating Ground Water Pollution Potential Using Hydrogeological Settings; US Environmental Protection Agency: Washington, DC, USA, 1987; pp. 1–455. [Google Scholar]
- Rupert, M. Calibration of the DRASTIC ground water vulnerability mapping method. Ground Water 2001, 39, 625–630. [Google Scholar] [CrossRef]
- Wu, C.; Yin, S.; Liu, H.; Chen, H. Groundwater vulnerability assessment and feasibility mapping under reclaimed water irrigation by a modified DRASTIC model. Water Resour. Manag. 2014, 28, 1219–1234. [Google Scholar] [CrossRef]
- Khan, A.; Khan, H.; Umar, R.; Khan, M. An integrated approach for aquifer vulnerability mapping using GIS and rough sets: Study from an alluvial aquifer in north India. Hydrogeol. J. 2014, 22, 1561–1572. [Google Scholar] [CrossRef]
- Wei, A.; Bi, P.; Guo, J.; Lu, S.; Li, D. Modified DRASTIC model for groundwater vulnerability to nitrate contamination in the Dagujia river basin, China. Water Supply 2021, 21, 1793–1805. [Google Scholar] [CrossRef]
- Pourkhosravani, M.; Jamshidi, F.; Sayari, N. Evaluation of groundwater vulnerability to pollution using DRASTIC, composite DRASTIC, and nitrate vulnerability models. Environ. Health Eng. Manag. 2021, 8, 129–140. [Google Scholar] [CrossRef]
- Guo, X.; Xiong, H.; Li, H.; Gui, X.; Hu, X.; Li, Y.; Cui, H.; Qiu, Y.; Zhang, F.; Ma, C. Designing dynamic groundwater management strategies through a composite groundwater vulnerability model: Integrating human-related parameters into the DRASTIC model using Lightgbm regression and SHAP analysis. Environ. Res. 2023, 236, 116871. [Google Scholar] [CrossRef] [PubMed]
- Gupta, T.; Kumari, R. Assessment of groundwater nitrate vulnerability using DRASTIC and modified DRASTIC in upper catchment of Sabarmati basin. Environ. Earth Sci. 2023, 82, 344. [Google Scholar] [CrossRef]
- Tian, H.; Xiao, C.; Xu, H.; Liang, X.; Zhao, H.; Zhao, Q.; Qiao, L.; Zhang, W. Groundwater vulnerability assessment for nitrate pollution based on modified DRASTIC method: A case study in southwest China. Appl. Ecol. Environ. Res. 2024, 22, 2339–2358. [Google Scholar] [CrossRef]
- Saaty, T.L. How to make a decision: The analytic hierarchy process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Thirumalaivasan, D.; Karmegam, M.; Venugopal, K. AHP-DRASTIC: Software for specific aquifer vulnerability assessment using DRASTIC model and GIS. Environ. Model. Softw. 2003, 18, 645–656. [Google Scholar] [CrossRef]
- Panagopoulos, G.P.; Antonakos, A.K.; Lambrakis, N.J. Optimization of the DRASTIC method for groundwater vulnerability assessment via the use of simple statistical methods and GIS. Hydrogeol. J. 2006, 14, 894–911. [Google Scholar] [CrossRef]
- Chen, S.-K.; Jang, C.-S.; Peng, Y.-H. Developing a probability-based model of aquifer vulnerability in an agricultural region. J. Hydrol. 2013, 486, 494–504. [Google Scholar] [CrossRef]
- Armengol, S.; Sanchez-Vila, X.; Folch, A. An approach to aquifer vulnerability including uncertainty in a spatial random function framework. J. Hydrol. 2014, 517, 889–900. [Google Scholar] [CrossRef]
- Pacheco, F.; Pires, L.; Santos, R.; Fernandes, L.S. Factor weighting in DRASTIC modeling. Sci. Total Environ. 2015, 505, 474–486. [Google Scholar] [CrossRef]
- Fijani, E.; Nadiri, A.A.; Moghaddam, A.A.; Tsai, F.T.-C.; Dixon, B. Optimization of DRASTIC method by supervised committee machine artificial intelligence to assess groundwater vulnerability for Maragheh-Bonab plain aquifer, Iran. J. Hydrol. 2013, 503, 89–100. [Google Scholar] [CrossRef]
- Stigter, T.Y.; Ribeiro, L.; Dill, A.M.M.C. Evaluation of an intrinsic and a specific vulnerability assessment method in comparison with groundwater salinisation and nitrate contamination levels in two agricultural regions in the south of Portugal. Hydrogeol. J. 2006, 14, 79–99. [Google Scholar] [CrossRef]
- Stuart, M.; Chilton, P.; Kinniburgh, D.; Cooper, D. Screening for long-term trends in groundwater nitrate monitoring data. Q. J. Eng. Geol. Hydrogeol. 2007, 40, 361–376. [Google Scholar] [CrossRef]
- Wang, L.; Stuart, M.E.; Bloomfield, J.P.; Butcher, A.S.; Gooddy, D.C.; McKenzie, A.A.; Lewis, M.A.; Williams, A.T. Prediction of the arrival of peak nitrate concentrations at the water table at the regional scale in Great Britain. Hydrol. Process. 2012, 26, 226–239. [Google Scholar] [CrossRef]
- Stevenazzi, S.; Masetti, M.; Nghiem, S.V.; Sorichetta, A. Groundwater vulnerability maps derived from a time-dependent method using satellite scatterometer data. Hydrogeol. J. 2015, 23, 631–647. [Google Scholar] [CrossRef]
- Wang, L.; Stuart, M.E.; Lewis, M.; Ward, R.; Skirvin, D.; Naden, P.; Collins, A.; Ascott, M. The changing trend in nitrate concentrations in major aquifers due to historical nitrate loading from agricultural land across England and Wales from 1925 to 2150. Sci. Total Environ. 2016, 542, 694–705. [Google Scholar] [CrossRef]
- Zhong, Z. A discussion of groundwater vulnerability assessment methods. Earth Sci. Front. 2005, 12, 3–13. [Google Scholar]
- Feng, W.; Wang, S.; Hu, C.; Li, L. Landform sedimentary contributed to groundwater nitrate vulnerability in multi-alluvial fan aquifer systems in a watershed. Environ. Earth Sci. 2023, 82, 232. [Google Scholar] [CrossRef]
- Kazakis, N.; Voudouris, K.S. Groundwater vulnerability and pollution risk assessment of porous aquifers to nitrate: Modifying the DRASTIC method using quantitative parameters. J. Hydrol. 2015, 525, 13–25. [Google Scholar] [CrossRef]
- Teso, R.R.; Poe, M.P.; Younglove, T.; McCool, P.M. Use of logistic regression and GIS modeling to predict groundwater vulnerability to pesticides. J. Environ. Qual. 1996, 25, 425–432. [Google Scholar] [CrossRef]
- Tesoriero, A.; Voss, F. Predicting the probability of elevated nitrate concentrations in the Puget Sound basin: Implications for aquifer susceptibility and vulnerability. Ground Water 1997, 35, 1029–1039. [Google Scholar] [CrossRef]
- Gentle, J.E. Random Number Generation and Monte Carlo Methods; Springer: New York, NY, USA, 2003. [Google Scholar] [CrossRef]
- Fishman, G.S. Monte Carlo: Concepts, Algorithms, and Applications; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- John, H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; The MIT Press: Cambridge, MA, USA, 1992. [Google Scholar] [CrossRef]
- Mitchell, M. An Introduction to Genetic Algorithms, 5th ed.; MIT Press: Cambridge, MA, USA; London, UK, 1999. [Google Scholar]
- Whitley, D. A genetic algorithm tutorial. Stat. Comput. 1994, 4, 65–85. [Google Scholar] [CrossRef]
- Eiben, A.E.; Smith, J.E. Introduction to Evolutionary Computing; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- McLay, C.; Dragten, R.; Sparling, G.; Selvarajah, N. Predicting groundwater nitrate concentrations in a region of mixed agricultural land use: A comparison of three approaches. Environ. Pollut. 2001, 115, 191–204. [Google Scholar] [CrossRef]
- Stigter, T.; Ribeiro, L.; Dill, A. Building factorial regression models to explain and predict nitrate concentrations in groundwater under agricultural land. J. Hydrol. 2008, 357, 42–56. [Google Scholar] [CrossRef]
- Zhu, Z.; Chen, D. Nitrogen fertilizer use in China—Contributions to food production, impacts on the environment and best management strategies. Nutr. Cycl. Agroecosyst. 2002, 63, 117–127. [Google Scholar] [CrossRef]
- Li, H.; Liu, Z.; Zheng, L.; Lei, Y. Resilience analysis for agricultural systems of North China Plain based on a dynamic system model. Sci. Agric. 2011, 68, 8–17. [Google Scholar] [CrossRef]
- Brauns, B.; Bjerg, P.L.; Song, X.; Jakobsen, R. Field scale interaction and nutrient exchange between surface water and shallow groundwater in the Baiyang lake region, North China Plain. J. Environ. Sci. 2016, 45, 60–75. [Google Scholar] [CrossRef]
- Wang, M.; Liu, D.G.; Wu, L.W.; Bao, Y.; Liu, N.W. Prediction of agriculture derived groundwater nitrate distribution in North China Plain with GIS-based BPNN. Environ. Geol. 2006, 50, 637–644. [Google Scholar] [CrossRef]
- Wang, S.; Tang, C.; Song, X.; Yuan, R.; Wang, Q.; Zhang, Y. Using major ions and δ15N-NO3− to identify nitrate sources and fate in an alluvial aquifer of the Baiyangdian lake watershed, North China Plain. Environ. Sci. Process. Impacts 2013, 15, 1430–1443. [Google Scholar] [CrossRef]
- Wu, C. Landform Environment and Its Formation in North China; Science Press: Beijing, China, 2008. (In Chinese) [Google Scholar]
- Pardo-Iguzquiza, E.; Dowd, P. Empirical Maximum Likelihood Kriging: The General Case. Math. Geol. 2005, 37, 477–492. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, 1–33. [Google Scholar] [CrossRef]
- Hirt, C.; Filmer, M.S.; Featherstone, W.E. Comparison and Validation of the Recent Freely Available ASTER-GDEM ver1, SRTM ver4.1 and GEODATA DEM-9S ver3 Digital Elevation Models over Australia. 2010. Available online: https://espace.curtin.edu.au/bitstream/20.500.11937/43846/2/137777_137777.pdf (accessed on 28 July 2009).
- Rexer, M.; Hirt, C. Comparison of free high resolution digital elevation data sets (ASTER GDEM2, SRTM v2.1/v4.1) and validation against accurate heights from the Australian National Gravity Database. Aust. J. Earth Sci. Int. Geosci. J. Geol. Soc. Aust. 2014, 61, 213–226. [Google Scholar] [CrossRef]
- Zhang, Z.; Fei, Y. (Eds.) Atlas of Groundwater Sustainable Utilization in North China Plain; China Cartographic Publishing House: Beijing, China, 2009. [Google Scholar]
- Cao, G.; Scanlon, B.R.; Han, D.; Zheng, C. Impacts of thickening unsaturated zone on groundwater recharge in the North China Plain. J. Hydrol. 2016, 537, 260–270. [Google Scholar] [CrossRef]
- Wang, H.; Pan, X.; Luo, J.; Luo, Z.; Chang, C.; Shen, Y. Using remote sensing to analyze spatiotemporal variations in crop planting in the North China Plain. Chin. J. Eco Agric. 2015, 23, 1199–1209. [Google Scholar]
- Min, L.; Shen, Y.; Pei, H.; Wang, P. Water movement and solute transport in deep vadose zone under four irrigated agricultural land-use types in the North China Plain. J. Hydrol. 2018, 559, 510–522. [Google Scholar] [CrossRef]
- Rosen, L. A study of the DRASTIC methodology with emphasis on Swedish conditions. Ground Water 1994, 32, 278–285. [Google Scholar] [CrossRef]
- Turkeltaub, T.; Jia, X.; Zhu, Y.; Shao, M.-A.; Binley, A. Recharge and nitrate transport through the deep vadose zone of the Loess Plateau: A regional-scale model investigation. Water Resour. Res. 2018, 54, 4332–4346. [Google Scholar] [CrossRef]


| Net Recharge (According to [11]) | Soil Media | |||
|---|---|---|---|---|
| DRASTIC Range (mm) | Range in This Paper (mm) | Score | Infiltration Coefficient | Score |
| 0–51 | 0–50 | 1 | 0.2 | 1 |
| 51–102 | 50–100 | 3 | 0.226 | 1.52 |
| 102–178 | 100–150 | 6 | 0.275 | 2.5 |
| – | 150–200 | 7 | 0.285 | 2.7 |
| 178–254 | 200–250 | 8 | 0.3 | 3 |
| >254 | >250 | 9 | 0.4 | 5 |
| 0.45 | 6 | |||
| 0.55 | 8 | |||
| 0.65 | 10 | |||
| Landforms | Land Use | ||||
| Geomorphic Units | NO3− (mg/L) | Score | Land Use Types | NO3− (mg/L) | Score |
| River belts | 12.06 | 1 | Cotton | – | 1 |
| Alluvial and flood plains | 13.21 | 1.24 | Woods | 12.19 | 1 |
| Lakes and depressions | 21.12 | 2.9 | Residential area | 16.32 | 1.88 |
| Alluvial-proluvial fans | 44.44 | 7.78 | Orchards | 21.67 | 3.02 |
| Proluvial fans | 55.03 | 10 | Wheat/maize | 29.91 | 4.78 |
| Vegetables | 54.33 | 10 | |||
| Version | Weights | |||||||
|---|---|---|---|---|---|---|---|---|
| D | R | A | S | T | I | C | L | |
| original | 5 | 4 | 3 | 2 | 1 | 5 | 3 | 5 |
| pesticide | 5 | 4 | 3 | 5 | 3 | 4 | 2 | 5 |
| Depth to the Water Table (D) | Net Recharge (R) | Aquifer Thickness (A) | ||||||
|---|---|---|---|---|---|---|---|---|
| Range (m) | NO3− (mg/L) | Score | Range (mm) | NO3− (mg/L) | Score | Range (m) | NO3− (mg/L) | Score |
| 0–30.5 | 47.37 | 10 | 0–102 | 29.64 | 9.87 | 0–45 | 55.64 | 10 |
| >30.5 | 20.45 | 4.32 | >102 | 30.02 | 10 | >45 | 25.67 | 4.61 |
| Infiltration coefficient (S) | Hydraulic Conductivity (C) | Land use (L) | ||||||
| Range | NO3− (mg/L) | Score | Range (m/d) | NO3− (mg/L) | Score | Types | NO3− (mg/L) | Score |
| 0–0.275 | 22.92 | 3.61 | 0–40.7 | 11.8 | 2.8 | All types except for vegetables | 27.71 | 5.1 |
| >0.275 | 63.45 | 10 | >40.7 | 42.07 | 10 | Vegetables | 54.33 | 10 |
| Topography slope (T) | Landform (I) | |||||||
| Range (%) | NO3− (mg/L) | Score | Geomorphic units | NO3− (mg/L) | Score | |||
| 0–2 | 22.66 | 4.31 | River belts | 12.06 | 2.19 | |||
| 2–6 | 32.61 | 6.2 | Alluvial and flood plains | 13.21 | 2.4 | |||
| 6–12 | 25.06 | 4.76 | Lakes and depressions | 21.12 | 3.84 | |||
| >12 | 52.59 | 10 | Alluvial-proluvial fans | 44.44 | 8.08 | |||
| Proluvial fans | 55.03 | 10 | ||||||
| Correlation Analysis | Logistic Regression Analysis | MC and GA | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameters | Spearman’s ρ | Sp a | Kendall’s τ | kp b | Weight | b Coefficients c | p-Value d | Weight | Weight (MC) | Weight (GA) | ||||
| 1 | 2 | 3 | 1 | 2 | 3 | |||||||||
| D | 0.413 | 0 * | 0.34 | 0 * | 4.225 | 0.08223 | 0.3312 | 0.093 | 4.993 | 4.855 | 4.802 | 5 | 4.787 | 4.839 |
| R | −0.163 | 0.039 * | −0.134 | 0.039 * | 1.666 | 4.42904 | 0.3144 | 5 | 0.086 | 0.03 | – | 0.171 | 0.232 | – |
| A | 0.316 | 0 * | 0.26 | 0 * | 3.231 | 0.05602 | 0.6178 | 0.063 | 2.252 | 2.414 | 2.446 | 2.251 | 2.491 | 2.5 |
| S | 0.426 | 0 * | 0.351 | 0 * | 4.358 | 0.14877 | 0.0778 | 0.168 | 2.624 | 2.522 | 2.467 | 2.483 | 2.474 | 2.452 |
| T | 0.113 | 0.151 | 0.09 | 0.15 | 1.14 | 0.17678 | 0.5116 | 0.2 | 2.749 | – | – | 2.808 | – | – |
| I | 0.47 | 0 * | 0.36 | 0 * | 4.638 | 0.14543 | 0.1753 | 0.164 | 1.759 | 1.379 | 1.431 | 1.664 | 1.391 | 1.419 |
| C | 0.488 | 0 * | 0.403 | 0 * | 5 | 0.16229 | 0.1341 | 0.183 | 3.864 | 3.8 | 3.797 | 3.889 | 3.848 | 3.848 |
| L | 0.207 | 0.007 ∗ | 0.17 | 0.008 * | 2.116 | 0.35728 | 0.0113 * | 0.403 | 5 | 5 | 5 | 4.998 | 5 | 5 |
| C-DRASTIC a | P-DRASTIC b | M-DRASTIC c | SPSA d | LRA e | CA f | MC g | GA h | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | ||||||
| Pearson’s relation coefficient | 0.513 | 0.502 | 0.647 | 0.646 | 0.591 | - | 0.633 | 0.634 | 0.658 | 0.656 | 0.656 | 0.658 | 0.656 | 0.656 |
| Spearman’s relation coefficient | 0.478 | 0.457 | 0.643 | 0.635 | 0.593 | - | 0.624 | 0.630 | 0.638 | 0.632 | 0.634 | 0.638 | 0.628 | 0.635 |
| Difficulty level | easy | easy | medium | medium+ | difficult | difficult | medium | medium | ||||||
| Computational efficiency | high | high | medium | medium− | lower than CA | low | medium+ | medium+ | ||||||
| Vulnerability Level | Aller’s Common DRASTIC | GA DRASTIC | ||
|---|---|---|---|---|
| Percentage (%) | Cumulative Percentage (%) | Percentage (%) | Cumulative Percentage (%) | |
| Very Low | 28.26 | 28.26 | 27.37 | 27.37 |
| Low | 25.62 | 53.89 | 39.35 | 66.72 |
| Medium | 23.54 | 77.43 | 17.81 | 84.53 |
| High | 16.83 | 94.26 | 10.88 | 95.41 |
| Very High | 5.74 | 100 | 4.59 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, X.; Peng, L.; Zhang, Y.; Zhang, Y.; Wang, Y.; Feng, W.; Yang, H. A Data-Driven Method for Determining DRASTIC Weights to Assess Groundwater Vulnerability to Nitrate: Application in the Lake Baiyangdian Watershed, North China Plain. Appl. Sci. 2025, 15, 2866. https://doi.org/10.3390/app15052866
Hou X, Peng L, Zhang Y, Zhang Y, Wang Y, Feng W, Yang H. A Data-Driven Method for Determining DRASTIC Weights to Assess Groundwater Vulnerability to Nitrate: Application in the Lake Baiyangdian Watershed, North China Plain. Applied Sciences. 2025; 15(5):2866. https://doi.org/10.3390/app15052866
Chicago/Turabian StyleHou, Xianglong, Liqin Peng, Yuan Zhang, Yan Zhang, Yunxia Wang, Wenzhao Feng, and Hui Yang. 2025. "A Data-Driven Method for Determining DRASTIC Weights to Assess Groundwater Vulnerability to Nitrate: Application in the Lake Baiyangdian Watershed, North China Plain" Applied Sciences 15, no. 5: 2866. https://doi.org/10.3390/app15052866
APA StyleHou, X., Peng, L., Zhang, Y., Zhang, Y., Wang, Y., Feng, W., & Yang, H. (2025). A Data-Driven Method for Determining DRASTIC Weights to Assess Groundwater Vulnerability to Nitrate: Application in the Lake Baiyangdian Watershed, North China Plain. Applied Sciences, 15(5), 2866. https://doi.org/10.3390/app15052866








