An Experimental Study on Physical and Mechanical Properties of Fractured Sandstone Grouting Reinforcement Body Under Freeze–Thaw Cycle
Abstract
1. Introduction
2. Experimental Materials and Methods
2.1. Materials and Sample Preparation
2.1.1. Experimental Materials
2.1.2. Sample Preparation
2.2. Experimental Procedure
2.2.1. Drying and Saturation Test
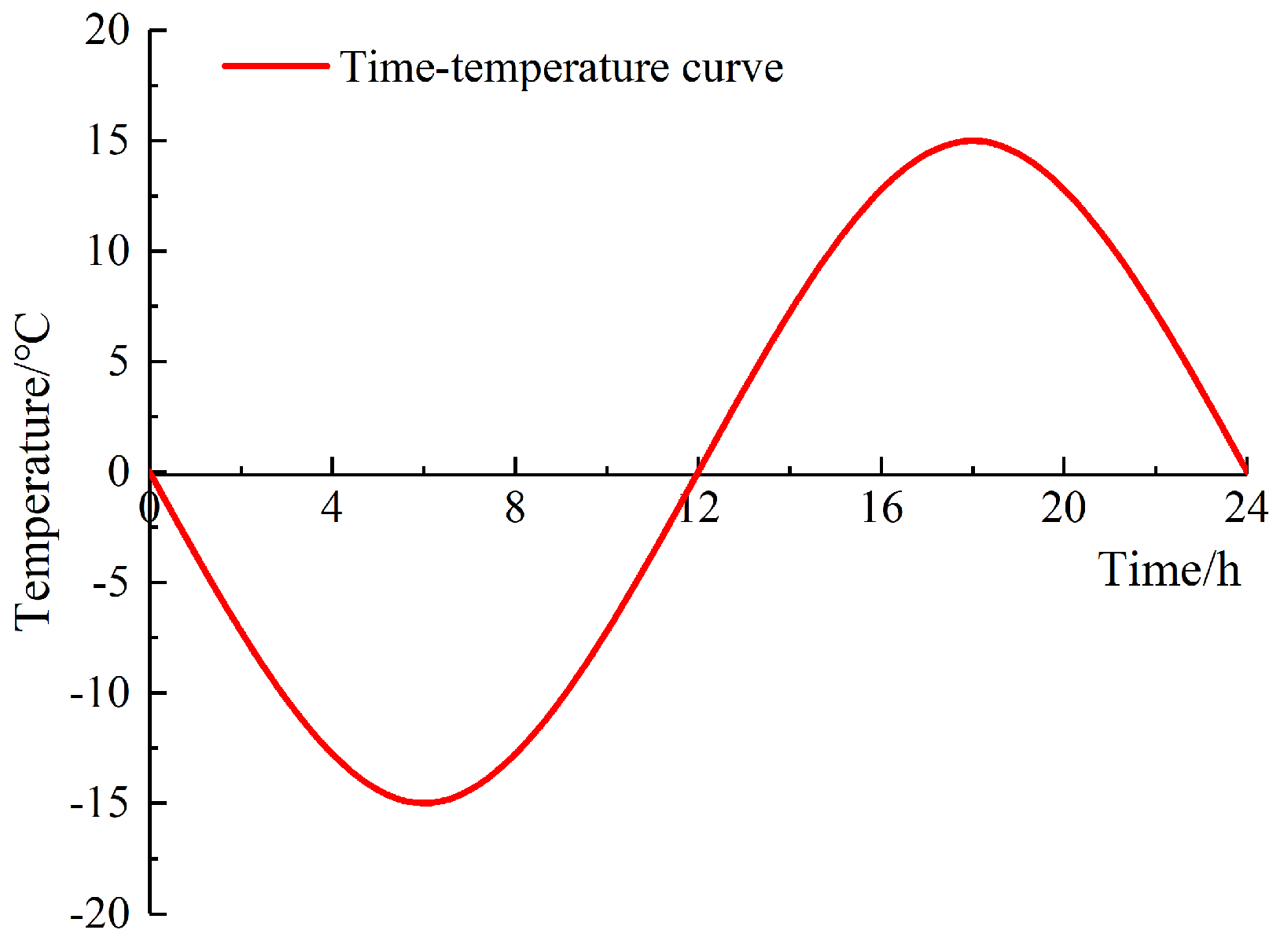
2.2.2. Freeze–Thaw Cycle Test
2.2.3. Nuclear Magnetic Resonance Principle and Test
2.2.4. Triaxial Compression Test
3. Results and Discussion
3.1. Physical Properties
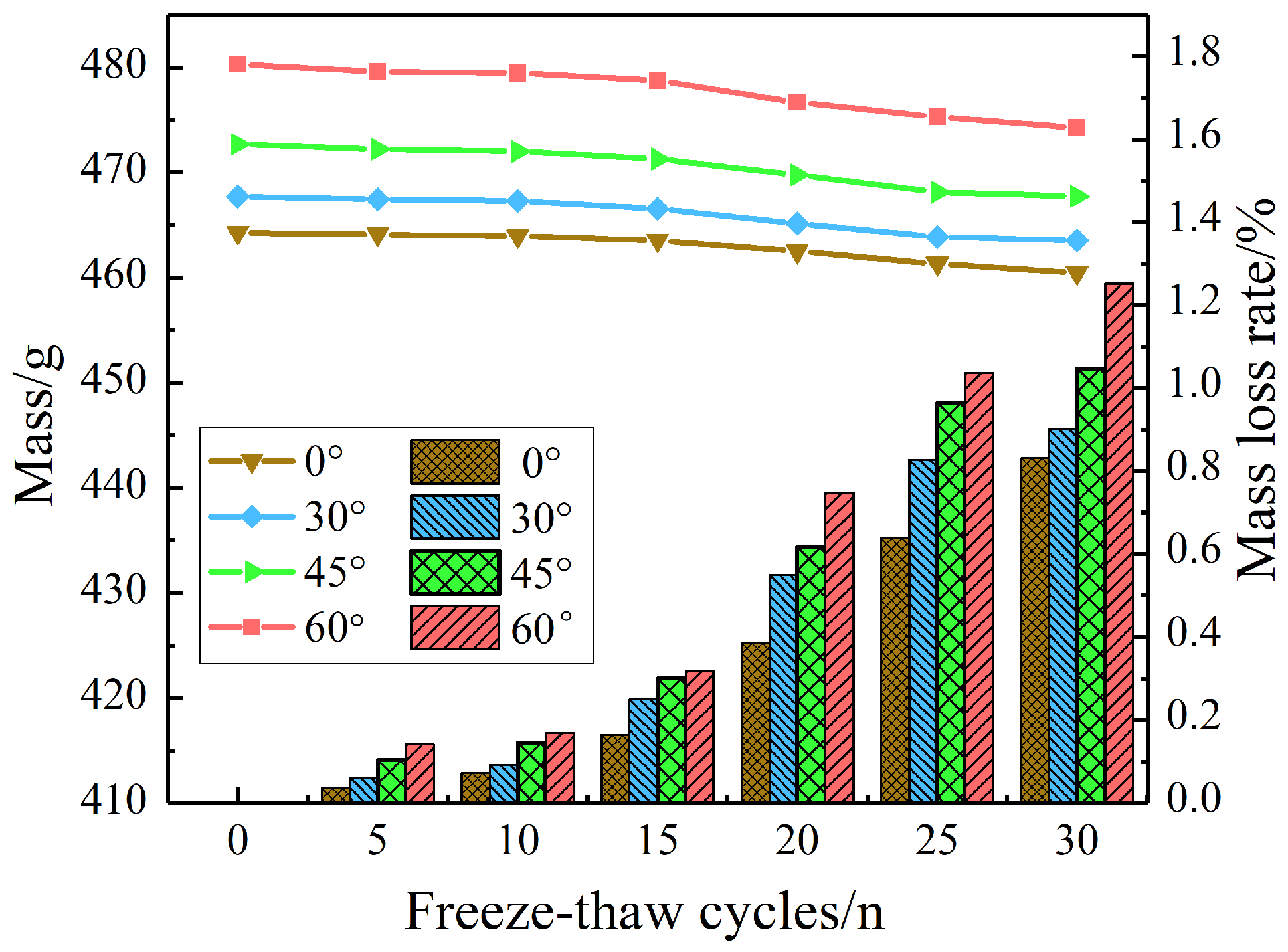
3.1.1. Mass
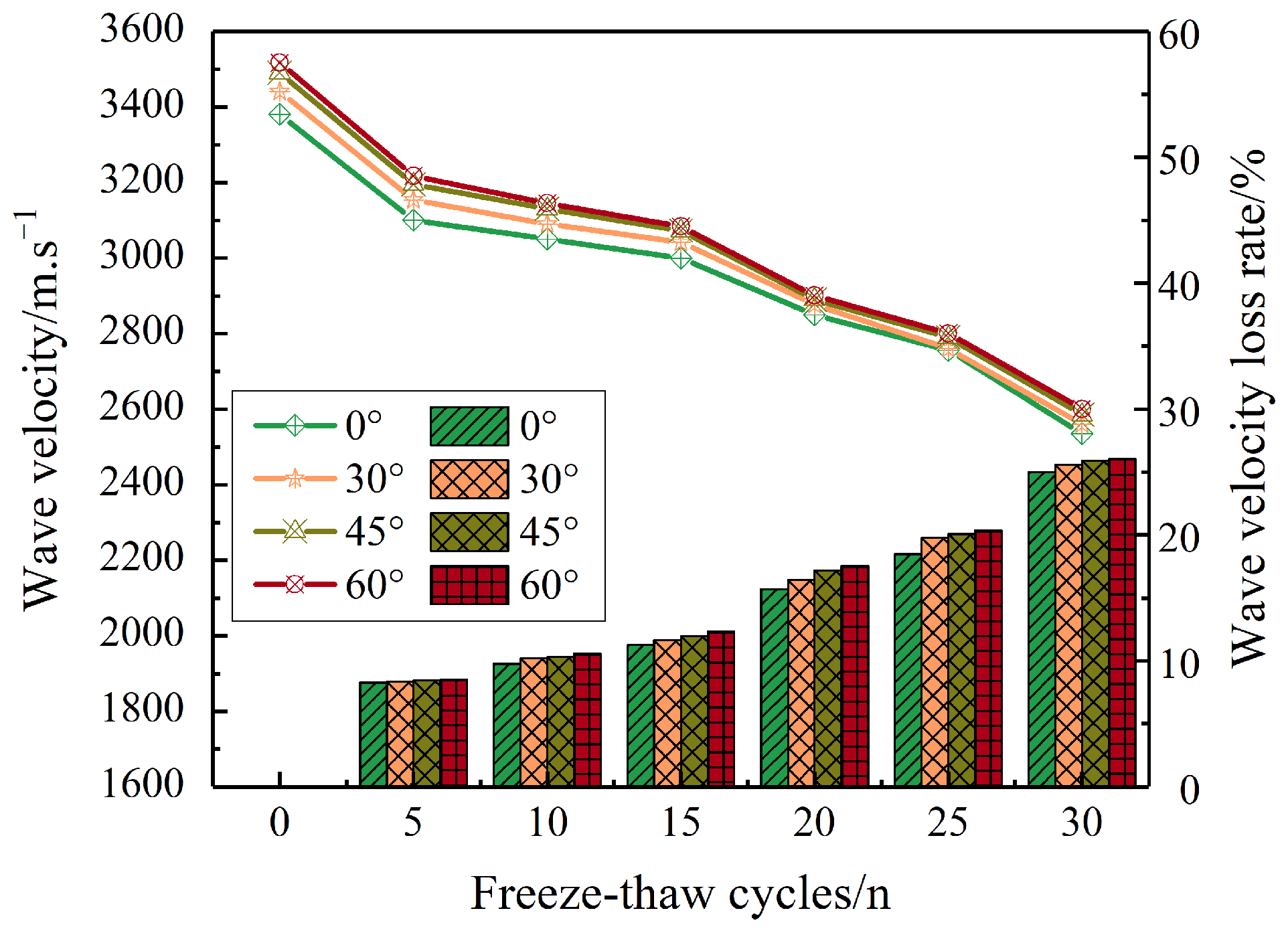
3.1.2. Wave Velocity
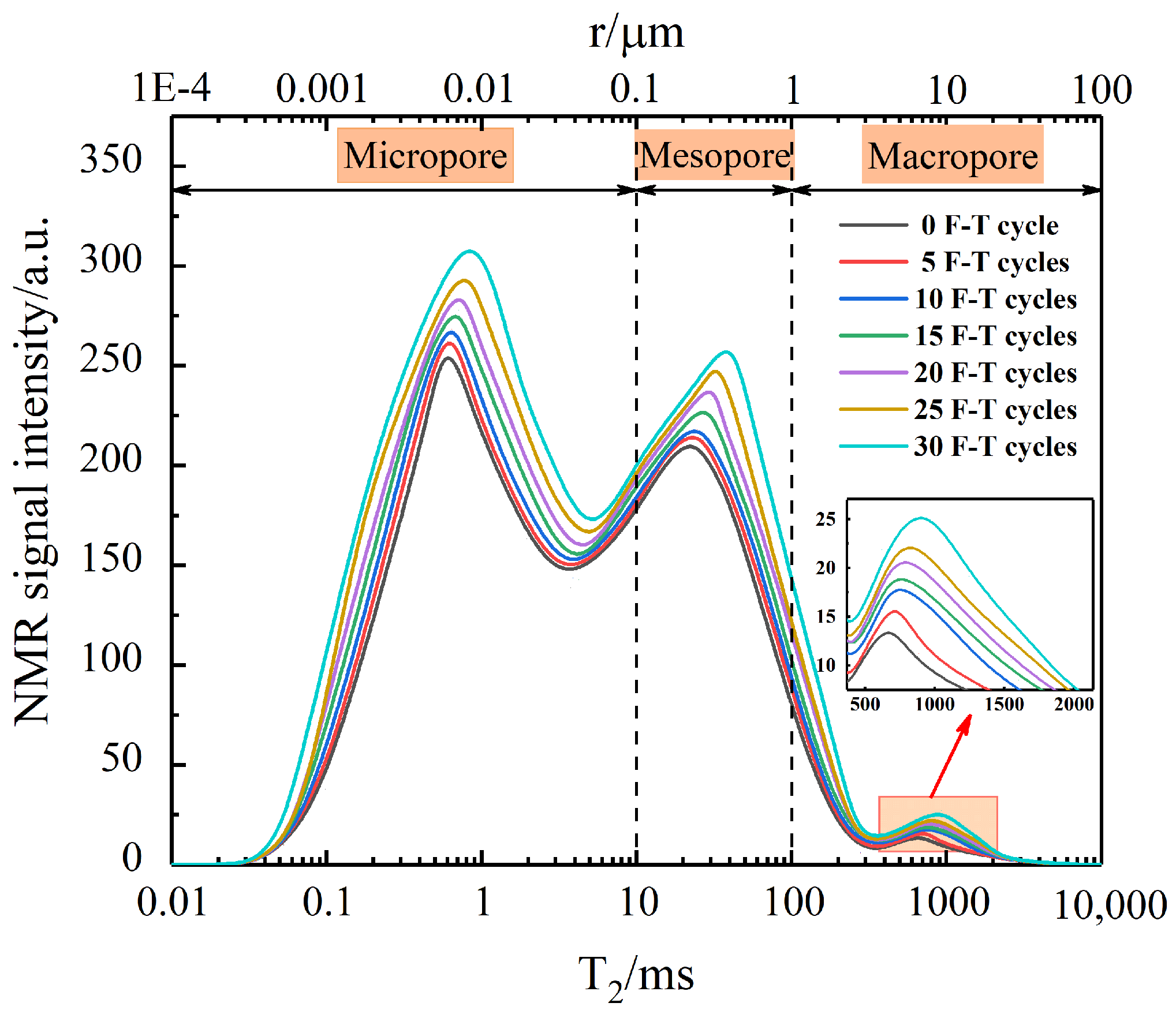
3.2. Microscopic Pore Characteristics
3.3. Mechanical Properties
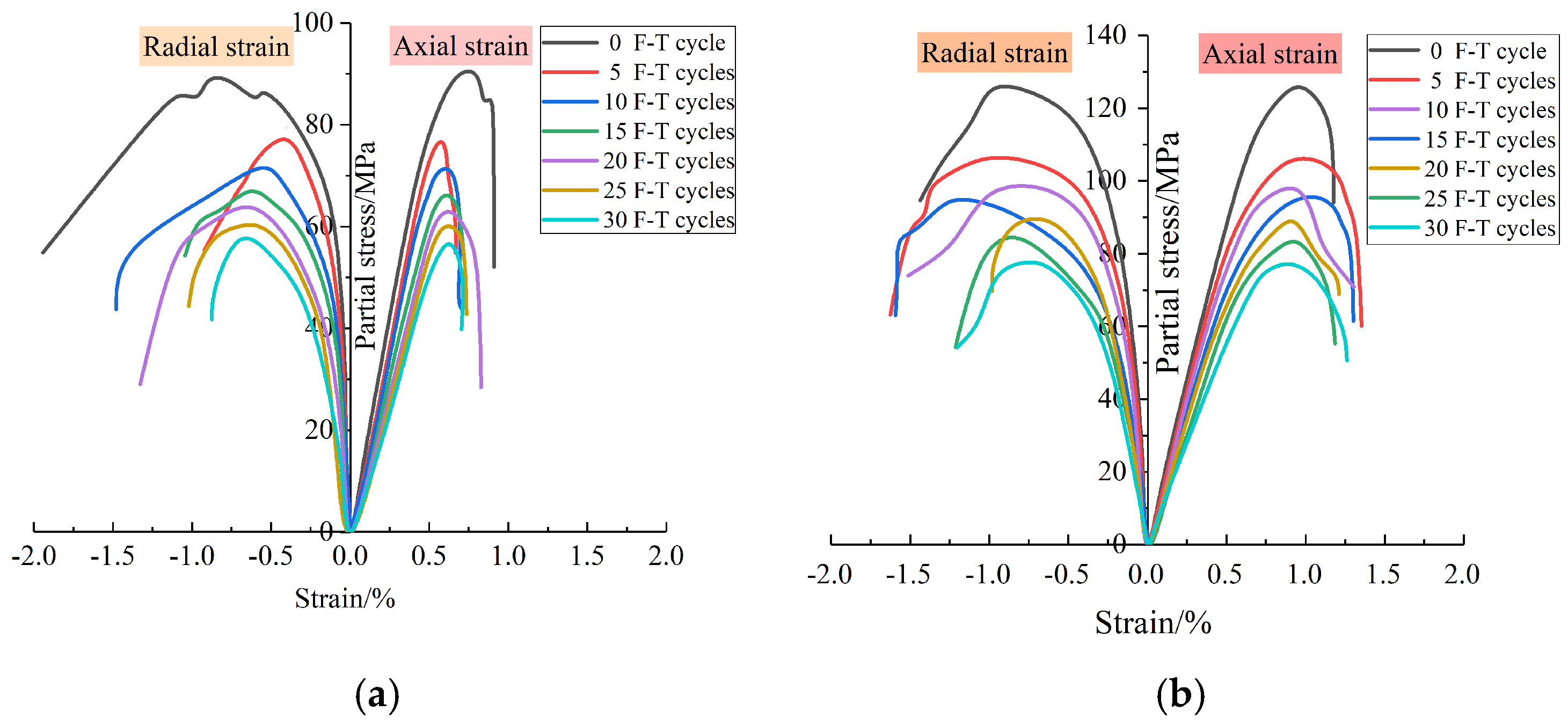
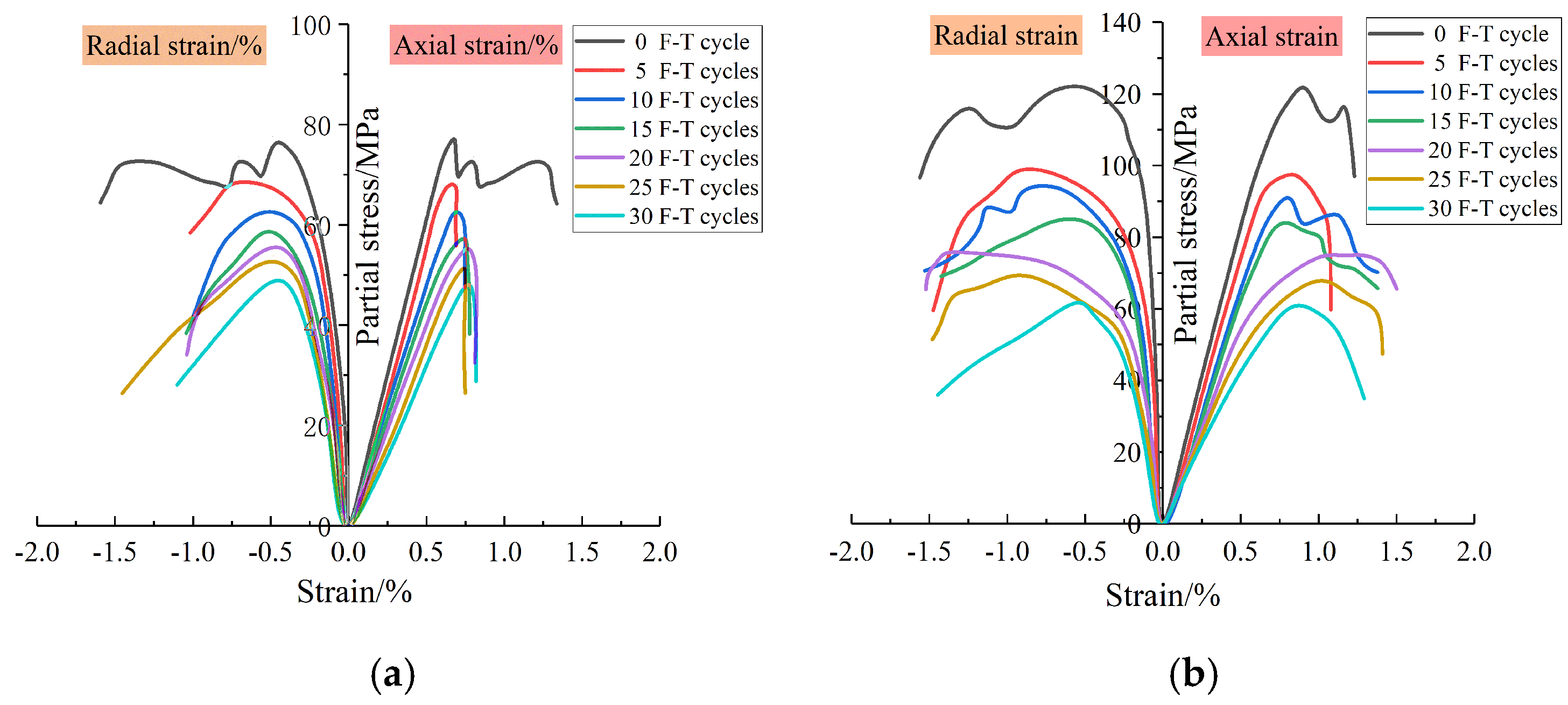
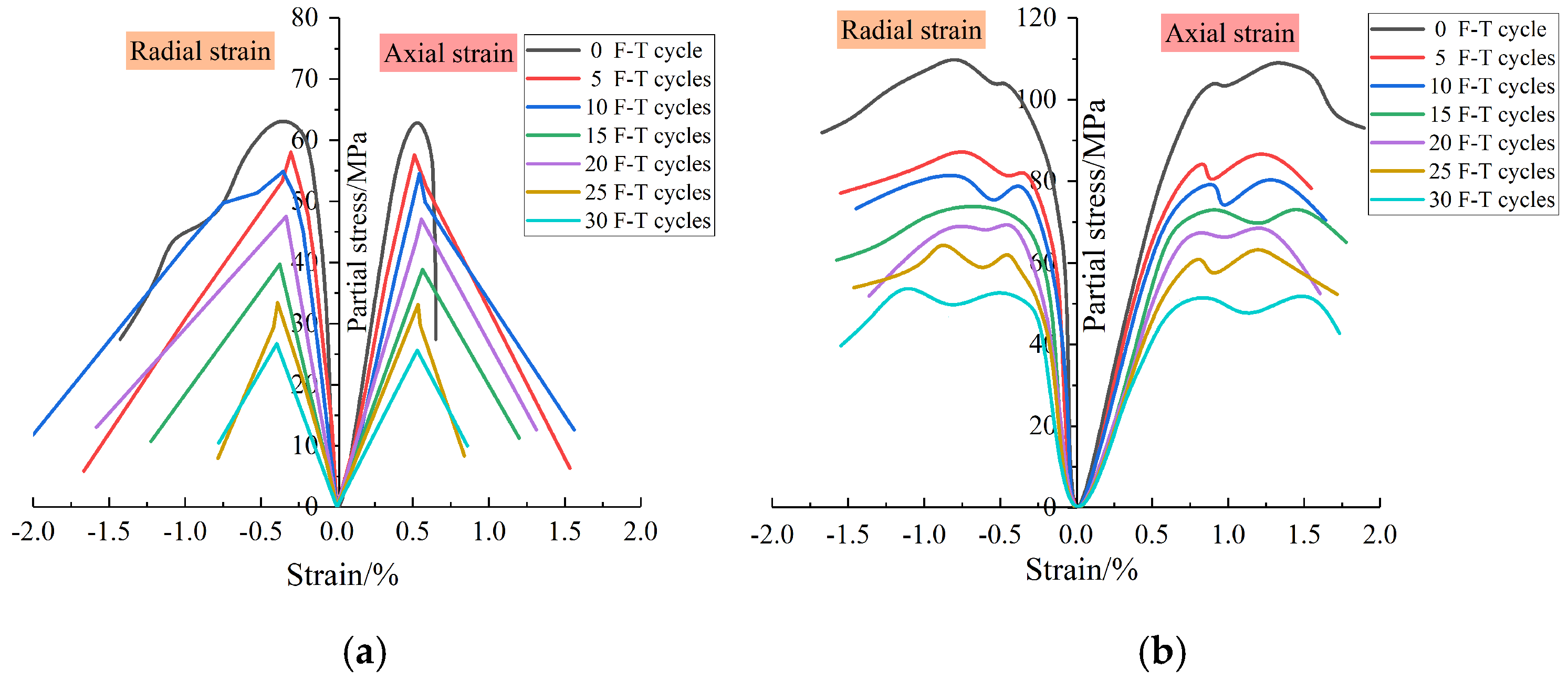
3.3.1. Stress–Strain Curve
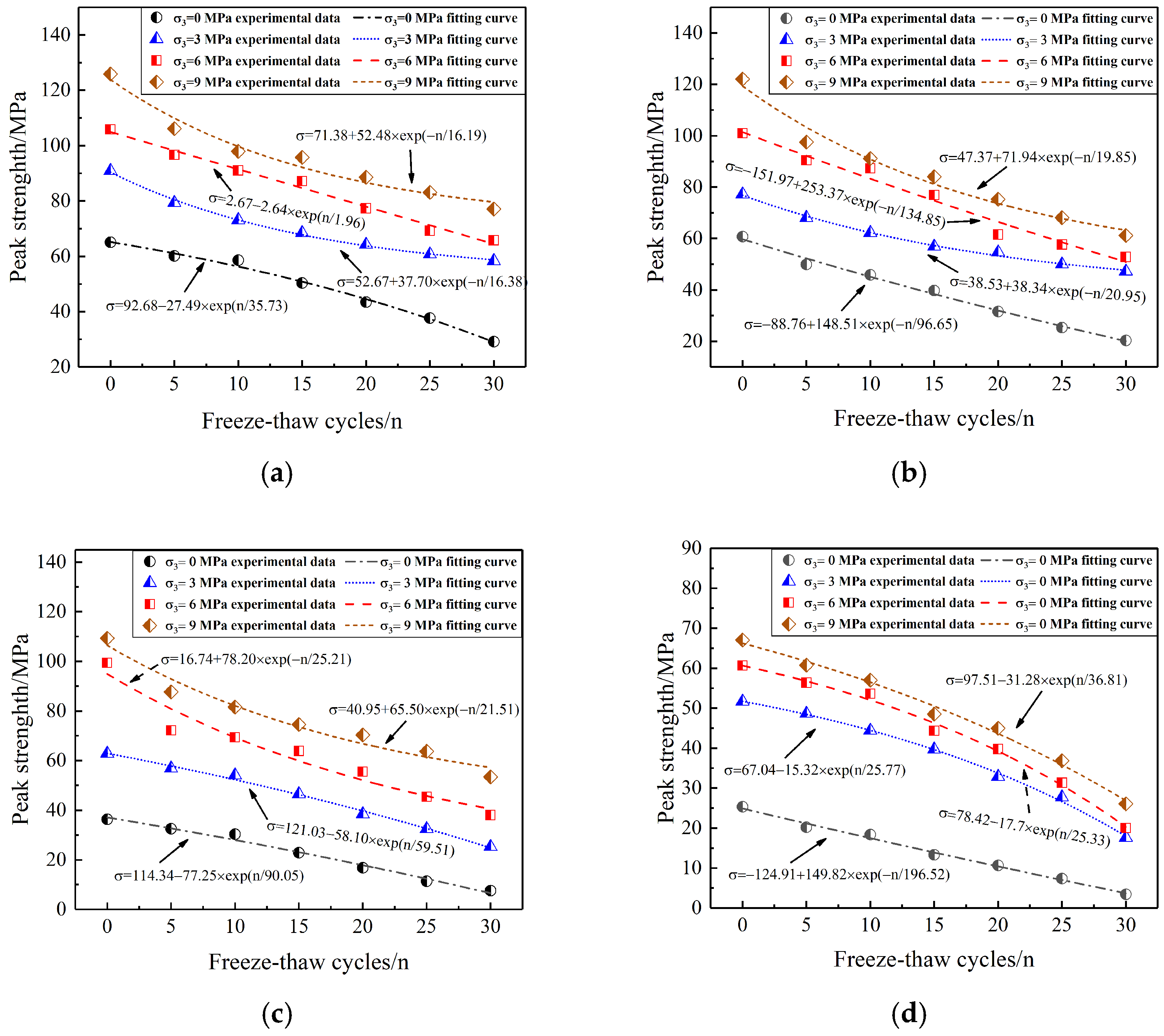
3.3.2. Peak Strength
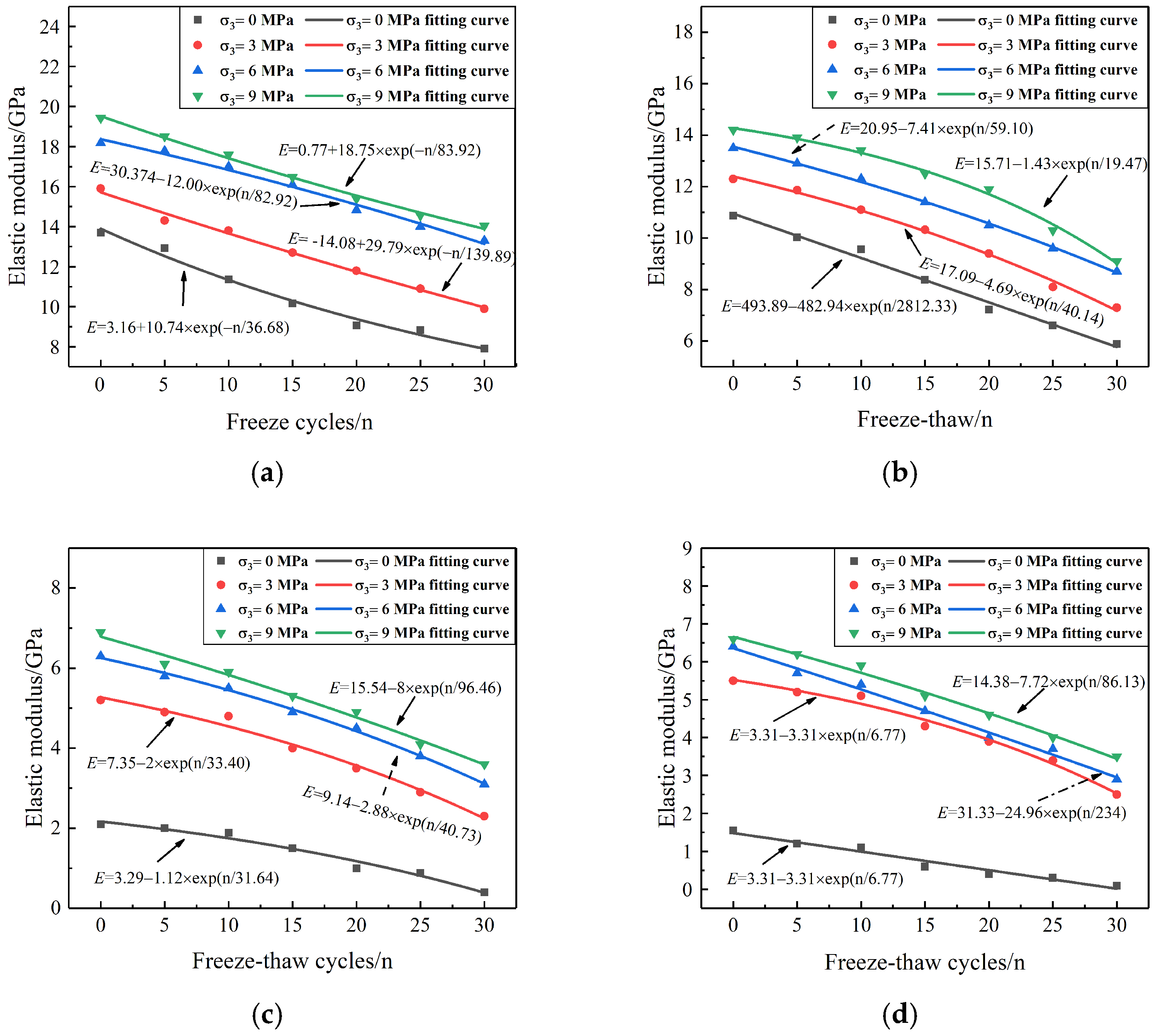
3.3.3. Elastic Modulus
3.3.4. Shear Strength Parameters
3.4. Discussion
3.4.1. The Influence Mechanism of Freeze–Thaw Cycle on Grouting Reinforcement Body
3.4.2. The Influence of Crack Dip Angle on Grouting Reinforcement Body
4. Conclusions
- As the number of freeze–thaw cycles increases, both the mass and wave velocity of the grouting reinforcement body decrease, while the mass loss rate and wave velocity loss rate increase. After 30 freeze–thaw cycles, the maximum mass loss rate of the sample is 1.25%, and the wave velocity loss rate exceeds 25%. Under the same number of freeze–thaw cycles, the mass loss rate increases with the increase in crack dip angle.
- The NMR T2 spectra curve of the grouting reinforcement body shifts to the right as the number of freeze–thaw cycles increases, indicating that the freeze–thaw process promotes the continuous initiation, development, and expansion of internal pores within the grouting reinforcement body. In the initial stages of the freeze–thaw cycle, pore size evolution progresses from micropores to mesopores and macropores. In the later stages of the freeze–thaw cycle, the evolution is primarily from mesopores to macropores.
- The freeze–thaw cycle weakens the mechanical properties of the grouting reinforcement body. As the number of freeze–thaw cycles increases, both the peak strength and elastic modulus of the grouting reinforcement body decline, following a negative exponential function under varying confining pressures. Cohesion and the internal friction angle progressively decrease with increasing freeze–thaw cycles. Under the same number of freeze–thaw cycles, the peak strength and elastic modulus of the grouting reinforcement body decrease as the crack dip angle increases but increases with higher confining pressures. The relationship between peak strength and confining pressure adheres to the Coulomb linear strength criterion.
- The crack dip angle and confining pressure significantly influence the failure mode of the grouting reinforcement body. Plastic flow is observed after the peak of the stress–strain curve for grouting reinforcement bodies subjected to high confining pressures with crack dip angles of 0°, 30°, or 45°, leading to a marked enhancement in ductility. In contrast, the stress–strain curves of grouting reinforcement bodies with a 45° crack dip angle under low confining pressure and a 60° crack dip angle exhibit a substantial decline after reaching the peak. This decline is primarily attributed to the stress exceeding the shear strength of the slurry–rock interface layer, resulting in shear slip along the fracture planes.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yuan, Y.; Pan, P.; Zhao, S.; Wang, B.; Song, G. The failure process of marble with filled crack under uniaxial compression based on digital image correlation. Chin. J. Rock Mech. Eng. 2018, 37, 339–351. [Google Scholar] [CrossRef]
- Pudasaini, S.P.; Krautblatter, M. A two-phase mechanical model for rock-ice avalanches. J. Geophys. Res. Earth Surf. 2014, 119, 2272–2290. [Google Scholar] [CrossRef]
- Krautblatter, M.; Funk, D.; Günzel, F.K. Why permafrost rocks become unstable: A rock-ice-mechanical model in time and space. Earth Surf. Process. Landf. 2013, 38, 876–887. [Google Scholar] [CrossRef]
- Huang, H.; Chen, J.; Zhang, D. Lateral asymptotic deflection evolution and mechanical behavior of secondary linings of freeze-thaw tunnels in cold regions. Chin. J. Geotech. Eng. 2019, 41, 2126–2132. [Google Scholar]
- Gustafson, G.; Ciaesson, J.; Fransson, A. Steering parameters for rock grouting. J. Appl. Math. 2013, 2013, 269594. [Google Scholar] [CrossRef]
- Tani, M.E. Grouting rock fractures with cement grout. Rock Mech. Rock Eng. 2012, 45, 547–561. [Google Scholar] [CrossRef]
- Hu, S.; Liu, Q.; Li, S. Advance and review on grouting critical problems in fractured rock mass. Coal Sci. Technol. 2022, 50, 112–126. [Google Scholar]
- Evdokimov, P.D.; Adamovich, A.N.; Fradkin, L.P.; Denisov, V.N. Shear strengths of fissures in ledge rock before and after grouting. Hydrotech. Constr. 1970, 4, 229–233. [Google Scholar] [CrossRef]
- Han, L.; Zong, Y.; Han, G.; Zhang, H. Study of shear properties of rock structure plane by grouting reinforcement body. Rock Soil Mech. 2011, 32, 2570–2576. [Google Scholar] [CrossRef]
- Liu, Q.; Zhou, Y.; Lu, C.; Zhang, J. Experimental study on mechanical properties of mudstone fracture before and after grouting. J. Min. Saf. Eng. 2016, 33, 509–514+520. [Google Scholar] [CrossRef]
- Salimian, M.H.; Baghbanan, A.; Hashemolhosseini, H.; Dehghanipoodeh, M.; Norouzi, S. Effect of grouting on shear behavior of rock joint. Int. J. Rock Mech. Min. Sci. 2017, 98, 159–166. [Google Scholar] [CrossRef]
- Sharafisafa, M.; Aliabadian, Z.; Tahmasebinia, F.; Shen, L. A comparative study on the crack development in rock-like specimens containing unfilled and filled flaws. Eng. Fract. Mech. 2021, 241, 107405. [Google Scholar] [CrossRef]
- Stavropoulou, E.; Dano, C.; Boulon, M. Shear Response of Wet Weak Carbonate Rock/Grout Interfaces Under Cyclic Loading. Rock Mech. Rock Eng. 2021, 54, 2791–2813. [Google Scholar] [CrossRef]
- Lu, H.; Zhu, C.; Liu, Q. Study on shear mechanical properties of structural planes grouted with different materials. Chin. J. Rock Mech. Eng. 2021, 40, 1803–1811. [Google Scholar] [CrossRef]
- Shen, J.; Liu, B.; Chen, J.; Li, Y.; Cheng, Y.; Song, Y. Experimental study on mechanical properties of diabase fracture-grouting mass. Chin. J. Rock Mech. Eng. 2020, 39 (Suppl. 1), 2804–2817. [Google Scholar] [CrossRef]
- Zong, Y.; Han, L.; Han, G. Experimental study on mechanical properties of confined grouting reinforcement body of fractured rock mass. J. Min. Saf. Eng. 2013, 30, 483–488. [Google Scholar]
- Wang, Z.; Qin, W.; Zhang, L. Experimental study on static and dynamic mechanical properties of cracked rock after grouting reinforcement body. Chin. J. Rock Mech. Eng. 2020, 39, 2451–2459. [Google Scholar] [CrossRef]
- Le, H.; Sun, S. Effects of grouting material and inclination angle of preexisting flaw on uniaxial compressive strength and failure mode of rock-like specimens. Rock Soil Mech. 2018, 39, 211–219. [Google Scholar] [CrossRef]
- Feng, G.; Ma, J.; Li, Z.; Qi, T.; Cui, J.; Guo, W.; Zhao, Y.; Hou, B. Bearing characteristics and damage mechanism of grouting reinforced body for broken surrounding rock. J. China Coal Soc. 2023, 48, 411–423. [Google Scholar] [CrossRef]
- Liu, R.; Zheng, Z.; Li, S.; Yang, H. Mechanical properties of fractured rock mass with consideration of grouting reinforcement. Chin. J. Highw. Transp. 2018, 31, 284–291. [Google Scholar]
- Rong, M. Study on the Mechanical Behavior and Failure Mechanism of the Fractured Surrounding Rock by Grouting Reinforcement Body. Ph.D. Dissertation, Shijiazhuang Tiedao University, Shijiazhuang, China, 2022. [Google Scholar]
- Hu, W.; Sui, W.; Wang, D.; Ma, L. Experimental investigation on mechanical properties and representative elementary volume for chemically grouted fractured rock masses. China Sci. Pap. 2013, 8, 408–412. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, W.; Zhao, A.; Guo, W. Shear Strength and Re-Failure Characteristics of Intact Red Sandstone and Grouting-Reinforced Body of Fractured Red Sandstone under Different Shear Angles. Minerals 2022, 12, 1580. [Google Scholar] [CrossRef]
- Wang, K.; Li, N. Numerical simulation on effects of reservoir characteristics and saturation on T2 spectra of nuclear magnetic resonance. Acta Pet. Sin. 2009, 30, 422–426. [Google Scholar]
- AlGhamdi, T.M.; Arns, C.H.; Eyvazzadeh, R.Y. Correlations between NMR-relaxation response and relative permeability from tomographic reservoir-rock images. SPE Reserv. Eval. Eng. 2013, 16, 369–377. [Google Scholar] [CrossRef]
- Li, J.; Kaunda, R.B.; Zhou, K. Experimental investigations on the effects of ambient freeze-thaw cycling on dynamic properties and rock pore structure deterioration of sandstone. Cold Reg. Sci. Technol. 2018, 154, 133–141. [Google Scholar] [CrossRef]
- Zhang, J.; Deng, H.; Deng, J.; Gao, R. Fractal analysis of pore structure development of sandstone: A nuclear magnetic resonance investigation. IEEE Access 2019, 7, 47282–47293. [Google Scholar] [CrossRef]
- De Quervain, F. Technische Gesteinskunde. In Lehrbücher und Monographien aus dem Gebiete der exakten Wissenschaften. Mineralogisch-geotechnische Reihe, Bd 1; Birkhäuser: Basel, Switzerland, 1967. [Google Scholar]
- Dubinin, M.M. Micropore structures of charcoal adsorbents. 1. A general characterization of micro- and supermicropores in the fissure model. Proc. Acad. Sci. USSR 1979, 8, 1691–1696. [Google Scholar]
- Gregg, S.J.; Sing, K.S.W. Adsorption, Surface Area and Porosity. Academic Press: London, UK, 1982. [Google Scholar]
- Klopfer, H. Feuchte. In Lehrbuch der Bauphysik; Lutz, P., Jenisch, R., Klopfer, H., et al., Eds.; Teubner Verlag: Stuttgart, Germany, 1985. [Google Scholar]
- DIN 66131; Bestimmung der spezifischen Oberfläche von Feststoffen durch Gasadsorption nach Brunauer, Emmett und Teller (BET). Beuth Verlag: Berlin, Germany, 1993.
- Kodikara, J.; Barbour, S.L.; Fredlund, D.G. Changes in clay structure and behavior due to wetting and drying. Aust. Geomech. 1999, 8. [Google Scholar]
- He, Y.; Mao, Z.; Xiao, L.; Zhang, Y. A new method for constructing capillary pressure curves by using T2 distribution of NMR. J. Jilin Univ. 2005, 35, 177–181. [Google Scholar]
- Lønøy, A. Making sense of carbonate pore systems. AAPG Bull. 2006, 90, 1381–1405. [Google Scholar] [CrossRef]
- Yan, J.; Wen, D.; Li, Z.; Bin, G.; Jin-Gong, C.; Qiang, L.; Yu, Y. Quantitative evaluation method for pore structure of low permeability sandstone based on NMR logging: Taking sand four segments of south slope of Dongying sag as an example. J. Geophys. 2016, 59, 1543–1552. [Google Scholar]
- Fang, T.; Zhang, L.; Liu, N.; Zhang, L.; Wang, W.; Yu, L.; Li, C.; Lei, Y. Quantitative characterization of pore structure of tight sandstone gas reservoirs by NMR technique: Taking Carboniferous-Permian tight sandstone reservoirs in eastern Linqing depression as an example. Acta Pet. Sin. 2017, 38, 902–915. [Google Scholar]
- Deprez, M.; De Kock, T.; De Schutter, G.; Cnudde, V. A review on freeze-thaw action and weathering of rocks. Earth-Sci. Rev. 2020, 203, 103143. [Google Scholar] [CrossRef]
- Momeni, A.; Abdilor, Y.; Khanlari, G.R.; Heidari, M.; Sepahi, A.A. The effect of freeze–thaw cycles on physical and mechanical properties of granitoid hard rocks. Bull. Eng. Geol. Environ. 2016, 75, 1649–1656. [Google Scholar] [CrossRef]
- Hosseini, M.; Khodayari, A.R. Effect of freeze-thaw cycle on strength and rock strength parameters (A Lushan sandstone case study). J. Min. Environ. 2019, 10, 257–270. [Google Scholar]
- Mousavi, S.Z.S.; Tavakoli, H.; Moarefvand, P.; Rezaei, M. Assessing the effect of freezing-thawing cycles on the results of the triaxial compressive strength test for calc-schist rock. Int. J. Rock Mech. Min. Sci. 2019, 123, 104090. [Google Scholar] [CrossRef]
- Webber, J.B.W.; Corbett, P.; Semple, K.T.; Ogbonnaya, U.; Teel, W.S.; Masiello, C.A.; Fisher, Q.J.; Valenza, J.J., II; Song, Y.Q.; Hu, Q. An NMR study of porous rock and biochar containing organic material. Microporous Mesoporous Mater. 2013, 178, 94–98. [Google Scholar] [CrossRef]
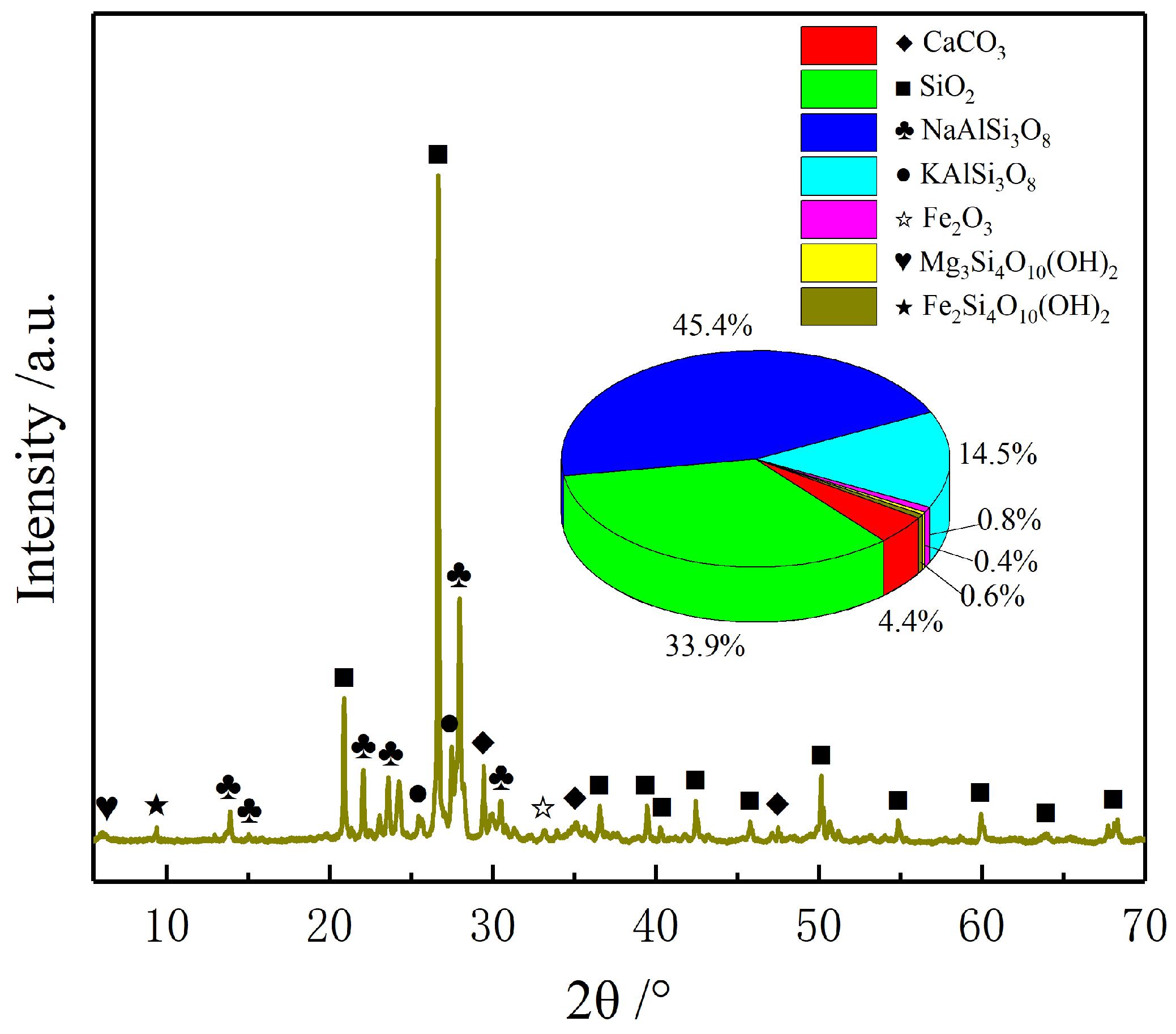

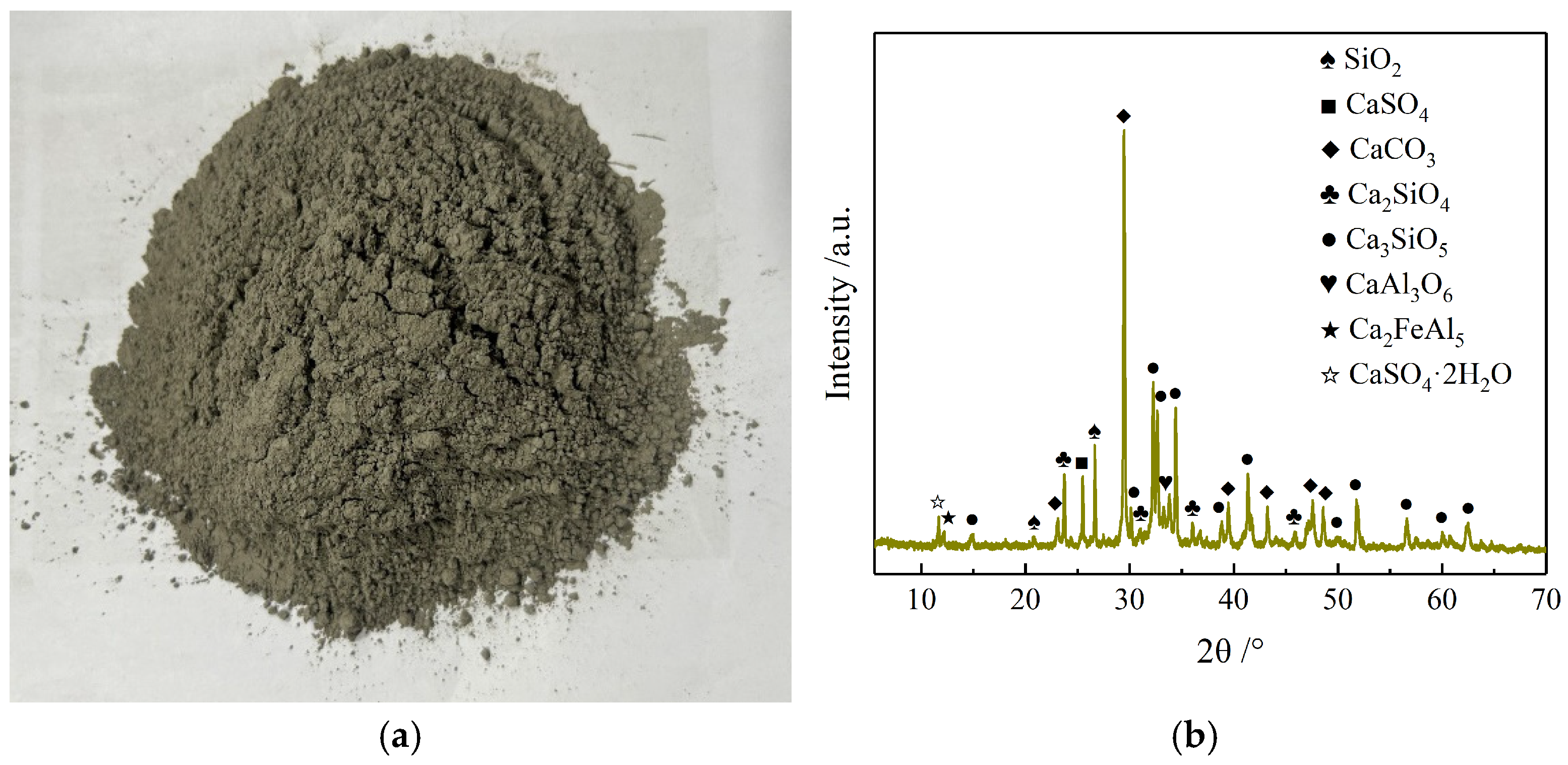











| Components | SiO2 | CaCO3 | Ca2(SiO4) | Ca3(SiO4)O | Ca2FeAlO5 | Ca3(Al2O6) | Ca(SO4)(H2O)2 | Ca(SO4) |
|---|---|---|---|---|---|---|---|---|
| Cement/% | 3.8 | 27.5 | 18.8 | 32.0 | 10.1 | 3.5 | 0.5 | 3.8 |
| (μm/ms) | Water | Clay | Solids |
|---|---|---|---|
| Water | 0.000 | 0.010 | 0.003 |
| Clay | 0.010 | 0.010 | 0.003 |
| Solids | 0.003 | 0.003 | 0.000 |
| Reference | Micropore/μm | Mesopor/μm | Macropore/μm |
|---|---|---|---|
| De Quervain (1967) [28] | <5 | 5–200 | 200–2000 |
| Dubinin (1979) [29] | (0.0012–0.0014) (0.003–0.0032) | (0.003–0.0032)– (0.2–0.4) | >(0.2–0.4) |
| IUPAC (Gregg and Sing1982) [30] | <0.002 | 0.002–0.05 | >0.05 |
| Klopfer (1985) [31] | <0.1 | 0.1–1000 | >1000 |
| DIN66131 (1993) [32] | <0.002 | 0.002–0.05 | >0.05 |
| Kodikara et al. (1999) [33] | 1–30 | — | 10–1000 |
| He Yudan et al. (2005) [34] | <10 | >10 | |
| Lonoy (2006) [35] | 10–50 | 50–100 | >100 |
| Yan Jianping et al. (2016) [36] | <0.1 | 0.1–1 | >1 |
| Fang Tao et al. (2017) [37] | <0.1 | 0.1–1 | 1–5 |
| Freeze–Thaw Cycles | Micropore | Mesopore | Macropore | Total T2 Spectral Area |
|---|---|---|---|---|
| 0 | 9931.66 | 3053.76 | 220.48 | 13,205.90 |
| 5 | 10,553.34 | 3454.50 | 324.23 | 14,332.07 |
| 10 | 11,098.72 | 4522.72 | 597.62 | 16,219.06 |
| 15 | 12,323.45 | 5610.13 | 1002.85 | 18,936.43 |
| 20 | 12,529.08 | 6304.11 | 1557.66 | 20,390.85 |
| 25 | 13,089.59 | 8455.29 | 2400.37 | 23,945.25 |
| 30 | 13,096.60 | 9293.20 | 3660.87 | 26,050.67 |
| Crack Dip Angle | Freeze–thaw Cycles | Fitting Equation | R2 | C/MPa | /° |
|---|---|---|---|---|---|
| 0° | 0 | 0.984 | 13.12 | 47.40 | |
| 5 | 0.969 | 13.69 | 42.52 | ||
| 10 | 0.961 | 14.04 | 39.67 | ||
| 15 | 0.965 | 11.49 | 42.48 | ||
| 20 | 0.967 | 10.36 | 41.60 | ||
| 25 | 0.943 | 9.33 | 41.02 | ||
| 30 | 0.910 | 7.77 | 41.98 | ||
| 30° | 0 | 0.992 | 11.24 | 48.37 | |
| 5 | 0.947 | 11.01 | 43.85 | ||
| 10 | 0.909 | 10.32 | 43.28 | ||
| 15 | 0.953 | 9.19 | 42.19 | ||
| 20 | 0.927 | 8.19 | 39.96 | ||
| 25 | 0.895 | 6.72 | 41.51 | ||
| 30 | 0.876 | 6.33 | 38.35 | ||
| 45° | 0 | 0.940 | 6.62 | 52.16 | |
| 5 | 0.978 | 7.18 | 45.65 | ||
| 10 | 0.964 | 7.06 | 44.29 | ||
| 15 | 0.958 | 5.45 | 44.69 | ||
| 20 | 0.988 | 3.82 | 45.31 | ||
| 25 | 0.988 | 2.66 | 44.44 | ||
| 30 | 0.944 | 1.90 | 41.85 | ||
| 30° | 0 | 0.890 | 7.34 | 39.37 | |
| 5 | 0.840 | 6.52 | 38.56 | ||
| 10 | 0.854 | 6.01 | 37.82 | ||
| 15 | 0.806 | 5.19 | 34.87 | ||
| 20 | 0.881 | 4.08 | 34.74 | ||
| 25 | 0.853 | 3.42 | 30.57 | ||
| 30 | 0.897 | 2.04 | 23.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Zhang, J.; Yu, Z.; Zhang, T.; Zhang, J. An Experimental Study on Physical and Mechanical Properties of Fractured Sandstone Grouting Reinforcement Body Under Freeze–Thaw Cycle. Appl. Sci. 2025, 15, 2801. https://doi.org/10.3390/app15052801
Liu S, Zhang J, Yu Z, Zhang T, Zhang J. An Experimental Study on Physical and Mechanical Properties of Fractured Sandstone Grouting Reinforcement Body Under Freeze–Thaw Cycle. Applied Sciences. 2025; 15(5):2801. https://doi.org/10.3390/app15052801
Chicago/Turabian StyleLiu, Shujie, Jiwei Zhang, Zhijie Yu, Tongzhao Zhang, and Jiahao Zhang. 2025. "An Experimental Study on Physical and Mechanical Properties of Fractured Sandstone Grouting Reinforcement Body Under Freeze–Thaw Cycle" Applied Sciences 15, no. 5: 2801. https://doi.org/10.3390/app15052801
APA StyleLiu, S., Zhang, J., Yu, Z., Zhang, T., & Zhang, J. (2025). An Experimental Study on Physical and Mechanical Properties of Fractured Sandstone Grouting Reinforcement Body Under Freeze–Thaw Cycle. Applied Sciences, 15(5), 2801. https://doi.org/10.3390/app15052801






