Entropy-Guided Distributional Reinforcement Learning with Controlling Uncertainty in Robotic Tasks

Abstract

This study proposes a novel approach to enhance the stability and performance of reinforcement learning (RL) in long-horizon tasks. Overestimation bias in value function estimation and high uncertainty within environments make it difficult to determine the optimal action. To address this, we improve the truncated quantile critics algorithm by managing uncertainty in robotic applications. Our dynamic method adjusts the discount factor based on policy entropy, allowing for fine-tuning that reflects the agent’s learning status. This enables the existing algorithm to learn stably even in scenarios with limited training data, ensuring more robust adaptation. By leveraging policy entropy loss, this approach effectively boosts confidence in predicting future rewards. Our experiments demonstrated an 11% increase in average evaluation return compared to traditional fixed-discount-factor approaches in the DeepMind Control Suite and Gymnasium robotics environments. This approach significantly enhances sample efficiency and adaptability in complex long-horizon tasks, highlighting the effectiveness of entropy-guided RL in navigating challenging and uncertain environments.

1. Introduction

Recently, there has been a surge in research focusing on managing uncertainty in long-horizon and high-dimensional reinforcement learning (RL) tasks [1,2,3,4,5]. High uncertainty can lead to instability in policy learning and make it difficult to determine the optimal action [6,7,8]. Uncertainty can be divided into two categories: aleatoric uncertainty and epistemic uncertainty. Aleatoric uncertainty refers to the inherent and unpredictable variability present in the environment, while epistemic uncertainty arises from incomplete or insufficient knowledge in the model. Distributional reinforcement learning has gained attention for its capability to improve agent performance by estimating aleatoric uncertainty. The approach considers the complete reward distribution rather than the expected reward value [1,9,10].

The distributional RL builds upon the traditional Q-learning algorithm by predicting the reward distribution for each state–action pair. This method facilitates better decision-making, particularly in highly uncertain environments, and allows agents to acquire more stable and robust policies. By modeling the entire reward function distribution and leveraging more information, agents can effectively estimate uncertainty about the reward. For instance, the categorical DQN (C51) estimates the distribution using fixed atom values [11], the QR-DQN estimates the entire distribution of rewards using fixed quantile levels [12], and the IQN approximates the distribution using implicit quantiles that learn sampled quantile fractions rather than fixed ones [13]. Offline RL is a crucial component for achieving broad generalization in various robot learning processes as it utilizes historical (offline) data without necessitating interaction with environments. However, the distribution shift, which refers to the difference between the distributions of the offline learned policy and the learning policy, is one of the main challenges [14,15,16]. Moreover, when previous experiences are shuffled and reused to improve sample efficiency, estimating uncertainty is particularly challenging [17,18,19].

In this study, we introduced a new method for managing uncertainty by adaptively modifying the discount factor using policy entropy within the MaxEnt framework [20], of the Soft Actor–Critic (SAC) algorithm [21]. The discount factor plays a crucial role in determining how much an agent values future rewards, impacting the performance of the RL algorithm and future uncertainty. If the agent learns consistently, and the entropy loss value decreases, the discount factor is increased to prioritize future rewards. Conversely, if the entropy loss value is high, indicating significant action randomness, the discount factor is decreased to reduce emphasis on future rewards. This method enhances sample efficiency by estimating epistemic uncertainty, thereby balancing reward maximization with exploration more effectively. Our aim is to modify this parameter by considering the policy entropy loss. This will help us evaluate the learning instability and estimate the environmental uncertainty, ultimately improving the overall performance and learning stability of the agent. We propose an enhanced algorithm called Entropy-Guided Truncated Quantile Critics (EG-TQC). It combines distributional RL with a method for adjusting the dynamic discount factor, which was previously used in the Truncated Quantile Critics (TQC) algorithm [22]. The TQC algorithm mitigates overestimation bias by combining the output distributions of multiple critics and eliminating extreme values. This approach is particularly effective in managing complex state–action spaces. However, the TQC algorithm has some limitations concerning epistemic uncertainty, including sensitivity to hyperparameters and reduced data efficiency during the learning process [23,24].

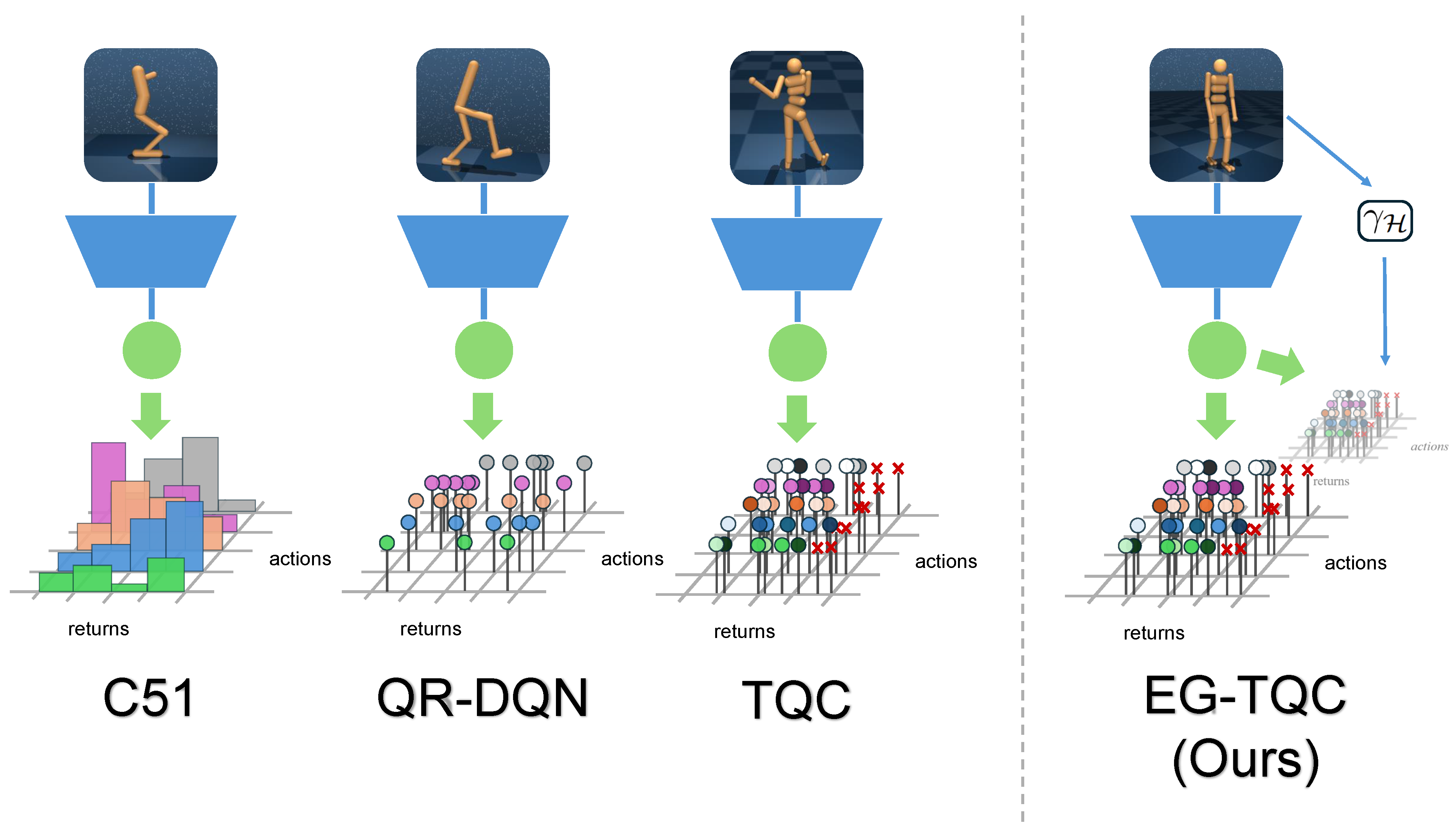
As shown in Figure 1, we enhanced the TQC algorithm by incorporating a dynamic discount factor adjustment method, leading to an improved and more consistent learning performance. In the distributional RL, the discount factor is essential in scaling the reward distribution, making it more effective than the generic hyperparameter tuning. Our approach involves evaluating the reliability of the future reward data based on policy entropy and adjusting the discount factor accordingly resulting in enhanced stability and data efficiency.

In our evaluation of the EG-TQC method using robotic tasks in the Mujoco environment of the DeepMind Control Suite, we found that it eliminates the need to search for the optimal discount factor for each environment. Additionally, it outperforms the TQC algorithm trained with various fixed discount factors. Furthermore, we extended the evaluation to more complex and higher-dimensional environments, specifically the robotic arm control tasks provided by Gymnasium robotics environments. Using our proposed method in combination with a Hindsight Replay Buffer [25], we demonstrated that the EG-TQC method performs exceptionally well, even in high-dimensional control environments.

The key contributions of this paper are as follows:

• Policy entropy-based adaptive discount factor adjustment:
  In conventional reinforcement learning algorithms, the discount factor ($\gamma$) is fixed, limiting its adaptability to different environments and learning states. In this study, we propose a method that dynamically adjusts the discount factor based on policy entropy, allowing the agent to reflect its learning state. This approach enables the agent to prioritize future rewards in stable learning conditions while focusing on short-term rewards in highly uncertain situations.
• Integration of distributional RL with adaptive discount factor adjustment:
  We integrate the proposed entropy-based adaptive discount factor adjustment into the TQC algorithm, enhancing its robustness in highly uncertain environments. This improvement allows the algorithm to achieve better learning efficiency and maintain stable performance across various environments compared to standard TQC.
• Empirical validation in robotic environments:
  To verify the performance of EG-TQC, we conducted extensive experiments in the Mujoco environment of the DeepMind Control Suite and the Gymnasium robotic control environments. The results show that EG-TQC achieves an average of 11% higher evaluation returns compared to TQC with fixed discount factors. Additionally, experiments incorporating Hindsight Replay Buffer demonstrated the generalizability of the proposed method, proving its superior performance and stability in high-dimensional environments.

2. Background

2.1. Distributional Reinforcement Learning

Standard RL models the expected value of a random return for a specific action in a given state using Q-learning. An agent is modeled as a Markov Decision Process (MDP) consisting of $(\mathcal{S},\mathcal{A},R,P,\gamma )$. $\mathcal{S}$ and $\mathcal{A}$ represent the state and action spaces, respectively. R is the reward, P is the transition probability, and $\gamma$ is the discount factor. The agent makes decisions based on a policy $\pi \left(a\right|s)$ that maps state $s\in S$ to actions $a\in A$.

The Q-learning method is to model the value function $Q_{\pi }$ as the following Bellman equation:

$$Q(s,a)=\mathbb{E}\left[R(s,a)\right]+\gamma \mathbb{E}\left[Q\left(S^{\prime },A^{\prime }\right)\right],$$

where the random variables $S^{\prime }$ and $A^{\prime }$ are distributed according to $P(·\mid s,a)$ and $\pi \left(·\mid s^{\prime }\right)$. RL aims to determine the optimal policy ${\pi }^{*}$ by maximizing the cumulative rewards, which in turn involves finding the optimal $Q^{*}$ function. This can be performed by iteratively applying the Bellman update to improve the estimated $Q_{\theta }$ as the parameterized optimal $Q^{*}$ function.

$$Q_{\theta }(s,a)\leftarrow \mathbb{E}\left[R(s,a)\right]+\gamma \mathbb{E}\left[\underset{a^{\prime }}{max}{Q}_{\theta }\left(s^{\prime },a^{\prime }\right)\right]$$

The distributional RL models the entire probability distribution of the random return rather than its expected value, showing improvements in sample diversity and performance. Rather than using the Q-function, the Z-distribution is used to model the return distribution for the state–action pairs.

$$Z^{\pi }(s,a)\stackrel{D}{=}R(s,a)+\gamma Z^{\pi }\left(S^{\prime },A^{\prime }\right),$$

where A $\stackrel{D}{=}$ B denotes the equality of the probability laws. The Q function is calculated as follows:

$$Q^{\pi }(s,a)=\mathbb{E}\left[Z^{\pi }(s,a)\right]=\mathbb{E}\left[\sum _{t=0}^{\infty }{\gamma }^{t}R(s_t,a_t)\right],$$

$$\begin{array}{c}\hfill x_t\sim P(·\mid s_{t-1},a_{t-1}),a_t\sim \pi (·\mid s_t),s_0=s,a_0=a.\end{array}$$

Modeling the entire probability distribution of returns can provide more information than before.

The C51 algorithm [11] utilizes a categorical distribution to represent the return distribution over a fixed set of equidistant points and aims to minimize the KL divergence to the projected distributional Bellman target.

$$Z^{\pi }(s,a):=\sum _{i=1}{p}_i{\delta }_{z_i},$$

where $z_i$ is a fixed set of return values and $\delta$ is the Dirac delta function. The C51 outperformed previous DQN variants on the Atari-57 benchmark.

QR-DQN [12] addresses the limitation of C51 by approximating the return distribution $Z^{\pi }(s,a)$ as follows:

$$Z_{\psi }(s,a):={\displaystyle \frac{1}{M}}\sum _{m=1}^M\delta \left({\theta }_{\psi }^m(s,a)\right),$$

where M denotes the number of atoms in the distribution and ${\theta }_{\psi }^m(s,a)$ is the Dirac delta function at locations. This is a mixture of atoms provided by a parametric model ${\theta }_{\psi }:S\times A\to {\mathbb{R}}^M$. The $\psi$ is the parameter of target network and can be optimized by minimizing the 1-Wasserstein distance [26] between the temporal difference target distribution $T^{\pi }{Z}_{\psi }$ and $Z_{\psi }$.

The distributional RL models the distribution of returns, enabling an agent to consider various potential returns. This increases the diversity of the sample data and improved the learning performance of the agent [27]. According to Clements et al. [1], the overall uncertainty of an agent can be divided into epistemic uncertainty and aleatoric uncertainty. By modeling the reward distribution, the agent gains a better understanding of aleatoric uncertainty. This involves comparing the return distributions using various probability metrics and studying the convergence properties of the distributional Bellman operator. As distributional reinforcement learning effectively estimates aleatoric uncertainty, we aim to enhance stability and efficiency further by utilizing policy entropy values to estimate epistemic uncertainty.

2.2. Truncated Quantile Critics

The TQC algorithm employs quantile regression to approximate the target distribution in the same manner as the QR-DQN.

$$Z(s,a)={\displaystyle \frac{1}{M}}\sum _{m=1}^M\delta \left({\theta }^m(s,a)\right)$$

TQC employs an ensemble of N networks where each network n predicts the distribution $Z_{{\psi }_n}$:

$$Z_{{\psi }_n}(s,a):={\displaystyle \frac{1}{M}}\sum _{m=1}^M\delta \left({\theta }_{{\psi }_n}^m(s,a)\right).$$

A single Bellman target distribution was computed for all networks. This is achieved by first computing all targets for all networks, pooling all targets $Z_{{\psi }_1}(s^{\prime },a^{\prime }),\dots ,Z_{{\psi }_N}(s^{\prime },a^{\prime })$ into one set, and then sorting them in ascending order. The $kN$ smallest of these targets $y_i$ are used to define the target distribution.

TQC approximates the locations for quantile fractions ${\tau }_m$, where $m\in [1\dots M]$ with ${\theta }_{{\psi }_n}^1(s,a),\dots ,{\theta }_{{\psi }_n}^M(s,a)$ by minimizing

$$J_Z\left({\psi }_n\right)={\mathbb{E}}_{\mathcal{D},\pi }\left[{\mathcal{L}}^k\left(s_t,a_t;{\psi }_n\right)\right].$$

The parameters ${\psi }_n$ are trained by minimizing the quantile Huber loss given by the following:

$${\mathcal{L}}^k\left(s,a;{\psi }_n\right)={\displaystyle \frac{1}{kNM}}\sum _{m=1}^M\sum _{i=1}^{kN}{\rho }_{{\tau }_m}^H\left(y_i(s,a)-{\theta }_{{\psi }_n}^m(s,a)\right),$$

where ${\rho }_{\tau }^H\left(u\right)=|\tau -\mathbb{I}(u<0)|{\mathcal{L}}_H^1\left(u\right)$ is the Huber quantile loss and ${\mathcal{L}}_H^1\left(u\right)$ is the Huber loss with parameter 1.

The rationale behind truncating some quantiles from the target distribution was to prevent overestimation bias. In TQC, the number of dropped targets per network $d=M-k$ is a hyperparameter that must be tuned per environment, allowing for fine-grained control of the bias.

The TQC algorithm utilizes multiple critic networks to effectively manage uncertainty. Each network is trained on distinct data subsets, leading to diverse predictions. This ensemble technique improved the stability of the model and prevented overfitting. Moreover, employing multiple networks aids in capturing environmental variability more effectively, thereby enabling more reliable decision-making in unexpected scenarios

The policy parameter $\varphi$ is trained similarly to SAC by maximizing the entropy-penalized estimate of the Q-value, which is the expectation over the distribution obtained from the critic:

$$J_{\pi }\left(\varphi \right)={\mathbb{E}}_{\mathcal{D},\pi }\left[\alpha \log {\pi }_{\varphi }(a\mid s)-{\displaystyle \frac{1}{NM}}\sum _{m,n=1}^{M,N}{\theta }_{{\psi }_n}^m(s,a)\right].$$

This method encourages the agent to explore more by maximizing entropy. This allows the agent to explore the environment better and reach new states, ultimately leading to the development of a better long-term strategy. Another important advantage of the TQC is its stability. The TQC algorithm gathers and uses more information for each state–action pair, improving the sample efficiency, which is crucial in data-limited scenarios. By explicitly modeling uncertainty, the TQC algorithm enables agents to make more reliable decisions and better handle the complexity and variability of the environment. Thus, TQC improves upon existing methods by explicitly modeling the distribution of returns and using an ensemble of networks to better handle inherent uncertainty and variability in RL environments. This helps reduce the overestimation bias and ultimately enhances the performance and stability of the agent. The TQC algorithm is particularly effective in high-dimensional and complex environments and can significantly improve the performance of RL agents in various applications.

However, since the target distribution is adjusted by removing extreme quantiles, some useful training data may be lost, reducing sample efficiency. This issue becomes more pronounced, especially in the early stages of training when data are limited, and it can cause TQC to require more data compared to conventional RL methods. Additionally, TQC requires experimental tuning of hyperparameters such as the number of quantiles (M), the number of retained quantiles (k), and the discount factor ($\gamma$). If appropriate values are not found during this process, training performance may degrade, making it difficult to ensure consistent optimal performance across various environments. To address these limitations, this study proposes EG-TQC, which integrates a dynamic discount factor adjustment mechanism based on policy entropy. This approach reduces the burden of hyperparameter tuning while maximizing the utilization of training data, thereby improving sample efficiency.

2.3. Discount Factor

The discount factor, denoted as $\gamma$, is a crucial parameter in RL. It determines the importance of future rewards in comparison to immediate rewards. The value of $\gamma$ falls within the range of 0 to 1. A value closer to 1 indicates that future rewards are considered almost as important as immediate rewards, while a value closer to 0 indicates that the agent prioritizes immediate rewards more significantly. In distributional RL, the discount factor is crucial for scaling the output distribution to calculate the reward accurately. It plays a pivotal role in considering the reliability of future rewards.

Research on analyzing and integrating the discount factor into RL is ongoing. Hu et al. [28] pointed out that in offline RL, lower values of $\gamma$ can introduce pessimism by optimizing policy performance under worst-case scenarios while also acting as a regularization term to improve sample efficiency. Fedus et al. [29] used a geometric discount factor to learn multiple values using an ensemble method. Tessler and Mannor [30] proposed a method to learn a surrogate reward function $\tilde{r}$ rather than using the discount factor for planning, to maintain optimal behavior. Furthermore, several studies explored dynamically adjusting the discount factor during training to better balance immediate and future rewards according to the agent’s situation [31,32,33,34,35]. Therefore, it was confirmed that the meaning of the discount factor can be broadly analyzed and, by combining it with other concepts to control it variably, the learning efficiency and stability of the agent can be enhanced according to its environment.

3. Entropy Guided Truncated Quantile Critics

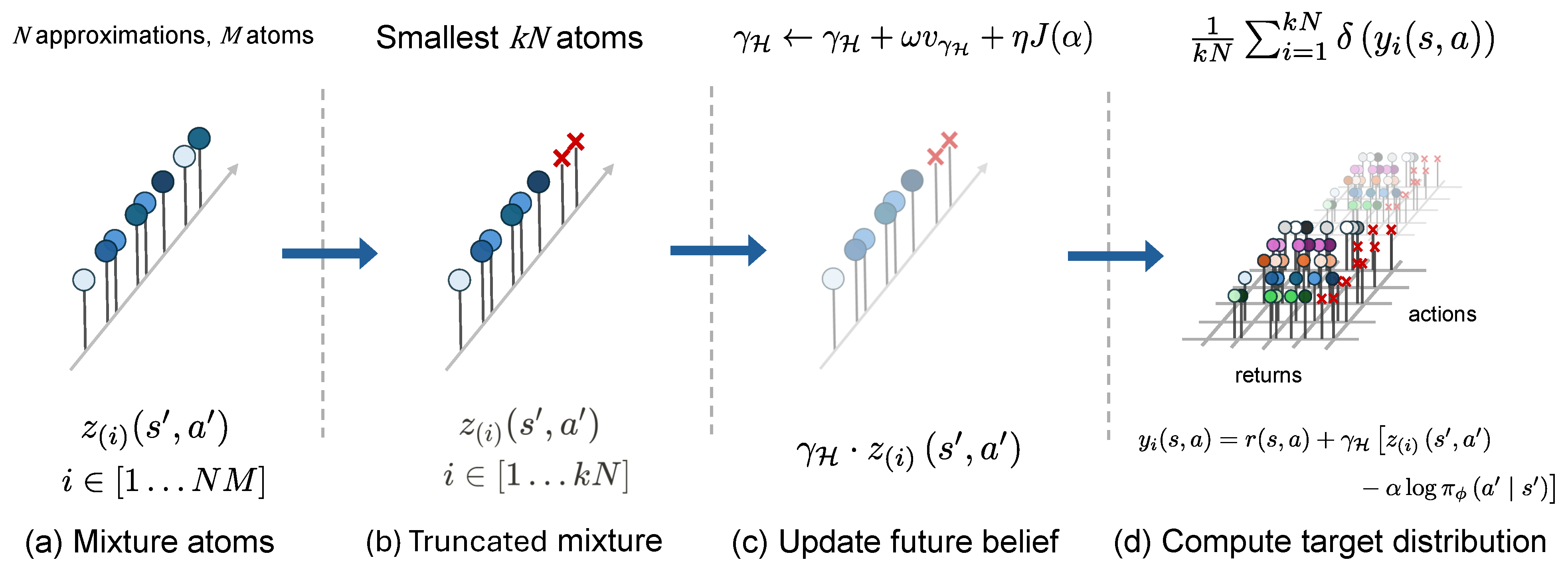
Typical RL training models use a static discount factor to uniformly decrease the weight of future rewards. However, this approach can be challenging for complex tasks where the significance of future rewards varies. In deep RL, the discount factor scales the future reward distribution, thereby making it more sensitive. To address these issues, we propose dynamically adjusting the discount factor based on policy entropy. This adjustment allows us to modify the trustworthiness of future rewards according to the learning situation of the agent. By integrating this approach with the TQC algorithm, our method helps control the overestimation bias and aleatoric uncertainty using multiple critics and truncating atoms. This combination mitigates sample efficiency degradation and aids in estimating the epistemic uncertainty (Figure 2).

3.1. Entropy Guided Discount Factor

We used entropy loss to assess the dependability of future rewards when an agent chooses an action in a given state. The entropy temperature coefficient $\alpha$ is determined by calculating the entropy loss, as defined by Haarnoja et al. (2018) [36] as follows:

$$J\left(\alpha \right)={\mathbb{E}}_{\mathcal{D},{\pi }_{\varphi }}\left[\log \alpha ·\left(-\log {\pi }_{\varphi }\left(a_t\mid s_t\right)-{\mathcal{H}}_T\right)\right],$$

where ${\mathcal{H}}_T$ is the target entropy with regard to the dimension of action space denoted by $-\dim \mathcal{A}$. If ${\mathcal{H}}_T$ is higher than the stochastic estimate of policy entropy $-\log {\pi }_{\varphi }\left(a_t\right|s_t)$, $\alpha$ is increased, and vice versa. We use this to measure the reliability of future rewards. As the agent learns, we use the entropy loss to measure the decrease in the predictability of future rewards. When the entropy loss is low, indicating reduced uncertainty, we decrease the discount factor to help the agent focus more on the current rewards in uncertain learning scenarios. Conversely, when the entropy loss is high, we increase the discount factor to reflect a higher certainty about rewards in the distant future. The method uses the already computed entropy loss to determine the entropy coefficient. This provides extra information about the reliability of future rewards without needing additional computation during the learning process. This approach helps to estimate the uncertainty of the agent.

Because the entropy loss value changes rapidly, we used the concept of momentum to track the trend of an agent’s action uncertainty in the learning process to avoid confusion.

$${\gamma }_{\mathcal{H}}\leftarrow {\gamma }_{\mathcal{H}}+\omega v_{{\gamma }_{\mathcal{H}}}+\eta J\left(\alpha \right)$$

where $\eta$ represents the learning rate of the discount factor, and $\omega$ is the momentum coefficient, and $v_{{\gamma }_t}$ represents the velocity of the discount factor. This approach allows the agent to dynamically adjust the discount factor based on the uncertainty during the learning process. The rate at which the discount factor changes varies depending on the task or the stage of learning. This is because the agent shows different learning tendencies based on the specific characteristics of tasks or whether the agent is in the early or mid-stage of training.

3.2. Entropy Guided TQC

We incorporated a variable discount factor based on entropy into the TQC algorithm. When compared to other algorithms, the TQC algorithm demonstrates lower sample efficiency when training an agent with a large number of samples accumulated at moderate performance levels [23]. It effectively mitigates overestimation bias and aleatoric uncertainty by ensembling and trimming the output distributions of multiple critics. However, it struggles to differentiate epistemic uncertainty and is sensitive to hyperparameters. In this paper, we use the entropy loss to adjust the reliability of the agent’s future rewards as shown in Algorithm 1. This discount factor update is efficient because it utilizes the pre-existing entropy loss $J\left(\alpha \right)$, which is already calculated during the process of computing the TQC policy loss. Therefore, no additional computation is required for the update term, providing additional information to the existing learning data and aiding the learning of the agent. This enhances the sample efficiency, facilitates faster learning convergence, and helps achieve a balance between exploration and exploitation. The reliability of the future reward obtained in this way is used as follows:

$$y_i(s,a)=r(s,a)+{\gamma }_{\mathcal{H}}\left[z_{\left(i\right)}\left(s^{\prime },a^{\prime }\right)-\alpha \log {\pi }_{\varphi }\left(a^{\prime }\mid s^{\prime }\right)\right],$$

where $z_{\left(i\right)}$ refers to the atoms used to approximate the return value distribution, which was then sorted. The smallest kN atoms are then used to define the target distribution $Y(s,a)$ as follows:

$$Y(s,a)={\displaystyle \frac{1}{kN}}\sum _{i=1}^{kN}\delta \left(y_i(s,a)\right).$$

The approach aims to enhance the accuracy of predicting future rewards for agents by adjusting the discount factor based on policy entropy. This ensures that the agent appropriately considers future rewards in light of uncertainty in the environment. Adaptive adjustment allows for more flexible and responsive learning, which is particularly beneficial for complex tasks where the significance of future rewards can vary widely. Furthermore, entropy-guided adjustments help the balance of the exploration-exploitation tradeoff more effectively. During the early stages of learning, when the agent is exploring the environment and the policy entropy is high, the discount factor increases to emphasize the potential long-term benefits of exploration. Conversely, as the agent gains more experience and the policy becomes more stable (as indicated by the lower entropy), the discount factor is decreased to prioritize immediate rewards.

This approach also helps reduce the sensitivity to hyperparameters, which is a common challenge in RL algorithms. Using an entropy-based approach, the need for extensive hyperparameter tuning is minimized because the discount factor automatically adjusts to the learning context. This results in a robust learning process that can adapt to various environments without manual intervention. In addition to enhancing sample efficiency, the entropy-guided TQC algorithm demonstrated improved convergence rates. The incorporation of the momentum term into the discount factor further smooths the rapid changes in entropy, preventing the learning process from becoming erratic. This stability is crucial for maintaining a consistent performance across different training sessions and ensuring reliable outcomes.

Algorithm 1 EG-TQC

1: Initialize critic networks $Z_{{\psi }_n}$, actor network ${\pi }_{\varphi }$, and target networks $Z_{{\overline{\psi }}_n}$, $n\in [1\dots N]$ 2: Set ${\mathcal{H}}_T=-dim\mathcal{A}$, $\alpha =1$, $\omega =0.9$, ${\gamma }_{\mathcal{H}}$ with initial value 3: Initialize discount factor velocity $v_{\gamma }=0$ 4: while not converged do 5:       Sample a batch of transitions $\left\{(s,a,r,s^{\prime })\right\}$ from replay buffer 6:       for each gradient step do 7:             Compute entropy coefficient: $$\alpha \leftarrow \alpha -{\lambda }_{\alpha }{\widehat{\nabla }}_{\alpha }J\left(\alpha \right)$$ 8:             Update discount factor: $${\gamma }_{\mathcal{H}}\leftarrow {\gamma }_{\mathcal{H}}+\omega v_{{\gamma }_{\mathcal{H}}}+\eta J\left(\alpha \right)$$ 9:             Compute target quantiles 10:           Update critics by minimizing quantile Huber loss 11:           Update actor by minimizing policy loss 12:           Update target networks 13:      end for 14: end while

4. Experiments

In this study, extensive experiments were conducted on robotic control to explore complex movements and interactions in unpredictable environments. These experiments are essential for understanding how well RL algorithms can adapt and perform in real-world applications. To achieve this, we tested our algorithms in the DeepMind Control Suite [37] and fetch environments from Gymnasium robotics [38]. The DeepMind control suite offers a set of standard tasks for continuous control that are commonly used to assess the performance of RL algorithms. The Fetch environment in the Gymnasium robotics provides a variety of robotic tasks, including manipulation and navigation, creating diverse and challenging scenarios for algorithm evaluation. Both environments use the MuJoCo physics engine (version 2.1.0, developed by DeepMind),which is ideal for accurately modeling the physical interactions and dynamics of complex robotic systems. By utilizing the same physics engine across different environments, we ensured consistent simulations, allowing for a more reliable comparison of the proposed algorithm’s performance.

The robotic tasks in the experimental environments are defined as MDP, which consist of a state space $\mathcal{S}$, an action space $\mathcal{A}$, a reward function R, state transition probabilities P, and a discount factor $\gamma$. For instance, in the Hopper task of the DeepMind Control Suite, the state space $\mathcal{S}$ includes the positions, velocities, and balance states of the robot’s joints. The action space $\mathcal{A}$ consists of the magnitude and direction of the forces applied to these joints. The reward function R is designed to encourage specific behaviors, such as maintaining balance or reaching a target location within a designated time frame. The state transitions P are governed by the dynamics modeled by the MuJoCo physics engine, which predicts the next state based on the robot’s actions. The discount factor $\gamma$ determines the importance of future rewards, which is dynamically adjusted in the proposed algorithm based on entropy.

In the FetchPickAndPlace task from the Gymnasium robotics environment, the state space includes the positions of the robotic arm, the target object, and the goal location. The action space consists of the movement directions for the robotic arm and grip control actions, such as opening or closing the gripper. The reward function provides feedback based on how closely the object approaches or successfully reaches the target location. These components highlight the complexity and physical interactions involved in robotic tasks, enabling the agent to learn effectively in various environments.

We utilized the TQC algorithm in all our experiments. The TQC aims to enhance the stability and performance of RL agents by better handling the uncertainty and variability in dynamic environments. To ensure a fair comparison, we kept all other codes and parameters identical across different experimental setups. This involved using the same network architectures, learning rates, and other hyperparameters as well as maintaining consistent training protocols and evaluation metrics. The hyperparameter settings according to our experiments are listed in

Table 1. Hyperparameters used for evaluation.

	Hyper Parameters
Optimizer	Adam
Learning rate	$3\times {10}^{-4}$
Replay Buffer size	${10}^6$
Number of critics N	2
Learning rate of discount factor $\eta$	${10}^{-8}$ (DM Control Suite) ${10}^{-7}$ (Fetch)
Number of Hidden Layer in critic networks	2
size of hidden layers in critic networks	256
Number of hidden layers in policy network	2
Size of hidden layers in policy network	256
Minibatch size	256
Entropy target ${\mathcal{H}}_T$	$-\dim \mathcal{A}$
Number of atoms M	25

. Our algorithm dynamically adjusts the discount factor based on the entropy loss. The discount factor is a crucial parameter in RL, because it determines the importance of future rewards. Traditional approaches often use a fixed discount factor, which can lead to suboptimal performance in environments with varying levels of uncertainty. In contrast, our approach allows the discount factor to vary in response to the entropy loss, providing a more adaptive and flexible learning process. This dynamic adjustment aims to balance the trade-off between exploration and exploitation more effectively, thereby enhancing an agent’s ability to learn from its environment.

The optimal value for the discount factor during training varies based on the size of the action space and the length of the horizon for each task. We compared our algorithm against various fixed discount factor settings and found that it demonstrated superior performance. Fixed discount factors do not account for the changing dynamics and uncertainties in the environment, often resulting in either excessive optimism or undue pessimism in an agent’s predictions. By dynamically adjusting the discount factor, our algorithm ensures a more balanced exploration, effectively managing uncertainty and improving both the efficiency and stability of the learning process.

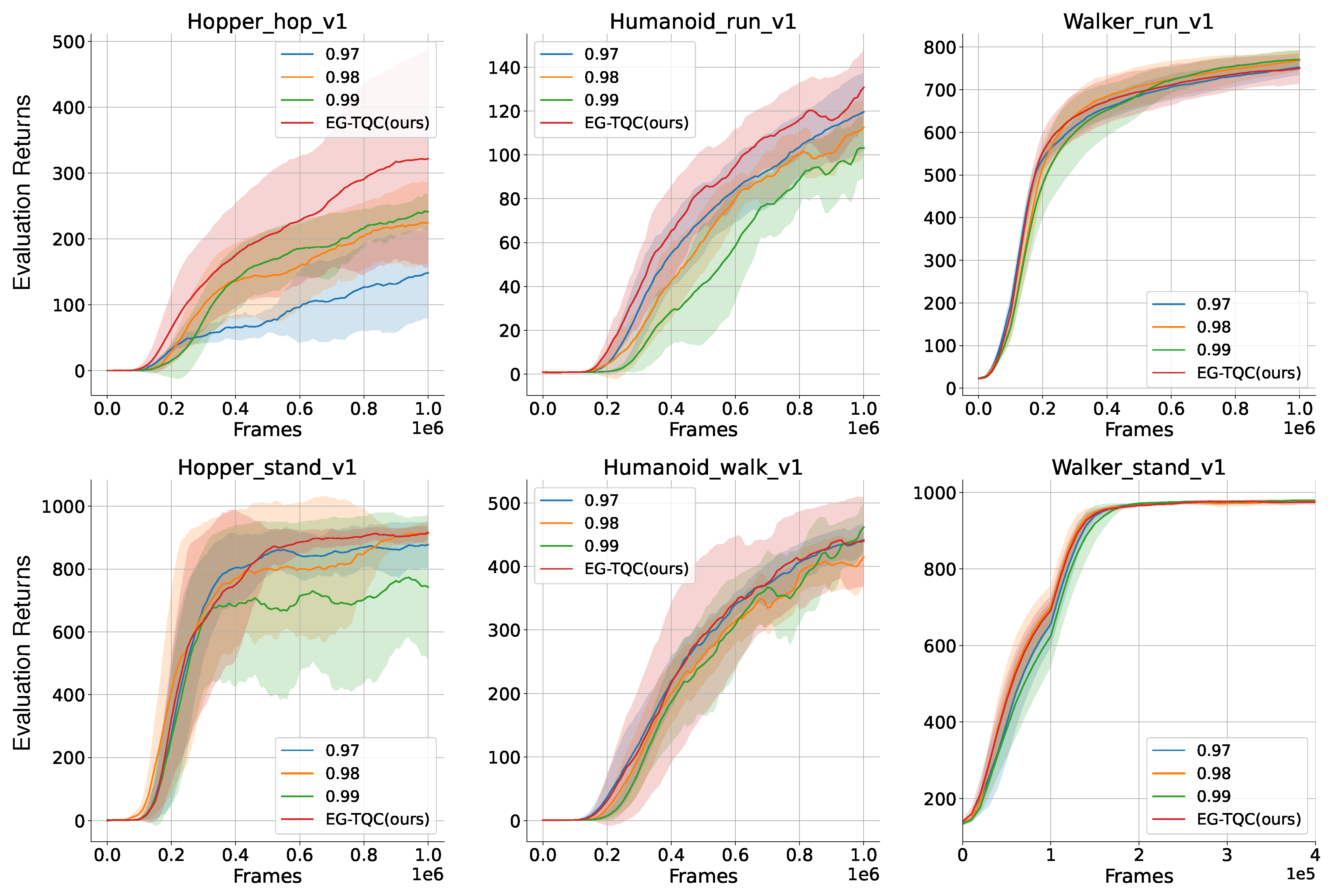
4.1. Comparative Evaluation in Robotic Task

To verify the applicability of our method across various robotic environments, we evaluated both the vanilla TQC and our EG-TQC on six benchmarks from the DeepMind control suite. The benchmarks comprised various manipulation tasks using Hopper, Humanoid, and Walker. The EG-TQC dynamically adjusts the discount factor values from ${\gamma }_{min}=0.97$ to ${\gamma }_{max}=0.99$ based on the uncertainty provided by the entropy. In contrast, the TQC was evaluated with fixed discount factor values of $\gamma =0.97$, $0.98$, and $0.99$. In Figure 3, the frames represent the amount of data the agent has processed during training, while the evaluation returns reflect the cumulative rewards received by the agent based on how well it performs the required actions. Our experimental results confirm that the EG-TQC method outperforms the basic fixed discount factor approach. The EG-TQC method enhances sample efficiency in the early stages of learning by adjusting future beliefs to modulate the contribution of learning data. Additionally, it positively impacts final learning performance and stability. Furthermore, the EG-TQC method eliminates the need for manually determining the appropriate discount factor for each task. It adjusts future reliability based on the specific situation, thereby improving overall performance.

4.2. Generality and Scalability Results

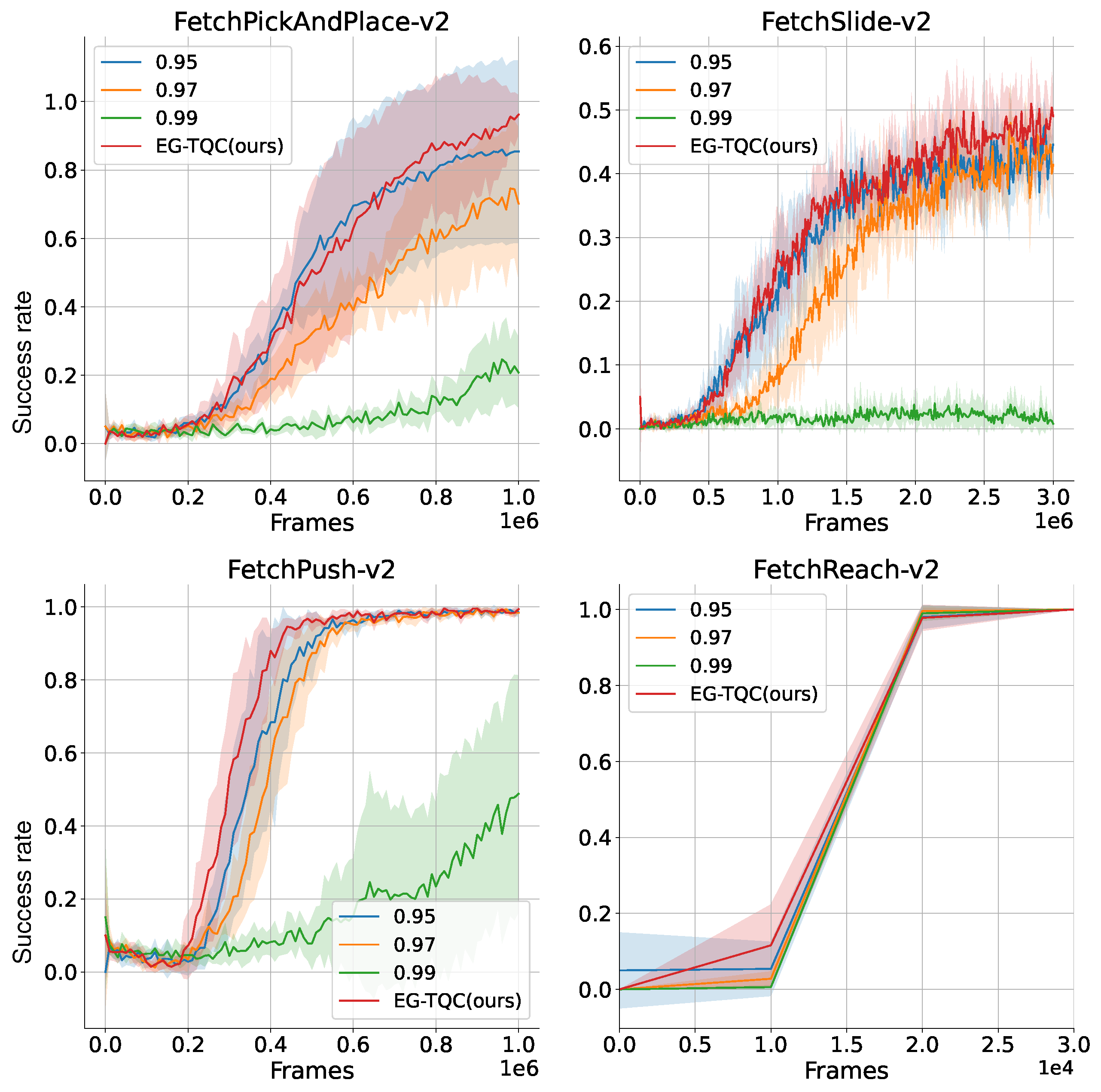
We evaluated the TQC algorithm using the Hindsight Replay Buffer on the FetchRobot of Gymnasium-robotics to assess its generality and performance in more complex environments. Owing to the complexity of the environment, the algorithm performed better with a smaller discount factor. Therefore, EG-TQC was applied variably based on the uncertainty provided by entropy, with the discount factor value ranging from ${\gamma }_{min}=0.95$ to ${\gamma }_{max}=0.99$. The TQC was evaluated with $\gamma$ values of 0.95, 0.97, and 0.99.

The robotics environments in the Gymnasium for this study are goal-oriented and feature sparse rewards, making it complex to balance exploration with exploitation. The success rate is determined by whether the robotic arm’s gripper or the object being moved is accurately placed at the target location; each environment has different objectives. As illustrated in Figure 4, the frames depict the amount of data the agent has learned, while the success rate reflects the proportion of tasks completed. The success rate ranges from 0 to 1, where 1 indicates that all attempts were successful.

The experimental results clearly show that our EG-TQC method surpassed the TQC method with a fixed discount factor (0.95) in the FetchPickAndPlace task, achieving an impressive success rate of 0.962 compared to 0.85. This reflects a notable improvement of about 11%. This enhancement not only increases sample efficiency but also allows for seamless adaptation to additional changes, such as the implementation of a hindsight replay buffer in the Gymnasium robotics environment. These findings robustly affirm the generality and scalability of our proposed approach.

4.3. Rendering Humanoid Results

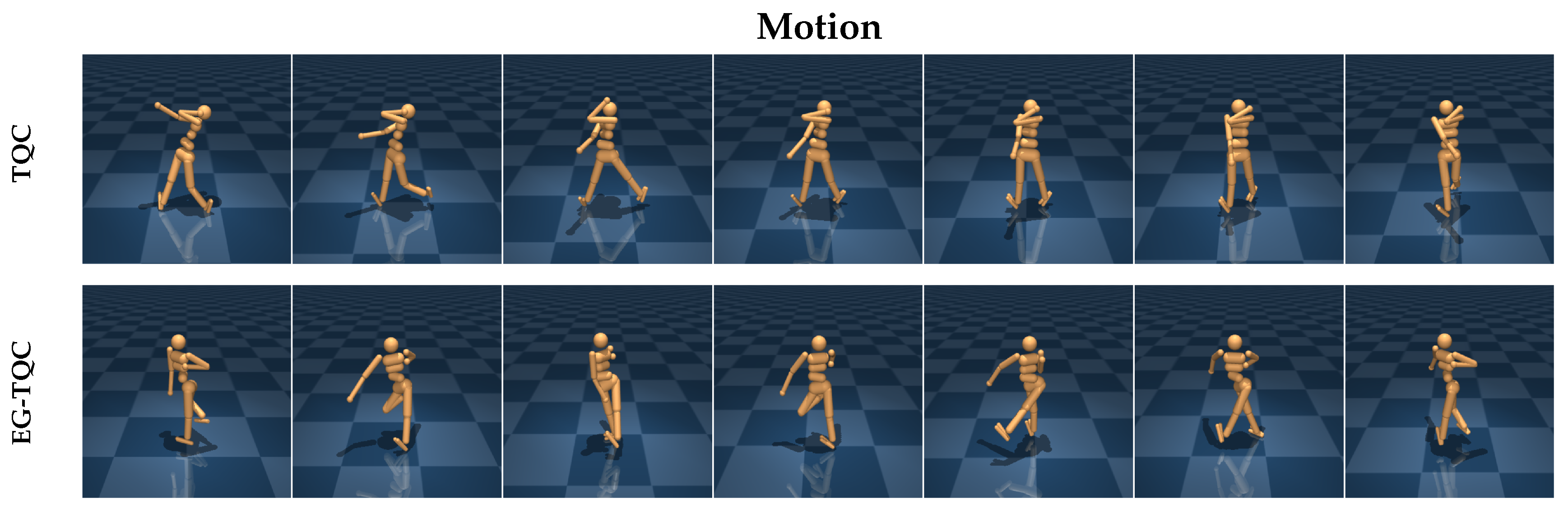
The rendering results of the trained models using the EG-TQC method are compared to those of the best-performing model that used a fixed discount factor, as shown in Figure 5. Although both methods achieved the same final reward, the humanoids trained with the EG-TQC exhibited more natural joint movements and made fewer errors. This indicates that the EG-TQC method allows for variations in the discount factor based on the specific task and the agent’s learning scenario. Moreover, it enhances the balance between exploration and exploitation, leading to better uncertainty estimation compared to the traditional TQC method, resulting in more stable learning.

5. Conclusions

In this paper, we present a new approach called the EG-TQC algorithm. This approach incorporates a dynamic discount factor adjustment, influenced by policy entropy, into the TQC framework. Our aim is to address overestimation bias and uncertainty in reinforcement learning by using policy entropy loss to dynamically adjust the discount factor. This adjustment is intended to enhance learning stability and performance. We carried out extensive experiments in DeepMind Control Suite and Gymnasium Robotic environments, and our results demonstrated that the EG-TQC algorithm outperformed traditional TQC methods with fixed discount factors. We observed significant improvements in sampling efficiency and adaptability, particularly in complex robotic control tasks. By dynamically adjusting the discount factor based on policy entropy, our approach eliminates the need for manual tuning of the discount factor and provides a more flexible and robust learning process.

Our proposed method is currently limited to the TQC algorithm, and further improvements are necessary to extend its applicability to a wider range of algorithms. Additionally, in environments where the task complexity is low and an optimal learning strategy can be easily derived, the dynamic discount factor adjustment may not be beneficial and could potentially degrade learning efficiency. In such simple scenarios where an agent can rapidly learn the optimal policy, dynamic discounting may introduce unnecessary variations, leading to confusion in the learning process. This highlights an area that requires further refinement.

Future research will focus on enhancing and expanding the entropy-based method to improve its adaptability and effectiveness across various reinforcement learning applications. Our findings underscore the potential of entropy-guided techniques for advancing RL, particularly in environments with high uncertainty and long planning horizons. Additionally, the EG-TQC algorithm demonstrates the ability to balance exploration and exploitation through adaptive discounting, making it a promising direction for future reinforcement learning research and applications.