Dynamics Modeling of Spalling Failure at the Non-Central Position of the Raceway for an Inner Ring of a Ball Bearing
Abstract
1. Introduction
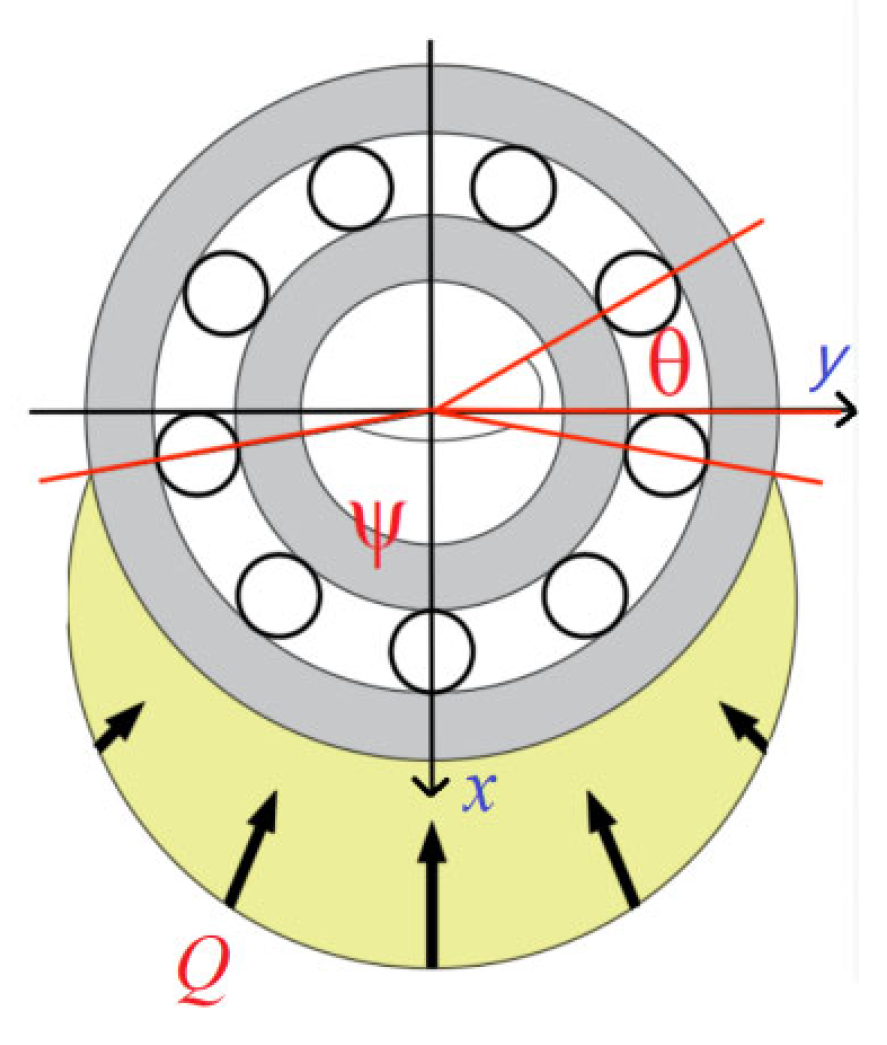
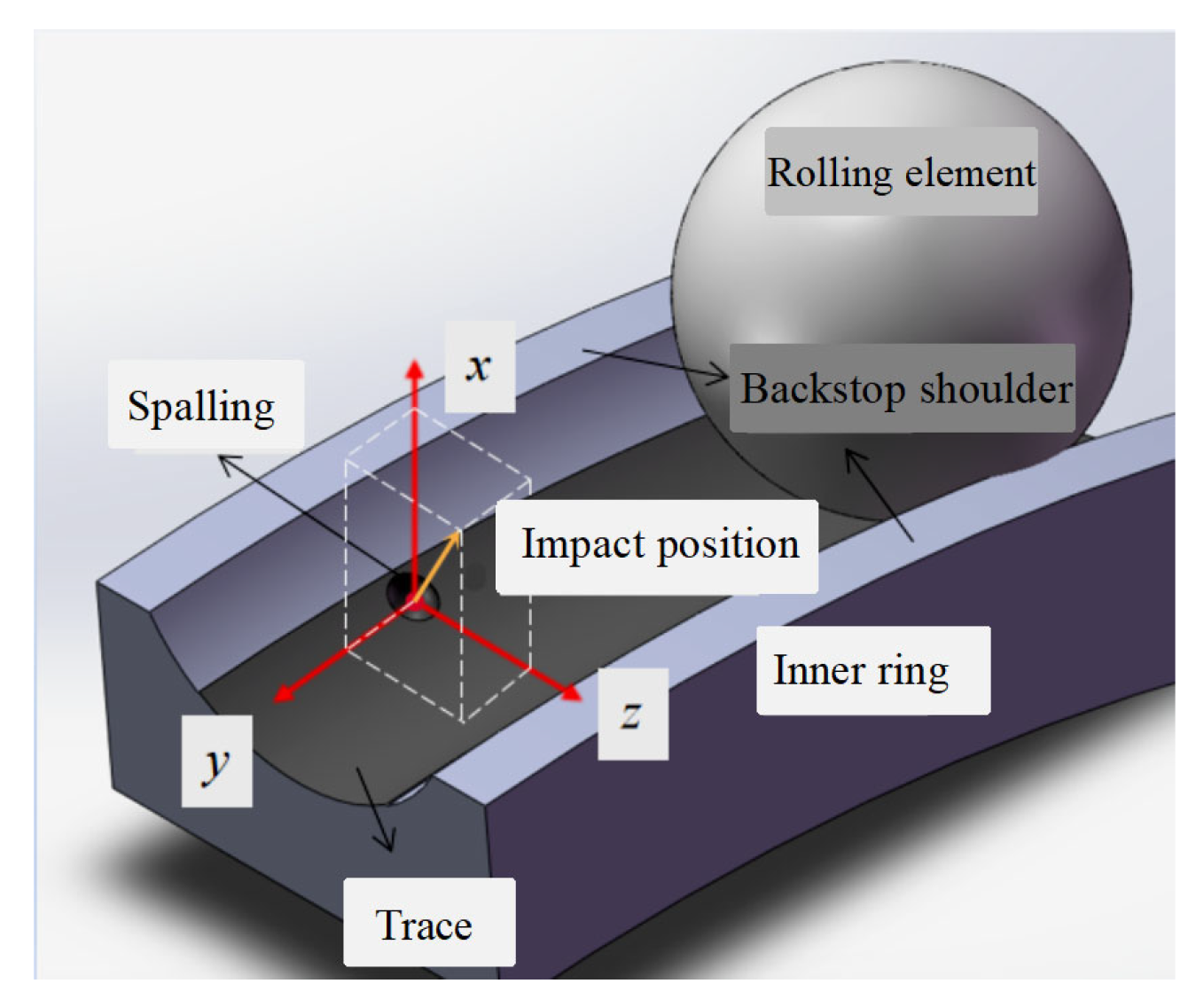
2. Dynamic Modeling of Spalling Faults at Non-Central Positions of the Inner-Ring Raceway
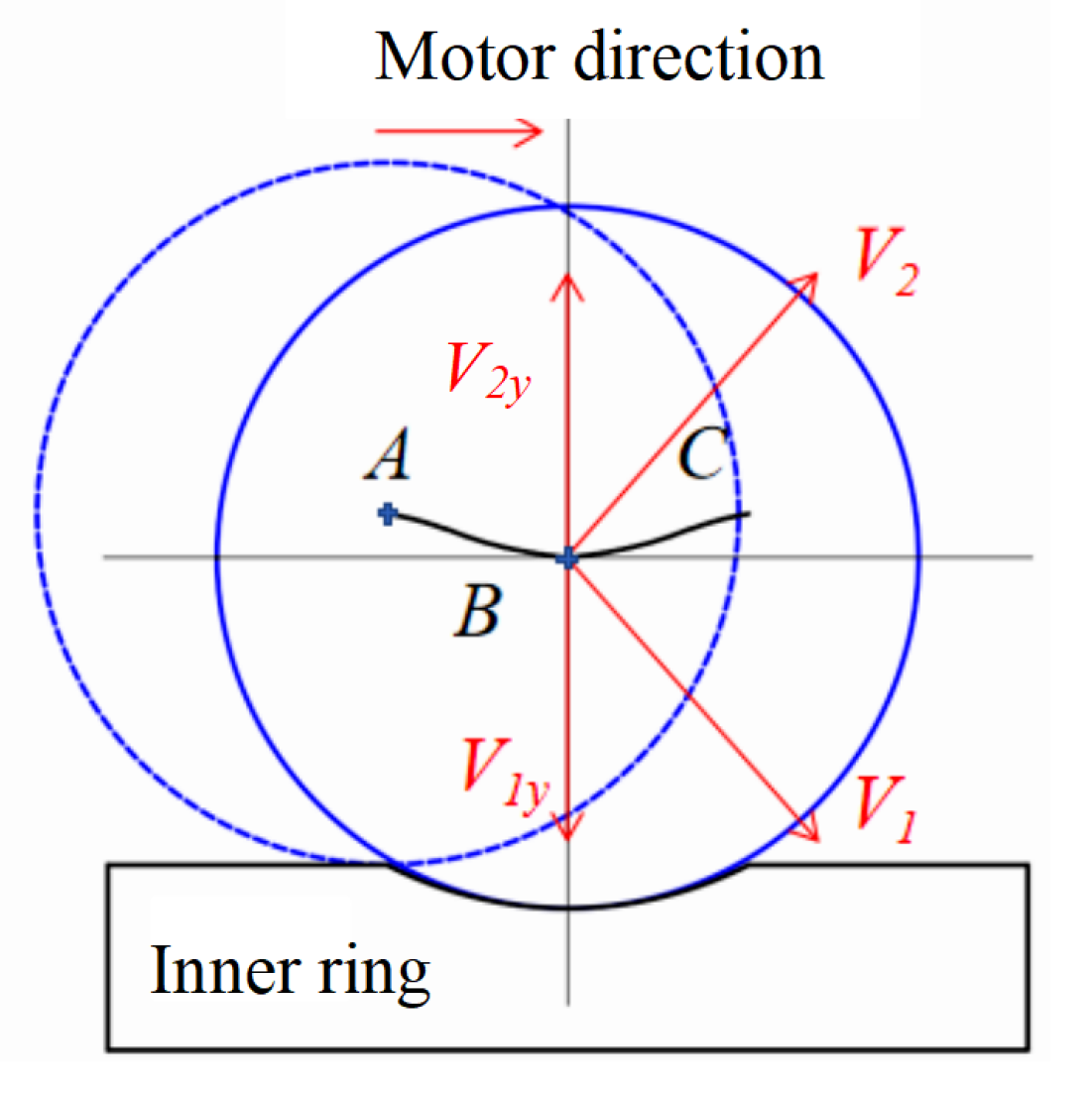
2.1. Rolling Element Deformation Quantity
2.2. Time-Varying Energy of Rolling Elements in Spalling Area
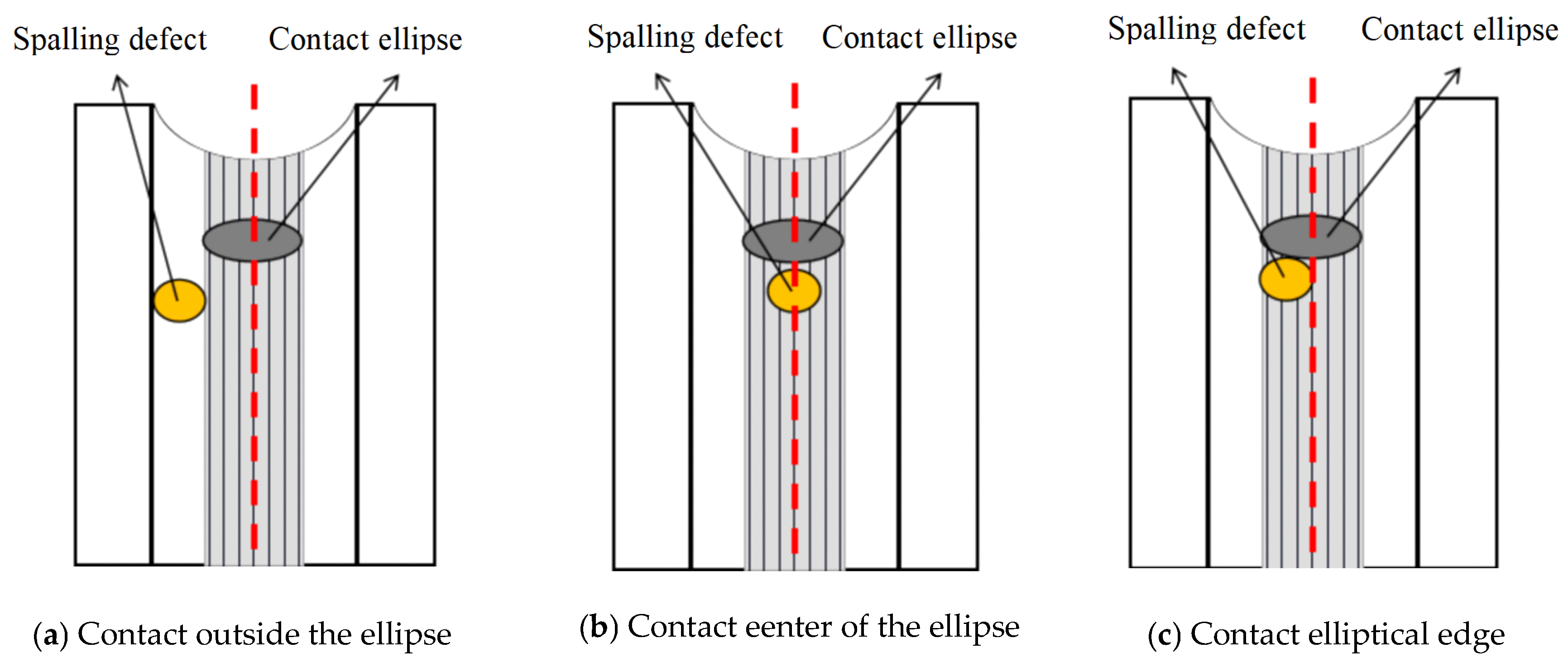
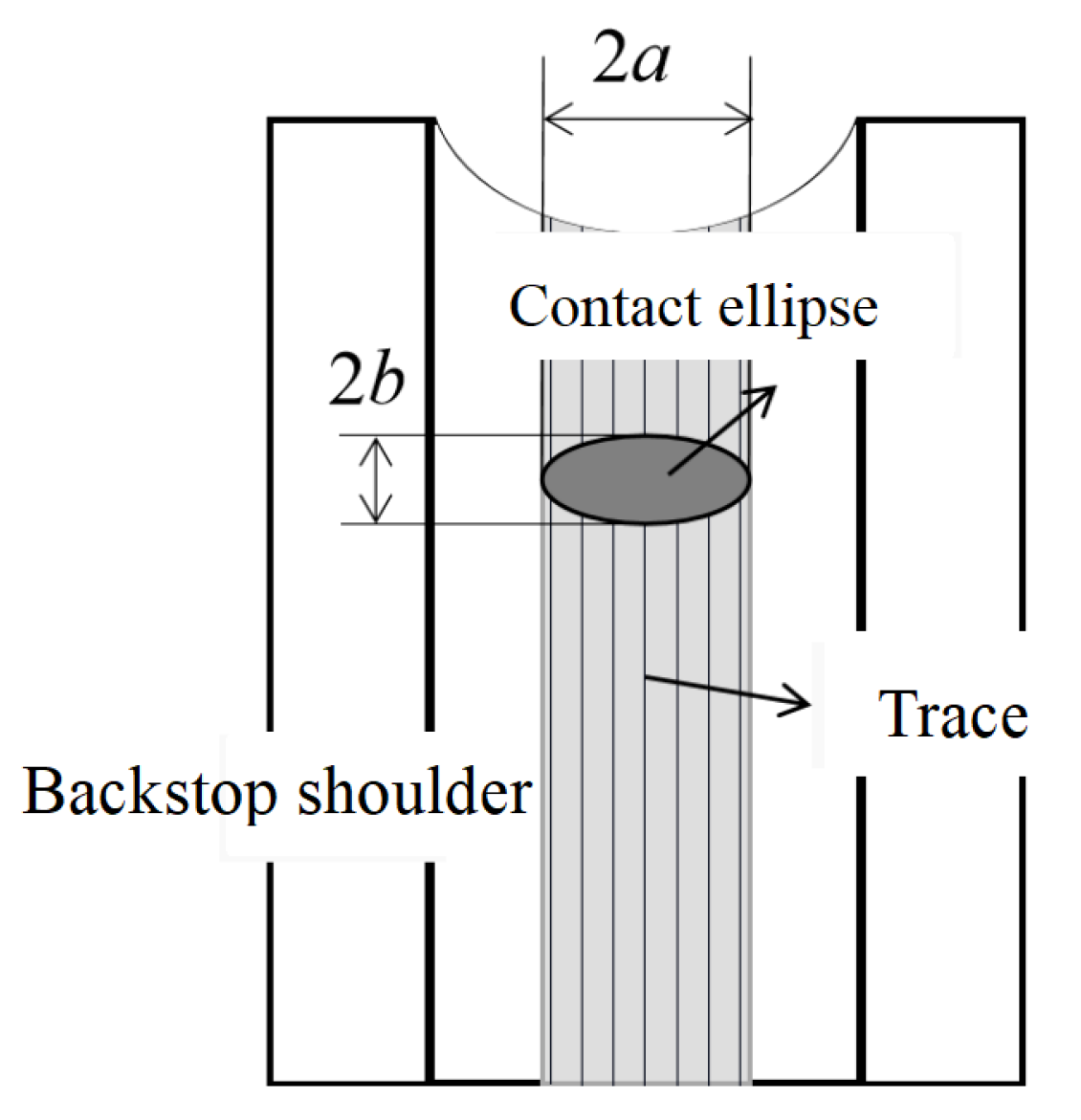
2.3. Rolling Element-Raceway Contact Area
2.4. Establish Fault Dynamics Equation
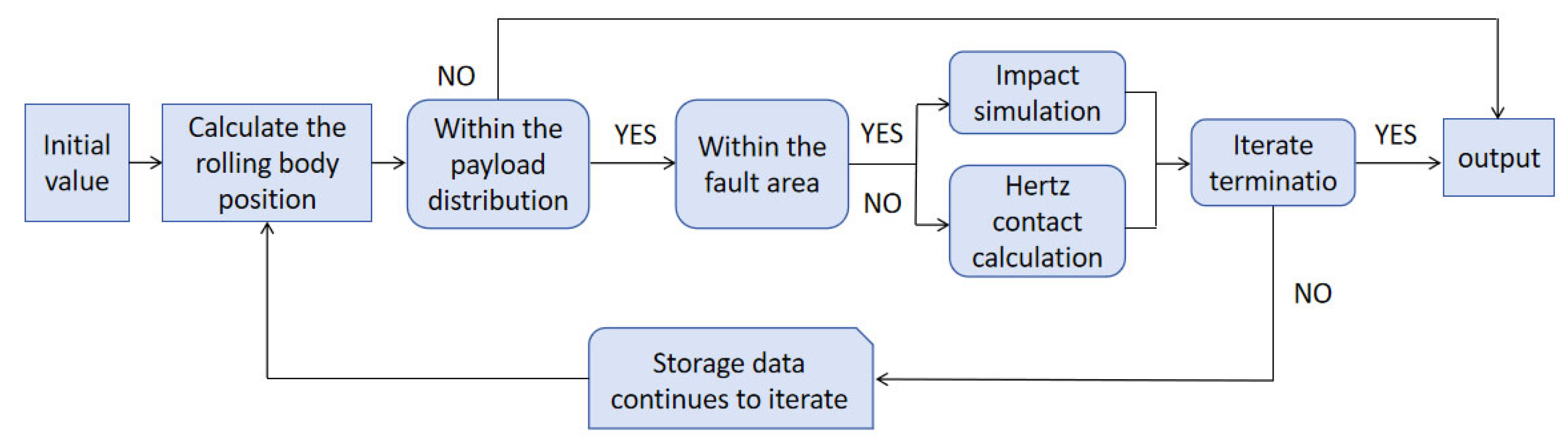
3. Model Calculation Results
4. Simulation and Experiment Validation
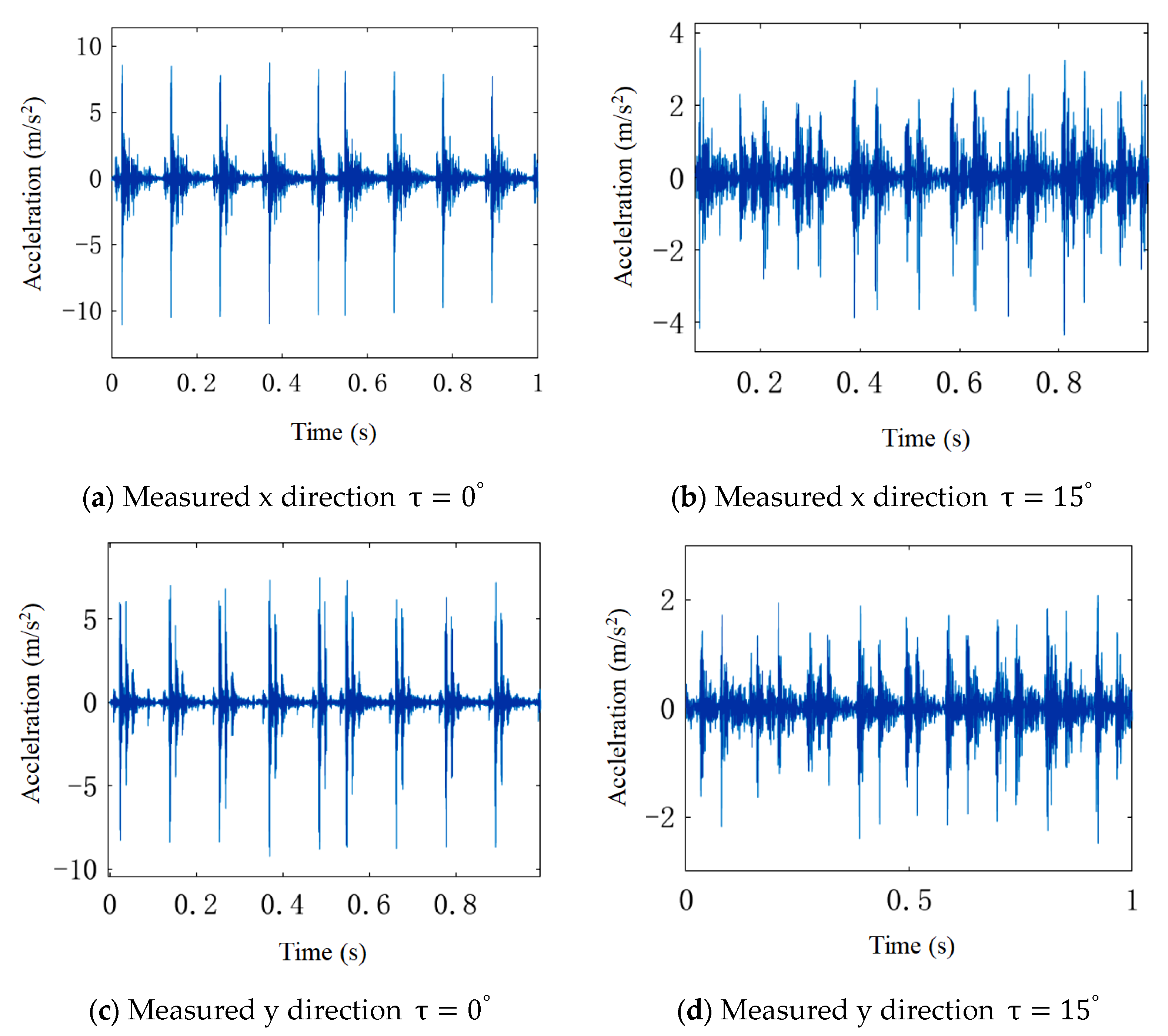
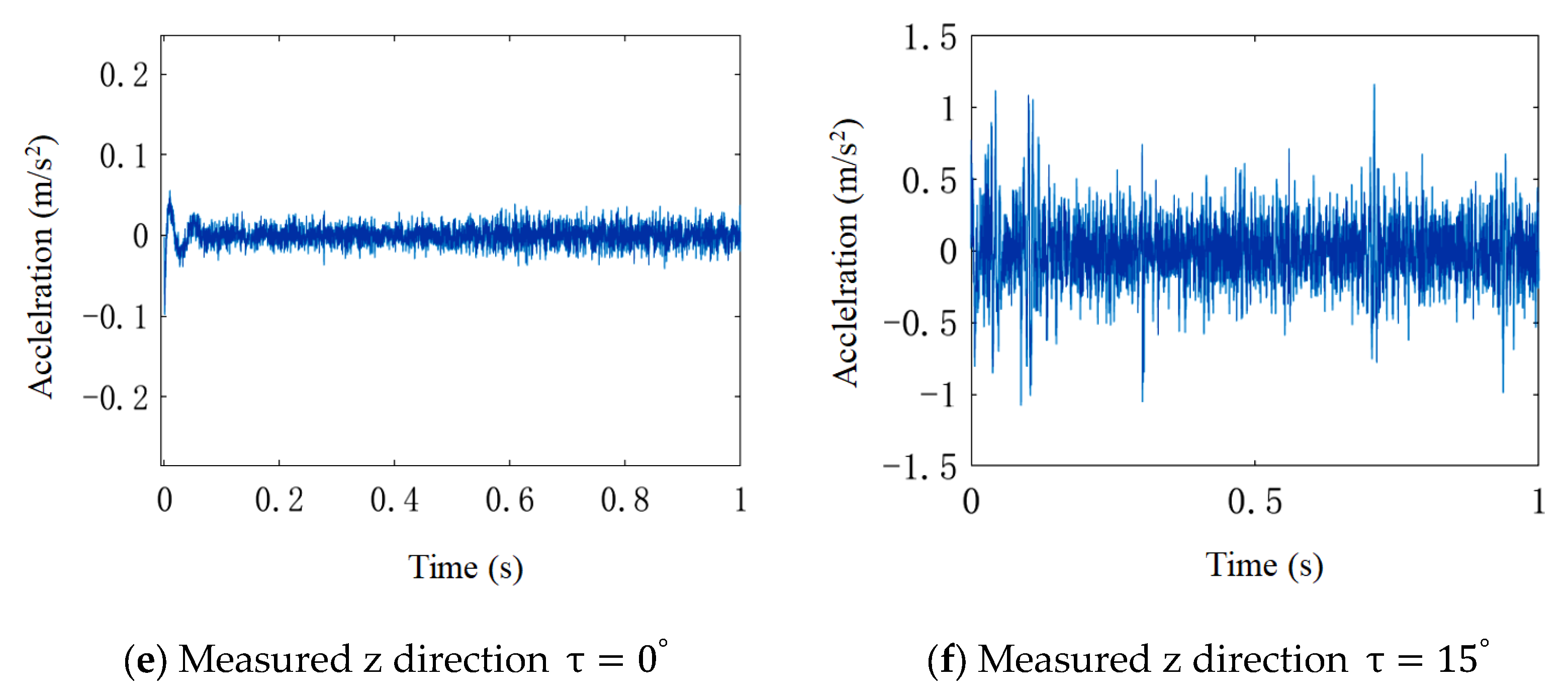
4.1. Experimental Procedure
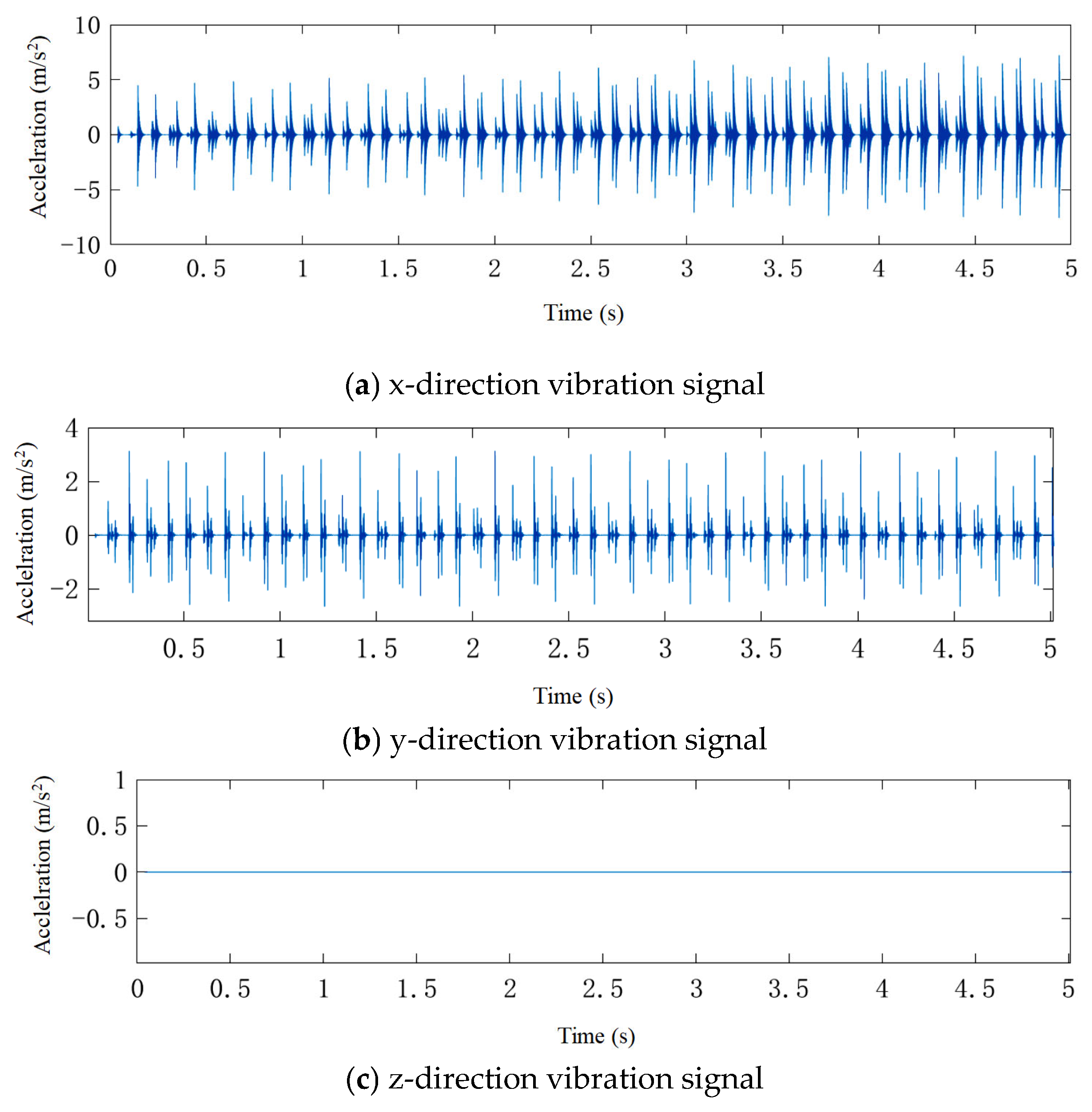
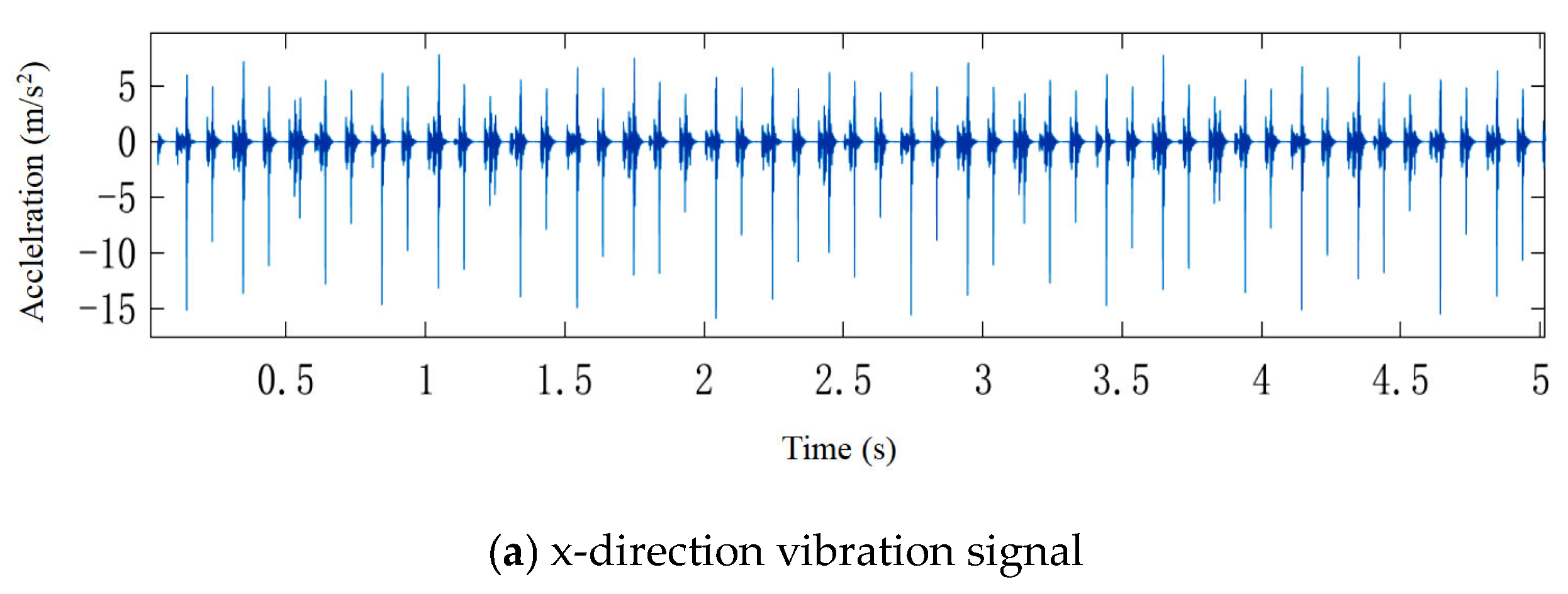
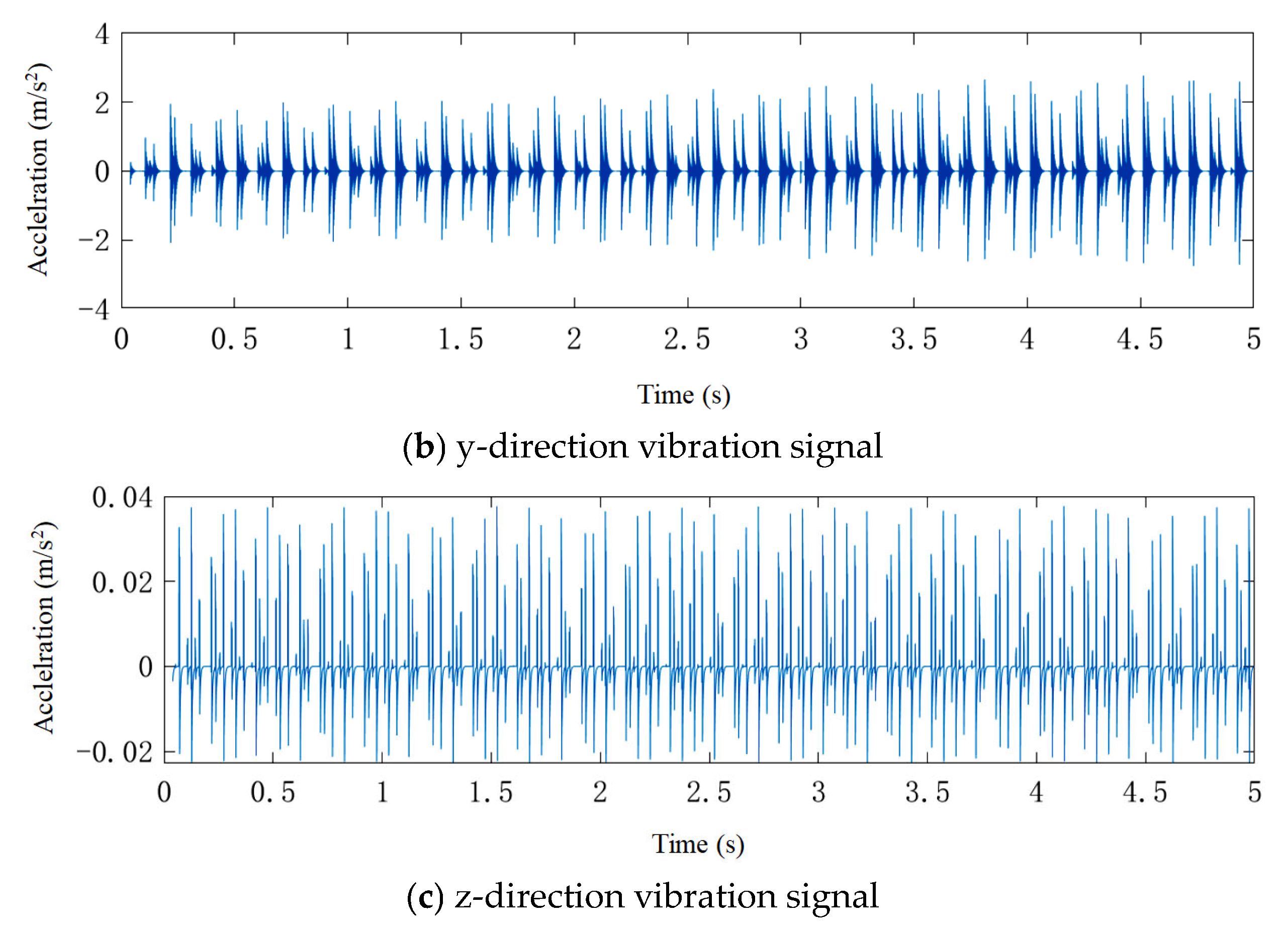
4.2. Envelope Spectrum Analysis of Simulated and Measured Signals
4.3. Amplitude Root Mean Square Analysis of Simulation and Measured Signals
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, H.; Jiang, D.; Zhuo, W.; Sun, H.; Ma, W. Failure Analysis of a Helicopter Engine Bearing Wear. Aviat. Maint. Eng. 2022, 12, 57–59. [Google Scholar] [CrossRef]
- Luo, M.; Guo, Y.; Andre, H.; Wu, X.; Na, J. Dynamic modeling and quantitative diagnosis for dual-impulse behavior of rolling element bearing with a spall on inner race. Mech. Syst. Signal Process. 2021, 158, 107711. [Google Scholar] [CrossRef]
- Desnica, E.; Ašonja, A.; Radovanović, L.; Palinkaš, I.; Kiss, I. Selection, Dimensioning and Maintenance of Roller Bearings. In 31st International Conference on Organization and Technology of Maintenance; Springer: Cham, Switzerland, 2022; Volume 592, pp. 133–142. [Google Scholar] [CrossRef]
- Wang, Y.; E, S.; Jia, Y.; Ma, X.; Xie, B. Improved model for quasi-static mechanical analysis of angular contact ball bearing under joint load. Bearing 2022, 11, 18–26. [Google Scholar] [CrossRef]
- Tian, J.; Ai, X.; Liu, L.; Zhang, F.; Wang, Z. Modeling of composite fault dynamics and vibration characteristic analysis of intermediary bearings. Vib. Impact 2022, 41, 144–151. [Google Scholar] [CrossRef]
- Mu, X.; Liu, Z. Dynamic response and life analysis of box bearing cage of EMU. Bearing 2023, 3, 18–26. [Google Scholar] [CrossRef]
- He, A.; Wang, X. Nonlinear dynamics modeling of the rotor with the bearing inner ring gap. Mech. Manuf. Autom. 2022, 51, 124–128. [Google Scholar] [CrossRef]
- Wan, C.; Zhang, K.; Tian, Z.; Chen, X.; Li, L. Study on the relationship between contact stress distribution characteristics and fatigue peeling of angle contact ball bearing at high speed. Mech. Drive 2021, 45, 38–44. [Google Scholar] [CrossRef]
- Pastukhov, A.; Timashov, E.; Stanojević, D. Temperature Conditions and Diagnostics of Bearings. Appl. Eng. Lett. 2023, 8, 45–51. [Google Scholar] [CrossRef]
- Ou, X.; Zhang, Y.; Zhang, K.; Wang, B. A deep groove ball bearing dynamics model considering unbalanced forces and disturbed dynamics. Mech. Des. Manuf. 2022, 12, 6–10. [Google Scholar] [CrossRef]
- Petersen, D.; Howard, C.; Sawalhi, N.; Ahmadi, A.M.; Singh, S. Analysis of Bearing Stiffness Variations, Contact Forces and Vibrations in Radially Loaded Double Row Rolling Element Bearings with Raceway Defects. Mech. Syst. Signal Process. 2015, 50–51, 139–160. [Google Scholar] [CrossRef]
- Dong, Q.Q.; Wei, H.J.; Ma, G.W. Failure Mechanism of S-Shaped Fissure In Brittle Materials Under Uniaxial Tension: Experimental and Numerical Analyses. Int. J. Solids Struct. 2020, 119–192, 486–496. [Google Scholar] [CrossRef]
- Cao, H.; Wang, D.; Zhu, Y.; Chen, X. Dynamic modeling and abnormal contact analysis of rolling ball bearings with double half-inner rings. Mech. Syst. Signal Process. 2021, 147, 107075. [Google Scholar] [CrossRef]
- Madar, E.; Galiki, O.; Klein, R.; Bortman, J.; Nickell, J.; Kirsch, M. A new model for bearing spall size estimation based on oil debris. Eng. Fail. Anal. 2022, 134, 106011. [Google Scholar] [CrossRef]
- Shi, J.; Yu, T.; Goebel, K.; Wu, D. Remaining Useful Life Prediction of Bearings Using Ensemble Learning: The Impact of Diversity in Base Learners and Features. J. Comput. Inf. Sci. Eng. 2021, 21, 021004. [Google Scholar] [CrossRef]
- Liu, Q.; Guo, Y.; Wu, X. Modeling of double impact characteristic mechanism of rolling bearing outer ring peeling fault. J. Vib. Eng. 2017, 30, 670–678. [Google Scholar] [CrossRef]
- Chang, B.; Yan, C.; Yuan, H.; Kang, J.; Wang, K.; Wu, L. Dynamic modeling of rolling bearing under multi event excitation. Vib. Impact 2018, 37, 16–24. [Google Scholar] [CrossRef]
- Xie, C.; Hao, L.; Deng, S.; Qian, D.; Hua, L. Nonlinear system of high-speed bearing rotor with outer race peeling off and its vibration response analysis. Vib. Shock 2022, 41, 262–269. [Google Scholar] [CrossRef]
- Cui, L.; Zhang, Y.; Zhang, F.; Zhang, J.; Lee, S. Vibration response mechanism of faulty outer race rolling element bearings for quantitative analysis. J. Sound Vib. 2016, 364, 67–76. [Google Scholar] [CrossRef]
- Jiang, Y.; Huang, W.; Luo, J.; Wang, W. An improved dynamic model of defective bearings considering the three-dimensional geometric relationship between the rolling element and defect area. Mech. Syst. Signal Process. 2019, 129, 694–716. [Google Scholar] [CrossRef]
- Shi, H.; Liu, Z.; Bai, X.; Li, Y.; Wu, Y. A Theoretical Model with the Effect of Cracks in the Local spall of Full Ceramic Ball Bearings. Appl. Sci. 2019, 9, 4142. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Tao, J.; Xu, B. Dynamic model of single point fault of outer ring of rolling bearing considering progressive deformation and lubricant. Bearing 2021, 9, 14–19. [Google Scholar] [CrossRef]
- Tu, W.; Liang, J.; Luo, Y.; Zhou, J.; Zhou, S. Research on dynamic load characteristics of rolling bearings under accelerated working conditions. Vib. Shock 2021, 40, 152–159. [Google Scholar] [CrossRef]





| Parameter | Numerical Value |
|---|---|
| The inner raceway diameter Di/mm | 25 |
| The outer raceway diameter Db/mm | 52 |
| Pitch circle diameter Dw/mm | 38.5 |
| Rolling element diameter db/mm | 7.9 |
| Number of rolling elements Z | 9 |
| Radial clearance Cr | 1 |
| Rolling element mass m0/g | 2.14 |
| Vibration Direction | Axial Position | Year-on-Year Growth | |
|---|---|---|---|
| x | 0.2590 | 0.1997 | −22.9% |
| y | 0.1113 | 0.1113 | 0% |
| z | 0 | 0.615 | ++ |
| Vibration Direction | Axial Position | Year-on-Year Growth | |
|---|---|---|---|
| x | 0.2677 | 0.2077 | −22.4% |
| y | 0.1259 | 0.1274 | +1.2% |
| z | 0.0073 | 0.0847 | ++ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Wang, L.; Meng, W.; Wang, J.; Gong, Z. Dynamics Modeling of Spalling Failure at the Non-Central Position of the Raceway for an Inner Ring of a Ball Bearing. Appl. Sci. 2025, 15, 2740. https://doi.org/10.3390/app15052740
Li S, Wang L, Meng W, Wang J, Gong Z. Dynamics Modeling of Spalling Failure at the Non-Central Position of the Raceway for an Inner Ring of a Ball Bearing. Applied Sciences. 2025; 15(5):2740. https://doi.org/10.3390/app15052740
Chicago/Turabian StyleLi, Sihui, Linghang Wang, Weiying Meng, Jiaying Wang, and Zhiheng Gong. 2025. "Dynamics Modeling of Spalling Failure at the Non-Central Position of the Raceway for an Inner Ring of a Ball Bearing" Applied Sciences 15, no. 5: 2740. https://doi.org/10.3390/app15052740
APA StyleLi, S., Wang, L., Meng, W., Wang, J., & Gong, Z. (2025). Dynamics Modeling of Spalling Failure at the Non-Central Position of the Raceway for an Inner Ring of a Ball Bearing. Applied Sciences, 15(5), 2740. https://doi.org/10.3390/app15052740






