1. Introduction
With the rapid advancement in communication, computer, and sensor technology, the vehicle–road–cloud cooperation cyber-physical system (VRCCPS) has undergone substantial development, which contributes to the maturity of autonomous vehicles (AVs) [
1]. Within VRCCPS, real-time traffic information is collected by both onboard and roadside sensors and aggregated on the dynamic high-definition (HD) map platform for building the digital twin of real traffic scenarios [
2]. On this basis, VRCCPS conducts predictive motion planning for AVs within the digital twin and employs the cloud control platform to guide real-world vehicles to improve traffic safety and efficiency. Thus, it is crucial for VRCCPS to accurately predict future traffic states based on the traffic environment perception provided by HD maps.
In contrast to conventional traffic detection systems, VRCCPS employs roadside perception devices to capture real-time motion information of traffic participants at a high frequency and aggregates these perceptions on the dynamic layer of HD maps. Therefore, the HD maps in VRCCPS can provide both real-time vehicle state information and comprehensive semantic information about vehicles and roads. However, there is a lack of research on leveraging HD maps for traffic state predictions, especially in complex urban traffic scenarios. Thus, we propose a model that utilizes structured data from HD maps to forecast future traffic states.
Currently, the mainstream frameworks for HD map creation include Lanelet2, OpenDRIVE, and Apollo Maps [
3]. These frameworks typically partition continuous road space into a series of lane segments with accurate geometric shapes and abundant semantic information, aiding in precise vehicle localization and motion planning. HD maps consist of multiple layers that successively update the states of various traffic objects at different frequencies [
4]. Based on real-time traffic information from HD maps, the VRCCPS needs to predict traffic state evolution to construct space–time corridors from unoccupied lane segments in the future for motion planning tasks [
5], as illustrated in
Figure 1. Thus, the prediction model proposed in this paper must forecast the future traffic states of the whole lane segments during the prediction horizon based on discrete spatial–temporal traffic information from HD maps.
As a classical traffic model, the cell transmission model (CTM) can forecast future traffic states in discrete space–time. In CTM, the road space is divided into a set of cells with various traffic states, and the transmission rules of vehicles between adjacent cells are determined by the fundamental diagram of traffic flow [
6]. Based on transmission rules, CTM can successively update the future states of the entire cells. However, the fundamental diagram of traffic flow fails to sufficiently leverage the real-time vehicle state and semantic information from HD maps, such as the azimuth and vehicle-type attribute, thereby limiting further improvement in the prediction accuracy of CTM. Thus, the model proposed in this paper employs the discrete spatial–temporal structure of CTM and innovates the method for updating the traffic state of lane segments.
By combining conventional CTM and Transformer networks, we propose a novel prediction model known as Cell Transformer (CeT). CeT can utilize the structured data from HD maps to forecast future traffic states. It first vectorizes the vehicle-type attributes to word encodings and applies the multi-head attention to embed them into vehicle-state vectors to generate vehicle-state embeddings (VSEs). Then, VSEs are padded and converted into lane segment states, which act as the initial encoding for the encoder–decoder structure. Meanwhile, CeT fuses the temporal attributes and dynamic topology graph to the spatial–temporal embeddings (STEs), which guide the extraction of spatial–temporal dependencies and correlations and the generation of future traffic states [
7].
We utilize the trajectory data from pNEUMA and the map from OpenStreetMap (OSM) to establish two traffic scenarios, containing two-phase signalized intersections and four-phase signalized intersections [
8]. Then, a map converter is employed to convert the OSM maps to Lanelet2 maps with appropriately sized lane segments [
9]. These lane segments can be considered cell space providing discretized spatial–temporal data for CeT. After training, CeT is compared with baseline models for predictive performance and subjected to ablation studies to investigate the contributions of its key components. Furthermore, the influences of hyperparameters and model sensitivity are also analyzed to verify the robustness of CeT. The contributions of CeT are summarized as follows:
This study presents a novel prediction framework that integrates the Cell Transmission Model with Transformer-based methodologies. By leveraging structured HD map data, the framework forecasts traffic states within discrete spatial–temporal systems, providing a robust solution for modeling dynamic traffic flows at signalized intersections.
The proposed method encodes vehicle-type attributes into vehicle-state embeddings, allowing the model to distinguish between different vehicle types and enhance prediction accuracy. By representing signal phase variations as dynamic connections in a directed graph and synthesizing spatial–temporal embeddings, CeT effectively captures the intricate interactions between spatial and temporal traffic dynamics.
The prediction performance of CeT is rigorously validated using real-world traffic data from the pNEUMA dataset. Experimental results demonstrate its superior predictive accuracy and robustness across various scenarios, highlighting the significant contributions of its key components to traffic state forecasting.
The remainder of this paper is structured as follows.
Section 2 reviews the relative research.
Section 3 introduces the conventional CTM and the architecture of CeT.
Section 4 describes the experiments and predictive performance evaluation methods.
Section 5 presents the experimental results and corresponding analysis. Finally,
Section 6 summarizes this paper and looks forward to further research.
2. Literature Review
A review of the existing research on CTM is presented in this section. It initially introduces the advent of the classical CTM and provides an overview of derived model-driven CTM for predicting traffic at signalized intersections. Moreover, some data-driven methods that utilize historical traffic data for traffic prediction are also presented in this section.
2.1. Model-Driven Methods
The classical CTM is derived from the Lighthill–Whitham–Richards (LWR) model, which pioneers the application of the continuity equation from fluid mechanics to model traffic flow [
10,
11]. Through the iterative solution to the LWR model, the trends in traffic volume, speed, and density changes can be acquired and used for predicting the future traffic state. To simplify the equation for the solution, the classical CTM discretizes the LWR model in both time and space [
6]. In this way, the continuous motion of vehicles is transformed into successive transmissions between adjacent cells, reducing the calculating pressure of model solving. Because of its simplicity and efficiency, the application of the classical CTM under various traffic scenarios is widely studied, leading to a series of extended CTMs [
12].
By describing the traffic flow at signalized intersections, some traffic flow model-based CTMs improve their predictive capabilities. For example, Srivastava et al. [
13] modify the right half of the demand function as a linear decreasing function to reflect various headways in different signal phases. Shirke et al. [
14] add compensatory terms to the function for startup loss time and dissipation waves to describe the capacity drop of cells at signalized intersections. Liu and Chang [
15] define the blocking matrix to reflect spatial queuing interactions between cells, allowing for an accurate description of the physical queue evolution at signalized intersections. These CTMs depict the operational characteristics of traffic flow at signalized intersections, which enhance their predictive performances. However, the traffic flow models on which model-driven CTM relies are often too idealistic to be met in real traffic, such as uniform traffic flow or equal headways [
12].
Further, some model-driven CTMs discuss the impact of cell size on predictive performances. For instance, Hu et al. [
16] model complex urban roads through cells with variable lengths and densities. These variable cells are connected by different types of cell connections, including simple connection, merge connection, and diverge connection. Wit and Ferrara [
17] utilize variable-length cells to model signalized intersections and reflected traffic states through the density of downstream congested cells, the density of upstream free cells, and the position of the congestion waves. These model-driven CTMs indicate that variable-sized cells are advantageous in discretizing road space at signalized intersections.
2.2. Data-Driven Methods
In contrast to model-driven CTMs, some approaches sight to directly derive traffic rules from real traffic data to predict traffic evolution without relying on explicit modeling. In the early research, Hamed et al. [
18] present the auto-regressive integrated moving average (ARIMA) model by employing the Box-Jenkins approach. The ARIMA constructs the traffic flow as an auto-regressive model for predicting future traffic evolution. On this basis, Williams and Hoel [
19] develop a seasonal ARIMA to reflect the seasonal patterns of traffic variation. While these regression models can capture the periodicity and trends in time series traffic data, their sensitivity to outliers and noise in actual data may lead to the instability of traffic predictions.
Apart from regression, some classic statistic methods are also used to capture evolution patterns from traffic data. For instance, Zhang and Poschinger [
20] employ the CTM to model urban roadways and extend the Kalman filter to estimate the traffic state and turning ratios within the cells. Kawasaki et al. [
21] adopt Bayesian filtering to fuse CTM and probe vehicle data to establish the state-space model that could estimate traffic states. Similarly, Wang et al. [
22] develop a framework that combines the traffic model and Bayesian network to estimate the overall traffic parameters based on partially observed vehicle trajectories and fundamental diagram parameters. These methods effectively manage the outliers and noise in traffic data and reduce the uncertainty of observation errors and model parameters. However, these methods rely on idealized assumptions and possess high computational complexity, which exhibits unsatisfying predictive performances in large-scale complex traffic scenes.
As computer science advances, certain machine learning and deep learning algorithms are also utilized for predicting traffic state evolution. For instance, Zhang and Liu [
23] employ support vector regression (SVR) to search for the optimal separating hyperplane in the feature space and regress a linear model for traffic prediction by minimizing the loss function. Further, Qi and Ishak [
24] apply the Hidden Markov Model to simulate the traffic evolution patterns between adjacent cells in a 2-dimensional state space consisting of mean and contrast of speed observations. Because of their flexible and adaptive architectures, these machine learning-based models improve their ability to model complex scenarios. Moreover, these approaches no longer solely rely on manual feature selection and construction but automatically extract valuable features from historical traffic data for predictions.
Compared to machine learning algorithms, deep learning algorithms utilize the perceptron that possesses stronger nonlinear fitting capabilities, improving performances in traffic predictions. Ye et al. [
25] provide a three-layer feedforward neural network (FNN) for traffic speed prediction based on input speed and acceleration. Polson and Sokolov [
26] optimize an architecture that combines a linear model and multiple tanh layers for predicting traffic state evolution. Azzouni and Pujolle [
27] apply Long Short-Term Memory (LSTM) architectures to accomplish short-term traffic flow prediction and establish the traffic matrices to describe the corresponding traffic states. The models based on deep learning algorithms are adept at extracting implicit high-dimensional features from traffic data and learning their temporal–spatial dependencies and correlations for accurate traffic predictions. However, these methods that solely rely on data training often lack interpretability and are prone to weak generalization ability due to overfitting.
In recent research, numerous data-driven approaches combine multiple fundamental models. For example, Pan et al. [
28,
29] proposed a hybrid interpretable model that combines the fundamental diagram, Markov, and LSTM for short-term traffic flow prediction. Guo et al. [
30] combine the 3-dimensional convolutional neuron network and recurrent neuron networks (RNN) to capture the spatial dependencies and temporal evolutions for network-wide urban traffic prediction. Xu et al. [
31] develop an adaptive graph convolutional recurrent network (AGCRN) that combines RNN and conventional graph neural network (GCN). The predictive model also incorporates adaptive parameters to GCN to capture the spatial correlations from dynamic graphs synthesized by the road segment connectivity and traffic states at each time step. Wu et al. [
32] propose a GCN architecture to predict traffic evolution named Graph WaveNet (GWN). They apply stacked 1-dimensional dilated convolutions and adaptive dependency matrices to enhance the predictive ability to extract the temporal and spatial dependencies and correlations. In general, these hybrid models are becoming mainstream in the field of traffic state predictions due to their balance between accuracy and interoperability. However, there is still a lack of discussions on the architectural optimization of traditional models using advanced data-driven methods.
In this paper, we propose CeT, a traffic prediction model that sufficiently integrates CTM and Transformer. CeT considers the lane segments in HD maps as not only the cell space in CTM but also the nodes in a directed graph network, which can simply capture the periodic changes in the phase of intersection signals [
33,
34]. Moreover, CeT also utilizes attention mechanisms to embed vehicle-type attributes into vehicle-state information to capture the differences between various types of vehicles, thereby enhancing prediction accuracy.
3. Method
This section presents a comprehensive introduction to CeT. Firstly, it outlines the structure of the conventional CTM and indicates its deficiencies. Subsequently, the section provides the appropriate problem formulation. Moreover, the section also introduces the architecture of CeT and its primate components in detail.
3.1. Cell Transmission Model
The conventional CTM discretizes continuous time into uniform time steps. It also partitions road space into a series of lane segments known as cells, as depicted in
Figure 2. The length of cells is typically longer than the distance a standard vehicle can travel within a time step to prevent vehicles from skipping over adjacent cells. Based on traffic flow theory, CTM can update cells to reflect the evolution of traffic states:
where
and
represent the inflow of cell
at time step
t. The calculation of
is expressed as follows:
where
denotes the maximum inflow to cell
at time step
t,
denotes the jam capacity of the cell
, and
w and
represent backward shockwave speed and free flow speed.
HD maps also possess discrete spatial–temporal structures [
4]. However, traditional CTM cannot adequately utilize traffic information from HP maps, such as azimuths and vehicle-type attributes. Meanwhile, traditional CTMs face challenges in capturing stable traffic information because signal phases intermittently disrupt the continuous traffic flow. Thus, we developed CeT, which inherits the discrete spatial–temporal framework of CTM but no longer models continuous traffic flow. Instead, it focuses on vehicle transmission patterns between cells and simplifies the prediction of traffic evolution to successive updates of cells within the prediction horizon. To this end, CeT fuses the inherent characteristics of lane segments, the motion characteristics of vehicles at each historical time step, and the vehicle-type attributes into the feature sequence that encodes the cell states over the historical horizon. Meanwhile, it represents the signal changes at intersections as dynamic connections between nodes corresponding to specific cells in a dynamic road graph, which are also embedded into the historical encoding sequence. Subsequently, CeT utilizes the Transformer architecture to extract the spatial–temporal correlations and dependencies from the historical encoding sequence to predict future cell states. In this way, CeT combines CTM and Transformer architecture while utilizing the structured traffic data from HD maps to forecast future traffic states in a discrete spatial–temporal system.
3.2. Problem Formulation
HD maps can provide a topology matrix to depict the adjacency of lane segments and real-time phases at signalized intersections. Therefore, the real-time connectivity among lane segments can be defined as a dynamic directed graph
, where
V is the set of lane segments,
is the set of directed edges for vehicle transmission between adjacent lane segments at time step
t, and
is the corresponding adjacency matrix of
:
where
denotes the lane segment
, and
denotes the lane segment count. For lane segment
, HD maps also provide its direction vector
, which represents the direction of the centerline of lane segment
. The instantaneous state of a vehicle is simplified as
, where
and
represent the spot speed and azimuth of vehicle
i in lane segment
at the time step
t. Based on this, a lane segment state at time step
t is defined as a feature vector set
, where
denotes the internal vehicle count of lane segment
at time step
t. Meanwhile, HD maps also supply vehicle-type attributes
, where
is a one-hot encoding corresponding to
. In this way, the state of road space at time step
t is represented as
and
. Moreover, HD maps provide the time attributes
, which is a one-hot encoding to reflect the position of time step
t in a week.
The future state of road space is defined as a set of the number of vehicles in each lane segment, expressed as . To this end, we take and as inputs, where denotes the historical time steps. The predictive goal is , where denotes the predictive time steps. The temporal attributes and spatial attributes are also input into CeT to guide spatial–temporal feature extraction and prediction result generation.
3.3. Model Architecture
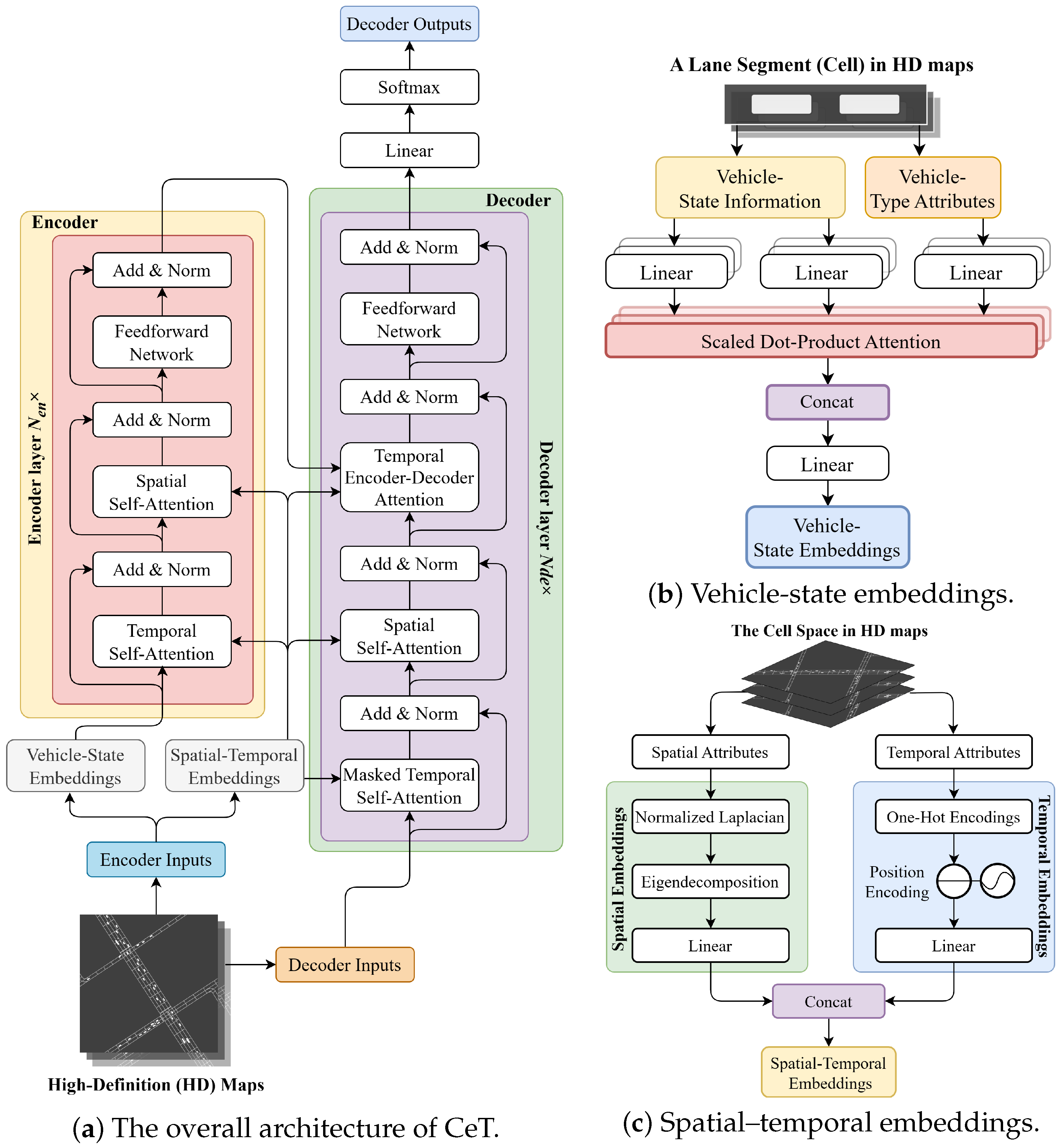
3.3.1. Model Overview
The architecture of CeT is demonstrated in
Figure 3a. Once inputs enter CeT, it first uses the angle between direction vector
and azimuth
to decompose the spot speed
and then converts it into the vehicle motion vector
, where
represents the feature dimension. Meanwhile, CeT converts vehicle-type attribute
into vehicle-type embedding
and fuses
and
to
. In this way, CeT reshapes and projects
to
, and the lane segment state at time step
t can be expressed as
. Then, CeT converts the
t-th temporal attribute
and spatial attribute
into the temporal embedding
and spatial embedding
, which guide the temporal self-attention (TSA) and spatial self-attention (SSA) computation on
. In this way, CeT can capture the encoding sequence
, which is input into the decoder. In the decoder, CeT takes
as initial input and utilize TSA and SSA to convert
into the decoding sequence
. Subsequently, CeT utilizes the temporal encoder–decoder attention (TEDA) and FNN to translate
and
into the traffic
prediction at time step
. Afterward, CeT updates the input of the decoder to
and conducts the next round of decoding. After
iterations of decoding, the final prediction of
Y is generated as
.
3.3.2. Vehicle-State Embeddings
CeT employs FNN and Multi-Head Attention (MHA) to fuse vehicle motion features, lane segment characteristics, and vehicle-type attributes to generate vehicle-state embeddings. Specifically, it decomposes vehicle speed into radial and lateral components based on the angle between the vehicle azimuths and the direction of lane segments, enabling more precise learning of the microscopic behavioral patterns of the vehicle. Subsequently, CeT applies FNN to transform the vehicle’s radial and lateral motion components into vehicle motion vectors and uses MHA to fuse them with vehicle-type attributes into vehicle-state embeddings. These embeddings, which combine the vehicle’s motion and type characteristics, enable CeT to better learn the evolution patterns of traffic states from traffic data.
Figure 3b demonstrates the fusion of the vehicle-state vector
and vehicle-type attribute
. When
enters CeT, it is decomposed and converted into the vehicle motion vector
as follows:
where
represents the activation function and
represents regularization. Meanwhile,
is linearly transformed into
. Subsequently,
is transformed into the query
, and
is projected to the key
and value
, where
and
denote the number of heads and the head dimension. Finally, an MHA computation is performed on
,
, and
:
where
represents the activation function. CeT applies
as the activation function for calculating attention weights because it can transform input values into a probability distribution, ensuring that the sum of all output values equals 1. Thus,
can reflect the relative importance among different input elements, thereby effectively allocating weights in attention mechanisms. In contrast, while
and
can also map inputs to a range between 0 and 1, they lack normalization properties and cannot directly generate probability distributions. Therefore,
is particularly suitable for multi-classification tasks and attention mechanisms, as it can better handle weight allocation among multiple elements.
3.3.3. Spatial–Temporal Embeddings
CeT employs a graph embedding technique called Eigenmaps and linear transformations to extract spatial and temporal embeddings from dynamic directed graphs and temporal labels provided by HD maps, respectively. Specifically, it performs eigen-decomposition on dynamic directed graphs representing the connectivity between lane segments at each time step to derive spatial feature embeddings. Simultaneously, it applies linear transformations to temporal labels to create temporal embeddings. These embeddings capture spatial and temporal features from historical traffic data, enabling CeT to learn variations in traffic evolution patterns across different periods, spatial connectivity between lane segments, and the impact of intersection signal phases on vehicle movement across specific lane segments.
Figure 3c demonstrates the extraction and generation of spatial embeddings
and temporals embeddings
from spatial attributes
and temporal attributes
. Specifically, CeT applies a graph embedding technique called Eigenmaps, which constructs the normalized Laplacian matrix
and conducts eigen-decomposition on
L to generate eigenvalue matrix
, where
represents the number of top neighbor nodes with the strongest spatial correlation to the node in dynamic directed graphs consisting of lane segments. In this way, CeT defines local neighborhoods for all lane segments treated as nodes in the dynamic directed graphs, thereby enhancing the accuracy of traffic evolution predictions. On this basis,
is linearly transformed into
. Meanwhile,
is transformed into
and concatenated with positional encoding
, which can be calculated as follows:
where
and
denote the position and dimension in
. The concatenated vector
is then linearly transformed into
.s.
3.3.4. Encoder
The encoder comprises encoder layers, each containing TSA, SSA, and FFN. TSA and SSA extract temporal and spatial dependencies and correlations while FNN conducts further spatial–temporal feature learning.
The TSA performs linear transformation on
to generate the query
, key
, and
. Then, a one-hidden-layer MLP projects
to three weighted matrices
,
, and
, which respectively guide the MHA computation on
,
and
:
Similarly, the SSA transforms the output of TSA into
,
, and
and transforms
into
,
, and
to perform MHA computation. After TSA and SSA computation, the encoder applies an FNN to convert the output sequence into the encoding sequence
.
3.3.5. Decoder
The decoder stacks
decoder layers, each containing TSA, SSA, TEDA, and FFN. In the decoder layer, TSA and SSA extract spatial–temporal dependencies and correlations from
to generate
. Subsequently, TEDA converts
into the query vector
, and it converts the encoder output
into the key vector
and value vector
. Next, TEDA utilizes multi-head cross-attention to capture the spatial–temporal correlations and dependencies from
,
, and
:
In this way, TEDA generates the decoding sequence and utilizes an FNN to convert it into the traffic prediction at the next time step within the predictive horizon. After
round of decoding, CeT can acquire the final traffic prediction sequence
.
4. Experiment
This section provides a detailed introduction to the experiment in this paper. Firstly, it introduces experimental datasets and scenarios. Then, the experiment setups are also presented in this section, including model parameters and implementation details of the experiment platform. Moreover, this section explains the baseline models and evaluation metrics.
4.1. Datasets and Scenarios
The experimental data is obtained from a comprehensive open-source dataset named pNEUMA, which contains approximately 500,000 real trajectories collected from the central business district of Athens, as displayed in
Figure 4 [
8]. These trajectories were derived from nearly 10 h of aerial video captured at 25 Hz by two five-drone swarms (H1 and H2) during the morning peak hours of weekdays and calibrated in the World Geodetic System 1984 (WGS84). The pNEUMA can provide vehicle-state information at any given timestamp and corresponding vehicle-type information for each trajectory. The dataset can be downloaded from
https://open-traffic.epfl.ch (accessed on 23 November 2019).
The official website of pNEMUA does not directly offer high-precision maps, so we download the OpenStreetMap (OSM) based on its WGS84 boundary coordinates, as shown in
Figure 5a. Then, the scenario designer in the composable benchmarks for motion planning on roads (CommonRoad) is employed to convert the OSM into a CommonRoad map [
9]. As demonstrated in
Figure 5b, the zones of drones 1, 2, 3, and 4 are selected to establish our research scenarios because these zones are densely populated with signalized intersections. Next, the trajectories of pNEUMA are smoothed by the Unscented Kalman Filter and matched with the CommonRoad map to reconstruct the actual traffic scenario, while simultaneously computing the azimuths [
35]. As shown in
Figure 5c, two two-phase signalized intersections and two four-phase signalized intersections are selected as the experimental scenarios, respectively named Scenario 1 and Scenario 2.
Utilizing the built-in map converter, the CommonRoad map is converted into the Lanelet2 format. The Lanelet2 map discretizes the road space into a series of lane segments, as depicted in
Figure 5d. The lane segment size is set to
m in length and the same width as the corresponding lane, providing sufficient space for a bus or heavy vehicle. It is worth noting that the connectivity matrix of lane segments is determined by both their topological relationships and signal phases at signalized intersections at each time step.
4.2. Experiment Setups
According to pNEUMA, we construct training, validation, and test sets of equal size for both Scenario 1 and Scenario 2, comprising 37,423, 5346, and 10,693 samples, respectively. For each sample, the temporal interval between two successive traffic states is set to 1 s based on the update frequency of HD maps [
4]. In the experiment, the number of previous states
and future states
are both set to 20. In CeT, the numbers of encoder layers
and decoder layers
are both set to 6, and the feature dimension
and jam capacity
are set to 16. The number of heads
in MHA is set to 4 and the head dimension
is equal to
. Moreover, the number of nodes
used to define the local neighborhood is set to 8.
CeT is deployed on a blade server equipped with an Intel Xeon Gold 5218 CPU, dual NVIDIA Tesla V100S GPUs, and Ubuntu 22.04.2 LTS runtime environment. It is implemented using the PyTorch 1.5 framework in the Python 3.8 programming environment. This work uses the mean absolute error (MAE) as the loss function to train CeT and applies the Adam optimizer to train the parameters in CeT with a learning rate set to
, batch set to 32, beta1 set to 0.9, beta2 set to 0.99, and epsilon set to
[
36]. After
rounds of iterative optimization, the training was completed.
4.3. Baseline Models
To assess the predictive performance of CeT, we select seven classic prediction methods to establish baseline models. These models are trained on the same dataset as CeT and compared against it during testing, providing an intuitive assessment of CeT’s predictive capabilities. To ensure a comprehensive evaluation, the selected methods span statistical, machine learning, and deep learning methods.
Historical Average (HA): As a fundamental statistical method, HA computes the average traffic states over the previous four signal phases to generate predictions. This method serves as a baseline to evaluate the performance of more sophisticated methods, providing insights into the benefits of leveraging historical patterns.
Autoregressive Integrated and Moving Average (ARIMA) [
18]: ARIMA is a widely adopted statistical model for time series forecasting. It captures linear dependencies in historical traffic data through its auto-regressive, differencing, and moving average components. Its inclusion ensures a comparison with traditional time series analysis techniques.
Support Vector Regression (SVR) [
37]: SVR is a robust machine learning method that constructs a hyperplane in kernel space to model nonlinear relationships in traffic data. It represents a classical approach to regression tasks and provides a baseline for evaluating the effectiveness of more advanced predictive techniques.
Random Forest (RF) [
38]: Implemented using Scikit-learn, RF is an ensemble learning method that combines 10 decision trees to improve predictive accuracy while controlling overfitting. This method is included as a representative of ensemble methods, which are widely recognized for their performance in traffic prediction tasks.
Feedforward Neural Network (FNN) [
25]: FNN is a deep learning model structured as an MLP with one hidden layer consisting of 256 neurons. It processes historical cell space states to predict future traffic states, serving as a baseline for evaluating the performance of more complex neural network architectures.
Adaptive Graph Convolutional Recurrent Network (AGCRN) [
31]: AGCRN enhances GCNs with node adaptive parameters to learn spatial dependencies and employs RNNs to capture temporal correlations. This method is included to represent advanced spatial–temporal modeling techniques.
Graph WaveNet (GWN) [
32]: GWN is an advanced deep learning method that combines 1-dimensional dilated convolutions to capture long-term temporal correlations and constructs an adaptive dependency matrix through learnable node embeddings to model spatial dependencies. It serves as a cutting-edge baseline for evaluating CeT’s performance against highly optimized architectures.
By including methods from diverse methodological groups, we ensure a thorough and balanced evaluation of CeT’s predictive performance. Each model is chosen to represent a distinct class of approaches, enabling a comprehensive comparison across statistical, machine learning, and deep learning paradigms.
4.4. Evaluation Metrics
This study applies MAE, root mean square error (RMSE), and accuracy (ACC) as evaluation metrics. The calculation formulas for MAE and RMSE are as follows:
where
represents the length of the estimated sequence. Further, the state of the lane segment is classified into the free state with less than 0.5 vehicles and the occupied state with more than 0.5 vehicles, and ACC is defined as the ratio of lane segments with accurately predicted states. Based on MAE, RMSE, and ACC, the predictive performance of CeT can be evaluated and compared to baselines.
5. Results and Analysis
This section presents the experimental results and corresponding analysis. It first compares the predictive performances of CeT with the baselines. Then, the section conducts ablation studies to examine the impact of different components of CeT on predictive results. Furthermore, the impacts of hyperparameters and model sensitivity are also discussed in this section.
5.1. Predictive Results
Table 1 presents a comparison of predictions between CeT and baseline models for two-phase signalized intersections (Scenario 1) and four-phase signalized intersections (Scenario 2), as described in
Section 4. The results demonstrate that the predictive performance of CeT outperforms all baselines in both Scenario 1 and Scenario 2. CeT enhances the best predictive performance in the baselines by 11.47%, 13.28%, and 4.36% in terms of MAE, RMSE, and ACC in Scenario 1. Similarly, CeT respectively improves MAE, RMSE, and ACC by 13.36%, 13.03%, and 4.78% in Scenario 2.
Figure 6 compares the predictive performance of the CeT model with baseline models (FNN, AGCRN, GWN) in two scenarios. Across three metrics—MAE, RMSE, and ACC—over a predictive horizon of 0 to 20 s, the CeT model consistently outperforms the baseline models, demonstrating lower prediction errors (MAE and RMSE) and higher accuracy (ACC). Furthermore, the performance of the CeT model degrades significantly less as the predictive horizon increases, showcasing greater robustness and stability.
As statistic methods, HA and ARIMA analyze historical traffic data at signalized intersections to identify periodic evolution patterns for future traffic state prediction. However, their neglect of previous traffic states hinders their ability to consider emergencies in forecasting. Further, these statistic models exhibit poor predictive performance at multi-signal intersections. In contrast to HA and ARIMA, SVR and RF establish the traffic state space and train the state evolution model based on historical data. By successively updating the state of cells, these machine learning methods can forecast future traffic states. However, these methods fail to sufficiently utilize the spatial relationship among cells, resulting in inferior predictive performance in Scenario 2 compared to Scenario 1. Compared to statistic and machine learning methods, deep learning-based approaches typically demonstrate superior predictive performance because of their strong non-linear fitting capabilities and flexible model structures. Through a fully connected network with one hidden layer, FNN can learn intricate spatial–temporal dependencies and correlations for future state prediction. In the experiment, FNN outcomes better predictive performance than the whole statistic and machine learning methods in Scenario 1. Nonetheless, the insufficient performance of FNN in Scenario 2 also indicates the need for deep learning-based approaches to improve predictive abilities in a broad spatial area. AGCRN effectively captures temporal and spatial correlations by employing RNN and GCN with adaptive parameters. Therefore, it exhibits excellent predictive performance, especially in Scenario 2. Similarly, GWN also adopts GCN and incorporates an adaptive dependency matrix to capture hidden spatial dependencies and correlations. Through stacked dilated causal convolution layers, GWN overcomes the challenge of long sequence dependencies in AGCRN, enabling it to accurately predict future traffic states in both Scenario 1 and Scenario 2. However, the GCNs employed in AGCRN and GWN fail to capture dynamic spatial changes at signalized intersections for their fixed architectures after training.
In comparison to the previously mentioned model, CeT primarily possesses three primate advantages. Firstly, CeT transforms vehicle-type information into word encodings and embeds them into vehicle-state information. Thus, CeT can comprehend the varying impacts of different vehicle types on traffic evolution. Secondly, CeT utilizes the dynamic topology graph to reflect different traffic patterns at intersections under various phases. With sufficient training, CeT can recognize signal phase changes from the topology graph and perform corresponding traffic prediction. Thirdly, CeT extracts spatial–temporal dependencies and correlations from the temporal attributes and spatial topology graph to guide the prediction. The experimental results in both Scenario 1 and Scenario 2 evidence the superiority of CeT.
5.2. Ablation Studies
Three independent ablation studies were conducted to research the crucial components of CeT. Apart from the studied components, the variants in these ablation studies share the same experiment setups with the complete model. Their experimental result is compared with that of the complete model to analyze the contributions of each component.
To investigate the contribution of vehicle-state embeddings, two variants are designed based on the complete model:
noVSE variant—VSE is deleted from the complete model to research the impacts of the embedding structure.
noVSA variant—The vehicle-state attributes in VSE are removed to study the impacts of the additional information.
Table 2 presents a detailed comparison of the performance of different model variants in two scenarios, focusing on the impact of VSE and VSA. The table evaluates the models using three metrics: MAE, RMSE, and ACC. In Scenario 1, the complete model with both VSE and VSA outperforms the variants that lack these components. Specifically, the CeT model achieves the lowest MAE of 0.247, the lowest RMSE of 0.565, and the highest accuracy of 84.81%. This indicates that incorporating both VSE and VSA significantly enhances the model’s performance in this scenario. Similarly, in Scenario 2, the complete model again demonstrates superior performance with an MAE of 0.272, RMSE of 0.512, and accuracy of 84.36%. These results suggest that the inclusion of both vehicle-state embeddings and attention is beneficial across different scenarios, consistently leading to improved predictive accuracy and reduced error compared to models that exclude either the noVSE variant or noVSA variant.
Figure 7 illustrates a detailed comparison of the MAE, RMSE, and ACC metrics at each time step within the predictive horizon for the complete model and its variants. The worst predictive performance of the noVSE variant can be attributed to the lack of vehicle-type embeddings. This deficiency makes it difficult for the noVSE variant to consider the differences among various types of vehicles in prediction. In comparison, the noVSA variant applies the same multi-head attention as the complete model to extract vehicle-state features, which significantly enhances predictive performance. Different from these variants, the complete model embeds the vehicle-type attributes into vehicle-state features and further improves the predictive performance, especially the initial states in the predicted result.
To research the impact of temporal and spatial feature extraction on prediction, two variants are constructed based on the complete model:
noTSA variant—TSA in both the encoder and decoder are removed from the complete model to study their function.
noSSA variant—SSA in both the encoder and decoder are removed from the complete model to test their effectiveness.
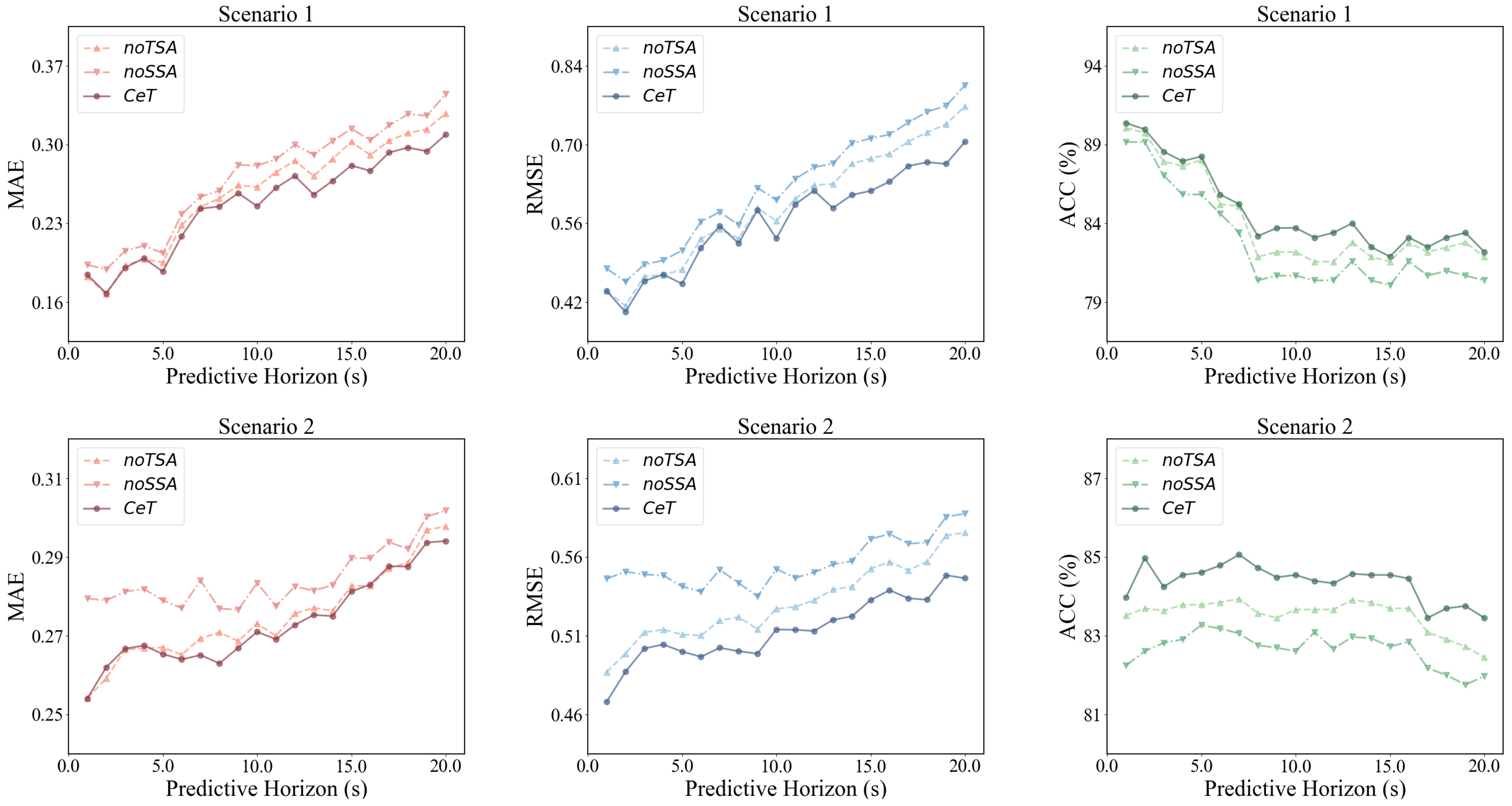
Table 3 provides a detailed comparison of the performance of different model variants in two scenarios, focusing on the impact of TSA and SSA. In Scenario 1, the complete model with both TSA and SSA outperforms the variants lacking these components. Specifically, CeT achieves the lowest MAE of 0.247, the lowest RMSE of 0.565, and the highest accuracy of 84.81%. This indicates that incorporating both types of self-attention significantly enhances the model’s performance in this scenario. Similarly, in Scenario 2, the complete model demonstrates superior performance with an MAE of 0.272, RMSE of 0.512, and accuracy of 84.36%.
Figure 8 illustrates a detailed comparison of the MAE, RMSE, and ACC metrics at each time step within the predictive horizon for the complete model and its variants. The experimental results demonstrate that the predictive performance of the noTSA variant is better than that of the noSSA variant but worse than that of the complete model. The experimental results confirm the significance of both TSA and SSA and indicate the greater contribution of SSA to enhancing predictive accuracy.
To investigate the guidance of temporal and spatial embeddings to prediction, three variants of the complete model are conducted as follows:
noSTE variant—SE and TE are deleted from the complete model to study their contribution.
noTE variant—TE are removed from the complete model to study their contribution.
noSE variant—The dynamic directed graph in SE is replaced by a static graph to study their contribution.
Table 4 compares the prediction performance of different variants in two scenarios. In Scenario 1, the complete model with both TE and SE outperforms the variants that lack these components. Specifically, CeT achieves the lowest MAE of 0.247, the lowest RMSE of 0.565, and the highest accuracy of 84.81%. This demonstrates that the integration of both TE and SE significantly enhances the model’s performance in this scenario. Similarly, in Scenario 2, the complete model shows superior performance with an MAE of 0.272, RMSE of 0.512, and accuracy of 84.36%. These results indicate that the inclusion of both TE and SE is beneficial across different scenarios, consistently leading to improved predictive accuracy and reduced error compared to models that exclude either noSTE, noTE, or noSE.
Figure 9 presents the step-by-step comparison between the complete model and variants. The result of the noSTE variant exhibits the worst predictive performance, which confirms the contribution of STEs. In contrast, the predictive performance of the noSE variant is slightly better than that of the noSTE variant and remarkably worse than that of the complete model. This phenomenon demonstrates the effective assistance of SEs in enabling CeT to comprehend signal variation and guide predictions across different phases. Surprisingly, the predictive performance of the noTE variant is significantly better than that of the noSE variant but only slightly less than that of the complete model. One possible explanation is that the data in pNEUMA is collected during the morning peak hours, which exhibit similar temporal patterns.
5.3. Hyperparameters Analysis
Figure 10 presents the results of three independent experiments designed to assess the impact of various hyperparameters on the model’s performance, specifically focusing on the model dimension
, the number of layers
in both the encoder and decoder, and the number of heads
. The experimental setup remains consistent with that described in
Section 4.2, ensuring that any observed variations in performance can be attributed to changes in these hyperparameters. The analysis of the results reveals that the metrics MAE, RMSE, and ACC exhibit similar trends across different prediction horizons. MAE values range from 0.25 to 0.31, gradually increasing as the prediction horizon extends. RMSE values follow a similar pattern, ranging from 0.46 to 0.58. Conversely, ACC values range from 81% to 85%, showing a slight decrease with longer prediction horizons. These consistent trends across varying hyperparameter settings suggest that the CeT model is relatively insensitive to changes in
,
, and
. This insensitivity is advantageous as it indicates that the model can maintain stable performance without extensive hyperparameter tuning.
5.4. Sensitivity Analysis
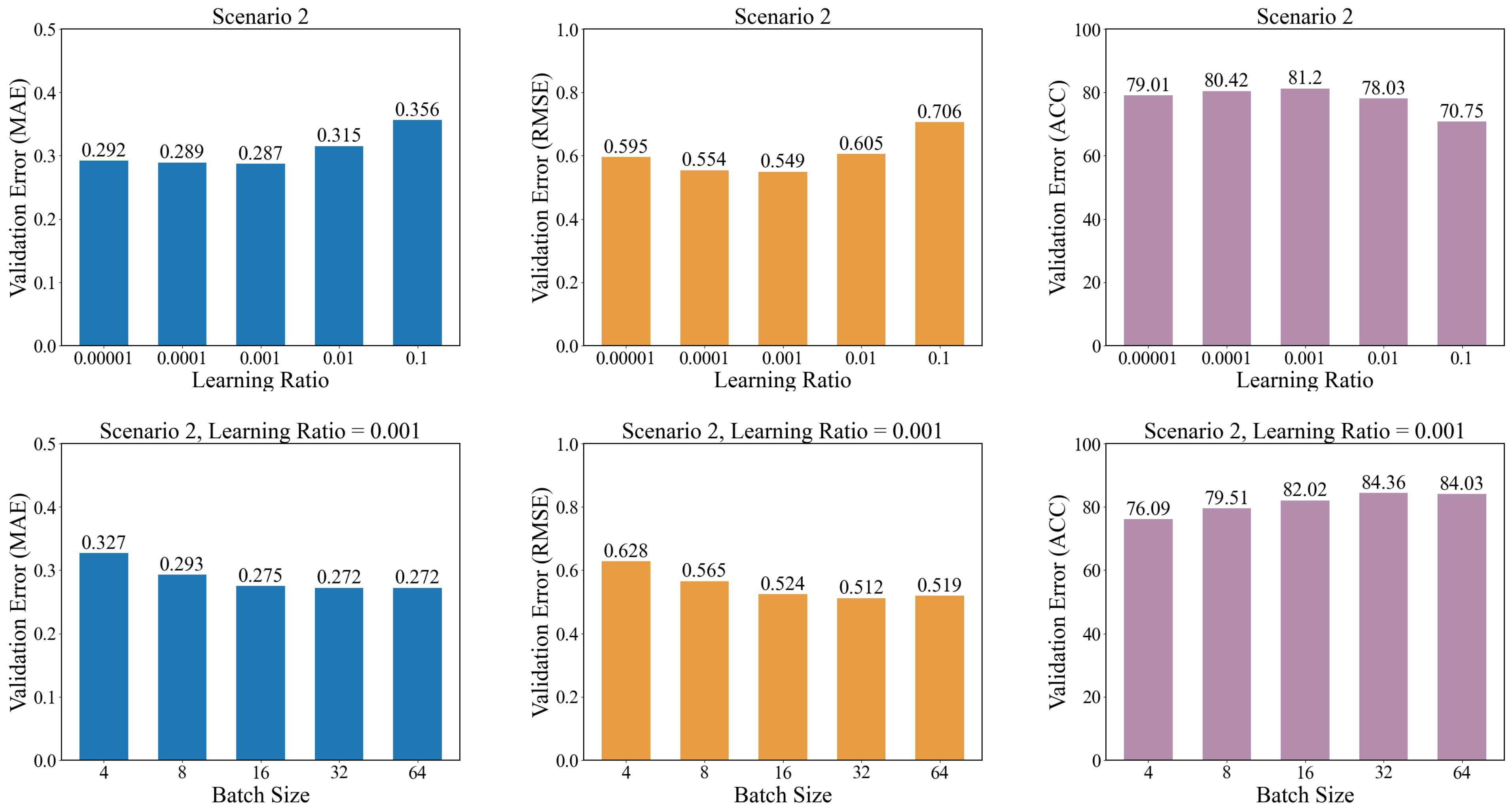
Two further investigations explore the impact of learning rate and batch size on the convergence behavior during training. A range of learning rates and batch sizes are tested to determine their effects on the convergence and predictive performance of the CeT model. As shown in
Figure 11, the results demonstrate that CeT achieves optimal predictive performance when the learning rate is set to 0.001. This learning rate strikes a balance between convergence speed and stability; a learning rate that is too high leads to divergence or oscillations in the loss function, while a learning rate that is too low results in excessively slow convergence, potentially causing the model to get stuck in suboptimal local minima. Similarly, the experiments reveal that a batch size of 32 is most suitable for CeT when paired with the optimal learning rate. A batch size that is too large leads to inefficient memory usage and slower updates, as it requires more computational resources and time per iteration. Conversely, a batch size that is too small introduces excessive noise in the gradient estimates, leading to unstable convergence and potentially poorer generalization. Therefore, selecting an appropriate batch size is crucial for achieving efficient and effective training. These findings highlight the importance of carefully tuning the learning rate and batch size to ensure robust model performance and efficient training dynamics.
6. Conclusions
This paper introduces CeT, a predictive framework designed to forecast future traffic states at signalized intersections. The model employs a discrete spatial–temporal structure, reminiscent of the traditional cellular transmission model, which proves effective in utilizing traffic data from high-definition maps. This includes vehicle-state information, vehicle-type attributes, temporal attributes, and spatial attributes. CeT first transforms the vehicle-type attributes into word encodings and embeds them into vehicle-state information, enabling the model to learn the effects of different vehicle types on traffic predictions. Subsequently, CeT converts vehicle-state embeddings into the state of the cell space, encompassing entire lane segments. Next, CeT utilizes the previous cell space states to construct the input sequence and perform spatial–temporal embeddings to the sequence based on the previous temporal attributes and spatial attributes. Under the guidance of spatial–temporal embeddings, CeT learns the interdependencies and correlations within the input sequence, employing multi-head attention to forecast the number of vehicles in each lane segment across the forecasting horizon.
We utilize the traffic data in pNEUMA to conduct two different signalized intersection scenarios to validate the effectiveness of CeT. Compared to the best predictive performance in baselines, the result indicates that CeT respectively improves MAE, RMSE, and ACC by 11.47%, 13.48%, and 4.36% in two-phase signalized intersections and 13.36%, 12.93%, and 4.78% in four-phase signalized intersections. Meanwhile, three independent ablation studies also confirm the advantages of CET over baseline models and the further contributions of vehicle-state embeddings, spatial–temporal embeddings, and spatial–temporal attention in enhancing predictive accuracy. Further, the studies on hyperparameters and model sensitivity also demonstrate the robustness of CeT.
Future research primarily focuses on three main directions. Firstly, we aim to enhance the model architecture to more effectively capture complex dependencies and correlations, thereby improving predictive performance. Secondly, we plan to integrate CeT with the motion planner of AVs. By leveraging the results of traffic state evolution prediction, we will generate space–time corridors to facilitate reference trajectory planning for autonomous vehicles. Furthermore, we will apply CeT in urban infrastructure monitoring for real-time condition evaluation or energy consumption prediction to optimize efficiency due to its outstanding ability in discrete spatial–temporal data processing.
Author Contributions
Conceptualization, A.L. and Y.P.; Methodology, A.L.; Software, Z.X.; Validation, W.L.; Formal analysis, A.L.; Investigation, Z.X.; Data curation, W.L.; Writing—original draft, A.L.; Writing—review & editing, Y.P.; Supervision, Y.C.; Funding acquisition, Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Key Science and Technology Projects in the Transportation Industry (2022-ZD6-116), and Technology Transfer Project of Beijing Municipal Engineering Design and Research Institute (40061000202417) and (40061000202503).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ding, F.; Zhang, N.; Li, S.; Bian, Y.; Tong, E.; Li, K. A survey of architecture and key technologies of intelligent connected vehicle-road-cloud cooperation system. Acta Autom. Sin. 2022, 48, 2863–2885. [Google Scholar] [CrossRef]
- Dong, J.; Xu, Q.; Wang, J.; Yang, C.; Cai, M.; Chen, C.; Liu, Y.; Wang, J.; Li, K. Mixed Cloud Control Testbed: Validating Vehicle-Road-Cloud Integration via Mixed Digital Twin. IEEE Trans. Intell. Veh. 2023, 8, 2723–2736. [Google Scholar] [CrossRef]
- Bao, Z.; Hossain, S.; Lang, H.; Lin, X. High-Definition Map Generation Technologies For Autonomous Driving. arXiv 2022, arXiv:2206.05400. [Google Scholar]
- Feng, C.; Du, Q.; Fan, X.; Ren, F.; Xiong, L.; Tian, Y.; Liu, W.; Wang, T.; Wang, Y.; Zhang, B. A Crowdsourcing Update Technology Route of HD Dynamic Map Basic Platform. J. Geomat. 2023, 48, 10–15. [Google Scholar] [CrossRef]
- Kiran, B.R.; Sobh, I.; Talpaert, V.; Mannion, P.; Sallab, A.A.A.; Yogamani, S.; Pérez, P. Deep Reinforcement Learning for Autonomous Driving: A Survey. IEEE Trans. Intell. Transp. Syst. 2022, 23, 4909–4926. [Google Scholar] [CrossRef]
- Daganzo, C.F. The cell transmission model, part II: Network traffic. Transp. Res. Part B Methodol. 1995, 29, 79–93. [Google Scholar] [CrossRef]
- Ye, X.; Fang, S.; Sun, F.; Zhang, C.; Xiang, S. Meta Graph Transformer: A Novel Framework for Spatial–Temporal Traffic Prediction. Neurocomputing 2022, 491, 544–563. [Google Scholar] [CrossRef]
- Barmpounakis, E.; Geroliminis, N. On the new era of urban traffic monitoring with massive drone data: The pNEUMA large-scale field experiment. Transp. Res. Part C Emerg. Technol. 2020, 111, 50–71. [Google Scholar] [CrossRef]
- Althoff, M.; Koschi, M.; Manzinger, S. CommonRoad: Composable benchmarks for motion planning on roads. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 719–726. [Google Scholar] [CrossRef]
- Lighthill, M.J.; Whitham, G.B. On kinematic waves II. A theory of traffic flow on long crowded roads. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1955, 229, 317–345. [Google Scholar] [CrossRef]
- Richards, P.I. Shock Waves on the Highway. Oper. Res. 1956, 4, 42–51. [Google Scholar] [CrossRef]
- Adacher, L.; Tiriolo, M. A macroscopic model with the advantages of microscopic model: A review of Cell Transmission Model’s extensions for urban traffic networks. Simul. Model. Pract. Theory 2018, 86, 102–119. [Google Scholar] [CrossRef]
- Srivastava, A.; Jin, W.L.; Lebacque, J.P. A modified Cell Transmission Model with realistic queue discharge features at signalized intersections. Transp. Res. Part B Methodol. 2015, 81, 302–315. [Google Scholar] [CrossRef][Green Version]
- Shirke, C.; Bhaskar, A.; Chung, E. Macroscopic modelling of arterial traffic: An extension to the cell transmission model. Transp. Res. Part C Emerg. Technol. 2019, 105, 54–80. [Google Scholar] [CrossRef]
- Liu, Y.; Chang, G.L. An arterial signal optimization model for intersections experiencing queue spillback and lane blockage. Transp. Res. Part C Emerg. Technol. 2011, 19, 130–144. [Google Scholar] [CrossRef]
- Hu, X.; Wang, W.; Sheng, H. Urban Traffic Flow Prediction with Variable Cell Transmission Model. J. Transp. Syst. Eng. Inf. Technol. 2010, 10, 73–78. [Google Scholar] [CrossRef]
- de Wit, C.C.; Ferrara, A. A variable-length Cell Transmission Model for road traffic systems. Transp. Res. Part C Emerg. Technol. 2018, 97, 428–455. [Google Scholar] [CrossRef]
- Hamed, M.M.; Al-Masaeid, H.R.; Said, Z.M.B. Short-Term Prediction of Traffic Volume in Urban Arterials. J. Transp. Eng. 1995, 121, 249–254. [Google Scholar] [CrossRef]
- Williams, B.M.; Hoel, L.A. Modeling and Forecasting Vehicular Traffic Flow as a Seasonal ARIMA Process: Theoretical Basis and Empirical Results. J. Transp. Eng. 2003, 129, 664–672. [Google Scholar] [CrossRef]
- Zhang, H.; Poschinger, A. Estimation of Turning Ratio at Intersections Based on Detector Data using Kalman Filter. Transp. Res. Procedia 2019, 41, 673–687. [Google Scholar] [CrossRef]
- Kawasaki, Y.; Hara, Y.; Kuwahara, M. Traffic state estimation on a two-dimensional network by a state-space model. Transp. Res. Part C Emerg. Technol. 2020, 113, 176–192. [Google Scholar] [CrossRef]
- Wang, S.; Patwary, A.; Huang, W.; LO, H.K. A general framework for combining traffic flow models and Bayesian network for traffic parameters estimation. Transp. Res. Part C Emerg. Technol. 2022, 139, 103664. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y. Traffic forecasting using least squares support vector machines. Transportmetrica 2009, 5, 193–213. [Google Scholar] [CrossRef]
- Qi, Y.; Ishak, S. A Hidden Markov Model for short term prediction of traffic conditions on freeways. Transp. Res. Part C Emerg. Technol. 2014, 43, 95–111. [Google Scholar] [CrossRef]
- Ye, Q.; Szeto, W.Y.; Wong, S.C. Short-Term Traffic Speed Forecasting Based on Data Recorded at Irregular Intervals. IEEE Trans. Intell. Transp. Syst. 2012, 13, 1727–1737. [Google Scholar] [CrossRef]
- Polson, N.G.; Sokolov, V.O. Deep learning for short-term traffic flow prediction. Transp. Res. Part C Emerg. Technol. 2017, 79, 1–17. [Google Scholar] [CrossRef]
- Azzouni, A.; Pujolle, G. A Long Short-Term Memory Recurrent Neural Network Framework for Network Traffic Matrix Prediction. arXiv 2017, arXiv:1705.05690. [Google Scholar]
- Pan, Y.A.; Guo, J.; Chen, Y.; Li, S.; Li, W. Incorporating Traffic Flow Model into A Deep Learning Method for Traffic State Estimation: A Hybrid Stepwise Modeling Framework. J. Adv. Transp. 2022, 2022. [Google Scholar] [CrossRef]
- Pan, Y.A.; Guo, J.; Chen, Y.; Cheng, Q.; Li, W.; Liu, Y. A fundamental diagram based hybrid framework for traffic flow estimation and prediction by combining a Markovian model with deep learning. Expert Syst. Appl. 2024, 238, 122219. [Google Scholar] [CrossRef]
- Guo, J.; Liu, Y.; Yang, Q.K.; Wang, Y.; Fang, S. GPS-based citywide traffic congestion forecasting using CNN-RNN and C3D hybrid model. Transp. A Transp. Sci. 2021, 17, 190–211. [Google Scholar] [CrossRef]
- Xu, Y.; Lu, Y.; Ji, C.; Zhang, Q. Adaptive Graph Fusion Convolutional Recurrent Network for Traffic Forecasting. IEEE Internet Things J. 2023, 10, 11465–11475. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Zhang, C. Graph WaveNet for Deep Spatial-Temporal Graph Modeling. arXiv 2019, arXiv:1906.00121. [Google Scholar]
- Kodupuganti, S.; Pulugurtha, S. Are facilities to support alternative modes effective in reducing congestion?: Modeling the effect of heterogeneous traffic conditions on vehicle delay at intersections. Multimodal Transp. 2023, 2, 100050. [Google Scholar] [CrossRef]
- Rahman, M.; Rifaat, S.; Sadeek, S.; Abrar, M.; Wang, D. Gated ensemble of spatio-temporal mixture of experts for multi-task learning in ride-hailing system. Multimodal Transp. 2024, 3, 100166. [Google Scholar] [CrossRef]
- Siebinga, O. TraViA: A Traffic data Visualization and Annotation tool in Python. J. Open Source Softw. 2021, 6, 3607. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, W.; Orabona, F.; Yang, T. Adam+: A Stochastic Method with Adaptive Variance Reduction. arXiv 2020, arXiv:2011.11985. [Google Scholar]
- Drucker, H.; Burges, C.J.C.; Kaufman, L.; Smola, A.; Vapnik, V. Support Vector Regression Machines. In Advances in Neural Information Processing Systems; Mozer, M., Jordan, M., Petsche, T., Eds.; MIT Press: Cambridge, MA, USA, 1996; Volume 9. [Google Scholar]
- Athey, S.; Tibshirani, J.; Wager, S. Generalized random forests. Ann. Stat. 2019, 47, 1148–1178. [Google Scholar] [CrossRef]
Figure 1.
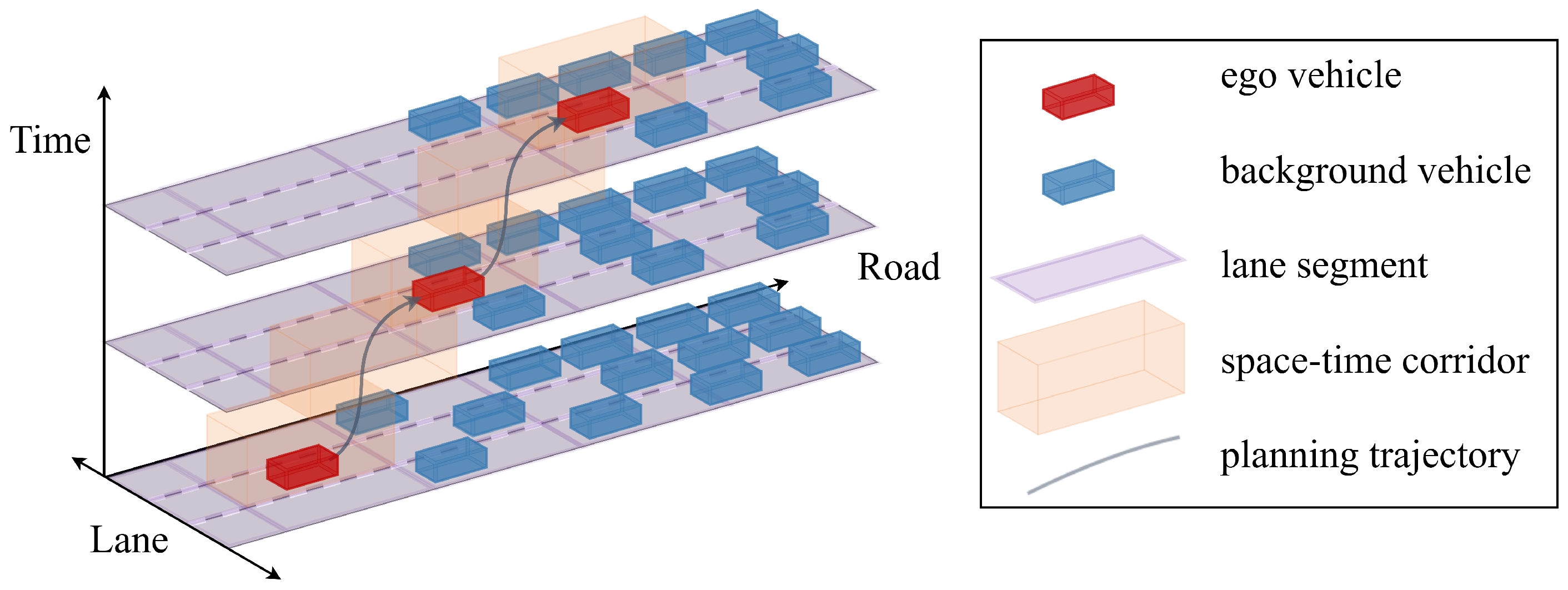
A three-dimensional representation in which the horizontal axis denotes lanes, the vertical axis indicates time, and the depth axis represents the road. The ego vehicle and background vehicles are situated along lane segments. The orange space–time corridor delineates the unoccupied future lane segments available for AV, while the gray curve illustrates the optimized planning trajectory within this corridor. This visualization emphasizes the consideration of future traffic states, which is essential for ensuring safe and efficient trajectory planning.
Figure 1.
A three-dimensional representation in which the horizontal axis denotes lanes, the vertical axis indicates time, and the depth axis represents the road. The ego vehicle and background vehicles are situated along lane segments. The orange space–time corridor delineates the unoccupied future lane segments available for AV, while the gray curve illustrates the optimized planning trajectory within this corridor. This visualization emphasizes the consideration of future traffic states, which is essential for ensuring safe and efficient trajectory planning.
Figure 2.
The illustration of the cell space in conventional CTM at a signalized intersection.
Figure 2.
The illustration of the cell space in conventional CTM at a signalized intersection.
Figure 3.
The architecture of CeT and its key components.
Figure 3.
The architecture of CeT and its key components.
Figure 4.
The data collection area in pNEUMA and the zone for each drone in the swarms.
Figure 4.
The data collection area in pNEUMA and the zone for each drone in the swarms.
Figure 5.
The establishment of the experimental scenarios. (a) The OSM map for the data collection area in pNEUMA. (b) The densely distributed zones of signalized intersections in CommonRoad. (c) The illustration of the two adjacent signalized intersections in Scenario 1. (d) The illustration of the constructed Scenario 1. The color ring denotes the azimuths of vehicles.
Figure 5.
The establishment of the experimental scenarios. (a) The OSM map for the data collection area in pNEUMA. (b) The densely distributed zones of signalized intersections in CommonRoad. (c) The illustration of the two adjacent signalized intersections in Scenario 1. (d) The illustration of the constructed Scenario 1. The color ring denotes the azimuths of vehicles.
Figure 6.
The comparison of predictive performance between CeT and baseline models in Scenario 1 and Scenario 2.
Figure 6.
The comparison of predictive performance between CeT and baseline models in Scenario 1 and Scenario 2.
Figure 7.
Ablation study for vehicle-state embeddings in Scenario 1 and Scenario 2.
Figure 7.
Ablation study for vehicle-state embeddings in Scenario 1 and Scenario 2.
Figure 8.
Ablation study for spatial-temporal embeddings in Scenario 1 and Scenario 2.
Figure 8.
Ablation study for spatial-temporal embeddings in Scenario 1 and Scenario 2.
Figure 9.
Ablation study for spatial and temporal attention in Scenario 1 and Scenario 2.
Figure 9.
Ablation study for spatial and temporal attention in Scenario 1 and Scenario 2.
Figure 10.
Analysis of the impact of hyperparameters on predictive performance in Scenario 2.
Figure 10.
Analysis of the impact of hyperparameters on predictive performance in Scenario 2.
Figure 11.
Analysis of learning rates and batch sizes on model convergence in Scenario 2.
Figure 11.
Analysis of learning rates and batch sizes on model convergence in Scenario 2.
Table 1.
The prediction comparison between CeT and baseline models. The best result is highlighted in bold, and the second-best result is labeled with an asterisk.
Table 1.
The prediction comparison between CeT and baseline models. The best result is highlighted in bold, and the second-best result is labeled with an asterisk.
| Scenario | Metric | HA | ARIMA | RF | SVR | FNN | AGCRN | GWN | CeT |
|---|
| Scenario 1 | MAE | 0.437 | 0.372 | 0.521 | 0.675 | 0.297 | 0.303 | 0.279 * | 0.247 |
| RMSE | 1.093 | 0.792 | 1.136 | 1.334 | 0.685 | 0.704 | 0.653 * | 0.565 |
| ACC | 61.13 | 67.54 | 74.51 | 73.07 | 77.21 | 78.49 | 81.27 * | 84.81 |
| Scenario 2 | MAE | 1.497 | 1.017 | 0.448 | 0.468 | 0.358 | 0.327 | 0.314 * | 0.272 |
| RMSE | 2.186 | 1.429 | 0.864 | 0.933 | 0.671 | 0.632 | 0.588 * | 0.512 |
| ACC | 58.38 | 61.86 | 68.23 | 68.33 | 76.98 | 78.72 | 80.51 * | 84.36 |
Table 2.
Ablation study for vehicle-state embeddings in Scenario 1 and Scenario 2. The best model is shown in bold font.
Table 2.
Ablation study for vehicle-state embeddings in Scenario 1 and Scenario 2. The best model is shown in bold font.
| Scenario | Metric | noVSE | noVSA | CeT |
|---|
| Scenario 1 | MAE | 0.272 | 0.263 | 0.247 |
| RMSE | 0.628 | 0.601 | 0.565 |
| ACC | 82.92 | 83.32 | 84.81 |
| Scenario 2 | MAE | 0.283 | 0.279 | 0.272 |
| RMSE | 0.543 | 0.533 | 0.512 |
| ACC | 83.11 | 83.52 | 84.36 |
Table 3.
Ablation study for temporal and spatial self-attention in Scenario 1 and Scenario 2. The best model is shown in bold font.
Table 3.
Ablation study for temporal and spatial self-attention in Scenario 1 and Scenario 2. The best model is shown in bold font.
| Scenario | Metric | noTSA | noSSA | CeT |
|---|
| Scenario 1 | MAE | 0.256 | 0.271 | 0.247 |
| RMSE | 0.592 | 0.626 | 0.565 |
| ACC | 84.07 | 82.69 | 84.81 |
| Scenario 2 | MAE | 0.276 | 0.284 | 0.272 |
| RMSE | 0.531 | 0.558 | 0.512 |
| ACC | 83.53 | 82.67 | 84.36 |
Table 4.
Ablation study for temporal and spatial embeddings in Scenario 1 and Scenario 2. The best model is shown in bold font.
Table 4.
Ablation study for temporal and spatial embeddings in Scenario 1 and Scenario 2. The best model is shown in bold font.
| Scenario | Metrics | noSTE | noTE | noSE | CeT |
|---|
| Scenario 1 | MAE | 0.281 | 0.262 | 0.278 | 0.247 |
| RMSE | 0.663 | 0.597 | 0.647 | 0.565 |
| ACC | 81.13 | 83.24 | 81.64 | 84.81 |
| Scenario 2 | MAE | 0.318 | 0.283 | 0.303 | 0.272 |
| RMSE | 0.598 | 0.534 | 0.569 | 0.512 |
| ACC | 80.49 | 82.82 | 81.56 | 84.36 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).