Sensitivity Analysis of Water Vapor in Near-Space Based on the SCIATRAN Atmospheric Radiative Transfer Model

Abstract

To achieve high-precision retrieval of water vapor concentration profiles in the near-space region, this study utilizes the high-resolution spectral radiative transfer model SCIATRAN to simulate water vapor observation spectra under different observational geometric parameters and atmospheric aerosol conditions. A comprehensive analysis is conducted on the influence of these parameters on spectral radiance. The results demonstrate that when the tangent height exceeds 40 km, water vapor absorption features significantly weaken. Spectral data acquired under conditions combining small solar zenith angles with large relative azimuth angles exhibit greater stability. Middle and upper atmospheric aerosols, predominantly composed of volcanic ash and particulate matter, induce strong sensitivity of water vapor spectral radiance to stratospheric and mesospheric aerosols. Notably, under extreme volcanic aerosol loading conditions, the differential-to-background ratio of spectral radiance surpasses 2000%. This investigation identifies key sensitive parameters and their mechanistic influences on near-space water vapor observation spectra. The findings provide a theoretical foundation for optimizing the design parameters of near-space sounders, while offering scientific guidance for formulating data screening strategies and conducting error traceability analysis during water vapor concentration retrieval processes.

1. Introduction

Near-space (20–100 km above the Earth’s surface) serves as the interface between the Earth’s atmosphere and the space environment, as well as a critical transition zone for aerospace activities. It holds significant application value in fields such as space exploration, communication, remote sensing, and target monitoring [1,2,3]. Although the atmosphere in this region is rarefied with extremely low water vapor content, atmospheric water vapor plays a vital role in the energy cycle and balance of the Earth-atmosphere system [4,5]. Its content and distribution directly affect atmospheric stratification, ionospheric physical properties, satellite communication and navigation performance, as well as the flight performance of near-space vehicles. Therefore, investigating the content, distribution, and variation patterns of atmospheric water vapor in near-space is of great significance for deepening the understanding of the physical and chemical environment in this region, improving climate prediction accuracy, and developing new remote sensing detection technologies [6].

Currently, space-based remote sensing has become the primary means of acquiring near-space atmospheric parameters due to its unique advantages of large-scale and all-day continuous observation [7]. Space-based detection mainly includes two methods: nadir sounding and limb sounding. For instance, the Total Ozone Mapping System (TOMS) and Solar Backscatter UV (SBUV) onboard the U.S. Nimbus-7 satellite, as well as the Atmospheric Interferometric Nadir Sounder on China’s Fengyun-4 satellite, all belong to the nadir sounding category. However, this detection method suffers from low vertical resolution, making it difficult to obtain accurate atmospheric profile data [8,9]. In contrast, limb sounding detects along the horizontal direction of the atmosphere, featuring high spatial coverage and vertical resolution, thus exhibiting distinct advantages in acquiring profile data of atmospheric parameters. Internationally, several countries have successively developed spaceborne limb sounders for water vapor detection. Examples include the Limb Infrared Monitor of the Stratosphere (LIMS) and the Stratospheric and Mesospheric Sounder (SAMS) onboard Nimbus-7; Remsberg et al. analyzed the impact of polar stratospheric clouds on the retrieval of ozone and other trace gases using Version 6 data from the LIMS instrument [10]. The Michelson Interferometer for Passive Atmospheric Sounding (MIPAS) onboard the European Space Agency’s ENVISAT satellite was utilized by Stefan Lossow et al. to evaluate the interannual variations in water vapor isotopes in the tropical lower stratosphere, with results indicating that vertical resolution is critical to the reliability of retrieval outcomes [11]. Additionally, the Spatial Heterodyne Observations of Water (SHOW) developed by Canada employs novel spatial heterodyne spectroscopy technology, demonstrating high-resolution potential in the upper troposphere and lower stratosphere. Nevertheless, Langille et al. pointed out that SHOW still exhibits shortcomings such as spectral aliasing and pointing accuracy in its first application on high-altitude platforms, which restrict its use in near-space and other regions with weak signals and complex environments [12,13]. The practical experiences not only verify the feasibility of limb sounding technology but also indicate that high-precision and high-vertical-resolution remote sensing detection remains an international technical challenge, particularly prominent in the Chinese context. Currently, China’s research on the environmental impact mechanisms of near-space vehicles is still immature, and there is no on-orbit satellite dedicated to near-space water vapor detection. Therefore, constructing a high-precision radiative transfer forward model and systematically analyzing the influence of various factors on water vapor detection are crucial for promoting the development and optimization of near-space water vapor sounders.

Currently, commonly used radiative transfer models in remote sensing research include MODTRAN, LOWTRAN, and SCIATRAN. Among them, MODTRAN is developed based on LOWTRAN with improved computational accuracy, but it still cannot meet the requirements of high-precision research [14]. SCIATRAN is a high-spectral-resolution atmospheric radiative transfer model developed by the University of Bremen, Germany, based on GOMETRAN++, specifically designed for the spaceborne passive remote sensing sensors SCIAMACHY and GOME [15]. This model adopts the line-by-line integration method to calculate the absorption contribution of spectral lines, enabling fast and accurate radiative transfer simulation. Many scholars have conducted sensitivity research and analysis on atmospheric trace gases such as CO₂ and NO₂ based on the SCIATRAN model combined with satellite-measured spectral data, providing effective references for satellite data processing and gas concentration retrieval [16,17]. However, there is still a lack of water vapor sensitivity analysis for near-space using this model. Based on this, this study intends to adopt the SCIATRAN radiative transfer model to quantitatively analyze the sensitivity influence laws of various factors on water vapor absorption spectra under limb observation conditions. The expected research results will provide a reliable simulation tool and theoretical basis for the design and optimization of future limb sounding instruments, as well as direct support for the development of retrieval algorithms.

2. Principles and Methods of Radiative Transfer Models

SCIATRAN is a high-spectral-resolution atmospheric radiative transfer model characterized by strong configurability, with a spectral range covering 175.44 nm to 40 μm and a spectral resolution reaching 0.24–0.5 nm [18]. Furthermore, the model provides extensive and detailed parameter settings for trace gases, observational geometry, aerosol properties, surface characteristics, and cloud parameters, meeting the precise configuration requirements for the parametric sensitivity analysis in this study. It also incorporates three atmospheric modes: spherical atmosphere, pseudo-spherical atmosphere, and plane-parallel atmosphere, supporting various observation geometries such as nadir, limb, and occultation, thereby enabling spectral simulations at arbitrary atmospheric altitudes. Since the limb observation geometry involves tangential viewing through the atmosphere and employs a limb-scanning technique for detection—using the tangent height to identify the line-of-sight—it offers extensive spatial coverage and high vertical spectral resolution [19]. Consequently, this study adopts the limb observation mode for simulations. Figure 1 shows the geometric configuration of limb observations. In the figure, ${\theta }_S$ represents the solar scattering angle, ${\theta }_Z$ the solar zenith angle, ${\theta }_A$ the solar azimuth angle, $Z_0$ the instrument altitude above the Earth’s surface, and $h_0$ the altitude of the tangent point (where the spectrometer’s line-of-sight is tangential to the atmospheric layers) above the Earth’s surface. The limb-scattered radiance $I_{\lambda }\left(h_0\right)$ received by the spectrometer at tangent height $h_0$ can be expressed as:

$$I_{\lambda }\left(h_0\right)=F_{\lambda }{\sigma }_{\lambda }\phi {\displaystyle \int d}\omega {\displaystyle {\int }_{-\infty }^{Sat}N[h\left(s\right)]}\times e^{-{\tau }_i\left(s\right)}ds$$

(1)

$${\tau }_i\left(s\right)={\sigma }_{\lambda }\left(i\right){\displaystyle {\int }_s^{Sat}{N}_i[h\left(s^{\prime }\right)]}d{s}^{\prime }$$

(2)

The definitions of each parameter in the formula are as follows: $F_{\lambda }$ represents the incident solar flux at wavelength $\lambda$, ${\sigma }_{\lambda }$ and $\phi$ denote the scattering cross-section and phase function, respectively, $\omega$ is the field of view of the instrument at the given tangent height, $N\left[h\left(s\right)\right]$ is the atmospheric density at altitude $h\left(s\right)$, while ${\tau }_i$ and ${\sigma }_{\lambda }\left(i\right)$ correspond to the optical depth and absorption cross-section of the atmospheric constituents, respectively. In practical observations, variations in solar azimuth and changes in atmospheric aerosol optical depth can lead to deviations in the radiative transfer path. Consequently, this alters the radiance received by the instrument and ultimately introduces biases in the retrieved water vapor concentration in the near-space region. Based on the above influence mechanisms, this study employs SCIATRAN as the forward model to systematically analyze the influence patterns of various parameters on the received radiance by simulating observation spectra of near-space water vapor under different geometric and aerosol parameters.

3. Simulation and Sensitivity Analysis

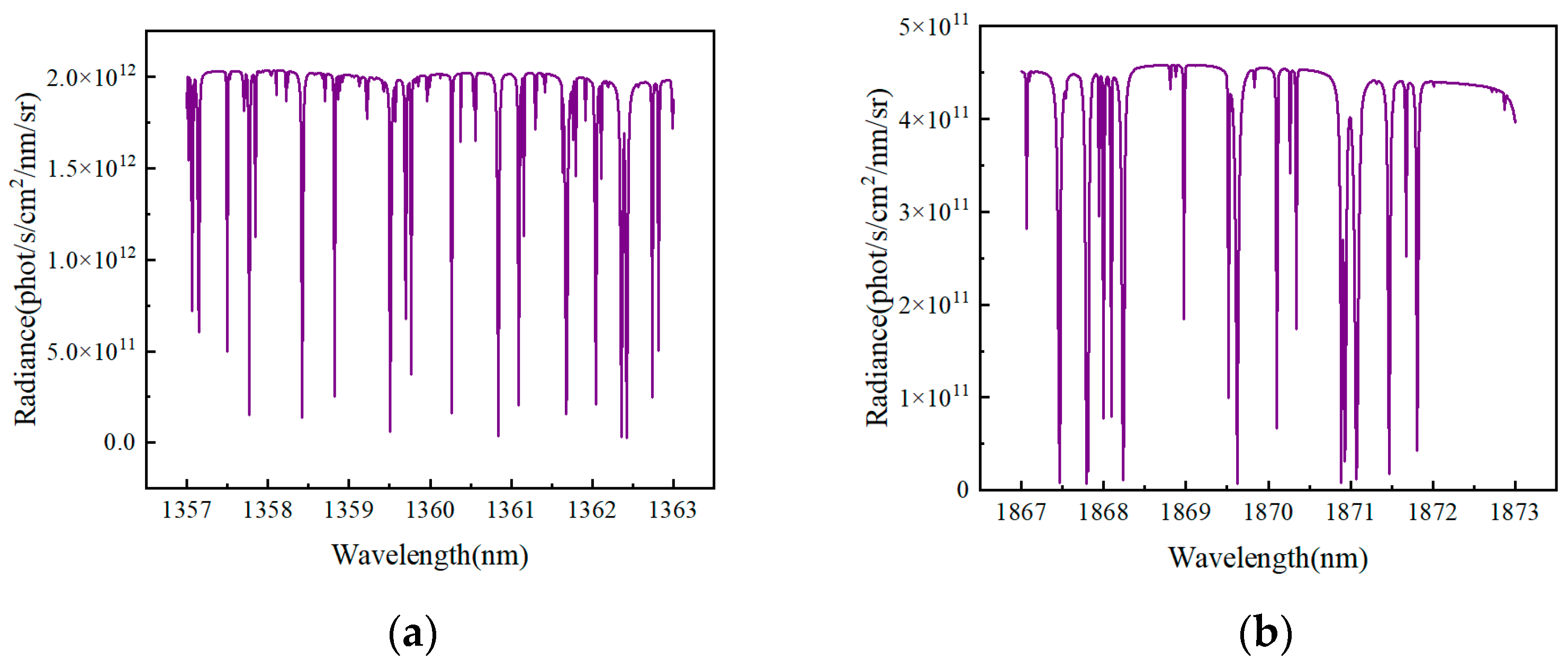
Atmospheric molecules interact with solar radiation through absorption and scattering. Therefore, selecting an appropriate water vapor absorption band for simulation is a primary step towards achieving high-precision retrieval. In atmospheric remote sensing, the 1.36 μm and 1.87 μm absorption bands are commonly used for monitoring atmospheric water vapor content. Simulation results presented in Figure 2 indicate that water vapor absorption in the 1.87 μm band is more intense, with its characteristic peaks approaching saturation, which can easily introduce errors in instrument detection. In contrast, the 1.36 μm band exhibits slightly weaker water vapor absorption and richer spectral features. 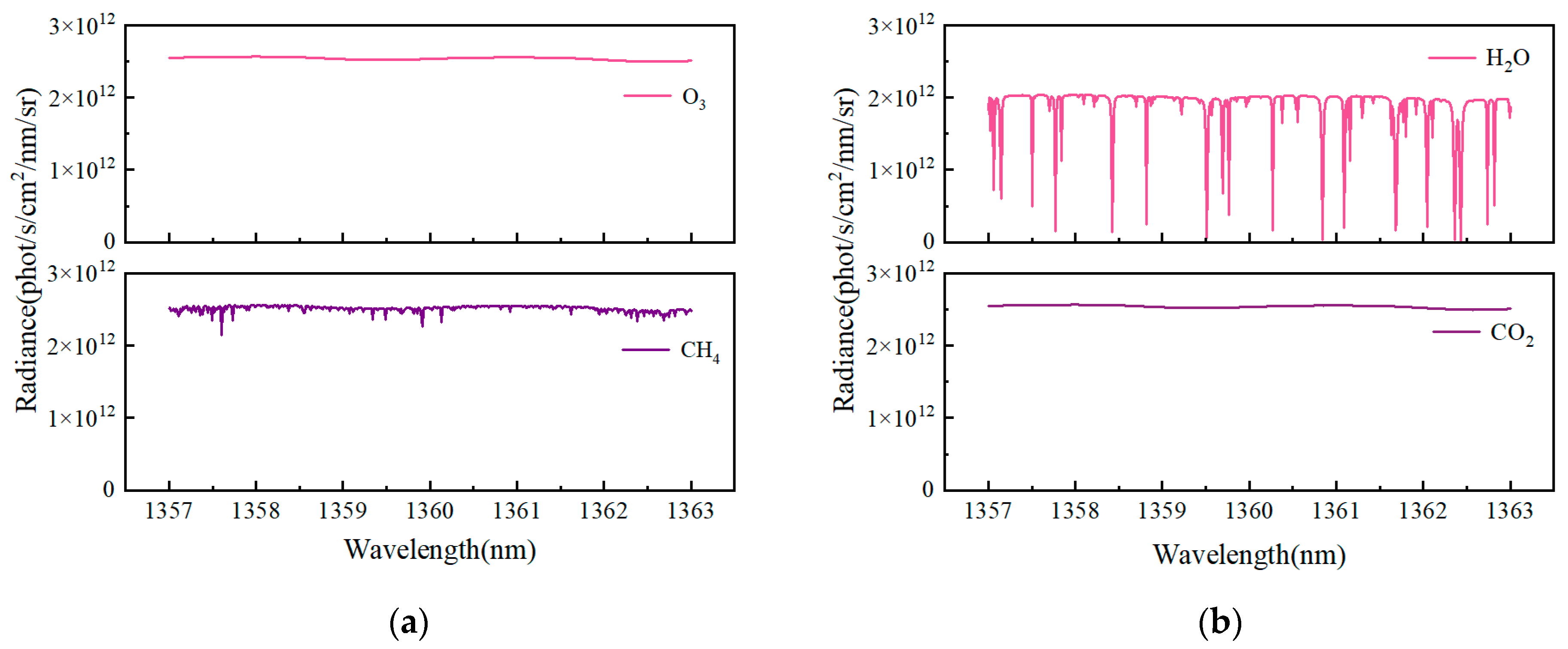Further analysis using Figure 3 reveals that the 1.36 μm band contains only a limited number of shallow absorption lines, thereby effectively avoiding saturation and detection biases caused by other atmospheric molecules. This makes it highly suitable for atmospheric water vapor detection and retrieval.

Based on the above analysis, this study utilizes atmospheric profile data for the mid-latitude summer and conducts simulations of spectral radiance for water vapor observations in the near-space region within the 1.36 μm band. By varying observational geometry parameters and aerosol parameters, changes in the spectral radiance are analyzed to establish a foundation for subsequent water vapor concentration retrieval in near-space. The configuration of background parameters for the SCIATRAN radiative transfer model in this study is shown in

Table 1. Parameter settings for SCIATRAN.

Parameters	Setting
RTM_TYPE	Spher_scat
RTM Mode	Int
RTM-CORE	DOM_S
Extra-terrestrial solar flux	sunbd.dat
Spectral segment	1357–1363 nm
Trace gas	${\mathrm{H}}_2\mathrm{O}$
Line absorber treatment	LBL
Position of the instrument	500 km

. The table indicates the use of the more accurate spherical atmospheric model (spher_scat) and the discrete ordinates method (DOM_S) as the solver, with radiance (Int) calculated using the line-by-line (LBL) method.

3.1. Influence of Observational Geometry Parameters on Water Vapor Observation Spectra

(1)

Influence of Tangent Height

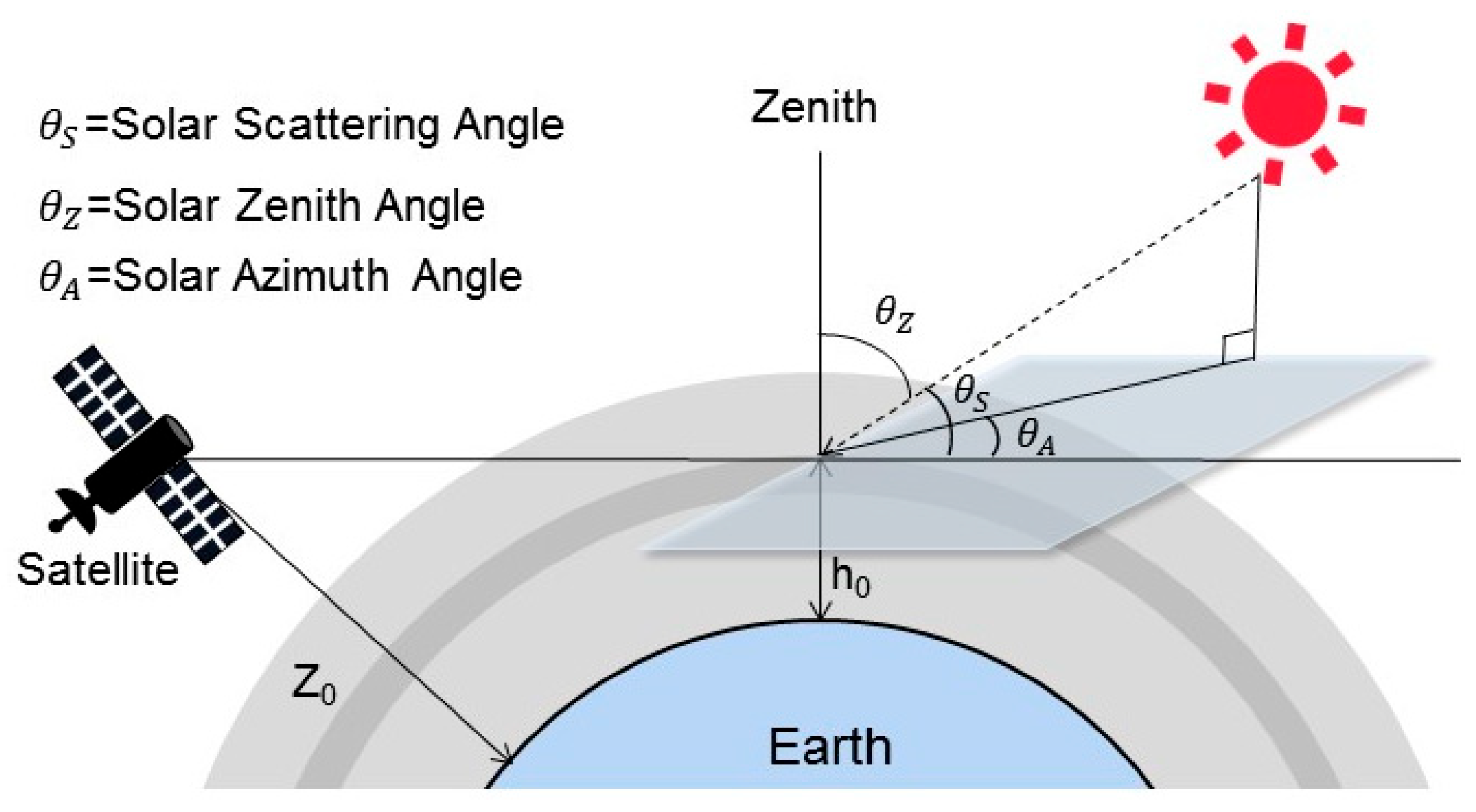
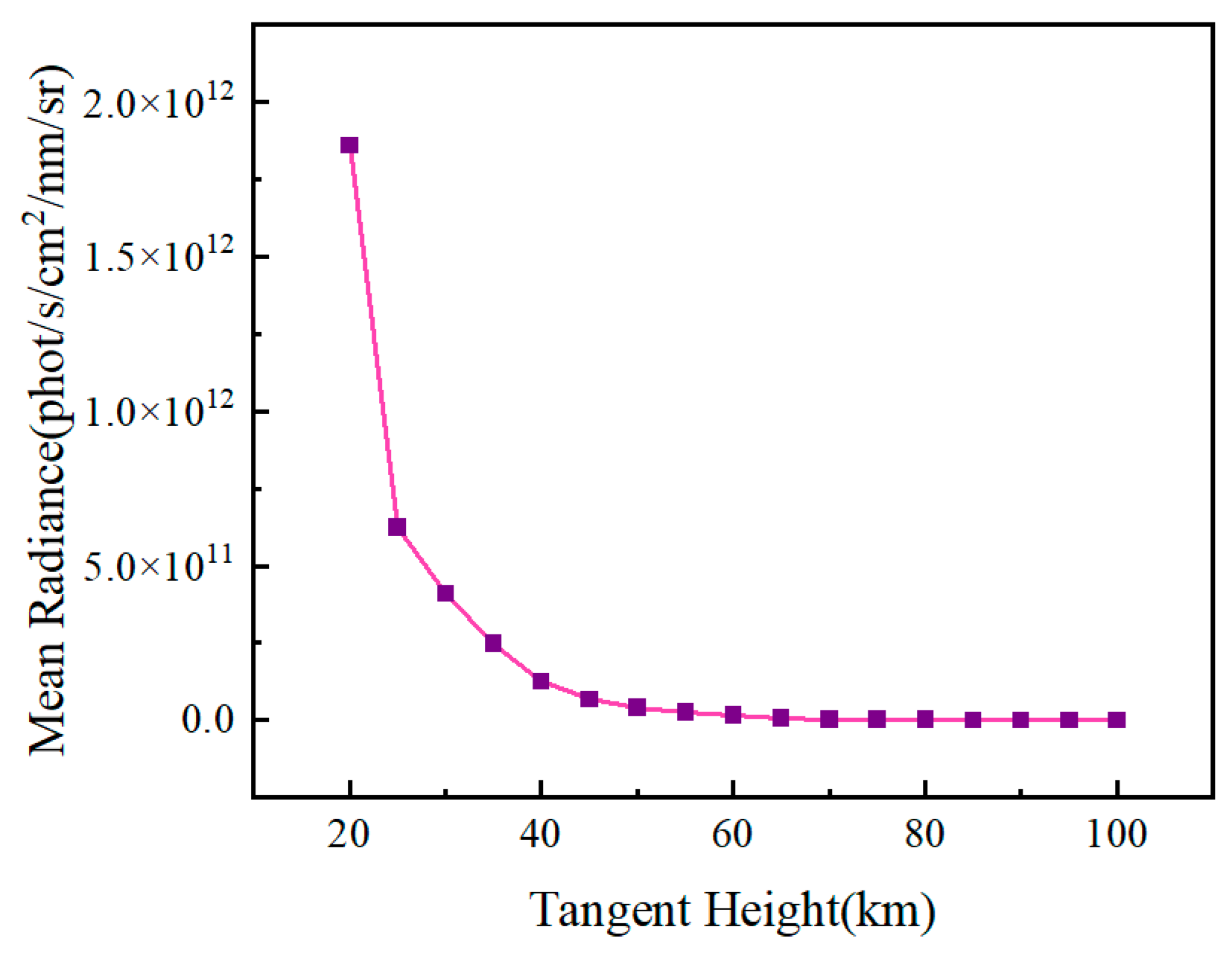
As illustrated in Figure 1, observational geometry is a crucial factor influencing water vapor detection. In the limb observation mode, the geometry is primarily described by three parameters: tangent height, solar zenith angle, and relative azimuth angle. This study selected 17 altitudes within the near-space region to conduct a sensitivity analysis of the tangent height on the water vapor observation spectrum. The average spectral radiance of water vapor observation spectra at different tangent heights, derived from integrating data under various solar positions, is shown in Figure 4. It can be observed from the figure that as the tangent height increases, the spectral radiance of the water vapor observations decreases approximately exponentially. When the altitude exceeds 60 km, the average radiance of the water vapor spectrum stabilizes at a relatively low level. This phenomenon occurs because atmospheric scattering of solar radiation primarily originates from Rayleigh scattering by air molecules and Raman scattering by cloud layers. As altitude increases, the concentration of atmospheric molecules decreases exponentially, weakening the scattering effect and ultimately leading to a reduction in atmospheric background radiation energy.

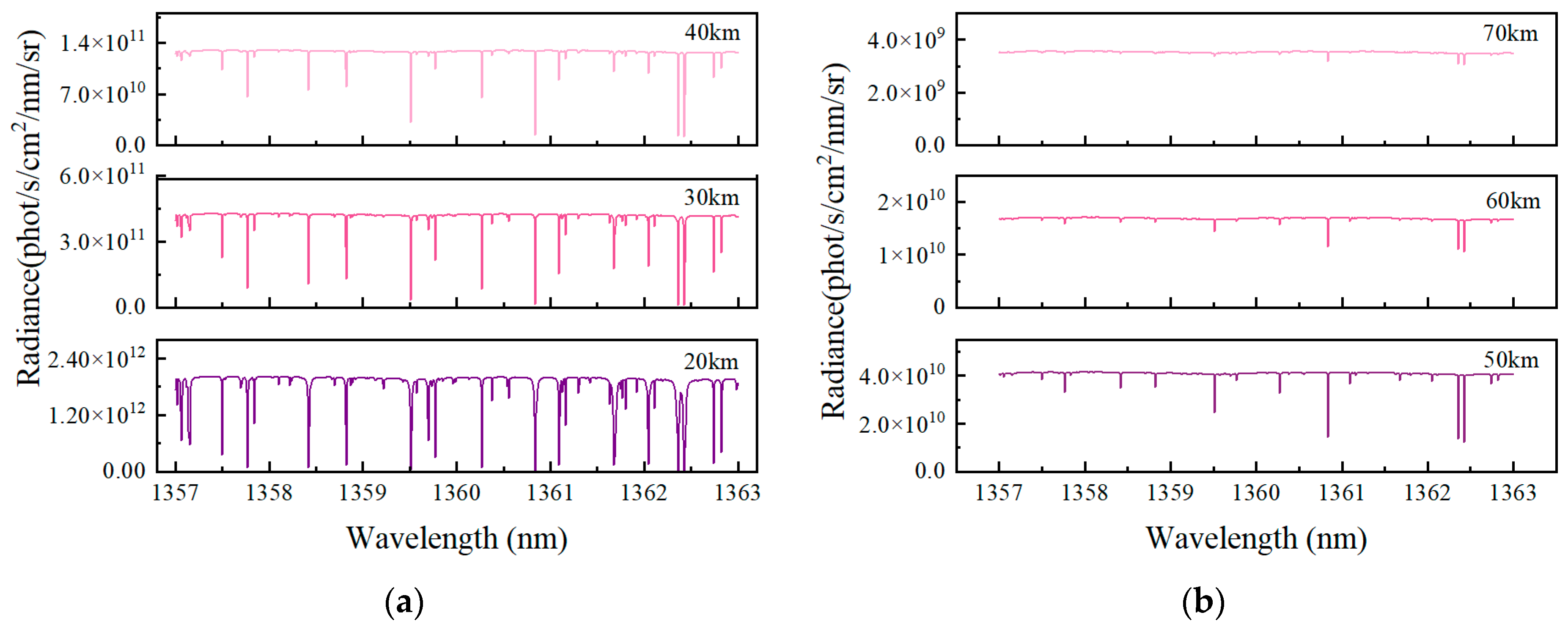
The water vapor observation spectra for tangent heights ranging from 20 km to 70 km are extracted and shown in Figure 5. The figure reveals that as the tangent height increases, the deep absorption features near 1359.5 nm, 1360.8 nm, and 1362.4 nm remain well-preserved, while the shallow absorption features gradually diminish. This is attributed to the lower water vapor content at higher atmospheric altitudes; the reduction in water vapor concentration causes its absorption features to gradually weaken. During the water vapor retrieval process, absorption features provide essential information. Since it becomes more challenging to extract these water vapor absorption features at higher tangent heights, retrieving water vapor concentration is more prone to errors at these altitudes. Therefore, based on the comprehensive analysis of Figure 4 and Figure 5, the spectral radiance is strongest and the absorption features are most pronounced at a tangent height of 20 km. To more accurately reflect the influence of other parameters on the water vapor observation spectrum, the subsequent sensitivity studies in this paper are all conducted at this tangent height.

(2)

Influence of Solar Geometry

Due to atmospheric scattering effects, the solar radiation received by a limb sounder includes not only direct radiation but also components from single scattering, reflection, and multiple scattering. The sun’s position influences the amount of radiation entering the sensor. Therefore, to precisely understand the impact of solar geometry on the limb observation of atmospheric water vapor in near-space, simulations of atmospheric water vapor radiance were conducted for different solar zenith angles (SZAs) and azimuth angles.

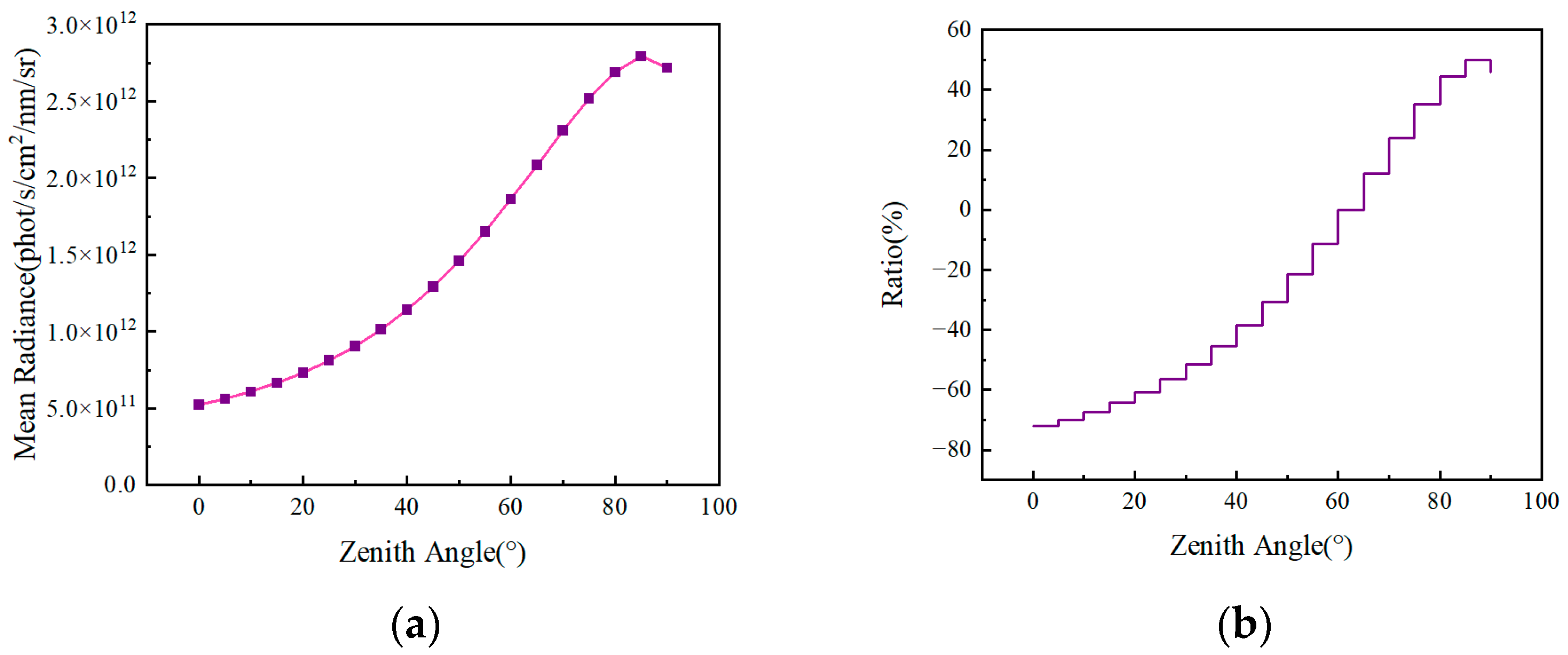
Under the experimental conditions of a relative azimuth angle of 30° and a tangent height of 20 km, the average spectral radiance for different SZAs is shown in Figure 6a. When the SZA is 0° (i.e., the sun is at the zenith), the average radiance of the water vapor observation spectrum is at its minimum. As the SZA increases, the spectral radiance gradually increases. The atmospheric water vapor spectral data within the 40–80° SZA range exhibit high sensitivity to changes in the SZA. When the SZA approaches 90°, a slight attenuation in average radiance occurs. This is attributed to the significantly elongated light path and the exponentially increasing atmospheric and ozone densities, which lead to dominant effects from ozone absorption and scattering attenuation. Figure 6b shows the relative difference in average spectral radiance for each SZA, using the average radiance at a 60° SZA as the reference. The results indicate that the change in the average spectral difference is relatively gradual when the SZA is less than 40°, while the difference is significantly larger within the 40–80° interval. This further confirms the high sensitivity of the spectra to the SZA within this range. Based on the above analysis, in practical observations, selecting small SZAs—determined by the target geographic location and observation time—can mitigate the interference of SZA-related errors from instrument calibration on the retrieval results.

In limb observation geometry, the relative azimuth angle is a key parameter describing the relative position between the satellite’s line-of-sight and the solar incidence direction. It is defined as the angle between the projections of the instrument’s line-of-sight and the solar incidence direction onto the horizontal plane. A relative azimuth angle of 0° indicates that the instrument and the sun are in the same direction, while an angle of 180° signifies that the instrument is opposite the sun. To systematically investigate the influence of this parameter on the water vapor observation spectra in the near-space region, this study fixed the solar zenith angle at 60° and the tangent height at 20 km, selecting 29 relative azimuth angles ranging from 0° to 180° for a sensitivity simulation study of the water vapor observation spectrum.

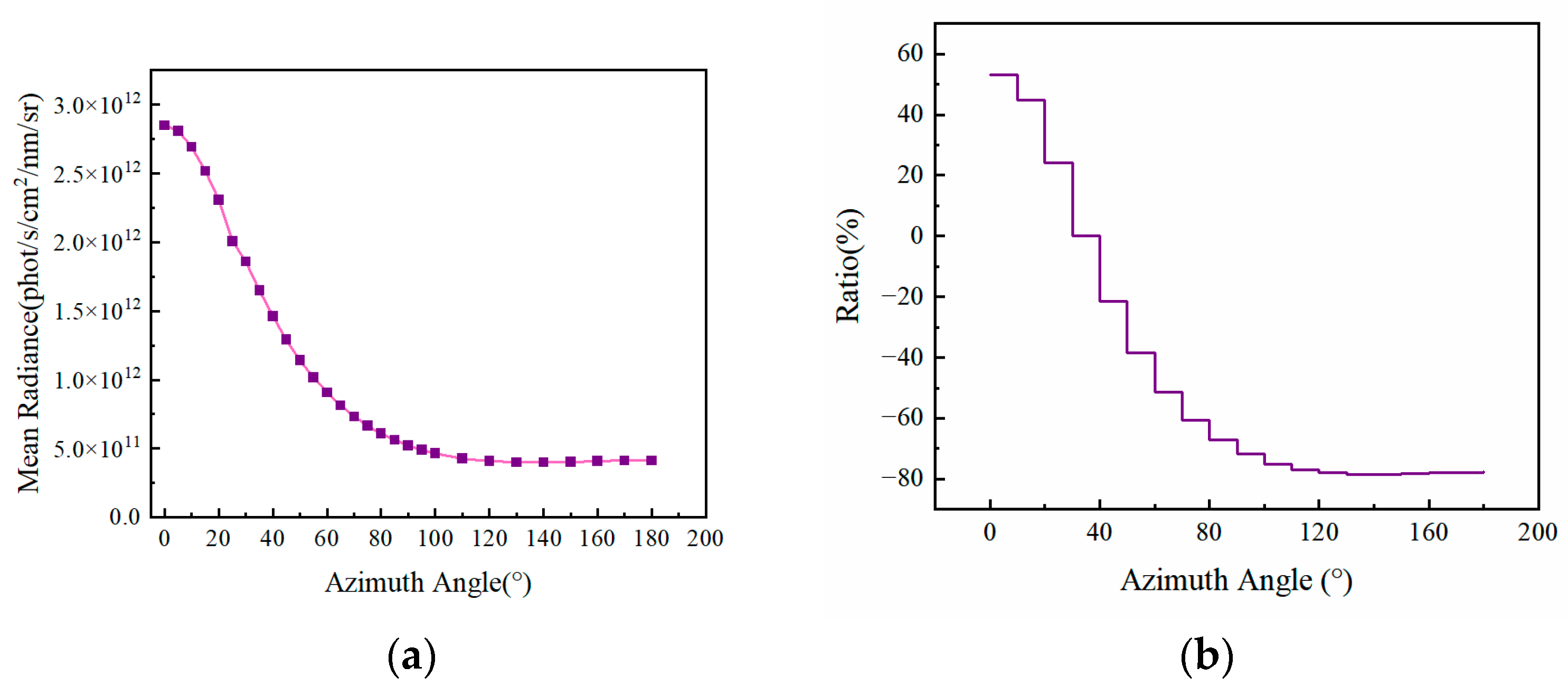
Figure 7a shows the average water vapor absorption spectra under different relative azimuth angles. Combined with the curve of the relative difference in spectral radiance across relative azimuth angles in Figure 7b, it can be observed that the influence of the relative azimuth angle on the spectral radiance exhibits distinct phased characteristics. When the relative azimuth angle is less than 140°, the spectral radiance shows a monotonically decreasing trend, with the rate of decrease gradually slowing. When the relative azimuth angle exceeds 140°, the relative radiance difference stabilizes, and the average spectral radiance shows a slight increase, indicating that the radiance within this range is largely insensitive to changes in the relative azimuth angle. Further analysis reveals that within the 10–60° range, the fluctuation amplitude of the relative radiance difference exceeds 15%, significantly higher than in other intervals, demonstrating strong sensitivity of the spectral radiance to changes in the relative azimuth angle within this range.

Based on the above patterns, in practical limb sounding missions, selecting large relative azimuth angles between 140° and 180° for observations can effectively reduce radiance deviations caused by fluctuations in the relative azimuth angle. Consequently, this approach helps minimize errors in geometric parameters during the water vapor concentration retrieval process, thereby enhancing the stability and accuracy of the retrieval results.

3.2. Influence of Aerosol Parameters on Water Vapor Observation Spectra

Aerosols possess diverse compositions and induce complex radiative effects through scattering and absorption. Understanding their impact on satellite-observed radiance is a critical step for the accurate retrieval of trace gases. This study divides the atmospheric altitude into the boundary layer (0–2 km), troposphere (2–10 km), stratosphere (20–30 km), and mesosphere (30–100 km) for discussion. Simulations of aerosol parameters within the boundary layer and troposphere revealed that the spectral radiance of the water vapor observations is not sensitive to changes in aerosols in these lower atmospheric regions. This is because the observation tangent height is situated in the near-space region, where variations in lower atmospheric aerosols have minimal impact on the observed radiance. Consequently, starting from a tangent height of 20 km, the focus shifts to the influence of aerosol seasonality, as well as stratospheric and mesospheric aerosols. To ensure the isolation of these effects from other environmental factors, all other parameters were maintained consistently at their default values, as shown in

Table 2. Aerosol Simulation Parameter Settings.

Parameters	Setting
Solar Zenith Angle	60°
Relative Azimuth Angle	30°
Boundary Layer Aerosol Type	Marine Aerosol Type
Visibility	23 km
Humidity	80%

.

(1)

Influence of Aerosol Seasonality

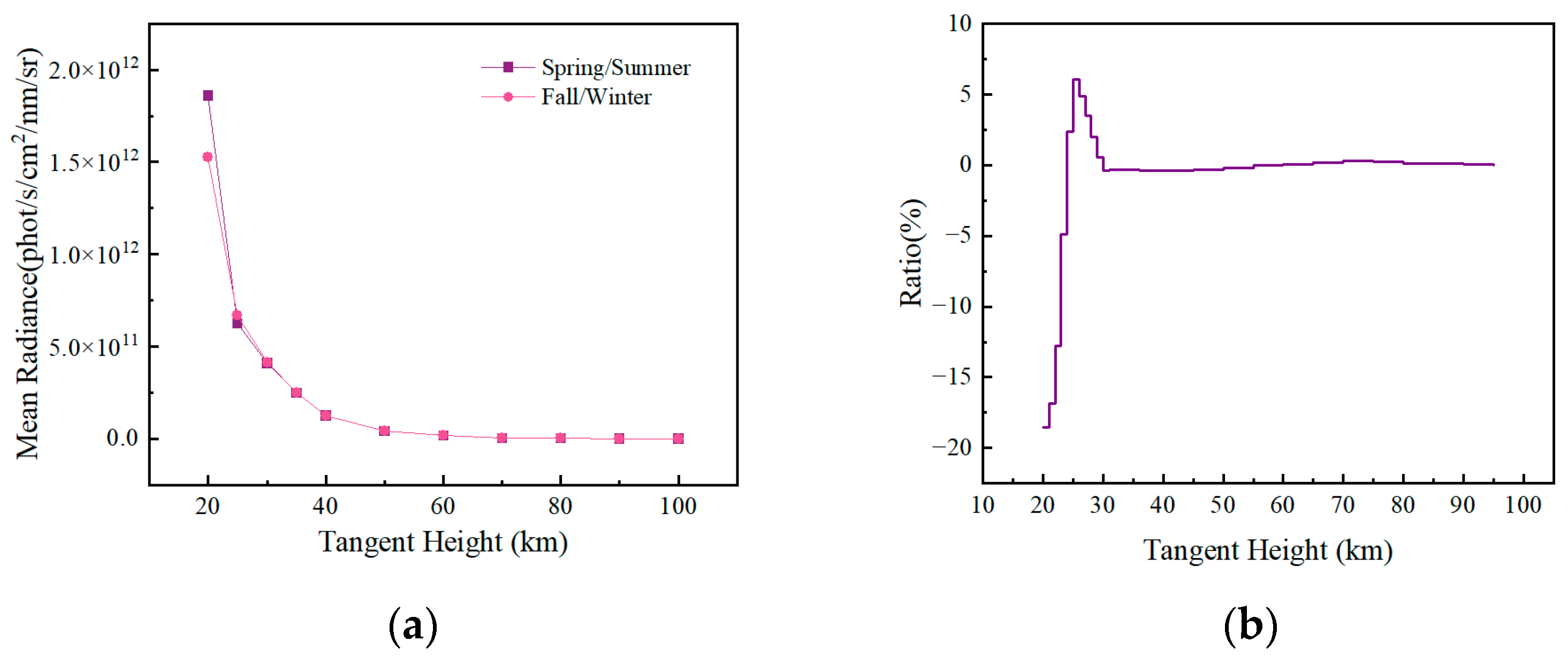
Influenced by climate change and human activities, the optical properties of aerosols exhibit significant seasonal variations. In the SCIATRAN model, aerosol seasons are categorized into spring-summer and autumn-winter types, with corresponding aerosol optical depths of 0.095 and 0.091, respectively. Figure 8a illustrates the variation trends of the average radiance corresponding to these two seasonal aerosol types across different tangent heights. To further quantify the impact of aerosol seasonal differences on the atmospheric water vapor observation spectrum, the average spectral radiance under the spring-summer aerosol type was used as a reference benchmark. The relative difference compared to the corresponding values under the autumn-winter aerosol type was calculated for different tangent heights, with the results shown in Figure 8b.

The figure indicates that the influence of aerosol seasonality on the spectral radiance of water vapor observations is primarily confined to tangent heights below 30 km. This is because the lower atmosphere is more significantly affected by natural climate variations and human activities, leading to pronounced seasonal changes in aerosol composition and concentration, which in turn cause seasonal differences in spectral radiance. Specifically, within the 20–24 km altitude range, the spectral radiance of spring-summer type aerosols is significantly higher than that of autumn-winter type aerosols. According to the climatological data built into the SCIATRAN model, within the 20–25 km altitude range, the optical thickness of spring-summer type aerosols is 0.1173, while that of autumn-winter type aerosols is 0.1066. The extinction coefficient of spring-summer type aerosols is approximately 39% higher than that of autumn-winter type aerosols. Higher aerosol optical thickness (AOT) and extinction coefficient indicate stronger atmospheric scattering of radiation in spring and summer. However, within the 24–28 km altitude range, the spectral radiance of autumn-winter type aerosols is slightly higher than that of spring-summer type aerosols, which is attributed to the fact that the extinction coefficient of autumn-winter type aerosols at this altitude is marginally higher than that of spring-summer type aerosols.

(2)

Influence of Stratospheric Aerosol Type

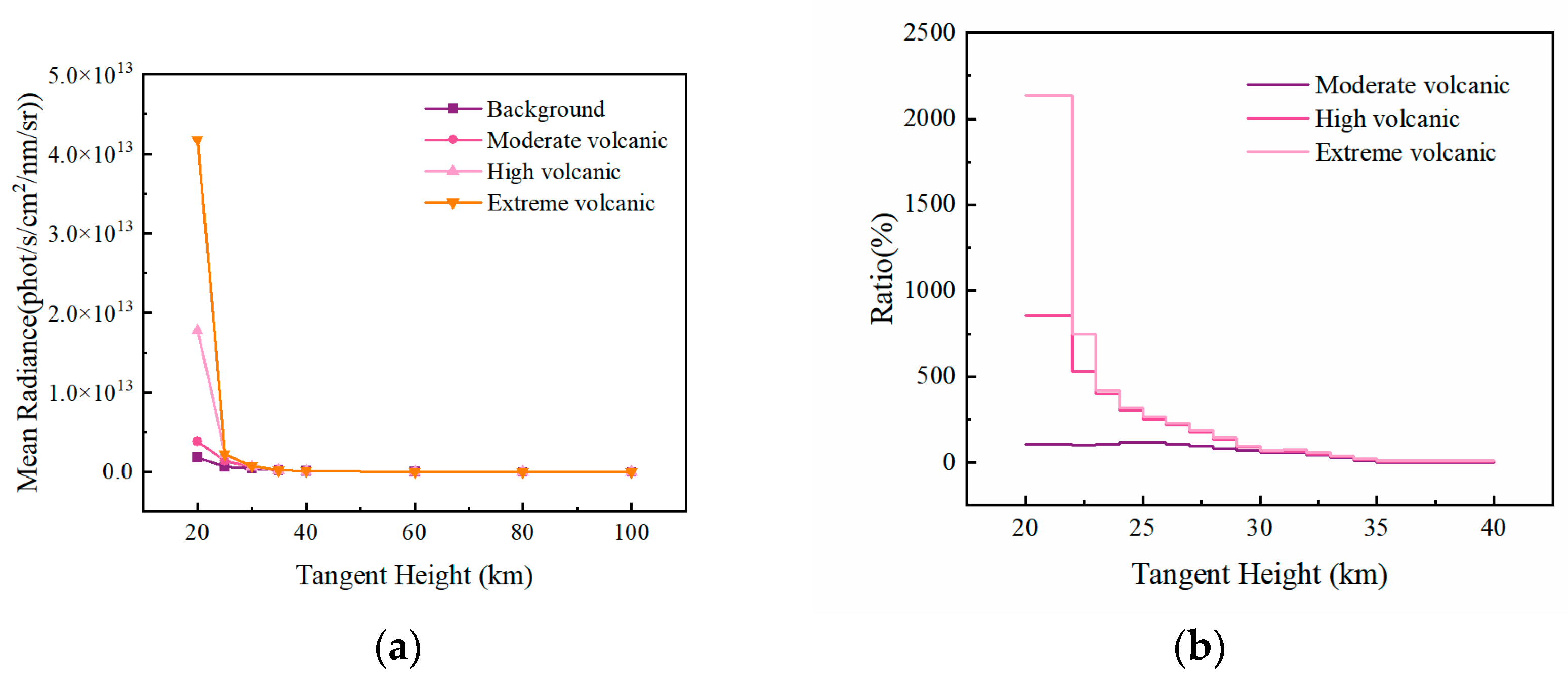
The stratosphere, primarily located between approximately 10 km and 50 km above the Earth’s surface, is significantly influenced by volcanic eruptions, with volcanic aerosols constituting its main particulate component. Its characteristics are described by aerosol load and aerosol type. Stratospheric aerosol loads are categorized into four types: Extreme Volcanic, High Volcanic, Moderate Volcanic, and Background. Figure 9a shows the trend of average spectral radiance with tangent height under these different aerosol loads. The figure indicates that when the tangent height is below 30 km, the average radiance decreases sequentially in the order of Extreme Volcanic, High Volcanic, Moderate Volcanic, and Background loads. This is because, according to the built-in parameters of the model, as the volcanic height increases, the corresponding aerosol optical thickness (AOT) increases sequentially. The aerosol optical thickness increases by 98% from moderate volcanoes to extremely high volcanoes, and at an altitude of 20 km, the extinction coefficient shows an order-of-magnitude change with the increase in volcanic height. However, when the tangent height exceeds 30 km, the average radiance for these four load types converges and remains stable. The reason is that the aerosol extinction coefficients of all volcanoes become identical, rendering their influence on aerosol concentration in the upper atmosphere negligible.

Figure 9b displays the curve of the relative difference in average spectral radiance compared to the Background load across different tangent heights for the other three stratospheric aerosol loads. The results show that particulate matter from extreme volcanic eruptions contributes significantly to the scattering of solar radiation. At a tangent height of 20 km, the relative difference between the Extreme Volcanic aerosol load and the Background load exceeds 2000%.

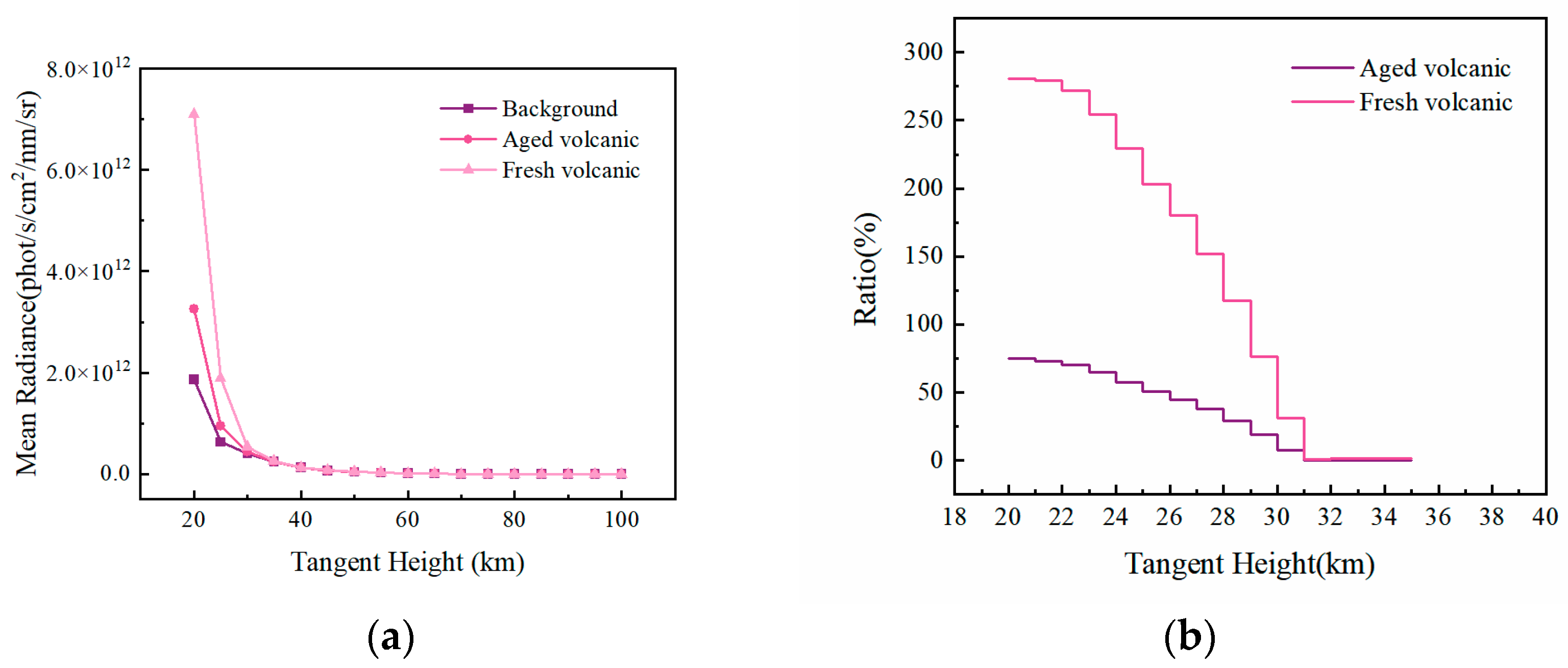
Stratospheric aerosol types are categorized into three classifications: Fresh Volcanic, Aged Volcanic, and Background. Figure 10a illustrates the variation trend of the average spectral radiance with tangent height for these different stratospheric aerosol types. Similar to the pattern observed with aerosol load types, when the tangent height is below 30 km, the Fresh Volcanic type exhibits the highest average radiance, followed by the Aged Volcanic type, with the Background type showing the lowest values. The reason for this difference lies in the distinct physical properties and scattering mechanisms of aerosol particles. According to the model’s built-in parameters, the single-scattering albedo (SSA) of old volcano-type aerosols is close to 0.95, indicating extremely strong scattering and weak absorption capabilities. When old volcano-type aerosols are encountered, intense scattering predominantly occurs, which scatters a large amount of radiation along the limb viewing path and results in attenuation of the signal received by the detector. In contrast, the single-scattering albedo of new volcano-type aerosols is approximately 0.91, with significantly stronger absorption than that of old volcano-type aerosols. Due to their stronger absorption and prominent forward scattering, new volcano-type aerosols not only attenuate the signal but may also enhance the radiation.

Figure 10b presents the relative difference curves of the average spectral radiance for the other stratospheric aerosol types, using the average spectral radiance of the Background aerosol as the reference benchmark. The results demonstrate that the Fresh Volcanic aerosol has the most significant impact on radiance. At a tangent height of 20 km, the relative difference in radiance between the Fresh Volcanic type and the Background type reaches 280.99%.

(3)

Influence of Mesospheric Aerosols

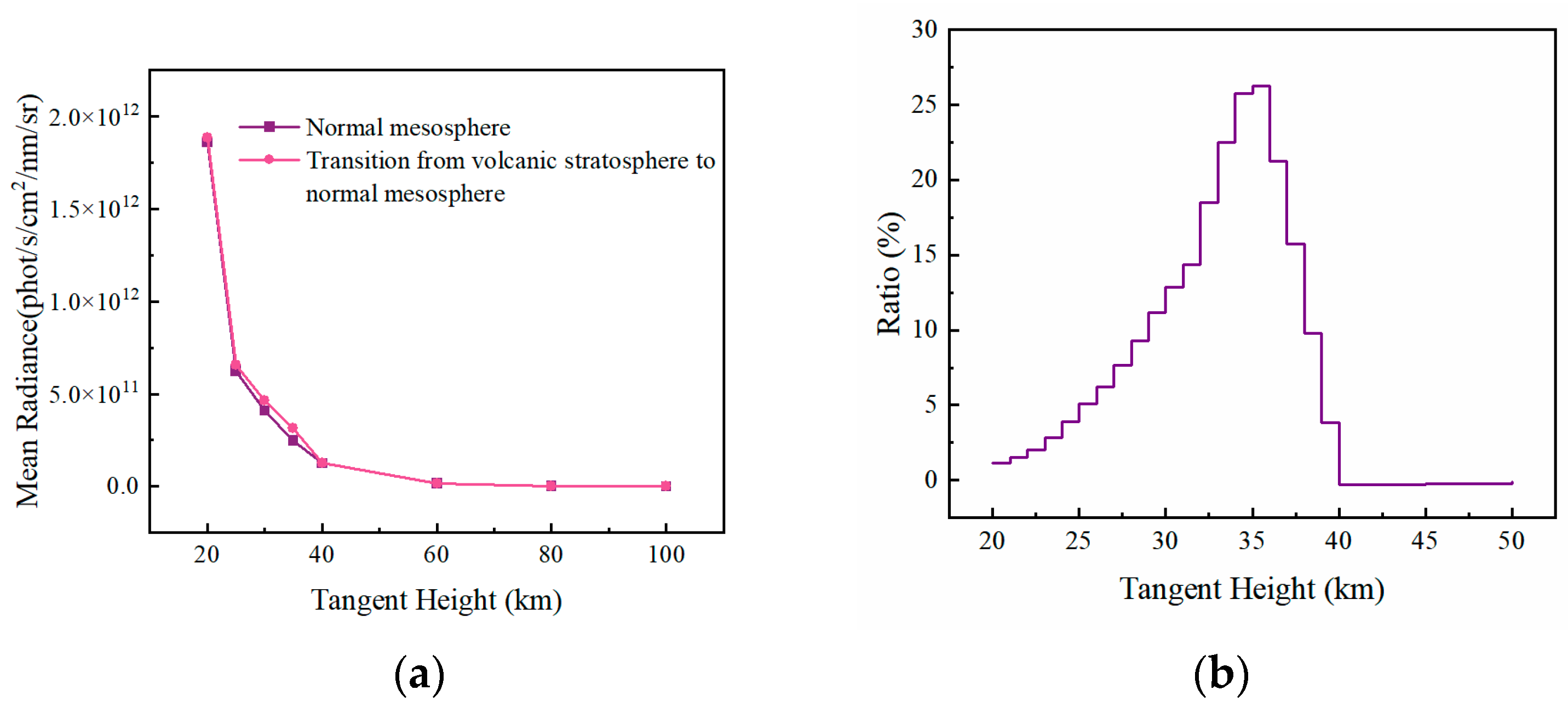
The properties of mesospheric aerosols are primarily characterized by their load types. In this study, mesospheric aerosols are classified into two categories: Normal Type and Volcanic Type. Figure 11a shows the trend of average spectral radiance with tangent height under different mesospheric aerosol load types. Using the average spectral radiance of the Normal Mesospheric type as a reference, the relative difference curve for the average spectral radiance of Volcanic Type aerosols that have entered the mesosphere from the stratosphere, across different tangent heights, is shown in Figure 11b.

The figures reveal that after volcanic aerosols enter the mesosphere from the stratosphere, they only cause a noticeable enhancement in the spectral radiance of water vapor observations within the 20–40 km altitude range. The influence peaks at 35 km, where the relative difference in radiance compared to the Normal Mesospheric aerosols reaches 26.23%. At other tangent heights, the impact of Volcanic Type aerosols on the spectral radiance is minimal and their contribution can be considered negligible.

4. Results and Discussion

Based on the radiative transfer principles elaborated in Section 2, limb radiance is primarily influenced by the combined effects of factors such as the incident solar spectrum, solar geometric position, and atmospheric path optical depth. Focusing on the aforementioned core physical parameters, this study systematically simulated the impacts of observation geometry and aerosol parameters on water vapor radiance. The results indicate that the water vapor observation spectrum exhibits significant systematic sensitivity to observation geometry, seasonal variations in aerosols, and aerosol parameters in the middle and upper atmospheres. Among the observation geometry parameters, the tangent height plays a dominant role in the radiative transfer path. Simulation results show that as the tangent height increases, the spectral radiance of water vapor observations presents an approximately exponential decay trend, gradually stabilizing at altitudes above 60 km. This variation law is consistent with the exponential decrease in atmospheric density with height, reflecting the intrinsic influence of the reduced number of Rayleigh scatterers on the radiative transfer process. Further spectral feature analysis reveals that when the tangent height exceeds 40 km, the water vapor absorption features weaken significantly, leading to a sharp increase in retrieval uncertainty. In addition to the tangent height, the solar geometric position also exerts an important effect on the observation results. The solar zenith angle has a significant impact on radiance within the range of 40–80°; the observed radiance fluctuates greatly when the relative azimuth angle is between 10–60°, while when the relative azimuth angle exceeds 140°, although the radiance level decreases, the observation stability is improved.

Regarding environmental parameters, changes in aerosols alter the optical depth of the atmospheric path, directly affecting the observed radiance. The study demonstrates that the influence of seasonal aerosol variations is mainly concentrated at altitudes below 30 km: within the 20–24 km altitude range, the spectral radiance corresponding to spring-summer type aerosols is significantly higher than that of autumn-winter type aerosols, whereas in the 24–28 km altitude range, the spectral radiance of autumn-winter type aerosols is slightly higher than that of spring-summer type. The impact of stratospheric aerosols is particularly prominent; when the tangent height is below 30 km, the average radiance under different aerosol loading conditions decreases in the order of extreme volcanic type, high volcanic type, moderate volcanic type, and background type. Specifically, at a tangent height of 20 km, the relative difference between the spectral radiance under extreme volcanic aerosol loading and the background value reaches as high as 2135.031%, fully demonstrating the influence of volcanic activities on near-space water vapor observations. Further type analysis shows that the radiance difference between new volcanic aerosols and background aerosols at 20 km altitude reaches 280.99%. In contrast, the impact of mesospheric aerosols is relatively limited, with the influence range mainly concentrated between 20 km and 40 km, and the maximum value appearing at 35 km (i.e., the radiance difference from ordinary mesospheric aerosols is 26.23%).

5. Conclusions

Based on the high-precision SCIATRAN radiative transfer model, this study systematically conducted a sensitivity analysis of near-space water vapor limb detection. The impacts of different observation geometric parameters and atmospheric aerosol parameters on the limb observation spectra of the 1.36 μm water vapor absorption band were quantitatively simulated. Combined with radiative transfer theory, this study thoroughly analyzed the physical mechanisms through which each parameter affects the observation spectra, and the following conclusions were drawn:

(1)

Among the observation geometric parameters, the tangent height is the decisive factor influencing the observation signal intensity and retrieval accuracy. Therefore, to obtain more accurate spectral information, priority should be given to spectral data with a tangent height below 40 km when retrieving water vapor concentration. Regarding solar orientation parameters, both the solar zenith angle and relative azimuth angle have sensitive angular ranges; selecting a relative azimuth angle greater than 140° can effectively improve observation stability and reduce the impact of geometric calibration errors on retrieval.

(2)

Aerosol parameters exert a significant modulation effect on near-space water vapor observations and exhibit obvious vertical stratification characteristics. Thus, the correction of middle and upper atmospheric aerosols, especially volcanic aerosols, should be prioritized in retrieval algorithms.

Although this study provides a systematic sensitivity analysis based on the SCIATRAN model, several limitations are noteworthy: Firstly, the model simulations are based on standard atmospheric profiles and idealized aerosol models, which exhibit certain differences from the actual atmospheric environment. Particularly under extreme weather conditions or in special geographical regions, actual atmospheric parameters may differ significantly from the model assumptions. Secondly, this study mainly focuses on the independent impacts of individual parameters, while the complex coupling relationships between various parameters in the actual atmosphere have not been fully considered. Additionally, the model does not fully account for the influence of clouds, especially thin clouds near the tropopause, which may have important effects on limb observations. Future research needs to verify and optimize the model by integrating more measured data.