Analyzing Students’ Academic Performance Based on Fuzzy Inference System

Abstract

Evaluating students’ knowledge and competencies to achieve the desired learning goals is one of the most important stages of the teaching process. The purpose of this study is to create a dataset consisting of programming questions and determine the level of these questions according to the Bloom taxonomy and the weight of each concept they contain, by taking expert opinion. The student’s score, question difficulty, and complexity levels are considered to determine the extent to which the student has learned a concept. A total of 96 students participated in this study, 51 in the experimental group and 45 in the control group. Random design for a pre-test–post-test control group was used to measure the students’ learning performance and self-efficacy regarding programming. While the experimental group students were given detailed feedback on how much they learned a concept, the control group students were only informed about the total score they received from the exam. The learning performance and self-efficacy perception regarding programming were analyzed using the paired samples t-test. Results show that the learning performance and self-efficacy perception regarding programming of the experimental group students improved significantly compared to the control group.

1. Introduction

The need to personalize each student’s learning experience has gained importance for the use of artificial intelligence in applications in the field of education. Artificial intelligence encompasses the development of systems capable of performing human-like functions, including cognitive learning, decision making, and adapting to the environment. Using artificial intelligence platforms, instructors were able to perform different administrative functions such as reviewing and grading students’ assignments more effectively and efficiently, resulting in high quality in teaching activities. As these systems leverage machine learning and adaptability, the curriculum and content are customized and personalized to the needs of the students, thereby improving the students’ experience and overall learning quality [1].

The use of artificial intelligence in education has created new opportunities to design productive learning activities and develop better technology-enhanced learning applications or environments. However, implementing relevant activities or systems remains a challenge for most researchers from education fields [2].

One of the most important indicators of the quality of education is the result obtained from presenting it as a grade based on an assessment of a student’s knowledge and skills. In addition to fulfilling a specific function, evaluation scores must be objective and unbiased. It should indicate that some important results were achieved and should be understandable to students, who should be informed in advance about the evaluation method and criteria. Additionally, the grades themselves should not be turned into a goal. It should provide information about the student’s progress, and the methods for calculating the grade should be objective and statistically valid [3].

A total of 96 students between the ages of 14–17 studying at a vocational high school in Izmir, Türkiye participated in this study. A total of 54 of the students were male (%56) and 42 were female (%44). About 53% (n = 51) of the students were in the experimental group and 47% (n = 45) were in the control group. A pre-test–post-test control group random design was used in the study. An exam consisting of questions selected from the data set prepared by the field teacher was applied to the experimental group students and the control group students and they were asked to answer them in the C Sharp programming language. Students in the experimental group received detailed feedback after completing the tasks. Individual interviews were conducted with each student to obtain information about their learning speed on the concepts. This increased students’ awareness of their learning gaps. Students were encouraged to review the textbook or other resources for missing information. The control group students were given the total score they received from the exam after the evaluation as feedback. In the research process, the test prepared to measure the learning performance and the computer programming self-efficacy scale were applied to the participants as pre-test and post-test and the results were analyzed using the paired sample t-test.

2. Related Works

From the University of California, Dr. Lotfi Zadeh’s use of fuzzy logic to determine colloquial ambiguity was first applied in 1965 [4]. Fuzzy logic technique, based on the clustering principle, has been used in many areas. In the classical set approach, an element is either an element of the set or it is not. In the fuzzy logic approach, the element may belong to defined clusters to a certain extent. Therefore, definitions that contain uncertainty and cannot be fully expressed with classical set definitions can be made. The theory of fuzzy logic is widely used in many fields, including in the field of education.

In this study, a performance evaluation method based on fuzzy logic systems is proposed. The results of the notes taken by twenty students from the control technique course at Marmara University Technical Education Faculty Electrical Education Department Control Technique Laboratory were compared with the results obtained by fuzzy logic and classical evaluation method.

To blur the exam results, the grades of the two exams were taken as input variables and their membership functions of fuzzy sets were used. Each input variable is expressed by five triangular membership functions.

Performance evaluation using fuzzy logic requires complex rules and additional software, but it also provides advantages for evaluation. The evaluation method with fuzzy logic is flexible and can allow many evaluation options [5].

In this study, the number of correct answers given by students preparing for the university exam in the mathematics course to the unit questions, the number of correct answers of other students taking the exam in the same unit and the course passing grades received by the student in previous years were evaluated as inputs of the fuzzy logic system, thus determining the student’s learning rates for each unit. Exams consisting of questions appropriate to the student’s level were produced according to the determined learning rates. This software aims to keep students’ motivation high. It has been observed that study motivation and student success increase with the studies conducted with exams specially produced for them [6].

In the study conducted by Barlybayev et al. [7], when calculating the final score, the weight ratios of the types of education received were multiplied by the arithmetic averages of the grades, and the obtained scores were accepted as inputs of the Mamdani-based fuzzy logic system. Therefore, it was seen that the evaluation of student performance with fuzzy calculation yielded more acceptable results.

In this study, a new fuzzy examination system was developed using Chen and Lee’s evaluation method, and this system was evaluated. In the new fuzzy exam system, there are questions that every student can answer, as each question has alternatives from easy to difficult. In this way, students at all levels will be able to answer the questions, which motivate them for subsequent exams [8].

To ensure fair evaluation of students’ grades, an exam system consisting of different sections was used in this study, each of which aimed to measure cognitive skills at different levels. In cases where a student’s scores on a test did not clearly belong to a specific set, the scores they received from open-ended questions were considered to decide which grade to give. The evaluation approach presented using the mathematical theory of fuzzy functions ensures that students are evaluated fairly, motivating them to succeed [9].

In this article, it is aimed to create a recommendation system based on fuzzy information to evaluate students’ competencies. This system consists of the inference and calculation module, which fuzzy calculates each competency, and the suggestion module, which aims to help educators evaluate the degree of development of their competencies and receive alternative improvement suggestions. The proposed solution was tested at the last two levels of science education in four Tunisian primary schools in different regions, showing that inquiry and collaborative learning should be implemented more in Tunisian classrooms [10].

Wu and Luo [11] used game-based learning to improve the quality of English language teaching in universities, considering that students have different needs and learning styles. The Enhanced Fuzzy Analytical Hierarchy Process (IF-AHP) is proposed to overcome the problem of evaluating the quality of teaching. Hierarchy models are created, the weight of the evaluation factors is calculated with AHP, and hierarchical evaluation is performed. With the proposed IF-AHP model, the online game-based learning system has shown good results in terms of system efficiency and satisfaction by helping students learn English quickly.

To develop a smart exam system based on fuzzy logic, a study was prepared by Ölmez [12] in which the teacher can choose the number of exam questions, the topics of the weeks and the difficulty level of the questions and accordingly the difficulty levels of the questions are calculated fuzzy. After each exam, the difficulty levels of the questions are updated again with the fuzzy logic method according to the number of correct answers. Thus, a smart exam system was created in which the difficulty level of a question that will be asked to the students for the first time is determined as medium and the difficulty levels change depending on the answer rates of the questions.

In this study, fuzzy logic and different fuzzy functions were used to determine whether students with borderline test scores would be given higher or lower grade scales. The goal is to give students a fairer grade in grading their tests. A system has been created that includes open-ended questions and whose weight is determined by considering the student’s knowledge and skills. Fuzzy grades are automatically calculated by considering the overall score of each student and the score of the open-ended question, the limit values of the membership functions. Thus, verifying that the grades received by each student are as fair as possible is very important for their motivation to study [3].

Evaluating students’ competencies is often inadequate in traditional evaluation methods. Research has focused on the effectiveness of fuzzy logic in assessing students’ competencies by considering uncertain factors. This study used a combination of fuzzy logic and hierarchical linear regression to analyze students’ performance. When students’ performance was compared to the traditional method, it was seen that more detailed and flexible feedback was obtained, and the learning method used also affected the students’ fuzzy grades [13].

Synchronous or asynchronous feedback provided in face-to-face and distance learning designs positively improves students’ cognitive skills, as well as their metacognitive and affective characteristics. Peer feedback and artificial intelligence-assisted feedback, which accompany teacher feedback, are known to have a greater impact on learning. Providing feedback can contribute to the development of students’ critical thinking skills, their ability to make objective assessments, their ability to revise their knowledge schemas, and their ability to translate theoretical knowledge into practical skills [14]. A review of the literature reveals that the effects of methods commonly used in programming education on different outcomes are often emphasized. However, a study providing detailed AI-supported feedback in this area is expected to address the gap in the literature and shed light on future studies. In the following section, a comparison of the fuzzy logic-based method used with other AI-based adaptive assessment systems is given.

Comparison of AI-Based Adaptive Assessment Systems

Fuzzy logic–based assessment systems and Item Response Theory (IRT) represent two distinct paradigms for modeling learner performance. Fuzzy logic approaches rely on linguistic rules and fuzzy inference mechanisms to address the uncertainty and imprecision inherent in educational data [4]. This rule-based reasoning makes fuzzy systems highly interpretable and adaptable to expert-defined knowledge, even in contexts with limited data [15]. In contrast, IRT provides a probabilistic and psychometrically grounded framework that models the probability of a correct response as a function of latent ability and item characteristics such as difficulty and discrimination [16]. IRT is particularly well suited to large-scale standardized and adaptive testing, where precise ability estimation and statistical validity are essential. Al-Lahibi [17] employed IRT to calibrate mathematics test items, focusing on psychometric precision by estimating item difficulty and discrimination parameters across a large student sample. However, while IRT yields robust and generalizable measures of proficiency, it is less flexible in handling qualitative or non-binary indicators of learning. Conversely, fuzzy logic offers greater interpretability and adaptability but lacks the rigorous statistical foundations and standardization that characterize IRT-based systems. As a result, fuzzy logic methods are often preferred for formative, classroom-oriented assessments, whereas IRT remains dominant in summative and standardized testing environments. While fuzzy logic excels in flexibility and interpretability, particularly in formative assessment and small-sample contexts, IRT provides standardized, statistically valid measures ideal for large-scale or high-stakes testing.

Bayesian Knowledge Tracing (BKT) was introduced by Corbett and Anderson [18]. According to BKT, the probability of a student correctly applying a skill on a future task is determined by four parameters: the probability of knowing the skill a priori (pInit), the probability of learning the skill after each opportunity to apply it (pLearn), the probability of making a mistake when applying an already known skill (pSlip), and the probability of luckily producing a correct response when the skill is not known (pGuess) [19]. A Bayesian network is a probabilistic graphical model for representing knowledge about an uncertain domain, where each node represents a random variable, and directed edges between nodes represent probabilistic dependencies between these variables. A Hidden Markov Model (HMM) is a specialized Bayesian network for tracking directly unobservable (hidden) nodes using observable node states. BKT provides a probabilistic learning model where hidden nodes represent student knowledge and observable nodes represent student performance [20]. BKT is generally used when the system is interactional/sequential (learners answer many skill-tagged items over time), one needs time-aware mastery estimation and automated item sequencing/personalization, and one can map interactions to discrete skills. Xu et al. [21] revealed that BKT’s value for adaptive training and outcome improvement in a domain where temporal tracking and personalized remediation matter. While fuzzy logic tends to be preferred in formative, small-scale educational environments that emphasize interpretability, BKT is more common in large-scale, data-driven intelligent tutoring systems that aim to track discrete skill mastery over time.

Artificial neural networks (ANN) form the basis of a framework inspired by the working principles of biological neural networks, forming one of the fundamental modeling tools in artificial intelligence. These networks can perform complex information processing tasks by enabling computer systems to use a structure similar to the neural networks of the human brain [22]. Neural network-based approaches, such as Deep Knowledge Tracing [23], learn complex, nonlinear relationships between student inputs and performance outcomes through data-driven optimization. While neural network models typically achieve superior predictive accuracy on large-scale datasets, they are computationally intensive, less transparent, and offer limited interpretability for educators [24]. Fuzzy logic and ANN models offer distinct advantages in predicting academic performance. The fuzzy logic approach, as demonstrated by Hegazi et al. [25], provides an interpretable and flexible mechanism to model uncertain educational data using linguistic rules. In contrast, ANN models, such as those presented by Baashar et al. [26], learn complex nonlinear patterns from large datasets, offering higher predictive accuracy but reduced transparency. While fuzzy logic is ideal for formative assessments and smaller data contexts where interpretability is critical, ANNs are better suited for large-scale educational data mining where predictive precision is prioritized. A fuzzy environment is a state associated with the uncertainty, ambiguity, and lack of information necessary for reasoning and computation of some elements. It can be used to describe observational features [27]. Consequently, fuzzy logic is preferred in scenarios requiring interpretability and low data demands, while neural networks are more effective for large, data-rich environments that focus on predictive accuracy rather than human-readable explanations.

Given the nature of the topic we were studying, the fuzzy logic method was used. This method, due to the limited data available, enabled the incorporation of expert knowledge through rules and was effective in the decision-making process and interpretation.

3. Method

Students are subjected to different types of assessments to measure their understanding of a topic. In this study, a weight value is assigned to exam questions according to their difficulty and complexity levels by considering fuzzy rules. After ensuring that these weight values affect the scores students receive, the degree of learning each concept is found. The method used in the study is explained below.

3.1. Preparing Data

A question database is created that shows the weight ratios of the concepts that each question is trying to measure in the question in the range [0, 1].

Table 1. Database consisting of programming questions and concept weights.

Question	Categories	Bloom Taxonomy Level	Data Types and Variables	Arithmetic Operators	Logical Operators	Assignment Operators	If else If	Loops	Methods	Foreach	Arrays	Database Design	Relational Databases	SQL Commands	Objects and Class
Write a program that prints numbers between 1–100 that can be divided by 3	Loops	Applying	0.1	0.1	0.1	0.1	0.3	0.3	0	0	0	0	0	0	0
Write a program that lists numbers between 1–100 that can be divided by 3 and 5	Loops	Applying	0.1	0.1	0.2	0.1	0.2	0.3	0	0	0	0	0	0	0
Write a program that prints numbers between 2 numbers entered by the user that can be divided by 3	Loops	Applying	0.1	0.1	0.1	0.1	0.3	0.3	0	0	0	0	0	0	0
Write a program that adds odd and even numbers between 1–100 separately	Loops	Applying	0.1	0.1	0.1	0.1	0.3	0.3	0	0	0	0	0	0	0
Implement a C# application that prints the largest and smallest of 10 numbers entered from the keyboard	Loops	Applying	0.1	0.1	0.2	0.1	0.4	0.2	0	0	0	0	0	0	0
Write a program For Loop that calculates the square of odd numbers and the cube of even numbers between 1–50 and prints them on the screen	Loops	Applying	0.1	0.2	0.1	0.1	0.3	0.2	0	0	0	0	0	0	0
Write a program for loop that lists numbers between 1–50 that can be divided by 5 or 8 and prints how many them are there	Loops	Applying	0.1	0.1	0.2	0.1	0.2	0.3	0	0	0	0	0	0	0
Find the number of even numbers out of 10 numbers entered by the user	Loops	Applying	0.1	0.1	0.1	0.1	0.3	0.3	0	0	0	0	0	0	0
Write C# codes that find the number of odd numbers and the average of even numbers generated randomly and display them on the screen	Loops	Applying	0.1	0.2	0.1	0.1	0.3	0.2	0	0	0	0	0	0	0
Write the program codes that calculate the average of the grades entered by the user using the method	Methods	Applying	0.1	0.3	0	0.1	0	0	0.5	0	0	0	0	0	0

shows a screenshot of the database consisting of programming questions and the weights of the concepts included in the questions.

The fact that the scoring of open-ended questions is based on the opinion of the teacher, or the rater is one of the important factors affecting the quality of written exams. These factors also affect the validity and reliability of the written exam [28]. In this study, to take precautions against all these factors, the concepts in the programming questions were scored according to their weight ratios, by taking the opinions of two more experts in addition to the researcher, and the final weight levels were determined by taking the average of the scores.

If we assume that there are m questions in an exam and each question consists of n concepts, the elements of the K matrix give the ratio of the concepts contained in the questions according to the prepared database as the following:

$$K=\begin{array}{c}{Q}_1\\ Q_2\\ ⋮\\ Q_m\end{array}\left[\begin{array}{cccc}{k}_{11}& k_{12}& \dots & k_{1n}\\ k_{21}& k_{22}& \dots & k_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ k_{m1}& k_{m2}& \dots & k_{mn}\end{array}\right]$$

$$\sum _{j=1}^n{k}_{ij}=1$$

(1)

where Q_i denotes the ith question where $1\le i\le m$ and k_ij denotes the weight of the concept in the question where $1\le j\le n.$ In this study, firstly the exam questions selected by the instructor are scored. It is expressed by the S matrix:

$$S=\begin{array}{c}{Q}_1\\ Q_2\\ ⋮\\ Q_m\end{array}\left[\begin{array}{c}{s}_1\\ s_2\\ ⋮\\ s_m\end{array}\right], \sum _{i=1}^m{s}_i=100, 1\le i\le m$$

(2)

$$L=S^{T}K, \left[l_j\right] 1\le j\le n.$$

(3)

The product of the S^T and K matrices gives the maximum score that can be obtained for each concept if the questions are answered correctly. l_j denotes the maximum score that can be obtained if the relevant concept section in the questions is answered correctly.

According to the weights of the concepts included in the exam questions, the full score to be received if the relevant section of each concept is answered correctly is calculated using the following equation:

$${k^{\prime }}_{ij}=k_{ij} \ast s_i$$

(4)

$$K^{\prime }=\begin{array}{c}{Q}_1\\ Q_2\\ ⋮\\ Q_m\end{array}\left[\begin{array}{cccc}{k^{\prime }}_{11}& {k^{\prime }}_{12}& \dots & {k^{\prime }}_{1n}\\ {k^{\prime }}_{21}& {k^{\prime }}_{22}& \dots & {k^{\prime }}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {k^{\prime }}_{m1}& {k^{\prime }}_{m2}& \dots & {k^{\prime }}_{mn}\end{array}\right].$$

The student’s answer to each question is scored by the instructor according to the accuracy rate of the sections related to the concepts included in the question. This scoring is done by considering the full scores calculated in the K’ matrix. It is expressed by the R matrix:

$$R=\begin{array}{c}{Q}_1\\ Q_2\\ ⋮\\ Q_m\end{array}\left[\begin{array}{cccc}{r}_{11}& r_{12}& \dots & r_{1n}\\ r_{21}& r_{22}& \dots & r_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ r_{m1}& r_{m2}& \dots & r_{mn}\end{array}\right].$$

The scores obtained by the student from the sections related to the concepts in each exam question are multiplied by the weight vector. The weight vector is obtained by applying the rules of fuzzy logic to the difficulty and complexity values of each question. The following explains how to obtain the difficulty and complexity attributes that describes with a crisp value for each question.

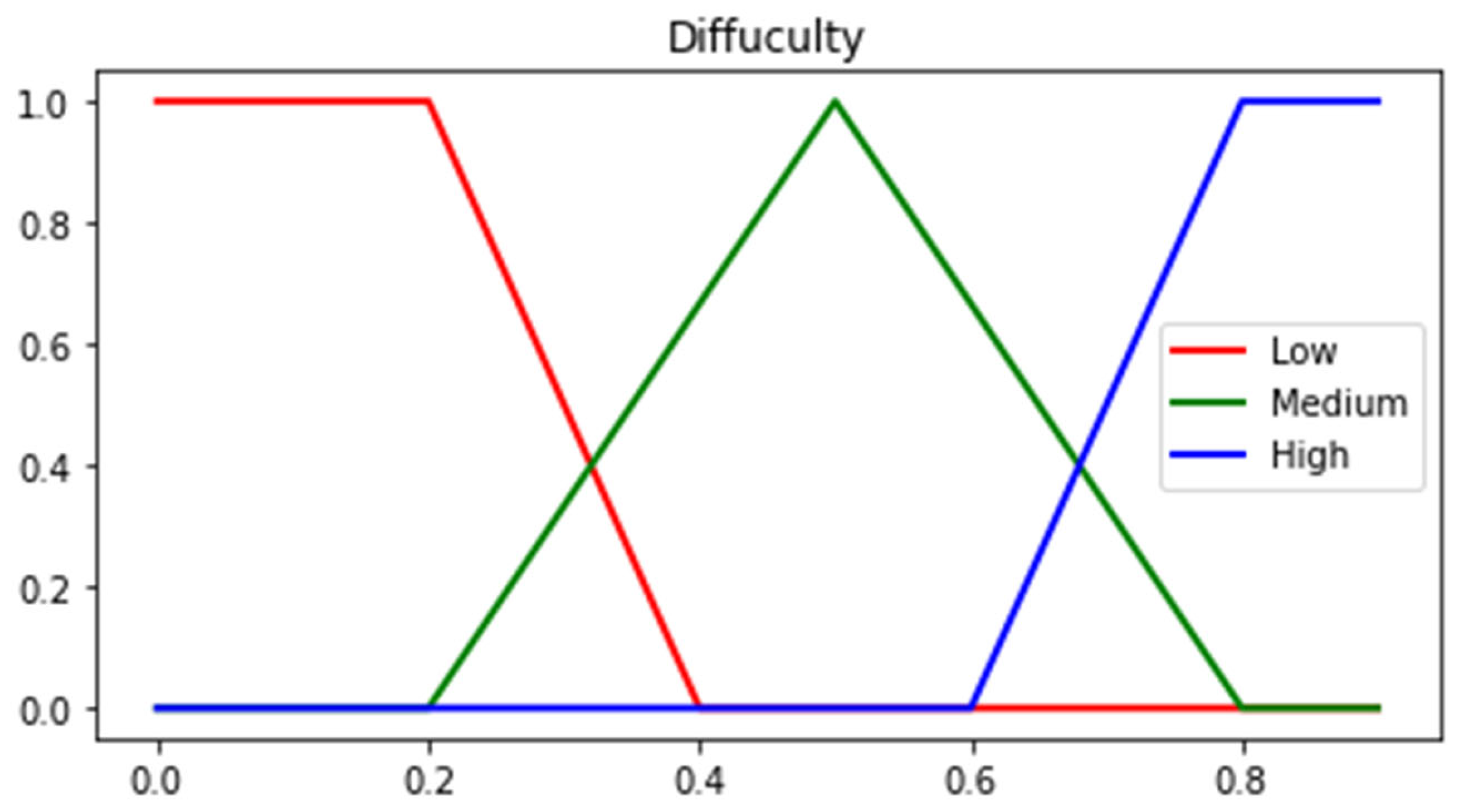
3.2. Difficulty Attribute

It is known that the rate of correct answers to a question indicates the difficulty level of the question. Item difficulty index is calculated as a percentage of the total number of correct responses to items and is calculated using the formula P = R/T. Here, P is the item difficulty index, R is the number of correct answers, and T is the total number of answers, both correct and incorrect. When a question is considered difficult, its difficulty index value is less than 30% and it is considered easy when the index value is greater than 80%. Based on this, the difficulty level of the question was tried to be determined according to the following equation [29]:

$$P_i={\displaystyle \frac{R_i}{T_i}}, 1\le i\le m$$

(5)

where P_i is the item difficulty index; R_i is the number of correct answers; and T_i is the total number of answers, both correct and incorrect.

In addition, in this study, the level of difficulty of the questions according to the Bloom taxonomy was considered in determining the difficulty level. In 1956, University of Chicago professor Benjamin Bloom classified the development of mental skills from low-level thinking skills to higher-level thinking skills to explain how the learning process develops. Bloom taxonomy shows that learning occurs in stages. Conceptual knowledge must be acquired to put it into practice. Learning to program is a difficult process because it requires cognitive actions such as analysis and synthesis. While writing the codes of a program, basic concepts are brought together to ensure the synthesis step. For the application and analysis steps, dividing the program codes into sections instead of printing them is deemed appropriate for the learners to understand the subject better [30,31]. The

Table 2. Classification of the stages of learning programming in the context of Bloom taxonomy.

Bloom Taxonomy	Learning to Program
Remembering	Interface, Structures, Syntax
Understanding	Comprehension, Related Concepts
Applying	Using the learned information (Understanding the program flow)
Analyzing	Understanding the problem situation
Synthesis	Creating Solutions
Evaluating	Evaluation of different solutions

below summarizes how the stages of learning programming are classified in the context of Bloom taxonomy.

In this study, a database consisting of programming questions was created and the learning stage of each question according to the Bloom taxonomy was determined by taking the opinions of the researcher and experts. The reason we carry out this is to assign a difficulty level according to the learning stage in which the questions are located. These difficulty levels are shown in

Table 3. Difficulty levels in the Bloom taxonomy.

Bloom Taxonomy	Difficulty Level
Remembering	1/6
Understanding	2/6
Applying	3/6
Analyzing	4/6
Synthesis	5/6
Evaluating	6/6

.

The final value of the difficulty level multiplied by the difficulty coefficient values given in Table 3. Increasing or decreasing the difficulty levels of the questions according to their level of the Bloom taxonomy is formulated as follows:

$$d_i=\left(1-P_i\right) \ast B_i, 1\le i\le m$$

(6)

where B_i is the Bloom’s taxonomy difficulty coefficient. P_i is the item difficulty index. d_i is the overall difficulty index.

The difficulty vector indicating the question difficulty level of each question is expressed as D as the following:

$$D=\begin{array}{c}{Q}_1\\ Q_2\\ ⋮\\ Q_m\end{array}\left[\begin{array}{c}{d}_1\\ d_2\\ ⋮\\ d_m\end{array}\right].$$

3.3. Complexity Attribute

One of the parameters affecting the determination of question difficulty levels is the number of concepts the question is related to and the number of correct or incorrect answers students give to the question [32]. In this study, it was assumed that the number of concepts the question is related to indicates the complexity of the question. The complexity vector showing how many concepts each question consists of is expressed as C as follows:

$$C=\begin{array}{c}{Q}_1\\ Q_2\\ ⋮\\ Q_m\end{array}\left[\begin{array}{c}{c}_1\\ c_2\\ ⋮\\ c_m\end{array}\right].$$

3.4. Fuzzyfication Process

After the difficulty and complexity values of the questions’ attributes are determined as vectors, triangular and trapezoidal fuzzy numbers and membership functions used to blur these values are determined. The fuzzy membership functions defined for difficulty and complexity attributes consist of triangular fuzzy numbers (a, b, c) and trapezoidal fuzzy numbers (a, b, c, d) and are formulated as follows:

$${\mu }_A\left(x\right)=\left\{\begin{array}{c}0, x\le a\\ {\displaystyle \frac{x-a}{b-a}}, a<x\le b\\ {\displaystyle \frac{c-x}{c-b}}, b<x<c\\ 0, x\ge c\end{array}\right.$$

(7)

$${\mu }_A\left(x\right)=\left\{\begin{array}{l}\hspace{1em} 0, \left(x<a\right) or (x>d) \\ {\displaystyle \frac{x-a}{b-a}}, a\le x\le b\\ \hspace{1em} 1, b\le x\le c\\ {\displaystyle \frac{d-x}{d-c}}, c\le x\le d\end{array}\right.$$

(8)

The numerical values obtained because of the formula to find the difficulty level of each question are expressed with linguistic variables at three different levels according to the value ranges specified in

Table 4. Linguistic variables and fuzzy numbers for difficulty.

Fuzzy Numbers	Linguistic Variables
0.0, 0.2, 0.4	Low
0.2, 0.5, 0.8	Medium
0.6, 0.8, 1.1	High

. Figure 1 shows the membership functions of these values.

The complexity values obtained according to the number of concepts contained in each question are expressed with three different levels of linguistic variables specified in

Table 5. Linguistic variables and fuzzy numbers for complexity.

Fuzzy Numbers	Linguistic Variables
0.0, 0.2, 0.4	Low
0.2, 0.5, 0.8	Medium
0.6, 0.8, 1.1	High

.

The difficulty and complexity values of the questions are expressed in fuzzy matrices, according to the values obtained from the membership functions. In this study, since the difficulty and complexity values are expressed with three different linguistic variables, the matrices are formed as follows:

$$DF=\begin{array}{c}{Q}_1\\ Q_2\\ ⋮\\ Q_m\end{array}\left[\begin{array}{ccc}{d}_{11}& d_{12}& d_{13}\\ d_{21}& d_{22}& d_{23}\\ ⋮& ⋮& ⋮\\ d_{m1}& d_{m2}& d_{m3}\end{array}\right]$$

$$CF=\begin{array}{c}{Q}_1\\ Q_2\\ ⋮\\ Q_m\end{array}\left[\begin{array}{ccc}{c}_{11}& c_{12}& c_{13}\\ c_{21}& c_{22}& c_{23}\\ ⋮& ⋮& ⋮\\ c_{m1}& c_{m2}& c_{m3}\end{array}\right]$$

3.5. Fuzzy Rules

While writing the fuzzy logic rules, all the fuzzy set connections that can be between the input data and the outputs are considered (

Table 6. Fuzzy rules.

Inclusiveness Level	Difficulty	Complexity
Very Low	Low	Low
Low	Low	Medium
	Medium	Low
	Low	Low
Sufficient	Low	Medium
	Medium	Low
	Medium	Medium
	Low	High
	High	Low
	Low	Low
Satisfactory	Medium	Medium
	Medium	Low
	Medium	High
	Low	High
	High	Low
	Low	Medium
	High	Medium
Good	Medium	Medium
	Medium	High
	Low	High
	High	Low
	High	Medium
	High	High
Very Good	Medium	High
	High	Medium
	High	High
Excellent	High	High

). The term inclusiveness level is used in this study to mean including all the features and subtleties. It refers to the level of importance achieved by considering all aspects of a question. For the fuzzy logic rules determined during the introduction process, the question difficulty was assigned a value of 0.6 based on expert opinion, and the complexity was assigned a value of 0.4. The difficulty value was determined based on other students’ exam scores and the ratio determined according to Bloom taxonomy. Therefore, the difficulty value was assigned a relatively higher value than the complexity value. Table 6 includes all the rules that can be written in the logical IF–THEN type that connect the inputs to the output variables.

Fuzzy rules for calculation in case the inclusiveness level of Q_i is very low are explained as the following:

IF difficulty is low, and complexity is low THEN question’s inclusiveness level is very low.

The formula that calculates the inclusiveness level of Q_i as very low is shown below:

$$h_{i1}=0.6\ast d_{i1}+0.4\ast c_{i1}.$$

(9)

Fuzzy rules for calculation in case the inclusiveness level of Q_i is low are explained as the following:

IF difficulty is low, and complexity is medium THEN question’s inclusiveness level is low.

IF difficulty is medium, and complexity is low THEN question’s inclusiveness level is low.

IF difficulty is low, and complexity is low THEN question’s inclusiveness level is low.

The formula that calculates the inclusiveness level of Q_i as low is shown below:

$$h_{i2}=Max\left(0.6\ast d_{i1}+0.4\ast c_{i2},0.6\ast d_{i2}+0.4\ast c_{i1}\right).$$

(10)

Fuzzy rules for calculation in case the inclusiveness level of Q_i is sufficient are explained as the following:

IF difficulty is low, and complexity is medium THEN question’s inclusiveness level is sufficient.

IF difficulty is medium, and complexity is low THEN question’s inclusiveness level is sufficient.

IF difficulty is medium, and complexity is medium THEN question’s inclusiveness level is sufficient.

IF difficulty is low, and complexity is high THEN question’s inclusiveness level is sufficient.

IF difficulty is high, and complexity is low THEN question’s inclusiveness level is sufficient.

IF difficulty is low, and complexity is low THEN question’s inclusiveness level is sufficient.

The formula that calculates the inclusiveness level of Q_i as sufficient is shown below:

$$h_{i3}=Max\left(\begin{array}{c}0.6\ast d_{i1}+0.4\ast c_{i2},0.6\ast d_{i2}+0.4\ast c_{i1}, 0.6\ast d_{i2}+0.4\ast c_{i2}, 0.6\ast d_{i1}+0.4\ast c_{i3},\\ 0.6\ast d_{i3}+0.4\ast c_{i1},0.6\ast d_{i1}+0.4\ast c_{i1}\end{array}\right).$$

(11)

Fuzzy rules for calculation in case the inclusiveness level of Q_i is satisfactory are explained as the following:

IF difficulty is medium, and complexity is medium THEN question’s inclusiveness level is satisfactory.

IF difficulty is medium, and complexity is low THEN question’s inclusiveness level is satisfactory.

IF difficulty is medium, and complexity is high THEN question’s inclusiveness level is satisfactory.

IF difficulty is low, and complexity is high THEN question’s inclusiveness level is satisfactory.

IF difficulty is high, and complexity is low THEN question’s inclusiveness level is satisfactory.

IF difficulty is low, and complexity is medium THEN question’s inclusiveness level is satisfactory.

IF difficulty is high, and complexity is medium THEN question’s inclusiveness level is satisfactory.

The formula that calculates the inclusiveness level of Q_i as satisfactory is shown below:

$$h_{i4}=Max\left(\begin{array}{c}0.6\ast d_{i2}+0.4\ast c_{i2},0.6\ast d_{i2}+0.4\ast c_{i1}, 0.6\ast d_{i2}+0.4\ast c_{i3}, 0.6\ast d_{i1}+0.4\ast c_{i3}, \\ 0.6\ast d_{i3}+0.4\ast c_{i1},0.6\ast d_{i1}+0.4\ast c_{i2},0.6\ast d_{i3}+0.4\ast c_{i2}\end{array}\right).$$

(12)

Fuzzy rules for calculation in case the inclusiveness level of Q_i is good are explained as the following:

IF difficulty is medium, and complexity is medium THEN question’s inclusiveness level is good.

IF difficulty is medium, and complexity is high THEN question’s inclusiveness level is good.

IF difficulty is low, and complexity is high THEN question’s inclusiveness level is good.

IF difficulty is high, and complexity is low THEN question’s inclusiveness level is good.

IF difficulty is high, and complexity is medium THEN question’s inclusiveness level is good.

IF difficulty is high, and complexity is high THEN question’s inclusiveness level is good.

The formula that calculates the inclusiveness level of Q_i as good is shown below:

$$h_{i5}=Max\left(\begin{array}{c}0.6\ast d_{i2}+0.4\ast c_{i2},0.6\ast d_{i2}+0.4\ast c_{i3}, 0.6\ast d_{i1}+0.4\ast c_{i3}, 0.6\ast d_{i3}+0.4\ast c_{i1},\\ 0.6\ast d_{i3}+0.4\ast c_{i2},0.6\ast d_{i3}+0.4\ast c_{i3}\end{array}\right).$$

(13)

Fuzzy rules for calculation in case the inclusiveness level of Q_i is very good are explained as the following:

IF difficulty is medium, and complexity is high THEN question’s inclusiveness level is very good.

IF difficulty is high, and complexity is medium THEN question’s inclusiveness level is very good.

IF difficulty is high, and complexity is high THEN question’s inclusiveness level is very good.

The formula that calculates the inclusiveness level of Q_i as very good is shown below:

$$h_{i6}=Max\left(0.6\ast d_{i2}+0.4\ast c_{i3},0.6\ast d_{i3}+0.4\ast c_{i2}, 0.6\ast d_{i3}+0.4\ast c_{i3}\right).$$

(14)

Fuzzy rules for calculation in case the inclusiveness level of Q_i is excellent are explained the following:

IF difficulty is high, and complexity is high THEN question’s inclusiveness level is excellent.

The formula that calculates the inclusiveness level of Q_i as excellent is shown below:

$$h_{i7}=Max\left(0.6\ast d_{i3}+0.4\ast c_{i3}\right).$$

(15)

3.6. Obtaining the Level of Inclusiveness of Each Question

The difficulty and complexity matrices are processed according to the formulas given for each question and the final form of the inclusiveness matrix H is obtained with the membership degrees found:

$$H=\begin{array}{c}{Q}_1\\ Q_2\\ ⋮\\ Q_m\end{array}\left[\begin{array}{cccc}{h}_{11}& h_{12}& \dots & h_{17}\\ h_{21}& h_{22}& \dots & h_{27}\\ ⋮& ⋮& \ddots & ⋮\\ h_{m1}& h_{m2}& \dots & h_{m7}\end{array}\right]$$

Using the formulas given below, an average value based on the H matrix is found for each question Q_i. Then, the score weight of each question is considered and multiplied by the obtained value:

$${Hw}_i={\displaystyle \frac{h_{i7}+h_{i6}+h_{i5}+h_{i4}-h_{i3}-h_{i2}-h_{i1}}{7}}, 1\le i\le m$$

(16)

$$S=\begin{array}{c}{Q}_1\\ Q_2\\ ⋮\\ Q_m\end{array}\left[\begin{array}{c}{s}_1\\ s_2\\ ⋮\\ s_m\end{array}\right], \sum _{i=1}^m{s}_i=100, {Sw}_i={\displaystyle \frac{s_i}{{\sum }_i^m{s}_i}}$$

(17)

$$W_i={Hw}_i\ast {Sw}_i, 1\le i\le m.$$

(18)

Thus, we obtain the W matrix, which shows the level of inclusiveness of each question:

$$W=\begin{array}{c}{Q}_1\\ Q_2\\ ⋮\\ Q_m\end{array}\left[\begin{array}{c}{w}_1\\ w_2\\ ⋮\\ w_m\end{array}\right]$$

3.7. Rearrangement of Student Scores

The points obtained by the student by answering each concept section of the questions correctly are multiplied by the weight values of the questions. Thus, if the level of inclusiveness of the question is high, the student’s score will increase, and in the opposite case, the score will decrease. Updated scores are expressed by the R′ matrix:

$${r^{\prime }}_{ij}=r_{ij}\ast \left(1+w_i\right)$$

(19)

$$If {r^{\prime }}_{ij}\ge {k^{\prime }}_{ij} then$$

(20)

$${r^{\prime }}_{ij}=={k^{\prime }}_{ij}$$

$$R^{\prime }=\begin{array}{c}{Q}_1\\ Q_2\\ ⋮\\ Q_m\end{array}\left[\begin{array}{cccc}{r^{\prime }}_{11}& {r^{\prime }}_{12}& \dots & {r^{\prime }}_{1n}\\ {r^{\prime }}_{21}& {r^{\prime }}_{22}& \dots & {r^{\prime }}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {r^{\prime }}_{m1}& {r^{\prime }}_{m2}& \dots & {r^{\prime }}_{mn}\end{array}\right].$$

Adding one to the weight value is to avoid obtaining a negative value.

3.8. Finding Student’s Learning Rate for Each Concept

The student scores updated according to the inclusiveness level of each question are represented by the R’ matrix. The sum of the values in each column of the R’ matrix is the sum of the scores the student received from the sections related to the concept of that column. The sum of the column values of the R’ matrix is found by multiplying all the values of the Z^T matrix by one and the R’ matrix. Dividing each value found by the maximum score that can be obtained by correctly answering the sections related to the relevant concept gives the student’s learning rate of the relevant concept.

$$Z=\begin{array}{c}{Q}_1\\ Q_2\\ ⋮\\ Q_m\end{array}\left[\begin{array}{c}{z}_1\\ z_2\\ ⋮\\ z_m\end{array}\right], z_i=1, 1\le i\le m$$

(21)

$$L^{\prime }=Z^T{R}^{\prime }, \left[{l^{\prime }}_j\right], 1\le j\le n$$

(22)

$${Lr}_j={\displaystyle \frac{\left[{l^{\prime }}_j\right]}{{[l}_j]}}, {Lr}_j\in \left[\mathrm{0,1}\right]$$

(23)

4. Instruments

The assessment tools used in this study consist of a pretest, a posttest focusing on learning performance, and a scale focusing on self-efficacy. The 7-point Likert Scale Computer Programming Self-Efficacy Scale was adapted to Turkish by Altun and Mazman [33] to examine the general self-efficacy perceptions of individuals regarding programming in terms of various variables. As a result of the validity and reliability studies conducted on the sample applied to the Turkish form of the study, the Cronbach Alpha coefficient for the entire scale was calculated as 0.928, and the McDonald’s ω (omega) coefficient, which is stated to give more appropriate results for congeneric measurements, was calculated as 0.956. As a result of the exploratory factor analysis, nine items explained 80.814% of the total variance, and the model related to this structure was also confirmed by confirmatory factor analysis.

A test consisting of ten questions was created with questions selected from relevant field tests created by the Ministry of National Education with teams consisting of academicians, field experts and measurement and assessment experts. The questions selected by two expert teachers were scored and applied to the experimental and control groups as pretest and posttest. The KR20 value of the pretest is 0.71 and the posttest is 0.73.

5. Results

5.1. Self-Efficacy

In this study, to observe the changes in the self-efficacy perceptions of the students in the experimental and control groups regarding programming, the relevant scale was applied as a pre-questionnaire and post-test and the results were analyzed using a paired sample t-test with a significance threshold of p < 0.05. Initially, an independent sample t-test was used to analyze whether there was a difference between the pre-test scores of the experimental and control groups and it was found that there was no difference (t = 0.12, p > 0.05). As it can be seen in

Table 7. Paired samples t-test of self-efficacy.

Group	Variable	N	Mean	SD	t	p
Experimental	Pre-test	51	4.56	1.29	−6.734	0.000
	Post-test	51	5.57	0.95
Control	Pre-test	45	4.59	1.17	−0.344	0.733
	Post-test	45	4.61	1.21

, the mean pre-test scores for the experimental group were 4.56 (standard deviation 1.29) and for the control group, 4.59 (standard deviation 1.17). When the post-test evaluations were examined, it was seen that there was a significant improvement in the self-efficacy perceptions of the experimental group students regarding programming. While the mean posttest score of the experimental group was 5.57 with a standard deviation of 0.95, the mean score of the control group was 4.61 with a standard deviation of 1.21. As a result of the analysis, it is found that there is a significant increase in the post-test scores of the experimental group compared to the control group (t = −6.734 p < 0.001). Accordingly, it has been proven that providing detailed feedback on the extent to which students have learned the concepts and informing them about their deficiencies significantly improves students’ self-efficacy perceptions regarding programming.

5.2. Learning Performance

In this study, it was seen by applying the independent sample t-test that there was no significant difference between the pretest results applied to the experimental and control groups at the beginning (t = 0.36, p = 0.71).

A paired sample t-test was used with a significance threshold of p < 0.05 to evaluate the pretest and posttest score differences between the experimental and control groups. As summarized in

Table 8. Paired samples t-test of learning performance.

Group	Variable	N	Mean	SD	t	p
Experimental	Pre-test	51	51.11	6.86	−7.293	0.000
	Post-test	51	62.50	8.69
Control	Pre-test	45	51.60	6.07	−1.727	0.091
	Post-test	45	53.22	7.52

, the pretest mean scores for the experimental group were 51.11 (standard deviation 6.86), for the control group 51.60 (standard deviation 6.07), and when the post-test evaluations are examined, it is seen that there is a significant improvement in the learning performance of the experimental group. While the average post-test score of the experimental group is 62.50 with a standard deviation of 8.69, the average score of the control group is 53.22 with a standard deviation of 7.52. As a result of the analysis, it is seen that there is a significant increase in the post-test scores of the experimental group compared to the control group (t = −7.293, p < 0.001). Accordingly, it has been proven that providing detailed feedback on the extent to which students have learned the concepts and informing them about their deficiencies significantly increases learning performance.

5.3. Limitations and Future Work

To overcome the limitations of this study, the number of students in the experimental and control groups could be increased, minimizing the impact of external factors on students. Furthermore, students’ work on the feedback provided could be monitored. To further automate the study in the future, the concepts and ratios contained in the questions could be determined using various natural language processing tools.

6. Conclusions

In education system, evaluating what students know and how they apply this knowledge is one of the important steps of the education process. Correct evaluation of students’ academic performance has significant effects on students’ education life and future. Despite this, we see that in our education system, the total score obtained from each exam is given to students as feedback during the evaluation phase. In this study, the points that students receive by answering the sections of the concepts correctly are increased or decreased by fuzzy membership functions depending on the difficulty and complexity level of the question, and the rate of learning each concept is given to the student as feedback. Additionally, student scores that increase and decrease depending on the degree of inclusiveness of the questions will ensure that rankings yield more accurate results in assessment methods that use systems, such as the bell curve. In this way, individualized evaluation for students can be made more accurately, and the way will be paved for correct guidance to complete their deficiencies.