Optimal Design of Anti-Collision Spacer Ring for Power Transmission Lines
Abstract
1. Introduction
2. Composition and Working Principle of the Spacer Ring System
3. The Optimization Model for Spacer Ring
3.1. Simulation Modeling of the Spacer Ring
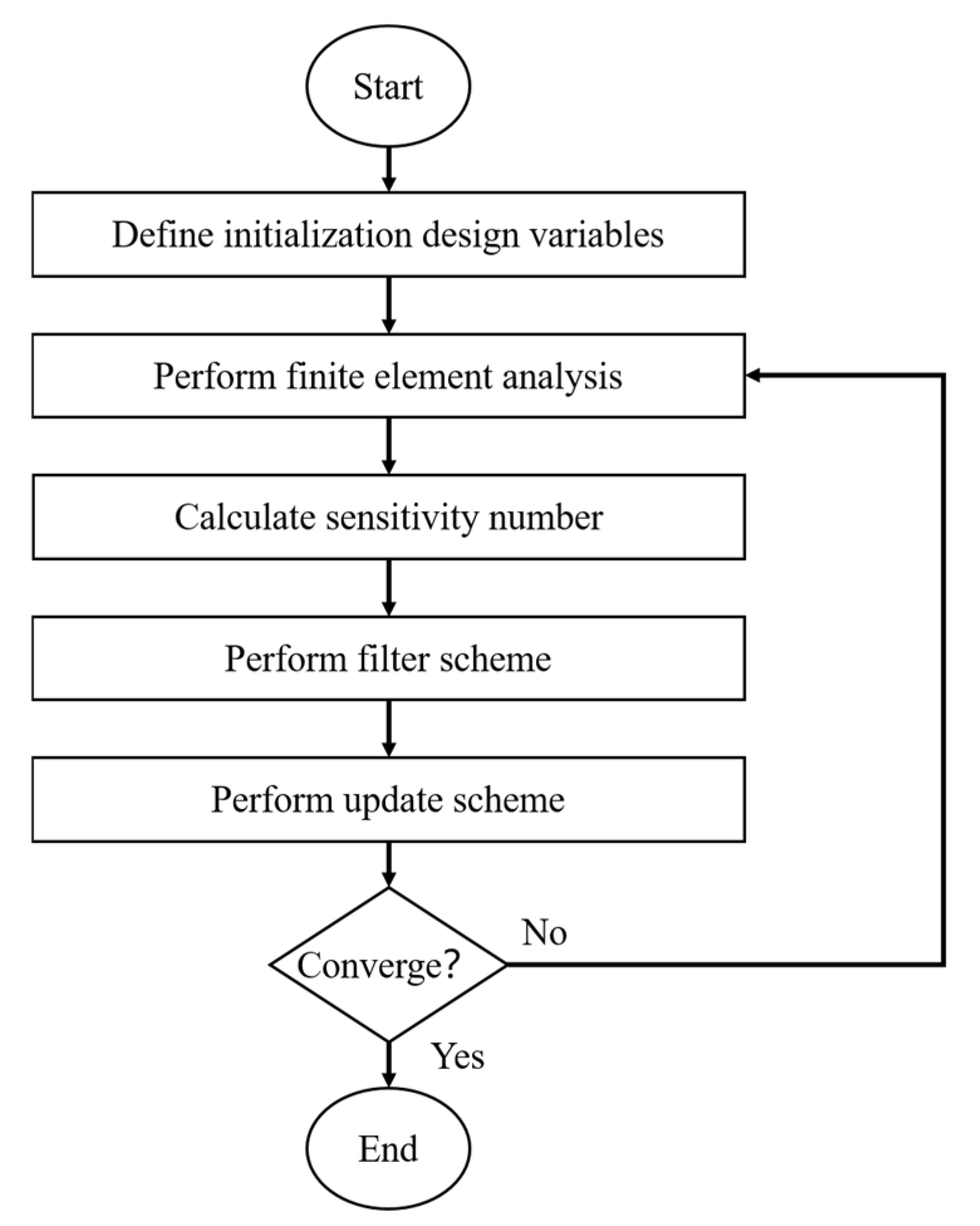
3.2. Topology Optimization Method Based on Variable Density Method
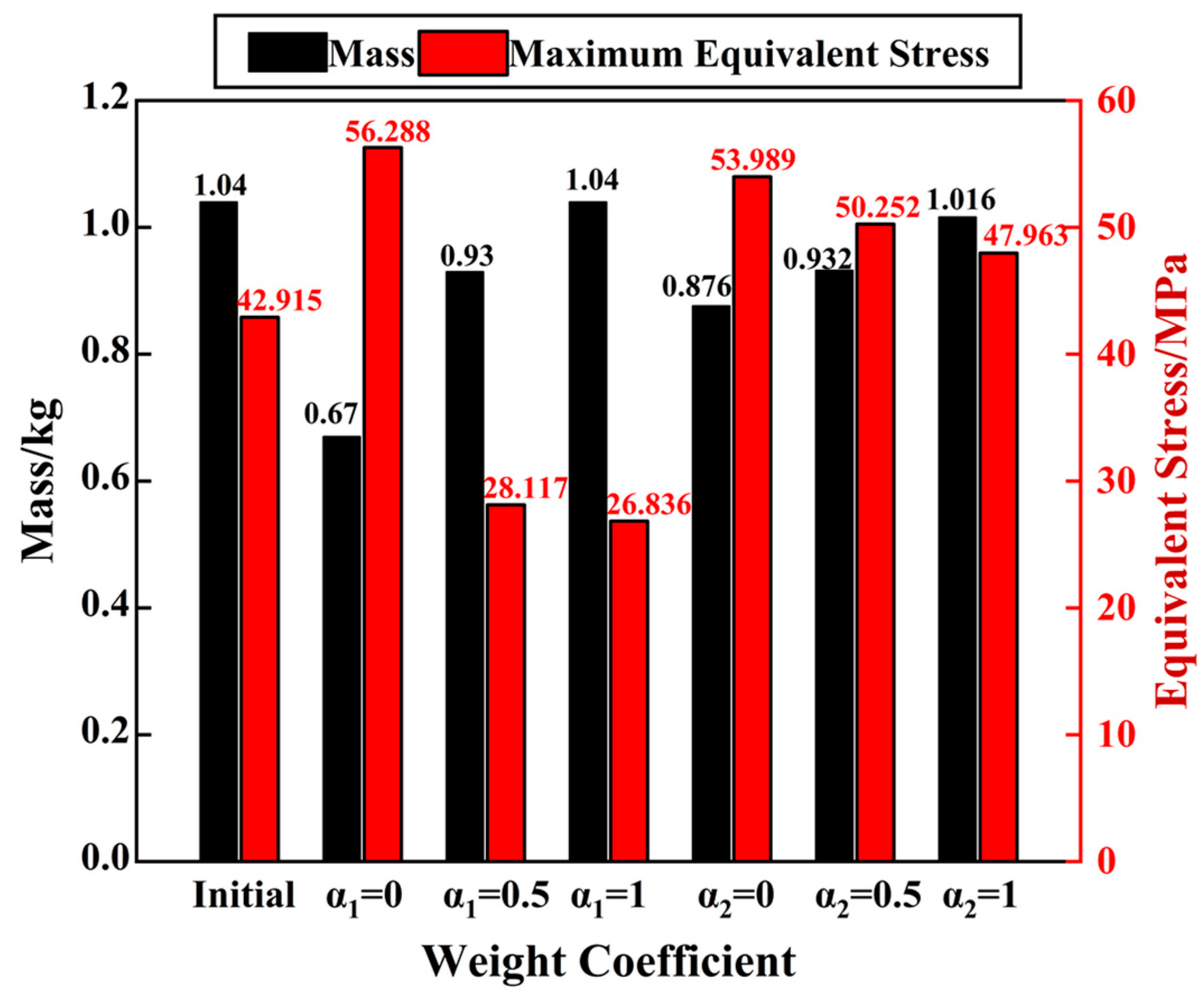
3.3. Mathematical Modeling for Topology Optimization
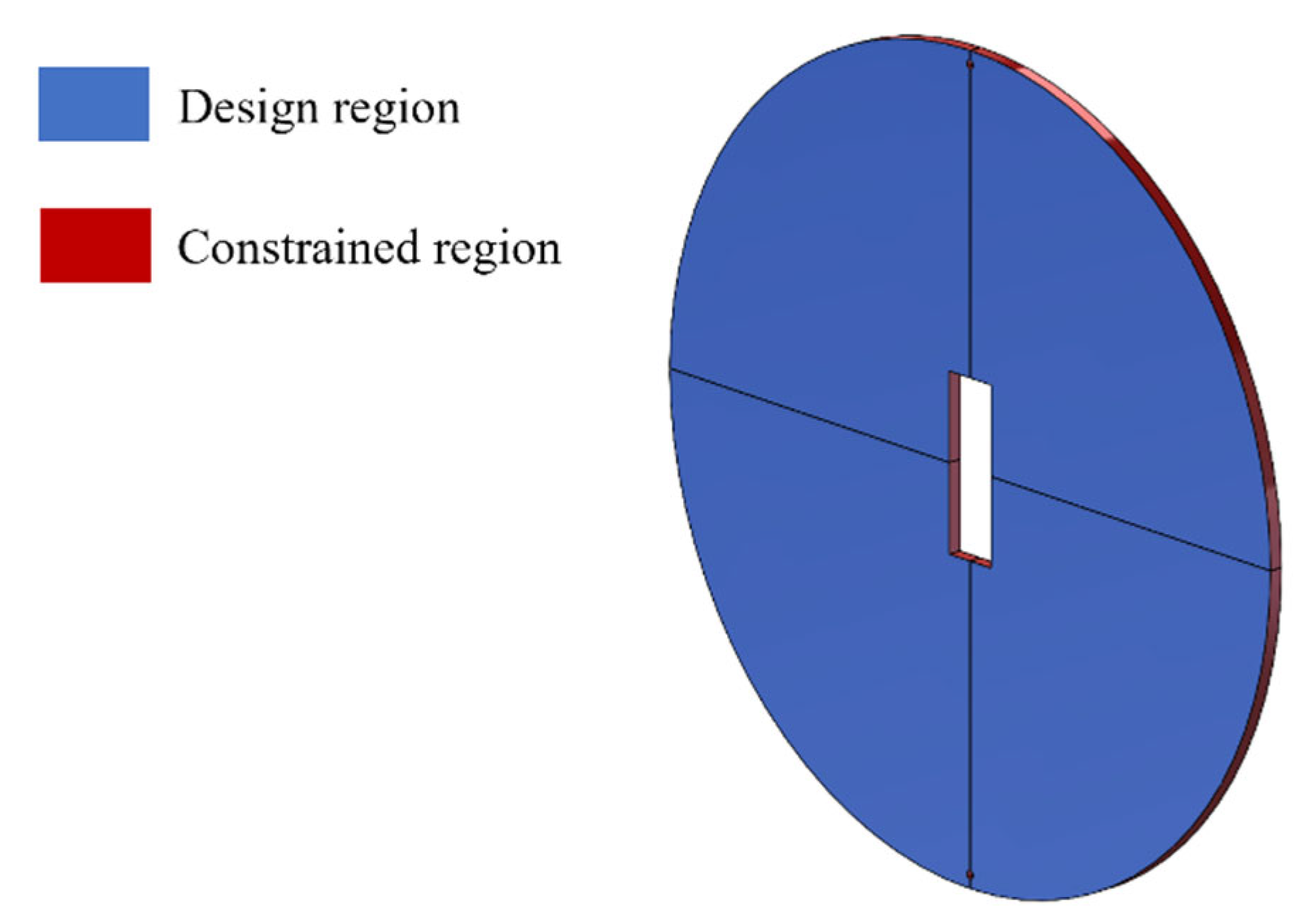
3.4. Boundary Conditions for Spacer Ring Structures
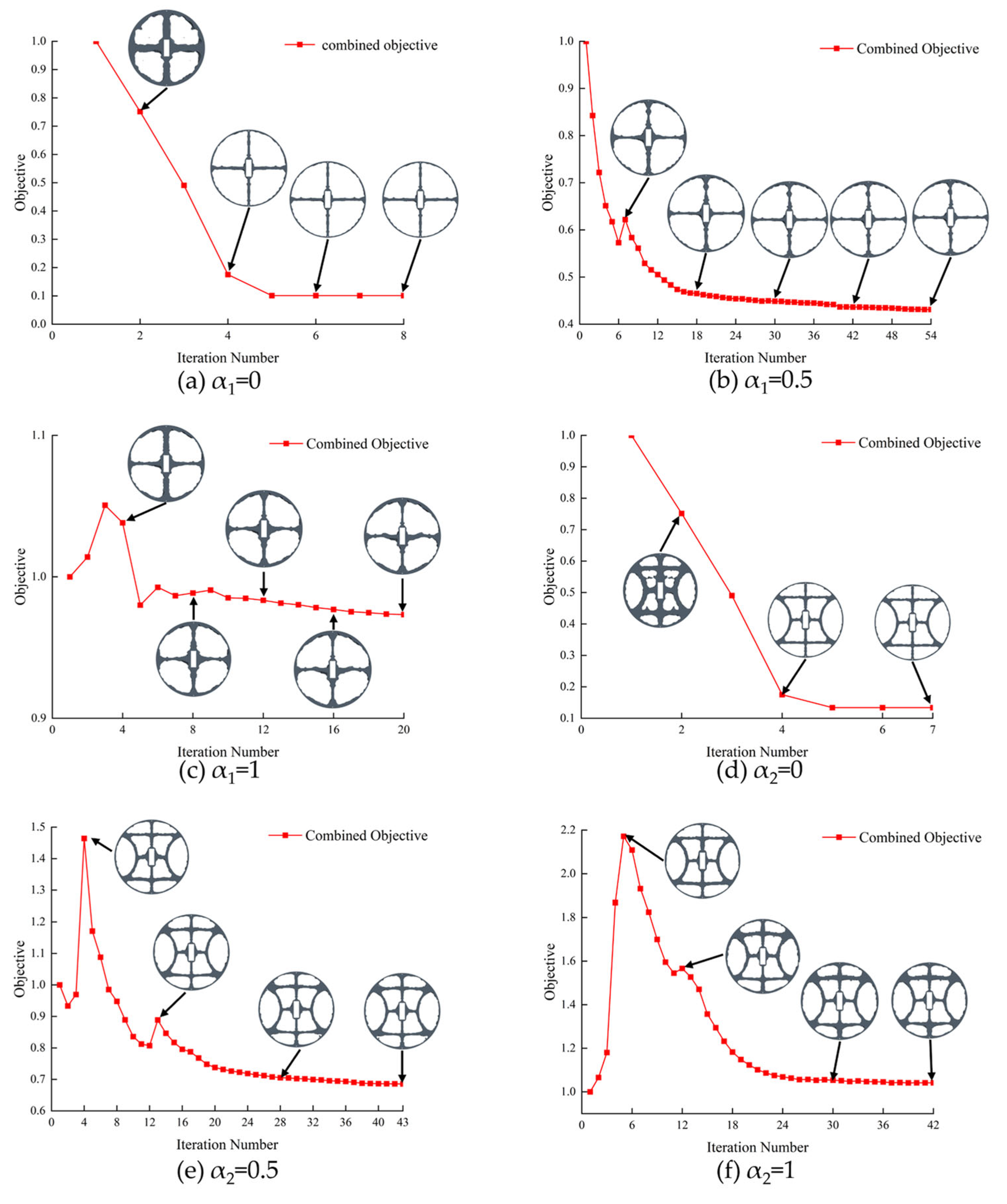
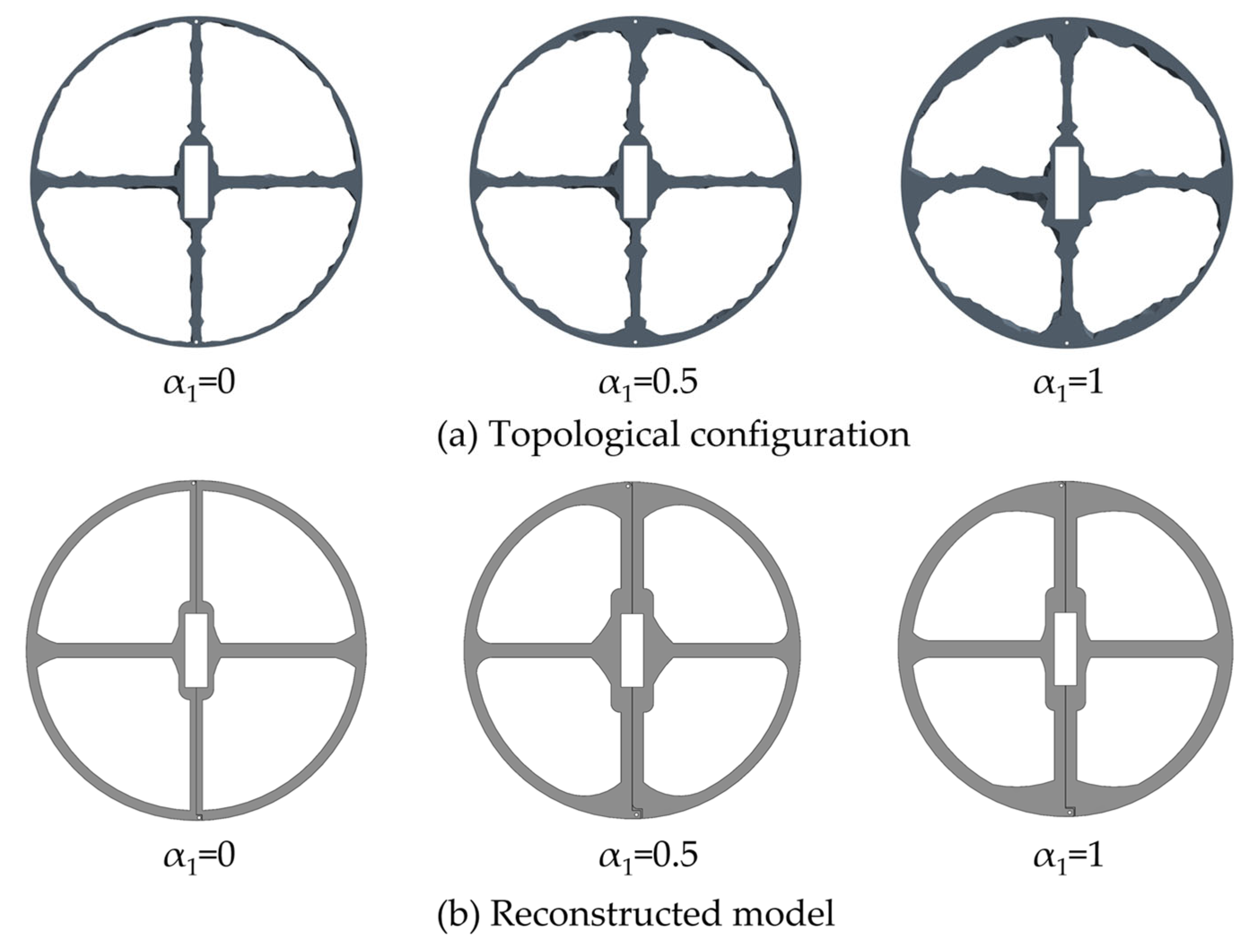
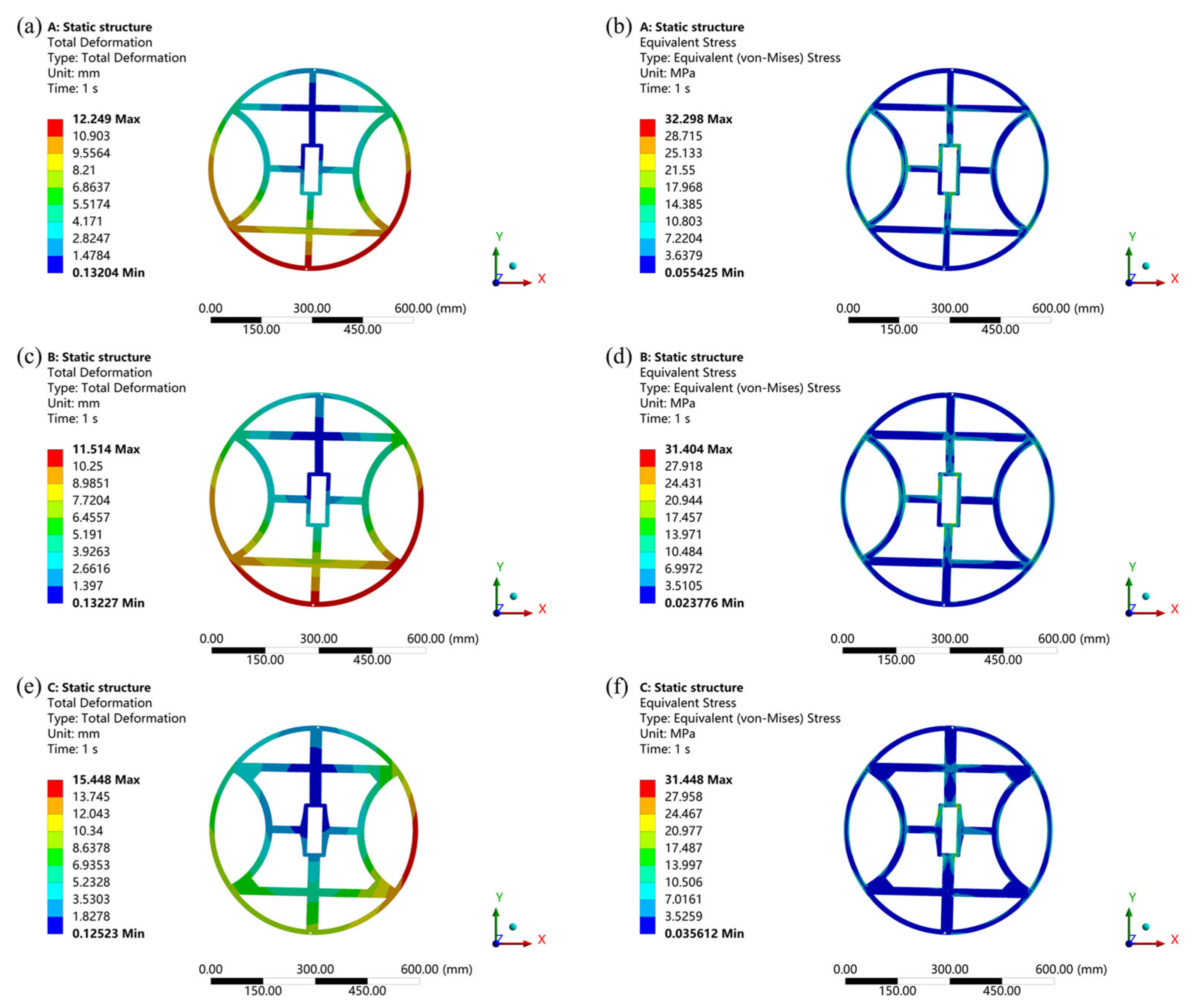
3.5. Topology Optimization Resulting Configurations
4. Spacer Ring Performance Simulation Analysis
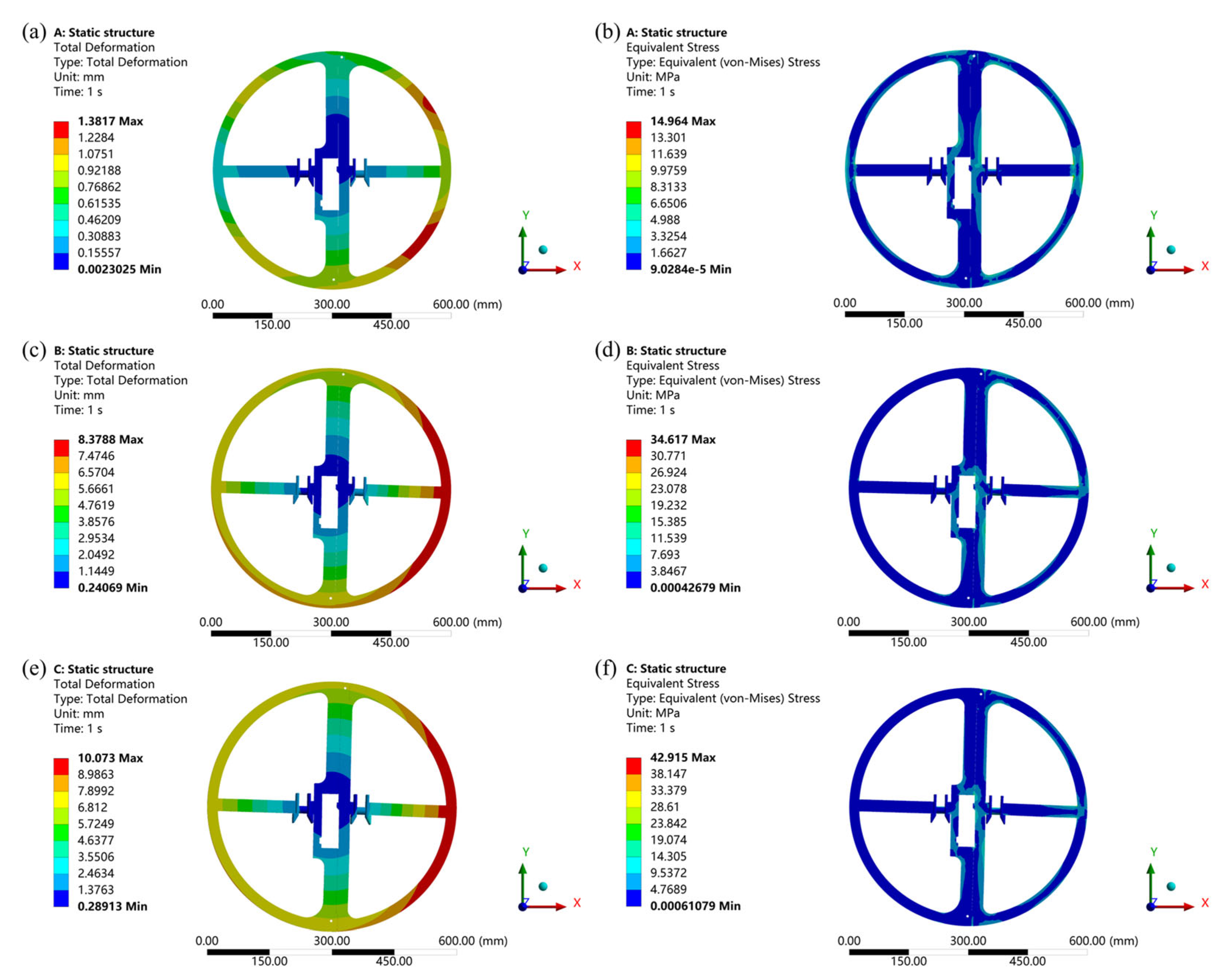
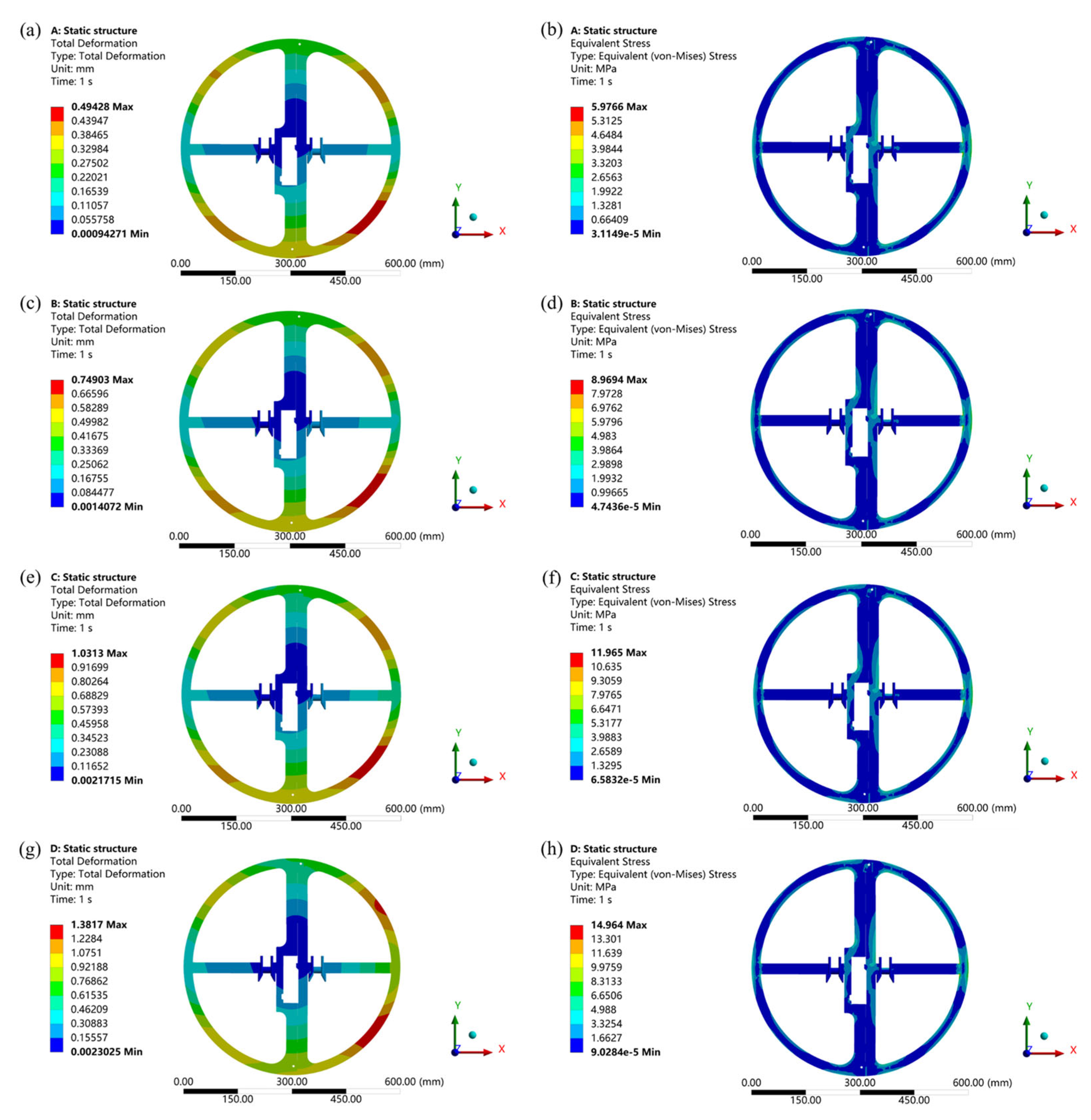
4.1. Static Analysis of the Spacer Ring
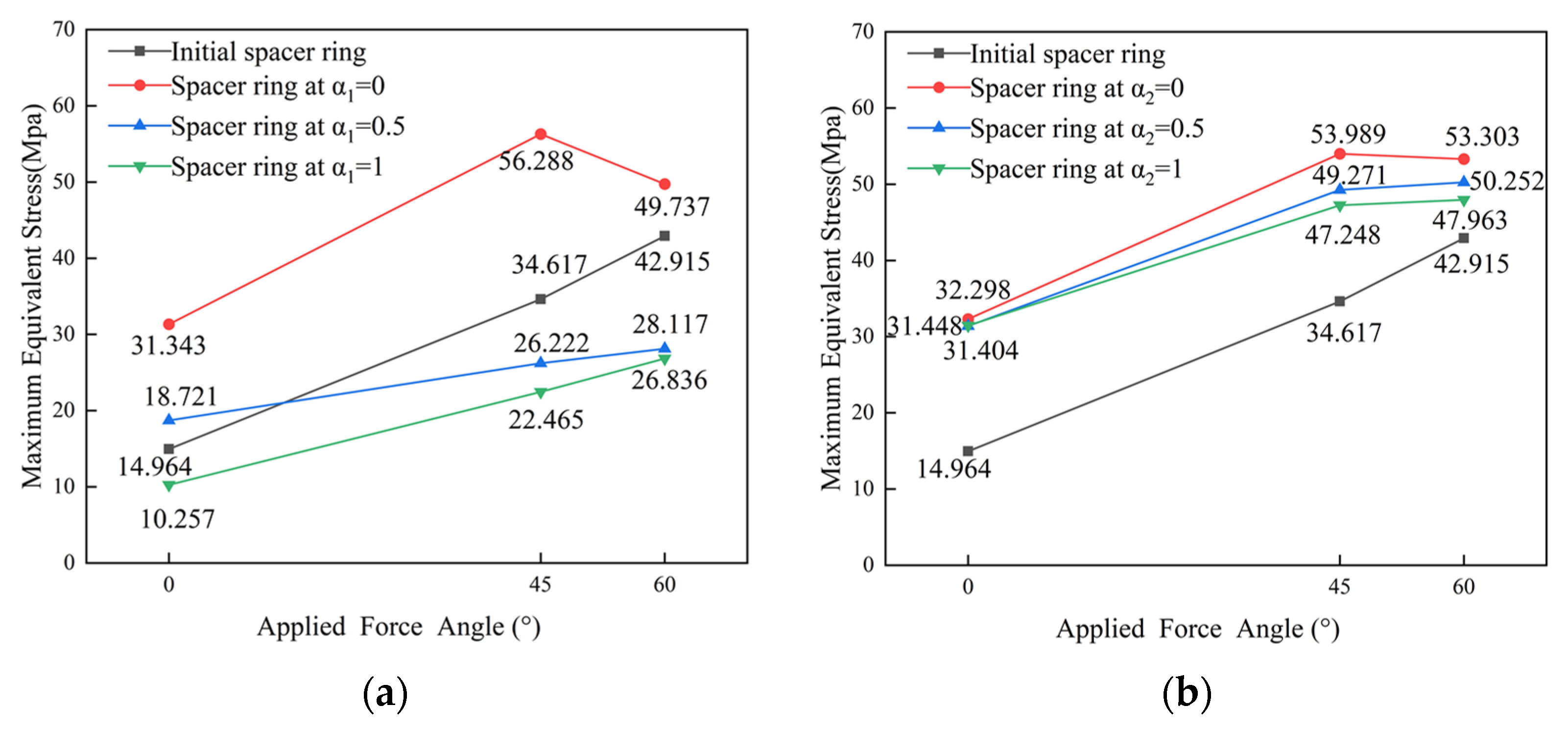
4.1.1. Deformation Characteristics and Stress Distribution of Spacer Ring at Different Applied Force Angles
4.1.2. Deformation Characteristics and Stress Distribution of the Spacer Ring in a Constant Direction
4.2. Spacer Ring Electrical Performance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tan, T.; Duan, C.; Liu, X.; Fan, D.; Ye, Z.; Xie, K.; Chai, Q.; Tian, Y.; Zhang, J. Research on Monitoring the Transmission Line Tension and Galloping Based on FBG Fitting Sensor. IEEE Trans. Instrum. Meas. 2022, 71, 1–8. [Google Scholar] [CrossRef]
- Lou, W.; Huang, C.; Huang, M.; Yu, J. An aerodynamic anti-galloping technique of iced 8-bundled conductors in ultra-high-voltage transmission lines. J. Wind Eng. Ind. Aerodyn. 2019, 193, 103972. [Google Scholar] [CrossRef]
- Si, J.; Rui, X.; Liu, B.; Zhou, L.; Liu, S. Study on a New Combined Anti-Galloping Device for UHV Overhead Transmission Lines. IEEE Trans. Power Deliv. 2019, 34, 2070–2078. [Google Scholar] [CrossRef]
- Xie, K.; Zhang, H.; Zhao, Y.; Tian, Y.; Lü, Z.; Wei, J.; Chai, Q.; Liu, Y.; Meng, Y.; Zhang, J.; et al. Structural Health Monitoring of Power Transmission System Based on Optical Fiber Sensor Under Transmission Line Galloping. Laser Optoelectron. Prog. 2018, 55, 070606. [Google Scholar] [CrossRef]
- Lou, W.; Huang, C.; Huang, M.; Liang, H.; Yu, J. Galloping Suppression of Iced Transmission Lines by Viscoelastic-Damping Interphase Spacers. J. Eng. Mech. 2020, 146, 04020135. [Google Scholar] [CrossRef]
- Sigmund, O.; Maute, K. Topology optimization approaches: A comparative review. Struct. Multidiscip. Optim. 2013, 48, 1031–1055. [Google Scholar] [CrossRef]
- Zargham, S.; Ward, T.A.; Ramli, R.; Badruddin, I.A. Topology optimization: A review for structural designs under vibration problems. Struct. Multidiscip. Optim. 2016, 53, 1157–1177. [Google Scholar] [CrossRef]
- Cai, J.; Huang, J.; Huang, L.; Li, Q.; Yin, L. Topology optimization of periodic structures under multiple dynamic uncertain loads. Adv. Eng. Softw. 2024, 198, 103777. [Google Scholar] [CrossRef]
- Hofmeyer, H.; Schevenels, M.; Boonstra, S. The generation of hierarchic structures via robust 3D topology optimisation. Adv. Eng. Inform. 2017, 33, 440–455. [Google Scholar] [CrossRef]
- Chen, A.; Cai, K.; Zhao, Z.-L.; Zhou, Y.; Xia, L.; Xie, Y.M. Controlling the maximum first principal stress in topology optimization. Struct. Multidiscip. Optim. 2021, 63, 327–339. [Google Scholar] [CrossRef]
- Vogel, A.; Junker, P. Adaptive thermodynamic topology optimization. Struct. Multidiscip. Optim. 2021, 63, 95–119. [Google Scholar] [CrossRef]
- Bokhari, A.H.; Mousavi, A.; Niu, B.; Wadbro, E. Topology optimization of an acoustic diode? Struct. Multidiscip. Optim. 2021, 63, 2739–2749. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, M.Y. Multimaterial structural topology optimization with a generalized Cahn–Hilliard model of multiphase transition. Struct. Multidiscip. Optim. 2006, 33, 89–111. [Google Scholar] [CrossRef]
- Tavakoli, R. Multimaterial topology optimization by Volume Constrained Allen–Cahn System and Regularized Projected Steepest Descent Method. Comput. Methods Appl. Mech. Eng. 2014, 276, 534–565. [Google Scholar] [CrossRef]
- Zhao, F. Topology optimization with meshless density variable approximations and BESO method. Comput. Aided Design. 2014, 56, 1–10. [Google Scholar] [CrossRef]
- Chu, S.; Xiao, M.; Gao, L.; Li, H.; Zhang, J.; Zhang, X. Topology optimization of multi-material structures with graded interfaces. Comput. Methods Appl. Mech. Eng. 2019, 346, 1096–1117. [Google Scholar] [CrossRef]
- Zhu, B.; Zhang, X.; Liu, M.; Chen, Q.; Li, H. Topological and Shape Optimization of Flexure Hinges for Designing Compliant Mechanisms Using the Level Set Method. Chin. J. Mech. Eng. 2019, 32, 13. [Google Scholar] [CrossRef]
- Xia, L.; Zhang, L.; Xia, Q.; Shi, T. Stress-based topology optimization using bi-directional evolutionary structural optimization method. Comput. Methods Appl. Mech. Eng. 2018, 333, 356–370. [Google Scholar] [CrossRef]
- Simonetti, H.L.; Almeida, V.S.; Neves, F.d.A.d. Smoothing evolutionary structural optimization for structures with displacement or natural frequency constraints. Eng. Struct. 2018, 163, 1–10. [Google Scholar] [CrossRef]
- Zhang, W.; Zhou, J.; Zhu, Y.; Guo, X. Structural complexity control in topology optimization via moving morphable component (MMC) approach. Struct. Multidiscip. Optim. 2017, 56, 535–552. [Google Scholar] [CrossRef]
- Zhao, F. A nodal variable ESO (BESO) method for structural topology optimization. Finite Elem. Anal. Des. 2014, 86, 34–40. [Google Scholar] [CrossRef]
- Xie, L.; Zhang, Y.; Ge, M.; Zhao, Y. Topology optimization of heat sink based on variable density method. Energy Rep. 2022, 8, 718–726. [Google Scholar] [CrossRef]
- Ma, W.; Lu, Y.; Wang, P.; Wang, Y.; Wang, J. Double Optimization Design of the Formula Racing Car Frame Based on the Variable Density Method and the Joint Variable Method. Appl. Sci. 2023, 13, 10155. [Google Scholar] [CrossRef]
- Liu, B.; Guo, D.; Jiang, C.; Li, G.; Huang, X. Stress optimization of smooth continuum structures based on the distortion strain energy density. Comput. Methods Appl. Mech. Eng. 2019, 343, 276–296. [Google Scholar] [CrossRef]
- Santos, d.; Batista, R.; Torii, A.J.; Novotny, A.A. Reliability-based topology optimization of structures under stress constraints. Int. J. Numer. Methods Eng. 2018, 114, 660–674. [Google Scholar] [CrossRef]
- Liu, J.; Luo, L.; Xiao, X.; Zhang, C.; Zhang, L.; Mi, C. Multi-Objectives topology optimization of frame in an electric mining dump truck based on fuzzy satisfaction variable weight coefficients method. J. Mech. Sci. Technol. 2022, 36, 3059–3069. [Google Scholar] [CrossRef]
- Zhao, Q.; Chen, X.; Wang, L.; Zhu, J.; Ma, Z.-D.; Lin, Y. Simulation and experimental validation of powertrain mounting bracket design obtained from multi-objective topology optimization. Adv. Mech. Eng. 2015, 7, 1–10. [Google Scholar] [CrossRef]
- Zhong, W.; Su, R.; Gui, L.; Fan, Z. Multi-objective topology and sizing optimization of bus body frame. Struct. Multidiscip. Optim. 2016, 54, 701–714. [Google Scholar] [CrossRef]
- Liu, C.-H.; Chung, F.-M.; Chen, Y.; Chiu, C.-H.; Chen, T.-L. Optimal Design of a Motor-Driven Three-Finger Soft Robotic Gripper. IEEEASME Trans. Mechatron. 2020, 25, 1830–1840. [Google Scholar] [CrossRef]
- Ferro, N.; Micheletti, S.; Perotto, S. POD-Assisted Strategies for Structural Topology Optimization. Comput. Math. Appl. 2019, 77, 2804–2820. [Google Scholar] [CrossRef]
- Du, Y.; Li, H.; Xie, H.; Tian, Q.; Zhou, X.; Luo, Z. Topology Optimization of Multiple Materials Compliant Mechanisms Based on Sequence Interpolation Model and Multigrid Method. J. Mech. Eng. 2018, 54, 47–56. [Google Scholar] [CrossRef]
- Wan, C.; Jiao, H.; Lv, L.; Lu, C. Multi-material topology optimization based on multiple simp of variable density method. J. Mech. Sci. Technol. 2024, 38, 749–759. [Google Scholar] [CrossRef]
- Lazarov, B.S.; Wang, F.; Sigmund, O. Length scale and manufacturability in density-based topology optimization. Arch. Appl. Mech. 2016, 86, 189–218. [Google Scholar] [CrossRef]
- Shu, J.; Fu, X. Optimal design of wind turbine’s base based on weight ratio. J. Mach. Des. 2024, 41, 128–135. [Google Scholar]
- Russ, J.B.; Waisman, H. Topology optimization for brittle fracture resistance. Comput. Methods Appl. Mech. Eng. 2019, 347, 238–263. [Google Scholar] [CrossRef]
- Park, J.J. Electrical Properties of Epoxy Composites with Micro-sized Fillers. Trans. Electr. Electron. Mater. 2018, 19, 475–480. [Google Scholar] [CrossRef]
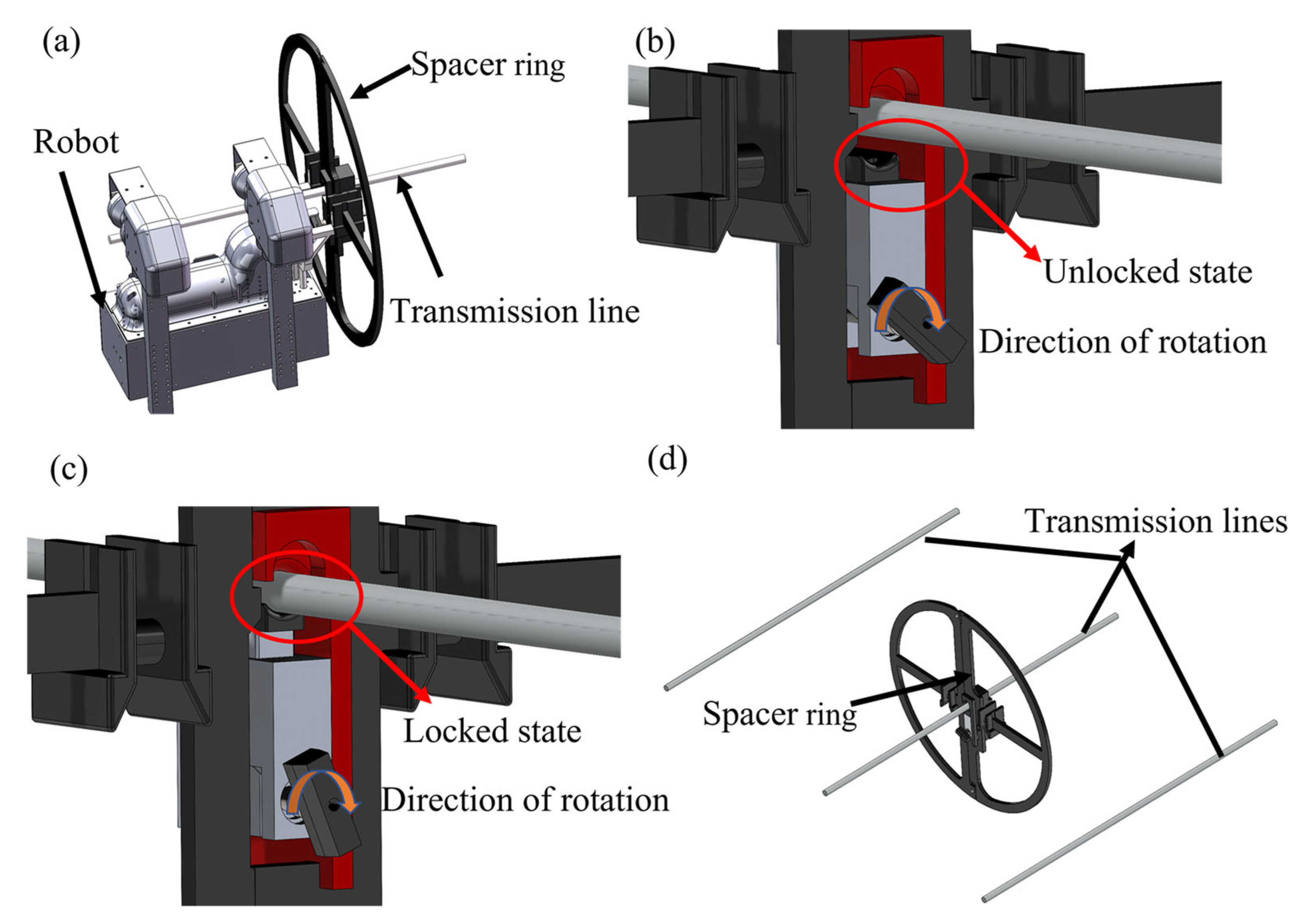
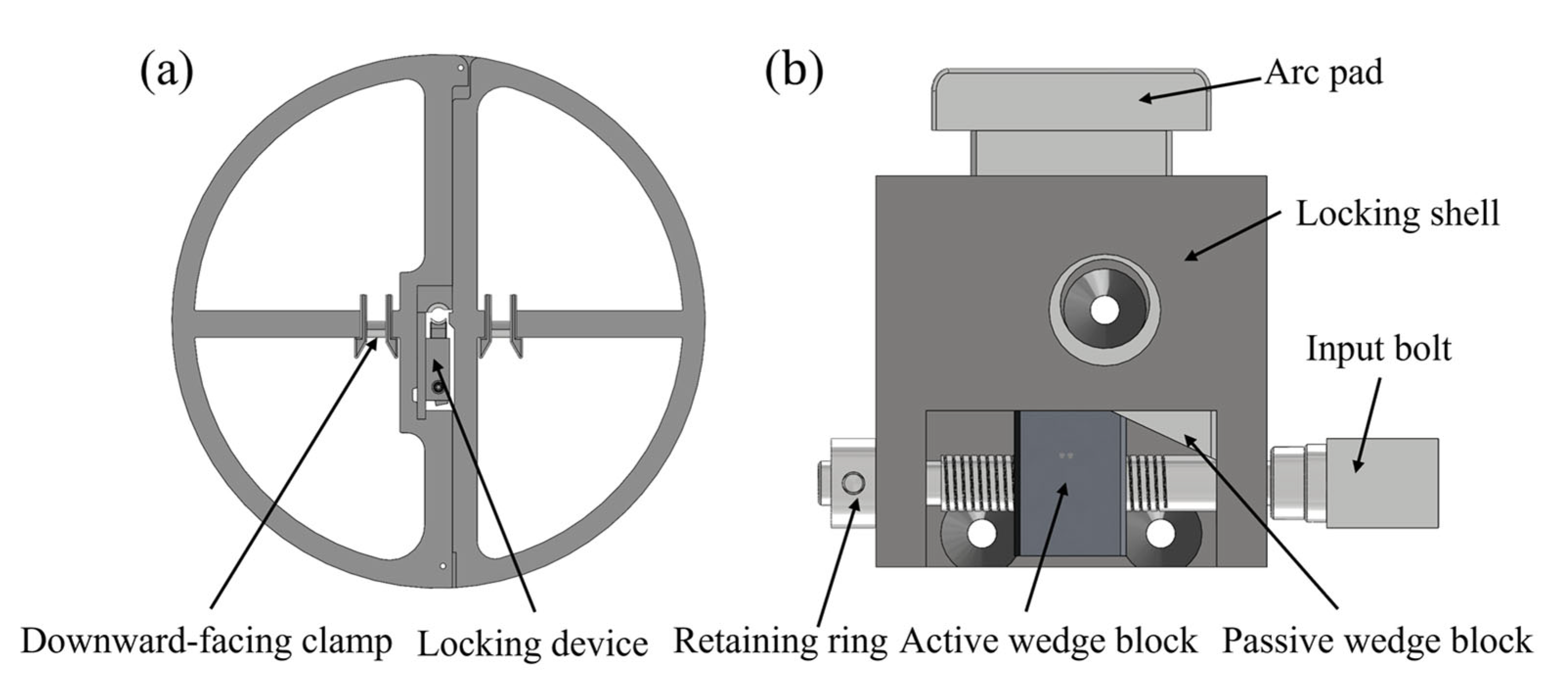





| Simulation Modeling of Spacer Ring | Materials | Modulus of Elasticity/MPa | Poisson’s Ratio |
|---|---|---|---|
| Spacer ring | Epoxy resin | 3780 | 0.35 |
| Spacer ring locking device | 7075 Aluminum alloy | 71,000 | 0.33 |
| Input bolt of locking device | 316 stainless steel | 193,000 | 0.28 |
| Transmission lines | 6061 Aluminum alloy | 69,040 | 0.33 |
| Density/(g/cm3) | Yield Strength/MPa | Relative Permittivity | Conductivity/(S/m) |
| 1.16 | 54.6 | 3.8 | / |
| 2.81 | 455 | / | 2.2 × 107 |
| 8.03 | 205 | / | 1.35 × 106 |
| 2.713 | 259.2 | / | 2.5 × 107 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Cheng, T.; Lian, H. Optimal Design of Anti-Collision Spacer Ring for Power Transmission Lines. Appl. Sci. 2025, 15, 12496. https://doi.org/10.3390/app152312496
Wang T, Cheng T, Lian H. Optimal Design of Anti-Collision Spacer Ring for Power Transmission Lines. Applied Sciences. 2025; 15(23):12496. https://doi.org/10.3390/app152312496
Chicago/Turabian StyleWang, Tianlei, Tianhui Cheng, and Huize Lian. 2025. "Optimal Design of Anti-Collision Spacer Ring for Power Transmission Lines" Applied Sciences 15, no. 23: 12496. https://doi.org/10.3390/app152312496
APA StyleWang, T., Cheng, T., & Lian, H. (2025). Optimal Design of Anti-Collision Spacer Ring for Power Transmission Lines. Applied Sciences, 15(23), 12496. https://doi.org/10.3390/app152312496






