Common Calibration of Solar Radiation and Net Longwave Radiation Is the Key to Accurately Estimating Reference Crop Evapotranspiration over the Tibetan Plateau
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of the Study Region
2.2. Data Collection
2.2.1. Data on Basic Meteorological Variables
2.2.2. Data on Radiation-Related Variables
2.2.3. Datasets Used for This Study
2.3. Description of FAO56-PM
2.4. Calculation Methods
2.4.1. AllenM Method
2.4.2. AllenO Method
2.4.3. AllenS Method
2.4.4. AllenL Method
2.4.5. AllenC Method
2.4.6. AllenR Method
2.5. Model Evaluation
3. Results
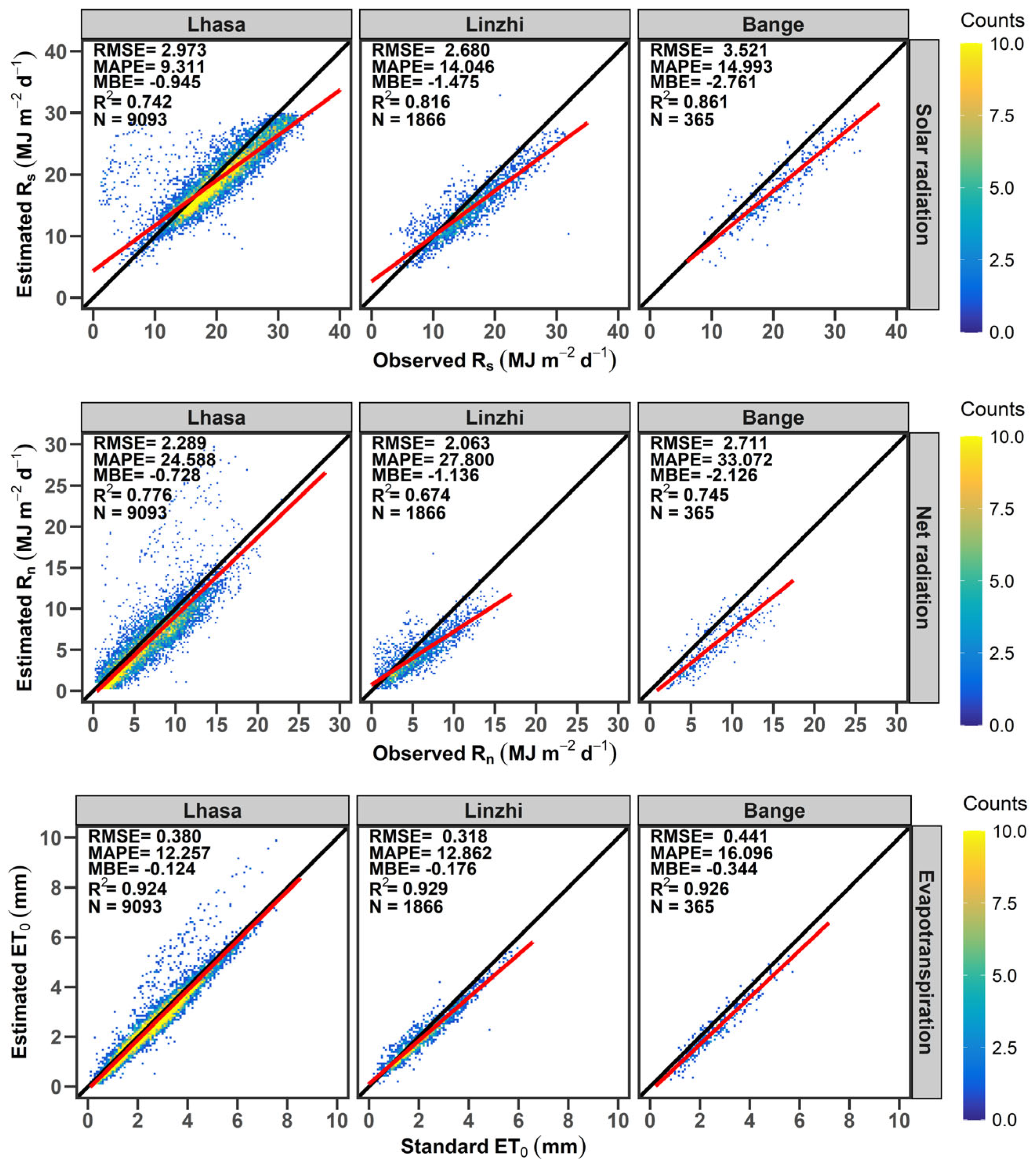
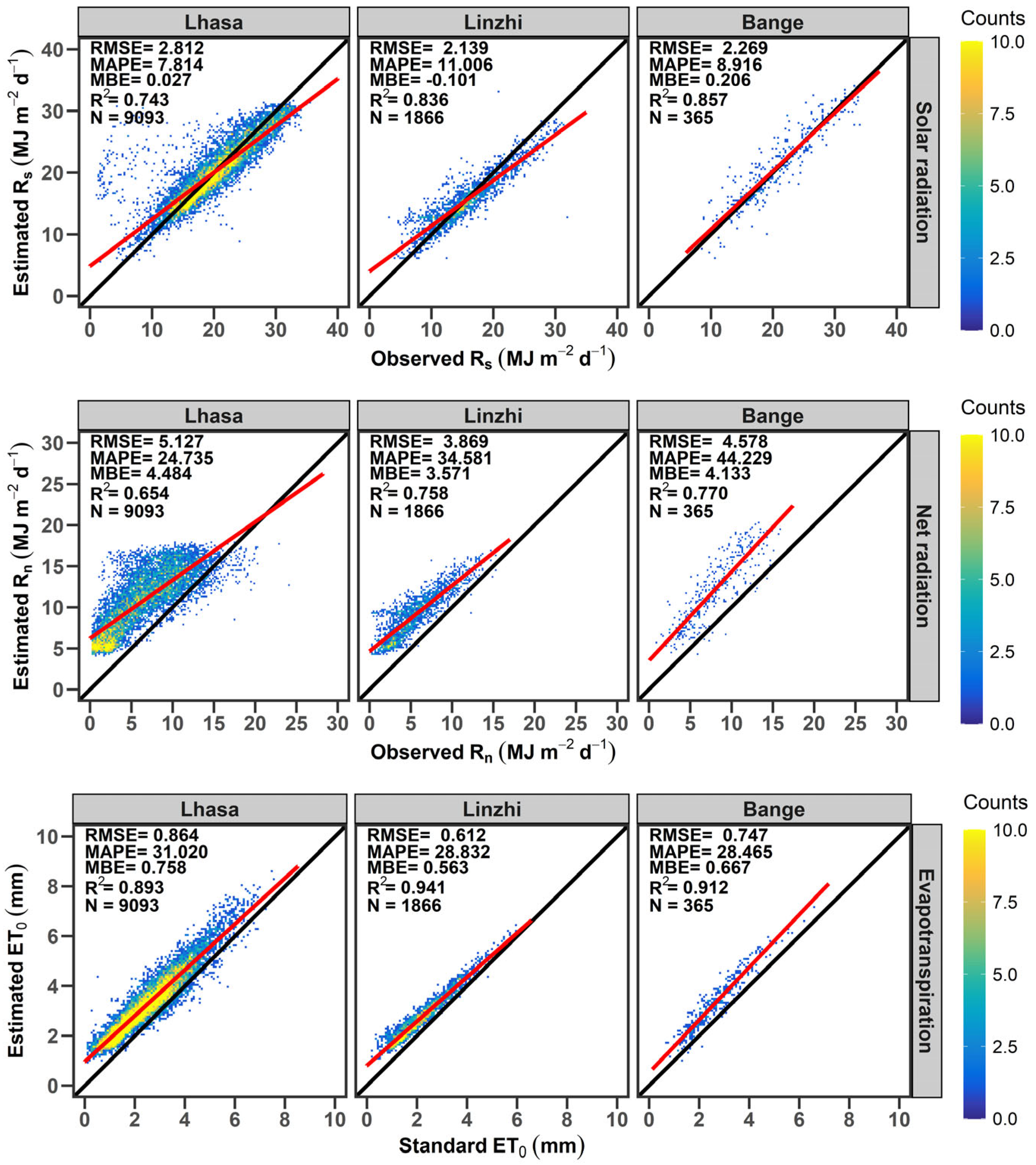
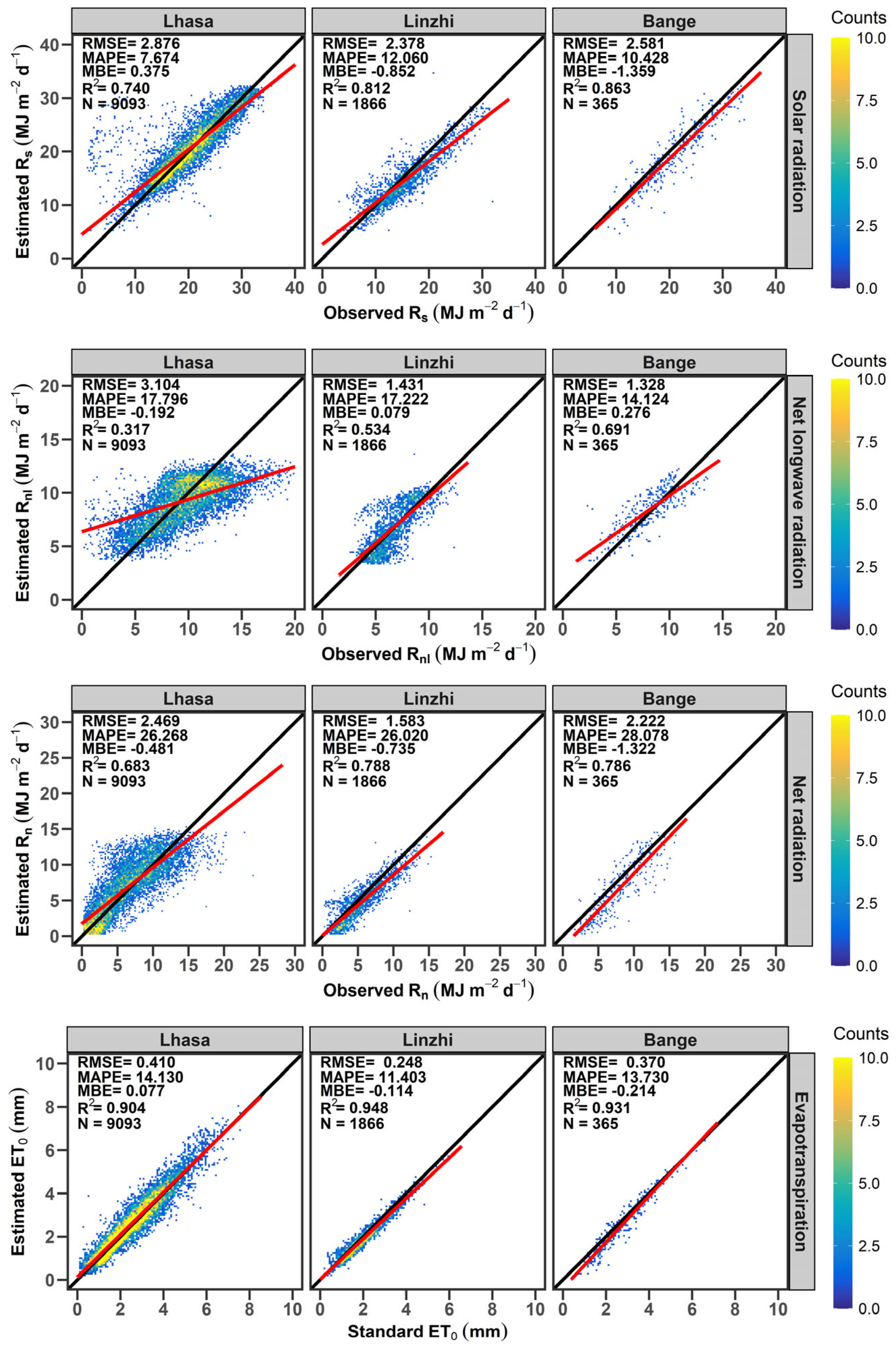
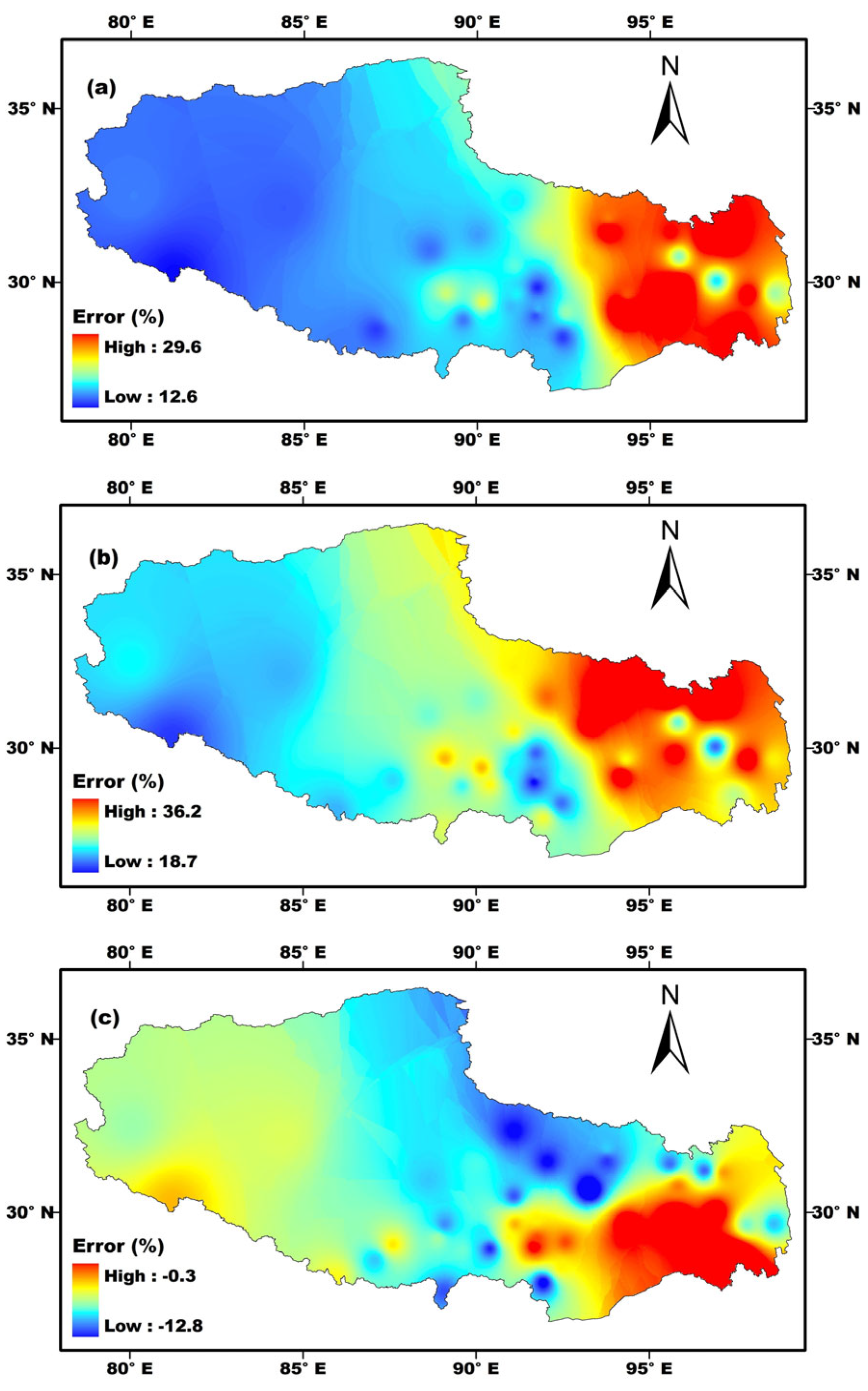
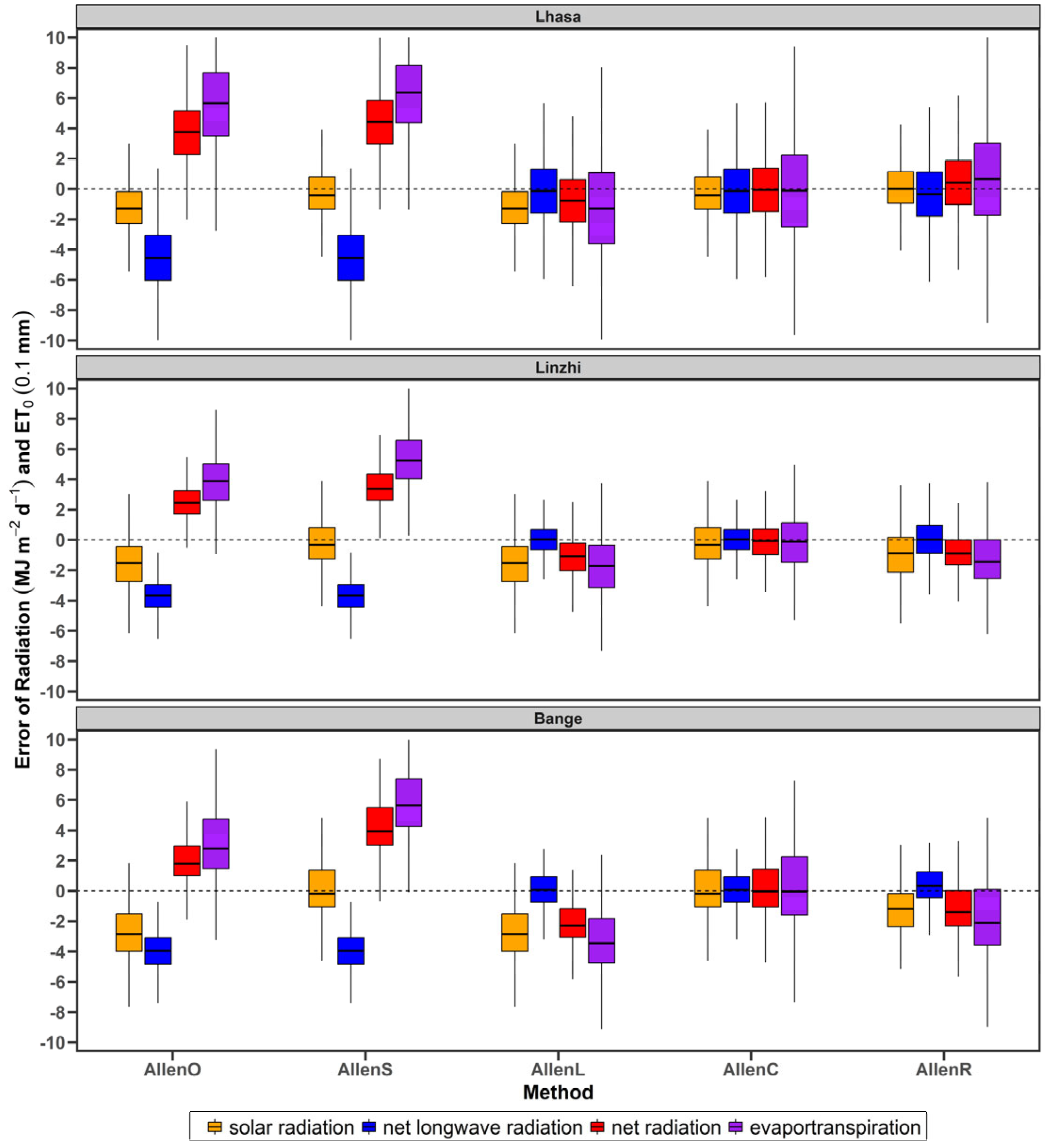
3.1. Errors in Estimated ET0 Resulting from Recommended Fs and Fnl
3.1.1. Errors in Estimated ET0 Resulting from Recommended Fs
3.1.2. Errors in Estimated ET0 Resulting from Recommended Fnl
3.1.3. Errors in Estimated ET0 Resulting from Both Recommended Fs and Fnl
3.2. Calibration of FAO56-PM
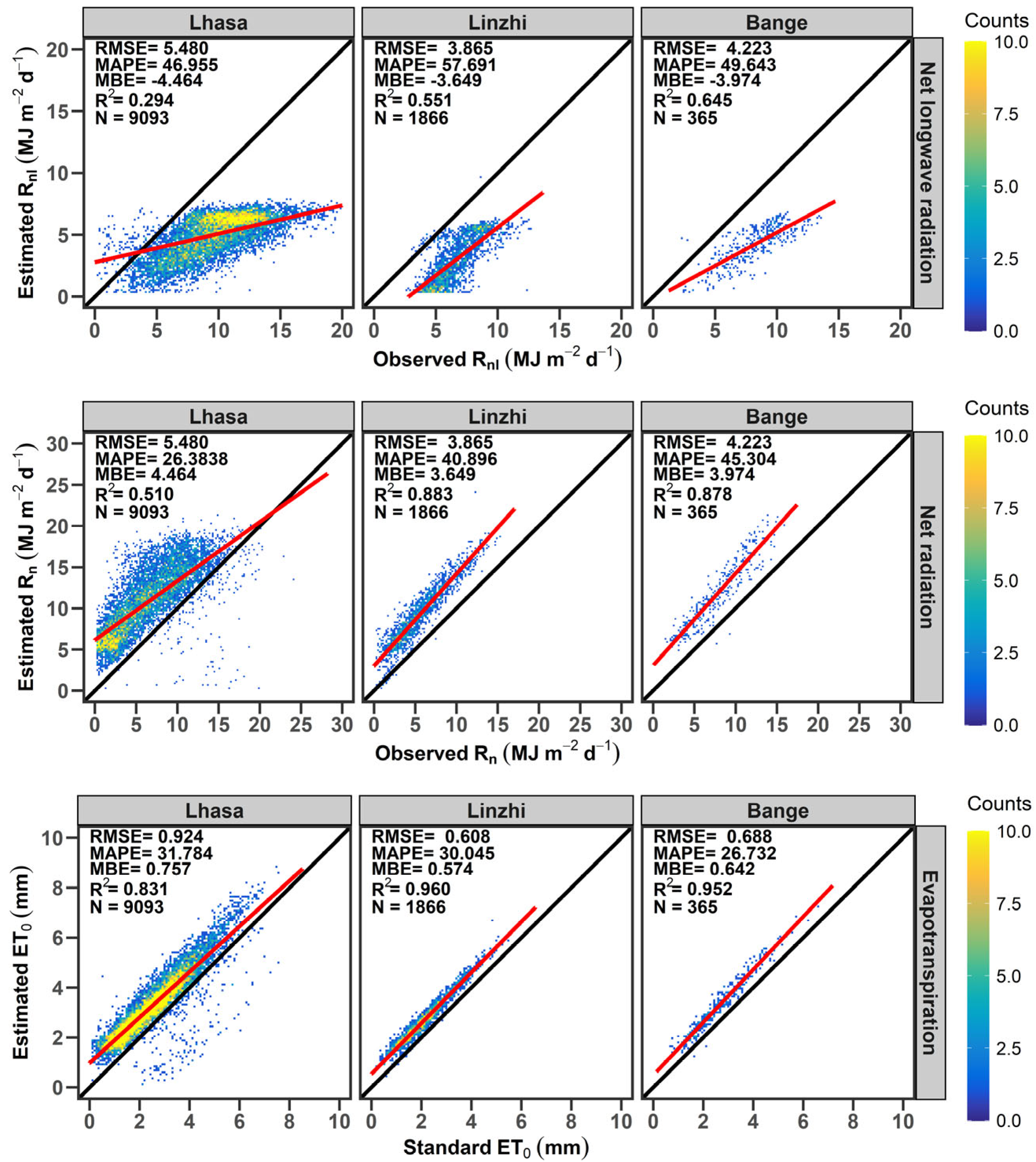
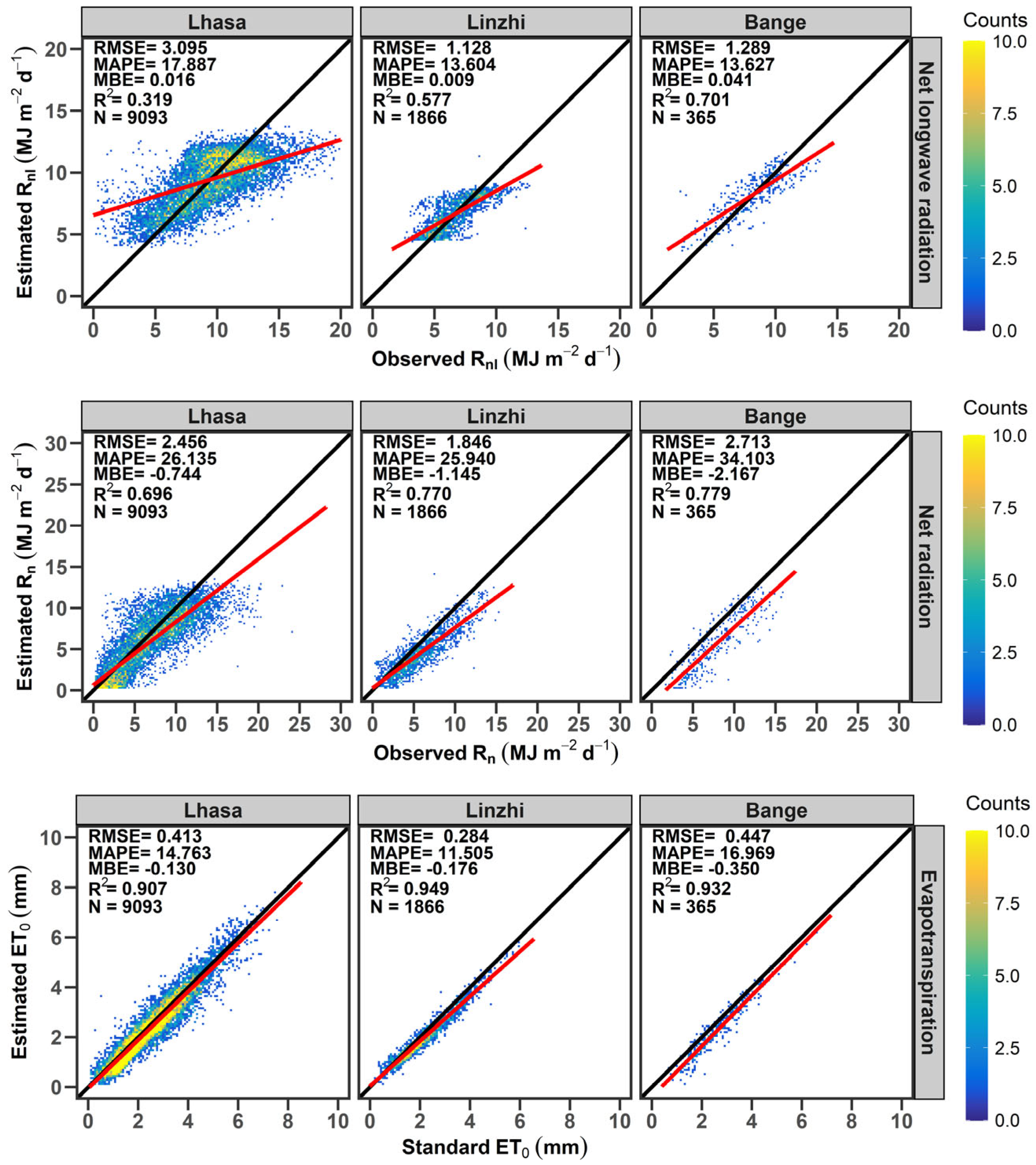
3.2.1. Mere Calibration of the Recommended Fs
3.2.2. Mere Calibration of the Recommended Fnl
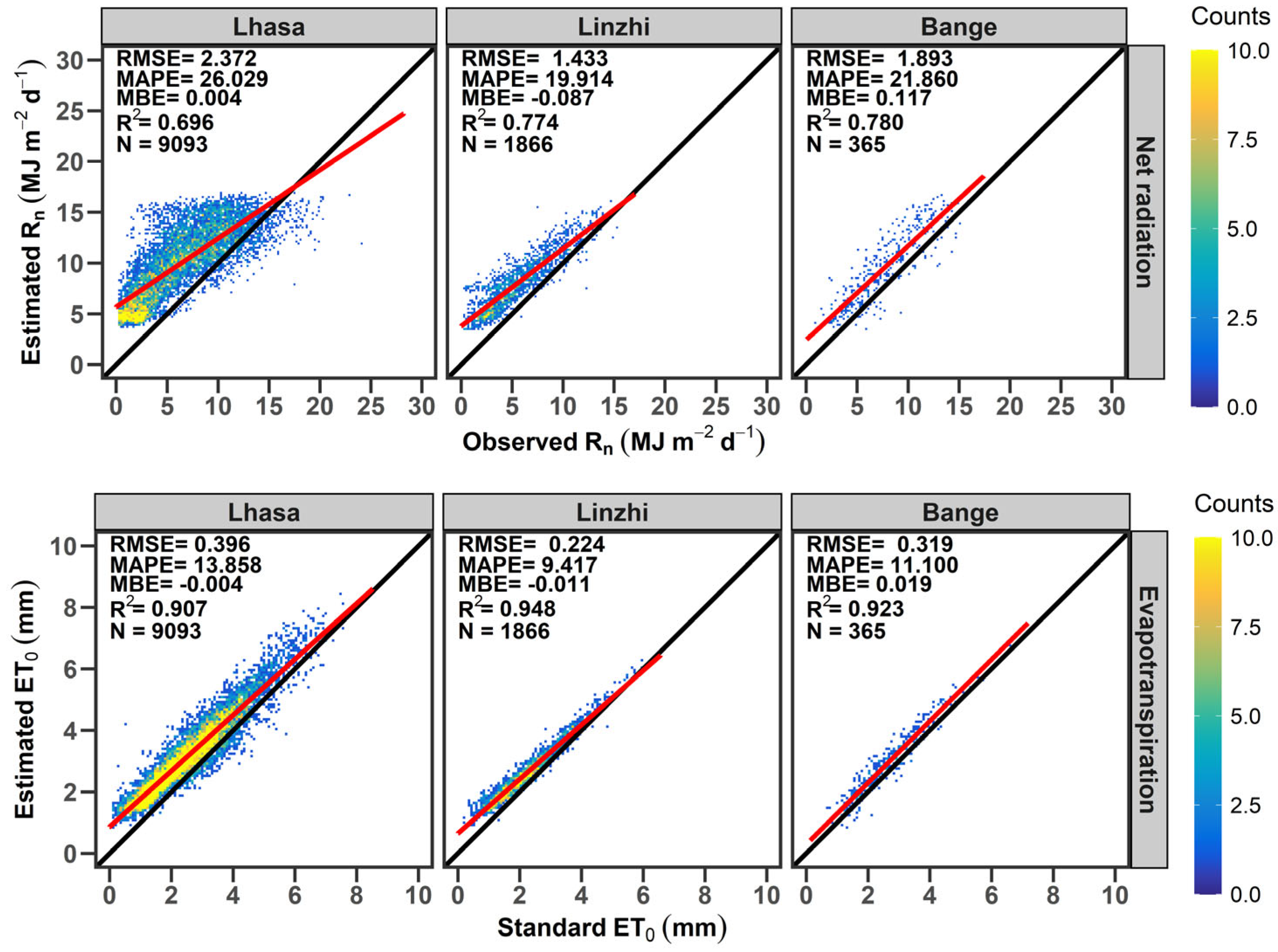
3.2.3. Comprehensive Calibration of Both Fs and Fnl
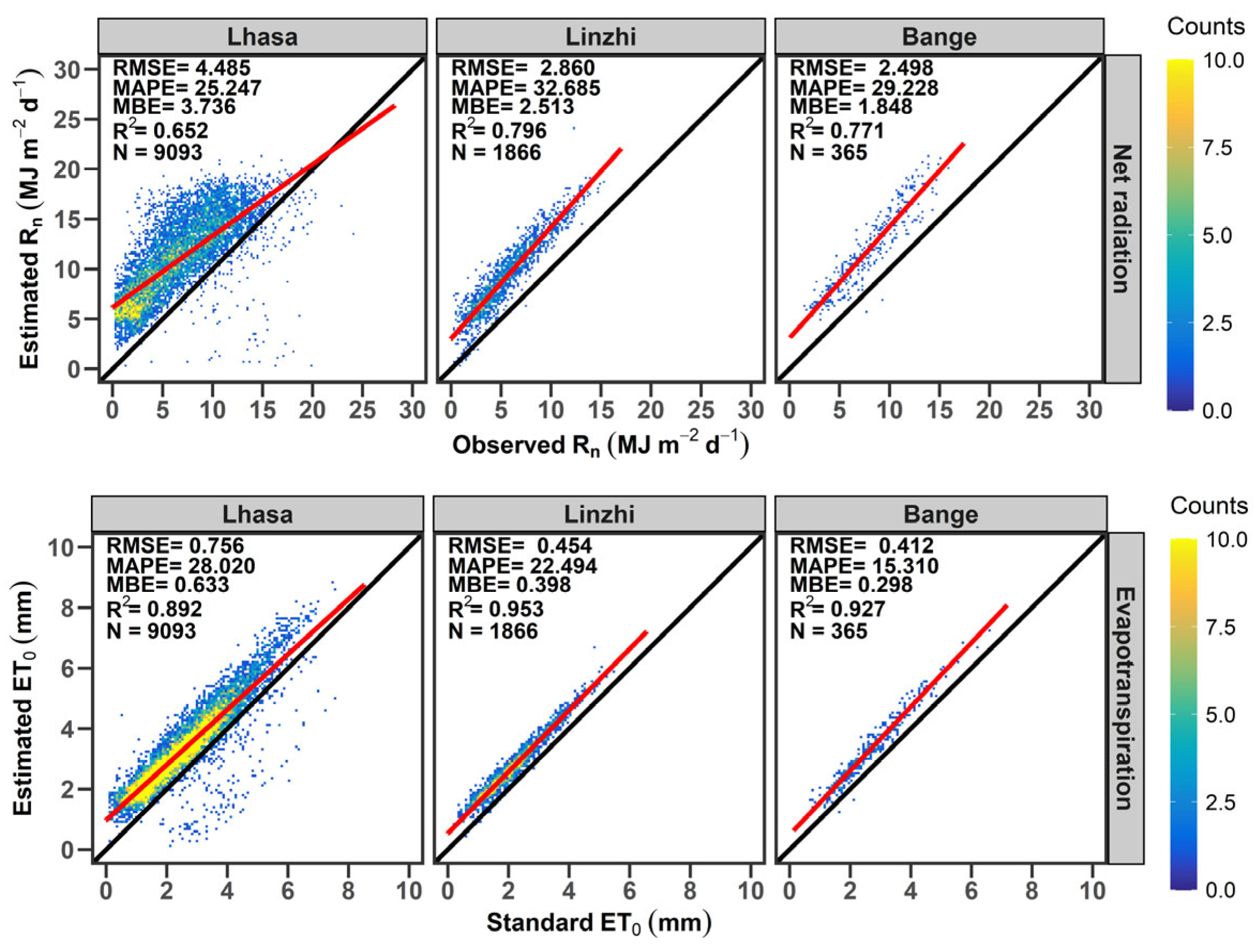
3.3. General Method Developed for Regional Application of FAO56-PM over the TP
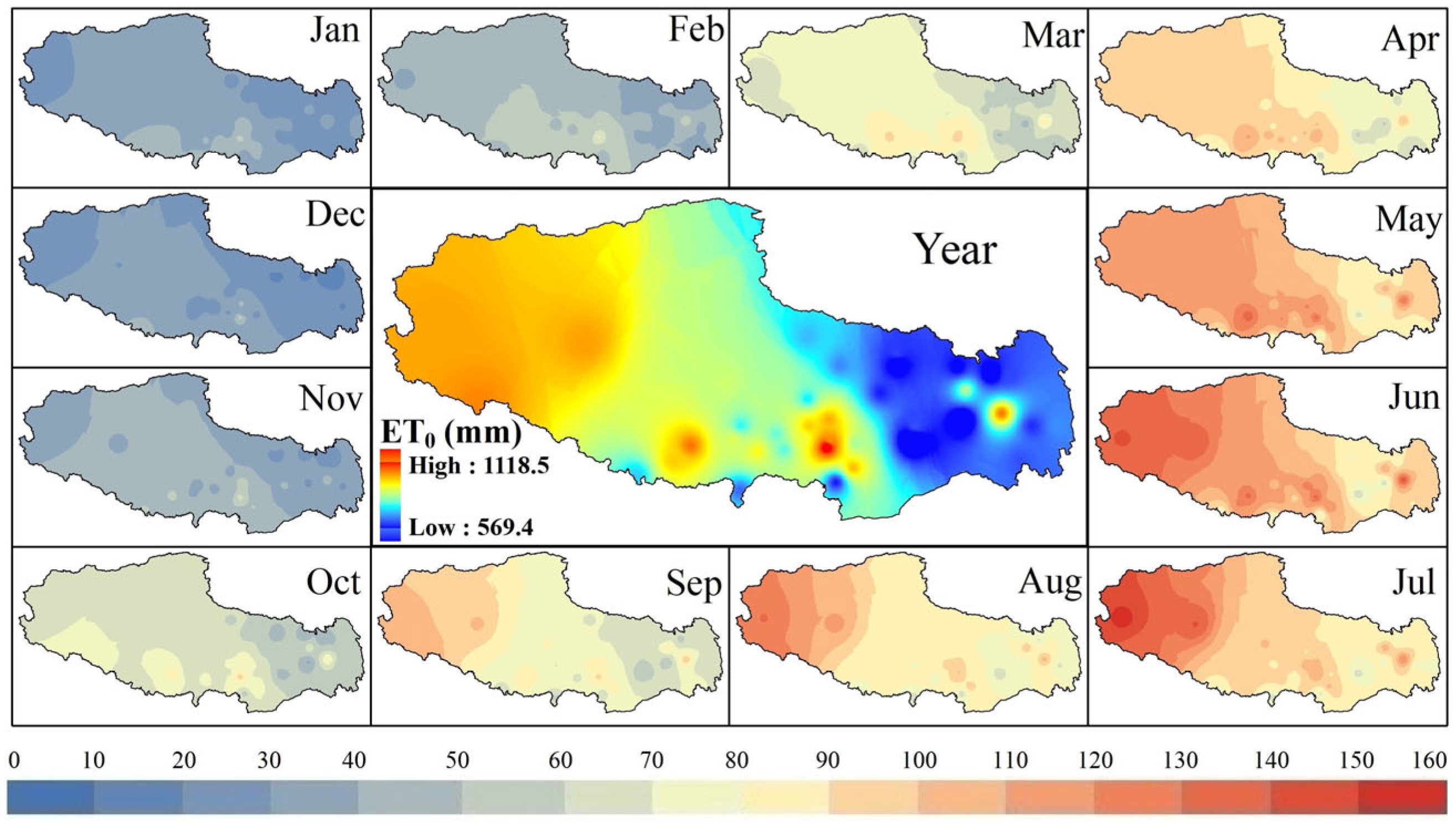
3.4. Spatial Distribution of ET0 over the TP
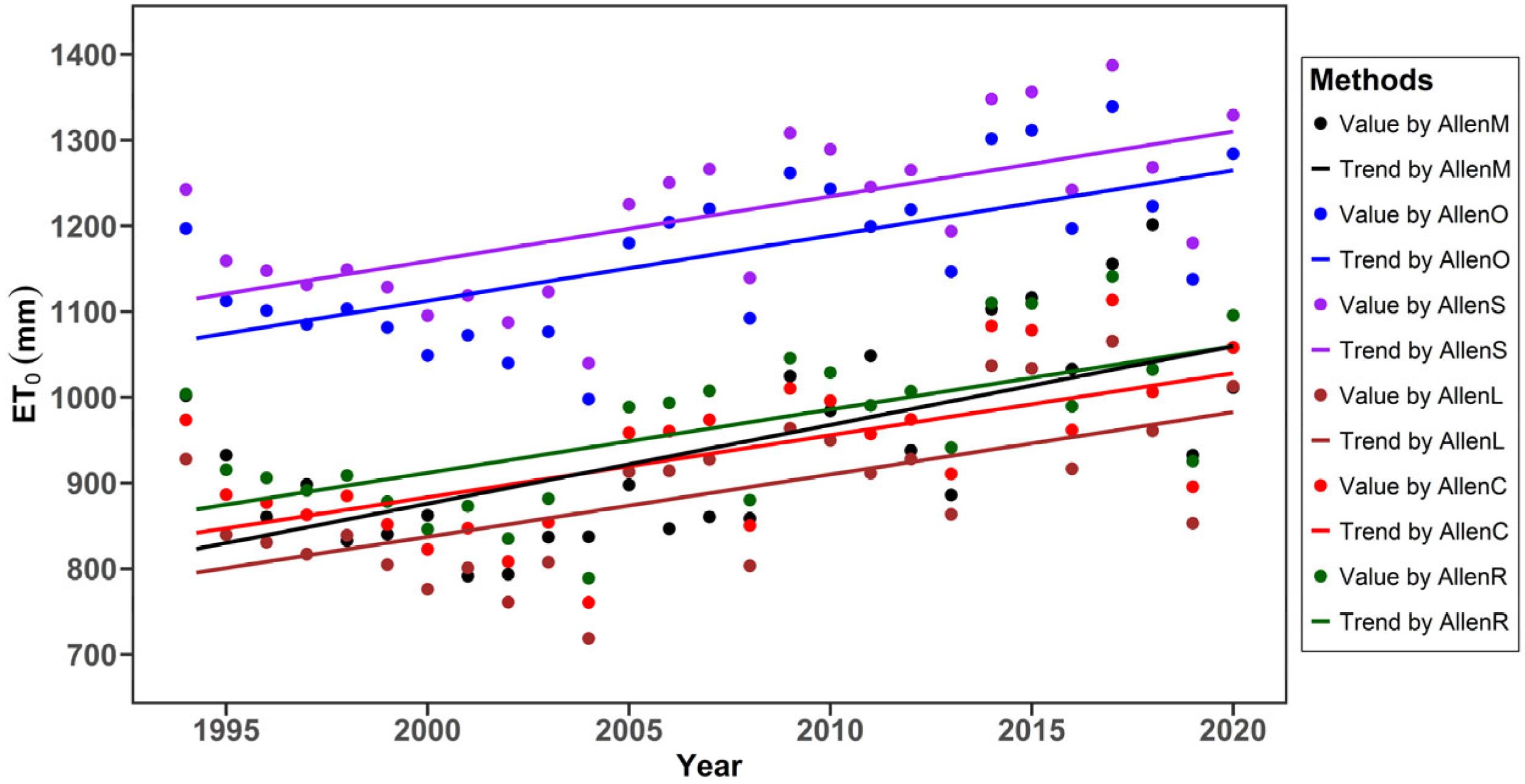
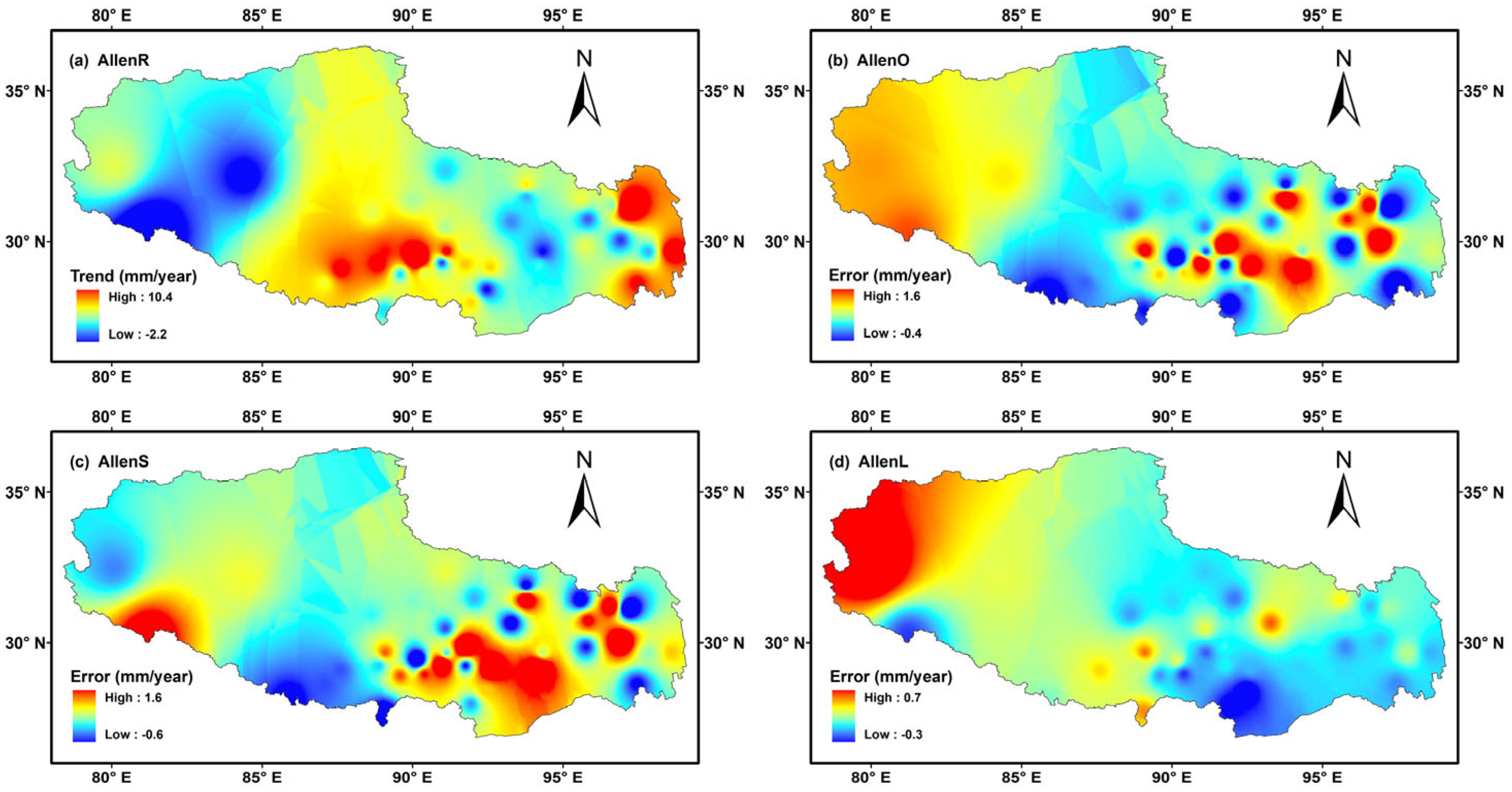
3.5. Trend Analysis of ET0 over the TP
4. Discussion
4.1. High Rs and Rnl over the TP
4.2. Offsetting Effects Between Errors in Estimated Rs and Rnl
4.3. Spatial Distribution and Temporal Trend of ET0 over the TP
4.4. Uncertainties and Future Studies
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mondal, S.; Mishra, A. Quantifying the precipitation, evapotranspiration, and soil moisture network’s interaction over global land surface hydrological cycle. Water Resour. Res. 2024, 60, e2023WR034861. [Google Scholar] [CrossRef]
- Hu, S.; Gao, R.; Zhang, T.; Bai, P.; Zhang, R. Spatio-temporal variation of reference evapotranspiration and its climatic drivers over the Tibetan Plateau during 1970–2018. Appl. Sci. 2021, 11, 8013. [Google Scholar] [CrossRef]
- Zhao, F.; Ma, S.; Wu, Y.; Qiu, L.; Wang, W.; Lian, Y.; Chen, J.; Sivakumar, B. The role of climate change and vegetation greening on evapotranspiration variation in the Yellow River Basen, China. Agric. For. Meteorol. 2022, 316, 108842. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Revisiting the global hydrological cycle: Is it intensifying? Hydrol. Earth Syst. Sci. 2020, 24, 3899–3932. [Google Scholar] [CrossRef]
- Labat, D. Oscillations in land surface hydrological cycle. Earth Planet. Sci. Lett. 2006, 242, 143–154. [Google Scholar] [CrossRef]
- Rast, M.; Johannessen, J.; Mauser, W. Review of understanding of Earth’s hydrological cycle: Observations, theory and modelling. Surv. Geophys. 2014, 35, 491–513. [Google Scholar] [CrossRef]
- Bouman, B.A.M.; Van Keulen, H.; Van Laar, H.H.; Rabbinge, R. The ‘School of de Wit’crop growth simulation models: A pedigree and historical overview. Agric. Syst. 1996, 52, 171–198. [Google Scholar] [CrossRef]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.A.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT cropping system model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- Keating, B.A.; Carberry, P.S.; Hammer, G.L.; Probert, M.E.; Robertson, M.J.; Holzworth, D.; Huth, N.I.; Hargreaves, J.N.G.; Meinke, H.; Hochman, G. An overview of APSIM, a model designed for farming systems simulation. Eur. J. Agron. 2003, 18, 267–288. [Google Scholar] [CrossRef]
- Bogawski, P.; Bednorz, E. Comparison and validation of selected evapotranspiration models for conditions in Poland (Central Europe). Water Resour. Manag. 2014, 28, 5021–5038. [Google Scholar] [CrossRef]
- Chen, A.; Orlov-Levin, V.; Meron, M. Applying high-resolution visible-channel aerial imaging of crop canopy to precision irrigation management. Agric. Water Manag. 2019, 216, 196–205. [Google Scholar] [CrossRef]
- Gao, H.; Liu, J.; Wang, H.; Mei, C.; Wang, J. Estimation of irrigated crop artificial irrigation evapotranspiration in China. Sci. Rep. 2024, 14, 16142. [Google Scholar] [CrossRef]
- Tang, P.; Xu, B.; Tian, D.; Ren, J.; Li, Z. Temporal and spatial variations of meteorological elements and reference crop evapotranspiration in Alpine regions of Tibet, China. Environ. Sci. Pollut. Res. 2021, 28, 36076–36091. [Google Scholar] [CrossRef]
- Liu, X.; Xu, C.; Zhong, X.; Li, Y.; Yuan, X.; Cao, J. Comparison of 16 models for reference crop evapotranspiration against weighing lysimeter measurement. Agric. Water Manag. 2017, 184, 145–155. [Google Scholar] [CrossRef]
- Zhao, W.L.; Qiu, G.Y.; Xiong, Y.J.; Paw U, K.T.; Gentine, P.; Chen, B.Y. Uncertainties caused by resistances in evapotranspiration estimation using high-density eddy covariance measurements. J. Hydrometeorol. 2020, 21, 1349–1365. [Google Scholar] [CrossRef]
- Azhar, A.H.; Perera, B.J.C. Evaluation of reference evapotranspiration estimation methods under Southeast Australian conditions. J. Irrig. Drain. Eng. 2011, 137, 268–279. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements–FAO Irrigation and Drainage Paper 56; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998. [Google Scholar]
- Anda, A.; Soos, G.; da Silva, J.A.T.; Kozma-Bognar, V. Regional evapotranspiration from a wetland in Central Europe, in a 16-year period without human intervention. Agric. For. Meteorol. 2015, 205, 60–72. [Google Scholar] [CrossRef]
- Doorenbos, J.; Pruitt, W.O. Guidelines for Predicting Crop Water Requirements. FAO Irrigation and Drainage Paper 24; Food and Agriculture Organization of the United Nations: Rome, Italy, 1977. [Google Scholar]
- Xue, Y.; Zhang, Z.; Li, X.; Liang, H.; Yin, L. A review of evapotranspiration estimation models: Advances and future development. Water Resour. Manag. 2025, 39, 3641–3657. [Google Scholar] [CrossRef]
- Tabari, H.; Grismer, M.E.; Trajkovic, S. Comparative analysis of 31 reference evapotranspiration methods under humid conditions. Irrig. Sci. 2013, 31, 107–117. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and environment. In Symposia of the Society for Experimental Biology; Cambridge University Press (CUP): Cambridge, UK, 1965. [Google Scholar]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. 1948, 193, 120–145. [Google Scholar]
- Jensen, M.E.; Haise, H.R. Estimating evapotranspiration from solar radiation. J. Irrig. Drain. Div. 1963, 89, 15–41. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Turc, L. Evaluation des besoins en eau irrigation, l’evapotranspiration potentielle. Ann. Agron. 1961, 12, 13–49. [Google Scholar]
- Hargreaves, G.L.; Hargreaves, G.H.; Riley, J.P. Irrigation water requirements for Senegal River basin. J. Irrig. Drain. Eng. 1985, 111, 265–275. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Xu, C.Y.; Singh, V.P. Cross comparison of empirical equations for calculating potential evapotranspiration with data from Switzerland. Water Resour. Manag. 2002, 16, 197–219. [Google Scholar] [CrossRef]
- Dalton, J. Experimental essays on the constitution of mixed gases. Manch. Lit. Philos. Soc. Memo 1802, 5, 535–602. [Google Scholar]
- Mahringer, W. Verdunstungsstudien am neusiedler See. Arch. Für Meteorol. Geophys. Und Bioklimatol. Ser. B 1970, 18, 1–20. [Google Scholar] [CrossRef]
- Singh, V.P.; Xu, C.Y. Evaluation and generalization of 13 masstransfer equations for determining free water evaporation. Hydrol. Process. 1997, 11, 311–323. [Google Scholar] [CrossRef]
- Chen, D.; Gao, G.; Xu, C.; Guo, J.; Ren, G. Comparison of the Thornthwaite method and pan data with the standard Penman–Monteith estimates of reference evapotranspiration in China. Clim. Res. 2005, 28, 123–132. [Google Scholar] [CrossRef]
- Liu, X.; Lin, E. Performance of the Priestley-Taylor equation in the semiarid climate of North China. Agric. Water Manag. 2005, 71, 1–17. [Google Scholar]
- Milly, P.C.D.; Dunne, K.A. Potential evapotranspiration and continental drying. Nat. Clim. Change 2016, 6, 946. [Google Scholar] [CrossRef]
- Sentelhas, P.C.; Gillespie, T.J.; Santos, E.A. Evaluation of FAO Penman–Monteith and alternative methods for estimating reference evapotranspiration with missing data in Southern Ontario, Canada. Agric. Water Manag. 2010, 97, 635–644. [Google Scholar] [CrossRef]
- Trajkovic, S.; Kolakovic, S. Evaluation of reference evapotranspiration equations under humid conditions. Water Resour. Manag. 2009, 23, 3057–3067. [Google Scholar] [CrossRef]
- Chen, S.; Liu, Y.; Thomas, A. Climatic change on the Tibetan Plateau: Potential evapotranspiration trends from 1961-2000. Clim. Change 2006, 76, 291–319. [Google Scholar]
- Liu, X.; Mei, X.; Li, Y.; Wang, Q.; Zhang, Y.; Porter, J.R. Variation in reference crop evapotranspiration caused by the Angstrom-Prescott coefficient: Locally calibrated versus the FAO recommended. Agric. Water Manag. 2009, 96, 1137–1145. [Google Scholar] [CrossRef]
- Yin, Y.; Wu, S.; Zheng, D.; Yang, Q. Radiation calibration of FAO56 Penman-Monteith model to estimate reference crop evapotranspiration in China. Agric. Water Manag. 2008, 95, 77–84. [Google Scholar] [CrossRef]
- Chen, S.; He, C.; Huang, Z.; Xu, X.; Jiang, T.; He, Z.; Liu, J.; Su, B.; Fenf, H.; Yu, Q.; et al. Using support vector machine to deal with the missing of solar radiation data in daily reference evapotranspiration estimation in China. Agric. For. Meteorol. 2022, 316, 108864. [Google Scholar] [CrossRef]
- Cunha, A.C.; Gabriel Filho, L.R.A.; Tanaka, A.A.; Goes, B.C.; Putti, F.F. Influence of the estimated global solar radiation on the reference evapotranspiration obtained through the penman-monteith fao 56 method. Agric. Water Manag. 2021, 243, 106491. [Google Scholar] [CrossRef]
- Paredes, P.; Pereira, L.S. Computing FAO56 reference grass evapotranspiration PM-ET0 from temperature with focus on solar radiation. Agric. Water Manag. 2019, 215, 86–102. [Google Scholar] [CrossRef]
- Sabziparvar, A.A.; Mousavi, R.; Marof, S.; Ebrahimipak, N.A.; Heidari, M. An improved estimation of the Angstrom-Prescott radiation coefficients for the FAO56 Penman-Monteith evapotranspiration method. Water Resour. Manag. 2013, 27, 2839–2854. [Google Scholar] [CrossRef]
- Duarte, H.F.; Dias, N.L.; Maggiotto, S.R. Assessing daytime downward longwave radiation estimates for clear and cloudy skies in Southern Brazil. Agric. For. Meteorol. 2006, 139, 171–181. [Google Scholar] [CrossRef]
- Kjaersgaard, J.H.; Plauborg, F.L.; Hansen, S. Comparison of models for calculating daytime long-wave irradiance using long term data set. Agric. For. Meteorol. 2007, 143, 49–63. [Google Scholar] [CrossRef]
- Matsui, H.; Osawa, K. Calibration effects of the net longwave radiation equation in Penman-type methods at Tateno, Japan. Hydrol. Res. Lett. 2015, 9, 113–117. [Google Scholar] [CrossRef]
- Zhu, X.; Qiu, X.; Zeng, Y.; Ren, W.; Tao, B.; Gao, J.; Liu, H.; Tan, Y. Effects of complex terrain on net surface longwave radiation in China. Theor. Appl. Climatol. 2018, 134, 251–264. [Google Scholar] [CrossRef]
- Liu, Z.F.; Yao, Z.J.; Yu, C.Q.; Zhong, Z.M. Assessing crop water demand and deficit for the growth of spring highland barley in Tibet, China. J. Integr. Agric. 2013, 12, 541–551. [Google Scholar] [CrossRef]
- Li, J.; Lu, C.; Chen, J.; Zhou, X.; Yang, K.; Li, J.; Wu, X.; Wu, S.; Hu, R.; Zhou, Z.; et al. The influence of complex terrain on cloud and precipitation on the foot and slope of the southeastern Tibetan Plateau. Clim. Dyn. 2024, 62, 3143–3163. [Google Scholar] [CrossRef]
- Liu, J.; Pan, T.; Chen, D.; Zhou, X.; Yu, Q.; Flerchinger, G.N.; Shen, Y. An improved Ångström-type model for estimating solar radiation over the Tibetan Plateau. Energies 2017, 10, 892. [Google Scholar] [CrossRef]
- Hans, V.S.; Francos, W.Z. Statistical Analysis in Climate Research; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Pan, X.; Guo, X.; Li, X.; Niu, X.; Yang, X.; Feng, M.; Che, T.; Jin, R.; Ran, Y.; Guo, J.; et al. National Tibetan Plateau Data Center: Promoting earth system science on the third pole. Bull. Am. Meteorol. Soc. 2021, 102, E2062–E2078. [Google Scholar] [CrossRef]
- Qian, X.; Yao, Y.; Wang, H.; Zou, L.; Li, Y. Statistics and analysis of high-altitude wind above the western Tibetan Plateau. Mon. Not. R. Astron. Soc. 2020, 498, 5786–5797. [Google Scholar] [CrossRef]
- Yao, T.; Thompson, L.; Chen, D.; Piao, S. Reflections and future strategies for third pole environment. Nat. Rev. Earth Environ. 2022, 3, 608–610. [Google Scholar] [CrossRef]
- Deng, M.; Meng, X.; Sheng, D.; Niu, H.; Wu, P.; Li, Z.; Chen, H.; Shang, L.; Wang, S.; Lyu, S. Observed surface heat fluxes partitioning during the local growing season over the Tibetan Plateau. Agric. For. Meteorol. 2024, 356, 110186. [Google Scholar] [CrossRef]
- Duan, A.; Wang, M.; Lei, Y.; Cui, Y. Trends in summer rainfall over China associated with the Tibetan Plateau sensible heat source during 1980-2008. J. Clim. 2013, 26, 261–275. [Google Scholar] [CrossRef]
- Yao, J.; Gu, L.; Yang, C.; Chen, H.; Wang, J.; Ding, Y.; Li, R.; Zhao, L.; Xiao, Y.; Qiao, Y.; et al. Estimation of surface energy fluxes in the permafrost region of the Tibetan Plateau based on in situ measurements and the surface energy balance system model. Int. J. Climatol. 2020, 40, 5783–5800. [Google Scholar] [CrossRef]
- Li, H.; Ma, W.; Lian, Y.; Wang, X.; Zhao, L. Global solar radiation estimation with sunshine duration in Tibet, China. Renew. Energy 2011, 36, 3141–3145. [Google Scholar] [CrossRef]
- Liu, J.; Liu, J.; Linderholm, H.W.; Chen, D.; Yu, Q.; Wu, D.; Haginoya, S. Observation and calculation of the solar radiation on the Tibetan Plateau. Energy Convers. Manag. 2012, 57, 23–32. [Google Scholar] [CrossRef]
- Pan, T.; Wu, S.; Dai, E.; Liu, Y. Estimating the daily global solar radiation spatial distribution from diurnal temperature ranges over the Tibetan Plateau in China. Appl. Energy 2013, 107, 384–393. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, X.; Jia, Y.; Cui, N.; Hao, W.; Li, H.; Gong, D. High-resolution assessment of solar radiation and energy potential in China. Energy Convers. Manag. 2021, 240, 114265. [Google Scholar] [CrossRef]
- Li, M.; Liu, H.; Guo, P.; Wu, W. Estimation of daily solar radiation from routinely observed meteorological data in Chongqing, China. Energy Convers. Manag. 2010, 51, 2575–2579. [Google Scholar] [CrossRef]
- Wang, Y.; Meng, Z.; Lyu, R.; Huang, G.; He, Q.; Cheng, T. Spatiotemporal changes of surface solar radiation: Implication for air pollution and rice yield in East China. Sci. Total Environ. 2020, 739, 140361. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, M.; Wang, L.; Qin, W.; Ma, Y.; Gong, W.; Yu, L. Investigating the all-sky surface solar radiation and its influencing factors in the Yangtze River Basin in recent four decades. Atmos. Environ. 2021, 244, 117888. [Google Scholar] [CrossRef]
- Yaghoubi, M.A.; Sabzevari, A. Further data on solar radiation in Shiraz, Iran. Renew. Energy 1996, 7, 393–399. [Google Scholar] [CrossRef]
- Jiao, Z.; Yan, G.; Zhao, J.; Wang, T.; Chen, L. Estimation of surface upward longwave radiation from MODIS and VIIRS clear-sky data in the Tibetan Plateau. Remote Sens. Environ. 2015, 162, 221–237. [Google Scholar] [CrossRef]
- Yang, K.; He, J.; Tang, W.; Qin, J.; Cheng, C.C. On downward shortwave and longwave radiations over high altitude regions: Observation and modeling in the Tibetan Plateau. Agric. For. Meteorol. 2010, 150, 38–46. [Google Scholar] [CrossRef]
- Li, R.; Zhao, L.; Wu, T.; Wu, X.; Xiao, Y.; Du, Y.; Qin, Y. The impacts of net long-wave radiation on the surface soil thermal regimes over the Qinghai-Tibetan Plateau, China. Environ. Earth Sci. 2016, 75, 271. [Google Scholar] [CrossRef]
- Gupta, S.K.; Ritchey, N.A.; Wilber, A.C.; Whitlock, C.H.; Gibson, G.G.; Stackhouse Jr, P.W. A climatology of surface radiation budget derived from satellite data. J. Clim. 1999, 12, 2691–2710. [Google Scholar] [CrossRef]
- Zhang, X.; Gu, S.; Zhao, X.; Cui, X.; Zhao, L.; Xu, S.; Du, M.; Jiang, S.; Gao, Y.; Ma, C.; et al. Radiation partitioning and its relation to environmental factors above a meadow ecosystem on the Qinghai-Tibetan Plateau. J. Geophys. Res. Atmos. 2010, 115, D10106. [Google Scholar] [CrossRef]
- Ma, Y.; Su, Z.; Koike, T.; Yao, T.; Ishikawa, H.; Ueno, K.I.; Menenti, M. On measuring and remote sensing surface energy partitioning over the Tibetan Plateau-from GAME/Tibet to CAMP/Tibet. Phys. Chem. Earth, Parts A/B/C 2003, 28, 63–74. [Google Scholar] [CrossRef]
- Chen, R.; Ersi, K.; Yang, J.; Lu, S.; Zhao, W. Validation of five global radiation models with measured daily data in China. Energy Convers. Manag. 2004, 45, 1759–1769. [Google Scholar] [CrossRef]
- Liu, Y.; Tan, Q.; Pan, T. Determining the parameters of the Angstrom-Prescott model for estimating solar radiation in different regions of China: Calibration and modeling. Earth Space Sci. 2019, 6, 1976–1986. [Google Scholar] [CrossRef]
- Zhang, X.; Ren, Y.; Yin, Z.Y.; Lin, Z.; Zheng, D. Spatial and temporal variation patterns of reference evapotranspiration across the Qinghai-Tibetan Plateau during 1971–2004. J. Geophys. Res. Atmos. 2009, 114, D15105. [Google Scholar] [CrossRef]
- Xie, H.; Zhu, X. Reference evapotranspiration trends and their sensitivity to climatic change on the Tibetan Plateau (1970–2009). Hydrol. Process. 2013, 27, 3685–3693. [Google Scholar] [CrossRef]
- Kay, A.; Davies, H. Calculating potential evaporation from climate model data: A source of uncertainty for hydrological climate change impacts. J. Hydrol. 2008, 358, 221–239. [Google Scholar] [CrossRef]
- Kingston, D.G.; Todd, M.C.; Taylor, R.G.; Thompson, J.R.; Arnell, N.W. Uncertainty in the estimation of potential evapotranspiration under climate change. Geophys. Res. Lett. 2009, 36, L20403. [Google Scholar] [CrossRef]
- Thompson, J.R.; Green, A.J.; Kingston, D.G. Potential evapotranspiration-related uncertainty in climate change impacts on river flow: An assessment for the Mekong River basin. J. Hydrol. 2014, 510, 259–279. [Google Scholar] [CrossRef]
- Shi, L.; Feng, P.; Wang, B.; Liu, D.; Cleverly, J.; Fang, Q.; Yu, Q. Projecting potential evapotranspiration change and quantifying its uncertainty under future climate scenarios: A case study in southeastern Australia. J. Hydrol. 2020, 584, 124756. [Google Scholar] [CrossRef]
- Wang, W.; Xing, W.; Shao, Q. How large are uncertainties in future projection of reference evapotranspiration through different approaches? J. Hydrol. 2015, 524, 696–700. [Google Scholar] [CrossRef]
- Xu, Y.P.; Pan, S.; Fu, G.; Tian, Y.; Zhang, X. Future potential evapotranspiration changes and contribution analysis in Zhejiang Province, East China. J. Geophys. Res. Atmos. 2014, 119, 2174–2192. [Google Scholar] [CrossRef]
- Jenkins, K.; Warren, R. Quantifying the impact of climate change on drought regimes using the Standardized Precipitation Index. Theor. Appl. Climatol. 2015, 120, 41–54. [Google Scholar] [CrossRef]
- Okkan, U.; Fistikoglu, O.; Ersoy, Z.B.; Noori, A.T. Analyzing the uncertainty of potential evapotranspiration models in drought projections derived for a semi-arid watershed. Theor. Appl. Climatol. 2024, 155, 2329–2346. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Begueria, S.; Lopez-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Pimentel, R.; Arheimer, B.; Crochemore, L.; Andersson, J.C.M.; Pechlivanidis, I.G.; Gustafsson, D. Which potential evapotranspiration formula to use in hydrological modeling world-wide? Water Resour. Res. 2023, 59, e2022WR033447. [Google Scholar] [CrossRef]
- Seiller, G.; Anctil, F. How do potential evapotranspiration formulas influence hydrological projections? Hydrol. Sci. J. 2016, 61, 2249–2266. [Google Scholar] [CrossRef]
- Zhao, L.; Xia, J.; Xu, C.Y.; Wang, Z.; Sobkowiak, L.; Long, C. Evapotranspiration estimation methods in hydrological models. J. Geogr. Sci. 2013, 23, 359–369. [Google Scholar] [CrossRef]
- Carmona, F.; Rivas, R.; Caselles, C. Estimation of daytime downward longwave radiation under clear and cloudy skies conditions over sub-humid region. Theor. Appl. Climatol. 2014, 115, 281–295. [Google Scholar] [CrossRef]
- Kofroňová, J.; Tesař, M.; Šípek, V. The influence of observed and modelled net longwave radiation on the rate of estimated potential evapotranspiration. J. Hydrol. Hydromech. 2019, 67, 280–288. [Google Scholar] [CrossRef]
- Kjaersgaard, J.H.; Cuenca, R.H.; Plauborg, F.L.; Hansen, S. Long-term comparisons of net radiation calculation schemes. Bound.-Layer Meteolol. 2007, 123, 417–431. [Google Scholar] [CrossRef]
- Kjaersgaard, J.H.; Cuenca, R.H.; Martinez-Cob, A.; Gavilan, P.; Plauborg, F.; Mollerup, M.; Hansen, S. Comparison of the performance of net radiation calculation models. Theor. Appl. Climatol. 2009, 98, 57–66. [Google Scholar] [CrossRef]
- Granata, F. Evapotranspiration evaluation models based on machine learning algorithms-A comparative study. Agric. Water Manag. 2019, 217, 303–315. [Google Scholar] [CrossRef]
- Yu, H.; Jiang, S.; Chen, M.; Wang, M.; Shi, R.; Li, S.; Wu, J.; Kui, X.; Zou, H.; Zhan, C. Machine learning models for daily net radiation prediction across different climatic zones of China. Sci. Rep. 2024, 14, 20454. [Google Scholar] [CrossRef]
- Sun, Z.; Sun, B.; Li, S.; Guo, Z.; Yang, Z.; Ding, Y.; Zhu, L. Estimation of daily reference crop evapotranspiration in China based on time-space-LSTM model. J. Hydrol. 2025, 660, 133430. [Google Scholar] [CrossRef]
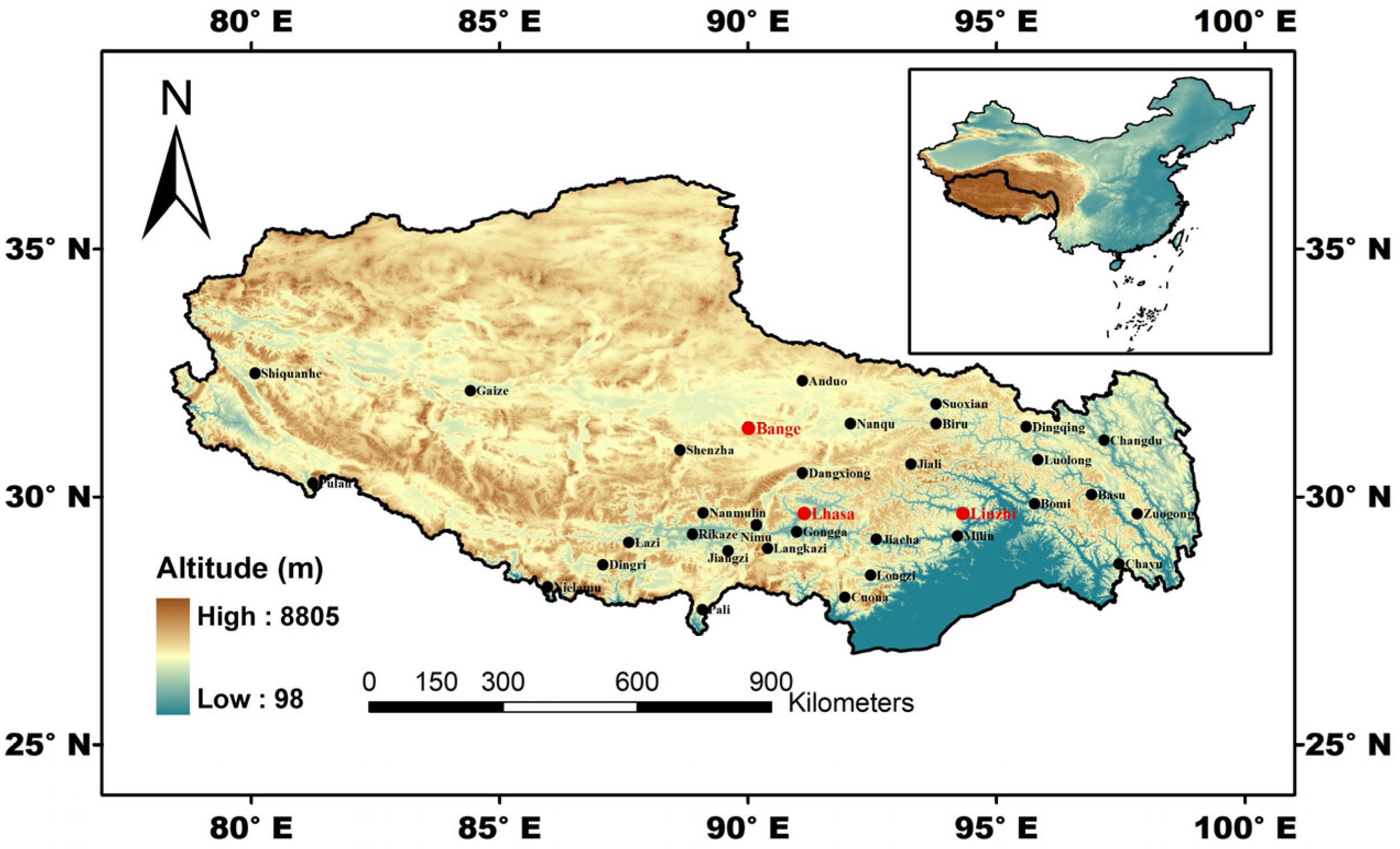
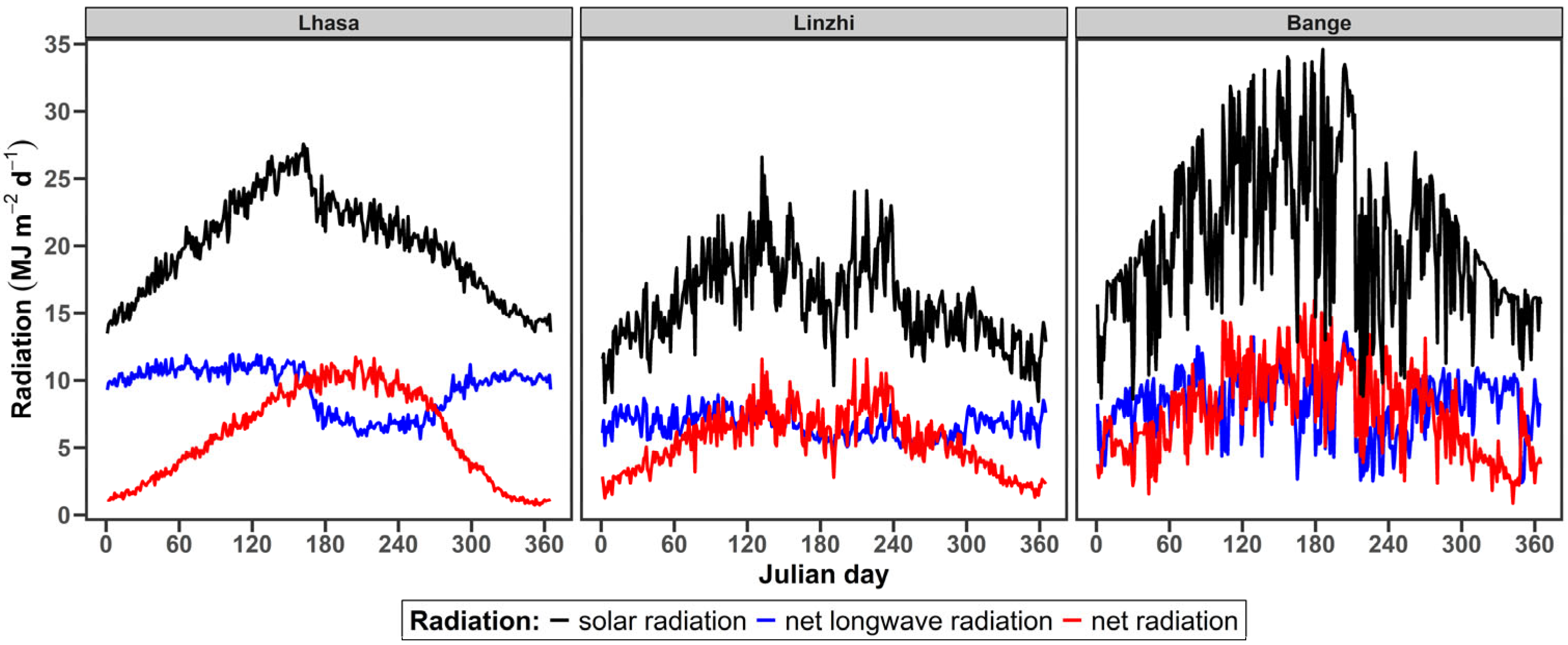
| Station | Latitude/N | Longitude/E | Altitude/m | Experimental Period/Recording Time |
|---|---|---|---|---|
| Lhasa | 29.67 | 91.13 | 3648.9 | 20 October 1993 to 31 December 2020 |
| Linzhi | 29.59 | 94.25 | 2991.8 | 1 September 2015 to 31 December 2020 |
| Bange | 31.38 | 90.02 | 4700.0 | 1 August 2014 to 31 July 2015 |
| Shiquanhe | 32.50 | 80.08 | 4278.6 | 1 January 1991 to 31 December 2020 |
| Gaize | 32.15 | 84.42 | 4414.9 | 1 January 1991 to 31 December 2020 |
| Anduo | 32.35 | 91.10 | 4800.0 | 1 January 1991 to 31 December 2020 |
| Nanqu | 31.48 | 92.07 | 4507.0 | 1 January 1991 to 31 December 2020 |
| Pulan | 30.28 | 81.25 | 3900.0 | 1 January 1991 to 31 December 2020 |
| Shenzha | 30.95 | 88.63 | 4672.0 | 1 January 1991 to 31 December 2020 |
| Dangxiong | 30.48 | 91.10 | 4200.0 | 1 January 1991 to 31 December 2020 |
| Lazi | 29.08 | 87.60 | 4000.0 | 1 January 1991 to 31 December 2020 |
| Nanmulin | 29.68 | 89.10 | 4000.1 | 1 January 1991 to 31 December 2020 |
| Rikaze | 29.25 | 88.88 | 3836.0 | 1 January 1991 to 31 December 2020 |
| Nimu | 29.43 | 90.17 | 3809.4 | 1 January 1991 to 31 December 2020 |
| Gongga | 29.30 | 90.98 | 3555.3 | 1 January 1991 to 31 December 2020 |
| Qongjie | 29.03 | 91.68 | 3740.0 | 1 January 1991 to 31 December 2020 |
| Zedang | 29.25 | 91.77 | 3551.7 | 1 January 1991 to 31 December 2020 |
| Nielamu | 28.18 | 85.97 | 3810.0 | 1 January 1991 to 31 December 2020 |
| Dingri | 28.63 | 87.08 | 4300.0 | 1 January 1991 to 31 December 2020 |
| Jiangzi | 28.92 | 89.60 | 4040.0 | 1 January 1991 to 31 December 2020 |
| Langkazi | 28.97 | 90.40 | 4431.7 | 1 January 1991 to 31 December 2020 |
| Cuona | 27.98 | 91.95 | 4280.3 | 1 January 1991 to 31 December 2020 |
| Longzi | 28.42 | 92.47 | 3860.0 | 1 January 1991 to 31 December 2020 |
| Pali | 27.73 | 89.08 | 4300.0 | 1 January 1991 to 31 December 2020 |
| Suoxian | 31.88 | 93.78 | 4022.8 | 1 January 1991 to 31 December 2020 |
| Biru | 31.48 | 93.78 | 3940.0 | 1 January 1991 to 31 December 2020 |
| Dingqing | 31.42 | 95.60 | 3873.1 | 1 January 1991 to 31 December 2020 |
| Leiwuqi | 31.22 | 96.60 | 3810.0 | 1 January 1991 to 31 December 2020 |
| Changdu | 31.15 | 97.17 | 3306.0 | 1 January 1991 to 31 December 2020 |
| Jiali | 30.67 | 93.28 | 4488.8 | 1 January 1991 to 31 December 2020 |
| Luolong | 30.75 | 95.83 | 3640.0 | 1 January 1991 to 31 December 2020 |
| Bomi | 29.87 | 95.77 | 2736.0 | 1 January 1991 to 31 December 2020 |
| Basu | 30.05 | 96.92 | 3260.0 | 1 January 1991 to 31 December 2020 |
| Jiacha | 29.15 | 92.58 | 3260.0 | 1 January 1991 to 31 December 2020 |
| Milin | 29.22 | 94.22 | 2950.0 | 1 January 1991 to 31 December 2020 |
| Zuogong | 29.67 | 97.83 | 3780.0 | 1 January 1991 to 31 December 2020 |
| Mangkang | 29.68 | 98.60 | 3870.0 | 1 January 1991 to 31 December 2020 |
| Chayu | 28.65 | 97.47 | 2327.6 | 1 January 1991 to 31 December 2020 |
| Method | Site | Fs | Fnl | ||||
|---|---|---|---|---|---|---|---|
| a | b | c | d | e | f | ||
| AllenO | All stations | 0.250 | 0.500 | 0.340 | 0.140 | 1.350 | 0.350 |
| Lhasa | 0.280 | 0.500 | 0.340 | 0.140 | 1.350 | 0.350 | |
| AllenS | Linzhi | 0.304 | 0.471 | 0.340 | 0.140 | 1.350 | 0.350 |
| Bange | 0.304 | 0.563 | 0.340 | 0.140 | 1.350 | 0.350 | |
| Lhasa | 0.250 | 0.500 | 0.630 | 0.296 | 0.673 | −0.149 | |
| AllenL | Linzhi | 0.250 | 0.500 | 0.280 | 0.076 | 0.997 | −0.324 |
| Bange | 0.250 | 0.500 500 | 0.846 | 0.345 | 0.507 | −0.054 | |
| Lhasa | 0.280 | 0.500 | 0.630 | 0.296 | 0.673 | −0.149 | |
| AllenC | Linzhi | 0.304 | 0.471 | 0.280 | 0.076 | 0.997 | −0.324 |
| Bange | 0.304 | 0.563 | 0.846 | 0.345 | 0.507 | −0.054 | |
| Lhasa | 0.253 | 0.556 | 0.582 | 0.264 | 0.721 | −0.149 | |
| AllenR | Linzhi | 0.258 | 0.530 | 0.582 | 0.264 | 0.721 | −0.149 |
| Bange | 0.238 | 0.598 | 0.582 | 0.264 | 0.721 | −0.149 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Zhou, G.; Du, J.; Li, M.; Song, Y.; Chen, S.; Ji, Y. Common Calibration of Solar Radiation and Net Longwave Radiation Is the Key to Accurately Estimating Reference Crop Evapotranspiration over the Tibetan Plateau. Appl. Sci. 2025, 15, 12449. https://doi.org/10.3390/app152312449
Liu J, Zhou G, Du J, Li M, Song Y, Chen S, Ji Y. Common Calibration of Solar Radiation and Net Longwave Radiation Is the Key to Accurately Estimating Reference Crop Evapotranspiration over the Tibetan Plateau. Applied Sciences. 2025; 15(23):12449. https://doi.org/10.3390/app152312449
Chicago/Turabian StyleLiu, Jiandong, Guangsheng Zhou, Jun Du, Mingxing Li, Yanling Song, Shang Chen, and Yuhe Ji. 2025. "Common Calibration of Solar Radiation and Net Longwave Radiation Is the Key to Accurately Estimating Reference Crop Evapotranspiration over the Tibetan Plateau" Applied Sciences 15, no. 23: 12449. https://doi.org/10.3390/app152312449
APA StyleLiu, J., Zhou, G., Du, J., Li, M., Song, Y., Chen, S., & Ji, Y. (2025). Common Calibration of Solar Radiation and Net Longwave Radiation Is the Key to Accurately Estimating Reference Crop Evapotranspiration over the Tibetan Plateau. Applied Sciences, 15(23), 12449. https://doi.org/10.3390/app152312449







