An Ambiguity in Child Body Surface Area Measurement
Featured Application
Abstract
1. Introduction
2. Current State of Knowledge
3. Methods and Applied Software
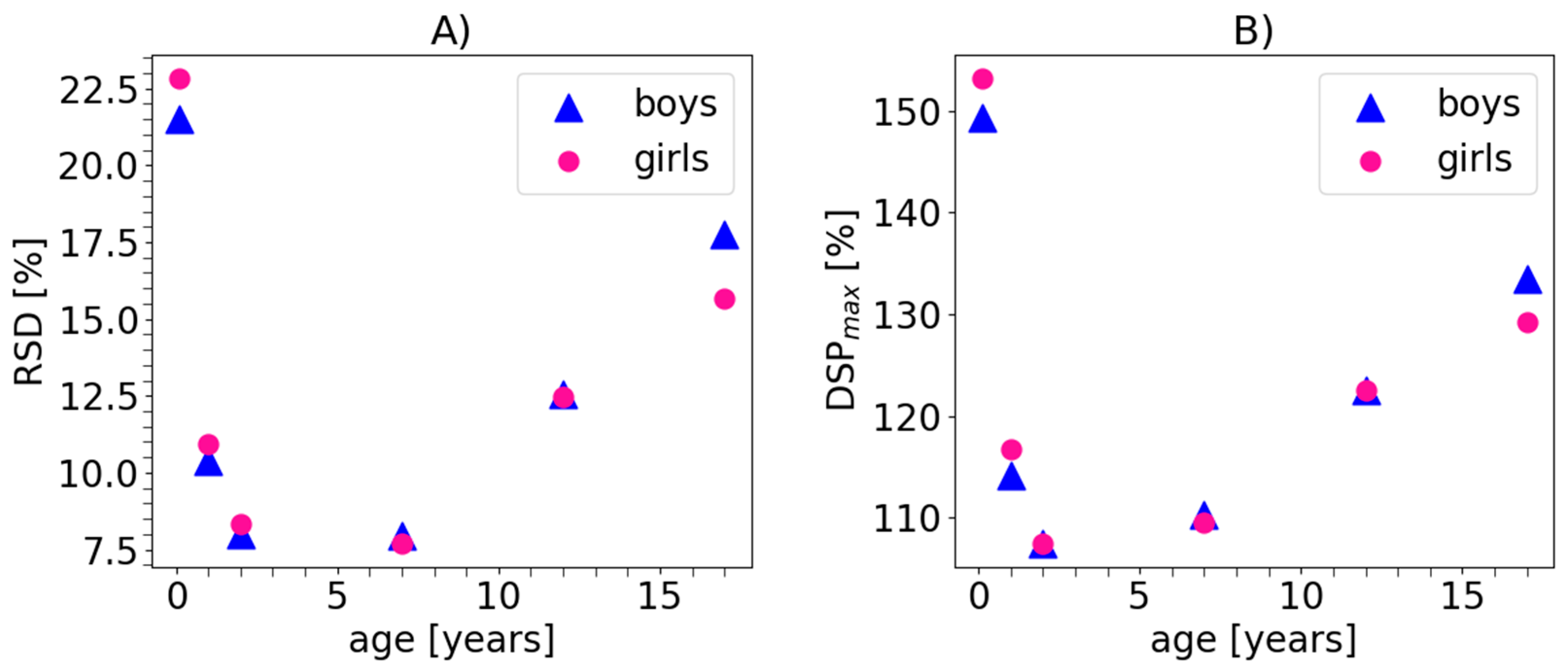
4. Results
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BSA | Body Surface Area |
| TBSA | Total Body Surface Area |
| GFR | Glomerular Filtration Rate |
| RSD | Relative standard deviation |
| DSPmax | Maximal discrepancy parameter |
Appendix A
| AGE | PERCENTILE | Weight (kg) | Height (cm) | Average BSA (m2) | σ (m2) | DSPMAX (m2) | RSD (%) | Relative DSPMAX (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Girls | Boys | Girls | Boys | Girls | Boys | Girls | Boys | Girls | Boys | Girls | Boys | Girls | Boys | ||
| 4 WEEKS | 3 | 3.1 | 3.4 | 49.7 | 50.7 | 0.233 | 0.243 | 0.066 | 0.065 | 0.396 | 0.403 | 28.45 | 26.67 | 169.82 | 166.00 |
| 25 | 3.7 | 4.0 | 52.1 | 53.1 | 0.258 | 0.270 | 0.064 | 0.063 | 0.410 | 0.417 | 24.71 | 23.24 | 159.15 | 154.75 | |
| 50 | 4.1 | 4.4 | 53.4 | 54.4 | 0.274 | 0.285 | 0.062 | 0.061 | 0.420 | 0.427 | 22.80 | 21.54 | 153.40 | 149.58 | |
| 75 | 4.5 | 4.8 | 54.7 | 55.7 | 0.289 | 0.300 | 0.061 | 0.060 | 0.429 | 0.436 | 21.16 | 20.08 | 148.40 | 145.04 | |
| 97 | 5.3 | 5.6 | 57 | 58 | 0.319 | 0.330 | 0.059 | 0.059 | 0.447 | 0.453 | 18.62 | 17.79 | 140.16 | 137.48 | |
| 1 year | 3 | 7.1 | 7.8 | 69.2 | 71.3 | 0.392 | 0.416 | 0.051 | 0.050 | 0.491 | 0.506 | 13.09 | 12.06 | 125.19 | 121.61 |
| 25 | 8.2 | 9.0 | 72.3 | 74.1 | 0.429 | 0.455 | 0.050 | 0.049 | 0.514 | 0.531 | 11.59 | 10.86 | 119.80 | 116.57 | |
| 50 | 8.9 | 9.6 | 74 | 75.7 | 0.452 | 0.475 | 0.049 | 0.049 | 0.529 | 0.543 | 10.92 | 10.37 | 116.94 | 114.37 | |
| 75 | 9.7 | 10.4 | 75.8 | 77.4 | 0.478 | 0.500 | 0.049 | 0.050 | 0.545 | 0.558 | 10.34 | 9.94 | 114.04 | 111.77 | |
| 97 | 11.3 | 11.8 | 78.9 | 80.2 | 0.527 | 0.542 | 0.051 | 0.051 | 0.575 | 0.586 | 9.69 | 9.49 | 109.19 | 108.11 | |
| 2 years | 3 | 9.3 | 9.8 | 79.6 | 82.1 | 0.471 | 0.488 | 0.046 | 0.044 | 0.540 | 0.552 | 9.67 | 9.08 | 114.79 | 112.93 |
| 25 | 10.8 | 11.3 | 83.5 | 85.8 | 0.519 | 0.536 | 0.045 | 0.044 | 0.571 | 0.582 | 8.67 | 8.25 | 110.06 | 108.57 | |
| 50 | 11.7 | 12.2 | 85.7 | 87.8 | 0.547 | 0.563 | 0.045 | 0.045 | 0.589 | 0.607 | 8.30 | 7.98 | 107.64 | 107.72 | |
| 75 | 12.7 | 13.1 | 87.9 | 89.9 | 0.577 | 0.591 | 0.047 | 0.046 | 0.623 | 0.637 | 8.06 | 7.79 | 107.95 | 107.93 | |
| 97 | 14.9 | 15.1 | 91.8 | 93.6 | 0.641 | 0.649 | 0.052 | 0.051 | 0.693 | 0.701 | 8.10 | 7.84 | 108.12 | 108.01 | |
| 7 years | 3 | 17.8 | 18.6 | 113 | 115 | 0.747 | 0.770 | 0.047 | 0.049 | 0.792 | 0.814 | 6.26 | 6.39 | 105.91 | 105.68 |
| 25 | 21.1 | 21.9 | 120 | 121 | 0.840 | 0.862 | 0.058 | 0.062 | 0.902 | 0.932 | 6.96 | 7.14 | 107.38 | 108.15 | |
| 50 | 23.5 | 24.4 | 123 | 125 | 0.903 | 0.927 | 0.069 | 0.073 | 0.992 | 1.026 | 7.65 | 7.89 | 109.80 | 110.60 | |
| 75 | 26.5 | 27.8 | 127 | 128 | 0.980 | 1.012 | 0.084 | 0.091 | 1.103 | 1.150 | 8.61 | 9.02 | 112.57 | 113.68 | |
| 97 | 34.7 | 37.6 | 133 | 134 | 1.172 | 1.236 | 0.134 | 0.154 | 1.397 | 1.499 | 11.43 | 12.44 | 119.19 | 121.27 | |
| 12 years | 3 | 30.0 | 29.7 | 141 | 139 | 1.085 | 1.074 | 0.097 | 0.096 | 1.237 | 1.225 | 8.93 | 8.95 | 113.97 | 114.05 |
| 25 | 37.4 | 37.1 | 149 | 148 | 1.263 | 1.254 | 0.139 | 0.138 | 1.506 | 1.495 | 10.99 | 10.98 | 119.27 | 119.22 | |
| 50 | 42.8 | 42.7 | 154 | 153 | 1.385 | 1.381 | 0.173 | 0.173 | 1.699 | 1.695 | 12.48 | 12.51 | 122.69 | 122.74 | |
| 75 | 49.6 | 50.0 | 158 | 158 | 1.531 | 1.538 | 0.219 | 0.222 | 1.938 | 1.952 | 14.30 | 14.45 | 126.61 | 126.90 | |
| 97 | 66.7 | 69.8 | 167 | 167 | 1.872 | 1.930 | 0.348 | 0.373 | 2.528 | 2.632 | 18.57 | 19.33 | 135.00 | 136.40 | |
| 17 years | 3 | 43.9 | 50.8 | 154 | 165 | 1.407 | 1.569 | 0.181 | 0.222 | 1.737 | 1.985 | 12.85 | 14.17 | 123.49 | 126.50 |
| 25 | 50.8 | 60.3 | 161 | 173 | 1.560 | 1.770 | 0.226 | 0.289 | 1.982 | 2.318 | 14.49 | 16.30 | 127.07 | 130.96 | |
| 50 | 55.7 | 66.9 | 165 | 178 | 1.663 | 1.903 | 0.260 | 0.337 | 2.153 | 2.546 | 15.64 | 17.73 | 129.46 | 133.81 | |
| 75 | 61.9 | 74.8 | 169 | 182 | 1.789 | 2.056 | 0.306 | 0.399 | 2.368 | 2.817 | 17.08 | 19.39 | 132.35 | 136.99 | |
| 97 | 77.5 | 93.9 | 176 | 190 | 2.088 | 2.406 | 0.429 | 0.557 | 2.900 | 3.461 | 20.53 | 23.14 | 138.88 | 143.82 | |
References
- Ivy, S.P.; Beumer, J.H. Ovarian cancer survival and chemotherapy dosing, body mass index, and body surface area: Are we there yet? JAMA Oncol. 2015, 1, 732–733. [Google Scholar] [CrossRef]
- Zafrir, B.; Goren, Y.; Salman, N.; Amir, O. Comparison of body mass index and body surface area as outcome predictors in patients with systolic heart failure. Cardiol. J. 2015, 22, 375–381. [Google Scholar] [CrossRef]
- Adler, A.C.; Nathanson, B.H.; Raghunathan, K.; McGee, W.T. Misleading indexed hemodynamic parameters: The clinical importance of discordant BMI and BSA at extremes of weight. Crit. Care 2012, 16, 471. [Google Scholar] [CrossRef] [PubMed]
- Du Bois, D.; Du Bois, E.F. A formula to estimate the approximate surface area if height and weight be known. Arch. Intern. Med. 1916, 17, 863–871. [Google Scholar] [CrossRef]
- Redlarski, G.; Palkowski, A.; Krawczuk, M. Body surface area formulae: An alarming ambiguity. Sci. Rep. 2016, 6, 27966. [Google Scholar] [CrossRef]
- Ho, H.L.; Halim, A.S.; Sulaiman, W.A.W.; Fatimah, M.J. Estimation of Total Body Surface Area Burned: A Comparison Between Burn Unit and Referring Facilities. Ann. Burns Fire Disasters 2023, 36, 19–28. [Google Scholar] [PubMed] [PubMed Central]
- Thelwell, M.; Masters, N.; Appleyard, R.; Bullas, A.M. Advanced Body Measurement Techniques Can Complement Current Methods of Cytotoxic Chemotherapy Dose Prescription. Appl. Sci. 2024, 14, 834. [Google Scholar] [CrossRef]
- Wu, Q.; Zhou, Y.; Fan, X.; Ma, H.; Gu, W.; Sun, F. Evaluation of nine formulas for estimating the body surface area of children with hematological malignancies. Front. Pediatr. 2022, 10, 989049. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Russell, J.; Grimes, J.P.; Teferi, S.; Pruitt, Z.M.; Howe, J.L.; Adams, K.T.; Nicol, N.; Krevat, S.; Busog, D.; Ratwani, R.M.; et al. Pediatric Dose Calculation Issues and the Need for Human Factors–Informed Preventative Technology Optimizations. Patient Saf. 2022, 4, 48–61. [Google Scholar] [CrossRef]
- Flint, B.; Das, J.M.; Hall, C.A. Body Surface Area; StatPearls [Internet]; StatPearls Publishing: Treasure Island, FL, USA, 2025. [Google Scholar]
- El Edelbi, R.A.; Lindemalm, S.; Nydert, P.; Eksborg, S. Estimation of body surface area in neonates, infants, and children using body weight alone. Int. J. Pediatr. Adolesc. Med. 2021, 8, 221–228. [Google Scholar] [CrossRef]
- Alvear-Vasquez, F.; Vidal-Espinoza, R.; Gomez-Campos, R.; de Campos, L.F.C.C.; Lazari, E.; Guzmán-Luján, J.F.; Pablos-Monzó, A.; Cossio-Bolaños, M. Body surface area is a predictor of maturity status in school children and adolescents. BMC Pediatr. 2023, 23, 410. [Google Scholar] [CrossRef]
- Piecuch, M.; Chylak, M.; Górski, M.; Garbicz-Kata, J.; Szczyrba, A.; Buczkowska, M.; Malinowska-Borowska, J.; Nowak, J.U.; Niedziela, J.T.; Gąsior, M.; et al. Comparison of the Effectiveness of Body Surface Area Estimation Formulas in Predicting the Risk of Death in Patients with Heart Failure. J. Clin. Med. 2024, 13, 6625. [Google Scholar] [CrossRef] [PubMed]
- Von Meeh, K. Oberflächenmessungen des menschlichen Körpers. Z. Biol. 1879, 15, 425–458. [Google Scholar]
- Fujimoto, S.; Watanabe, T.; Sakamoto, A.; Yukawa, K.; Morimoto, K. Studies on the physical surface area of Japanese: Part 18 calculation formulas in three stages over all ages. Nippon Eiseigaku Zasshi 1968, 23, 443–450. [Google Scholar] [CrossRef]
- Lissauer, W. Über Oberflächenmessungen an Säuglingen und ihre Bedeutung für den Nahrungsbedarf. Jahrb. Kinderheilkd. Phys. Erzieh. Neue Folge 1903, 58, 392–411. [Google Scholar]
- Costeff, H. A simple empirical formula for calculating approximate surface area in children. Arch. Dis. Child. 1966, 41, 681–683. [Google Scholar] [CrossRef]
- Boyd, E. The Growth of the Surface Area of the Human Body; University Minnesota Press: Minneapolis, MN, USA, 1935. [Google Scholar]
- Haycock, G.B.; Schwartz, G.J.; Wisotsky, D.H. Geometric method for measuring body surface area: A height-weight formula validated in infants, children, and adults. J. Pediatr. 1978, 93, 62–66. [Google Scholar] [CrossRef] [PubMed]
- Nwoye, L.O.; Al-Shehri, M.A. The body surface area of Saudi newborns. J. Egypt. Public Health Assoc. 2005, 80, 153–168. [Google Scholar]
- Rubner, M.; Heubner, O. Die natürliche Ernährung eines Säuglings. Z. Biol. 1898, 36, 1–55. [Google Scholar]
- Banerjee, S.; Bhattacharya, A.K. Determination of body surface area in Indian Hindu children. J. Appl. Physiol. 1961, 16, 969–970. [Google Scholar] [CrossRef]
- Meban, C. The surface area and volume of the human fetus. J. Anat. 1983, 137, 271–278. [Google Scholar]
- Mosteller, R.D. Simplified calculation of body surface area. N. Engl. J. Med. 1987, 317, 1098. [Google Scholar]
- Vaughan, V.C., III; Litt, I.F. Developmental pediatrics: Assessment of growth and development. In Nelson Textbook of Pediatrics; Behrman, R.E., Vaughan, V.C., III, Eds.; WB Saunders: Philadelphia, PA, USA, 1987; pp. 24–33. [Google Scholar]
- Current, J.D. A linear equation for estimating the body surface area in infants and children. Internet J. Anesthesiol. 1998, 2, e9453. [Google Scholar] [CrossRef]
- The WHO Child Growth Standards. (n.d.). Available online: https://www.who.int/tools/child-growth-standards/standards (accessed on 8 November 2025).
- Singh, G.K.; Kogan, M.D.; Van Dyck, P.C. Changes in state-specific childhood obesity and overweight prevalence in the United States from 2003 to 2007. Arch. Pediatr. Adolesc. Med. 2010, 164, 598–607. [Google Scholar] [CrossRef]
- Wang, Y.; Lobstein, T. Worldwide trends in childhood overweight and obesity. Int. J. Pediatr. Obes. 2006, 1, 11–25. [Google Scholar] [CrossRef]
- Stamatakis, E.; Wardle, J.; Cole, T.J. Childhood obesity and overweight prevalence trends in England: Evidence for growing socioeconomic disparities. Int. J. Obes. 2010, 34, 41–47. [Google Scholar] [CrossRef] [PubMed]
- Gerina-Berzina, A.; Vikmanis, U.; Teibe, U.; Umbraško, S. Anthropometric measurements of the body composition of cancer patients determine the precise role of the body surface area and the calculation of the dose of chemotherapy. Pap. Anthropol. 2012, 21, 84–94. [Google Scholar] [CrossRef]
- Gurney, H. How to calculate the dose of chemotherapy. Br. J. Cancer 2002, 86, 1297–1302. [Google Scholar] [CrossRef] [PubMed]
- Chatelut, E.; White-Koning, M.L.; Mathijssen, R.H.; Puisset, F.; Baker, S.D.; Sparreboom, A. Dose banding as an alternative to body surface area-based dosing of chemotherapeutic agents. Br. J. Cancer 2012, 107, 1100–1106. [Google Scholar] [CrossRef] [PubMed]
- Fukazawa, K.; Nishida, S.; Shigematsu, A.; Levi, D.M.; Nishida, T.; Tzakis, A.G. Determination of the safe range of graft size mismatch using body surface area index in deceased liver transplantation. Transplant. Int. 2013, 26, 724–733. [Google Scholar] [CrossRef]
- Urata, K.; Kawasaki, S.; Matsunami, H.; Hashikura, Y.; Ikegami, T.; Ishizone, S.; Momose, Y.; Komiyama, A.; Makuuchi, M. Calculation of child and adult standard liver volume for liver transplantation. Hepatology 1995, 21, 1317–1321. [Google Scholar] [CrossRef]
- West, D.P.; Worobec, S.; Solomon, L.M. Pharmacology and toxicology of infant skin. J. Investig. Dermatol. 1981, 76, 147–150. [Google Scholar] [CrossRef]
- Iversen, L.; Lange, M.; Bissonette, R.; Carvalho, A.; van de Kerkhof, P.; Kirby, B.; Kleyn, C.; Lynde, C.; van der Walt, J.; Wu, J. Topical treatment of psoriasis: Questionnaire results on topical therapy accessibility and influence of body surface area on usage. J. Eur. Acad. Dermatol. Venereol. 2017, 31, 1188–1195. [Google Scholar] [CrossRef]
- Speeckaert, R.; van Geel, N.; Vermaelen, K.; van Hoecke, L.; Brochez, L.; Lambert, J. Comparison of methods to estimate the affected body surface area and the dosage of topical treatments in psoriasis and atopic dermatitis: The advantage of a picture-based tool. J. Eur. Acad. Dermatol. Venereol. 2019, 33, 1726–1732. [Google Scholar] [CrossRef]
- Saadeh, S.A.; Alhawiti, N.M.; El-Metwally, A.; Alamro, R.A.; Khalil, A. Weight or body surface area dosing of steroids in nephrotic syndrome: Is there an outcome difference? Pediatr. Nephrol. 2011, 26, 2167–2171. [Google Scholar] [CrossRef] [PubMed]
- Bayley, E.W.; Chung, Y.T.; O’Mara, M.S.; Walker, A.C.; Serghiou, M.A. Research priorities for burn nursing: Rehabilitation, discharge planning, and follow-up care. J. Burn Care Rehabil. 1992, 13, 471–476. [Google Scholar] [CrossRef] [PubMed]
- Parvizi, D.; Kamolz, L.P.; Giretzlehner, M.; Trop, M.; Lumenta, D.B. The potential impact of wrong TBSA estimations on fluid resuscitation in patients suffering from burns: Things to keep in mind. Burns 2014, 40, 241–245. [Google Scholar] [CrossRef]
- Mündlein, M.; Eberhardt, J.; Farkas, A.; Dörfler, M.; Ulmer, H.; Lothar, H. Comparison of transepidermal water loss (TEWL) measurements with two novel sensors based on different sensing principles. Sens. Actuators A Phys. 2008, 142, 67–72. [Google Scholar] [CrossRef]
- Tsai, P.-J.; Shieh, H.-Y.; Lee, W.-J.; Lai, S.-O. Health-risk assessment for workers exposed to polycyclic aromatic hydrocarbons (PAHs) in a carbon black manufacturing industry. Sci. Total Environ. 2001, 278, 137–150. [Google Scholar] [CrossRef]
- Udristioiu, A.; Nanu, M.; Nanu, C.; Udristioiu, I.; Popescu, F.; Galescu, L. Variability of biological parameters in blood samples between two consecutive schedules of hemodialysis. In Basic Nephrology and Acute Kidney Injury; InTech: Rijeka, Croatia, 2012; pp. 53–60. [Google Scholar]
- Starship Children’s Health. Wilms Tumour PI Wilms 1 Protocol. Available online: https://starship.org.nz/guidelines/wilms-tumour-pi-wilms-1-protocol/ (accessed on 15 March 2024).
- Wang, J.; Li, M.; Tang, J.; Jiang, S.; Wang, C. Current treatment for Wilms tumor: COG and SIOP standards. World J. Pediatr. Surg. 2019, 2, e000038. [Google Scholar] [CrossRef]
- Dix, D.B.; Seibel, N.L.; Chi, Y.-Y.; Khanna, G.; Gratias, E.; Anderson, J.R.; Mullen, E.A.; Geller, J.I.; Kalapurakal, J.A.; Paulino, A.C.; et al. Treatment of stage IV favorable histology Wilms tumor with lung metastases: A report from the Children’s Oncology Group AREN0533 study. J. Clin. Oncol. 2018, 36, JCO2017771931. [Google Scholar] [CrossRef]
- Ademola-Popoola, D.; Opocher, E.; Reddy, A. Contemporary management of retinoblastoma in the context of a low-resource country. Niger. Postgrad. Med. J. 2019, 26, 69–73. [Google Scholar] [CrossRef] [PubMed]
- Ancona Lezama, D.A.; Dalvin, L.A.; Shields, C.L. Modern treatment of retinoblastoma: A 2020 review. Indian J. Ophthalmol. 2020, 68, 2356–2365. [Google Scholar] [CrossRef]
- Whelan, J.S.; Burcombe, R.; Janinis, J.; Baldelli, A.M.; Cassoni, A.M. Interval compressed vincristine, doxorubicin, cyclophosphamide alternating with ifosfamide, etoposide in patients with advanced Ewing’s and other small round cell sarcomas. Clin. Sarcoma Res. 2012, 2, 12. [Google Scholar] [CrossRef]
- Imaya, M.; Muramatsu, H.; Narita, A.; Yamamori, A.; Wakamatsu, M.; Yoshida, T.; Miwata, S.; Narita, K.; Ichikawa, D.; Hamada, M.; et al. Combination chemotherapy consisting of irinotecan, etoposide, and carboplatin for refractory or relapsed neuroblastoma. Cancer Med. 2022, 11, 1956–1964. [Google Scholar] [CrossRef]
- Khan, S.; Ahmed, A.; Al-Salem, A.H.; Al-Zahrani, A.S.; Al-Hussein, K. Pediatric high-risk neuroblastoma with autologous stem cell transplant—20 years of experience. Int. J. Pediatr. Adolesc. Med. 2021, 8, 253–257. [Google Scholar] [CrossRef]
- Schmiegelow, K.; Nielsen, S.N.; Frandsen, T.L.; Nersting, J. Mercaptopurine/methotrexate maintenance therapy of childhood acute lymphoblastic leukemia: Clinical facts and fiction. J. Pediatr. Hematol. Oncol. 2014, 36, 503–517. [Google Scholar] [CrossRef] [PubMed]
- National Comprehensive Cancer Network. Acute Lymphoblastic Leukemia. Available online: https://www.nccn.org/guidelines/guidelines-detail?category=1&id=1410 (accessed on 8 November 2025).
- Rinke, M.L.; Shore, A.D.; Morlock, L.; Hicks, R.W.; Miller, M.R. Characteristics of pediatric chemotherapy medication errors in a national error reporting database. Cancer 2007, 110, 186–195. [Google Scholar] [CrossRef] [PubMed]
- Yosipovitch, G.; DeVore, A.; Dawn, A. Obesity and the skin: Skin physiology and skin manifestations of obesity. J. Am. Acad. Dermatol. 2007, 56, 901–916. [Google Scholar] [CrossRef]
- Redlarski, G.; Kozieł, S.; Krawczuk, M.; Siebert, J.; Tałałaj, M.; Pałkowski, A.; Tojza, P.; Cieślikowska, Z.; Litzbarski, L.S. An improvement of body surface area formulas using the 3D scanning technique. Int. J. Occup. Med. Environ. Health 2024, 37, 205–219. [Google Scholar] [CrossRef]
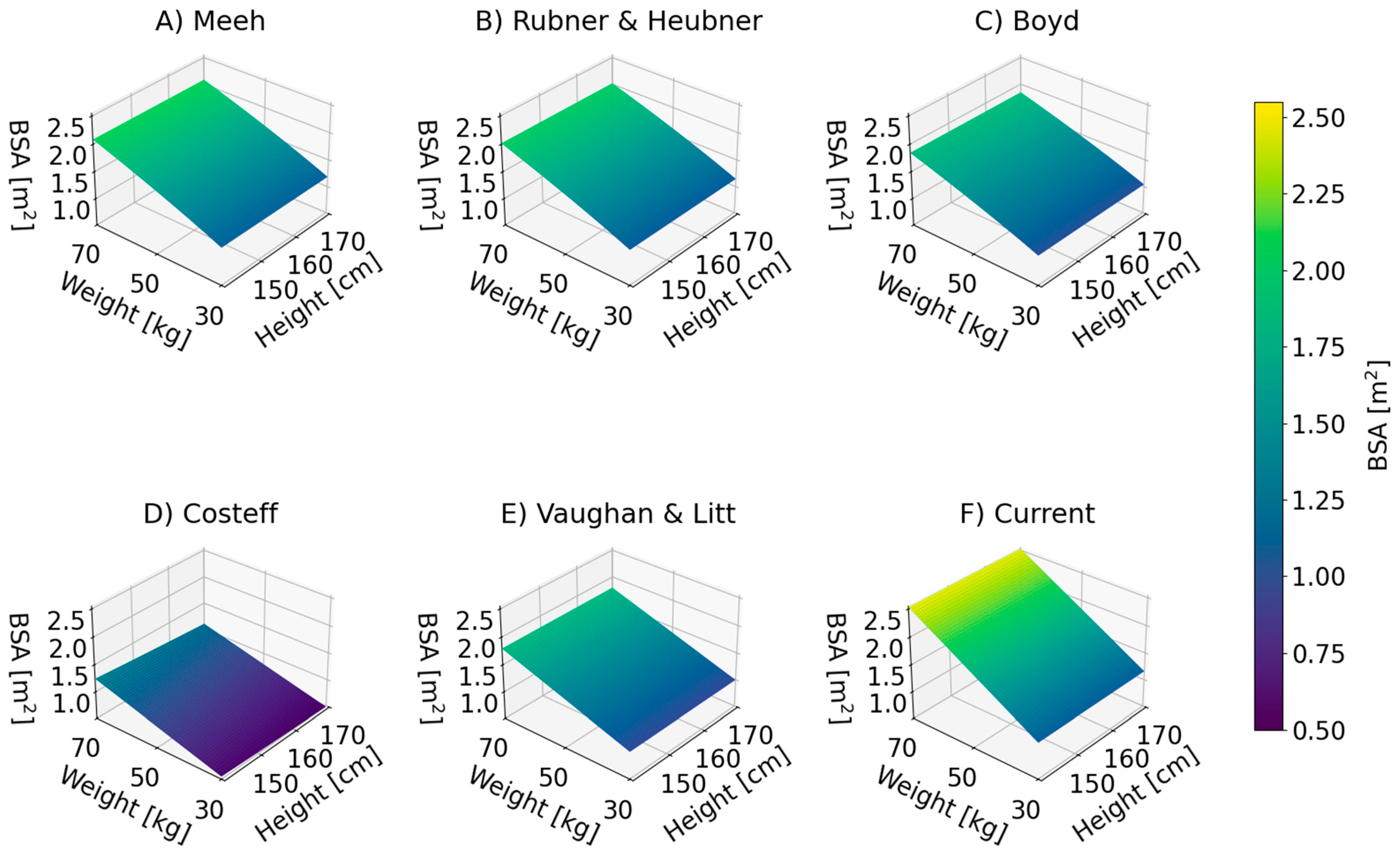
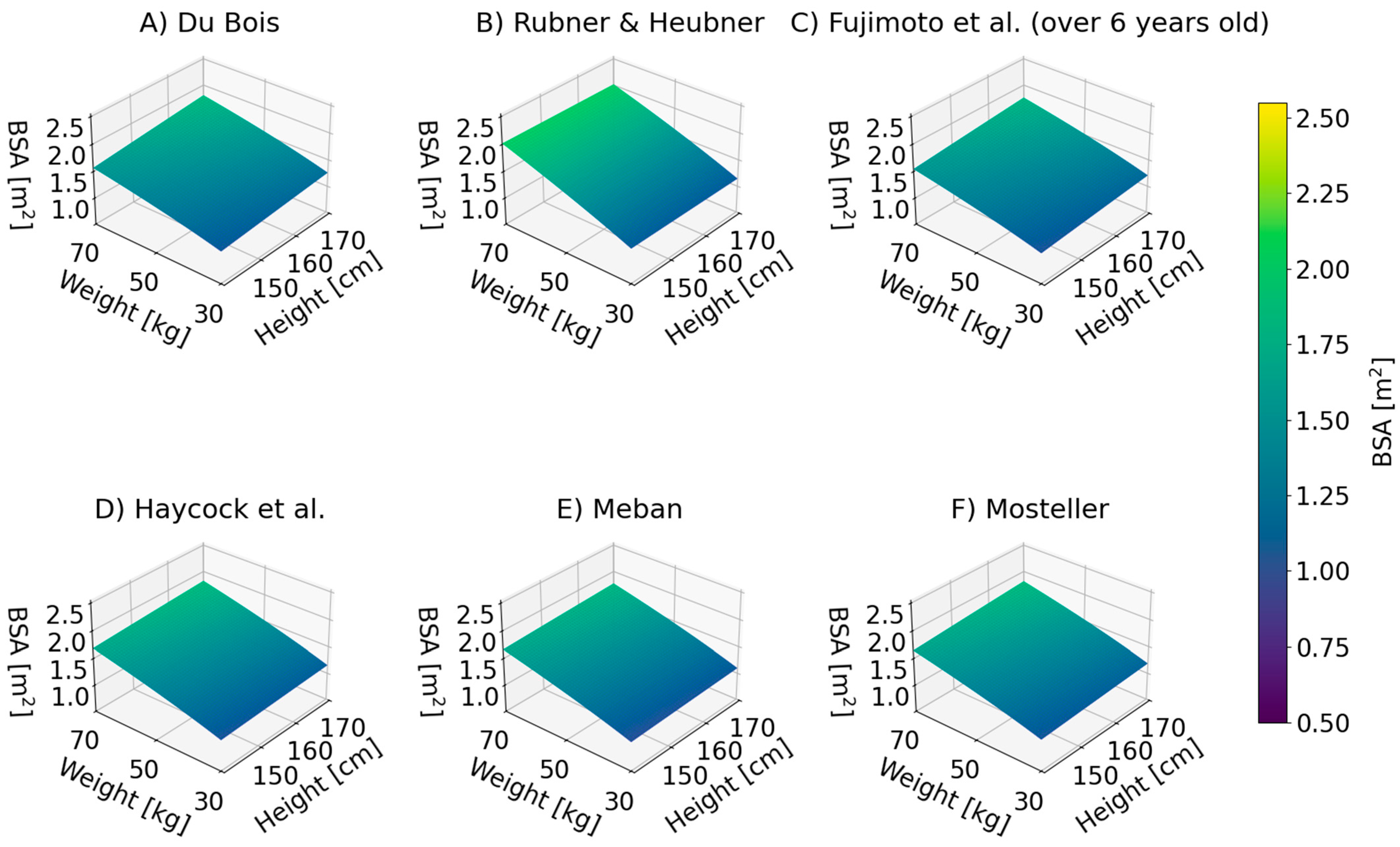
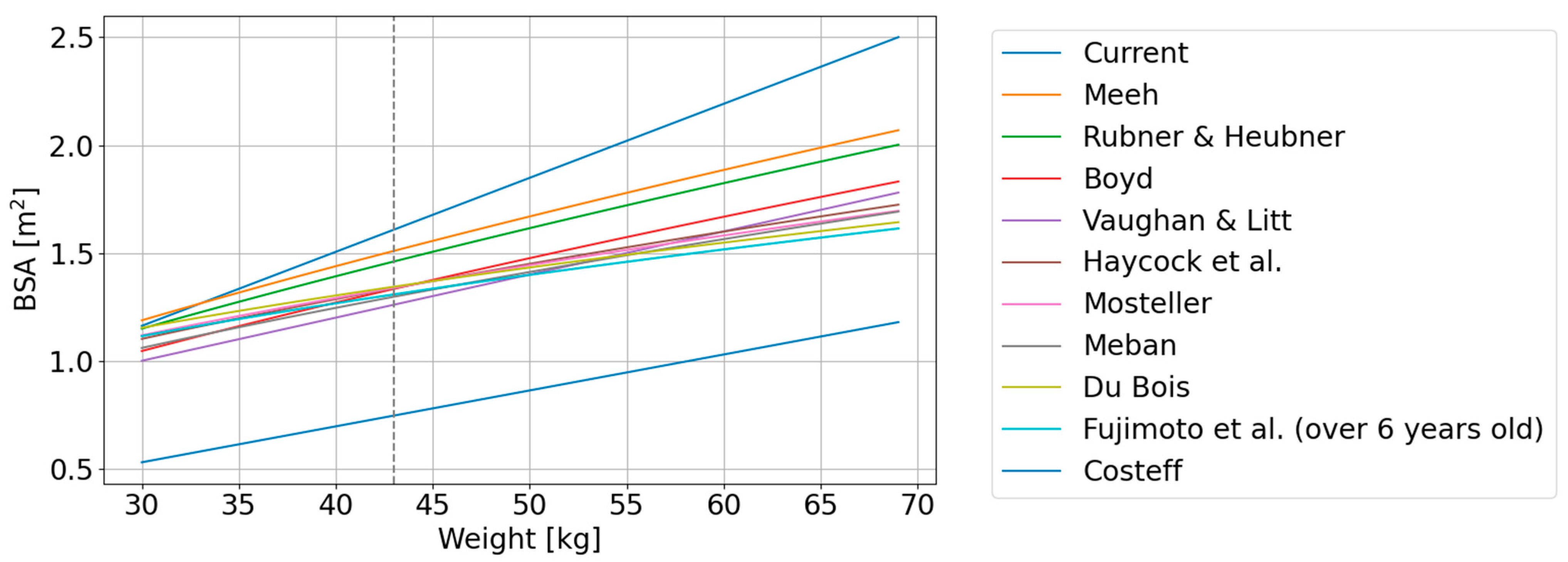
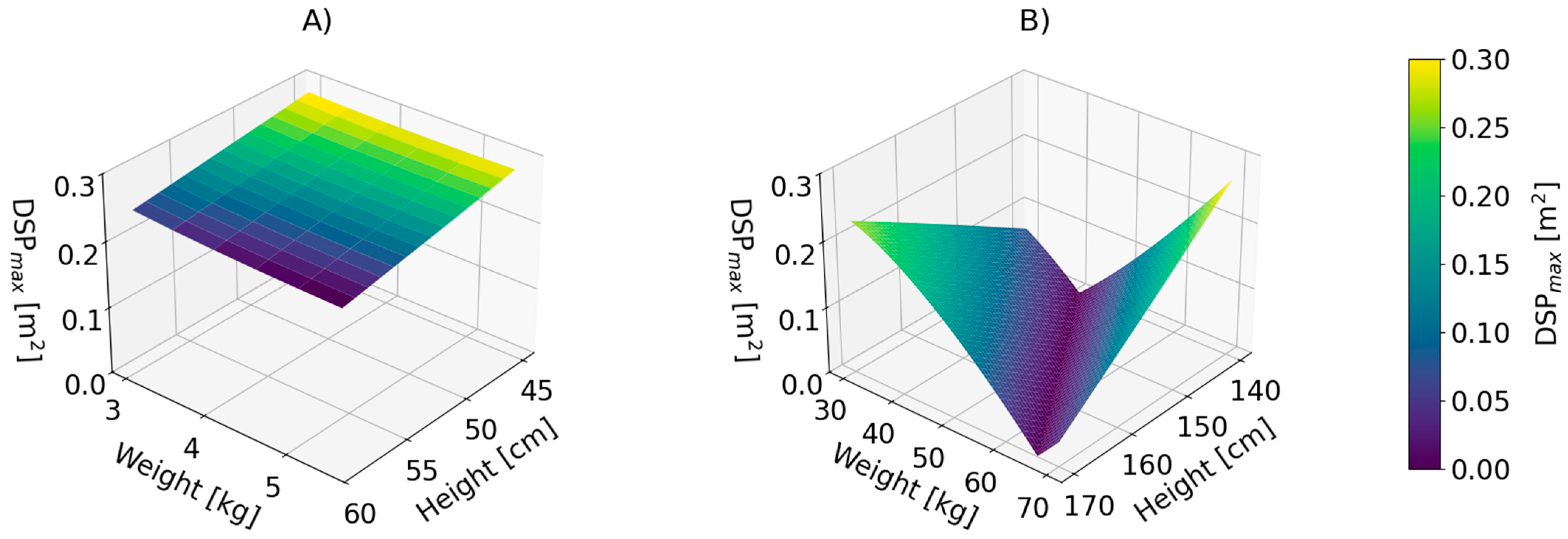
| No. | Authors | Year | Formula | Reference |
|---|---|---|---|---|
| 1 | Meeh | 1879 | 0.123 × W2/3 | [14] |
| 2 | Rubner & Heubner | 1898 | 0.119 × W2/3 | [21] |
| 3 | Lissauer | 1903 | neonates: 0.103 × W2/3 toddlers: 0.1 × W2/3 | [16] |
| 4 | DuBois & DuBois | 1916 | 0.007184 × W0.425 × H0.725 | [4] |
| 5 | Boyd | 1935 | 0.0004688 × (1000 × W) 0.8168−0.0154×log10(1000×W) | [18] |
| 6 | Banerjee & Bhattacharya | 1961 | 0.007 × W0.425 × H0.725 | [22] |
| 7 | Costeff | 1966 | [17] | |
| 8 | Fujimoto et al. | 1968 | infants: 0.009568 × W0.473 × H0.655 1–5 years: 0.0381 × W0.423 × H0.362 over 6 years: 0.008883 × W0.444 × H0.663 | [15] |
| 9 | Haycock et al. | 1978 | 0.024265 × W0.5378 × H0.3964 | [19] |
| 10 | Meban | 1983 | 0.00064954 × (1000 × W)0.562 × H0.32 | [23] |
| 11 | Mosteller | 1987 | [24] | |
| 12 | Vaughan & Litt | 1987 | 0.02 × W +0.4 | [25] |
| 13 | Current | 1998 | 0.03433 × W + 0.1321 | [26] |
| 14 | Nwoye & AlShehri | 2005 | Neonates: 0.03614 × W0.529 × H0.294 Neonates (simplified): 0.042 × W + 0.074 | [20] |
| Disease | Regimen | Reference | Drug | Therapeutic Singular Doses | Dosage | Comments/Assumptions | ||
|---|---|---|---|---|---|---|---|---|
| MIN | AVG | MAX | ||||||
| Wilms’ tumour [45,46] | EE4A | [45] | vincristine | 1.5 mg/m2 | 1.884 mg | 2.078 mg | 2.4 mg | |
| dactinomycin | 1.35 mg/m2 | 1.696 mg | 1.87 mg | 2.161 mg | ||||
| DD4A | vincristine | 1.5 mg/m2 | 1.884 mg | 2.078 mg | 2.4 mg | |||
| dactinomycin | 1.35 mg/m2 | 1.696 mg | 1.87 mg | 2.161 mg | ||||
| doxorubicin | 40 mg/m2 | 50.24 mg | 55.4 mg | 64.04 mg | ||||
| M | [47] | vincristine | 1.5 mg/m2 | 1.884 mg | 2.078 mg | 2.4 mg | dosage of dactinomycin given in mg/kg | |
| dactinomycin | 0.045 mg/kg | 1.935 mg | ||||||
| doxorubicin | 45 mg/m2 | 56.52 mg | 62.325 mg | 72.045 mg | ||||
| cyclophosphamide | 440 mg/m2 | 552.64 mg | 609.4 mg | 704.44 mg | ||||
| etoposide | 100 mg/m2 | 125.6 mg | 138.5 mg | 160.1 mg | ||||
| Retinoblastoma | VEC | [48,49] | vincristine | 1.5 mg/m2 | 1.884 mg | 2.078 mg | 2.4 mg | unilateral, intraocular retinoblastoma |
| carboplatin | 560 mg/m2 | 703.36 mg | 775.6 mg | 896.56 mg | ||||
| etoposide | 100 mg/m2 | 125.6 mg | 138.5 mg | 160.1 mg | ||||
| Ewing sarcoma | VDC-IE | [50] | vincristine | 1.4 mg/m2 | 1.758 mg | 1.939 mg | 2.241 mg | |
| doxorubicin | 75 mg/m2 | 94.2 mg | 103.875 mg | 120.075 mg | ||||
| cyclophosphamide | 1200 mg/m2 | 1507.2 mg | 1662 mg | 1921.2 mg | ||||
| ifosfamide | 9 mg/m2 | 11.304 mg | 12.465 mg | 14.409 mg | ||||
| etoposide | 500 mg/m2 | 628 mg | 692.5 mg | 800.5 mg | ||||
| Neuroblastoma | IrEC | [51] | irinotecan | 100 mg/m2 | 125.6 mg | 138.5 mg | 160.1 mg | 2nd line, proposed for relapse |
| etoposide | 100 mg/m2 | 125.6 mg | 138.5 mg | 160.1 mg | ||||
| carboplatin | 80 mg/m2 | 100.48 mg | 110.8 mg | 128.08 mg | ||||
| CEM | [52] | carboplatin | 800 mg/m2 | 1004.8 mg | 1108 mg | 1280.8 mg | bone marrow conditioning before HSCT in high-risk neuroblastoma | |
| etoposide | 500 mg/m2 | 628 mg | 692.5 mg | 800.5 mg | ||||
| melphalan | 70 mg/m2 | 87.92 mg | 96.95 mg | 112.07 mg | ||||
| ALL | EsPHALL + Berlin Frankfurt Munster | [53] | dexamethasone | 20 mg/m2 | 25.12 mg | 27.7 mg | 32.02 mg | not all drugs used simultaneously; not all of drugs used in all cycles |
| vincristine | 1.5 mg/m2 | 1.884 mg | 2.078 mg | 2.4 mg | ||||
| methotrexate | 5000 mg/m2 | 6280 mg | 6925 mg | 8005 mg | ||||
| cytarabine | 2000 mg/m2 | 2512 mg | 2770 mg | 3202 mg | ||||
| L-asparaginase | 25.000 IU/m2 | 31400 IU | 34625 IU | 40025 IU | ||||
| cyclophosphamide | 200 mg/m2 | 251.2 mg | 277 mg | 320.2 mg | ||||
| imatinib | 300 mg/m2 | 376.8 mg | 415.5 mg | 480.3 mg | ||||
| daunorubicin | 30 mg/m2 | 37.68 mg | 41.55 mg | 48.03 mg | ||||
| ifosfamide | 800 mg/m2 | 1004.8 mg | 1108 mg | 1280.8 mg | ||||
| MTX/6MP | [54] | methotrexate | 20 mg/m2 | 25.12 mg | 27.7 mg | 32.02 mg | maintenance regimen; different dosage variants | |
| 40 mg/m2 | 50.24 mg | 55.40 mg | 64.04 mg | |||||
| 6-mercaptopurine | 50 mg/m2 | 62.8 mg | 69.25 mg | 80.05 mg | ||||
| 75 mg/m2 | 94.2 mg | 103.875 mg | 120.075 mg | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Litzbarski, L.S.; Redlarski, G.; Tojza, P.M.; Cieślikowska, Z.; Czapliński, M. An Ambiguity in Child Body Surface Area Measurement. Appl. Sci. 2025, 15, 12454. https://doi.org/10.3390/app152312454
Litzbarski LS, Redlarski G, Tojza PM, Cieślikowska Z, Czapliński M. An Ambiguity in Child Body Surface Area Measurement. Applied Sciences. 2025; 15(23):12454. https://doi.org/10.3390/app152312454
Chicago/Turabian StyleLitzbarski, Leszek Sławomir, Grzegorz Redlarski, Piotr Mateusz Tojza, Zuzanna Cieślikowska, and Mieszko Czapliński. 2025. "An Ambiguity in Child Body Surface Area Measurement" Applied Sciences 15, no. 23: 12454. https://doi.org/10.3390/app152312454
APA StyleLitzbarski, L. S., Redlarski, G., Tojza, P. M., Cieślikowska, Z., & Czapliński, M. (2025). An Ambiguity in Child Body Surface Area Measurement. Applied Sciences, 15(23), 12454. https://doi.org/10.3390/app152312454







