Bearing Fault Diagnosis Based on Multi-Channel WOA-VMD and Tucker Decomposition
Abstract
1. Introduction
2. Methods
2.1. Principle of Variational Mode Decomposition and Adaptability Analysis for Tensor Construction
- denotes the partial derivative with respect to time t;
- is the dirac dalta function;
- is the k-th mode component;
- is its center frequency, and j is the imaginary unit.
- is a step-size parameter controlling convergence;
- is the pre-set convergence tolerance.
2.2. Adaptive Parameter Optimization Strategy for VMD Based on Whale Optimization Algorithm (WOA)
- b is the spiral constant;
- l ∈ [−1, 1] is a random number.
- D is the distance between the simulation and the target.
- represents the current position of the whale;
- denotes the current global best position;
- refers to a randomly selected whale from the population.
- and are random numbers uniformly distributed in [0, 1];
- is a linearly decreasing factor over the iterations.
2.3. Tensor Dimensionality Reduction and Feature Extraction Based on Tucker Decomposition
- denotes the mode-n product between a tensor and a matrix;
- is the core tensor;
- , , and are the factor matrices along the mode (modal), time, and channel dimensions, respectively.
- is core tensor;
- , , and are and factor matrices
- denotes the i-the sample;
- μ is the sample mean;
- N is the length of the signal.
2.4. Construction of Fault Classification Model Based on SVM
- is the slack variable to allow misclassification;
- C is the regularization parameter (penalty factor) that controls the trade-off between maximizing the margin and minimizing the classification error.
- α is the Lagrange multiplier.
- is the input vector;
- is the corresponding label;
- is the kernel function used to compute the inner product in the high-dimensional feature space.
- is the kernel width parameter that controls the smoothness of the decision boundary.
2.5. Diagnostic Process
- (1)
- The signals were decomposed using WOA-VMD, with key parameters adaptively optimized via the WOA.
- (2)
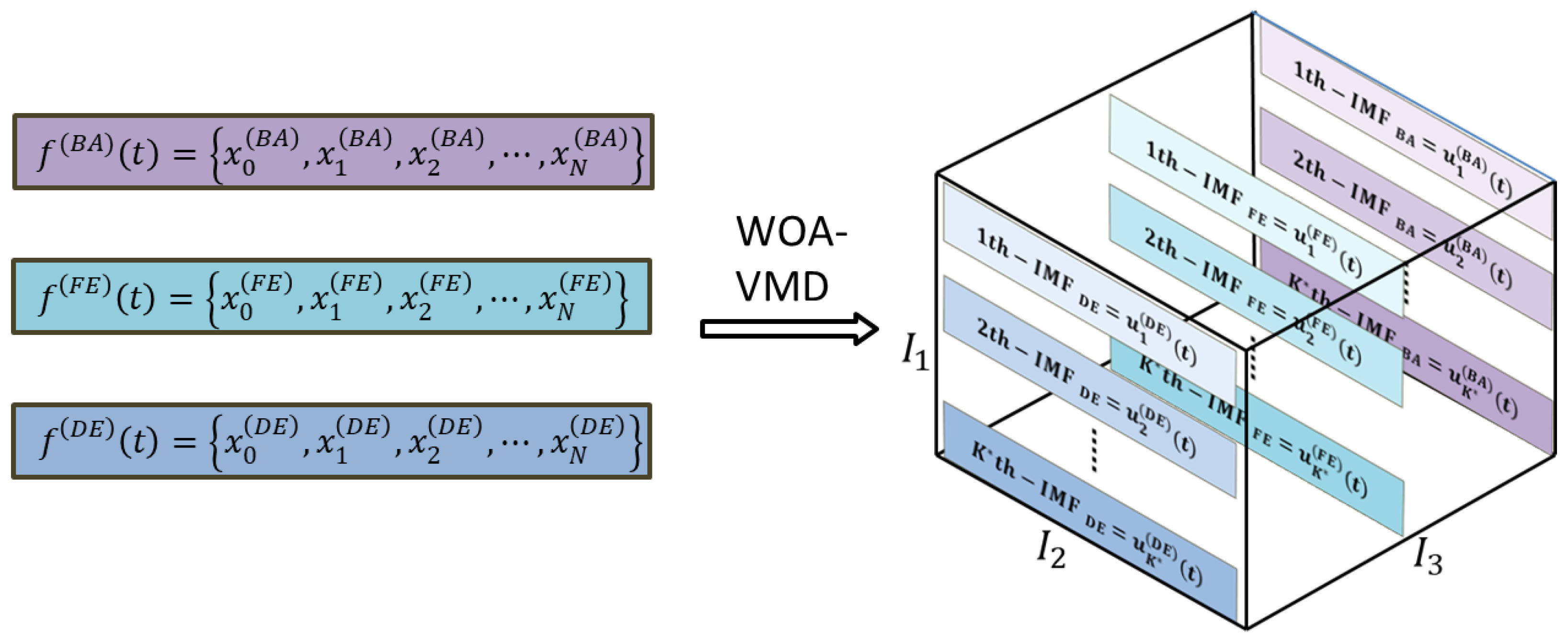
- The IMFs from all channels were stacked along the channel dimension to construct a third-order tensor (mode × time × channel), preserving both temporal and spatial information.
- (3)
- Tucker decomposition was applied to the constructed tensor to extract compact and discriminative features, from which statistical indicators, including standard deviation, kurtosis, and waveform factor, were calculated.
- (4)
- The extracted features were divided into training and testing sets and input into SVM classifier for model training and fault diagnosis, enabling accurate identification of different bearing fault types.
3. Experimental Analysis
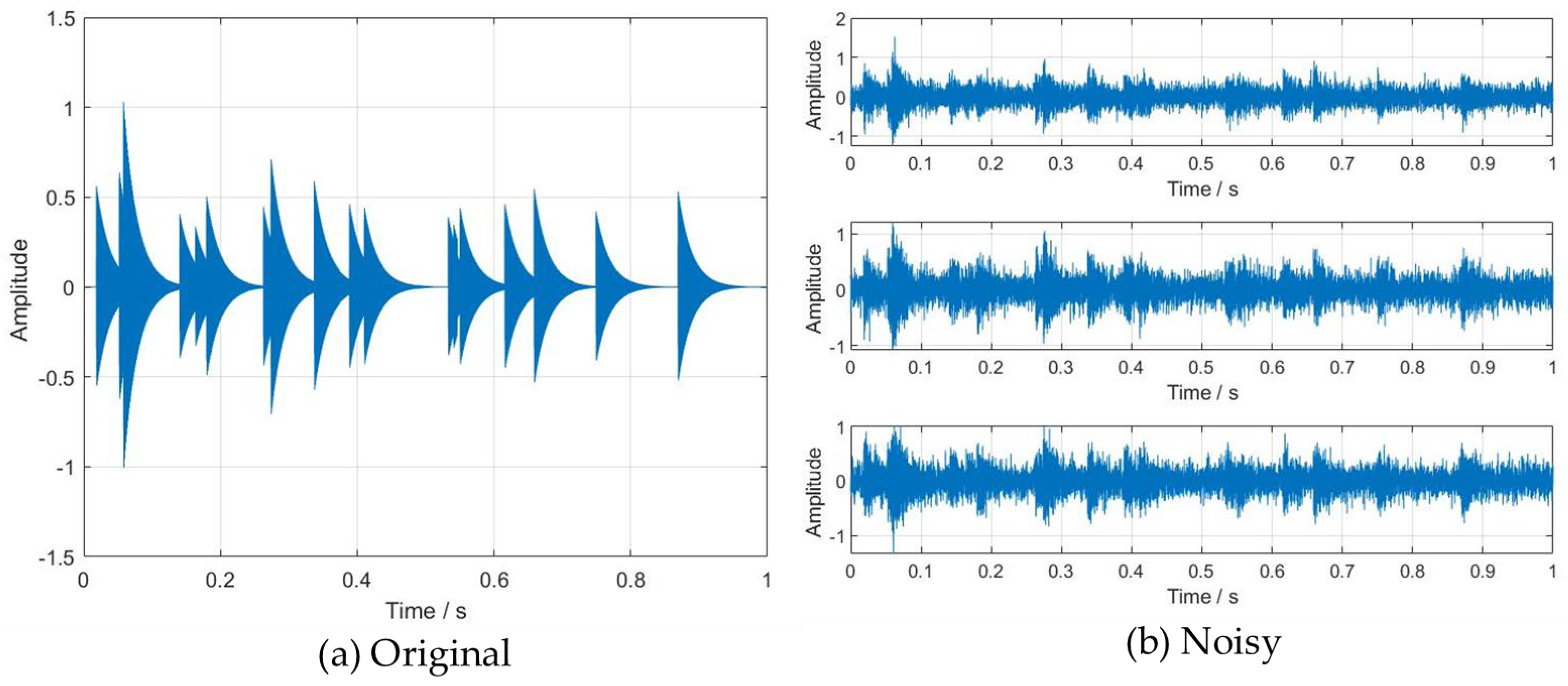
3.1. Denoising Performance Verification Based on Simulated Signals
- P is the number of impact pulses;
- is the amplitude of the i-th pulse;
- is the occurrence time of the i-th pulse;
- is the attenuation coefficient that controls the decay rate of each impact;
- is the resonance frequency;
- represents Gaussian white noise added to mask the impulsive features and simulate various levels of signal-to-noise ratio (SNR) across channels.
- Psignal and Pnoise represent the average power of the clean signal and noise, respectively.
| Method | SNR (dB) |
|---|---|
| VMD | 7.02 |
| GA-VMD | 9.14 |
| AO-VMD | 9.19 |
| ALO-VMD | 10.17 |
| WOA-VMD | 13.35 |
3.2. Fault Diagnosis Verification Based on Real Multi-Channel Signals
3.2.1. Dataset Description
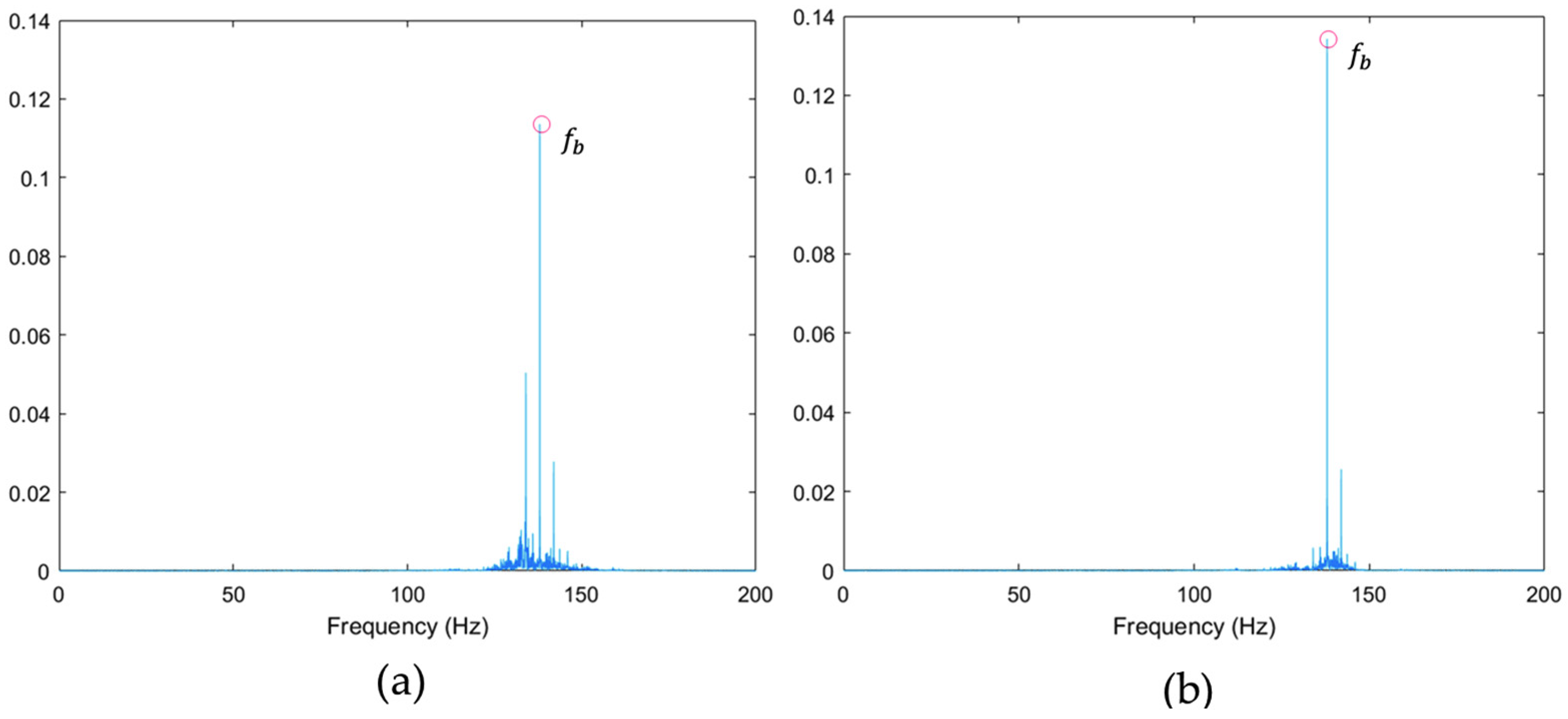
3.2.2. Effectiveness of the WOA-VMD Method in Fault Signal Denoising
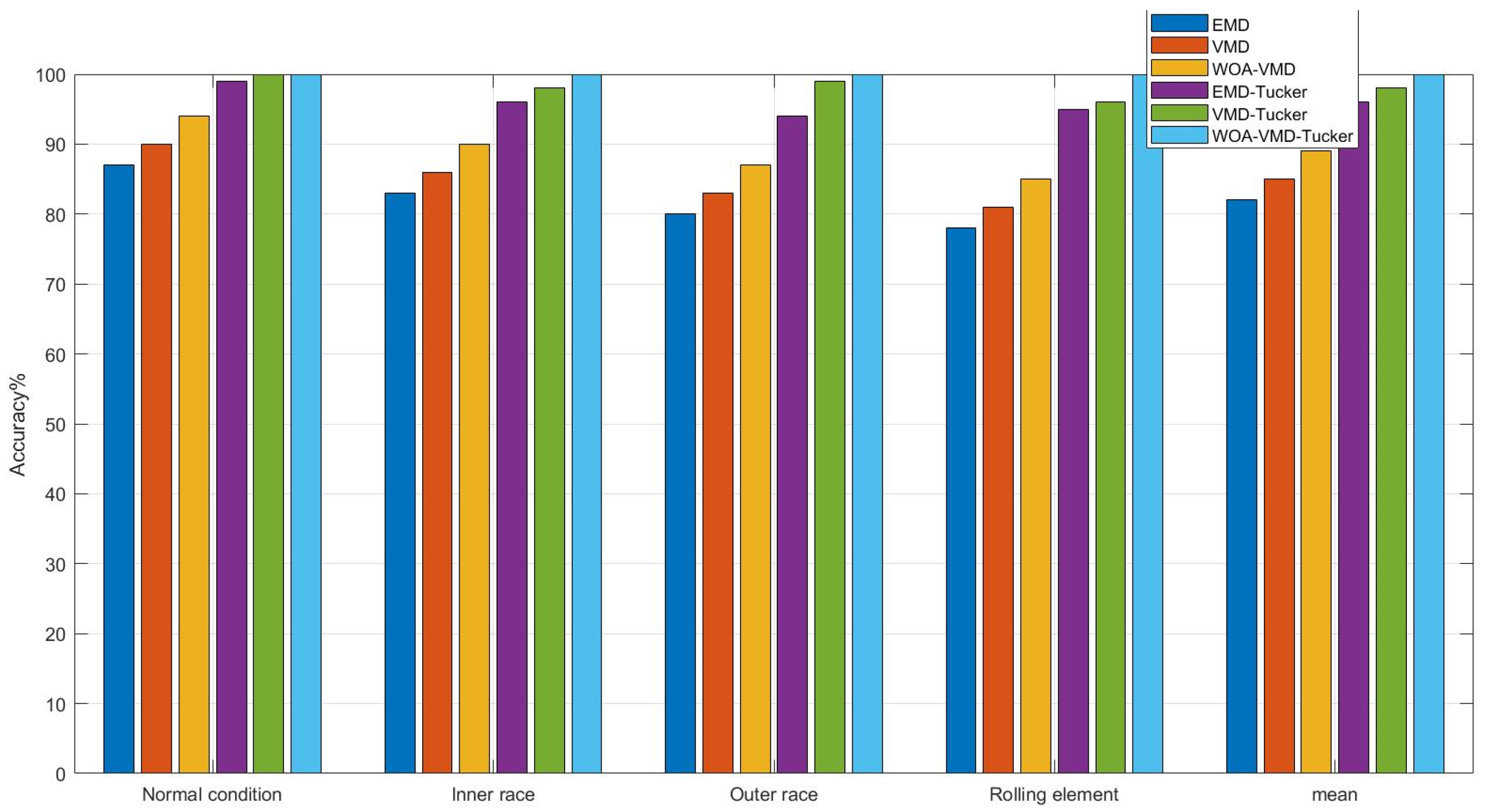
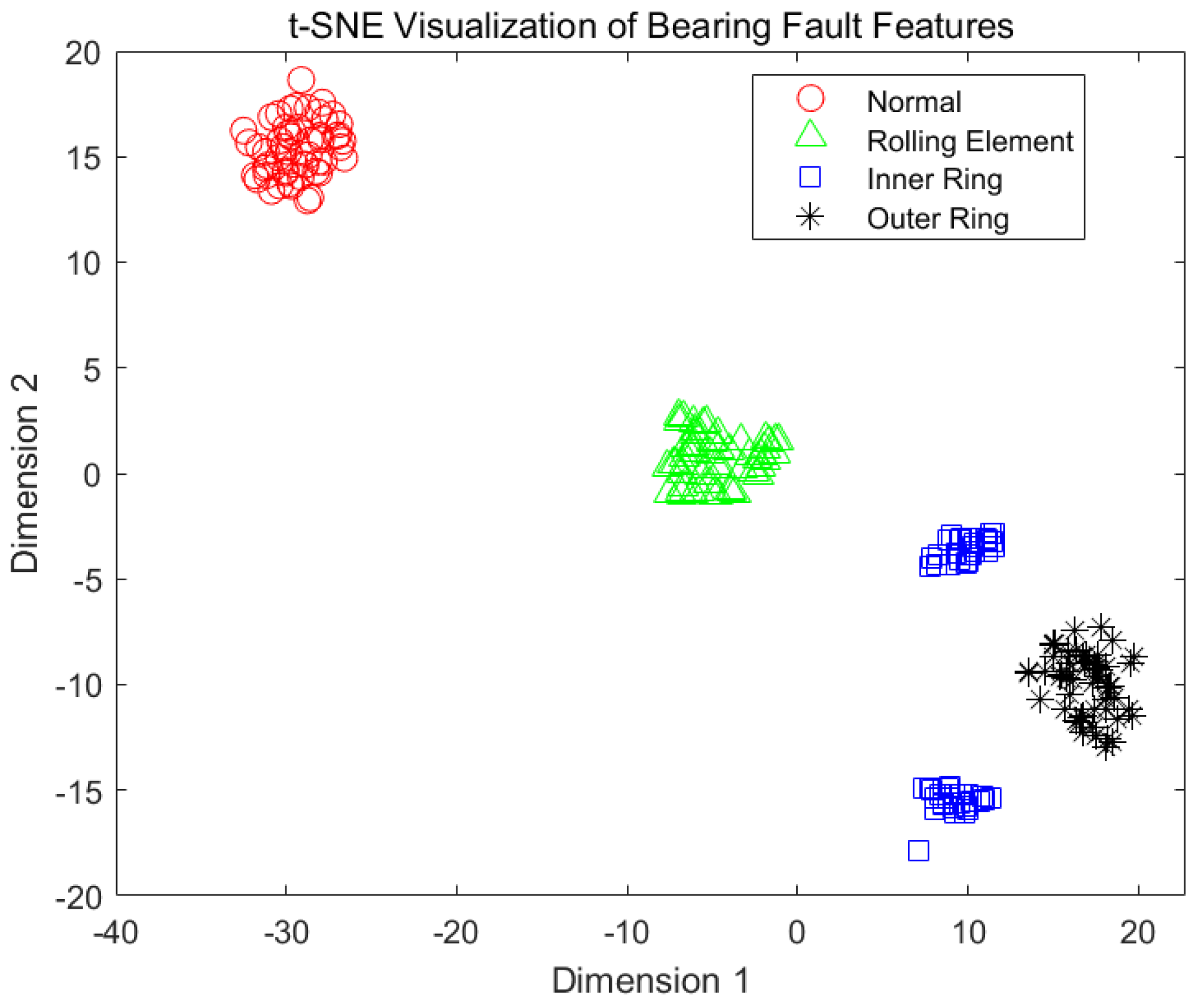
3.3. Comparative Analysis of Fault Diagnosis Performance Using Different Feature Extraction Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fang, Z.; Wu, Q.-E.; Wang, W.; Wu, S. Research on Improved Fault Detection Method of Rolling Bearing Based on Signal Feature Fusion Technology. Appl. Sci. 2023, 13, 12987. [Google Scholar] [CrossRef]
- Sacerdoti, D.; Strozzi, M.; Secchi, C. A Comparison of Signal Analysis Techniques for the Diagnostics of the IMS Rolling Element Bearing Dataset. Appl. Sci. 2023, 13, 5977. [Google Scholar] [CrossRef]
- Wang, N.; Ma, P.; Zhang, H.; Wang, C. Fault Feature Enhancement and Diagnosis of Rolling Bearing Based on Complex Network. In Proceedings of the 2021 CAA Symposium on Fault Detection, Supervision, and Safety for Technical Processes (SAFEPROCESS), Chengdu, China, 17–18 December 2021; pp. 1–6. [Google Scholar]
- Xia, P.; Xu, H.; Lei, M.; Zhang, S. An Improved Underdamped Asymmetric Bistable Stochastic Resonance Method and its Application for Spindle Bearing Fault Diagnosis. IEEE Access 2020, 8, 46824–46836. [Google Scholar] [CrossRef]
- Wen, J.; Xu, F. Decision-Level Fusion-Based Compressor Blade Crack Detection Method Using Acoustic and Vibration Signals. In Proceedings of the 2023 6th International Conference on Mechatronics, Robotics and Automation (ICMRA), Xiamen, China, 17–19 November 2023. [Google Scholar]
- Tang, H.; Lu, S.; Qian, G.; Ding, J.; Liu, Y.; Wang, Q. IoT-Based Signal Enhancement and Compression Method for Efficient Motor Bearing Fault Diagnosis. IEEE Sens. J. 2021, 21, 1820–1828. [Google Scholar] [CrossRef]
- Nadide, G.; Mahmut, O. Diagnosis of Major Depressive Disorder from EEG Signals Using Empirical Wavelet Transform and Machine Learning Methods. In Proceedings of the 2024 Medical Technologies Congress (TIPTEKNO), Mugla, Turkiye, 10–12 October 2024; pp. 1–4. [Google Scholar]
- Alimuradov, A.; Tychkov, A. EMD-Based Noise-Robust Method For Speech/Pause Segmentation. In Proceedings of the 2021 3rd International Youth Conference on Radio Electronics, Electrical and Power Engineering (REEPE), Moscow, Russia, 11–13 March 2021; pp. 1–8. [Google Scholar]
- Chen, X.; Guo, Y.; Na, J. Proportional Selection Scheme: A Frequency Band Division Tool for Rolling Element Bearing Diagnostics. IEEE Trans. Ind. Electron. 2022, 69, 9504–9513. [Google Scholar] [CrossRef]
- Kucukselbes, H.; Sayilgan, E. Analysing SCI Patients’EEG Signal Using Manifold Learning Methods For Triple Command BCI Design. In Proceedings of the 2024 International Conference on INnovations in Intelligent SysTems and Applications (INISTA), Craiova, Romania, 4–6 September 2024; pp. 1–5. [Google Scholar]
- Wu, Q.; Gao, Q.; Lu, Y.; Zhu, D.; Sun, D.; Zhao, D. Incipient Fault Diagnosis Method via Joint Adaptive Signal Decomposition. IEEE Sens. J. 2024, 24, 24308–24318. [Google Scholar] [CrossRef]
- Huang, Y.; Xu, Z.; Jie, Z.; Shen, T.; Cao, L.; Wang, J. Bearing Fault Diagnosis Based on Time-Varying Targeted Enhancement of Stress Wave Signal. In Proceedings of the 2024 IEEE International Conference on Sensing, Diagnostics, Prognostics, and Control (SDPC), Shijiazhuang, China, 26–28 July 2024; pp. 57–62. [Google Scholar]
- Liao, Z.; Liang, G.; Song, X.; Li, X.; Huang, Z. AC Motor Fault Diagnosis Based on Multi-Source Signal Fusion SDP. In Proceedings of the 2024 Global Reliability and Prognostics and Health Management Conference (PHM-Beijing), Beijing, China, 11–13 October 2024; pp. 1–8. [Google Scholar]
- Hsieh, N.-K.; Yu, T.-Y. Fault Detection in Harmonic Drive Using Multi-Sensor Data Fusion and Gravitational Search Algorithm. Machines 2024, 12, 831. [Google Scholar] [CrossRef]
- Ma, H.; Li, J.; Huang, J.; Wang, R.; Ge, R.; Zhang, F. Adaptive Embedded Flexible Tensor Singular Spectrum Decomposition. Electronics 2025, 14, 21. [Google Scholar] [CrossRef]
- Yin, Y.; Yuan, R.; Lv, Y.; Wu, H.; Li, H.; Zhu, W. Low-Rank Tensor Train Dynamic Mode Decomposition: An Enhanced Multivariate Signal Processing Method for Mechanical Fault Diagnosis. IEEE Trans. Instrum. Meas 2025, 74, 1–16. [Google Scholar] [CrossRef]
- Jiang, H.; Wu, Y.; Yuan, J.; Zhao, Q.; Chen, J. Adaptive Low-Rank Tensor Estimation Model Based Multichannel Weak Fault Detection for Bearings. Sensors 2024, 24, 3762. [Google Scholar] [CrossRef] [PubMed]
- Chu, Z.; Guo, Q.; Wang, C. The PID Control Algorithm based on Whale Optimization Algorithm Optimized BP Neural Network. In Proceedings of the 2023 IEEE 7th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 15–17 September 2023; pp. 2450–2453. [Google Scholar]
- Zou, Y.; Zhang, X.; Zhao, W.; Liu, T. Rolling Bearing Fault Diagnosis Based on Optimized VMD Combining Signal Features and Improved CNN. World Electr. Veh. J. 2024, 15, 544. [Google Scholar] [CrossRef]
- Yang, L.; Wang, J.; Xie, X.; Kuang, J. Application of tucker decomposition in speech signal feature extraction. In Proceedings of the 2013 International Conference on Asian Language Processing, Urumqi, China, 17–19 August 2013; pp. 155–158. [Google Scholar]
- Zhang, M.; Yin, J.; Chen, W. Rolling Bearing Fault Diagnosis Based on Time-Frequency Feature Extraction and IBA-SVM. IEEE Access 2022, 10, 85641–85654. [Google Scholar] [CrossRef]



| SNR (dB) | Methods | Vibration | |||
|---|---|---|---|---|---|
| ACC (%) | PC (%) | RC (%) | F1 (%) | ||
| (−10, −5, 0) | VMD | 92.5 ± 0.6 | 93.0 ± 0.5 | 92.0 ± 0.7 | 92.5 ± 0.6 |
| GA-VMD | 95.4 ± 0.4 | 94.8 ± 0.6 | 96.2 ± 0.5 | 95.5 ± 0.4 | |
| AO-VMD | 96.1 ± 0.5 | 95.5 ± 0.5 | 95.8 ± 0.4 | 95.6 ± 0.5 | |
| ALO-VMD | 96.8 ± 0.4 | 97.1 ± 0.3 | 95.9 ± 0.4 | 96.5 ± 0.3 | |
| WOA-VMD | 98.4 ± 0.3 | 98.6 ± 0.3 | 98.2 ± 0.3 | 98.4 ± 0.2 | |
| (−10, −8, −5) | VMD | 91.0 ± 0.7 | 89.5 ± 0.8 | 88.9 ± 0.7 | 89.2 ± 0.8 |
| GA-VMD | 95.0 ± 0.4 | 95.3 ± 0.5 | 94.7 ± 0.4 | 95.0 ± 0.4 | |
| AO-VMD | 96.3 ± 0.3 | 96.5 ± 0.3 | 96.1 ± 0.3 | 96.3 ± 0.3 | |
| ALO-VMD | 96.5 ± 0.3 | 96.5 ± 0.3 | 96.1 ± 0.4 | 96.3 ± 0.3 | |
| WOA-VMD | 98.9 ± 0.4 | 99.1 ± 0.4 | 98.6 ± 0.3 | 98.8 ± 0.3 | |
| SNR (dB) | Fault Type | Vibration | |||
|---|---|---|---|---|---|
| ACC (%) | PC (%) | RC (%) | F1 (%) | ||
| (−10, −5, 0) | Inner race fault | 98.2 ± 0.3 | 98.0 ± 0.4 | 98.1 ± 0.4 | 98.1 ± 0.3 |
| Outer race fault | 98.4 ± 0.4 | 98.3 ± 0.3 | 98.2 ± 0.3 | 98.3 ± 0.3 | |
| Ball fault | 98.6 ± 0.4 | 98.5 ± 0.3 | 98.4 ± 0.4 | 98.5 ± 0.3 | |
| (−10, −8, −5) | Inner race fault | 98.7 ± 0.3 | 98.5 ± 0.4 | 98.7 ± 0.3 | 98.7 ± 0.3 |
| Outer race fault | 98.9 ± 0.3 | 98.8 ± 0.4 | 98.9 ± 0.5 | 98.9 ± 0.4 | |
| Ball fault | 99.1 ± 0.4 | 99.0 ± 0.4 | 99.1 ± 0.3 | 99.0 ± 0.3 | |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Outer race diameter (mm) | 52 | Inner race diameter (mm) | 25 |
| Pitch diameter (mm) | 38.5 | Ball diameter (mm) | 7.94 |
| Number of balls | 9 | Cotact angle/(°) | 0 |
| Fault Type | Vibration | |||
|---|---|---|---|---|
| ACC (%) | PC (%) | RC (%) | F1 (%) | |
| Inner race fault | 99.5 ± 0.5 | 99.0 ± 0.3 | 98.5 ± 0.4 | 98.8 ± 0.3 |
| Outer race fault | 99.6 ± 0.4 | 98.5 ± 0.3 | 98.0 ± 0.3 | 98.3 ± 0.3 |
| Ball fault | 99.7 ± 0.3 | 99.2 ± 0.3 | 98.8 ± 0.4 | 99.0 ± 0.3 |
| Methods | Vibration | |||
|---|---|---|---|---|
| ACC (%) | PC (%) | RC (%) | F1 (%) | |
| MEMD-SVM | 82.0 ± 0.8 | 82.3 ± 0.9 | 81.8 ± 0.7 | 81.9 ± 0.8 |
| VMD-SVM | 84.2 ± 0.5 | 84.8 ± 0.6 | 83.9 ± 0.7 | 84.0 ± 0.6 |
| WOA-VMD-CNN | 82.3 ± 0.9 | 83.7 ± 1.1 | 82.5 ± 0.8 | 82.5 ± 1.0 |
| WOA-VMD-SVM | 86.3 ± 0.7 | 87.0 ± 0.9 | 85.8 ± 0.6 | 86.1 ± 0.7 |
| VMD-Tucker-CNN | 88.5 ± 0.4 | 89.7 ± 0.5 | 88.5 ± 0.6 | 86.9 ± 0.6 |
| VMD-Tucker-SVM | 93.3 ± 0.3 | 94.5 ± 0.4 | 93.3 ± 0.4 | 92.9 ± 0.5 |
| WOA-VMD-Tucker-CNN | 90.2 ± 0.6 | 91.5 ± 0.5 | 87.0 ± 0.8 | 90.1 ± 0.6 |
| WOA-VMD-Tucker-SVM | 99.6 ± 0.4 | 98.8 ± 0.4 | 98.5 ± 0.3 | 98.6 ± 0.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Pan, W.; Wu, Y.; Xiao, D.; Xu, M.; Qin, H.; Wang, Z. Bearing Fault Diagnosis Based on Multi-Channel WOA-VMD and Tucker Decomposition. Appl. Sci. 2025, 15, 12232. https://doi.org/10.3390/app152212232
Chen L, Pan W, Wu Y, Xiao D, Xu M, Qin H, Wang Z. Bearing Fault Diagnosis Based on Multi-Channel WOA-VMD and Tucker Decomposition. Applied Sciences. 2025; 15(22):12232. https://doi.org/10.3390/app152212232
Chicago/Turabian StyleChen, Lingjiao, Wenxin Pan, Yuezhong Wu, Danjing Xiao, Mingming Xu, Hualian Qin, and Zhongmei Wang. 2025. "Bearing Fault Diagnosis Based on Multi-Channel WOA-VMD and Tucker Decomposition" Applied Sciences 15, no. 22: 12232. https://doi.org/10.3390/app152212232
APA StyleChen, L., Pan, W., Wu, Y., Xiao, D., Xu, M., Qin, H., & Wang, Z. (2025). Bearing Fault Diagnosis Based on Multi-Channel WOA-VMD and Tucker Decomposition. Applied Sciences, 15(22), 12232. https://doi.org/10.3390/app152212232






