Novel Method to Improve the Convergence of Physics-Informed Neural Networks for Complex Thermal Simulations
Abstract
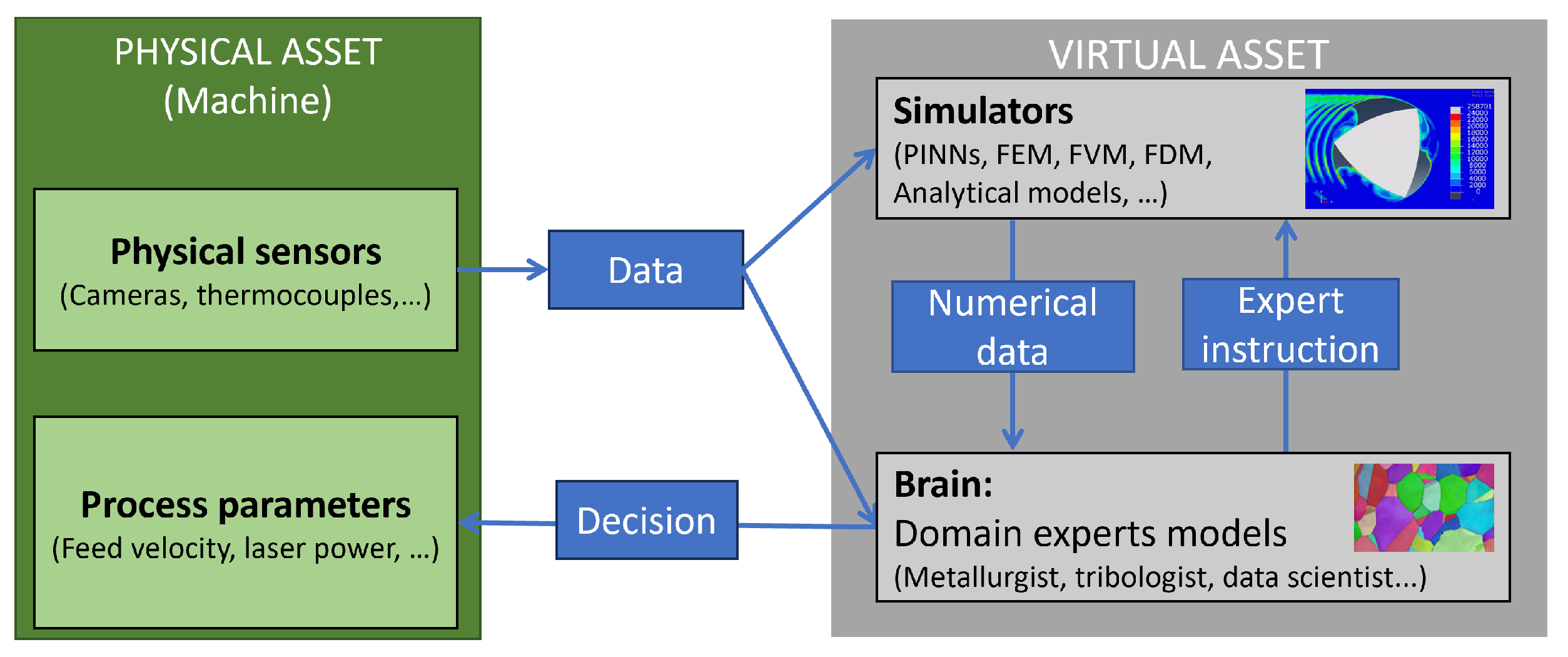
1. Introduction
- Real-time calculations: To enable real-time decision-making, predictions must be made in real time.
- Incorporating domain knowledge: The digital twin must integrate domain knowledge such as metallurgy, tribology, numerical analysis, and data science to make informed decisions [9].
- Online knowledge development: Some information is only available online and must be processed in real time, which creates the challenge of handling large volumes of data.
- Multi-scale models: The digital twin must cover all scales, from microstructure to machine level, to identify defects.
2. Modeling and Methods
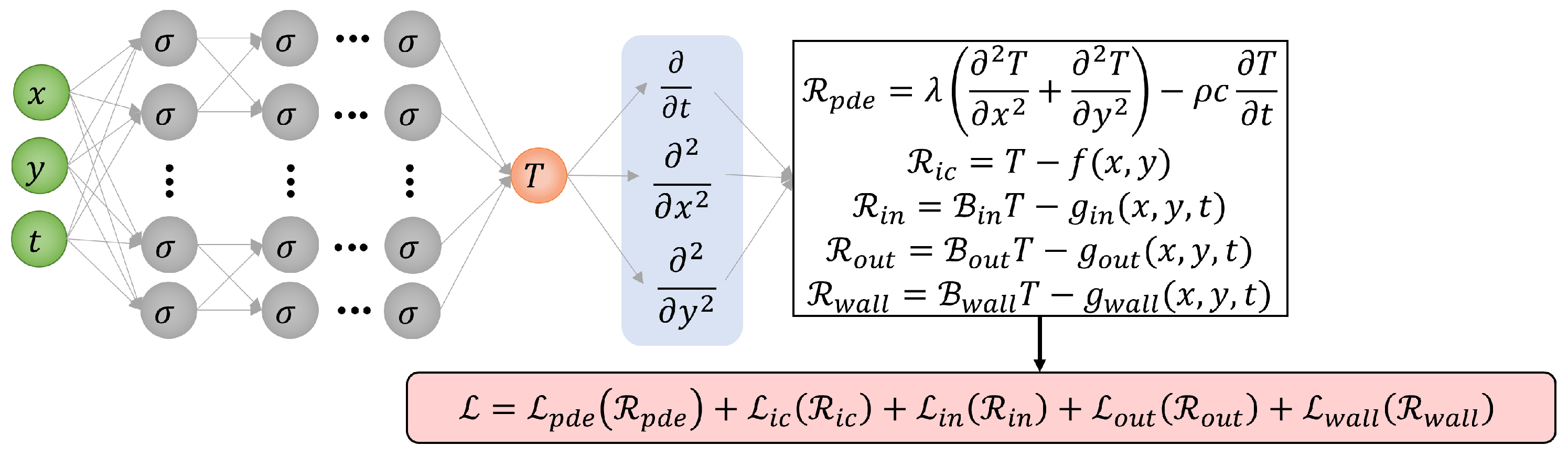
2.1. Classical PINN Method
2.2. SD-PINN Method
2.3. SDFEET-PINN Method
3. Benchmark Problems for Evaluation
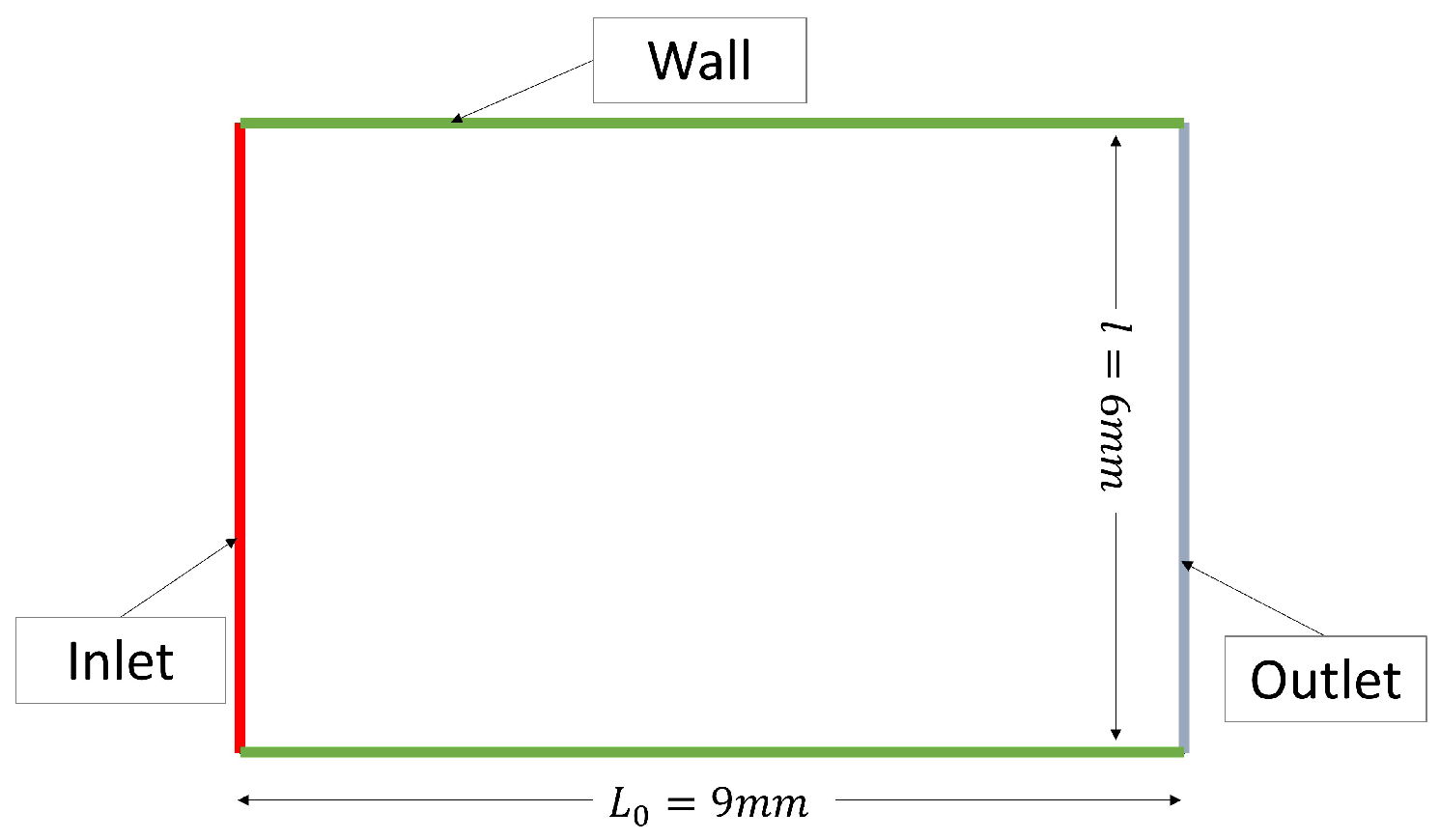
3.1. Problem with Dirichlet Boundary Conditions
3.2. Problem with Dirichlet and Newton Boundary Conditions
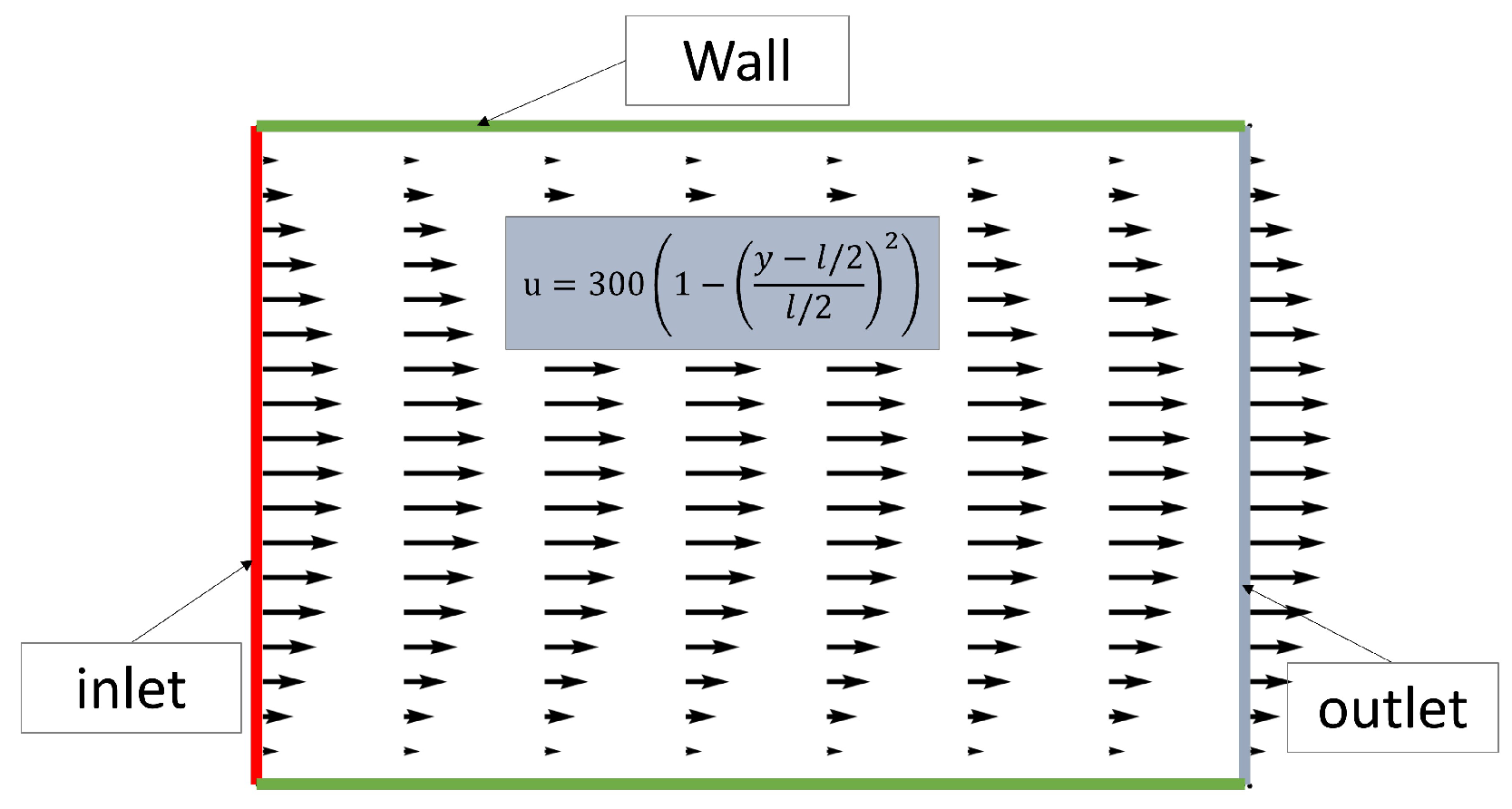
3.3. Problemwith Advection, Dirichlet, and Newton Boundary Conditions
3.4. Application to a Complex 3D Geometry
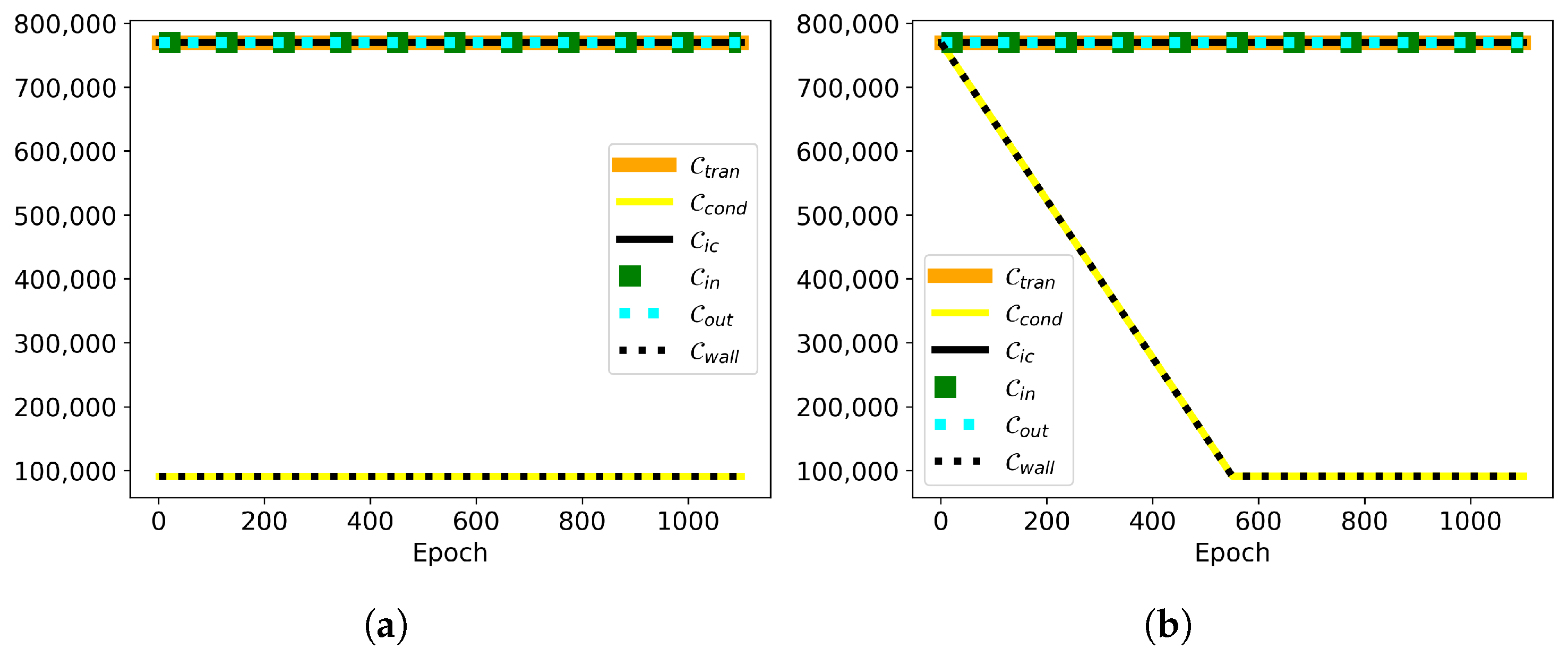
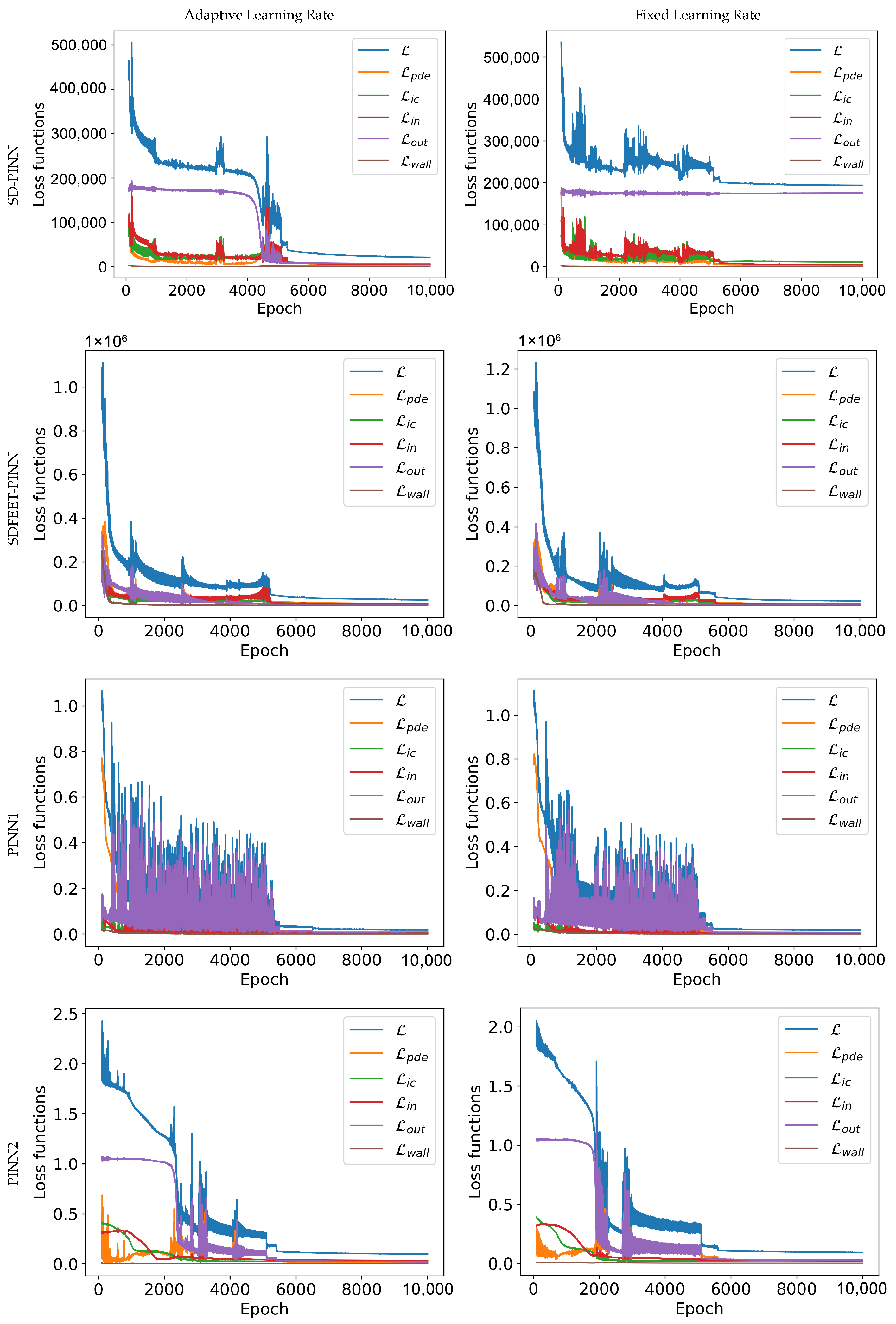
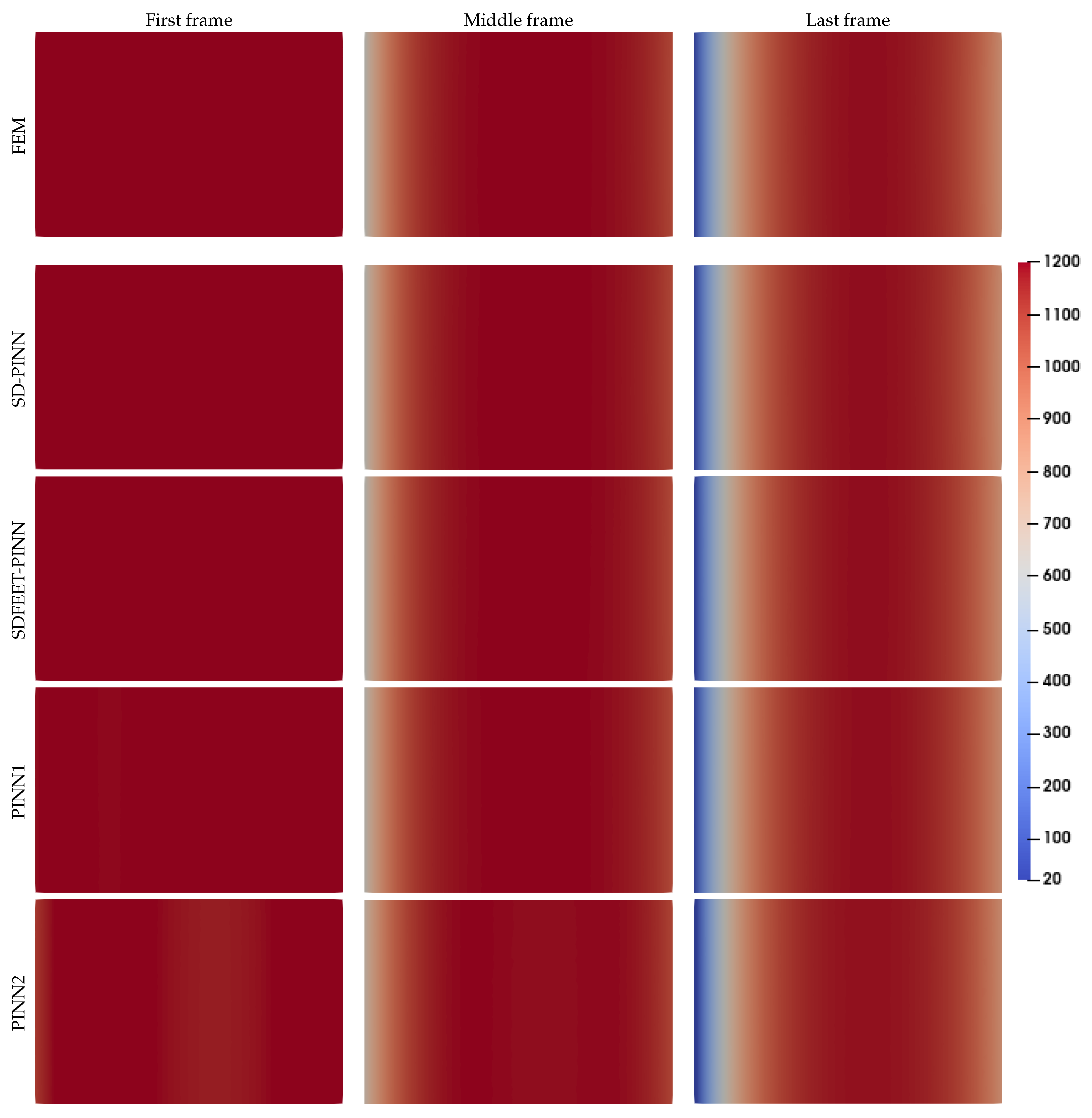
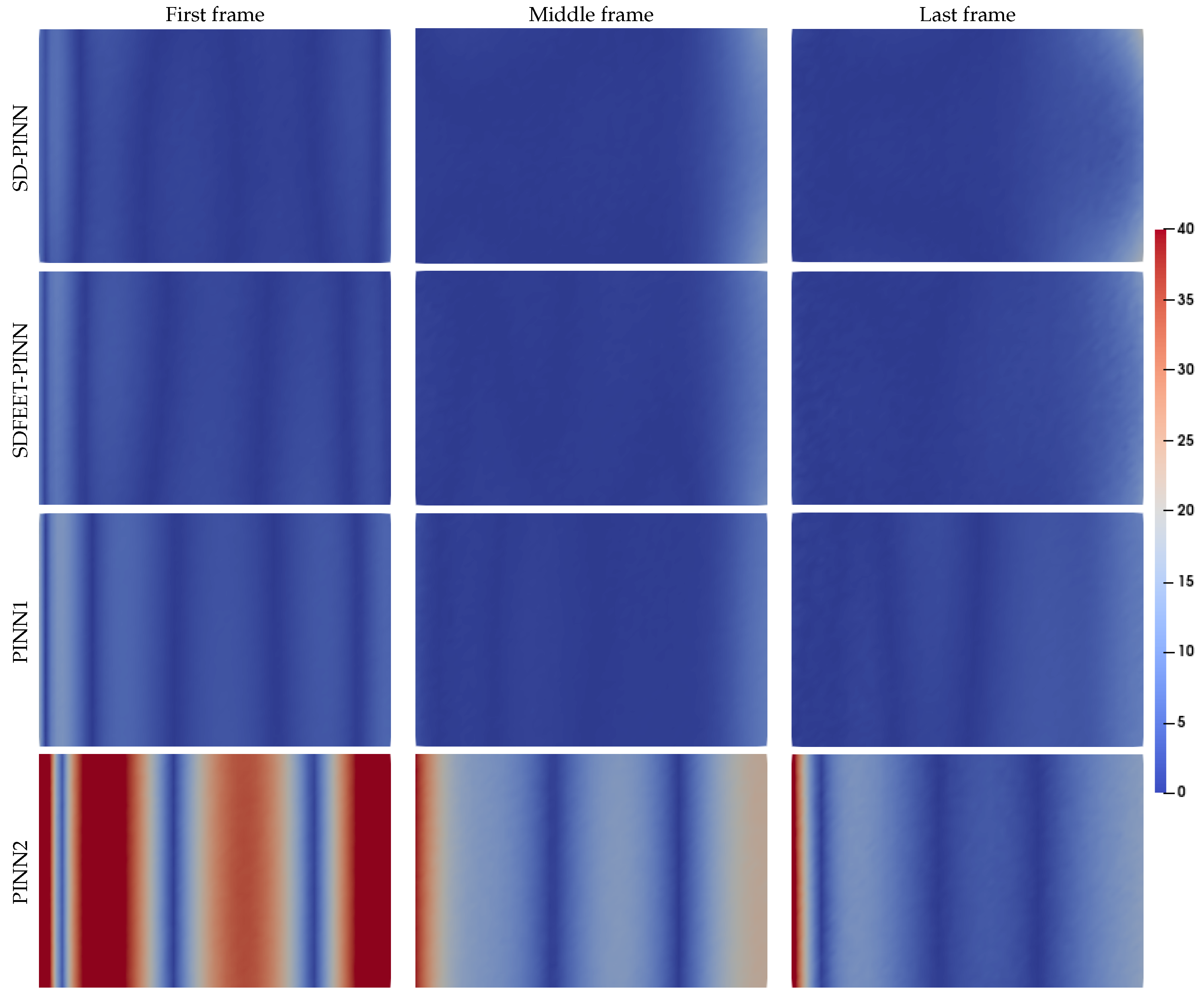
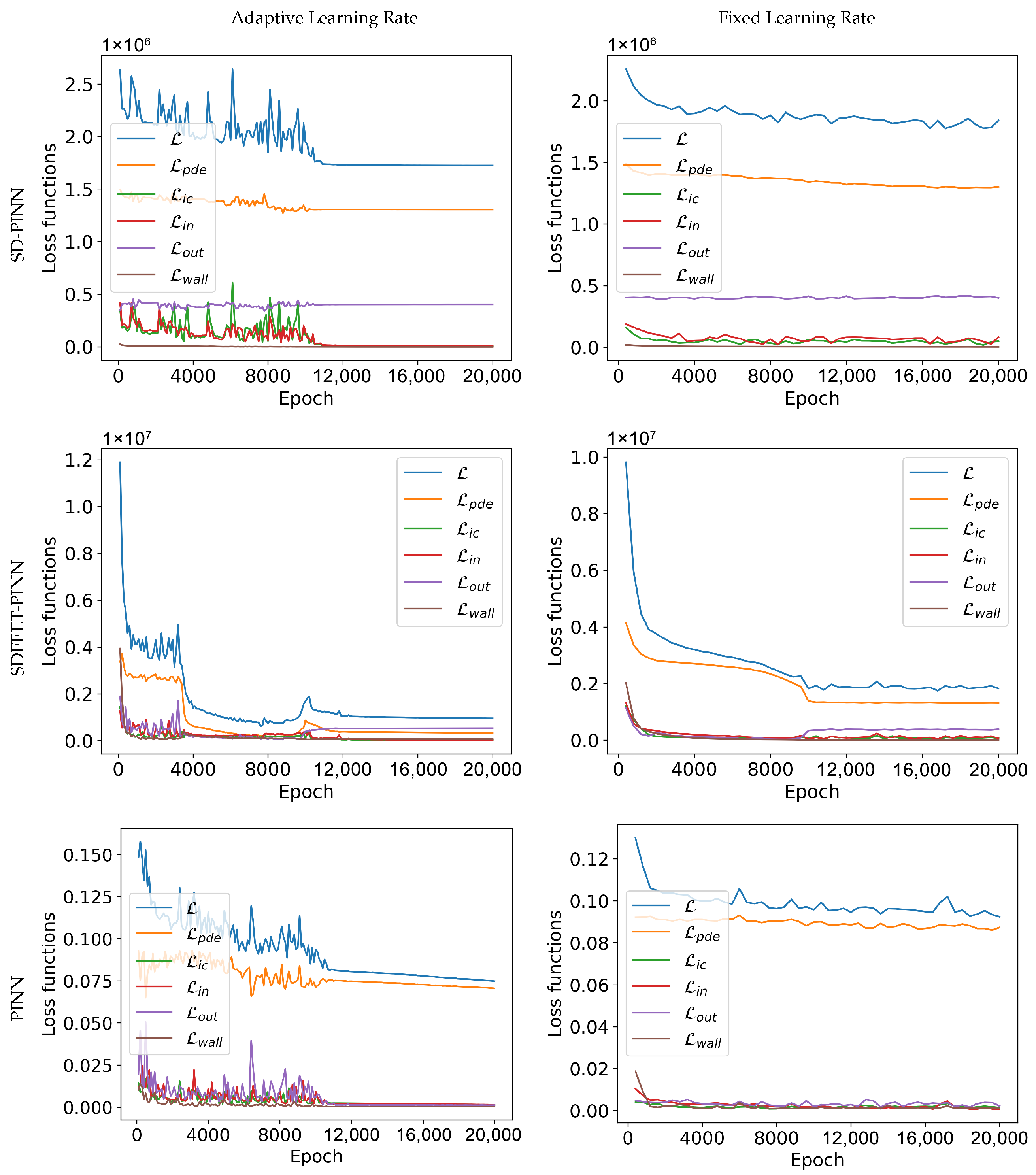
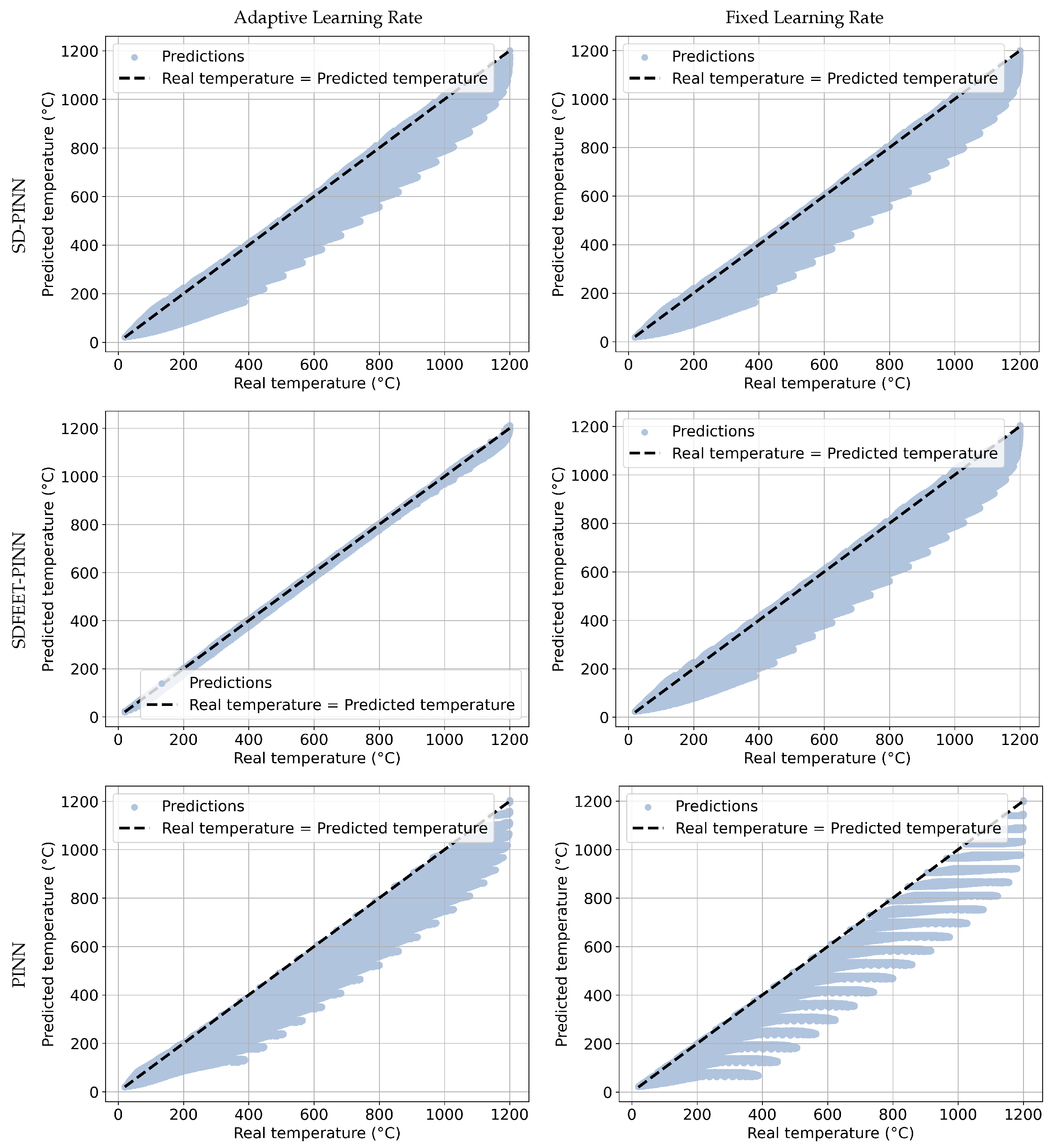
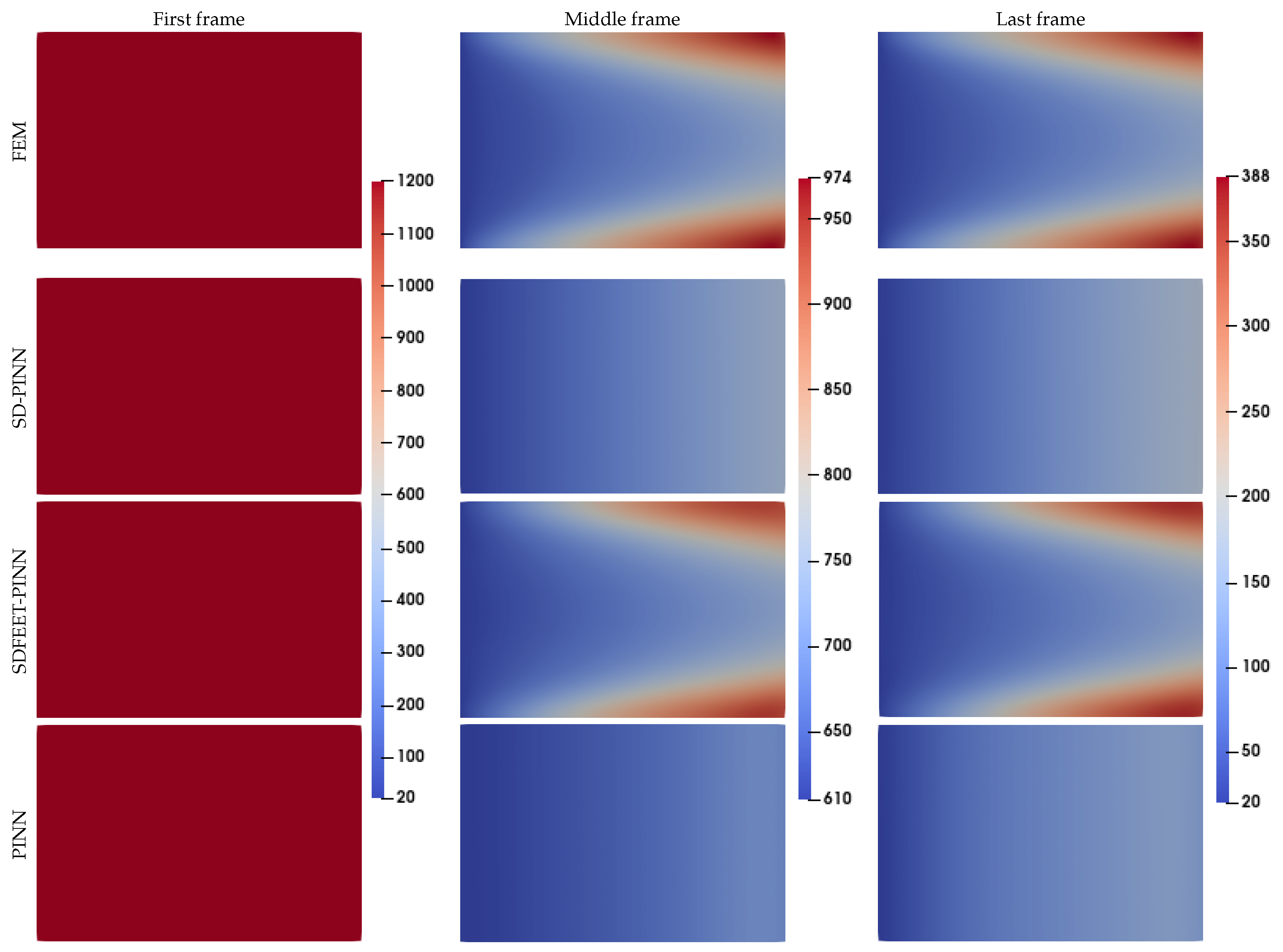
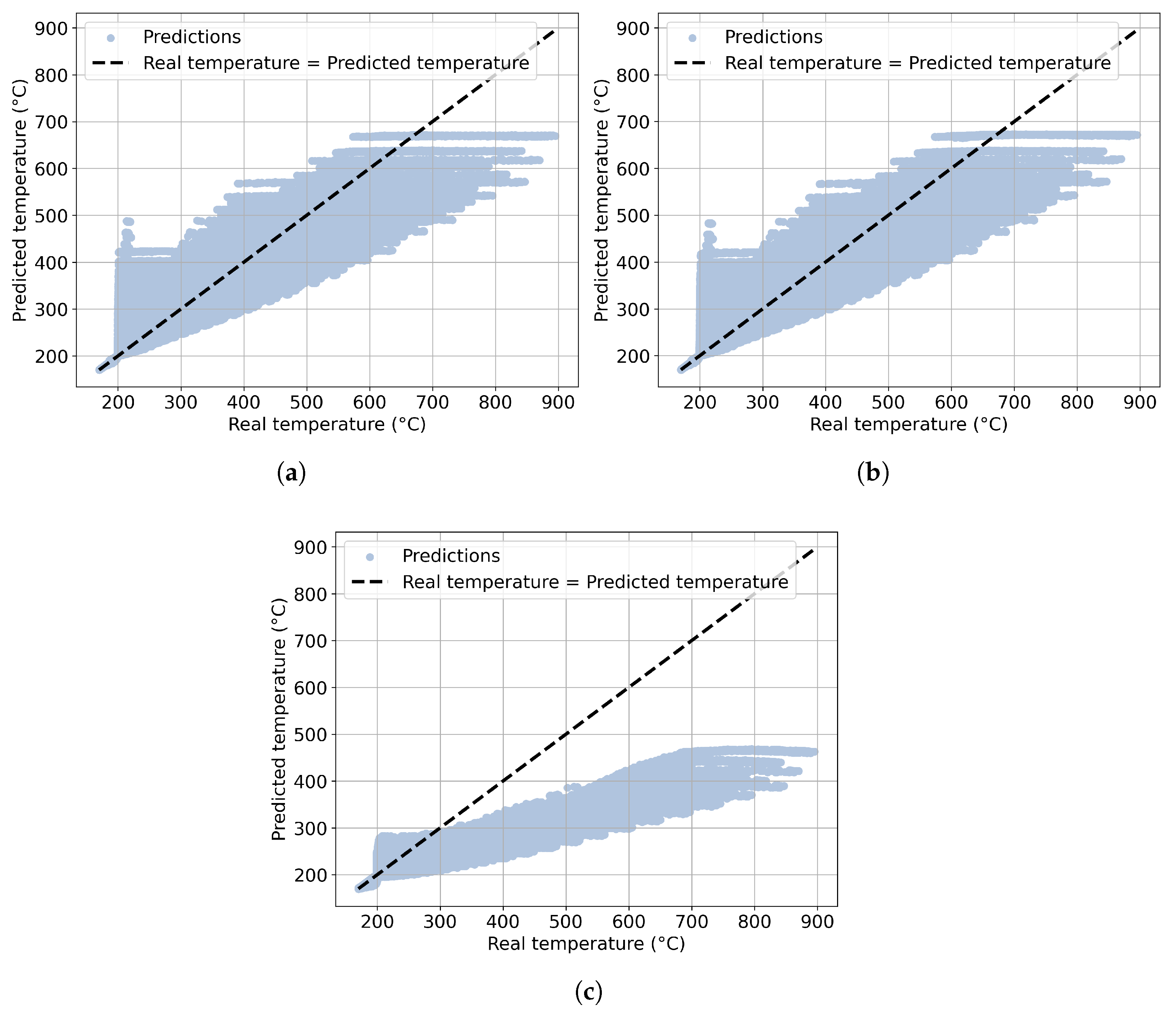
4. Results and Discussions
4.1. Problem with Dirichlet Boundary Conditions
4.2. Problem with Dirichlet and Newton Boundary Conditions
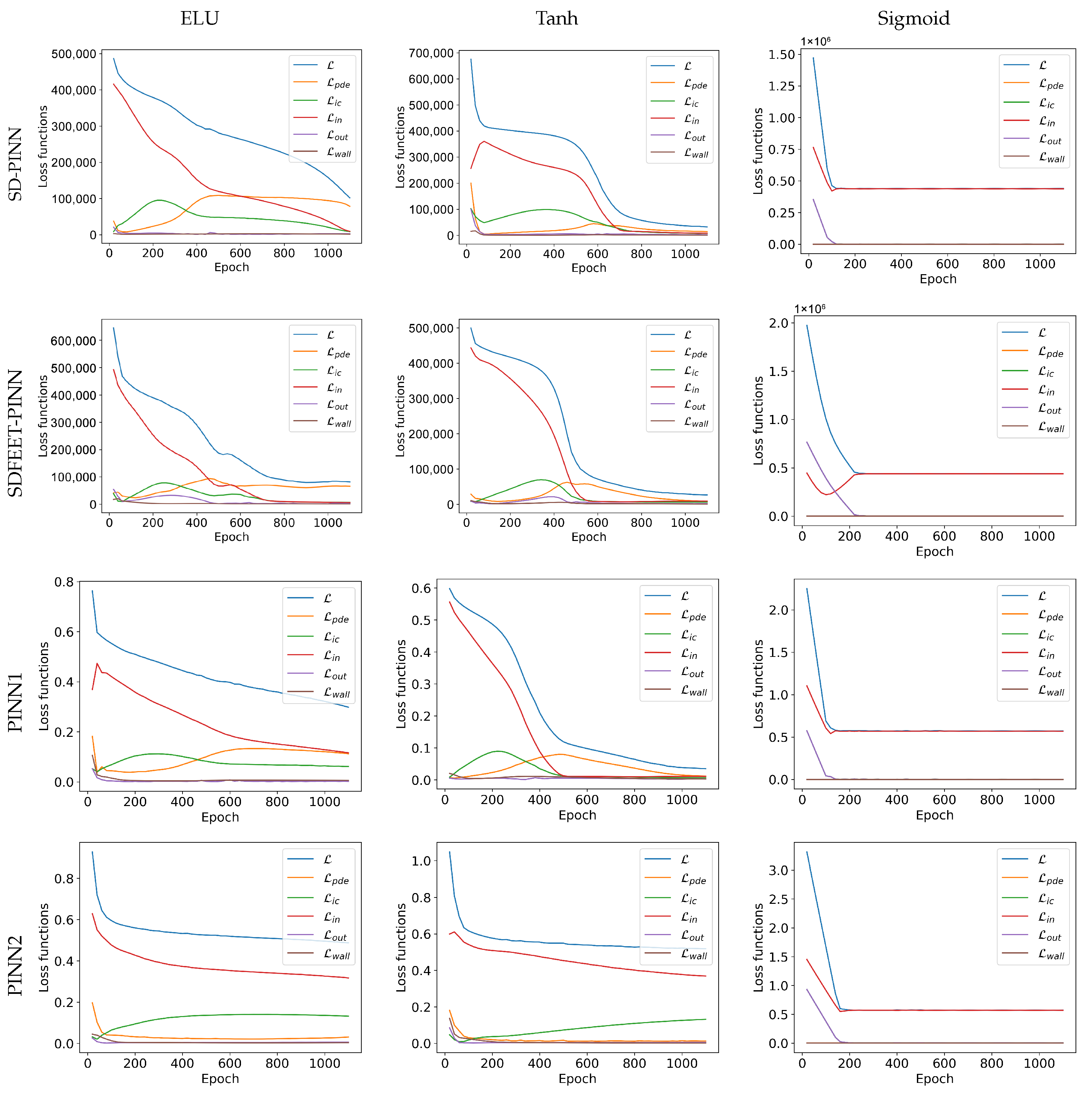
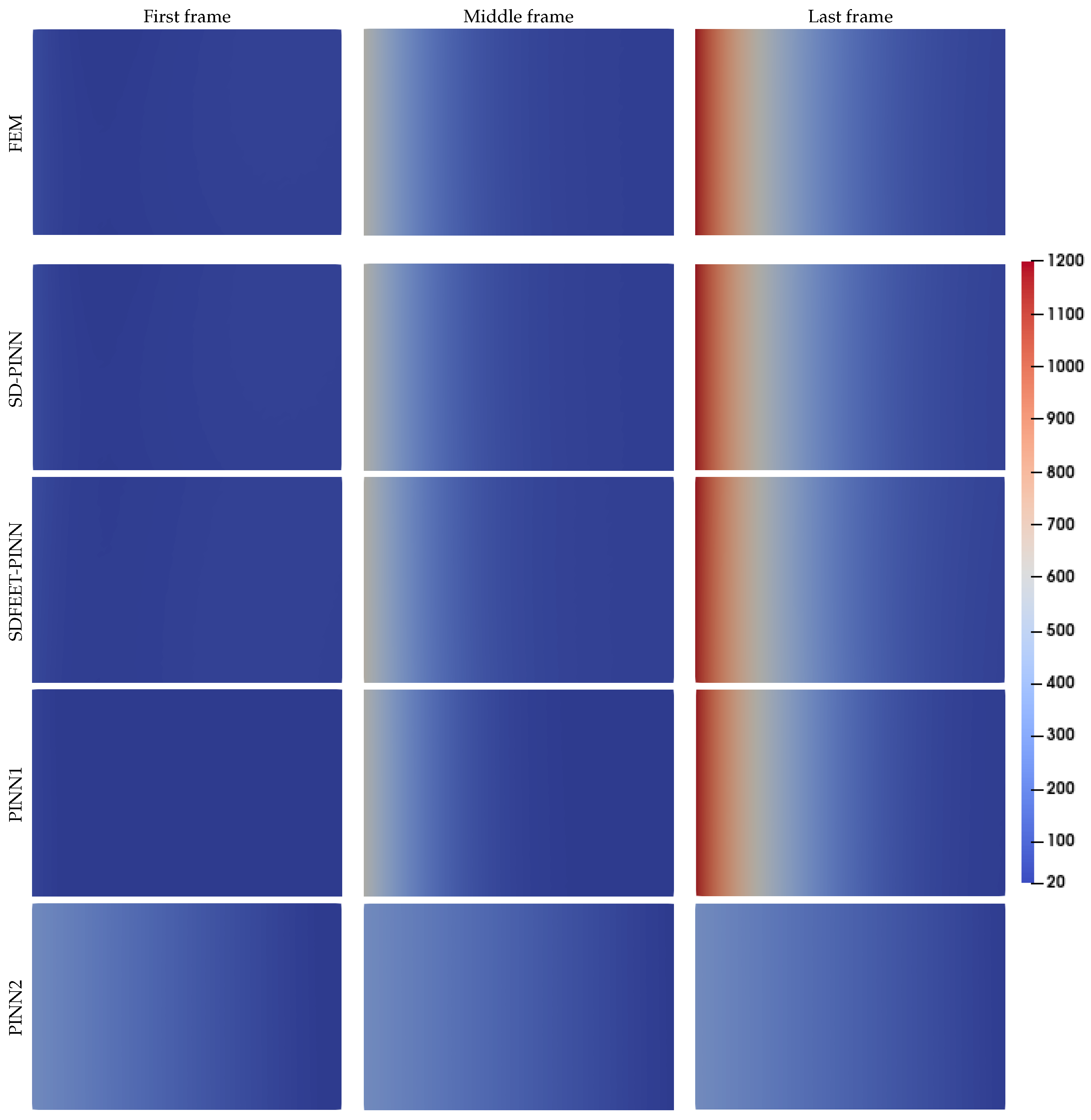
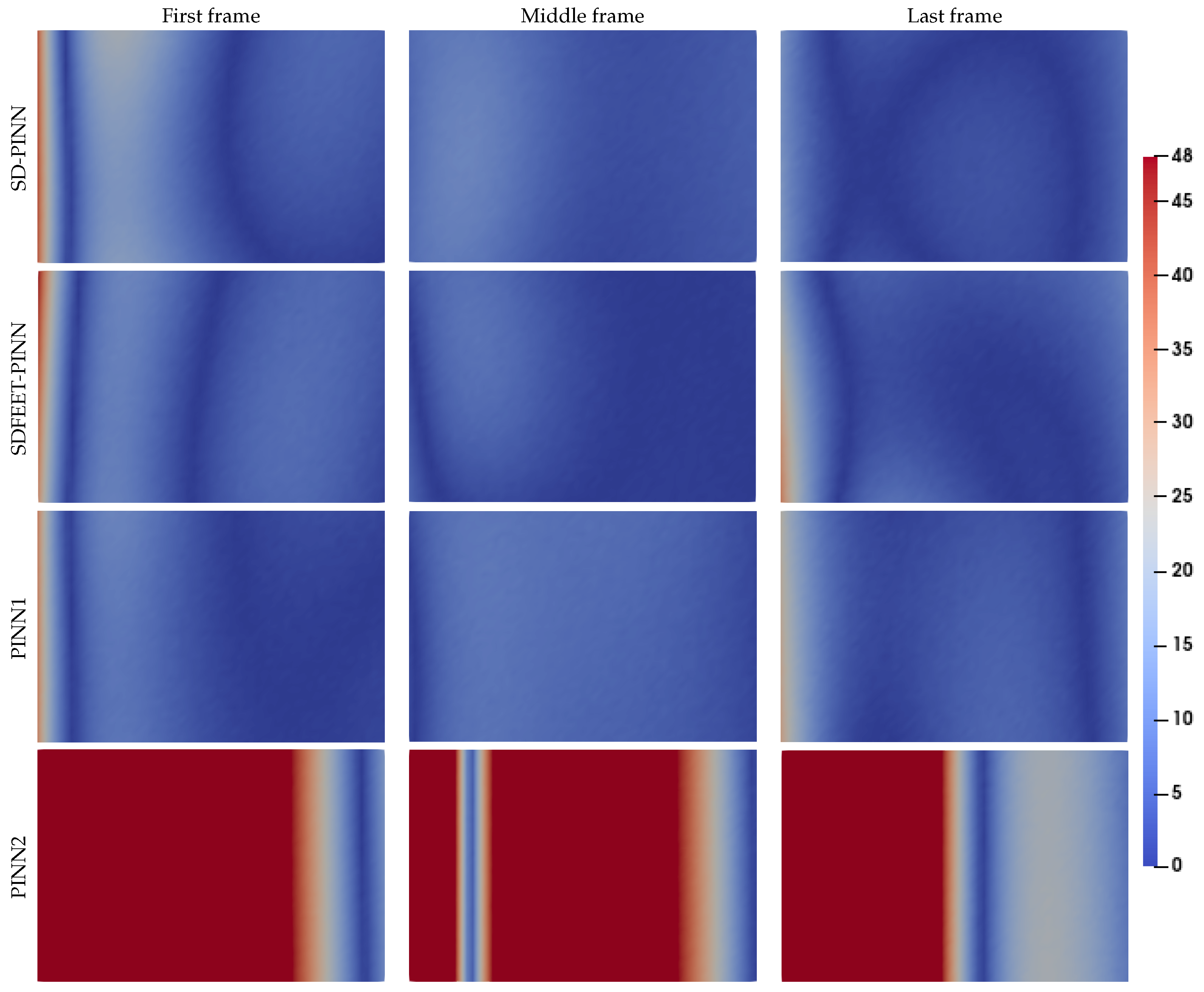
4.3. Problem with Advection, Dirichlet, and Newton Boundary Conditions
4.4. Application to a Complex 3D Geometry
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| Abbreviation | Description |
| L-PBF | Laser Powder Bed Fusion |
| PINN | Physics-Informed Neural Networks |
| FEM | Finite Element Method |
| FVM | Finite Volume Method |
| FDM | Finite Difference Method |
| SD-PINN | Same Dimensions PINN |
| PDE | Partial Differential Equation, specifically the heat equation. |
| ADAM | Adaptive Moment Estimation. |
| L-BFGS | Limited-memory Broyden–Fletcher–Goldfarb–Shanno. |
| SDFEET-PINN | Same Dimensions From Equal Equation Terms PINN |
| FEET | From Equal Equation Terms PINN |
| Symbols | |
| Symbol | Description |
| l | The width of the model geometry. |
| The length of the model geometry, also used as the reference length. | |
| Prescribed initial temperature function. | |
| Prescribed temperature or flux, depending on the operator . | |
| Density. | |
| c | Specific heat. |
| Heat conductivity. | |
| Boundary condition operator | |
| Exponent * denotes the dimensionless variables. | |
| Subscript 0 denotes the reference constants. | |
| Residual related to i ∈ {pde, ic, in, out, wall, bot, pow, top}. | |
| Loss related to i ∈ {pde, ic, in, out, wall, bot, pow, top}. | |
| Dimensional coefficients related to i ∈ {tran, conv, cond, ic, in, out, out/h, out/k, bot, pow/h, pow/k, top/p, top/h}. | |
| Subscript indicating variables related to the transient term in the heat equation. | |
| Subscript indicating variables related to the convection term in the heat equation. | |
| Subscript indicating variables related to the conduction term in the heat equation. | |
| Subscript indicating variables related to the Partial Differential Equation or the heat equation. | |
| Subscript indicating variables related to the initial conditions. | |
| Subscript indicating variables related to the inlet boundary condition. | |
| Subscript indicating variables related to the outlet boundary condition. | |
| Subscripts of the coefficients for the convection and conduction terms in the Newton boundary condition at the outlet, respectively. | |
| Subscript indicating variables related to the wall boundary condition. | |
| Subscript indicating variables related to the bottom boundary condition. | |
| Subscripts of the coefficients for the convection and conduction terms in the Newton boundary condition at the surface in contact with the powder, respectively. | |
| , and | Subscripts of the coefficients for the prescribed heat flux power, convection, and conduction terms in the Newton boundary condition at the top surface of the 3D hydraulic joint, respectively. |
References
- Gao, S.; Li, Z.; Petegem, S.V.; Ge, J.; Goel, S.; Vas, J.V.; Luzin, V.; Hu, Z.; Seet, H.L.; Sanchez, D.F.; et al. Additive manufacturing of alloys with programmable microstructure and properties. Nat. Commun. 2023, 14, 6752. [Google Scholar] [CrossRef]
- Bajaj, P.; Hariharan, A.; Kini, A.; Kürnsteiner, P.; Raabe, D.; Jägle, E.A. Steels in additive manufacturing: A review of their microstructure and properties. Mater. Sci. Eng. A 2020, 772, 138633. [Google Scholar] [CrossRef]
- Delahaye, J.; Tchuindjang, J.T.; Lecomte-Beckers, J.; Rigo, O.; Habraken, A.M.; Mertens, A. Influence of Si precipitates on fracture mechanisms of AlSi10Mg parts processed by Selective Laser Melting. Acta Mater. 2019, 175, 160–170. [Google Scholar] [CrossRef]
- Pauza, J.G.; Tayon, W.A.; Rollett, A.D. Computer simulation of microstructure development in powder-bed additive manufacturing with crystallographic texture. Model. Simul. Mater. Sci. Eng. 2021, 29, 055019. [Google Scholar] [CrossRef]
- Khdoudi, A.; Masrour, T.; Hassani, I.E.; Mazgualdi, C.E. A Deep-Reinforcement-Learning-Based Digital Twin for Manufacturing Process Optimization. Systems 2024, 12, 38. [Google Scholar] [CrossRef]
- Zhu, Q.; Liu, Z.; Yan, J. Machine learning for metal additive manufacturing: Predicting temperature and melt pool fluid dynamics using physics-informed neural networks. Comput. Mech. 2021, 67, 619–635. [Google Scholar] [CrossRef]
- Nath, P.; Mahadevan, S. Probabilistic Digital Twin for Additive Manufacturing Process Design and Control. J. Mech. Des. 2022, 144, 1–15. [Google Scholar] [CrossRef]
- Go, M.S.; Lim, J.H.; Lee, S. Physics-informed neural network-based surrogate model for a virtual thermal sensor with real-time simulation. Int. J. Heat Mass Transf. 2023, 214, 124392. [Google Scholar] [CrossRef]
- Zhou, G.; Zhang, C.; Li, Z.; Ding, K.; Wang, C. Knowledge-driven digital twin manufacturing cell towards intelligent manufacturing. Int. J. Prod. Res. 2020, 58, 1034–1051. [Google Scholar] [CrossRef]
- Bresson, Y.; Tongne, A.; Baili, M.; Arnaud, L. Global-to-local simulation of the thermal history in the laser powder bed fusion process based on a multiscale finite element approach. Int. J. Adv. Manuf. Technol. 2023, 127, 4727–4744. [Google Scholar] [CrossRef]
- De Lozzo, M. Substitution de modèle et approche multifidélité en expérimentation numérique [Surrogate modeling and multifidelity approach in computer experimentation]. J. Société Française Stat. 2015, 156, 21–55. [Google Scholar]
- Aymerich, E.; Pisano, F.; Cannas, B.; Sias, G.; Fanni, A.; Gao, Y.; Böckenhoff, D.; Jakubowski, M. Physics Informed Neural Networks towards the real-time calculation of heat fluxes at W7-X. Nucl. Mater. Energy 2023, 34, 101401. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Xu, R.; Zhang, D.; Rong, M.; Wang, N. Weak form theory-guided neural network (TgNN-wf) for deep learning of subsurface single- and two-phase flow. J. Comput. Phys. 2021, 436, 110318. [Google Scholar] [CrossRef]
- Rong, M.; Zhang, D.; Wang, N. A Lagrangian dual-based theory-guided deep neural network. Complex Intell. Syst. 2022, 8, 4849–4862. [Google Scholar] [CrossRef]
- Zhou, H.; Wu, H.; Sheil, B.; Wang, Z. A self-adaptive physics-informed neural networks method for large strain consolidation analysis. Comput. Geotech. 2025, 181, 107131. [Google Scholar] [CrossRef]
- Hou, J.; Li, Y.; Ying, S. Enhancing PINNs for solving PDEs via adaptive collocation point movement and adaptive loss weighting. Nonlinear Dyn. 2023, 111, 15233–15261. [Google Scholar] [CrossRef]
- Guo, Y.; Cao, X.; Song, J.; Leng, H.; Peng, K. An efficient framework for solving forward and inverse problems of nonlinear Partial Differential Equations via enhanced physics-informed neural network based on adaptive learning. Phys. Fluids 2023, 35, 106603. [Google Scholar] [CrossRef]
- Xiang, Z.; Peng, W.; Liu, X.; Yao, W. Self-adaptive loss balanced Physics-informed neural networks. Neurocomputing 2022, 496, 11–34. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, X.; Feng, X.; Xu, H. An improved physics-informed neural network with adaptive weighting and mixed differentiation for solving the incompressible Navier–Stokes equations. Nonlinear Dyn. 2024, 112, 16113–16134. [Google Scholar] [CrossRef]
- Gao, B.; Yao, R.; Li, Y. Physics-informed neural networks with adaptive loss weighting algorithm for solving partial differential equations. Comput. Math. Appl. 2025, 181, 216–227. [Google Scholar] [CrossRef]
- Hooshyar, S.; Elahi, A. Sequencing Initial Conditions in Physics-Informed Neural Networks. J. Chem. Environ. 2024, 3, 98–108. [Google Scholar] [CrossRef]
- Chen, X.; Yang, J.; Liu, X.; He, Y.; Luo, Q.; Chen, M.; Hu, W. Hemodynamics modeling with physics-informed neural networks: A progressive boundary complexity approach. Comput. Methods Appl. Mech. Eng. 2025, 438, 117851. [Google Scholar] [CrossRef]
- Guo, Y.; Min, J.; Lin, S.; Liu, X.; Fu, Z. Curriculum-Transfer-Learning Based Physics-Informed Neural Networks for Long-Term Simulation of Physical and Mechanical Behaviors. Chin. J. Theor. Appl. Mech. 2024, 56, 763–773. [Google Scholar] [CrossRef]
- Münzer, M.; Bard, C. A Curriculum-Training-Based Strategy for Distributing Collocation Points during Physics-Informed Neural Network Training. In Proceedings of the Machine Learning and the Physical Sciences Workshop, New Orleans, LA, USA, 3 December 2022. [Google Scholar]
- Peng, B.; Panesar, A. Multi-layer thermal simulation using physics-informed neural network. Addit. Manuf. 2024, 95, 104498. [Google Scholar] [CrossRef]
- Ghungrad, S.; Gould, B.; Wolff, S.; Haghighi, A. Physics-Informed Artificial Intelligence for Temperature Prediction in Metal Additive Manufacturing: A Comparative Study. In Volume 1: Additive Manufacturing Biomanufacturing; Life Cycle Engineering; Manufacturing Equipment and Automation; Nano/Micro/Meso Manufacturing; American Society of Mechanical Engineers: New York, NY, USA, 2022. [Google Scholar] [CrossRef]
- Huang, Y.H.; Xu, Z.; Qian, C.; Liu, L. Solving free-surface problems for non-shallow water using boundary and initial conditions-free physics-informed neural network (bif-PINN). J. Comput. Phys. 2023, 479, 112003. [Google Scholar] [CrossRef]
- Kashefi, A.; Mukerji, T. Physics-informed PointNet: A deep learning solver for steady-state incompressible flows and thermal fields on multiple sets of irregular geometries. J. Comput. Phys. 2022, 468, 111510. [Google Scholar] [CrossRef]
- Bolandi, H.; Sreekumar, G.; Li, X.; Lajnef, N.; Boddeti, V.N. Physics informed neural network for dynamic stress prediction. Appl. Intell. 2023, 53, 26313–26328. [Google Scholar] [CrossRef]
- Bresson, Y.; Tongne, A.; Selva, P.; Arnaud, L. Numerical modelling of parts distortion and beam supports breakage during selective laser melting (SLM) additive manufacturing. Int. J. Adv. Manuf. Technol. 2022, 119, 5727–5742. [Google Scholar] [CrossRef]
- Benoist, V.; Arnaud, L.; Baili, M.; Faye, P. Topological optimization design for additive manufacturing, taking into account flexion and vibrations during machining post processing operations. In Proceedings of the 14th International Conference on High Speed Machining, San Sebastián, Spain, 17–18 April 2018; pp. 1–4. [Google Scholar]
- Lou, Q.; Meng, X.; Karniadakis, G.E. Physics-informed neural networks for solving forward and inverse flow problems via the Boltzmann-BGK formulation. J. Comput. Phys. 2021, 447, 110676. [Google Scholar] [CrossRef]
- Pratama, D.A.; Abo-Alsabeh, R.R.; Bakar, M.A.; Salhi, A.; Ibrahim, N.F. Solving partial differential equations with hybridized physic-informed neural network and optimization approach: Incorporating genetic algorithms and L-BFGS for improved accuracy. Alex. Eng. J. 2023, 77, 205–226. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tongne, A.; Arnaud, L. Novel Method to Improve the Convergence of Physics-Informed Neural Networks for Complex Thermal Simulations. Appl. Sci. 2025, 15, 12234. https://doi.org/10.3390/app152212234
Tongne A, Arnaud L. Novel Method to Improve the Convergence of Physics-Informed Neural Networks for Complex Thermal Simulations. Applied Sciences. 2025; 15(22):12234. https://doi.org/10.3390/app152212234
Chicago/Turabian StyleTongne, Amèvi, and Lionel Arnaud. 2025. "Novel Method to Improve the Convergence of Physics-Informed Neural Networks for Complex Thermal Simulations" Applied Sciences 15, no. 22: 12234. https://doi.org/10.3390/app152212234
APA StyleTongne, A., & Arnaud, L. (2025). Novel Method to Improve the Convergence of Physics-Informed Neural Networks for Complex Thermal Simulations. Applied Sciences, 15(22), 12234. https://doi.org/10.3390/app152212234





