UGV Formation Path Planning Based on DRL-DWA in Off-Road Environments †
Abstract
1. Introduction
1.1. Research Motivation
1.2. Literature Review
1.3. Contributions
- A hierarchical large-scale off-road path planning scheme is presented in this paper, which consists of two components: (1) a global path planner based on D* Lite for calculating a roughly feasible global path, and (2) a local motion controller for calculating a dynamically feasible path and conducting obstacle avoidance.
- DRL and DWA are combined to complement each other’s strengths and overcome their respective limitations. The weighting factors of the DWA evaluation functions are adaptively adjusted by the DRL network, and the final optimal control velocities are calculated by DWA, which ensures that they are dynamically feasible.
- We expand the single UGV into a multi-UGV system and compare the proposed algorithm to prior navigation methods using real-world terrain data. Experimental results demonstrate that the proposed method considerably enhances the success rate of path planning while avoiding various obstacles and non-traversable terrain when the sacrifice of trajectory length and travel time is almost negligible.
1.4. Organization
2. Problem Formulation
3. Proposed Solution
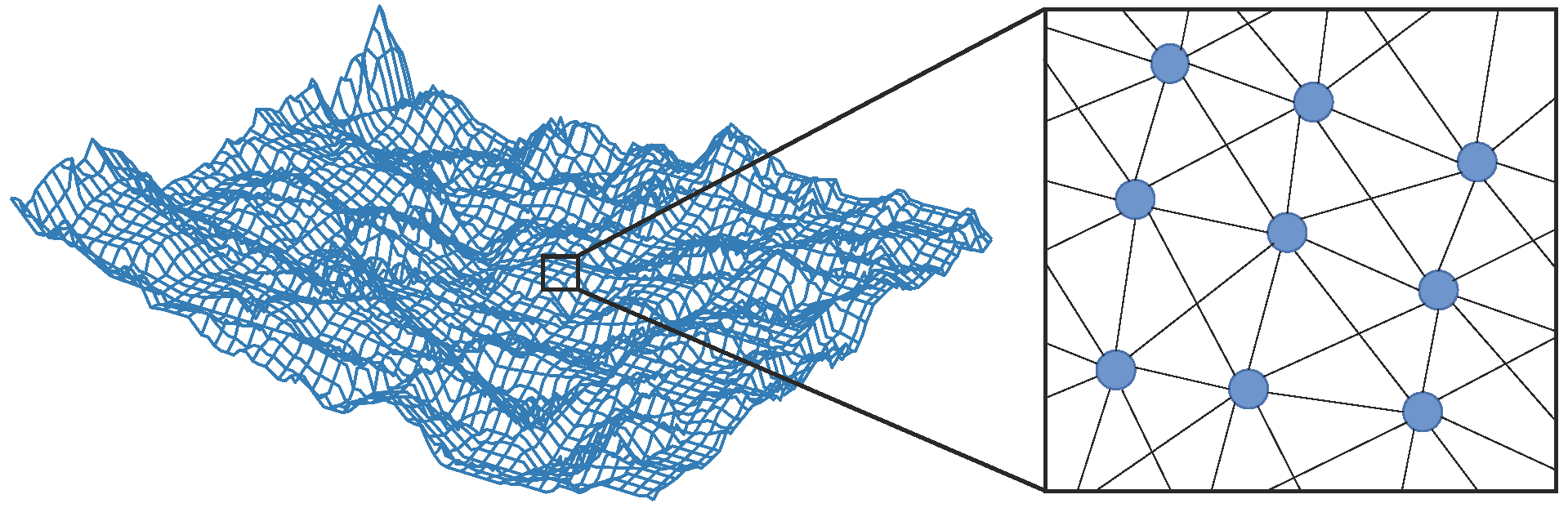
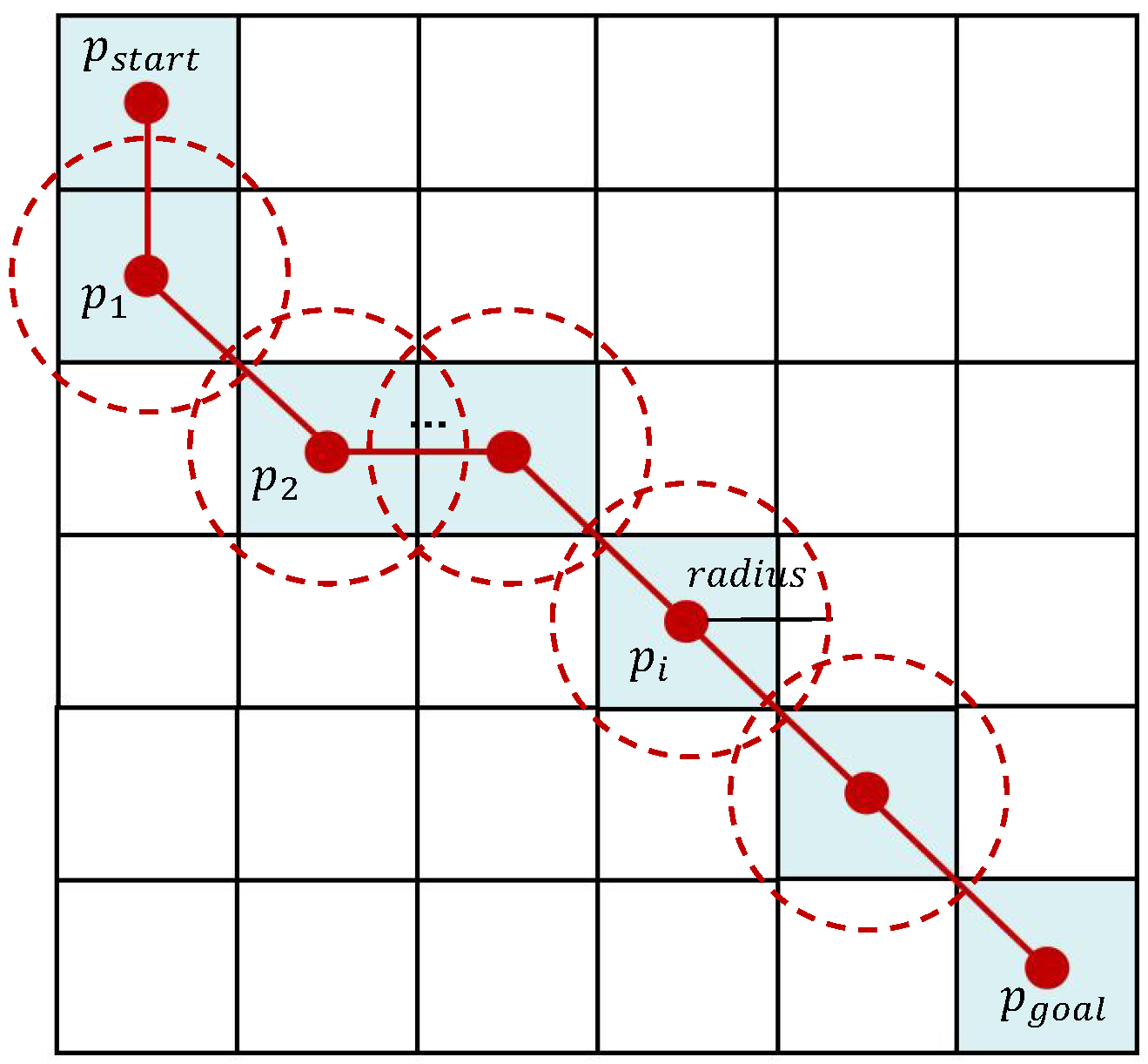
3.1. Global Path Planning
3.2. Local Path Planning
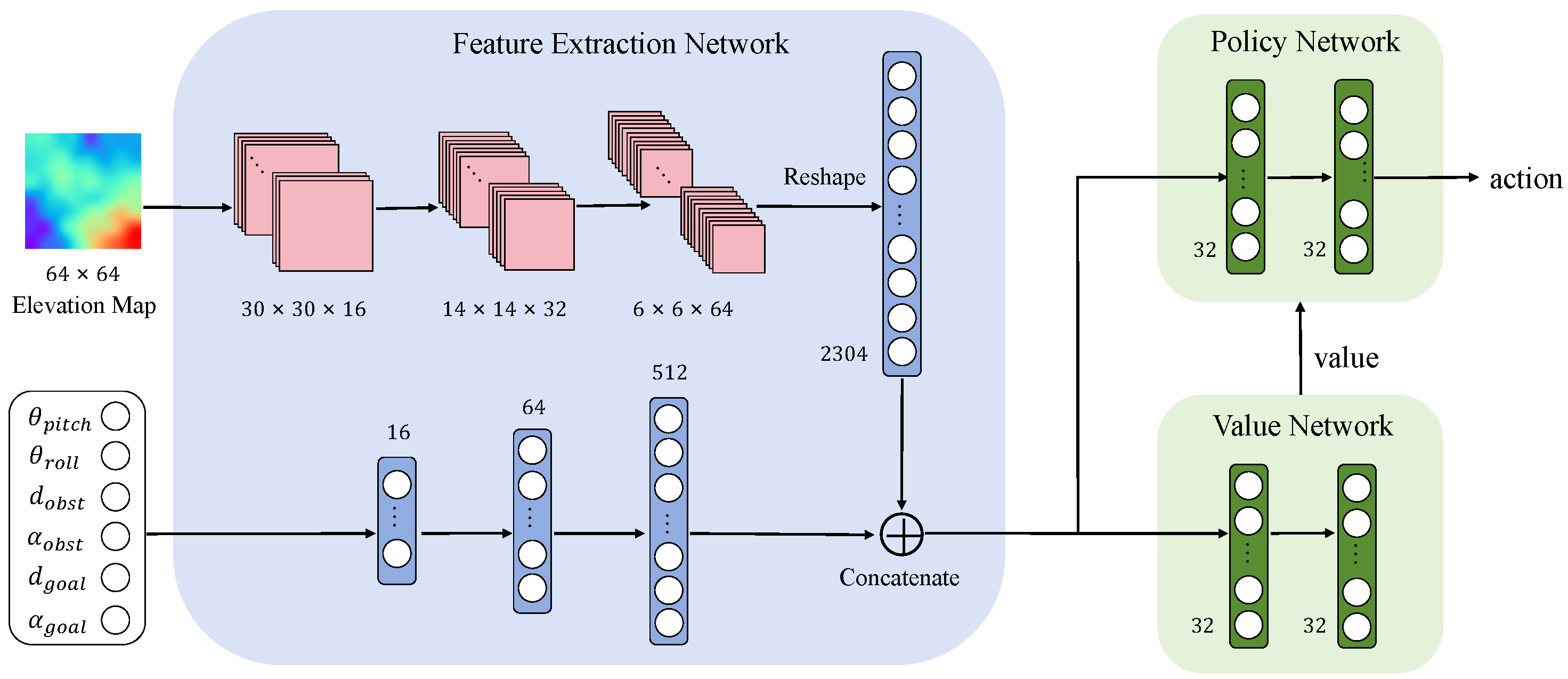
3.3. DRL Design
| Algorithm 1 Path planning based on DRL-DWA. |
| Initialization: Policy network with random parameters , value network with random parameters , discount factor Training:
|
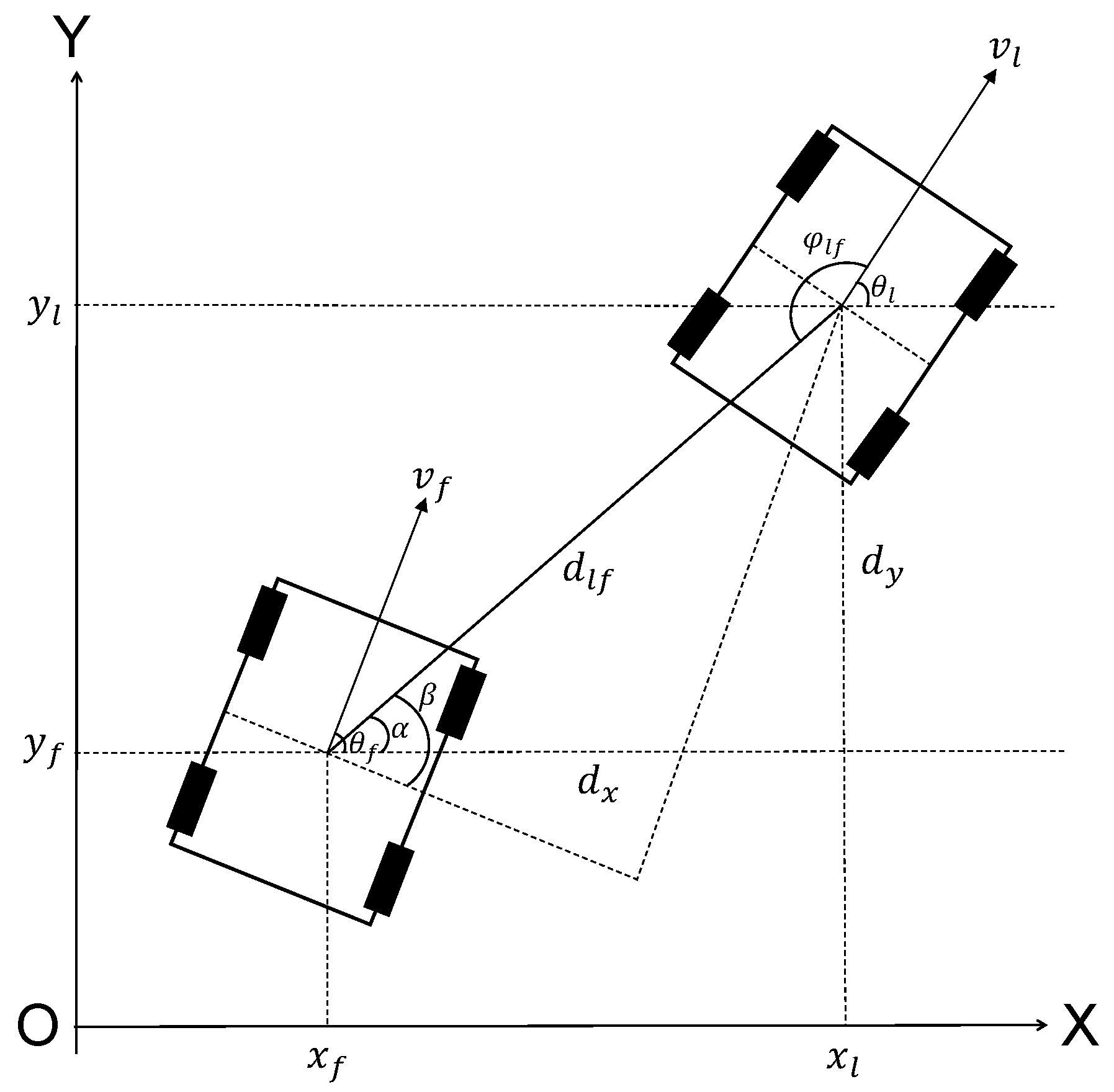
3.4. Formation Control
| Algorithm 2 A formation algorithm combining DRL-DWA-based path planning and leader–follower method. |
| Output: Global cost map, UGV position, obstacle information, target information Input: Formation trajectory
|
4. Simulation and Analysis
4.1. Implementation
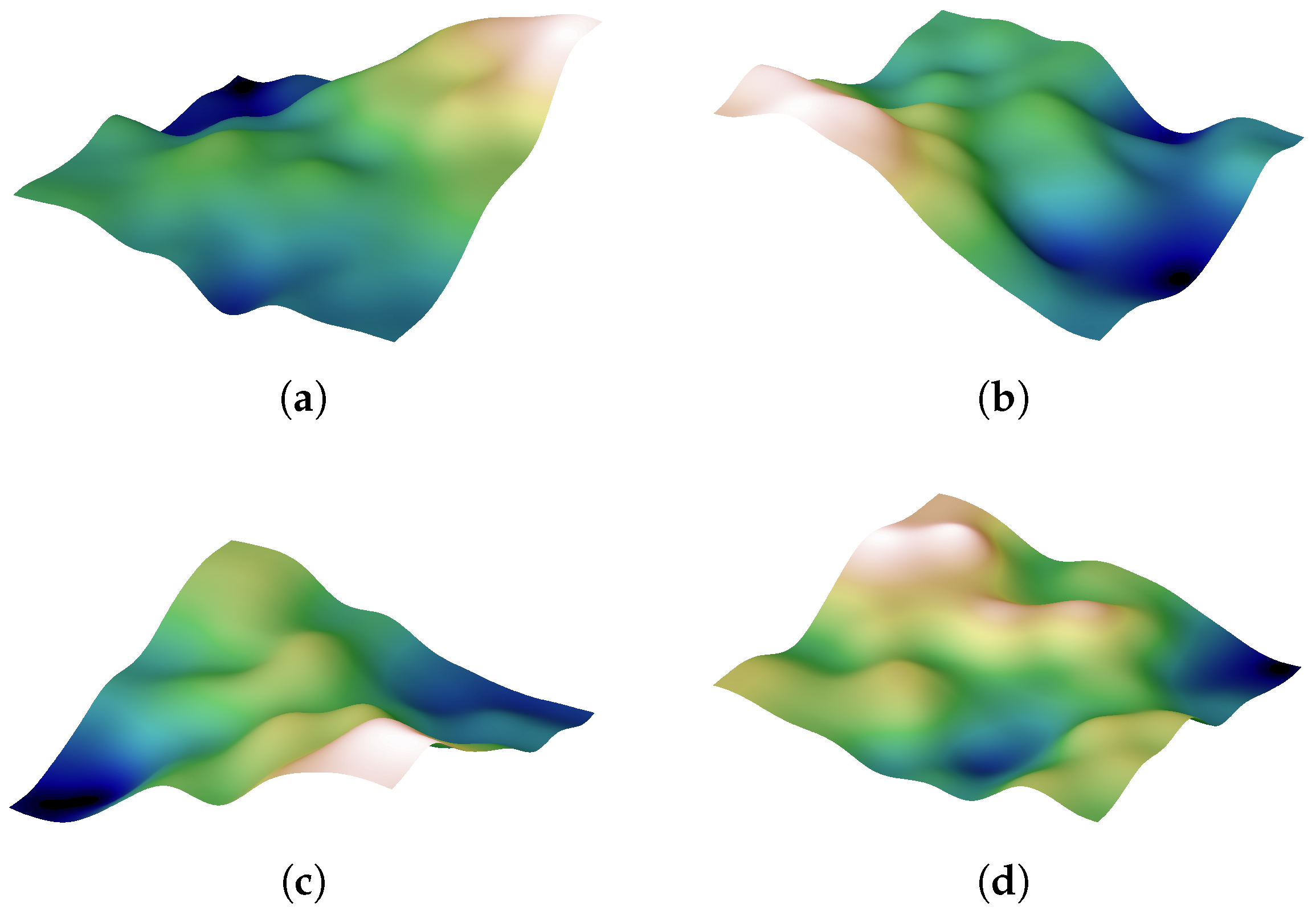
4.2. Training Scenarios
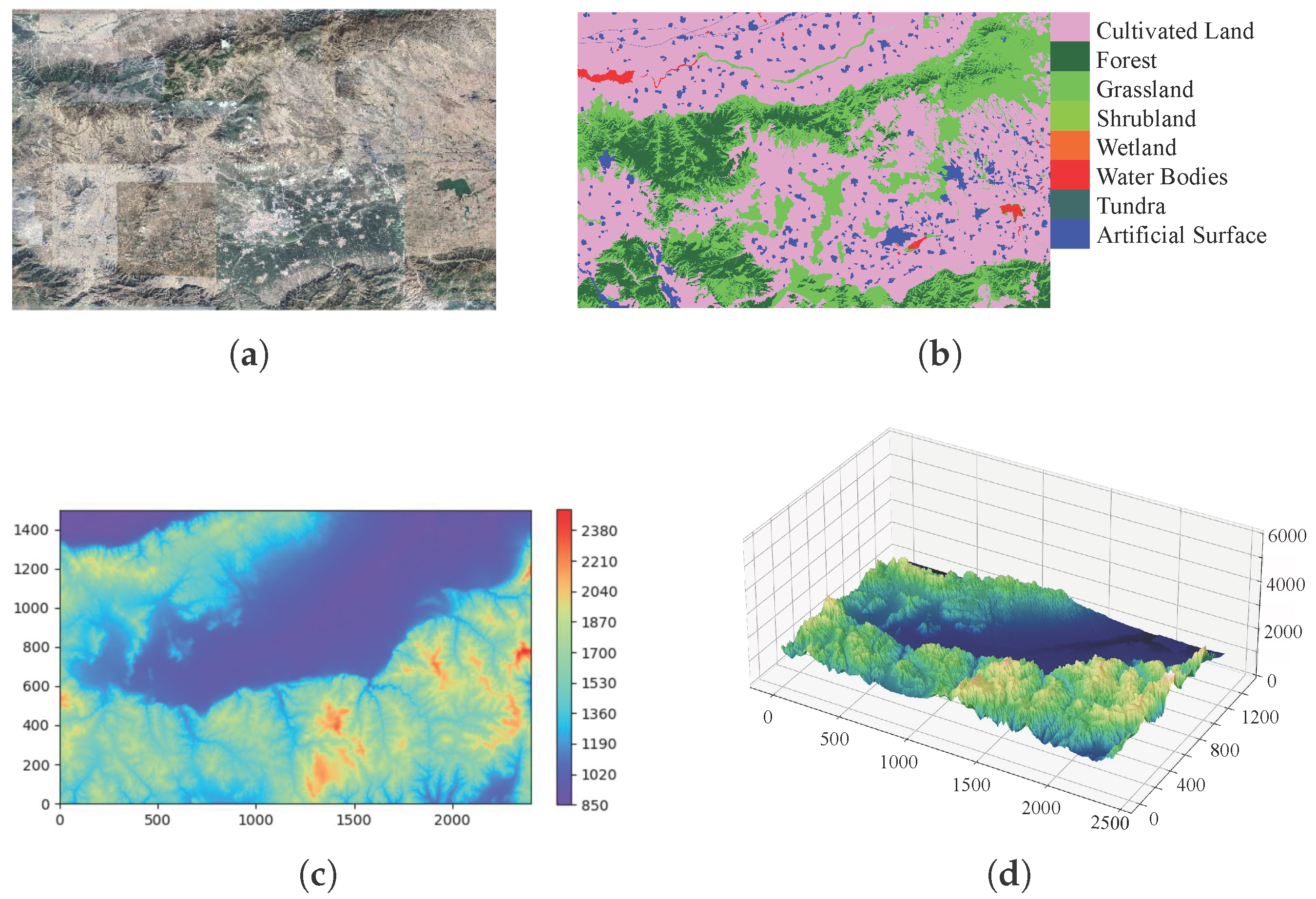
4.3. Testing Scenarios and Evaluation Metrics
- Success rate—The percentage of trials in which the UGV successfully navigates to the target while avoiding obstacles and restricted zones.
- Average trajectory length—The average distance traveled by the UGV from the start to the target, calculated across successful trials.
- Average travel time—The total time traveled by the UGV from the start to the target, averaged over the number of successful trials.
- Average elevation gradient—The elevation gradient encountered by the UGV along its trajectory, averaged over the successful trials.
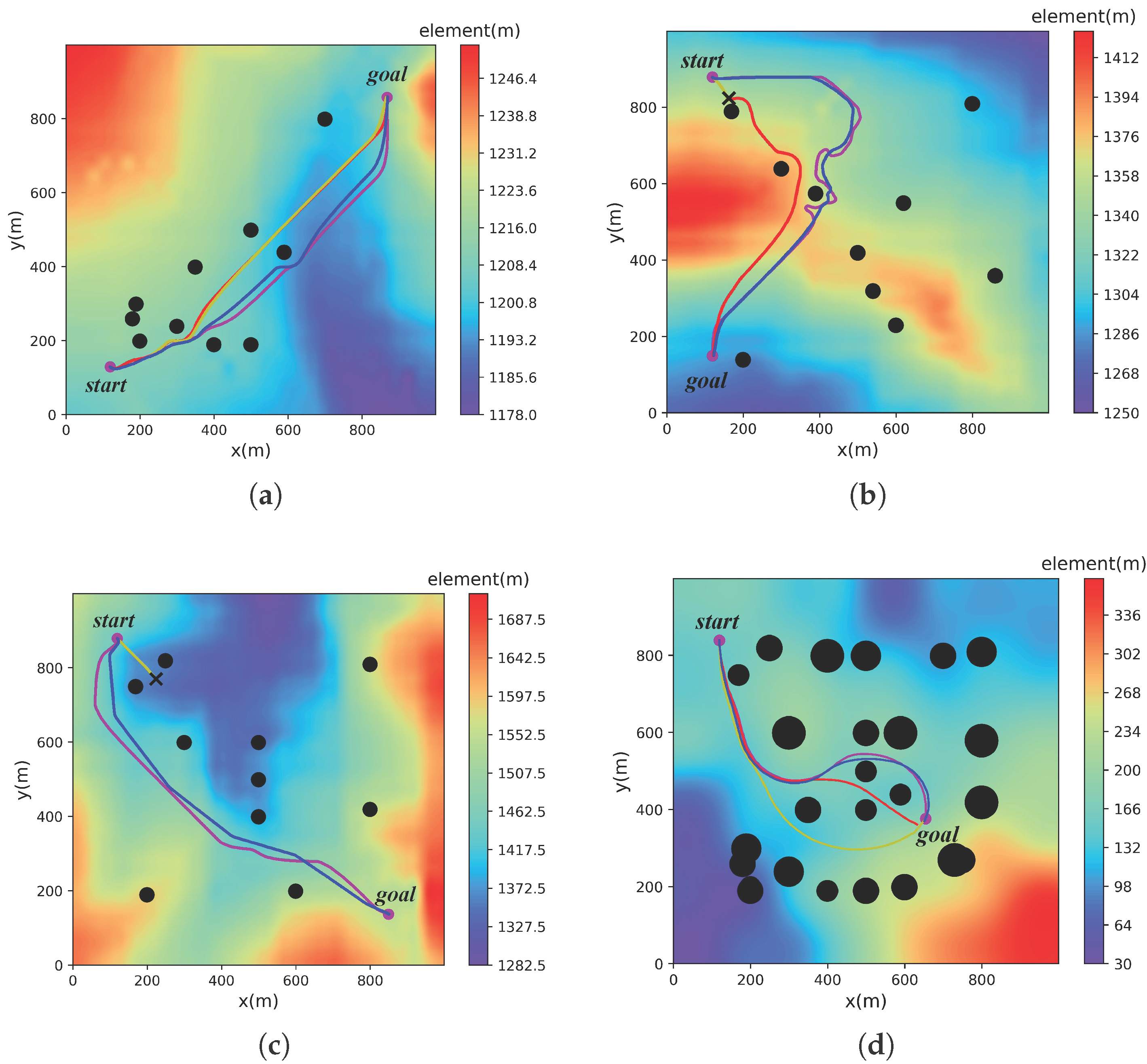
4.4. Analysis and Comparison
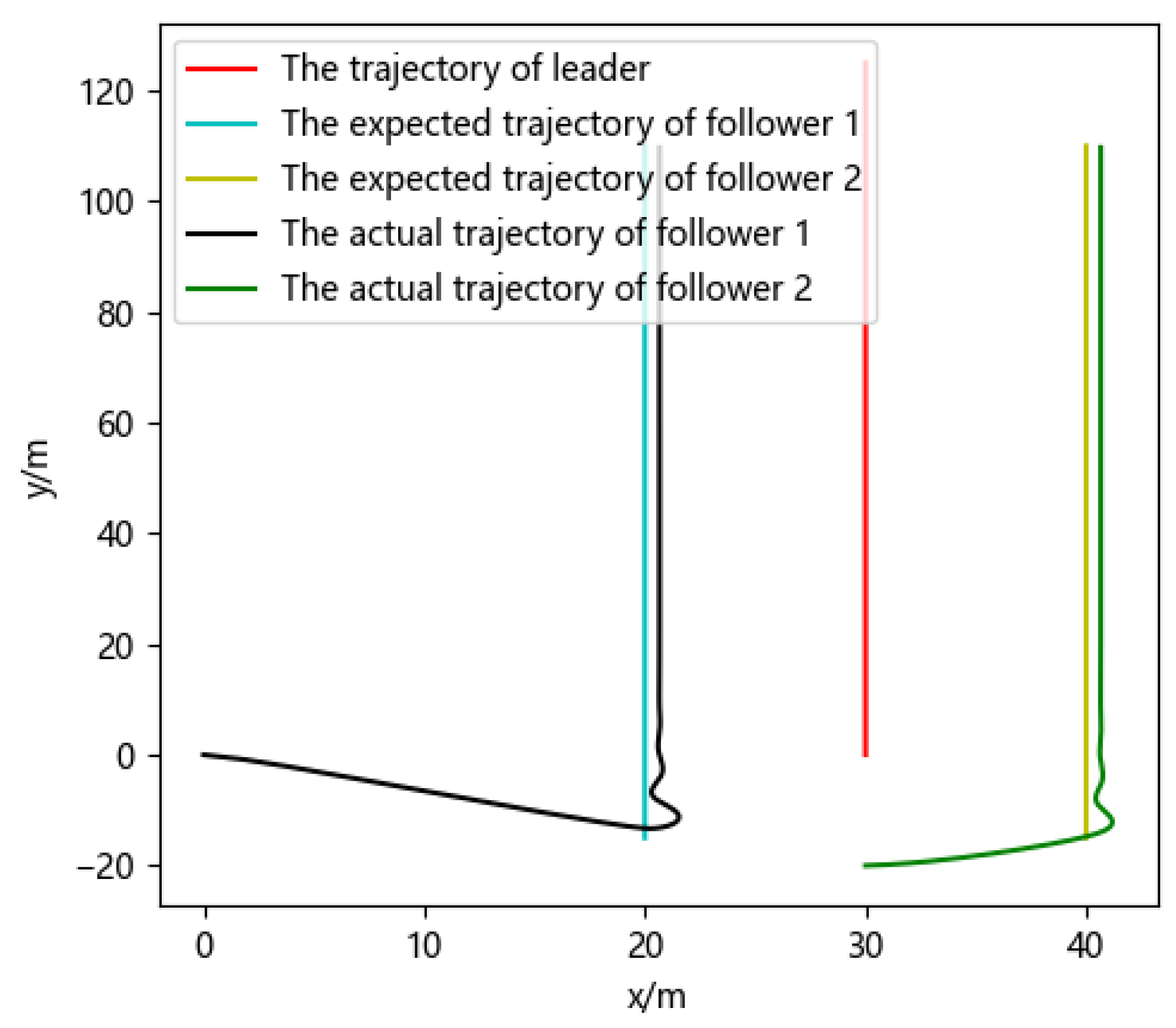
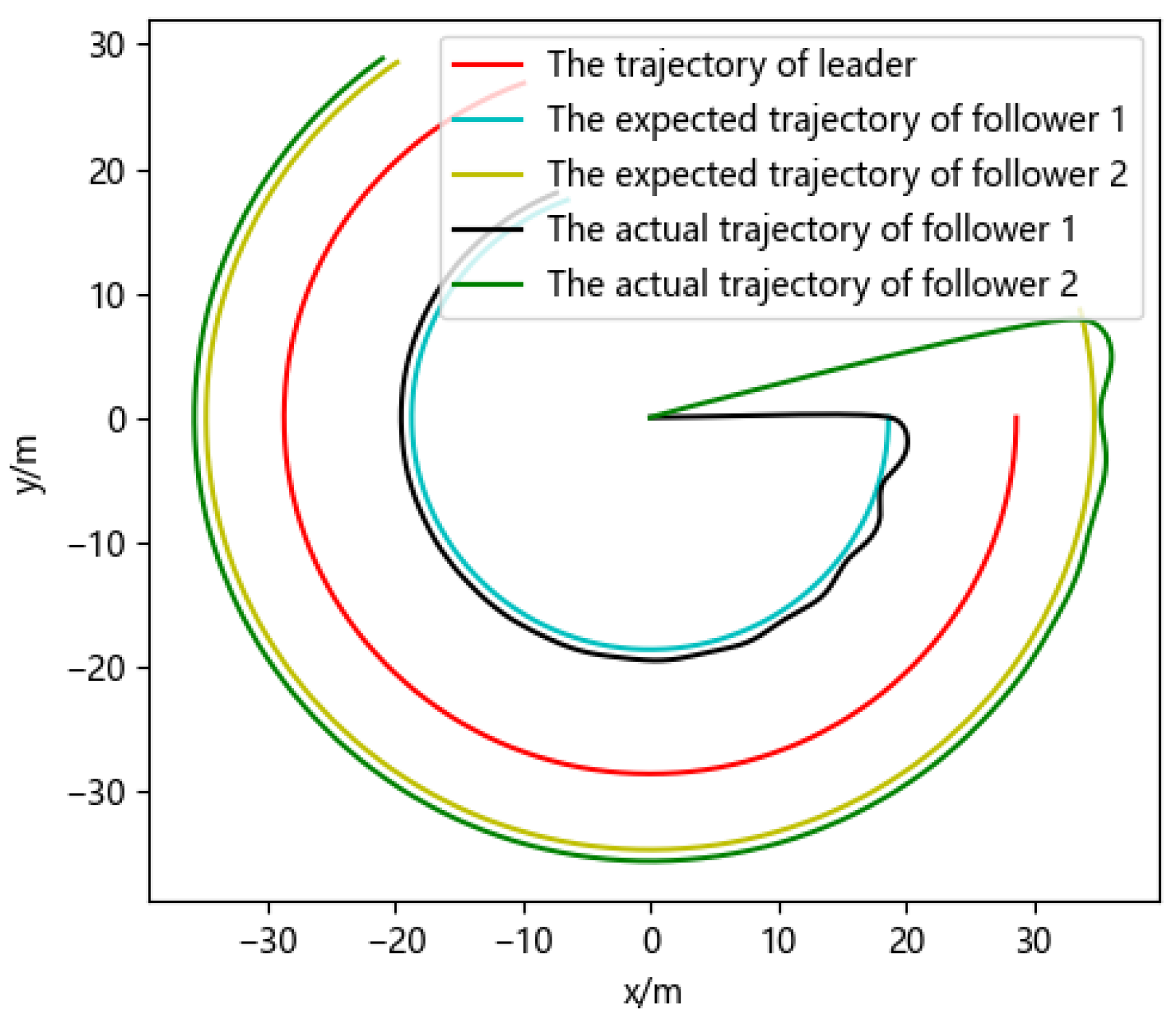
4.5. Formation Path Planning
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gan, X.; Huo, Z.; Li, W. DP-A*: For Path Planing of UGV and Contactless Delivery. IEEE Trans. Intell. Transp. Syst. 2023, 25, 907–919. [Google Scholar] [CrossRef]
- Park, C.; Park, J.S.; Manocha, D. Fast and bounded probabilistic collision detection for high-DOF trajectory planning in dynamic environments. IEEE Trans. Autom. Sci. Eng. 2018, 15, 980–991. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, S.; Akbar, A. Ground feature oriented path planning for unmanned aerial vehicle mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1175–1187. [Google Scholar] [CrossRef]
- Waibel, G.G.; Löw, T.; Nass, M.; Howard, D.; Bandyopadhyay, T.; Borges, P.V.K. How rough is the path? Terrain traversability estimation for local and global path planning. IEEE Trans. Intell. Transp. Syst. 2022, 23, 16462–16473. [Google Scholar] [CrossRef]
- Koenig, S.; Likhachev, M.; Furcy, D. Lifelong planning A*. Artif. Intell. 2004, 155, 93–146. [Google Scholar] [CrossRef]
- Koenig, S.; Likhachev, M. Fast replanning for navigation in unknown terrain. IEEE Trans. Robot. 2005, 21, 354–363. [Google Scholar] [CrossRef]
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Gammell, J.D.; Srinivasa, S.S.; Barfoot, T.D. Informed RRT: Optimal sampling-based path planning focused via direct sampling of an admissible ellipsoidal heuristic. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2997–3004. [Google Scholar]
- Katrakazas, C.; Quddus, M.; Chen, W.H.; Deka, L. Real-time motion planning methods for autonomous on-road driving: State-of-the-art and future research directions. Transp. Res. Part C Emerg. Technol. 2015, 60, 416–442. [Google Scholar] [CrossRef]
- Hu, J.; Hu, Y.; Lu, C.; Gong, J.; Chen, H. Integrated path planning for unmanned differential steering vehicles in off-road environment with 3D terrains and obstacles. IEEE Trans. Intell. Transp. Syst. 2021, 23, 5562–5572. [Google Scholar] [CrossRef]
- Fox, D.; Burgard, W.; Thrun, S. The dynamic window approach to collision avoidance. IEEE Robot. Autom. Mag. 1997, 4, 23–33. [Google Scholar] [CrossRef]
- Xu, X.; Cai, P.; Ahmed, Z.; Yellapu, V.S.; Zhang, W. Path planning and dynamic collision avoidance algorithm under COLREGs via deep reinforcement learning. Neurocomputing 2022, 468, 181–197. [Google Scholar] [CrossRef]
- Francis, A.; Faust, A.; Chiang, H.T.L.; Hsu, J.; Kew, J.C.; Fiser, M.; Lee, T.W.E. Long-range indoor navigation with prm-rl. IEEE Trans. Robot. 2020, 36, 1115–1134. [Google Scholar] [CrossRef]
- Sathyamoorthy, A.J.; Liang, J.; Patel, U.; Guan, T.; Chandra, R.; Manocha, D. Densecavoid: Real-time navigation in dense crowds using anticipatory behaviors. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 11345–11352. [Google Scholar]
- Zhu, Y.; Mottaghi, R.; Kolve, E.; Lim, J.J.; Gupta, A.; Fei-Fei, L.; Farhadi, A. Target-driven visual navigation in indoor scenes using deep reinforcement learning. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3357–3364. [Google Scholar]
- Zhou, S.; Xi, J.; McDaniel, M.W.; Nishihata, T.; Salesses, P.; Iagnemma, K. Self-supervised learning to visually detect terrain surfaces for autonomous robots operating in forested terrain. J. Field Robot. 2012, 29, 277–297. [Google Scholar] [CrossRef]
- Shan, Y.; Fu, Y.; Chen, X.; Lin, H.; Zhang, Z.; Lin, J.; Huang, K. LiDAR Based Traversable Regions Identification Method for Off-Road UGV Driving. IEEE Trans. Intell. Veh. 2024, 9, 3544–3557. [Google Scholar] [CrossRef]
- Guastella, D.C.; Muscato, G. Learning-based methods of perception and navigation for ground vehicles in unstructured environments: A review. Sensors 2020, 21, 73. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, A.; Nguyen, N.; Tran, K.; Tjiputra, E.; Tran, Q.D. Autonomous navigation in complex environments with deep multimodal fusion network. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 5824–5830. [Google Scholar]
- Mayuku, O.; Surgenor, B.W.; Marshall, J.A. A self-supervised near-to-far approach for terrain-adaptive off-road autonomous driving. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 14054–14060. [Google Scholar]
- Zhang, K.; Niroui, F.; Ficocelli, M.; Nejat, G. Robot navigation of environments with unknown rough terrain using deep reinforcement learning. In Proceedings of the 2018 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Philadelphia, PA, USA, 6–8 August 2018; pp. 1–7. [Google Scholar]
- Josef, S.; Degani, A. Deep reinforcement learning for safe local planning of a ground vehicle in unknown rough terrain. IEEE Robot. Autom. Lett. 2020, 5, 6748–6755. [Google Scholar] [CrossRef]
- Weerakoon, K.; Sathyamoorthy, A.J.; Patel, U.; Manocha, D. Terp: Reliable planning in uneven outdoor environments using deep reinforcement learning. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 9447–9453. [Google Scholar]
- Zhu, L.; Huang, K.; Wang, Y.; Hu, Y. A Multi-Objective Path Planning Framework in Off-Road Environments Based on Deep Reinforcement Learning. IEEE Trans. Intell. Transp. Syst. 2025, 1–19. [Google Scholar] [CrossRef]
- Fan, J.; Fan, L.; Ni, Q.; Wang, J.; Liu, Y.; Li, R.; Wang, Y.; Wang, S. Perception and Planning of Intelligent Vehicles Based on BEV in Extreme Off-Road Scenarios. IEEE Trans. Intell. Veh. 2024, 9, 4568–4572. [Google Scholar] [CrossRef]
- Patel, U.; Kumar, N.K.S.; Sathyamoorthy, A.J.; Manocha, D. Dwa-rl: Dynamically feasible deep reinforcement learning policy for robot navigation among mobile obstacles. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 6057–6063. [Google Scholar]
- Langer, D.; Rosenblatt, J.; Hebert, M. A behavior-based system for off-road navigation. IEEE Trans. Robot. Autom. 1994, 10, 776–783. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, C. On Hierarchical Path Planning Based on Deep Reinforcement Learning in Off- Road Environments. In Proceedings of the 2024 10th International Conference on Automation, Robotics and Applications (ICARA), Athens, Greece, 22–24 February 2024; pp. 461–465. [Google Scholar]
- Rowe, N.C.; Ross, R.S. Optimal grid-free path planning across arbitrarily-contoured terrain with anisotropic friction and gravity effects. IEEE Trans. Robot. Autom. 1990, 6, 540–553. [Google Scholar] [CrossRef]
- Ganganath, N.; Cheng, C.T.; Chi, K.T. A constraint-aware heuristic path planner for finding energy-efficient paths on uneven terrains. IEEE Trans. Ind. Inform. 2015, 11, 601–611. [Google Scholar] [CrossRef]
- Thrun, S.; Littman, M.L. Reinforcement learning: An introduction. AI Mag. 2000, 21, 103. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar] [CrossRef]
- Perlin, K. An image synthesizer. ACM Siggraph Comput. Graph. 1985, 19, 287–296. [Google Scholar] [CrossRef]
- Jain, A.; Sharma, A.; Rajan. Adaptive & Multi-Resolution Procedural Infinite Terrain Generation with Diffusion Models and Perlin Noise. In Proceedings of the Thirteenth Indian Conference on Computer Vision, Graphics and Image Processing, Gandhinagar, India, 8–10 December 2022; pp. 1–9. [Google Scholar]
- Lacaze, A.; Moscovitz, Y.; DeClaris, N.; Murphy, K. Path planning for autonomous vehicles driving over rough terrain. In Proceedings of the 1998 IEEE International Symposium on Intelligent Control (ISIC) Held Jointly with IEEE International Symposium on Computational Intelligence in Robotics and Automation (CIRA) Intell, Gaithersburg, MD, USA, 17 September 1998; pp. 50–55. [Google Scholar]
- Chang, L.; Shan, L.; Jiang, C.; Dai, Y. Reinforcement based mobile robot path planning with improved dynamic window approach in unknown environment. Auton. Robot. 2021, 45, 51–76. [Google Scholar] [CrossRef]



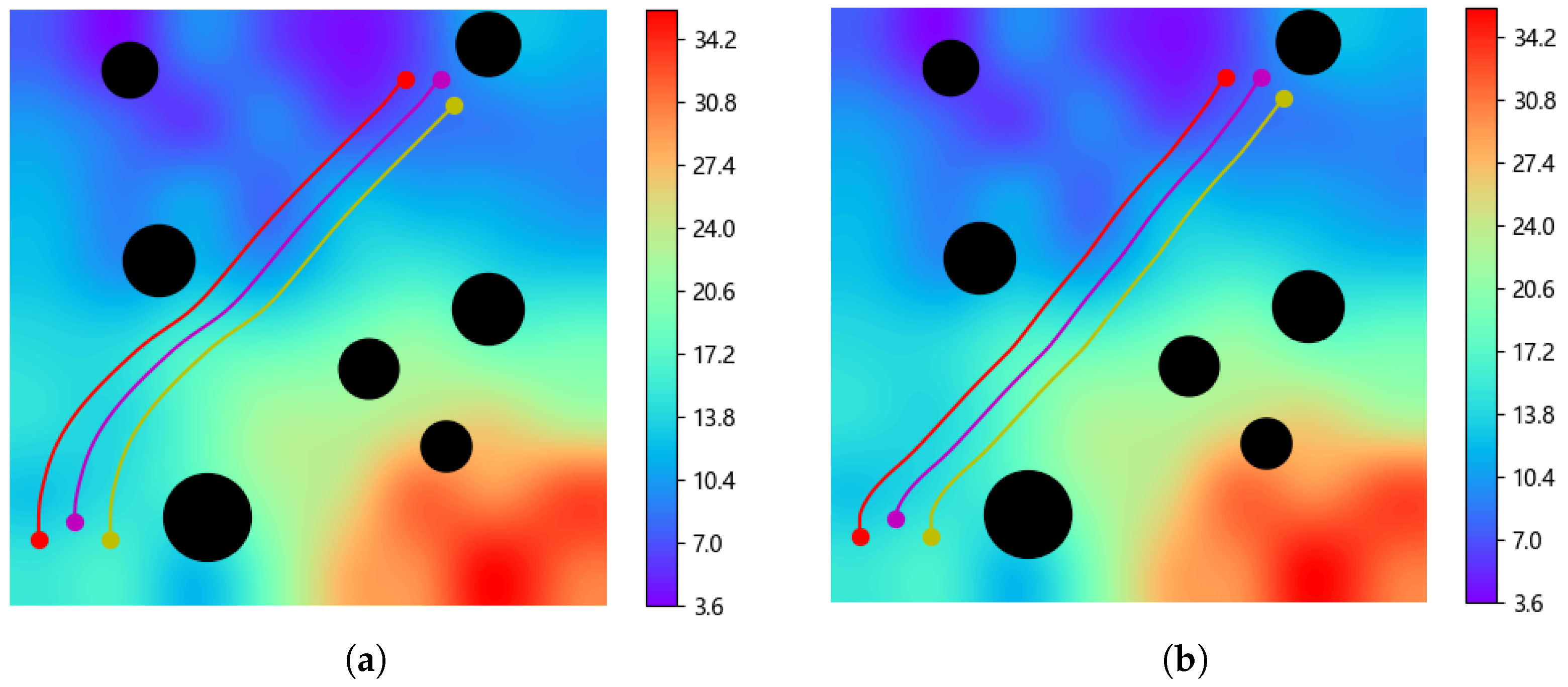
| Scenarios | Method | Success Rate (%) | Average Trajectory Length (m) | Average Traveled Time (s) | Average Elevation Gradient |
|---|---|---|---|---|---|
| Low Elevation | DWA [11] | 85 | 1364.34 | 132.64 | 1.79 |
| Ego-graph Method [35] | 88 | 1357.76 | 132.93 | 1.74 | |
| DWA-RL with D* Lite [36] | 94 | 1398.54 | 133.21 | 1.68 | |
| Proposed | 94 | 1423.65 | 129.84 | 1.66 | |
| Medium Elevation | DWA [11] | 72 | 1085.98 | 139.84 | 3.46 |
| Ego-graph Method [35] | 69 | 1126.63 | 147.53 | 3.25 | |
| DWA-RL with D* Lite [36] | 79 | 1294.26 | 143.28 | 3.03 | |
| Proposed | 82 | 1320.21 | 143.57 | 2.98 | |
| High Elevation | DWA [11] | 31 | 1259.32 | 142.17 | 4.06 |
| Ego-graph Method [35] | 39 | 1243.65 | 143.25 | 3.82 | |
| DWA-RL with D* Lite [36] | 53 | 1298.43 | 152.14 | 3.46 | |
| Proposed | 59 | 1306.42 | 150.34 | 3.31 | |
| Numerous Obstacles | DWA [11] | 54 | 775.41 | 97.32 | 1.95 |
| Ego-graph Method [35] | 55 | 754.54 | 90.43 | 1.87 | |
| DWA-RL with D* Lite [36] | 70 | 794.02 | 88.65 | 1.80 | |
| Proposed | 71 | 802.82 | 89.01 | 1.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Zhang, Y.; Song, D.; Zhang, N.; Chen, L.; Yang, J.; Wang, L.; Zhai, X.B. UGV Formation Path Planning Based on DRL-DWA in Off-Road Environments. Appl. Sci. 2025, 15, 12212. https://doi.org/10.3390/app152212212
Li C, Zhang Y, Song D, Zhang N, Chen L, Yang J, Wang L, Zhai XB. UGV Formation Path Planning Based on DRL-DWA in Off-Road Environments. Applied Sciences. 2025; 15(22):12212. https://doi.org/10.3390/app152212212
Chicago/Turabian StyleLi, Congduan, Yiqi Zhang, Dan Song, Nanfeng Zhang, Lei Chen, Jingfeng Yang, Li Wang, and Xiangping Bryce Zhai. 2025. "UGV Formation Path Planning Based on DRL-DWA in Off-Road Environments" Applied Sciences 15, no. 22: 12212. https://doi.org/10.3390/app152212212
APA StyleLi, C., Zhang, Y., Song, D., Zhang, N., Chen, L., Yang, J., Wang, L., & Zhai, X. B. (2025). UGV Formation Path Planning Based on DRL-DWA in Off-Road Environments. Applied Sciences, 15(22), 12212. https://doi.org/10.3390/app152212212






