Numerical Simulation and Mechanism Study of Liquid Nitrogen Flow Instability in a Sudden Expansion–Contraction Channel
Abstract
1. Introduction
- (i)
- Vortex-induced flow separation and reattachment.
- (ii)
- High-amplitude pressure fluctuations.
- (iii)
- Strong thermo-hydrodynamic coupling.
- (1)
- Jet dynamics and phase-change phenomena
- (2)
- Turbulence–thermal coupling in a constrained channel
- (3)
- Nonlinear instability mechanisms
2. Physical and Mathematical Model
2.1. Physical Model
2.2. Mathematical Model
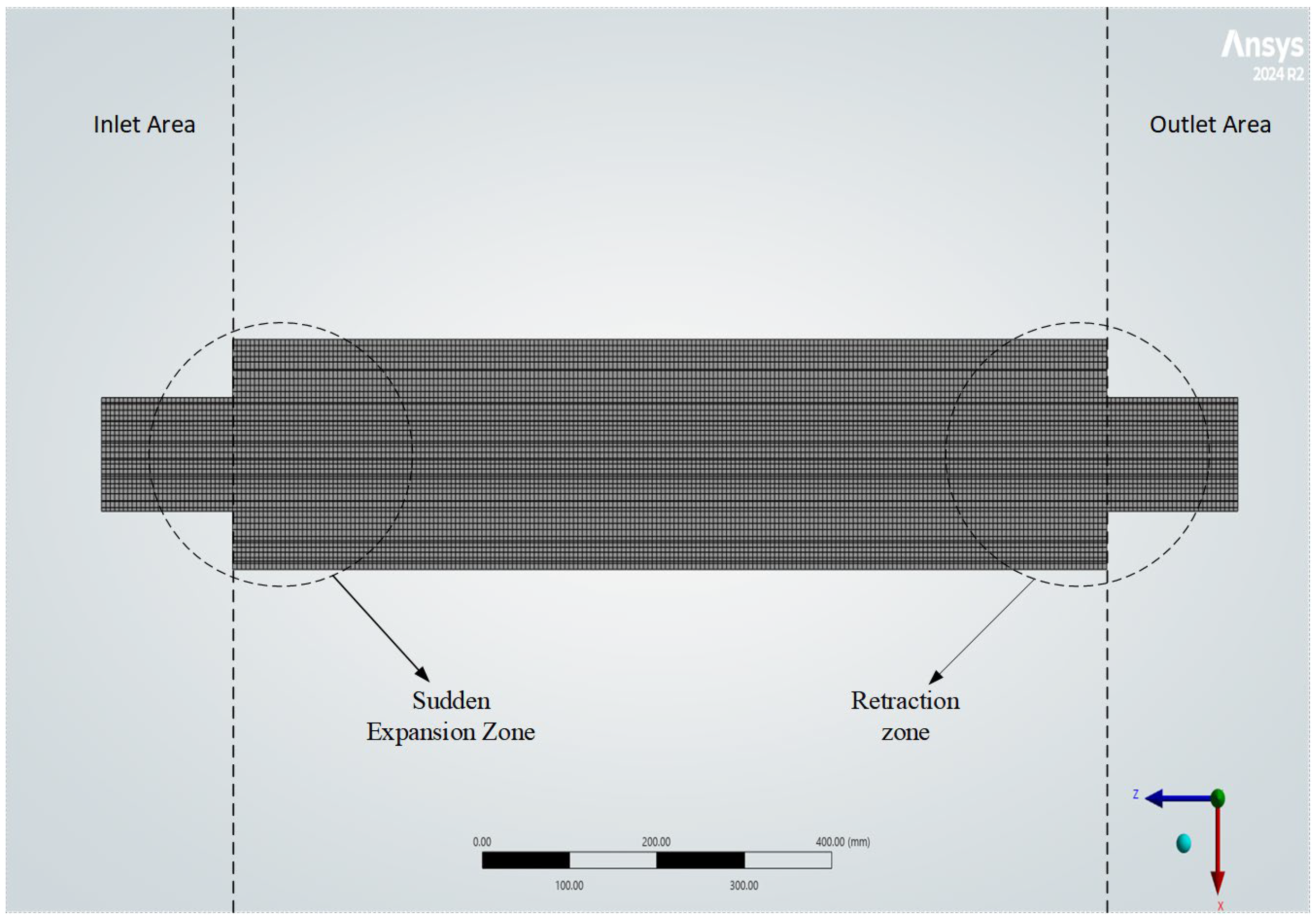
3. Grid Division and Condition
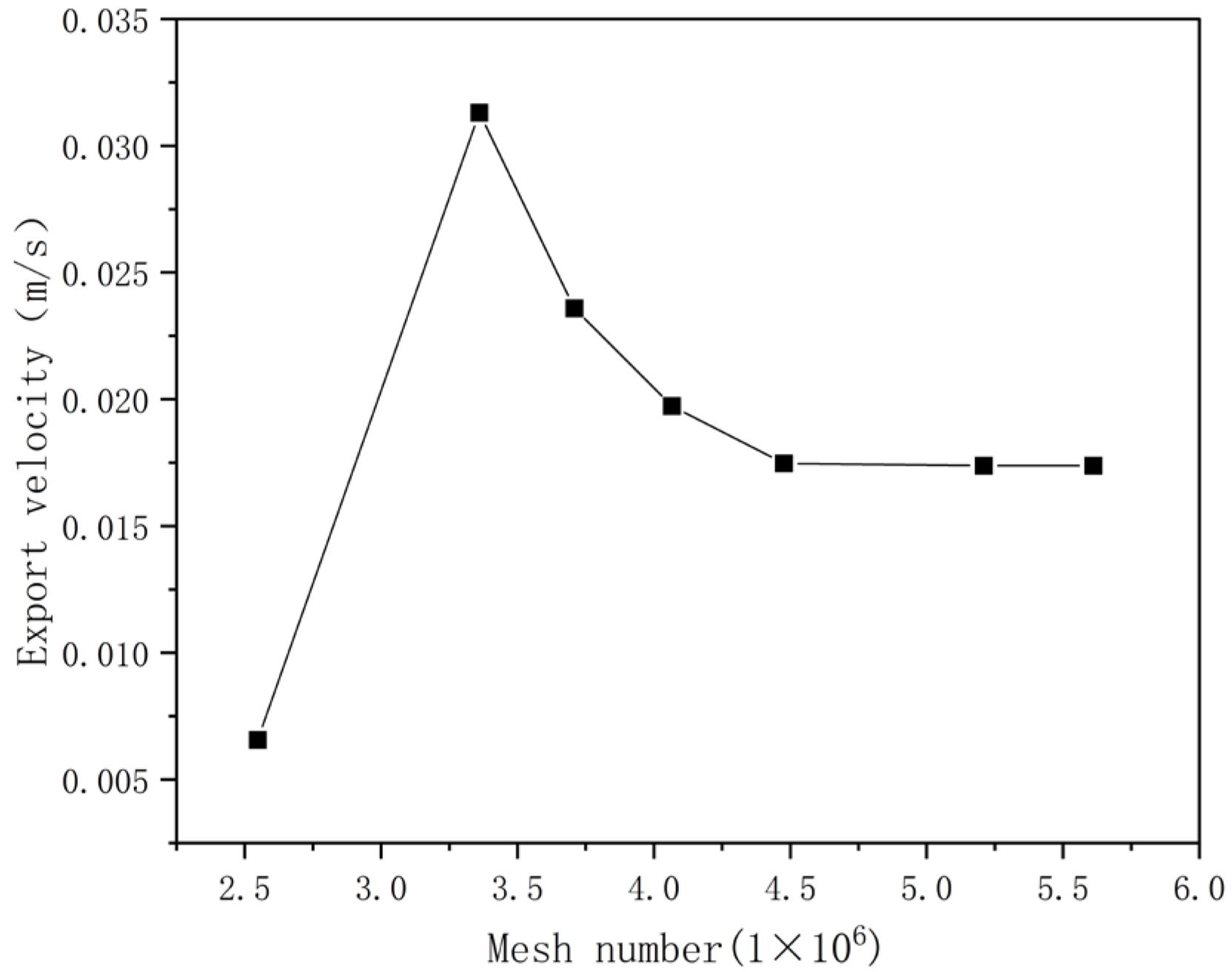
3.1. Grid-Independent Verification
3.2. Boundary Conditions
4. Analysis and Results
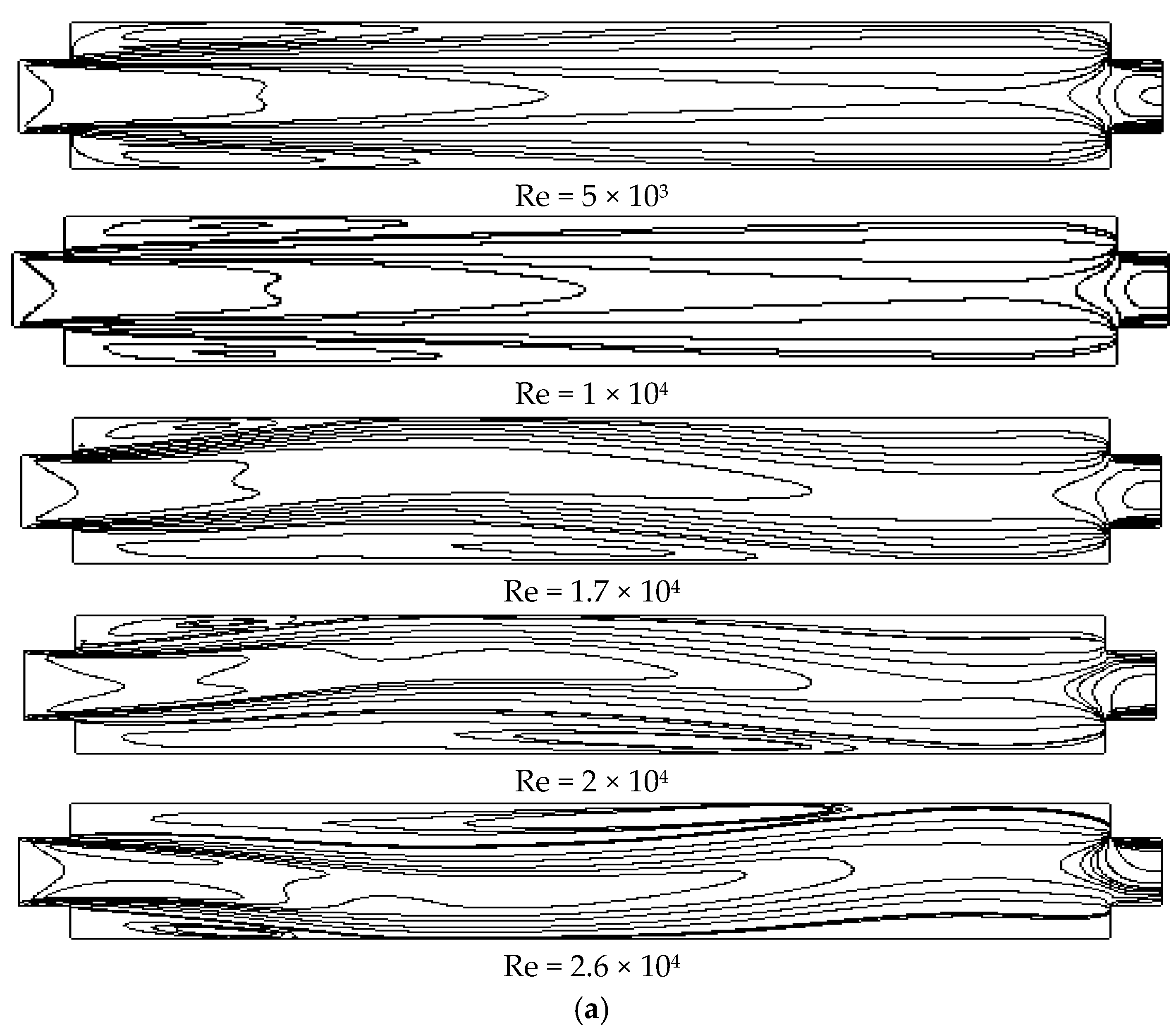
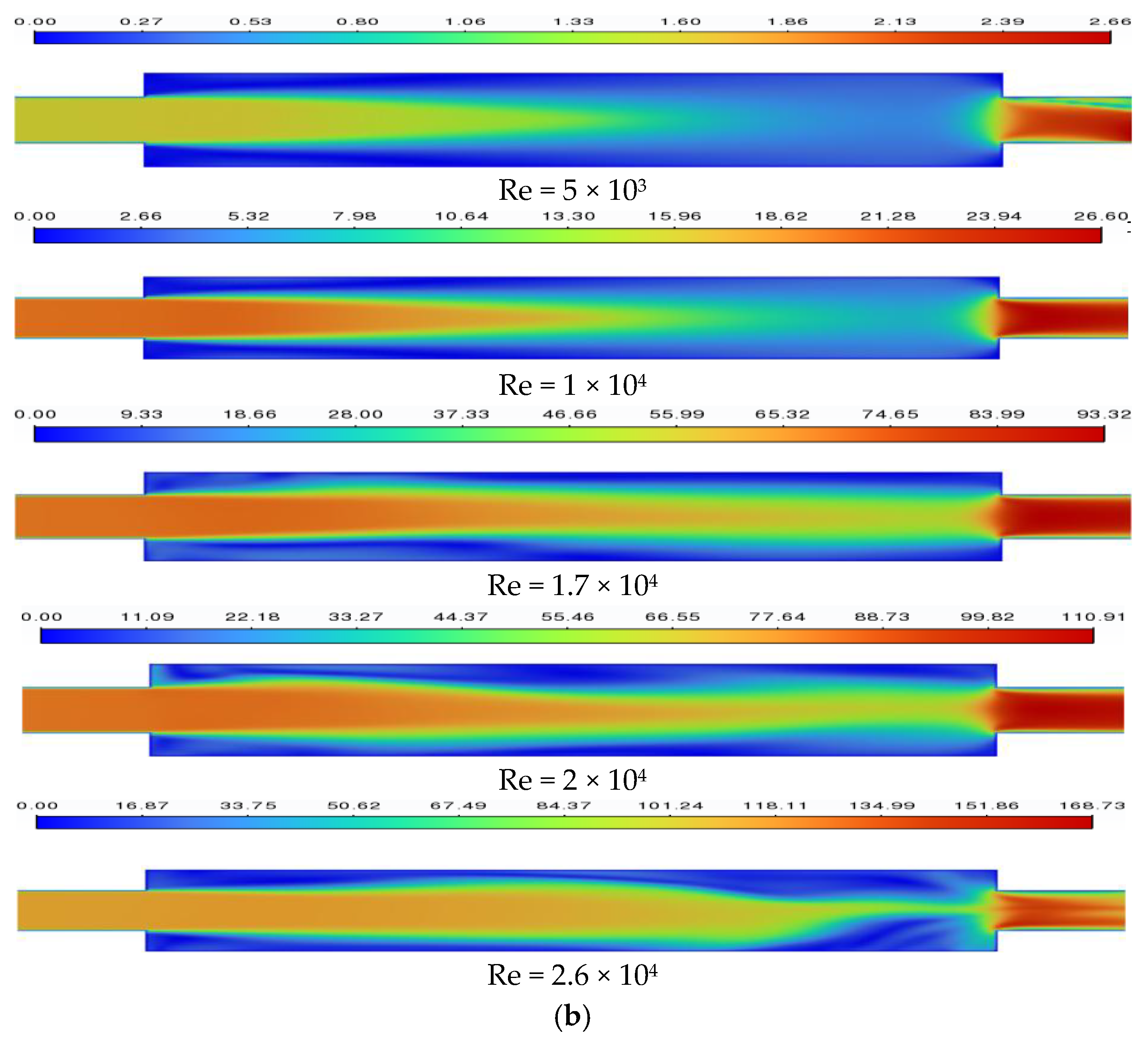
4.1. Flow Characteristics of the Sudden Expansion–Contraction Channel in Different Re
4.1.1. Analysis of Fluid Flow Under Different Re
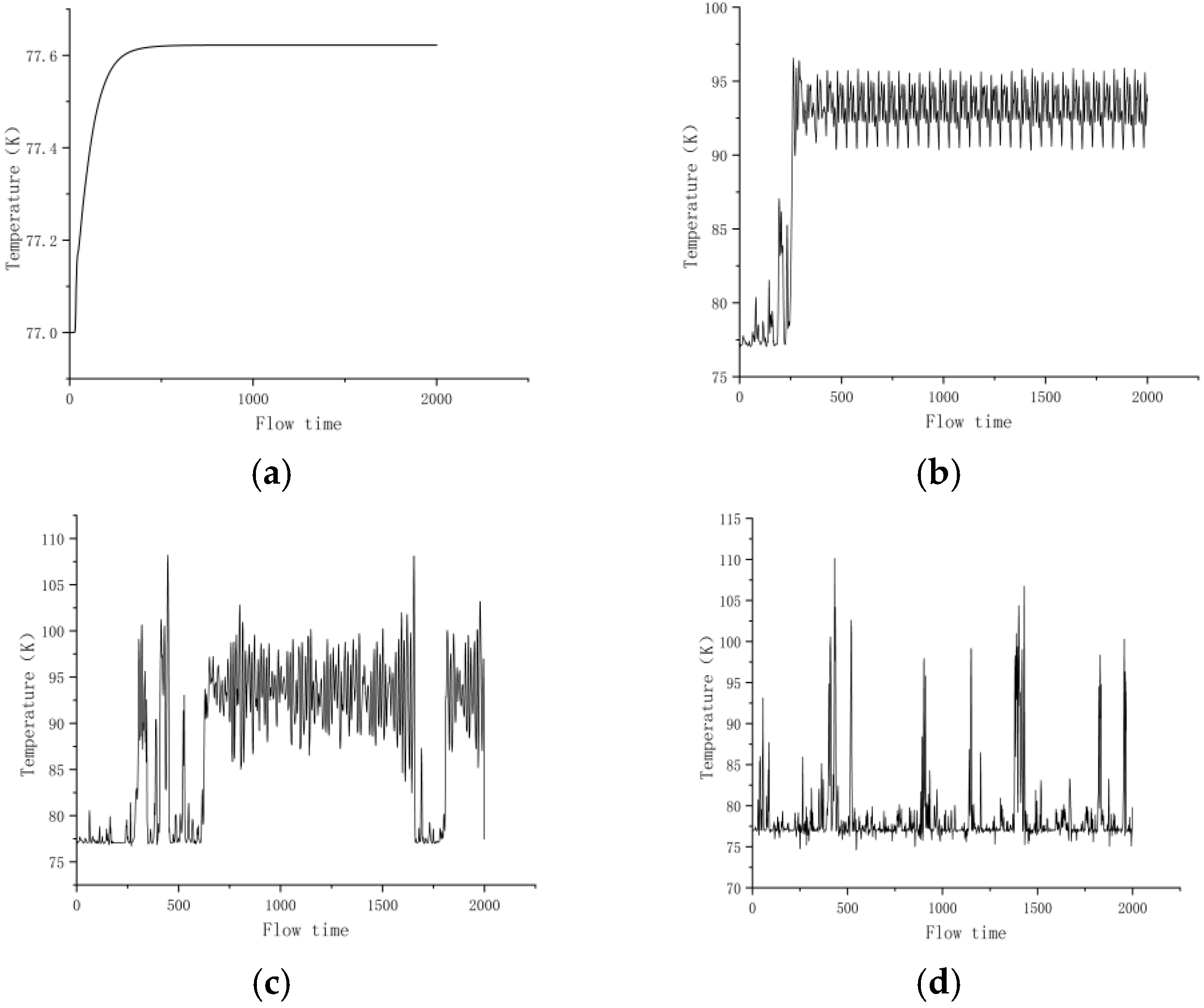
4.1.2. Evolution of Fluid Temperature Under Different Re
4.2. Analysis of Fluid Flow with Different Structural Parameters
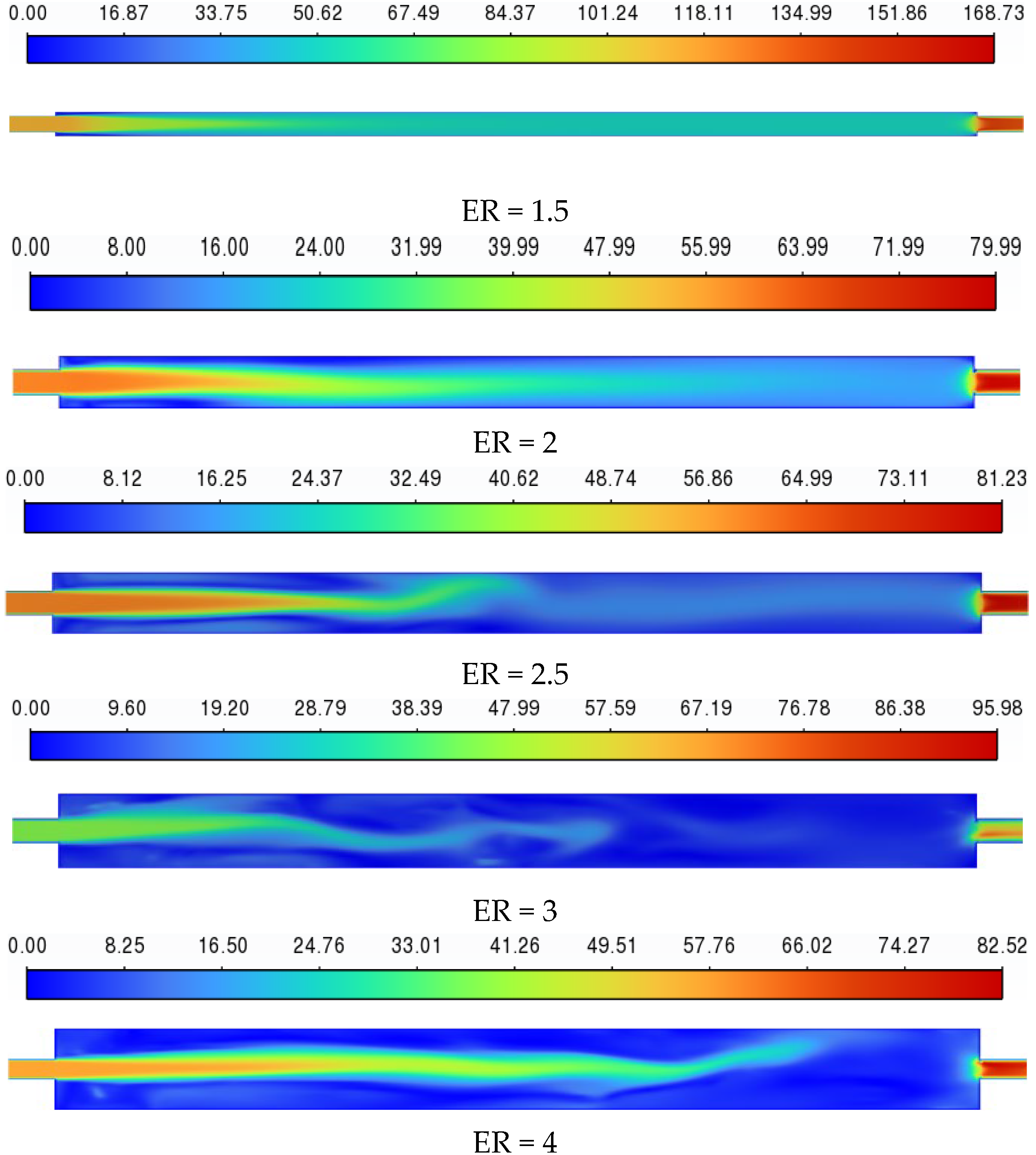
4.2.1. Fluid Flow of the Expansion–Contraction Channel with the Different ER
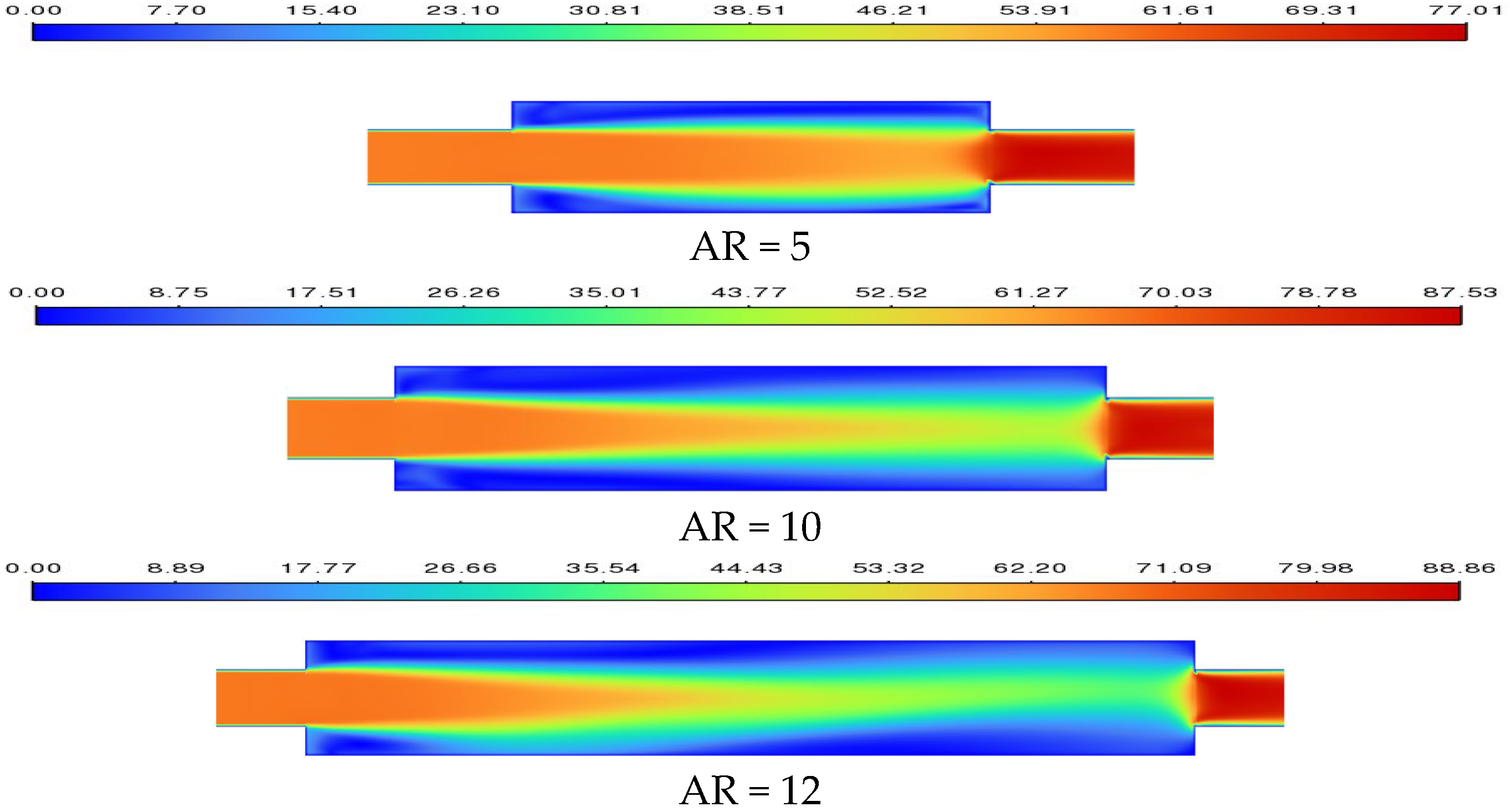
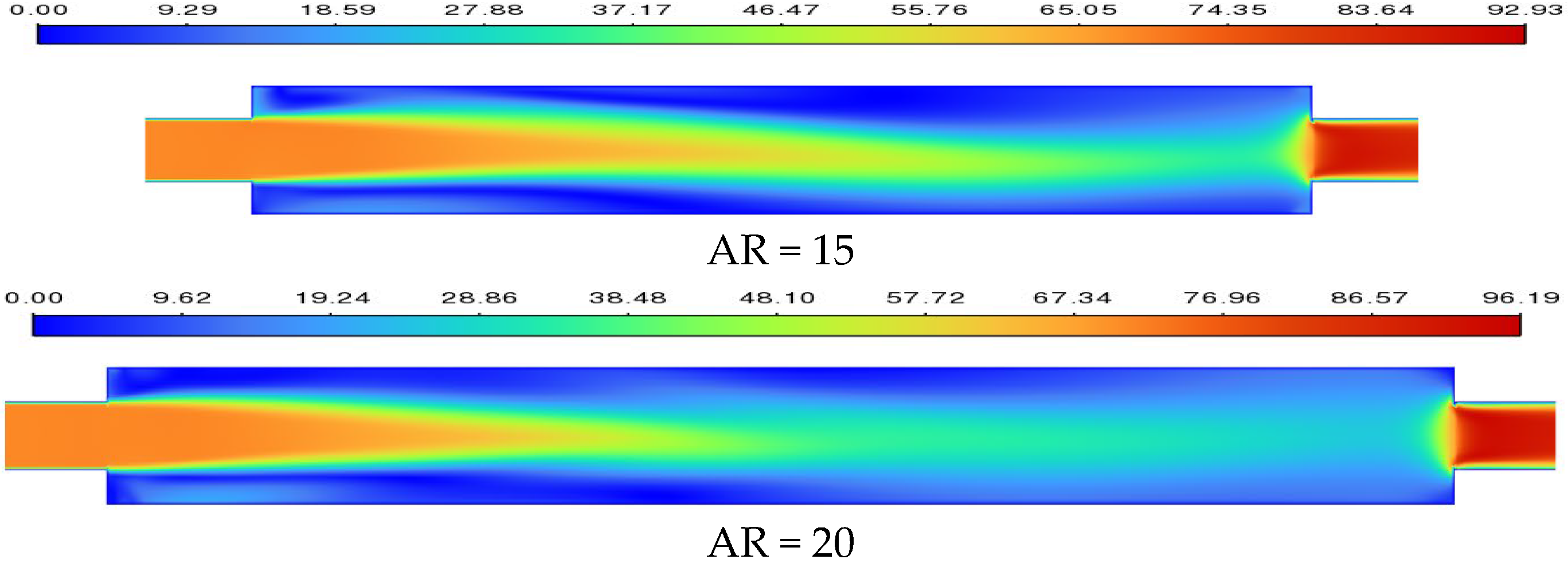
4.2.2. Fluid Flow of the Expansion–Contraction Channel with Different Ars
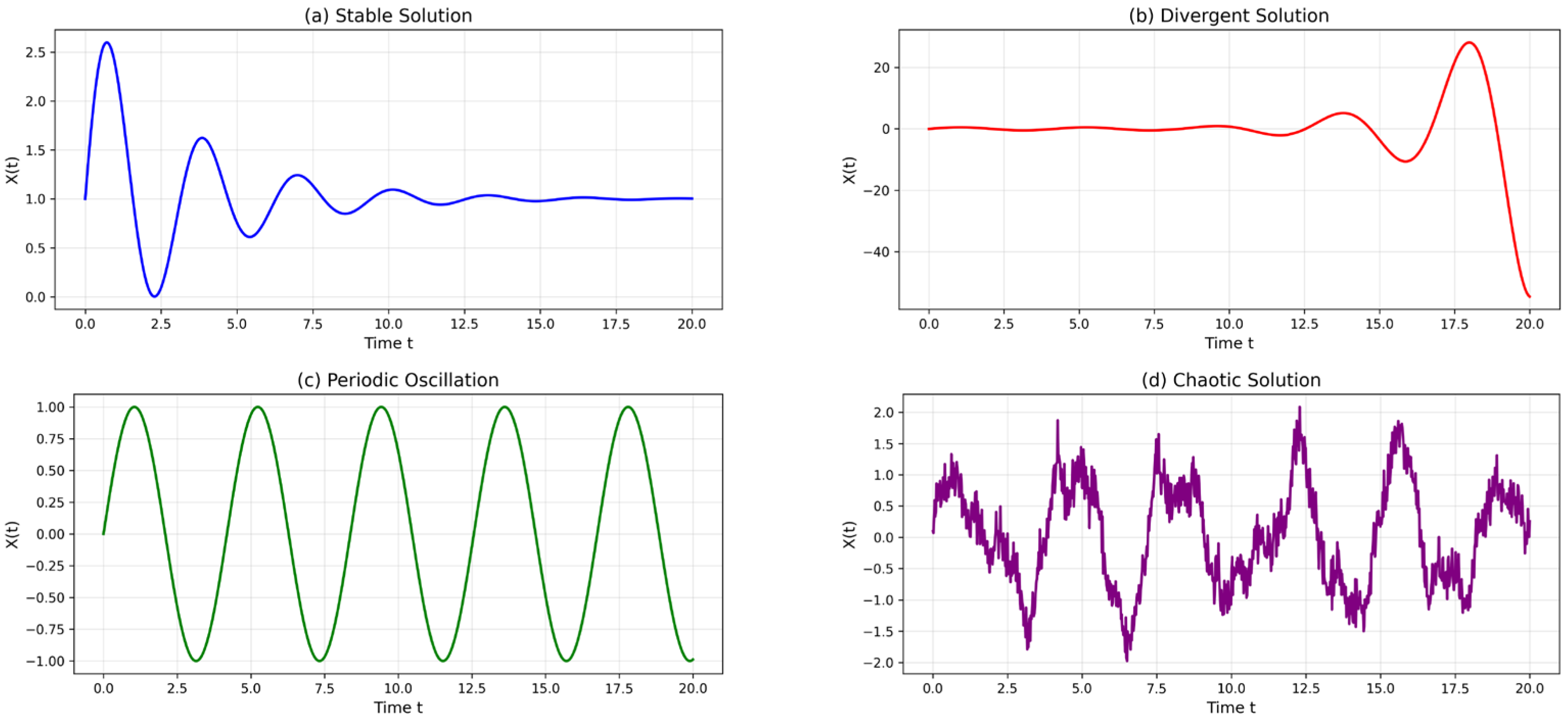
4.3. Analysis of Flow Characteristics and Nonlinear Characteristics
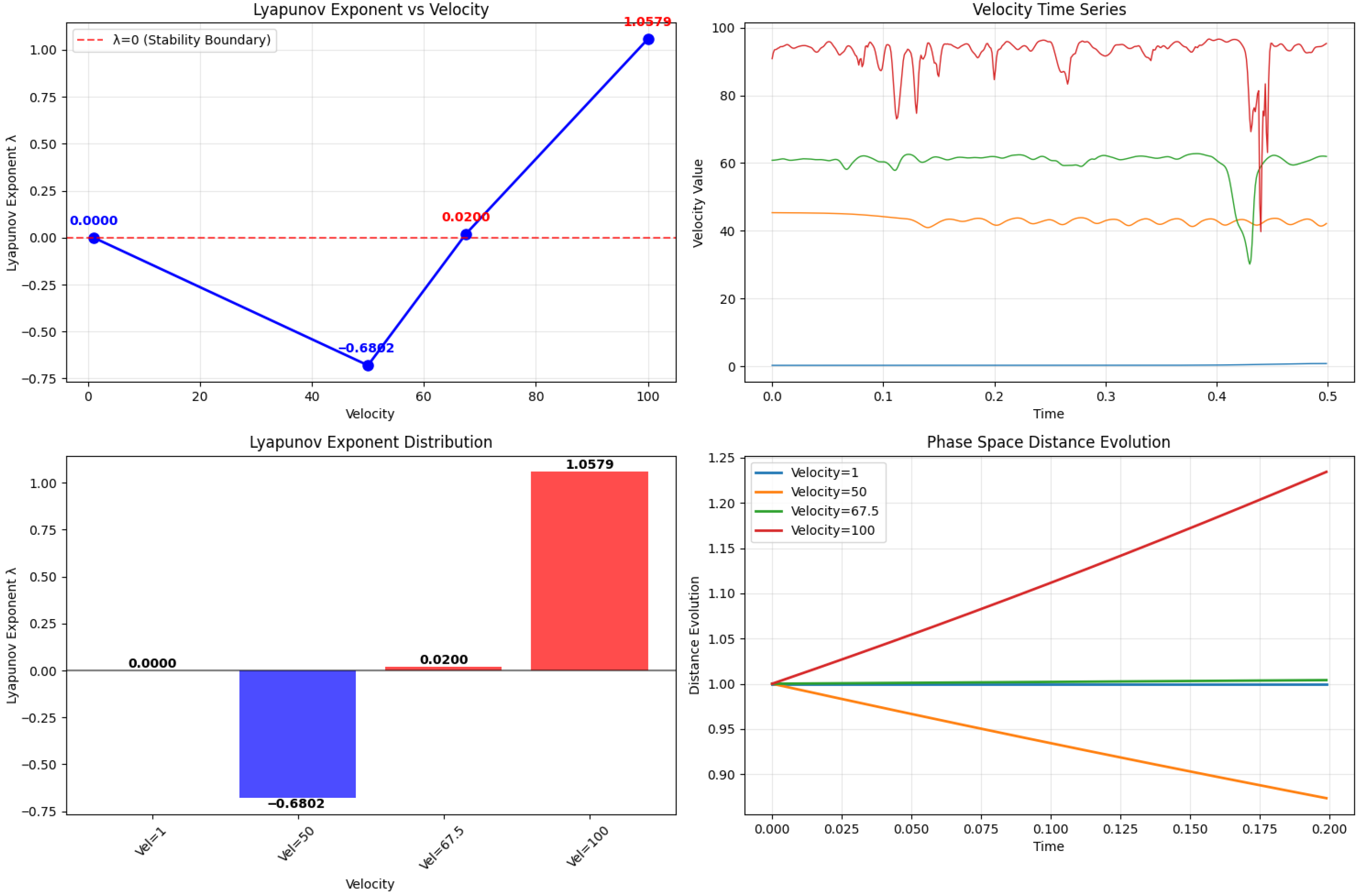
4.3.1. Physical Mechanisms of Parameters
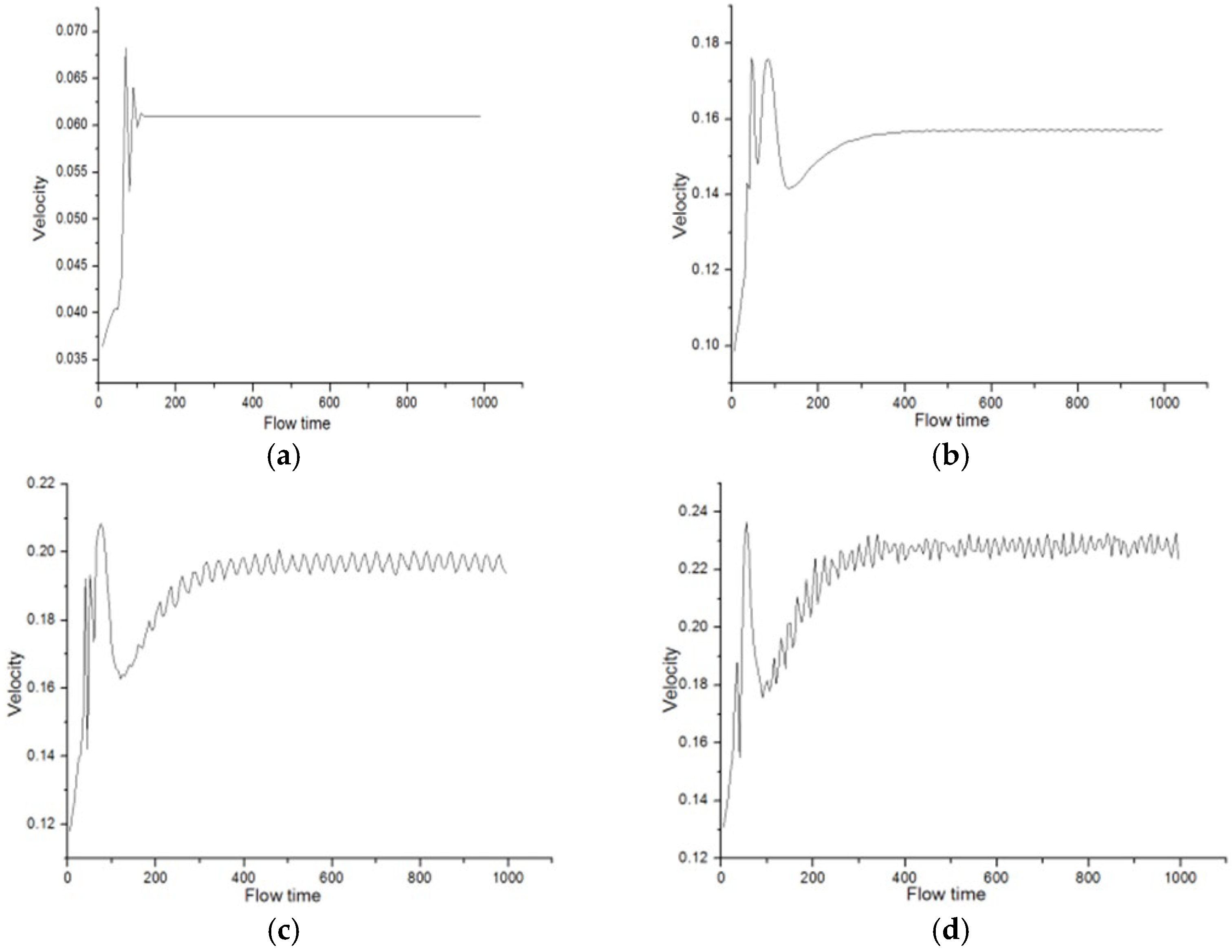
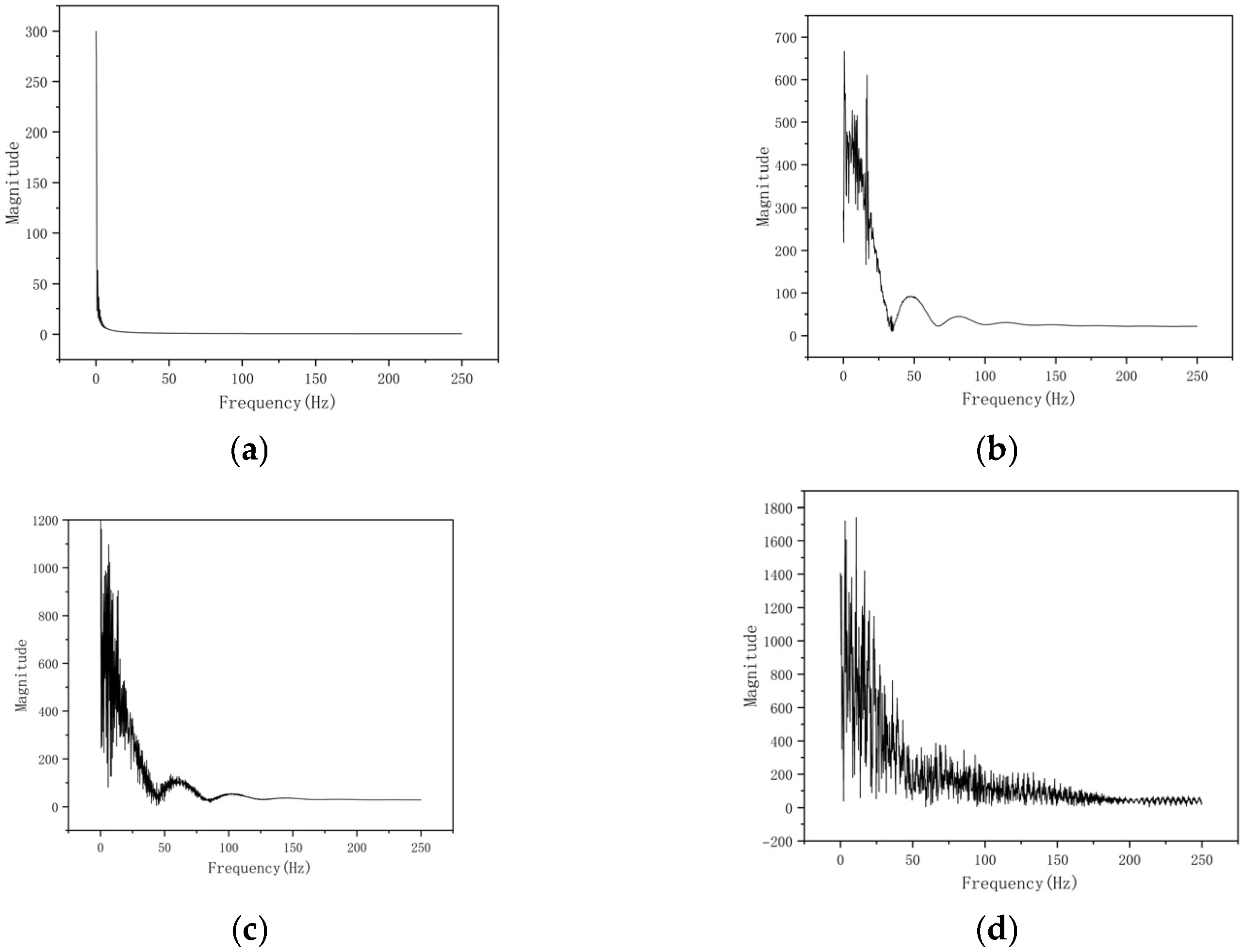
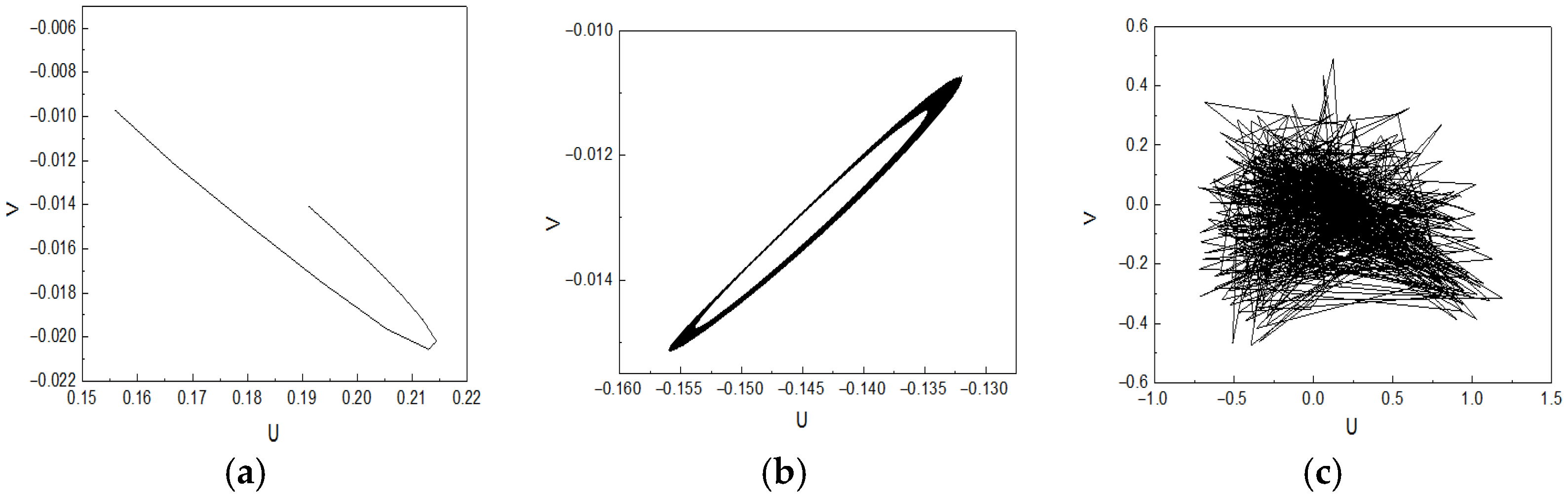
4.3.2. Spectral Analysis and Velocity Phase Diagram Analysis
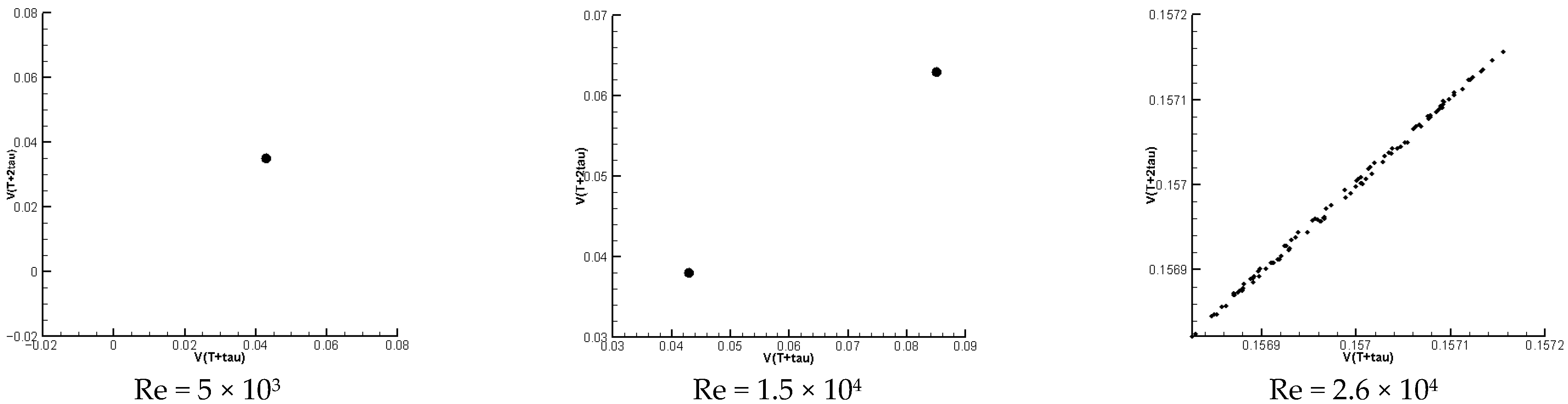
4.3.3. Poincaré Section
5. Conclusions
- (1)
- As the Re increases, the fluid flow transitions from a stable symmetric flow state to the gradual emergence of oscillations and eventually to a chaotic state. Specifically, when Re is less than 1.7 × 104, the flow exhibits higher stability, characterized by a uniform and symmetric jet flow. When Re exceeds 2.6 × 104, turbulence significantly intensifies, accompanied by pronounced oscillatory behavior, resulting in entirely irregular flow within the channel. Lyapunov exponent analysis of the velocity time series validates the system’s transition from stable to chaotic states.
- (2)
- Alterations in structural parameters influence the Rec for flow heat transfer. An increase in ER leads to a monotonically decreasing Rec, eventually saturating; under different parameter evolutions, the system consistently exhibits the same transition from a stable state to a chaotic state. Therefore, in nonlinear dynamical systems with structural symmetry, the result is independent of variations in geometric parameters.
- (3)
- Nonlinear phenomena in flow heat transfer are investigated using spectral analysis, velocity phase space, and Poincaré sections. The analysis elucidates the general characteristics and underlying mechanisms of nonlinearity, demonstrating how the existence of multiple solutions in nonlinear systems influences heat transfer within fluid flows. Analysis of critical state transitions in flow heat transfer provides new insights and data references for solving practical engineering problems.
- (4)
- Subsequent research will construct an experimental apparatus featuring a sudden expansion–contraction channel and employ particle image velocimetry (PIV) and laser-induced fluorescence temperature measurement techniques to obtain precise measurements of velocity and temperature fields. These measurements can then be directly compared with current numerical simulation results to further validate the model’s accuracy. The nonlinear characteristics will be analyzed from the perspectives of thermofluid dynamics or fluid–structure interaction, employing more precise parameters to assess the nonlinear state quantitatively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| U | Streamwise velocity |
| V | Transverse velocity |
| W | Vertical velocity |
| T | Temperature |
| AR | Aspect ratio |
| ER | Expansion ratio |
| Re | Reynolds number |
| Rec | Critical Reynolds number |
| Recf | First critical Reynolds number |
| Recs | Second critical Reynolds number |
| H | expansion diameter |
| h | shrinkage diameter |
| L | Length |
| ω | Vorticity |
| μ | Dynamic viscosity |
| k | Turbulent kinetic energy |
| ε | Turbulent dissipation rate |
References
- Tilton, D.E.; Kearns, D.A.; Tilton, C.L. Liquid nitrogen spray cooling of a simulated electronic chip. In Advances in Cryogenic Engineering; Springer: Berlin/Heidelberg, Germany, 1994; pp. 1779–1786. [Google Scholar]
- Wei, A.; Qiu, L.; Zhang, X. On the unsteady cavitation characteristics of compressible liquid nitrogen flows through a venturi tube. Int. J. Multiph. Flow 2024, 170, 104630. [Google Scholar] [CrossRef]
- Wei, A.; Wang, W.; Hu, Y.; Feng, S.; Qiu, L.; Zhang, X. Numerical and experimental analysis of the cavitation and flow characteristics in liquid nitrogen submersible pump. Phys. Fluids 2024, 36, 042109. [Google Scholar] [CrossRef]
- Sehmbey, M.S.; Chow, L.C.; Hahn, O.J.; Pais, M.R. Effect of spray characteristics on spray cooling with liquid nitrogen. J. Thermophys. Heat Transf. 1995, 9, 757–765. [Google Scholar] [CrossRef]
- Sehmbey, M.S.; Chow, L.C.; Hahn, O.J.; Pais, M.R. Spray cooling of power electronics at cryogenic temperatures. J. Thermophys. Heat Transf. 1995, 9, 123–128. [Google Scholar] [CrossRef]
- Cen, K.; Li, Y.; Wei, L.; Li, W.; Wang, Y.; Dai, M. Evaporation of single moving liquid nitrogen droplet: Experimental study and numerical simulation. Int. J. Heat Mass Transf. 2023, 201, 123584. [Google Scholar] [CrossRef]
- Moosavian, D.; Ghassemi, H.; Mostofizadeh, A. Experimental study of atomization of liquid nitrogen jet impingement. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 302. [Google Scholar] [CrossRef]
- Cai, C.; Ren, K.; Li, Q. Numerical simulation of the flow field structure of liquid nitrogen jet. Therm. Sci. 2019, 23, 1337–1343. [Google Scholar] [CrossRef]
- Banerjee, S.; Banik, A.; Rajak, V.K.; Bandyopadhyay, T.K.; Nayak, J.; Jasinski, M.; Kumar, R.; Jeon, B.-H.; Siddiqui, M.R.; Khan, M.A. Two-Phase Crude Oil–Water Flow Through Different Pipes: An Experimental Investigation Coupled with Computational Fluid Dynamics Approach. ACS Omega 2024, 9, 11181–11193. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, Z.; Li, Y.; Ma, E.; Yu, H. Flow boiling of liquid nitrogen in a horizontal macro-tube at low pressure: Part I-flow pattern, two-phase flow instability, and pressure drop. Int. J. Heat Fluid Flow 2024, 107, 109335. [Google Scholar] [CrossRef]
- Zhang, X.; Zeng, X.; He, C.; Liu, Y. Large-eddy simulation of turbulent channel flows with antifouling-featured bionic microstructures. Int. J. Heat Fluid Flow 2023, 104, 109228. [Google Scholar] [CrossRef]
- Cai, H.; Xu, L.; Yang, Y.; Li, L. Analytical solution and numerical simulation of the liquid nitrogen freezing-temperature field of a single pipe. AIP Adv. 2018, 8, 055119. [Google Scholar] [CrossRef]
- Mohammadshahi, S.; Samsam-Khayani, H.; Cai, T.; Kim, K.C. Experimental and numerical study on flow characteristics and heat transfer of an oscillating jet in a channel. Int. J. Heat Fluid Flow 2020, 86, 108701. [Google Scholar] [CrossRef]
- Jia, H.W.; Zhang, P.; Guo, T.; Fu, X.; Jiang, S. Flow-boiling heat transfer experiments with liquid nitrogen in microchannel heat sinks. J. Shanghai Jiao Tong Univ. 2014, 48, 1274–1278. [Google Scholar]
- Zhang, P. Flow boiling of liquid nitrogen in narrow annular channels. J. Korean Inst. Supercond. Cryog. 2008, 10, 1–5. [Google Scholar]
- Sun, S.; Wu, Y.; Zhao, R. The numerical calculation of heat transfer performance for annular flow of liquid nitrogen in a vertical annular channel. Cryogenics 2001, 41, 231–237. [Google Scholar] [CrossRef]
- Sun, B.; Song, J.W. Coupled heat transfer characteristics of stepped cooling channels in liquid oxygen/methane engines. J. Aeronaut. Propuls. 2016, 31, 2972–2978. [Google Scholar]
- Wang, L.; Shi, S.; Qu, M.; Ni, Y.; Ma, Y.; Li, Y. Variation of Leidenfrost temperature in liquid nitrogen pipe chilldown process and its application in chilldown performance analysis. Int. J. Multiph. Flow 2022, 156, 104225. [Google Scholar] [CrossRef]
- Chen, J.C.; Chen, T.R.; Liang, W.D.; Tan, S.L.; Geng, H. Experimental study on the evolution of cavitation flow process of liquid nitrogen in systolic dilatation tubes. J. Mech. 2022, 54, 1242–1256. [Google Scholar]
- Zhang, J.; Lei, L.; Li, H.; Xin, G.; Wang, X. Experimental and numerical studies of liquid-liquid two-phase flows in microchannel with sudden expansion/contraction cavities. Chem. Eng. J. 2022, 433, 133820. [Google Scholar] [CrossRef]
- Erturk, E.; Allahviranloo, T. Bifurcation and Multiplicity of Solutions of the Navier–Stokes Equations in Driven Semi-Elliptical Cavity Flow. Mathematics 2022, 10, 4242. [Google Scholar] [CrossRef]
- Trefethen, L.N.; Trefethen, A.E.; Reddy, S.C.; Driscoll, T.A. Hydrodynamic stability without eigenvalues. Science 1993, 261, 578–584. [Google Scholar] [CrossRef] [PubMed]
- Straughan, B. The Energy Method, Stability, and Nonlinear Convection; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 91. [Google Scholar]
- Rionero, S.; Mulone, G. On the non-linear stability of parallel shear flows. Contin. Mech. Thermodyn. 1991, 3, 1–11. [Google Scholar] [CrossRef]
- Guan, F. Nonlinear Stability Study of Two Classical Flow Problems in Fluid Mechanics; Beijing University of Chemical Technology: Beijing, China, 2024. [Google Scholar]
- Roshchin, D.; Kravchenko, I.; Fu, T.; Patlazhan, S. Effect of flow bifurcation transitions of shear-thinning fluids on hydrodynamic resistance of channels with sudden contraction and expansion. Chem. Eng. Sci. 2023, 281, 119169. [Google Scholar] [CrossRef]
- Kumar, R.; Das, A.K. Numerical study of boiling of liquid nitrogen at solid and liquid contact planes. Int. J. Heat Mass Transf. 2022, 183, 122075. [Google Scholar] [CrossRef]
- Yang, L.; Yang, M.; Huang, W. Nonlinear Phenomena of Fluid Flow in a Bioinspired Two-Dimensional Geometric Symmetric Channel with Sudden Expansion and Contraction. Mathematics 2024, 12, 553. [Google Scholar] [CrossRef]


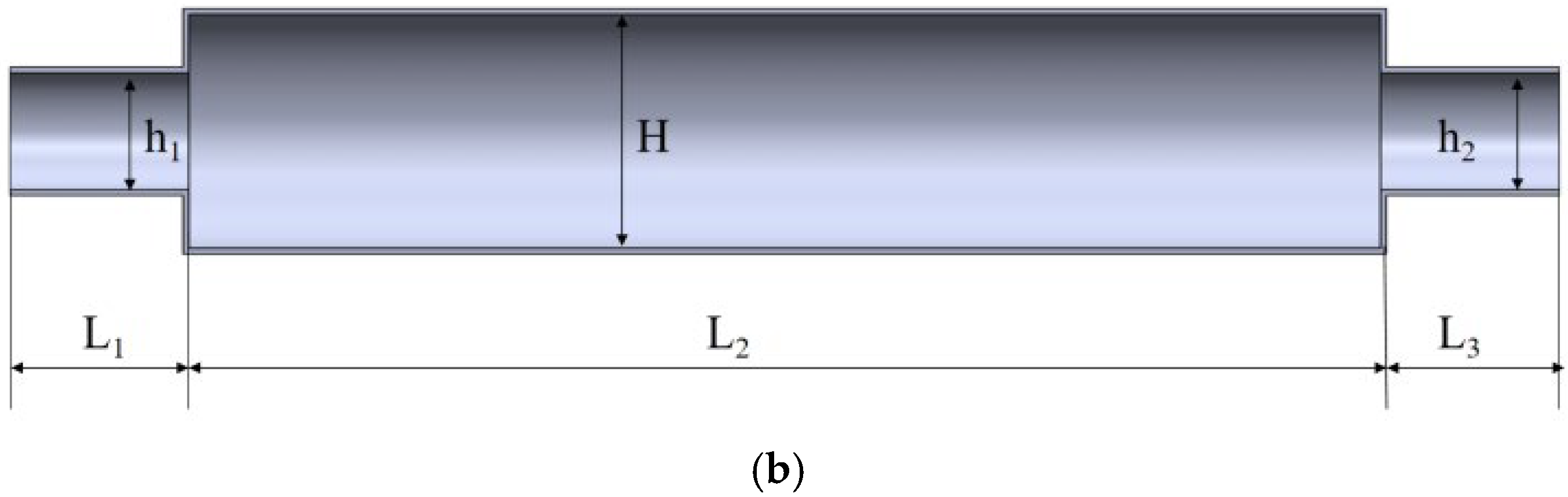






| Parameters | Values (mm) | |
|---|---|---|
| Entry channel | Diameter h1 | 100 |
| Length L1 | 150 | |
| Exit channel | Diameter h2 | 100 |
| Length L3 | 150 | |
| Internal channel | Diameter H | 200 |
| Length L2 | 1000 | |
| wall thickness h3 | 5 | |
| Domain | Boundary Condition Type | Parameters and Values |
|---|---|---|
| inlet | Velocity Inlet | Velocity: Varied to achieve target Re (5 × 103–2.6 × 104) Temperature: 77 K |
| outlet | Pressure Outlet | Temperature: 300 K |
| Channel Walls | No-Slip Wall | wall temperature: 300 K |
| Two-Phase Model | Volume-of-Fluid (VOF) | Phases: Primary Phase—LN2 Secondary Phase—Air Volume Fraction (LN2): 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, C.; Yang, C.; Tian, Z.; Zhang, J.; Zhang, Z.; Su, C. Numerical Simulation and Mechanism Study of Liquid Nitrogen Flow Instability in a Sudden Expansion–Contraction Channel. Appl. Sci. 2025, 15, 12211. https://doi.org/10.3390/app152212211
Shen C, Yang C, Tian Z, Zhang J, Zhang Z, Su C. Numerical Simulation and Mechanism Study of Liquid Nitrogen Flow Instability in a Sudden Expansion–Contraction Channel. Applied Sciences. 2025; 15(22):12211. https://doi.org/10.3390/app152212211
Chicago/Turabian StyleShen, Chunyun, Chao Yang, Zhongxu Tian, Jiajun Zhang, Zheming Zhang, and Chengxuan Su. 2025. "Numerical Simulation and Mechanism Study of Liquid Nitrogen Flow Instability in a Sudden Expansion–Contraction Channel" Applied Sciences 15, no. 22: 12211. https://doi.org/10.3390/app152212211
APA StyleShen, C., Yang, C., Tian, Z., Zhang, J., Zhang, Z., & Su, C. (2025). Numerical Simulation and Mechanism Study of Liquid Nitrogen Flow Instability in a Sudden Expansion–Contraction Channel. Applied Sciences, 15(22), 12211. https://doi.org/10.3390/app152212211






