Transient Prediction Model of Wellbore Temperature in Ultra-Deep Wells Considering Cementing Quality
Abstract
1. Introduction
2. Model Development
2.1. Physical Model and Assumption
- (a)
- (b)
- The drilling fluid is incompressible.
- (c)
- The static formation temperature is maintained at a sufficient distance from the wellbore.
- (d)
- The drill string is centered, and the wellbore has a regular shape.
2.2. Mathematical Model
- (1)
- Drilling fluids in drill pipe
- (2)
- Drill pipe wall
- (3)
- Drilling fluids in the annulus
- (4)
- Casing
- (5)
- Cement
- (6)
- Formation
2.3. Initial and Boundary Conditions
- (1)
- Initial condition
- (2)
- Boundary conditions
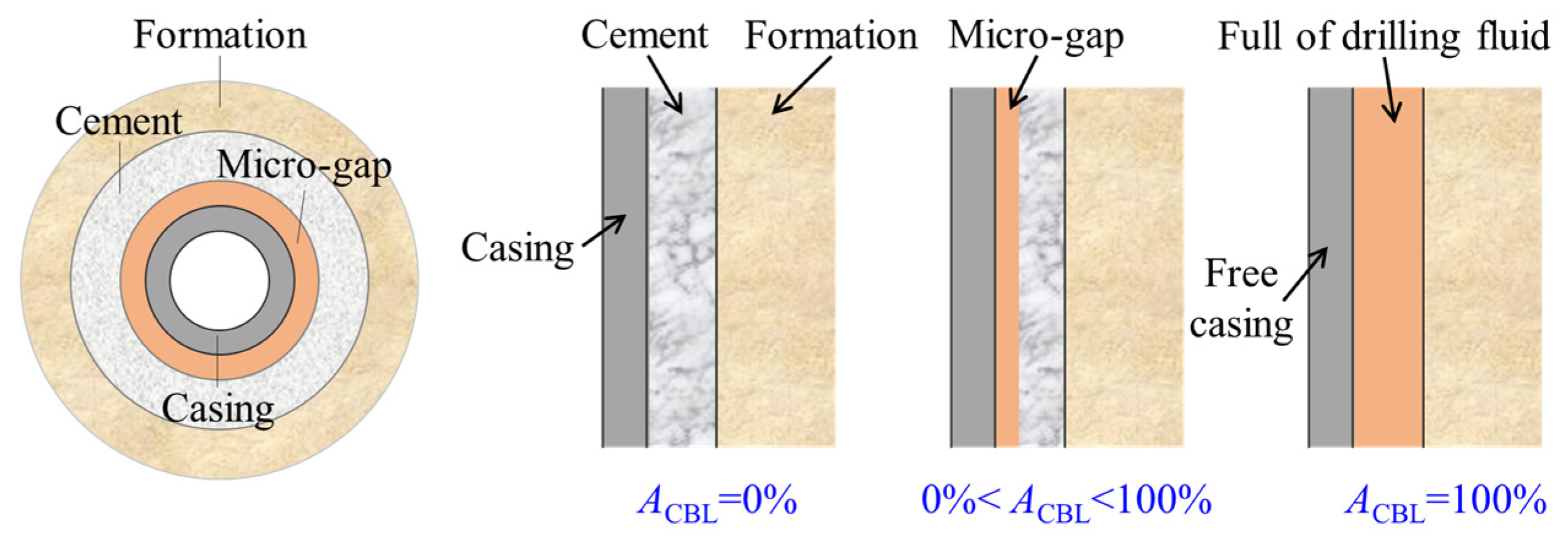
2.4. Overall Thermal Conductivity of the Cement Considering Cement Quality
2.5. Convective Heat Transfer Coefficient
2.6. Auxiliary Equations
- (1)
- Drilling fluid properties
- (2)
- Formation properties
3. Model Solution and Validation
3.1. Model Solution
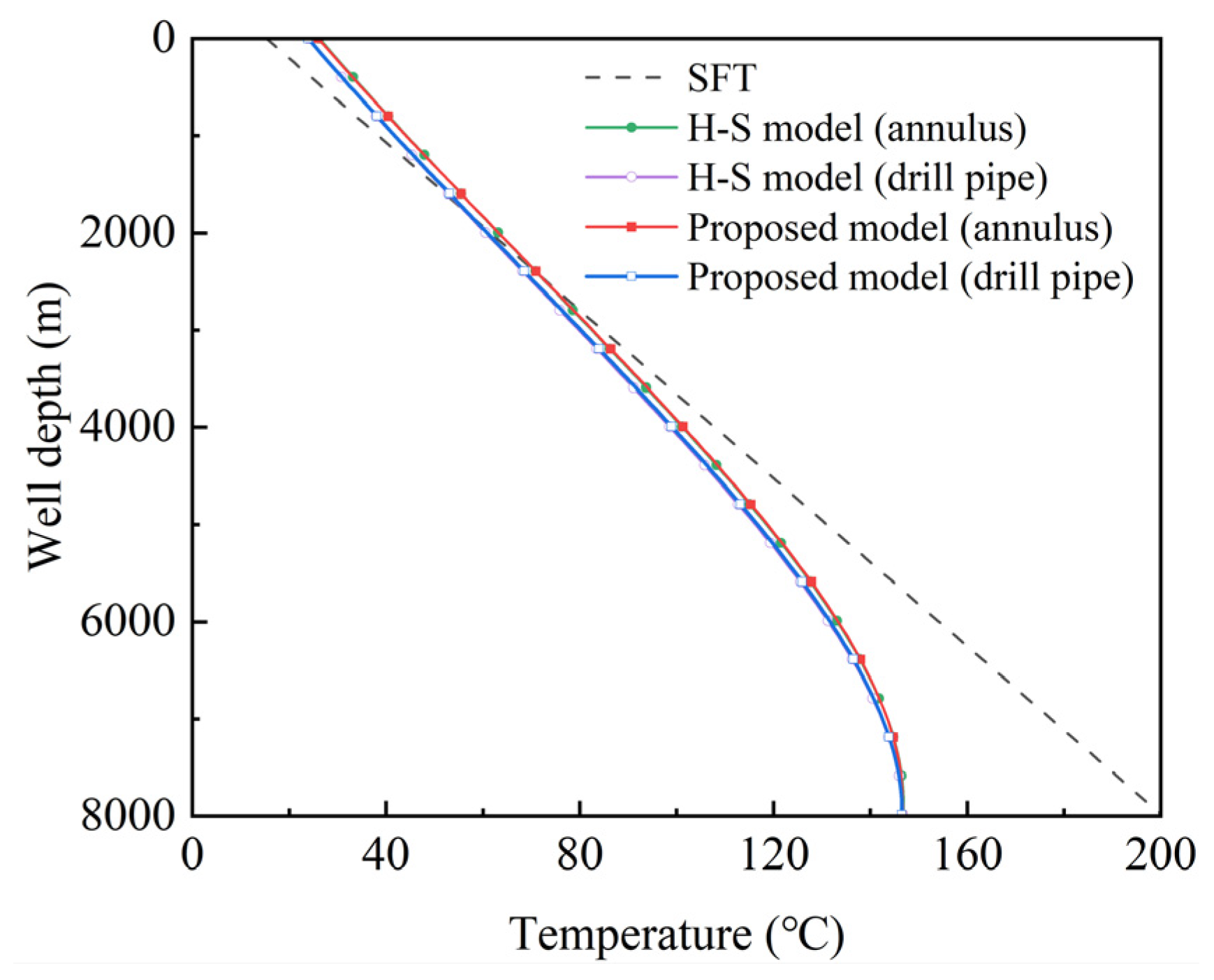
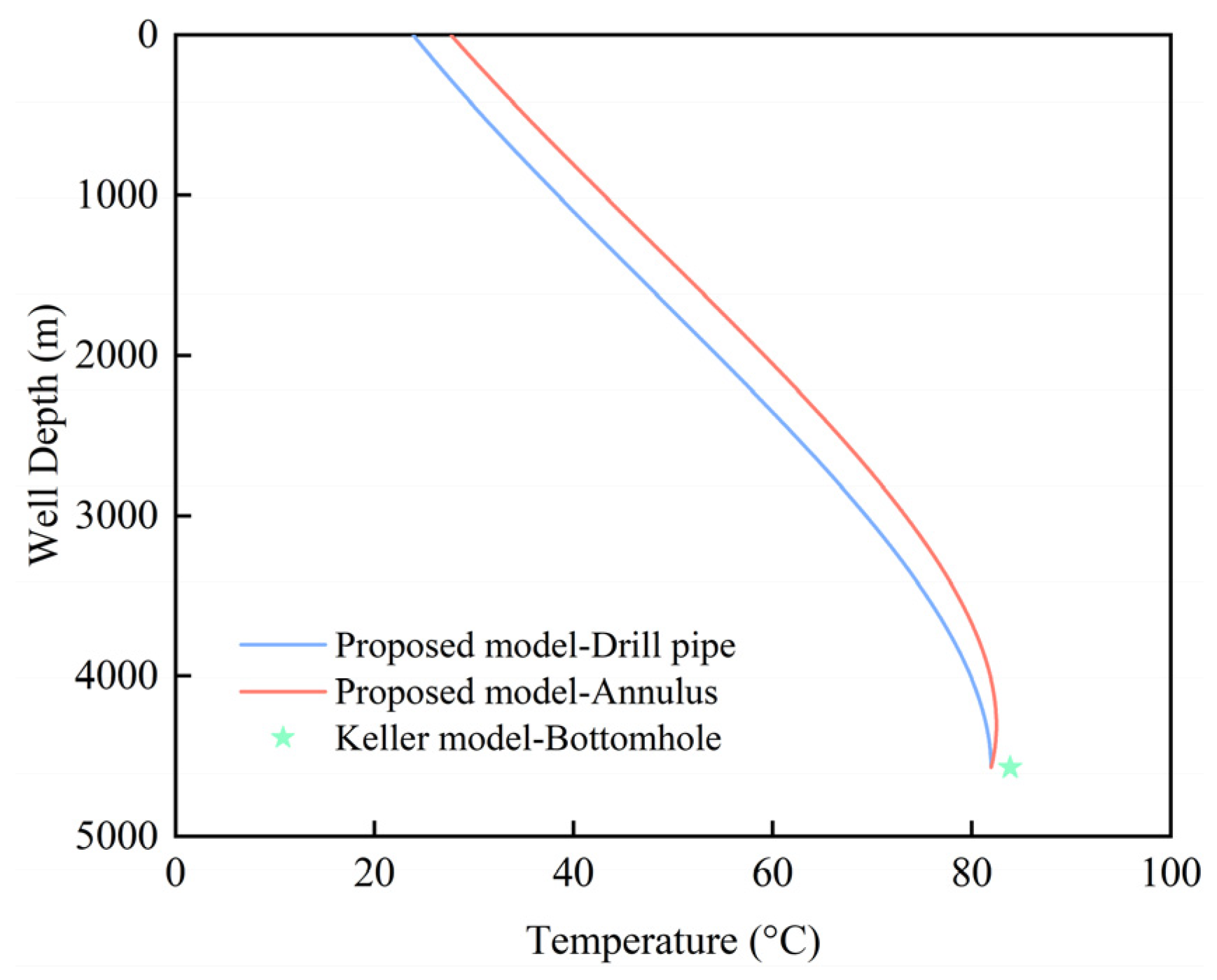
3.2. Model Validation
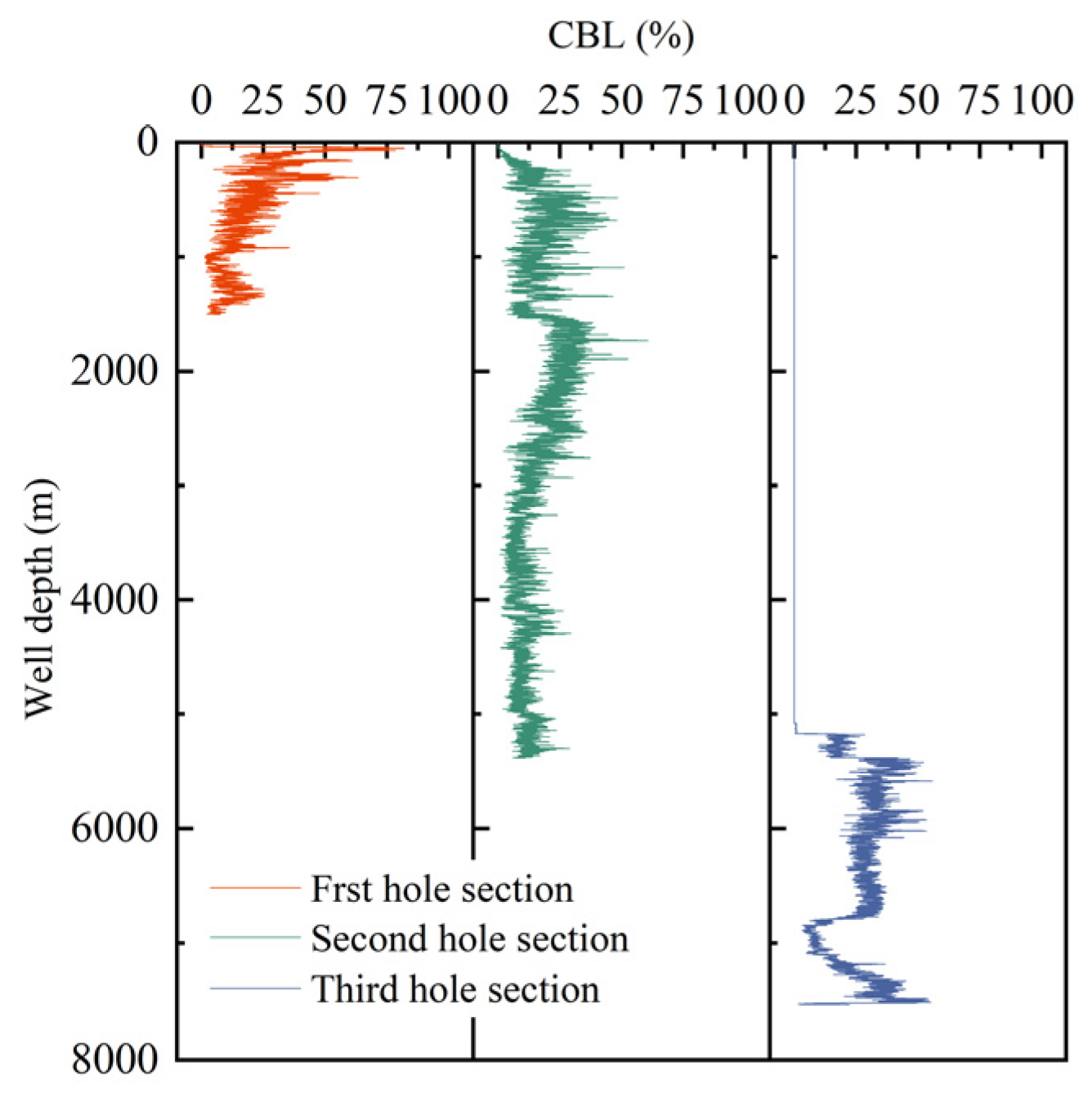
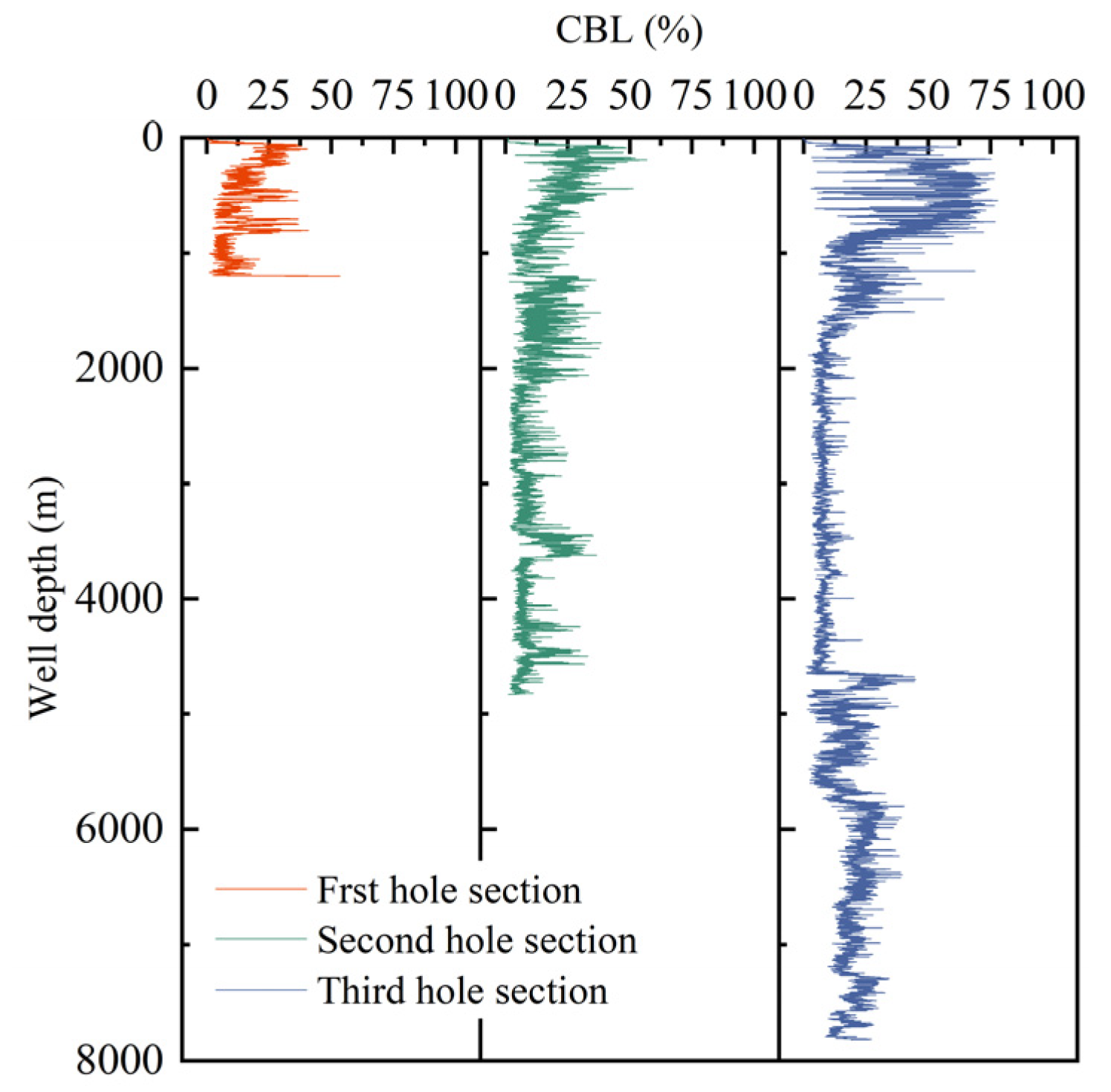
4. Application Cases of Shunbei Oilfield
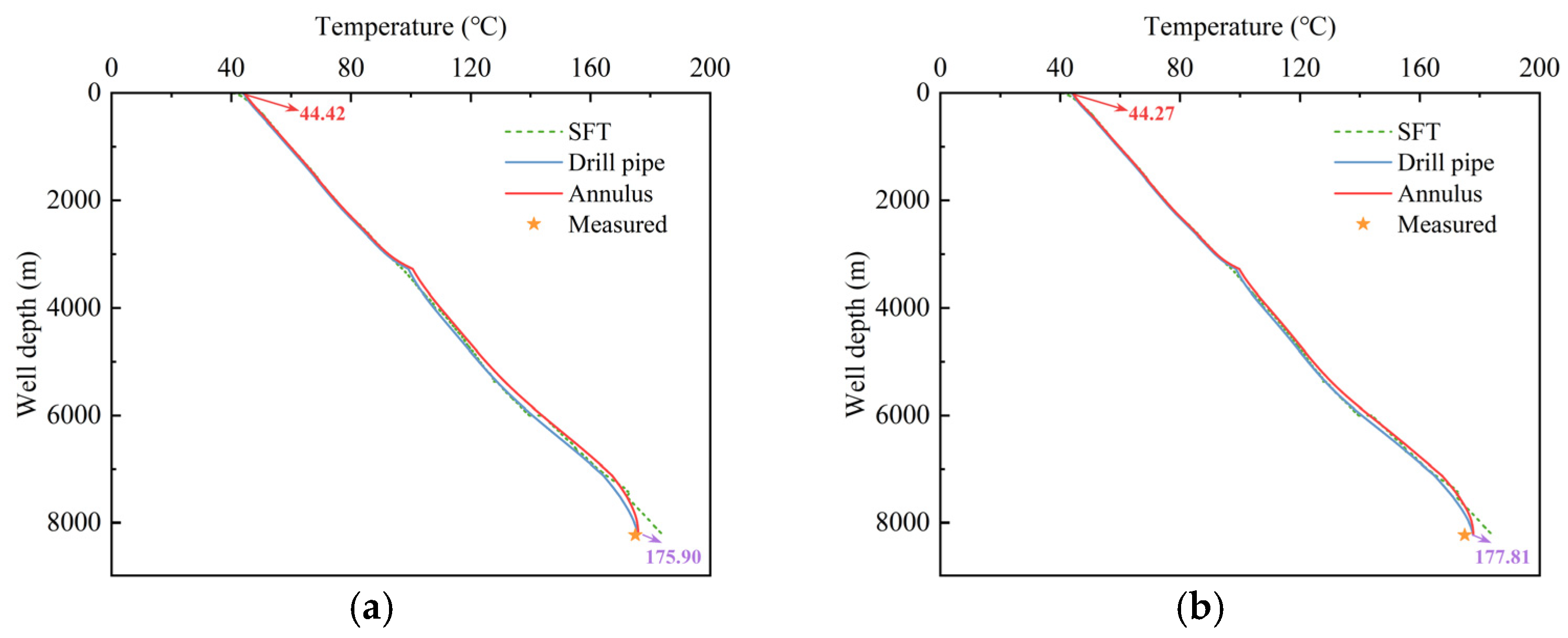
4.1. Case Study—Shunbei Well A
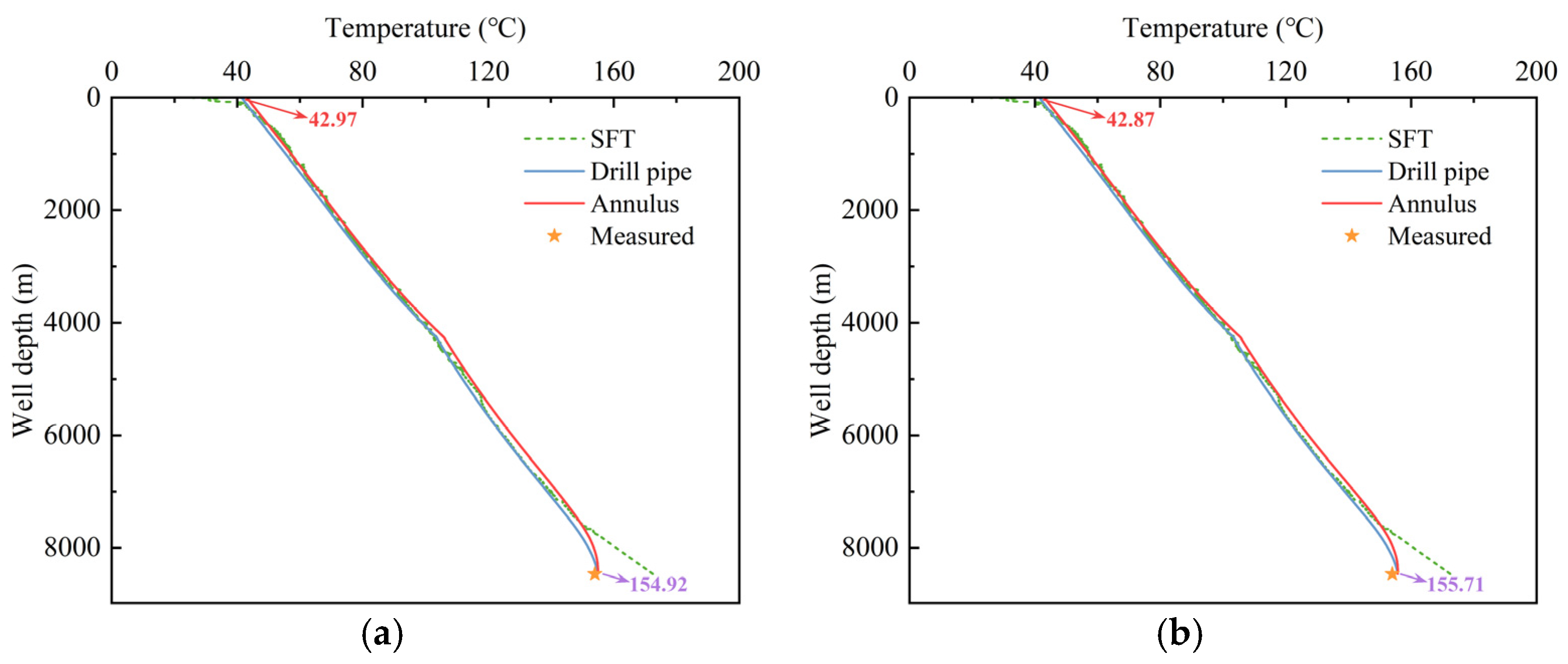
4.2. Case Study—Shunbei Well B
4.3. Case Study—Shunbei Well C
5. Conclusions
- (1)
- Based on the principle of energy conservation, a formation–wellbore heat transfer model was established and compared with the Holmes & Swift and Keller models. The results show that, relative to the Holmes & Swift model, the RMSE of the predicted drill pipe and annulus temperatures are 0.149 °C and 0.323 °C, respectively. Compared with the Keller model, the AE of the predicted BHT is 1.93 °C, corresponding to a RE of 2.3%.
- (2)
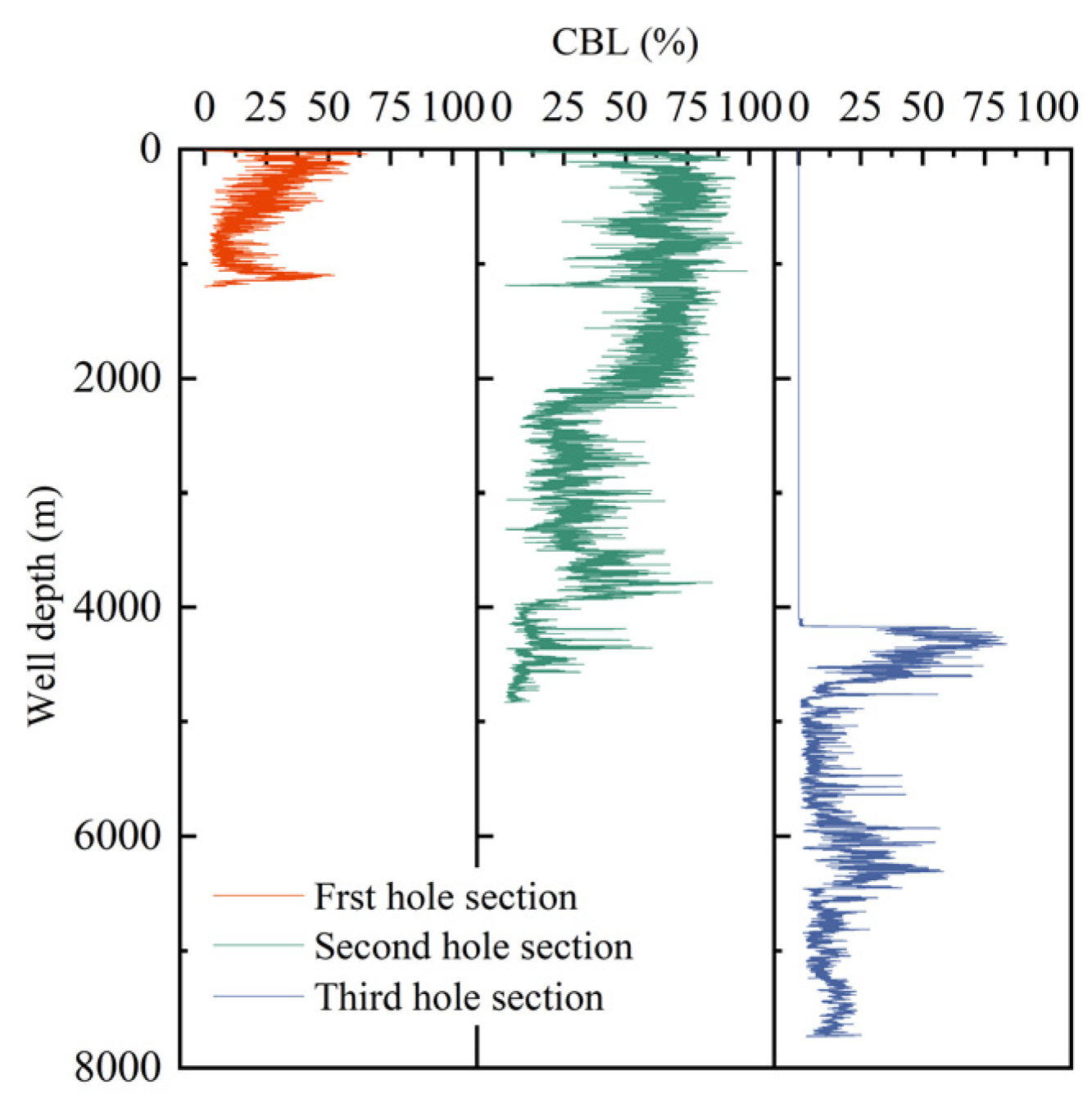
- Using CBL data, the percentage of micro-gap in the cement is determined. Based on heat transfer resistance, an overall thermal conductivity model for micro-gap and cement is established, and embedded into the formation–wellbore heat transfer model.
- (3)
- The formation–wellbore heat transfer model considering cementing quality is validated using data from three ultra-deep wells. The results showed that the MAE in BHTs prediction is 1.24 °C, with a MRE of 0.77%. The MAE in OLT prediction is 1.31 °C, with a MRE of 3.06%. Considering cementing quality improves the prediction accuracy of bottomhole temperature by 1.03% and outlet temperature by 0.35%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| ρm | Density of drilling fluid, kg/m3 |
| Cm | Specific heat capacity of drilling fluid, J/kg/°C |
| rdp,i | Inner radius of the drill pipe, m |
| Tm | Temperature of drilling fluid in the drill pipe, °C |
| t | Time, s |
| Vm | Velocity of the drilling fluid in the drill pipe, m/s |
| z | Depth, m |
| hm-dp | CHTC of the wall of the drill pipe, W/m2/°C |
| Tdp | Temperature of the wall of the drill pipe, °C |
| ρdp | Density of the drill pipe, kg/m3 |
| Cdp | Specific heat capacity of the drill pipe, J/kg/°C |
| rdp,o | Outer radius of the drill pipe, m |
| λdp | Thermal conductivity of the drill pipe, W/m/°C |
| hdp-a | CHTC between the drilling fluid in annulus and the drill pipe, W/m2/°C |
| Ta | Temperature of the drilling fluid in the annulus, °C |
| rca1,i | Inner radius of the first casing or the radius of the borehole, m |
| Va | Velocity of the drilling fluid in the annulus, m/s |
| ha-ca | CHTC between drilling fluid in the annulus and the casing, W/m2/°C |
| Tca1 | Temperature of the first casing or the borehole wall, °C |
| ρca | Density of the casing, kg/m3 |
| Cca | Specific heat capacity of the casing, J/kg/°C |
| rca1,o | Outer radius of the first casing, m |
| λca | Thermal conductivity of the casing, W/m/°C |
| rca2,i | Inner radius of the second layer of casing, m |
| Tce | Temperature of the first layer of cement, °C |
| λca1-ce1 | Overall thermal conductivity between the first casing and the first cement, W/m/°C |
| k | Overall thermal conductivity of the cement, W/m/°C |
| ρce | Density of the cement, kg/m3 |
| Cce | Specific heat capacity of the cement, J/kg/°C |
| rca2,o | Outer radius of the second layer of casing, m |
| Tca2 | Temperature of the second layer of casing °C |
| λce1-ca2 | Overall thermal conductivity between the first cement and the second casing, W/m/°C |
| ρf | Density of the formation, kg/m3 |
| Cf | Specific heat capacity of the formation, J/kg/°C |
| Tf | Temperature of the formation, °C |
| Tg | Temperature of the surface, °C |
| Gf | Temperature gradient of the stratum, °C/m |
| Tin | ILT of drilling fluid in the drill pipe, °C |
| L | Well depth, m |
| Φ | Heat flux, W |
| A | Surface area, m2 |
| ACBL | Acoustic amplitude, % |
| rca,o | Outer radius of the casing, m |
| rf | Radius of the formation, m |
| Ts | Temperature at the micro-gap inner wall (cement inner wall), °C |
| λce | Thermal conductivity of the cement, W/m/°C |
| h | Convective heat transfer coefficient, W/m2/°C |
| Nu | Nusselt number, - |
| λ | Thermal conductivity, W/m/°C |
| Dh | Hydrodynamic diameter, m |
| Redp | Reynolds number of turbulence in the circular tube, - |
| Prdp | Prandtl number, - |
| fdp | Friction factor in drill pipe, - |
| Rean | Reynolds number of turbulence in the circular tube, - |
| Pran | Prandtl number, - |
| fan | Friction factor in annulus, - |
| Fan | Correction factor, - |
| η | Gap ratio annulus, - |
| ro | Outer radius of the annulus space, m |
| ri | Inner radius of the annulus space, m |
| P | Pressure, Pa |
| T | Drilling fluid temperature in the drill pipe or annulus, °C |
| ρ0 | Initial density of drilling fluid, kg/m3 |
| T0 | Test temperature, °C |
| P0 | Test pressure, Pa |
| μ | Drilling fluid plastic viscosity, Pa·s |
| μ0 | Initial plastic viscosity of drilling fluid, Pa·s |
| C | Specific heat capacity, J/kg/°C |
| A, B, C, D, E, F | Coefficients of the control equations of the unit control body, - |
| nt | Time node, - |
| i | Spatial node on the radial direction of the wellbore, - |
| j | Space node on the axial direction of the wellbore, - |
Abbreviations
| BHT | Bottomhole temperature |
| API | American petroleum institute |
| SFT | Static formation temperature |
| ILT | Inlet temperature |
| OLT | Outlet temperature |
| RE | Relative error |
| PDM | Positive displacement motor |
| NMDC | Non-magnetic drill collar |
| HWDP | Heavy-weight drill pipe |
| AE | Absolute error |
| MWD | Measurement while drilling |
References
- Guo, X.; Hu, D.; Li, Y.; Duan, J.; Zhang, X.; Fan, X.; Duan, H.; Li, W. Theoretical progress and key technologies of onshore ultra-deep oil/gas exploration. Engineering 2019, 5, 458–470. [Google Scholar] [CrossRef]
- Xu, C.; Zou, W.; Yang, Y.; Duan, Y.; Shen, Y.; Luo, B.; Ni, C.; Fu, X.; Zhang, J. Status and prospects of deep oil and gas resources exploration and development onshore China. J. Nat. Gas Geosci. 2018, 3, 11–24. [Google Scholar] [CrossRef]
- Zongqi, C.; Xianghua, L.; Binzhen, B.; Hao, Y. Technical progress and development consideration of drilling and completion engineering for ultra-deep wells in the Shunbei Oil & Gas Field. Pet. Drill. Tech. 2022, 50, 1–10. [Google Scholar]
- Wang, X.; Dong, M.; Sun, B.; Wang, Z.; Gao, Y.; Li, H. Cement Slurry Displacement Efficiency in Ultra-Deep Wells: A Thermal-Pressure-Dependent Rheology Model. Case Stud. Therm. Eng. 2025, 74, 106884. [Google Scholar] [CrossRef]
- Liu, R.; Yu, J.; Liu, L.; Wang, Z.; Zhou, S.; Zhu, Z. A Cement Bond Quality Prediction Method Based on a Wide and Deep Neural Network Incorporating Embedded Domain Knowledge. Appl. Sci. 2025, 15, 5493. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, W.; Song, L.; Wu, J.; Wu, Y. Study on sealing integrity of cement sheath in ultra deep well reservoir reconstruction. Energy Sci. Eng. 2023, 11, 2630–2641. [Google Scholar] [CrossRef]
- Spindler, R. Analytical models for wellbore-temperature distribution. SPE J. 2011, 16, 125–133. [Google Scholar] [CrossRef]
- Kabir, C.; Hasan, A.; Kouba, G.; Ameen, M. Determining circulating fluid temperature in drilling, workover, and well control operations. SPE Drill. Complet. 1996, 11, 74–79. [Google Scholar] [CrossRef]
- Wang, Z.; Horne, R.N. Analyzing wellbore temperature distributions using nonisothermal multiphase flow simulation. In Proceedings of the SPE Western Regional Meeting, Anchorage, Alaska, 4–7 May 2011; p. SPE–144577-MS. [Google Scholar]
- Yang, H.; Li, J.; Liu, G.; Wang, C.; Li, M.; Jiang, H. Numerical analysis of transient wellbore thermal behavior in dynamic deepwater multi-gradient drilling. Energy 2019, 179, 138–153. [Google Scholar] [CrossRef]
- Holmes, C.S.; Swift, S.C. Calculation of circulating mud temperatures. J. Pet. Technol. 1970, 22, 670–674. [Google Scholar] [CrossRef]
- Hasan, A.R.; Kabir, C. Aspects of wellbore heat transfer during two-phase flow. SPE Prod. Facil. 1994, 9, 211–216. [Google Scholar] [CrossRef]
- Xiangyang, Z.; Cong, Z.; Peng, W.; Xiaoyang, L.; Mou, Y. A comparative study on the calculation accuracy of numerical and analytical models for wellbore temperature in ultra-deep wells. Pet. Drill. Tech. 2022, 50, 69–75. [Google Scholar]
- Abdelhafiz, M.M.; Hegele Jr, L.A.; Oppelt, J.F. Numerical transient and steady state analytical modeling of the wellbore temperature during drilling fluid circulation. J. Pet. Sci. Eng. 2020, 186, 106775. [Google Scholar] [CrossRef]
- Yang, M.; Zhao, X.; Meng, Y.; Li, G.; Zhang, L.; Xu, H.; Tang, D. Determination of transient temperature distribution inside a wellbore considering drill string assembly and casing program. Appl. Therm. Eng. 2017, 118, 299–314. [Google Scholar] [CrossRef]
- Yang, M.; Tang, D.; Chen, Y.; Li, G.; Zhang, X.; Meng, Y. Determining initial formation temperature considering radial temperature gradient and axial thermal conduction of the wellbore fluid. Appl. Therm. Eng. 2019, 147, 876–885. [Google Scholar] [CrossRef]
- Zhongming, C.; Rudolf, J. Accurate prediction wellbore transient temperature profile under multiple temperature gradients: Finite difference approach and case history. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 5–8 October 2003; p. 84583. [Google Scholar]
- Zhang, Z.; Xiong, Y.; Gao, Y.; Liu, L.; Wang, M.; Peng, G. Wellbore temperature distribution during circulation stage when well-kick occurs in a continuous formation from the bottom-hole. Energy 2018, 164, 964–977. [Google Scholar] [CrossRef]
- Zhang, Z.; Wei, Y.; Xiong, Y.; Peng, G.; Wang, G.; Lu, J.; Zhong, L.; Wang, J. Influence of the location of drilling fluid loss on wellbore temperature distribution during drilling. Energy 2022, 244, 123031. [Google Scholar] [CrossRef]
- Li, G.; Yang, M.; Meng, Y.; Wen, Z.; Wang, Y.; Yuan, Z. Transient heat transfer models of wellbore and formation systems during the drilling process under well kick conditions in the bottom-hole. Appl. Therm. Eng. 2016, 93, 339–347. [Google Scholar] [CrossRef]
- Yao, X.; Song, X.; Zhou, M.; Xu, Z.; Duan, S.; Li, Z.; Li, H. A modified heat transfer model for predicting wellbore temperature in ultra-deep drilling with insulated drill pipe. Energy 2025, 331, 136981. [Google Scholar] [CrossRef]
- Dang, Z.; Chen, X.; Yao, X.; Xu, Z.; Zhou, M.; Yang, W.; Song, X. Wellbore temperature prediction model and influence law of ultra-deep wells in Shunbei field, China. Processes 2024, 12, 1715. [Google Scholar] [CrossRef]
- YANG, M.M.; DENG, J.Z. A transient heat transfer model of wellbore and formation during the whole drilling process. Acta Pet. Sin. 2013, 34, 366. [Google Scholar]
- Xu, Z.; Wu, K.; Song, X.; Li, G.; Zhu, Z.; Sun, B. A unified model to predict flowing pressure and temperature distributions in horizontal wellbores for different energized fracturing fluids. SPE J. 2019, 24, 834–856. [Google Scholar] [CrossRef]
- Xuezhe, Y.; Xianzhi, S.; Zhengming, X.; Mengmeng, Z.; Shiming, D.; Yueqi, C.; Haobo, W. An inversion-while-drilling method for the static formation temperature of ultra-deep wells based on differential evolution algorithm. Acta Pet. Sin. 2025, 46, 1805–1816. [Google Scholar] [CrossRef]
- Willhite, G.P. Over-all heat transfer coefficients in steam and hot water injection wells. J. Pet. Technol. 1967, 19, 607–615. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer; New York John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1990; Volume 1072. [Google Scholar]
- Gnielinski, V. Neue Gleichungen für den Wärme-und den Stoffübergang in turbulent durchströmten Rohren und Kanälen. Forsch. Im. Ingenieurwesen A 1975, 41, 8–16. [Google Scholar] [CrossRef]
- Sorelle, R.R.; Jardiolin, R.A.; Buckley, P.; Barrios, J.R. Mathematical Field Model Predicts Downhole Density Changes in Static Drilling Fluids. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 5–8 October 1997. [Google Scholar]
- Minton, R.C.; Bern, P.A. Field Measurement and Analysis of Circulating System Pressure Drops with Low-Toxicity Oil-Based Drilling Fluids. In Proceedings of the IADC/SPE Drilling Conference, Dallas, TX, USA, 7–9 September 1988. [Google Scholar]
- Mao, L.; Wei, C.; Jia, H.; Lu, K. Prediction model of drilling wellbore temperature considering bit heat generation and variation of mud thermophysical parameters. Energy 2023, 284, 129341. [Google Scholar] [CrossRef]
- Tiskatine, R.; Bougdour, N.; Idoum, A.; Bazgaou, A.; Oaddi, R.; Ihlal, A.; Aharoune, A. Experimental investigation on rock thermal properties under the influence of temperature. Thermochim. Acta 2023, 720, 179424. [Google Scholar] [CrossRef]
- Yao, X.; Song, X.; Xu, Z.; Zhou, M.; Wang, Q. Research on the influence mechanism of heat-Insulating coating parameters in temperature-controlled drilling of ultra-deep well. Pet. Drill. Tech. 2024, 52, 126–135. [Google Scholar]



| Lithologies | Density (kg/m3) | Specific Heat Capacity (J/kg/°C) | Thermal Conductivity (W/m/°C) |
|---|---|---|---|
| Limestone | 2655 | ||
| Sandstone | 2486 | ||
| Mudstone | 2718 | ||
| Granite | 2586 | ||
| Basalt | 2602 | ||
| Marble | 2597 | ||
| Quartzite | 2670 | ||
| Gabbro | 2644 |
| Parameters | Value Unit | Parameters | Value Unit |
|---|---|---|---|
| Depth | 8000 m | Drill pipe specific heat | 400 J/kg/°C |
| Drill pipe inner diameter | 151 mm | Formation specific heat | 837 J/kg/°C |
| Drill pipe outer diameter | 168 mm | Drilling fluid thermal conductivity | 1.73 W/m/°C |
| Borehole diameter | 213 mm | Drill pipe thermal conductivity | 43.75 W/m/°C |
| Drilling fluid density | 1200 kg/m3 | Formation thermal conductivity | 2.25 W/m/°C |
| Drill pipe density | 7800 kg/m3 | Surface temperature | 15.3 °C |
| Formation density | 2645 kg/m3 | Geothermal gradient | 2.31 °C/100 m |
| Drilling fluid viscosity | 45.4 mPa·s | Inlet temperature | 24 °C |
| Drilling fluid specific heat | 1675 J/kg/°C | Flow rate | 13.2 L/s |
| Type | Bit Diameter (mm) | Depth (m) | Casing Outer Diameter (mm) | Casing Setting Depth (m) | Cement Top Depth (m) | Hole Enlargement Ratio (%) |
|---|---|---|---|---|---|---|
| Surface casing | 660.4 | 105 | 508 | 105 | 0 | / |
| Intermediate casing | 444.5 | 1199.5 | 339.7 | 1199.15 | 0 | / |
| Intermediate casing | 311.2 | 4363 | 250.8 | 4362 | 0 | 3.94 |
| Intermediate casing | 215.9 | 7728 | 177.8 | 7726.77 | 4162 | 4.14 |
| Open-hole section | 149.2 | 8543 | / | / | / | 3.43 |
| Medium | Density (kg/m3) | Specific Heat (J/kg/°C) | Thermal Conductivity (W/m/°C) |
|---|---|---|---|
| Drilling fluid | 1600 1 & Equation (27) | Equation (30) | Equation (29) |
| Drill pipe | 7800 2 | 500 2 | 48 2 |
| Casing | 7800 2 | 500 2 | 48 2 |
| Cement | 2140 3 | 2000 3 | 0.7 3 |
| Formation rock | 2655 4 | 985 4 | 2.021 4 |
| Type | Bit Diameter (mm) | Depth (m) | Casing Outer Diameter (mm) | Casing Setting Depth (m) | Cement Top Depth (m) | Hole Enlargement Ratio (%) |
|---|---|---|---|---|---|---|
| Surface casing | 660.4 | 100 | 508 | 100 | 0 | / |
| Intermediate casing | 444.5 | 1507 | 339.7 | 1506.33 | 0 | / |
| Intermediate casing | 311.2 | 5382 | 250.8 | 5381.37 | 0 | 7.88 |
| Intermediate casing | 215.9 | 7528 | 177.8 | 7527.76 | 5167.56 | 3.78 |
| Open-hole section | 149.2 | 8287 | / | / | / | 3.12 |
| Medium | Density (kg/m3) | Specific Heat (J/kg/°C) | Thermal Conductivity (W/m/°C) |
|---|---|---|---|
| Drilling fluid | 1290 1 & Equation (27) | Equation (30) | Equation (29) |
| Drill pipe | 7800 2 | 500 2 | 48 2 |
| Casing | 7800 2 | 500 2 | 48 2 |
| Cement | 2140 3 | 2000 3 | 0.7 3 |
| Formation rock | 2655 4 | 985 4 | 2.021 4 |
| Type | Bit Diameter (mm) | Depth (m) | Casing Outer Diameter (mm) | Casing Setting Depth (m) | Cement Top Depth (m) | Hole Enlargement Ratio (%) |
|---|---|---|---|---|---|---|
| Surface casing | 660.4 | 110 | 508 | 110 | 0 | / |
| Intermediate casing | 444.5 | 1201 | 365.1 | 1200.75 | 0 | / |
| Intermediate casing | 333.4 | 4834 | 273.1 | 4832.38 | 0 | 4.87 |
| Intermediate casing | 241.3 | 7821 | 193.7 | 7819.85 | 0 | 5.56 |
| Open-hole section | 165.1 | 8479 | / | / | / | 3.37 |
| Density (kg/m3) | Specific Heat (J/kg/°C) | Thermal Conductivity (W/m/°C) | |
|---|---|---|---|
| Drilling fluid | 1110 1 & Equation (27) | Equation (30) | Equation (29) |
| Drill pipe | 7800 2 | 500 2 | 48 2 |
| Casing | 7800 2 | 500 2 | 48 2 |
| Cement | 2140 3 | 2000 3 | 0.7 3 |
| Formation rock | 2655 4 | 985 4 | 2.021 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dang, Z.; Chen, X.; Yao, X.; Zhou, M.; Xu, Z.; Li, Z. Transient Prediction Model of Wellbore Temperature in Ultra-Deep Wells Considering Cementing Quality. Appl. Sci. 2025, 15, 12029. https://doi.org/10.3390/app152212029
Dang Z, Chen X, Yao X, Zhou M, Xu Z, Li Z. Transient Prediction Model of Wellbore Temperature in Ultra-Deep Wells Considering Cementing Quality. Applied Sciences. 2025; 15(22):12029. https://doi.org/10.3390/app152212029
Chicago/Turabian StyleDang, Zhigang, Xiuping Chen, Xuezhe Yao, Mengmeng Zhou, Zhengming Xu, and Zengjia Li. 2025. "Transient Prediction Model of Wellbore Temperature in Ultra-Deep Wells Considering Cementing Quality" Applied Sciences 15, no. 22: 12029. https://doi.org/10.3390/app152212029
APA StyleDang, Z., Chen, X., Yao, X., Zhou, M., Xu, Z., & Li, Z. (2025). Transient Prediction Model of Wellbore Temperature in Ultra-Deep Wells Considering Cementing Quality. Applied Sciences, 15(22), 12029. https://doi.org/10.3390/app152212029







