Multi-Polar Approach to Parasitic Suppression in Smart Electromagnetic Skins (SESs)
Abstract
1. Introduction
2. SES Radiation Mechanism Modeling
2.1. Homogenized Effective Medium Model
2.2. Multipole Scattering Model
2.3. Comparison of Radiation Mechanism Analytical Models
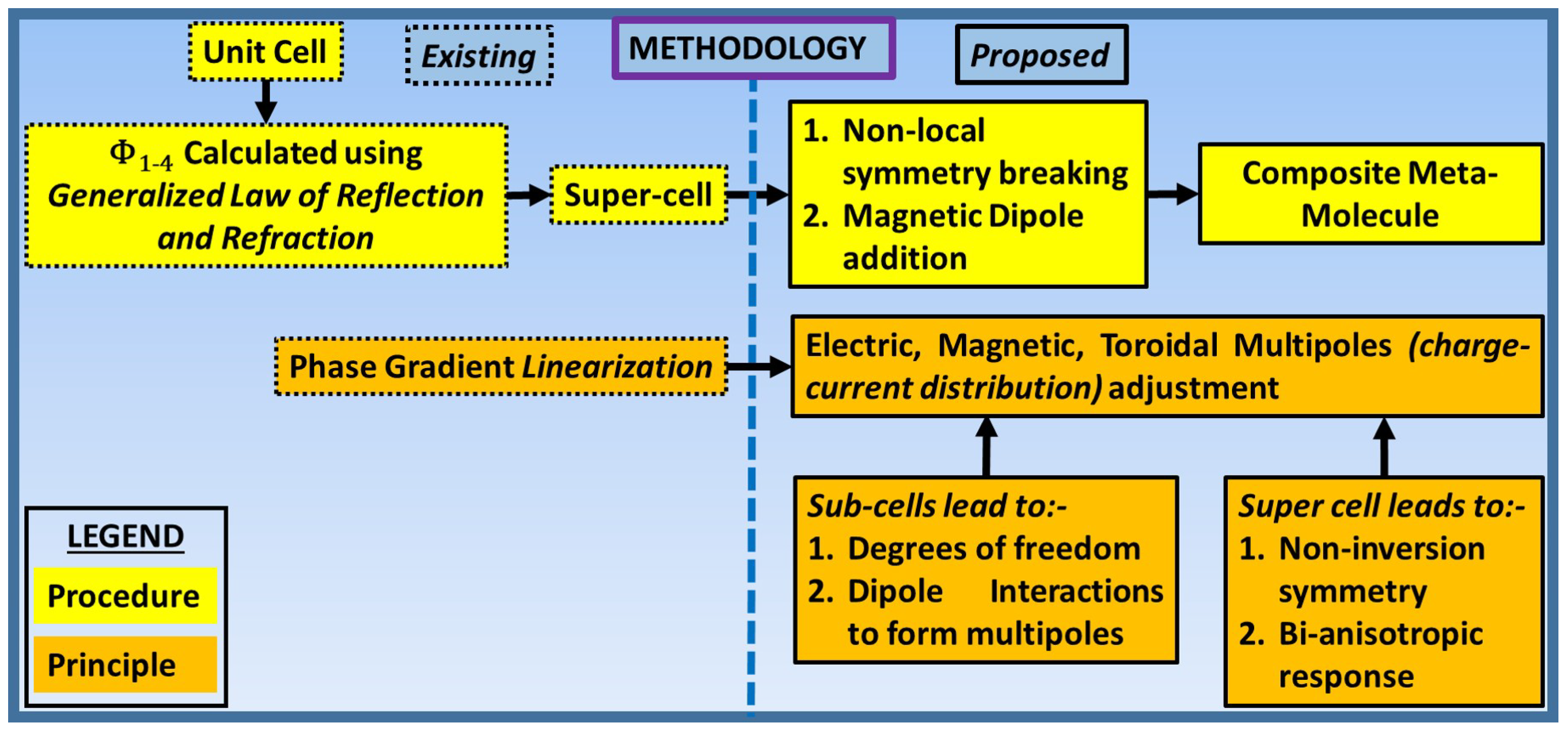
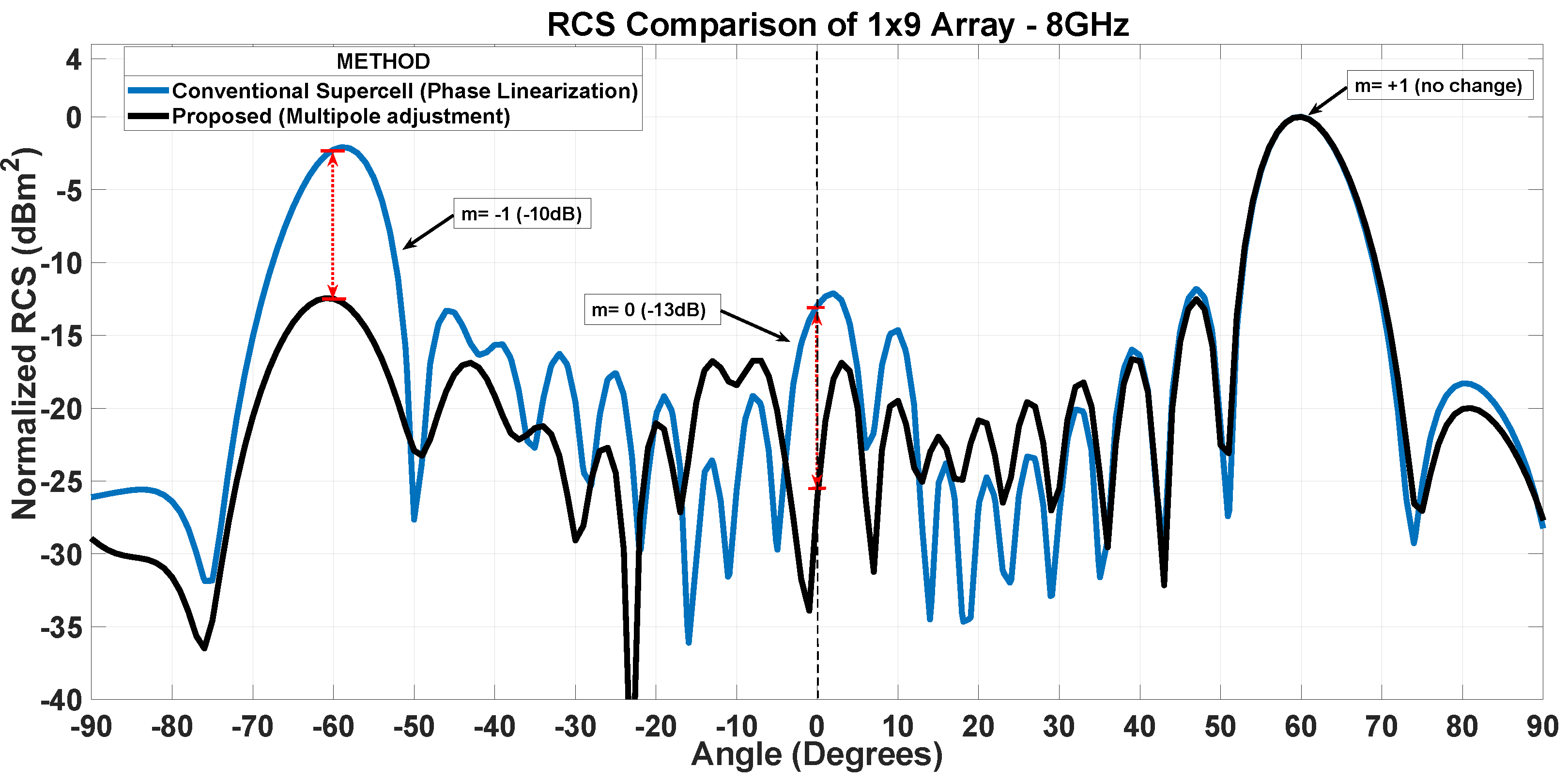
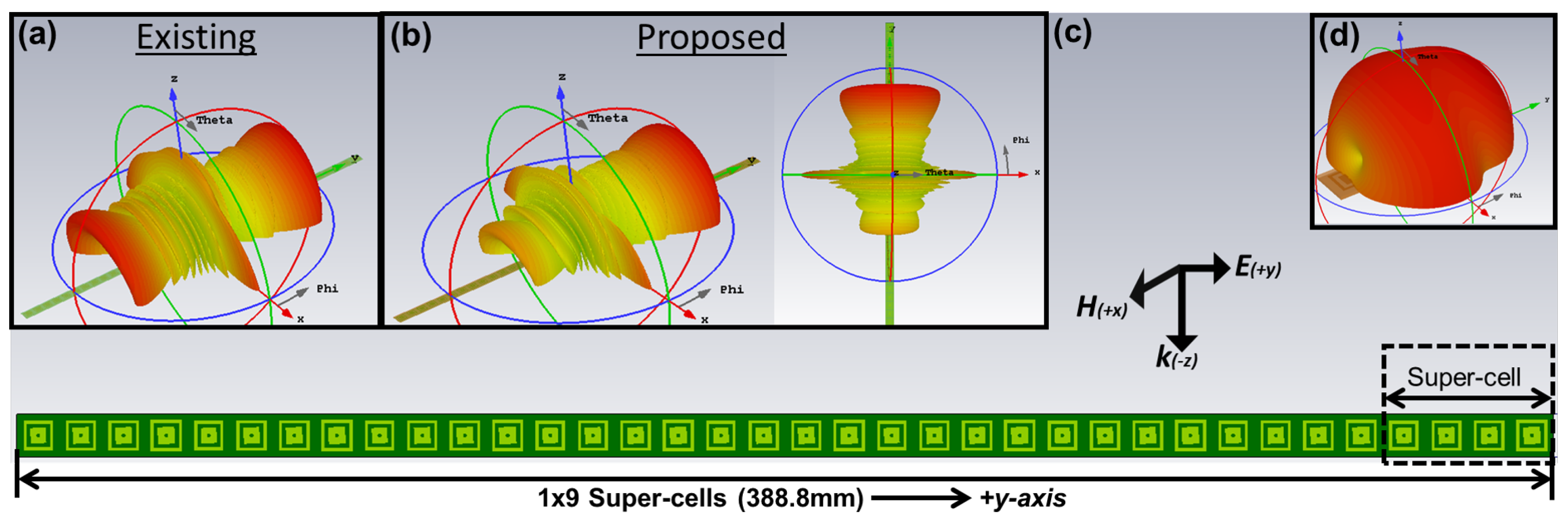
3. Proposed Approach
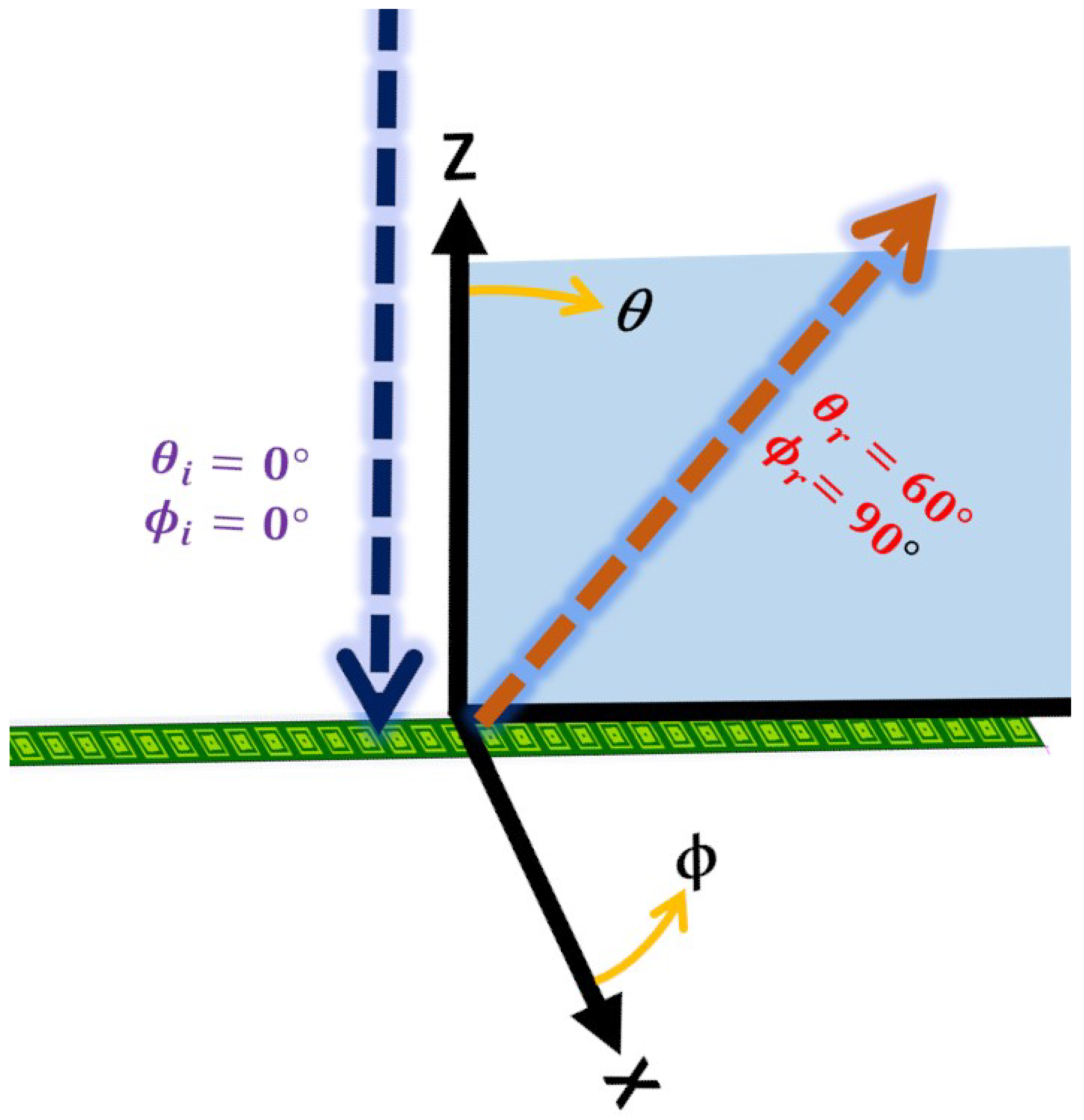
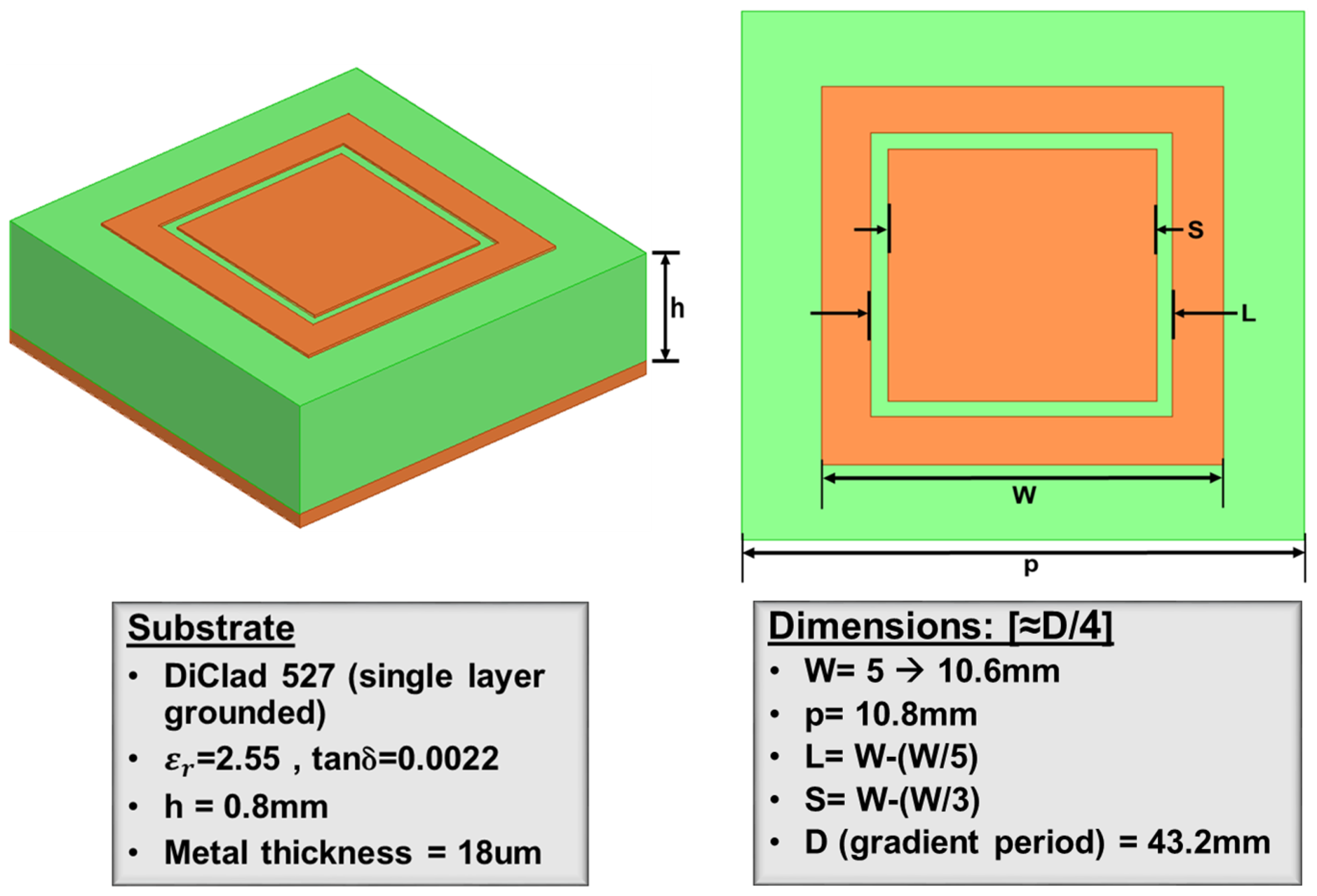
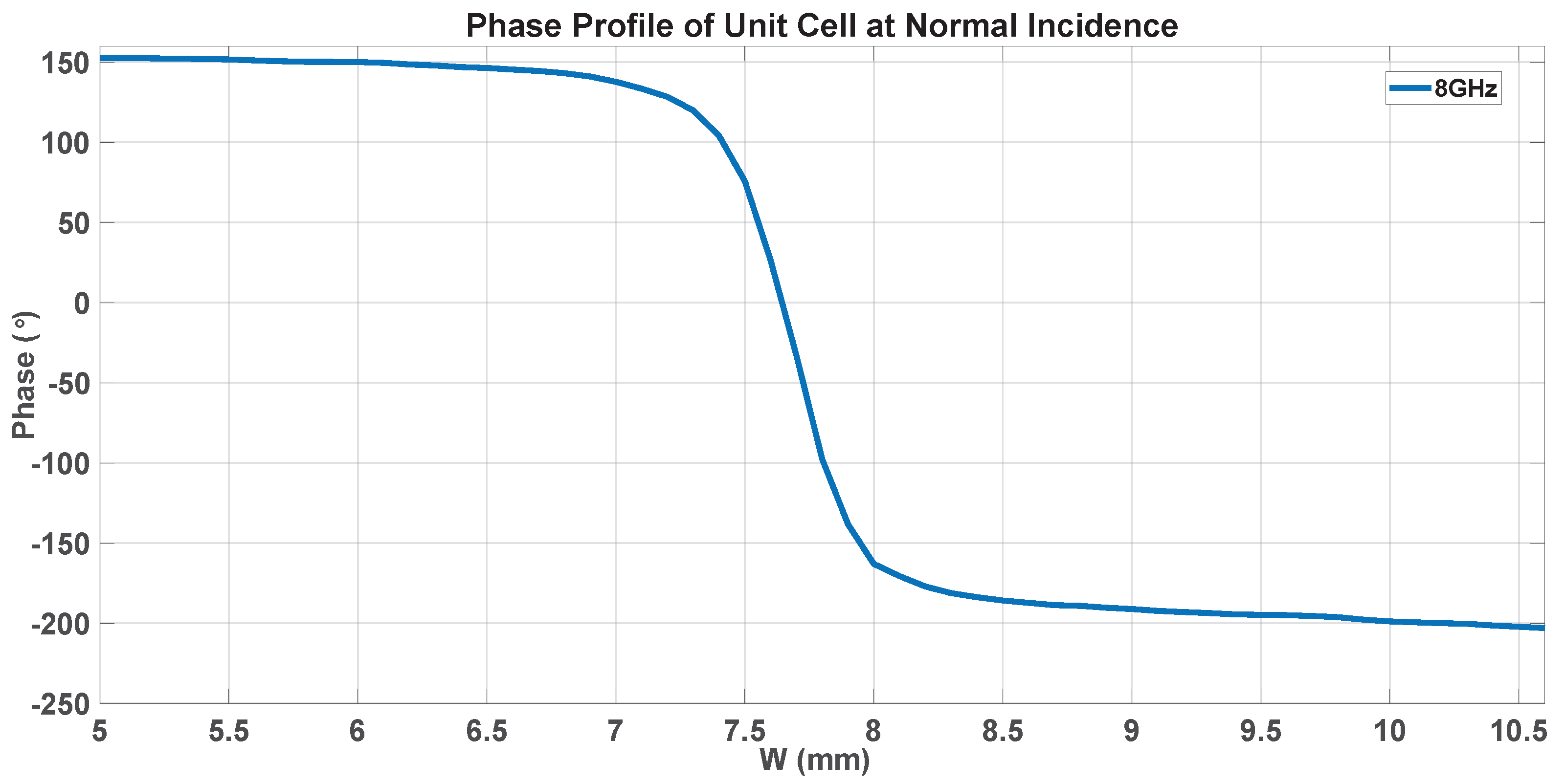
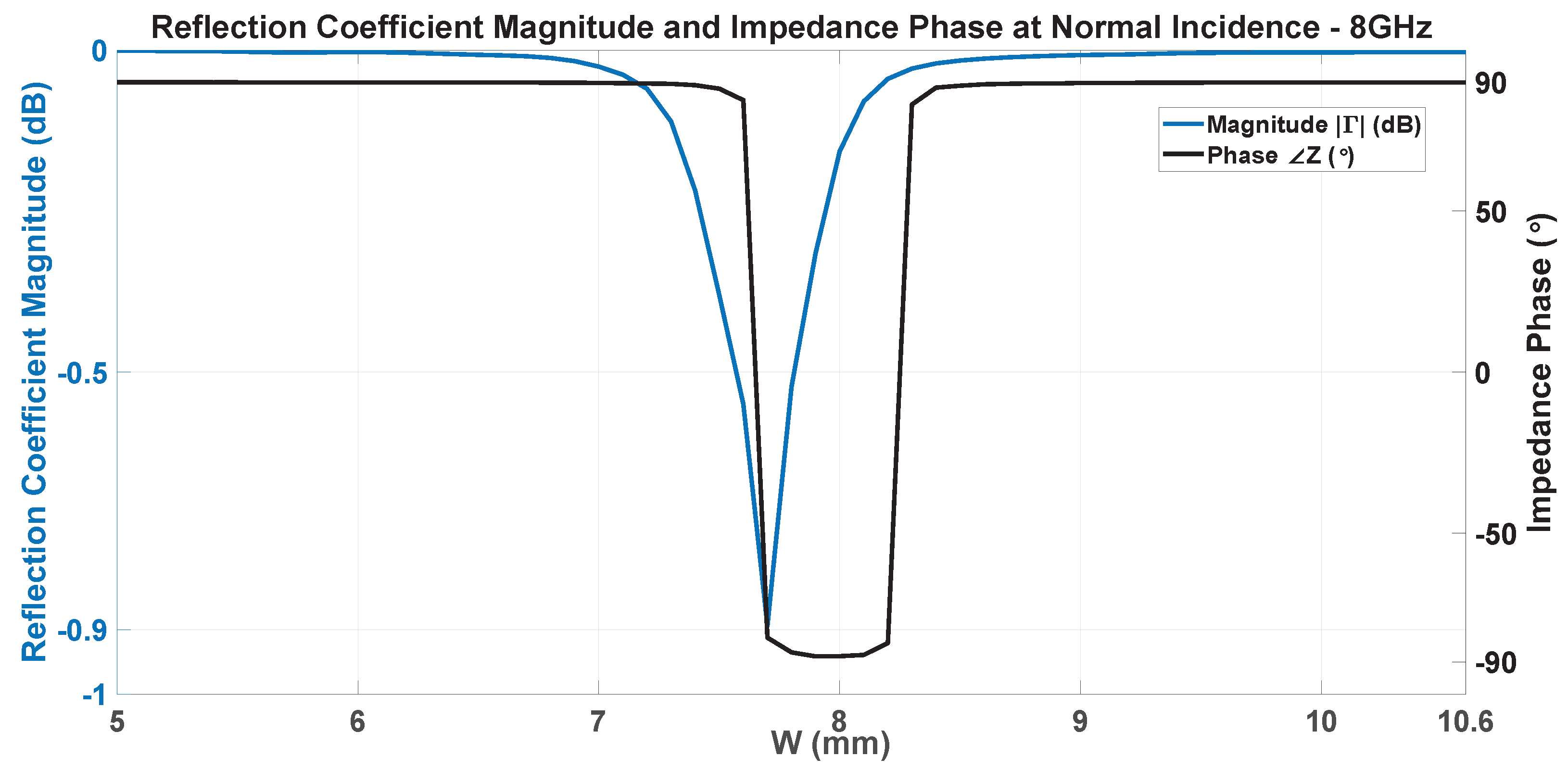
3.1. Initial Unit Cell
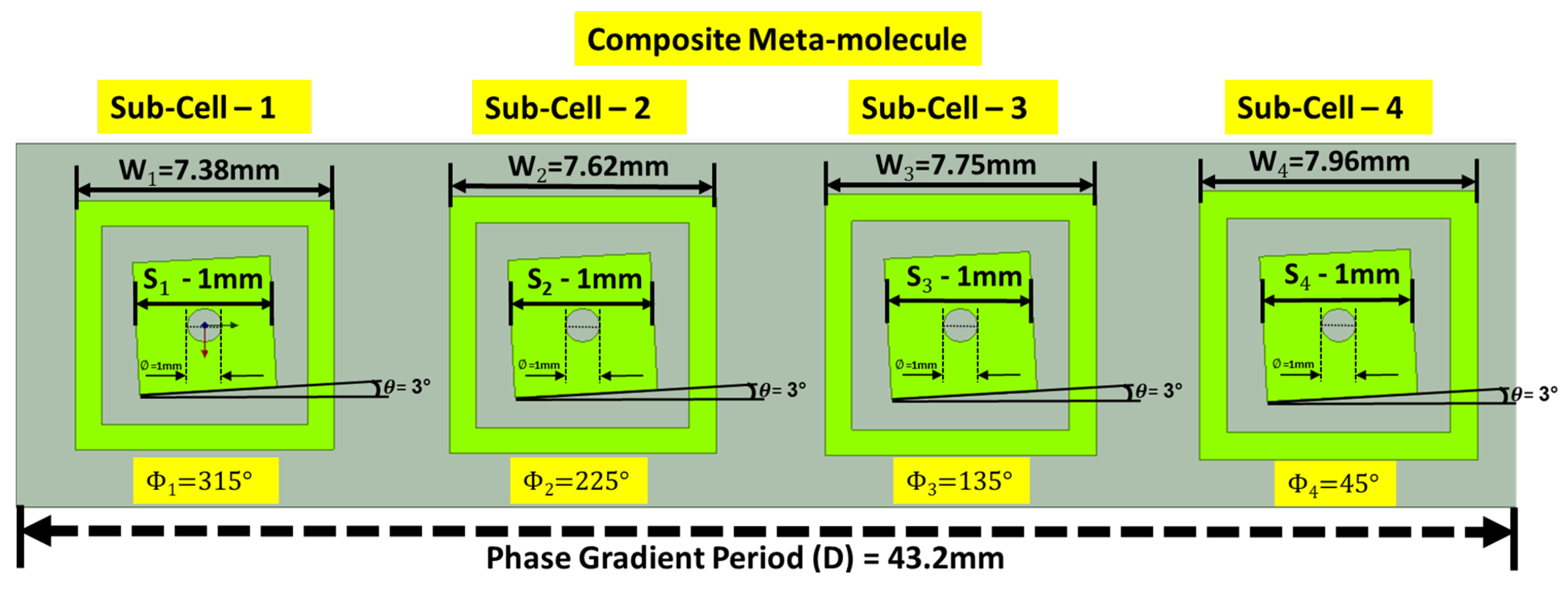
3.2. PG Super-Cell Definition
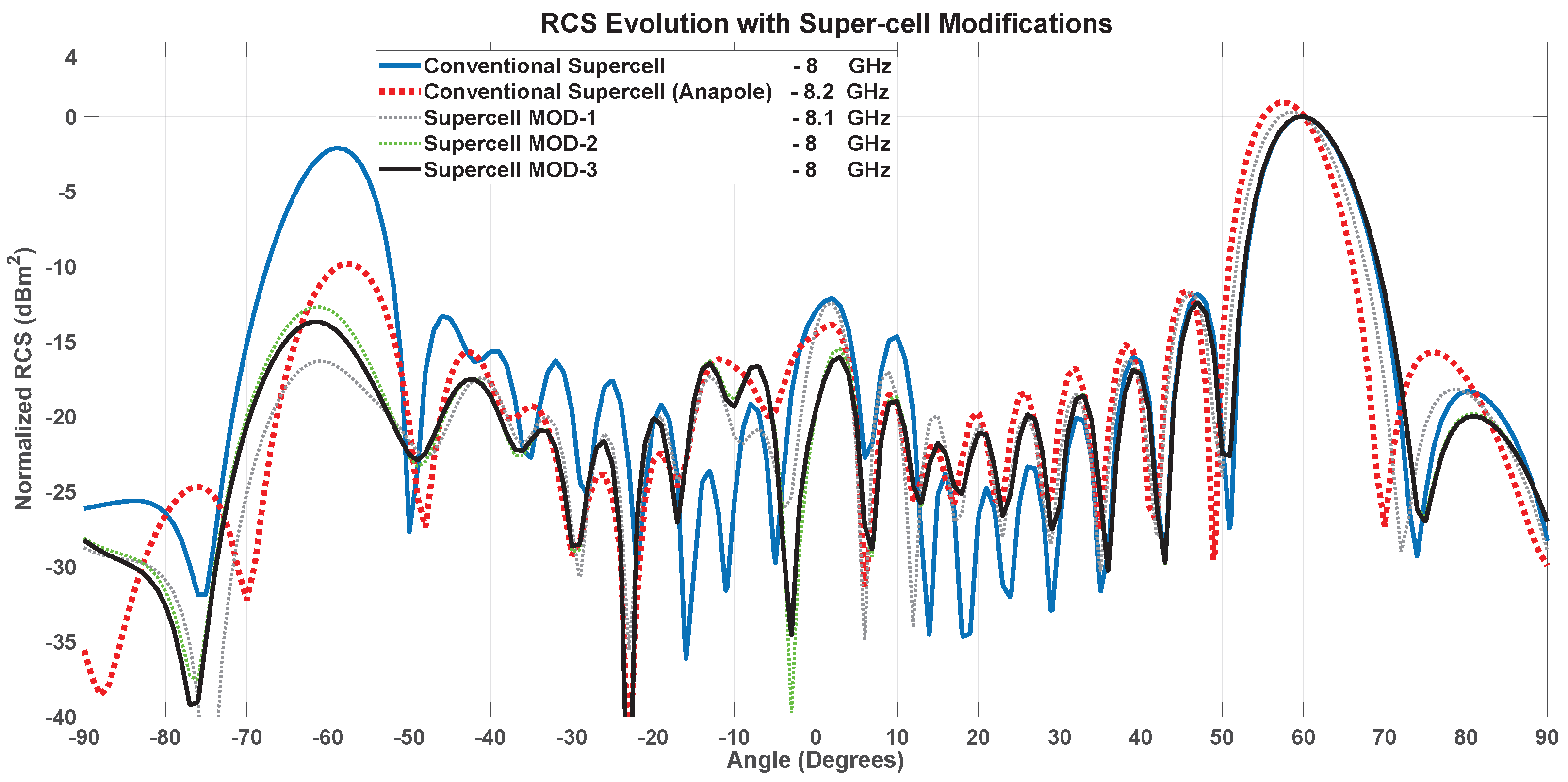
3.3. UC and Super-Cell Modifications and Effects on the SES Performance
3.3.1. Inner Patch Size Reduction
3.3.2. Inner Patch Tilting
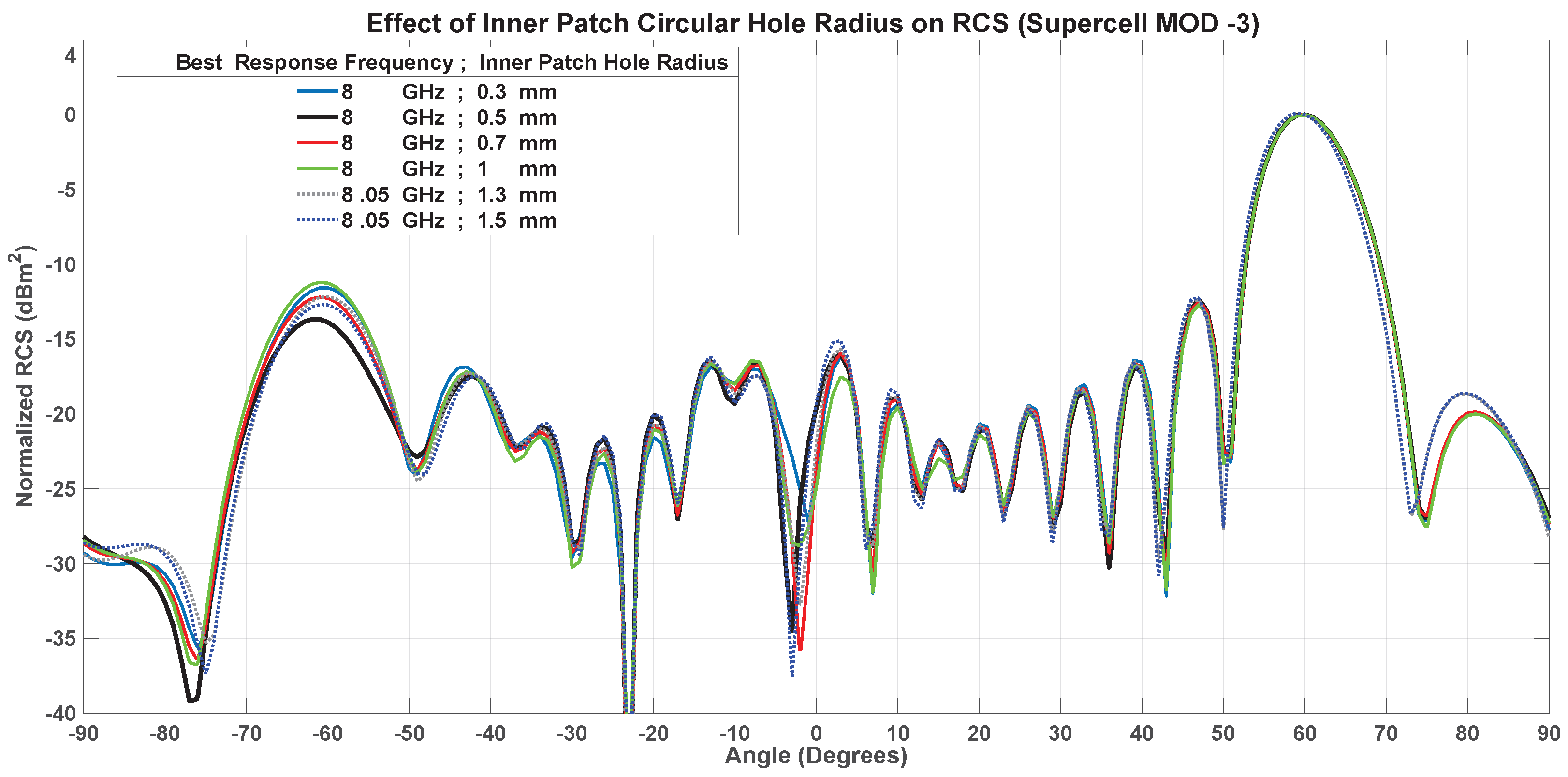
3.3.3. Introduction of Inner Patch Hole
3.3.4. Modification Effects and Discussion
- (a)
- Outer rings–unmodified–Local design–anomalous reflection
- (b)
- Inner patch–modified–Non-local design–undesired radiation suppression
4. Application of Theory of Multipoles to Anomalous Reflective SES
- (a)
- Area of dynamic charge-currents distributions i.e., super-cell size, (at 8 GHz for normal incidence and pointing angle of is 53 mm, when the pointing angle is the area becomes 43.2 mm, for is 40 mm and for is 37.6 mm) becomes comparable to or larger than effective wavelength ( mm at 8 GHz). This configuration makes the contributions of higher order multipoles non-negligible in the structure response [50,61].
- (b)
- The structure loses inversion symmetry along the gradient period, i.e., super-cell length, , Figure 16h. This non-inversion symmetry introduces bi-anisotropy at the super-cell level [48] and contribution of charge-current distributions and TD in far-field radiations becomes non-negligible. This super-cell level bi-anisotropy due to non-inversion symmetry is different from UC level bi-anisotropy which can be possible in symmetric UCs.
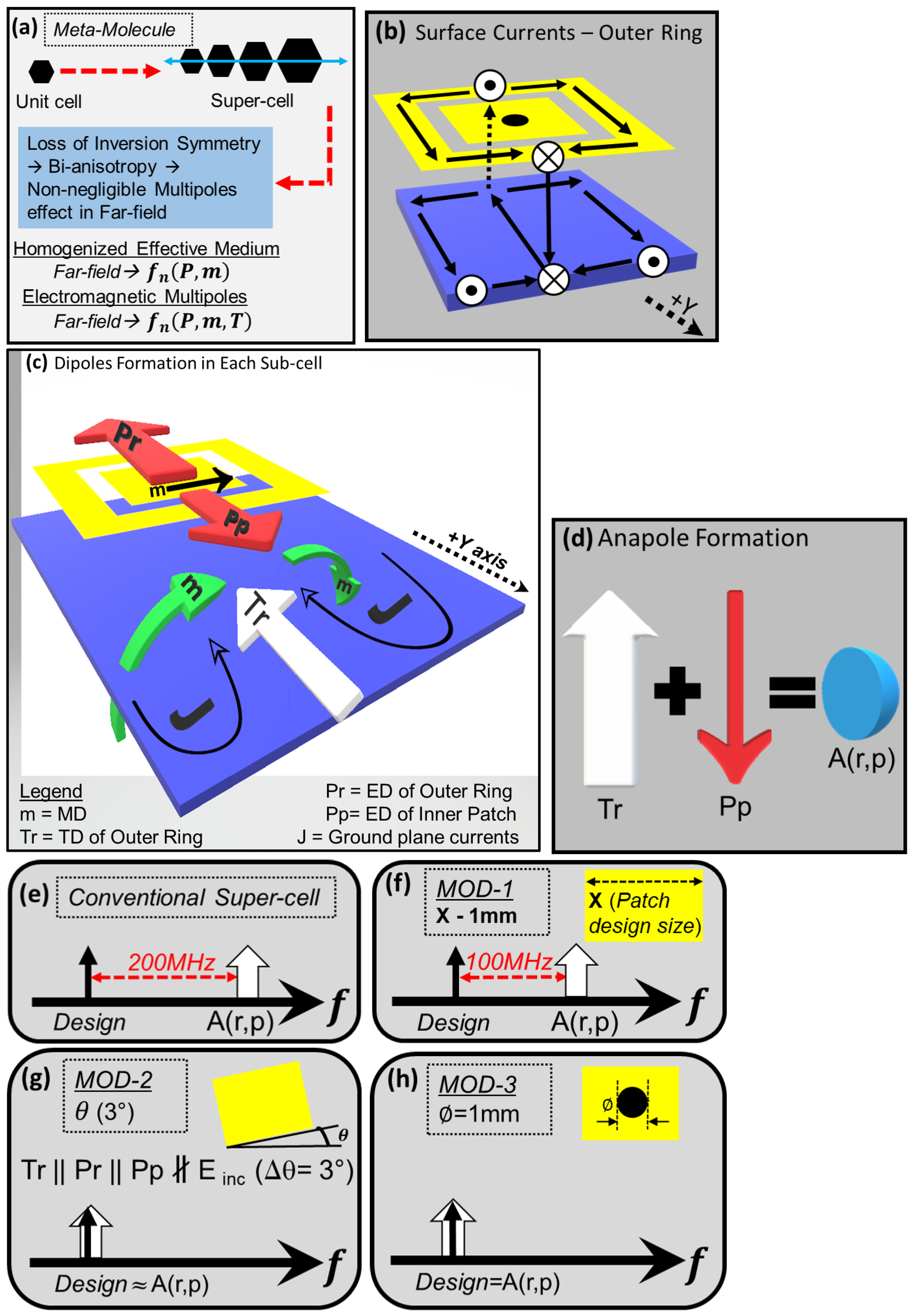
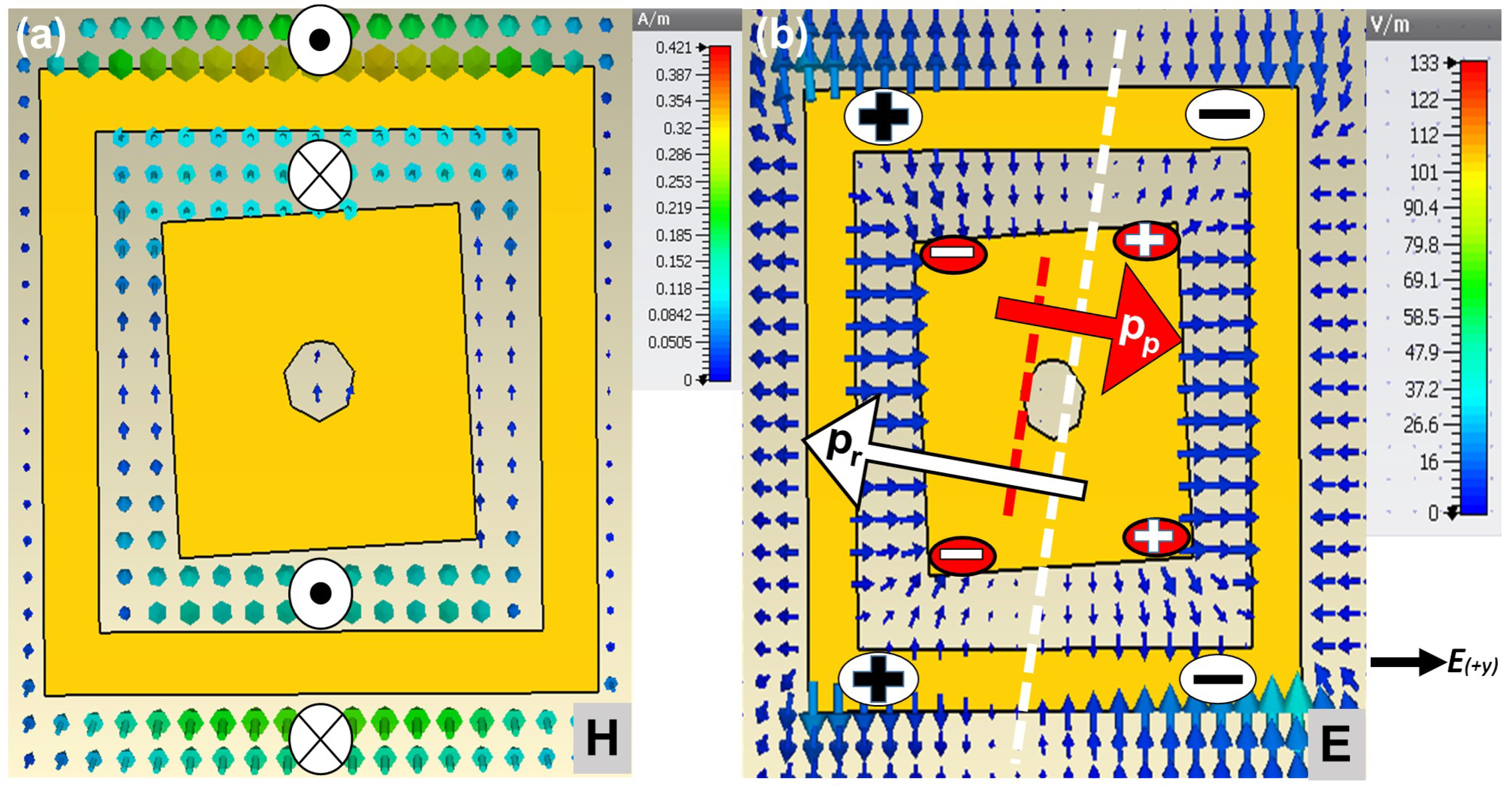
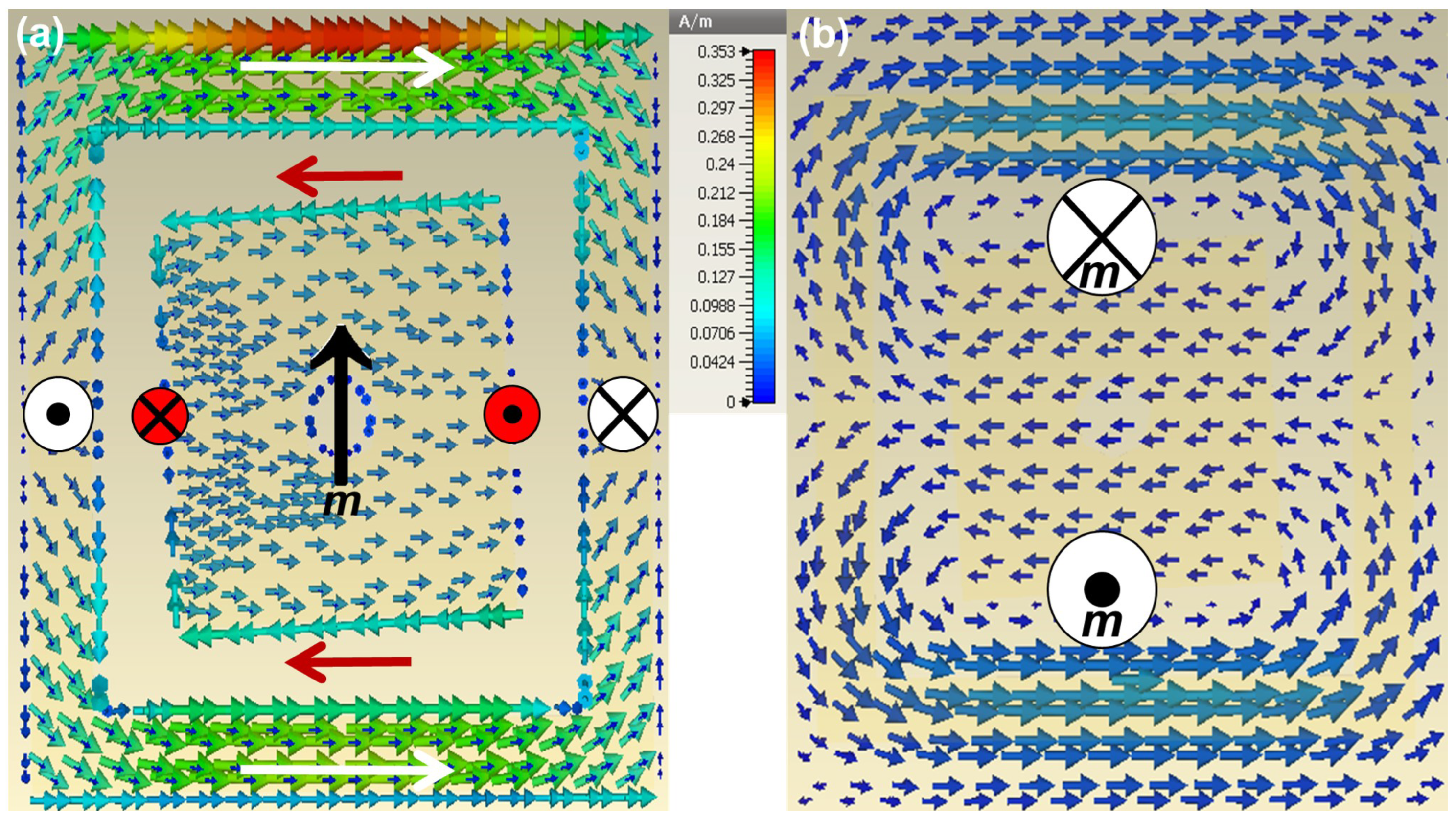
4.1. Charge-Current Distribution and Dipoles Formation
4.2. Controlling Dipole Interactions for Radiation and Suppression Management
- (a)
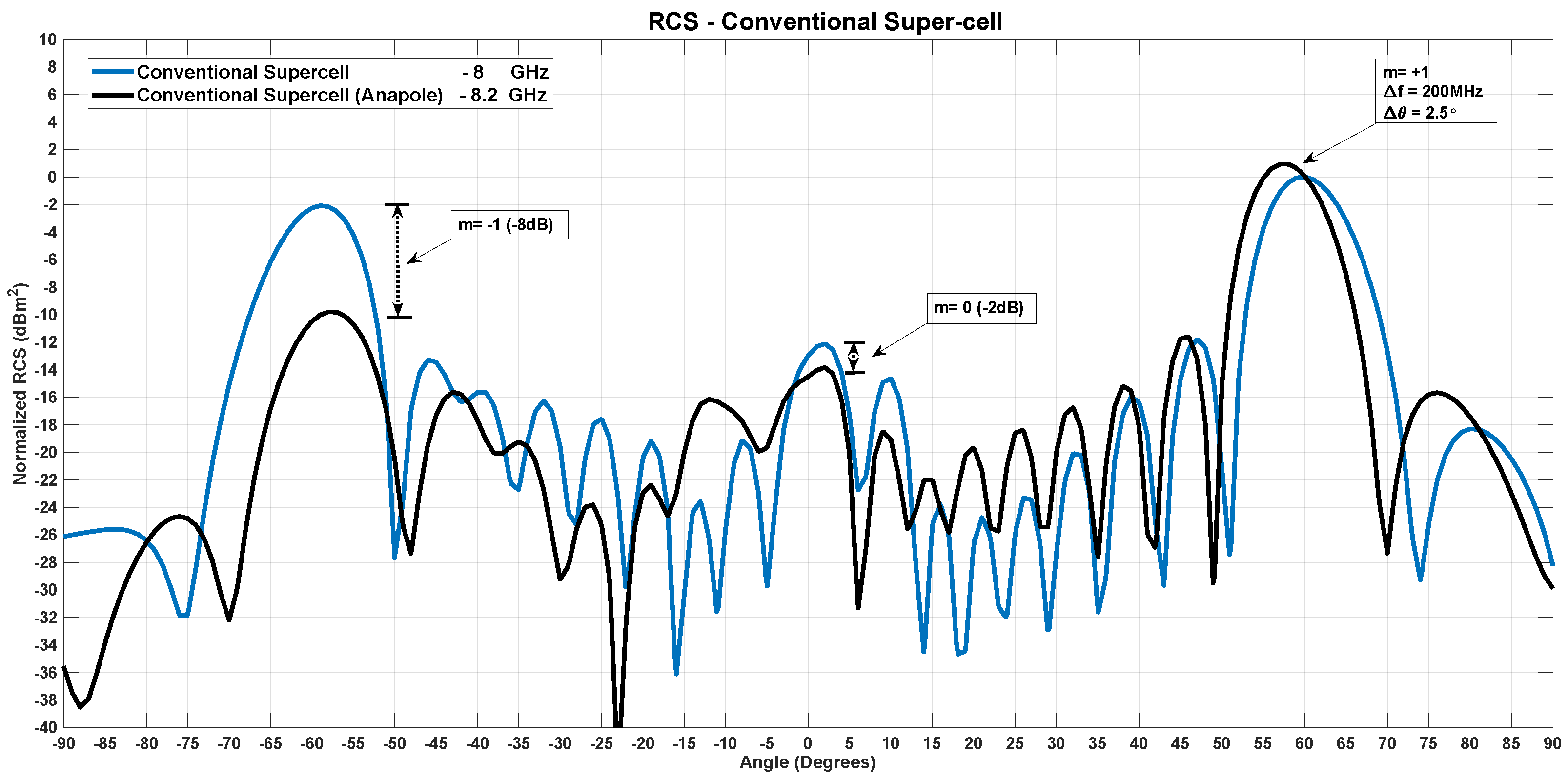
- = Anapole (undesired radiation suppression)
- (b)
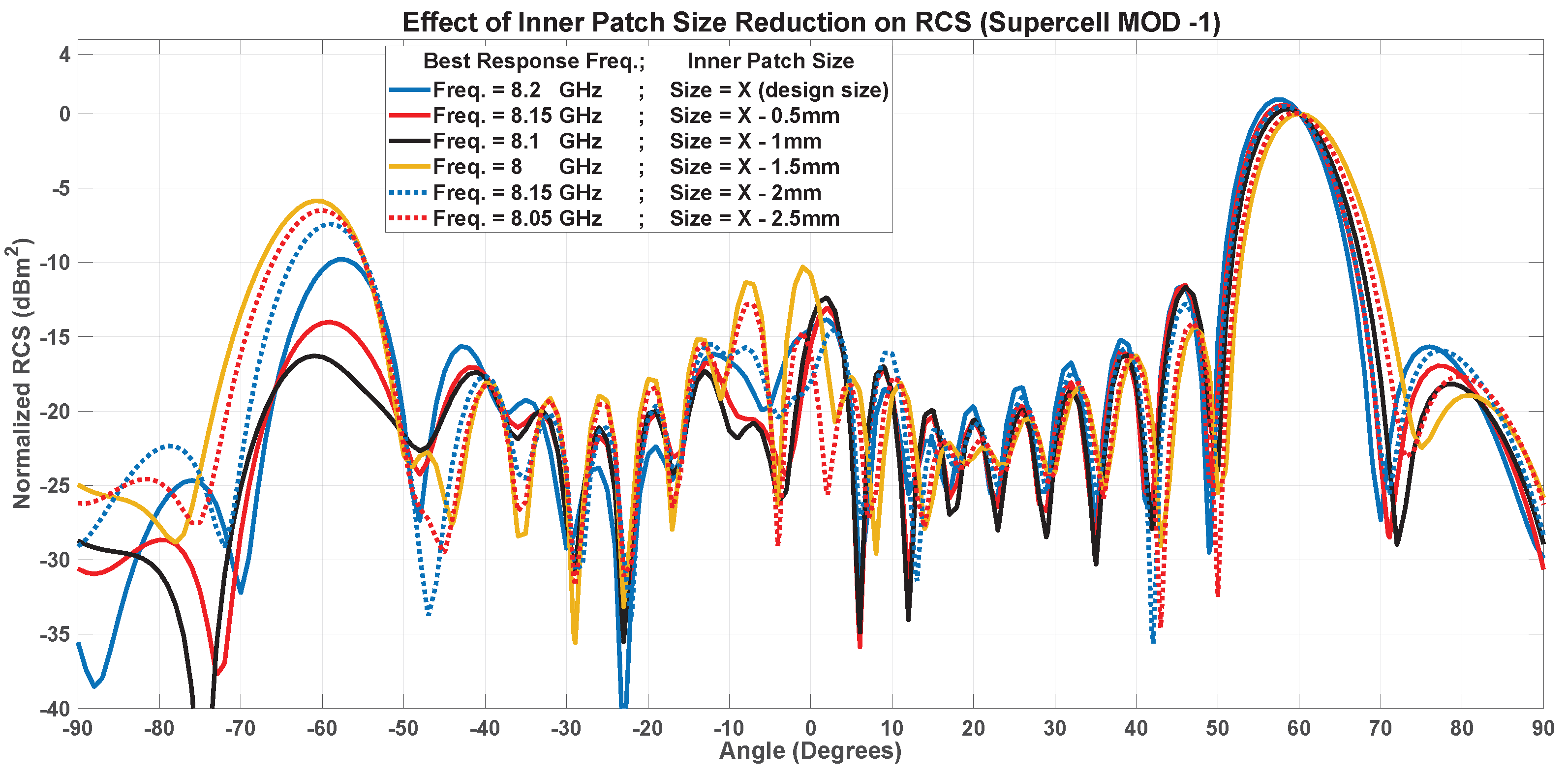
- Inner patch size reduction (frequency shifting of anapole)–modification–1
- (c)
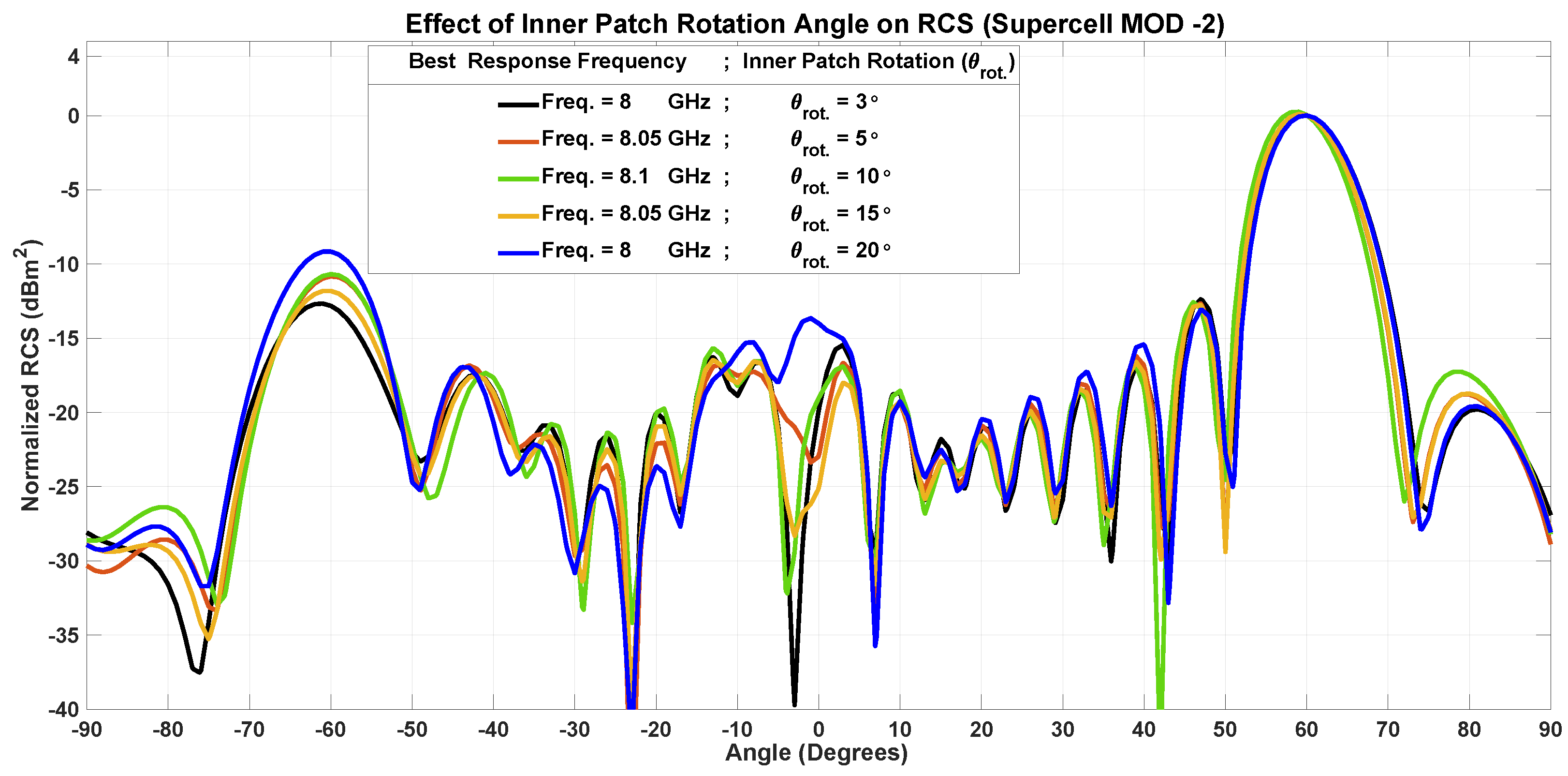
- Inner patch tilt (frequency shifting of anapole)–modification–2
- (d)
- m, magnetic dipole of inner patch (frequency shifting of anapole)–modification–3
- (e)
- for desired radiation
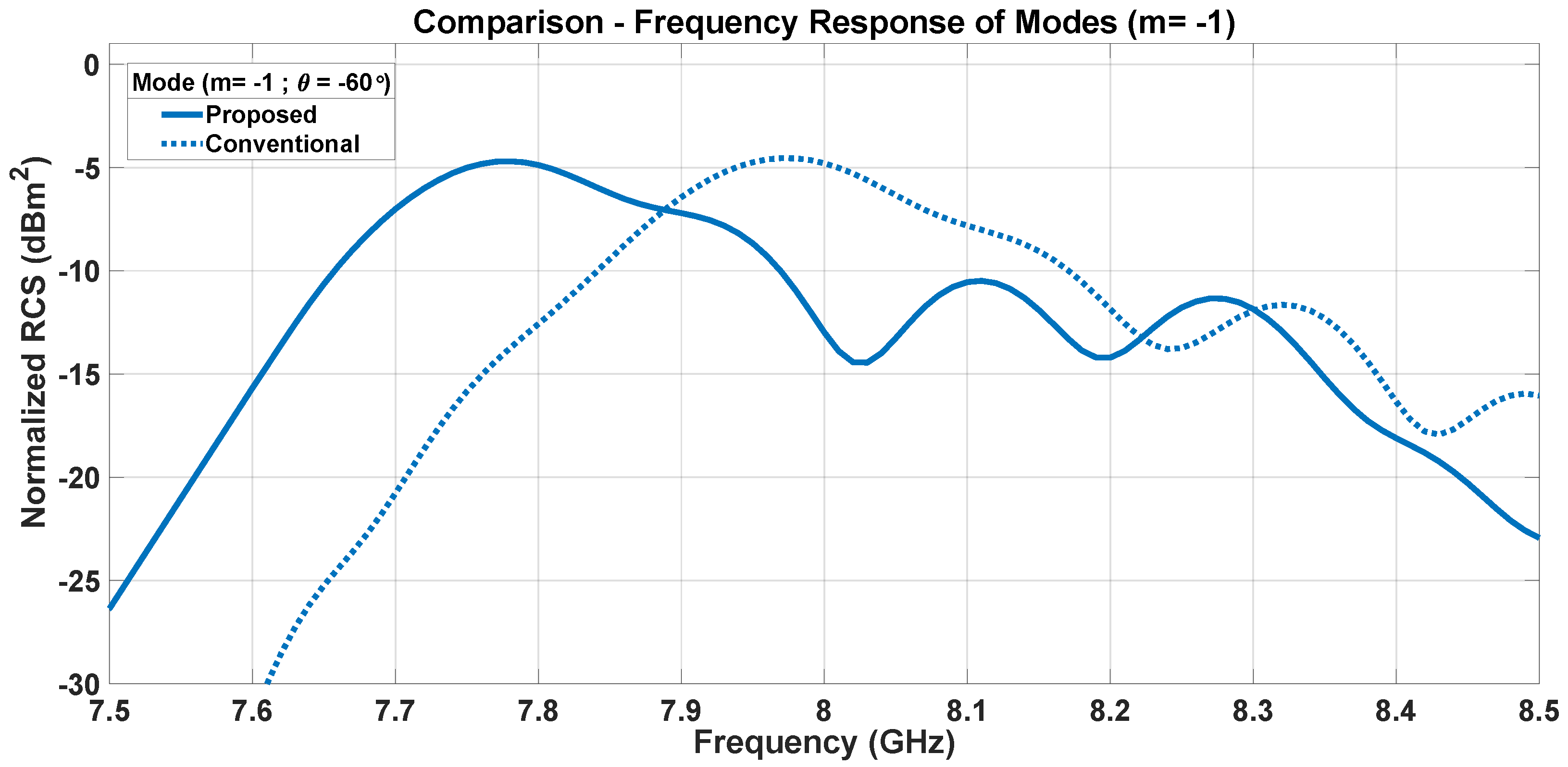
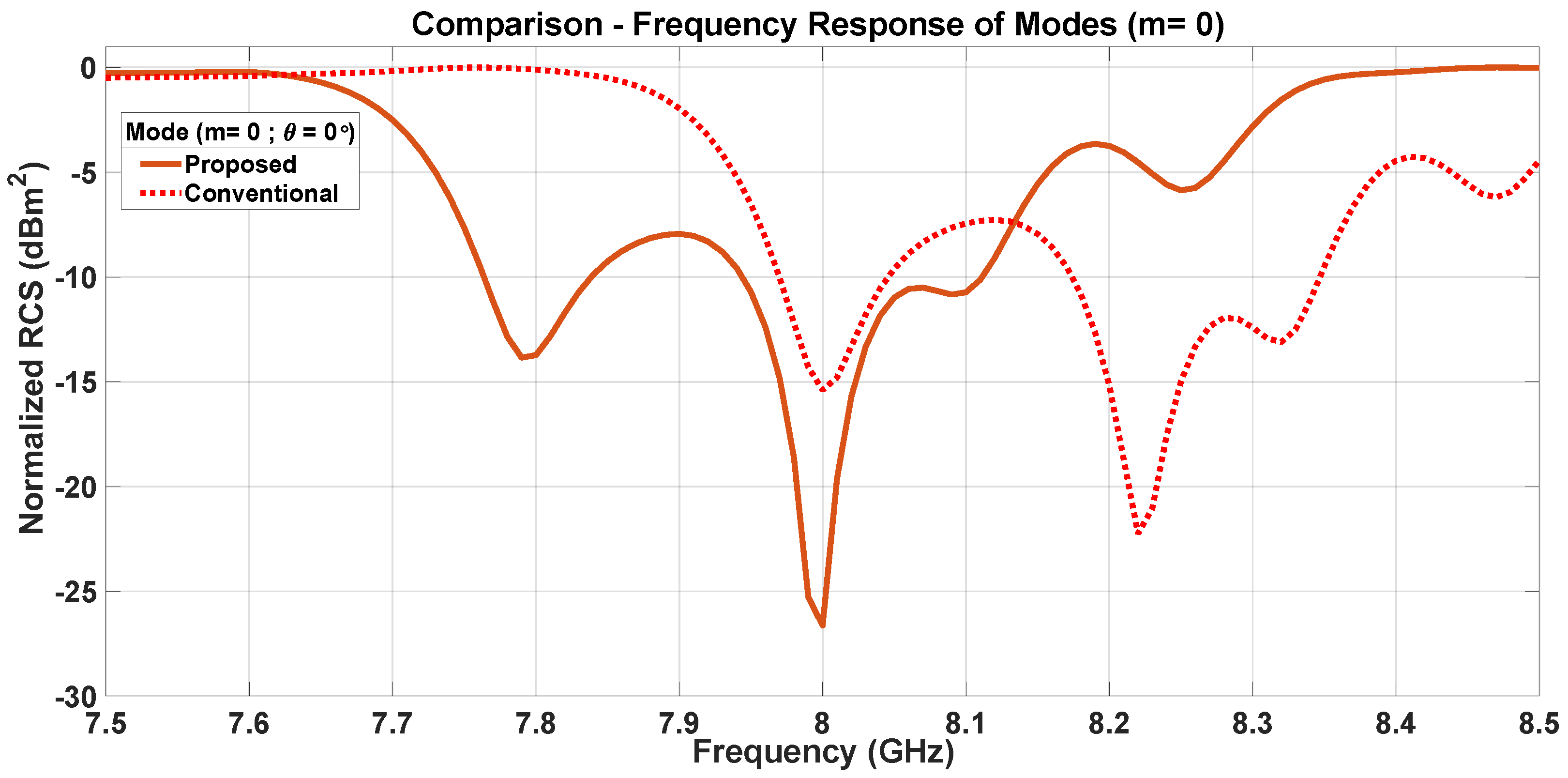
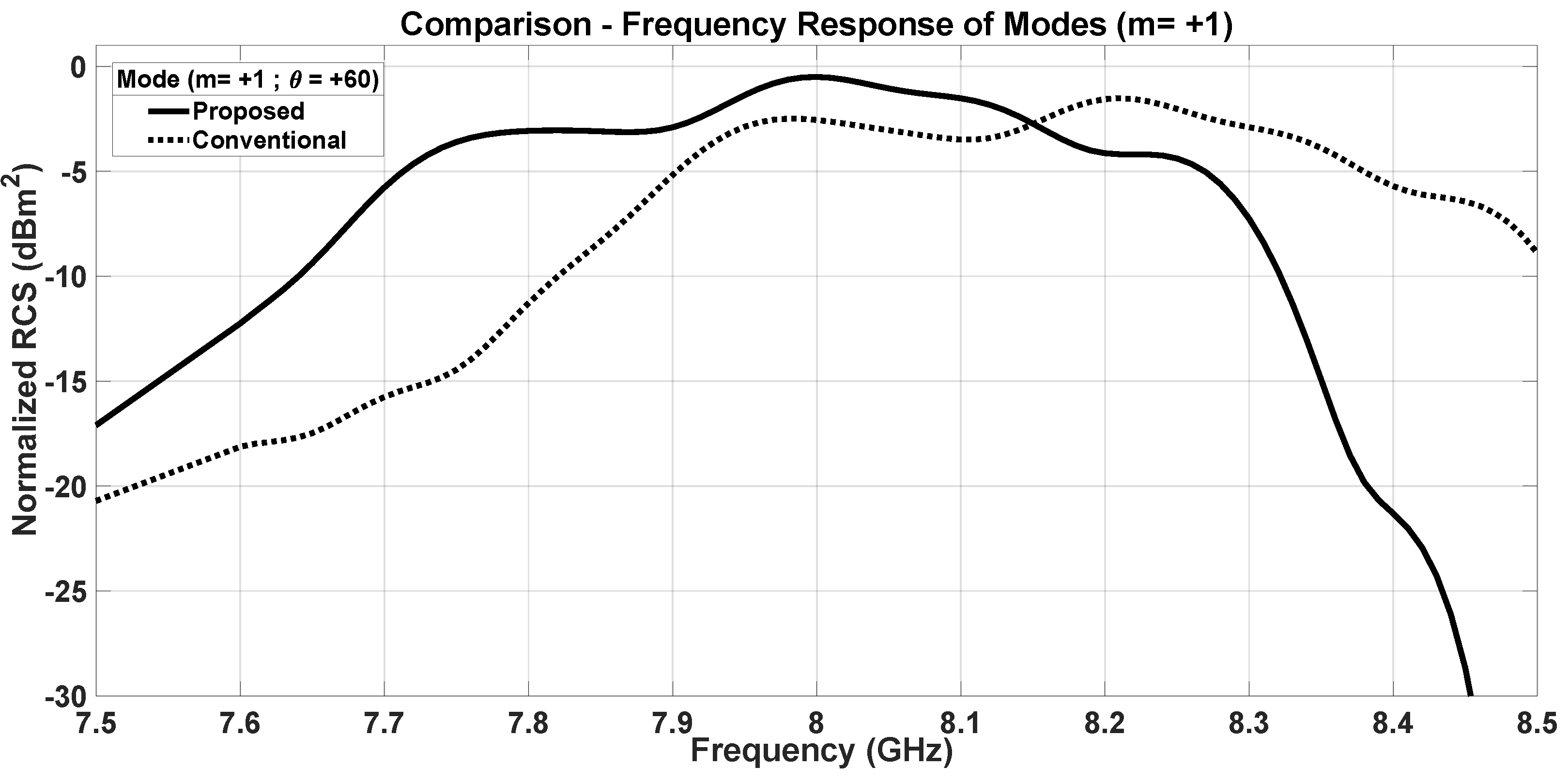
5. Effect of Dipole Interactions on Frequency Response of Modes
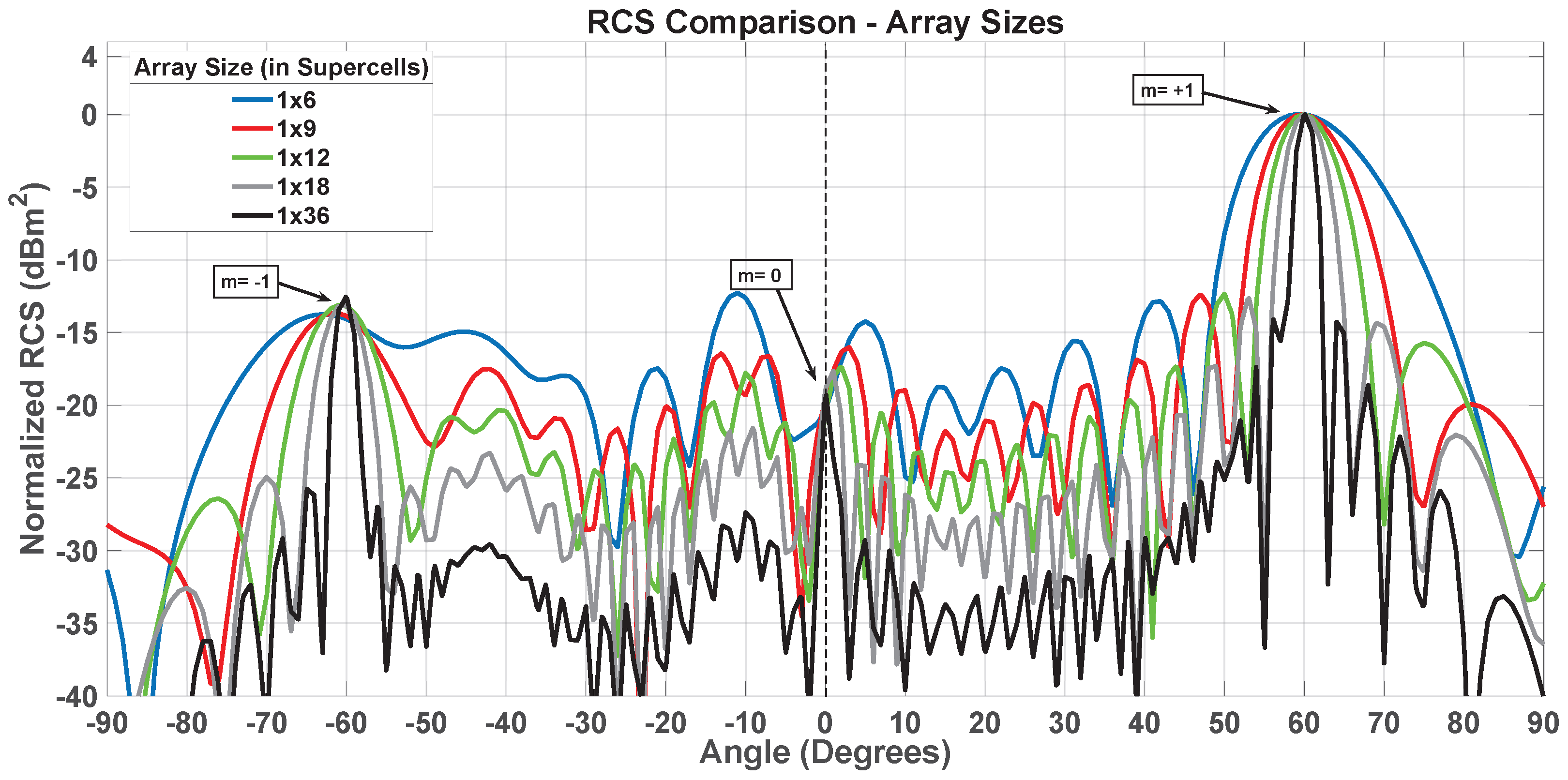
6. Diffraction Grating-like Behavior
7. Sensitivity Analysis
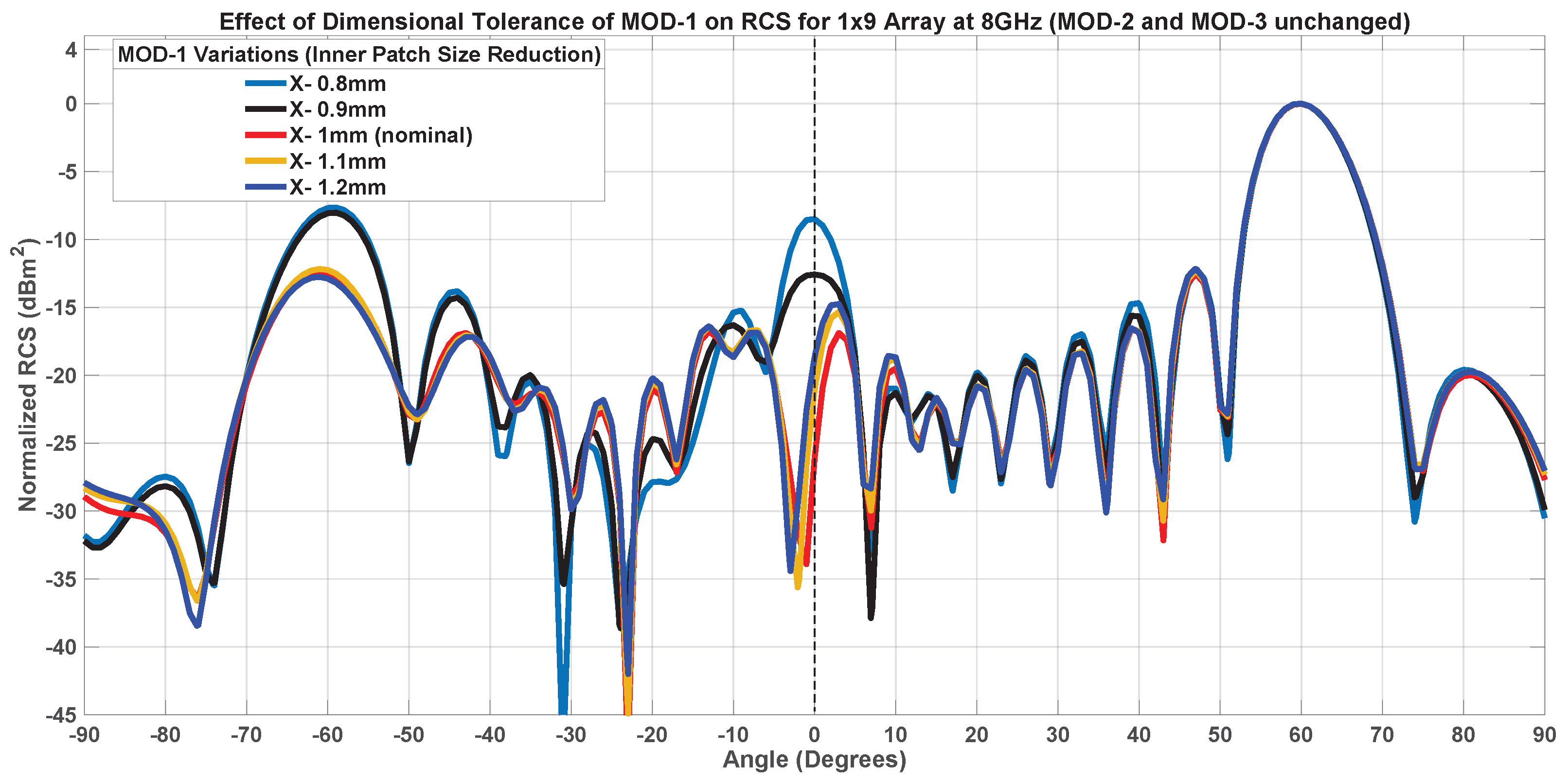
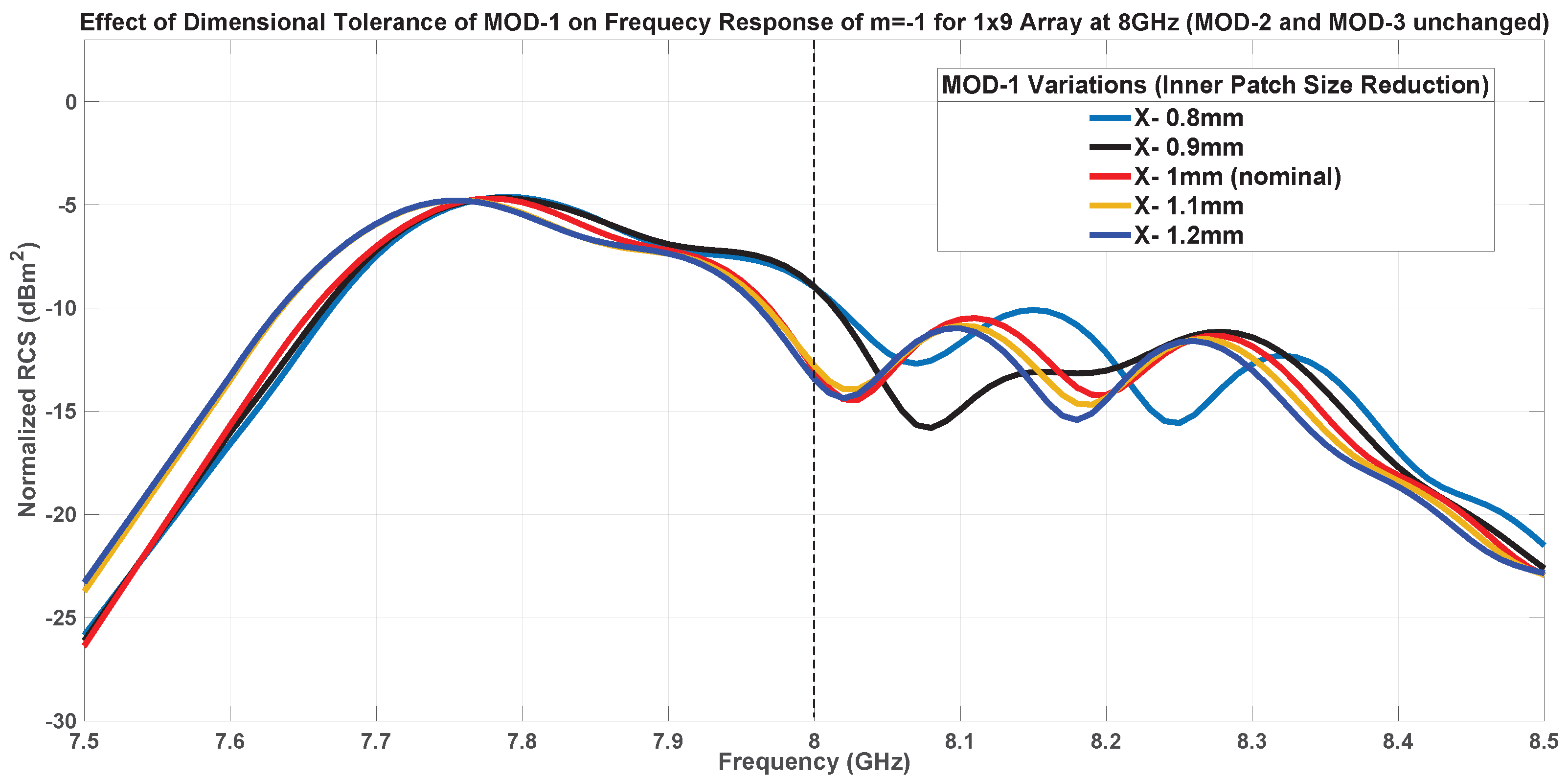
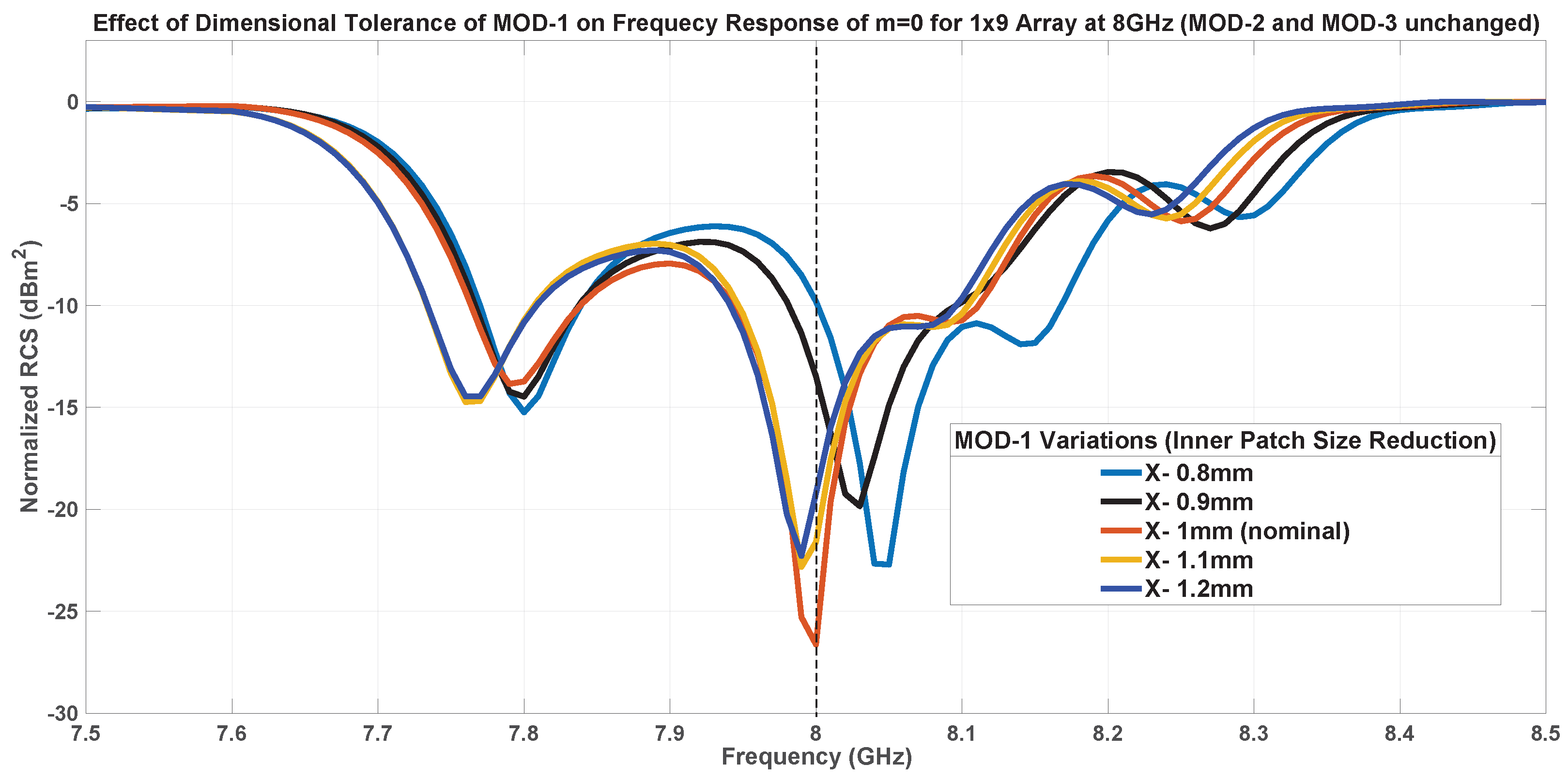
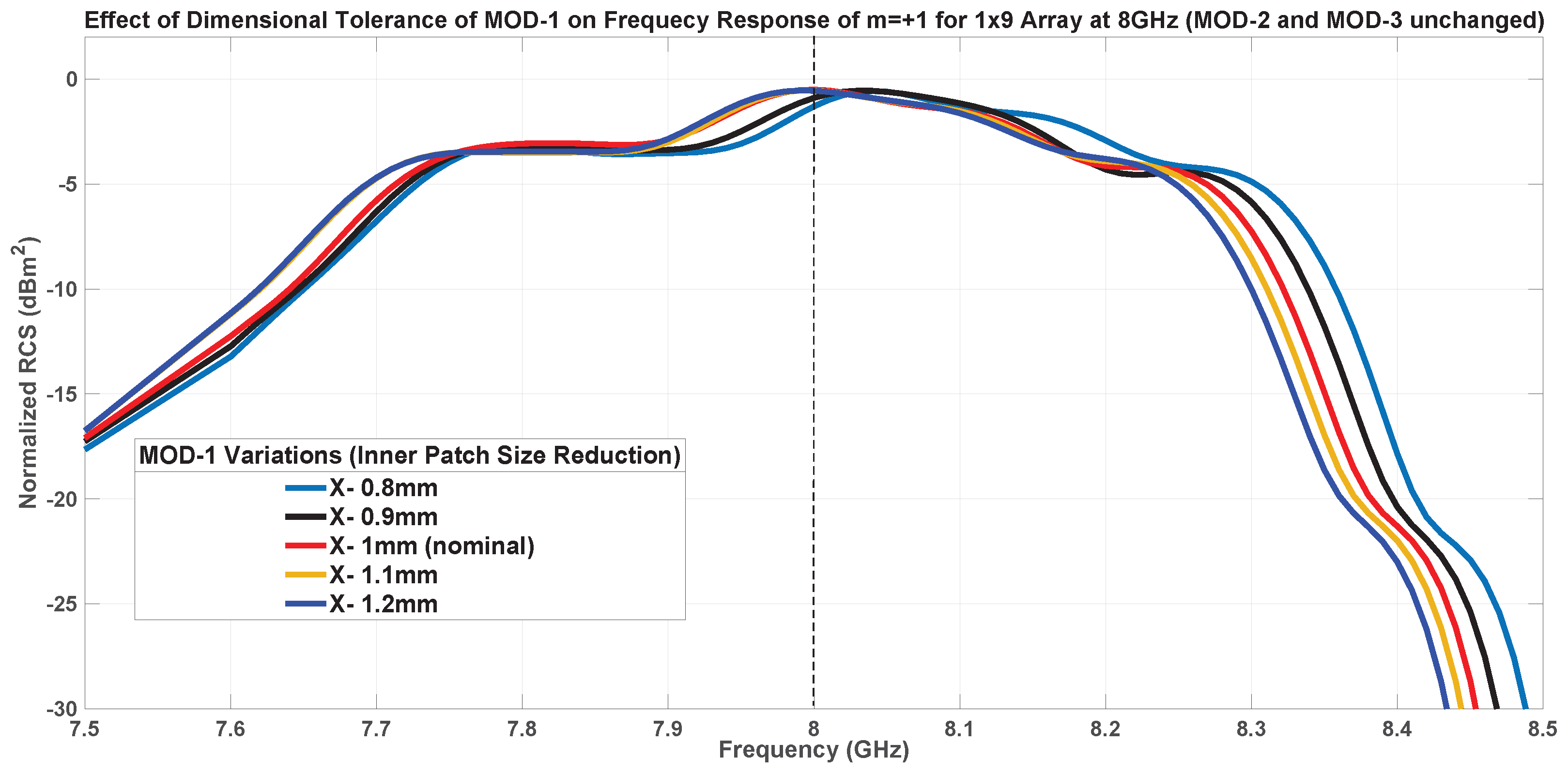
7.1. Fabrication Tolerance Analysis
7.1.1. Inner Patch Size-MOD-1
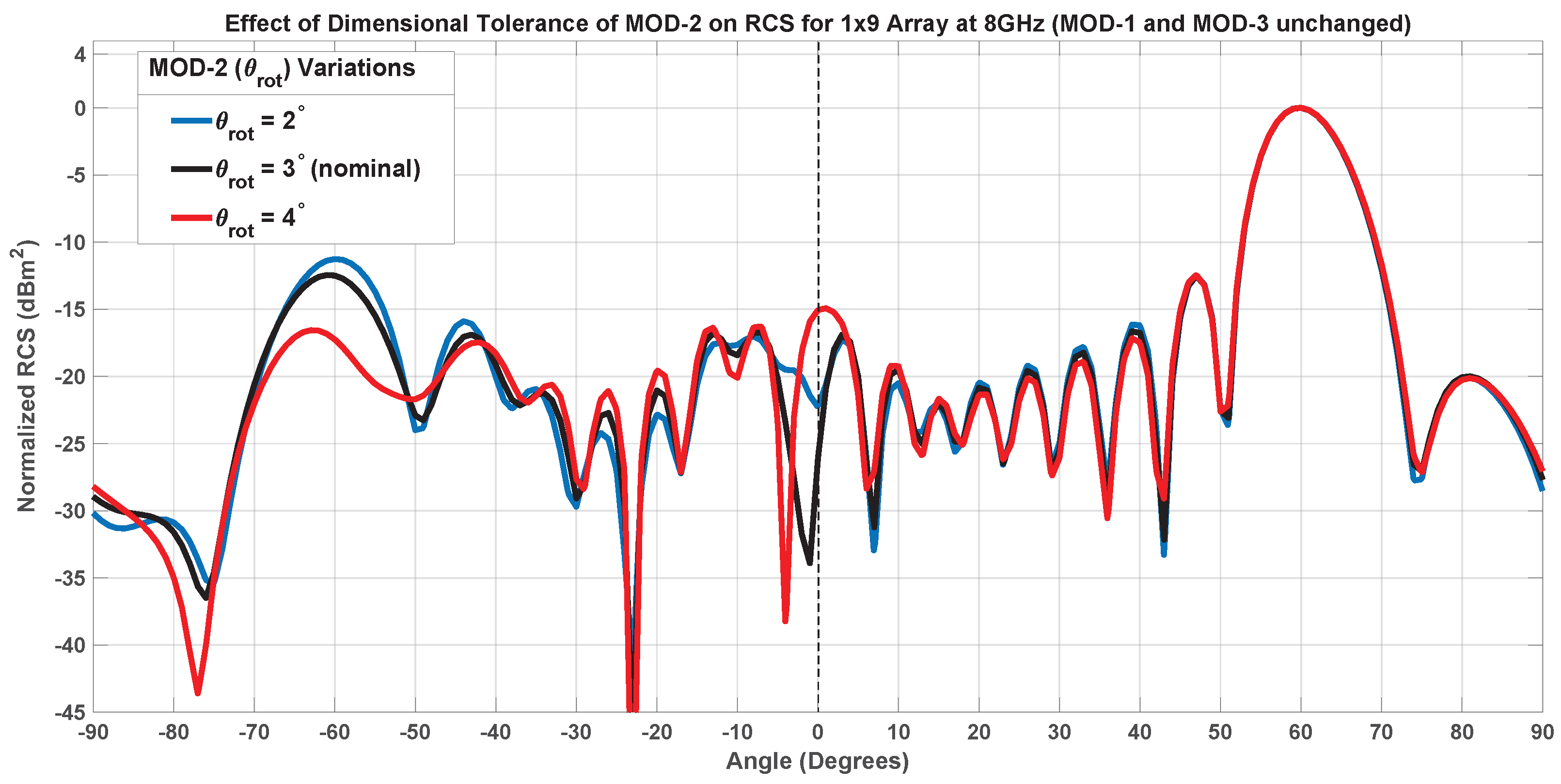
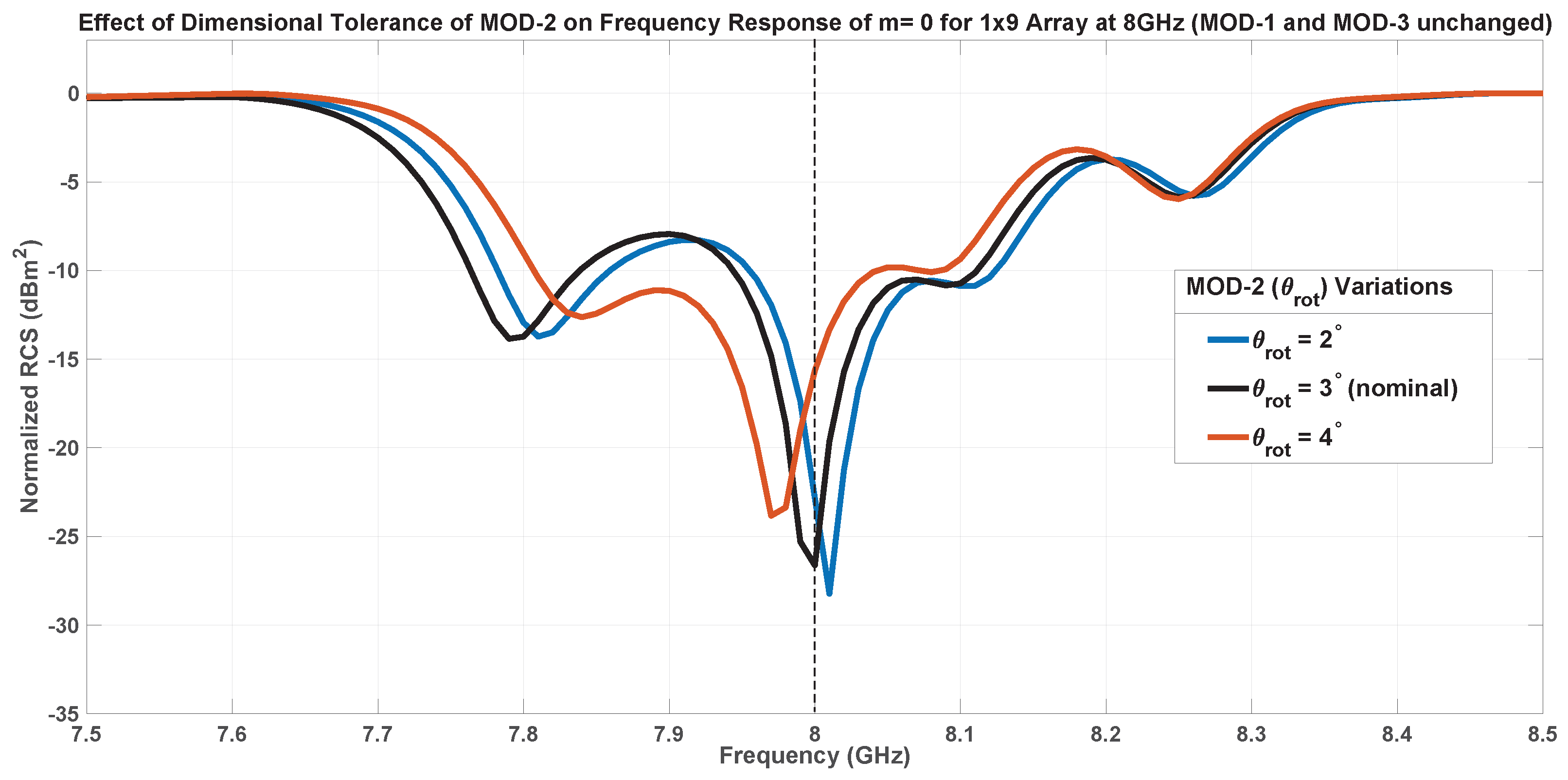
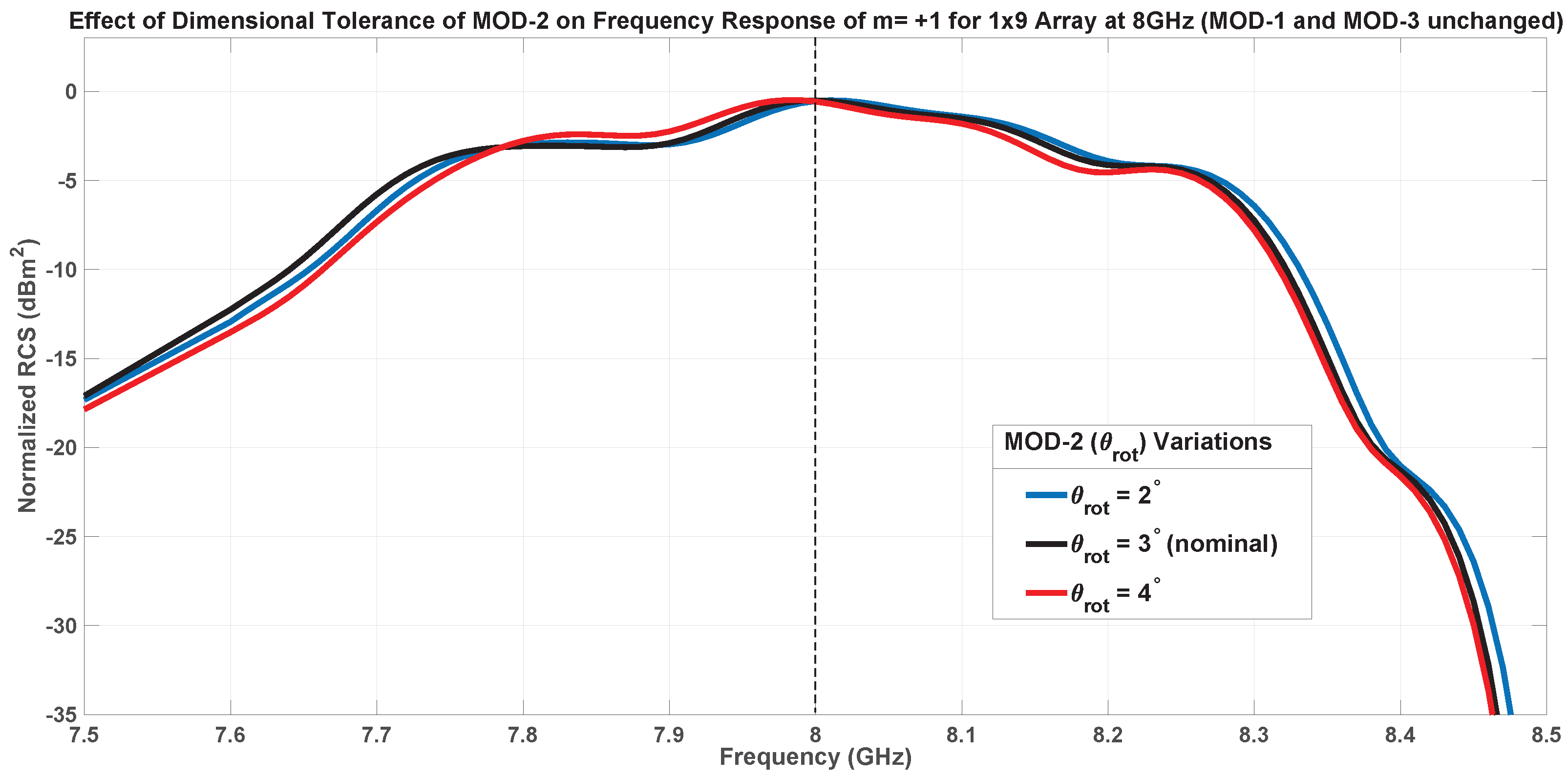
7.1.2. Inner Patch Tilting-MOD-2
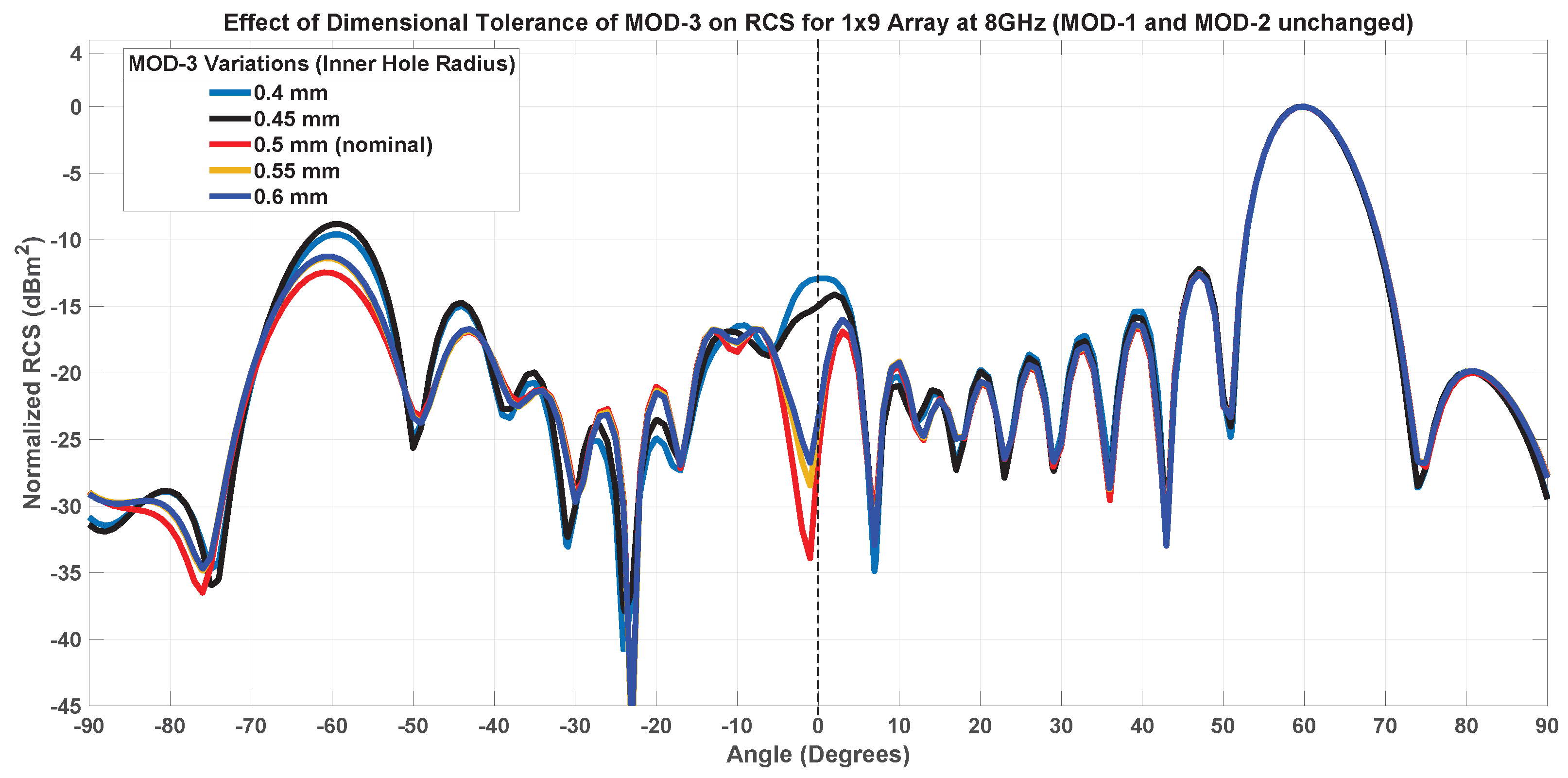
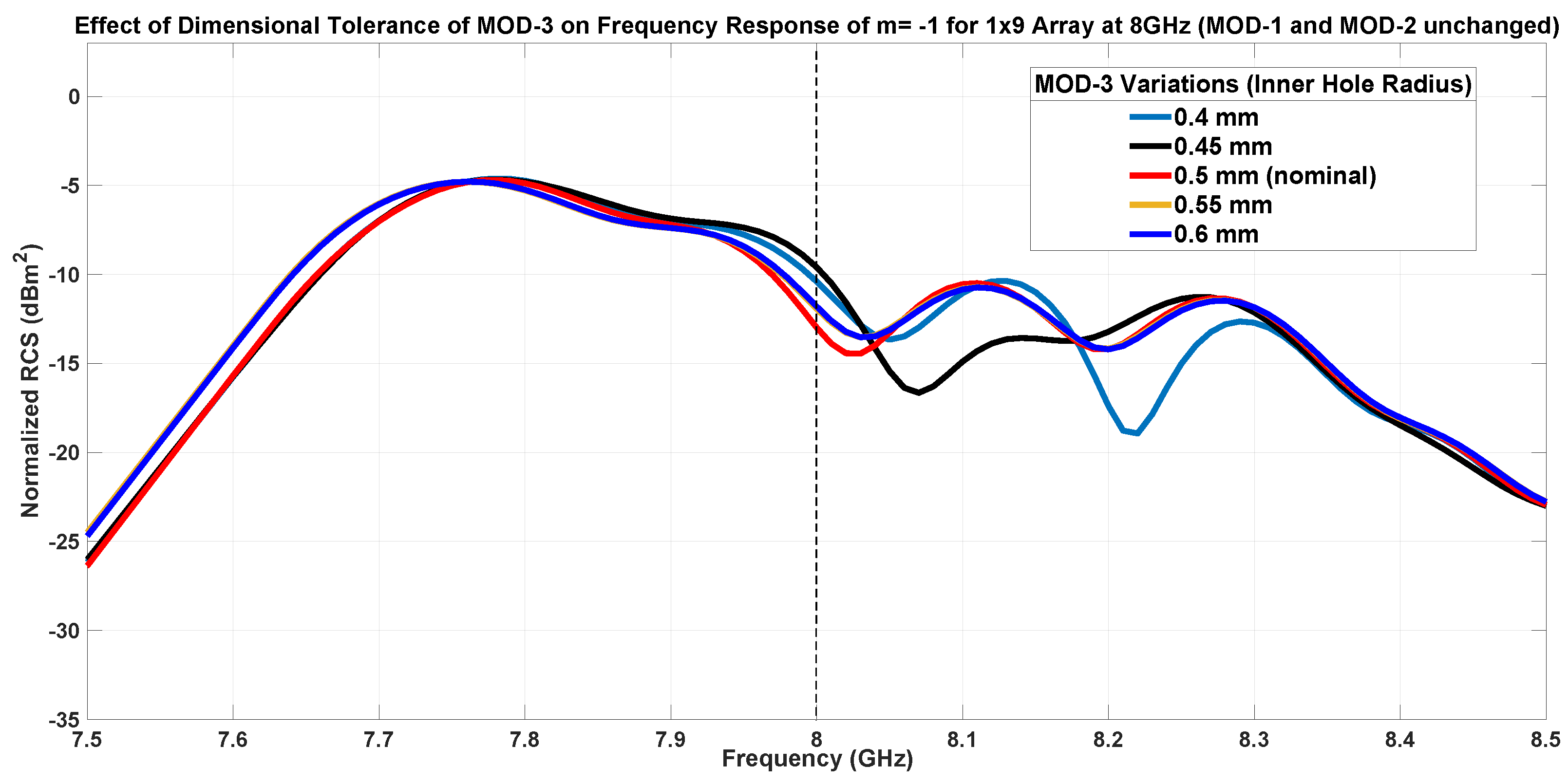
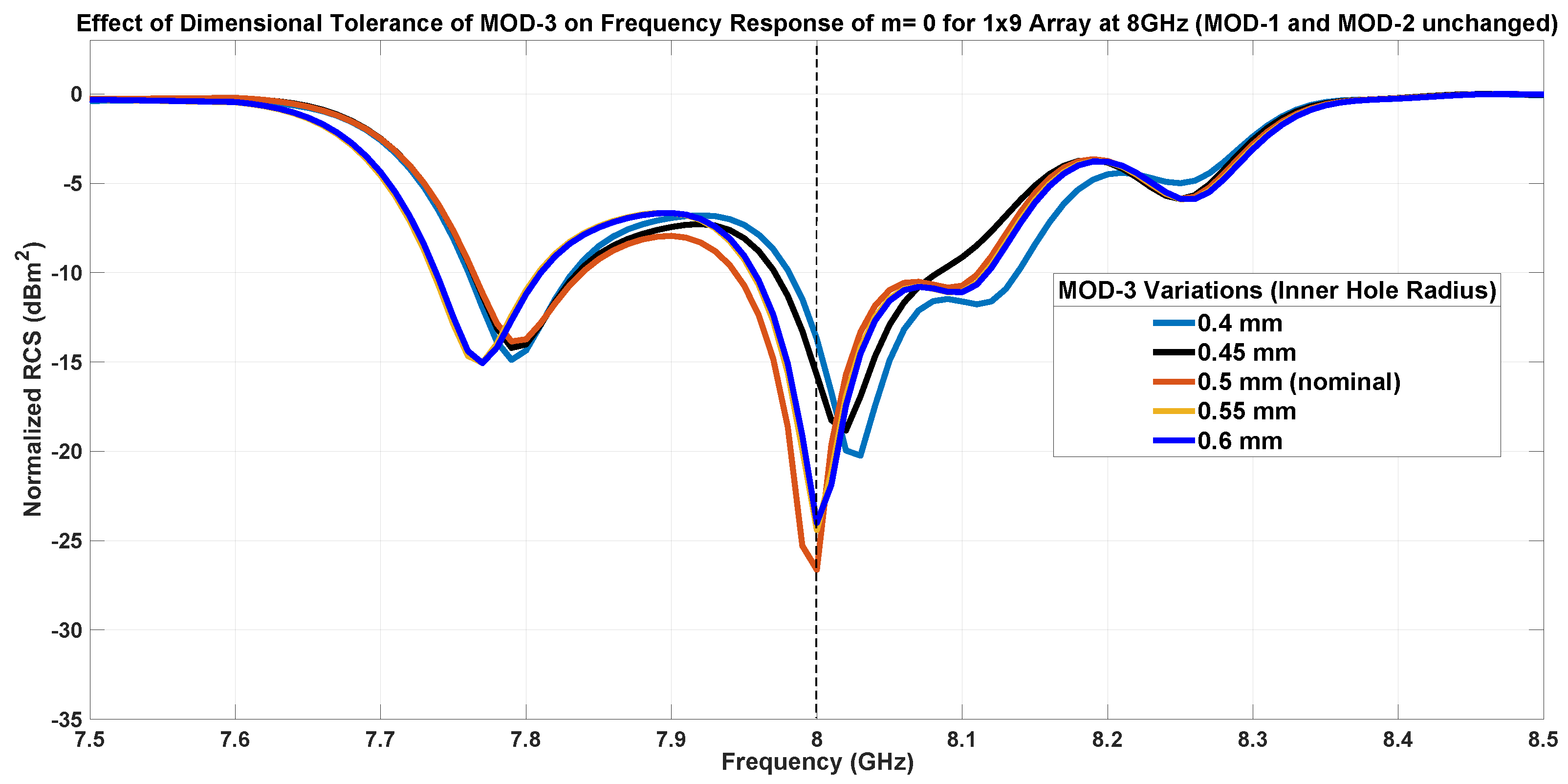
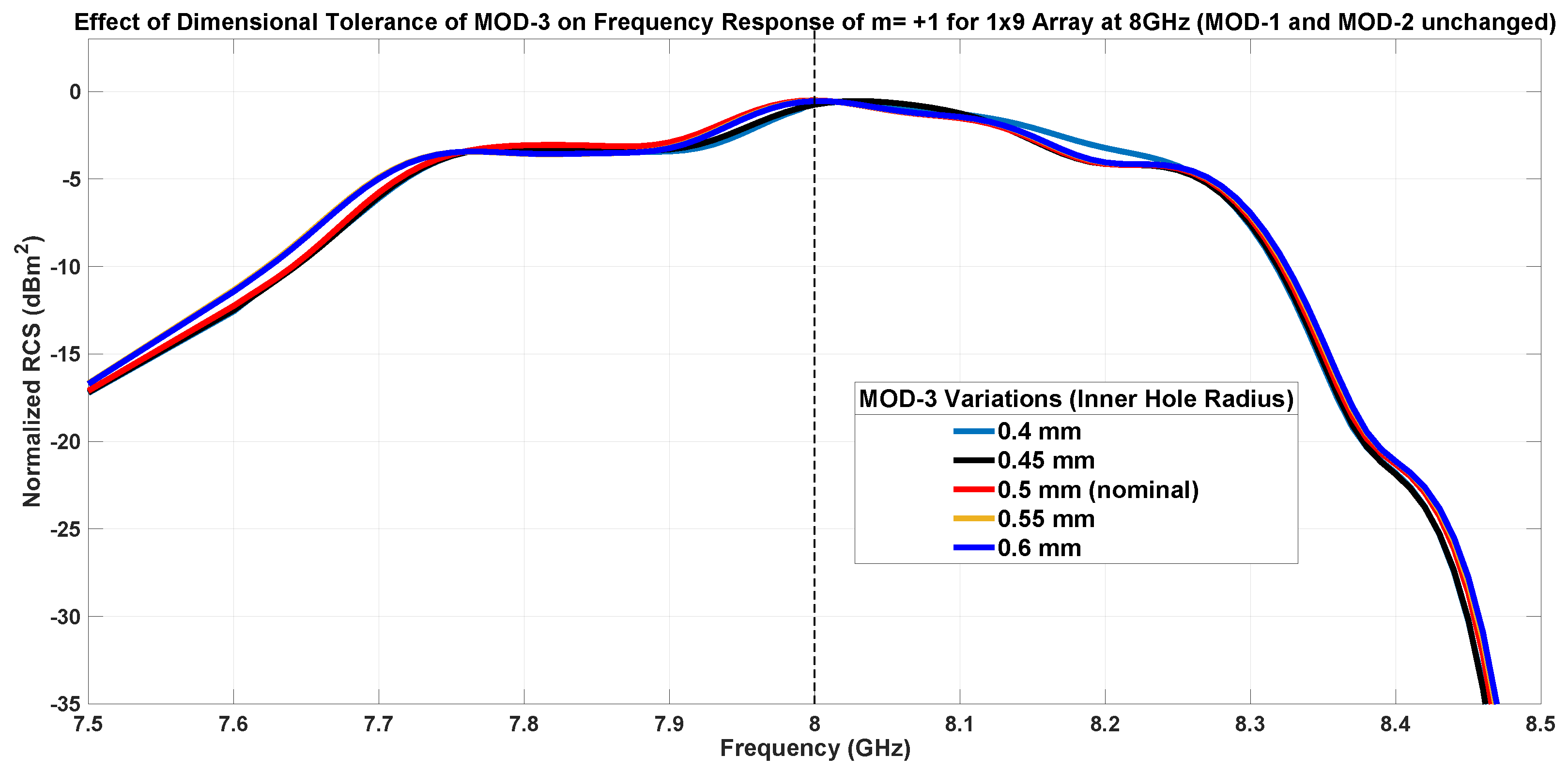
7.1.3. Inner Patch Hole Size-MOD-3
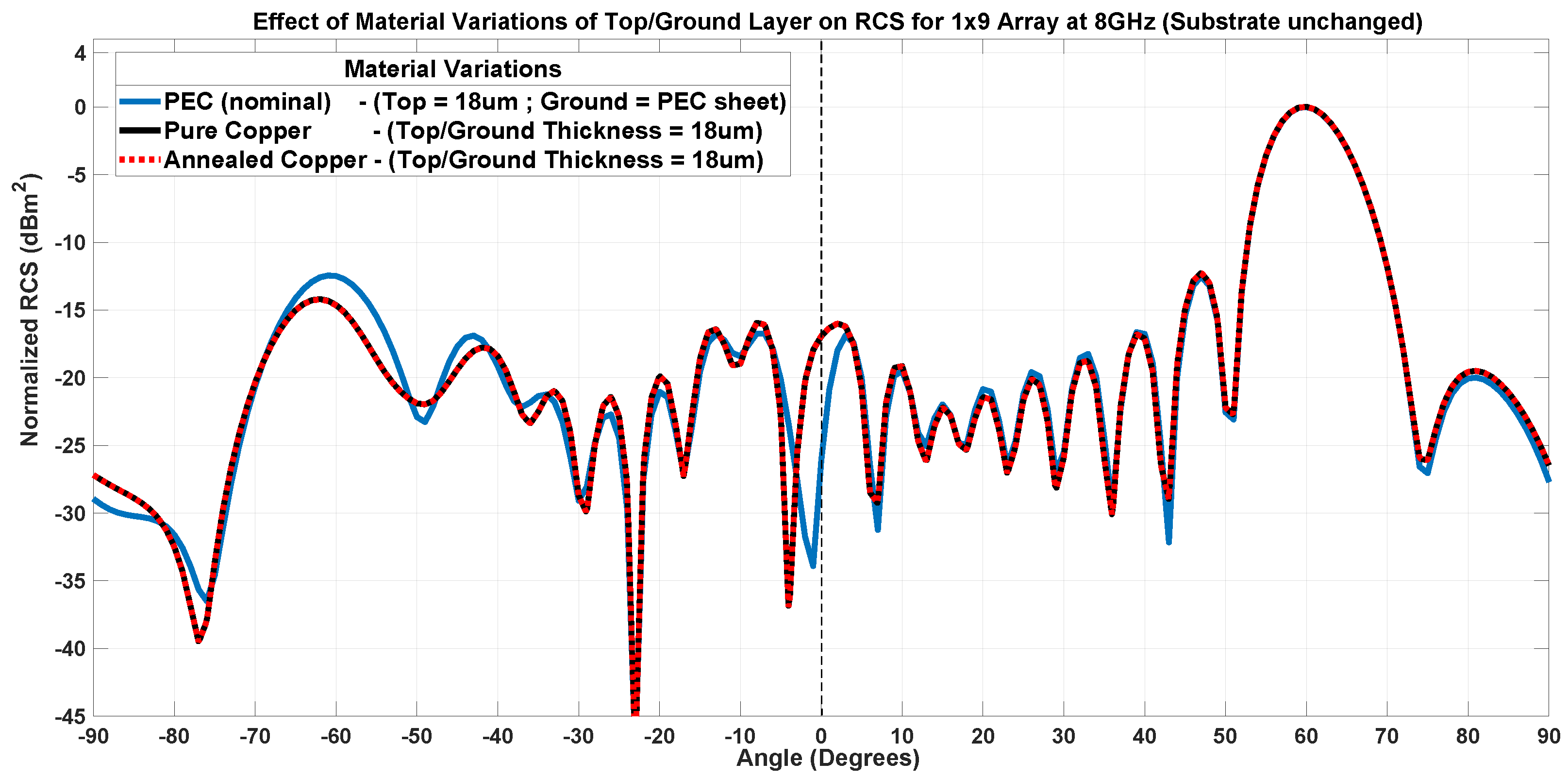
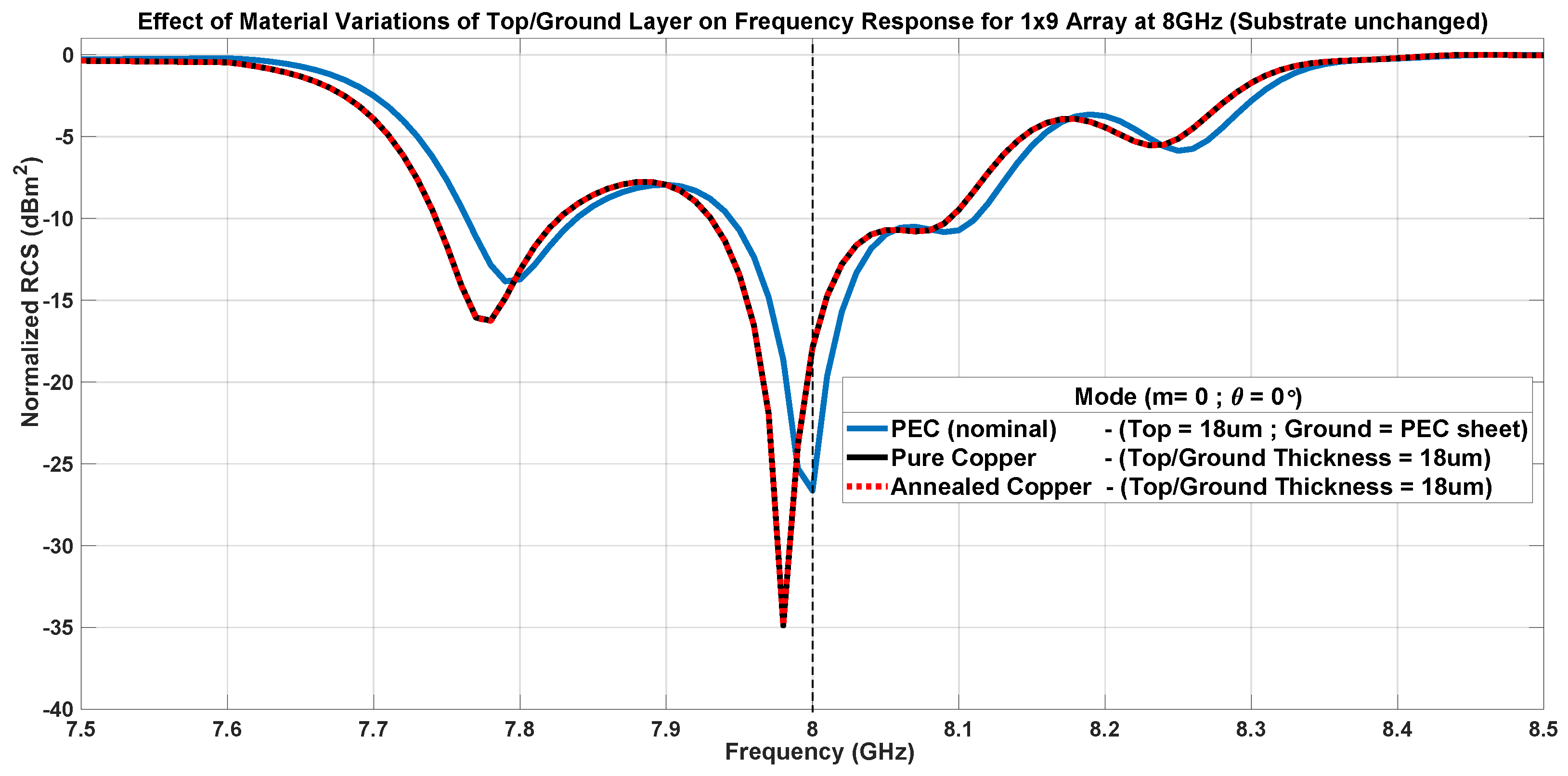
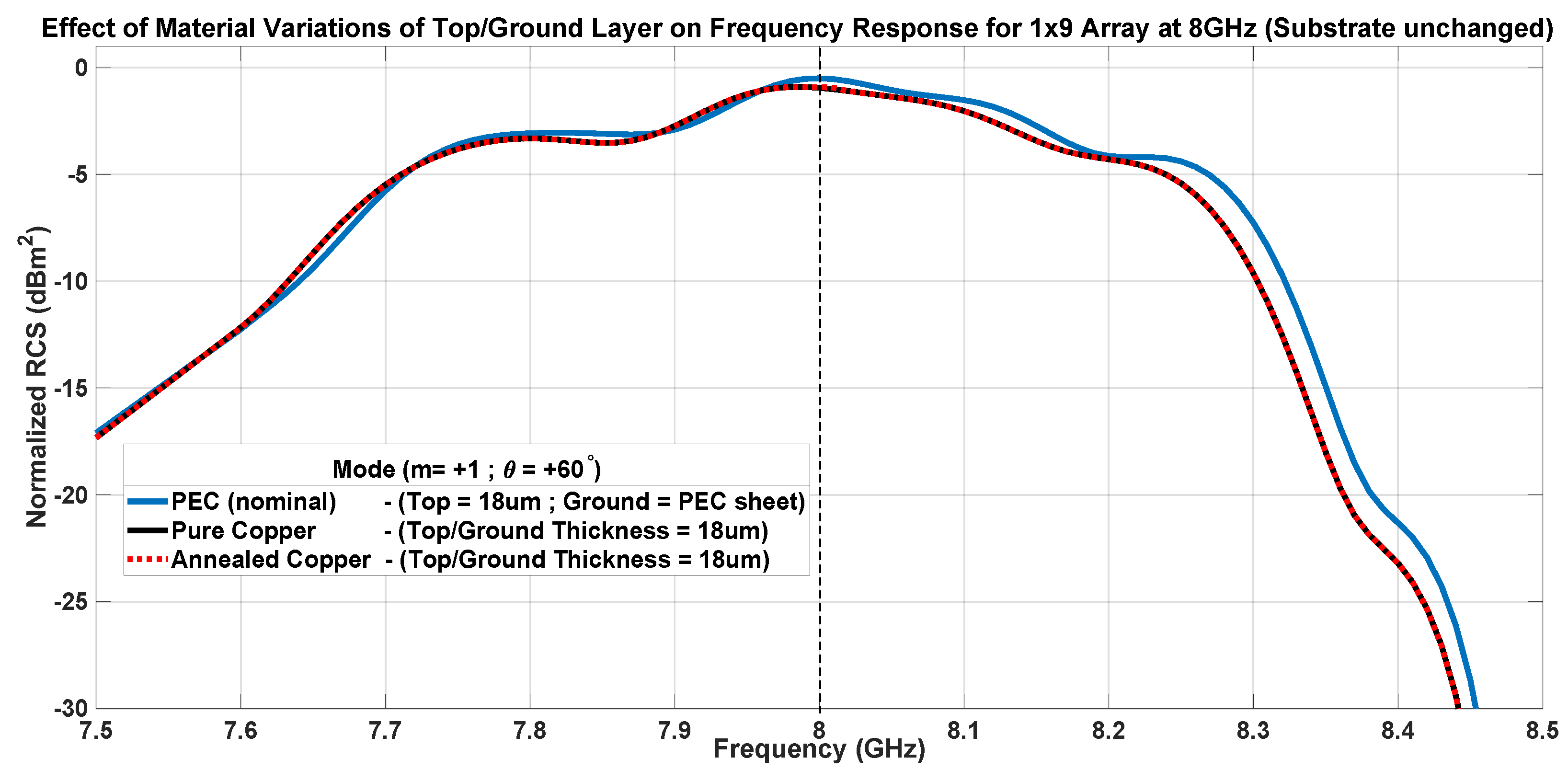
7.2. Method Stability
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tishchenko, A.; Khalily, M.; Shojaeifard, A.; Burton, F.; Björnson, E.; Di Renzo, M.; Tafazolli, R. The Emergence of Multi-Functional and Hybrid Reconfigurable Intelligent Surfaces for Integrated Sensing and Communications—A Survey. IEEE Commun. Surv. Tutor. 2024, 27, 2895–2936. [Google Scholar] [CrossRef]
- Umer, A.; Müürsepp, I.; Alam, M.M.; Wymeersch, H. Reconfigurable Intelligent Surfaces in 6G Radio Localization: A Survey of Recent Developments, Opportunities, and Challenges. IEEE Commun. Surv. Tutor. 2025. [Google Scholar] [CrossRef]
- Zaoutis, E.A.; Liodakis, G.S.; Baklezos, A.T.; Nikolopoulos, C.D.; Ioannidou, M.P.; Vardiambasis, I.O. 6G Wireless Communications and Artificial Intelligence-Controlled Reconfigurable Intelligent Surfaces: From Supervised to Federated Learning. Appl. Sci. 2025, 15, 3252. [Google Scholar] [CrossRef]
- Martini, E.; Maci, S. Theory, Analysis, and Design of Metasurfaces for Smart Radio Environments. Proc. IEEE 2022, 110, 1227–1243. [Google Scholar] [CrossRef]
- Di Renzo, M. Smart radio environments empowered by reconfigurable intelligent surfaces: How it works, state of research, and the road ahead. IEEE J. Sel. Areas Commun. 2020, 38, 2450–2525. [Google Scholar] [CrossRef]
- Ayoubi, R.A.; Moro, E.; Mizmizi, M.; Tagliaferri, D.; Filippini, I.; Spagnolini, U. Optimal Planning for Heterogeneous Smart Radio Environments. arXiv 2024, arXiv:2411.15629. [Google Scholar] [CrossRef]
- Lee, J.Y.; Wu, D.; Guo, X.; Tan, J.D.; Yew, T.J.; Ng, Z.N.; Bhuiyan, M.A.S.; Miraz, M.H. 6G communications through sub-Terahertz CMOS power amplifiers: Design challenges and trends. Heliyon 2025, 11, e43393. [Google Scholar] [CrossRef]
- Thomas, S.; Virdi, J.S.; Babakhani, A.; Roberts, I.P. A Survey on Advancements in THz Technology for 6G: Systems, Circuits, Antennas, and Experiments. IEEE Open J. Commun. Soc. 2025, 6, 1998–2016. [Google Scholar] [CrossRef]
- Oliveri, G.; Zardi, F.; Rocca, P.; Salucci, M.; Massa, A. Building a Smart EM Environment-AI-Enhanced Aperiodic Micro-Scale Design of Passive EM Skins. IEEE Trans. Antennas Propag. 2022, 70, 8757–8770. [Google Scholar] [CrossRef]
- Benoni, A.; Capra, F.; Salucci, M.; Massa, A. Toward real-world indoor smart electromagnetic environments–A large-scale experimental demonstration. IEEE Trans. Antennas Propag. 2023, 71, 8450–8463. [Google Scholar] [CrossRef]
- Freni, A.; Beccaria, M.; Mazzinghi, A.; Massaccesi, A.; Pirinoli, P. Low-Profile and Low-Visual Impact Smart Electromagnetic Curved Passive Skins for Enhancing Connectivity in Urban Scenarios. Electronics 2023, 12, 4491. [Google Scholar] [CrossRef]
- Beccaria, M.; Freni, A.; Mazzinghi, A.; Pirinoli, P. On the features of curved, passive reconfigurable smart electromagnetic skins. Sci. Rep. 2025, 15, 32277. [Google Scholar] [CrossRef]
- Huang, J.; Encinar, J. Reflectarray Antennas; Wiley-IEEE Press: Hoboken, NJ, USA, 2007; pp. 1–216. [Google Scholar]
- Martinez-de-Rioja, E.; Vaquero, A.F.; Arrebola, M.; Carrasco, E.; Encinar, J.A.; Achour, M. Passive intelligent reflecting surfaces based on reflectarray panels to enhance 5G millimeter-wave coverage. Int. J. Microw. Wirel. Technol. 2023, 15, 3–14. [Google Scholar] [CrossRef]
- Li, A.; Singh, S.; Sievenpiper, D. Metasurfaces and their applications. Nanophotonics 2018, 7, 989–1011. [Google Scholar] [CrossRef]
- Liaskos, C.; Nie, S.; Tsioliaridou, A.; Pitsillides, A.; Ioannidis, S.; Akyildiz, I. A new wireless communication paradigm through software-controlled metasurfaces. IEEE Commun. Mag. 2018, 56, 162–169. [Google Scholar] [CrossRef]
- Yang, F.; Rahmat-Samii, Y. Surface Electromagnetics, With Applications in Antenna, Microwave, and Optical Engineering; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Glybovski, S.B.; Tretyakov, S.A.; Belov, P.A.; Kivshar, Y.S.; Simovski, C.R. Metasurfaces: From microwaves to visible. Phys. Rep. 2016, 634, 1–72. [Google Scholar] [CrossRef]
- Tang, W. Subject Editor spotlight on programmable metasurfaces: The future of wireless? IET Electron. Lett. 2019, 55, 360–361. [Google Scholar] [CrossRef]
- Hu, J.; Bandyopadhyay, S.; Liu, Y.H.; Shao, L.Y. A review on metasurface: From principle to smart metadevices. Front. Phys. 2021, 8, 586087. [Google Scholar] [CrossRef]
- Chen, H.T.; Taylor, A.J.; Yu, N.F. A review of metasurfaces: Physics and applications. Rep. Prog. Phys. 2016, 79, 076401. [Google Scholar] [CrossRef]
- Wong, A.M.H.; Christian, P.; Eleftheriades, G.V. Binary Huygens’ metasurfaces: Experimental demonstration of simple and efficient near-grazing Retroreflectors for TE and TM polarizations. IEEE Trans. Antennas Propag. 2018, 66, 2892. [Google Scholar] [CrossRef]
- Estakhri, N.M.; Neder, V.; Knight, M.W.; Polman, A.; Alù, A. Visible Light, Wide-angle graded metasurface for back reflection. ACS Photonics 2017, 4, 228. [Google Scholar] [CrossRef]
- Xu, G.; Ataloglou, V.G.; Hum, S.V.; Eleftheriades, G.V. Extreme Beam-Forming With Impedance Metasurfaces Featuring Embedded Sources and Auxiliary Surface Wave Optimization. IEEE Access 2022, 10, 28670–28684. [Google Scholar] [CrossRef]
- Rabinovich, O.; Epstein, A. Analytical Design of Printed Circuit Board (PCB) Metagratings for Perfect Anomalous Reflection. IEEE Trans. Antennas Propag. 2018, 66, 4086–4095. [Google Scholar] [CrossRef]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.P.; Capasso, F.; Gaburro, Z. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef]
- Elineau, M.; Loison, R.; Méric, S.; Gillard, R.; Pagani, P.; Mazé-Merceur, G.; Pouliguen, P. RCS prediction and optimization for anomalous reflection metasurfaces using Floquet analysis. Int. J. Microw. Wirel. Technol. 2023, 15, 966–974. [Google Scholar] [CrossRef]
- Islam, N.A.; Choi, S. Compact folded dipole metasurface for high anomalous reflection angles with low harmonic levels. Sci. Rep. 2020, 10, 18125. [Google Scholar] [CrossRef]
- Asadchy, V.S.; Albooyeh, M.; Tcvetkova, S.N.; Díaz-Rubio, A.; Ra’di, Y.; Tretyakov, S.A. Perfect control of reflection and refraction using spatially dispersive metasurfaces. Phys. Rev. B 2016, 94, 075142. [Google Scholar] [CrossRef]
- Díaz-Rubio, A.; Asadchy, V.S.; Elsakka, A.; Tretyakov, S.A. From the generalized reflection law to the realization of perfect anomalous reflectors. Sci. Adv. 2017, 3, e1602714. [Google Scholar] [CrossRef]
- Asadchy, V.S.; Wickberg, A.; Díaz-Rubio, A.; Wegener, M. Eliminating Scattering Loss in Anomalously Reflecting Optical Metasurfaces. ACS Photonics 2017, 4, 1264–1270. [Google Scholar] [CrossRef]
- Ra’di, Y.; Alù, A. Metagratings for Efficient Wavefront Manipulation. IEEE Photonics J. 2022, 14, 2207513. [Google Scholar] [CrossRef]
- Popov, V.; Boust, F.; Burokur, S.N. Controlling diffraction patterns with metagratings. Phys. Rev. Appl. 2018, 10, 011002. [Google Scholar] [CrossRef]
- Ra’di, Y.; Alù, A. Reconfigurable metagratings. ACS Photonics 2018, 5, 1779–1785. [Google Scholar] [CrossRef]
- Panagiotidis, E.; Almpanis, E.; Stefanou, N.; Papanikolaou, N. Multipolar interactions in Si sphere metagratings. J. Appl. Phys. 2020, 128, 093103. [Google Scholar] [CrossRef]
- Huang, T.; Yin, L.Z.; Zhao, J.; Liu, P.K. High-order multipoles in all-dielectric metagrating enabling ultralarge-angle light bending with unity efficiency. Nanophotonics 2021, 10, 2859–2873. [Google Scholar] [CrossRef]
- Fan, Z.; Shcherbakov, M.R.; Allen, M.; Allen, J.; Wenner, B.; Shvets, G. Perfect diffraction with multiresonant bianisotropic metagratings. ACS Photonics 2018, 5, 4303–4311. [Google Scholar] [CrossRef]
- Wang, S.; Chen, K.; Zhang, X.; Dong, S.; Tang, K.; Yang, W.; Zhao, J.; Jiang, T.; Feng, Y. Metagrating-assisted dual-polarized hybrid metalens with near-unity numerical aperture. Phys. Rev. Appl. 2025, 23, 064011. [Google Scholar] [CrossRef]
- Niemi, T.; Karilainen, A.O.; Tretyakov, S.A. Synthesis of Polarization Transformers. IEEE Trans. Antennas Propag. 2013, 61, 3102–3111. [Google Scholar] [CrossRef]
- Liu, W.; Kivshar, Y.S. Generalized Kerker effects in nanophotonics and meta-optics [Invited]. Opt. Express 2018, 26, 13085–13105. [Google Scholar] [CrossRef]
- Lee, J.Y.; Miroshnichenko, A.E.; Lee, R.-K. Reexamination of Kerker’s conditions by means of the phase diagram. Phys. Rev. A 2017, 96, 043846. [Google Scholar] [CrossRef]
- Chen, Y.; Fleury, R.; Seppecher, P.; Hu, G.; Wegener, M. Nonlocal metamaterials and metasurfaces. Nat. Rev. Phys. 2025, 7, 299–312. [Google Scholar] [CrossRef]
- Estakhri, N.M.; Alù, A. Wave-front transformation with gradient metasurfaces. Phys. Rev. X 2016, 6, 041008. [Google Scholar] [CrossRef]
- Saue, T. Post Dirac-Hartree-Fock methods-Properties. In Theoretical and Computational Chemistry; Schwerdtfeger, P., Ed.; Elsevier: Amsterdam, The Netherlands, 2002; Volume 11, pp. 332–400. [Google Scholar]
- Alaee, R.; Rockstuhl, C.; Fernandez-Corbaton, I. An electromagnetic multipole expansion beyond the long-wavelength approximation. Opt. Commun. 2018, 407, 17–21. [Google Scholar] [CrossRef]
- Grahn, P.; Shevchenko, A.; Kaivola, M. Electromagnetic multipole theory for optical nanomaterials. New J. Phys. 2012, 14, 093033. [Google Scholar] [CrossRef]
- Achouri, K.; Caloz, C. Electromagnetic Metasurfaces: Theory and Applications; Wiley-IEEE Press: Hoboken, NJ, USA, 2021. [Google Scholar]
- Papasimakis, N.; Fedotov, V.A.; Savinov, V.; Raybould, T.A.; Zheludev, N.I. Electromagnetic toroidal excitations in matter and free space. Nat. Mater. 2016, 15, 263–271. [Google Scholar] [CrossRef]
- Poleva, M.; Frizyuk, K.; Baryshnikova, K.; Evlyukhin, A.; Petrov, M.; Bogdanov, A. Multipolar theory of bianisotropic response of meta-atoms. Phys. Rev. B 2023, 107, L041304. [Google Scholar] [CrossRef]
- Kaelberer, T.; Fedotov, V.A.; Papasimakis, N.; Tsai, D.P.; Zheludev, N.I. Toroidal Dipolar Response in a Metamaterial. Science 2010, 330, 1510–1512. [Google Scholar] [CrossRef]
- Baryshnikova, K.V.; Smirnova, D.A.; Luk’yanchuk, B.S.; Kivshar, Y.S. Optical anapoles: Concepts and applications. Adv. Opt. Mater. 2019, 7, 1801350. [Google Scholar] [CrossRef]
- Guo, S.; Talebi, N.; Campos, A.; Kociak, M.; van Aken, P.A. Radiation of Dynamic Toroidal Moments. ACS Photonics 2019, 6, 467–474. [Google Scholar] [CrossRef]
- Talebi, N.; Guo, S.; van Aken, P.A. Theory and applications of toroidal moments in electrodynamics: Their emergence, characteristics, and technological relevance. Nanophotonics 2018, 7, 93–110. [Google Scholar] [CrossRef]
- Muhammad, N.; Su, Z.; Jiang, Q.; Wang, Y.; Huang, L. Radiationless optical modes in metasurfaces: Recent progress and applications. Light: Sci. Appl. 2024, 13, 192. [Google Scholar] [CrossRef]
- Savinov, V.; Fedotov, V.A.; Zheludev, N.I. Toroidal dipolar excitation and macroscopic electromagnetic properties of metamaterials. Phys. Rev. B 2014, 89, 205112. [Google Scholar] [CrossRef]
- Wang, X.; Chen, D.; Ma, W.; You, S.; Zhou, M.; Wang, L.; Zhang, Q.; Luo, S.; Zhou, C. Tuning the magnetic toroidal dipole response in dielectric metasurfaces. J. Opt. Soc. Am. B 2023, 40, 560–566. [Google Scholar] [CrossRef]
- Maleki, J.; Fathi, D. Refractive index sensor based on fano-magnetic toroidal quadrupole resonance enabled by bound state in the continuum in all-dielectric metasurface. Sci. Rep. 2024, 14, 4110. [Google Scholar] [CrossRef] [PubMed]
- Evlyukhin, A.B.; Reinhardt, C.; Evlyukhin, E.; Chichkov, B.N. Multipole analysis of light scattering by arbitrary-shaped nanoparticles on a plane surface. J. Opt. Soc. Am. B 2013, 30, 2589–2598. [Google Scholar] [CrossRef]
- Guo, L.; Gao, Y. High-Q Resonances Induced by Toroidal Dipole Bound States in the Continuum in Terahertz Metasurfaces. Crystals 2025, 15, 96. [Google Scholar] [CrossRef]
- Ji, J.; Lv, X.; Li, C.; Yang, X.; Guo, Y. Asymmetric Orthogonal Metasurfaces Governed by Toroidal Dipole Bound States in the Continuum. Photonics 2023, 10, 1194. [Google Scholar] [CrossRef]
- Algorri, J.F.; Dmitriev, V.; Hernández-Figueroa, H.E.; Rodríguez-Cobo, L.; Dell’Olio, F.; Cusano, A.; López-Higuera, J.M.; Zografopoulos, D.C. Polarization-independent hollow nanocuboid metasurfaces with robust quasi-bound states in the continuum. Opt. Mater. 2024, 147, 114631. [Google Scholar] [CrossRef]
- Gupta, M.; Singh, R. Toroidal metasurfaces in a 2D flatland. Rev. Phys. 2020, 5, 100040. [Google Scholar] [CrossRef]
- Li, S.-Q.; Crozier, K.B. Origin of the anapole condition as revealed by a simple expansion beyond the toroidal multipole. Phys. Rev. B 2018, 97, 245423. [Google Scholar] [CrossRef]
- Zanganeh, E.; Evlyukhin, A.; Miroshnichenko, A.; Song, M.; Nenasheva, E.; Kapitanova, P. Anapole meta-atoms: Nonradiating electric and magnetic sources. Phys. Rev. Lett. 2021, 127, 096804. [Google Scholar] [CrossRef]
- Savinov, V.; Papasimakis, N.; Tsai, D.P.; Zheludev, N.I. Optical anapoles. Commun. Phys. 2019, 2, 69. [Google Scholar] [CrossRef]
- Miroshnichenko, A.E.; Evlyukhin, A.B.; Yu, Y.F.; Bakker, R.M.; Chipouline, A.; Kuznetsov, A.I.; Luk’yanchuk, B.; Chichkov, B.N.; Kivshar, Y.S. Nonradiating anapole modes in dielectric nanoparticles. Nat. Commun. 2015, 6, 8069. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Bozhevolnyi, S.I. Nonradiating anapole states in nanophotonics: From fundamentals to applications. Nanotechnology 2019, 30, 204001. [Google Scholar] [CrossRef] [PubMed]
- Gupta, M.; Singh, R. Toroidal versus Fano Resonances in High Q planar THz Metamaterials. Adv. Opt. Mater. 2016, 4, 2119–2125. [Google Scholar] [CrossRef]
- Basharin, A.A.; Chuguevsky, V.; Volsky, N.; Kafesaki, M.; Economou, E.N. Extremely high Q-factor metamaterials due to anapole excitation. Phys. Rev. B 2017, 95, 035104. [Google Scholar] [CrossRef]
- Totero Gongora, J.S.; Miroshnichenko, A.E.; Kivshar, Y.S.; Fratalocchi, A. Anapole nanolasers for mode-locking and ultrafast pulse generation. Nat. Commun. 2017, 8, 15535. [Google Scholar] [CrossRef]
- Wu, P.C.; Liao, C.Y.; Savinov, V.; Chung, T.L.; Chen, W.T.; Huang, Y.W.; Wu, P.R.; Chen, Y.H.; Liu, A.Q.; Zheludev, N.I.; et al. Optical anapole metamaterial. ACS Nano 2018, 12, 1920–1927. [Google Scholar] [CrossRef]
- Algorri, J.F.; Zografopoulos, D.C.; Ferraro, A.; García-Cámara, B.; Vergaz, R.; Beccherelli, R.; Sánchez-Pena, J.M. Anapole Modes in Hollow Nanocuboid Dielectric Metasurfaces for Refractometric Sensing. Nanomaterials 2019, 9, 30. [Google Scholar] [CrossRef]


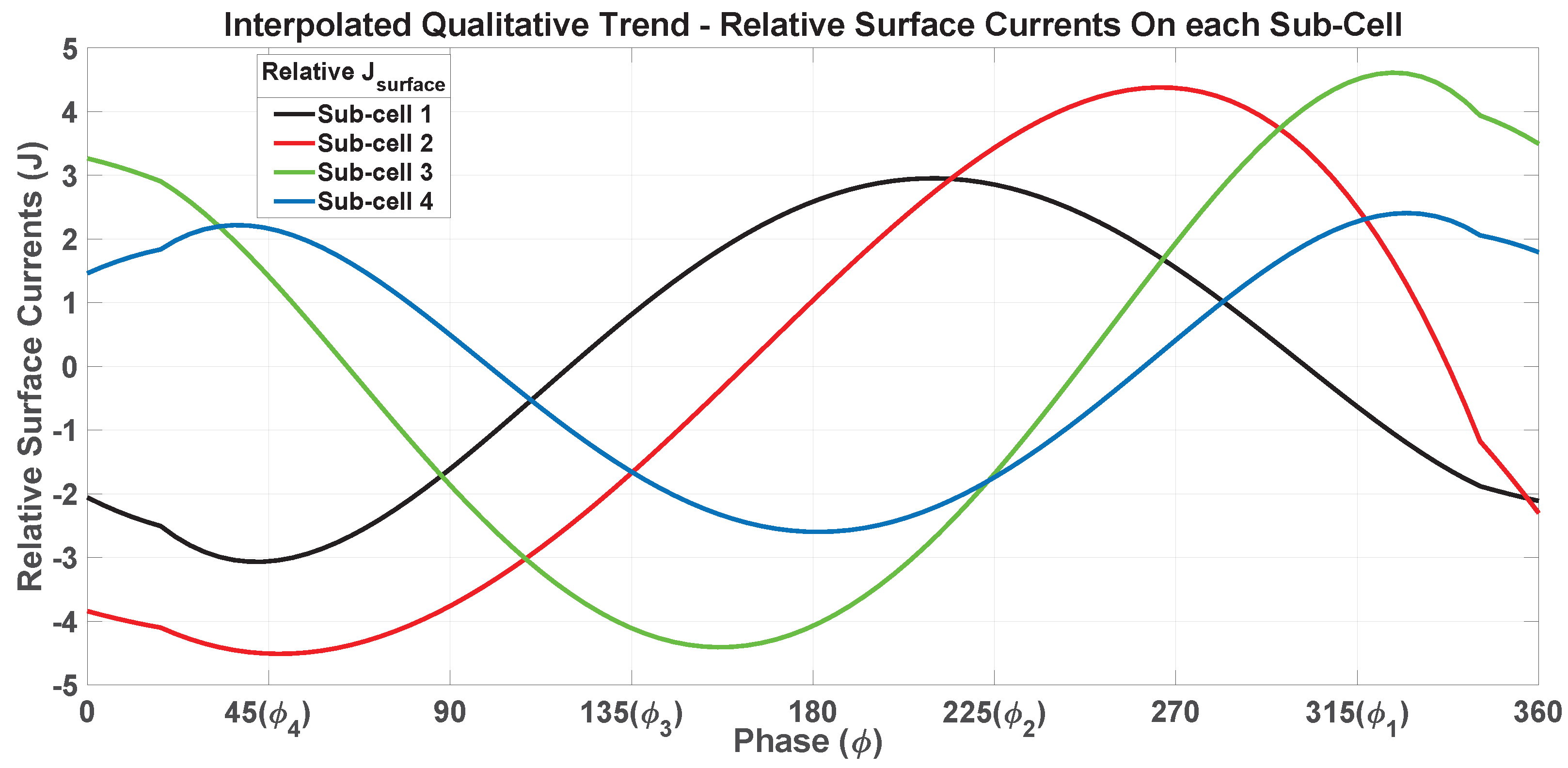


| No. | Phase | UC-1 | UC-2 | UC-3 | UC-4 | Ground Plane Surface Currents Mutual Coupling () | Remarks |
|---|---|---|---|---|---|---|---|
| 1. | J3 ← | J1 ← | J2 → | J4 → | |||
| 2. | J3 ← | J1 ← | J2 → | J4 → | |||
| 3. | J2 ← | J1 ← | J3 → | J4 → | |||
| 4. | J2 ← | J1 ← | 0 | J3 → | |||
| 5. | J3 ← | J1 ← | J2 ← | 0 | |||
| 6. | 0 | J2 ← | J1 ← | J3 ← | |||
| 7. | J4 → | J2 ← | J1(−max) ← | J3 ← | |||
| 8. | J3 → | 0 | J1 ← | J2 ← | |||
| 9. | J2 → | J4 → | J1 ← | J3 ← | |||
| 10. | J3 → | J1 → | J2 ← | J4 ← | |||
| 11. | J2 → | J1 → | J3 ← | J4 ← | |||
| 12. | J2 → | J1 → | 0 | J3 ← | |||
| 13. | J3 → | J1 → | J2 → | 0 | |||
| 14. | 0 | J2 → | J1 → | J3 → | |||
| 15. | J4 ← | J2 → | J1(+max) → | J3 → | |||
| 16. | J3 ← | 0 | J1 → | J2 → |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayaz, S.; Pirinoli, P. Multi-Polar Approach to Parasitic Suppression in Smart Electromagnetic Skins (SESs). Appl. Sci. 2025, 15, 11977. https://doi.org/10.3390/app152211977
Ayaz S, Pirinoli P. Multi-Polar Approach to Parasitic Suppression in Smart Electromagnetic Skins (SESs). Applied Sciences. 2025; 15(22):11977. https://doi.org/10.3390/app152211977
Chicago/Turabian StyleAyaz, Shahid, and Paola Pirinoli. 2025. "Multi-Polar Approach to Parasitic Suppression in Smart Electromagnetic Skins (SESs)" Applied Sciences 15, no. 22: 11977. https://doi.org/10.3390/app152211977
APA StyleAyaz, S., & Pirinoli, P. (2025). Multi-Polar Approach to Parasitic Suppression in Smart Electromagnetic Skins (SESs). Applied Sciences, 15(22), 11977. https://doi.org/10.3390/app152211977







