Non-Steady-State Coupled Model of Viscosity–Temperature–Pressure in Polymer Flooding Injection Wellbores
Abstract
1. Introduction
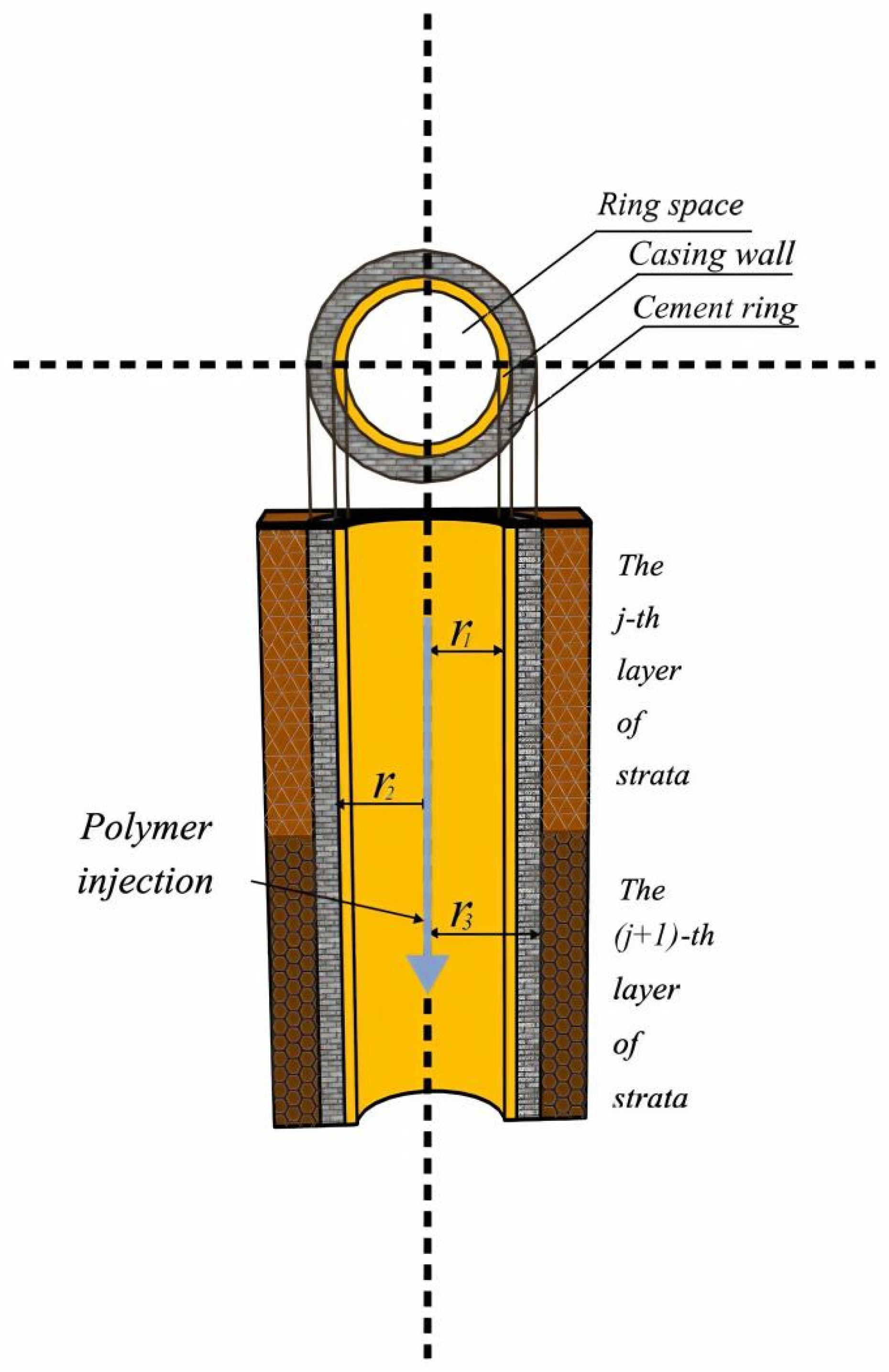
2. Structural Model Analysis
3. Mathematical Model Development
3.1. Model Assumptions
- Before the injection of fluid, the fluid inside the casing had reached a thermal equilibrium state with the formation.
- The temperature and pressure at the same horizontal section within the casing are the same.
- Throughout the entire construction process, the injection flow rate, injection temperature and injection pressure remained constant
- Below the surface lies the constant-temperature layer; after reaching a certain depth, the temperature of the strata changes linearly with depth.
- Apart from viscosity, the thermal physical parameters of the polymer solutions remain constant in the wellbore.
3.2. Wellbore Temperature–Pressure–Viscosity Coupling Model
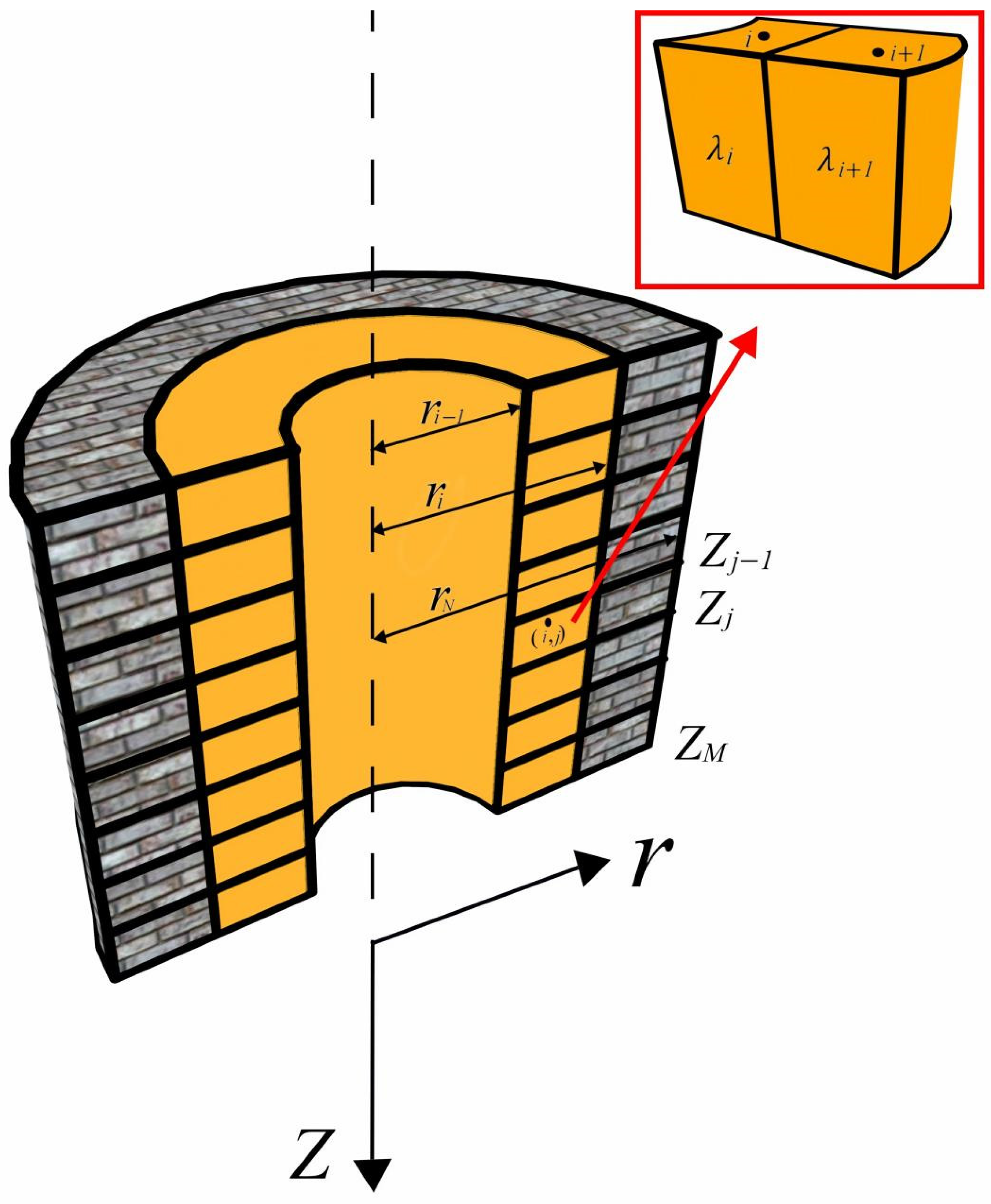
3.2.1. Casing Heat Transfer Model
- (1)
- In the axial direction, the net heat transfer caused by fluid flow, that is, the difference between the heat entering and the heat leaving.
- (2)
- In the radial direction, the heat generated by the convective heat transfer between the fluid and the casing wall.
- (3)
- According to the law of conservation of energy, within a unit of time, the difference between the heat flowing into and out of the control unit is equal to the increase in the energy of the control unit.
3.2.2. Pressure Drop Model
3.2.3. Other Parameters
- (1)
- Reynolds number
- (2)
- Prandtl number
- (3)
- Friction factor
- (4)
- Fluid velocity
- (5)
- Frictional Internal Heat Source
- (6)
- Casing Internal Convective Heat Transfer Coefficient
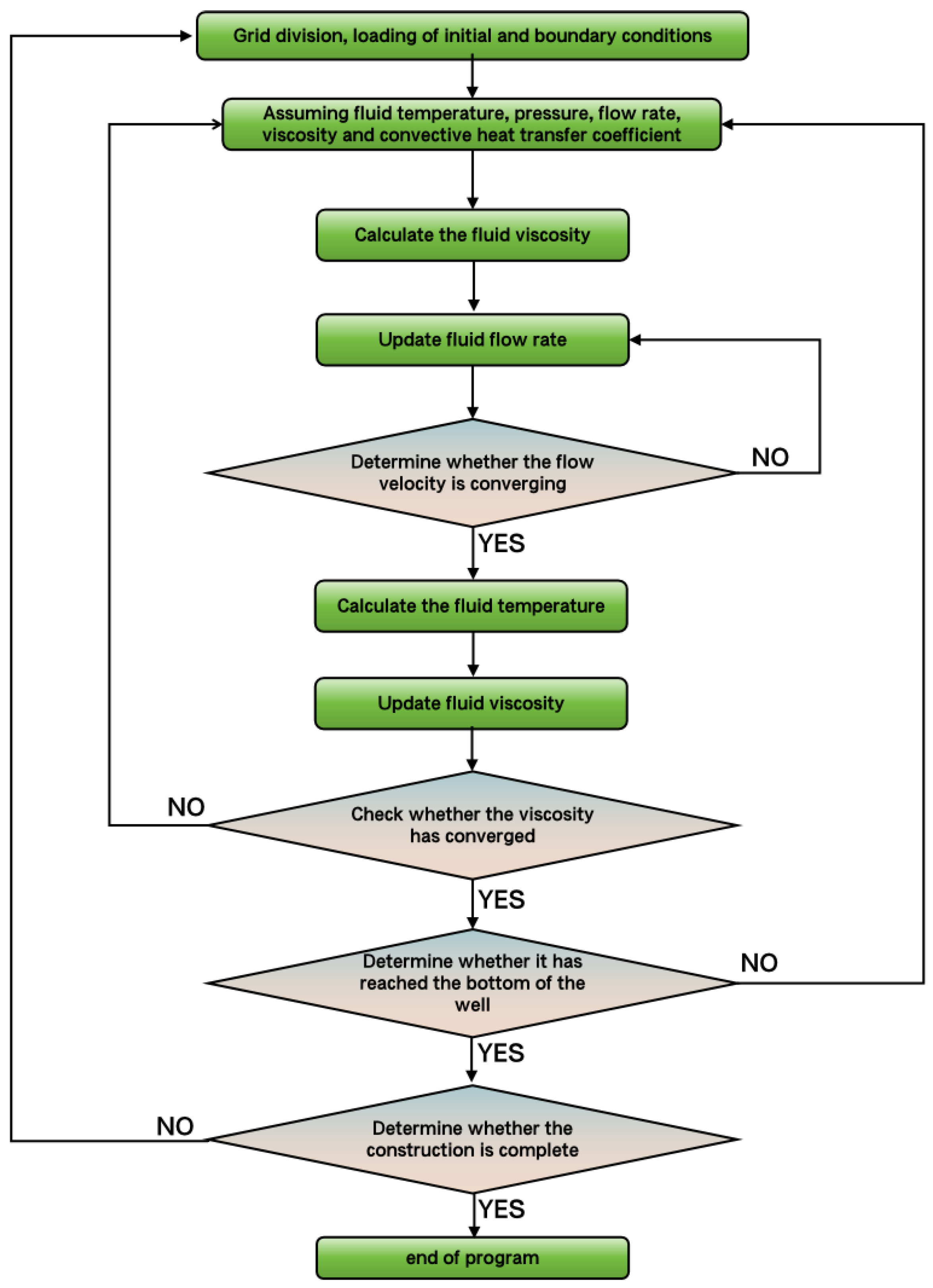
3.3. Model Solving Methodology
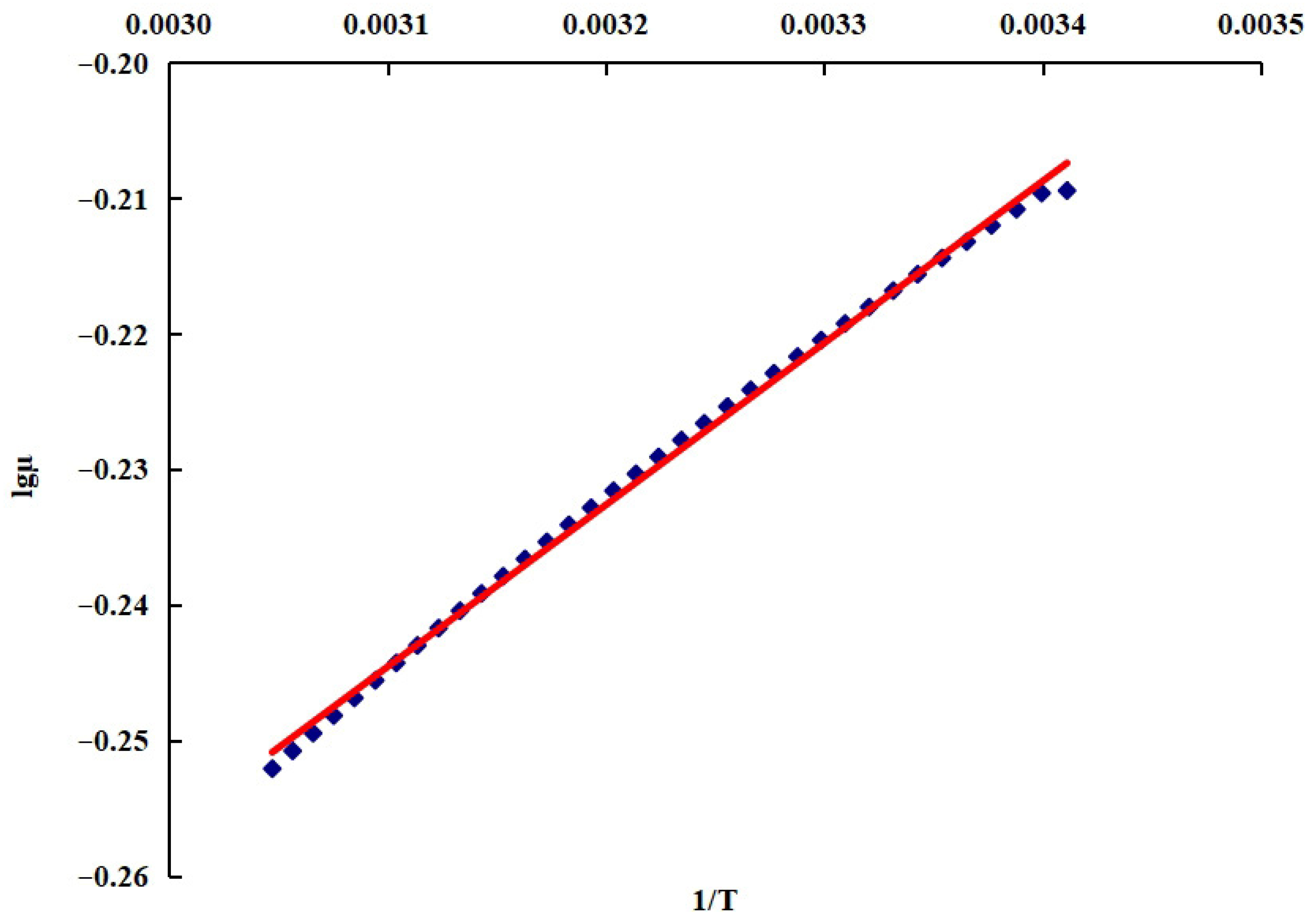
3.3.1. Viscosity–Temperature Model
3.3.2. Solution Methodology
3.3.3. Computational Solution Procedure
4. Analysis of Model Results
4.1. Case Study
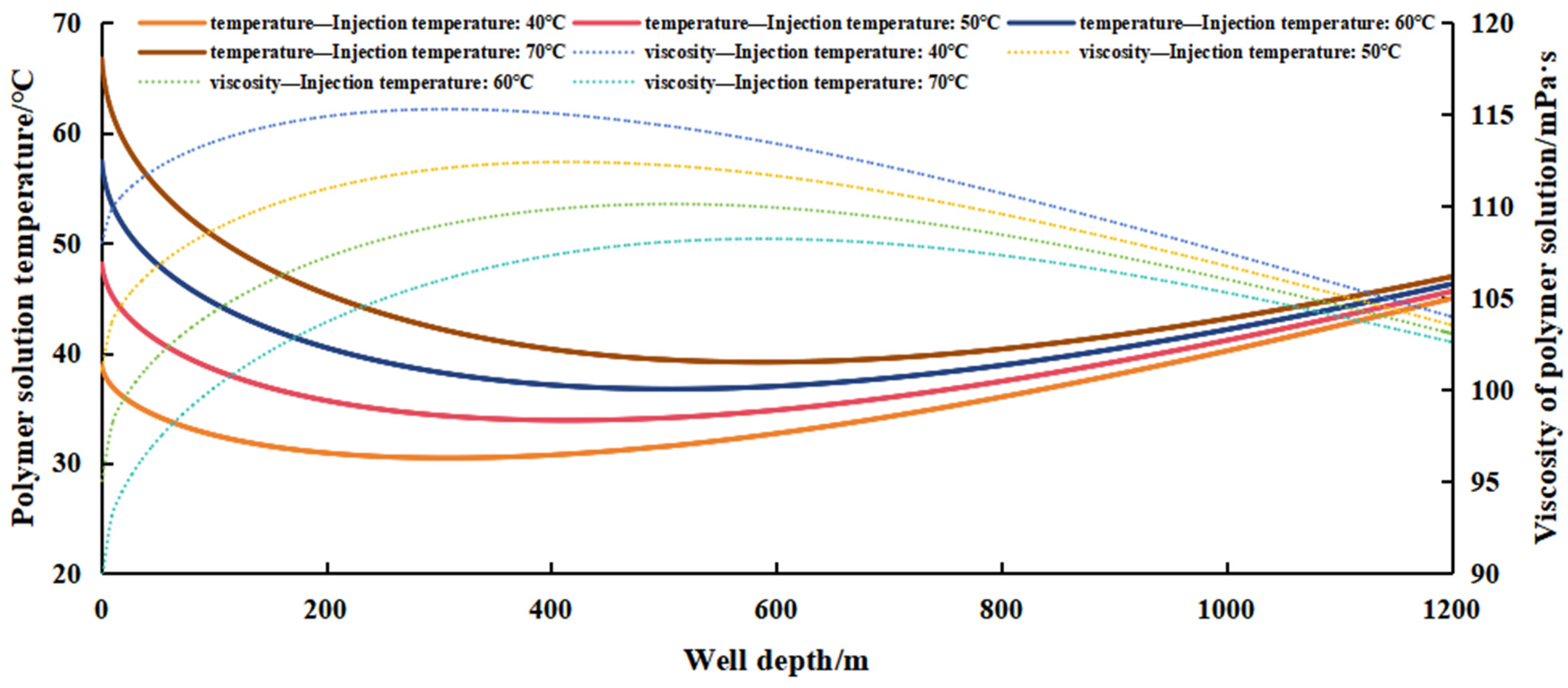
4.2. Effect of Injection Temperature on Polymer Flooding Wellbore
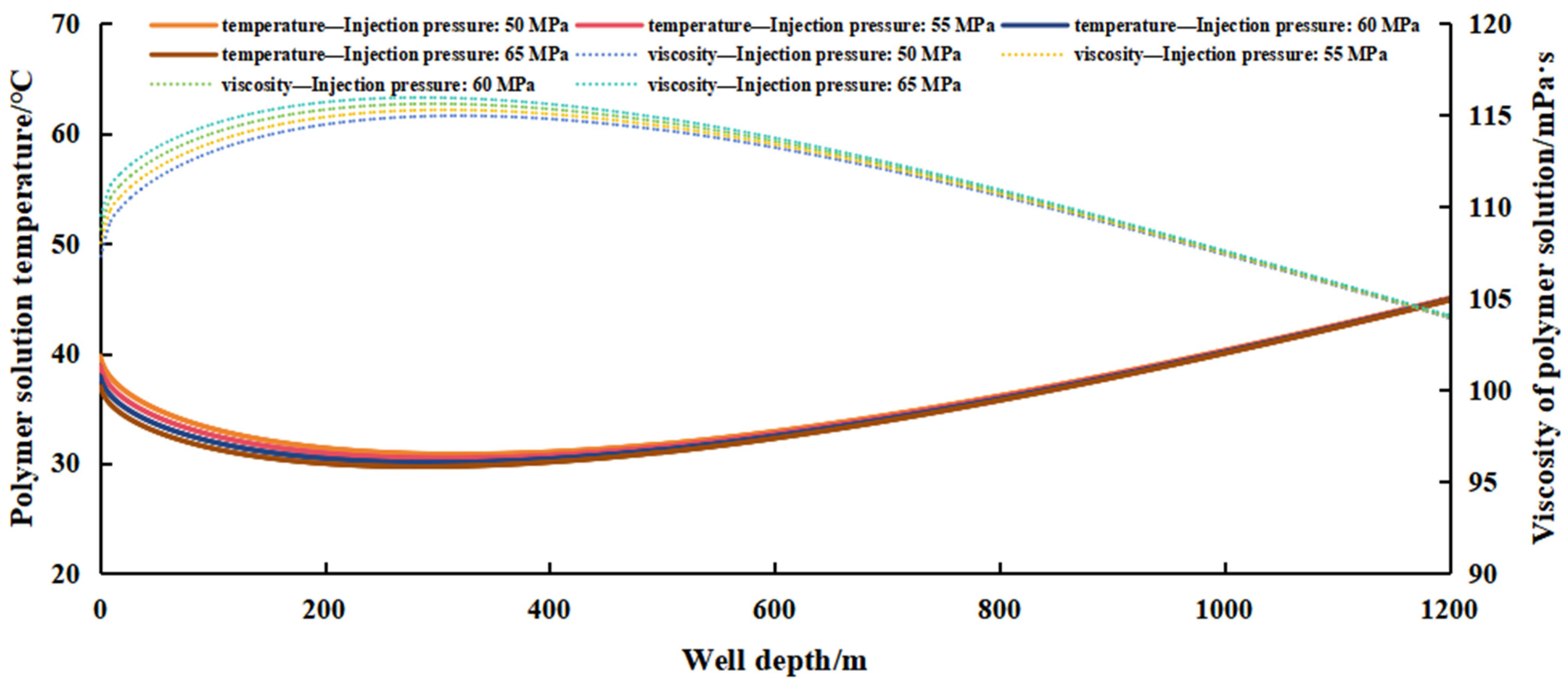
4.3. Effect of Injection Pressure on Polymer Flooding Wellbore
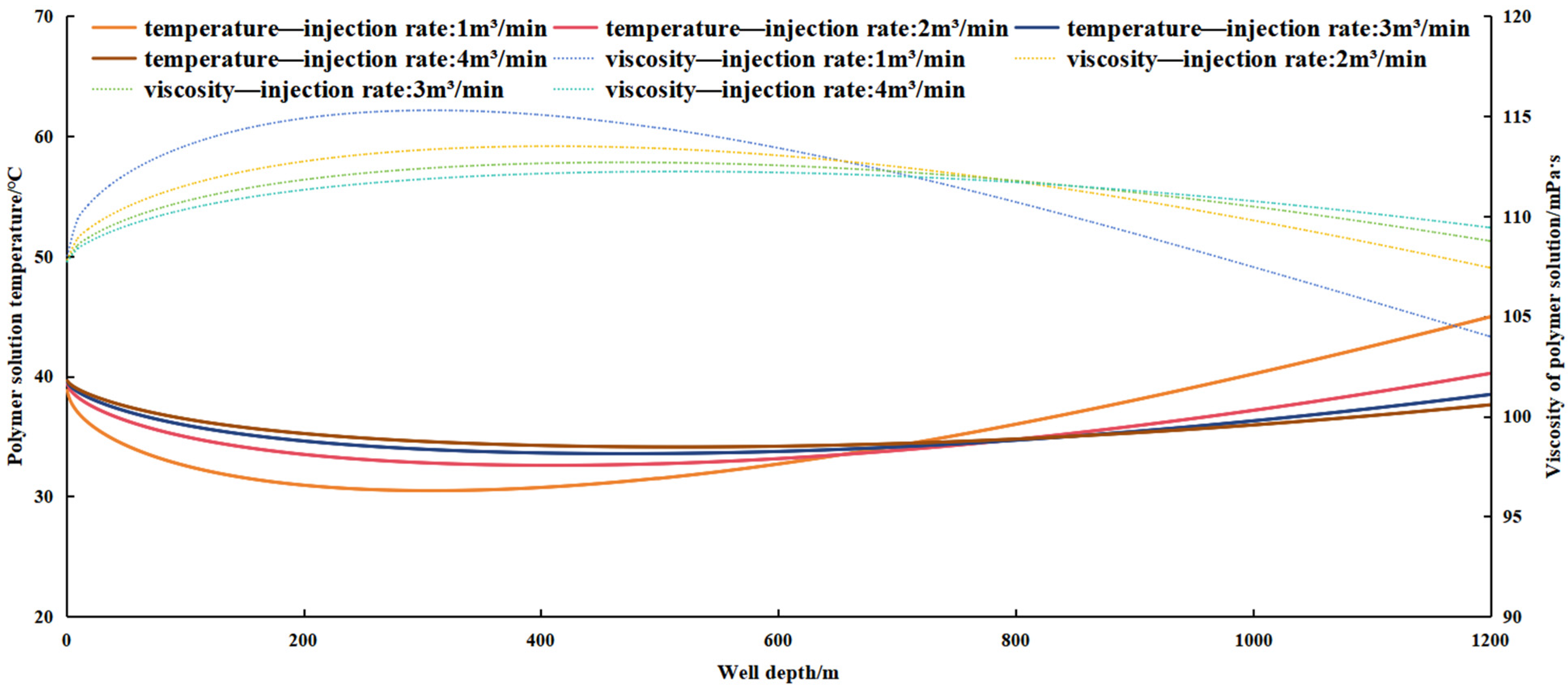
4.4. Effect of Injection Rate on Polymer Flooding Wellbore
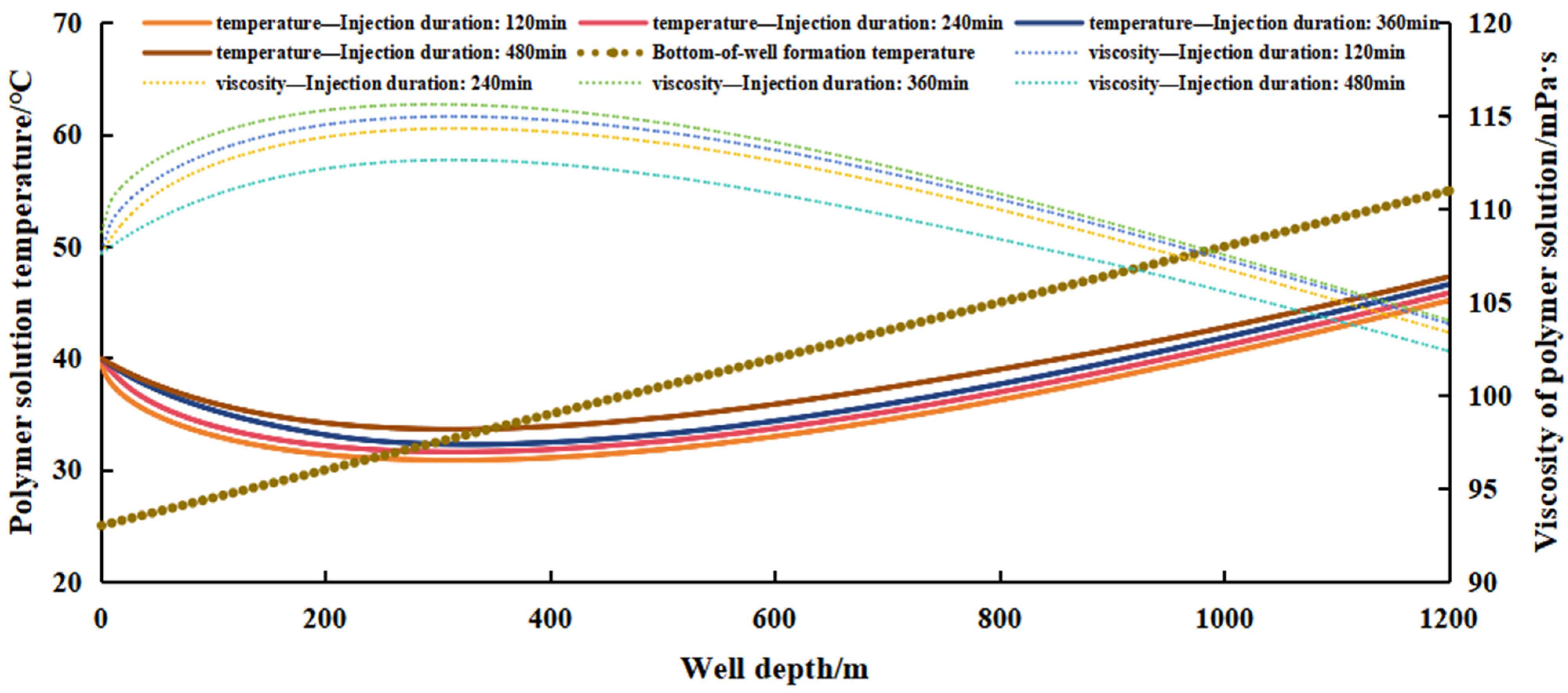
4.5. Effect of Injection Duration on Polymer Flooding Wellbore
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Feng, Y.; Li, B.; Han, P. Enhancing oil recovery from low-permeability reservoirs with a self-adaptive polymer: A proof-of-concept study. Fuel 2019, 251, 136–146. [Google Scholar] [CrossRef]
- Mishra, S.; Bera, A.; Mandal, A. Effect of polymer adsorption on permeability reduction in enhanced oil recovery. J. Pet. Eng. 2014, 2014, 395857. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y.; Sun, X.; Liu, Z.; Liu, J.; Liu, S. Investigation of polymer-assisted CO2 flooding to enhance oil recovery in low-permeability reservoirs. Polymers 2023, 15, 3886. [Google Scholar] [CrossRef]
- Zhang, X.; Li, B.; Pan, F.; Su, X.; Feng, Y. Enhancing oil recovery from low-permeability reservoirs with a thermoviscosifying water-soluble polymer. Molecules 2021, 26, 7468. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Y.; Liu, Y.; Liu, P. Enhancing oil recovery in low-permeability reservoirs using a low-molecular-weight amphiphilic polymer. Polymers 2024, 16, 1036. [Google Scholar] [CrossRef]
- Song, H.; Ghosh, P.; Bowers, A.; Niu, F.; Mohanty, K. Low-salinity polymer flood for enhanced oil recovery in low-permeability carbonates. SPE J. 2024, 29, 443–454. [Google Scholar] [CrossRef]
- Lu, G.; Bao, C.; Xie, K.; Cao, W.; Liu, Y.; Zhang, Y.; Wang, X.; Zhang, J. Enhanced oil recovery mechanisms of polymer flooding in a heterogeneous oil reservoir. Pet. Explor. Dev. 2021, 48, 169–178. [Google Scholar] [CrossRef]
- Zhang, X.; Fan, Z.; Cai, L.; Fu, Y.; Liu, J.; Liu, Q.; Tong, Q.; Qiao, S.; Sun, A. Polyacrylamide structural instability and degradation induced by nanobubbles: A molecular simulation study. Phys. Fluids 2025, 37, 026601. [Google Scholar] [CrossRef]
- Juárez, J.L.; Bertin, H.; Omari, A.; Romero, C.; Bourdarot, G.; Jouenne, S.; Morel, D.; Neillo, V. Polymer Injection for EOR: Influence of Mobility Ratio and Slug Size on Final Oil Recovery. In SPE Europec Featured at EAGE Conference and Exhibition; SPE: London, UK, 2020; pp. 1–9. [Google Scholar] [CrossRef]
- Firozjaii, A.M.; Saghafi, H.R. Review on chemical enhanced oil recovery using polymer flooding: Fundamentals, experimental and numerical simulation. Petroleum 2020, 6, 115–122. [Google Scholar] [CrossRef]
- Davarpanah, A. Parametric Study of Polymer-Nanoparticles-Assisted Injectivity Performance for Axisymmetric Two-Phase Flow in EOR Processes. Nanomaterials 2020, 10, 1818. [Google Scholar] [CrossRef] [PubMed]
- Aitkulov, A.; Mohanty, K.K. Investigation of alkaline-surfactant-polymer flooding in a quarter five-spot sandpack for viscous oil recovery. J. Pet. Sci. Eng. 2019, 175, 706–718. [Google Scholar] [CrossRef]
- Tie, L.; Yu, M.; Li, X.; Liu, W.; Zhang, B.; Chang, Z.; Zheng, Y. Research on polymer solution rheology in polymer flooding for Qikou reservoirs in a Bohai Bay oilfield. J. Pet. Explor. Prod. Technol. 2019, 9, 703–715. [Google Scholar] [CrossRef]
- Yang, L.; Li, B.; Chen, X.; Yu, L.; Jing, F.-M.; Zhang, D. Experimental and numerical study of the rheological characteristics and flow law of water-based drilling fluids in high-temperature and high-pressure wellbores. J. Hydrodyn. 2024, 36, 954–967. [Google Scholar] [CrossRef]
- Ramirez, A. Numerical Investigation of Polymer Injection Effects on Geomechanical Reservoir Properties During Enhanced Oil Recovery. 2017. Available online: https://hdl.handle.net/11124/172043 (accessed on 1 November 2025).
- Magzoub, M.I.; Salehi, S.; Hussein, I.A.; Nasser, M.S. Loss circulation in drilling and well construction: The significance of applications of crosslinked polymers in wellbore strengthening: A review. J. Pet. Sci. Eng. 2020, 185, 106653. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, S.L.; Xie, H.; Jiang, Y.; Cheng, S.Q.; Zhang, J. Dynamic characterization of viscoelasticity during polymer flooding: A two-phase numerical well test model and field study. Pet. Sci. 2025, 22, 2493–2501. [Google Scholar] [CrossRef]
- Sandiford, B.B. Laboratory and field studies of water floods using polymer solutions to increase oil recoveries. J. Pet. Technol. 1964, 16, 917–922. [Google Scholar] [CrossRef]
- Smith, J.E. Closing the lab-field gap: A look at near-wellbore flow regimes and performance of 57 field projects. In Proceedings of the SPE Improved Oil Recovery Conference, Tulsa, OK, USA, 17–19 April 1994; Society of Petroleum Engineers: Richardson, TX, USA, 1994. SPE-27774-MS. [Google Scholar] [CrossRef]
- Muruaga, E.; Flores, M.; Norman, C.; Romero, J.L. Combining bulk gels and colloidal dispersion gels for improved volumetric sweep efficiency in a mature waterflood. In Proceedings of the SPE Improved Oil Recovery Conference, Tulsa, OK, USA, 24–28 April 2008; Society of Petroleum Engineers: Richardson, TX, USA, 2008. SPE-113334-MS. [Google Scholar] [CrossRef]
- Dobrynin, A.V.; Sayko, R.; Colby, R.H. Viscosity of polymer solutions and molecular weight characterization. ACS Macro Lett. 2023, 12, 773–779. [Google Scholar] [CrossRef] [PubMed]
- Pearson, J.R.A.; Tardy, P.M.J. Models for flow of non-Newtonian and complex fluids through porous media. J. Non-Newton. Fluid Mech. 2002, 102, 447–473. [Google Scholar] [CrossRef]
- Sun, G.; Li, D.; Zhang, D.; Xu, T.H. Study on improving viscosity of polymer solution based on complex reaction. IOP Conf. Ser. Mater. Sci. Eng. 2018, 369, 012045. [Google Scholar] [CrossRef]
- Yang, Y.; Shu, Z.; Ye, Z.; Wang, X.; Wang, Z.; Liang, S. An improved study of near-well zone flooding for polymer solution through the mechanical shearing and Forchheimer flow simulation. Mater. Today Commun. 2024, 38, 107634. [Google Scholar] [CrossRef]
- Yang, W.; Yu, H.; Fan, N. Transient pressure analysis of polymer flooding fractured wells with oil-water two-phase flow. Pet. Explor. Dev. 2023, 50, 175–182. [Google Scholar] [CrossRef]
- Konyukhov, V.M.; Konyukhov, I.V.; Chekalin, A.N. Numerical modeling and parallel computations of heat and mass transfer during polymer flooding of non-uniform oil reservoir developing by system of producing and injecting wells. In Proceedings of the Journal of Physics: Conference Series, Moscow, Russia, 15–17 October 2019; IOP Publishing: Bristol, UK, 2019; Volume 1158, p. 032018. [Google Scholar] [CrossRef]
- Peng, L.; Han, G.; Chen, Z.; Pagou, A.L.; Zhu, L.; Abdoulaye, A.M. Dynamically coupled reservoir and wellbore simulation research in two-phase flow systems: A critical review. Processes 2022, 10, 1778. [Google Scholar] [CrossRef]
- Guo, J.; Zeng, J. Unsteady-state temperature-pressure coupling model for fractured wellbores under supercritical carbon dioxide pressure. Chin. J. Pet. 2015, 36, 203–209. [Google Scholar] [CrossRef]
- Aarvik, A.; Djuve, S.; Valle, A. Steady state calculations of wellbore and wellhead temperatures. In Proceedings of the BHR International Conference on Multiphase Production Technology, Edinburgh, UK, 23–25 June 2009; BHR Group: Cranfield, UK, 2009. BHR-2009-E1. [Google Scholar]
- Hasan, A.R.; Kabir, C.S.; Wang, X. A robust steady-state model for flowing-fluid temperature in complex wells. SPE Prod. Oper. 2009, 24, 269–276. [Google Scholar] [CrossRef]
- Abdelhafiz, M.M.; Hegele, L.A., Jr.; Oppelt, J.F. Numerical transient and steady state analytical modeling of the wellbore temperature during drilling fluid circulation. J. Pet. Sci. Eng. 2020, 186, 106775. [Google Scholar] [CrossRef]
- Zhang, S.; Fu, J.; Peng, C.; Su, Y.; Zhang, H.; Yang, M. The analysis of transient temperature in the wellbore of a deep shale gas horizontal well. Processes 2024, 12, 1402. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, N.; Liang, H.; Wei, M.; Ma, B.; Qiu, D. The Wellbore Temperature and Pressure Behavior during the Flow Testing of Ultra-Deepwater Gas Wells. Fluid. Dyn. Mater. Proc. 2024, 20, 2523–2540. [Google Scholar] [CrossRef]
- Tang, L.; Luo, P. The effect of the thermal stress on wellbore stability. In Proceedings of the SPE Oil and Gas India Conference and Exhibition, New Delhi, India, 17–19 February 1998. SPE-39505-MS. [Google Scholar] [CrossRef]
- Yu, S.; Du, A.; Ye, C.; Xiang, J.; Chen, Y.; Guo, Y.; Shen, L. Temperature and Pressure Profiles during Prolonged Working Fluid Injection in Wellbores: Mechanisms and Key Influencing Factors. Fluid. Dyn. Mater. Proc. 2025, 21, 1623–1639. [Google Scholar] [CrossRef]
- Wei, W.; Wang, M.; Cheng, J.; Hu, Y.; Li, Y.; Zheng, J. Digital twinning of temperature fields for modular multilayer multiphase pipeline structures. Digital Twin. 2025, 4, 2530307. [Google Scholar] [CrossRef]
- Chen, N.H. An explicit equation for friction factor in pipe. Ind. Eng. Chem. Fundam. 1979, 18, 296–297. [Google Scholar] [CrossRef]
- Huang, W.X. Engineering Fluid Mechanics; Chemical Industry Press: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Jia, J.; Sogabe, T.; Li, S. A generalized symbolic Thomas algorithm for the solution of opposite-bordered tridiagonal linear systems. J. Comput. Appl. Math. 2015, 290, 423–432. [Google Scholar] [CrossRef]
- Yang, Z.; Yan, W.; Lv, W.; Tang, Q.; Duan, J.; Li, M.; Zhou, P.; Li, J.; Yang, T. Study on the phase state and temperature-pressure distribution of CO2 injection wellbore and its effect on tubing stress conditions. Geoenergy Sci. Eng. 2024, 241, 213155. [Google Scholar] [CrossRef]

| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Reservoir depth | 1200 m | Fluid Specific Heat Capacity | 4.2 J/(kg·K) |
| Total construction time | 240 min | Inner Diameter Ratio (Dimensionless) | 1.6 |
| Injection rate | 0.05 m3/min | Casing Inner Diameter | 0.0809 m |
| Injection temperature | 40 °C | Casing Outer Diameter | 0.0909 m |
| Injection pressure | 60 MPa | Cement Sheath Outer Diameter | 0.1209 m |
| Average Casing Roughness | 0.0000153 m | Casing Density | 7800 kg/m3 |
| Geothermal Gradient | 0.03 °C | Cement Sheath Density | 1900 kg/m3 |
| Isothermal Point Depth | 20 m | Specific Heat Capacity | 445.5 J/(kg·K) |
| Isothermal Point Temperature | 25 °C | Specific Heat Capacity | 880.6 J/(kg·K) |
| Fluid Density | 1000 kg/m3 | Casing Thermal Conductivity | 45 W/(m·K) |
| Fluid Thermal Conductivity | 0.59 W/(m·K) | Cement Sheath Thermal Conductivity | 1.2 W/(m·K) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Fan, J.; Hao, M.; Zhang, X.; Liu, F.; Zhang, X. Non-Steady-State Coupled Model of Viscosity–Temperature–Pressure in Polymer Flooding Injection Wellbores. Appl. Sci. 2025, 15, 11831. https://doi.org/10.3390/app152111831
Huang Y, Fan J, Hao M, Zhang X, Liu F, Zhang X. Non-Steady-State Coupled Model of Viscosity–Temperature–Pressure in Polymer Flooding Injection Wellbores. Applied Sciences. 2025; 15(21):11831. https://doi.org/10.3390/app152111831
Chicago/Turabian StyleHuang, Yutian, Jiawei Fan, Ming Hao, Xinlei Zhang, Fuzhen Liu, and Xuesong Zhang. 2025. "Non-Steady-State Coupled Model of Viscosity–Temperature–Pressure in Polymer Flooding Injection Wellbores" Applied Sciences 15, no. 21: 11831. https://doi.org/10.3390/app152111831
APA StyleHuang, Y., Fan, J., Hao, M., Zhang, X., Liu, F., & Zhang, X. (2025). Non-Steady-State Coupled Model of Viscosity–Temperature–Pressure in Polymer Flooding Injection Wellbores. Applied Sciences, 15(21), 11831. https://doi.org/10.3390/app152111831





