B-Value Spatiotemporal Changes and Aftershock Correlation Prior to the Mwg 7.1 Dingri Earthquake in Southern Tibet: Implications for Land Deformation and Seismic Risk
Abstract
1. Introduction
2. Data and Methods
2.1. Seismic Data
2.2. Magnitude Scale Adoption
2.3. b Value Calculation Method
2.4. Granger Causality Analysis for Seismic Interaction Networks
2.4.1. Data Preparation: From Catalog to Multivariate Time Series
2.4.2. Model Estimation: Vector Autoregression (VAR)
2.4.3. Causality Testing and Network Construction
3. Results
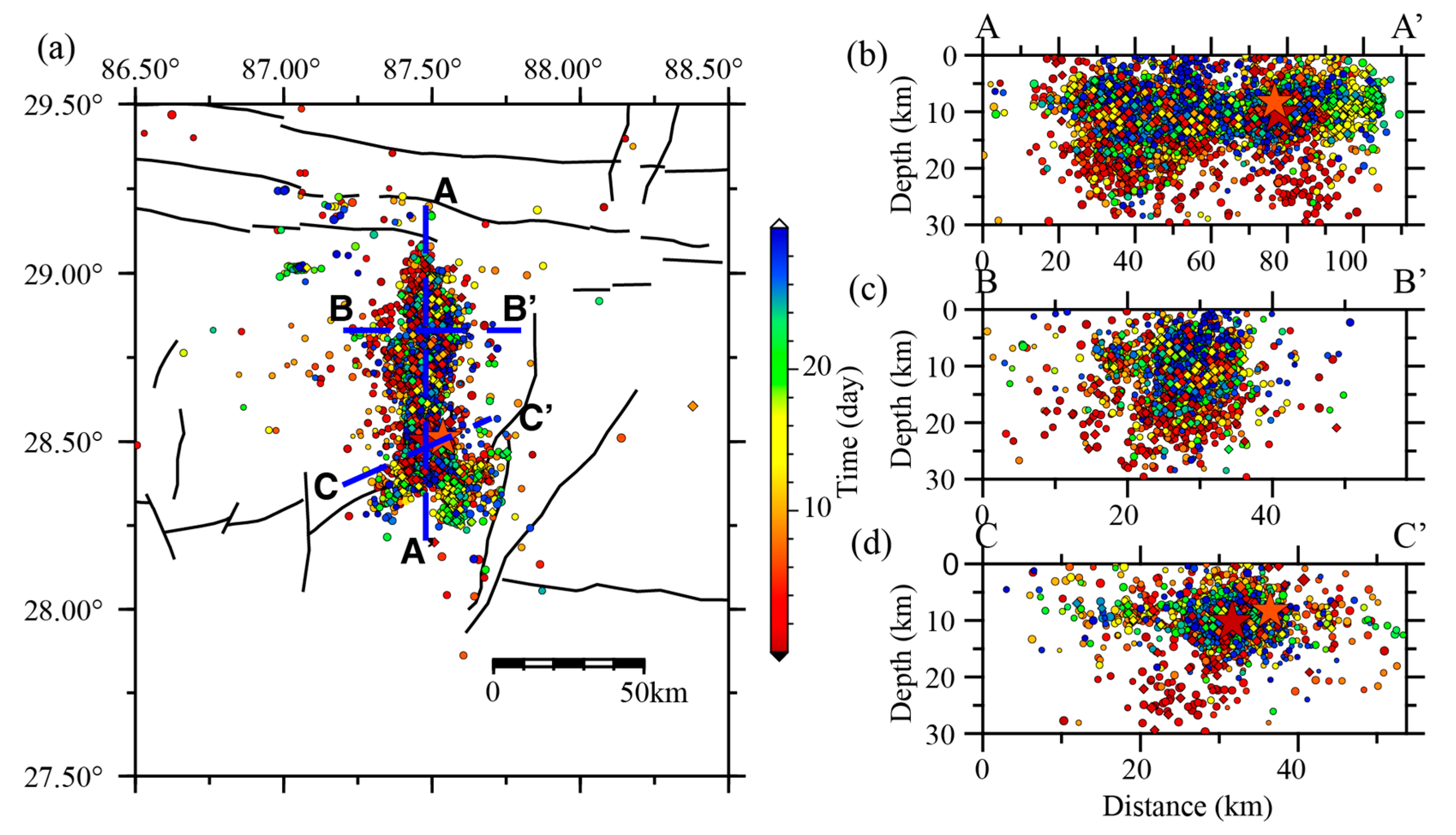
3.1. Earthquake Relocation and Aftershock Distribution
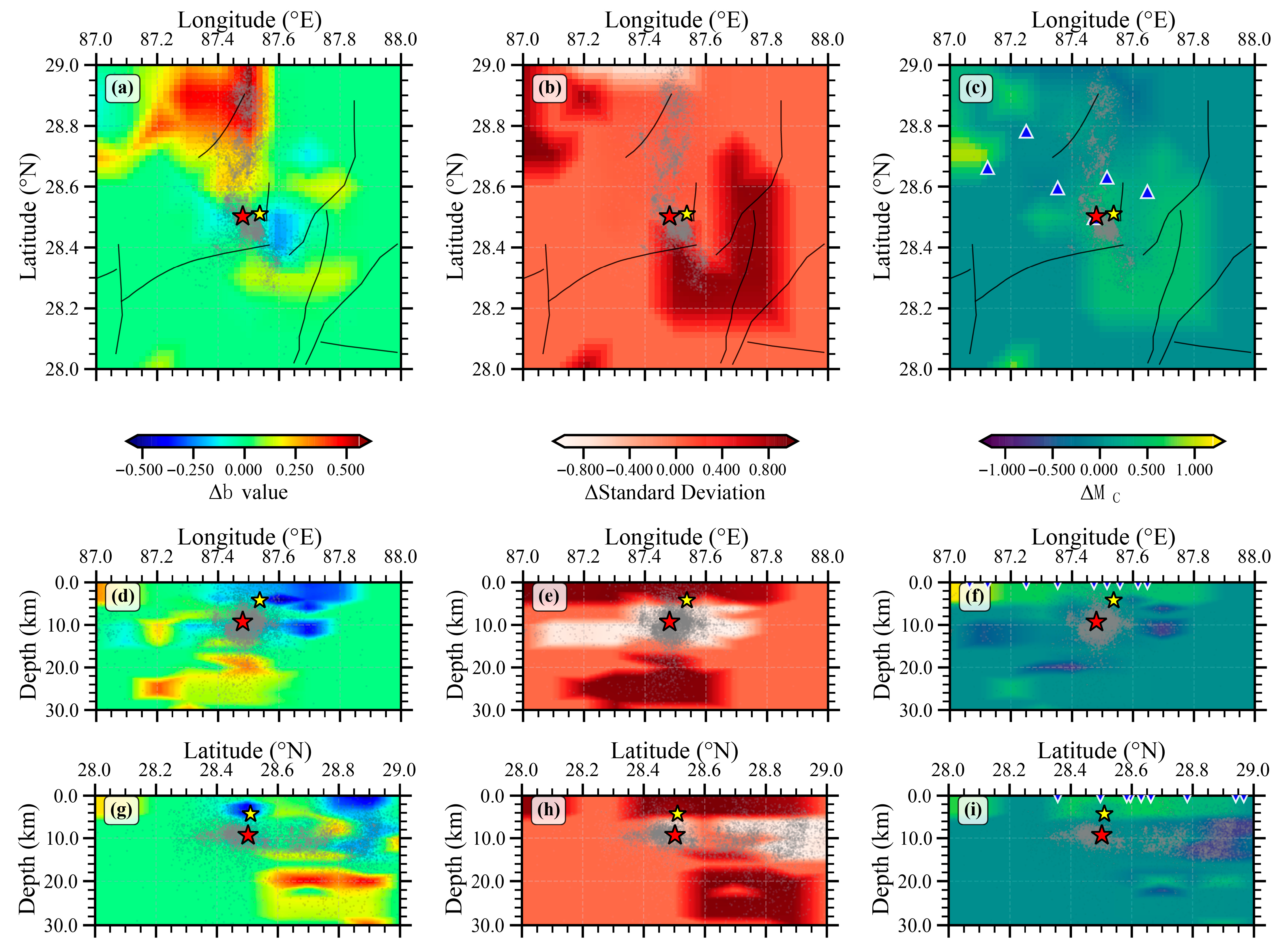
3.2. Spatiotemporal Variation in the b Value
3.3. Evolution of Seismic Interaction Networks
4. Discussion
4.1. Spatiotemporal Evolution of b Values and Earthquake Occurrence
4.2. Dynamic Evolution of Seismic Interaction Networks
4.3. Physical Interpretation: From System-Wide Adjustment to Pre-Failure Lock-In
4.4. Integrated Validation Through Aftershock Sequence Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ishimoto, M. Observation of Earthquakes Registered with the Microseissmograph Constructed Recently (I). Bull. Earthq. Res. Inst. Univ. Tokyo 1939, 17, 443. [Google Scholar]
- Gutenberg, B.; Richter, C. Seismicity of the Earth and Associated Phenomena; Princeton University Press: Princeton, NJ, USA, 1954; ISBN 0-598-97720-1. [Google Scholar]
- Lay, T.; Wallace, T.C. Modern Global Seismology; Elsevier: Amsterdam, The Netherlands, 1995; Volume 58, ISBN 0-08-053671-9. [Google Scholar]
- Ogata, Y.; Katsura, K. Analysis of Temporal and Spatial Heterogeneity of Magnitude Frequency Distribution Inferred from Earthquake Catalogues. Geophys. J. Int. 1993, 113, 727–738. [Google Scholar] [CrossRef]
- Schorlemmer, D.; Wiemer, S.; Wyss, M. Earthquake Statistics at Parkfield: 1. Stationarity of b Values. J. Geophys. Res. Solid Earth 2004, 109, B12307. [Google Scholar] [CrossRef]
- Sanchez, J.J.; McNutt, S.R.; Power, J.A.; Wyss, M. Spatial Variations in the Frequency-Magnitude Distribution of Earthquakes at Mount Pinatubo Volcano. Bull. Seismol. Soc. Am. 2004, 94, 430–438. [Google Scholar] [CrossRef]
- Wiemer, S.; McNutt, S.R. Variations in the Frequency-magnitude Distribution with Depth in Two Volcanic Areas: Mount St. Helens, Washington, and Mt. Spurr, Alaska. Geophys. Res. Lett. 1997, 24, 189–192. [Google Scholar] [CrossRef]
- Wyss, M.; Stefansson, R. Nucleation Points of Recent Mainshocks in Southern Iceland, Mapped by b values. Bull. Seismol. Soc. Am. 2006, 96, 599–608. [Google Scholar] [CrossRef]
- Wyss, M.; Schorlemmer, D.; Wiemer, S. Mapping Asperities by Minima of Local Recurrence Time: San Jacinto-Elsinore Fault Zones. J. Geophys. Res. Solid Earth 2000, 105, 7829–7844. [Google Scholar] [CrossRef]
- Smith, W.D. The b-Value as an Earthquake Precursor. Nature 1981, 289, 136–139. [Google Scholar] [CrossRef]
- Schorlemmer, D.; Wiemer, S.; Wyss, M. Variations in Earthquake-Size Distribution across Different Stress Regimes. Nature 2005, 437, 539–542. [Google Scholar] [CrossRef] [PubMed]
- Jiang, C.; Jiang, C.; Yin, F.; Zhang, Y.; Bi, J.; Long, F.; Si, Z.; Yin, X. A New Method for Calculating B-Value of Time Sequence Based on Data-Driven (TbDD): A Case Study of the 2021 Yangbi MS 6.4 Earthquake Sequence in Yunnan. Chin. J. Geophys. 2021, 64, 3126–3134. (In Chinese) [Google Scholar]
- Yin, F.; Jiang, C. Enhanced B-Value Time-Series Calculation Method Using Data-Driven Approach. Geophys. J. Int. 2024, 236, 78–87. [Google Scholar] [CrossRef]
- Xu, X.; Wang, S.; Cheng, J.; Wu, X. Shaking the Tibetan Plateau: Insights from the MW 7.1 Dingri earthquake and its implications for active fault mapping and disaster mitigation. NPJ Nat. Hazards 2025, 2, 16. [Google Scholar] [CrossRef]
- Yin, X.; Zhang, X.; Cai, R.; Wang, H.; Liu, F. Fast 1-D Velocity Optimization Inversion to 3D Velocity Imaging: A Case Study of Sichuan Maerkang Earthquake Swarm in 2022. Sustainability 2022, 14, 15909. [Google Scholar] [CrossRef]
- Scholz, C.H. On the stress dependence of the earthquake b value. Geophys. Res. Lett. 2015, 42, 1399–1402. [Google Scholar] [CrossRef]
- Goebel, T.H.W.; Schorlemmer, D.; Becker, T.W.; Dresen, G.; Sammis, C.G. Acoustic emissions document stress changes over many seismic cycles in stick-slip experiments. Geophys. Res. Lett. 2017, 44, 2967–2974. [Google Scholar] [CrossRef]
- Bi, J.; Cao, F.; Ma, Y. Seismicity characteristics based on the spatiotemporal ETAS model in North China from the perspective of different cut-off magnitude. PLoS ONE 2025, 20, e0327295. [Google Scholar] [CrossRef]
- Yin, X.; Jiang, C.; Yin, F.; Zhai, H.; Zheng, Y.; Wu, H.; Liu, X.; Li, J. Assessment and optimization of maximum magnitude forecasting models for induced seismicity in enhanced geothermal systems: The Gonghe EGS project in Qinghai, China. Tectonophysics 2024, 886, 230438. [Google Scholar] [CrossRef]
- Granger, C.W. Investigating Causal Relations by Econometric Models and Cross-Spectral Methods. Econom. J. Econom. Soc. 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Waldhauser, F.; Ellsworth, W.L. A Double-Difference Earthquake Location Algorithm: Method and Application to the Northern Hayward Fault, California. Bull. Seismol. Soc. Am. 2000, 90, 1353–1368. [Google Scholar] [CrossRef]
- Cai, M.; Chen, J.; Yin, X. Three-dimensional velocity structure and relocation of earthquakes in Luding area, Sichuan Province. China Earthq. Eng. J. 2023, 45, 552–564. (In Chinese) [Google Scholar]
- Yin, X.; Wang, S.; Liang, X.; Ma, G. Impact of fault complexity on aftershock decay: A case study of the Wushi MS 7.1 earthquake. China Earthq. Eng. J. 2024, 46, 965–972+991. (In Chinese) [Google Scholar]
- Xin, H.; Zhang, H.; Kang, M.; He, R.; Gao, L.; Gao, J. High-resolution Lithospheric Velocity Structure of Continental China by Double-difference Seismic Travel-time Tomography. Seismol. Res. Lett. 2019, 90, 229–241. [Google Scholar] [CrossRef]
- China Earthquake Administration. Earthquake Cataloging Specifications (DB/T 66-2016); Seismological Press: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Purcaru, G.; Berckhemer, H. A magnitude scale for very large earthquakes. Tectonophysics 1978, 49, 189–198. [Google Scholar] [CrossRef]
- Hanks, T.C.; Kanamori, H. A moment magnitude scale. J. Geophys. Res. 1979, 84, 2348–2350. [Google Scholar] [CrossRef]
- Das, A.; Das, T.; Chaudhuri, C.H.; Choudhury, D. Integrated study on buried pipelines, co-seismic landslides, and magnitude conversion for 2023 Türkiye earthquake. Eng. Geol. 2024, 337, 107599. [Google Scholar] [CrossRef]
- Thatcher, W.; Hanks, T.C. Source parameters of southern California earthquakes. J. Geophys. Res. 1973, 78, 8547–8576. [Google Scholar] [CrossRef]
- Hutton, L.K.; Boore, D.M. The ML scale in southern California. Bull. Seismol. Soc. Am. 1987, 77, 2074–2094. [Google Scholar] [CrossRef]
- Choy, G.L.; Boatwright, J.L. Global patterns of radiated seismic energy and apparent stress. J. Geophys. Res. 1995, 100, 18205–18228. [Google Scholar] [CrossRef]
- Ristau, J.; Rogers, G.C.; Cassidy, J.F. Moment magnitude-local magnitude calibration for earthquakes in western Canada. Bull. Seismol. Soc. Am. 2003, 93, 2994–3000. [Google Scholar] [CrossRef]
- Keir, D.; Hamling, I.J.; Ayele, A.; Calais, E.; Ebinger, C.; Wright, T.J.; Jacques, E.; Mohamed, K.; Hammond, J.O.; Belachew, M. Evidence for focused magmatic accretion at segment centers from lateral dike injections captured beneath the Red Sea rift in Afar. Geology 2009, 37, 59–62. [Google Scholar] [CrossRef]
- Kanamori, H. The energy release in great earthquakes. J. Geophys. Res. 1977, 82, 2981–2987. [Google Scholar] [CrossRef]
- Das, R.; Sharma, M.L.; Wason, H.R.; Choudhury, D.; Gonzalez, G. A seismic moment magnitude scale. Bull. Seismol. Soc. Am. 2019, 109, 1542–1555. [Google Scholar] [CrossRef]
- Kanamori, H. Magnitude scale and quantification of earthquakes. Tectonophysics 1983, 93, 185–199. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Magnitude and energy of earthquakes. Nature 1955, 176, 795. [Google Scholar] [CrossRef]
- Mignan, A.; Woessner, J. Estimating the Magnitude of Completeness for Earthquake Catalogs. Community Online Resour. Stat. Seism. Anal. 2012, 1–45. [Google Scholar] [CrossRef]
- Woessner, J.; Wiemer, S. Assessing the Quality of Earthquake Catalogues: Estimating the Magnitude of Completeness and Its Uncertainty. Bull. Seismol. Soc. Am. 2005, 95, 684–698. [Google Scholar] [CrossRef]
- Ak, K. Maximum likelihood estimate of b in the formula log N = a-bM and its confidence limits. Bull. Earthquake Res. Inst. Tokyo Univ. 1965, 43, 237–239. [Google Scholar]
- Bengoubou-Valerius, M.; Gibert, D. Bootstrap determination of the reliability of b values: An assessment of statistical estimators with synthetic magnitude series. Nat. Hazards 2013, 65, 443–459. [Google Scholar] [CrossRef]
- Engle, R.F.; Granger, C.W.J. Co-integration and error correction: Representation, estimation, and testing. Econometrica 1987, 55, 251–276. [Google Scholar] [CrossRef]
- Huang, M.H.; Fielding, E.J.; Liang, C.; Milillo, P.; Bekaert, D.; Dreger, D.; Salzer, J. Coseismic deformation and triggered landslides of the 2016 Mw 6.2 Amatrice earthquake in Italy. Geophys. Res. Lett. 2017, 44, 1266–1274. [Google Scholar] [CrossRef]
- Elliott, J.R.; Walters, R.J.; England, P.C.; Jackson, J.A.; Li, Z.; Parsons, B. Extension on the Tibetan plateau: Recent normal faulting measured by InSAR and body wave seismology. Geophys. J. Int. 2010, 183, 503–535. [Google Scholar] [CrossRef]
- King, G.; Nábělek, J. Role of fault bends in the initiation and termination of earthquake rupture. Science 1985, 228, 984–987. [Google Scholar] [CrossRef]
- Wesnousky, S.G. Predicting the endpoints of earthquake ruptures. Nature 2006, 444, 358–360. [Google Scholar] [CrossRef] [PubMed]
- Main, I.G.; Meredith, P.G.; Jones, C. A Reinterpretation of the Precursory Seismic b Value Anomaly from Fracture Mechanics. Geophys. J. Int. 1989, 96, 131–138. [Google Scholar] [CrossRef]
- Henderson, J.; Main, I.G.; Pearce, R.G.; Takeya, M. Seismicity in North-Eastern Brazil: Fractal Clustering and the Evolution of the b Value. Geophys. J. Int. 1994, 116, 217–226. [Google Scholar] [CrossRef]
- Scheffer, M.; Bascompte, J.; Brock, W.A.; Brovkin, V.; Carpenter, S.R.; Dakos, V.; Held, H.; Van Nes, E.H.; Rietkerk, M.; Sugihara, G. Early-Warning Signals for Critical Transitions. Nature 2009, 461, 53–59. [Google Scholar] [CrossRef]
- Qiao, X.; Lu, Z.; Yan, S.; Shi, H.; Zhi, M.; Zhao, D. The 2025 MW 7.0 Dingri Earthquake: Conjugate Normal Faulting of a Graben Structure in the Southern Xainza-Dinggye Rift. Geophys. Res. Lett. 2025, 52, e2025GL116154. [Google Scholar] [CrossRef]
- Yu, S.; Zhang, S.; Luo, J.; Li, Z.; Ding, J. The Tectonic Significance of the MW 7.1 Earthquake Source Model in Tibet in 2025 Constrained by InSAR Data. Remote Sens. 2025, 17, 936. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Lu, Y.; Yin, X.; Cai, R.; Zhou, L.; Wang, S.; Liu, F. B-Value Spatiotemporal Changes and Aftershock Correlation Prior to the Mwg 7.1 Dingri Earthquake in Southern Tibet: Implications for Land Deformation and Seismic Risk. Appl. Sci. 2025, 15, 11685. https://doi.org/10.3390/app152111685
Wang X, Lu Y, Yin X, Cai R, Zhou L, Wang S, Liu F. B-Value Spatiotemporal Changes and Aftershock Correlation Prior to the Mwg 7.1 Dingri Earthquake in Southern Tibet: Implications for Land Deformation and Seismic Risk. Applied Sciences. 2025; 15(21):11685. https://doi.org/10.3390/app152111685
Chicago/Turabian StyleWang, Xiaojuan, Yating Lu, Xinxin Yin, Run Cai, Liyuan Zhou, Shuwang Wang, and Feng Liu. 2025. "B-Value Spatiotemporal Changes and Aftershock Correlation Prior to the Mwg 7.1 Dingri Earthquake in Southern Tibet: Implications for Land Deformation and Seismic Risk" Applied Sciences 15, no. 21: 11685. https://doi.org/10.3390/app152111685
APA StyleWang, X., Lu, Y., Yin, X., Cai, R., Zhou, L., Wang, S., & Liu, F. (2025). B-Value Spatiotemporal Changes and Aftershock Correlation Prior to the Mwg 7.1 Dingri Earthquake in Southern Tibet: Implications for Land Deformation and Seismic Risk. Applied Sciences, 15(21), 11685. https://doi.org/10.3390/app152111685





