Leveraging Artificial Intelligence for Real-Time Risk Detection in Ship Navigation
Abstract
1. Introduction
1.1. Literature Review
1.2. Aim of the Work
2. Materials and Methods
2.1. Materials
2.2. Methods for Dataset Creation
- To reverse the COG of the ships (addition of 180° to the route), keeping all the other features unchanged.
- To assign very low SOG value to those ships that were in navigation with a SOG greater to a certain threshold, by replacing the original value with a new random value between 0 and 0.2 kn.
- To assign high SOG value to those that had very low speed, by replacing the original value with a new random value between 5 and 30 kn.
2.3. Methods for ML
3. Results
4. Discussion
5. Conclusions
- Decision tree is a tool that can be used for detection of anomalies in the Strait of Messina,
- The most used equation of cost loss function used by the algorithm is the Entropy one,
- The accuracy of the trained model in validation and test phase are 99.53% and 95.9%,
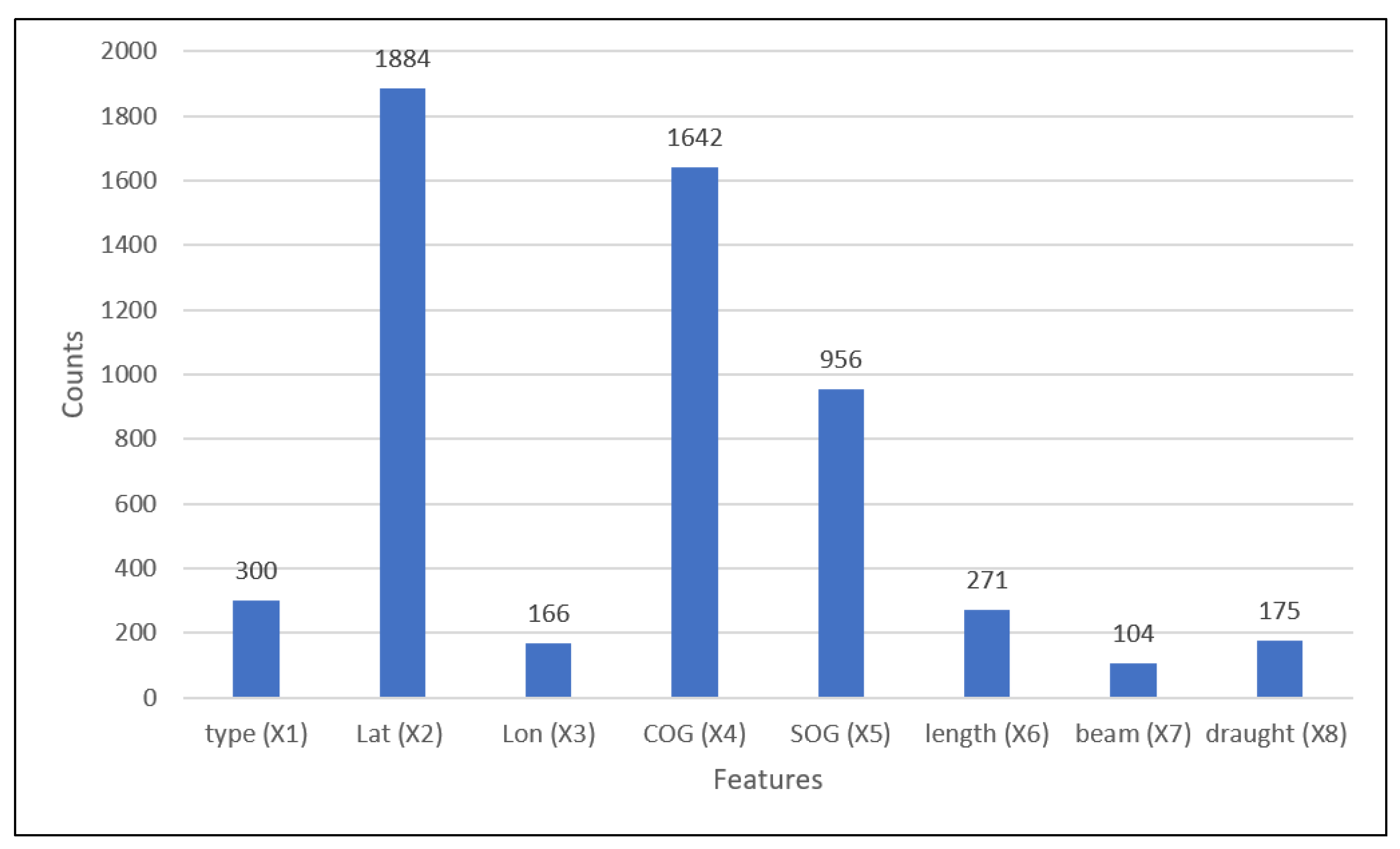
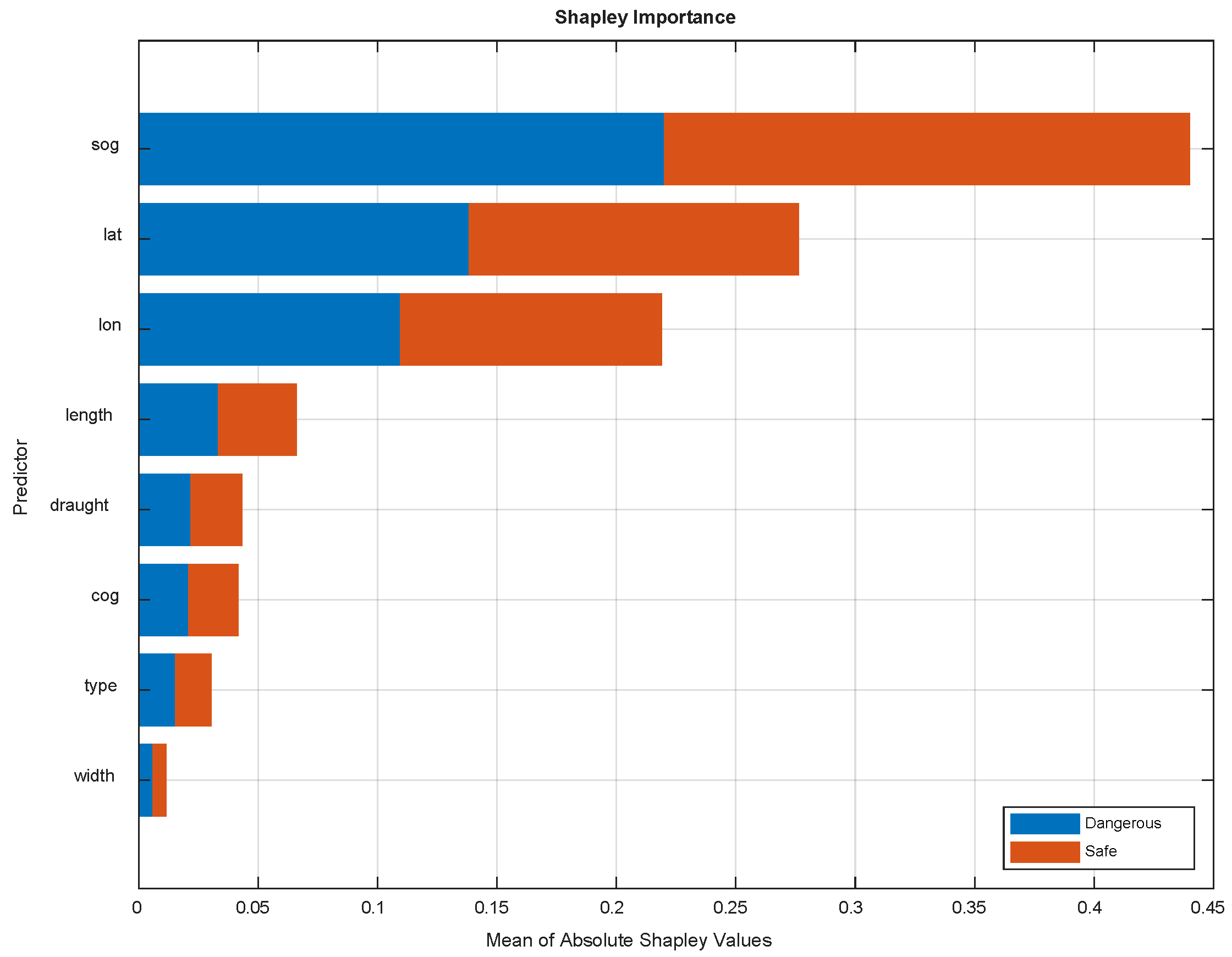
- The most used features for building the tree have been: Latitude, Cog, and Sog
- The parameters relative to the dimension of the ship and draught are little used during the building of the tree.
- Up to a depth of 20, the Longitude parameter has been used intensively but with the increase in the depth of the tree this feature was used less, probably for the particular shape of the channel of the Strait of Messina,
- The algorithm can be a starting point for introducing the use of Machine Learning as instrument for VTS operators.
- The system can be used to integrate the human experience as a Decision Support Tool (DST).
- The AIS data provided by the Port Authority have low number of instances in the group of anomalies.
- Artificial anomalies have been added in order to balance the dataset.
- The artificial anomalies can be improved with more realistic situations of risk with the help of the port authority.
- The results of the decision tree can be improved with an ensemble method like Random Forest algorithm.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| ANN | Artificial Neural Network |
| AIS | Automatic Identification System |
| CNN | Convolutional Neural Network |
| COG | Course Over Ground |
| DST | Decision Support Tool |
| DL | Deep Learning |
| FN | False Negative |
| FP | False Positive |
| HSC | High-Speed Craft |
| IALA | International Association of Lighthouse Authorities |
| IWRAP | International Association of Lighthouse Authorities Waterways Risk Assessment Program |
| IMO | International Maritime Organization |
| ML | Machine Learning |
| MMSI | Maritime Mobile Service Identities |
| NC | Negative Class |
| PC | Positive Class |
| RNN | Recurrent Neural Network |
| SMIGL | Ship Movement Image Generation and Labelling |
| SOG | Speed Over Ground |
| TSS | Traffic Separation Scheme |
| TN | True Negative |
| TP | True Positive |
| VTS | Vessel Traffic Service |
References
- UNCTAD. Review of Maritime Transport 2022; UNCTAD: Geneva, Switzerland, 2022; ISBN 9789211130737. [Google Scholar]
- Rodrigue, J.-P. The Geography of Transport Systems, 5th ed.; Routledge: Oxfordshire, UK; New York, NY, USA, 2020; ISBN 9780429346323. [Google Scholar]
- Yu, J.Y.; Sghaier, M.O.; Grabowiecka, Z. Deep Learning Approaches for AIS Data Association in the Context of Maritime Domain Awareness. In Proceedings of the 2020 23rd International Conference on Information Fusion, FUSION 2020, Rustenburg, South Africa, 6–9 July 2020. [Google Scholar] [CrossRef]
- HUMAN ERROR AND MARITIME SAFETY. Available online: https://maredu.hcg.gr/modules/document/file.php/MAK265/Dissertations%20in%20English/Human%20Error%20And%20Maritime%20Safety.pdf (accessed on 1 October 2025).
- Macduff, T. The Probability of Vessel Collisions. Ocean Ind. 1974, 9, 144–148. [Google Scholar]
- Dominguez-Péry, C.; Tassabehji, R.; Corset, F.; Chreim, Z. A Holistic View of Maritime Navigation Accidents and Risk Indicators: Examining IMO Reports from 2011 to 2021. J. Shipp. Trade 2023, 8, 11. [Google Scholar] [CrossRef]
- Xiao, F.; Ma, Y. Artificial Forces for Virtual Autonomous Ships with Encountering Situations in Restricted Waters. Marit. Policy Manag. 2020, 47, 687–702. [Google Scholar] [CrossRef]
- Zhang, T.; Yin, J.; Wang, X.; Min, J. Prediction of Container Port Congestion Status and Its Impact on Ship’s Time in Port Based on AIS Data. Marit. Policy Manag. 2024, 51, 669–697. [Google Scholar] [CrossRef]
- Munim, Z.H.; Dushenko, M.; Jimenez, V.J.; Shakil, M.H.; Imset, M. Big Data and Artificial Intelligence in the Maritime Industry: A Bibliometric Review and Future Research Directions. Marit. Policy Manag. 2020, 47, 577–597. [Google Scholar] [CrossRef]
- Robards, M.; Silber, G.; Adams, J.; Arroyo, J.; Lorenzini, D.; Schwehr, K.; Amos, J. Conservation Science and Policy Applications of the Marine Vessel Automatic Identification System (AIS)—A Review. Bull. Mar. Sci. 2016, 92, 75–103. [Google Scholar] [CrossRef]
- Berking, B. Potential and Benefits of AIS to Ships and Maritime Administrations. WMU J. Marit. Aff. 2003, 2, 61–78. [Google Scholar] [CrossRef]
- Bhurtyal, S.; Bui, H.; Hernandez, S.; Eksioglu, S.; Asborno, M.; Mitchell, K.N.; Kress, M. Prediction of Waterborne Freight Activity with Automatic Identification System Using Machine Learning. Comput. Ind. Eng. 2025, 200, 110757. [Google Scholar] [CrossRef]
- Somalvico, M. L’Intelligenza Artificiale; Rusconi Editore: Milano, Italy, 1987. [Google Scholar]
- Obradović, I.; Miličević, M.; Žubrinić, K. Machine Learning Approaches to Maritime Anomaly Detection. Naše More Znan. Časopis Pomor. 2014, 61, 96–101. [Google Scholar]
- Knapp, S.; van de Velden, M. Exploration of Machine Learning Methods for Maritime Risk Predictions. Marit. Policy Manag. 2023, 51, 1443–1473. [Google Scholar] [CrossRef]
- Xu, S.; Hu, H. Development of a Maritime Safety Management Database Using Relational Database Approach. Int. J. Shipp. Transp. Logist. 2019, 11, 334. [Google Scholar] [CrossRef]
- Singh, S.K.; Heymann, F. Machine Learning-Assisted Anomaly Detection in Maritime Navigation Using AIS Data. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, Oregon, 20–23 April 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 832–838. [Google Scholar]
- Jia, H.; Prakash, V.; Smith, T. Estimating Vessel Payloads in Bulk Shipping Using AIS Data. Int. J. Shipp. Transp. Logist. 2019, 11, 25. [Google Scholar] [CrossRef]
- Vanneschi, L.; Castelli, M.; Re, A. Prediction of Ships’ Position by Analysing AIS Data: An Artificial Intelligence Approach. Int. J. Web Eng. Technol. 2017, 12, 253. [Google Scholar] [CrossRef]
- Smith, M.; Reece, S.; Roberts, S.; Rezek, I. Online Maritime Abnormality Detection Using Gaussian Processes and Extreme Value Theory. In Proceedings of the 2012 IEEE 12th International Conference on Data Mining, Brussels, Belgium, 10–13 December 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 645–654. [Google Scholar]
- Ristic, B.; Scala, B.L.; Morelande, M.; Gordon, N. Statistical Analysis of Motion Patterns in AIS Data: Anomaly Detection and Motion Prediction. In Proceedings of the 2008 11th International Conference on Information Fusion, Cologne, Germany, 30 June–3 July 2008. [Google Scholar]
- Lane, R.O.; Nevell, D.A.; Hayward, S.D.; Beaney, T.W. Maritime Anomaly Detection and Threat Assessment. In Proceedings of the 2010 13th International Conference on Information Fusion, Edinburgh, UK, 26–29 July 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–8. [Google Scholar]
- Özlem, Ş.; Altan, Y.C.; Otay, E.N.; Or, İ. Grounding Probability in Narrow Waterways. J. Navig. 2020, 73, 267–281. [Google Scholar] [CrossRef]
- Yan, R.; Wang, S. Study of Data-Driven Methods for Vessel Anomaly Detection Based on AIS Data. In Smart Transportation Systems 2019; Springer: Singapore, 2019; pp. 29–37. [Google Scholar]
- Ginoulhac, R.; Barbaresco, F.; Schneider, J.-Y.; Pannier, J.-M.; Savary, S. Coastal Radar Target Recognition Based On Kinematic Data (AIS) With Machine Learning. In Proceedings of the 2019 International Radar Conference (RADAR), Toulon, France, 23–27 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar]
- Zhang, C.; Bin, J.; Wang, W.; Peng, X.; Wang, R.; Halldearn, R.; Liu, Z. AIS Data Driven General Vessel Destination Prediction: A Random Forest Based Approach. Transp. Res. Part C Emerg. Technol. 2020, 118, 102729. [Google Scholar] [CrossRef]
- Zhang, M.; Kujala, P.; Hirdaris, S. A Machine Learning Method for the Evaluation of Ship Grounding Risk in Real Operational Conditions. Reliab. Eng. Syst. Saf. 2022, 226, 108697. [Google Scholar] [CrossRef]
- Tritsarolis, A.; Chondrodima, E.; Pelekis, N.; Theodoridis, Y. Vessel Collision Risk Assessment Using AIS Data: A Machine Learning Approach. In Proceedings of the 2022 23rd IEEE International Conference on Mobile Data Management (MDM), Paphos, Cyprus, 6–9 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 425–430. [Google Scholar]
- Tritsarolis, A.; Kontoulis, Y.; Theodoridis, Y. The Piraeus AIS Dataset for Large-Scale Maritime Data Analytics. Data Brief 2022, 40, 107782. [Google Scholar] [CrossRef]
- Rawson, A.; Brito, M.; Sabeur, Z.; Tran-Thanh, L. A Machine Learning Approach for Monitoring Ship Safety in Extreme Weather Events. Saf. Sci. 2021, 141, 105336. [Google Scholar] [CrossRef]
- Xie, G.G.; Blauwkamp, D.; Nguyen, T.D. Toward a Deep Learning Approach to Behavior-Based AIS Traffic Anomaly Detection. In Proceedings of the Dynamic and Novel Advances in Machine Learning and Intelligent Cyber Security (DYNAMICS) Workshop 2018, San Juan, PR, USA, 3–4 December 2018. [Google Scholar] [CrossRef]
- Yang, C.-H.; Lin, G.-C.; Wu, C.-H.; Liu, Y.-H.; Wang, Y.-C.; Chen, K.-C. Deep Learning for Vessel Trajectory Prediction Using Clustered AIS Data. Mathematics 2022, 10, 2936. [Google Scholar] [CrossRef]
- Nguyen, D.; Vadaine, R.; Hajduch, G.; Garello, R.; Fablet, R. GeoTrackNet—A Maritime Anomaly Detector Using Probabilistic Neural Network Representation of AIS Tracks and A Contrario Detection. IEEE Trans. Intell. Transp. Syst. 2022, 23, 5655–5667. [Google Scholar] [CrossRef]
- Chen, X.; Liu, Y.; Achuthan, K.; Zhang, X. A Ship Movement Classification Based on Automatic Identification System (AIS) Data Using Convolutional Neural Network. Ocean Eng. 2020, 218, 108182. [Google Scholar] [CrossRef]
- Murray, B.; Perera, L.P. An AIS-Based Deep Learning Framework for Regional Ship Behavior Prediction. Reliab. Eng. Syst. Saf. 2021, 215, 107819. [Google Scholar] [CrossRef]
- de Vries, G.K.D.; van Someren, M. Machine Learning for Vessel Trajectories Using Compression, Alignments and Domain Knowledge. Expert Syst. Appl. 2012, 39, 13426–13439. [Google Scholar] [CrossRef]
- Dobrkovic, A.; Iacob, M.-E.; van Hillegersberg, J. Maritime Pattern Extraction and Route Reconstruction from Incomplete AIS Data. Int. J. Data Sci. Anal. 2018, 5, 111–136. [Google Scholar] [CrossRef]
- Zhang, M.; Conti, F.; Le Sourne, H.; Vassalos, D.; Kujala, P.; Lindroth, D.; Hirdaris, S. A Method for the Direct Assessment of Ship Collision Damage and Flooding Risk in Real Conditions. Ocean Eng. 2021, 237, 109605. [Google Scholar] [CrossRef]
- Rong, H.; Teixeira, A.P.; Guedes Soares, C. Ship Collision Avoidance Behaviour Recognition and Analysis Based on AIS Data. Ocean Eng. 2022, 245, 110479. [Google Scholar] [CrossRef]
- Durczak, W.; Filina-Dawidowicz, L. A Review of Vessel Traffic Services Systems Operating in Poland in Terms of Their Compliance with International Legislation. Appl. Sci. 2025, 15, 797. [Google Scholar] [CrossRef]
- Wan, C.; Yan, X.; Zhang, D.; Yang, Z. Analysis of Risk Factors Influencing the Safety of Maritime Container Supply Chains. Int. J. Shipp. Transp. Logist. 2019, 11, 476. [Google Scholar] [CrossRef]
- Kowalska, K.; Peel, L. Maritime Anomaly Detection Using Gaussian Process Active Learning. In Proceedings of the 2012 15th International Conference on Information Fusion, Singapore, 9–12 July 2012. [Google Scholar]
- Kraus, P.; Mohrdieck, C.; Schwenker, F. Ship Classification Based on Trajectory Data with Machine-Learning Methods. In Proceedings of the 2018 19th International Radar Symposium (IRS), Bonn, Germany, 20–22 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–10. [Google Scholar]
- Mantecon, T.; Casals, D.; Navarro-Corcuera, J.J.; del-Blanco, C.R.; Jaureguizar, F. Deep Learning to Enhance Maritime Situation Awareness. In Proceedings of the 2019 20th International Radar Symposium (IRS), Ulm, Germany, 26–28 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–8. [Google Scholar]
- Liang, Q.; Tvete, H.A.; Brinks, H.W. Prediction of Vessel Propulsion Power Using Machine Learning on AIS Data, Ship Performance Measurements and Weather Data. J. Phys. Conf. Ser. 2019, 1357, 012038. [Google Scholar] [CrossRef]
- Cucinotta, F.; Guglielmino, E.; Sfravara, F. Frequency of Ship Collisions in the Strait of Messina through Regulatory and Environmental Constraints Assessment. J. Navig. 2017, 70, 1002–1022. [Google Scholar] [CrossRef]
- Fuji, Y.; Yamanouchi, H.; Mizuki, N. Some Factors Affecting the Frequency of Accidents in Marine Traffic. J. Navig. 1974, 27, 239–247. [Google Scholar]
- Bokau, J.R.K.; Camliyurt, G.; Priadi, A.A.; Park, Y.; Kim, D. Enhancing Safety of Navigation: Redesigning Precautionary Areas into Roundabouts in Marine Traffic Separation Schemes. Appl. Sci. 2024, 14, 11588. [Google Scholar] [CrossRef]
- Cunningham, P.; Cord, M.; Delany, S.J. Supervised Learning. In Machine Learning Techniques for Multimedia; Springer: Berlin/Heidelberg, Germany, 2008; pp. 21–49. [Google Scholar]

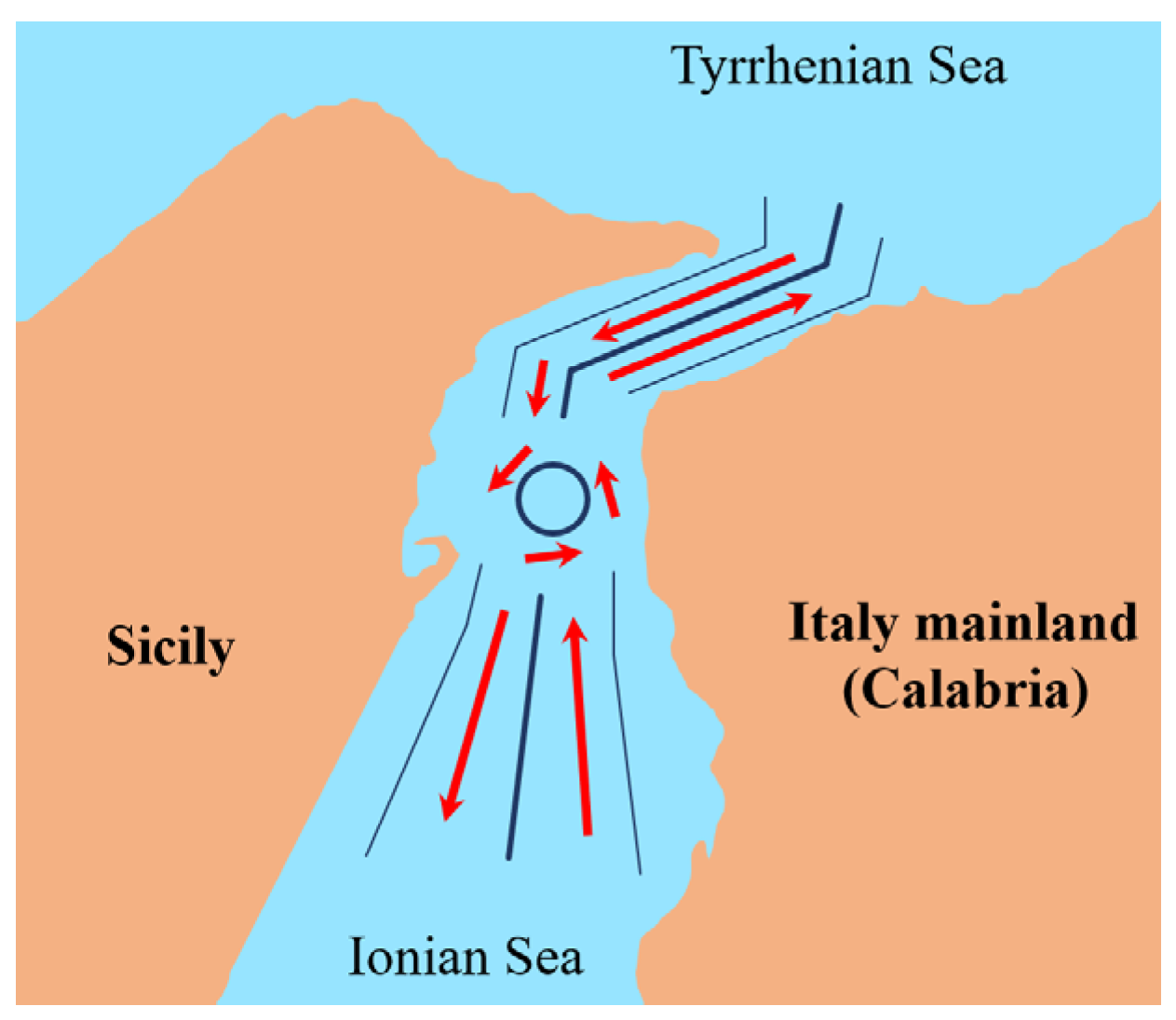
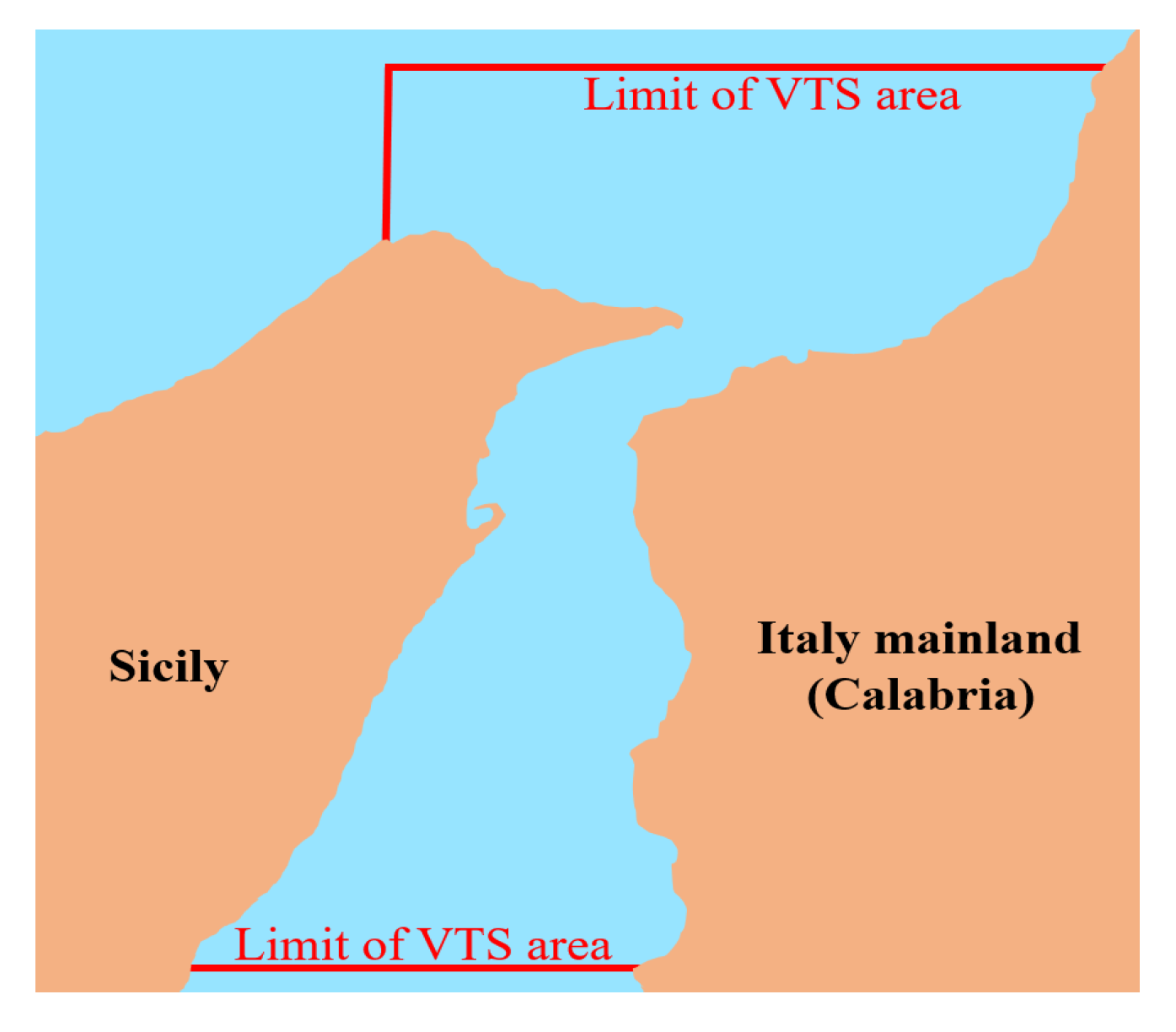
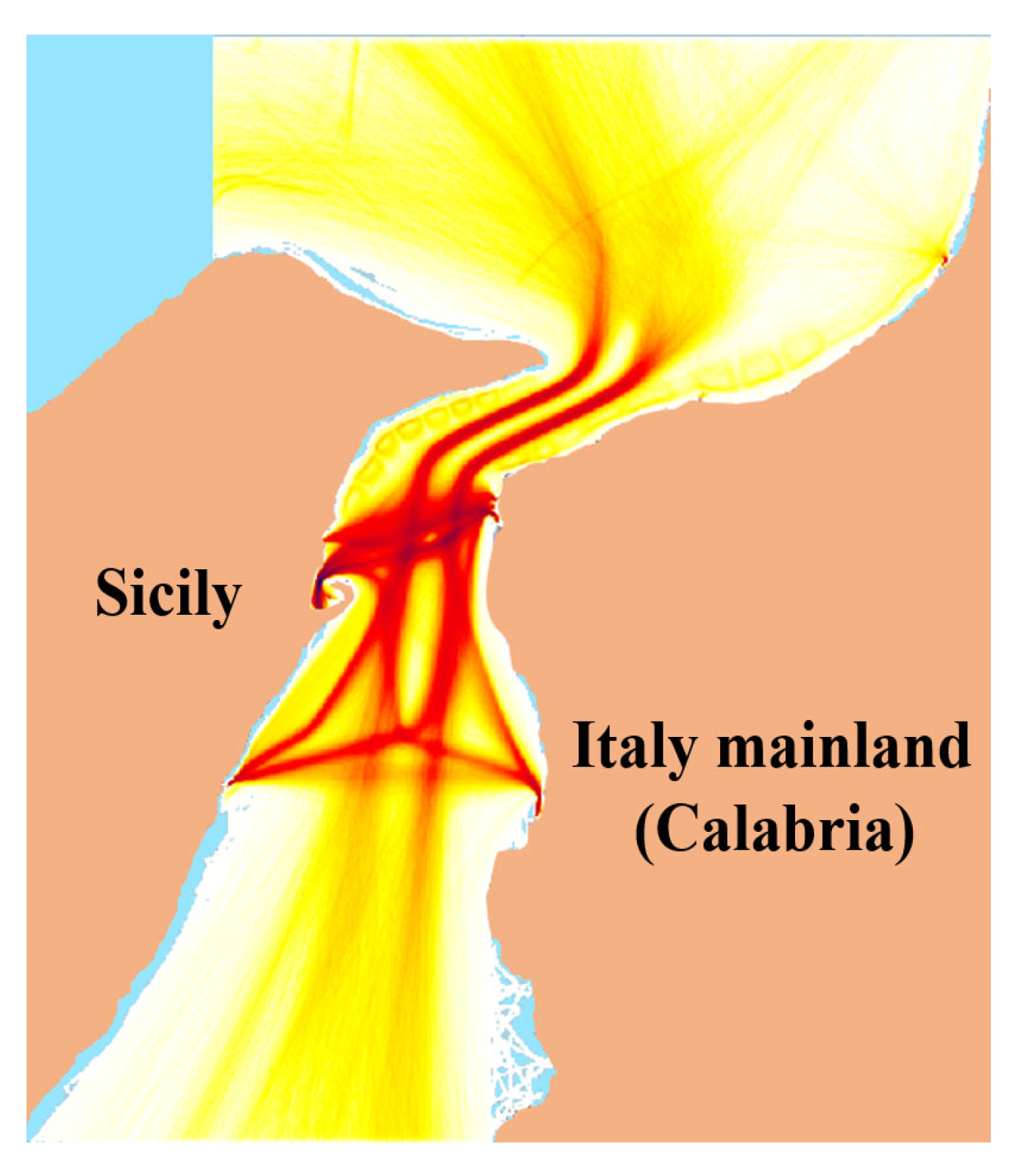
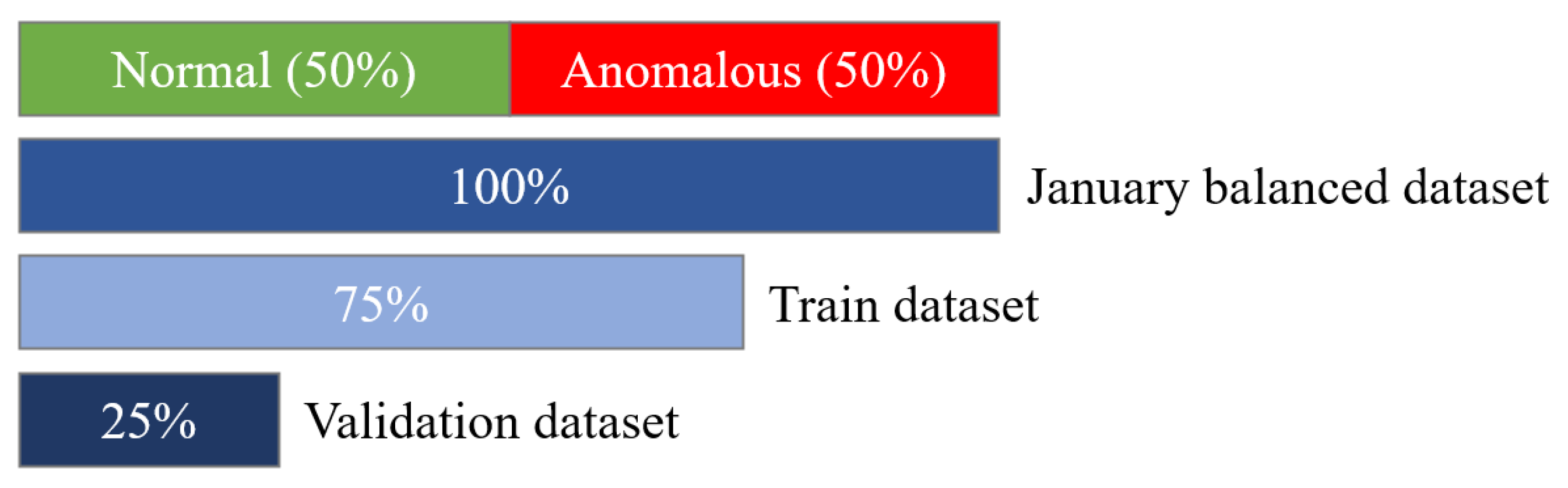
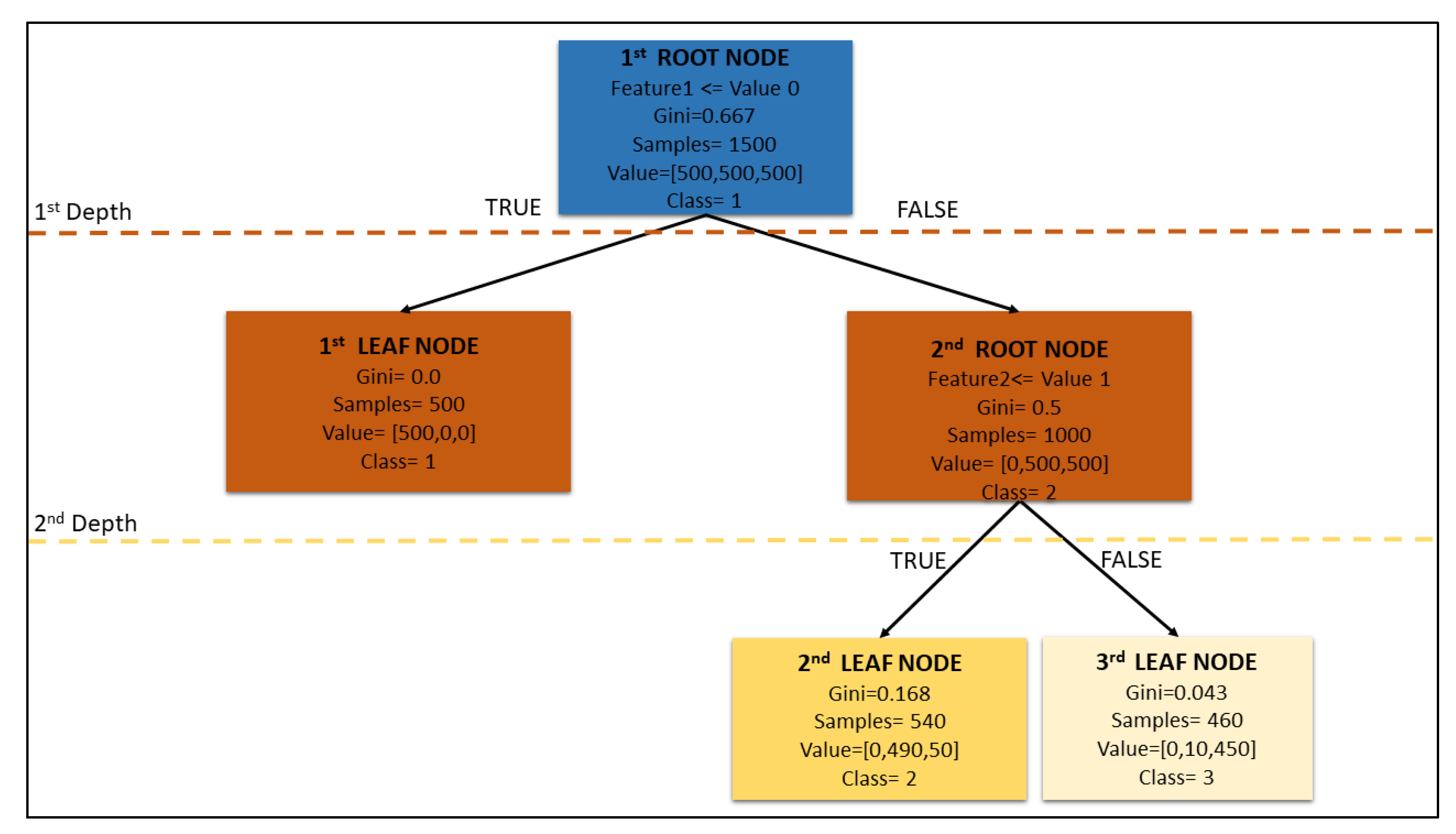
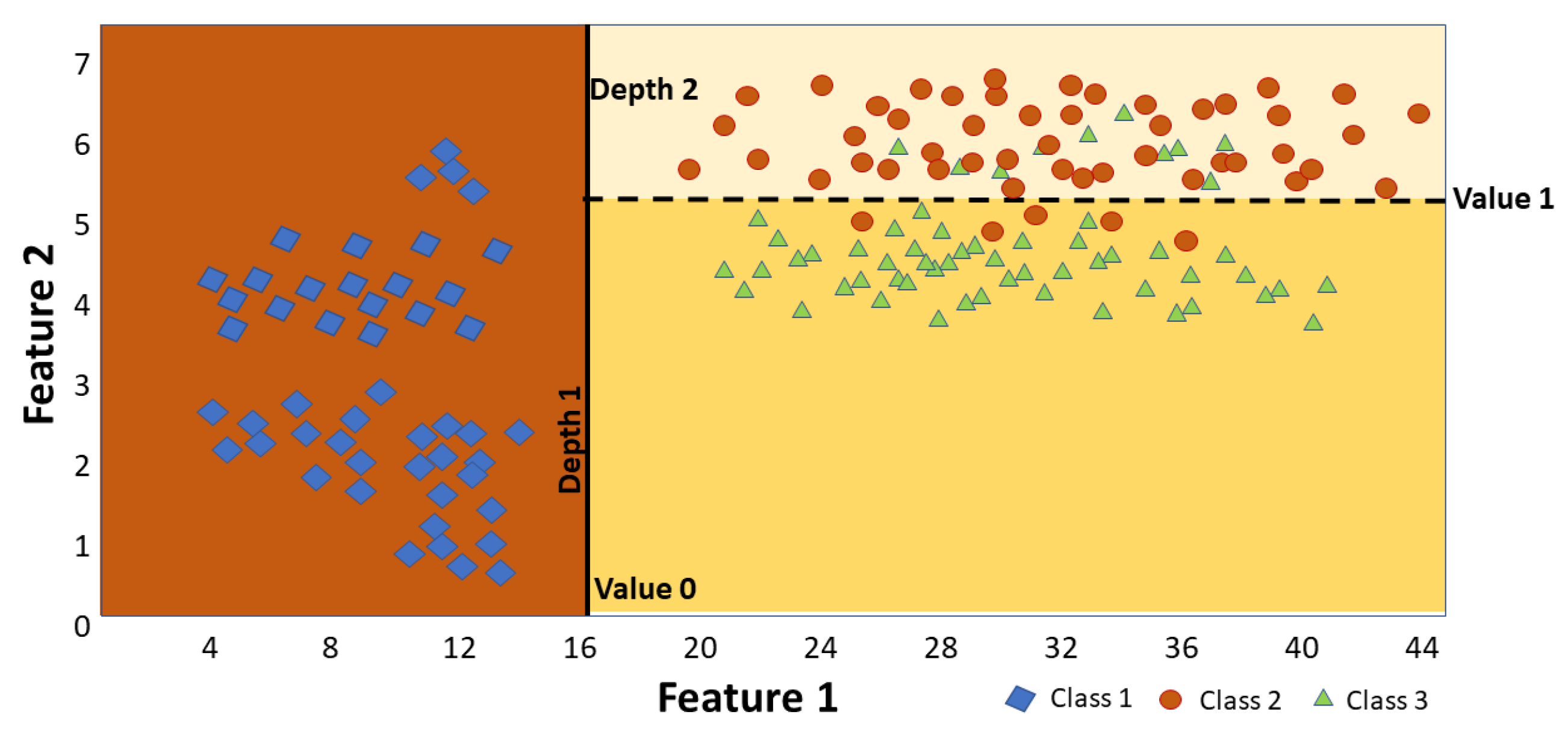

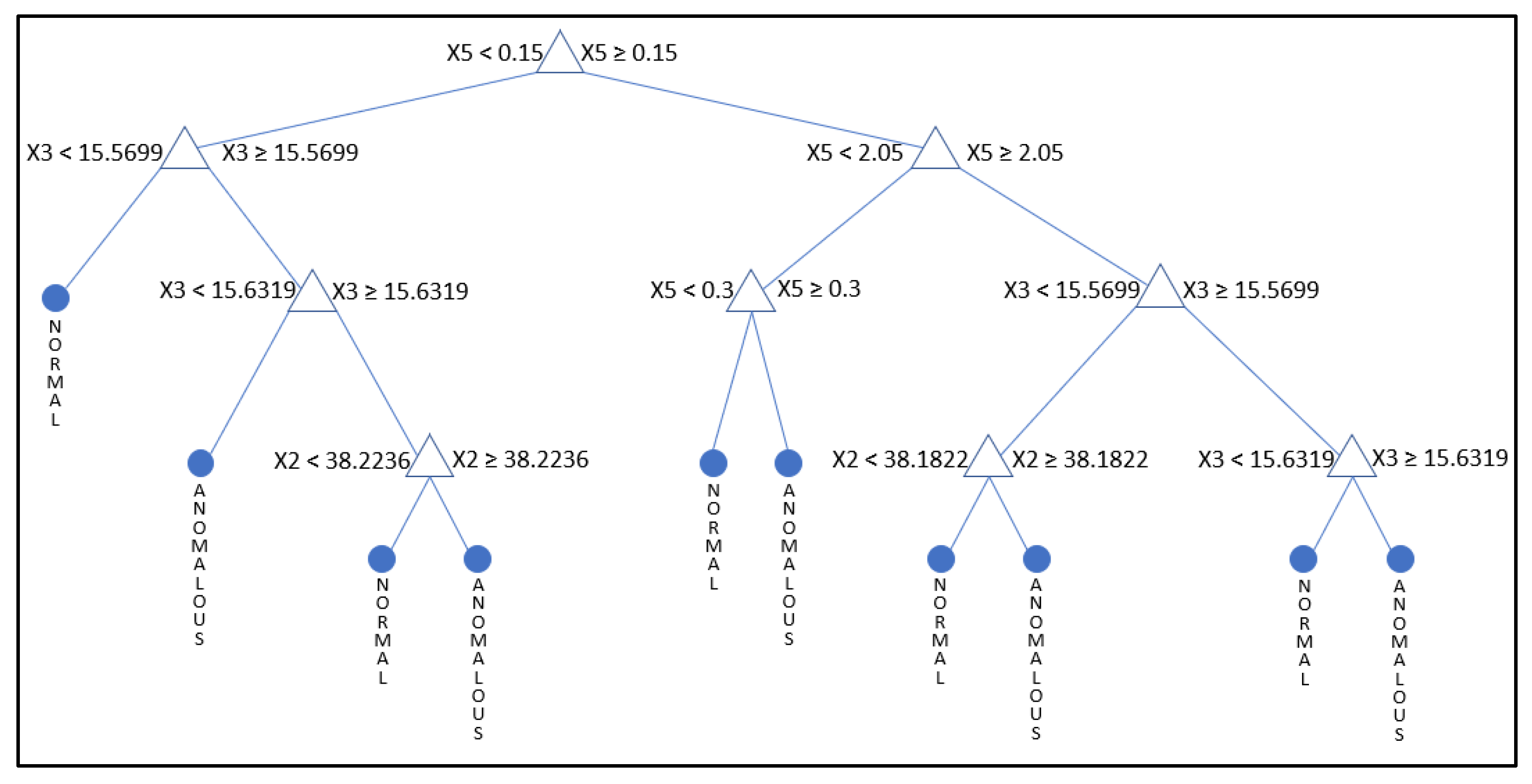
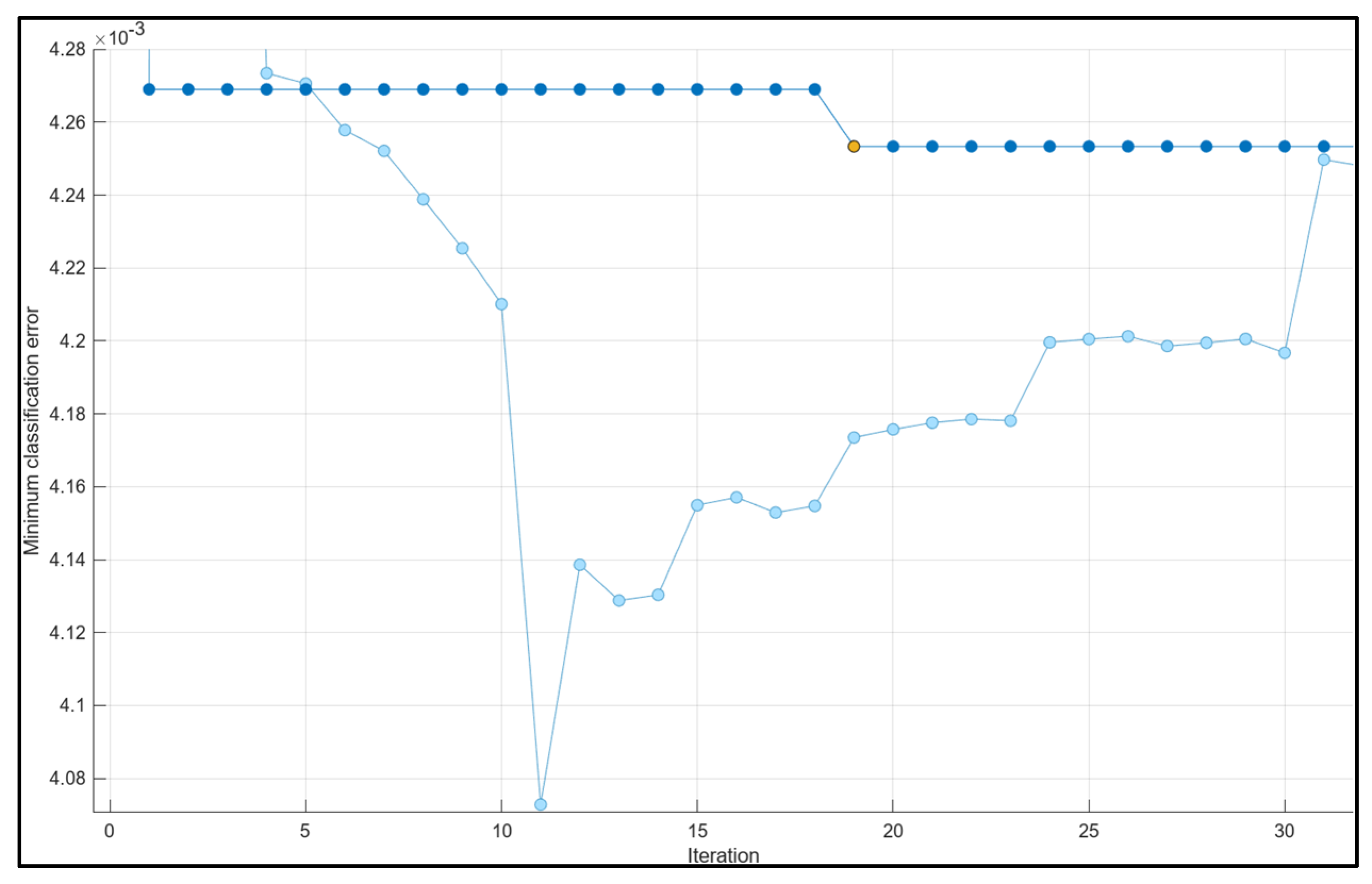
| Works | Position | Time | Route | Speed | Type | Size | Status |
|---|---|---|---|---|---|---|---|
| [20] | X | X | |||||
| [21] | X | ||||||
| [22] | X | X | X | X | |||
| [42] | X | X | X | ||||
| [25] | X | X | X | X | X | ||
| [43] | X | X | X | X | |||
| [26] | X | X | |||||
| [17] | X | X | X | X | |||
| [34] | X | X | X | X | X | ||
| [35] | X | X | X | X | |||
| [44] | X | X | |||||
| [45] | X | X | X | X | |||
| [36] | X | X | X | X | |||
| [37] | X | ||||||
| This work | X | X | X | X | X | X |
| Year | Event Number |
|---|---|
| 1950s | 4 |
| 1960s | 11 |
| 1970s | 17 |
| 1980s | 7 |
| 1990s | 3 |
| 2000s | 2 |
| Type | Information | Data Type |
|---|---|---|
| Static | MMSI number | Number [Integer] |
| Static | Call sign and name | Text [Character] |
| Static | IMO Number | Number [Integer] |
| Static | Length and Beam | Number [Float] |
| Static | Type of Ship | Categorical Number [Integer] (in according to AIS Specifications) |
| Static | Location of Electronic Position Fixing System (EPFS) antenna | Number [Float] |
| Dynamic | Ship position Latitude | Number [Float] |
| Dynamic | Ship position Longitude | Number [Float] |
| Dynamic | Position Time Stamp in UTC | Number [DateTime] |
| Dynamic | Course over ground (COG) | Number [Float] |
| Dynamic | Speed over ground (SOG) | Number [Float] |
| Dynamic | Heading | Number [Integer] |
| Dynamic | Navigational Status | Categorical data [Integer] (in according to AIS Specifications) |
| Dynamic | Rate of turn (ROT) | Number [Integer] |
| Voyage-related | Ship’s draught | Number [Float] |
| Voyage-related | Hazardous Cargo | Categorical data [Integer] (in according to AIS Specifications) |
| Voyage-related | Destination and ETA (Estimated Time of Arrival) | Text in both cases [Character] |
| Voyage-related | Route plan | |
| Safety-related | Free from short text messages | Text [Character] |
| Dataset | No. AIS Data |
|---|---|
| January | 1,786,822 |
| January balanced | 3,573,644 |
| Train (75% of January balanced) | 2,680,233 |
| Validation (25% of January balanced) | 893,411 |
| March | 1,875,403 |
| Test ≡ March balanced | 3,750,806 |
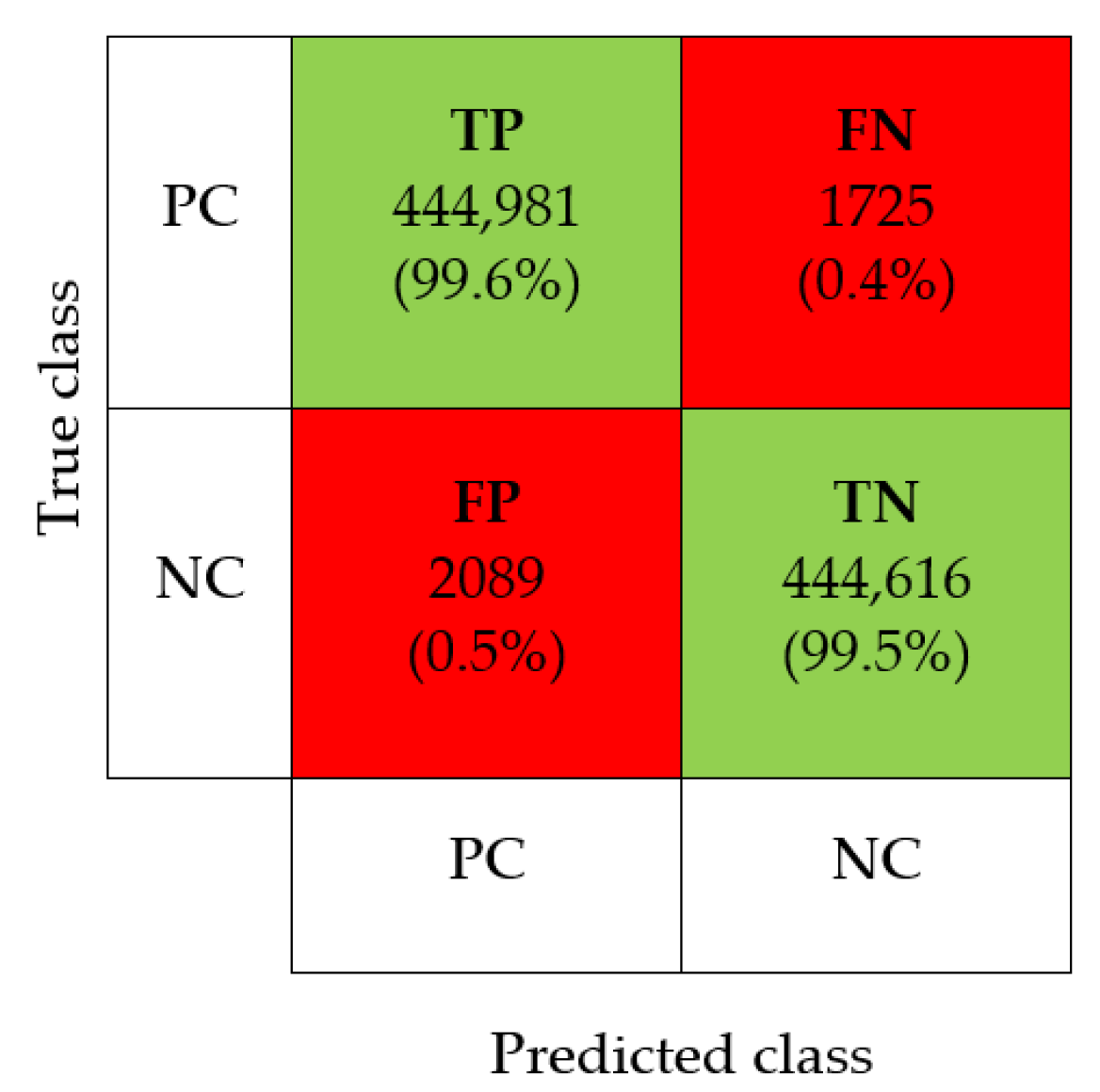
| TP | FN | FP | TN | Accuracy | Precision | Sensitivity | Specificity | F1-Score |
|---|---|---|---|---|---|---|---|---|
| 444,981 | 1725 | 2089 | 444,616 | 99.57% | 99.53% | 99.61% | 99.53% | 99.57% |
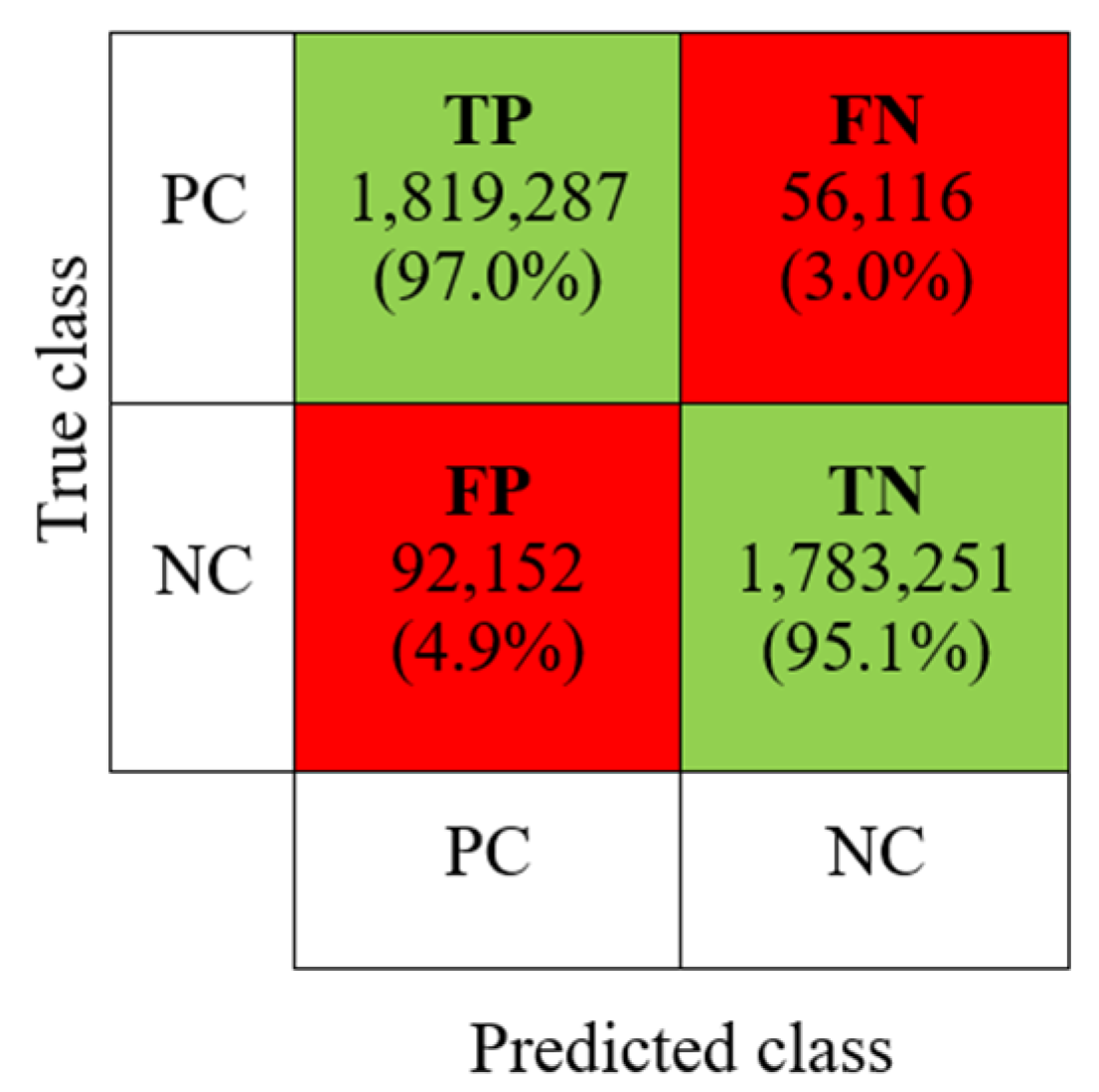
| TP | FN | FP | TN | Accuracy | Precision | Sensitivity | Specificity | F1-Score |
|---|---|---|---|---|---|---|---|---|
| 1,819,287 | 56,116 | 92,152 | 1,783,251 | 95.96% | 95.18% | 97.01% | 95.06% | 96.09% |
| k-Fold | No. Instances (Train–Validation) | TP | FN | FP | TN | ACC [%] | PRE [%] | SEN [%] | SPE [%] | F1-Score [%] |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2,858,916–714,728 | 355,897 | 1773 | 1467 | 355,591 | 99.55 | 99.59 | 99.50 | 99.59 | 99.54 |
| 2 | 2,858,915–714,729 | 355,933 | 1685 | 1431 | 355,680 | 99.56 | 99.60 | 99.53 | 99.60 | 99.56 |
| 3 | 2,858,915–714,729 | 355,829 | 1607 | 1535 | 355,758 | 99.56 | 99.57 | 99.55 | 99.57 | 99.56 |
| 4 | 2,858,915–714,729 | 356,007 | 1880 | 1358 | 355,484 | 99.55 | 99.62 | 99.47 | 99.62 | 99.54 |
| 5 | 2,858,915–714,729 | 356,046 | 1746 | 1319 | 355,618 | 99.57 | 99.63 | 99.51 | 99.63 | 99.57 |
| tot | 14,294,576–3,573,644 | 1,779,712 | 8691 | 7110 | 1,778,131 | 99.56 | 99.60 | 99.51 | 99.60 | 99.55 |
| Feature | Type (X1) | Lat (X2) | Lon (X3) | COG (X4) | SOG (X5) | Length (X6) | Beam (X7) | Draught (X8) |
|---|---|---|---|---|---|---|---|---|
| No. splits | 0 | 6 | 9 | 0 | 3 | 1 | 0 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barberi, E.; Chillemi, M.; Cucinotta, F.; Raffaele, M.; Salmeri, F.; Sfravara, F. Leveraging Artificial Intelligence for Real-Time Risk Detection in Ship Navigation. Appl. Sci. 2025, 15, 11674. https://doi.org/10.3390/app152111674
Barberi E, Chillemi M, Cucinotta F, Raffaele M, Salmeri F, Sfravara F. Leveraging Artificial Intelligence for Real-Time Risk Detection in Ship Navigation. Applied Sciences. 2025; 15(21):11674. https://doi.org/10.3390/app152111674
Chicago/Turabian StyleBarberi, Emmanuele, Massimiliano Chillemi, Filippo Cucinotta, Marcello Raffaele, Fabio Salmeri, and Felice Sfravara. 2025. "Leveraging Artificial Intelligence for Real-Time Risk Detection in Ship Navigation" Applied Sciences 15, no. 21: 11674. https://doi.org/10.3390/app152111674
APA StyleBarberi, E., Chillemi, M., Cucinotta, F., Raffaele, M., Salmeri, F., & Sfravara, F. (2025). Leveraging Artificial Intelligence for Real-Time Risk Detection in Ship Navigation. Applied Sciences, 15(21), 11674. https://doi.org/10.3390/app152111674










