1. Introduction
With the rapid advancement of Micro-Electro-Mechanical System (MEMS) technology, the attitude and heading reference system (AHRS) has been widely used in various fields such as indoor positioning [
1], mobile robots [
2], wearable devices [
3], autonomous driving [
4], unmanned aerial vehicles [
5], resource exploration [
6], virtual reality [
7], attitude capture [
8], and stone and earthen materials testing [
9]. Therefore, how to obtain accurate attitude information by MEMS-AHRS is a current research hotspot in applied sciences.
At present, MEMS-AHRS’s accuracy remains limited under dynamic conditions [
10]. Although MEMS gyroscopes offer benefits such as low cost, low power consumption, and small size, the significant zero drift of MEMS gyroscopes can lead to Euler angle divergence when used alone [
11]. To address this difficulty, magnetometer, accelerometer, and rate gyro (MARG) sensors are commonly used to improve the attitude estimation accuracy based on the specific geophysical field, viz., the gravitational field and the geomagnetic field [
12].
Currently, numerous data fusion algorithms are applied for MARG attitude estimation, such as complementary filters [
13], Kalman filters [
14], and neural networks [
15]. The complementary filter is simple but relies on manually tuned parameters, making it hard to adapt to complex conditions [
16]. Neural networks have strong fitting ability but require large datasets and lack interpretability, limiting their use on resource-constrained platforms [
17]. In contrast, the Kalman filter provides optimal estimation based on system models and noise statistics, offering both accuracy and stability. From the perspective of selecting a filter state vector, the general options are algorithms based on attitude representation parameters, such as the Euler angle [
18], rotation matrix [
19], or quaternion [
20]. N.Y. Ko et al. [
18] proposed a Euler angle-based extended Kalman filter algorithm, which modifies the gyroscope-predicted Euler angle using the Euler angle measurement calculated by the specific force and magnetic vector. However, Euler angle-based algorithms involve a lot of inverse trigonometric functions during each attitude update and are prone to Gimbal Lock [
21]. G. Shaaban et al. [
19] proposed a rotation-matrix-based invariant extended Kalman filter algorithm, which derives a rotation matrix propagation equation based on the angular rate measured by the gyroscopes and fuses the specific force and magnetic vector measurement through non-linear transformation. However, rotation-matrix-based algorithms encounter high-dimensional and multi-constraint challenges, resulting in low computational efficiency [
22]. Unlike the Euler angle and rotation matrix, quaternion-based algorithms do not suffer from these problems. X. Xu et al. [
20] proposed a quaternion-based double extended Kalman filter algorithm, which decomposes the quaternion into the inclination quaternion and the yaw quaternion and corrects inclination and yaw using an extended Kalman filter. In contrast, quaternion-based algorithms require decoupling of the influence of magnetic interference on inclination estimation, which is caused by the presence of magnetic inclination. Therefore, S. Zhang et al. [
23] proposed a geophysical-field-based Kalman filter (GKF) algorithm, which avoids using attitude representation parameters as the filter state vector. Instead, the algorithm estimates the specific force and magnetic vector information in the body frame based on the propagation equations of the gravitational field and geomagnetic field. Finally, the attitude information is calculated from the estimated specific force and magnetic vector.
In addition, the external acceleration [
24] during vehicle movement and the soft/hard magnetic anomalies [
12] caused by external factors such as metal and electronic equipment can disturb the attitude information obtained from MARG sensors. Hence, adaptive algorithms are needed to suppress the impact of external acceleration and magnetic anomalies on inclination and yaw estimation, respectively [
25].
To solve the above problem, many scholars have carried out a lot of research and improvement on adaptive strategies. Y. Sun et al. [
26] proposed a decoupled orientation estimation approach (DOEA) based on the threshold-based adaptive (TA) strategy, which judges the reliability of accelerometers by the modulus value of the accelerometer-sensed gravity field vector. Similarly, X. Wang et al. [
27] proposed an adaptive robust error-state Kalman filter algorithm to enhance yaw estimation in complex magnetic disturbance environments, which dynamically adjusts the magnetic vector measurement noise by calculating the changes in magnetic field intensity and magnetic inclination. Nonetheless, Y. Xu et al. [
28] believe that TA strategy may lead to misjudgment, which cannot ensure the reliability of measurements. The derivative of the output vector of the accelerometers and magnetometers should be regarded as an additional judgment criterion. A. Lotfy et al. [
29] used the Chi-square test adaptive (CA) Kalman filter algorithm to monitor the measurement variance using the measurement information and the mean square error matrix. However, the determination of the detection threshold in CA is challenging due to the principle of binary measurement anomaly judgment, which may lead to false alarms or a reduction in the probability of detecting measurement anomalies. S. Sarkka et al. [
30] proposed the Variational Bayesian adaptive (VBA) Kalman filter algorithm, which estimates the inaccurate and slowly varying measurement noise covariance matrix by choosing an appropriate conjugate prior to distribution. A. Makni et al. [
31] used the Sage–Husa adaptive filter algorithm to estimate the measured noise parameters of the system in real time through the output of the accelerometers. However, the Sage–Husa adaptive filter is sensitive to initial value selection. The measurement noise covariance matrix easily loses positive quality, which can lead to filter divergence. As a result, X. Lin et al. [
32] proposed a robust error-state Kalman filter (RESKF) algorithm based on the improved sequential adaptive (SA) strategy for MARG attitude estimation, which uses a sequential structure to reduce adaptive parameters and impose upper and lower boundary limits to ensure that the measure noise covariance matrix remains within a reasonable range and achieve fault isolation to rapidly reduce the measurement credibility. However, the noise covariance of a specific force and magnetic vector in the RESKF algorithm is not propagated to the Euler angle measurement, which impacts the optimal estimation of the filter. In addition, MARG adaptive attitude estimation can also be achieved by updating the magnetometer calibration parameters. H. Ke et al. [
33] proposed a gyroscope-aided magnetometer calibration algorithm, which updates the calibration parameters based on the consistency of spatial rotation perception between the gyroscopes and the magnetometers. Z. Wu et al. [
34] proposed an adaptive anti-disturbance algorithm, which estimates the magnetometer zero bias and the rate of change in the magnetic field to dynamically calibrate the magnetometer parameters, thereby maintaining filter stability under long-term stable magnetic interference.
In this work, a sequential adaptive geophysical-field-based Kalman filter (SA-GKF) algorithm for MARG attitude estimation is proposed. The SA-GKF algorithm estimates the specific force and magnetic vector based on the linear system model of the specific geophysical field and uses the sequential Sage–Husa adaptive strategy to estimate the measurement noise parameters in real time, which suppresses the maximum error of yaw estimation by more than 94% and inclination estimation by more than 21%. Furthermore, compared with three adaptive strategies and two algorithms, the proposed algorithm shows superior accuracy, confirming its advancement in attitude estimation under challenging conditions.
This paper is organized as follows: In
Section 2, the preliminaries of the rotation matrix calculation, the inclination calculation, and the yaw calculation are reviewed. In
Section 3, the sequential adaptive geophysical-field-based Kalman filter (SA-GKF) algorithm for MARG attitude estimation is introduced. In
Section 4, a set of experiments are designed to verify the effectiveness and advancement of the SA-GKF algorithm. In
Section 5, the conclusions are presented.
3. Sequential Adaptive Geophysical-Field-Based Kalman Filter Algorithm for Robust MARG Attitude Estimation
The purpose of this study is to suppress the effects of external acceleration and the soft/hard magnetic anomalies on the attitude estimation, for which the SA-GKF algorithm is proposed. Based on the principles outlined in
Section 2, this section mainly describes the proposed SA-GKF algorithm for robust MARG attitude estimation.
In the SA-GKF algorithm, the geophysical field prediction
is obtained from the propagation equation constructed by the gyroscope-sensed angular rate
at time
, and the geophysical field measurement
is obtained from the accelerometer-sensed specific force
and the magnetometer-sensed magnetic vector
. The measurement noise covariance matrix
is adaptively estimated in a sequential structure according to
, which is calculated by
and
. Finally, the geophysical field estimation
is obtained, and the Euler angle can be further calculated based on it. The block diagram of the SA-GKF algorithm is shown in
Figure 1. In this section, the block diagram will be explained explicitly.
3.1. System Model
3.1.1. Process Model
The rotation matrix of frame {
} at time
relative to frame {
} at time
, i.e.,
, can be expressed as follows:
where
stands for the three-order identity matrix;
stands for the rotation vector of frame {
} at time
relative to frame {
} at time
, which can be expressed by the calibrated gyroscope-sensed angular rate
and gyroscope noise
in frame {
} at time
:
where
stands for the sampling interval of gyroscopes.
Hence, the specific force in frame {
}’s transformation between time
and time
can be expressed using Equations (6) and (7), i.e., [
23]
Similarly, the magnetic vector in frame {
}’s transformation between time
and time
can be obtained as follows [
23]:
In summary, the process model of the SA-GKF algorithm can be abbreviated as follows:
where
In Equation (11),
and
are the state vector at time
and time
, respectively;
is the state one-step transition matrix;
is the process noise distribution matrix; and
is the process noise vector. The covariance matrix of
is defined as
, which can be expressed as follows:
where
,
, and
are the variances of
,
, and
, which can be calculated by collecting gyroscope measurements for a long time under static conditions.
significantly affects filtering performance [
35]. An undersized
makes the filter over-rely on the model and respond slowly to real state changes, whereas an oversized
causes excessive dependence on measurements and degrades estimation smoothness.
3.1.2. Measurement Model
The calibrated accelerometer-sensed specific force and the calibrated magnetometer-sensed magnetic vector are defined as
and
, which can be expressed by
as follows [
23]:
where
is the accelerometer noise and
is the magnetometer noise.
Therefore, the measurement model of the SA-GKF algorithm can be abbreviated as follows:
where
In Equation (15),
is the measurement vector at time
;
is the measurement matrix; and
is the measurement noise vector. The covariance matrix of
is defined as
, which can be expressed as follows:
where
,
,
,
,
, and
are the variances of
,
,
,
,
, and
, which can be calculated by collecting accelerometer and magnetometer measurements for a long time under static and stable conditions.
3.1.3. System State Space Model
From Equations (10) and (14), we can obtain the system state space model of the SA-GKF algorithm as follows:
3.2. SA-GKF Algorithm
3.2.1. Time Update
According to the state estimation
at time
and the process model in Equation (10), the state at time
, i.e., the process of state one-step prediction, can be predicted as follows:
where
is the zero-mean white noise, which contributes nothing to the state prediction.
Then, the state covariance matrix at time
can be predicted by the state estimation covariance matrix at time
, i.e., the process of the one-step state prediction covariance matrix, which is defined as follows:
3.2.2. Adaptive Measurement Update
The external acceleration and magnetic anomalies can significantly affect the estimation accuracy of the inclination and yaw, respectively. Therefore, adaptive algorithms must be used to solve the interference problem. The Sage–Husa adaptive filter algorithm is commonly used in practice, and the specific implementation is as follows [
32]:
where
is the measurement innovation;
is the fading factor, so that the filter can always maintain the adaptive ability of
[
36]. Based on a series of comparative experiments,
was set to 0.95.
However, the Sage–Husa adaptive filter is sensitive to the initial value selection. If the actual measurement noise is too low compared to the theoretical modeling value or the initial state noise setting is too high,
may lose its positive definiteness and cause a filter anomaly [
32].
In addition, in practical applications, the number of adaptive parameters should be reduced to maintain the reliability of the filter. A simple and effective method is to use a sequential structure to reduce adaptive parameters and impose upper and lower boundary limits on each diagonal component of to ensure that it remains within a reasonable range.
From Equation (14), the measurement equation at time
can be decomposed into six groups as follows:
The measurement noise covariance matrix can be expressed in the following component block diagonal matrix form:
Therefore, when the
i-th scalar sequential measurement is updated, the scalar measurement equation is
Further, the
i-th scalar sequential measurement innovation can be expressed as follows:
The
i-th scalar sequential measurement innovation covariance is
Equation (25) is used for setting upper and lower boundary restrictions with the following conditions on each
diagonal component [
32]:
where the lower boundary
is used to ensure the positive quality of
, and the upper boundary
is used to quickly reduce the reliability of measurement information
and test whether
is abnormal. If
,
is regarded as abnormal, and the measurement update is abandoned.
Through the above processing, the system noise parameters can be estimated quickly in real time, and the impact of external acceleration and magnetic anomalies on the inclination and yaw estimation can be suppressed, with good adaptability and reliability.
The
i-th sequential filter gain is the weight matrix that balances the contribution of the predicted and measured state values, i.e.,
where
is the
i-th sequential one-step state prediction covariance matrix.
The
i-th sequential state at time
can be further modified by
on the basis of the
i-th sequential state prediction
, i.e., the process of state estimation, as follows:
The
i-th sequential state estimation covariance matrix can be obtained as follows:
To sum up, the final filtered value is
where
is the dimension of the measurement vector.
3.3. Euler Angle Estimation
In summary, the Euler angle estimation
can be obtained from (3) and (5) and
Table 1 and
Table 2 by
.
The proposed SA-GKF algorithm runs recursively by combining (3), (5), (11)–(12), (15)–(16), and (18)–(30). The implementation pseudocode of the SA-GKF algorithm is shown in Algorithm 1.
| Algorithm 1: Sequential adaptive geophysical-field-based Kalman filter |
Input
, , , , , , , , , .
1: ; //State-one-step prediction.
2: ; //State-one-step prediction covariance matrix.
3: ;
For i = 1:n
4: ; //the i-th measurement.
5: ; //the i-th measurement innovation.
6: ; //the i-th measurement innovation covariance.
7: Calculate from (24); //the i-th measurement covariance.
8: if , ; else , ; //Measurement fault isolation.
9: ; //Measurement fault isolation.
End
10: , ; //Final filtered value.
11: Calculate , , and from (3), (5), Table 1 and Table 2 by ; //Inclination and yaw calculation.
12: .
Output
, , , , . |
For the sequential Sage–Husa adaptive linear Kalman filter with a state vector of dimension and measurement vector of dimension , the computational complexity is , and the memory complexity is . The proposed SA-GKF algorithm, with , has been successfully deployed on an embedded system based on an the STM32F411RET6 microcontroller produced by STMicroelectronics in Geneva, Switzerland (100 MHz main frequency, 128 KB SRAM) at an execution frequency of 100 Hz, demonstrating its feasibility and efficiency in resource-constrained systems.
In summary, the SA-GKF algorithm combines geophysical field modeling with the sequential adaptive filter to achieve strong robustness against external acceleration and magnetic anomalies. The effectiveness of this algorithm will be verified by the experiments presented below.
4. Experiments and Discussion
In order to verify the effectiveness of the proposed SA-GKF algorithm, a set of experiments was designed. This section presents the experimental platform, design, process, results, and discussion.
4.1. Experimental Platform
In order to verify the effectiveness of the SA-GKF algorithm, a set of experiments were designed based on our self-developed MARG-AHRS module [
37], which integrates with XV7001BB gyroscopes (produced by Epson in Suwa, Japan), LIS3LV02DL accelerometers (produced by STMicroelectronics in Geneva, Switzerland), RM3100 magnetometers (produced by PNI in Windsor, CT, USA), a LM75A thermometer (produced by Texas Instruments in Dallas, TX, USA), a STM32F411RET6 microcontroller, and a high-precision orthogonal housing (see
Figure 2a). Gyroscopes, accelerometers, and magnetometers are calibrated by the multi-angle-rate method [
38], the six-positions method [
39], and the error separation method [
40], respectively. After testing, the root mean square error of the calibrated gyroscope measurement, accelerometer measurement, and magnetometer measurement are 0.2°/s, 0.0004 g, and 0.003 h. Under static conditions, the inclination accuracy is 0.25°, and the yaw accuracy is 0.3°. Only calibrated MARG data fusion can ensure the stability of the filter. In the experiment, to ensure the effectiveness of the generated measurement interference, the attitude error caused by external acceleration and magnetic anomalies will be made greater than the module’s attitude accuracy. The sampling rate of the module is 100 Hz, and the main performance parameters of the sensors in the MARG module are shown in
Table 3. In addition, an experimental platform based on a three-axis non-magnetic turntable and the upper computer was built (see
Figure 2b).
4.2. Experimental Design
A 0.02 mm/m air-level was used to strictly level the yaw axis (i.e., Z-axis), pitch axis (i.e., X-axis), and roll axis (i.e., Y-axis) of the three-axis non-magnetic turntable. Then, the MARG-AHRS module was fixed on the turntable plane to execute the experiment.
Two sets of experiments were designed: (a) In the pitch dynamic experiment, the X-axis of the turntable was manually rotated, and the MARG-AHRS module’s outputs of roll and yaw were recorded. (b) In the roll dynamic experiment, the Y-axis of the turntable was manually rotated, and the MARG-AHRS module’s outputs of pitch and yaw were ecorded. In these experiments, external acceleration and magnetic anomalies were realized by rotating the X-/Y-axes of the three-axis non-magnetic turntable and introducing a magnet.
At first, the effectiveness of the SA-GKF algorithm is verified by comparing it with the GKF algorithm (i.e., an SA-GKF algorithm without an adaptive strategy). Secondly, the rationality of choosing an SA strategy is verified by comparing the SA-GKF algorithm with the threshold-based adaptive GKF (TA-GKF) algorithm, Chi-square test adaptive GKF (CA-GKF) algorithm, and Variational Bayesian adaptive GKF (VBA-GKF) algorithm. Finally, the advancement of the SA-GKF algorithm is verified by comparing it with the DOEA and the RESKF algorithm.
The quantitative index of attitude estimation robustness is the maximum error of the Euler angle. The Euler angle errors were obtained from the difference between the reference value and the algorithm estimate. In the experimental results, Reference stands for the Euler angles reference value.
4.3. Anti-Interference Experiments
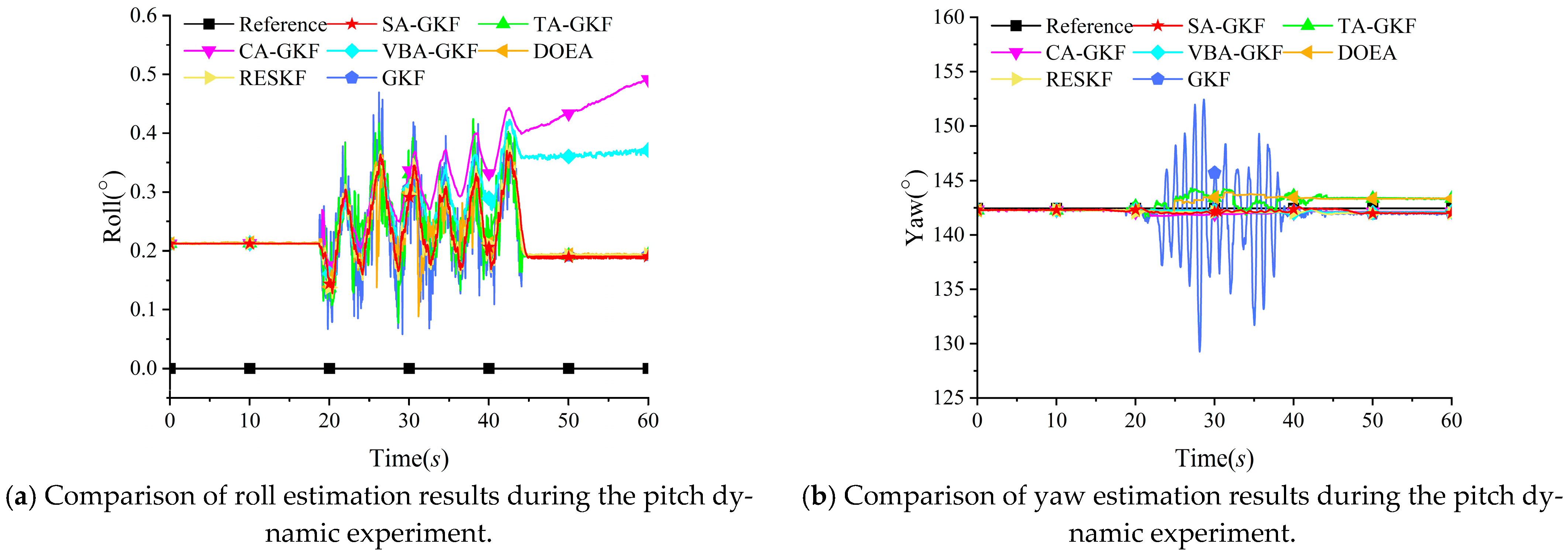
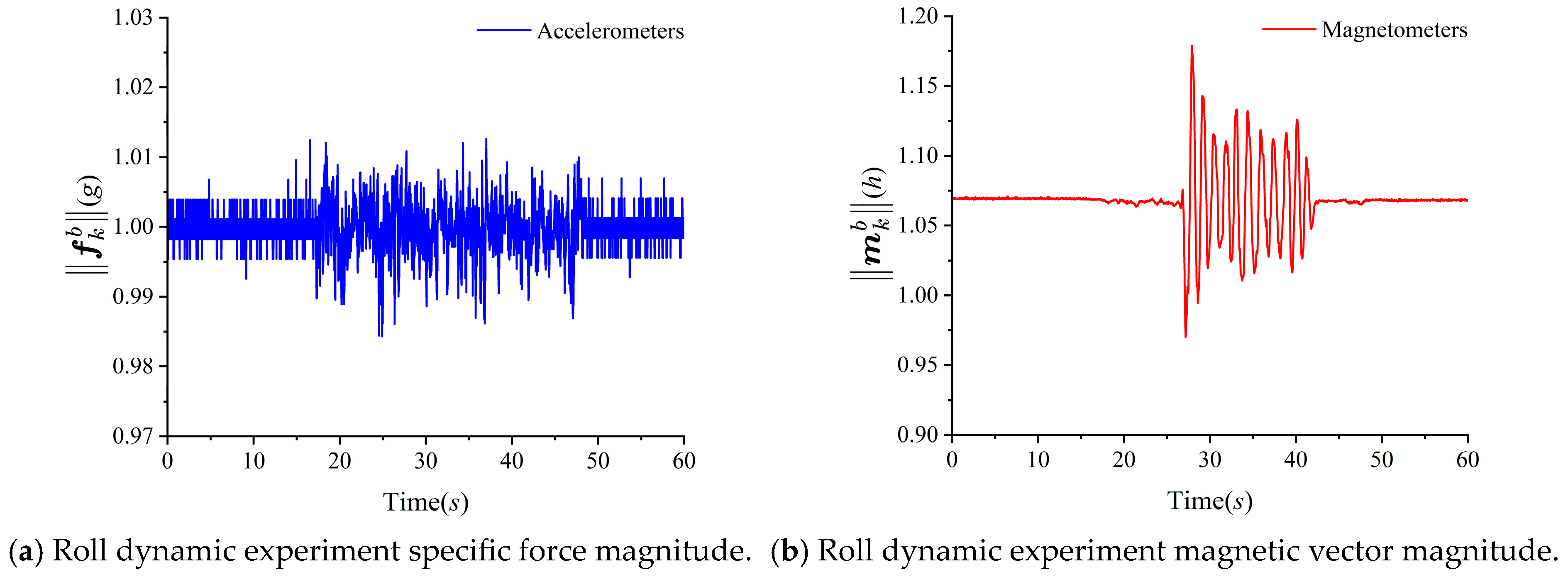
4.3.1. Pitch Dynamic Experiment
In this experiment, the Y-axis and Z-axis were kept stationary. The reference values of roll are zero, and the reference value of yaw is the scale value of the magnetic north, corresponding to the turntable’s 142.45°.
The magnitudes of the specific force and magnetic vector in the pitch dynamic experiment are shown in
Figure 3a,b, respectively.
As shown in
Figure 4 and
Table 4, in the pitch dynamic experiment, compared with the GKF algorithm, the SA-GKF algorithm’s maximum roll error is reduced by 21.08%, and its maximum yaw error is reduced by 96.24%. In addition, compared with the TA-GKF algorithm, the CA-GKF algorithm, the VBA-GKF algorithm, the DOEA, and the RESKF algorithm, the SA-GKF algorithm works better and is more stable.
4.3.2. Roll Dynamic Experiment
In this experiment, the X-axis and Z-axis were kept stationary. The reference values of the pitch are zero, and the reference value of yaw is the scale value of the magnetic north, corresponding to the turntable’s 142.45°.
The magnitudes of the specific force and magnetic vector in the pitch dynamic experiment are shown in
Figure 5a,b, respectively.
As shown in
Figure 6 and
Table 5, in the roll dynamic experiment, compared with the GKF algorithm, the SA-GKF algorithm’s maximum pitch error is reduced by 31.00%, and its maximum yaw error is reduced by 94.26%. In addition, compared with the TA-GKF algorithm, the CA-GKF algorithm, the VBA-GKF algorithm, the DOEA, and the RESKF algorithm, the SA-GKF algorithm works better and is more stable.
4.4. Experimental Discussions
From the experimental results in
Section 4.3, we can see that the proposed SA-GKF algorithm can effectively suppress the influence of external acceleration and soft/hard magnetic anomalies on the estimation inclination and yaw estimation, respectively. When interference occurs, the SAGKF algorithm constructs the measurement innovation in real time by calculating the difference between the prediction and measurement of the geophysical fields. Then, the SAGKF algorithm estimates the measurement noise covariance matrix and combines the fault isolation to shield abnormal measurements, rapidly reducing the credibility of abnormal measurements and significantly enhancing the robustness of MARG attitude estimation.
Furthermore, compared with the TA, CA, and VBA strategies, the SA strategy exhibits stronger adaptability and is more suitable for combination with the GKF algorithm. The TA and CA strategies suffer from the binarity problem, making it difficult to determine the appropriate threshold. Therefore, both are prone to false alarms or missed detections, which can result in filter anomaly or even divergence. The VBA strategy relies on the factorization assumption and has no boundary constraints, resulting in reduced stability when the noise characteristics vary rapidly.
Finally, the experimental results show that the SA-GKF algorithm strategy has a higher attitude estimation accuracy than the DOEA and the RESKF algorithm, showing that the SA-GKF algorithm has certain advantages. The adaptive strategy of the DOEA is consistent with the TA strategy, and therefore DOEA has the same binarity problem. In the RESKF algorithm, both the state and measurement vectors are represented in the Euler angle, making it difficult to accurately model the noise statistics, which further limits its estimation precision.
The above analysis confirms that the proposed SA-GKF algorithm achieves superior performance and robustness.
5. Conclusions
Based on the theoretical analysis and experimental validation presented in the previous sections, the main contributions and future perspectives are summarized as follows:
In this work, a sequential adaptive linear Kalman filter algorithm based on the geophysical field for MARG attitude estimation was proposed, which suppresses the maximum error of yaw estimation by more than 94% and that of inclination estimation by more than 21%. Compared with the existing three adaptive strategies and two algorithms, the SA-GKF represents certain advancements. The SA-GKF algorithm can provide a strongly robust MARG attitude estimation solution for resource exploration, navigation and positioning, motion control, and stone and earthen materials testing, promoting the development of related industries.
However, the SA-GKF algorithm only performs online estimation of the measurement noise covariance matrix, without considering the effect of inaccuracies in the process noise covariance matrix. Moreover, when long-term disturbances occur, the filter relies solely on the time update process. After the disturbance ends, the filter may have already diverged, causing normal measurements to be misidentified as abnormal ones, thereby preventing the system from returning to stable filtering. In future work, the adaptive MARG attitude estimation algorithm will be studied further under conditions where both measurement noise and process noise are uncertain. In addition, long-term stable magnetic interference can be suppressed by combining the algorithm with the updated magnetic declination. Both are conducive to preventing filter divergence and improving the robustness of MARG attitude estimation.