Abstract
With the expansion of network scale, the distance between routing nodes increases, and various routing constraints cause significant interference to the optimization process of traditional routing algorithms. To address this issue, based on the DSR routing protocol, this paper proposes a multi-constraint QoS routing algorithm based on an improved whale optimization algorithm. Specifically, the linear convergence factor in the original WOA is adjusted to a nonlinear one, which balances the global exploration capability and local exploitation capability of the algorithm. Additionally, an inertia weight strategy is introduced: this not only accelerates the convergence of the population but also enables the algorithm to escape local optimal solutions in a timely manner. Simulation results demonstrate that the routing protocol based on the improved WOA ensures QoS routing optimization capability and improves the efficiency of optimal path search.
1. Introduction
With the advancement of network technologies and wireless communications, the current demand for wireless networks among users has reached an unprecedented high, accompanied by increasingly stringent requirements for the Quality of Service (QoS) of wireless networks [1]. The multi-constraint QoS problem has been proven to be an NP-Complete challenge in the literature [2]. Currently, studies have revealed the prominent advantages of various intelligent algorithms. Scholars both at home and abroad have conducted in-depth research on network routing by integrating the characteristics of intelligent algorithms and have proposed a variety of algorithms.
The Multipath Data Transfer (MPDT) protocol proposed in [3] maximizes the lifetime of wireless multimedia networks by distributing the load evenly among various nodes. This protocol consists of two phases: the route establishment phase and the data transmission phase. In the route establishment phase, multiple paths are constructed; during the data transmission phase, data is transmitted through different selected paths. The Reliable, Real-time Routing (3R) protocol presented in [4] takes both multipath and time-constrained routing into account. It puts forward the theory that transmission delay can be reduced through parallel transmission. By using the packet reception rate to estimate the necessary paths that can ensure successful data arrival, the protocol achieves reduced delay and improved reliability, albeit at the cost of relatively high energy consumption.
The Mobility Aware Routing With Partial Route Preservation (PARTROUTE) protocol proposed in [5] takes the energy level of sensor nodes as the basis for route selection and determines the route through Multipath Route Request (MREQ) messages. When an MREQ packet is broadcast from the source node to the destination node, it detects the energy level of each intermediate node it passes through; the higher the energy level of a node, the faster the MREQ message is forwarded. The Energy-Efficient and QoS-Based Routing (EQSR) protocol introduced in [6] is a routing protocol that incorporates energy level, available buffer size, and signal-to-noise ratio into route selection simultaneously, and determines the next-hop forwarding node on a hop-by-hop basis.
A multipath routing protocol based on multi-objective evolutionary algorithms was proposed in [7]. Considering the energy constraints of wireless sensor networks, this protocol calculates the optimal trade-off between energy consumption and reliability using multi-objective evolutionary algorithms and obtains the optimal multipath routes by pruning the k-shortest path algorithm. Reference [8] proposed an adaptive multipath routing algorithm based on the shuffled frog leaping algorithm to address congestion issues in wireless sensor networks. In [9], a routing algorithm based on the Genetic Algorithm (GA) was presented, which provides a relatively practical solution to the routing addressing problem of multi-constraint discrete network nodes; however, its obvious drawback lies in insufficient positive feedback capability.
Reference [10] proposed a multipath selection scheme for QoS-aware routing in mobile ad hoc networks based on fractional cuckoo search. By considering QoS constraints such as energy, link lifetime, distance, and delay, a new fitness function was developed, but the scheme has low feasibility. References [11,12,13,14,15] optimized multi-constraint QoS routing algorithms based on ant colony algorithms, and the performance of the optimized algorithms was improved from various perspectives. Nevertheless, these algorithms have certain limitations to some extent: for instance, in the early stage of search, the content of pheromone is relatively scarce, which easily leads to problems such as blind search and local optimization.
To sum up, in multipath basic protocols, MPDT focuses on resource efficiency (load balancing to extend network lifetime) but lacks real-time performance and reliability, while 3R emphasizes real-time performance and reliability (parallel transmission to reduce latency) but comes at the cost of high energy consumption. The single-index optimization protocol PARTROUTE only focuses on node energy but neglects real-time performance, reliability and load balancing. The multi-index fusion protocol covers energy, signal-to-noise ratio and cache, but lacks real-time performance and is prone to falling into local optimum. In the intelligent optimization protocol, the multi-objective evolutionary algorithm weighs energy consumption and reliability but lacks real-time performance and has high complexity. The leapfrog algorithm only solves congestion problems. The GA has weak positive feedback and slow convergence. The fractional cuckoo search index covers all aspects but has low feasibility. The ant colony algorithm has strong global exploration but has problems of blind search in the early stage and local optima. Overall, the existing protocols generally have common problems such as incomplete index coverage, single optimization logic, and rigid scenario adaptation, making it difficult to meet the comprehensive QoS requirements of complex wireless networks.
Therefore, in order to enhance the transmission efficiency, quality and data integrity of wireless Mesh network transmission, ensure the QoS service volume of the network, and provide an expandable intelligent solution for the growing demand of modern service composition. This paper proposes a multi-constraint QoS routing algorithm based on an improved whale algorithm. The main contents of this study include:
- An improved multipath DSR routing algorithm (WDSR) was designed based on the DSR protocol. A calculation method for the link overlap degree has been developed. Under the principle of minimum hop count in the DSR protocol, the path with the minimum hop count is taken as the main path. According to the designed overlap calculation method, two paths with the lowest overlap degree and the smallest hop count are selected as auxiliary paths, thereby achieving multi-path routing and improving the performance and QoS of the mobile AD hoc network.
- To further enhance the network performance of the WDSR routing algorithm when the network congestion is high, based on the WDSR algorithm, by improving the convergence factor in the whale algorithm and introducing inertia weight, a multipath QoS routing algorithm (YWDSR) based on the improved whale optimization algorithm is proposed.
2. Materials and Methods
2.1. QoS Routing Mathematical Model
To study the problem of network QoS, an abstract mathematical model of this problem is established. The core objective of multi-constraint QoS routing is to start from the source node and find a transmission path that can reach the destination node and satisfy all the preset routing constraints. This study adopts the network model in Reference [16].
As shown in Figure 1, an undirected graph G(V,E) is adopted to represent the network model of multi-constraint QoS routing, where V represents all routing nodes in the network,E represents all communicable links in the network, r is the interactive range of nodes, and d represents the distance between nodes. If d < r, then there exists a communicable link e between two nodes, and . Given an undirected graph G(V,E), the set of paths from the source node to the destination node is P. For a path p ∈ P, the edge set is E(p), and the node set is N(p).
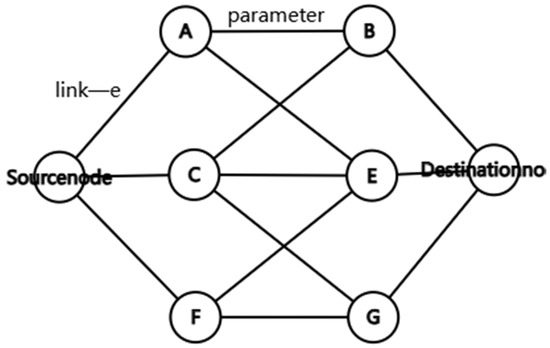
Figure 1.
QoS network model.
In practical applications, indicators such as delay, packet loss rate, Bandwidth and overhead are commonly used to measure the QoS performance of links. The corresponding formulas are as follows:
Time Delay:
Bandwidth:
Packet Loss Rate:
Overhead:
Equations (1)–(4) express the four most important constraints in the network in the form of mathematical formulas, respectively, and the purpose of the QoS routing algorithm is to find a routing path that satisfies the following conditions :
Delay constraint:
Bandwidth constraint:
Packet loss rate constraint:
The overhead constraint achieves its minimum value under the premise that indicators such as delay, bandwidth, and packet loss rate meet the constraint conditions.
2.2. Improved Multipath DSR Routing Algorithm
In the process of route discovery, the DSR routing protocol selects the path with the smallest hop count, that is, the single-path routing protocol. However, in scenarios with large-scale networks, high dynamic requirements, and low latency demands, the quality of service will significantly decline.
To enhance the QoS performance of the network, this chapter continues to optimize based on the DSR protocol and proposes a multipath WDSR protocol, enabling it to find multiple routes that meet the conditions during the route establishment process. When one of them is disconnected due to the movement of the network topology, data can continue to be transmitted by choosing other alternative paths, reducing the delay in restarting the route establishment.
2.2.1. Stability Analysis of Multipath
Multipath routing protocols [17] can be classified into three types [18] based on their correlation characteristics: path-dependent, path-uncorrelated, and node-uncorrelated.
As shown in Figure 2, S denotes the source node and D denotes the destination node. The three path types are defined and illustrated as follows:

Figure 2.
Schematic diagram of multipath routing.
Path-related types refer to the existence of a shared link between two different paths, as shown in paths S-A-B-D and S-B-D in Figure 2. The path-uncorrelated type refers to the situation where there is no shared link between two different paths, as shown in paths S-A-B-D and S-B-E-D in Figure 2. The node-unrelated type refers to the situation where there is no shared intermediate node between two different paths, as shown by the paths S-A-B-D and S-C-E-D in the figure.
The stability of Mesh networks is affected by many factors such as the movement of node positions and interference from wireless channels. The following will analyze the stability of path types and find the optimal path criterion [18]
Suppose the Path is PATH (a1, a2…), if the probability of path breakage caused by movement and other reasons for each node is p, then the stability of the single-path routing is:
The probability of path failure is:
According to probability knowledge, it is known that , Therefore:
That is, , indicating that the greater the number of nodes in the path, the less stable the path.
Let a multipath composed of two paths be called MPi, where i represents the number of common nodes of the two paths. Let the number of nodes in one path be m and the number of nodes in the other path be n then .
MP0 indicates that the two included paths have no shared intermediate node, and its failure rate is
MP1 indicates that the two included paths share a common intermediate node, and its failure rate is:
By analogy, MPk indicates that the two paths it contains have k intermediate nodes, and its failure rate is:
Then compare the failure rates of MPk and MPk-1
It can be seen from Equation (14) that the more common intermediate nodes there are in a multipath, the higher the failure rate. Therefore, the stability of the node uncorrelated type of multipath is the best. When transmitting data through multipath routing algorithms, efforts should be made to select paths where nodes are not correlated, and the number of intermediate nodes should be as few as possible [19].
2.2.2. Multipath Selection Strategy
- Calculation of Link Overlap Degree
This paper designs a calculation method for link overlap. By specifically quantifying the correlation degree among multiple communicable routing paths obtained by the routing algorithm, the required multiple paths are selected based on the size relationship of the overlap degree. The specific calculation method for the degree of overlap. As shown below
Suppose there are two paths, Pa and Pb. L(P) represents the set of links contained in path P, and L(Pa) ∩ L(Pb) represents the shared set of links of the two paths. L(Pa) ∪ L(Pb) represents the set of all unique links contained in the two paths.
For the two paths Pa and Pb, the calculation formula for the weighted link overlap degree E(Pa,Pb) is:
- 2.
- Multipath Selection Strategy
It can be known from reference [20] that when the number of paths in multipath routing is three, the best network performance can be achieved. Conversely, not only does it fail to improve the network performance, but it also increases the routing overhead of the protocol. Therefore, after the destination node receives multiple path information, only three of the best node-unrelated paths are selected from them.
The DSR protocol is a single-path routing protocol that uses the minimum hop count as the routing criterion. To better adapt it to wireless Mesh networks, its routing discovery rules are changed to make it a multipath routing protocol. The strategy is as follows:
- (1)
- If the routing cache of the intermediate node contains a path to the destination node, the RREQ packet continues to be forwarded along this path, and the intermediate node does not need to return the RREP message to the source node.
- (2)
- Intermediate nodes refuse to forward RREQ messages that have already recorded the addresses of intermediate nodes to avoid forming routing loops.
- (3)
- The destination node should receive RREQ messages as much as possible within the specified time, select the path with the minimum hop count as the master path, calculate the link overlap degree between other paths and the master path, and choose the two paths with the lowest overlap degree as the slave paths. If there is more than one path, choose the one with the fewest hops.
2.3. QoS Routing Algorithm Based on Improved Whale Optimization Algorithm
The previous text proposed an improved multipath DSR routing algorithm, WDSR, which can adapt to the characteristics of wireless Mesh networks. However, the algorithm still follows the DSR protocol and selects around the path with the minimum hop count. The number of hops in a path does not directly affect the QoS parameters of the path. When the distance from the source node to the target node remains unchanged, the average distance between nodes on the path selected based on the principle of minimum hop count may be greater than that on other paths. When the distance between nodes exceeds a certain level, it leads to poor wireless connection signals between nodes and cannot guarantee the stability of the connection. Therefore, this paper proposes a multi-constraint QoS routing algorithm, YWDSR, for wireless Mesh networks based on the improved whale algorithm.
2.3.1. Whale Optimization Algorithm
The whale optimization algorithm [21] was proposed by Mirjalili et al. in 2016 as a novel swarm intelligence optimization algorithm. Its inspiration comes from the hunting behavior of humpback whales, especially their unique “bubble-net feeding strategy”. This algorithm achieves an efficient solution of complex optimization problems by simulating the encirclement, spiral attack and random search mechanism of whales. Compared with other intelligent algorithms, WOA has certain advantages. Compared with the Genetic Algorithm (GA), WOA does not require complex crossover and mutation operations, has fewer parameters (mainly relying on the search agent position update), and is easier to adjust parameters. Compared with the Particle Swarm Optimization (PSO) algorithm, the spiral mechanism of WOA can more precisely balance exploration and development in path search, avoiding premature convergence.
Specifically, WOA mainly simulates three behaviors of whales: surrounding prey (EncirclingPrey): the whale gradually approaches the optimal solution (prey) by adjusting its position; Bubble net attack (bubble-netAttacking): Using a spiral movement mode for fine search and random search within a local range (Searchfor prey): When no clear target is found, whales will randomly swim to explore new areas (global search). The position of each whale represents a feasible solution, and in the D-dimensional solution space, its position is Xsd = (X1, X2, X3, …) (XD), where Xj ∈ Xsd represents a valid path from the source node to the target node. Combining the traditional WOA, the multi-path routing discovery optimization model of mobile AD hoc networks consists of two sub-models: bubble net attack and prey search [17]. The following is a detailed introduction to the mathematical representation of whale behavior:
- (1)
- Bubble Net attack
The whale approaches the current optimal individual (prey).
In the formula, t represents the number of iterations; is the current optimal position vector; X(t) is the current search agent set vector; A and C are coefficient vectors, and the formula is:
r1 and r2 are random vectors on [0, 1]. By reducing the value of a in the formula, the behavior of shrinking and enclosing can be achieved. a is the convergence factor, and its relationship with t is shown in Equation (20):
In the formula, represents the maximum number of iterations.
Spiral position update stage:
The process by which whales approach their prey satisfies the spiral equation:
Among them: b is a constant used to define the shape of the logarithmic helix, and r is a random number on [−1, 1].
Since the contraction and encirclement mechanism and the spiral position update occur simultaneously during the bubble net attack, assuming that the probability of the whale performing any one of these behaviors is 50%, the position update formula of the whale is:
Here, p is a random number in [0, 1].
- (2)
- Search for prey
When prey is scarce or unevenly distributed, humpback whales conduct extensive random searches. The expression at this stage is
Among them: is the position of the randomly selected whale individual in the group.
2.3.2. Adaptability of WOA
Compared with other meta-heuristic algorithms, the WOA has natural adaptability in routing optimization due to its two-stage search and dynamic following characteristics. The specific comparison is shown in Table 1:

Table 1.
Comparison of the compatibility of WOA.
2.3.3. Improved Whale Optimization Algorithm
- Convergence Factor
In the Whale Optimization Algorithm (WOA), humpback whales perform predation behavior according to Equation (17). Specifically, when |A| ≥ 1, the algorithm conducts a random global search with a probability of 0.5; when |A| < 1, it switches to local exploitation. This mechanism makes it difficult to balance exploration and exploitation in complex optimization problems, potentially leading to premature convergence to local optima.
As indicated in Equation (18), the value of A is dynamically adjusted with the convergence factor a. Since the linear convergence factor a decreases linearly with the increase in iteration, it results in insufficient global search time in the early stage of the algorithm and fixed local exploitation step size in the later stage, which fails to dynamically adapt to the multi-stage search requirements of complex environments.
To address this issue, a piecewise function convergence factor a′ is proposed to optimize this balance, as shown in Equation (24) below:
To further verify the effectiveness of a′ in algorithm search, a comparative is conducted with the convergence factor of the original WOA.
As shown in Figure 3, At the beginning of the iteration, the downward trend of a’ is relatively gentle, which can maintain A large value for a long time, promoting the A value to remain at a high level and effectively extending the global search time. The global search ability and convergence speed of the algorithm rapidly decay from a higher value to a lower value in the middle of the iteration, achieving a rapid transition from global search to local search. Maintain a relatively low value in the later stage of iteration to ensure the local search performance of the algorithm.
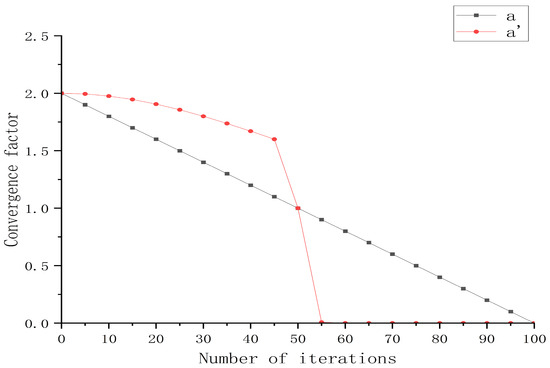
Figure 3.
Convergence factor comparison curve.
- 2.
- Inertia weight
The inertia weight ω is an important parameter of the Particle Swarm Optimization (PSO) algorithm and plays a significant role in the convergence of the algorithm. In PSO, the larger the ω value, the stronger the global search ability. Conversely, the smaller the ω value, the stronger the local search ability and the weaker the global search ability. The inertia weight ω of the PSO algorithm is introduced as the guide weight to improve the convergence accuracy and better adjust the global search ability and local search ability of the algorithm. The inertia weight ω value of synergy a decreases with the increase in the number of iterations and is controlled by the convergence factor a, making the ω value positively correlated with the a value. It is defined as follows:
Among them: is the maximum value of convergence factor a, and amin is the minimum value of convergence factor a; is the maximum value of the inertia weight, and is the minimum value of the inertia weight. tmax represents the maximum number of iterations.
After introducing the inertia weight ω, the search methods of WOA were changed from Formulas (14) and (15) to Formulas (18) and (19), respectively:
Adaptive inertia weights, through dynamic adjustment, can encourage broader global search in the early stage of the algorithm and enhance local search near the known optimal solution in the later stage. This dynamic adjustment helps the algorithm strike a balance between global search and local search, thereby enhancing the algorithm’s optimization ability, laying a solid foundation for finding high-quality QoS routing solutions in complex wireless Mesh networks.
- 3.
- Fitness function
- (1)
- Time delay:
Among them, is the delay of the generated path, and is the maximum delay of all candidate paths.
- (2)
- Bandwidth:
Here, represents the bandwidth of the generated path, and represents the minimum bandwidth of all candidate paths.
- (3)
- Packet loss rate:
Here, represents the bandwidth of the generated path, and represents the minimum bandwidth of all candidate paths.
- (4)
- Hop count
As can be seen from the above, the smaller the delay, the larger the bandwidth, the smaller the packet loss rate, and the smaller the hop count, the more likely this path is to be chosen as the candidate path. Therefore, the fitness function is:
Among them, , the weight selection is flexibly adjusted according to the application scenario, and is the number of path hops.
To sum up, the WOA flow is shown in the following figure.
As shown in Figure 4, The improvement of multipath DSR protocols using whale optimization algorithms mainly consists of the following three stages:

Figure 4.
Flowchart of the WOA.
- 1.
- Initialization stage.
- (1)
- Start: Initiate the algorithm process.
- (2)
- Initialize the population: Randomly generate a set of initial solutions (whale individual positions) to cover the solution space and serve as the search starting point.
- (3)
- Calculate fitness: Use the objective function to evaluate the “advantages and disadvantages” of each individual.
- 2.
- Iterative optimization stage.
- (1)
- Update parameters: Adjust key parameters of the algorithm.a: Decreasing in the form of piecewise functions, the control search mode shifts from “global exploration” to “local development”.
- (2)
- Behavioral selection (hunting strategy);p is a random number in [0, 1]. Select “encircle the prey” or “spiral update” based on p.p < 0.5 (encircling development stage): Then judge (|A| < 1). If it is satisfied, perform the encircling behavior, gather towards the optimal individual according to Formula (17), and converge towards the current optimal solution.p ≥ 0.5 (exploration stage): Perform spiral update and expand the search range using the spiral curve according to Formula (21).
- 3.
- Selection of the best and iterative termination.
- (1)
- Calculate the new fitness: After updating the position, recalculate the individual fitness.
- (2)
- Update the optimal solution: If the fitness of the new individual is better than the historical optimum, replace the optimal solution and record the position.
- (3)
- Determine the termination condition: Check whether the number of iterations t has reached its maximum value.
2.3.4. Improvement of Data Structure
In order to achieve QoS support for the YWDSR routing protocol, this section modifies the data structure of the RREQ message of the existing DSR routing protocol.
The data structure of the RREQ message of the DSR protocol is modified to form the RREQ message of the YWDSR protocol. The modified routing request frame is shown in Table 2. Five main fields have been added: the minimum bandwidth field required by the service, the maximum delay field acceptable to the service, the delay accumulation field during the transmission process, and the bandwidth record field during the transmission process. When a service is initiated, the minimum bandwidth and the maximum acceptable delay required by the service are first estimated. After obtaining the results, they are recorded in the corresponding fields and remain unchanged as the QoS limit threshold for pathfinding in the subsequent process. The values of the two cumulative fields are initially 0 and change as the path-seeking process progresses. Once the values of the two cumulative fields exceed the QoS limit threshold, it indicates that the path passed by this message does not meet the QoS requirements, and this RREQ message will be directly discarded.

Table 2.
RREQ message data structure.
- Data Structure of RREP Messages
As shown in Table 3, The RREQ message of the YWDSR algorithm increases the comprehensive cost function value F of the path, and the source node can select the path based on the F value.

Table 3.
RREP message data structure.
3. Results
3.1. Performance Analysis of WDSR Algorithm
In order to analyze the performance of the WDSR routing algorithm, this paper uses NS-2 simulation software to conduct simulation experiments. NS-2 is a network simulation emulator developed by the University of California, Berkeley. The simulation function of NS2 can simulate most of the existing transport layer network protocols. The NS2 development languages are C++ and OTCL, which include the simulated event scheduler, the network component object library, and the model library of the built network.
It is compared with the traditional DSR protocol and an improved algorithm, NDMR, to analyze the performance in terms of average end-to-end delay, packet loss rate and average throughput. The experiment is set in a space of 1000 m × 1000 m, with a total of 50 wireless Mesh network nodes. The communication radius of each node is set at 250 m. The nodes are mobile and move in a randomly selected direction according to the RandomWaypoint model [21]. Suppose the minimum bandwidth required for the business is 64 kHz, that is, Bmin = 0.128 Mbps, and the maximum delay is 200 ms, that is, Delaymax = 200 ms. The destination node is allowed to collect routing paths within 50 ms and select two paths with larger fitness functions from them as multipath routes. Other parameter Settings of the network environment are shown in Table 4.

Table 4.
Simulation Parameter Setting.
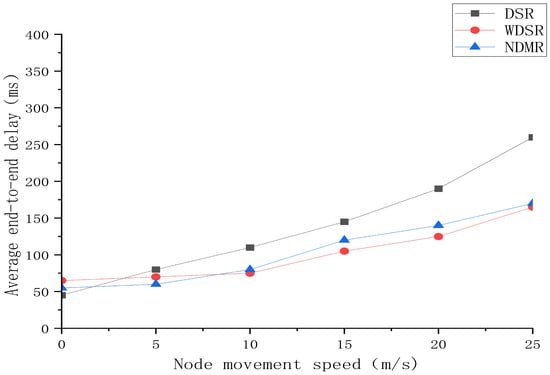
Figure 5.
The average end-to-end latency of DSR, WDSR and NDMR.
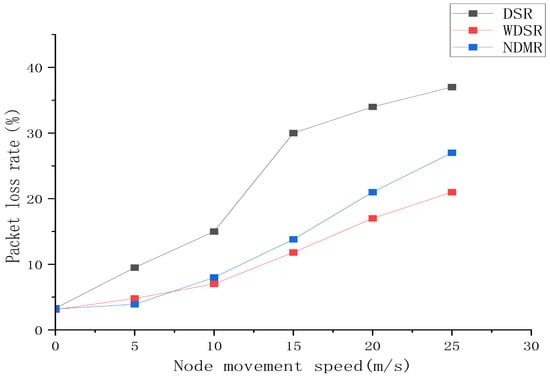
Figure 6.
The packet loss rates of DSR, WDSR and NDMR.

Figure 7.
The average throughput of DSR, WDSR and NDMR.
It can be seen from Figure 5 that when the node movement speed of the wireless Mesh network is relatively slow, the average end-to-end delay of the DSR protocol is the smallest. This is because the DSR protocol does not need to frequently search for new routing paths. However, even when nodes are stationary, the WDSR protocol needs to continuously detect the state of the network, which makes its average end-to-end delay higher than that of the DSR protocol. However, as the speed of node movement increases, the topological structure of the network begins to change frequently. The DSR protocol requires frequent route discovery, while the WDSR protocol can promptly sense changes in the network topology. At this point, the average end-to-end delay of the WDSR protocol is superior to the other two algorithms.
Figure 6 shows the packet loss rate varying with the speed of node movement. When the speed is 0, the packet loss rates of these three protocols are basically the same. However, as the speed of node movement increases, the network topology becomes unstable. The packet loss rate growth rate of the WDSR protocol is significantly lower than that of the DSR protocol. The NDMR protocol adopts a multipath routing strategy to balance network load and improve fault tolerance, so the increase in packet loss rate is relatively slow. The WDSR protocol was modified to a multipath routing protocol based on these important parameter indicators from the very beginning of its design. After comprehensive consideration, the communication connection performance selected by the WDSR protocol is better, thereby improving the fault tolerance rate of the network.
Figure 7 shows the variation in the average network throughput as the node movement speed increases. From the image, it can be seen that the average throughput of the three algorithms is gradually decreasing. This is due to the reduced stability of the links in the network. Within a relatively short period of time, the entire system network needs to be constantly discovered and maintained, which leads to a continuous decrease in the received data streams. With the further increase in node speed, the WDSR protocol, due to the adoption of an improved multipath routing strategy, makes the stability of the routing path higher than that of the DSR protocol and the NDMR protocol. Therefore, the reduction in the average throughput of the WDSR protocol is significantly smaller than that of the DSR protocol.
3.2. Performance Analysis of the YWDSR Algorithm
The multipath QoS routing algorithm based on the Whale Optimization Algorithm is an improvement on the WDSR algorithm. Therefore, the proposed WDSR algorithm is used as a benchmark, and the QAMR (Ant colony optimization algorithm) algorithm is selected as a second benchmark algorithm.
The network environment Settings for the simulation experiment in this section are the same as before. In the experiment of the improved multipath QoS routing algorithm, the population size is set to 30, and the Settings of other parameters are as follows: t = 100, ω_1 = 0.4, ω_2 = 0.4, ω_3 = 0.2, N = 50.
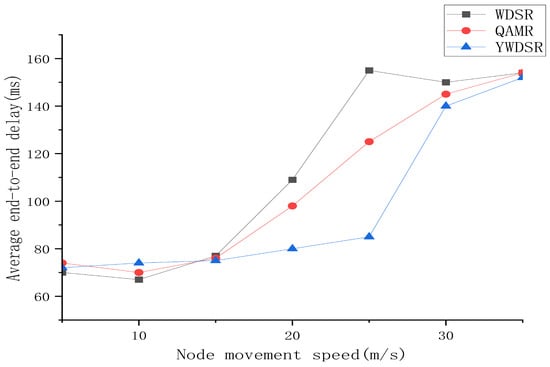
Figure 8.
The average end-to-end latency of WDSR, QAMR and YWDSR.
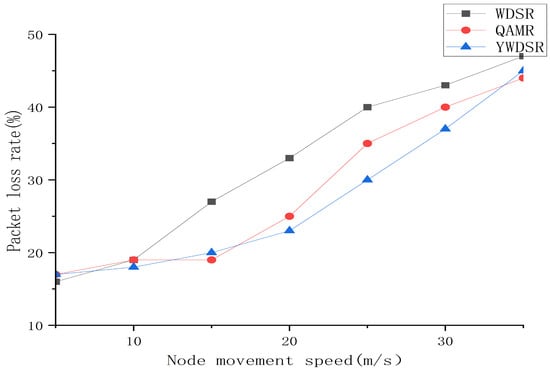
Figure 9.
The packet loss rates of WDSR, QAMR and YWDSR.

Figure 10.
The average throughput of WDSR, QAMR and YWDSR.
Figure 8 shows that the average end-to-end delay of the three routing algorithms varies as the number of data streams in the network increases. The continuous increase in the number of data streams in the network indicates that the network load and network congestion are deteriorating. When the degree of network congestion is low. The whale algorithm needs to be constantly optimized to select the optimal path, while the ant colony algorithm selects the optimal path through the continuous accumulation and iterative search of pheromones, which leads to the average end-to-end delay of the YWDSR and QAMR algorithms being higher than that of the WDSR algorithm. As can be seen from the figure, when network congestion reaches a certain level, the average end-to-end delay of the two optimization algorithms is better than that of WDSR. This is because the number of data streams keeps increasing, and the number of data streams on the path with the minimum hop count selected by WDSR keeps accumulating. The congestion degree of this path keeps rising, resulting in a continuous decline in network performance. The YWDSR algorithm balances global search and local search, and selects the optimal path at this time as the transmission path, resulting in better network performance.
Figure 9 shows that the packet loss rates of the three algorithms change as the number of data streams in the network increases. When the degree of network congestion is low, the packet loss rates of the three algorithms do not differ much. As the degree of network congestion continues to increase, the packet loss rate of algorithms gradually shows differences. YWDSR and QAMR transmit data packets by choosing the optimal path, so the increase in packet loss rate is relatively low. However, the WDSR algorithm is based on the principle of minimum hop count and only selects the path that meets the minimum hop count. It does not specifically consider that when the number of network data streams increases, more data streams are transmitted through the path with the minimum hop count, resulting in a rapid increase in the congestion degree of the path with the minimum hop count. This will lead to a greater decline in network performance. Compared with the QAMR algorithm, the packet loss rate performance of the YWDSR algorithm does not improve much, mainly because both select the optimal path as the transmission path.
Figure 10 shows the variation in the average throughput of the three algorithms as the number of data streams in the network increases. In the initial stage, the number of data streams in the network is relatively small, and the average throughput does not differ much. It can be seen from the figure that as the number of data streams increases, the average throughput reaches a relatively large level and then decreases. This is caused by the intensification of network congestion and the overall decline in network performance. Overall, in a harsh network environment, the network performance of the optimal path selected by the optimization algorithm is superior to that of the path with the smallest hop count. Compared with the QAMR algorithm, the average throughput of the YWDSR algorithm is relatively higher, and its overall performance is better than that of the QAMR algorithm.
4. Discussion
This study focuses on wireless Mesh networks by investigating their structural characteristics, performance advantages, and limitations. Combined with the practical requirements for network QoS routing, two improved routing algorithms are proposed to address the challenges of stability and efficiency in dynamic network environments, with the following key findings:
- Design and Performance of the WDSR Algorithm
An improved multipath DSR routing algorithm (WDSR) is proposed based on the traditional DSR protocol. Through an analysis of multipath link stability, it is confirmed that fewer overlapping links between paths correspond to higher link stability. Guided by this principle, a method for calculating link overlap degree is designed to quantify the correlation between candidate paths.
In the path selection phase, WDSR selects the minimum-hop path as the primary path and two secondary paths with the lowest overlap degree relative to the primary path, thereby realizing multipath routing. Simulation experimental results demonstrate that WDSR is better adapted to the dynamic characteristics of wireless Mesh networks: compared with the traditional single-path DSR protocol, it significantly improves network performance in three core QoS metrics—reducing average end-to-end delay, lowering packet loss rate, and enhancing average throughput.
- 2.
- Design and Performance of the YWDSR Algorithm
To further optimize routing performance under multi-constraint QoS requirements, a multi-constraint QoS improved multipath DSR routing algorithm (YWDSR) is proposed by integrating an improved Whale Optimization Algorithm. The original WOA is enhanced in two key aspects to better match the needs of routing path optimization:
Nonlinear convergence factor: Designed to dynamically adjust the search step size with the progress of iterations. In the early iteration stage, it maintains a large value to support extensive global exploration of the solution space; in the late stage, it decreases adaptively to enable precise local exploitation around potential optimal solutions.
Adaptive inertia weight strategy: Adjusts the weight dynamically according to the distribution of the current population. This strategy balances the algorithm’s early exploration and late exploitation processes, avoiding both the inefficiency of blind global search and the risk of premature convergence to local optima.
Simulation experiments verify that YWDSR further enhances the adaptability of wireless Mesh networks. Under scenarios with high node mobility or heavy network congestion, it outperforms the WDSR algorithm in end-to-end delay control, packet loss rate suppression, and throughput maintenance, providing more reliable QoS guarantees for data transmission.
“Although the research results are encouraging, this study still has some limitations: high overhead under low congestion conditions, the contradiction between iterative optimization features and the real-time requirements of routing, and the contradiction between manual configuration of multi-objective optimization and dynamic scene adaptation. Future research will focus on breakthroughs in four major directions: lightweight computing, adaptive weights, dynamic topology awareness, and protocol stack compatibility, in order to enhance the universality, sustainability, and scalability of the proposed methods. At the same time, in response to the adaptation boundary issues in the Internet of Vehicles (which needs to be restructured into a distributed predictive optimization architecture to bridge the gap in mobility and reliability) and 5G/6G (which only supports non-real-time service slicing and requires cross-layer collaboration of edge computing), ultimately, a “scene-parameter” dynamic matching model and an “edge-terminal” collaborative optimization architecture are constructed. And paths such as the fitness function for cross-layer indicator fusion, which transform limitations into practical improvement paths, provide specific guidance for engineering deployment, and achieve value upgrading.”
Author Contributions
Conceptualisation, D.S. and Y.N.; methodology, Y.N.; software, Y.N.; validation, D.S. and Y.N.; formal analysis, Y.N.; investigation, Y.N.; resources, D.S. and Y.N.; data curation, Y.N.; writing—original draft preparation, Y.N.; writing—review and editing, D.S.; visualisation, Y.N.; supervision, D.S.; project administration, D.S.; funding acquisition, D.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Shandong Province Major Scientific and Technological Innovation Project No. 2019TSLH0315; Project Contract of Shandong Provincial Key Research and Development Program (Major Scientific and Technological Innovation Project) Project Number: 2023CXGC010701.
Data Availability Statement
Data available on request due to privacy. The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zeng, F.; Zhao, N.; Li, W. Joint interference optimization and user PAtisQAction improvement for multicast routing and channel assignment in wireless mesh networks. Clust. Comput. 2019, 22, 15059–15072. [Google Scholar] [CrossRef]
- Jing, Z. Research on QoS Routing Security Algorithm Based on QAODV Protocol. In Proceedings of the 4th International Conference on Intelligent Structure and Vibration Control (ISVC 2014), Chongqing, China, 25–28 July 2014; Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences: Beijing, China, 2014; pp. 245–250. [Google Scholar]
- Poojary, S.; Pai, M.M.M. Multipath Data Transfer in Wireless Multimedia Sensor Network. In Proceedings of the 2010 International Conference on Broadband, Wireless Computing, Communication and Applications, Fukuoka, Japan, 4–6 November 2010; IEEE: New York, NY, USA, 2010; pp. 379–383. [Google Scholar]
- Krogmann, M.; Heidrich, M.; Bichler, D.; Barisic, D.; Stromberg, G. Reliable, Real-Time Routing in Wireless Sensor and Actuator Networks. ISRN Commun. Netw. 2011, 2011, 1–8. [Google Scholar] [CrossRef][Green Version]
- Sarangi, S.; Kar, S. Mobility Aware Routing with Partial Route Preservation in Wireless Sensor Networks. Ubiquitous Comput. Commun. J. 2011, 6, 848–856. [Google Scholar][Green Version]
- Ben-Othman, J.; Yahya, B. Energy efficient and QoS based routing protocol for wireless sensor networks. J. Parallel Distrib. Comput. 2010, 70, 849–857. [Google Scholar] [CrossRef]
- Rahat, A.A.M.; Everson, R.M.; Fieldsend, J.E. Evolutionary Multi-Path Routing for NetworkLifetime and Robustness in Wireless Sensor Networks. Ad Hoc Netw. 2016, 52, 130–145. [Google Scholar] [CrossRef]
- Krishna Kishore, K.; Rajesh Kumar, P. Comprehensive Analysis of PAPR Reduction in OFDM, UFMC and Signal Scrambling UFMC Technique using Shuffled Frog Leaping Algorithm. IETE J. Res. 2023, 69, 272–283. [Google Scholar]
- Ghaemi, Y.; Ocla, E.H. Time delay-based routing protocol using genetic algorithm in vehicular Ad Hoc networks. Clust. Comput. 2024, 28, 146. [Google Scholar] [CrossRef]
- Rama, R.A.; Patyananda, R.; Valli Kumari, V. Multipath selection based on fractional cuckoo search algorithm for QoS aware routing in MANET. Sens. Rev. 2019, 39, 218–232. [Google Scholar]
- He, J.; Teng, Z.; Zhang, F. Research on Power Control Routing Algorithm for Wireless Sensor Networks Based on Ant Colony Optimization. Wirel. Pers. Commun. 2024, 137, 1119–1139. [Google Scholar] [CrossRef]
- Palman, M.F.; Lehmoud, M.A.A.; Joda, A.F. Adaptation of the Ant Colony Algorithm to Avoid Congestion in Wireless Mesh Networks. J. Cyber Secur. Mobil. 2023, 12, 785–812. [Google Scholar]
- Suresh Kumar, M.; Sathish Kumar, G.A. Enhanced ant colony optimization algorithm for packet delivery with improved energy efficiency in wireless sensor networks. J. Intell. Fuzzy Syst. 2023, 44, 7909–7917. [Google Scholar] [CrossRef]
- Dorathy, I.E.P.; Chandrasekaran, M. Ant-based Energy Efficient Routing Algorithm for Mobile Ad hoc Networks. Intell. Autom. Soft Comput. 2022, 33, 1423–1438. [Google Scholar] [CrossRef]
- Wang, W.; Tong, G. Multi-path unequal clustering protocol based on ant colony algorithm in wireless sensor networks. IET Netw. 2020, 9, 56–63. [Google Scholar] [CrossRef]
- Chen, K.; Hu, X. Relay Routing Method Based on Genetic Adaptive Ant Colony System Algorithm. J. Cent. South Univ. (Nat. Sci. Ed.) 2013, 44, 571–579. [Google Scholar]
- Jinglun, S. An Independent Multipath Routing Algorithm in Ad hoc Networks. Comput. Eng. 2003, 29, 14–15. [Google Scholar]
- Wang, L.; Zhang, L. Multipath Source Routing in Wireless Ad hoc Networks. In Proceedings of the 2000 Canadian Conference on Electrical and Computer Engineering, Halifax, NS, Canada, 7–10 May 2000; Volume 1, pp. 79–83. [Google Scholar]
- Yang, X.; Fan, Z.; Min, G. In the satellite network SDN based multipath routing algorithm research. J. Mod. Inf. Technol. 2025, 9, 1–4. [Google Scholar] [CrossRef]
- Zheng, S. Research on QoS Routing Protocol and NS2 Simulation in Ad Hoc Networks. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2008. [Google Scholar]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 1–67. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).