Early Prediction of Student Performance Using an Activation Ensemble Deep Neural Network Model
Abstract
1. Introduction
2. Literature Review
2.1. Challenges
- Improving a model’s predictive accuracy is widely known to be difficult. Various factors play a role in enhancing predictive accuracy [3].
- The uneven distribution of classes in educational data is a frequent issue that can significantly impact the efficiency of models. Additionally, creating new ensembles and hybrid classifiers for the scenario poses a challenge [9].
- Examining and contrasting the effectiveness of classifiers is an important process. While it may seem easy to assess their performance, the results can be deceiving. Thus, determining the most optimal method that results in their strengths is a crucial task [4].
- Even though artificial neural networks help to reveal connections between neurons, a major drawback is the challenge of interpreting the relationships between independent and dependent variables [5].
2.2. Problem Statement
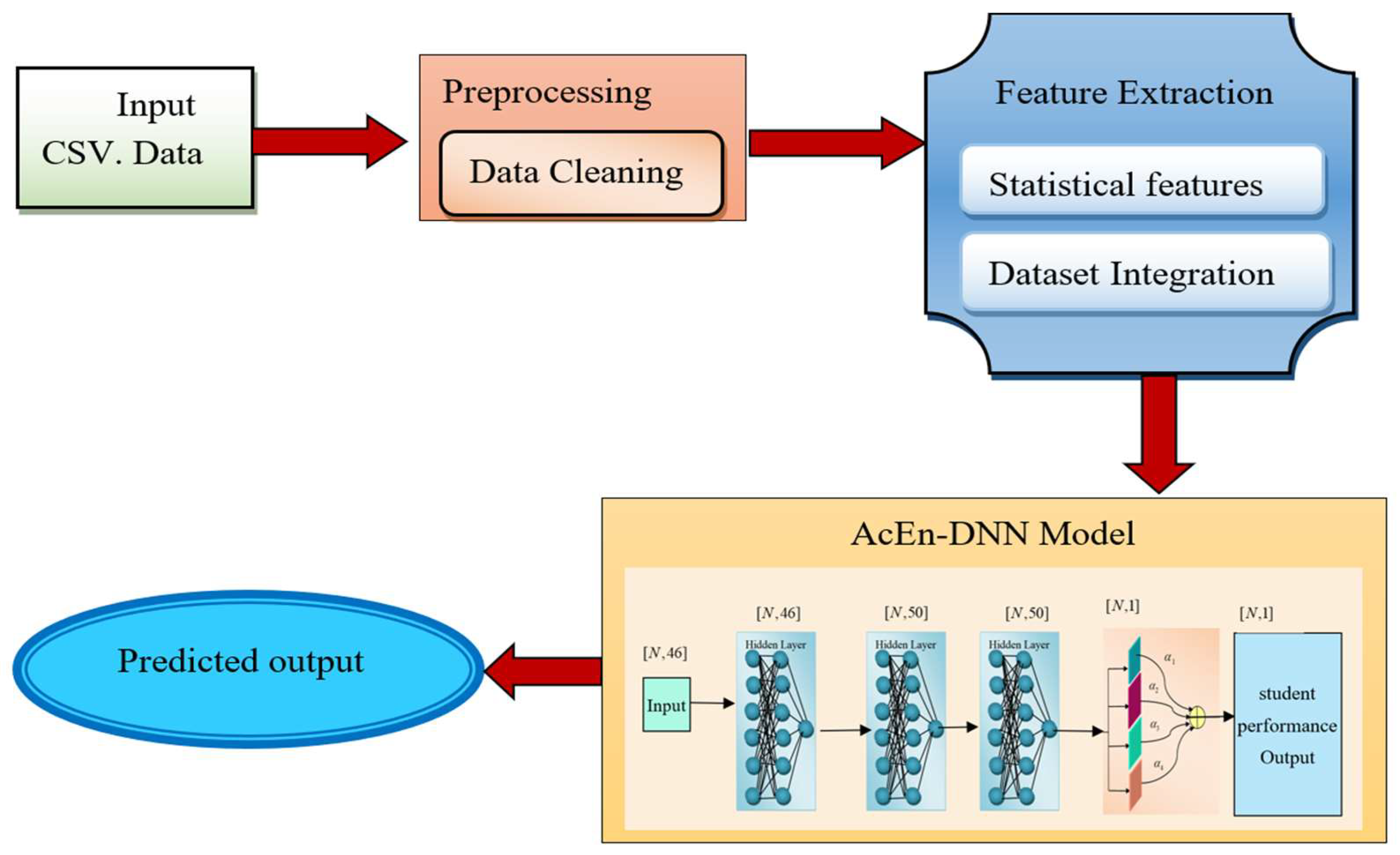
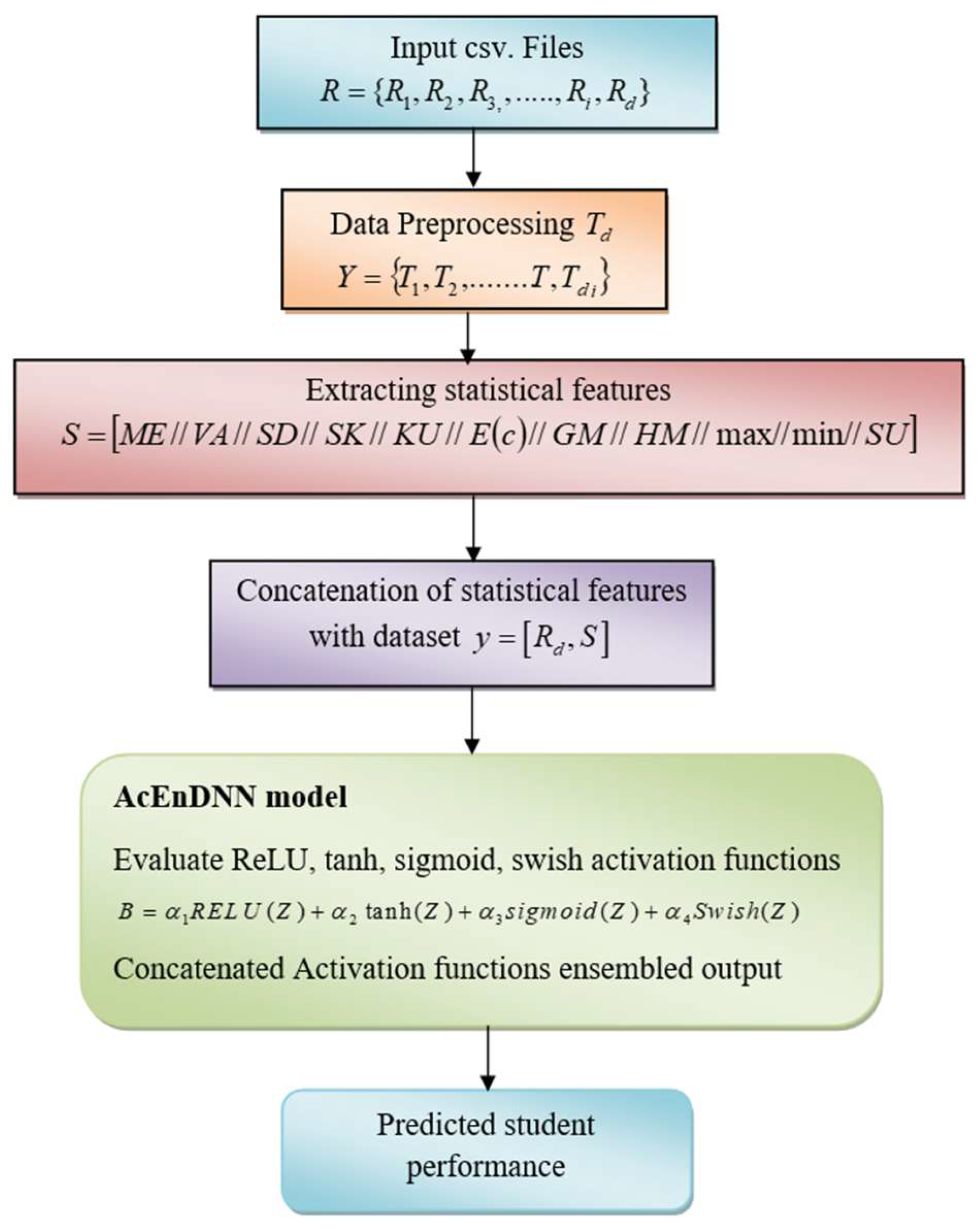
3. Methodology
3.1. Input Data for Students’ Performance Prediction
3.2. Preprocessing Data Mining for Students’ Performance Prediction
3.3. Statistical Feature Extraction for Students’ Performance Prediction
- (i)
- Mean:
- (ii)
- Variance:
- (iii)
- Standard Deviation (SD):
- (iv)
- Skewness:
- (v)
- Kurtosis:
- (vi)
- Entropy:
- (vii)
- Geometric Mean:
- (viii)
- Harmonic Mean:
- (ix)
- Maximum:
- (x)
- Minimum:
- (xi)
- Sum:
3.4. Data Integration
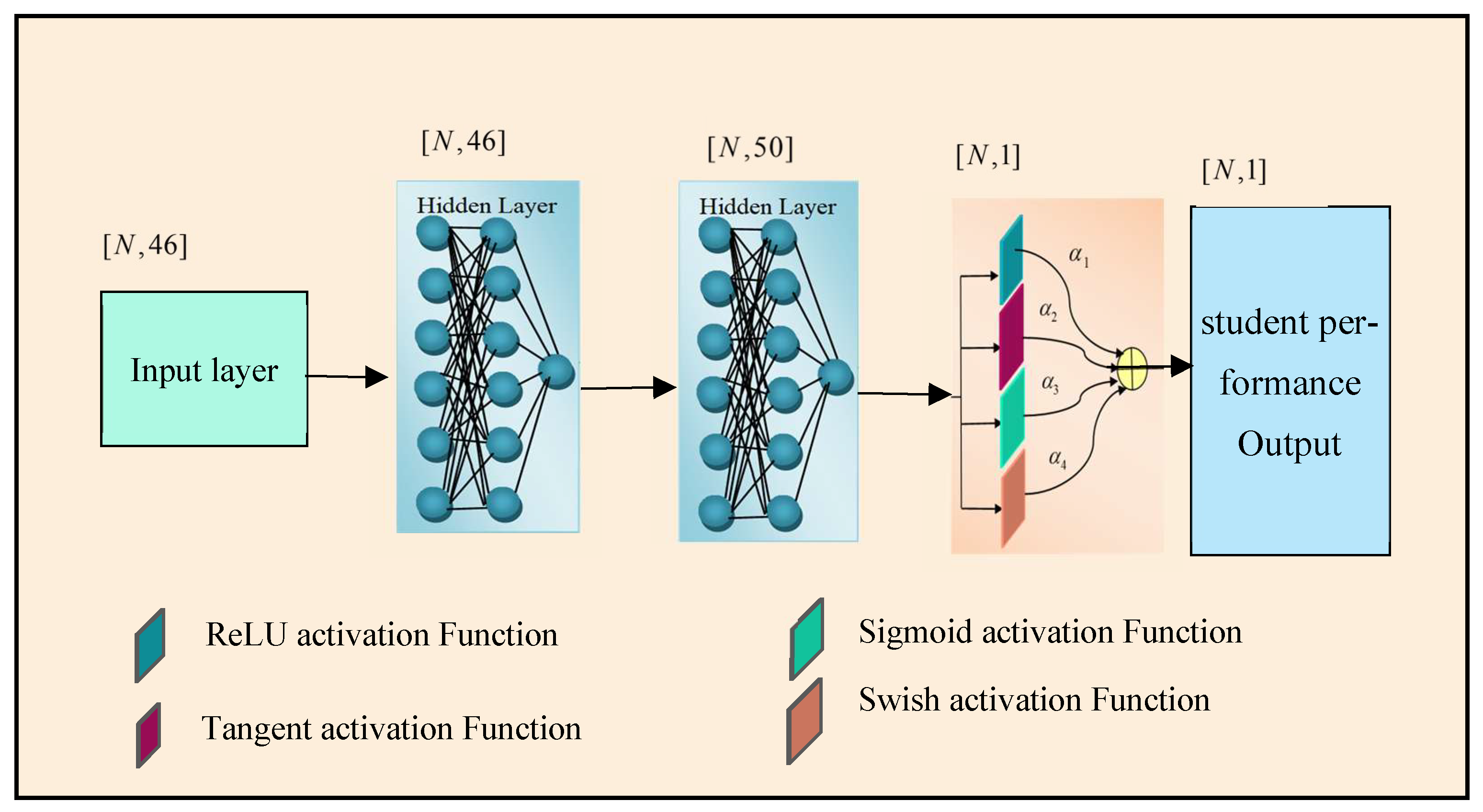
4. Activation Ensemble Neural Network in Student Performance Prediction
Activation Ensemble Deep Neural Network Model
5. Results and Discussion
5.1. Experimental Setup
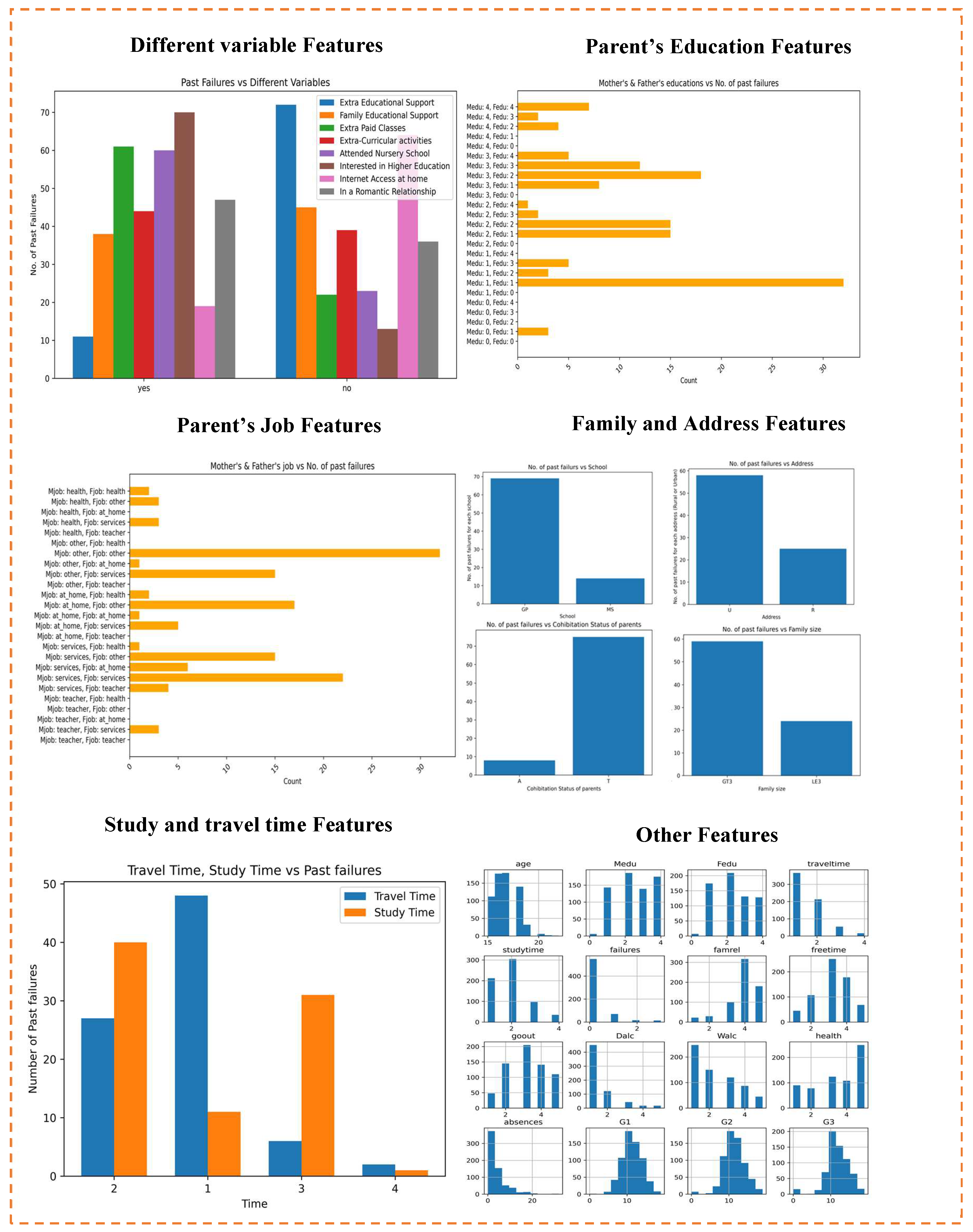
5.2. Dataset Description
5.3. Performance Metrics
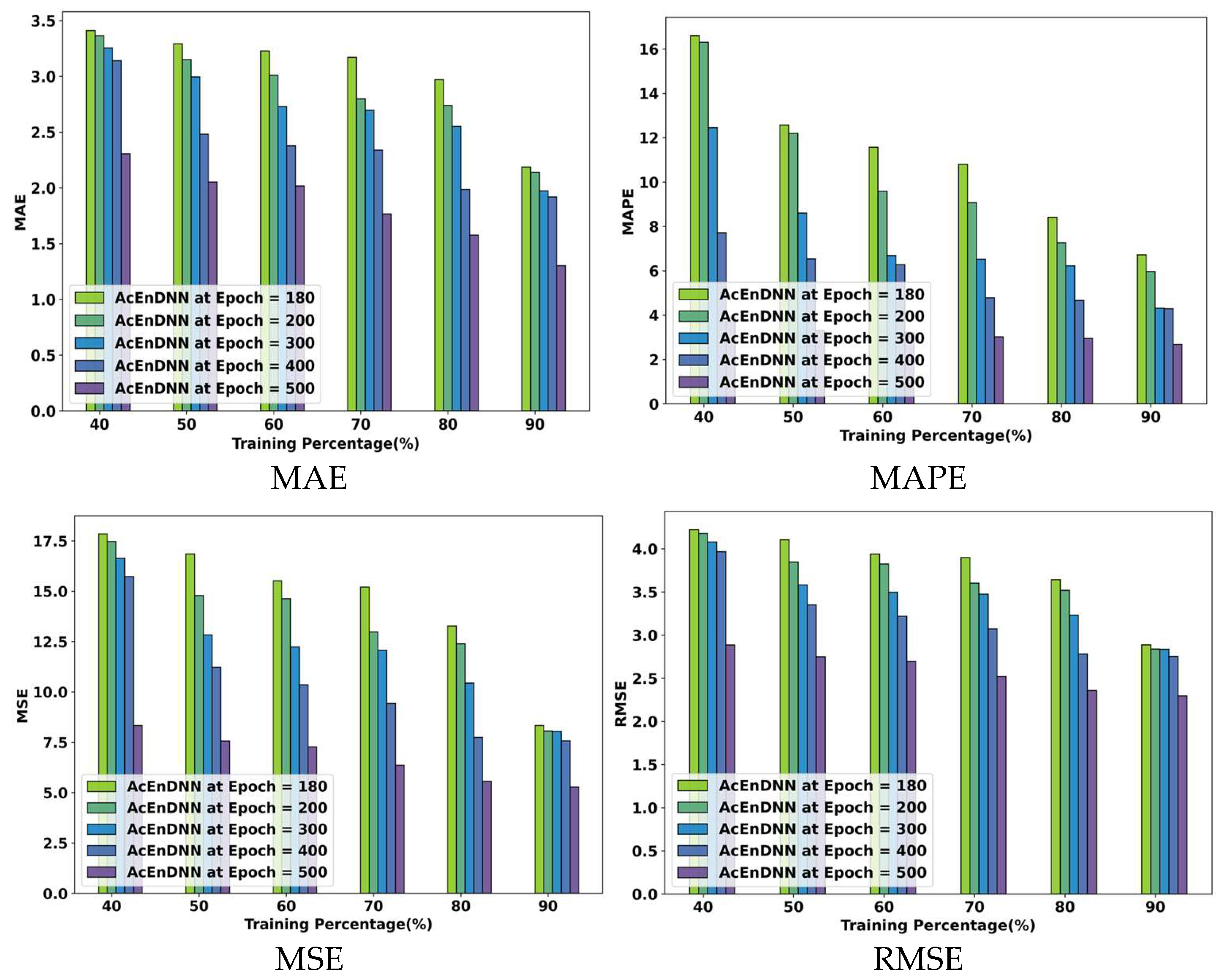
5.4. Performance Analysis of the AcEn-DNN Model Using Student-mat.csv Dataset
5.5. Performance Analysis of the AcEn-DNN Model Using Student-por.csv Dataset
5.6. Comparative Methods
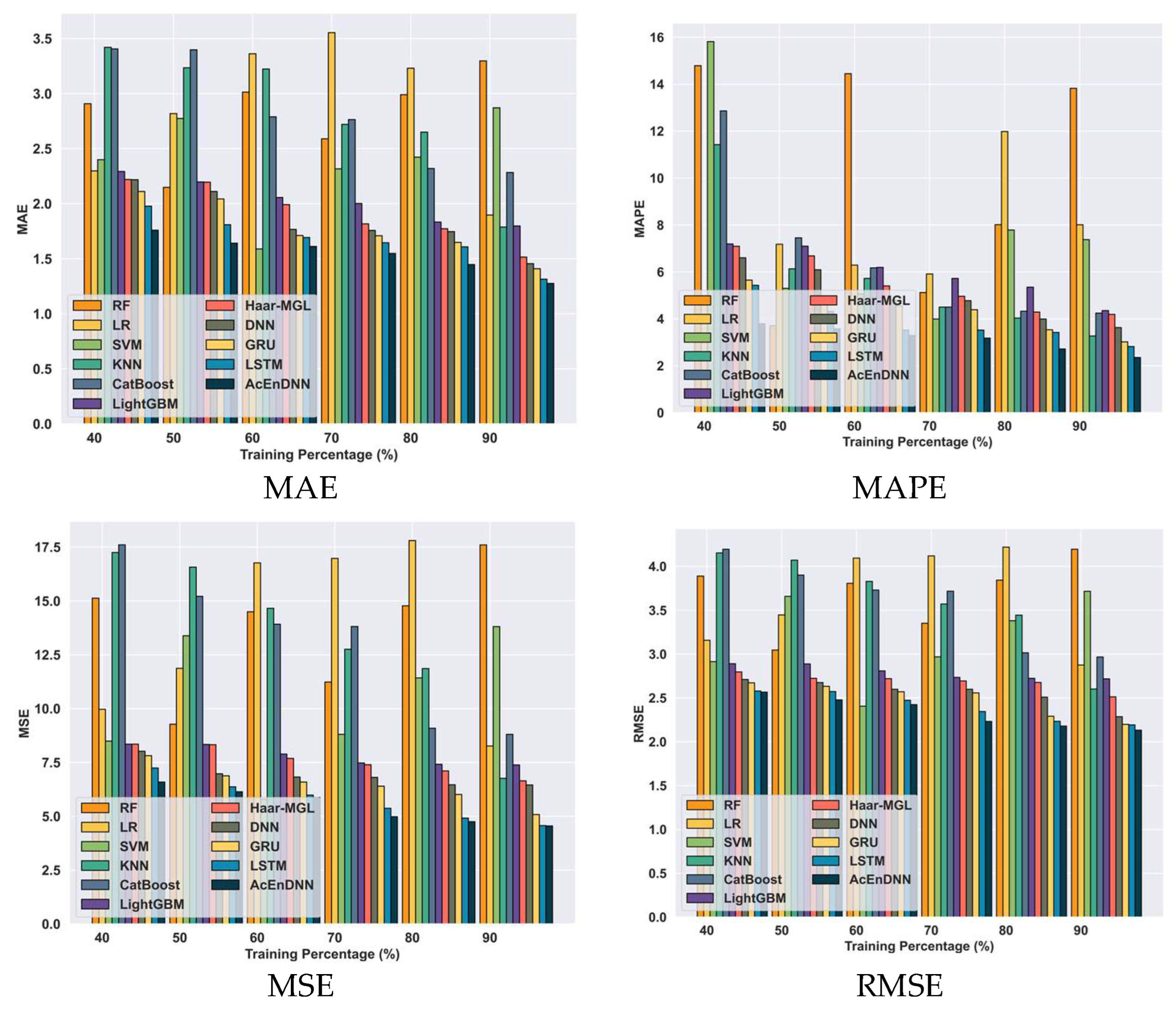
5.6.1. Comparative Analysis Using Student-mat.csv Dataset Based on TP
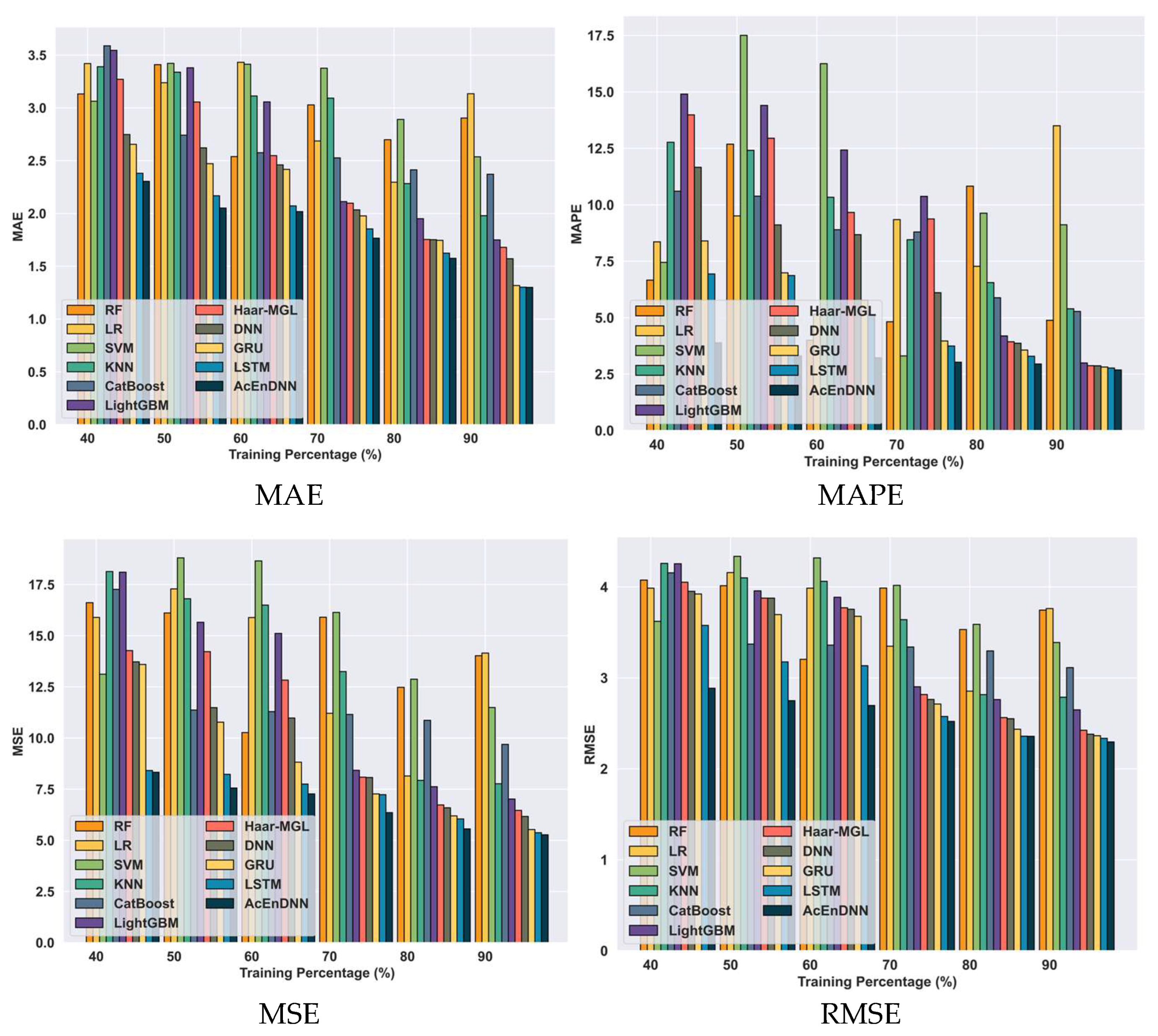
5.6.2. Comparative Analysis Using Student-por.csv Dataset Based on Training Percentage
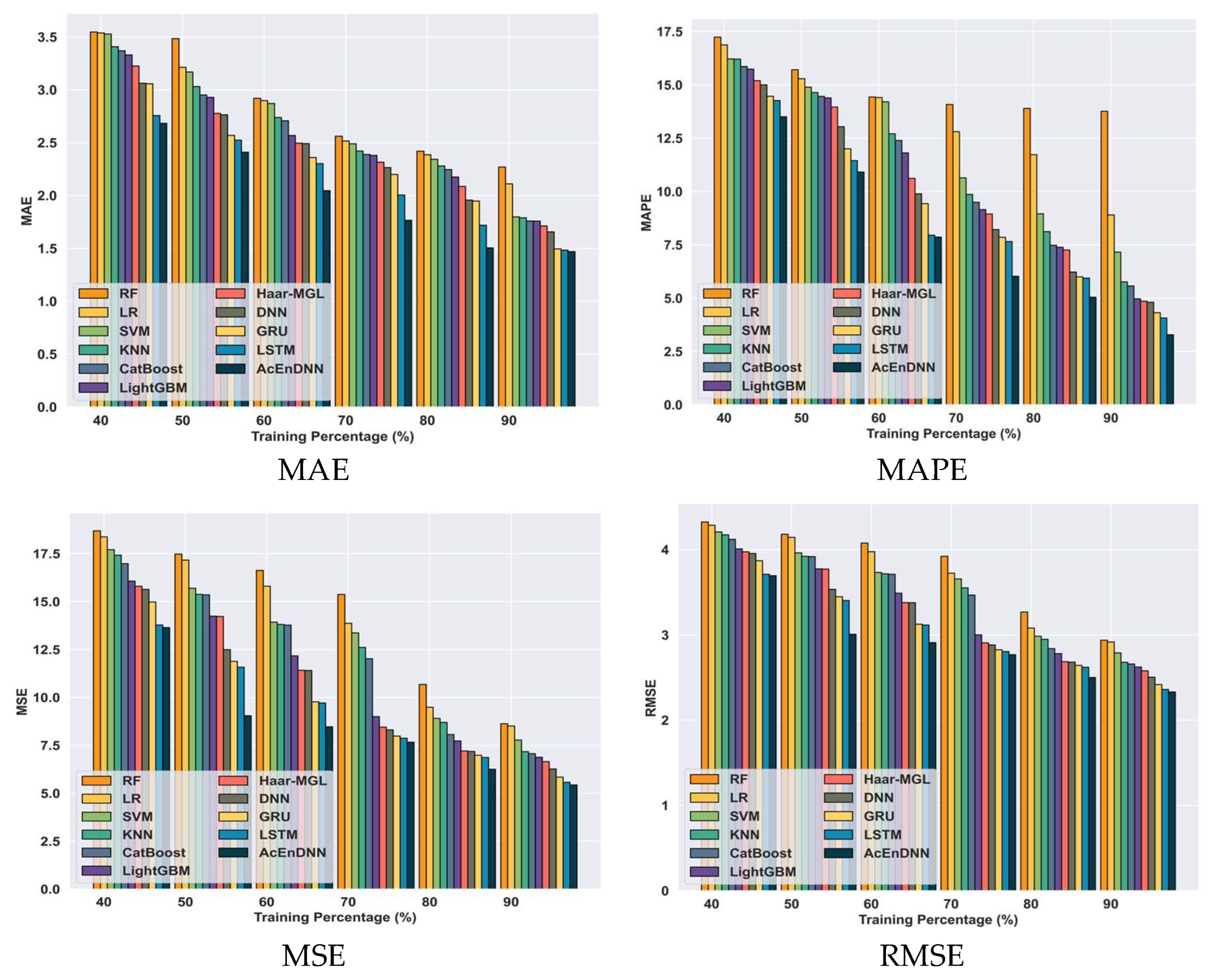
5.6.3. Comparative Analysis Using the Real-Time Dataset Based on Training Percentage
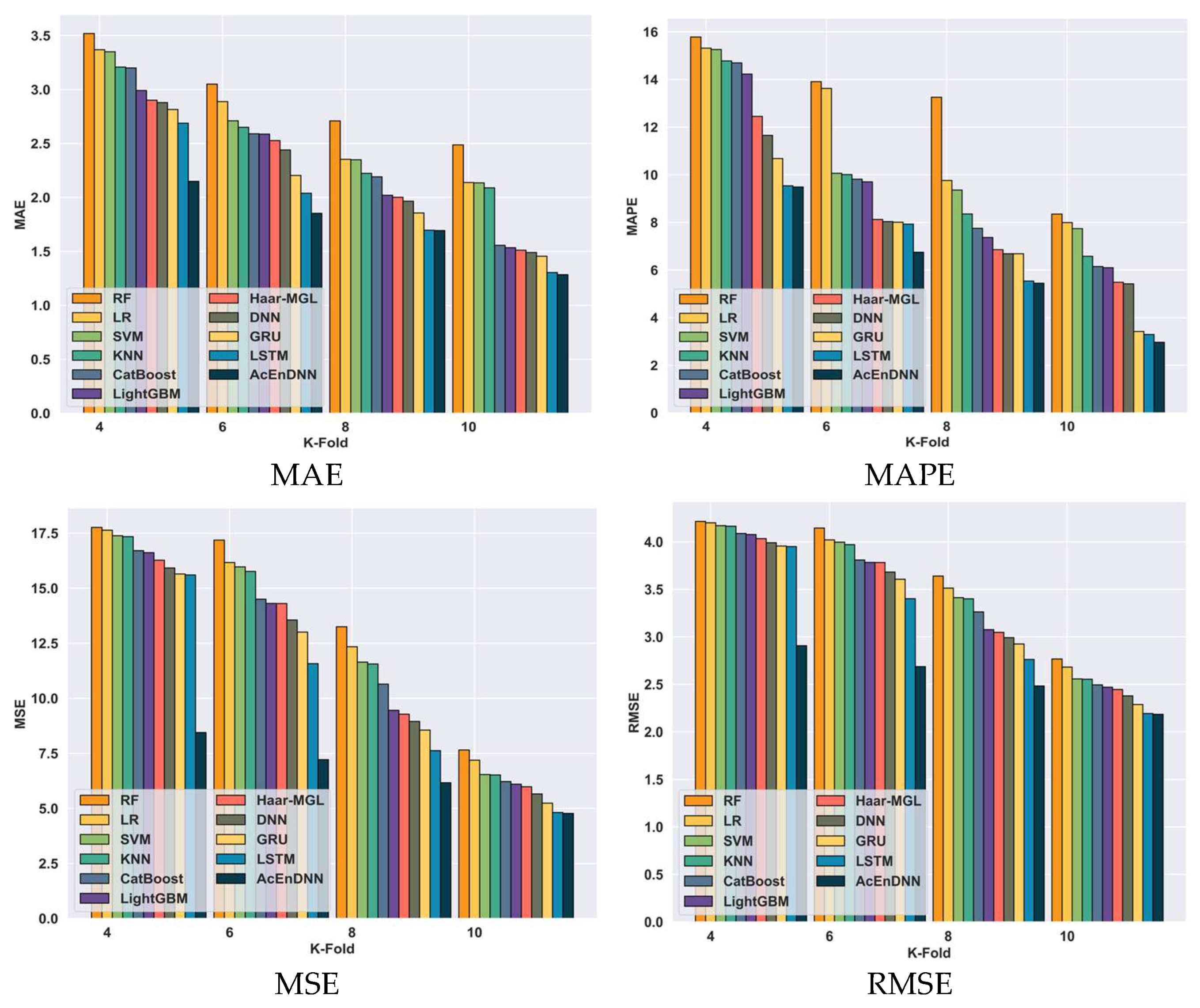
5.6.4. Comparative Analysis Based on K-Fold Value for Student-mat.csv Dataset
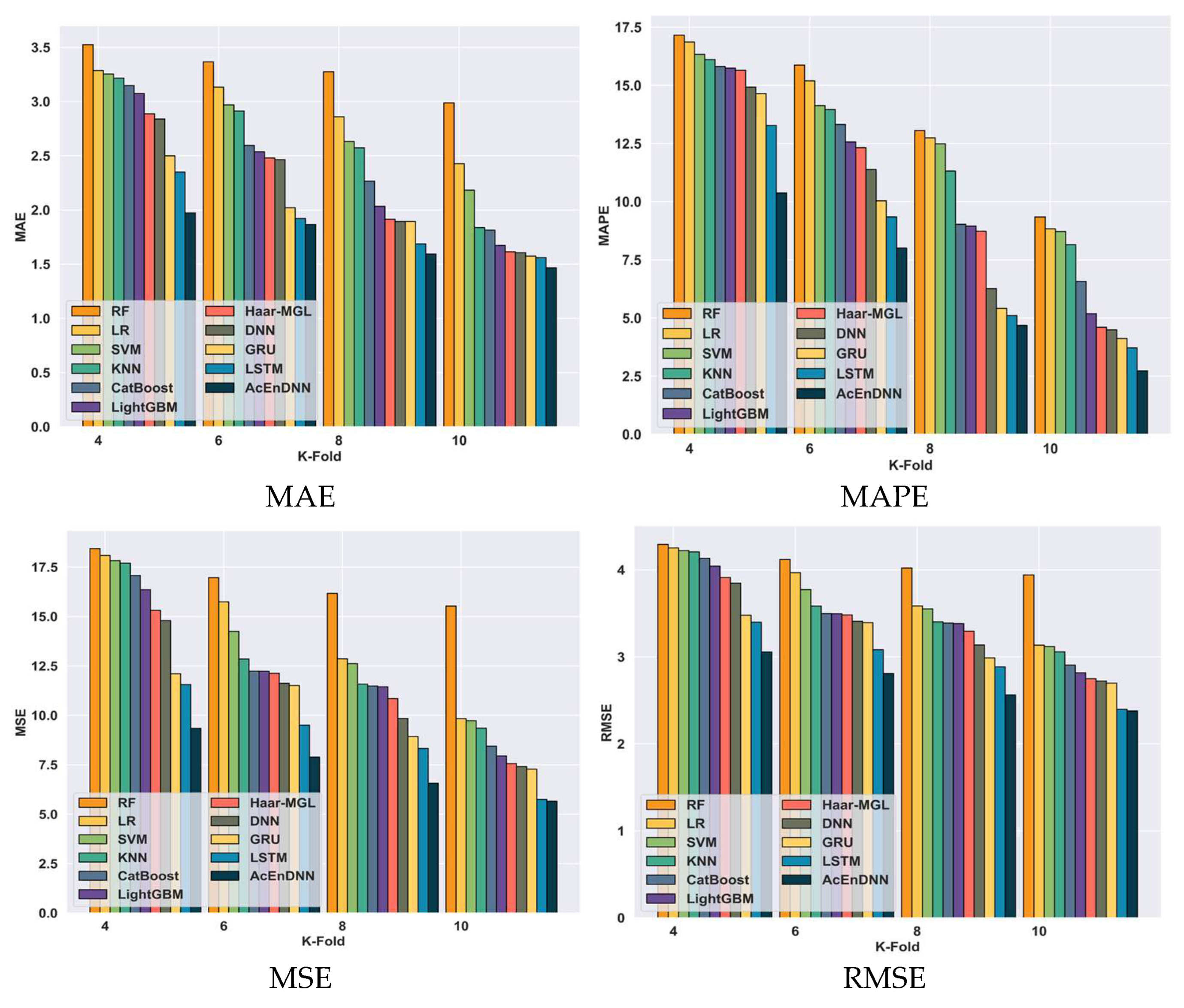
5.6.5. Comparative Analysis Based on K-Fold Value Using Student-por.csv Dataset
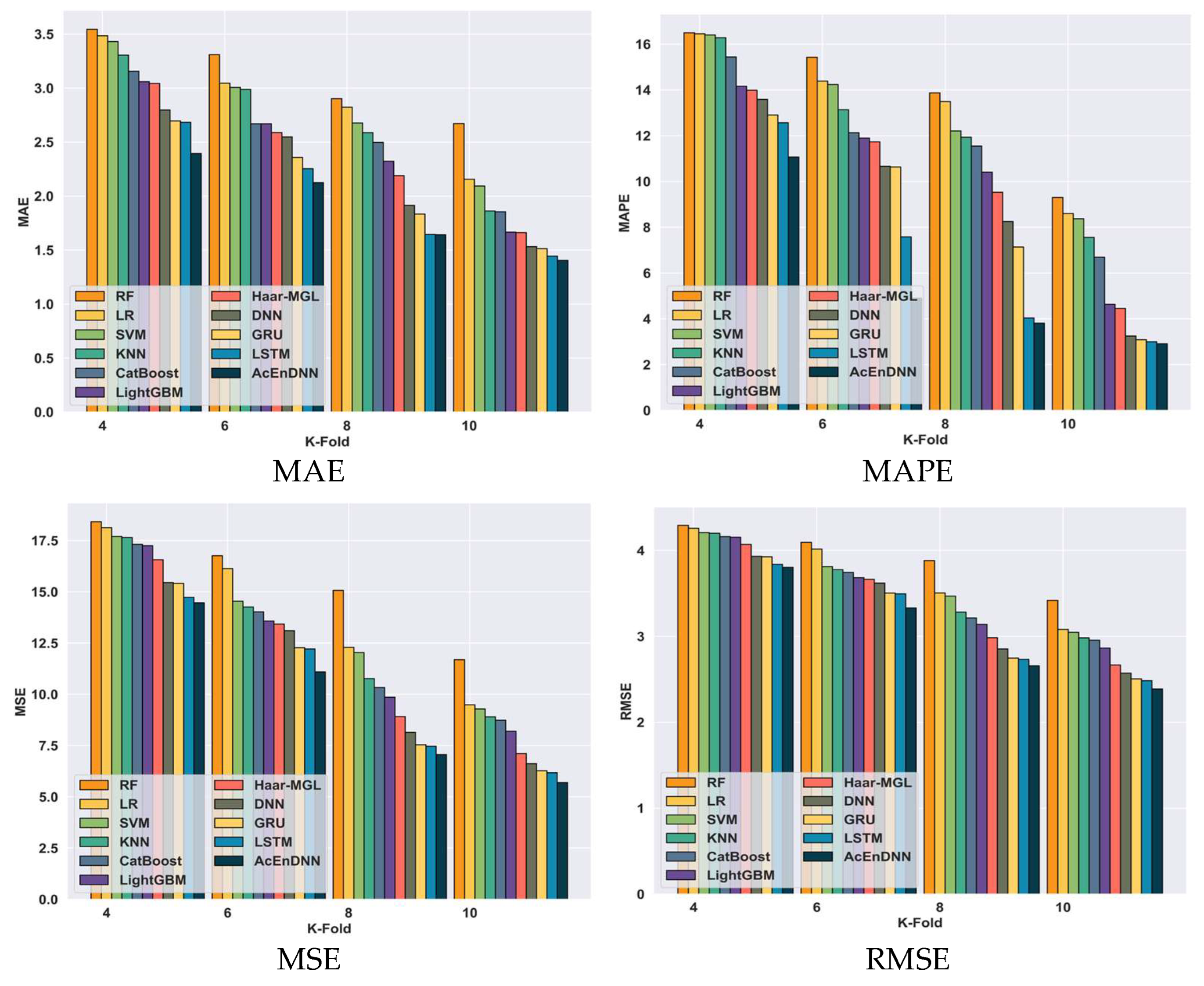
5.6.6. Comparative Analysis Based on K-Fold Value Using Real-Time Dataset
5.7. Comparative Discussion
5.8. Statistical Analysis
5.9. Ablation Study
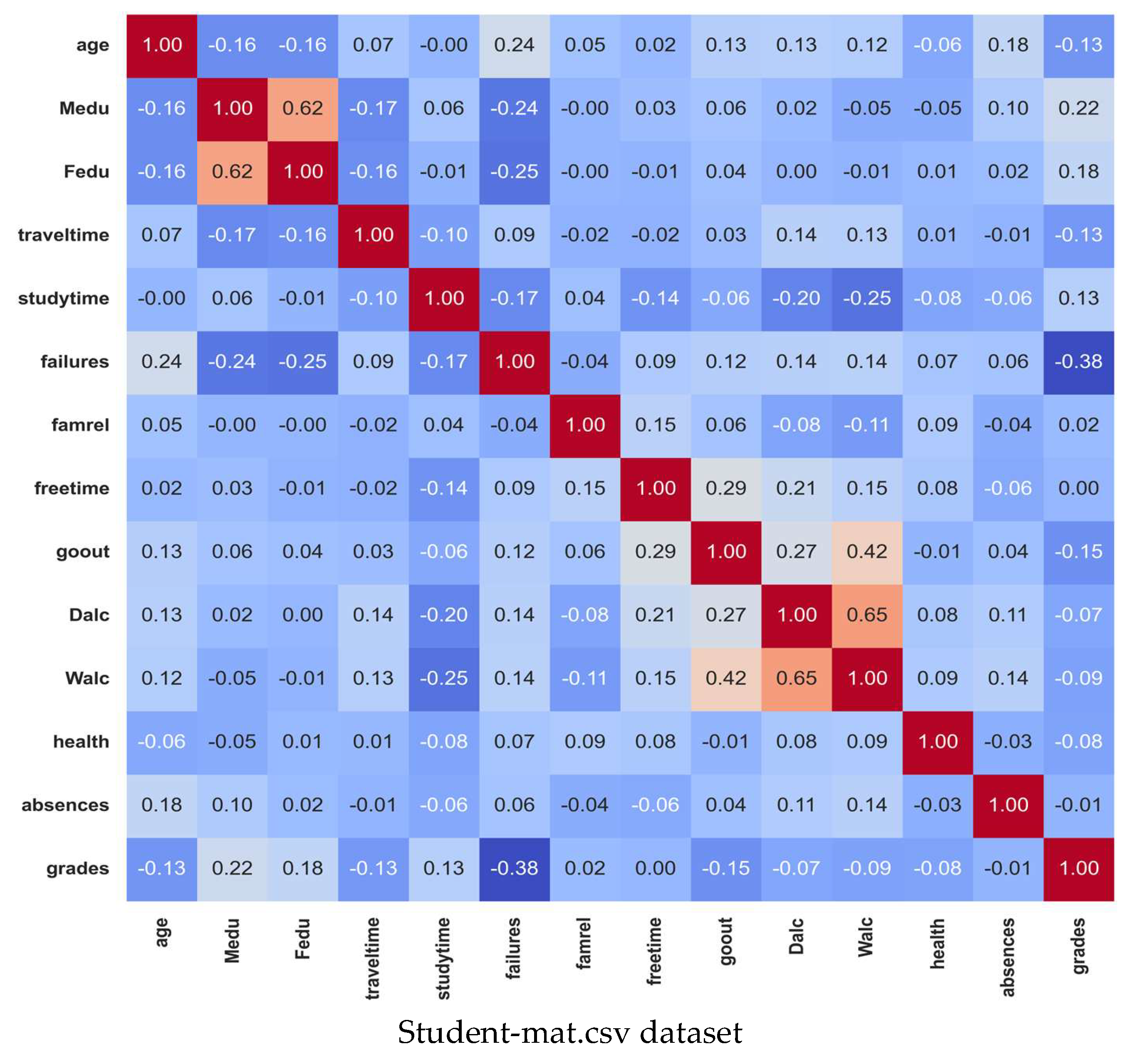
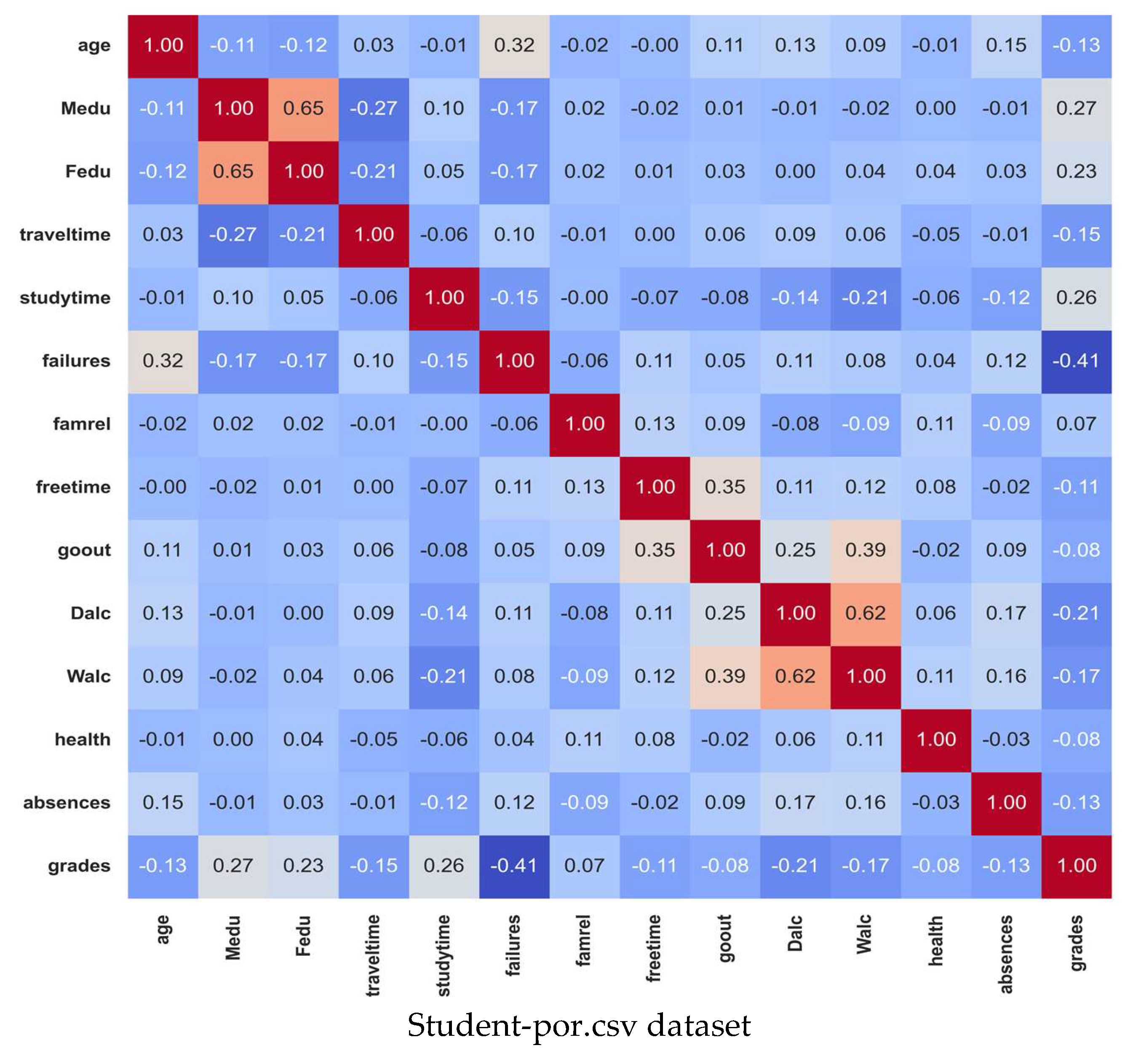
5.10. Correlation Matrix
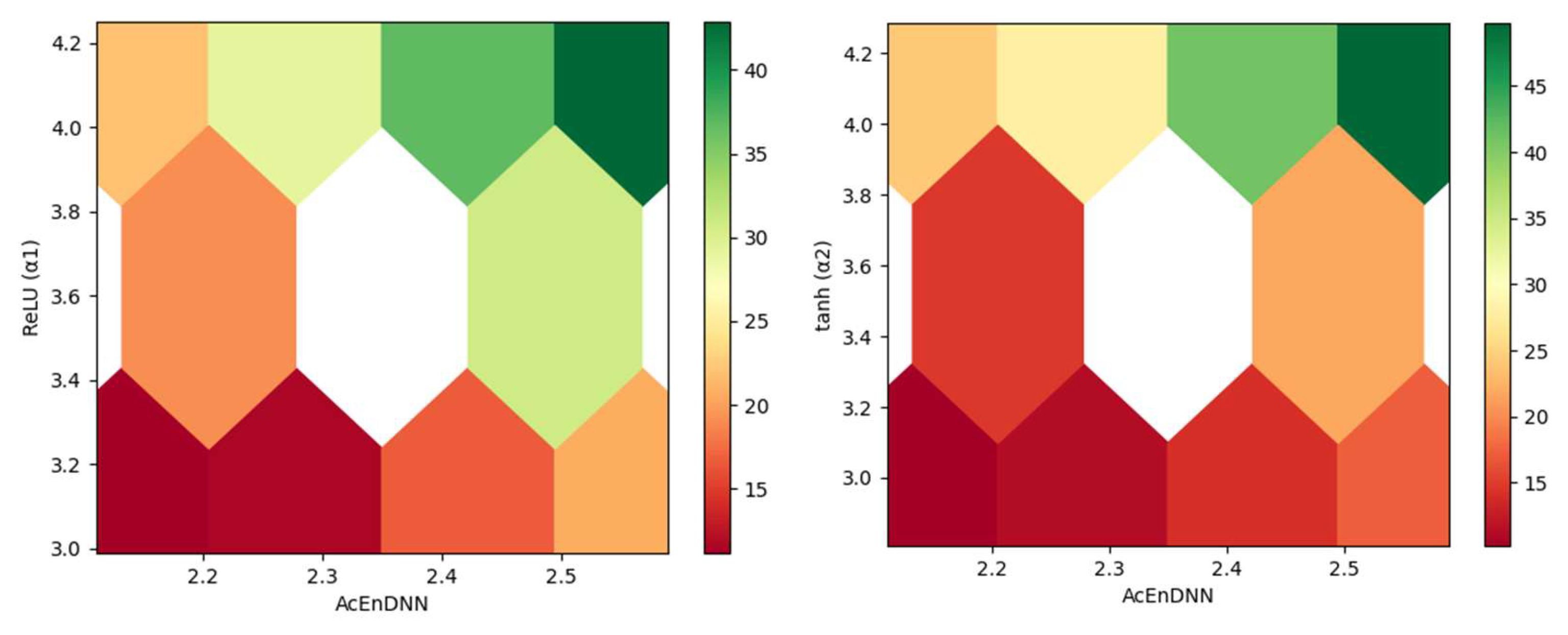
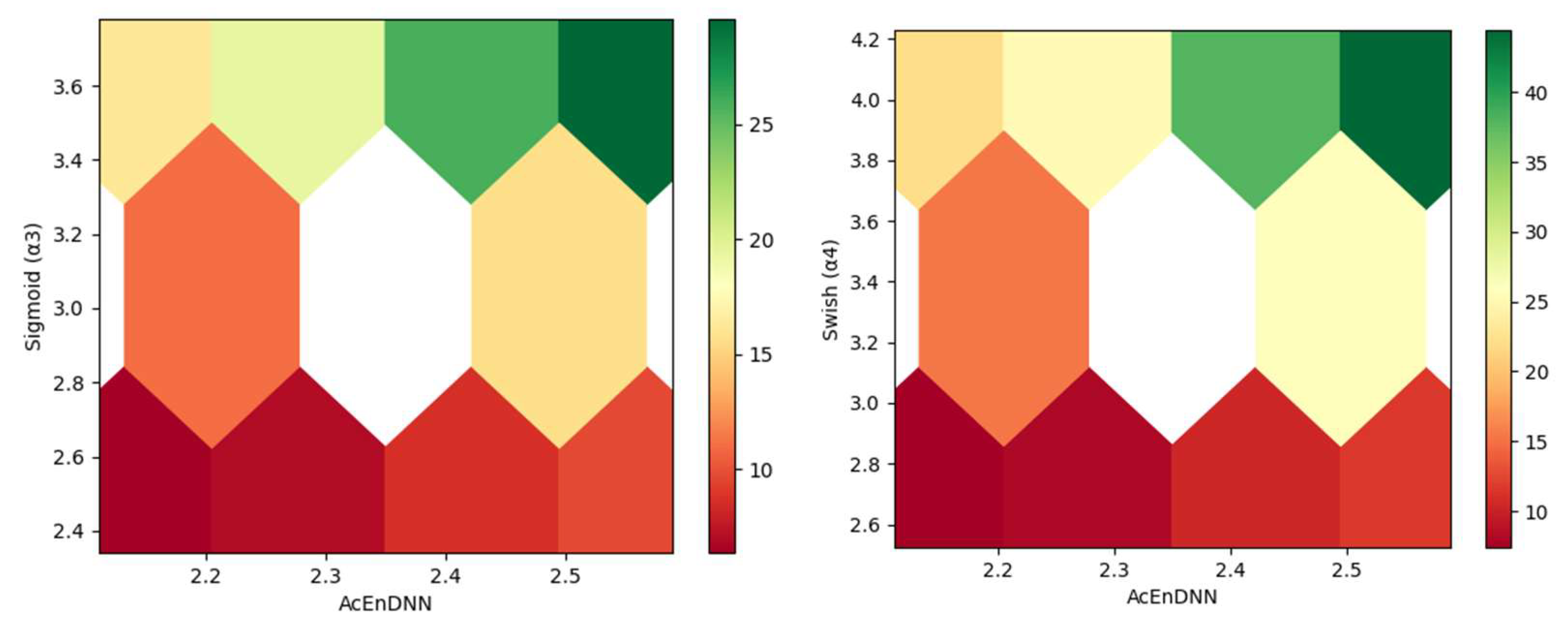
5.11. Sensitivity Analysis
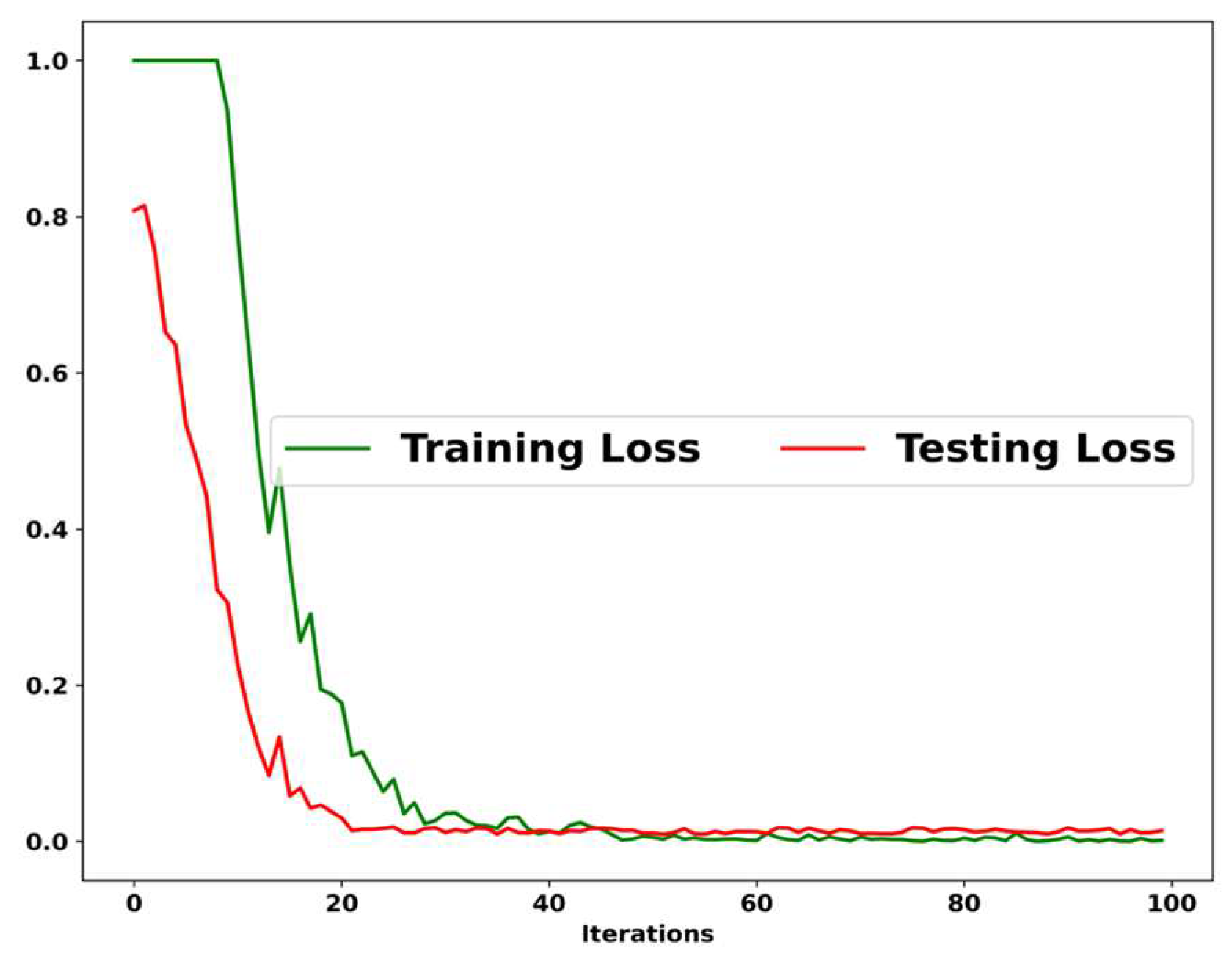
5.12. Training and Testing Loss Analysis
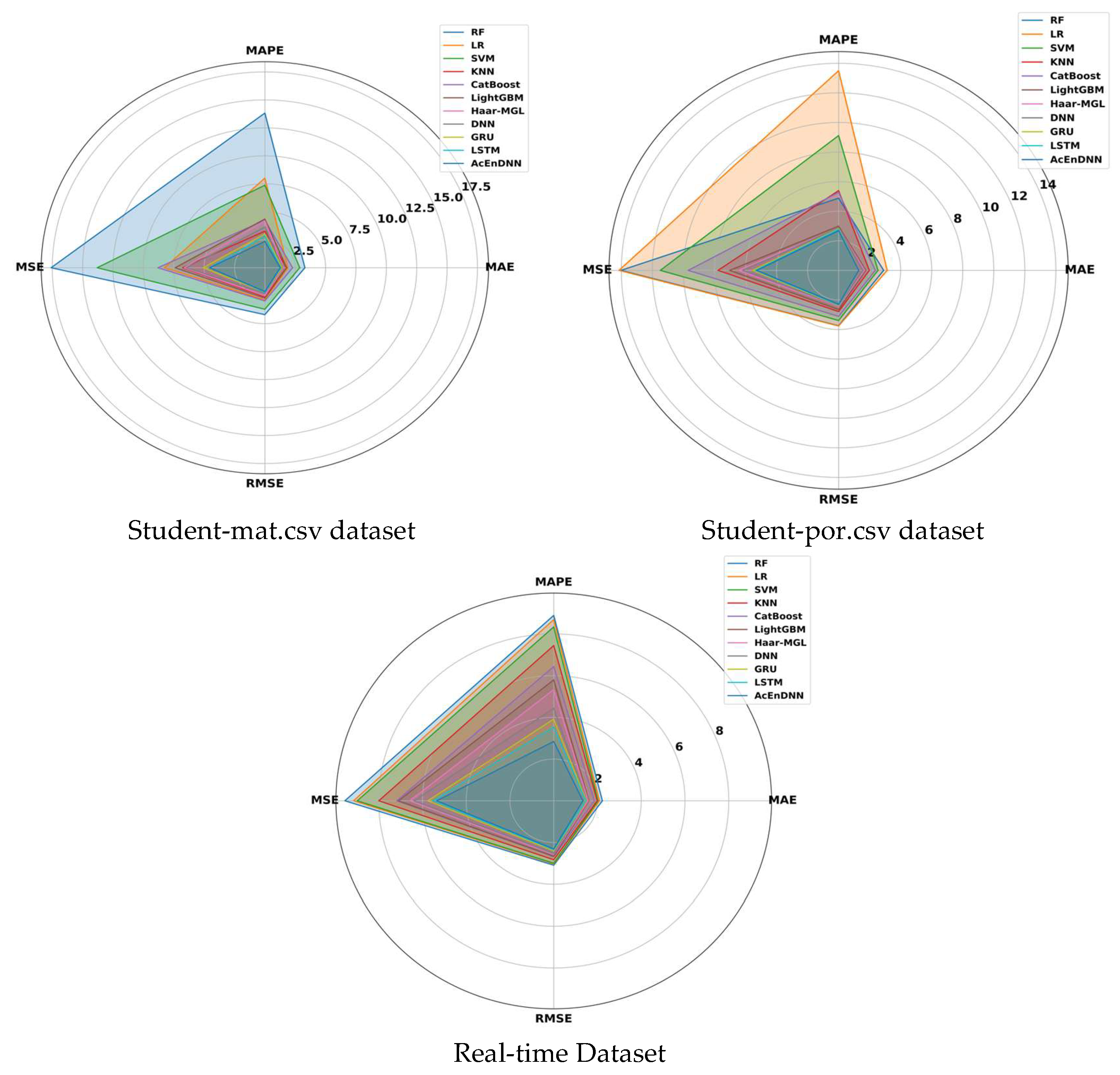
5.13. Spider Plot Analysis
5.14. Computational Complexity
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zohair, A.; Mahmoud, L. Prediction of Student’s performance by modelling small dataset size. Int. J. Educ. Technol. High. Educ. 2019, 16, 1–8. [Google Scholar] [CrossRef]
- Mengash, H.A. Using data mining techniques to predict student performance to support decision making in university admission systems. IEEE Access 2020, 8, 55462–55470. [Google Scholar] [CrossRef]
- Ghorbani, R.; Ghousi, R. Comparing different resampling methods in predicting students’ performance using machine learning techniques. IEEE Access 2020, 8, 67899–67911. [Google Scholar] [CrossRef]
- Tomasevic, N.; Gvozdenovic, N.; Vranes, S. An overview and comparison of supervised data mining techniques for student exam performance prediction. Comput. Educ. 2020, 143, 103676. [Google Scholar] [CrossRef]
- Lau, E.T.; Sun, L.; Yang, Q. Modelling, prediction and classification of student academic performance using artificial neural networks. SN Appl. Sci. 2019, 1, 982. [Google Scholar] [CrossRef]
- Liu, Q.; Huang, Z.; Yin, Y.; Chen, E.; Xiong, H.; Su, Y.; Hu, G. Ekt: Exercise-aware knowledge tracing for student performance prediction. IEEE Trans. Knowl. Data Eng. 2019, 33, 100–115. [Google Scholar] [CrossRef]
- Yağcı, M. Educational data mining: Prediction of students’ academic performance using machine learning algorithms. Smart Learn. Environ. 2022, 9, 11. [Google Scholar] [CrossRef]
- Aydoğdu, Ş. Predicting student final performance using artificial neural networks in online learning environments. Educ. Inf. Technol. 2020, 25, 1913–1927. [Google Scholar] [CrossRef]
- Bisri, A.; Heryatun, Y.; Navira, A. Educational Data Mining Model Using Support Vector Machine for Student Academic Performance Evaluation. J. Educ. Learn. 2025, 19, 478–486. [Google Scholar] [CrossRef]
- Ghorbani, R.; Ghousi, R. Predictive data mining approaches in medical diagnosis: A review of some diseases prediction. Int. J. Data Netw. Sci. 2019, 3, 47–70. [Google Scholar] [CrossRef]
- Zhou, R.; Wang, Q.; Cao, L.; Xu, J.; Zhu, X.; Xiong, X.; Zhang, H.; Zhong, Y. Dual-Level Viewpoint-Learning for Cross-Domain Vehicle Re-Identification. Electronics 2024, 13, 1823. [Google Scholar] [CrossRef]
- Ni, L.; Wang, S.; Zhang, Z.; Li, X.; Zheng, X.; Denny, P.; Liu, J. Enhancing student performance prediction on learnersourced questions with sgnn-llm synergy. Proc. AAAI Conf. Artif. Intell. 2024, 38, 23232–23240. [Google Scholar] [CrossRef]
- Adekitan, A.I.; Noma-Osaghae, E. Data mining approach to predicting the performance of first year student in a university using the admission requirements. Educ. Inf. Technol. 2019, 24, 1527–1543. [Google Scholar] [CrossRef]
- Fernandes, E.; Holanda, M.; Victorino, M.; Borges, V.; Carvalho, R.; Van Erven, G. Educational data mining: Predictive analysis of academic performance of public school students in the capital of Brazil. J. Bus. Res. 2019, 94, 335–343. [Google Scholar] [CrossRef]
- Mai, J.; Wei, F.; He, W.; Huang, H.; Zhu, H. An Explainable Student Performance Prediction Method Based on Dual-Level Progressive Classification Belief Rule Base. Electronics 2024, 13, 4358. [Google Scholar] [CrossRef]
- Gao, J.; Chen, M.; Xiang, L.; Xu, C. A comprehensive survey on evidential deep learning and its applications. arXiv 2024, arXiv:2409.04720. [Google Scholar] [CrossRef]
- Chen, P.; Lu, Y.; Zheng, V.W.; Pian, Y. Prerequisite-driven deep knowledge tracing. In Proceedings of the 2018 IEEE International Conference on Data Mining, Singapore, 17–20 November 2018; pp. 39–48. [Google Scholar]
- Chen, Y.; Liu, Q.; Huang, Z.; Wu, L.; Chen, E.; Wu, R.; Su, Y.; Hu, G. Tracking knowledge proficiency of students with educational priors. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, Singapore, 6–10 November 2017; pp. 989–998. [Google Scholar]
- Corbett, A.T.; Anderson, J.R. Knowledge tracing: Modeling the acquisition of procedural knowledge. User Model. User-Adapt. Interact. 1994, 4, 253–278. [Google Scholar] [CrossRef]
- Cui, P.; Liu, S.; Zhu, W. General knowledge embedded image representation learning. IEEE Trans. Multimed. 2017, 20, 198–207. [Google Scholar] [CrossRef]
- Cui, P.; Wang, X.; Pei, J.; Zhu, W. A survey on network embedding. IEEE Trans. Knowl. Data Eng. 2018, 31, 833–852. [Google Scholar] [CrossRef]
- Liu, X.; Wu, W.; Hu, Z.; Sun, Y. SCECNet: Self-correction feature enhancement fusion network for remote sensing scene classification. Earth Sci. Inform. 2024, 17, 4555–4573. [Google Scholar] [CrossRef]
- Liu, Y.; Ren, Z.; Liu, X.; Wang, X.; Wang, Y.; Wang, H. Research on Multimodal Link Prediction Method Based on Vision Transformer and Convolutional Neural Network. Available online: https://www.researchsquare.com/article/rs-4489200/v1 (accessed on 11 June 2024).
- Junejo, N.U.; Huang, Q.; Dong, X.; Wang, C.; Zeb, A.; Humayoo, M.; Zheng, G. SAPPNet: Students’ academic performance prediction during COVID-19 using neural network. Sci. Rep. 2024, 14, 24605. [Google Scholar] [CrossRef] [PubMed]
- Junejo, N.U.; Huang, Q.; Dong, X.; Wang, C.; Humayoo, M.; Zheng, G. SLPNet: Student Learning Performance Prediction During the COVID-19 Pandemic via a Deep Neural Network. In Proceedings of the CCF National Conference of Computer Applications, Harbin, China, 15–18 July 2024; pp. 65–75. [Google Scholar]
- Baniata, L.H.; Kang, S.; Alsharaiah, M.A.; Baniata, M.H. Advanced deep learning model for predicting the academic performances of students in educational institutions. Appl. Sci. 2024, 14, 1963. [Google Scholar] [CrossRef]
- Vives, L.; Cabezas, I.; Vives, J.C.; Reyes, N.G.; Aquino, J.; Cóndor, J.B.; Altamirano, S.F.S. Prediction of students’ academic performance in the programming fundamentals course using long short-term memory neural networks. IEEE Access 2024, 12, 5882–5898. [Google Scholar] [CrossRef]
- Sugiarto, H.S.; Tjandra, Y.G. Uncovering University Application Patterns Through Graph Representation Learning 2024. Available online: https://www.researchsquare.com/article/rs-4820733/v1 (accessed on 29 July 2024).
- Dataset Description. Available online: https://www.kaggle.com/datasets/larsen0966/student-performance-data-set/data (accessed on 14 March 2024).
- Shaban, W.M.; Ashraf, E.; Slama, A.E. SMP-DL: A novel stock market prediction approach based on deep learning for effective trend forecasting. Neural Comput. Appl. 2024, 36, 1849–1873. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, Y.; Cheng, M.; Zhu, J.; Meng, Y.; Mu, X. Performance prediction and parameter optimization of alumina-titanium carbide ceramic micro-EDM hole machining process based on XGBoost. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2024, 238, 310–319. [Google Scholar] [CrossRef]
- Batool, S.; Rashid, J.; Nisar, M.W.; Kim, J.; Mahmood, T.; Hussain, A. A random forest students’ performance prediction (rfspp) model based on students’ demographic features. In Proceedings of the 2021 Mohammad Ali Jinnah University International Conference on Computing (MAJICC), Karachi, Pakistan, 15–17 July 2021; pp. 1–4. [Google Scholar]
- Roy, K.; Farid, D.M. An adaptive feature selection algorithm for student performance prediction. IEEE Access 2024, 12, 75577–75598. [Google Scholar] [CrossRef]
- Sarwat, S.; Ullah, N.; Sadiq, S.; Saleem, R.; Umer, M.; Eshmawi, A.A.; Mohamed, A.; Ashraf, I. Predicting students’ academic performance with conditional generative adversarial network and deep SVM. Sensors 2022, 22, 4834. [Google Scholar] [CrossRef] [PubMed]
- Al-Shehri, H.; Al-Qarni, A.; Al-Saati, L.; Batoaq, A.; Badukhen, H.; Alrashed, S.; Alhiyafi, J.; Olatunji, S.O. Student performance prediction using support vector machine and k-nearest neighbor. In Proceedings of the 2017 IEEE 30th Canadian Conference on Electrical and Computer Engineering (CCECE), Windsor, ON, Canada, 30 April–3 May 2017; pp. 1–4. [Google Scholar]
- Tirumanadham, N.K.; Thaiyalnayaki, S.; SriRam, M. Evaluating boosting algorithms for academic performance prediction in E-learning environments. In Proceedings of the 2024 International Conference on Intelligent and Innovative Technologies in Computing, Electrical and Electronics (IITCEE), Bangalore, India, 24–25 January 2024; pp. 1–8. [Google Scholar]
- Wang, C.; Chang, L.; Liu, T. Predicting student performance in online learning using a highly efficient gradient boosting decision tree. In Proceedings of the International Conference on Intelligent Information Processing, Qingdao, China, 27–30 May 2022; pp. 508–521. [Google Scholar]
- Afzaal, M.; Zia, A.; Nouri, J.; Fors, U. Informative feedback and explainable AI-based recommendations to support students’ self-regulation. Technol. Knowl. Learn. 2024, 29, 331–354. [Google Scholar] [CrossRef]
- Li, M.; Zhuang, X.; Bai, L.; Ding, W. Multimodal graph learning based on 3D Haar semi-tight framelet for student engagement prediction. Inf. Fusion 2024, 105, 102224. [Google Scholar] [CrossRef]



| Sl.No | Author | Method | Advantage | Disadvantage | Achievement |
|---|---|---|---|---|---|
| 1. | Ramin Ghorbani and Rouzbeh Ghousi [3] | Machine Learning Models | The models perform better when dealing with fewer classes and nominal features. | The models obtain poor performance due to single classifiers. | Median-69.56 Sum of Ranks-37 |
| 2. | Nikola Tomasevic et al. [4] | Supervised Data Mining Technique | The model demonstrates high accuracy in making these predictions. | The model suffers from profiling, which can arise from improper application. | F1-0.94 RMSE-14.59 |
| 3. | E. T. Lau et al. [5] | Artificial Neural Network | The model performs with better accuracy in this prediction. | According to gender, the model performs poorly in the classification of students. | Accuracy-84.8% |
| 4. | Qi Liu et al. [6] | Exercise-aware Knowledge Tracing (EKT) | The prediction accuracy is enhanced by including an attention mechanism. | However, the model found that predicting student performance still faced challenges due to the cold start problem. | MAE-0.32 RMSE-0.41 |
| 5. | Hanan Abdullah’s [2] | ANN | Popular data mining techniques are utilized to generate four prediction models. | However, input variables such as pre-admission tests are rarely used to predict student performance | Accuracy-79% |
| 6. | Lubna Mahmoud Abu Zohair [1] | KNN | The model achieves better accuracy by using a small dataset. | However, the model faces challenges in computational complexity. | Accuracy-72% |
| 7. | Mustafa Yagci [7] | ML Algorithms | The predictions are made using the parameters of midterm grades, department data, and faculty data. | The model faces challenges in overfitting. | Accuracy-75% |
| 8. | Seyhmus Aydogdu [8] | ANN | The model could benefit struggling students by giving them a chance to improve. | The model suffers from computational issues. | Accuracy-80.47% |
| 9. | N.U. Rehman Junejo et al. [24] | SAPPNet | The model improves educational results in real-time situations. | The model has poor resilience and flexibility. | Accuracy-93% |
| 10. | N.U. Rehman Junejo et al. [25] | SLPNet | The model predicts students who are at risk of dropping out early and helps to improve their academic scores. | The model obtains computational complexity. | Accuracy-89% |
| Model/Metric | RF | LR | SVM | KNN | Cat Boost | LightGBM | Haar-MGL | DNN | GRU | LSTM | AcEnDNN | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Student-mat.csv | TP-90% | MAE | 3.30 | 1.90 | 2.87 | 1.79 | 2.28 | 1.80 | 1.52 | 1.46 | 1.41 | 1.31 | 1.28 |
| MAPE | 13.83 | 8.01 | 7.38 | 3.27 | 4.25 | 4.35 | 4.19 | 3.63 | 3.02 | 2.82 | 2.36 | ||
| MSE | 17.60 | 8.26 | 13.81 | 6.76 | 8.80 | 7.38 | 6.65 | 6.45 | 5.08 | 4.57 | 4.55 | ||
| RMSE | 4.20 | 2.87 | 3.72 | 2.60 | 2.97 | 2.72 | 2.51 | 2.29 | 2.20 | 2.19 | 2.13 | ||
| K-fold 10 | MAE | 2.49 | 2.14 | 2.14 | 2.09 | 1.56 | 1.53 | 1.51 | 1.49 | 1.46 | 1.31 | 1.28 | |
| MAPE | 8.35 | 8.00 | 7.74 | 6.58 | 6.15 | 6.10 | 5.49 | 5.42 | 3.42 | 3.30 | 2.97 | ||
| MSE | 7.65 | 7.19 | 6.54 | 6.52 | 6.22 | 6.10 | 5.98 | 5.66 | 5.24 | 4.81 | 4.77 | ||
| RMSE | 2.77 | 2.68 | 2.56 | 2.55 | 2.49 | 2.47 | 2.45 | 2.38 | 2.29 | 2.19 | 2.18 | ||
| Student-por.csv | TP-90% | MAE | 2.9 | 3.13 | 2.54 | 1.98 | 2.37 | 1.75 | 1.68 | 1.57 | 1.32 | 1.3 | 1.30 |
| MAPE | 4.88 | 13.5 | 9.11 | 5.4 | 5.28 | 2.99 | 2.87 | 2.87 | 2.81 | 2.77 | 2.69 | ||
| MSE | 14.02 | 14.15 | 11.49 | 7.77 | 9.69 | 7.02 | 6.47 | 6.17 | 5.53 | 5.37 | 5.28 | ||
| RMSE | 3.74 | 3.76 | 3.39 | 2.79 | 3.11 | 2.65 | 2.43 | 2.38 | 2.36 | 2.34 | 2.30 | ||
| K-fold 10 | MAE | 2.99 | 2.43 | 2.18 | 1.84 | 1.81 | 1.67 | 1.61 | 1.61 | 1.57 | 1.56 | 1.47 | |
| MAPE | 9.34 | 8.84 | 8.71 | 8.15 | 6.56 | 5.18 | 4.60 | 4.49 | 4.12 | 3.72 | 2.73 | ||
| MSE | 15.53 | 9.83 | 9.73 | 9.35 | 8.44 | 7.94 | 7.56 | 7.41 | 7.28 | 5.75 | 5.65 | ||
| RMSE | 3.94 | 3.14 | 3.12 | 3.06 | 2.91 | 2.82 | 2.75 | 2.72 | 2.70 | 2.40 | 2.38 | ||
| Real-time dataset | TP-90% | MAE | 2.27 | 2.11 | 1.80 | 1.79 | 1.76 | 1.76 | 1.71 | 1.66 | 1.50 | 1.48 | 1.47 |
| MAPE | 13.76 | 8.90 | 7.16 | 5.77 | 5.58 | 4.97 | 4.86 | 4.81 | 4.32 | 4.07 | 3.29 | ||
| MSE | 8.63 | 8.51 | 7.78 | 7.18 | 7.07 | 6.88 | 6.66 | 6.27 | 5.85 | 5.58 | 5.44 | ||
| RMSE | 2.94 | 2.92 | 2.79 | 2.68 | 2.66 | 2.62 | 2.58 | 2.50 | 2.42 | 2.36 | 2.33 | ||
| K-fold 10 | MAE | 2.67 | 2.16 | 2.09 | 1.86 | 1.85 | 1.67 | 1.66 | 1.53 | 1.51 | 1.44 | 1.40 | |
| MAPE | 9.30 | 8.60 | 8.37 | 7.56 | 6.69 | 4.63 | 4.46 | 3.25 | 3.09 | 3.00 | 2.91 | ||
| MSE | 11.69 | 9.49 | 9.29 | 8.90 | 8.74 | 8.20 | 7.12 | 6.62 | 6.28 | 6.17 | 5.70 | ||
| RMSE | 3.42 | 3.08 | 3.05 | 2.98 | 2.96 | 2.86 | 2.67 | 2.57 | 2.51 | 2.48 | 2.39 | ||
| Dataset | Model/Metric | RF | LR | SVM | KNN | Cat Boost | LightGBM | Haar-MGL | DNN | GRU | LSTM | AcEnDNN | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Student-mat.csv | Best | MAE | 3.30 | 3.55 | 2.87 | 3.42 | 3.41 | 2.29 | 2.22 | 2.22 | 2.11 | 1.98 | 1.76 |
| MAPE | 14.79 | 11.98 | 15.81 | 11.42 | 12.86 | 7.19 | 7.09 | 6.61 | 5.65 | 5.43 | 3.79 | ||
| MSE | 17.60 | 17.80 | 13.81 | 17.25 | 17.61 | 8.35 | 8.35 | 8.02 | 7.82 | 7.24 | 6.59 | ||
| RMSE | 4.20 | 4.22 | 3.72 | 4.15 | 4.20 | 2.89 | 2.80 | 2.71 | 2.67 | 2.58 | 2.57 | ||
| Mean | MAE | 2.82 | 2.86 | 2.40 | 2.84 | 2.83 | 2.03 | 1.92 | 1.84 | 1.77 | 1.67 | 1.55 | |
| MAPE | 9.98 | 7.33 | 7.56 | 5.85 | 6.59 | 5.99 | 5.44 | 4.98 | 4.30 | 3.84 | 3.15 | ||
| MSE | 13.75 | 13.61 | 10.28 | 13.31 | 13.07 | 7.81 | 7.58 | 6.92 | 6.46 | 5.74 | 5.48 | ||
| RMSE | 3.69 | 3.65 | 3.17 | 3.61 | 3.59 | 2.79 | 2.69 | 2.56 | 2.49 | 2.40 | 2.34 | ||
| Variance | MAE | 0.13 | 0.35 | 0.17 | 0.30 | 0.20 | 0.03 | 0.06 | 0.06 | 0.06 | 0.04 | 0.02 | |
| MAPE | 20.79 | 5.44 | 15.37 | 7.15 | 9.21 | 0.98 | 1.23 | 1.12 | 0.71 | 0.70 | 0.24 | ||
| MSE | 7.44 | 13.95 | 8.15 | 12.21 | 10.08 | 0.17 | 0.38 | 0.28 | 0.69 | 0.82 | 0.58 | ||
| RMSE | 0.14 | 0.27 | 0.21 | 0.27 | 0.20 | 0.01 | 0.01 | 0.02 | 0.03 | 0.02 | 0.03 | ||
| Student-por.csv | Best | MAE | 3.41 | 3.43 | 3.42 | 3.39 | 3.59 | 3.55 | 3.27 | 2.75 | 2.66 | 2.38 | 2.30 |
| MAPE | 12.68 | 13.50 | 17.50 | 12.77 | 10.60 | 14.90 | 13.99 | 11.66 | 8.40 | 6.93 | 3.89 | ||
| MSE | 16.61 | 17.29 | 18.81 | 18.14 | 17.27 | 18.11 | 14.28 | 13.72 | 13.59 | 8.41 | 8.33 | ||
| RMSE | 4.08 | 4.16 | 4.34 | 4.26 | 4.16 | 4.26 | 4.05 | 3.95 | 3.92 | 3.58 | 2.89 | ||
| Mean | MAE | 2.95 | 3.03 | 3.12 | 2.87 | 2.70 | 2.63 | 2.40 | 2.20 | 2.10 | 1.90 | 1.84 | |
| MAPE | 7.31 | 8.86 | 10.54 | 9.32 | 8.31 | 9.88 | 8.80 | 7.05 | 5.25 | 4.79 | 3.18 | ||
| MSE | 14.23 | 13.76 | 15.18 | 13.40 | 11.94 | 11.99 | 10.44 | 9.50 | 8.70 | 7.17 | 6.73 | ||
| RMSE | 3.76 | 3.68 | 3.88 | 3.61 | 3.44 | 3.40 | 3.25 | 3.21 | 3.13 | 2.86 | 2.58 | ||
| Variance | MAE | 0.08 | 0.17 | 0.11 | 0.29 | 0.17 | 0.51 | 0.37 | 0.19 | 0.22 | 0.13 | 0.11 | |
| MAPE | 10.79 | 6.45 | 24.31 | 7.72 | 4.20 | 22.04 | 17.34 | 9.44 | 3.94 | 2.74 | 0.14 | ||
| MSE | 5.14 | 9.94 | 8.22 | 17.54 | 5.99 | 19.52 | 11.63 | 7.59 | 7.77 | 1.25 | 1.19 | ||
| RMSE | 0.10 | 0.20 | 0.14 | 0.36 | 0.11 | 0.42 | 0.44 | 0.44 | 0.42 | 0.22 | 0.04 | ||
| Real-time dataset | Best | MAE | 3.55 | 3.54 | 3.53 | 3.41 | 3.37 | 3.33 | 3.23 | 3.06 | 3.06 | 2.76 | 2.68 |
| MAPE | 17.24 | 16.88 | 16.22 | 16.21 | 15.86 | 15.74 | 15.20 | 15.00 | 14.47 | 14.27 | 13.51 | ||
| MSE | 18.69 | 18.38 | 17.71 | 17.42 | 16.98 | 16.07 | 15.80 | 15.64 | 14.98 | 13.78 | 13.65 | ||
| RMSE | 4.32 | 4.29 | 4.21 | 4.17 | 4.12 | 4.01 | 3.98 | 3.95 | 3.87 | 3.71 | 3.69 | ||
| Mean | MAE | 2.87 | 2.78 | 2.70 | 2.61 | 2.57 | 2.52 | 2.44 | 2.37 | 2.27 | 2.13 | 1.98 | |
| MAPE | 14.85 | 13.34 | 12.01 | 11.22 | 10.88 | 10.58 | 10.14 | 9.53 | 9.01 | 8.56 | 7.78 | ||
| MSE | 14.58 | 13.87 | 12.90 | 12.52 | 12.21 | 11.02 | 10.63 | 10.22 | 9.58 | 9.23 | 8.42 | ||
| RMSE | 3.79 | 3.69 | 3.56 | 3.50 | 3.45 | 3.28 | 3.22 | 3.16 | 3.06 | 3.00 | 2.87 | ||
| Variance | MAE | 0.25 | 0.24 | 0.32 | 0.27 | 0.27 | 0.26 | 0.23 | 0.22 | 0.24 | 0.20 | 0.20 | |
| MAPE | 1.55 | 6.67 | 10.93 | 13.34 | 13.60 | 14.39 | 13.00 | 12.89 | 11.89 | 11.52 | 12.23 | ||
| MSE | 13.46 | 13.82 | 12.40 | 12.84 | 13.12 | 11.54 | 12.08 | 10.73 | 9.62 | 7.87 | 6.98 | ||
| RMSE | 0.26 | 0.27 | 0.26 | 0.28 | 0.29 | 0.26 | 0.28 | 0.26 | 0.24 | 0.21 | 0.19 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bin Nuweeji, H.; Alzubi, A.B. Early Prediction of Student Performance Using an Activation Ensemble Deep Neural Network Model. Appl. Sci. 2025, 15, 11411. https://doi.org/10.3390/app152111411
Bin Nuweeji H, Alzubi AB. Early Prediction of Student Performance Using an Activation Ensemble Deep Neural Network Model. Applied Sciences. 2025; 15(21):11411. https://doi.org/10.3390/app152111411
Chicago/Turabian StyleBin Nuweeji, Hassan, and Ahmad Bassam Alzubi. 2025. "Early Prediction of Student Performance Using an Activation Ensemble Deep Neural Network Model" Applied Sciences 15, no. 21: 11411. https://doi.org/10.3390/app152111411
APA StyleBin Nuweeji, H., & Alzubi, A. B. (2025). Early Prediction of Student Performance Using an Activation Ensemble Deep Neural Network Model. Applied Sciences, 15(21), 11411. https://doi.org/10.3390/app152111411






