Softening Deformation Characteristics of Tuff Gully Tunnels Under Heavy Rainfall Infiltration and Their Influence on Stability
Abstract
1. Introduction
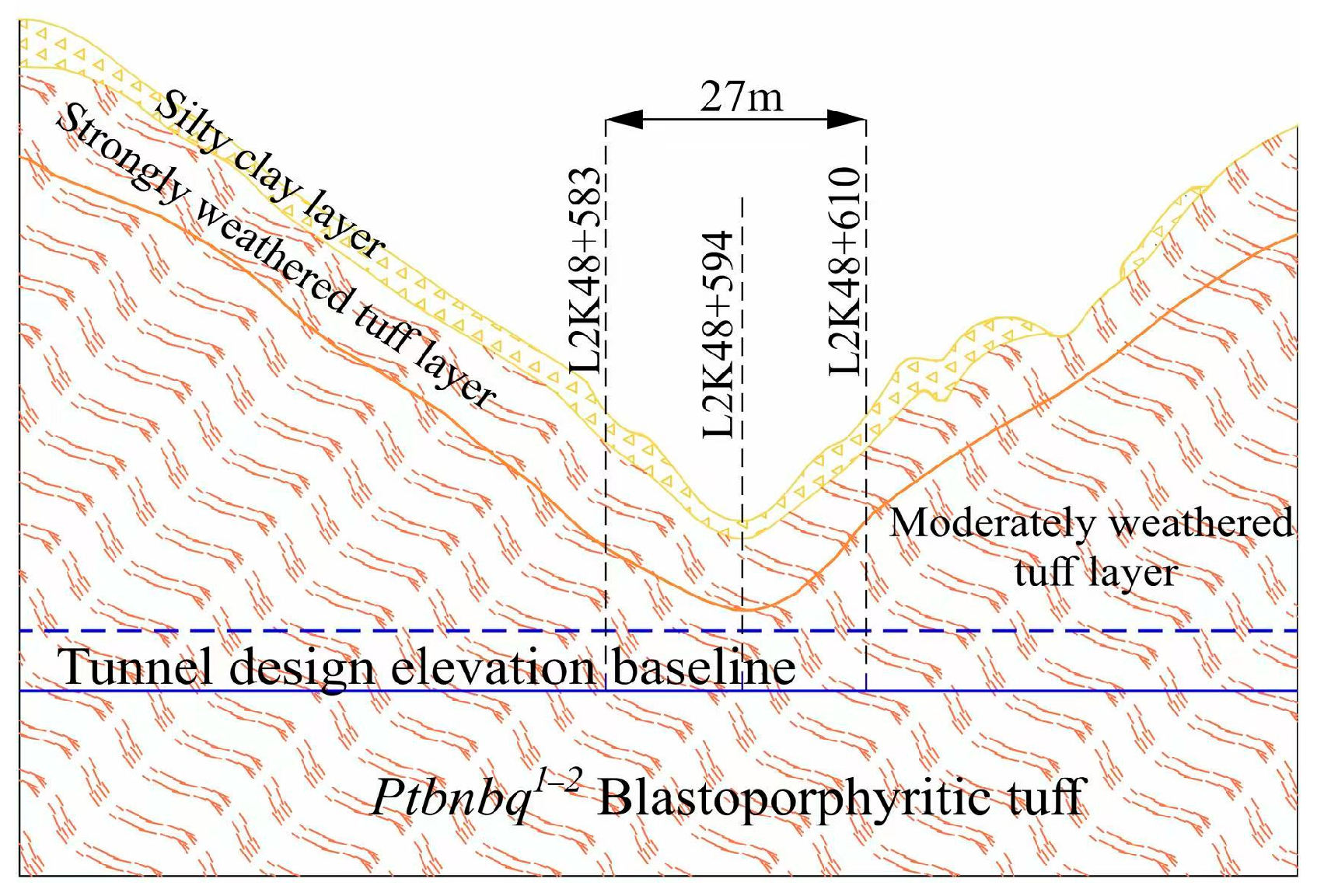
2. Engineering Overview
3. Tunnel Support Design Scheme
- Design of advanced small pipe support
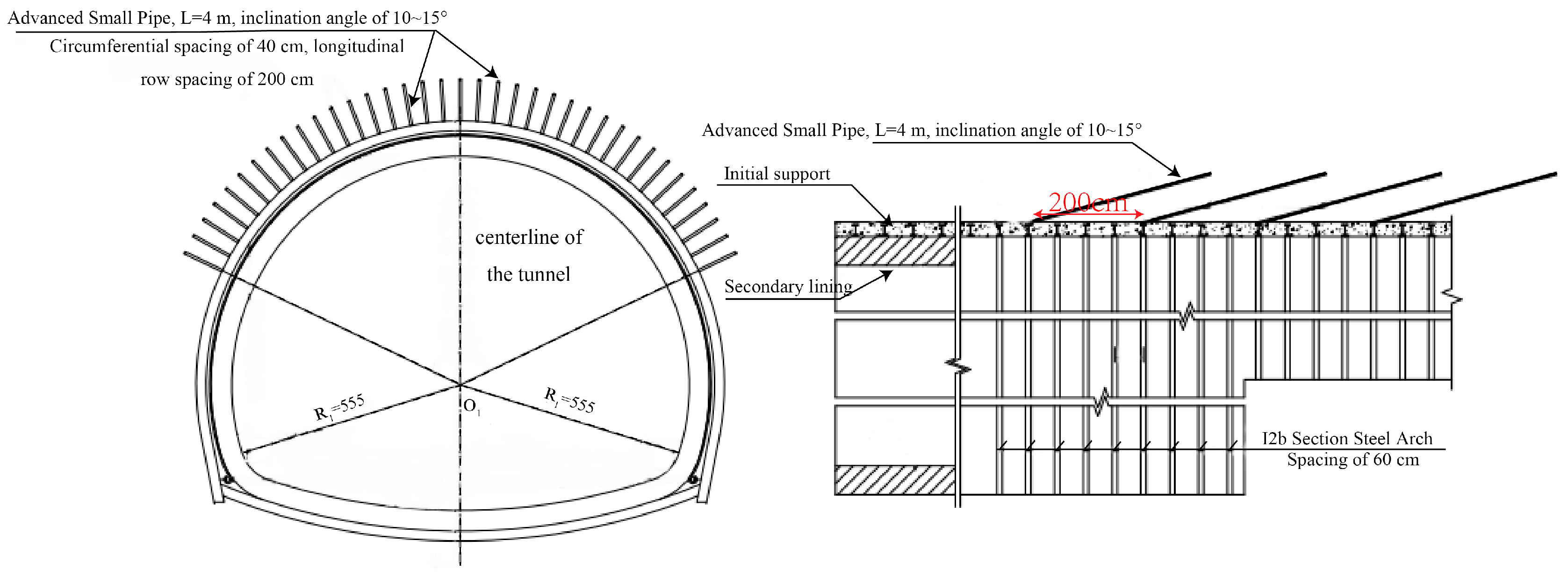
- 2.
- Design of Lining Support

4. Study on Softening Law of Tuff Under Rainfall Infiltration
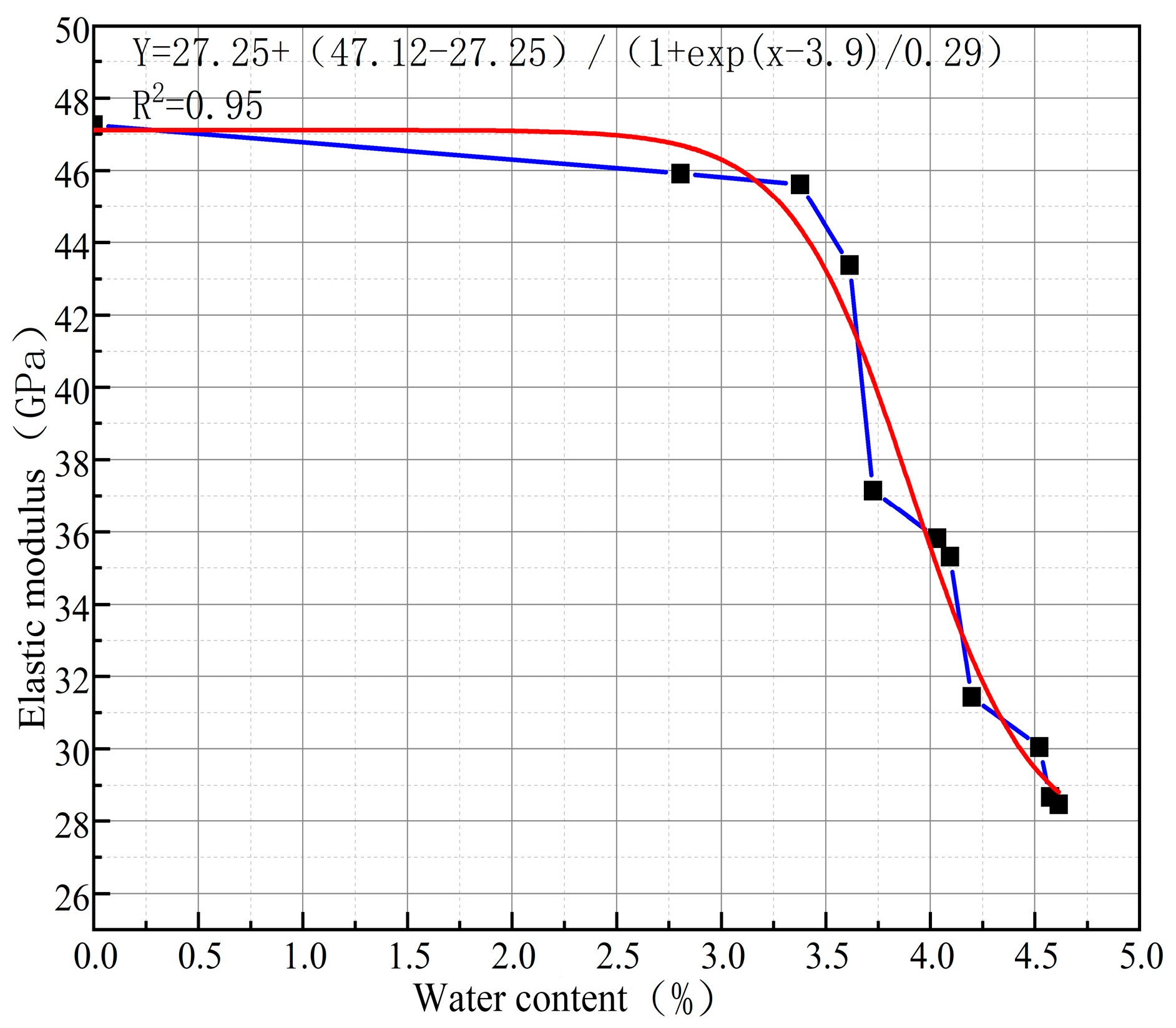
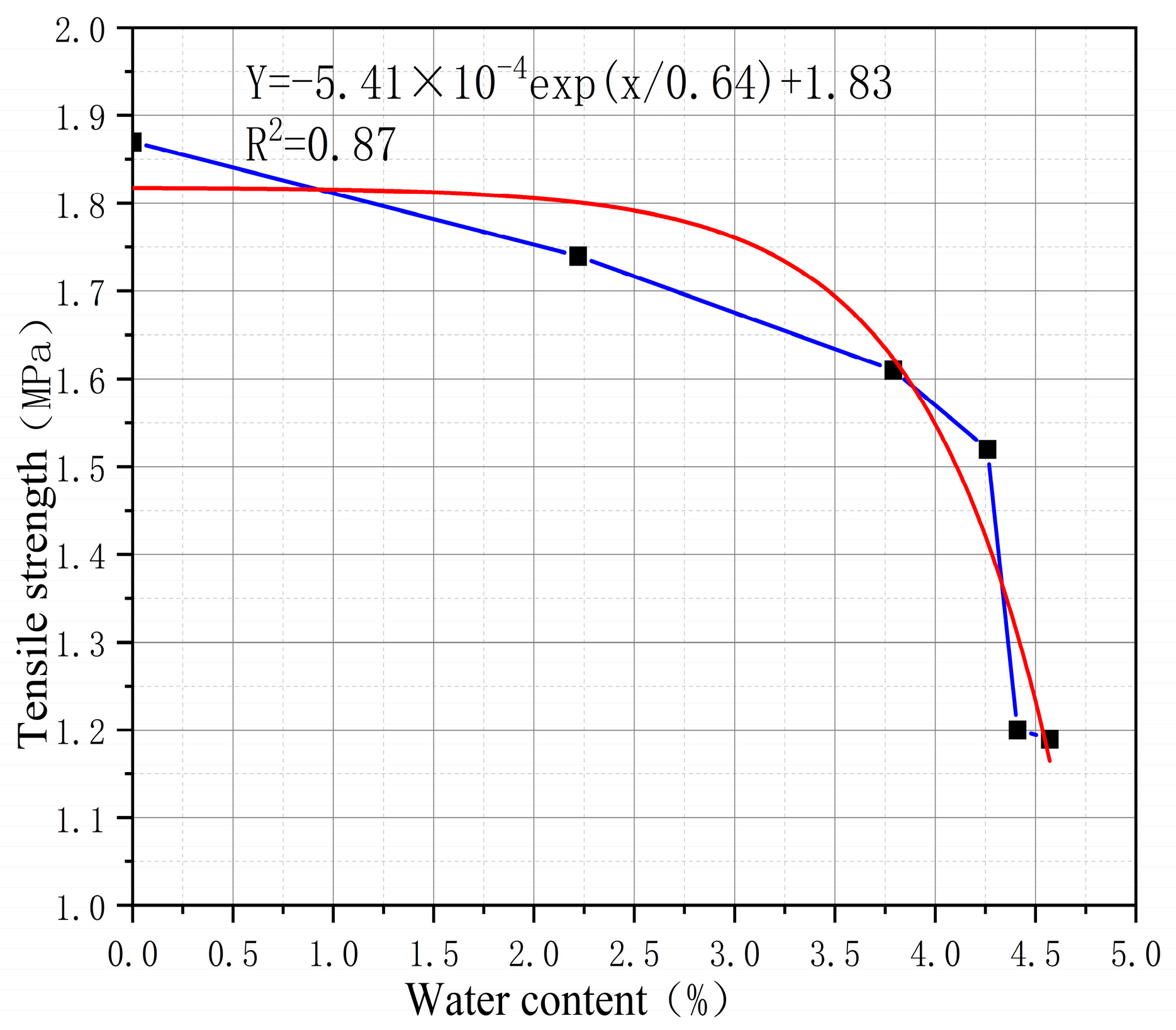
4.1. Relationship Between Elastic Modulus, Cohesion and Water Content
4.2. Relationship Between Softening Coefficient and Water Content
5. Study on Heavy Rainfall Infiltration in Gullies
5.1. Construction of Numerical Test Model for Gully Valley Tunnel
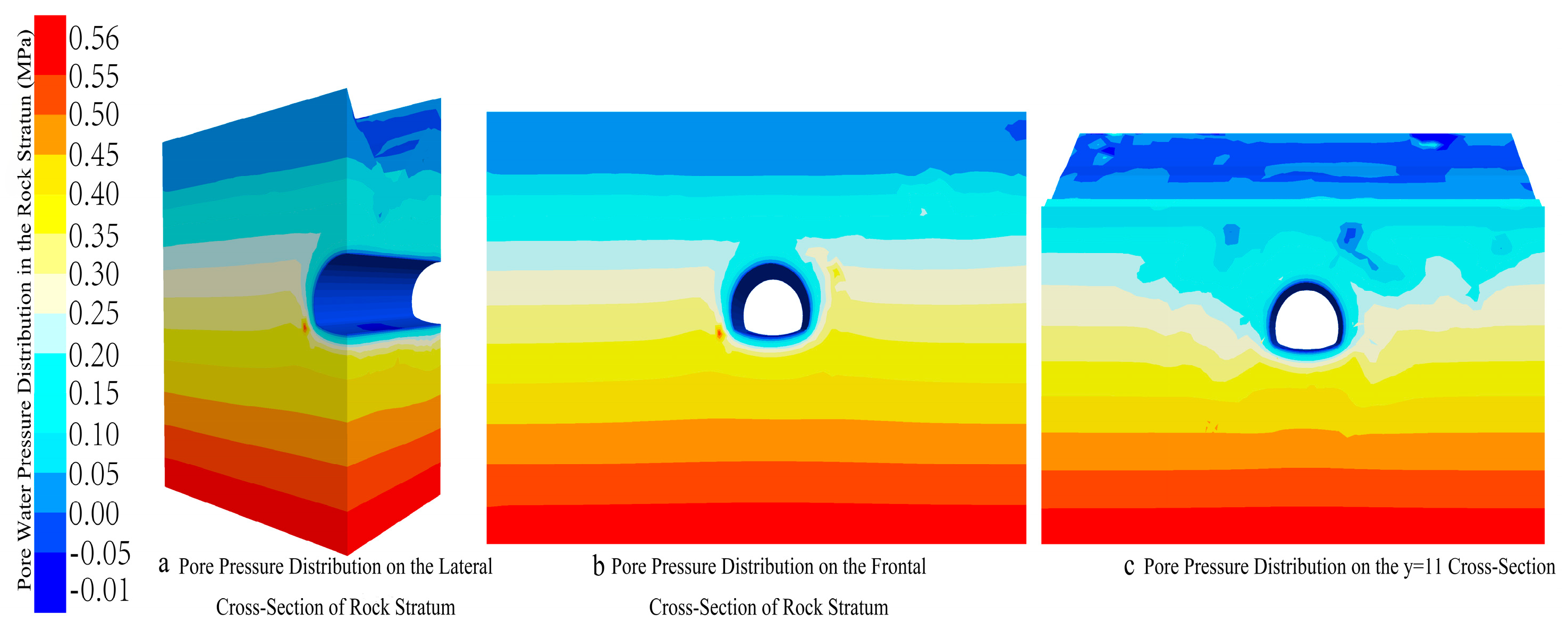
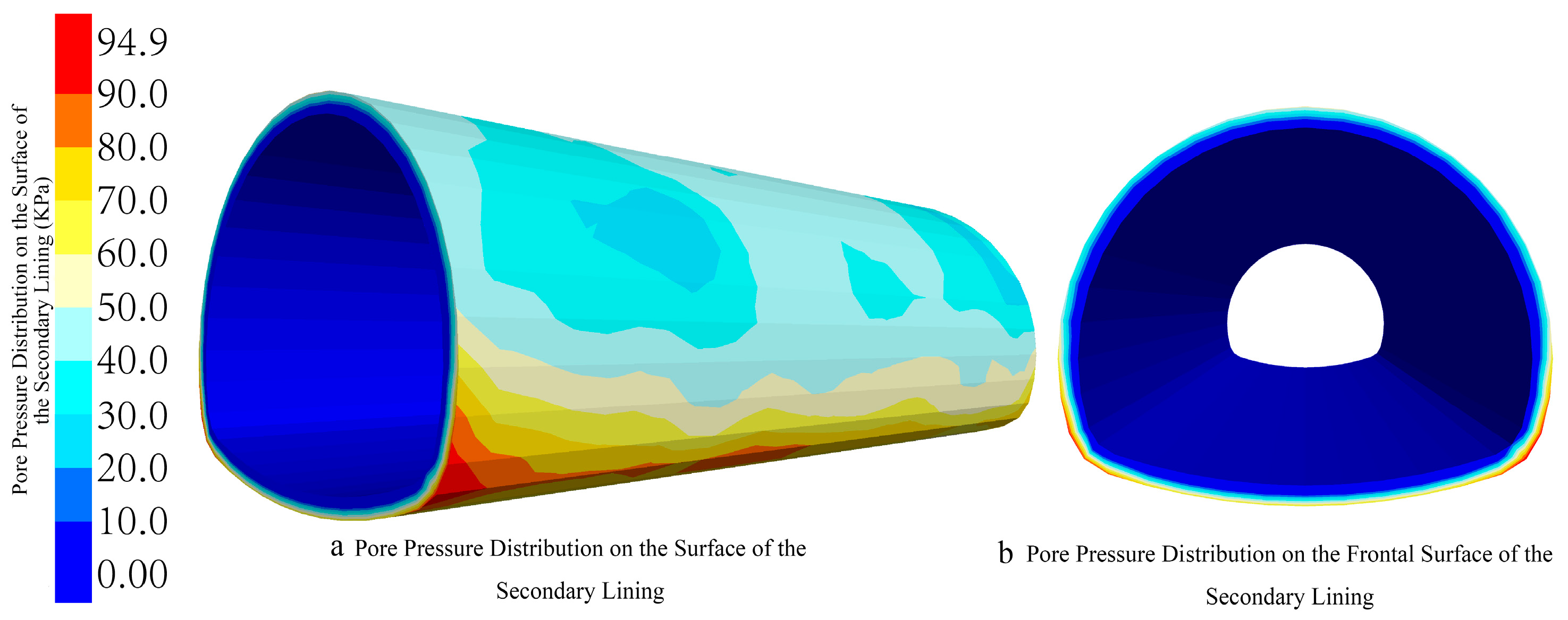
5.2. Pore Water Pressure Distribution in Rock Strata
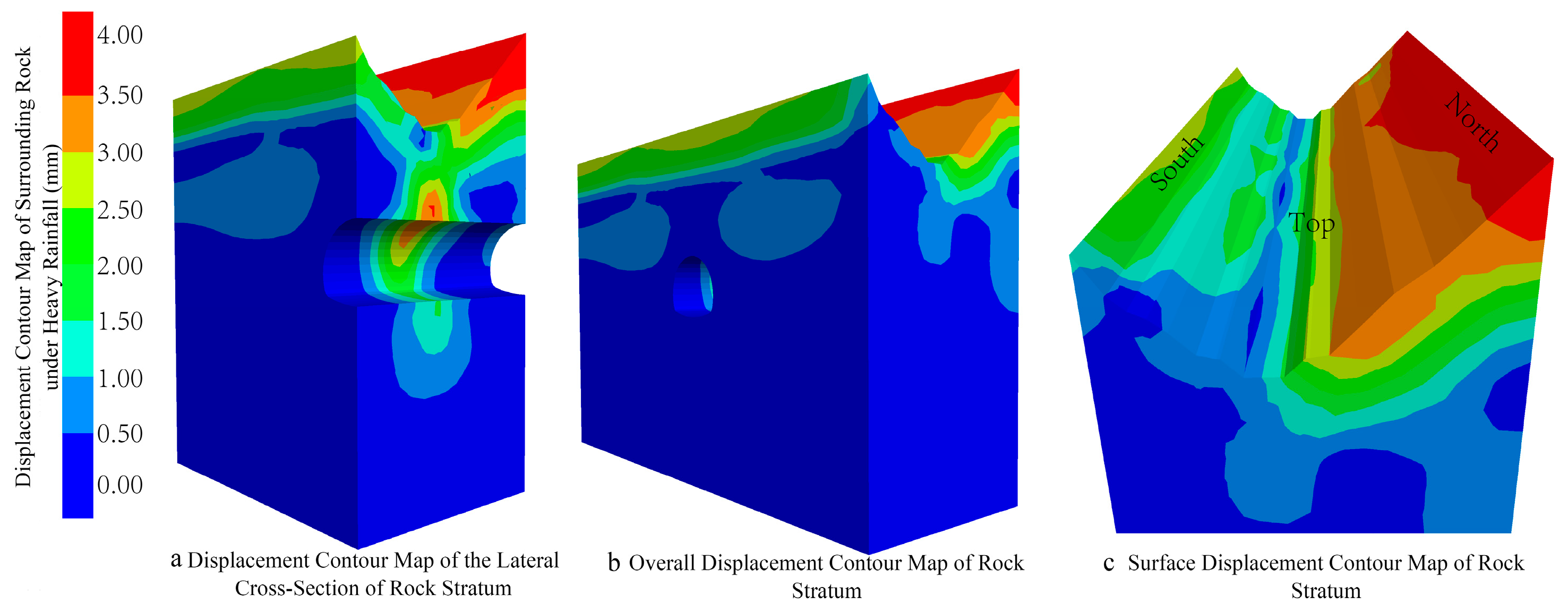
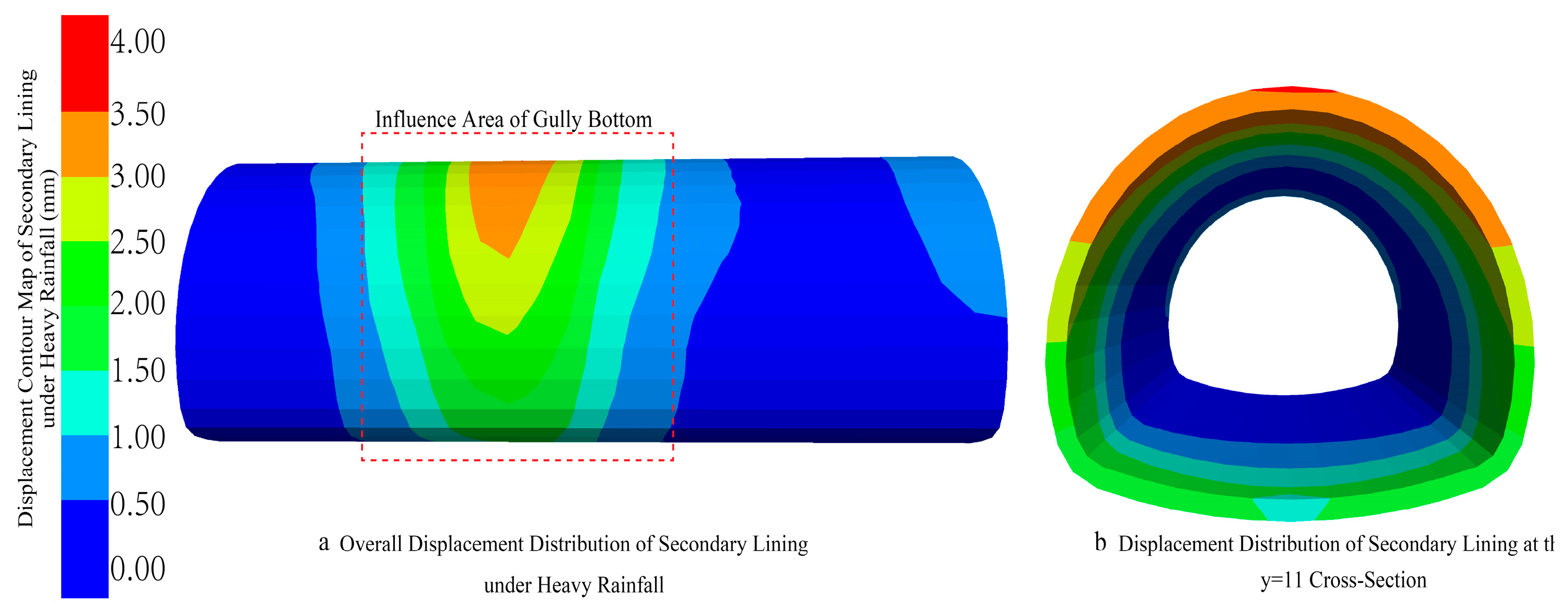
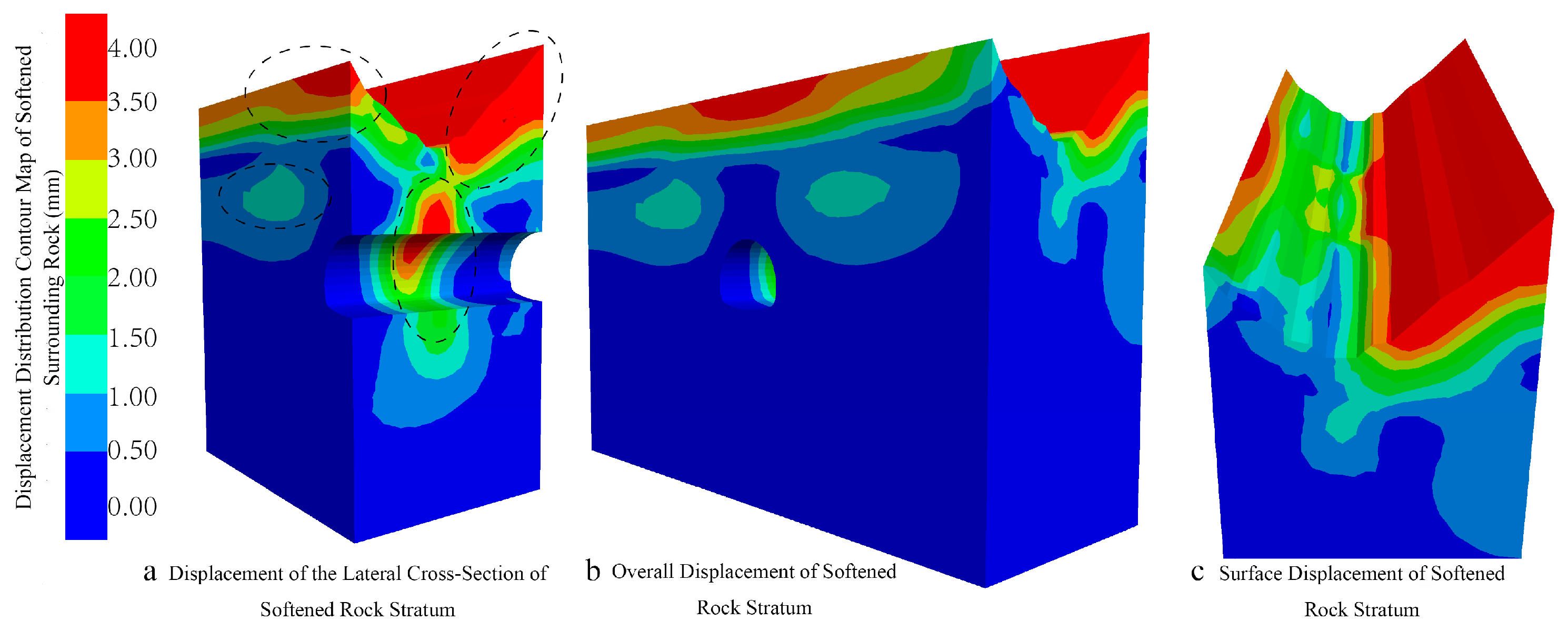
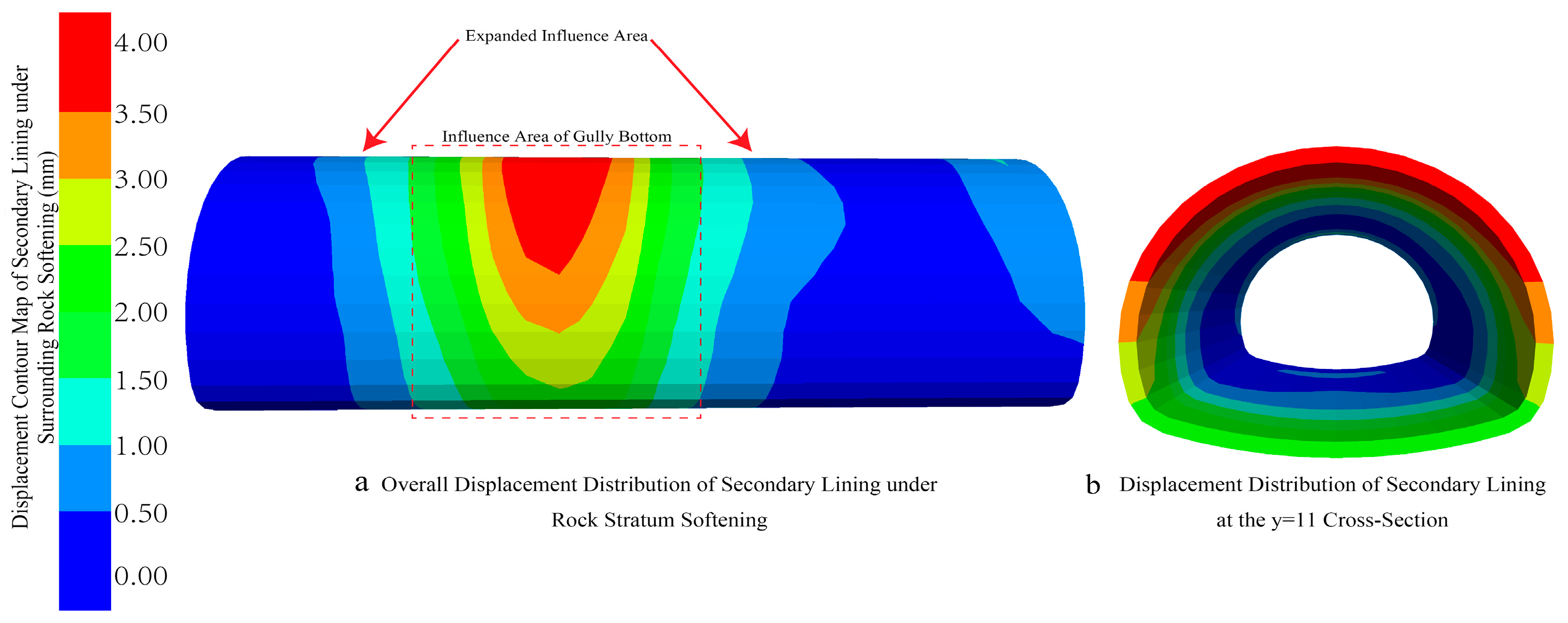
5.3. Displacement and Deformation Characteristics of Surrounding Rock and Support Structure
5.4. Influence of Rock Stratum Softening on Tunnel Stability
6. Conclusions
- (1)
- It reveals the “water content threshold effect” and softening law of tuff mechanical properties. Through systematic unsaturated mechanical tests, the phased attenuation characteristics of the mechanical parameters of the local blastotuff with water content were quantified. The critical water content for significant strength deterioration was determined to be 2.5%, and the saturated softening coefficient was measured as 0.59. This law provides a key theoretical and data basis for the stability evaluation and early warning of tunnel surrounding rock during the rainy season.
- (2)
- It clarifies the “seepage-control and convergence” effect of gully topography and the redistribution law of pore water pressure under heavy rainfall infiltration. Numerical simulations reveal that rainfall converges at the gully bottom under the control of the gully’s “concave” topography, causing the pore water pressure of the rock stratum to increase from the top to the bottom, with the maximum reaching 0.55 MPa at the bottom. For the first time, it systematically presents a binary distribution pattern of “uniform below, disordered above” bounded by the tunnel, especially forming a significant pore water pressure extension zone directly below the aqueduct. This law clarifies that the reconstruction of the seepage field is the primary external environmental factor affecting tunnel stability.
- (3)
- It reveals the deformation synergy mechanism and stability-sensitive zones under the “seepage-softening” coupling effect. The study clarifies for the first time that the special seepage field controlled by topography and the strength softening effect of tuff are coupled with each other, leading to non-uniform distribution of deformations in the surrounding rock and support structures. Instead, deformations are highly concentrated in three key stability-sensitive zones: directly below the gully bottom, arch haunches, and arch crown. This mechanism explains the cause of the spatial differentiation of deformations and provides a reference for precise prevention and control.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, X.; Luo, Q.; Yan, F.; Qi, C. Dynamic compressive micro-macro fracture mechanism with the water-saturated strengthening and weakening effect in brittle rocks. Theor. Appl. Fract. Mech. 2025, 137, 104871. [Google Scholar] [CrossRef]
- Yujing, J.; Lugen, C.; Dong, W.; Hengjie, L.; Guangchao, Z.; Ling, D.; Bin, L. Mechanical properties and acoustic emission characteristics of soft rock with different water contents under dynamic disturbance. Int. J. Coal Sci. Technol. 2024, 11, 36. [Google Scholar] [CrossRef]
- Ning, L.; Zhijun, J.; Haibo, W.; Yushi, Z.; Shicheng, Z.; Fengxia, L.; Tong, Z.; Minqu, J. Investigation into shale softening induced by water/CO2-rock interaction. Int. J. Rock Mech. Min. Sci. 2023, 161, 105299. [Google Scholar]
- Li, T.; Jiang, M.; Thornton, C. Three-dimensional discrete element analysis of triaxial tests and wetting tests on unsaturated compacted silt. Comput. Geotech. 2018, 97, 90–102. [Google Scholar] [CrossRef]
- Moore, D.E.; Lockner, D.A. Crystallographic controls on the frictional behavior of dry and water-saturated sheet structure minerals. J. Geophys. Res. Solid Earth 2004, 109, B03401. [Google Scholar] [CrossRef]
- Jiao, L.; Hao, C.; Duan, D.; Lu, W.; Gan, Y.; Qi, J.; Yang, W.; Chen, Y. Molecular dynamics simulation of water absorption and mechanical weakening in coal rocks based on Monte Carlo methods. Solid State Ion. 2024, 418, 116743. [Google Scholar] [CrossRef]
- Liang, N.; Jin, T.; Zhang, J.; Lu, D. Mechanism Study on the Intrinsic Damage and Microchemical Interactions of Argillaceous Siltstone Under Different Water Temperatures. Appl. Sci. 2024, 14, 11747. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, Z.; Yin, Y.; Wen, J. Comparative Evaluation of Presented Strength Criteria of Anisotropic Rocks Based on Triaxial Experiments. Appl. Sci. 2025, 15, 5308. [Google Scholar] [CrossRef]
- Baud, P.; Louis, L.; David, C.; Rawling, G.C.; Wong, T.-F. Effects of Bedding and Foliation on Mechanical Anisotropy, Damage Evolution and Failure Mode; Geological Society, London, Special Publications: Bath, UK, 2005; Volume 245, pp. 223–249. [Google Scholar] [CrossRef]
- Wei, H.; Rui, F.; Huanran, F.; Jingyu, C.; Zili, F. Mechanical Properties of Soft Rocks Subjected to Water-Rock Reaction and Cyclic Pressure. Adv. Civ. Eng. 2022, 2022, 1533464. [Google Scholar]
- Xu, H.; Liu, J.; Wang, L.; Yang, B.; Yang, H. The weakening effect of hydrostatic pressure on rock mass of different lithology. Environ. Earth Sci. 2015, 74, 2489–2497. [Google Scholar] [CrossRef]
- Heap, M.J.; Harnett, C.; Farquharson, J.; Baud, P.; Rosas-Carbajal, M.; Komorowski, J.C.; Violay, M.E.S.; Gilg, H.A.; Reuschlé, T. The influence of water-saturation on the strength of volcanic rocks and the stability of lava domes. J. Volcanol. Geotherm. Res. 2023, 444, 107962. [Google Scholar] [CrossRef]
- Pan, Y.; Wu, G.; Zhao, Z.; He, L. Analysis of rock slope stability under rainfall conditions considering the water-induced weakening of rock. Comput. Geotech. 2020, 128, 103806. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, H.; Jiang, M. Theoretical study on the water-induced weakening of rock based on microstructural mechanics approach. Eur. J. Environ. Civ. Eng. 2025, 29, 89–111. [Google Scholar] [CrossRef]
- Ding, C.; Zhang, Y.; Yang, X.; Hu, D.; Zhou, H.; Lu, J. Permeability evolution of tight sandstone under high confining pressure and high pore pressure and its microscopic mechanism. Rock Soil Mech. 2019, 40, 3300–3308. [Google Scholar]
- Zheng, J.; Zheng, L.; Liu, H.-H.; Ju, Y. Relationships between permeability, porosity and effective stress for low-permeability sedimentary rock. Int. J. Rock Mech. Min. Sci. 2015, 78, 304–318. [Google Scholar] [CrossRef]
- Zhang, R.; Ning, Z.; Yang, F.; Zhao, H.; Wang, Q. A laboratory study of the porosity-permeability relationships of shale and sandstone under effective stress. Int. J. Rock Mech. Min. Sci. 2016, 81, 19–27. [Google Scholar] [CrossRef]
- Mao, W.; Ren, Z.L.; Liu, X.J.; Muhemaier, R.; Li, Y.J.; Jiang, C.T. Research on the Stability of Lining Structures Under Different Fault Moments Based on FDM-DEM. Build 2024, 14, 16. [Google Scholar] [CrossRef]
- Wang, J.-A.; Park, H.D. Fluid permeability of sedimentary rocks in a complete stress–strain process. Eng. Geol. 2002, 63, 291–300. [Google Scholar] [CrossRef]
- Jiang, C.T.; Mao, W.; Zhang, Y.K.; Liu, X.J.; Muhemaier, R.; Xie, L.F. Influence of external insert angle on structural deformation of long pipe shed with shallow hole. Sci. Rep. 2023, 13, 18. [Google Scholar] [CrossRef]
- Xing, J.; Zhao, C.; Yu, S.; Matsuda, H.; Ma, C. Experimental Study on Rock-Like Specimens with Single Flaw under Hydro-Mechanical Coupling. Appl. Sci. 2019, 9, 3234. [Google Scholar] [CrossRef]
- JTG D70-2004; Code for Design of Road Tunnel. Chongqing Transportation Research and Design Institute: Chongqing, China, 2004.
- GB/T 50081-2019; Standard for Test Methods of Concrete Physical and Mechanical Properties. China Architecture & Building Press: Beijing, China, 2019.
- Guo-Ping, X.; Hong-Zhou, L.; Bai-Yong, F.; Jian-Gang, Y. Research and prospect of post-peak strain-softening characteristics of rocks. IOP Conf. Ser. Earth Environ. Sci. 2021, 787, 012135. [Google Scholar]
- Liu, Z.; He, X.; Fan, J.; Zhou, C. Study on the Softening Mechanism and Control of Red-Bed Soft Rock under Seawater Conditions. J. Mar. Sci. Eng. 2019, 7, 235. [Google Scholar] [CrossRef]
- Shipiao, C.; Sumin, Z. Handbook of Engineering Geology; China Architecture&Building Press: Beijing, China, 2007. [Google Scholar]


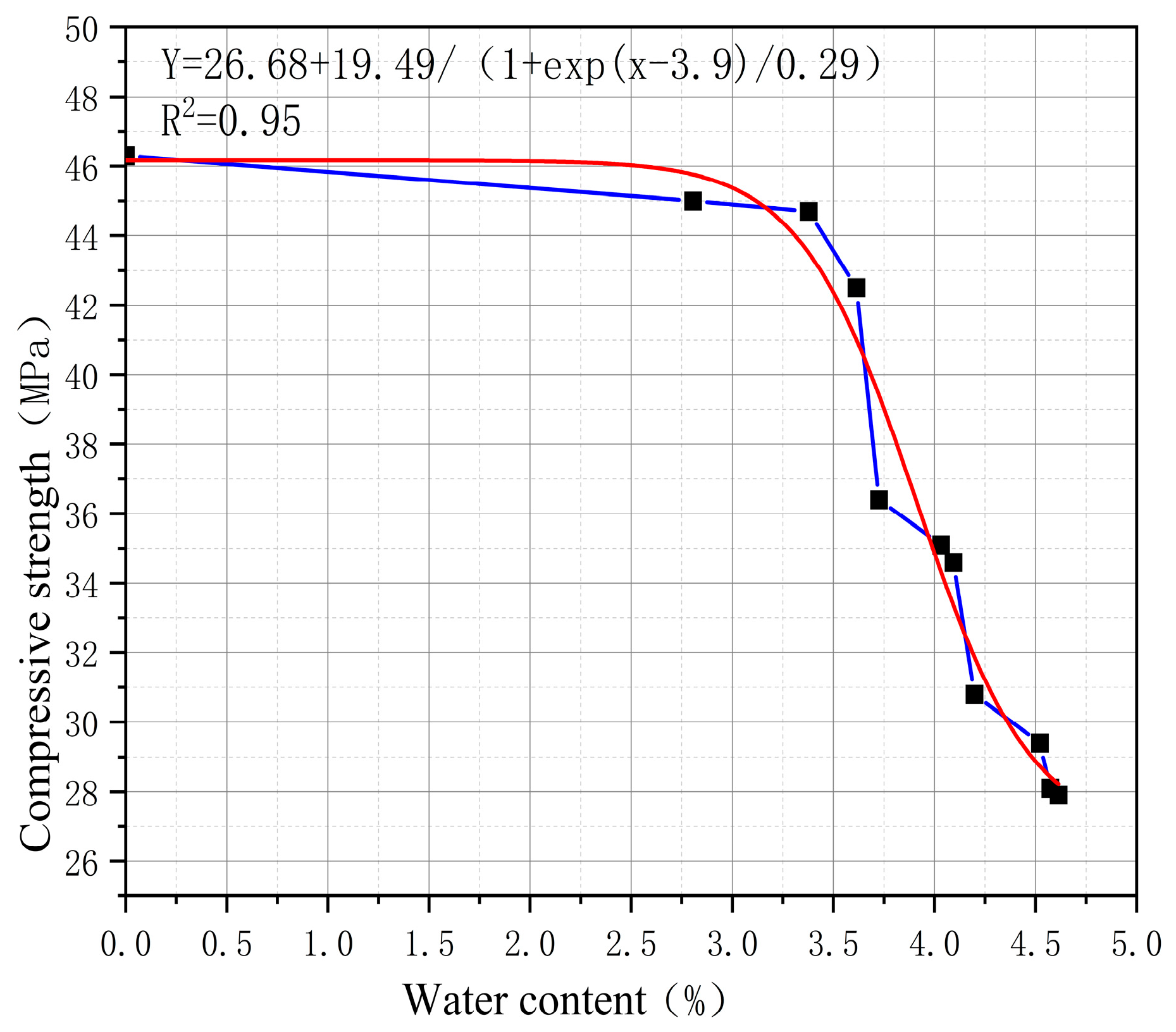
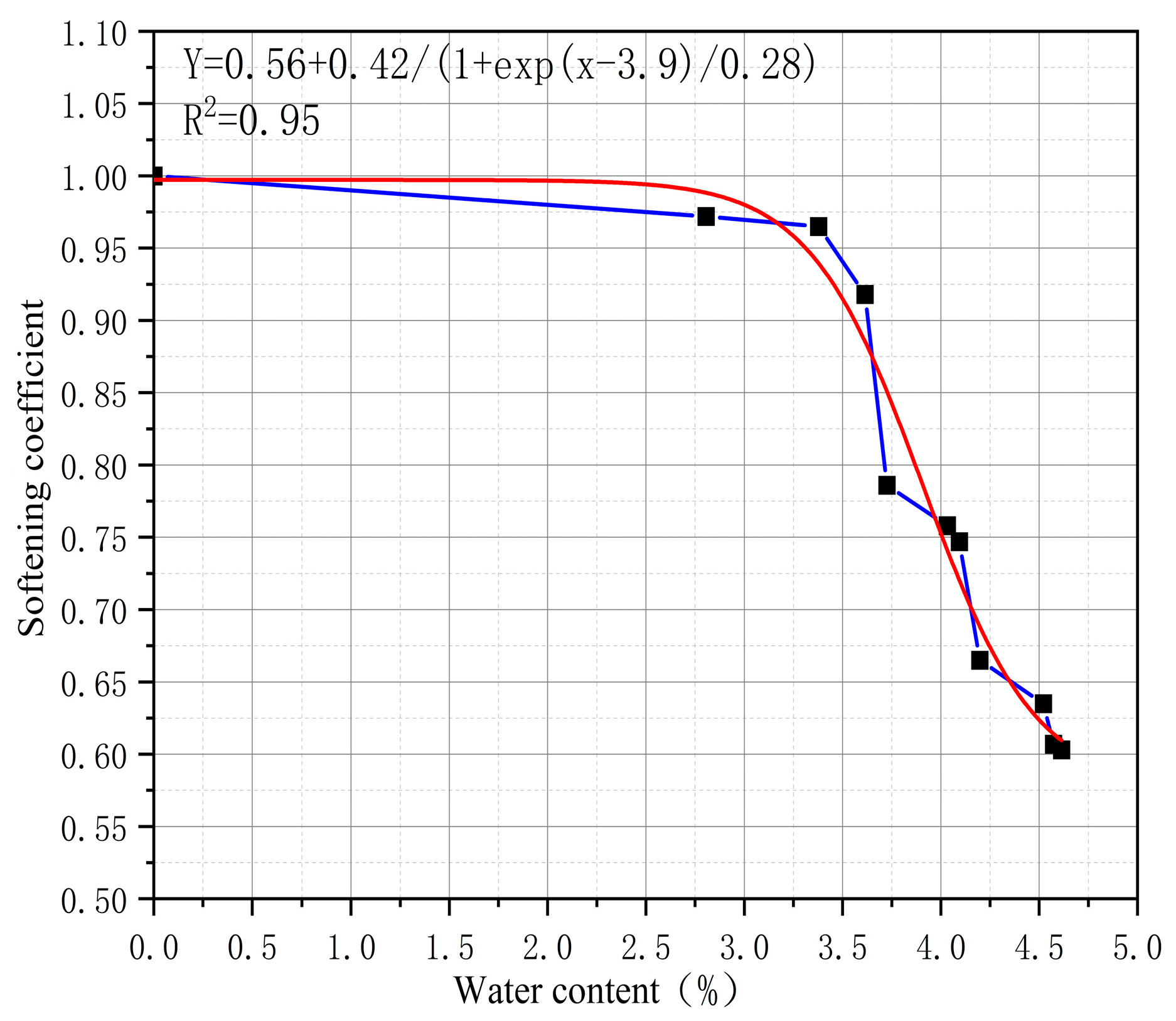

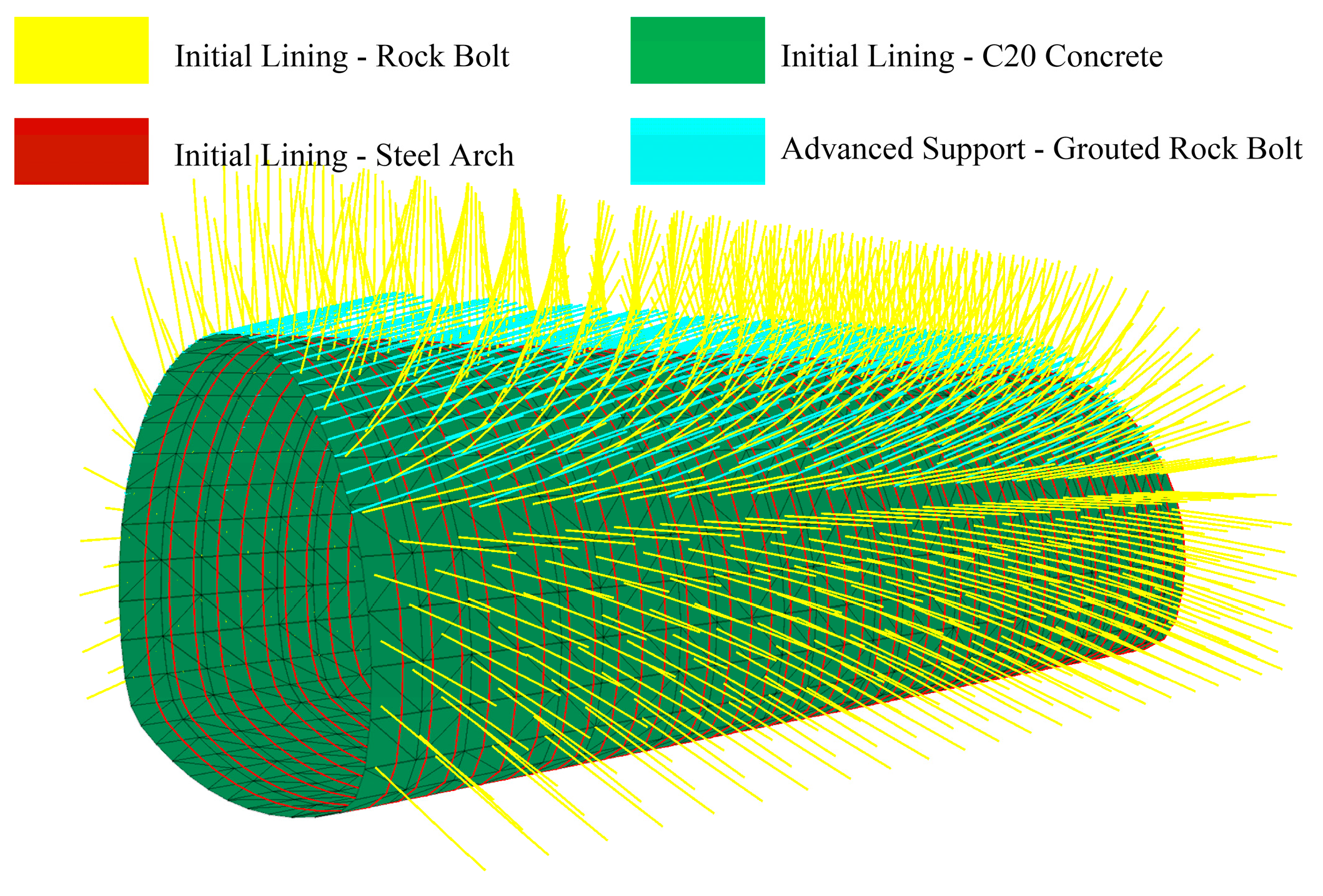
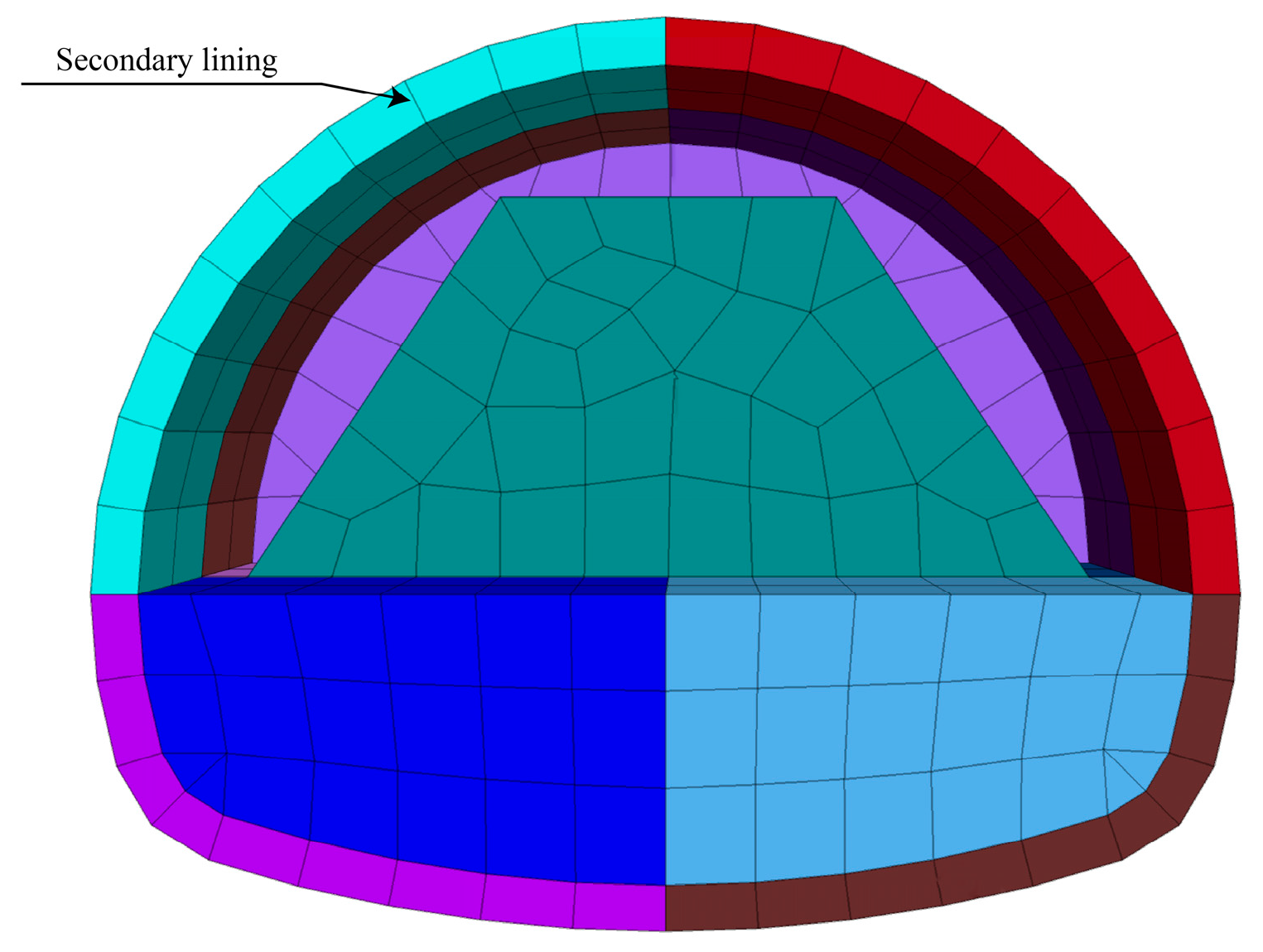

| Item | Water Content % | Failure Load kN | Compressive Strength MPa | Elastic Modulus GPa |
|---|---|---|---|---|
| undisturbed rock core | 0 | 90.887 | 46.3 | 47.245 |
| soaked1 | 2.805 | 88.335 | 45.0 | 45.918 |
| soaked2 | 3.378 | 87.746 | 44.7 | 45.612 |
| soaked3 | 3.614 | 83.427 | 42.5 | 43.376 |
| soaked4 | 3.725 | 71.453 | 36.4 | 37.143 |
| soaked5 | 4.032 | 68.901 | 35.1 | 35.816 |
| soaked6 | 4.094 | 67.919 | 34.6 | 35.306 |
| soaked7 | 4.197 | 60.460 | 30.8 | 31.429 |
| soaked8 | 4.521 | 57.712 | 29.4 | 30.052 |
| soaked9 | 4.573 | 55.168 | 28.1 | 28.673 |
| soaked10 | 4.613 | 54.762 | 27.9 | 28.469 |
| Item | Water Content% | Failure Load KN | Tensile Strength MPa |
|---|---|---|---|
| undisturbed rock core | 0 | 7.34 | 1.87 |
| soaked1 | 2.22 | 6.83 | 1.74 |
| soaked2 | 3.79 | 6.29 | 1.61 |
| soaked3 | 4.26 | 5.98 | 1.52 |
| soaked4 | 4.41 | 4.71 | 1.20 |
| soaked5 | 4.57 | 4.67 | 1.19 |
| Softening Coefficient | Evaluation of Water Influence Degree on Rock |
|---|---|
| <0.40 | Water exerts severe influence on rock |
| 0.40~0.65 | Water exerts significant influence on rock |
| 0.65~0.80 | Water exerts moderate influence on rock |
| 0.80~0.95 | Water exerts slight influence on rock |
| >0.95 | Water exerts no influence on rock |
| Item | Density /(kg/m3) | Elastic Modulus E/GPa | Poisson’s Ratio | Cohesion/MPa | Friction Angle/° |
|---|---|---|---|---|---|
| Blastoporphyritic Tuff | 2650 | 47.1 | 0.15 | 7.3 | 45.8 |
| Aqueduct | 2500 | 0.3 | 0.2 | ||
| C30 Secondary Lining | 2500 | 30 | 0.2 | ||
| C20 Shotcrete | 2400 | 28 | 0.13 | ||
| Steel Arch | 7850 | 206 | 0.3 | ||
| Φ25Rock Bolt | 7850 | 200 | 0.3 | ||
| Φ50Rock Bolt | 7850 | 200 | 0.3 | ||
| Φ42Rock Bolt | 7850 | 200 | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Wang, S.; Mao, W.; Shao, P.; Muhemaier, R.; Li, Y.; Xie, L. Softening Deformation Characteristics of Tuff Gully Tunnels Under Heavy Rainfall Infiltration and Their Influence on Stability. Appl. Sci. 2025, 15, 11385. https://doi.org/10.3390/app152111385
Liu X, Wang S, Mao W, Shao P, Muhemaier R, Li Y, Xie L. Softening Deformation Characteristics of Tuff Gully Tunnels Under Heavy Rainfall Infiltration and Their Influence on Stability. Applied Sciences. 2025; 15(21):11385. https://doi.org/10.3390/app152111385
Chicago/Turabian StyleLiu, Xuejun, Shuo Wang, Wei Mao, Peng Shao, Ruheiyan Muhemaier, Yanjun Li, and Liangfu Xie. 2025. "Softening Deformation Characteristics of Tuff Gully Tunnels Under Heavy Rainfall Infiltration and Their Influence on Stability" Applied Sciences 15, no. 21: 11385. https://doi.org/10.3390/app152111385
APA StyleLiu, X., Wang, S., Mao, W., Shao, P., Muhemaier, R., Li, Y., & Xie, L. (2025). Softening Deformation Characteristics of Tuff Gully Tunnels Under Heavy Rainfall Infiltration and Their Influence on Stability. Applied Sciences, 15(21), 11385. https://doi.org/10.3390/app152111385







