On the Use of Machine Learning Methods for EV Battery Pack Data Forecast Applied to Reconstructed Dynamic Profiles
Featured Application
Abstract
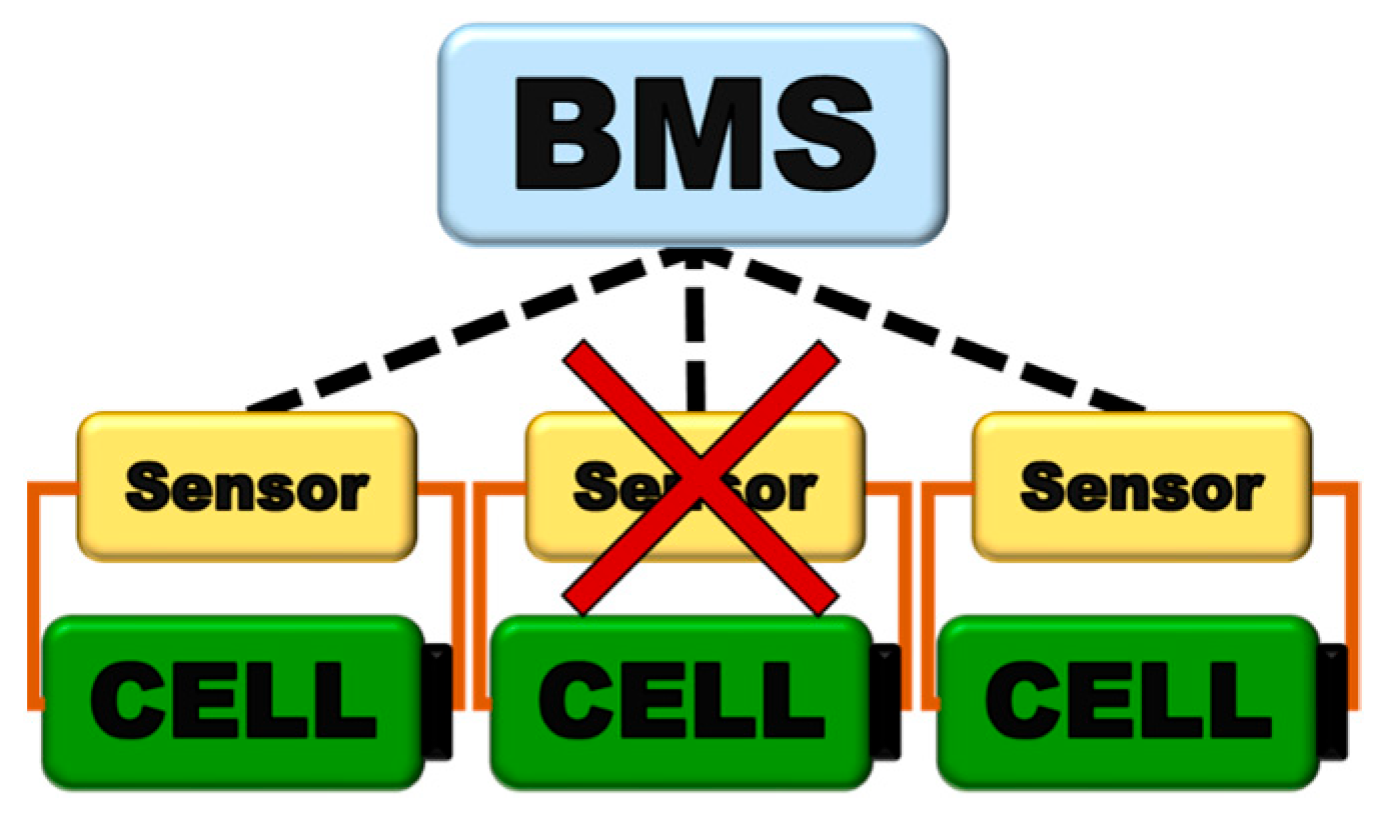
1. Introduction
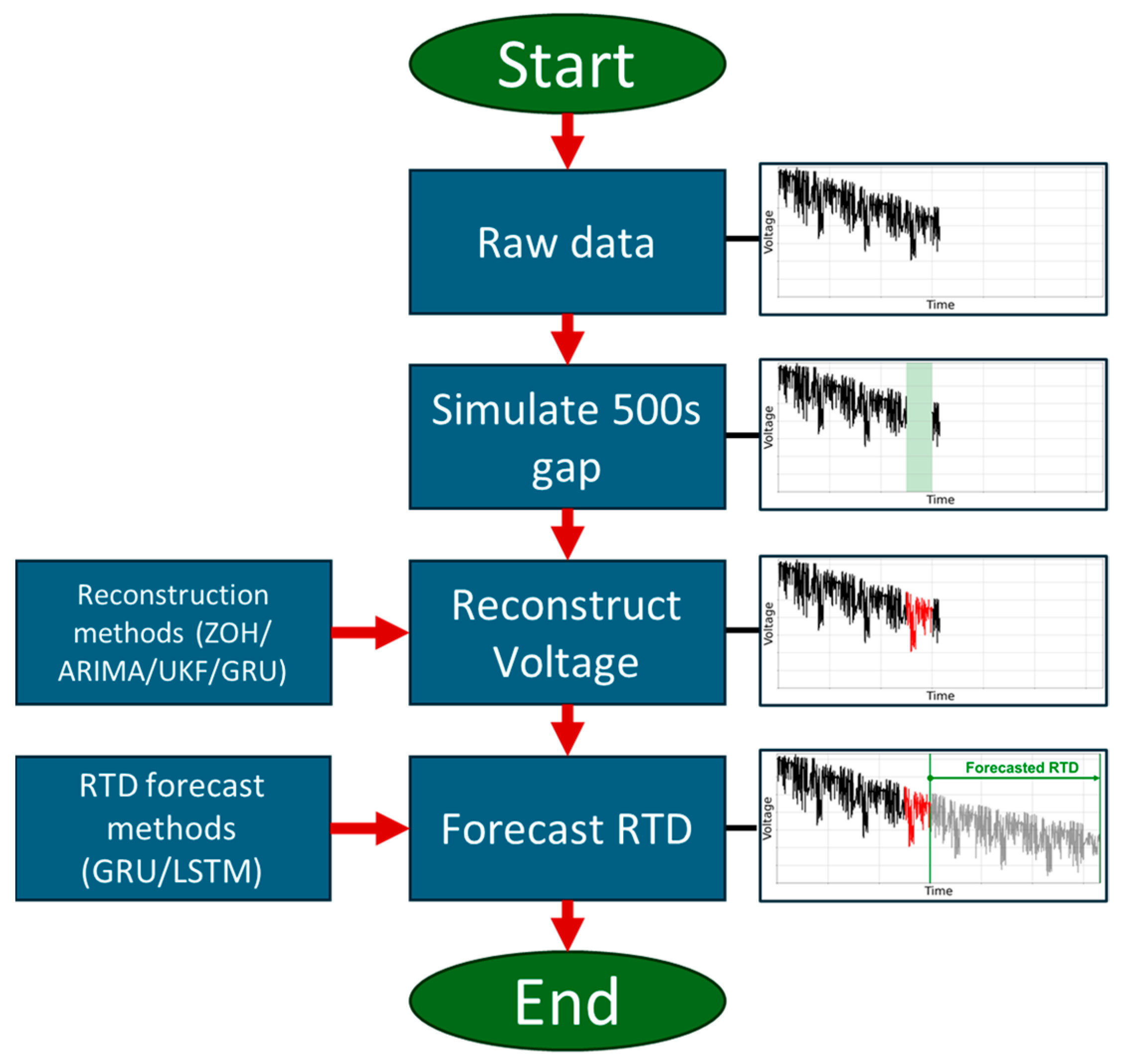
2. Materials and Methods
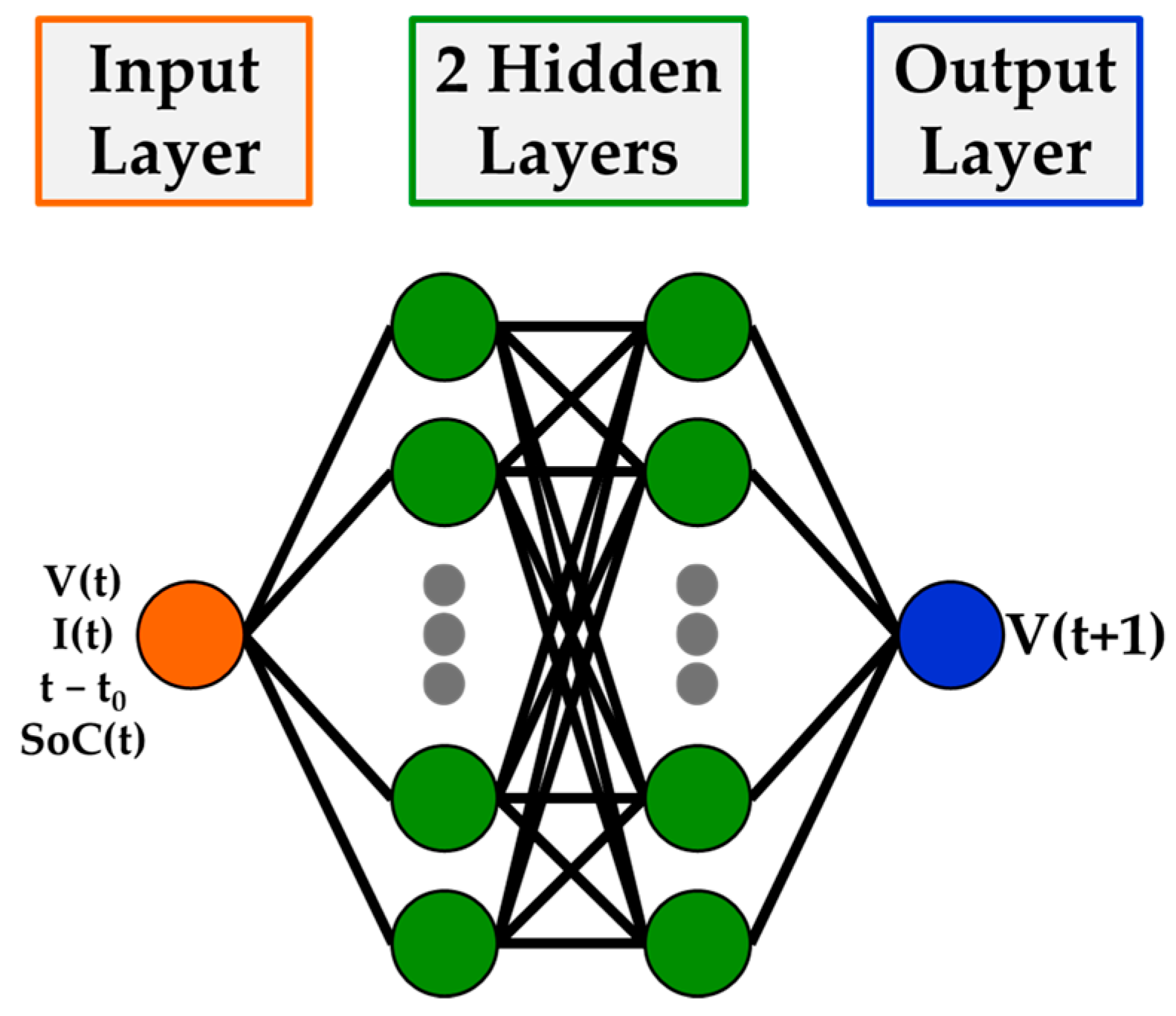
2.1. Analyzed Reconstruction Methods
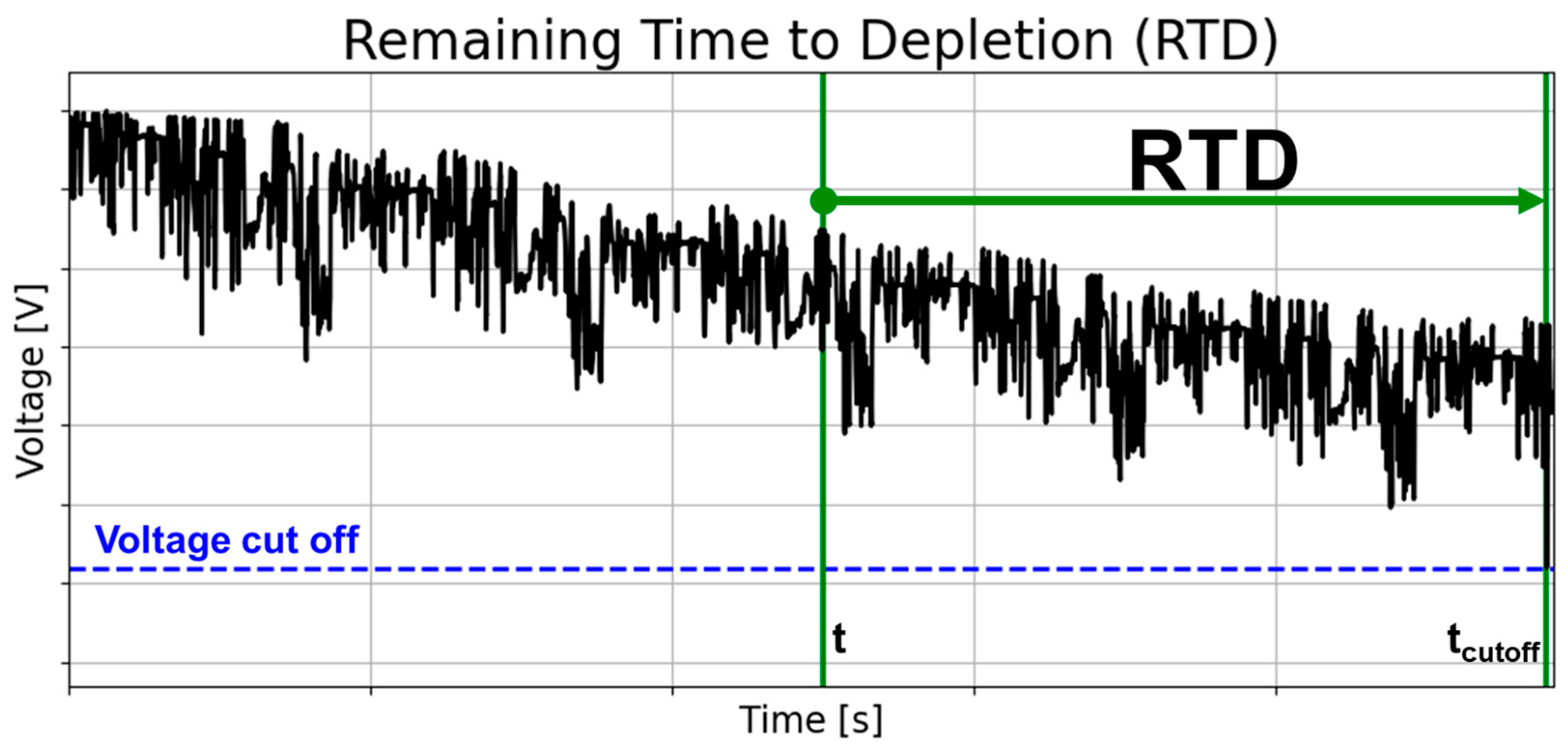
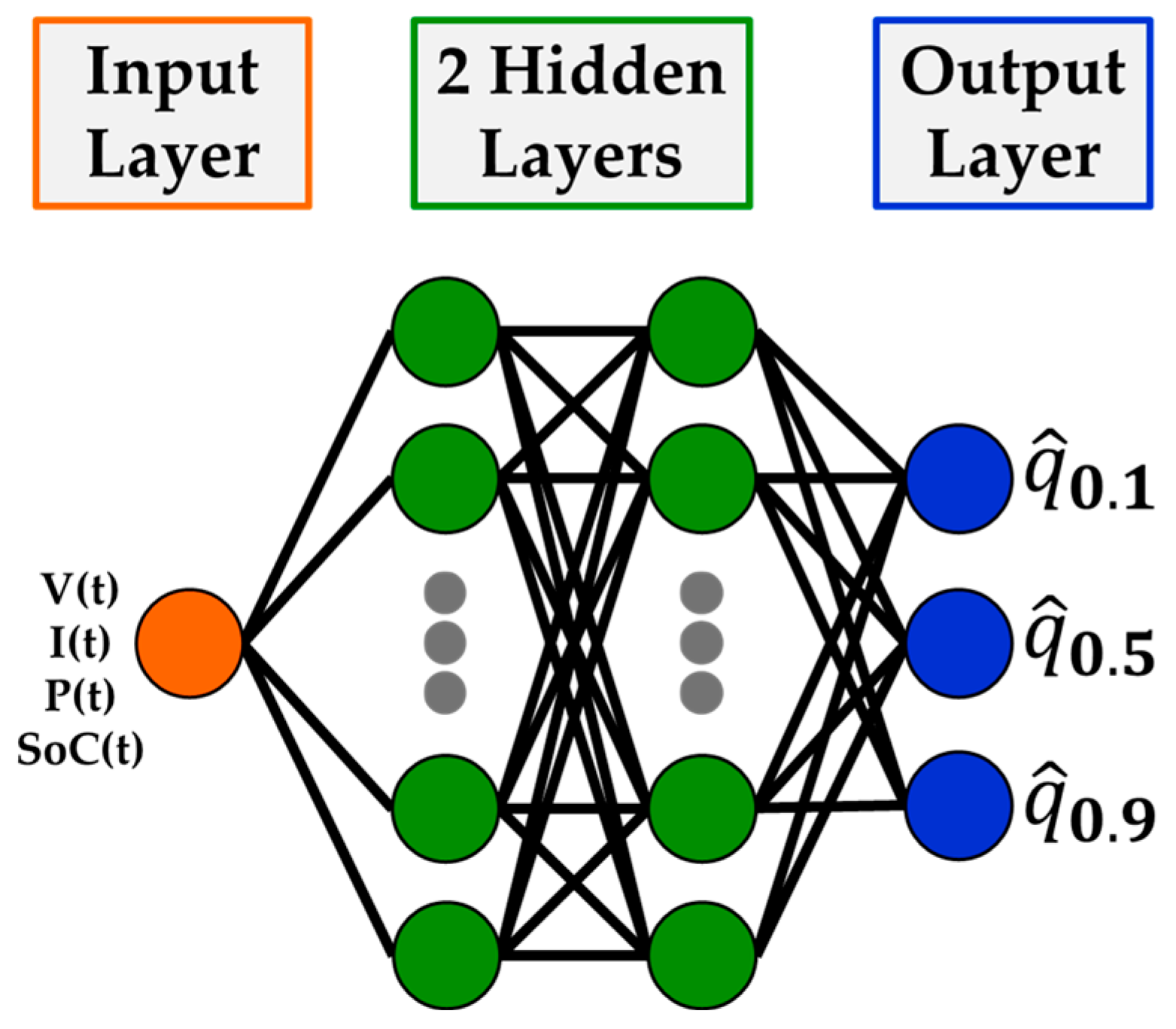
2.2. Analyzed RTD Forecasting Methods
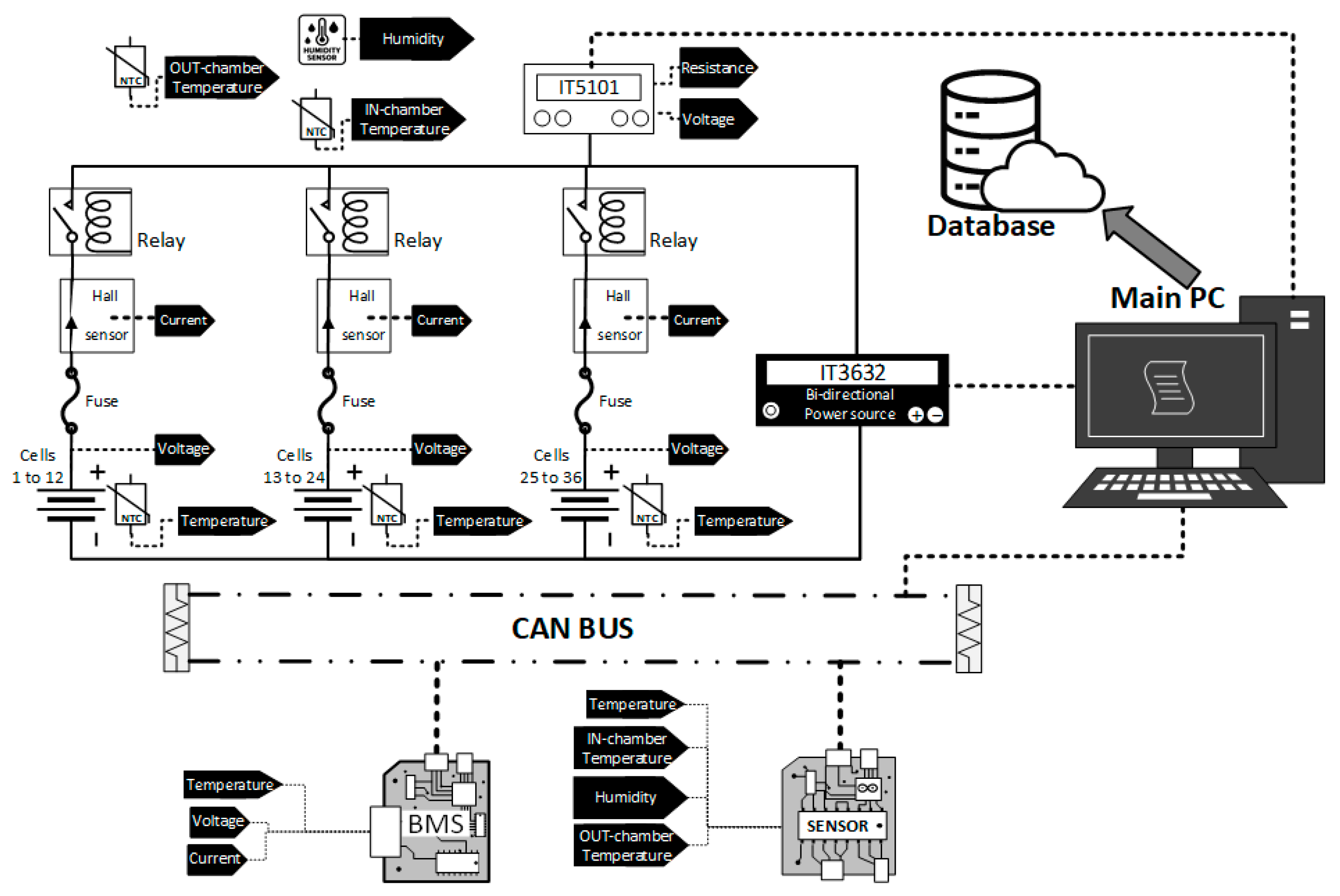
3. Dataset
- Chemistry: NCA;
- Nominal capacity: 3.2 Ah;
- Nominal voltage: 3.6 V;
- Charge conditions: CC-CV at 0.5C (cut off at 65 mA or after 4 h).
- Training set (WLTP driving cycles 249 to 300): This set is used for training data-driven reconstruction methods such as GRUs, as well as for training the RNN models for RTD forecasting.
- Evaluation set (WLTP driving cycles 301 to 350): This set is reserved exclusively for testing all reconstruction methods and assessing their impact on RTD forecasting accuracy.
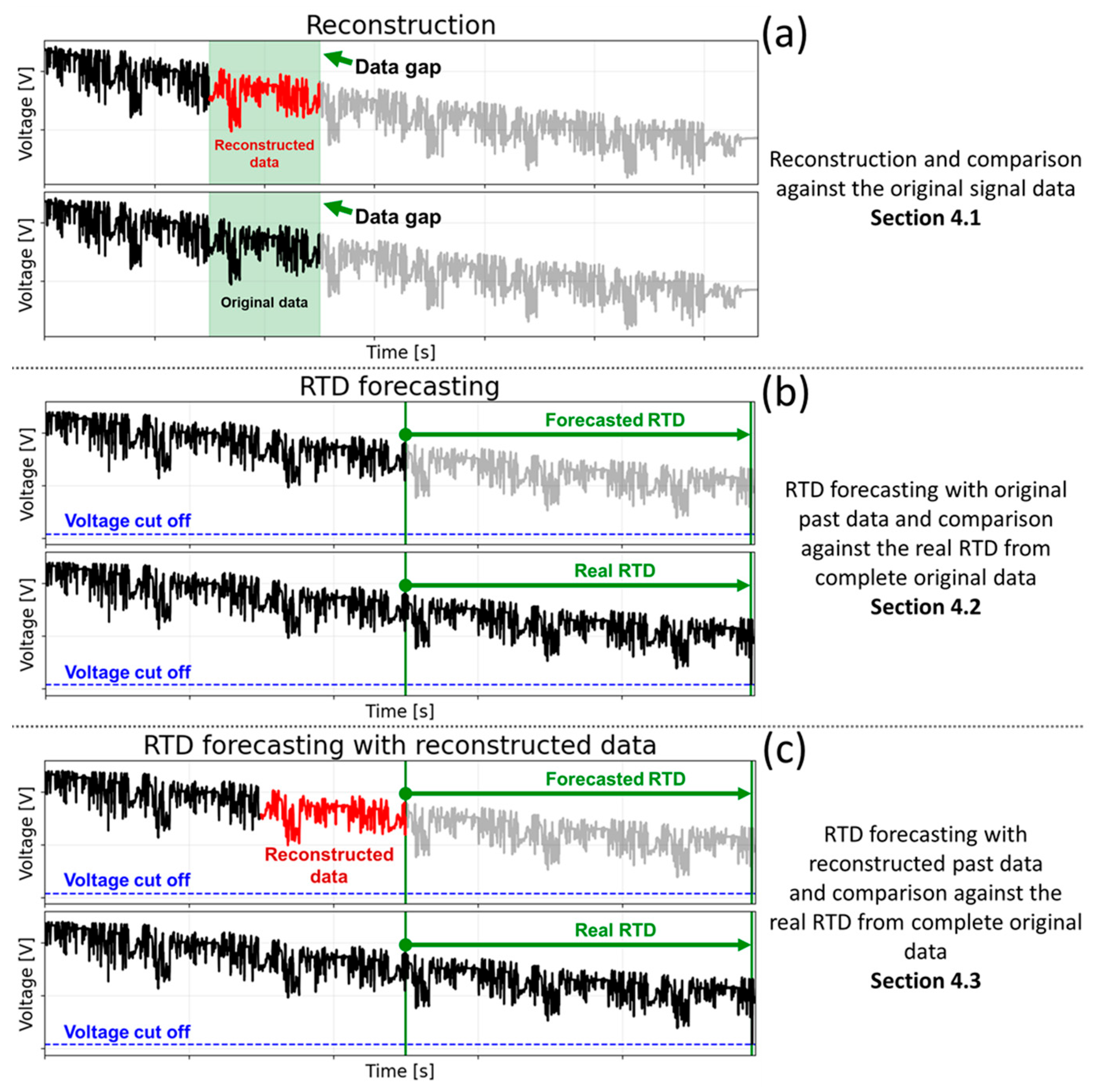
4. Results
4.1. Reconstruction Results
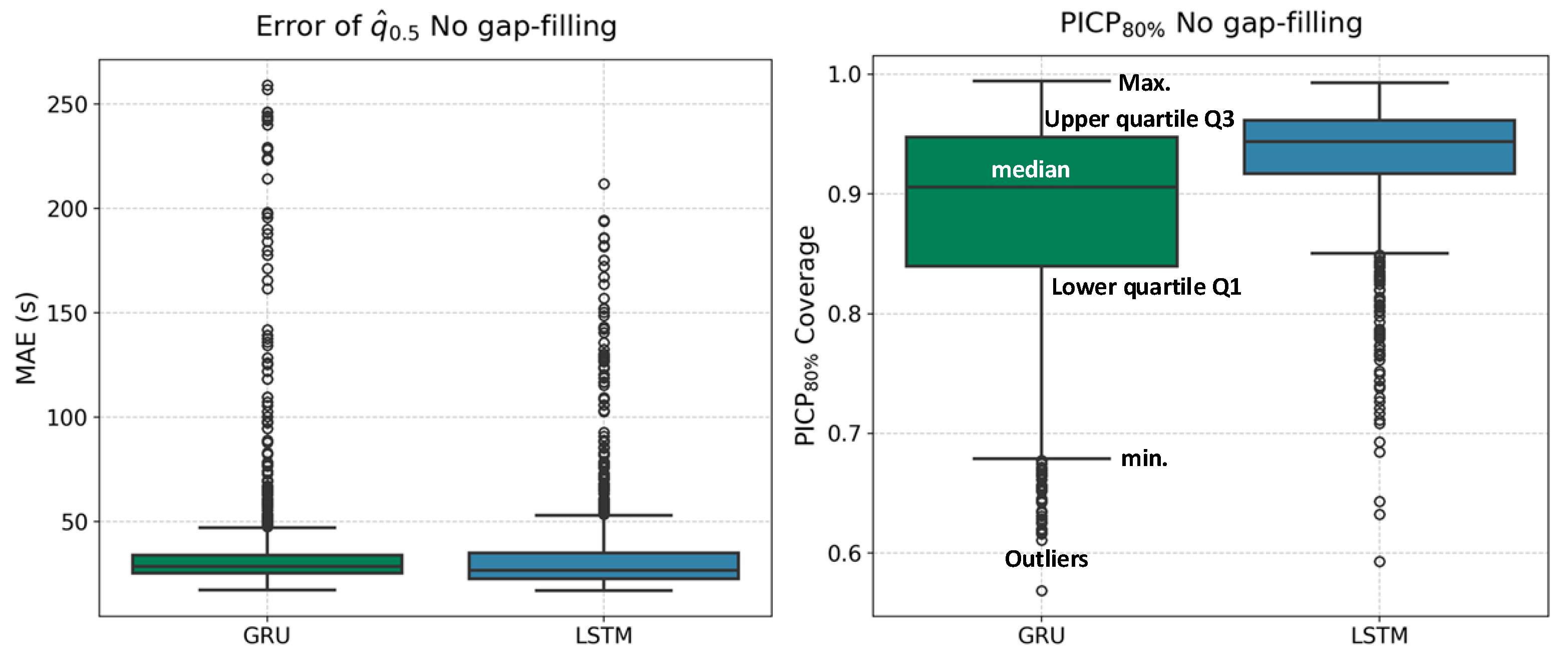
4.2. RTD Forecast Based on the Original Signal of Past Data
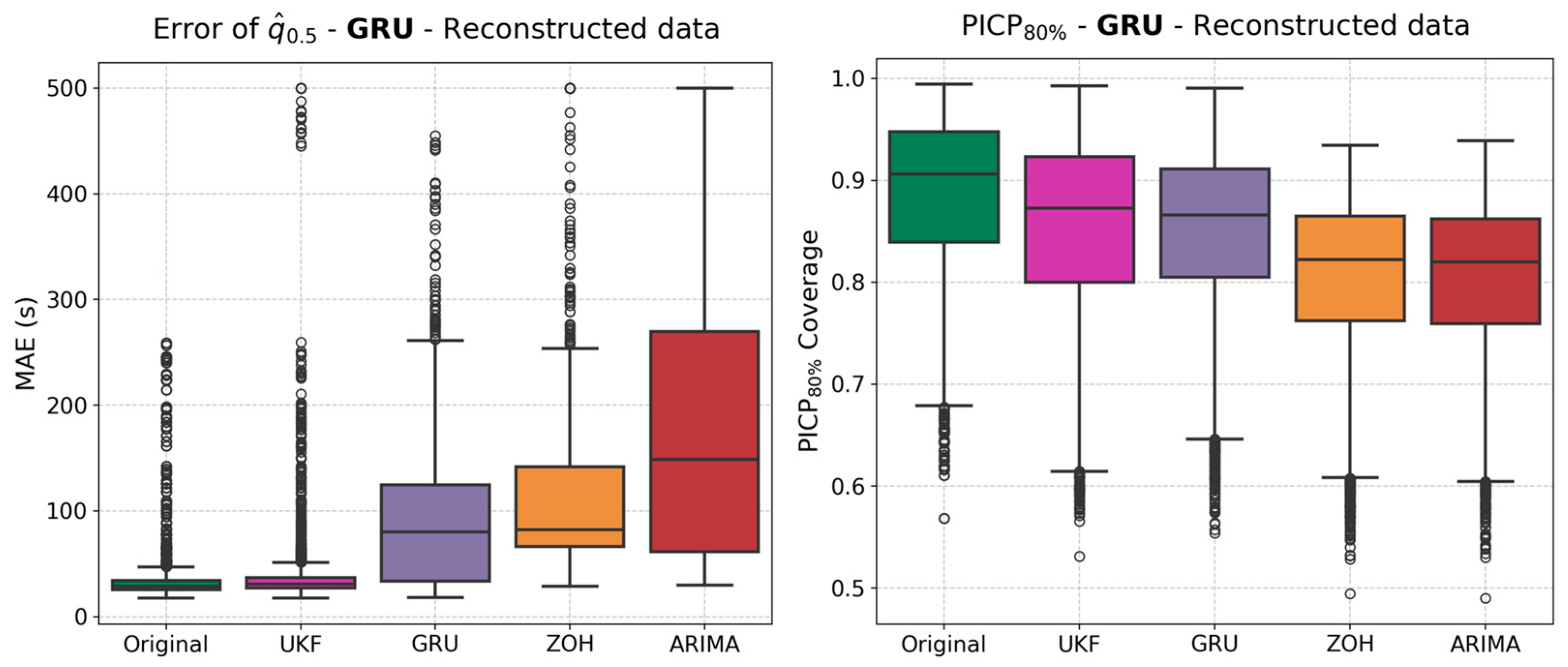
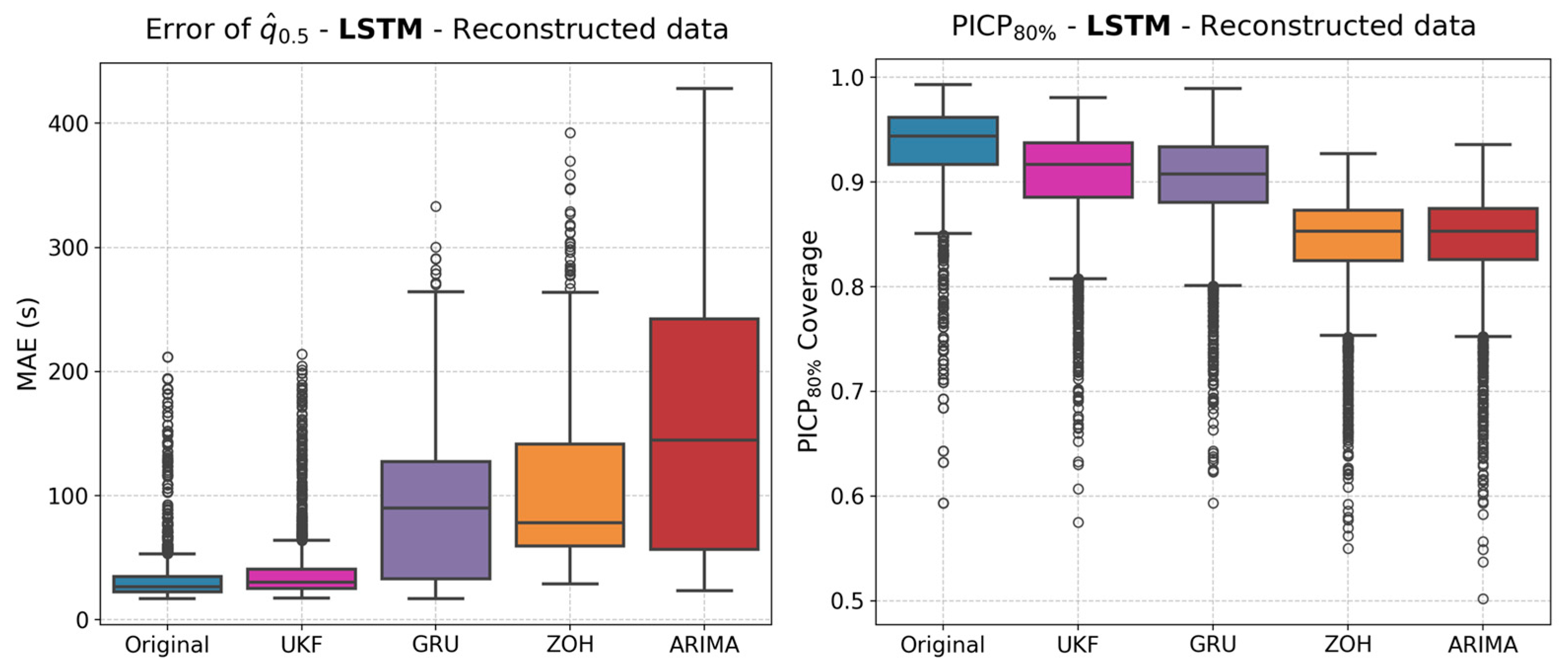
4.3. RTD Forecast Based on the Reconstructed Signal of Past Data
4.4. Assessment of the Computational Cost
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ostadi, A.; Kazerani, M.; Chen, S.K. Optimal sizing of the Energy Storage System (ESS) in a Battery-Electric Vehicle. In Proceedings of the 2013 IEEE Transportation Electrification Conference and Expo (ITEC), Detroit, MI, USA, 16–19 June 2013. [Google Scholar]
- Ranjith Kumar, R.; Bharatiraja, C.; Udhayakumar, K.; Devakirubakaran, S.; Sekar, K.S.; Mihet-Popa, L. Advances in Batteries, Battery Modeling, Battery Management System, Battery Thermal Management, SOC, SOH, and Charge/Discharge Characteristics in EV Applications. IEEE Access 2023, 11, 105761–105809. [Google Scholar] [CrossRef]
- Xiong, R.; Yu, Q.; Shen, W.; Lin, C.; Sun, F. A Sensor Fault Diagnosis Method for a Lithium-Ion Battery Pack in Electric Vehicles. IEEE Trans. Power Electron. 2019, 34, 9709–9718. [Google Scholar] [CrossRef]
- Spoorthi, B.; Pradeepa, P. Review on Battery Management System in EV. In Proceedings of the 2022 International Conference on Intelligent Controller and Computing for Smart Power (ICICCSP), Hyderabad, India, 21–23 July 2022. [Google Scholar]
- Prada, E.; Di Domenico, D.; Creff, Y.; Sauvant-Moynot, V. Towards Advanced BMS Algorithms Development for (P)HEV and EV by Use of a Physics-Based Model of Li-ion Battery Systems. In Proceedings of the 2013 World Electric Vehicle Symposium and Exhibition (EVS27), Barcelona, Spain, 17–20 November 2013. [Google Scholar]
- Li, B.; Fu, Y.; Shang, S.; Li, Z.; Zhao, J.; Wang, B. Research on Functional Safety of Battery Management System (BMS) for Electric Vehicles. In Proceedings of the 2021 International Conference on Intelligent Computing, Automation and Applications (ICAA), Nanjing, China, 25–27 June 2021; pp. 267–270. [Google Scholar]
- Popp, A.; Fechtner, H.; Schmuelling, B.; Kremzow-Tennie, S.; Scholz, T.; Pautzke, F. Battery Management Systems Topologies: Applications: Implications of Different Voltage Levels. In Proceedings of the 2021 IEEE 4th International Conference on Power and Energy Applications (ICPEA), Busan, Republic of Korea, 9–11 October 2021; pp. 43–50. [Google Scholar]
- Khan, F.I.; Hossain, M.M.; Lu, G. Sensing-based monitoring systems for electric vehicle battery—A review. Meas. Energy 2025, 6, 100050. [Google Scholar]
- Kosuru Rahul, V.S.; Kavasseri Venkitaraman, A. A Smart Battery Management System for Electric Vehicles Using Deep Learning-Based Sensor Fault Detection. World Electr. Veh. J. 2023, 14, 101. [Google Scholar] [CrossRef]
- Li, J.; Che, Y.; Zhang, K.; Liu, H.; Zhuang, Y.; Liu, C.; Hu, X. Efficient battery fault monitoring in electric vehicles: Advancing from detection to quantification. Energy 2024, 313, 134150. [Google Scholar] [CrossRef]
- Jeevarajan, J.A.A.; Joshi, T.; Parhizi, M.; Rauhala, T.; Juarez-Robles, D. Battery Hazards for Large Energy Storage Systems. ACS Energy Lett. 2022, 7, 2725–2733. [Google Scholar] [CrossRef]
- Haider, S.N.N.; Zhao, Q.; Li, X. Data driven battery anomaly detection based on shape based clustering for the data centers class. J. Energy Storage 2020, 29, 101479. [Google Scholar] [CrossRef]
- Bhaskar, K.; Kumar, A.; Bunce, J.; Pressman, J.; Burkell, N.; Rahn, C. Data-Driven Thermal Anomaly Detection in Large Battery Packs. Batteries 2023, 9, 70. [Google Scholar] [CrossRef]
- Liu, J.; He, L.; Zhang, Q.; Xie, Y.; Li, G. Real-world cross-battery state of charge prediction in electric vehicles with machine learning: Data quality analysis, data repair and training data reconstruction. Energy 2025, 335, 138322. [Google Scholar]
- Sherstinsky, A. Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar]
- Saha, P.; Dash, S.; Mukhopadhyay, S. Physics-incorporated convolutional recurrent neural networks for source identification and forecasting of dynamical systems. Neural Netw. 2021, 144, 359–371. [Google Scholar]
- Karafyllis, I.; Krstic, M. Nonlinear stabilization under sampled and delayed measurements, and with inputs subject to delay and zero-order hold. IEEE Trans. Automat. Contr. 2012, 57, 1141–1154. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, M. Lithium-ion batteries remaining useful life prediction based on a mixture of empirical mode decomposition and ARIMA model. Microelectron. Reliab. 2016, 65, 265–273. [Google Scholar] [CrossRef]
- Riba, J.R.; Gómez-Pau, Á.; Martínez, J.; Moreno-Eguilaz, M. On-Line Remaining Useful Life Estimation of Power Connectors Focused on Predictive Maintenance. Sensors 2021, 21, 3739. [Google Scholar] [CrossRef] [PubMed]
- pmdarima: ARIMA Estimators for Python—Pmdarima 2.0.4 Documentation. Available online: https://alkaline-ml.com/pmdarima/ (accessed on 29 September 2025).
- He, Z.; Dong, C.; Pan, C.; Long, C.; Wang, S. State of charge estimation of power Li-ion batteries using a hybrid estimation algorithm based on UKF. Electrochim. Acta 2016, 211, 101–109. [Google Scholar]
- Xiong, K.; Zhang, H.Y.; Chan, C.W. Performance evaluation of UKF-based nonlinear filtering. Automatica 2006, 42, 261–270. [Google Scholar] [CrossRef]
- de la Vega, J.; Riba, J.R.; Ortega-Redondo, J.A. Real-Time Lithium Battery Aging Prediction Based on Capacity Estimation and Deep Learning Methods. Batteries 2023, 10, 10. [Google Scholar] [CrossRef]
- Hussein, A.A.H.; Batarseh, I. An overview of Generic Battery Models. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011. [Google Scholar]
- Liu, S.; Deng, J.; Yuan, J.; Li, W.; Li, X.; Xu, J.; Zhang, S.; Wu, J.; Wang, Y.G. Probabilistic quantile multiple fourier feature network for lake temperature forecasting: Incorporating pinball loss for uncertainty estimation. Earth Sci. Inform. 2024, 17, 5135–5148. [Google Scholar] [CrossRef]
- Bauer, I.; Haupt, H.; Linner, S. Pinball boosting of regression quantiles. Comput. Stat. Data Anal. 2024, 200, 108027. [Google Scholar] [CrossRef]
- de la Vega Hernández, J.; Ortega Redondo, J.A.; Riba Ruiz, J.-R. Lithium-Ion Battery Pack Cycling Dataset with CC-CV Charging and WLTP/Constant Discharge Profiles. 2025. Available online: https://dataverse.csuc.cat/dataset.xhtml?persistentId=doi:10.34810/data2395 (accessed on 30 July 2025).
- de La Vega, J.; Riba, J.-R.; Ortega, J.A. Advanced Battery Test Bench for Realistic Vehicle Driving Conditions Assessment; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2025; pp. 1–6. [Google Scholar]
- Ma, C.; Wang, A.; Chen, G.; Xu, C. Hand joints-based gesture recognition for noisy dataset using nested interval unscented Kalman filter with LSTM network. Vis. Comput. 2018, 34, 1053–1063. [Google Scholar] [CrossRef]
- Liu, X.; Gao, Z.; Tian, J.; Wei, Z.; Fang, C.; Wang, P. State of Health Estimation for Lithium-Ion Batteries Using Voltage Curves Reconstruction by Conditional Generative Adversarial Network. IEEE Trans. Transp. Electrif. 2024, 10, 10557–10567. [Google Scholar] [CrossRef]
- Mu, J.; Han, Y.; Zhang, C.; Yao, J.; Zhao, J. An Unscented Kalman Filter-Based Method for Reconstructing Vehicle Trajectories at Signalized Intersections. J. Adv. Transp. 2021, 2021, 6181242. [Google Scholar] [CrossRef]
- Li, J.; Zhang, C.; Cao, Q.; Qi, C.; Huang, J.; Xie, C. An Experimental Study on Deep Learning Based on Different Hardware Configurations. In Proceedings of the 2017 International Conference on Networking, Architecture, and Storage (NAS), Shenzhen, China, 7–9 August 2017. [Google Scholar]

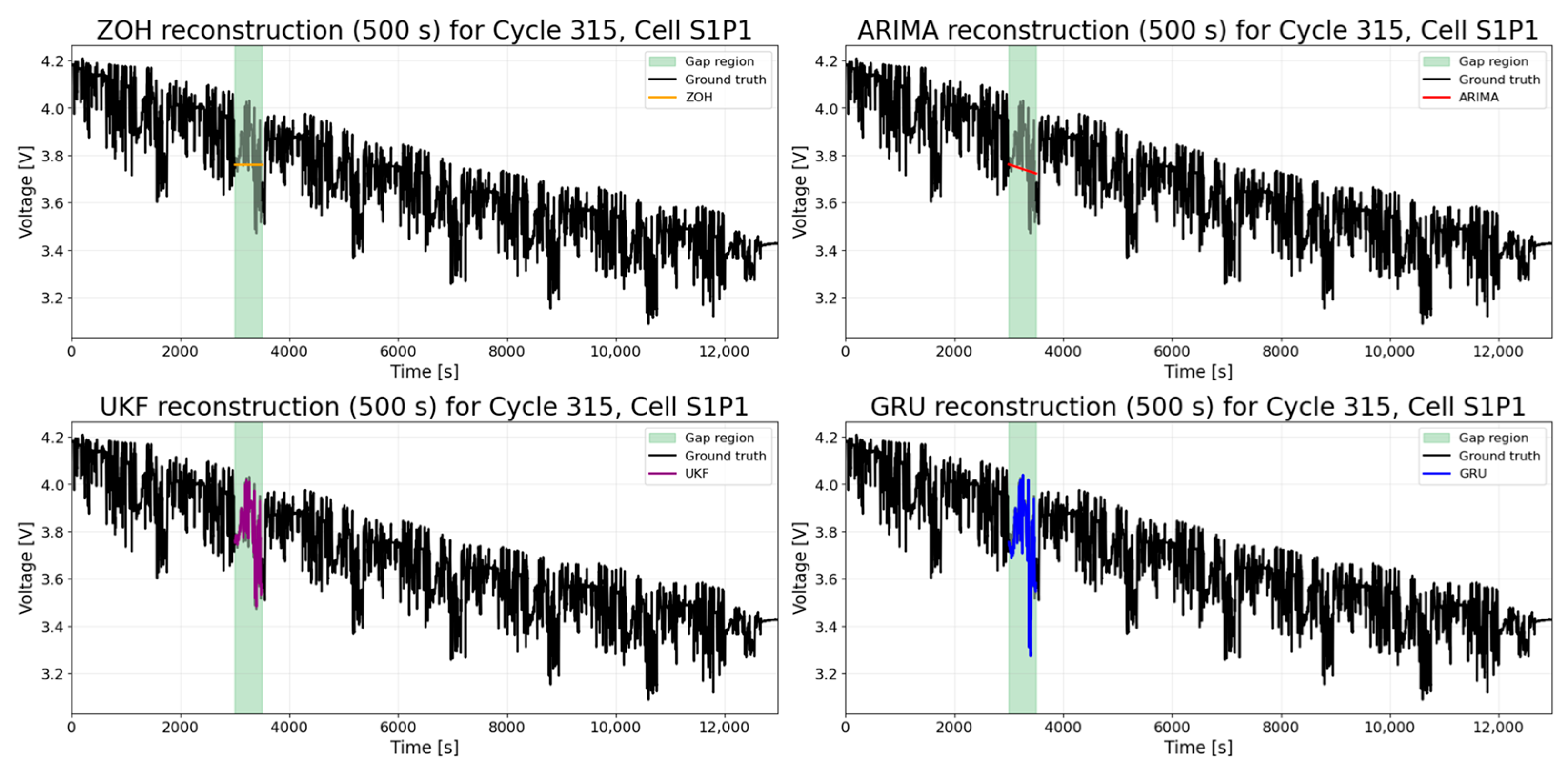
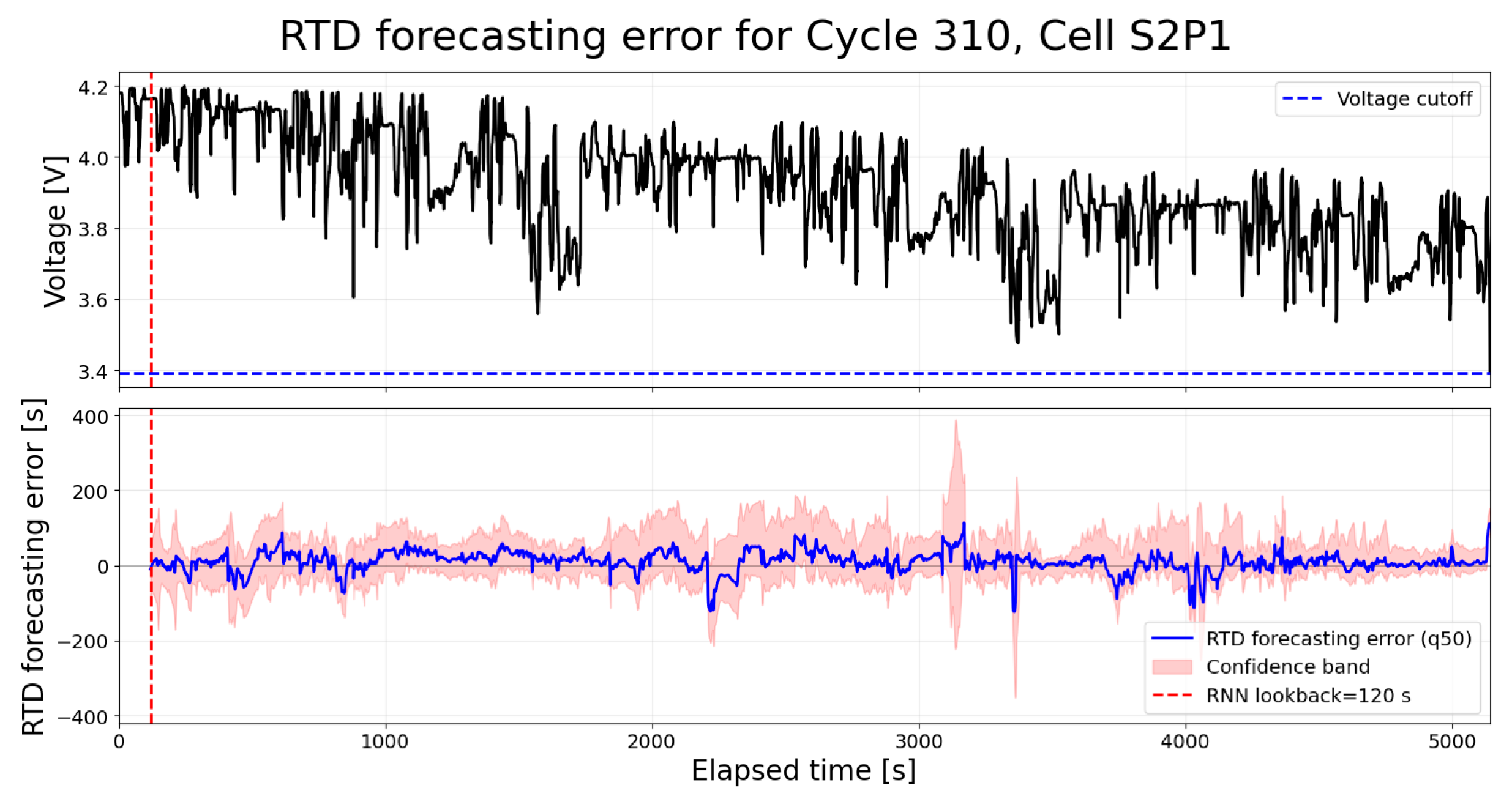
| Model | Average R2 | Average/Maximum RMSE | Average/Maximum MAE |
|---|---|---|---|
| ARIMA | −1.7104 | 0.0797/0.5238 | 0.0813/0.4847 |
| GRU (RNN) | 0.7936 | 0.0385/0.1145 | 0.0287/0.0735 |
| UKF | 0.9134 | 0.0266/0.1077 | 0.0127/0.0803 |
| ZOH | −1.1822 | 0.0764/0.4757 | 0.0783/0.4408 |
| Model | Mean Values (s) | Median Values (s) | PICP80% Mean Values (%) | PICPwidth Mean Values (s) |
|---|---|---|---|---|
| GRU | 36.2 s | 28.6 s | 88.2% | 159.06 s |
| LSTM | 34.5 s | 26.7 s | 93.1% | 126.56 s |
| Model | Reconstruction Method | Mean Values (s) | Median Values (s) | PICP80% Mean Values (%) | PICPwidth Mean Values (s) |
|---|---|---|---|---|---|
| GRU | UKF | 39.2 s | 30.9 s | 85.2% | 157.1 s |
| GRU | 88.5 s | 79.9 s | 84.8% | 159.6 s | |
| ZOH | 113.7 s | 82.5 s | 80.3% | 161.6 s | |
| ARIMA | 167.1 s | 148.8 s | 80.1% | 164.1 s | |
| LSTM | UKF | 37.8 s | 30.4 s | 90.4% | 125.9 s |
| GRU | 88.3 s | 90.1 s | 90.1% | 129.0 s | |
| ZOH | 105.6 s | 78.0 s | 84.3% | 122.0 s | |
| ARIMA | 153.5 s | 144.7 s | 84.4% | 121.4 s |
| Reconstruction Method | Data Preprocessing Stage Computational Cost in Seconds | Reconstruction Stage Computational Cost in Seconds |
|---|---|---|
| UKF | 0.003 | 0.402 |
| GRU | 0.065 | 10.146 |
| ZOH | 0.000 | 0.001 |
| ARIMA | 22.360 | 0.012 |
| Forecasting Method | Model Loading Time in Seconds | Forecasting Time (RTD Evaluation) in Seconds |
|---|---|---|
| LSTM | 0.077 | 5.524 |
| GRU | 0.080 | 7.891 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de la Vega, J.; Riba, J.-R.; Ortega-Redondo, J.A. On the Use of Machine Learning Methods for EV Battery Pack Data Forecast Applied to Reconstructed Dynamic Profiles. Appl. Sci. 2025, 15, 11291. https://doi.org/10.3390/app152011291
de la Vega J, Riba J-R, Ortega-Redondo JA. On the Use of Machine Learning Methods for EV Battery Pack Data Forecast Applied to Reconstructed Dynamic Profiles. Applied Sciences. 2025; 15(20):11291. https://doi.org/10.3390/app152011291
Chicago/Turabian Stylede la Vega, Joaquín, Jordi-Roger Riba, and Juan Antonio Ortega-Redondo. 2025. "On the Use of Machine Learning Methods for EV Battery Pack Data Forecast Applied to Reconstructed Dynamic Profiles" Applied Sciences 15, no. 20: 11291. https://doi.org/10.3390/app152011291
APA Stylede la Vega, J., Riba, J.-R., & Ortega-Redondo, J. A. (2025). On the Use of Machine Learning Methods for EV Battery Pack Data Forecast Applied to Reconstructed Dynamic Profiles. Applied Sciences, 15(20), 11291. https://doi.org/10.3390/app152011291








