Numerical Investigation of the Bond–Slip Mechanism Between Deformed CFRP Bars and Ultra-High Performance Concrete
Abstract
1. Introduction
2. Materials and Methods
2.1. Bond–Slip Tests
- Center-pull test: As a recommended method specified in the Standard for Test Methods of Concrete Structures (GB50152–92) [17], the center-pull test is also the most widely used experimental approach. Specimens are typically prismatic or cylindrical in shape, with the steel bar positioned at the geometric center of the specimen. The casting process is performed horizontally, and the bond length is controlled by encasing the steel bar in PVC sleeves. This method is characterized by operational simplicity and facilitated data analysis, thereby being widely employed in contemporary bond–slip research.
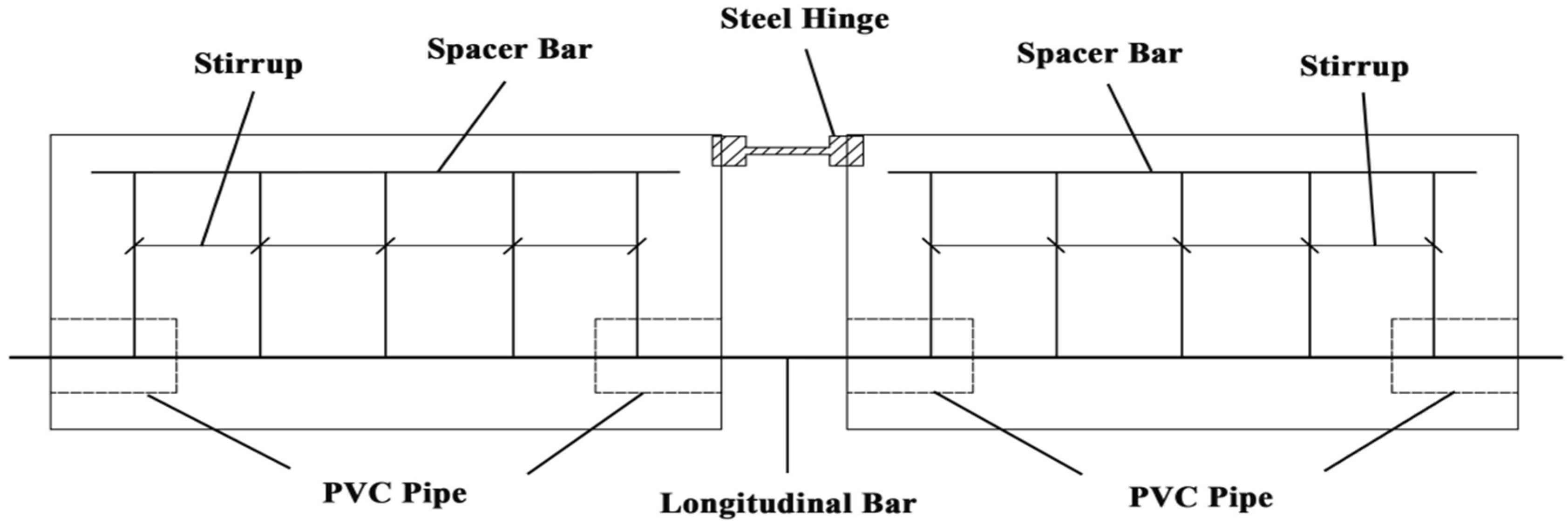
- Beam Tests: Beam tests (as shown in Figure 1) are categorized into full-beam tests and half-beam tests. Specifically, the full-beam test investigates the bond behavior between reinforcing bars and concrete through the bending of supported beams. Compared with the central pull-out test, this method can more accurately reflect the actual stress states of reinforcing bars and concrete in practical engineering scenarios. Nevertheless, its application remains limited, primarily due to the complexity of specimen fabrication and the high associated costs. The half-beam test offers relatively simplified specimen fabrication. It not only allows for the adjustment of the bending moment-to-shear force ratio but also enables the application of “dowel force”, making it a commonly used method for determining the development length of reinforcing bars. However, the presence of size effects may lead to discrepancies in strength and crack width between the scaled-down model and the prototype, as the material properties of the scaled model may not be consistent with those of the original.
- 3.
- Axial Tension Test: The axial tension test is primarily employed to characterize the bond behavior across cracks and the evolution of cracking. In this test, the reinforcing bar is subjected to pure tensile loading; however, this loading condition does not replicate the stress states experienced by reinforcing bars under complex loading scenarios in practical engineering. Furthermore, the test typically quantifies global slip, making it challenging to capture local slip at the interface between the reinforcing bar and the concrete.
2.2. Finite Element Model for Bond–Slip
3. Finite Element Model
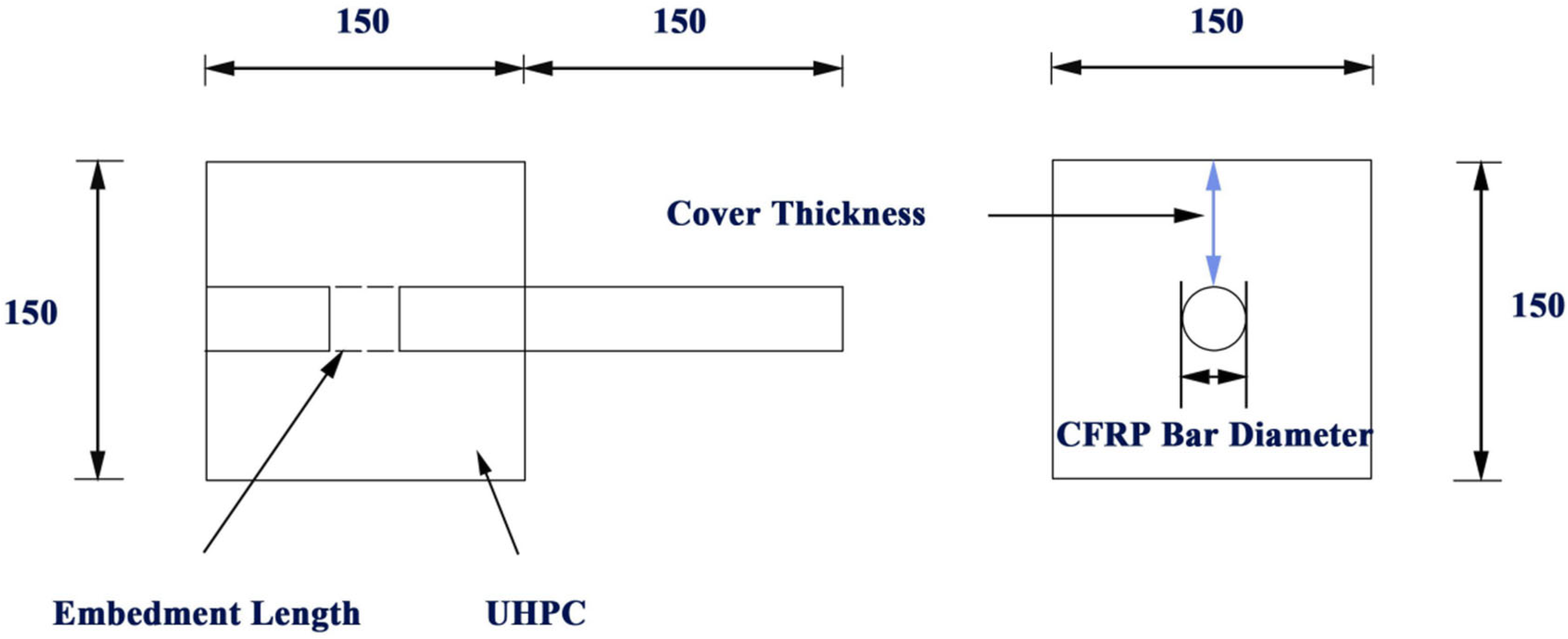
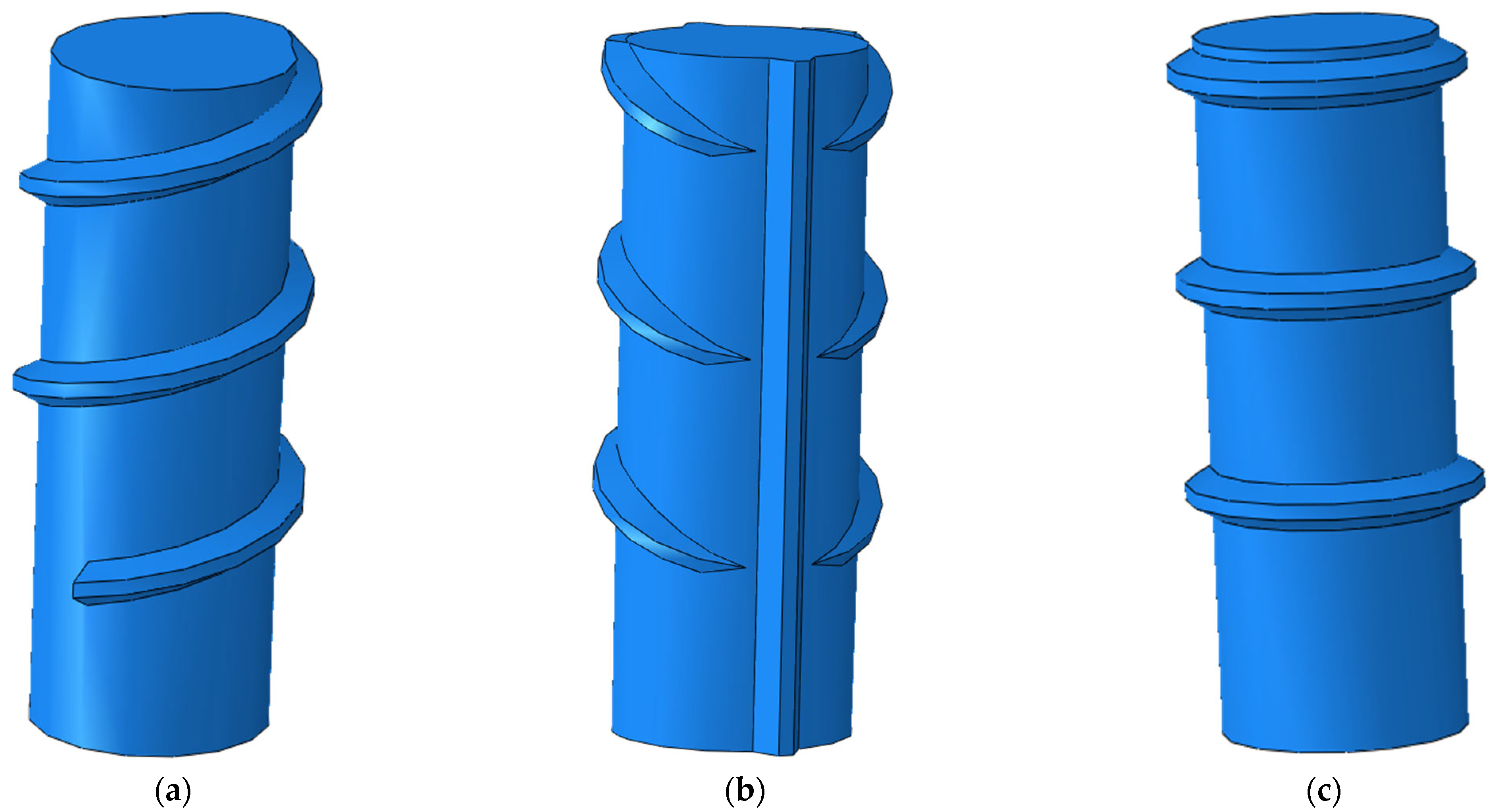
3.1. Geometric Model
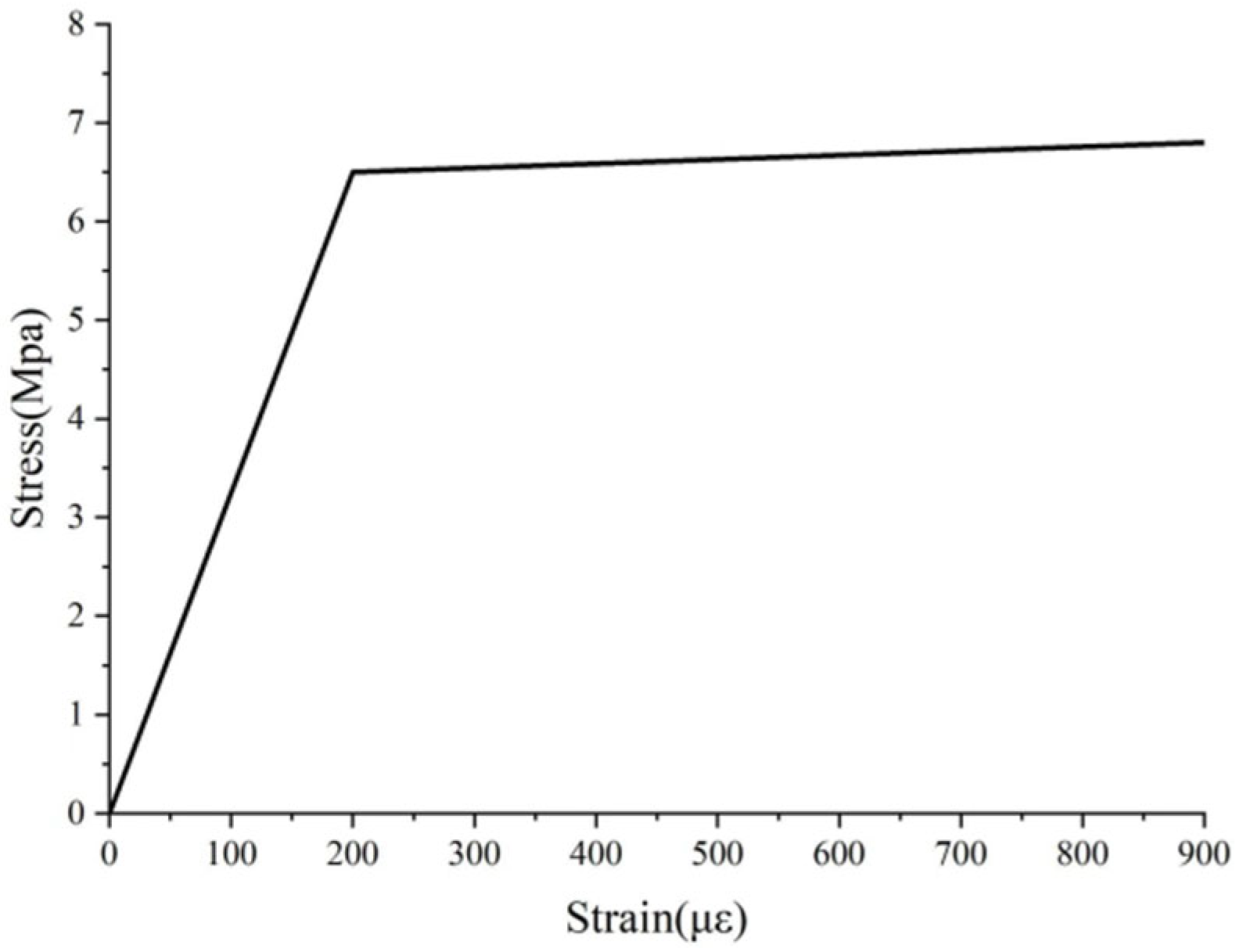
3.2. Constitutive Relations
- Dilatation angle: Set to 30°.
- Eccentricity of the flow potential: This parameter characterizes the deviation between the plastic flow potential function and the hyperbolic asymptote; its value was specified as 0.1 in this study.
- Biaxial compressive strength ratio (fb0/fc0): This ratio reflects the strength degradation behavior of the material under multiaxial stress states. Based on the strength criterion established by Chiew et al. [19] through classical biaxial compression tests, it was set to 1.16.
- Parameter k: This parameter represents the ratio of the second invariant of stress on the tensile and compressive meridians at the initial yielding stage, and characterizes the relative position of the tension–compression meridians on the π-plane. By integrating the elastoplastic theoretical framework proposed by Sarikaya [20] and the numerical validation results from Kmiecik [21], a value of 2/3 was adopted as its characteristic parameter.
- Viscosity parameter (μ): This parameter governs the convergence stability of the viscoplastic regularization process. To satisfy the computational accuracy requirements for quasi-static analysis, it was set to 0.0001.
3.3. Contact Conditions
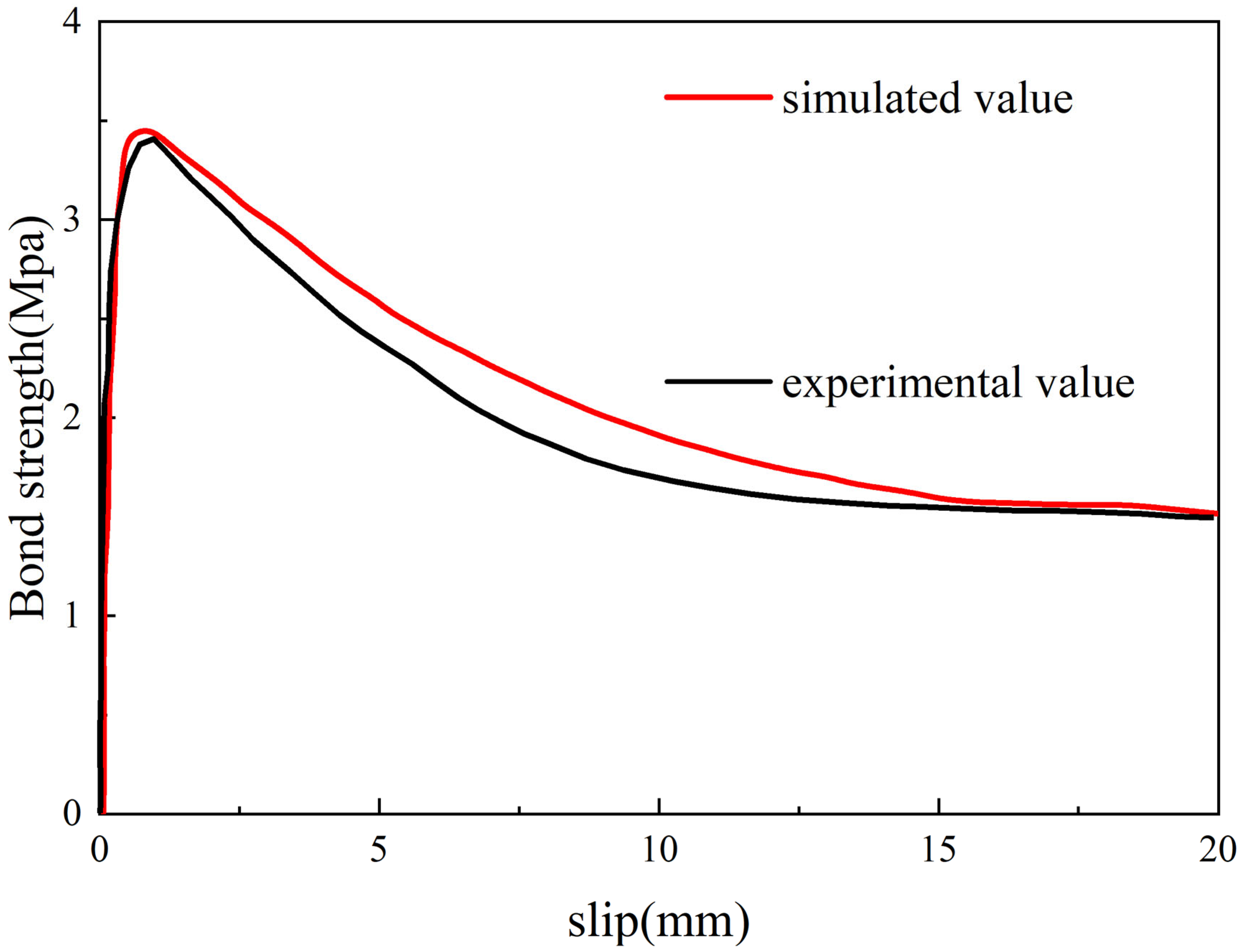
3.4. Validation of the Finite Element Model for Bond–Slip Between CFRP Bars and UHPC
- τ—bond strength (MPa);
- P—axial tensile force (kN);
- d—diameter of CFRP bars (mm);
- ld—anchorage length of CFRP bars (mm).
4. Bond–Slip Performance of CFRP Bars and UHPC
4.1. Influencing Factors
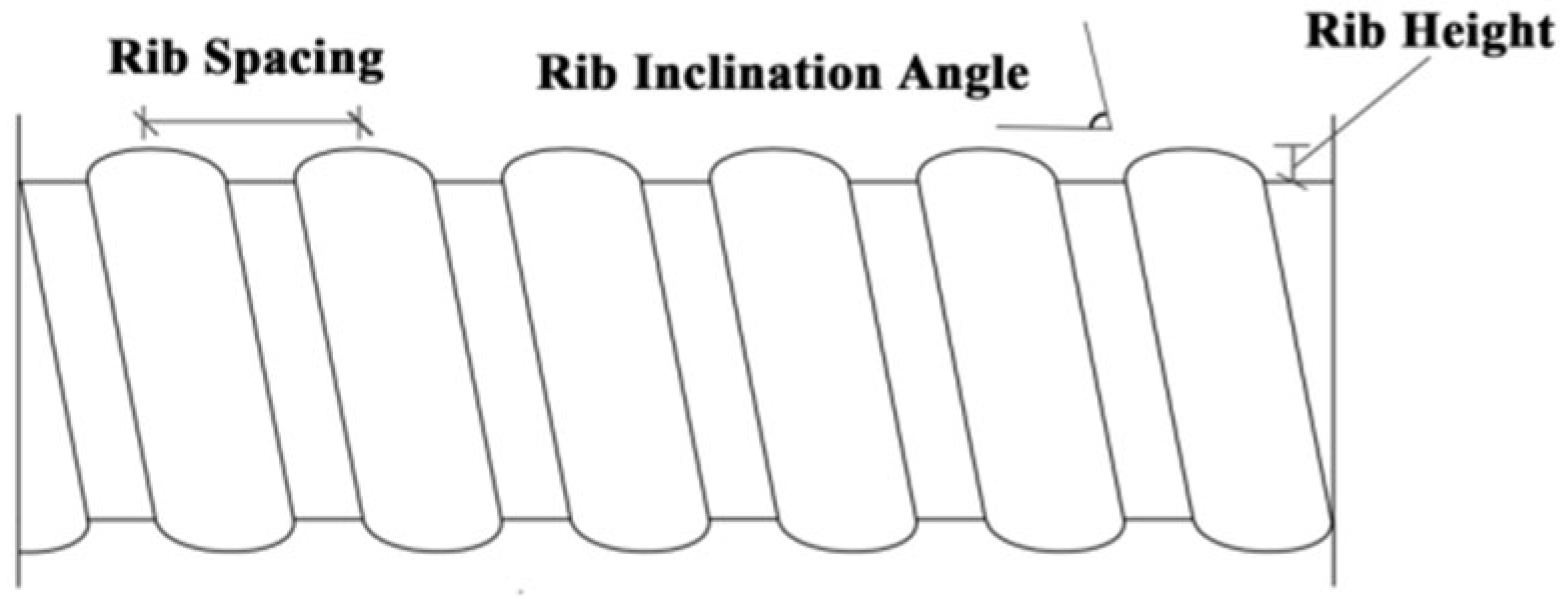
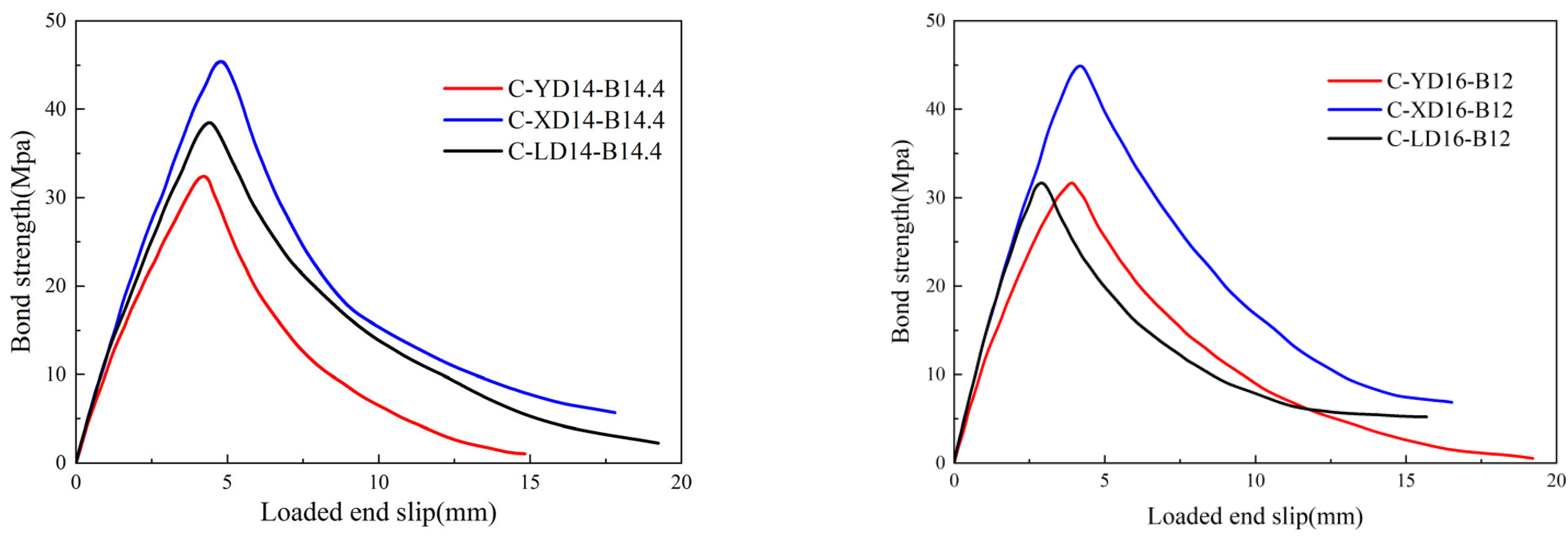
4.2. Effect of Bar Surface Morphology
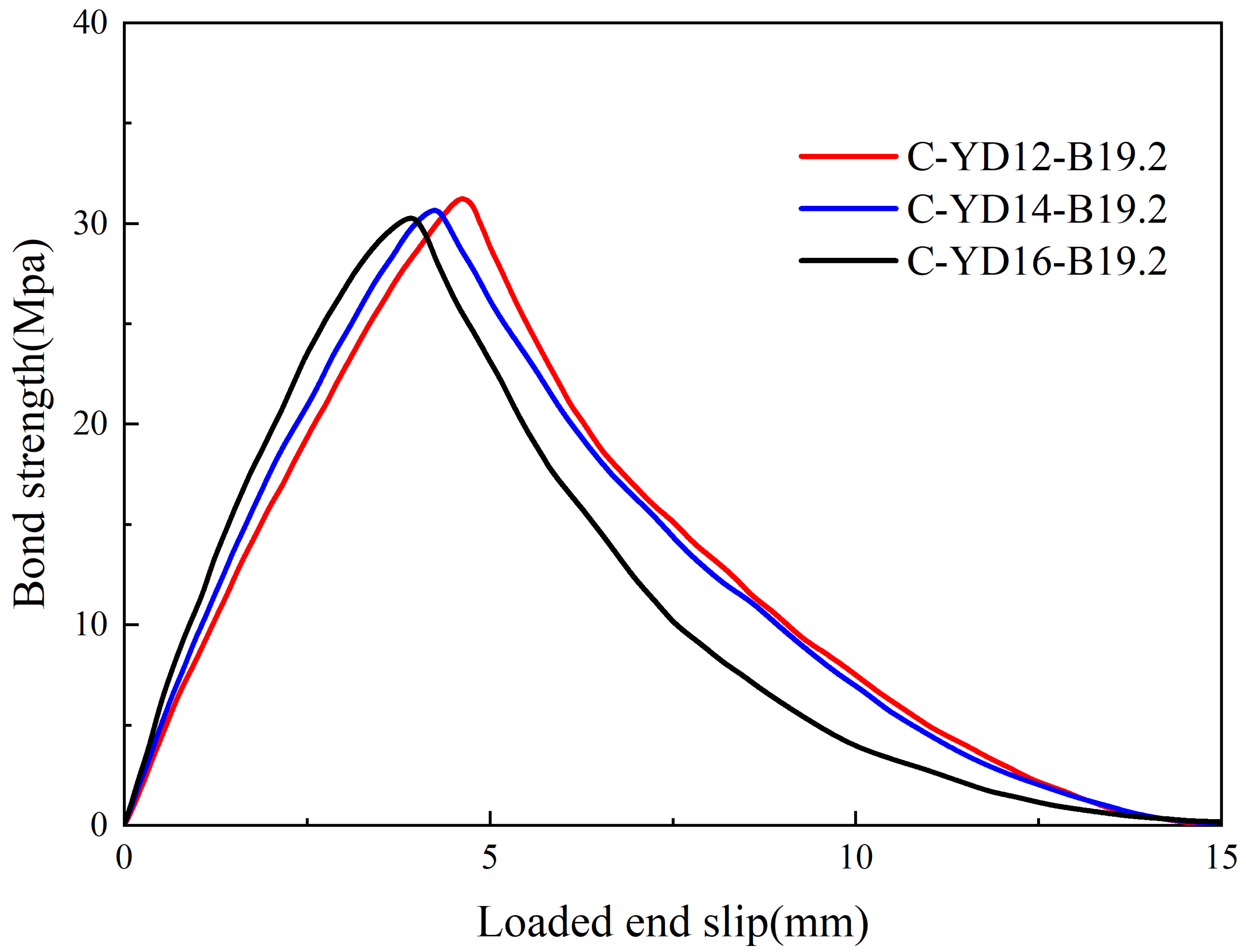
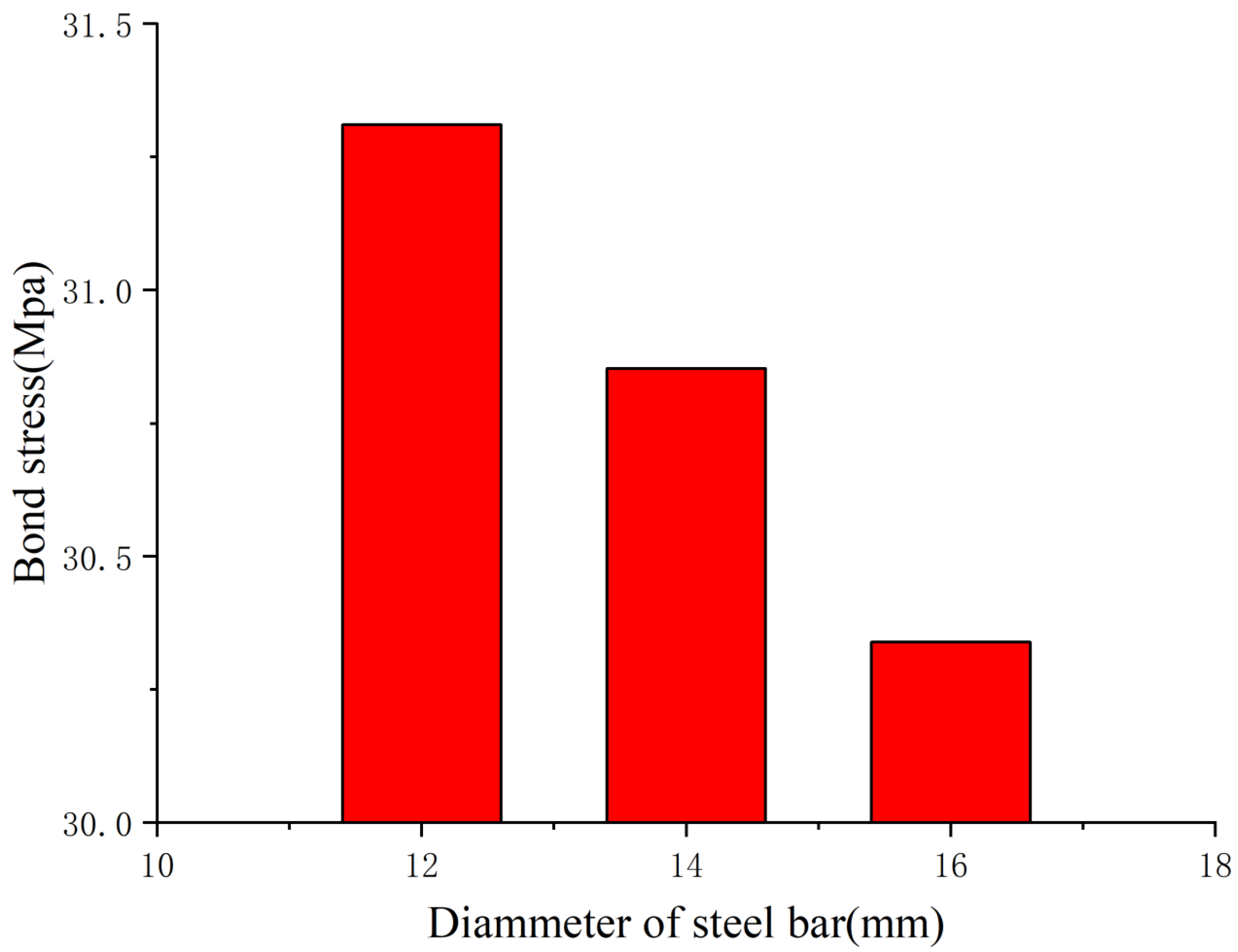
4.3. Effect of CFRP Bar Diameter
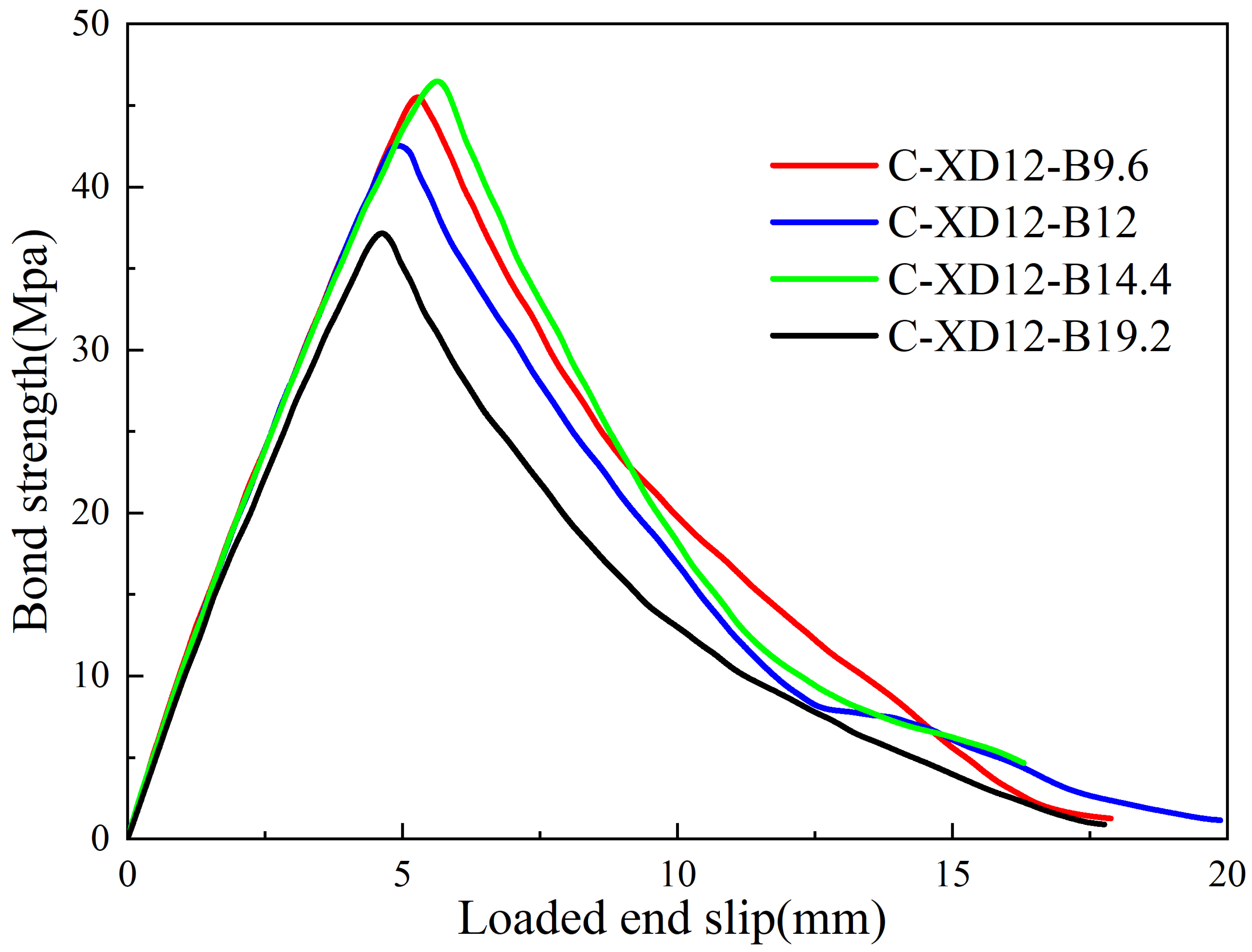
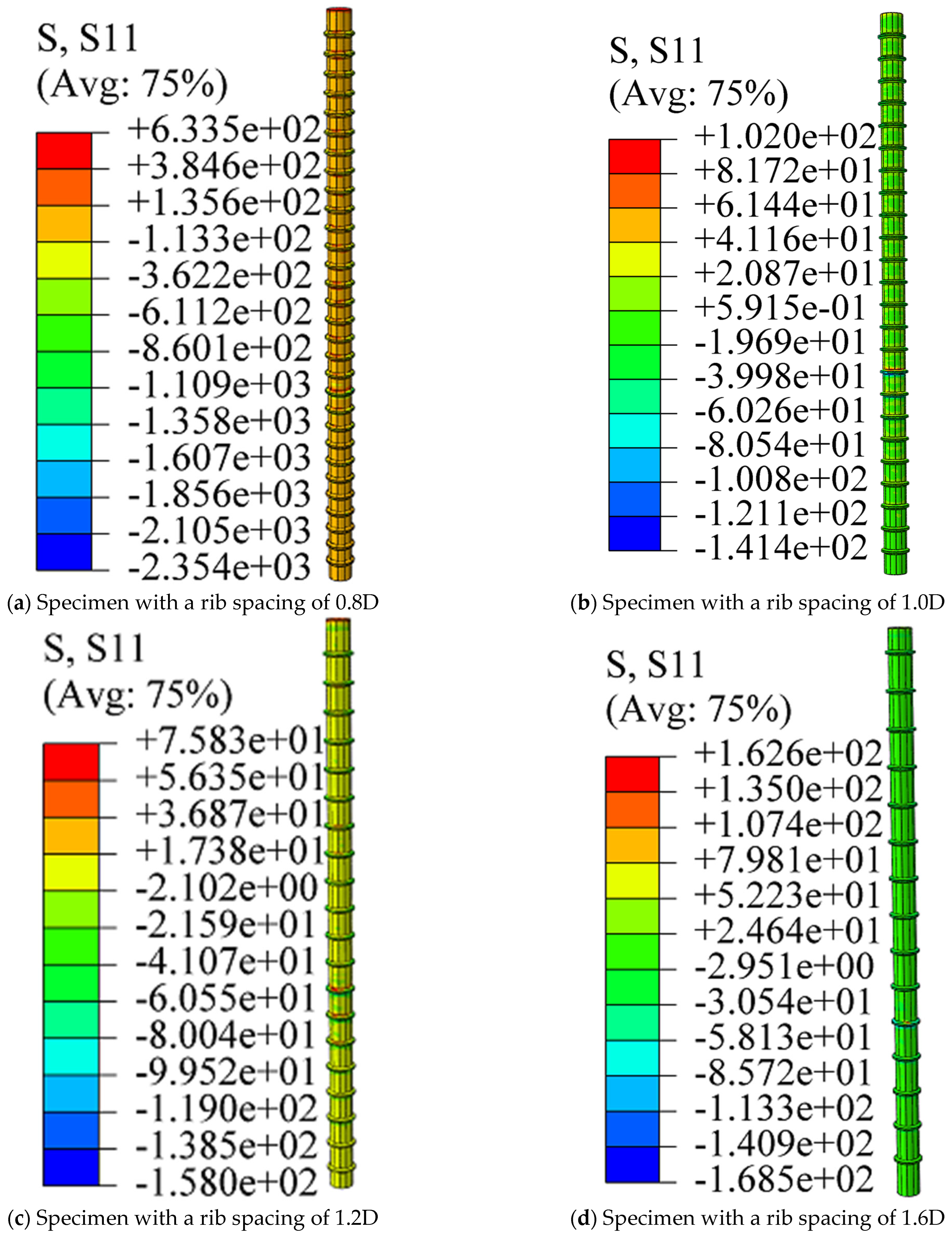
4.4. Effect of Rib Spacing
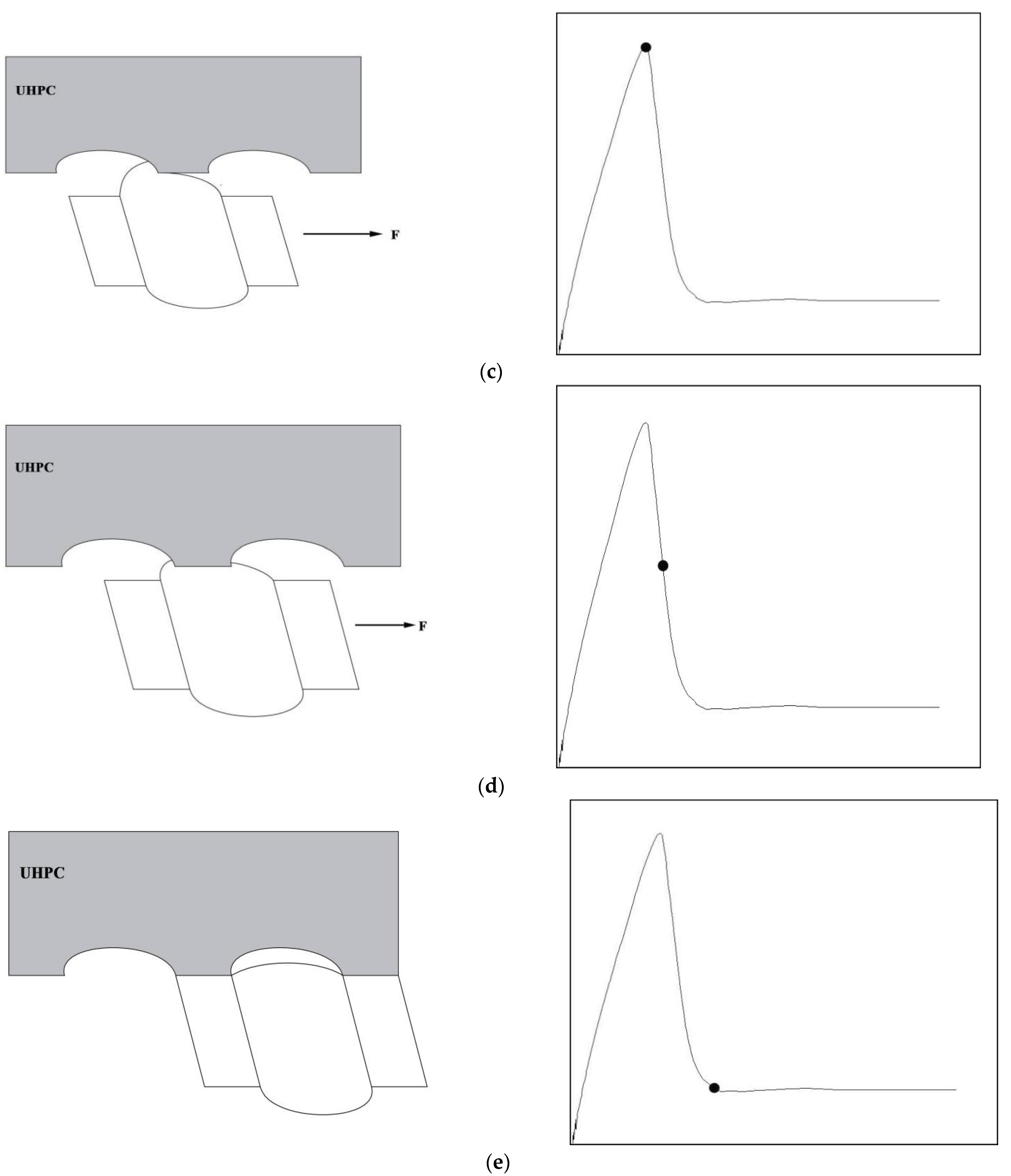
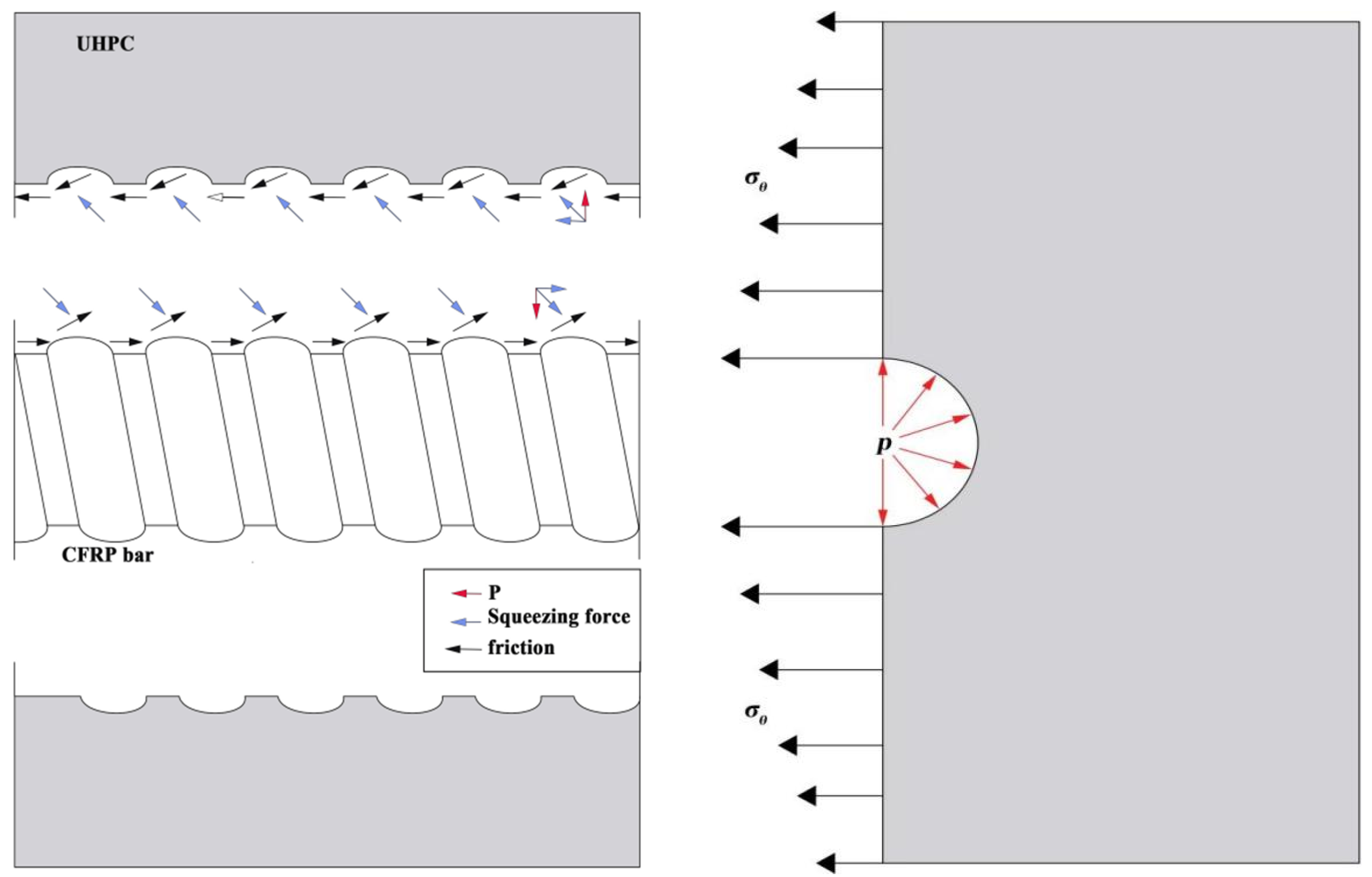
5. Bonding Mechanism and Force Transfer Mechanism Between UHPC and CFRP Bars
5.1. Analysis of Bonding Mechanism
5.2. Bond Force Transfer Mechanism
6. Conclusions and Discussion
- For CFRP bars with diameters of 16 mm and 14 mm, and corresponding rib spacings of 1.0D and 1.2D, the bond strength of equal-height-ribbed bars exceeded that of crescent-ribbed bars by 40.6–45.9% and that of spiral-ribbed bars by 17.3–41.8%.
- The surface morphology of CFRP bars exerted a significant influence on the interfacial bond strength between CFRP bars and UHPC. Benefiting from the uniform stress distribution induced by their geometric symmetry, equal-height-ribbed CFRP bars exhibited the optimal bond behavior and thus possessed greater reliability in engineering applications.
- Within a specific range of bar diameters, the interfacial bond strength between CFRP bars and UHPC decreased with an increase in CFRP bar diameter; however, the overall influence of diameter was relatively minor. For CFRP bars with diameters ranging from 12 mm to 16 mm, the interfacial bond strength decreased by 12–15% for every 4 mm increase in diameter.
- For 12 mm-diameter equal-height-ribbed CFRP bars with a rib spacing of 14.4 mm, the interface between the CFRP bars and UHPC achieved the peak interfacial bond strength. Furthermore, the slip magnitude corresponding to the peak interfacial bond strength exhibited a positive correlation with the peak interfacial bond strength itself.
- During the bond–slip process between CFRP bars and UHPC, the stress of the CFRP bars along the anchorage length exhibited a distinct nonlinear distribution characteristic. As the slip magnitude increased, the bar stress gradually increased, with stress values being higher at locations closer to the loading end.
- This study investigated three factors influencing the bond–slip behavior between UHPC and CFRP bars. Several other factors, however, were not considered, such as concrete cover thickness, the volume fraction of steel fibers in UHPC, and anchorage length. Future research could delve deeper into the effects of these unaddressed factors on the bond–slip performance between UHPC and CFRP bars.
- This work primarily focused on the bond performance between UHPC and CFRP bars under monotonic static loading. In practical engineering applications, however, these materials are subjected to various factors such as freeze–thaw cycles, chloride ion erosion, and dynamic loads. Subsequent studies are encouraged to investigate the bond degradation mechanisms under individual or even coupled multi-factor conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fan, D.Q.; Yu, R.; Fu, S.Y.; Yue, L.; Wu, C.F.; Shui, Z.H.; Liu, K.N.; Song, Q.L.; Sun, M.J.; Jiang, C.Y. Precise design and characteristics prediction of Ultra-High Performance Concrete (UHPC) based on artificial intelligence techniques. Concr. Compos. 2021, 122, 104171. [Google Scholar] [CrossRef]
- Abellan-Garcia, J.; Abbas, Y.M.; Khan, M.I.; Martínez-Lirón, V. Ductility characteristics of strain-hardening ultra-high-performance concrete: ANN and empirical approaches. Comput. Concr. 2025, 35, 603–617. [Google Scholar] [CrossRef]
- Lyu, X.; Ayough, P.; Nawaz, W.; Elchalakani, M. Development and characterization of printable rubberised ultra-high-performance concrete. J. Build. Eng. 2025, 111, 113192. [Google Scholar] [CrossRef]
- Qiu, Z.T.; Deng, M.K.; Wei, D.; Tian, X.L.; Li, R.Z. Axial compressive behaviour of H-shaped steel members strengthened with ultra-high performance concrete with coarse aggregates (CA-UHPC): Experimental study and theoretical analysis. Constr. Build. Mater. 2025, 493, 143257. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Zhang, Q.; Xu, L.Y.; Hou, W.; Miao, Y.S.; Liu, Y.; Huang, B.T. Transfer learning for intelligent design of lightweight Strain-Hardening Ultra-High-Performance Concrete (SH-UHPC). Autom. Constr. 2025, 175, 106241. [Google Scholar] [CrossRef]
- Yoo, S.J.; Hong, S.H.; Yoon, Y.S. Bonding behavior and prediction of helically ribbed CFRP bar embedded in ultra high-performance concrete (UHPC). CASE Stud. Constr. Mater. 2023, 19, e02253. [Google Scholar] [CrossRef]
- Wu, M.Z.; Xu, J.C.; Li, W.Y.; Li, W.W.; Wang, C.G.; Wang, P. Axial compression behaviour of concrete columns with CFRP-mesh fabric (CFRP-MF) stirrup and steel-FRP composite bar (SFCB): Experimental investigation and mechanism research. Constr. Build. Mater. 2024, 436, 136853. [Google Scholar] [CrossRef]
- Zhou, Y.W.; Zheng, X.B.; Xing, F.; Sui, L.L.; Zheng, Y.W.; Huang, X.X. Investigation on the electrochemical and mechanical performance of CFRP and steel-fiber composite bar used for impressed current cathodic protection anode. Constr. Build. Mater. 2020, 255, 119377. [Google Scholar] [CrossRef]
- Li, S.; Sun, J.R.; Guo, Y.Q. Method of measuring the mechanical impact loads of lightning on CFRP composites. Acta Mater. Compos. Sin. 2025, 42, 5994–6005. [Google Scholar] [CrossRef]
- Yuan, J.Q.; Graybeal, B. Bond of Reinforcement in Ultra-High-Performance Concrete. ACI Struct. J. 2015, 112, 851–860. [Google Scholar] [CrossRef]
- Xie, J.; Wang, X.H.; Liu, Y. Numerical analysis on bonding performance between CFRP bar and concrete at polar low temperatures. J. Harbin Inst. Technol. 2024, 56, 1–13. [Google Scholar] [CrossRef]
- Ouyang, L.Z.; Song, X.B.; Yin, C.R.; Xiao, X.W.; Qi, L.G. Bond behavior between CFRP bars with different surface characteristics and concrete. China Civ. Eng. J. 2025, 1–11. [Google Scholar] [CrossRef]
- Chen, J.X.; Fang, Z.; Fang, W.C.; Wang, Q.W.; Tan, X.Y. Experimental Study on the Bond Behavior of the CFRP Bar-UHPC Interface in Composite Anchorage. J. Compos. Constr. 2025, 29, 04025015. [Google Scholar] [CrossRef]
- Fahmy, M.F.M.; Ahmed, S.A.S.; Wu, Z.S. Bar surface treatment effect on the bond-slip behavior and mechanism of basalt FRP bars embedded in concrete. Constr. Build. Mater. 2021, 289, 122844. [Google Scholar] [CrossRef]
- Jafari, A.; Shahmansouri, A.A.; Abdulridha, H.A.; Issa, B.I.; Bengar, H.A. Effect of CFRP confinement on bond-slip behavior of steel rebar in low-strength concrete: Experimentation, prediction and parametric study. Constr. Build. Mater. 2025, 477, 141333. [Google Scholar] [CrossRef]
- Shahmansouri, A.A.; Jafari, A.; Bengar, H.A.; Zhou, Y. Steel rebar bond-slip behavior in CFRP-strengthened low-strength concrete: ML-driven solution and reliability analysis. Constr. Build. Mater. 2025, 490, 142302. [Google Scholar] [CrossRef]
- GB50152-2012; Standard for Test Method of Concrete Structures. Ministry of Housing and Urban-Rural Development PRC: Beijing, China, 2012. (In Chinese)
- Gu, J.F.; Ren, Q.W. Study on hydraulic concrete cracking criterion in smeared crack numerical model. Eng. Mech. 2015, 32, 84–91. [Google Scholar]
- Chiew, S.M.; Ibrahim, I.S.; Jamaluddin, N.; Sarbini, N.N.; Ma, C.K.; Ahmad, Y. Behavior of Steel Fiber-Reinforced Concrete under Biaxial Stresses. ACI Struct. J. 2020, 117, 267–278. [Google Scholar] [CrossRef]
- Sarikaya, A.; Erkmen, R.E. A plastic-damage model for concrete under compression. Int. J. Mech. Sci. 2019, 150, 584–593. [Google Scholar] [CrossRef]
- Kmiecik, P.; Kaminski, M. Modelling of reinforced concrete structures and composite structures with concrete strength degradation taken into consideration. Arch. Civ. Mech. Eng. 2011, 11, 623–636. [Google Scholar] [CrossRef]
- Hassan, M.; Benmokrane, B.; ElSafty, A.; Fam, A. Bond durability of basalt-fiber-reinforced-polymer (BFRP) bars embedded in concrete in aggressive environments. Compos. Part B Eng. 2016, 106, 262–272. [Google Scholar] [CrossRef]
- Karataş, M.A.; Gökkaya, H. A review on machinability of carbon fiber reinforced polymer (CFRP) and glass fiber reinforced polymer (GFRP) composite materials. Def. Technol. 2018, 14, 318–326. [Google Scholar] [CrossRef]
- Shan, B. Experimental Studies on Long-Term Behavior of FRP Retrofitted RC Columns with Earthquake Loading Damage. Ph.D. Thesis, Hunan University, Changsha, China, 2002. [Google Scholar]
- Zhang, Z. Bending Behaviors of Composite Bridge Deck System Composed of OSD and Reinforced UHPC Layer. Ph.D.Thesis, Hunan University, Changsha, China, 2016. [Google Scholar]
- Guan, P.; Tu, Y.; Zhang, P.; Tang, G. A review on constitutive relationship of ultra-high-performance concrete under uniaxial compression and tension. Acta Mater. Compos. Sin. 2019, 36, 1295–1305. [Google Scholar]
- Jin, L.; Liu, K.X.; Zhang, R.B.; Yu, W.X.; Du, X.L. Bond behavior between steel bar and concrete considering cryogenic temperatures and confinement. CASE Stud. Constr. Mater. 2023, 18, e01856. [Google Scholar] [CrossRef]
- Jiang, Z.W.; Liu, P.J.; Fang, Z.; Fang, Y.W.; Wang, Z.W. Experimental study on bonding behavior between CFRP smooth bar and UHPC under impact loading. Acta Mater. Compos. Sin. 2024, 41, 858–870. [Google Scholar] [CrossRef]
- Hsu, T.T. Unified Theory of Reinforced Concrete; Routledge: London, UK, 2017. [Google Scholar]
- Pan, R.S.; Zou, J.Y.; Liao, P.; Li, C.X. Experimental study and calculating method for bond strength between helically ribbed GFRP bar and UHPC. Zhongguo Gonglu Xuebao/China J. Highw. Transp. 2023, 36, 144–156. [Google Scholar]



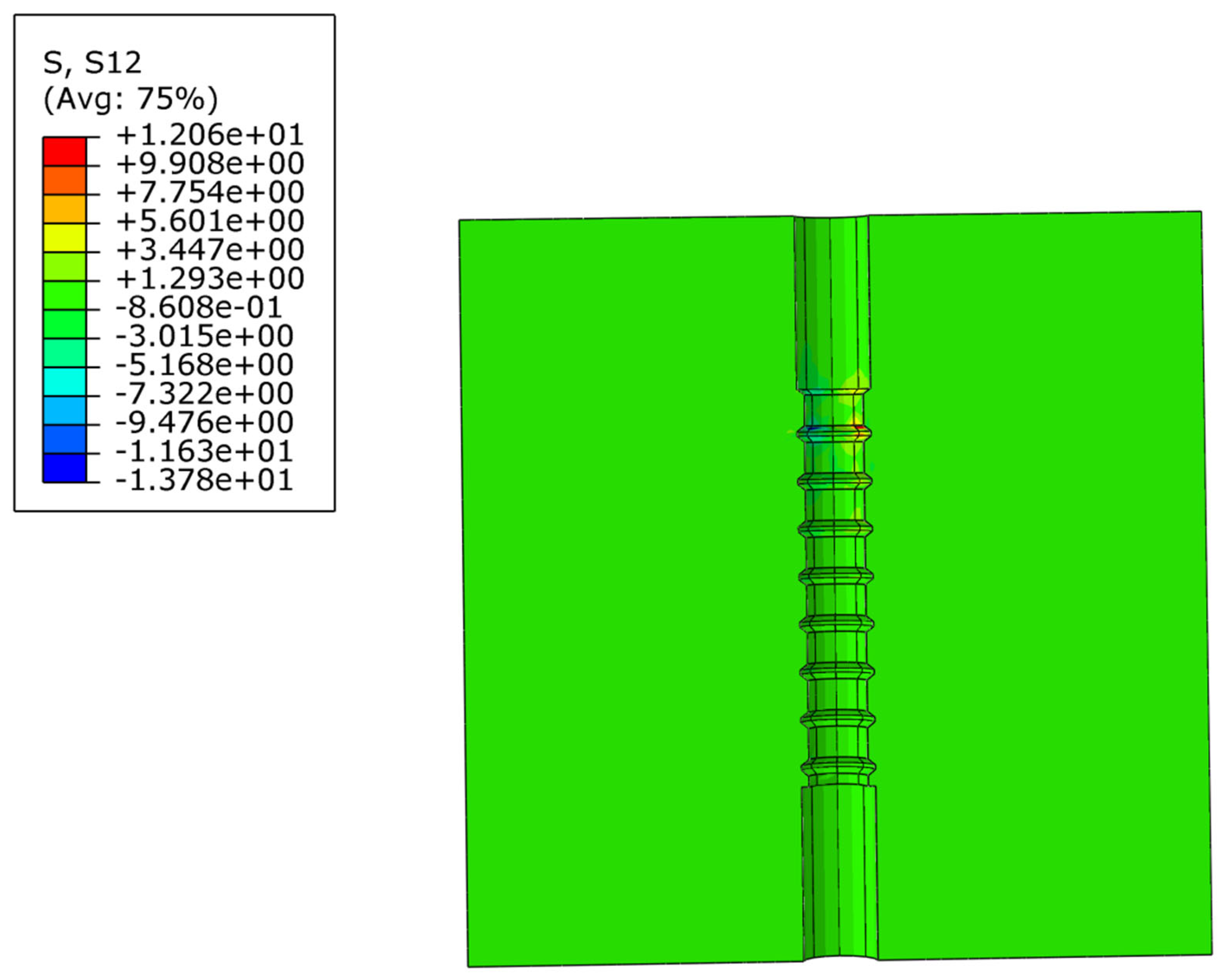
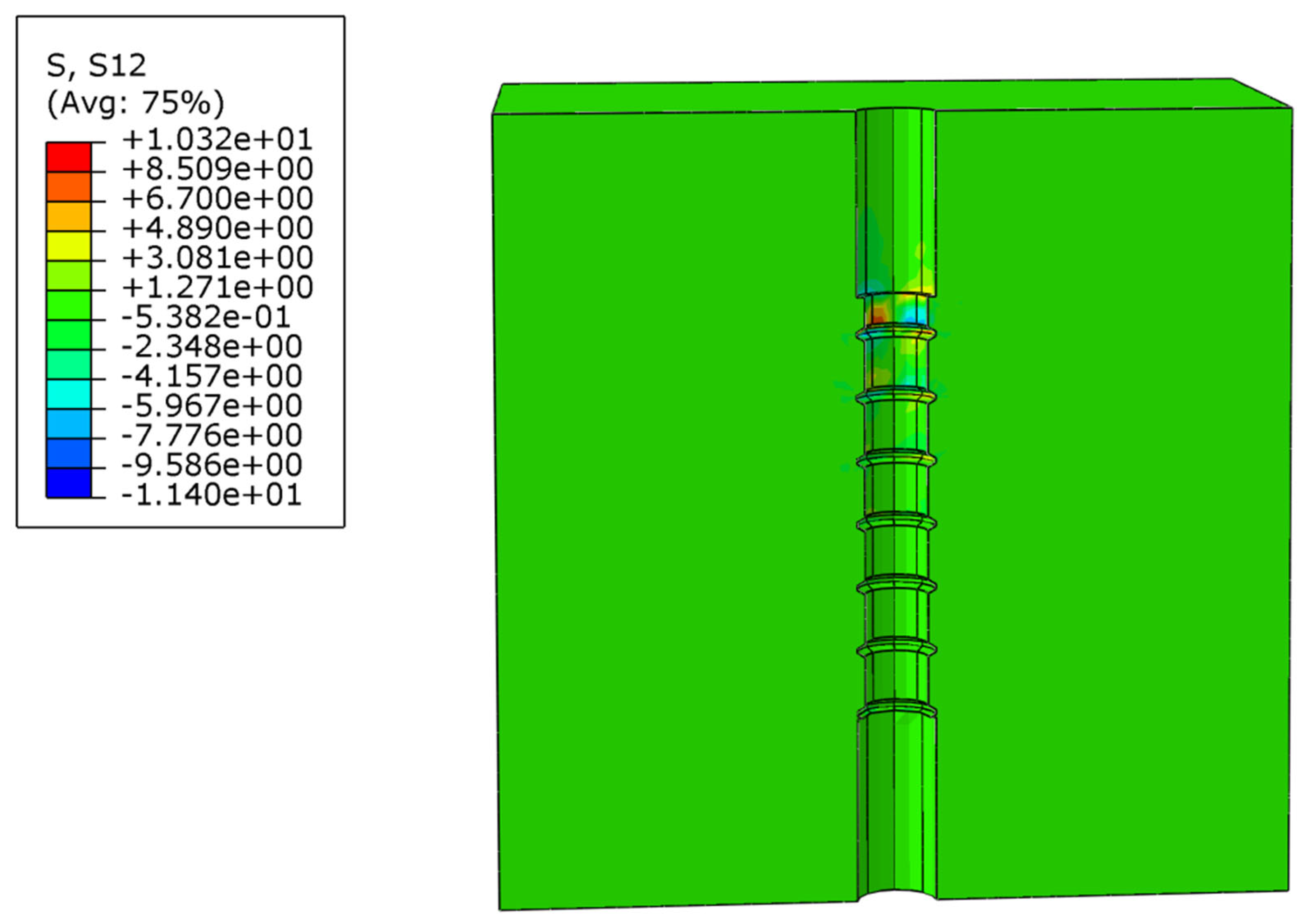

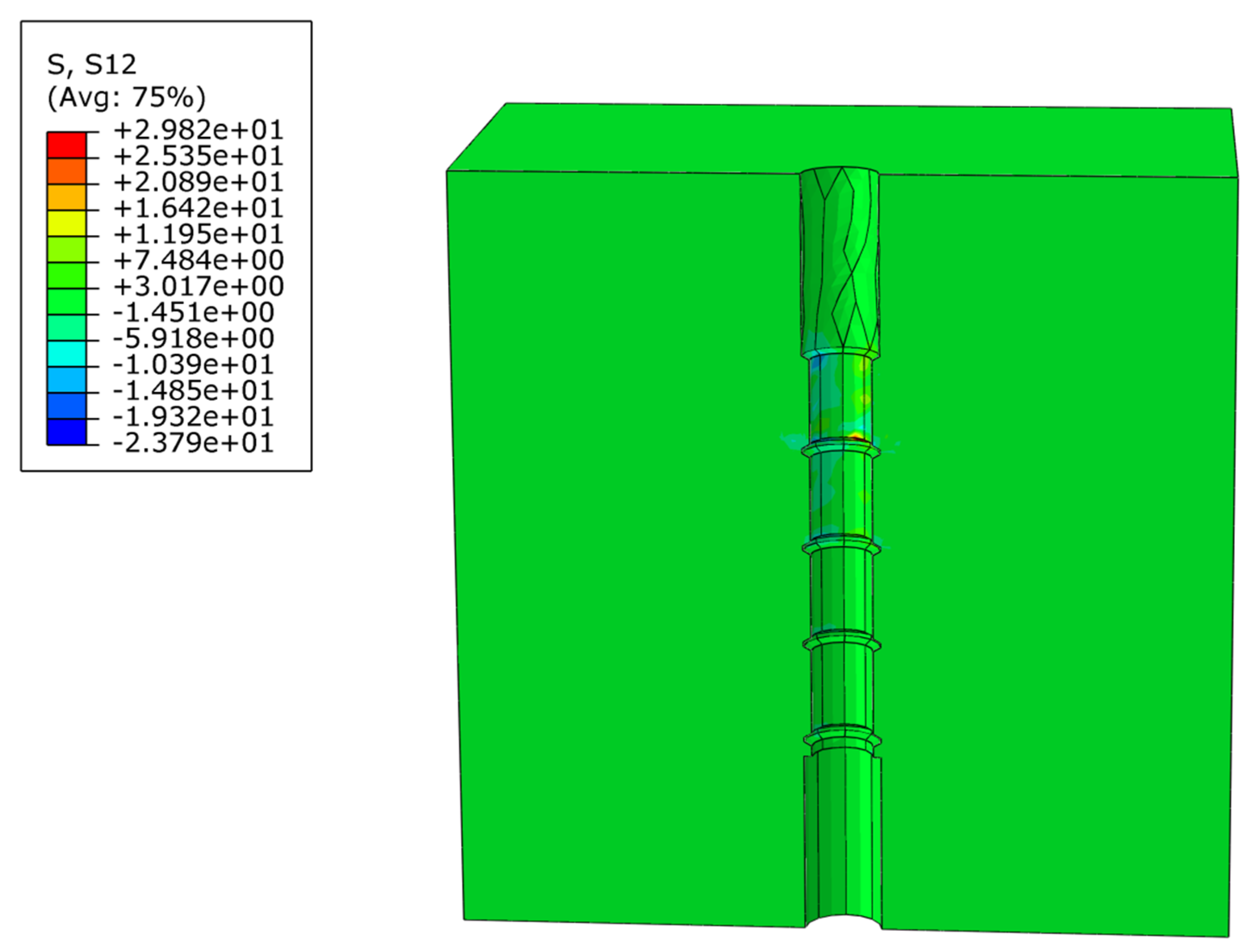

| Category | Experimental Value | Numerical Simulation Value | Error Value |
|---|---|---|---|
| Peak Bond Strength (Mpa) | 3.41 | 3.46 | 0.05 |
| Peak Bond Slip (mm) | 0.97 | 0.85 | 0.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, J.; Liu, N.; Ke, C. Numerical Investigation of the Bond–Slip Mechanism Between Deformed CFRP Bars and Ultra-High Performance Concrete. Appl. Sci. 2025, 15, 11066. https://doi.org/10.3390/app152011066
Jiang J, Liu N, Ke C. Numerical Investigation of the Bond–Slip Mechanism Between Deformed CFRP Bars and Ultra-High Performance Concrete. Applied Sciences. 2025; 15(20):11066. https://doi.org/10.3390/app152011066
Chicago/Turabian StyleJiang, Junling, Nachuan Liu, and Changren Ke. 2025. "Numerical Investigation of the Bond–Slip Mechanism Between Deformed CFRP Bars and Ultra-High Performance Concrete" Applied Sciences 15, no. 20: 11066. https://doi.org/10.3390/app152011066
APA StyleJiang, J., Liu, N., & Ke, C. (2025). Numerical Investigation of the Bond–Slip Mechanism Between Deformed CFRP Bars and Ultra-High Performance Concrete. Applied Sciences, 15(20), 11066. https://doi.org/10.3390/app152011066





