Distributed Photovoltaic Short-Term Power Forecasting Based on Seasonal Causal Correlation Analysis
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Methodology Overview
1.3. Contribution and Framework in This Article
- (1)
- Combining CEEMDAN and gray relational analysis, a feature analysis and power reconstruction algorithm is proposed under complex meteorological conditions, establishing a new and effective set of input features.
- (2)
- A two-stage feature selection method containing causality is proposed, which deeply considers the feature changes in different seasons and dynamically adjusts model inputs.
- (3)
- A shape-based clustering algorithm is used for weather classification, significantly improving the effectiveness of weather segmentation.
- (4)
- A combined model for distributed PV power forecasting under complex meteorological conditions is proposed. This model effectively integrates complex features, extracts key factors, and is capable of adapting to time series forecasting with strong generalization ability.
2. Related Methods
2.1. Data Reconstruction
- (1)
- The original power data are decomposed into IMFs via CEEMDAN, as expressed in Equation (1):where M denotes the number of IMFs, IMF_k(t) represents the set of quasi-orthogonal intrinsic mode functions, and R(t) is the residual.
- (2)
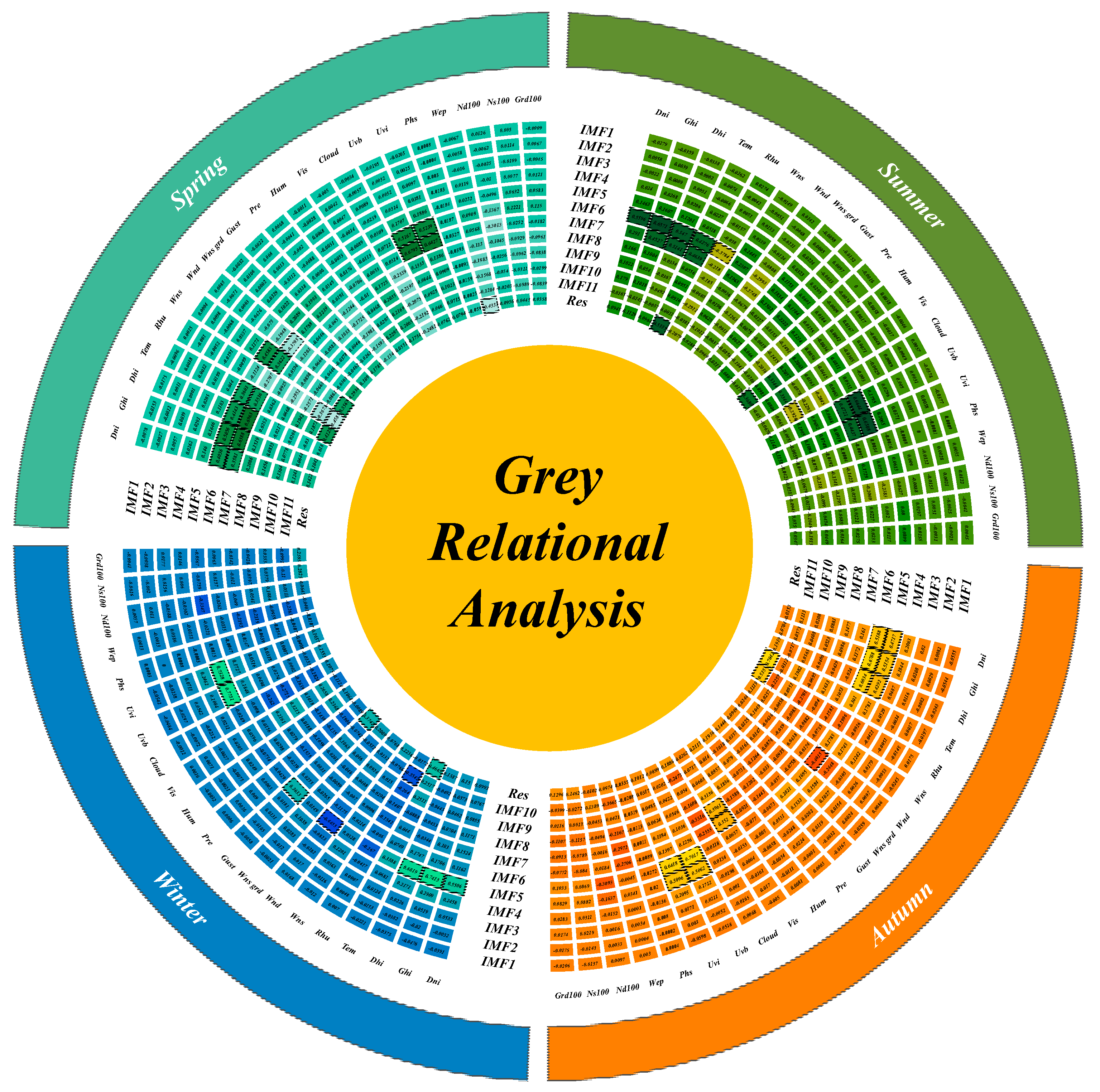
- Based on Step 1, the correlation between the future weather sequences of each season and the modal components is calculated. GRA [26] analysis is performed on the weather sequences of each season’s future period and each IMF_k(t). First, the sequence is dimensionless, and then the correlation coefficients are calculated. The formula is as follows:
- (3)
- Based on Step 2, the reconstructed data is matched with modal components that have similar features. Compared to traditional statistical methods, this approach is simpler and focuses more on the similarity of nonlinear features. The calculation process is as follows:
2.2. Two Stage Feature Selection
- (1)
- Construct the feature set TF for each modal component and weather feature using gray relational analysis:
- (2)
- Construction of the original feature set for the reconstructed features:
- (3)
- Feature selection for the reconstructed components:
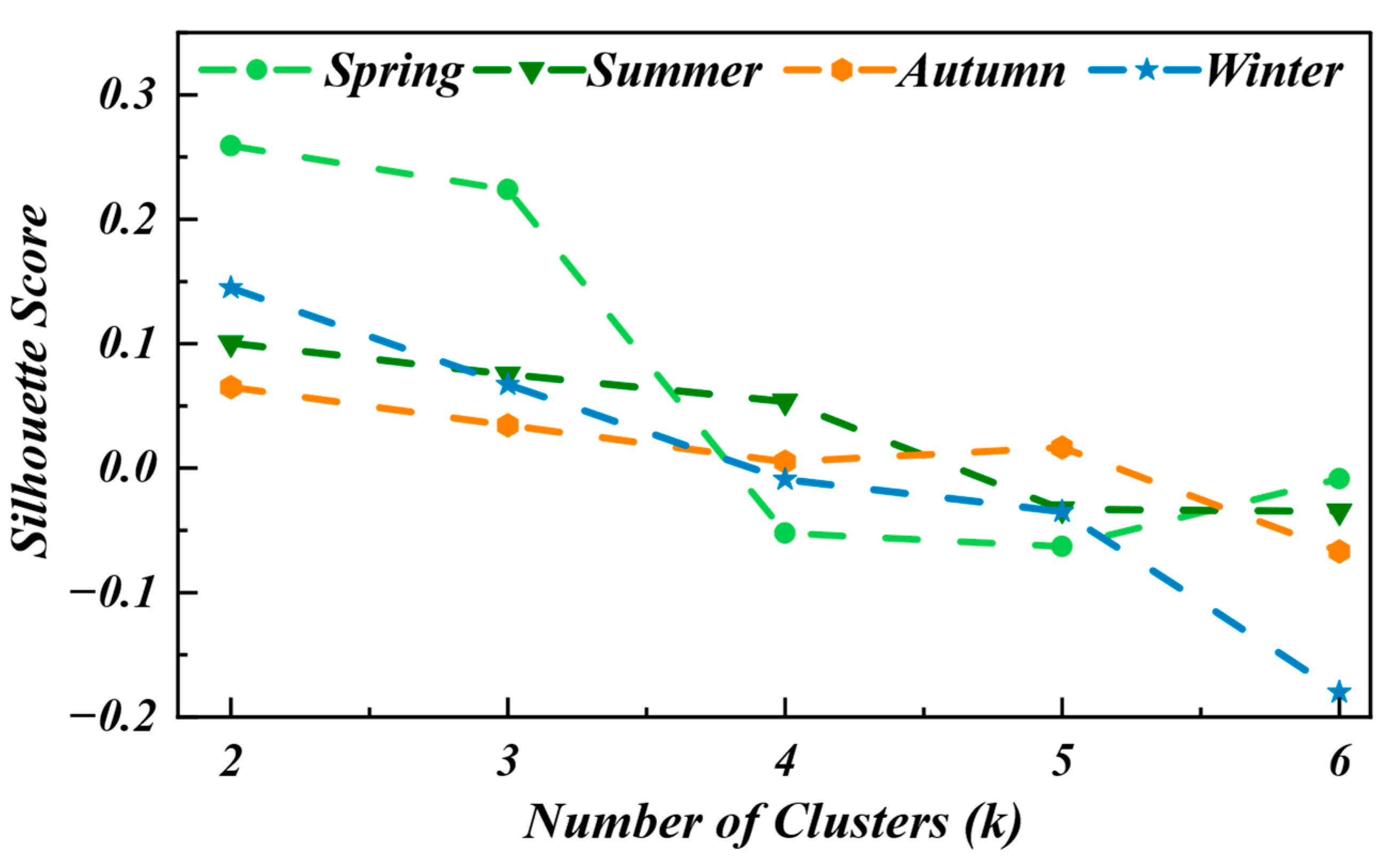
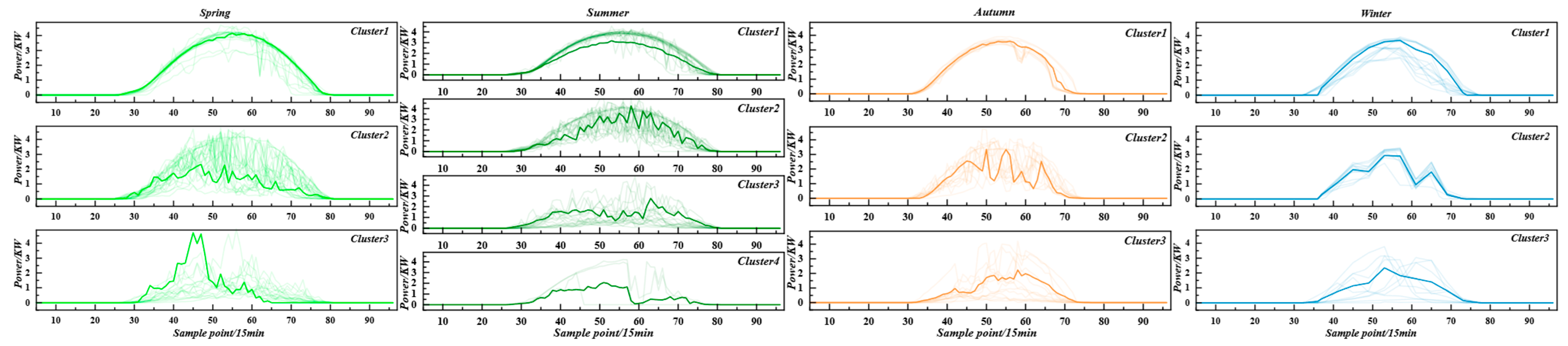
2.3. K-Shape Clustering Method
2.4. CNN-BiLstm-KAN
2.4.1. Convolutional Neural Network
2.4.2. BiLstm Layer
2.4.3. Kolmogorov Arnold Network Layer
2.5. Model Structure of the Proposed Methodology
- (1)
- Gray-relational filtering: for each IMF, retain the weather variables whose correlation exceeds a season-specific threshold; the intersection of these per-IMF sets yields the first-stage candidate pool.
- (2)
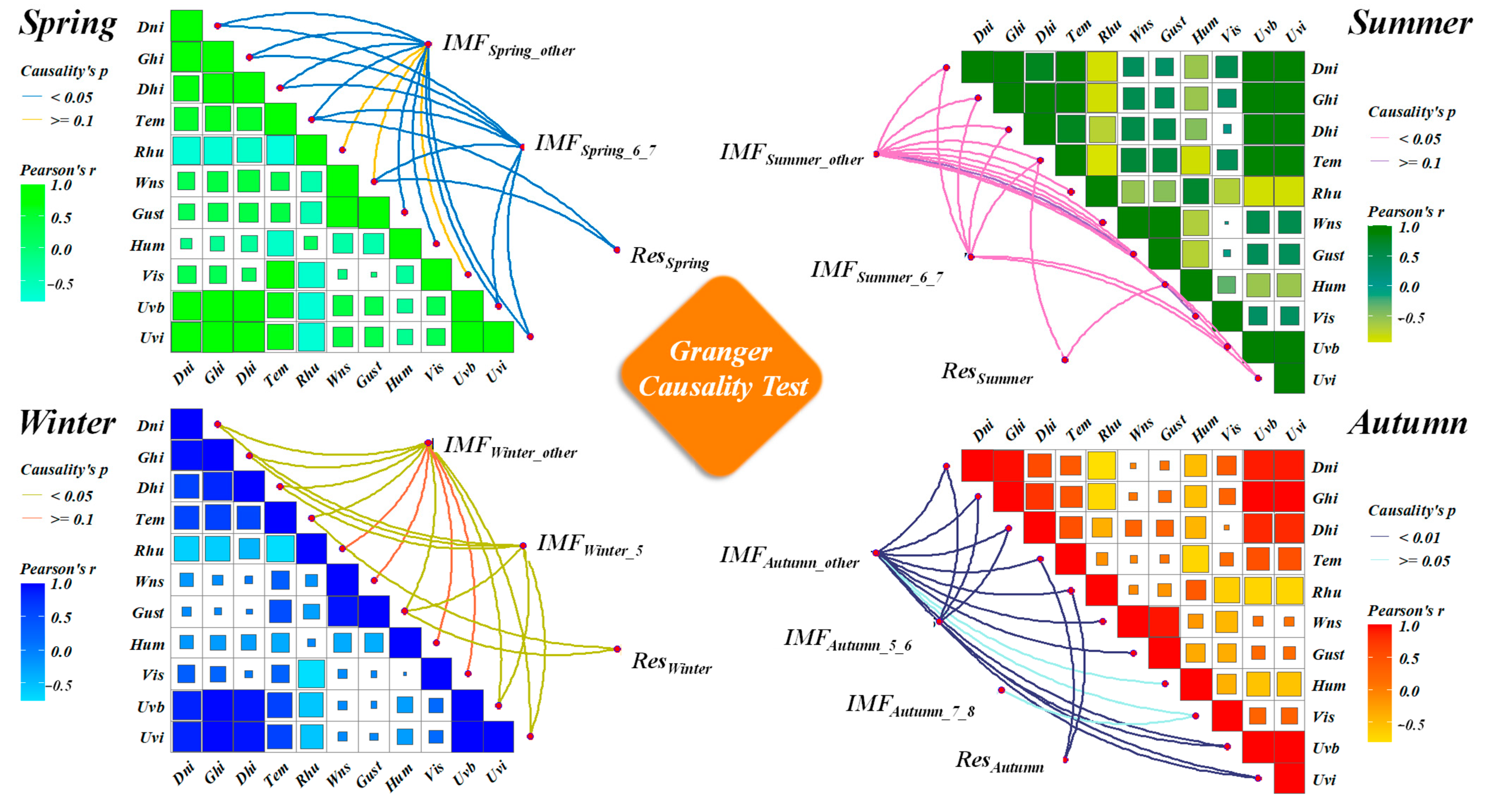
- Nonlinear causality test: run a convergent-cross-map test between every reconstructed components and the first-stage candidates, keeping only variables with statistically significant causal influence to form the final input set.
3. Experiments and Analysis
3.1. Data Description and Preprocessing
3.2. Data Decomposition and Feature Mining
3.2.1. Data Decomposition and Permutation Entropy Fusion
3.2.2. Feature Analysis Based on Causal Association
3.3. Weather Type Classification
3.4. Predictive Error Evaluation Metrics
4. PV Forecasting and Error Analysis
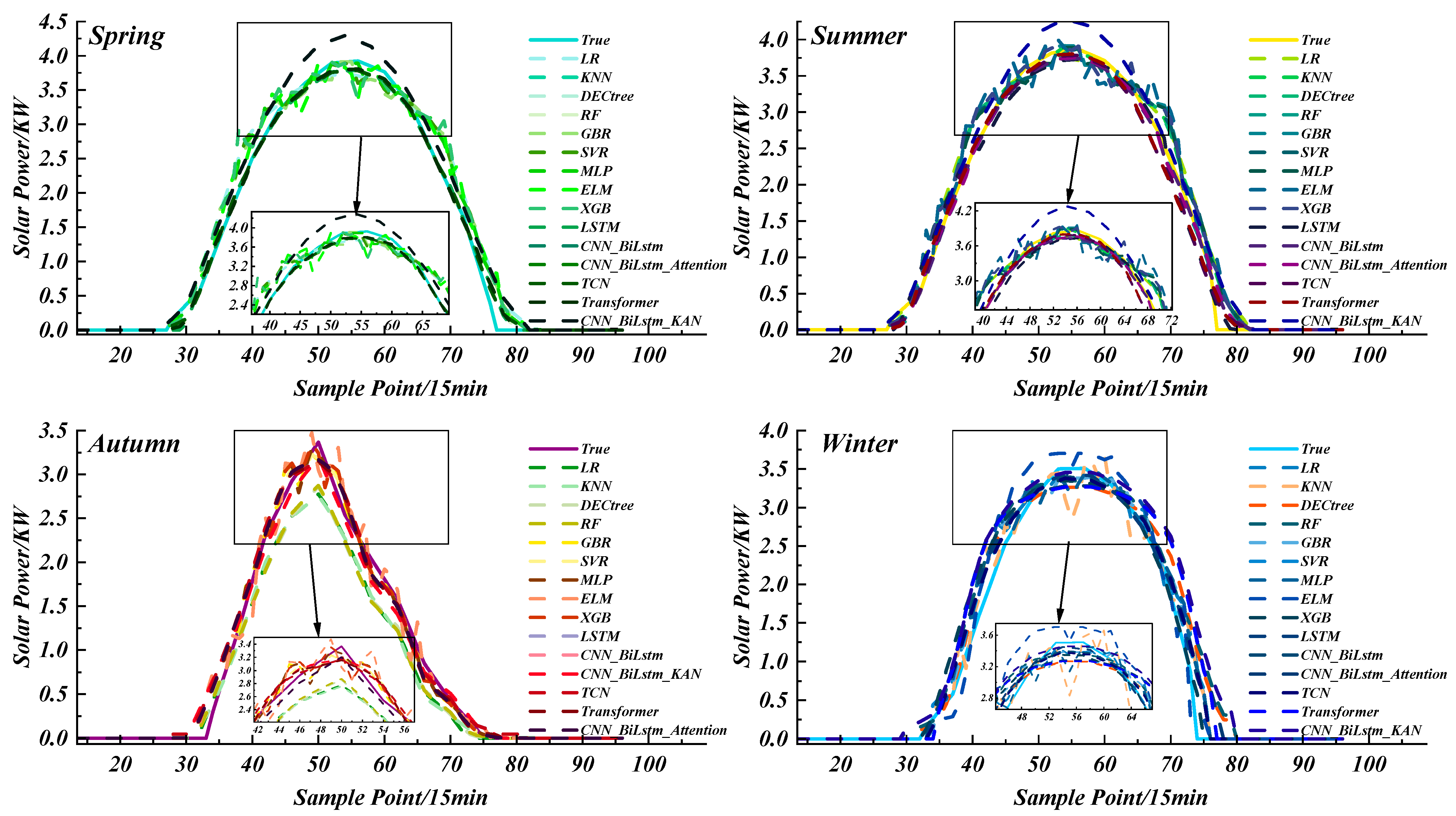
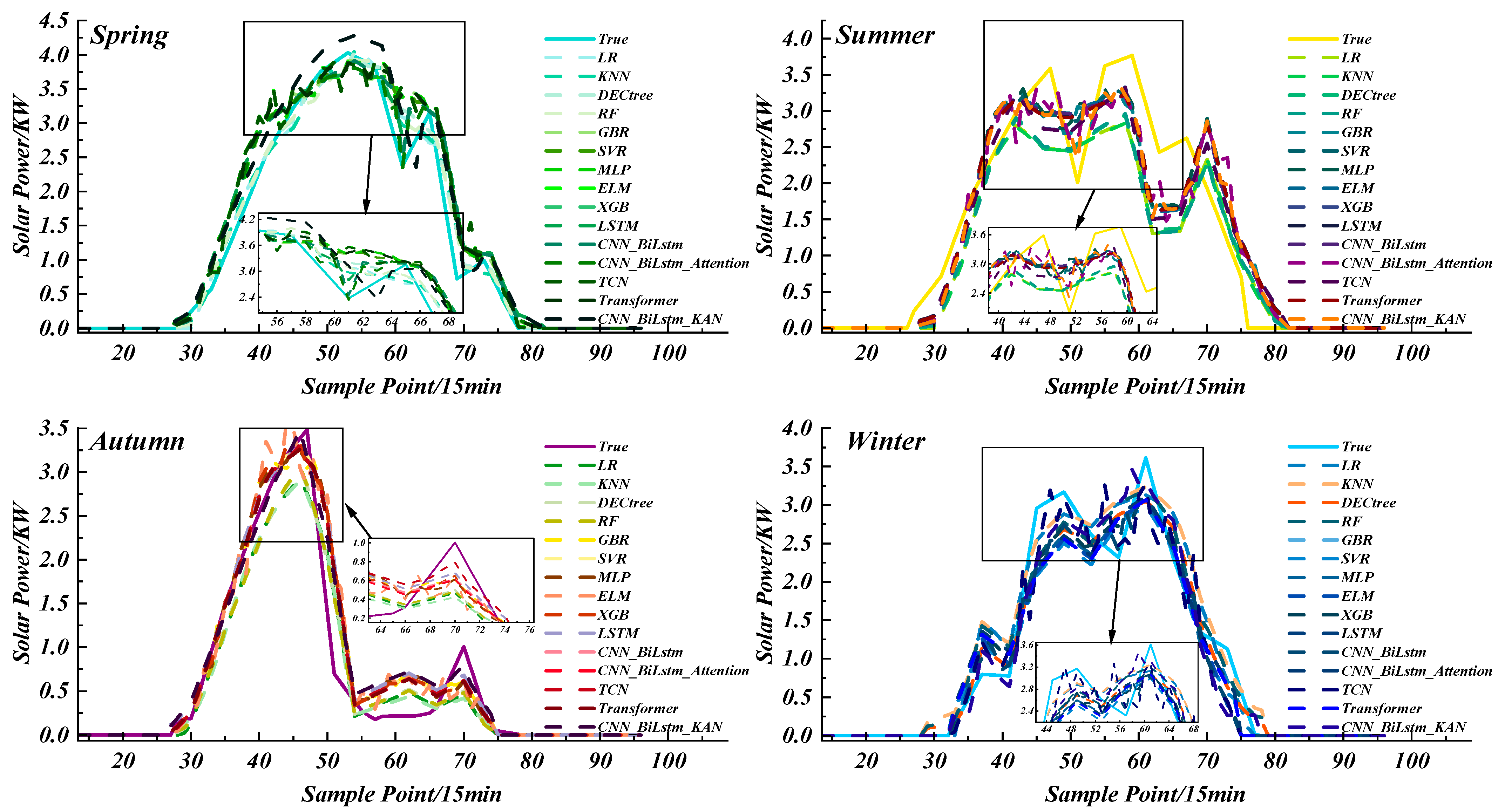
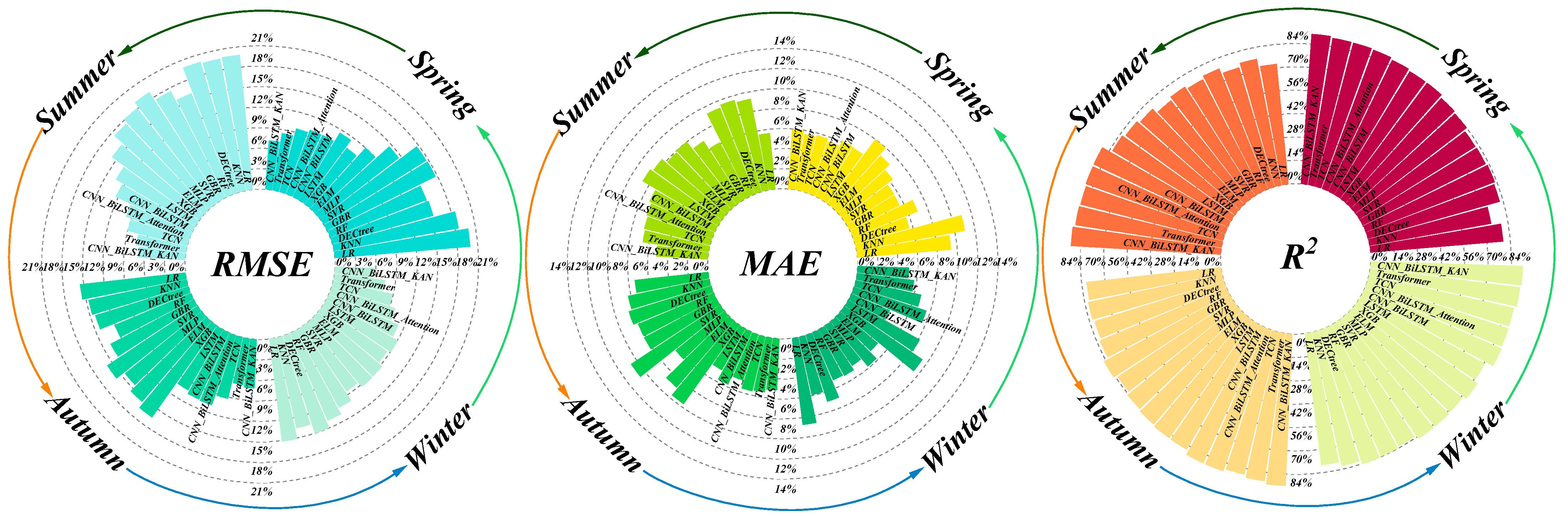
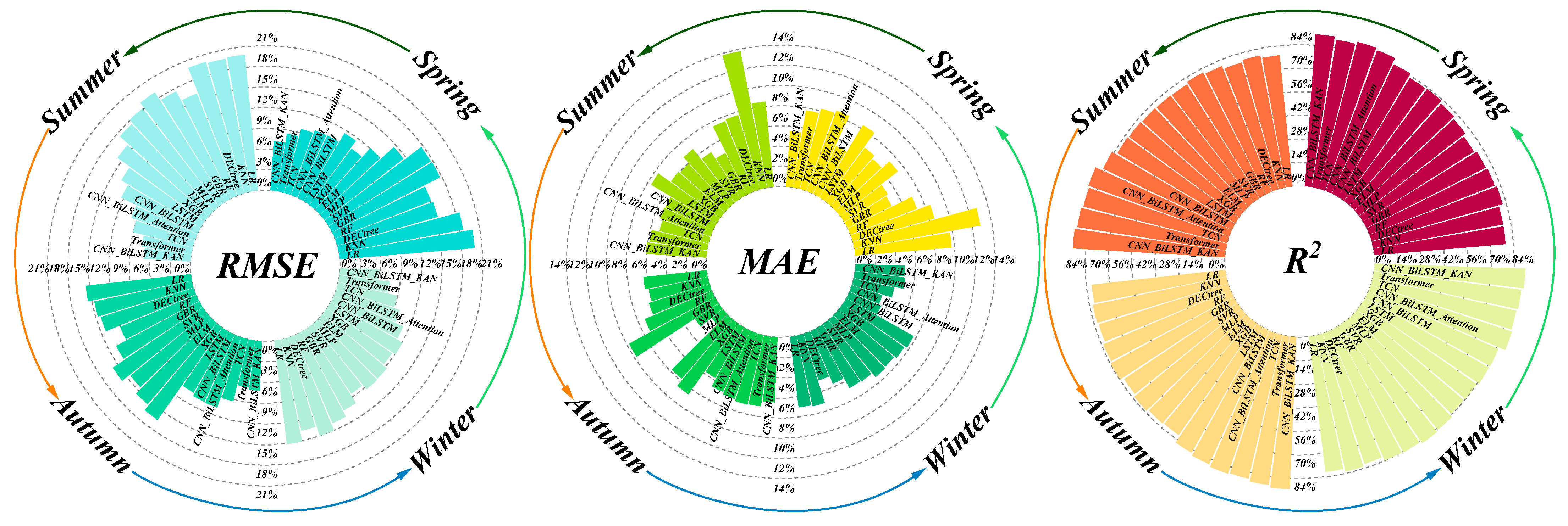
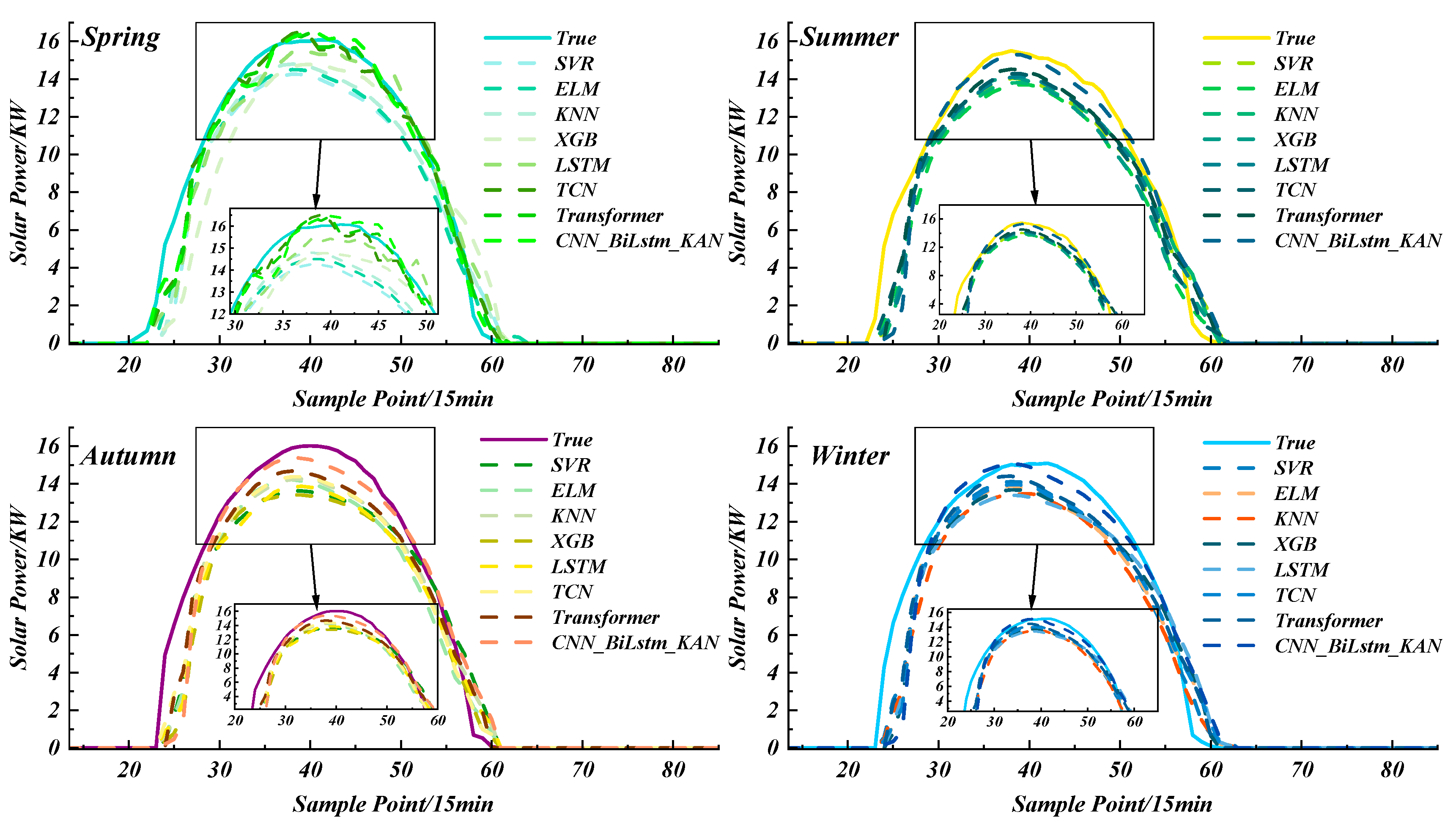
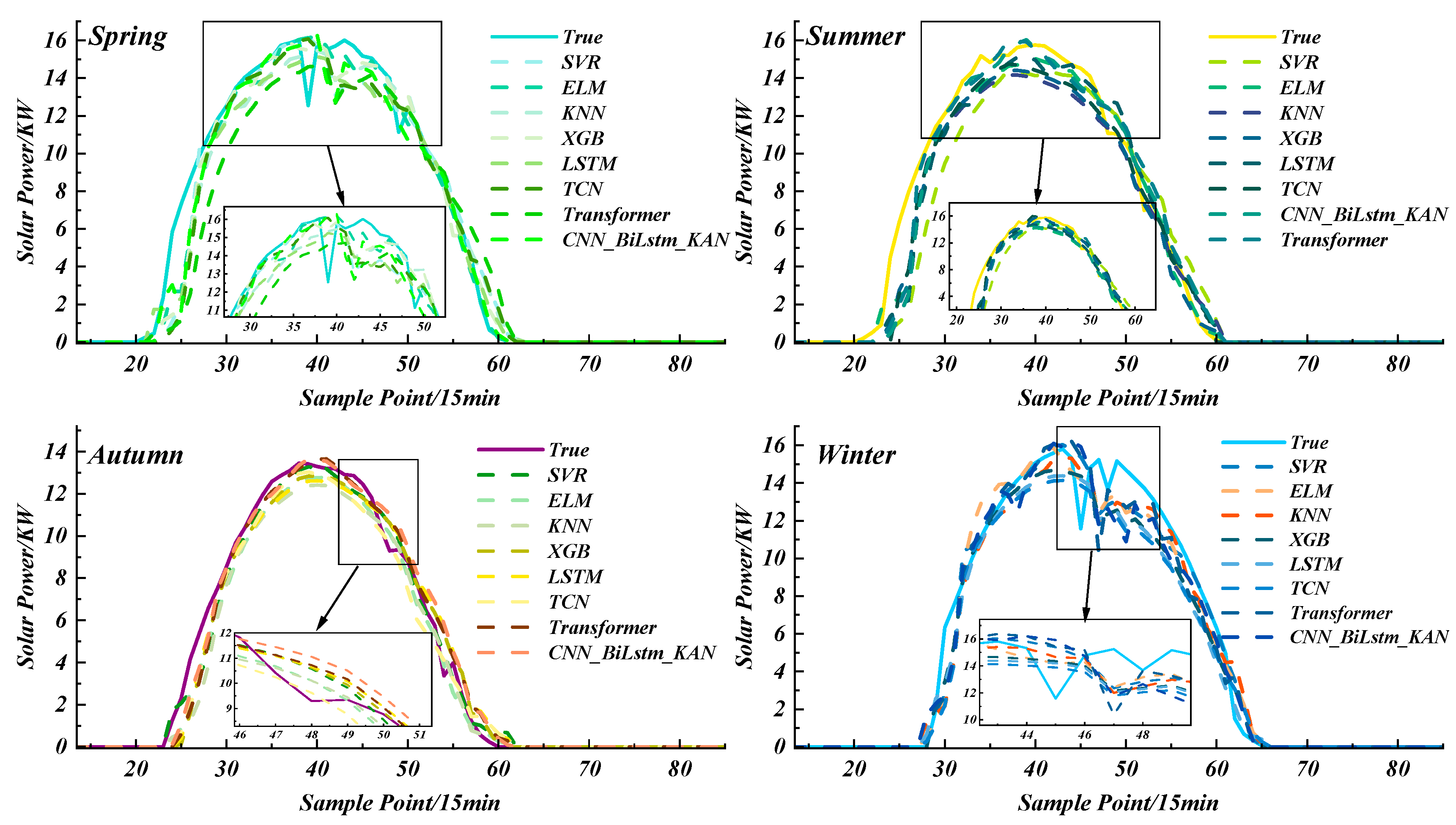
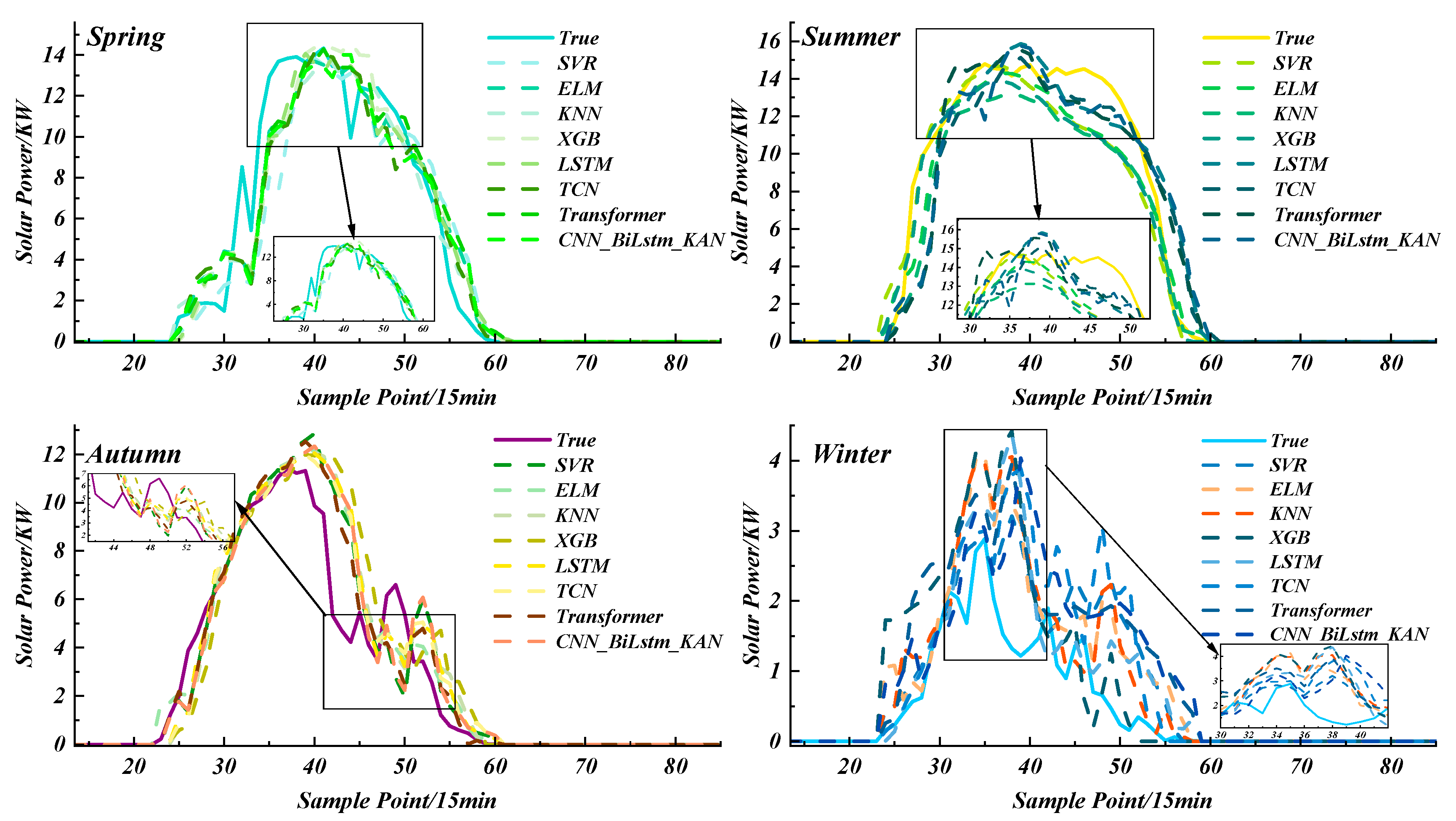
4.1. Comparison Results of Seasonal Models
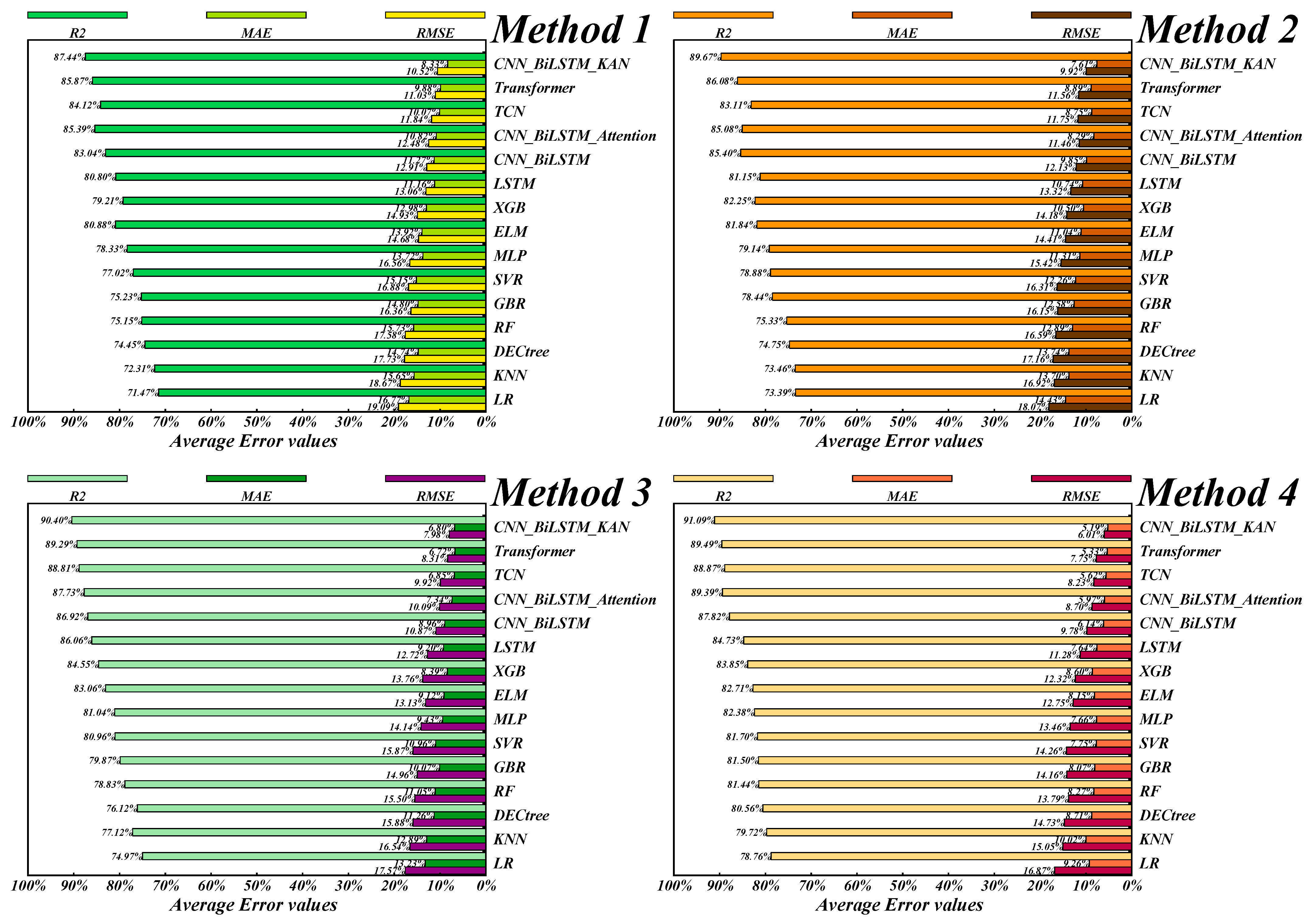
4.2. Ablation Study
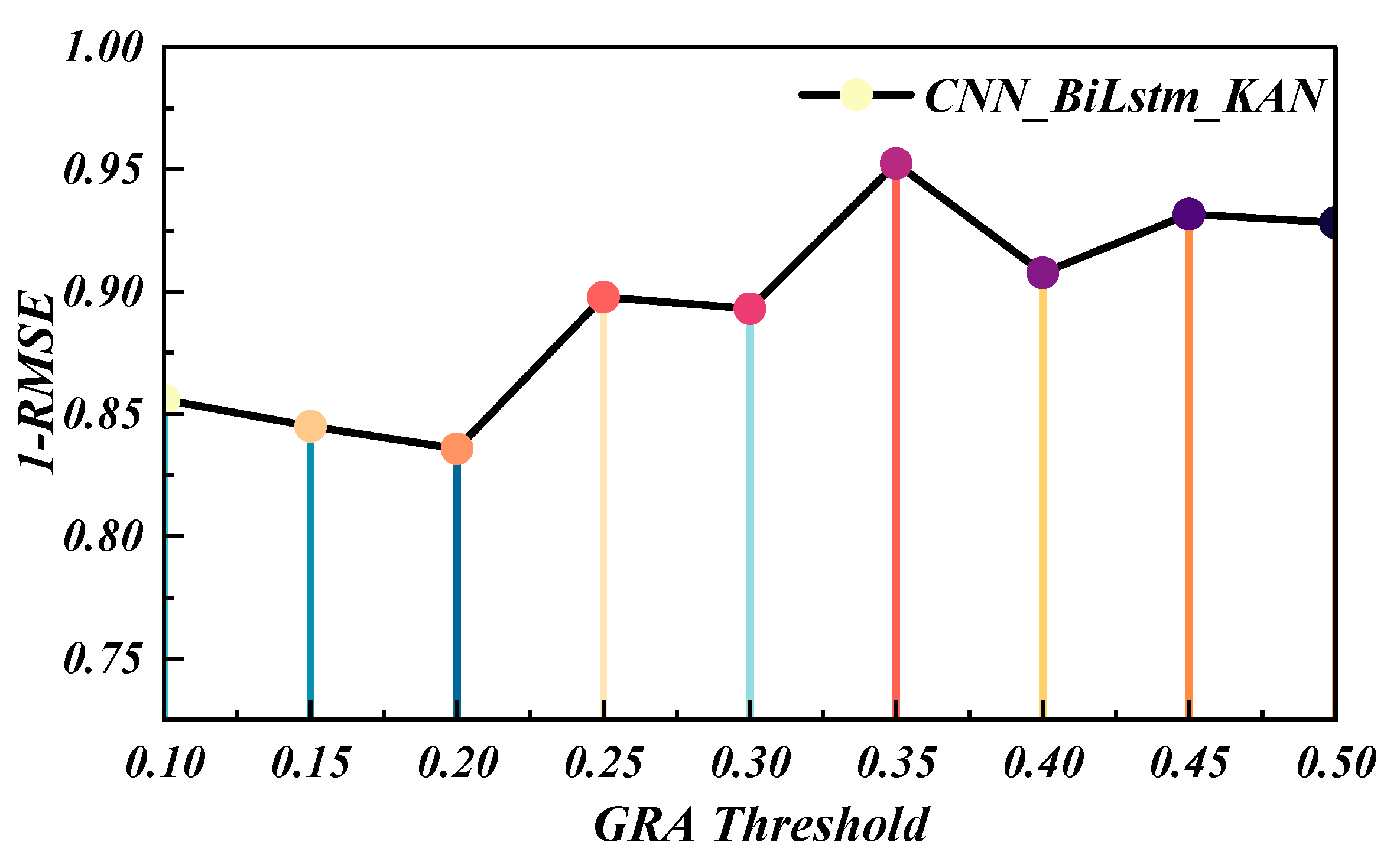
4.3. Influence of the Gray Relational Threshold
4.4. Other-Region Experiments for Distributed-PV User
5. Conclusions
- (1)
- The CEEMDAN method is used to decompose and reconstruct power data divided by season, revealing seasonal fluctuations within the series. Compared to the data reconstruction method, the prediction model’s RMSE improved by an average of 4.51%, MAE decreased by 3.14%, and R2 increased by 3.65%.
- (2)
- The GRA and NGC methods are used to correlate the time series with weather features for each season, uncovering difficult-to-identify nonlinear relationships between the time series and weather features. Compared to the method without weather type division, the average RMSE for sunny-like, cloudy, and rainy weather environments decreased by 4.69%, 1.93%, and 2.61%, respectively, and the average MAE decreased by 3.77%, 3.15%, and 3.24%. Meanwhile, the average R2 increased by 3% to 9%.
- (3)
- The K-Shape algorithm is used to classify power sequences into weather types, obtaining representative weather event meteorological features and high-precision similar-day datasets. This allows for short-term forecasting of distributed PV power under different weather scenarios, reducing the impact of PV output uncertainty, lowering the data computation load, and improving operational efficiency.
- (4)
- Compared to traditional machine learning models, the proposed method based on CNN_BiLSTM_KAN demonstrates better prediction performance. CNN_BiLSTM_KAN reduces RMSE by 7.09%, MAE by an average of 2.83%, and increases R2 by an average of 8.21% across all seasons and weather types, showing a clear forecasting advantage over traditional models.
6. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PV | Photovoltaic Power |
| NWP | Numerical Weather Prediction |
| GRA | Gray Relation Analysis |
| KAN | Kolmogorov Arnold Network |
| GC | Granger Causality |
| NGC | Nonlinear Granger Causality |
| CNN | Convolution Neural Network |
| LSTM | Long Short Term Memory |
| BiLstm | Bidirectional LSTM |
| ED | Euclidean Distance |
| PE | Permutation Entropy |
| EMD | Empirical Mode Decomposition |
| EEMD | Ensemble EMD |
| CEEMDAN | Complete EEMD with Adaptive Noise |
| VMD | Variational Mode Decomposition |
| LR | Logistic Regression |
| KNN | K Near Neighbor |
| DECtree | Decision tree |
| Xgboost | Extreme gradient boosting |
| GBR | Gradient Boosting Regression |
| ELM | Extreme Learning Machine |
| GRU | Gated Recurrent Units |
| MLP | Multi-Layer Perceptron |
| RF | Random Forest |
| SVR | Support Vector Regression |
| RMSE | Root Mean Square Error |
| MAE | Mean Absolute Error |
| R2 | R square |
| IMF | Intrinsic Mode Function |
| Res | Residual |
| Dni | Direct Normal Irradiance |
| Ghi | Global Horizontal Irradiance |
| Dhi | Diffuse Horizontal Irradiance |
| Tem | Temperature |
| Rhu | Relative Humidity |
| Wns | Wind Speed |
| Gust | Gust |
| Hum | Humidity |
| Vis | Visibility |
| Uvb | Ultraviolet Radiation Short |
| Uvi | Ultraviolet Radiation Long |
References
- Yang, M.; Jiang, Y.; Xu, C.; Wang, B.; Wang, Z.; Su, X. Day-ahead wind farm cluster power prediction based on trend categorization and spatial information integration model. Appl. Energy 2025, 388, 125580. [Google Scholar] [CrossRef]
- Kang, K.; Jia, H.; Hui, H.; Liu, D. Two-stage optimization configuration of shared energy storage for multi-distributed photovoltaic clusters in rural distribution networks considering self-consumption and self-sufficiency. Appl. Energy 2025, 394, 126174. [Google Scholar] [CrossRef]
- Yang, M.; Guo, Y.; Fan, F. Ultra-Short-Term Prediction of Wind Farm Cluster Power Based on Embedded Graph Structure Learning With Spatiotemporal Information Gain. IEEE Trans. Sustain. Energy 2025, 16, 308–322. [Google Scholar] [CrossRef]
- Dai, H.; Zhen, Z.; Wang, F.; Lin, Y.; Xu, F.; Duić, N. A short-term PV power forecasting method based on weather type credibility prediction and multi-model dynamic combination. Energy Convers. Manag. 2025, 326, 116501. [Google Scholar] [CrossRef]
- Wang, Y.; Fu, W.; Wang, J.; Zhen, Z.; Wang, F. Ultra-short-term distributed PV power forecasting for virtual power plant considering data-scarce scenarios. Appl. Energy 2024, 373, 123890. [Google Scholar] [CrossRef]
- Zhao, H.; Huang, X.; Xiao, Z.; Shi, H.; Li, C.; Tai, Y. Week-ahead hourly solar irradiation forecasting method based on ICEEMDAN and TimesNet networks. Renew. Energy 2024, 220, 119706. [Google Scholar] [CrossRef]
- Yang, M.; Shen, X.; Huang, D.; Su, X. Fluctuation Classification and Feature Factor Extraction to Forecast Very Short-Term Photovoltaic Output Powers. CSEE J. Power Energy Syst. 2025, 11, 661–670. [Google Scholar]
- Deng, F.; Wang, J.; Wu, L.; Gao, B.; Wei, B.; Li, Z. Distributed photovoltaic power forecasting based on personalized federated adversarial learning. Sustain. Energy Grids Netw. 2024, 40, 101537. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, Y.; Wu, J.; Zhang, X. A regional distributed photovoltaic power generation forecasting method based on grid division and TCN-Bilstm. Renew. Energy 2026, 256, 123935. [Google Scholar] [CrossRef]
- Chen, D.; Shi, X.; Jiang, M.; Zhu, S.; Zhang, H.; Zhang, D.; Chen, Y.; Yan, J. Selecting effective NWP integration approaches for PV power forecasting with deep learning. Sol. Energy 2025, 301, 113939. [Google Scholar] [CrossRef]
- Tang, Y.; Yang, K.; Zhang, S.; Zhang, Z. Photovoltaic power forecasting: A dual-attention gated recurrent unit framework incorporating weather clustering and transfer learning strategy. Eng. Appl. Artif. Intell. 2024, 130, 107691. [Google Scholar] [CrossRef]
- Ouyang, J.; Chu, L.; Chen, X.; Zhao, Y.; Zhu, X.; Liu, T. A K-means cluster division of regional photovoltaic power stations considering the consistency of photovoltaic output. Sustain. Energy Grids Netw. 2024, 40, 101573. [Google Scholar] [CrossRef]
- Sun, F.; Li, L.; Bian, D.; Ji, H.; Li, N.; Wang, S. Short-term PV power data prediction based on improved FCM with WTEEMD and adaptive weather weights. J. Build. Eng. 2024, 90, 109408. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Yang, M.; Huang, Y.; Wang, Z.; Wang, B.; Su, X. A Framework of Day-Ahead Wind Supply Power Forecasting by Risk Scenario Perception. IEEE Trans. Sustain. Energy 2025, 16, 1659–1672. [Google Scholar] [CrossRef]
- Zhou, F.; Huang, Z.; Zhang, C. Carbon price forecasting based on CEEMDAN and LSTM. Appl. Energy 2022, 311, 118601. [Google Scholar] [CrossRef]
- Liu, Q.; Lou, X.; Yan, Z.; Qi, Y.; Jin, Y.; Yu, S.; Yang, X.; Zhao, D.; Xia, J. Deep-learning post-processing of short-term station precipitation based on NWP forecasts. Atmos. Res. 2023, 295, 107032. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Kong, X.; Ma, L.; Besheer, A.H.; Lee, K.Y. Deep neural network for forecasting of photovoltaic power based on wavelet packet decomposition with similar day analysis. Energy 2023, 271, 126963. [Google Scholar] [CrossRef]
- Cui, S.; Lyu, S.; Ma, Y.; Wang, K. Improved informer PV power short-term prediction model based on weather typing and AHA-VMD-MPE. Energy 2024, 307, 132766. [Google Scholar] [CrossRef]
- Li, J.; Rao, C.; Gao, M.; Xiao, X.; Goh, M. Efficient calculation of distributed photovoltaic power generation power prediction via deep learning. Renew. Energy 2025, 246, 122901. [Google Scholar] [CrossRef]
- Lin, H.; Gao, L.; Cui, M.; Liu, H.; Li, C.; Yu, M. Short-term distributed photovoltaic power prediction based on temporal self-attention mechanism and advanced signal decomposition techniques with feature fusion. Energy 2025, 315, 134395. [Google Scholar] [CrossRef]
- Gao, B.; Huang, X.; Shi, J.; Tai, Y.; Zhang, J. Hourly forecasting of solar irradiance based on CEEMDAN and multi-strategy CNN-LSTM neural networks. Renew. Energy 2020, 162, 1665–1683. [Google Scholar] [CrossRef]
- Yang, M.; Jiang, R.; Wang, B.; Fang, G.; Jia, Y.; Fan, F. Multi-channel attention mechanism graph convolutional network considering cumulative effect and temporal causality for day-ahead wind power prediction. Energy 2025, 332, 137023. [Google Scholar] [CrossRef]
- Mayer, M.J.; Yang, D. Calibration of deterministic NWP forecasts and its impact on verification. Int. J. Forecast. 2023, 39, 981–991. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Z.; Feng, B.; Sui, X.; Zhang, S. Granger-guided reduced dual attention long short-term memory for travel demand forecasting during coronavirus disease 2019. Eng. Appl. Artif. Intell. 2025, 153, 110950. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, Z. A Deep Attention Convolutional Recurrent Network Assisted by K-Shape Clustering and Enhanced Memory for Short Term Wind Speed Predictions. IEEE Trans. Sustain. Energy 2022, 13, 856–867. [Google Scholar] [CrossRef]
- Paparrizos, J.; Gravano, L. k-Shape: Efficient and Accurate Clustering of Time Series. In Proceedings of the 2015 ACM SIGMOD International Conference on Management of Data, New York, NY, USA, 31 May–4 June 2015; pp. 1855–1870. [Google Scholar]
- Gao, Y.; Hu, Z.; Chen, W.-A.; Liu, M.; Ruan, Y. A revolutionary neural network architecture with interpretability and flexibility based on Kolmogorov–Arnold for solar radiation and temperature forecasting. Appl. Energy 2025, 378, 124844. [Google Scholar] [CrossRef]
- Wei, C.; Li, H.; Luo, Z.; Wang, T.; Yu, Y.; Wu, M.; Qi, B.; Yu, M. Quantitative analysis of flame luminance and explosion pressure in liquefied petroleum gas explosion and inerting: Grey relation analysis and kinetic mechanisms. Energy 2024, 304, 132046. [Google Scholar] [CrossRef]
- Li, C.; Xie, W.; Zheng, B.; Yi, Q.; Yang, L.; Hu, B.; Deng, C. An enhanced CLKAN-RF framework for robust anomaly detection in unmanned aerial vehicle sensor data. Knowl.-Based Syst. 2025, 319, 113690. [Google Scholar] [CrossRef]
- Hasnat, M.A.; Asadi, S.; Alemazkoor, N. A graph attention network framework for generalized-horizon multi-plant solar power generation forecasting using heterogeneous data. Renew. Energy 2025, 243, 122520. [Google Scholar] [CrossRef]
- Dou, W.; Wang, K.; Shan, S.; Li, C.; Zhang, K.; Wei, H.; Sreeram, V. A correction framework for day-ahead NWP solar irradiance forecast based on sparsely activated multivariate-shapelets information aggregation. Renew. Energy 2025, 244, 122638. [Google Scholar] [CrossRef]
- Tank, A.; Covert, I.; Foti, N.; Shojaie, A.; Emily, B. Fox Neural Granger Causality. Trans. Pattern Anal. Mach. Intell. 2022, 44, 4267–4279. [Google Scholar]
- Sui, Q.; Wang, Y.; Liu, C.; Wang, K.; Sun, B. Attribution-Aided Nonlinear Granger Causality Discovery Method and Its Industrial Application. IEEE Trans. Ind. Inform. 2025, 21, 6147–6157. [Google Scholar] [CrossRef]
- Ma, L.; Wang, M.; Peng, K. Nonlinear Dynamic Granger Causality Analysis Framework for Root-Cause Diagnosis of Quality-Related Faults in Manufacturing Processes. IEEE Trans. Autom. Sci. Eng. 2024, 21, 3554–3563. [Google Scholar] [CrossRef]
- Long, C.L.; Guleria, Y.; Alam, S. Air passenger forecasting using Neural Granger causal Google trend queries. J. Air Transp. Manag. 2021, 95, 102083. [Google Scholar] [CrossRef]
- Guo, C.; Chen, Y.; Fu, Y. FPGA-based component-wise LSTM training accelerator for neural granger causality analysis. Neurocomputing 2025, 615, 128871. [Google Scholar] [CrossRef]
- Zhang, T.; Liao, Q.; Tang, F.; Li, Y.; Wang, J. Wide-area Distributed Photovoltaic Power Forecast Method Based on Meteorological Resource Interpolation and Transfer Learning. Proc. CSEE 2023, 43, 7929–7940. [Google Scholar]
- Shi, M.; Xu, K.; Wang, J.; Yin, R.; Zhang, P. Short-Term Photovoltaic Power Forecast Based on Grey Relational Analysis and GeoMAN Model. Trans. CHINA Electrotech. Soc. 2021, 36, 2298–2305. [Google Scholar]
- Lin, Y.E.; Ming, P.E.; Peng, L.U.; Jinlong, Z.H.O.; Boyu, H.E. Combination Forecasting Method of Short-term Photovoltaic Power Based on Weather Classification. Autom. Electr. Power Syst. 2021, 45, 44–54. [Google Scholar]
- Yu, B.; Guo, H.; Shi, J. Remaining useful life prediction based on hybrid CNN-BiLSTM model with dual attention mechanism. Int. J. Electr. Power Energy Syst. 2025, 172, 111152. [Google Scholar] [CrossRef]
- Li, Z.-Q.; Yin, Y.; Li, X.; Nie, L.; Li, Z. Prediction of tunnel surrounding rock deformation using CNN-BiLSTM-attention model incorporating a novel index: Excavation factor. Tunn. Undergr. Space Technol. 2025, 166, 106974. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, M.; Chen, Y.; Kong, W. Short-term power load forecasting for industrial buildings based on decomposition reconstruction and TCN-Informer-BiGRU. Energy Build. 2025, 347, 116317. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, L.; Wang, C. Parallel ResBiGRU-transformer fusion network for multi-energy load forecasting based on hierarchical temporal features. Energy Convers. Manag. 2025, 345, 120360. [Google Scholar] [CrossRef]







| Ref. | Core Techniques | Key Strengths | Main Limitations | Typical Application Scenarios |
|---|---|---|---|---|
| LR [31] | Linear regression + NWP | Ultra-fast; interpretable coefficients | Misses nonlinearity & ramps | Day-ahead coarse scheduling |
| KNN [32] | Euclidean nearest-day search | Zero training; easy to deploy | Storage grows with data; metric sensitive | Small residential PV |
| DECtree [33] | Single CART on raw features | Human-readable rules | High variance; over-fits noise | Exploratory analysis |
| RF [34] | Bagging CART ensemble | Robust to outliers; handles interaction | Biased toward majority weather class | Regional fleet forecasting |
| GBR [35] | Gradient-boosting trees | Captures complex nonlinearity | Slow; hyper-parameters sensitive | Utility short-term markets |
| SVR [36] | RBF-kernel SV regression | Convex optimum; global solution | Quadratic memory; kernel choice critical | Limited-data sites |
| MLP [37] | 2-layer feed-forward | Simple deep baseline | Vanishing gradients; needs tuning | Research baseline |
| ELM [38] | Random hidden neurons | Extreme training speed | Random weights → unstable | Ultra-fast prototype |
| XGB [39] | Boosted trees with regularization | state-of-the-art tabular accuracy | Requires careful early-stopping | Commercial forecasting |
| LSTM [40] | Vanilla LSTM | Long-term temporal memory | No exogenous causality; over-fits ramps | Single-site hourly |
| CNN_ BiLstm [41] | 1-D CNN + BiLSTM | Local + global spatio-temporal | Fixed topology; no weather-type filter | Day-ahead bidding |
| CNN_BiLstm_Attention [42] | + Self-attention | Focus on key time-steps | Attention noise; extra parameters | Research benchmark |
| TCN [43] | Dilated causal CNN | Long receptive field; parallel training | Struggles with seasonal drift | Intra-day trading |
| Transformer [44] | Encoder–decoder self-attention | Captures global dependencies | Data-hungry; quadratic complexity | Large-scale farms |
| The proposed methodology | CEEMDAN-GRA-NGC + K-shape + CNN-BiLSTM-KAN | Season-weather matched; causal feature pruning; interpretable KAN | Higher pre-training time | Distributed rooftops with scarce data and fast ramps |
| Feature (p-Value) | Dni | Ghi | Dhi | Tem | Rhu | Wns | Gust | Hum | Vis | Uvb | Uvi | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Spring | IMFSpring_other | 0.0061 | 0.0013 | 0.0004 | 0.0207 | 0.1831 | 0.5066 | 0.0883 | 0.1025 | 0.5940 | 0.0038 | 0.0072 |
| IMFSpring_6_7 | 0.0035 | 0.0077 | 0.0081 | 0.0372 | / | 0.0274 | / | / | / | 0.0004 | 0.0094 | |
| RESSpring | / | / | / | 0.0289 | / | 0.0017 | / | / | / | / | / | |
| Summer | IMFSummer_other | 0.0008 | 0.0068 | 0.0089 | 0.0345 | 0.1269 | 0.0316 | 0.0688 | 0.0318 | 0.8473 | 0.0020 | 0.0047 |
| IMFSummer_6_7 | 0.0056 | 0.0046 | 0.0021 | 0.0071 | / | / | / | / | / | 0.0053 | 0.0018 | |
| RESSummer | / | / | / | 0.0503 | / | / | / | 0.0285 | / | / | / | |
| Autumn | IMFAutumn_other | 0.0035 | 0.0036 | 0.0013 | 0.0656 | 0.0060 | 0.1565 | 0.0113 | 0.4971 | 0.7401 | 0.0088 | 0.0009 |
| IMFAutumn_5_6 | 0.0086 | 0.0007 | 0.0035 | / | / | / | / | / | / | 0.0073 | 0.0063 | |
| IMFAutumn_7_8 | / | / | / | / | / | / | / | / | 0.0099 | / | / | |
| RESAutumn | / | / | / | 0.0957 | 0.0040 | / | / | / | / | / | / | |
| Winter | IMFWinter_other | 0.0019 | 0.0012 | 0.0028 | 0.1045 | 0.4622 | 0.9949 | 0.0019 | 0.9922 | 0.9988 | 0.0006 | 0.0011 |
| IMFWinter_5 | 0.0042 | 0.0086 | 0.0081 | / | / | / | 0.0049 | / | / | 0.0062 | 0.0052 | |
| RESWinter | / | / | / | 0.0856 | / | / | 0.0026 | / | / | / | / | |
| Season | Spring | Summer | Autumn | Winter |
|---|---|---|---|---|
| Silhouette Score | 0.2238 | 0.0535 | 0.0343 | 0.0670 |
| Number of Cluster | 3 | 4 | 3 | 3 |
| Model | Index | Spring | Summer | Autumn | Winter | Average |
|---|---|---|---|---|---|---|
| LR | RMSE | 17.01% | 16.07% | 17.31% | 18.04% | 17.11% |
| MAE | 12.65% | 11.53% | 12.61% | 11.74% | 12.13% | |
| R2 | 77.27% | 79.28% | 78.67% | 78.54% | 78.44% | |
| KNN | RMSE | 14.38% | 13.44% | 14.69% | 14.72% | 14.31% |
| MAE | 13.26% | 10.39% | 11.55% | 10.78% | 11.50% | |
| R2 | 79.15% | 80.58% | 79.47% | 79.11% | 79.58% | |
| DECtree | RMSE | 13.78% | 15.26% | 13.72% | 13.95% | 14.18% |
| MAE | 12.39% | 11.84% | 11.63% | 10.63% | 11.62% | |
| R2 | 80.22% | 81.12% | 80.77% | 80.11% | 80.56% | |
| RF | RMSE | 14.16% | 13.84% | 12.62% | 13.74% | 13.59% |
| MAE | 12.47% | 10.25% | 9.12% | 10.35% | 10.55% | |
| R2 | 80.07% | 80.67% | 81.27% | 81.16% | 80.79% | |
| GBR | RMSE | 15.05% | 16.36% | 13.45% | 14.98% | 14.96% |
| MAE | 11.27% | 12.25% | 9.49% | 12.66% | 11.42% | |
| R2 | 81.61% | 79.94% | 80.86% | 80.09% | 80.63% | |
| SVR | RMSE | 13.52% | 15.04% | 14.84% | 12.96% | 14.09% |
| MAE | 11.53% | 11.58% | 11.47% | 10.16% | 11.19% | |
| R2 | 82.56% | 80.27% | 81.32% | 82.96% | 81.78% | |
| MLP | RMSE | 13.93% | 14.46% | 12.89% | 11.98% | 13.32% |
| MAE | 11.41% | 11.45% | 10.71% | 9.22% | 10.70% | |
| R2 | 81.96% | 81.61% | 82.72% | 84.02% | 82.58% | |
| ELM | RMSE | 15.53% | 12.76% | 12.08% | 10.72% | 12.77% |
| MAE | 12.44% | 11.48% | 9.54% | 8.69% | 10.54% | |
| R2 | 79.93% | 82.27% | 84.49% | 83.94% | 82.66% | |
| XGB | RMSE | 12.66% | 10.92% | 11.45% | 11.06% | 11.52% |
| MAE | 10.44% | 9.13% | 8.55% | 10.83% | 9.74% | |
| R2 | 80.69% | 85.22% | 83.65% | 86.84% | 84.10% | |
| LSTM | RMSE | 10.76% | 9.07% | 10.91% | 10.61% | 10.34% |
| MAE | 9.42% | 7.38% | 8.31% | 9.56% | 8.67% | |
| R2 | 82.55% | 87.13% | 84.95% | 86.88% | 85.38% | |
| CNN_ BiLstm | RMSE | 7.39% | 8.81% | 9.69% | 7.55% | 8.36% |
| MAE | 7.44% | 8.88% | 6.52% | 7.01% | 7.46% | |
| R2 | 88.55% | 89.93% | 87.47% | 90.54% | 89.12% | |
| CNN_BiLstm_Attention | RMSE | 6.19% | 7.75% | 8.98% | 5.42% | 7.09% |
| MAE | 6.42% | 6.37% | 4.59% | 5.51% | 5.72% | |
| R2 | 90.81% | 90.17% | 88.81% | 91.61% | 90.35% | |
| TCN | RMSE | 5.16% | 6.97% | 7.16% | 5.01% | 6.08% |
| MAE | 5.24% | 6.18% | 6.37% | 4.59% | 5.60% | |
| R2 | 90.95% | 89.83% | 90.27% | 90.68% | 90.43% | |
| Transformer | RMSE | 6.83% | 5.44% | 6.33% | 4.58% | 5.80% |
| MAE | 5.33% | 5.07% | 5.27% | 4.81% | 5.12% | |
| R2 | 91.04% | 89.87% | 91.54% | 89.73% | 90.55% | |
| CNN_ BiLstm_KAN | RMSE | 4.06% | 5.93% | 5.88% | 3.16% | 4.76% |
| MAE | 5.03% | 4.35% | 3.62% | 4.92% | 4.48% | |
| R2 | 92.26% | 91.42% | 91.74% | 92.66% | 92.02% |
| Weather Type Label | Sunny-Like | Cloudy Day | Rainy Day | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 |
| LR | 17.11% | 12.13% | 78.44% | 15.94% | 7.76% | 78.05% | 17.58% | 7.89% | 79.79% |
| KNN | 14.31% | 11.50% | 79.58% | 14.25% | 8.61% | 78.68% | 16.59% | 9.95% | 80.89% |
| DECtree | 14.18% | 11.62% | 80.56% | 13.91% | 7.69% | 80.43% | 16.11% | 6.83% | 80.70% |
| RF | 13.59% | 10.55% | 80.79% | 13.52% | 7.38% | 81.63% | 14.27% | 6.89% | 81.90% |
| GBR | 14.96% | 11.42% | 80.63% | 12.02% | 6.28% | 81.54% | 15.51% | 6.51% | 82.33% |
| SVR | 14.09% | 11.19% | 81.78% | 12.69% | 7.03% | 81.89% | 15.98% | 5.04% | 81.45% |
| MLP | 13.32% | 10.70% | 82.58% | 12.23% | 6.60% | 82.39% | 14.85% | 5.67% | 82.18% |
| ELM | 12.77% | 10.54% | 82.66% | 11.17% | 7.13% | 83.61% | 14.30% | 6.79% | 81.87% |
| XGB | 11.52% | 9.74% | 84.10% | 11.97% | 8.87% | 85.12% | 13.48% | 7.19% | 82.34% |
| LSTM | 10.34% | 8.67% | 85.38% | 11.69% | 6.92% | 84.93% | 11.82% | 7.35% | 83.88% |
| CNN_BiLstm | 8.36% | 7.46% | 89.12% | 9.96% | 5.80% | 88.61% | 11.03% | 5.15% | 85.72% |
| CNN_BiLstm_Attention | 7.09% | 5.72% | 90.35% | 8.91% | 6.22% | 88.80% | 10.10% | 5.97% | 89.02% |
| TCN | 8.11% | 5.11% | 91.13% | 8.01% | 5.98% | 89.23% | 9.24% | 5.15% | 90.18% |
| Transformer | 6.37% | 5.02% | 90.77% | 7.65% | 5.42% | 90.20% | 7.78% | 5.98% | 91.22% |
| CNN_BiLstm_KAN | 4.76% | 4.48% | 92.02% | 6.53% | 5.35% | 90.51% | 6.75% | 5.73% | 90.74% |
| Model | Key Parameter(s) | Value | Train Samples (Days) | Time(s) |
|---|---|---|---|---|
| LR | fit_intercept | True | 288 | 0.002 |
| KNN | n_neighbors, weights | 10, distance | 288 | 0.006 |
| DECtree | max_depth, min_samples_split | None, 10 | 288 | 0.185 |
| RF | n_estimators, max_depth, min_samples_split | 500, 30, 5 | 288 | 0.093 |
| GBR | n_estimators, learning_rate, max_depth | 400, 0.05, 5 | 288 | 9.5171 |
| SVR | Kernel, C, ε | RBF, 100, 0.01 | 288 | 12.1877 |
| MLP | hidden_layer_sizes, activation, solver, learning_rate_init | (128, 64), ReLU, Adam, 1 × 10−3 | 288 | 7.1446 |
| ELM | n_hidden, activation_func | 500, sigmoid | 288 | 1.4033 |
| XGB | n_estimators, max_depth, learning_rate, subsample | 500, 6, 0.05, 0.8 | 288 | 0.055 |
| LSTM | hidden_units, layers, dropout, optimizer, learning_rate, epochs | 128, 2, 0.2, Adam, 1 × 10−3, 30 | 288 | 133.0592 |
| CNN_ BiLstm | CNN filters, kernel_size, BiLSTM units, layers, dropout, epochs | 64, 3, 128, 2, 0.2, 30 | 288 | 183.4738 |
| CNN_BiLstm_Attention | Same as CNN_BiLstm, attention heads, epochs | -, 8, 30 | 288 | 80.389 |
| TCN | dilated causal filters, kernel size, dilation rates, dropout, optimizer, learning_rate, epochs | 64, 3, [1,2,4,8], 0.2, Adam, 1 × 10−3, 30 | 288 | 758.939 |
| Transformer | d_model, n_heads, e_layers, d_layers, d_ff, dropout, positional encoding, optimizer, earning_rate, epochs | 128, 8, 2, 1, 256, 0.1, sine, Adam, 1 × 10−4, 30 | 288 | 483.192 |
| CNN_ BiLstm_KAN | Same as CNN_BiLstm, KAN basis functions, polynomial order, λ_reg, epochs | -, 16, 3, 1 × 10−4, 30 | 288 | 436.6235 |
| Weather Type Label | Sunny-Like | Cloudy Day | Rainy Day | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 |
| SVR | 10.72% | 4.86% | 84.97% | 11.23% | 7.99% | 75.73% | 13.92% | 6.25% | 84.46% |
| ELM | 10.67% | 9.41% | 86.93% | 11.61% | 7.85% | 79.13% | 12.08% | 8.77% | 85.47% |
| KNN | 11.85% | 8.15% | 84.46% | 13.12% | 8.44% | 80.79% | 11.45% | 9.65% | 86.27% |
| XGB | 9.87% | 4.17% | 89.41% | 12.16% | 8.73% | 82.37% | 10.91% | 4.74% | 86.45% |
| LSTM | 9.99% | 7.59% | 89.03% | 9.59% | 7.17% | 88.55% | 9.69% | 5.73% | 89.15% |
| TCN | 7.32% | 6.68% | 88.91% | 8.15% | 6.92% | 88.43% | 8.98% | 4.82% | 89.23% |
| Transformer | 6.17% | 5.73% | 90.37% | 7.98% | 6.76% | 90.93% | 9.02% | 5.59% | 87.71% |
| CNN_BiLstm_KAN | 6.03% | 5.13% | 91.12% | 7.74% | 6.64% | 91.42% | 8.64% | 5.46% | 89.32% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Yang, M.; Che, J.; Xu, W.; He, W.; Wu, K. Distributed Photovoltaic Short-Term Power Forecasting Based on Seasonal Causal Correlation Analysis. Appl. Sci. 2025, 15, 11063. https://doi.org/10.3390/app152011063
Wang Z, Yang M, Che J, Xu W, He W, Wu K. Distributed Photovoltaic Short-Term Power Forecasting Based on Seasonal Causal Correlation Analysis. Applied Sciences. 2025; 15(20):11063. https://doi.org/10.3390/app152011063
Chicago/Turabian StyleWang, Zhong, Mao Yang, Jianfeng Che, Wei Xu, Wei He, and Kang Wu. 2025. "Distributed Photovoltaic Short-Term Power Forecasting Based on Seasonal Causal Correlation Analysis" Applied Sciences 15, no. 20: 11063. https://doi.org/10.3390/app152011063
APA StyleWang, Z., Yang, M., Che, J., Xu, W., He, W., & Wu, K. (2025). Distributed Photovoltaic Short-Term Power Forecasting Based on Seasonal Causal Correlation Analysis. Applied Sciences, 15(20), 11063. https://doi.org/10.3390/app152011063







