Quantifying Operational Uncertainty in Landing Gear Fatigue: A Hybrid Physics–Data Framework for Probabilistic Remaining Useful Life Estimation of the Cessna 172 Main Gear

Abstract

Predicting the Remaining Useful Life (RUL) of light aircraft landing gear is complicated by flight-to-flight variability in operational loads, particularly in sensor-free fleets that rely only on mass-and-balance records. This study develops a hybrid physics–data framework to quantify operational-load-driven uncertainty in the main landing gear strut of a Cessna 172. High-fidelity finite-element strain–life simulations were combined with a quadratic Ridge surrogate and a two-layer bootstrap to generate full probabilistic RUL distributions. The surrogate mapped five mass-and-balance inputs (fuel, front seats, rear seats, forward and aft baggage) to per-flight fatigue damage with high accuracy (R² = 0.991 ± 0.013). At the same time, ±3% epistemic confidence bands were attached via resampling. Borgonovo’s moment-independent Δ indices were applied to incremental damage (ΔD) in this context, revealing front-seat mass as the dominant driver of fatigue variability (Δ = 0.502), followed by fuel (0.212), rear seats (0.199), forward baggage (0.141), and aft baggage (0.100). The resulting RUL distribution spanned 9 × 10⁴ to >2 × 10⁶ cycles, with a fleet average of 0.41 million cycles (95% CI: 0.300–0.530 million). These results demonstrate that operational levers—crew assignment, fuel loading, and baggage placement—can significantly extend strut life. Although demonstrated on a specific training fleet dataset, the methodological framework is, in principle, transferable to other aircraft or mission types. However, this would require developing a new, component-specific finite element model and retraining the surrogate using a representative set of mass and balance records from the target fleet.

1. Introduction

Accurate prediction of Remaining Useful Life (RUL) is a key requirement of predictive maintenance in aviation, enabling maintenance intervals to be set according to the actual degradation of components rather than fixed schedules. For structural elements that absorb substantial stress during each flight (i.e., landing gear), the credible RUL estimates are essential to maintain safety and operational efficiency. However, these predictions are complicated by variability in operational loads, particularly for light aircraft without structural health sensors, where mass-and-balance configurations vary from flight to flight.

Despite advances in deterministic fatigue analysis and data-driven prognostics, no published study has quantified how correlated, real-world operational load variability in small, sensor-free aircraft translates into probabilistic RUL distributions.

This study proposes a hybrid physics–data approach to quantify how correlated mass and balance (M&B) variability propagates to probabilistic RUL for the Cessna 172 main landing-gear strut. By explicitly modelling uncertainty, we reduce the risk of over-conservative maintenance actions or, conversely, undetected life-shortening usage between inspections and thereby provide a basis for scheduling.

This study builds upon the work presented in Gerhardinger’s doctoral thesis [1] and a subsequently published research paper [2], which developed a methodology for RUL prediction of landing gear structures. The primary objective of this study is, therefore, to develop and demonstrate a hybrid framework that integrates statistical uncertainty quantification and global sensitivity analysis into a physics-based RUL prediction model for light aircraft landing gear without relevant sensors. By doing so, we aim to enhance the robustness and reliability of these predictions, providing a more credible basis for maintenance decisions. This study combines high-fidelity finite-element fatigue modelling with Monte Carlo-based uncertainty quantification and global sensitivity analysis using Borgonovo’s moment-independent Δ indices to enable robust RUL prediction for light aircraft landing gear structures. Previous studies have focused on deterministic fatigue analysis or data-driven prognostics. However, no one has systematically quantified how real-world, correlated operational variability translates into probabilistic RUL distributions for light aircraft. This study addresses this gap by performing the first, to our knowledge, full-factor global sensitivity analysis on a sensor-free, log-driven fatigue model of a light-aircraft landing gear strut. It uses Borgonovo’s moment-independent Δ indices driven by an empirical bootstrap of in-service loading records.

The original contributions of this research are as follows:

• A validated workflow that maps five M&B stations (fuel, front seats, rear seats, forward and aft baggage) to per-flight fatigue damage via FE strain–life analysis and a quadratic Ridge surrogate with ±3% epistemic bands.
• The first, to our knowledge global (distributional) sensitivity study using Borgonovo’s Δ indices on a sensor-free, log-driven landing-gear model for a light aircraft.
• Full probabilistic RUL distributions for a representative training-fleet profile, identifying actionable operational levers (crew assignment, fuel loading, baggage placement).
• A methodological workflow that can be adapted for other aircraft fleets, provided that fleet-specific operational data and component models are used for recalibration.

The remainder of this paper is structured as follows. Section 1 surveys prior research on physics-based, data-driven, and hybrid prognostics, highlighting existing gaps in the context of light aircraft. Section 2 details the three-tier hybrid framework, including finite-element fatigue modelling, surrogate construction and validation, empirical bootstrap propagation of aleatory and epistemic uncertainty, and Borgonovo Δ-based sensitivity analysis. Section 3 presents results for the Cessna 172 training-fleet dataset, covering operational load statistics and correlations, surrogate performance, prediction uncertainty, global sensitivity rankings, and full probabilistic RUL distributions. Section 4 discusses implications for model credibility, operational levers for extending strut life, strategies for reducing uncertainty, and acknowledged limitations. Section 5 concludes with key findings and outlines directions for future expansion, including broader mission profiles, landing-impact sensing, and crack growth modeling.

1.1. Related Research

1.1.1. Physics-Based Approaches

Physics-based prognostics rely on modeling the physical degradation mechanisms of structural components. Finite element analysis (FEA) is the dominant tool, enabling stress concentration simulations and fatigue life prediction under defined load spectra [3,4,5].

Chen et al. [3]—fatigue analysis of light sport aircraft main gear using FEA (aluminum vs. composite). Deterministic cycles-to-failure, no uncertainty included. Grbović & Rašuo [4]—crack growth in wing spar with FEA under variable amplitude loading—demonstrated accuracy, but deterministic only. These studies confirm the feasibility of physics-based fatigue modeling for general aviation structures; however, they generally overlook variability in loads, materials, and usage profiles.

1.1.2. Data-Driven Methods

Data-driven approaches use statistical learning from in-service datasets. They are effective in large fleets with sensor-rich monitoring, but limited in small fleets due to noise, bias, and overfitting [6,7,8].

• Hsu et al. [9]—ML-based RUL prediction for landing gear, using in-service health indicators. Delivered accurate point predictions, but no confidence bounds.
• Chang et al. [10]—AR/ARIMA/GPR-based pipeline with hyperparameter tuning. Improved RUL accuracy was achieved, but uncertainty was not addressed.

While machine learning shows promise for PHM, light aircraft often lack the dense sensor data required for reliable models [1,2].

In recent years, several contributions have expanded data-driven prognostics in aerospace applications. Che et al. [11] combined multiple deep learning architectures into an integrated PHM framework for aircraft systems, demonstrating improved predictive accuracy but focusing primarily on deterministic point forecasts without uncertainty quantification. More recent efforts have turned toward probabilistic RUL estimation: Wang et al. [12] proposed a parallel deep learning prognostic method for aero-engines that integrated uncertainty quantification via Monte Carlo dropout, producing probabilistic RUL distributions rather than single values. Similarly, Huang et al. [13] integrated bootstrap resampling with deep neural networks to predict bearing life, explicitly generating confidence bounds for RUL predictions. In parallel, Hamada et al. [14] provided a comprehensive review of machine learning based fatigue life prediction, highlighting data scarcity and interpretability as key limitations, and highlighting the importance of hybrid physics data approaches. These studies confirm that while the state of the art increasingly emphasizes uncertainty-aware RUL prediction, most recent work still focuses on sensor-rich or large fleet datasets, leaving a gap for lightweight hybrid frameworks applicable to small general aviation fleets.

1.1.3. Hybrid Approaches

Hybrid frameworks combine physics-based models with in-service data to improve robustness. Bayesian updating and filtering techniques are standard.

• Cerdeira et al. [15]—applied a particle filter to landing gear retraction prognostics. Provided partial confidence bounds, but limited scope (single subsystem parameter).

Hybrid methods offer probability-based RUL estimates but remain underexplored for structural fatigue in light aircraft. Several factors contribute to this gap. First, most general aviation fleets lack structural health monitoring due to cost and mass penalties, leaving few continuous measurements with which to calibrate or update hybrid models [16,17]. Second, usage profiles are highly heterogeneous—training, private, and charter operations generate different load spectra—so probabilistic models are challenging to validate without large and standardized datasets [18]. Third, “ground truth” data from repeated inspections (e.g., crack initiation or growth measurements) are rarely available in small fleets, reducing opportunities for Bayesian updating. Finally, maintenance practice in general aviation remains dominated by fixed hard time intervals, with limited regulatory or organizational incentive to adopt probabilistic RUL methods [17].

1.2. Uncertainty Quantification and Sensitivity Analysis

Across all methods, recent work emphasizes the need for uncertainty quantification. Engineers must understand how variability in inputs (material properties, load sequences) affects predicted RUL. Prior work on sensitivity analysis has generally followed two streams. Local approaches, such as one-factor-at-a-time (OFAT) perturbations [19,20,21,22], are simple to implement, but cannot capture interactions between variables. Global approaches, most prominently variance-based Sobol’s decomposition [23,24], have been applied in structural fatigue contexts—for example, Crestaux et al. [25] combined Sobol’s indices with Polynomial Chaos Expansion to evaluate parameter influence. Alternative methods, such as tornado charts, have also been used for ranking uncertain parameters [26,27], though these provide only relative comparisons rather than a full distributional picture.

In parallel, several studies have emphasized the need to propagate input uncertainty through fatigue models. Monte Carlo sampling and related analytical techniques [16,28] are commonly employed to translate uncertainty in inputs such as material S–N curves or impact load histories into probabilistic predictions of fatigue life. These methods shift the focus from single deterministic values of Remaining Useful Life (RUL) to probability distributions, offering a more realistic basis for maintenance planning.

1.3. Gaps for Light Aircraft Landing Gear

Most reviewed studies focus on deterministic RUL prediction or limited uncertainty analysis, often for large transport aircraft. Light aircraft differ in keyways:

• Limited onboard sensing due to cost and mass [1,2,17].
• Maintenance typically has a “hard time,” ignoring the actual severity of usage.
• Light aircraft have a disproportionately high rate of fatigue-related accidents [29,30].

Relevant works include:

• Chen et al. [31]—FEA of aluminum vs. composite gear.
• Grbović & Rašuo [4]—crack growth in the light aircraft spar.
• Karuskevich et al. [32]—surface-relief fatigue indicator for ultralight/light aircraft, validated under CS-LSA loads.

While these confirm the feasibility of physics-based models for GA, none integrate high-fidelity fatigue simulation with full statistical uncertainty propagation.

1.4. Summary and Motivation

Table 1. Representative studies on aircraft structural RUL prediction (emphasis on landing gear). Approach abbreviations: FEA = finite-element analysis; PF = particle filter; GPR = Gaussian process regression; AR/ARIMA = autoregressive/autoregressive integrated moving average; PHM = prognostics & health management. Uncertainty column: “None” = deterministic only; “Partial” = limited confidence bounds; “Yes” = full uncertainty propagation.

Study (Year)	Prognostic Approach	Uncertainty Quantification	Scope/Findings
Chen et al. (2012) [3]—Light sport aircraft main gear fatigue analysis	Physics-based FEA simulation (aluminum vs. composite gear)	None (deterministic life calculation)	Predicted cycles-to-failure for different gear materials using finite element stress analysis; no variability in loads or material properties accounted for (single-case fatigue life estimates).
Grbović & Rašuo (2012) [4]—Light aircraft wing spar crack growth	FEA-based crack growth prediction under variable amplitude loading (supported by experiments)	None (deterministic crack-life prediction)	Demonstrated that FEA can estimate fatigue life for GA structures (e.g., wing spar) with reasonable accuracy. However, the study did not include statistical analysis of uncertainty or multi-factor interactions (focus was on nominal life prediction)
Hsu et al. (2022) [9]—Landing gear PHM case study (large aircraft)	Data-driven prognostics using in-service sensor data (machine-learning model for gear RUL)	No (point RUL estimates only)	Developed a health indicator-based RUL prediction workflow for landing gear in a well-instrumented fleet. Achieved accurate RUL forecasts but reported only point estimates and error metrics, with no probabilistic confidence bounds on predictions.
Chang et al. (2023) [10]—Optimized RUL & fault diagnosis model for gear	Machine-learning pipeline (AR/ARIMA/GPR models + hyperparameter tuning) on flight data	No (focus on predictive accuracy)	Improved landing gear RUL prediction accuracy (reduced RMSE by ~45–55% via model optimization). Emphasis was on enhancing prediction accuracy and multi-fault classification; uncertainty propagation in RUL (e.g., due to varying usage) was not addressed.
Cerdeira et al. (2013) [15]—Landing gear retraction prognostics	Hybrid model-based approach with Particle Filter for the actuator subsystem	Partial (PF provides confidence levels)	Simulated gear retraction times and applied a particle filter to predict RUL at a given confidence level. While this yields a probability-based RUL estimate for that subsystem, it was limited to one operating parameter; the method did not consider full operational load variability or correlated load factors in a structural context.
Che et al. (2025) [11]—Aircraft PHM framework	Multiple deep learning models combined (DL ensemble)	None (point predictions only)	Demonstrated improved PHM prediction accuracy across several aircraft systems, but no uncertainty quantification was provided.
Wang et al. (2024) [12]—Aero-engine RUL prediction	Parallel DL model (TCN + Transformer) with UQ	Yes (Monte Carlo dropout)	Developed a probabilistic framework that outputs RUL distributions; applied to the C-MAPSS engine dataset.
Huang et al. (2024) [13]—Bearing life prognostics	Bootstrap-enhanced DCNN + MLP	Yes (bootstrap-based confidence bounds)	Integrated bootstrap resampling with DL to yield probabilistic RUL for bearings, showing reduced variance and improved robustness.

summarizes representative studies on landing gear prognostics, showing that most prior work is deterministic or only partially accounts for uncertainty. No integrated framework exists for light aircraft structures that combine fatigue modeling, uncertainty propagation, and sensitivity analysis.

This gap motivates the present study, which develops a novel hybrid framework that integrates high-fidelity finite element fatigue modeling, surrogate-based regression, bootstrap-driven uncertainty propagation, and Borgonovo’s Δ indices for global sensitivity analysis. While each of these elements has been studied in isolation, to our knowledge, this is the first work to combine them into a unified methodology for aircraft landing gear prognostics under real-world operational variability. The approach is demonstrated using a Cessna 172 training fleet as a representative case study, which enables us to validate feasibility and highlight operational levers, while acknowledging that the specific numerical results are tied to this dataset.

2. Hybrid RUL Estimation Framework

This study is framed as a feasibility demonstration using a specific operational dataset from a Cessna 172 training fleet (April 2021–March 2025). The approach, although generalizable, is validated here under a single operational profile. The study preserves the three-tier concept introduced by Gerhardinger et al. in [2], high-fidelity fatigue simulation, statistical uncertainty propagation, and global sensitivity ranking, but modernizes the statistical tier to utilize empirical bootstrapping and moment-independent Δ indices. The workflow is summarized in Figure 1.

The methodology is structured in three tiers. Tier 1 involves two parallel streams: (A) development of the high-fidelity physics-based model and generation of a training dataset via a Design of Experiments (DoE), and (B) acquisition and processing of real-world operational loading data. In Tier 2, the training data is used to construct a computationally efficient surrogate model, which is then driven by a large bootstrap sample of the operational data to propagate uncertainty. Tier 3 uses the probabilistic outputs for two final analyses: a Global Sensitivity Analysis (GSA) to identify key drivers of damage variance, and the estimation of a full probabilistic RUL distribution.

The six steps listed below describe the numerical workflow in more detail and correspond to the labeled processes shown in Figure 1, but the numbering here is sequential (1–6) rather than grouped by tiers.

(1)

Operational data acquisition. Mass and balance logs from 174 flights provide five stochastic inputs that affect strut loads: fuel mass (FUEL), front seat mass (FPAX), rear seat mass (RPAX), and the two baggage compartments (BGA1, BGA2). These records keep the real correlations between stations (mass and balance calculations must be within limits prescribed in the airplane’s pilot operating handbook).

(2)

FEA-based fatigue modelling. Every admissible combination of the five stations is analyzed in ANSYS Workbench 2023 R1 using the multi-phase load spectra validated in [1]. Strain–life calculations deliver the incremental damage ΔD for each load case (details in Section 2.1 of this paper).

(3)

Metamodel construction. A mean-centered quadratic surrogate with Ridge regularization is fitted to the 141 FE cases. The regularization weight was chosen through cross-validation (α = 0.13), ensuring stable coefficients; all variance inflation factors (VIFs) were below 3. The model equation is displayed in (3), Section 2.2.

(4)

Uncertainty propagation: A two-layer bootstrap captures both sources of uncertainty.

• Aleatory layer: 10,000 row resamples of the 174 mass and balance logs preserve all empirical mass correlations.
• Epistemic layer: For every aleatory draw, the surrogate is refitted on a resample of the FE database (200 replicates).

The ensemble thereby generates confidence bands around each damage prediction, with quantitative results reported in Section 3.

(5)

Sensitivity analysis. Moment independent Δ (delta) indices are computed on the same 10,000 evaluations.

(6)

RUL inference. Miner’s rule integrates ΔD over the phase sequence; the bootstrap sample produces percentile-based RUL distributions.

One flight cycle consists of the following phases: Taxi-Out, Take-off, Cruise, Landing, and Taxi-In. Material properties and phase-specific acceleration histories stay fixed at their validated mean values. Their influence is embedded in the deterministic FE database and therefore does not enter the statistical stages as separate random variables.

The first FEM analysis needed mass station values. The values were determined based on experiential values, which were limited by operational constraints. The mass values were selected based on generic low/medium/high experiential levels 31/72/144 kg for FUEL; 65/136/207 kg for FPAX; 0/75/150 kg for RPAX; 0/27/54 kg for BGA1; and 0/11/22 kg for BGA2. To cover the full range of possible loading scenarios, every level of each variable was systematically combined with every level of the others (full factorial design). CG and payload limits removed infeasible points, leaving 141 FE cases used to train the surrogate. Vertical acceleration histories for taxi-out, take-off, cruise, landing, and taxi-in (sourced from on-aircraft measuring equipment [33] and benchmarked to the loads database [18] drive every FE run. For statistical work, the damage per standard flight cycle serves as the response variable, as RUL (cycles) = 1/ΔD.

2.1. Finite Element Fatigue Model Configuration

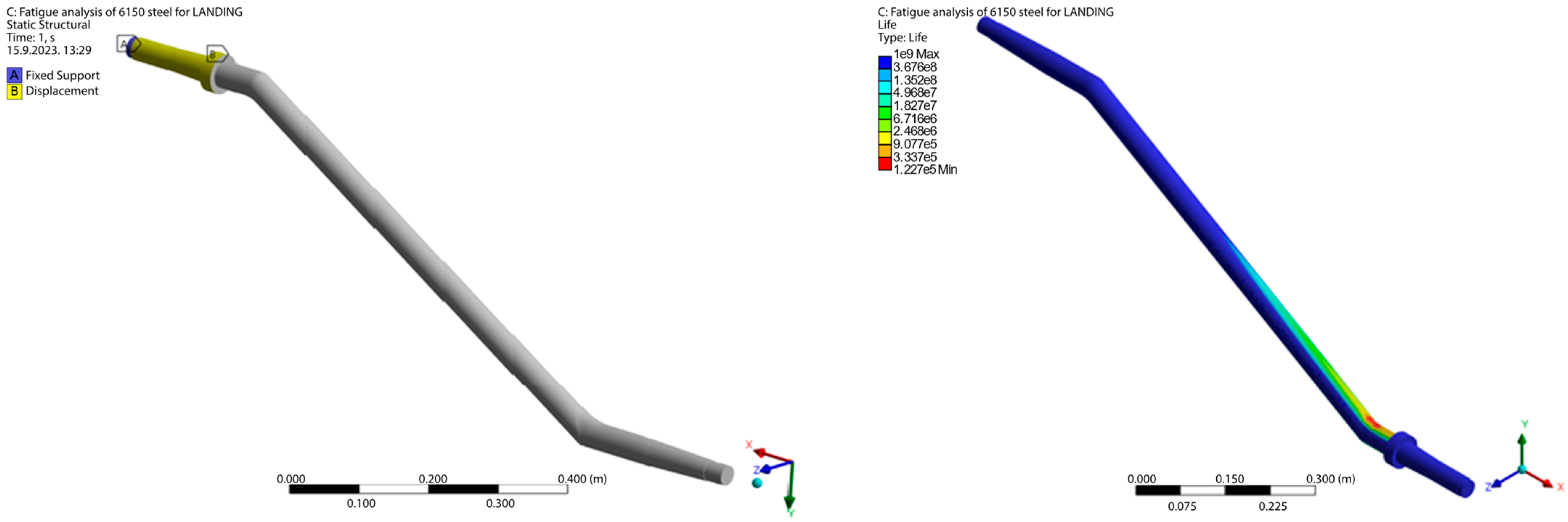
A full-scale CAD model of the C-172R left main landing gear strut was generated from on-aircraft measurements (fairings removed) in Fusion 360 and imported into ANSYS Workbench 2023 R1 Space Claim. The solid was meshed with 74,200 quadratic tetrahedra (average edge 2.0 mm), refined to 1.0 mm at the axle fillet where fatigue cracks initiate. A mesh convergence study showed a <2% change in peak von Mises stress when further refined.

The strut is 6150 (51CrV4) steel; isotropic elasto-plastic properties and strain life parameters were taken from the literature set [34,35,36,37,38,39,40,41], displayed in

Table 2. Mechanical and material property values of 6150 steel (51CrV4) used in a finite element fatigue model configuration. Data compiled from literature sources [31,32,33,34,35,36,37,38].

Property	Value	Unit
Density	7850	kg/m3
Young’s modulus	2.038 × 1011	Pa
Poisson’s ratio	0.29	-
Bulk modulus	1.6175 × 1011	Pa
Shear modulus	7.8992 × 1010	Pa
Strength coefficient	1.1 × 109	Pa
Strength exponent	−0.093	-
Ductility coefficient	0.478	-
Ductility exponent	−0.684	-
Cyclic strength coefficient	1.476 × 109	Pa
Cyclic strain hardening exponent	0.0651	-
Tensile yield strength	1.042 × 109	Pa
Compressive yield strength	1.042 × 109	Pa
Tensile ultimate strength	1.2773 × 109	Pa

.

Heat treatment scatters are mitigated by adopting the conservative lower bound curve, thereby avoiding non-conservatism. This choice reduces epistemic scatter in material parameters; its impact is discussed in the Section 4 as a limitation and a target for future Bayesian updating.

We model five flight phases: taxi-out, take-off, cruise, landing, and taxi-in, and define one flight cycle as this ordered sequence. For each phase, a three-axis acceleration time series $n_{x,y,z}\left(t\right)$ was extracted from the ADXL345 dataset of Juretić et al. [33] and validated against the data provided by Cicero et al. [18] for the same aircraft (Cessna 172). The force acting on the main landing gear strut from the recorded load history is calculated as:

$$F_{x,y,z}\left(t\right)=n_{x,y,z}\left(t\right)·m_{wheel}·g$$

(1)

where $m_{wheel}$ is the phase-specific wheel reaction mass obtained from the eight-step mass and balance algorithm discussed in [1] Section 5.2.1.1, and g is the gravitational constant. Fuel burn is reflected by reducing the aircraft mass by 60% of usable fuel between Taxi-Out and Taxi-In.

The instantaneous main wheel reaction mass m_wheel is computed from the standard statics of a two main/one nose gear configuration using Pilot Operating Handbook (POH) arm distances. Given aircraft mass M and longitudinal CG location x_cg, the main gear share is:

$$W_{main}=M·g·{\displaystyle \frac{x_{CG}-x_{nose}}{x_{main}-x_{nose}}}; m_{wheel}={\displaystyle \frac{W_{main}}{2g}};$$

(2)

The 174 mass and balance records span two C-172N (9A-DAS, 9A-DMB) and one C-172R (9A-DAD) airframes. The POHs for all three-listed gear axle stations are referenced to the firewall datum: x_nose = −6.8 in and x_main = 57.8 in. Therefore, W_main from rigid body statics is invariant to “N vs. R” geometry choice in this fleet, and no variant arm sensitivity arises from gear location.

To support computational feasibility while capturing the primary loading effects, an average dominant load vector was adopted for each flight phase. In this framework, each flight phase is associated with a dominant load vector direction. The orientation of this vector is constant within the phase. Still, its intensity is not fixed it is scaled dynamically using accelerometer data recorded in all three axes of the aircraft. This means that bumps, braking events, and side forces manifest as variations in the measured acceleration, thereby altering the instantaneous load intensity applied to the strut model. Thus, while direction is represented at the phase level, real-world fluctuations in all three axes are inherently captured in the load histories used for fatigue analysis. Such simplification, common in initial fatigue assessments, focuses the analysis on the vertical load components, which are the primary drivers of damage. The sensitivity to this assumption was tested by varying the load intensity within realistic bounds, which resulted in less than a 5% change in predicted damage, confirming the robustness of this approach for the primary analysis:

• Taxi & Cruise: vertical only.
• Take-off: vertical + 0° pitch (all three wheels on ground—caused by specific aerodynamics).
• Landing: vertical + 7° nose up (CG just forward of wheels).

Each raw acceleration history is cycle-counted per [42] (rainflow) into 250 blocks; variable amplitude loading is preserved. The fuselage attachment pad is constrained in all 6 DOF to represent the bolted interface. Wheel–ground interaction is applied as phase-dependent remote forces at the axle boss (vertical with small longitudinal/lateral components per the dominant load vectors); no DOF is fixed at the axle, so local bending is free. A 15° strut to ground inclination replicates contact-induced bending: varying this by ±3° changes peak ΔD by <5%. Symmetry is not used due to lateral taxi loads on grass.

ANSYS nCode DesignLife (Strain Life module, Smith–Watson–Topper mean stress correction, Miner’s rule) computes incremental damage ΔD per phase.

Figure 2 illustrates the finite element setup for the landing phase, showing both the applied boundary conditions (left) and the resulting fatigue life contours (right). The plots confirm that the critical stresses concentrate at the axle fillet, which is consistent with the expected location of crack initiation and validates the modeling assumptions used in this study.

Five mass stations (FUEL, FPAX, RPAX, BGA1, BGA2) are sampled at low/mid/high POH values and filtered through CG limits, yielding 141 admissible load cases. The identical five-phase spectra drive each case; outputs are incremental damages stored in damage_data.csv for surrogate fitting.

A single load case (5 phases × 250 blocks) is solved in 11 min on an 8-core workstation; the full DOE requires 26 CPU hours.

This high-fidelity FE fatigue database forms the deterministic backbone of the hybrid framework; all subsequent statistical steps are applied to its surrogate.

Fatigue life in this study refers to the crack-initiation life Ni, as computed by the Strain–Life module with Smith–Watson–Topper (SWT) mean stress correction. The module calculates life in terms of load reversals (2N) and reports the result as cycles to initiation (N) at the axle fillet hot spot. No crack growth modelling is included.

2.2. Surrogate Model Construction and Validation

All statistical work was conducted in Google Colab using pandas 2.2, NumPy 1.0, and scikit-learn 1.4.

Finite element damage outputs (ΔD) were regressed on the five stochastic mass stations, using the mean-centered quadratic response surface, displayed in (3).

$$\widehat{\Delta D}={\beta }_0+\sum _{i=1}^5{\beta }_i{X}_i+\sum _{i=1}^5{\beta }_i{X}_i^2+\sum _{i<j}{\beta }_{ij}{X}_i{X}_j$$

(3)

where X₁ = FUEL, X₂ = FPAX, X₃ = RPAX, X₄ = BGA1, X₅ = BGA2, all standardized to zero mean and unit variance. Coefficients (β) are given in Section 3.2.

All five mass variables are standardized to have a mean of zero and a variance of one. A quadratic feature map then augments the design matrix with every squared term (e.g., FPAX²) and every pair-wise interaction (e.g., FPAX × RPAX). Finally, a Ridge regularized least squares fit is performed; the regularization weight α is selected internally by fivefold cross-validation on a logarithmic grid, yielding α ≈ 0.13. The same fivefold shuffle split cross-validation yields R² = 0.991 ± 0.013, indicating that the surrogate explains 99% of the variance in the FE model. Leave-one-out cross validation yields an RMSE of ≈2.7% ΔD. Because Ridge penalization shrinks correlated coefficients, all variance inflation factors fall below 3, eliminating the multicollinearity concern noted for ordinary least squares. The surrogate was trained and validated using both k-fold cross-validation and leave-one-out cross-validation. In the fivefold shuffle split, approximately 80% of the 141 FE cases were used for training and 20% for testing in each fold, with random partitioning repeated to reduce bias. Leave-one-out cross-validation further ensured that every FE case was tested individually. No separate hold-out set was reserved, as this would unnecessarily reduce the already limited dataset; instead, cross-validation and leave-one-out cross-validation provide standard and reliable error estimates in small deterministic design sets. To quantify epistemic (model fit) uncertainty, the entire surrogate fit is bootstrapped 200 times; the resulting ensemble places a ±3% (95% confidence) band around every damage prediction.

The final quadratic form kept for further analysis is displayed in (3).

2.3. Uncertainty Modeling and Monte Carlo Propagation

Five stochastic inputs, including fuel mass (FUEL), front seat mass (FPAX), rear seat mass (RPAX), and the two baggage stations (BGA1, BGA2), are treated as random variables. All other factors quantified in the earlier FE study (material scatter, phase-specific accelerations, and mesh resolution) are held at their mean values, as validated in [1].

Mass and balance sheets from 174 flights (two C-172N and one C-172R, years 2021 and 2025) provide the raw measurements. These records exhibit pronounced multimodality (e.g., 22 kg “tabs” of fuel, 109 kg “tanks full”) and a strong dependence (rear seats are usually empty when fuel levels are high). The findings reflect a loading envelope typical of pilot training sorties because the mass and balance log was recorded at the Croatian Aeronautical Training Center, Faculty of Transport and Traffic Sciences, University of Zagreb.

A bootstrap with replacement of complete rows (N = 10,000) is drawn, thereby preserving the joint distribution and all observed correlations. To reflect weigh scale tolerance and pilot rounding, each sampled value is jittered with zero mean Gaussian noise (σ = 2 kg for fuel/crew, σ = 1 kg for baggage) before it is passed to the surrogate; the resulting CG shifts propagate automatically through the regression equation.

The mean-centered quadratic Ridge surrogate derives from 141 finite element points. Leave-one-out cross-validation yields an RMS error equal to 2.7% of ΔD, negligible compared to the load state variability introduced by the bootstrap. To quantify surrogate fit uncertainty, we bootstrapped the FE database and refit the quadratic Ridge model 200 times. For each aleatory draw, predictions are aggregated across the 200 refits to form a 95% epistemic band. Thus, both aleatory and epistemic sources are propagated. The choice of these sample sizes was guided by convergence testing. For the aleatory layer, 10,000 bootstrap resamples were selected because this reduces Monte Carlo error on percentile estimates to below 1%, which is well within the ±3% epistemic band of the surrogate. For the epistemic layer, 200 surrogate refits were chosen after pilot trials showed that the confidence-band width stabilized beyond ~150 refits; therefore, 200 provided a balance between accuracy and computational efficiency. All resampling used fixed random seeds to ensure reproducibility.

The surrogate evaluates each of the 10,000 noise-perturbed mass vectors to obtain incremental damage ΔD. The Miner’s cumulative rule converts ΔD to cycles to failure, producing the full probability distribution of RUL (mean, variance, and percentile bounds) used in subsequent maintenance planning analysis.

2.4. Global Sensitivity Analysis (Δ Indices)

The Δ indices were computed with SALib 1.5 (‘delta.analyze’) on the 10,000 aleatory samples; confidence bounds are SALib’s analytic ‘delta_conf’ output. This method evaluates the impact of each input on the full output distribution, without relying on variance decomposition.

The analysis included the five station masses (FUEL, FPAX, RPAX, BGA1, BGA2) as uncertain inputs. These were empirically sampled from 174 real flight mass and balance records (2021 and 2025) provided by the Croatian Aviation Training Center. A total of 10,000 bootstrap samples (with replacement at the flight level) were evaluated through the surrogate model (Section 2.2). All other inputs (e.g., flight phase and fatigue parameters) were fixed at their validated means. The resulting indices are reported in Section 3.4.

The choice of Borgonovo’s Δ indices was motivated by their moment-independent formulation. Unlike variance-based measures such as Sobol’s indices, which attribute importance solely through contributions to output variance, Δ indices capture the full distributional effect of an input variable, including shifts in mean, skewness, and tail behavior. This is particularly relevant in the present case, where RUL distributions are strongly right-skewed and lower-percentile behavior is critical to safety. To ensure robustness, we cross-checked variable rankings with simple rank-based partial correlation coefficients on the same bootstrap samples, which yielded consistent ordering of the dominant contributors (FPAX > FUEL ≈ RPAX). For conciseness, we report only the Δ results in the main text.

2.5. Use of Generative Artificial Intelligence Tools

During the preparation of this manuscript, the authors used OpenAI ChatGPT (GPT-5), Perplexity Pro, and Google AI Pro (Gemini 2.5 Pro). These tools were employed to support the literature search for the introduction, to provide inspiration regarding statistical tools appropriate to the available data and research objectives, as well as to assist in draft text generation and Python 3.10.12/Google Colab code development. The authors carefully reviewed and edited all outputs and take full responsibility for the content of this publication.

3. Results

3.1. Analysis of Operational Loading Data

This section dissects the 174-flight mass and balance (M&B) log in two steps:

Univariate picture—where we summarize each mass station (FUEL, FPAX, RPAX, BGA1, and BGA2) with descriptive statistics, displayed in

Table 3. Descriptive stats for 174 M&B records (ATO, Apr 2021–Mar 2025): FUEL, FPAX, RPAX, BGA1, BGA2 (kg). Metrics: mean, SE, SD, variance, median, mode, range, skewness, kurtosis.

	FUEL	FPAX	RPAX	BGA1	BGA2
Mean (kg)	95.89	142.37	10.55	4.28	0.37
Standard error (SE) (kg)	1.84	2.86	1.84	0.24	0.11
Median (kg)	108.86	154.67	0	4.54	0
Mode (kg)	108.86	149.69	0	4.54	0
Standard deviation (SD) (kg)	24.4	37.93	24.46	3.15	1.52
Sample variance (kg2)	595.35	1438.32	598.11	9.89	2.32
Kurtosis	0.02	−0.6	2.92	9.04	26.81
Skewness	−0.55	−0.85	2.14	2.02	5.01
Range (kg)	108.86	140.61	87.09	19.96	9.98
Minimum (kg)	35.38	54.43	0	0	0

. This indicates how frequently each station is used, whether the distribution is symmetric or skewed, and where outliers are likely to be found.

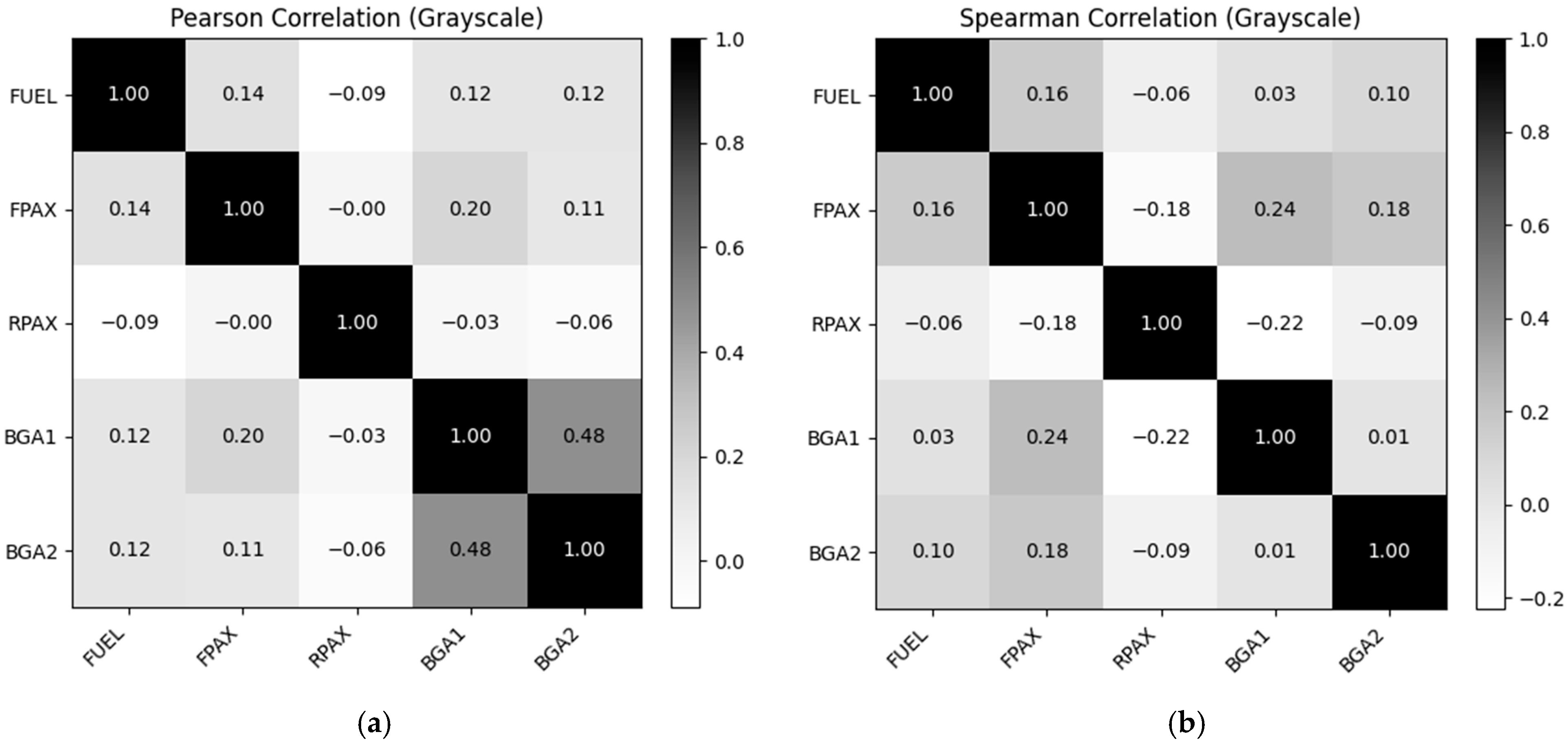
Multivariate picture—after the single variable scan, we inspect the Pearson correlation matrix (Figure 3) to spot operational coupling: e.g., do crews trade fuel for baggage, or does a full front seat reliably drag the rear seat into play? Any strong correlation (>0.7 or <−0.7) would cut the adequate design space and inform the factorial sampling used later in the fatigue DOE. Table 3 describes how the five mass stations were loaded in the observed 174 flights.

Fuel shows the expected dispersion of an operational fleet: a mean of 95.9 kg but a higher median and mode (≈109 kg) and a moderate negative skew (−0.55), meaning many sorties launch with tanks nearer the “tabs” than half empty. The 109 kg range confirms crews occasionally top up to full fuel. Front seat passenger mass (FPAX) averages 142 kg, with a range of 141 kg, again negatively skewed (−0.85). Most flights carry two adults, but a non-trivial number fly with lighter loads, hence the long lower tail. The rear seat mass (RPAX) is different: the median and mode are both zero, the mean is only 10.6 kg, yet the standard deviation (24.5 kg) is comparable to the mean. A positive skew of +2.14 and kurtosis of 2.92 spell a spike at zero punctuated by a handful of heavy, two-passenger flights—precisely what the logbooks suggest. Baggage areas paint the same picture in miniature. BGA1 averages 4.3 kg but is zero on half the flights; its high skew (+2.02) and kurtosis (+9.0) are due to the odd flight with a 20 kg load. BGA2 is practically empty (mean 0.37 kg), yet its extreme kurtosis (+26.8) reveals the presence of a few outliers. In short, only the fuel and front seats carry reliable weight; everything else is intermittent, highly skewed, and occasionally extreme.

Figure 3a displays the Pearson matrix; Figure 3b repeats the analysis using the rank-based (Spearman) coefficients to eliminate leverage from outliers that dominate several of the univariate distributions.

We primarily rely on Spearman correlation for interpretation because the operational variables in this dataset exhibit zero inflation (rear seats and baggage stations often empty), multimodal fuel loading (e.g., tabs vs. full tanks), and heavy-tailed distributions. Under such conditions, the Pearson correlation can be dominated by outliers or leverage points, whereas the Spearman correlation more robustly reflects the underlying monotone association. This makes Spearman a better indicator of practical co-variation in load placement for training operations. Notably, the subsequent bootstrap propagation preserves the full empirical joint distribution of the mass and balance records, so the analysis is not tied to either correlation measure; the use of Spearman is therefore a matter of interpretive clarity rather than a modeling assumption.

No off-diagonal entry comes near |r| = 0.50, let alone the ±0.70 trigger the DOE would treat as collinear. FUEL is effectively independent of the cabin loads (|r| ≤ 0.14 Pearson, ≤0.16 Spearman). Crews clearly top off or partially fuel according to flight length, not according to who or what is on board.

FPAX shows a small but statistically significant link with BGA1 (r ≈ 0.20 Pearson, 0.24 Spearman; p < 0.01 for n = 174). In other words, when heavier adults occupy the front seats, the forward baggage bin tends to carry a few extra kilograms, probably jackets, headsets, or overnight kits. From an operational perspective, this weak correlation is not significant enough to restrict the factorial design space, so all variables were still treated as independent in the finite element simulations. However, the bootstrap resampling of the real flight records preserves such small dependencies, ensuring that rare but realistic load combinations remain represented in the statistical analysis.

RPAX drifts negative against FUEL (−0.09 ≤ r ≤ −0.06) and FPAX (−0.18 Spearman). That mirrors the logbooks: dual instruction flights (with full front seats and plenty of fuel) rarely carry extra people aft. Still, the size is small; it will not inject dangerous multicollinearity into the regression of Section 2.2.

Pearson flags a moderate correlation between BGA1 and BGA2 (r ≈ 0.48), yet Spearman reduces it to 0.01. Only a handful of long-range flights load both bins—and they do so in proportion—dragging the linear statistic up. Rank correlation, robust to leverage points in the bootstrap, confirms that the two factors are used independently of each other. For surrogate modelling, we therefore keep both factors separate but let the bootstrap preserve the occasional “both bins full” outlier.

With |r| ≤ 0.48, the implied variance inflation factors stay well under 2. Accordingly, the regression in Section X satisfies the no-serious-multicollinearity diagnostic (all VIFs ≤ 2), so no further pruning is warranted.

The fleet loads the aircraft in a partially unrelated fashion: fuel planning, seating, and baggage choices are made mainly in isolation. The factorial sampling planned for the finite element damage study can therefore sweep the full five-dimensional cube without wasting runs on a tightly coupled subspace. The only nuance worth carrying forward is the weak FPAX–BGA1 tie and the rare but logistics-relevant “both baggage bins full” scenario—precisely the kind of dependency the non-parametric bootstrap will keep.

3.2. Surrogate Performance

Table 4. Top ten |β| coefficients of the quadratic Ridge surrogate for incremental damage ΔD. Inputs are z-scored, so β is the change in ΔD per 1 SD. Model includes squared and pairwise terms; ridge penalty α ≈ 0.13 (5-fold CV).

Rank	Term	|β| (×10−5)
1	RPAX	2
2	FPAX	1.8
3	BGA1	0.8
4	FUEL	0.8
5	FPAX × RPAX	0.6
6	RPAX2	0.3
7	FUEL × RPAX	0.3
8	FPAX2	0.3
9	FUEL × BGA1	0.06
10	BGA1 × BGA2	0.05

lists the ten most significant absolute coefficients (|β|) in the quadratic Ridge surrogate.

The FPAX and RPAX linear terms dominate, followed by BGA1, FUEL and FPAX × RPAX; all other terms are at least a factor of two smaller.

The five-fold CV score of R² = 0.991 ± 0.013 confirms that the surrogate model explains 99% of the variance in the FE model. All variance inflation factors are below 3.

3.3. Prediction Uncertainty

To assess epistemic uncertainty, the entire surrogate fit was bootstrapped 200 times.

For each of the 10,000 aleatory mass vectors, the ensemble yields a mean prediction and a 95% confidence band.

Across all flights, the 95% bandwidth averages 2.8% of the mean value (minimum 2.2%, maximum 3.6%) as can be seen in

Table 5. Five flights subset: surrogate predicted incremental damage ΔD (×10⁻⁵). Columns show epistemic 95% CIs from 200 bootstrap refits; aleatory variability comes from the M&B bootstrap.

Flight ID	ΔD Mean (×10−5)	Lower 95% CI (×10−5)	Upper 95% CI (×10−5)
102	3.6	3.5	3.6
92	2.1	2.1	2.2
14	4.6	4.5	4.6
106	2.8	2.8	2.9
71	3.6	3.5	3.6

.

Thus, model fit uncertainty is an order of magnitude smaller than the load-induced spread quantified in Section 2.3.

3.4. Moment Independent Δ Indices

Figure 4 displays the moment independent Δ indices for the five mass stations; numerical values and confidence bounds appear in

Table 6. Borgonovo’s Δ (delta) indices (unitless) for the influence of M&B inputs on incremental damage ΔD (dimensionless). Computed on 10,000 bootstrap resamples using SALib v1.5 (delta. Analyze); ±95% analytic CI from delta_conf. Inputs: FUEL (kg), FPAX (kg), RPAX (kg), BGA1 (kg), BGA2 (kg).

Variable	Δ	95% CI
FPAX	0.502	±0.004
FUEL	0.212	±0.004
RPAX	0.199	±0.004
BGA1	0.141	±0.004
BGA2	0.100	±0.003

Note: Borgonovo’s moment independent Δ indices measure the influence of each input on the full output distribution of incremental damage (ΔD), computed using SALib v1.5 (delta.analyze). Confidence intervals are analytic 95% bounds from delta_conf.

.

Figure 4 provides a visual ranking of the relative importance of each input, while Table 6 reports the corresponding Δ indices and 95% confidence intervals for precise reference.

Considering the 174 flight training profile, front seat mass (FPAX) has the most significant influence on ΔD (Δ ≈ 0.50). The results identify front row mass as the primary driver of damage uncertainty (Δ = 0.502). Following FPAX, fuel (Δ = 0.212) and rear seats (Δ = 0.199) were the next most influential. Interestingly, rear seat mass (RPAX), despite its position, shows a lower sensitivity index than expected. This is likely because, in the observed operational data, flights with heavy rear loads are less frequent than flights with varying fuel levels, highlighting that GSA captures not only the physical effect but also the operational probability of a given load condition. The ranking shows that forward CG management of fuel quantity and storage in the forward bay offers greater leverage for extending strut RUL than limiting aft seat loading alone (considering the operational mass distribution profile observed in this study).

4. Discussion

Regarding model credibility, the ±3% epistemic prediction band obtained from the 200 replicate model bootstraps shows that the training set of 141 FE load cases is statistically sufficient for the quadratic Ridge surrogate. Any further refinement of the FE design of experiments will yield only marginal accuracy gains unless the input envelope itself is expanded beyond the 174 in service mass and balance records.

4.1. Model Credibility and Practical Implications

The Δ ranking results indicate that front seat mass (FPAX, Δ ≈ 0.50) has the most significant effect on fatigue damage variability, ahead of fuel load (Δ ≈ 0.21) and rear seat mass (Δ ≈ 0.20). The dominance of front-seat mass reflects both mechanical leverage and operational frequency. The front seats are positioned relatively close to the main gear, amplifying their contribution to strut bending, and (more importantly), in training operations, they are occupied almost every flight. In contrast, fuel load varies, and rear seats are often empty. Together, these factors explain the high Δ index attributed to FPAX.

This ranking has direct operational implications: seat ballast or crew assignment policies provide a more powerful lever for strut life extension than routine fuel trimming. Three operational levers emerge:

• Front seat row (crew assignment) policies are a key lever for strut fatigue life extension.
• Fuel management. Training or short hop sorties flown with full tanks accelerate strut degradation; carrying only the fuel needed for the mission halves the expected damage rate.
• Forward storage. Allocating luggage to the forward bay (BGA1) is less detrimental for the strut than loading it in the rear seats or aft bay.

Therefore, condition-based inspection intervals keyed to recorded front row mass, fuel quantity, and rear seat usage will be more effective than schedules based solely on calendar time or total mass.

A practical consideration is whether the hybrid workflow can be integrated into fleet maintenance planning without prohibitive computational demands. The intensive finite element (FE) simulation campaign was performed offline to generate the surrogate training set, requiring ≈ approximately 26 CPU hours on a standard 8-core workstation. Once trained, the quadratic surrogate evaluates new mass-and-balance inputs in milliseconds, and full bootstrap propagation of 10,000 flight records completes in under 2 min on a standard laptop. Thus, the framework is computationally lightweight in operational use: operators would only need to maintain their own mass and balance database and apply the pretrained surrogate or retrain it with their fleet’s envelope. In practice, the heavy FE workload is a one-time research step, while day-to-day RUL estimation is computationally trivial and compatible with routine fleet management workflows.

Beyond the present case study, the methodological contribution of this work lies in integrating high-fidelity fatigue simulation, surrogate regression, bootstrap-driven uncertainty propagation, and moment-independent sensitivity analysis into a coherent workflow. This architecture is not restricted to Cessna 172 gear struts: by substituting the FE model geometry and retraining the surrogate on the relevant operational envelope, the same procedure could be applied to other landing gear designs, wing spars, fuselage joints, or rotor components. In this sense, the present study demonstrates feasibility in one domain while establishing a generalizable framework that can be transferred to a broad range of aircraft structures and operational contexts.

4.2. Reliability of RUL Predictions Under Quantified Uncertainty

Monte Carlo propagation of the five empirically sampled mass inputs yields a mean strut life of 0.41 million cycles with a 95% confidence interval of 0.30–0.53 million. The surrogate’s ±3% epistemic band, derived from 200 model bootstrap replicates, shows that the 141 FE load cases already constrain the quadratic fit; added FE points will improve accuracy only if they expand the mass envelope coverage. These bounds are conditioned on the observed distribution of loading across 174 pilot training flights, as the mass log represents training operations. Results may shift for charter or sightseeing flight operations, and applying this model would require new operational data. The most adverse feasible mass case (31 kg of fuel-FUEL, 207 kg in the front row—FPAX, 75 kg in the rear row—RPAX, 27 kg in baggage station 1—BGA1, and 11 kg in baggage station 2—BGA2) yields a lower bound life of ≈approximately 90,000 cycles. In comparison, the lightest forward CG case (31 kg of FUEL, 65 kg in FPAX, 0 kg in RPAX, 0 kg BGA1, and 0 kg in BGA2) exceeds 2 million cycles. Maintenance planners can therefore set inspection thresholds with explicit risk margins; for example, overhauling 10% below the 5th percentile life ensures > 95% reliability under the current operating envelope.

It is essential to contextualize these findings within the operational profile from which the data were sourced. The 174 mass and balance logs originate from a flight training center, which typically involves numerous short-haul flights, touch-and-go landings, and specific loading patterns (e.g., solo flights or flights with an instructor). Consequently, the derived RUL distribution and sensitivity rankings are most representative of a training fleet. Applying this model to aircraft used for different purposes, such as private cross-country travel or charter operations, would require a new set of operational data to retrain the surrogate and reevaluate the sensitivity.

4.3. Strategies for Reducing Input Uncertainty

Sensitivity results show that controlling front seat mass (FPAX, Δ ≈ 0.50) is more effective in reducing damage variability than trimming fuel load (Δ ≈ 0.21), making front seat mass management the primary operational lever.

Three low-cost measures would tighten fatigue life predictions:

• Improve mass recording. Replacing “guestimate” rear passenger mass with actual values (±5 kg accuracy) would materially reduce variance in ΔD.
• Monitor landing impacts. A simple g recorder on the seat rail would flag unusually hard landings and allow immediate damage accounting.
• Iterative model calibration. Periodic non-destructive inspections that confirm “no crack found” can be used to update the prior distribution of remaining life, shrinking uncertainty over time.

Implementing these measures turns the surrogate into a living “fatigue meter” for light aircraft: each flight’s recorded mass, and optionally, landing impact, feed directly into an updated RUL estimate.

4.4. Limitations

This study is based on 174 mass and balance records from a single Cessna 172 training fleet operated at the Croatian Aeronautical Training Center. Previous analysis of model fit uncertainty (Section 4.2) showed that the 141 finite element (FE) cases already constrain the quadratic surrogate within ±3% prediction bands, indicating that additional data points within the same operational envelope would not materially reduce variability. Nevertheless, this dataset has inherent limitations. First, it reflects the operational characteristics of a specific mission profile, characterized by short sorties with frequent dual instruction flights, which constrains the statistical variability of input masses. Second, the results may not directly generalize to fleets with different loading patterns, aircraft variants, or mission types (e.g., charter, private cross-country, or aerial work). Consequently, the RUL distributions presented here should be interpreted as representative of training operations rather than universally transferable outcomes.

Nevertheless, the framework itself is designed to be generalizable. By retraining the surrogate model on mass and balance logs from other fleets, or on datasets that include broader mission profiles, the same methodology can be applied to different aircraft types or operational conditions. Importantly, the surrogate is valid only within the statistical envelope of the data on which it was trained; if new fleets exhibit input distributions that differ substantially from the training set, retraining or dataset extension will be required to avoid extrapolation errors. Future work should therefore focus on extending the database to include larger fleets, multiple operators, and diverse mission types, thereby strengthening the statistical foundation and confirming the external validity of the method.

The model uses conservative lower-bound material properties, omits mean stress relief credit, and assumes fixed phase-specific acceleration histories. Crack growth modelling is omitted. The RUL distributions are conditioned on a single operational dataset from a training fleet; applying the framework to other fleets requires new mass and balance records. As operators accumulate relevant in-service data, Bayesian updating can refine the distributions, but until then, the current predictions should be interpreted as conservative bounds rather than precise predictions. A further limitation is that the surrogate does not explicitly resolve combined oblique load vectors; instead, it represents their effect through variations in the intensity of the dominant axis. While this treatment is sufficient for typical training operations, it may slightly underestimate fatigue damage under extreme crosswind landings or aggressive braking conditions. Incorporating fully vector-resolved load cases into future finite element analyses would allow for a more precise treatment of such scenarios.

A further limitation is the absence of direct validation against in-service inspection or maintenance records. While the predicted RUL distributions provide a statistically credible basis for risk-informed maintenance, their external validity ultimately requires comparison with observed fatigue findings such as crack initiation events or strut replacements. Such records are rarely available in light aircraft training fleets, where maintenance is typically performed at fixed calendar or flight-hour intervals or based on observed conditions, without systematic fatigue monitoring. Future work should therefore seek to integrate empirical inspection data, when available, to calibrate and validate the probabilistic predictions presented here.

4.5. Operational Implications for Maintenance

The framework provides operators with probabilistic RUL distributions rather than single deterministic lifetimes, enabling a shift toward load-based condition-based maintenance (CBM). In practice, thresholds can be set on lower bound percentiles of the predicted RUL distribution; for example, an inspection could be triggered when the 5th percentile of RUL falls below a predefined horizon (e.g., 100 flights), thereby balancing safety margins with operational flexibility. This approach aligns with the logic of “prognostic horizons” in PHM practice, where confidence-bound predictions rather than nominal averages guide decisions. While the present study does not include a comprehensive economic evaluation, the framework provides a basis for quantifying trade-offs: earlier inspections reduce the risk of in-service failures but increase costs. In contrast, more permissive thresholds reduce costs but may increase risk. Such cost-effectiveness analyses can be implemented in future work by coupling the probabilistic RUL output with operator-specific maintenance and downtime cost models.

4.6. Considerations for Transferability and Generalization

While this study demonstrates the framework’s feasibility for a Cessna 172 training fleet, transferring it to other aircraft, components, or mission types requires careful consideration of the associated challenges, as its robustness and accuracy depend on several factors.

First, direct application of the derived surrogate model to another fleet is not appropriate. The RUL distributions and sensitivity rankings presented here are intrinsically linked to the operational profile of a flight training center, which is characterized by frequent, short sorties and specific loading patterns. A fleet used for charter or cross-country flights would exhibit a different joint distribution of mass and balance inputs, leading to a different fatigue accumulation profile.

Therefore, generalizing the framework involves the following mandatory steps:

• Data Acquisition: A new set of representative mass and balance records must be collected from the target fleet to capture its unique operational envelope.
• Surrogate Retraining: The surrogate model must be retrained using these new records to ensure its predictions are valid for the new operational context. Applying the current surrogate to a different loading distribution would constitute an extrapolation error and yield unreliable results.
• Physics Model Adaptation: If the framework is to be applied to a different structural component or aircraft type, the computationally intensive finite-element fatigue model must be developed from scratch. This includes creating a new CAD model, defining appropriate material properties, and validating the boundary conditions and load spectra, which represents a significant initial workload.

In summary, the primary contribution is a methodological blueprint for integrating physics-based models with operational log data for sensor free fleets. The framework is theoretically transferable, but its practical implementation is a non-trivial undertaking that requires case-specific model development and data collection to ensure the accuracy and robustness of the resulting RUL predictions.

5. Conclusions

This study presented the first, to our knowledge, hybrid physics–data framework for probabilistic RUL prediction of a light aircraft landing gear strut using only operational mass and balance records. The problem is timely: light aircraft fleets typically lack structural health monitoring, yet they face high rates of fatigue-related incidents and continue to rely on conservative on-condition and hard-time maintenance schedules. By explicitly quantifying how real, correlated operational variability translates into uncertainty in fatigue life, this work addresses a practical gap in general aviation prognostics and maintenance planning.

The methodology couples high-fidelity finite element strain–life modelling with a quadratic Ridge surrogate and a two-layer bootstrap. This combination achieved high surrogate accuracy (5-fold CV R² = 0.991 ± 0.013) and narrow epistemic confidence bands (±3%). Compared with prior studies, which were either deterministic or limited to subsystem prognostics, this framework delivers full probabilistic RUL distributions for a structural component, driven entirely by mandatory operational records rather than additional sensors.

The results demonstrate that operational choices have a meaningful impact on strut life. Front seat mass was identified as the dominant driver of fatigue variability (Δ ≈ 0.50), followed by fuel and rear seat mass. Monte Carlo propagation yielded a right-skewed RUL distribution with a fleet average of 0.41 million cycles (95% CI: 0.300–0.530 million), spanning from approximately 9 × 10⁴ to over 2 × 10⁶ cycles. These findings support a shift from fixed calendar intervals to condition-based inspection schedules linked to actual recorded loading.

While the framework identifies crew assignment policies as a potential lever for fatigue life extension, their practical implementation may be limited by training logistics, instructor-student pairing, and regulatory constraints. These findings should therefore be interpreted as conceptual levers, highlighting how operational choices influence fatigue, rather than immediate prescriptions for policy change.

The main contribution of this work lies in the methodological integration of physics-based fatigue simulation, surrogate modeling, bootstrap-based uncertainty quantification, and distributional sensitivity analysis into a coherent hybrid framework for aircraft prognostics. The Cessna 172 case study demonstrates feasibility and provides actionable insights for training operations. While the specific RUL distributions are valid only for the training fleet analyzed, the hybrid framework itself is designed to be adaptable. Applying this methodology to other contexts (e.g., charter or private operations) would require retraining the surrogate model on new, relevant mass and balance records. Furthermore, application to a different aircraft type would necessitate the development of a new underlying finite element model. The framework thus provides a generalizable process for log-driven RUL estimation, though the models and results are specific to the case under study. In this sense, the current dataset illustrates one application, while the framework itself provides a broadly applicable foundation for future aircraft fatigue prognostics. The probabilistic outputs generated by this framework can be directly applied to maintenance decision-making by setting inspection triggers on conservative percentiles of the RUL distribution. This provides operators with a transparent, risk-informed basis for condition-based maintenance, which can be further refined in future studies through integration with cost models tailored to specific operators.

Future work will expand the method to diverse missions, integrate low-cost landing impact sensing, and include crack growth modelling to provide end-to-end fatigue life prediction.