Real-Time Prediction of S-Wave Accelerograms from P-Wave Signals Using LSTM Networks with Integrated Fragility-Based Structural Damage Alerts for Induced Seismicity
Abstract
1. Introduction
- Integrated real-time framework: Combines LSTM-based seismic wave prediction with structural fragility analysis to provide immediate, actionable damage alerts.
- Advanced temporal modeling: Uses initial P-wave data to accurately forecast full S-wave accelerograms, capturing nonlinear ground motion evolution.
- Rapid, validated risk estimation: Demonstrates high predictive accuracy and effective early classification of structural damage, offering possible crucial lead time for automated decision-making in induced seismicity scenarios.
2. Materials and Methods
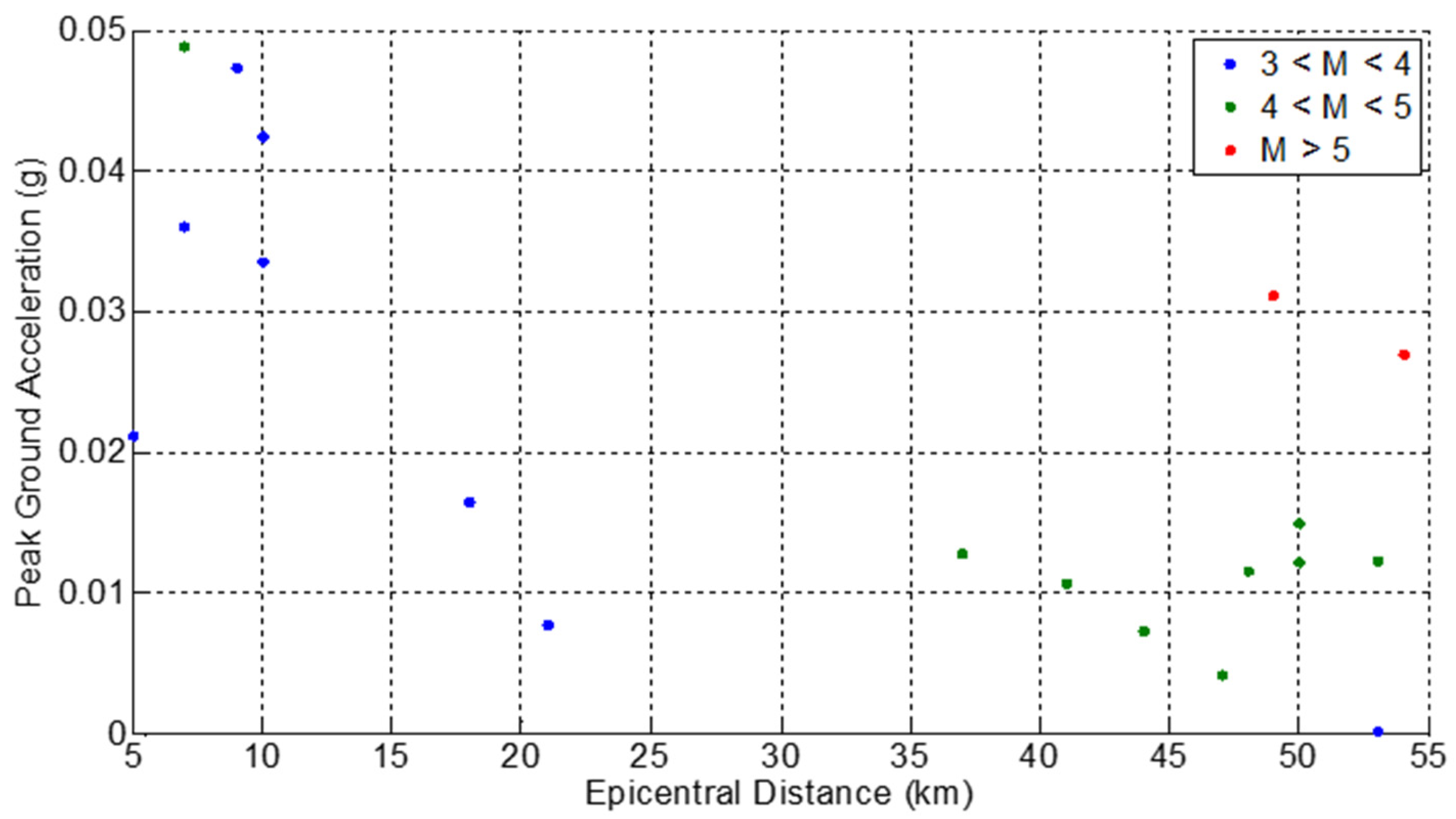
2.1. Induced Ground Motion Database
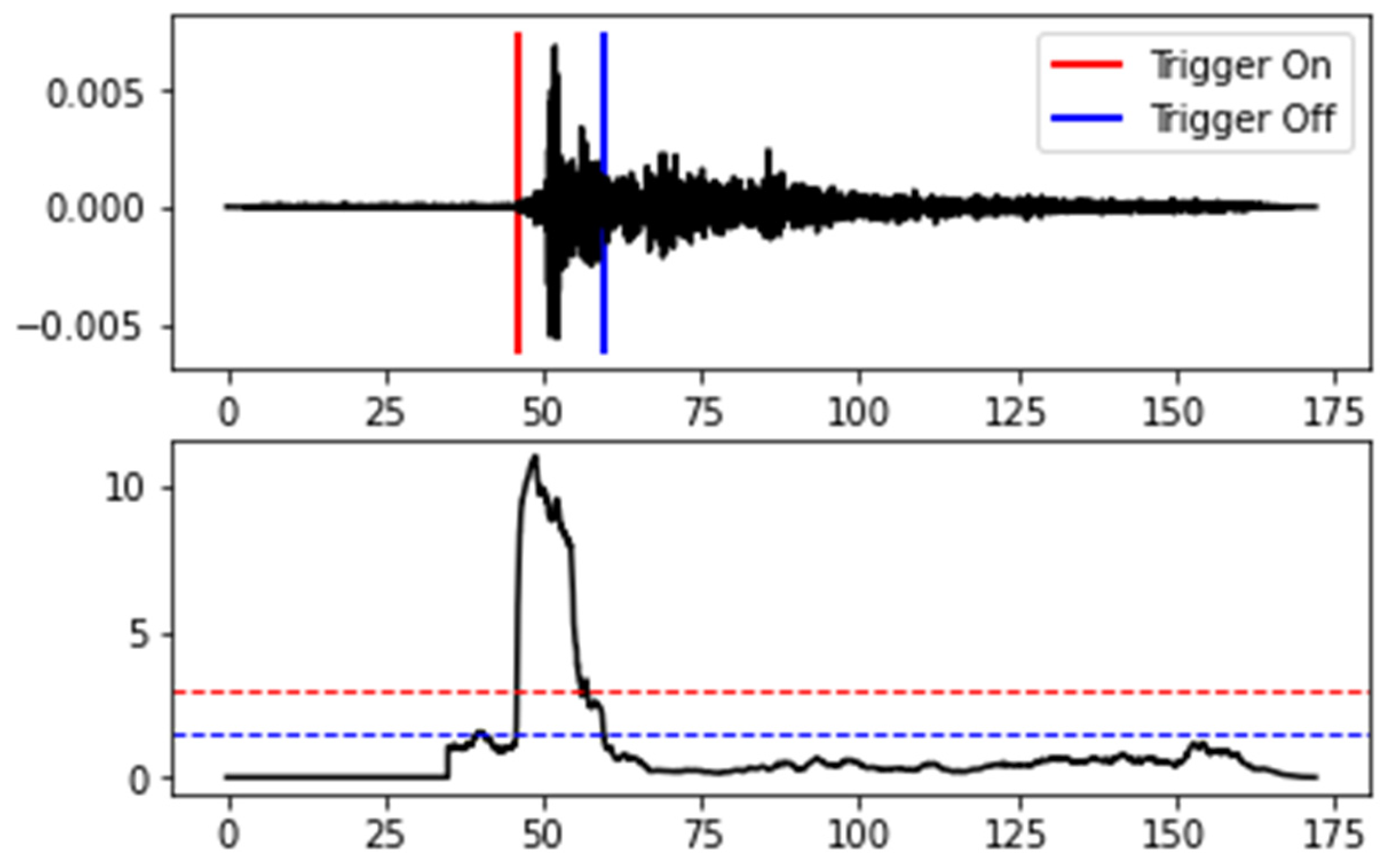
2.2. Short-Term Average over Long-Term Average (STA/LTA) for Induced Seismic Event Detection
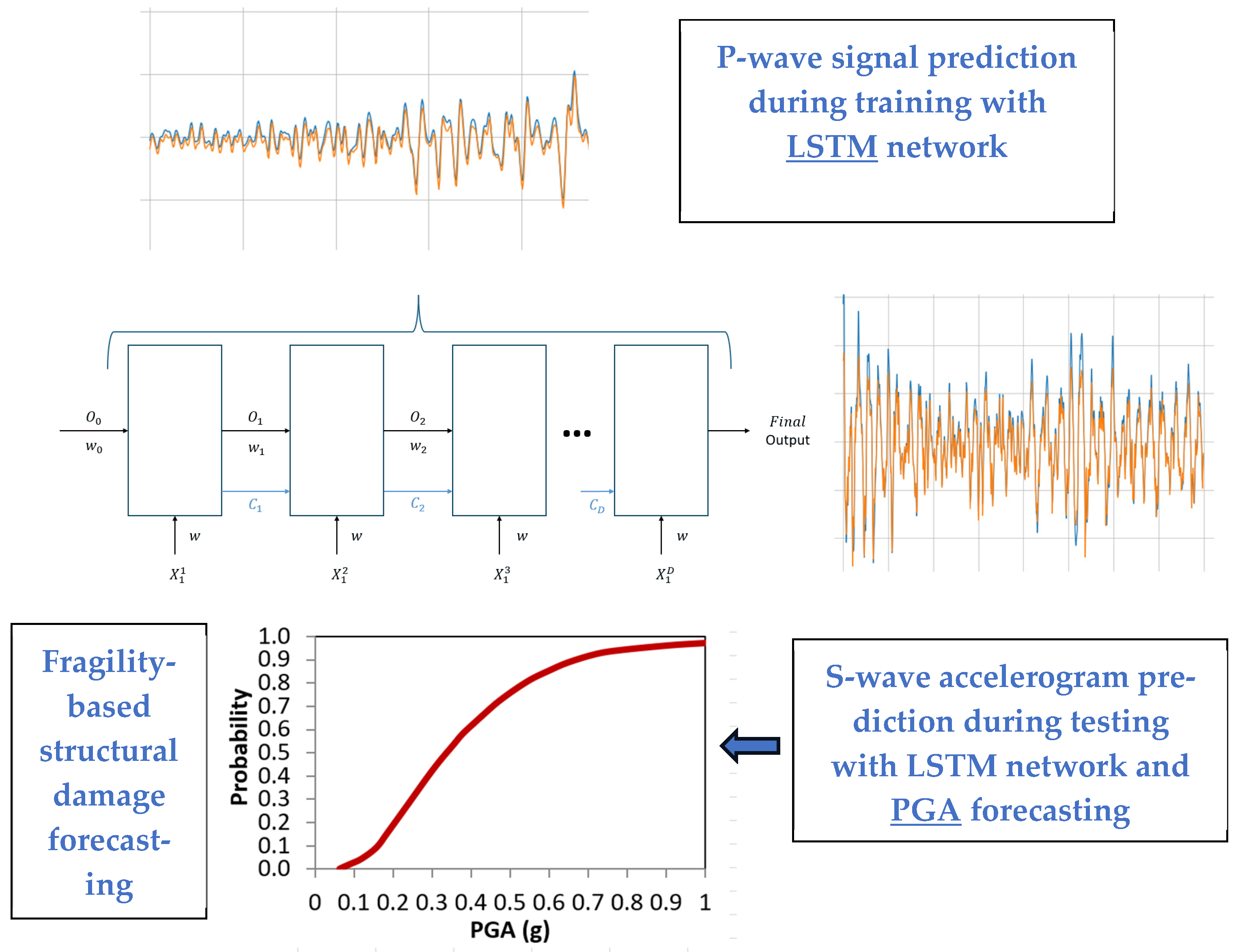
2.3. Description and Input–Output Design of LSTM Machine Learning Model
3. Results
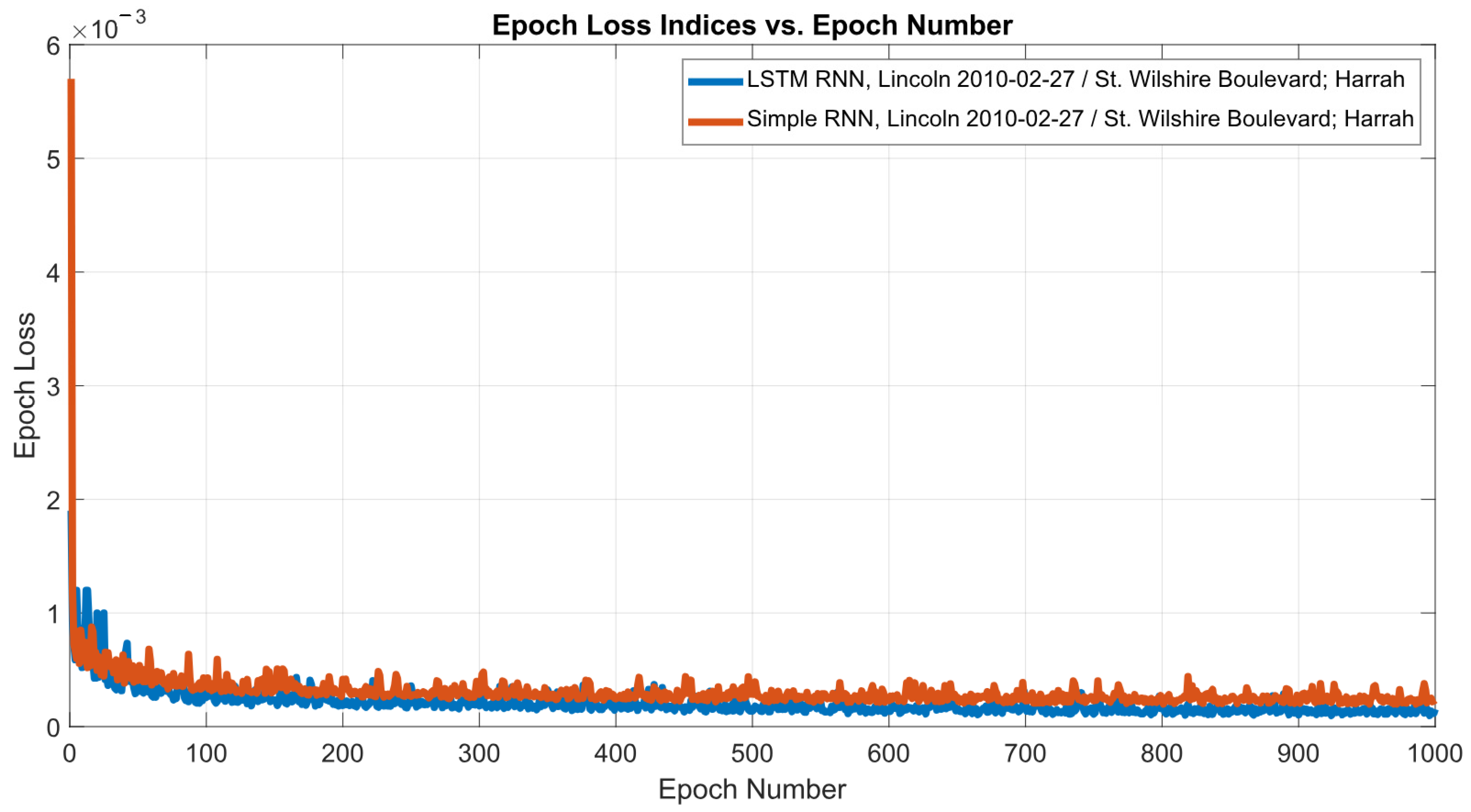
3.1. Application of LSTM RNN Network with Python
- Formulating the problem and identifying the required data.
- Collecting the data in a usable format.
- Detecting and addressing data gaps or uncertainties.
- Preprocessing and preparing the data for model input.
- Training the model on the designated training dataset.
- Using the trained model to generate predictions on the test dataset.
- Comparing the predictions with the actual test outcomes and calculating performance metrics.
- Refining the model, expanding the dataset, or considering alternative modeling strategies if results are not satisfactory.
- Each record in the training set is passed through the LSTM RNN, and the network produces a prediction of the target variable.
- These predictions are then used to compute the Cost Function, which measures the prediction error of the model. A commonly used choice is the Mean Squared Error (MSE).
- Following forward propagation, backward propagation is performed. In this step, the model’s parameters are updated to reduce the Cost Function value. The updates are carried out in reverse order—starting from the output layer and moving back toward the input layer.
- The combination of forward propagation, cost calculation, and backward propagation for the entire training set constitutes a single epoch.
- The next epoch begins using the updated parameters from the previous iteration. Training continues for the specified number of epochs, and the parameter values obtained after the final backward propagation are taken as the trained LSTM RNN model parameters.
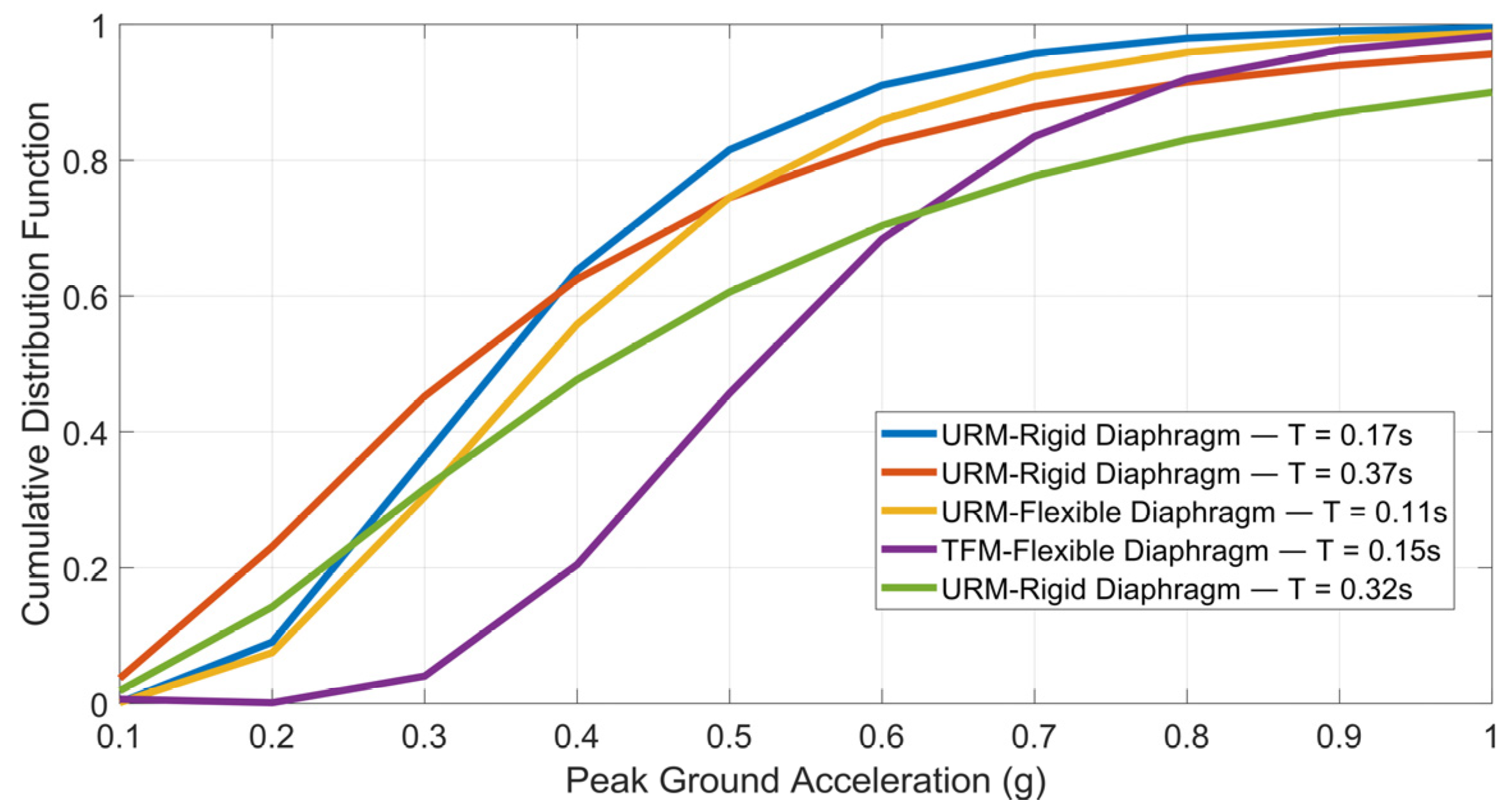
3.2. Adopted Fragility Curves near Geothermal Platforms in France
4. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EEW | Earthquake Early Warning |
| PEER | Pacific Earthquake Engineering Research Center |
| LSTM | Long Short-Term Memory neural network |
| CNN | Convolutional Neural Network |
| RNN | Recurrent Neural Network |
| PGA | Peak Ground Acceleration |
| AI | Artificial Intelligence |
| ML | Machine Learning |
| STA/LTA | Short-Term Average over Long-Term Average |
| TFM | Timber-Framed Masonry |
| URM | Unreinforced Masonry |
| ESDOF | Equivalent Single-Degree-Of-Freedom |
| MSE | Mean Squared Error |
| MAE | Mean Absolute Error |
References
- Zhou, W.; Lanza, F.; Grigoratos, I.; Schultz, R.; Cousse, J.; Trutnevyte, E.; Muntendam-Bos, A.; Wiemer, S. Managing induced seismicity risks from enhanced geothermal systems: A good practice guideline. Rev. Geophys. 2024, 62, e2024RG000849. [Google Scholar] [CrossRef]
- Qin, Y.; Chen, T.; Ma, X.; Chen, X. Forecasting induced seismicity in Oklahoma using machine learning methods. Sci. Rep. 2022, 12, 9319. [Google Scholar] [CrossRef] [PubMed]
- Fujinawa, Y.; Noda, Y. Japan’s Earthquake Early Warning System on 11 March 2011: Performance, Shortcomings, and Changes. Earthq. Spectra 2013, 29, S341–S368. [Google Scholar] [CrossRef]
- Cuéllar, A.; Espinosa-Aranda, J.M.; Suarez, R.; Ibarrola, G.; Uribe, A. The Mexican Seismic Alert System (SASMEX): Its Alert Signals, Broadcast Results and Performance During the M 7.4 Punta Maldonado Earthquake of March 20th, 2012. In Early Warning for Geological Disasters; Wenzel, F., Zschau, Z., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 71–87. [Google Scholar]
- Yamada, M.; Tamaribuchi, K.; Wu, S. Faster and More Accurate Earthquake Early Warning System. J. Jpn. Assoc. Earthq. Eng. 2014, 14, 21–24. [Google Scholar] [CrossRef]
- Kodera, Y.; Saitou, J.; Hayashimoto, N.; Adachi, S.; Morimoto, M.; Nishimae, Y.; Hoshiba, M. Earthquake Early Warning for the 2016 Kumamoto Earthquake: Performance Evaluation of the Current System and the Next-Generation Methods of the Japan Meteorological Agency. Earth Planets Space 2016, 68, 202. [Google Scholar] [CrossRef]
- Hsu, T.-Y.; Wang, H.-H.; Lin, P.-Y.; Lin, C.-M.; Kuo, C.-H.; Wen, K.-L. Performance of the NCREE’s On-Site Warning System during the 5 February 2016Mw6.53 Meinong Earthquake. Geophys. Res. Lett. 2016, 43, 8954–8959. [Google Scholar] [CrossRef]
- Hsu, T.Y.; Lin, P.Y.; Wang, H.H.; Chiang, H.W.; Chang, Y.W.; Kuo, C.H. Comparing the Performance of the NEEWS Earthquake Early Warning System against the CWB System during the 6 February 2018 Mw 6.2 Hualien Earthquake. Geophys. Res. Lett. 2016, 45, 6001–6007. [Google Scholar]
- Wu, Y.M.; Mittal, H.; Huang, T.C.; Yang, B.M.; Jan, J.C.; Chen, S.K. Performance of a Low-Cost Earthquake Early Warning System (P-Alert) and Shake Map Production during the 2018 Mw 6.4 Hualien, Taiwan, Earthquake. Seismol. Res. Lett. 2019, 90, 19–29. [Google Scholar] [CrossRef]
- Kodera, Y.; Yamada, Y.; Hirano, K.; Tamaribuchi, K.; Adachi, S.; Hayashimoto, N.; Morimoto, M.; Nakamura, M.; Hoshiba, M. The Propagation of Local Undamped Motion (PLUM) Method: A Simple and Robust Seismic Wavefield Estimation Approach for Earthquake Early Warning. Bull. Seismol. Soc. Am. 2018, 108, 983–1003. [Google Scholar] [CrossRef]
- Kodera, Y. An Earthquake Early Warning Method Based on Huygens Principle: Robust Ground Motion Prediction Using Various Localized Distance-Attenuation Models. J. Geophys. Res. Solid Earth 2019, 124, 12981–12996. [Google Scholar] [CrossRef]
- Hsu, T.-Y.; Kuo, C.-H.; Wang, H.-H.; Chang, Y.-W.; Lin, P.-Y.; Wen, K.-L. The Realization of an Earthquake Early Warning System for Schools and its Performance during the 2019 ML 6.3 Hualien (Taiwan) Earthquake. Seismol. Res. Lett. 2021, 92, 342–351. [Google Scholar] [CrossRef]
- Allen, R.M.; Melgar, D. Earthquake Early Warning: Advances, Scientific Challenges, and Societal Needs. Annu. Rev. Earth Planet. Sci. 2019, 47, 361–388. [Google Scholar] [CrossRef]
- Cremen, G.; Galasso, C. Earthquake Early Warning: Recent Advances and Perspectives. Earth-Sci. Rev. 2020, 205, 103184. [Google Scholar] [CrossRef]
- Wald, D.J. Practical Limitations of Earthquake Early Warning. Earthq. Spectra 2020, 36, 1412–1447. [Google Scholar] [CrossRef]
- Böse, M.; Heaton, T.; Hauksson, E. Rapid Estimation of Earthquake Source and Ground-Motion Parameters for Earthquake Early Warning Using Data from a Single Three-Component Broadband or Strong-Motion Sensor. Bull. Seismol. Soc. Am. 2012, 102, 738–750. [Google Scholar] [CrossRef]
- Hsu, T.-Y.; Huang, S.-K.; Chang, Y.-W.; Kuo, C.-H.; Lin, C.-M.; Chang, T.-M.; Wen, K.-L.; Loh, C.-H. Rapid On-Site Peak Ground Acceleration Estimation Based on Support Vector Regression and P-Wave Features in Taiwan. Soil Dyn. Earthq. Eng. 2013, 49, 210–217. [Google Scholar] [CrossRef]
- Hsu, T.-Y.; Huang, C.-W. Onsite Early Prediction of PGA Using CNN with Multi-Scale and Multi-Domain P-Waves as Input. Front. Earth Sci. 2021, 9, 626908. [Google Scholar] [CrossRef]
- Chiang, Y.-J.; Chin, T.-L.; Chen, D.-Y. Neural Network-Based Strong Motion Prediction for On-Site Earthquake Early Warning. Sensors 2022, 22, 704. [Google Scholar] [CrossRef]
- Fayaz, J.; Galasso, C. A Deep Neural Network Framework for Real-Time On-Site Estimation of Acceleration Response Spectra of Seismic Ground Motions. Comput.-Aided Civ. Infrastruct. Eng. 2022, 38, 87–103. [Google Scholar] [CrossRef]
- Jozinović, D.; Lomax, A.; Štajduhar, I.; Michelini, A. Rapid Prediction of Earthquake Ground Shaking Intensity Using Raw Waveform Data and a Convolutional Neural Network. Geophys. J. Int. 2020, 222, 1379–1389. [Google Scholar] [CrossRef]
- Münchmeyer, J.; Bindi, D.; Leser, U.; Tilmann, F. The Transformer Earthquake Alerting Model: A New Versatile Approach to Earthquake Early Warning. Geophys. J. Int. 2021, 225, 646–656. [Google Scholar] [CrossRef]
- Hsu, T.Y.; Pratomo, A. Early Peak Ground Acceleration Prediction for On-Site Earthquake Early Warning Using LSTM Neural Network. Front. Earth Sci. 2022, 10, 911947. [Google Scholar] [CrossRef]
- Sak, H.; Senior, A.W.; Beaufays, F. Long Short-Term Memory Recurrent Neural Network Architectures for Large Vocabulary Speech Recognition. arXiv 2014, arXiv:1402.1128. [Google Scholar]
- Murtaza, R.; Patel, H.; Varma, S. Predicting Stock Prices Using LSTM. Int. J. Sci. Res. 2017, 6, 1754–1756. [Google Scholar]
- Zhao, Z.; Chen, W.; Wu, X.; Chen, P.C.Y.; Liu, J. LSTM Network: A Deep Learning Approach for Short-term Traffic Forecast. IET Intell. Transp. Syst. 2017, 11, 68–75. [Google Scholar] [CrossRef]
- Wang, C.Y.; Huang, T.C.; Wu, Y.M. A LSTM Neural Network for On-Site Earthquake Early Warning. EGU Gen. Assem. 2020, 2020, 3696. [Google Scholar]
- Megalooikonomou, K.G.; Parolai, S.; Pittore, M. Toward performance-driven seismic risk monitoring for geothermal platforms: Development of ad hoc fragility curves. Geotherm Energy 2018, 6, 8. [Google Scholar] [CrossRef]
- PEER-NGA-East Database; Pacific Earthquake Engineering Research Center. University of California: Berkeley, CA, USA, 2025. Available online: https://peer.berkeley.edu/research/nga-east (accessed on 5 June 2025).
- Beyreuther, M.; Barsch, R.; Krischer, L.; Megies, T.; Behr, Y.; Wassermann, J. ObsPy: A Python Toolbox for Seismology. Seismol. Res. Lett. 2010, 81, 530–533. [Google Scholar] [CrossRef]
- Burkov, A. The Hundred-Page Machine Learning Book. 2019. Available online: https://themlbook.com/ (accessed on 1 July 2025).
- Vamvatsikos, D.; Cornell, C.A. Incremental Dynamic Analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Pantazopoulou, S.J. Development of a simplified mechanical model to estimate the seismic vulnerability of heritage unreinforced masonry buildings. J. Earthq. Eng. Taylor Fran 2015, 20, 298–325. [Google Scholar] [CrossRef]
- MATLAB: User’s Guide, Version R2024b; Mathworks Inc.: Natick, MA, USA, 2024.
- Filippou, F.C.; Constantinides, M. FEDEAS Lab—Getting Started Guide and Simulation Examples, NEESgrid Report 2004-22 and SEMM Report 2004-05, 2004. Available online: http://www.neesgrid.org/news/documents.php (accessed on 20 July 2025).
- Boxberger, T.; Fleming, K.; Pittore, M.; Parolai, S.; Pilz, M.; Mikulla, S. The Multi-Parameter Wireless Sensing System (MPwise): Its description and application to earthquake risk mitigation. Sensors 2017, 17, 2400. [Google Scholar] [CrossRef]
- DESTRESS: Demonstration of Soft Stimulation Treatments of Geothermal Reservoirs, EU Research Project H2020, 2020. Available online: https://www.destress-h2020.eu/en/home/ (accessed on 25 August 2025).

| EQ-ID | EQ-ID Database | Year | Name | Location | Mw | Epicenter Latitude (Deg) | Epicenter Longitude (Deg) | Depth (km) |
|---|---|---|---|---|---|---|---|---|
| 1 | 57 | 2010 | Lincoln_2010-02-27 | Lincoln OK | 4.18 | 35.553 | −96.752 | 4 |
| 2 | 66 | 2010 | Slaughterville _2010-10-13 | Slaughterville OK | 4.36 | 35.202 | −97.309 | 14 |
| 3 | 67 | 2010 | Guy_2010-10-15 | Guy AR | 3.86 | 35.276 | −92.322 | 5 |
| 4 | 73 | 2010 | Arcadia_2010-11-24 | Arcadia OK | 3.96 | 35.627 | −97.246 | 3 |
| 5 | 74 | 2010 | BethelAcres_ 2010-12-12 | Bethel Acres OK | 3.23 | 35.392 | −96.995 | 4 |
| 6 | 76 | 2010 | Guy_2010-11-20 | Guy AR | 3.90 | 35.316 | −92.317 | 5 |
| 7 | 80 | 2011 | Greenbrier_2011-02-28 | Greenbrier AR | 4.68 | 35.265 | −92.34 | 4 |
| 8 | 91 | 2011 | Sparks_2011-11-06 | Sparks OK | 5.68 | 35.537 | −96.747 | 9 |
| 9 | 92 | 2011 | Comal_2011-10-20 | Comal TX | 4.71 | 28.81 | −98.15 | 4 |
| Activation Function | Equation | Application |
|---|---|---|
| ReLu | F(x) = max(0, x) | Regression problems with many hidden layers |
| Cost Function | Equation | Application |
|---|---|---|
| Mean Absolute Error (MAE) | Regression problems: less strict compared to Mean Squared Error (MSE), since it does not quantify the error as the square of prediction’s deviation, but as an absolute distance. |
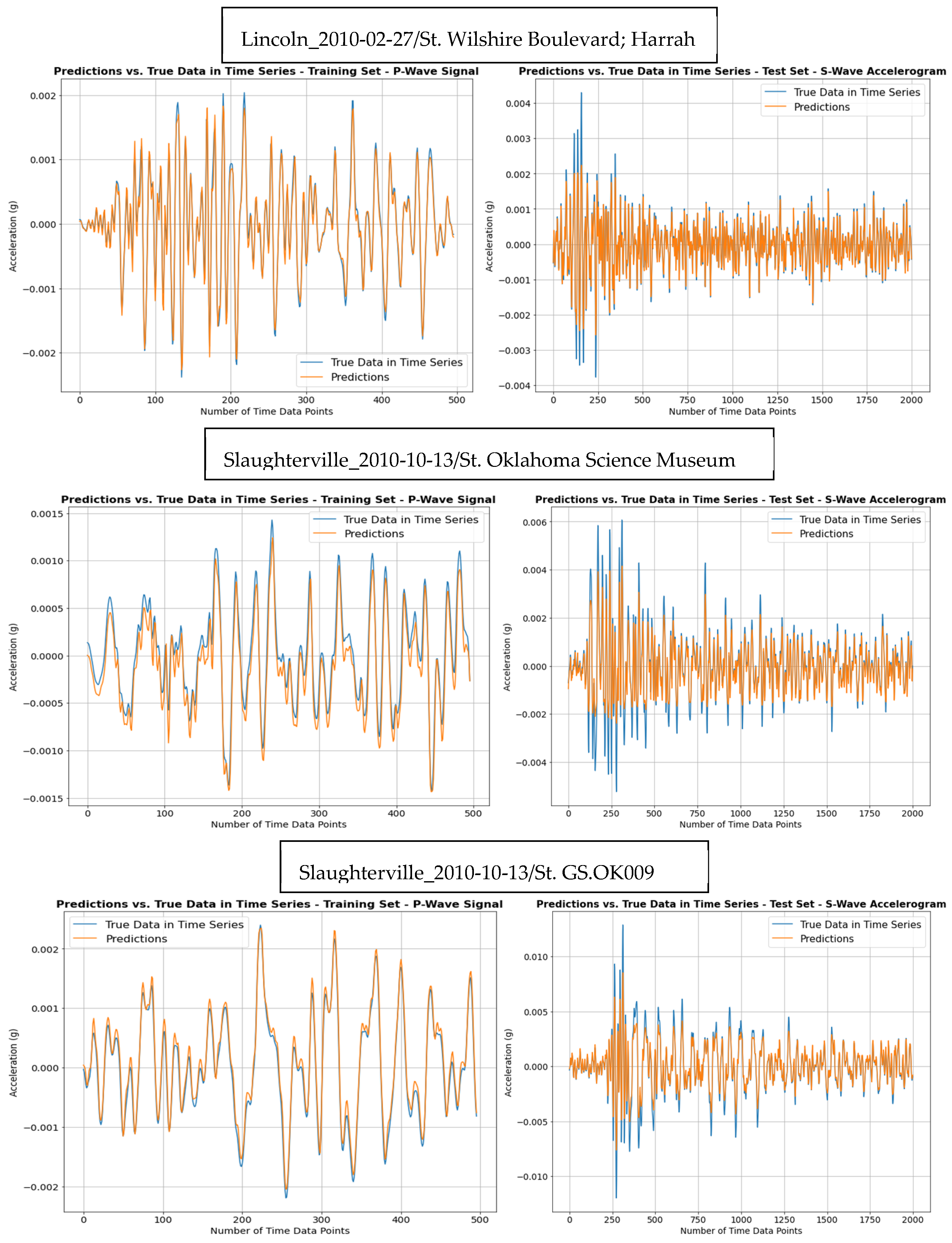
| EQ Name and Recording Station | MSE Training Set | MSE Testing Set |
|---|---|---|
| Lincoln_2010-02-27/St. Wilshire Boulevard; Harrah | 9.2268 × 10−5 | 7.1828 × 10−5 |
| Slaughterville_2010-10-13/St. Oklahoma Science Museum | 0.0001374 | 0.0002488 |
| Slaughterville_2010-10-13/St. GS.OK009 | 0.0001115 | 0.0003106 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Megalooikonomou, K.G.; Beligiannis, G.N. Real-Time Prediction of S-Wave Accelerograms from P-Wave Signals Using LSTM Networks with Integrated Fragility-Based Structural Damage Alerts for Induced Seismicity. Appl. Sci. 2025, 15, 11017. https://doi.org/10.3390/app152011017
Megalooikonomou KG, Beligiannis GN. Real-Time Prediction of S-Wave Accelerograms from P-Wave Signals Using LSTM Networks with Integrated Fragility-Based Structural Damage Alerts for Induced Seismicity. Applied Sciences. 2025; 15(20):11017. https://doi.org/10.3390/app152011017
Chicago/Turabian StyleMegalooikonomou, Konstantinos G., and Grigorios N. Beligiannis. 2025. "Real-Time Prediction of S-Wave Accelerograms from P-Wave Signals Using LSTM Networks with Integrated Fragility-Based Structural Damage Alerts for Induced Seismicity" Applied Sciences 15, no. 20: 11017. https://doi.org/10.3390/app152011017
APA StyleMegalooikonomou, K. G., & Beligiannis, G. N. (2025). Real-Time Prediction of S-Wave Accelerograms from P-Wave Signals Using LSTM Networks with Integrated Fragility-Based Structural Damage Alerts for Induced Seismicity. Applied Sciences, 15(20), 11017. https://doi.org/10.3390/app152011017







